Abstract
Early detection and treatment of skin cancer are important for patient recovery and survival. Dermoscopy images can help clinicians for timely identification of cancer, but manual diagnosis is time-consuming, costly, and prone to human error. To conduct this, an innovative deep learning-based approach has been proposed for automatic melanoma detection. The proposed method involves preprocessing dermoscopy images to remove artifacts, enhance contrast, and cancel noise, followed by feeding them into an optimized Convolutional Neural Network (CNN). The CNN is trained using an innovative metaheuristic called the Improved Chameleon Swarm Algorithm (CSA) to optimize its performance. The approach has been validated using the SIIM-ISIC Melanoma dataset and the results have been confirmed through rigorous evaluation metrics. Simulation results demonstrate the efficacy of the proposed method in accurately diagnosing melanoma from dermoscopy images by highlighting its potential as a valuable tool for clinicians in early cancer detection.
Keywords: Melanoma, Skin Cancer, Medical Imaging, Dermoscopy, Early Detection, CNN, Improved Chameleon Swarm Algorithm
Subject terms: Medical research, Engineering
Introduction
When the body requires more cells, they naturally proliferate and expand. However, owing to genetic alterations and mutations in cell structure, they begin to grow and proliferate abnormally, resulting in cancer. A huge mass of cells is formed as a result of this irregular development1. This mass is toxic to the body and depletes its resources, attacking and killing tissues everywhere around it2. Each country has different cancer prevalence rates. Although, some malignancies, such as skin cancer, are, of course, found all over the world3. Exposure to sunlight causes abnormal growth of skin cells, called skin cancer4. In fact, the cause of skin cancer is that a mutation (an error) appears in the DNA of skin cells5. A mass of cancer cells is generated. Skin cancer can also occur in areas of the skin that are not normally exposed to sunlight. Avoiding or limiting exposure to Ultraviolet (UV) radiation can decrease the risk of skin cancer6.
The thin layer that acts as a protective covering for skin cells is called the epidermis. It should be noted that the body constantly sheds skin cells7–9. The epidermis consists of three major cell kinds around Squamous cells that are placed right below the outward surface and operate as the inner lining of the skin10.
Basal cells that produce novel skin cells are found under the squamous cells. Melanocytes that produce melanin. Melanin is a pigment which provides the skin its natural color and is positioned in the lower portion of the epidermis11. Melanocytes generate more melanin once the body is exposed to sunlight to assist in shielding the deeper layers of the skin. This is why the skin darkens in the sun.
The most severe kind of skin cancer is melanoma which occurs in melanocyte cells that produce melanin. It can even be created within the eyes and seldom in internal organs like the intestines. The precise reason of it is still unknown; however, being exposed to diffuse UV light from sunlight or solarium lamps and beds raises the danger of evolving melanoma. Restraining UV exposure can assist in decreasing the danger of melanoma.
The risk of melanoma appears to be growing in people under 40, especially women. Awareness of the warning signs of skin cancer helps to identify and treat cancerous changes before cancer has extended. If melanoma is diagnosed early, it can be successfully treated. Examining the skin for doubtful changes can aid to diagnose skin cancer in its early steps. Early detection of skin cancer provides the best chance of successfully treating skin cancer.
Many malignancies are now entirely curable or treated. The importance of early cancer detection in this case are not overstated. If cancer is detected early, the chances of a complete cure are quite high. Faster therapy, better treatment outcomes, less problems following treatment, and no need to remove or eliminate the patient’s limb are all advantages of early cancer identification.
Diagnostic radiography has evolved greatly as a result of the development of new equipment and procedures, allowing for better cancer detection and surgery avoidance. Radiology is the technique of creating pictures of the body’s organs and organ systems12,13. This approach is used to detect tumors and other abnormalities in order to diagnose the disease and assess therapy success. During sampling and other surgical operations, photography may also be employed.
Analysis of medicinal images using processing of image allows for finer identification of tumors with the progress of cancer cell diagnosis technologies by employing engineering sciences. Processing medicinal images regularly requires the utilization of a computer system and existence of expert software.
Image processing mechanisms are basic, non-invasive ways for detecting cancer cells that help to speed up early diagnosis and, as a result, enhance the chances of cancerous patients’ survival. Different types of medical imaging systems have been proposed for accurate diagnosis of the skin cancers.
Zghal et al.14 identified melanoma disease through processing scanned CT images. One of the illnesses that causes death is cancer. One of these cancers is called skin cancer. Therefore, using a reliable method to diagnose melanoma in the early stages is essential to save the patient’s life. Their goal was to provide a reliable computer method for diagnosing the disease. They used computer methods and image processing to identify malignant skin blemishes by employing three stages of preprocessing, extraction, and finally classification of damaged and healthy skin. The mentioned process was executed in MATLAB software environment. The outcomes of the analysis illustrated that the presented technique’s accuracy was about 90%.
Salah et al.15 tested a fuzzy neural technique in detecting cancerous spots on the skin. Using a powerful method to identify the type of skin blemishes could save the patient from death. Due to the complexity of identifying this disease, they used computational methods to solve diagnostic problems. The method they used was called the neural fuzzy system. They used a neural-fuzzy network approach to process images and identify malignant skin lesions. Analysis and processing of images of different patients by this approach showed that the neural-fuzzy network could identify abnormal lesions on the skin with the accuracy level of 91.3%.
Roffman et al.16 classified cancerous spots on the skin by getting assistant from an Artificial Neural Network. Direct Ultraviolet rays on the skin cause abnormal spots on the skin that form thick melanoma. Detection of abnormal spots from natural spots on the skin can lead to early diagnosis and complete cure of the disease. They utilized an NN for solving the problem of detecting cancer spots. This method has the ability to solve some complex problems in identifying the disease. They used patient data from 1997 to 2015 to perform this technique. Factors such as age, gender, diabetes status, and smoking status were employed to detect the disease. The outcomes of the model validation index were estimated to be 0.81%, which indicated the reliability of the model for disease identification.
Dorj et al.17 segmented the cancerous lesions on the skin using a CNN. In this study, they developed an intelligent and computational system for rapid diagnosis of a disease called convulsive neural network. Their goal was to present a technique for detecting malignant skin lesions. They used RGB skin cancer images to run the smart system. The results of the implementation showed that the smart grid could detect the lesions.
Li et al.18 detected skin cancer using optimal Support Vector Machine (SVM). Among the riskiest cancers in the universe is skin cancer. This disease is one of the leading reasons of death in the universe. Accurate and early detection of cancerous spots on the skin can save the lives of most infected patients to some extent. In this study, they presented an intelligent and automated technique for detecting disease. This automated method was based on complex computer calculations. The method presented was called a backup vector machine. This intelligent approach used a fluid search optimizer based on turbulence theory to improve its performance. The results of automatic detection of intelligent technique showed that this optimal model could detect skin spots to the optimal and maximum accuracy by increasing convergence and preventing local optimization.
It can be deduced that numerous processes have been proposed for skin cancer diagnosis. However, selecting the best diagnostic procedure was not easy, and each had its own set of benefits and drawbacks. The purpose of this study is designing a new form of the deep neural network (DNN) system to diagnose skin cancer from dermoscopy images with superior accurateness. The major goal is creating a tool based on deep learning for timely skin cancer recognition. The paper’s key contribution is using an enhanced algorithm for optimizing of the CNN for skin cancer diagnosis.
Materials and methods
Convolutional neural network (CNN)
Fine-tuning the CNN hyperparameters is a multimodal optimization problem19. Therefore, improper selection policy of hyper-parameter configuration will make unsatisfactory performance20. One of the most popular techniques for optimal hyperparameter selection is using metaheuristics21. Recently, there are some metaheuristic techniques, which have been proposed for this purpose. For example, PSO (Particle Swarm Optimization)22, Equilibrium Optimization (EO)23, and Manta Ray Foraging Optimization (MRFO) algorithm24. Metaheuristics and their variants attempt to optimize hyperparameters of the CNN. In this study, a recently presented metaheuristic, called Chameleon Swarm Algorithm (CSA) has been proposed for this purpose.
Incidentally, CNN’s high training cost and the CSA’s tendency for generating premature solution can limit the CSA’s performance for optimal selection of the hyperparameters of the CNN. Deep CNN training often entails a large number of iterations for modifying weights and biases, making the evaluation of the quality of a hyperparameter configuration costly and difficult. Therefore, a faster model of the CSA based on pseudorandom values is proposed instead of random values. This can increase the candidate generation. Nevertheless, the CSA has sometimes weak initializing. So, an opposite learning-based method has been used for solving this issue. Therefore, the CSA has been improved for adjusting the CNN hyperparameters to reach to the following necessities:
For saving time and calculation resources while maintaining a reliable optimization, the CNN training process should be terminated in an appropriate point.
To decrease the CNN’s quantity of instances in each iteration, the population number of chameleon swarms should be as much as possible.
This technique can achieve a suboptimal solution for the proposed CNN.
These needs cause a necessity to develop a method that can, first and foremost, properly adjust the CNN hyper-parameters by considering a narrow confidence interval.
Secondly, several hyper-parameter ranges must be considered, and the suboptimal hyper-parameter arrangement must be identified at a reasonable cost.
Problem Statement
The optimal hyperparameter selection in the convolutional neural network is regarded as an integer programming issue. The chief notion is achieving optimum hyper-variable amounts to reach the minimum error rate and maximum accuracy, i.e.,
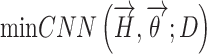 |
1 |
Subject to:
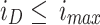 |
2 |
where, 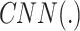 describes the structure of the CNN.
describes the structure of the CNN. 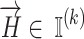 is a k-dimensional hyper-parameter vector,
is a k-dimensional hyper-parameter vector, 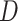 specifies the data collection for the purpose of training and validation of the Convolutional Neural Network, and
specifies the data collection for the purpose of training and validation of the Convolutional Neural Network, and 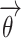 signifies vector of learned parameters (i.e., CNN biases and weights). The limitation of CNN is the number of training iterations.
signifies vector of learned parameters (i.e., CNN biases and weights). The limitation of CNN is the number of training iterations. 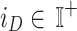 defines the quantity of iterations in the present network’s training stage on database
defines the quantity of iterations in the present network’s training stage on database 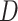 , and the upper limitation of the iteration is defined by
, and the upper limitation of the iteration is defined by 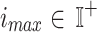 .
.
All iterations take the input data’s mini-batch and update the CNN’s parameters. Each epoch can have tens to hundreds of iterations. Iterations are more accurate measuring scale of CNN’s cost of training than epoch. Training a CNN is time-consuming due to the large number of parameters that require updating, which necessitates a substantial amount of data. As a result, determining the objective costs a lot of money. The constraint helps to avoid impractical optimization strategies that are able identify configurations of hyper-parameter that are of high quality but with an excessive computing cost. The search for the best values of hyper-parameter under the limitation is driven by the purpose of reducing value of error to the least.
The dropout ratio in the CNN models is represented as a continuous floating-point number, and the methodology relied on integer programming. To modify the suggested algorithm for the optimization of continuous floating-point variables, discretization technique has been implemented. Discretization involves transforming a continuous variable into a discrete one by segmenting the continuous range into distinct intervals. In this scenario, the dropout ratio range has been divided into a series of discrete values. The algorithm has been adjusted to function with these discretized dropout ratio values. Rather than considering the dropout ratio as a continuous floating-point variable, it has been regarded as a discrete variable with ten potential values. The algorithm would then identify one of these discrete values as the optimal dropout ratio. To ensure that the discretization process did not limit the algorithm’s performance, a strategy has been adopted that permitted the algorithm to investigate the continuous range of dropout ratio values. Specifically, neighborhood search method is used to seek the optimal dropout ratio value in the vicinity of the current best solution.
Developed chameleon swarm algorithm
In this part of the article, the mathematical models of the algorithm are stated. In this section, how chameleons forage is modeled. This performance consists of bait tracking, bait search, and bait hunting. The suggested algorithm is then specified.
Initialization and function assessment
In the optimization approach based on population such as CSA, the initial population is first determined. In this algorithm, a population of 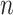 individuals is initially formed within the d-dimensional solution space, where any individual acts as an individual solution. A population of chameleons is expressed within a 2-dimensional matrix
individuals is initially formed within the d-dimensional solution space, where any individual acts as an individual solution. A population of chameleons is expressed within a 2-dimensional matrix 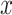 that its scope is
that its scope is 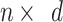 . The location of
. The location of 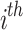 individual with iteration
individual with iteration 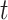 within the solution space is illustrated in the following way:
within the solution space is illustrated in the following way:
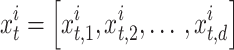 |
3 |
where, the dimension of the problem is indicated by 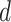 , the present iteration number is expressed by
, the present iteration number is expressed by 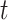 ,
, 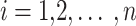 , the location of the
, the location of the 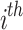 chameleon is specified by
chameleon is specified by 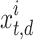 .
.
The issue’s dimension with unchanging haphazard initializing and the creation of the primary population are presented below:
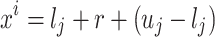 |
4 |
Where, 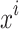 stands for the initial vector of the
stands for the initial vector of the 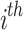 chameleon, and the highest and the lowest limitations of the search space within the
chameleon, and the highest and the lowest limitations of the search space within the 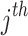 dimension have been indicated by
dimension have been indicated by 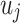 and
and 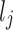 , respectively. In addition,
, respectively. In addition, 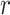 is a uniformly formed haphazard number between 0 and 1.
is a uniformly formed haphazard number between 0 and 1.
Fitness performance appraisal determines the solution quality of every recent chameleon’s location. According to the quality obtained, the current location will be replaced with a new location with better solution quality. Nevertheless, the chameleon in the CSA model stays at its existing location when quality of its solution has been found to be the best one.
Prey searching
Employing the location updating strategy, the motion of chameleons during food search can be simulated as follows:
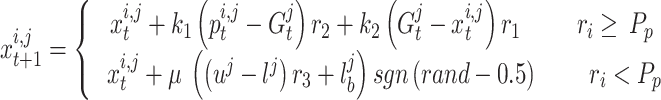 |
5 |
Where:
The new location of the
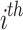 individual within the
individual within the 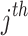 dimension and the
dimension and the 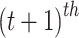 iteration stage has been defined through
iteration stage has been defined through 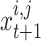 ,
,The present situation of the chameleon
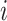 in the
in the 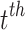 iteration stage and dimension
iteration stage and dimension 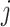 is represented by
is represented by 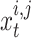 ,
,The perfect location that has been gained thus far by chameleon
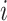 in the
in the 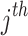 dimension at epoch loop
dimension at epoch loop 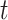 is described by
is described by 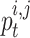 ,
,The global finest location within the dimension
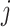 gained ever via every individual within iteration
gained ever via every individual within iteration 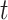 ,
,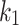 and
and 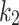 manage exploration phase and are positive amount,
manage exploration phase and are positive amount,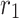 ,
, 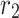 and
and 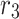 are haphazard numbers rendered uniformly in the interval [0,1],
are haphazard numbers rendered uniformly in the interval [0,1],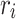 indicates a haphazard number rendered within
indicates a haphazard number rendered within  index within the range [0,1] in uniform way,
index within the range [0,1] in uniform way,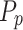 defines the possibility of the individual finding bait that is 0.1, and the current amount was found through a broad empirical test,
defines the possibility of the individual finding bait that is 0.1, and the current amount was found through a broad empirical test,The direction of exploitation and exploration is affected by
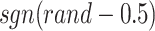 that is equal to 1 or -1,
that is equal to 1 or -1,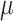 indicates a variable that describes a function of epoch and reduces with the number of the epochs as shown in Eq. (6),
indicates a variable that describes a function of epoch and reduces with the number of the epochs as shown in Eq. (6),
In the case of 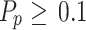 , the organization of a plate within an affine region is considered. A specific plane has been defined by three non-collinear points, specifically the green (G), red (R), and purple (P) positions within the affine region. The 3 positions
, the organization of a plate within an affine region is considered. A specific plane has been defined by three non-collinear points, specifically the green (G), red (R), and purple (P) positions within the affine region. The 3 positions 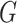 ,
, 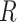 , and
, and 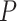 are within an affine region. The segment of line that connects the locations
are within an affine region. The segment of line that connects the locations 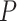 and
and 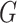 is illustrated in Eq. (6).
is illustrated in Eq. (6).
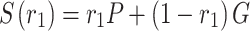 |
6 |
where, 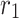 is a random amount between 0 and 1. A location on this line has been selected randomly and has created a direction from this location to
is a random amount between 0 and 1. A location on this line has been selected randomly and has created a direction from this location to 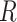 . The positions along this path are determined utilizing
. The positions along this path are determined utilizing 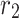 , which is expressed in the following equation:
, which is expressed in the following equation:
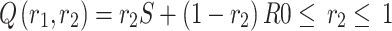 |
7 |
As can be seen from Eqs. (6) and (7), there is a great ability to explore any location on this line way. The simulation of this property of the affine space is done through contrasting the major symbols of Eq. (5) with the symbols expressed above. So that, 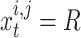 ,
, 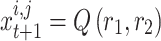 ,
, 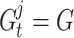 , and
, and 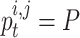 . So, chameleons can explore all probable positions in the search space. To control the exploration strength in the chameleon swarm algorithm,
. So, chameleons can explore all probable positions in the search space. To control the exploration strength in the chameleon swarm algorithm, 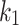 and
and 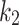 scale factors are presented in Eq. (3). By assigning small and large amounts to each of these parameters, CSA is able to switch between global search and local search. In the case of
scale factors are presented in Eq. (3). By assigning small and large amounts to each of these parameters, CSA is able to switch between global search and local search. In the case of 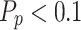 , to increase the search potency of CSA, chameleons are allowed to explore the haphazard positions in the solution space.
, to increase the search potency of CSA, chameleons are allowed to explore the haphazard positions in the solution space.
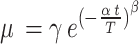 |
8 |
Where, 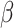 ,
, 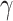 and
and 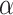 are constant amounts for controlling exploitation and exploration ability, the maximum and current number of iterations are indicated by
are constant amounts for controlling exploitation and exploration ability, the maximum and current number of iterations are indicated by 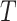 and
and 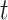 .
.
As a result of increasing the exploitation and exploration capacities and decreasing the search speed through Eq. (6), convergence is assured. The amount of variables 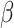 ,
, 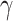 and
and 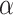 for each of the test functions are equal to 3.0, 1.0 and 3.5, respectively. These variables were obtained for a subset of problems through experimental testing. Nonetheless, they can be applied for other optimization issues as required. The amount of
for each of the test functions are equal to 3.0, 1.0 and 3.5, respectively. These variables were obtained for a subset of problems through experimental testing. Nonetheless, they can be applied for other optimization issues as required. The amount of 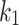 and
and 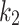 are equal to 0.25 and 1.5. These amounts were also obtained during the experimental research, and they can be applied for other optimization issues as necessary.
are equal to 0.25 and 1.5. These amounts were also obtained during the experimental research, and they can be applied for other optimization issues as necessary.
In Eq. (5), 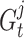 denotes that the present individual solution proximate to the optimal problem solver, since the global optimum problem solver has not been recognized within the solution space.
denotes that the present individual solution proximate to the optimal problem solver, since the global optimum problem solver has not been recognized within the solution space. 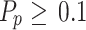 expresses that individuals are able to alter their location pursuant to catch the target within the solution space. In contrast, when
expresses that individuals are able to alter their location pursuant to catch the target within the solution space. In contrast, when 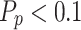 , individual stochastically explore the solution space within diverse locations and directions during hunting. So, they can identify any close prey that represents optimal prey.
, individual stochastically explore the solution space within diverse locations and directions during hunting. So, they can identify any close prey that represents optimal prey.
Eyes’ rotation of chameleon
Chameleons have the power to turn their eyes more than 360 degrees, they use this ability to find prey and hunt. After identifying the prey, they enhance their locations on the basis of the situation of the target. The rotation and movement of chameleons toward the prey are simulated during the subsequent stages.
The main situation of the individual is translated to the center of gravity;
The rotation matrix which specifies the situation of the target is discovered;
The location of the chameleons is updated by employing the matrix of rotation in the middle of gravity; and ultimately.
The individuals move back to the main location.
Using translation and rotation of vectors in space, four stated stages are executed to update the location of chameleons. The locations of the target and chameleons can be described as vectors. To update the location of the chameleons, the following processes were employed to rotate the 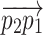 vector within the 3-Dimensional search space at a predetermined angle:
vector within the 3-Dimensional search space at a predetermined angle:
Translate the vector
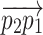 to the point of reference. It is achieved via deducting the vector’s tail from tip of it,
to the point of reference. It is achieved via deducting the vector’s tail from tip of it, 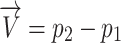 .
.Spin
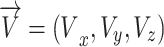 that its tip is at situation (1) and its tail is at the point of the reference within the
that its tip is at situation (1) and its tail is at the point of the reference within the 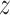 -axis compared to the angle
-axis compared to the angle 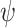 . This phase results in the vector
. This phase results in the vector 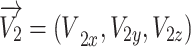 that is located at the
that is located at the 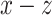 plane (location 2). The angle of rotation
plane (location 2). The angle of rotation  has been gained from the elements
has been gained from the elements 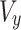 and
and 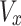 of vector
of vector 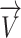 through the next formula:
through the next formula:
 |
9 |
According to the right-hand law for the positive value of 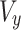 and the
and the 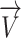 rotation, the angle
rotation, the angle 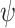 has been found to be negative. The rotated vector
has been found to be negative. The rotated vector 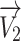 ’s element
’s element 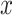 at situation (2) can be expressed in the following manner:
at situation (2) can be expressed in the following manner:
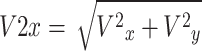 |
10 |
where, 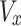 and
and 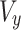 are the components
are the components 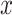 and
and 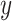 of the vector
of the vector 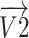 and equal
and equal 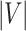 and 0, respectively.
and 0, respectively.
-
c.
The vector must be spun to
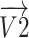 at location (2) within the
at location (2) within the 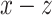 plane via an angle
plane via an angle 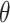 for arraying it with the
for arraying it with the 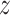 -axis. The current phase results in the vector
-axis. The current phase results in the vector 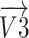 (position 3).
(position 3).
The angle 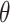 is computed according to the Eq. (15).
is computed according to the Eq. (15).
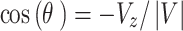 |
11 |
where, 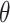 is the angle of spin
is the angle of spin 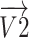 at location (2) to generate
at location (2) to generate 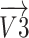 within situation (3), the
within situation (3), the 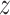 element of
element of 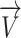 has been indicated through
has been indicated through 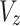 , and
, and 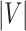 represents the vector
represents the vector 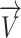 ’s magnitude.
’s magnitude.
It has been observed from Eq. (15) that the angle 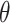 is negative because of the rule of right-hand for rotation of vector. The
is negative because of the rule of right-hand for rotation of vector. The 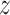 component of the vector
component of the vector 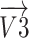 that has been rotated within situation (3), has been clarified subsequently:
that has been rotated within situation (3), has been clarified subsequently:
 |
12 |
where, both 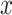 and
and 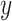 components of
components of 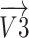 (
(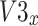 and
and 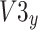 ) are equal to 0.
) are equal to 0.
Chameleon hunting is modeled when using eye rotation and position updating through the above steps, during which a vector rotates from one position to another. The new location of a candidate has been updated through employing the subsequent formula:
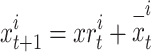 |
13 |
The new location of a chameleon is indicated by 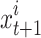 , the middle of the existing situation of the individual prior to rotation has been defined via
, the middle of the existing situation of the individual prior to rotation has been defined via 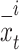 , and the centered coordinates of rotating of the individual within the solution space is expressed by
, and the centered coordinates of rotating of the individual within the solution space is expressed by 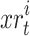 which can be obtained as follows:
which can be obtained as follows:
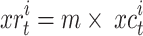 |
14 |
where, 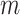 represents a matrix of rotation and show the individual’s rotation, and the centering coordinates at epoch
represents a matrix of rotation and show the individual’s rotation, and the centering coordinates at epoch 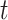 is expressed by
is expressed by 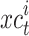 . The definition of these components is as follows:
. The definition of these components is as follows:
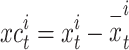 |
15 |
The present situation of the chameleons within iteration 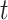 has been indicated via
has been indicated via 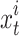 .
.
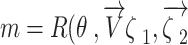 |
16 |
where, 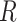 expresses the matrices of rotation within the relevant axes,
expresses the matrices of rotation within the relevant axes, 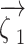 and
and 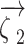 are 2 orthonormal candidates within the n-dimensional solution space, in which the sizes of all vectors are
are 2 orthonormal candidates within the n-dimensional solution space, in which the sizes of all vectors are 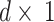 , and a chameleon’s angle of rotation has been specified by
, and a chameleon’s angle of rotation has been specified by 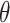 :
:
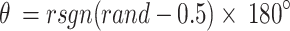 |
17 |
where, 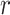 is a random amount between [0,1], and it is used to execute a rotation angle from
is a random amount between [0,1], and it is used to execute a rotation angle from 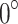 to
to 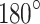 , the direction of rotation is shown by
, the direction of rotation is shown by 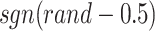 , which is equal to 1 or -1.
, which is equal to 1 or -1.
The matrix presented below is related to the rotation along the 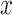 -axis and
-axis and 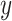 -axis:
-axis:
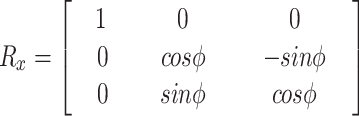 |
18 |
Where the angle of rotation around the  -axis is indicated by
-axis is indicated by 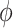 .
.
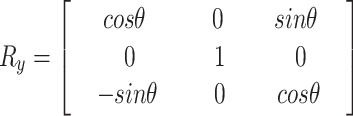 |
19 |
Where the angle of rotation around the 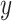 -axis is indicated
-axis is indicated 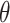 .
.
Prey hunting
The best chameleon is the closest to the target, which is called the optimal chameleon, and the prey is hunted once it is very near the chameleon. The regarded chameleon assaults the prey with its tongue. It is capable of stretching its tongue twice as long, so its location changes slightly. This process helps chameleons for exploiting the solution space by efficiently catching prey. The equation that simulates the pace of a candidate’s tongue as it drops on the target is calculated subsequently:
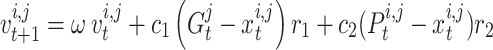 |
20 |
The new pace of the 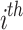 individual within the
individual within the 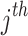 dimension at iteration
dimension at iteration 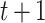 is defined by
is defined by 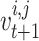 , the present speed of the
, the present speed of the 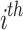 individual within the
individual within the 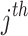 dimension is expressed by
dimension is expressed by 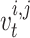 , the
, the 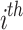 chameleon’s finest identified location is indicated by
chameleon’s finest identified location is indicated by 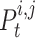 , the finest global location identified thus far to the chameleons is represented by
, the finest global location identified thus far to the chameleons is represented by 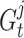 ,
, 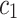 and
and 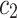 are positive constants that manage the impact of
are positive constants that manage the impact of 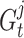 and
and 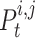 on falling the chameleon’s tongue,
on falling the chameleon’s tongue, 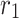 and
and 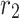 indicate two random numbers between 0 and 1.
indicate two random numbers between 0 and 1. 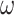 indicates the inertia weight that is linearly reduced during the iterations:
indicates the inertia weight that is linearly reduced during the iterations:
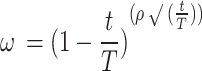 |
21 |
For controlling exploitation ability, 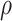 is used that is a positive number. The value of
is used that is a positive number. The value of 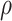 for every benchmark issue solved in this article is considered 1.
for every benchmark issue solved in this article is considered 1.
The position of the chameleon is specified by the position of its tongue when hurried toward the prey and can be obtained based on the third equation of motion, as follows:
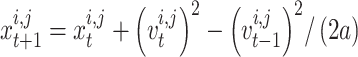 |
22 |
The former speed of the 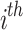 chameleon in the
chameleon in the 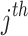 dimension is specified by
dimension is specified by 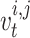 , the proportion of acceleration of the individual’s tongue that slowly rises is represented by
, the proportion of acceleration of the individual’s tongue that slowly rises is represented by 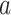 , and its max amount is 2,590 m per second squared. The equation of the present proportion is in the following manner:
, and its max amount is 2,590 m per second squared. The equation of the present proportion is in the following manner:
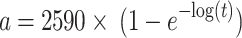 |
23 |
The three formulas (5), (13), and (22) presented above describe the exploration of distinct positions within the search space by chameleons. As a consequence, the most promising places in which the optimal prey exists are discovered. In other words, these equations simulate chameleon foraging. The parameters that exist in the algorithm for describing the exploration step are as follows:
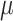 : This restraints the quantity of explorations of the algorithm. It determines to what scope the novel location would be to the target. This variable prevents premature convergence, increases exploitation capacity, and prevents solutions from getting stuck in local optima. Exploration capacity rises with high amounts of
: This restraints the quantity of explorations of the algorithm. It determines to what scope the novel location would be to the target. This variable prevents premature convergence, increases exploitation capacity, and prevents solutions from getting stuck in local optima. Exploration capacity rises with high amounts of 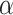 and
and 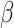 . Exploration ability declines when the number is more than four. According to experimental experiments, searching at borders is possible by search agents with numbers greater than four.
. Exploration ability declines when the number is more than four. According to experimental experiments, searching at borders is possible by search agents with numbers greater than four.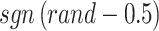 in Eq. (5): This influences the orientation of global search. Owing to that
in Eq. (5): This influences the orientation of global search. Owing to that 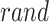 is between 0 and 1 with a distribution that is uniform, negative and positive symptoms are equally likely.
is between 0 and 1 with a distribution that is uniform, negative and positive symptoms are equally likely.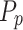 : The value assigned to this variable is obtained from experimental studies, which values less than 0.15 and reduces the performance of the exploration. Each individual is far away from targets within the early stages. Their location is updated according to Eq. (5), which enhances the algorithm’s ability to search the space globally.
: The value assigned to this variable is obtained from experimental studies, which values less than 0.15 and reduces the performance of the exploration. Each individual is far away from targets within the early stages. Their location is updated according to Eq. (5), which enhances the algorithm’s ability to search the space globally.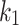 and
and 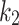 : Chameleon location updates are affected by these parameters. The impact of the best situation of individuals is controlled through the variable
: Chameleon location updates are affected by these parameters. The impact of the best situation of individuals is controlled through the variable 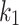 , and the effect of the global best position attained thus far is controlled by
, and the effect of the global best position attained thus far is controlled by 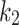 . The values of these parameters can be selected between 0 and 2. if
. The values of these parameters can be selected between 0 and 2. if 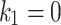 or
or 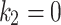 , it is indicated that a part of Eq. (3) never contributes to the operation of optimality that increases the getting stuck possibility within local optimum. The case of
, it is indicated that a part of Eq. (3) never contributes to the operation of optimality that increases the getting stuck possibility within local optimum. The case of 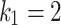 and
and 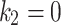 and inversely highlights sensible global search capability that may result in non-accurate problem solvers. According to empirical experiment,
and inversely highlights sensible global search capability that may result in non-accurate problem solvers. According to empirical experiment, 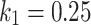 or
or 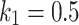 , and
, and 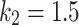 or
or 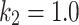 give a rational equilibrium between exploration and exploitation stages.
give a rational equilibrium between exploration and exploitation stages.
Improved chameleon swarm algorithm
To provide a higher accuracy of the metaheuristics, different techniques have been proposed. These techniques are proposed for resolving different issue of the algorithms, like getting stuck in the local optimum point, raw convergence, and increasing the correct convergence25. Although the chameleon swarm algorithm is a newly published technique, it can be improved to get more accurate and precise results. The present study uses two adjustments for this purpose that are explained in the following.
To obtain more global search, the OBL (Opposition-Based Learning) approach has been utilized. Tizhoosh et al.26 were the first to introduce the OBL technique. Each produced candidate is treated as solutions, which contains the candidate and its balance value. Then, as the new candidate, the best candidate between the two values has been chosen. It has been accomplished by determining the cost value of the two substitutions. The following equation yields the opposing candidate for the suggested method based on OBL:
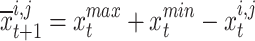 |
24 |
where, 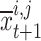 signifies the opposite of the
signifies the opposite of the 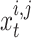 , and
, and 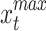 and
and 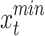 denote the maximum and minimum decision variable constraints, respectively. The next candidate, in particular, is a superior problem solver.
denote the maximum and minimum decision variable constraints, respectively. The next candidate, in particular, is a superior problem solver.
Chaos theory has been also used for increasing the algorithm efficiency. Instead of full stochastic values, theory of chaos adds number with pseudo-stochastic values. This aids the algorithm’s pace and reduces the optimizer’s temporal complication. For chaotic mechanisms, several maps have been introduced. The current study gets optimized using a sinusoidal map. The following equation was used to create the sinusoidal map mathematically:
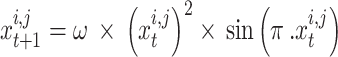 |
25 |
where, 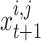 denotes the chaotic pseudo-stochastic value made within the current iteration, whereas
denotes the chaotic pseudo-stochastic value made within the current iteration, whereas 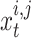 denotes the chaotic stochastic amount created within the previous iteration. The control parameter is described as
denotes the chaotic stochastic amount created within the previous iteration. The control parameter is described as 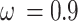 , and
, and 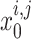 is assumed to be 0.4.
is assumed to be 0.4.
Authentication
The computational analysis of the algorithm is described within the present part. Testing of the suggested ICSA is implemented to a laptop environment with Intel® Core™ i5-7500 CPU 3.40 GHz, 3.41 GHz; with 16 GB RAM, and 64-bit Windows 10 OS. This system is used for validation of the proposed ICSA with a total of five existing metaheuristic algorithms, including Locust Swarm (LS) optimization27, Lion Optimization Algorithm (LOA)28, IPOP-CMA-ES29, LSHADE-SPACMA30, and the original Chameleon Swarm Algorithm31 to be developed and tested. To ensure impartiality in the evaluation of each method, this study was run fifteen times. Each run also included a total of 200 iterations. The average values for all measures were calculated using 25 runs for each algorithm. The parameter values of the algorithms are given in Table 1.
Table 1.
Parameter values of the algorithms.
| Algorithm | Parameter | Value |
|---|---|---|
| IPOP-CMA-ES 29 |
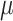 32
32
|
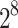
|
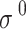
|
2 | |
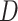
|
5 | |
| LSHADE-SPACMA 30 |
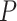
|
0.6 |
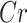
|
0.8 | |
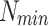
|
6 | |
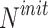
|
34 | |
| Locust Swarm (LS) optimization 27 | F | 0.8 |
| L | 0.9 | |
| g | 18 | |
| Lion Optimization Algorithm (LOA) 28 | Number of prides | 4 |
| Percent of nomad lions | 0.4 | |
| Roaming percent | 0.5 | |
| Mutate probability | 0.6 | |
| Sex rate | 0.75 | |
| Mating probability | 0.5 | |
| Immigrate rate | 0.6 |
The hyperparameters of the algorithms are considered their default downloaded codes. However, the maximum number of iterations and the population size of the algorithms are set equal to provide more fair evaluations. All of the algorithms were run for 25 times to provide more fair analysis.
According to the stochastic nature of the metaheuristic algorithms, amounts of parameters are randomly set. To evaluate the efficiency of the recommended ICSA, this study applied “CEC-BC-2017 test suite”33. The number of variables in the cost functions is set 10. The suggested ICSA, which is proposed in this research, has been evaluated by reducing 10 stochastic fitness functions to the least by using the “CEC-BC-2017 test suite”. The limitation range for all functions is between − 100 and 100. To supply a sensible measurement, the maximum number of iterations and population size for all algorithms are set 200 and 50, respectively. The comparison experiments have been performed to the functions F1, F3, F5, F7, F9, F11, F13, F15, F17, and F19, randomly. Table 2 indicates the average (Avg) amount and the StD amount of the outcomes for all algorithms in reference to the defined benchmark functions.
Table 2.
Comparison of average and standard deviation values for the studied algorithms employed in CEC-BC-2017.
| Function | Indicator | ICSA | CSA 31 | LOA 28 | LS 27 | LSHADE-SPACMA 30 | IPOP-CMA-ES 29 |
|---|---|---|---|---|---|---|---|
| F1 | Avg | 2015.43 | 2264.59 | 2574.83 | 2863.18 | 1863.96 | 100.0 |
| StD | 1364.44 | 1537.52 | 1919.50 | 2015.44 | 1182.42 | 50.0 | |
| F3 | Avg | 1050.0 | 1266.0 | 1940.36 | 1530.15 | 1450.09 | 500.0 |
| StD | 5.63e-6 | 6.12e-6 | 238.53 | 133.37 | 262.86 | 10.0 | |
| F5 | Avg | 777.66 | 833.41 | 925.22 | 1012.47 | 751.83 | 50.15 |
| StD | 250.02 | 315.19 | 523.17 | 800.0 | 120.0 | 25.0 | |
| F7 | Avg | 600.0 | 800.66 | 700.12 | 800.0 | 623.0 | 33.73 |
| StD | 300.34 | 480.0 | 664.53 | 593.0 | 420.90 | 10 | |
| F9 | Avg | 370.55 | 420.11 | 500.9 | 460.0 | 380.0 | 90.0 |
| StD | 126.38 | 238.8 | 310.3 | 312.4 | 247.39 | 21.28 | |
| F11 | Avg | 1200.72 | 1362.56 | 1590.60 | 1800.01 | 1021.33 | 100.2 |
| StD | 708.36 | 980.15 | 1000.11 | 1539.16 | 936.14 | 50.0 | |
| F13 | Avg | 1560.06 | 1633.43 | 1700.77 | 1816.30 | 2055.66 | 500.0 |
| StD | 1054.51 | 1222.45 | 1663.55 | 1713.40 | 1667.43 | 200.0 | |
| F15 | Avg | 1262.12 | 1360.22 | 1511.24 | 1833.47 | 1288.82 | 50.52 |
| StD | 1143.5 | 1210.42 | 1382.44 | 1540.83 | 1009.77 | 10.0 | |
| F17 | Avg | 1639.33 | 1945.36 | 2672.72 | 2588.64 | 1636.25 | 400.0 |
| StD | 1120.72 | 1430.44 | 1864.88 | 2000.0 | 1000.22 | 100.0 | |
| F19 | Avg | 1933.11 | 2374.42 | 2637.53 | 2815.28 | 2546.82 | 500 |
| StD | 1518.45 | 1939.45 | 2444.14 | 2336.74 | 2242.63 | 300 | |
| Friedman mean rank | “7.36” | “5.46” | “6.21” | “6.46” | “5.71” | “8.32” | |
| Rank | 2 | 3 | 5 | 4 | 6 | 1 | |
The results of Table 2 indicate that the offered Improved Chameleon Swarm Algorithm accomplished the finest accuracy value, followed via IPOP-CMA-ES algorithm, that is the winner of the CEC. These results showed that the proposed method achieved higher efficiency toward the others in solving the CEC benchmark functions. Furthermore, by examining the standard deviation value of these algorithms, it can be observed that the proposed method provided one of the minimum values. It has been illustrated the suggested approach achieved the better reliability for solving the optimization problems during different runs. These results drive us to utilize the algorithm for optimally arranging the hyperparameters of the CNN for providing a proper skin cancer diagnosis system.
Data preprocessing
Various imaging techniques in medicine are designed for specific purposes, the most common of which is the dermoscopy, which is mostly used to diagnose skin cancer. Although, medical imaging has some problems after capturing. Indeed, the raw images input should be preprocessed before starting the main evaluation to get easier and more accurate results. This is done for noise elimination and improving the images’ quality regarding contrast. Several methodologies have been proposed for preprocessing of the medical pictures. Within the current study, noise deletion and contrast enhancement have been used for improving the images quality.
Hair removal
Raw images input in dermoscopy usually include some artifacts like hair that hardens the processing stages. To resolve this issue, hair removal technique has been utilized. The method of hair removal is given in Fig. 1.
Fig. 1.
The pseudocode of the hair removal technique.
Based on Fig. 1, the method uses thickening mathematical morphology for solidifying the objects by addition of the pixels to the external part of the edges in the objects pending to connect all separated objects in the 8-pixel neighboring. Similar to any mathematical morphology, the thickening mathematical morphology uses a structural element. This method uses verbose hit-and-miss binary transform to thickening. For employing thickening operation in an image 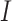 and assuming a structural element as
and assuming a structural element as 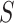 , the following formula is employed:
, the following formula is employed:
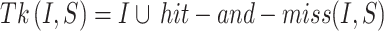 |
26 |
As a result, the thickened pictures include the actual picture plus any extra center pixels that the transform of the hit-and-miss has turned on.
By assuming 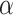 and
and 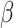 as two structural elements, where,
as two structural elements, where, 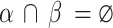 , these two elements are named complex structuring component. Then, the transform of the hit-or-miss for picture
, these two elements are named complex structuring component. Then, the transform of the hit-or-miss for picture 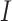 by
by 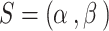 is achieved as follows:
is achieved as follows:
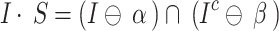 |
27 |
where, 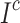 and
and  represent the complement of the image
represent the complement of the image 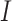 and the mathematical erosion, respectively
and the mathematical erosion, respectively
A simple example of the removal of Hair is shown in Fig. 2.
Fig. 2.
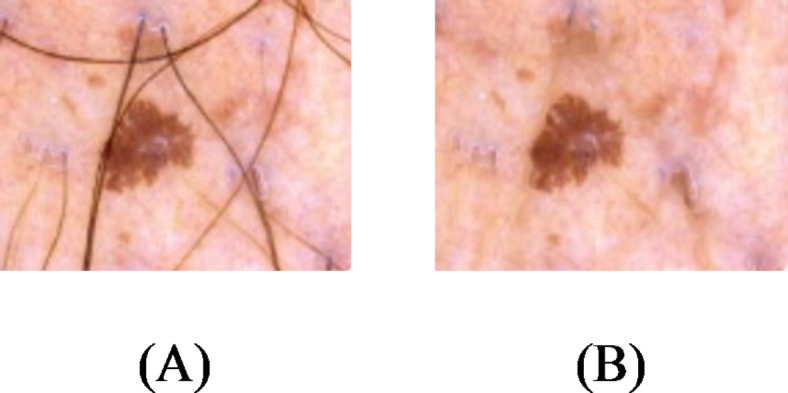
Simple instance of the removal of Hair for dermoscopy picture.
Noise deletion based on Non-local means (NLM)
Noise is a random and unwanted change that affects the image pixels, leading to the loss of image information and detail. As mentioned before, dermoscopy images may face some noises during the imaging which can be generated because of different reason, like the device itself. One of the most significant issues of the noise is its effect on the medical imaging. The main purpose in noise removal technique is to find the noise and to improve the Signal to Noise Ratio (SNR).
Noise removal technologies are critical since the existence of noise in photographs is unavoidable. It has to be probable to maintain the image’s original construction within the reduction of noise process such that the actual picture and its features have not been affected. Various noise deletion strategies have been proposed in this endeavor. The present study uses Non-Local Means (NLM) filter for this purpose. The utilized filter for NLM is Yaroslavsky filter34. This filter uses pixels with closer intensity level to recover the pixels’ factual value.
The main advantage of the NLM is that it is reliable regarding similarity criterion in the presence of noise. Indeed, this method performs well for all images that their noise can be modeled as Gaussian generator.
The weights of all pixels within the pictures, according to the resemblance of their neighbors, are the foundation of the NLM approach. Therefore, the weight assigned to an image’s pixel is higher, indicating that its neighbors and the refined pixel neighbor are more comparable. Lastly, the total of the weights discovered in another pixel is utilized for specifying the number of processed pixels.
The Gaussian kernel with NLM Euclidean weighted principle has been used as the neighborhood similarity criterion in the approach, as illustrated in the equation below.
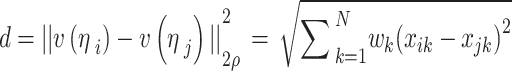 |
28 |
where, 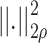 specifies Gaussian kernel with the operator of the Euclidean distance-weighted, and
specifies Gaussian kernel with the operator of the Euclidean distance-weighted, and 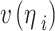 and
and 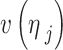 represent the vector of the neighborhood of pixels and the processed pixels, respectively.
represent the vector of the neighborhood of pixels and the processed pixels, respectively.
Therefore, the pixel in the middle has a bigger value when computing neighborhood similarity, and the significance of the pixels reduces as it moves far away. The neighboring pixel similarity for the 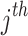 pixel has been evaluated as follows:
pixel has been evaluated as follows:
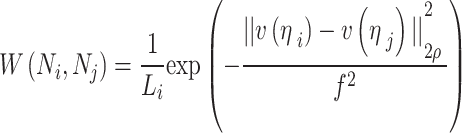 |
29 |
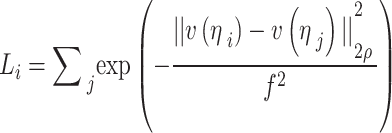 |
30 |
where, 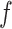 defines the smoothing parameter, and
defines the smoothing parameter, and 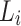 stands for the normalization of the parameter, which makes sure that the sum of the allocated weights is one.
stands for the normalization of the parameter, which makes sure that the sum of the allocated weights is one.
Finally, the NLM filter has been evaluated by employing the weight coefficients as follows:
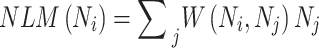 |
31 |
Because of the time-consuming procedure of allocating weight to the pixels, the weighting process is performed in a specific space known as the window of search in the vicinity of all pixels in processing. NLM is a constant filter with three parameters of smoothing, search window radius (here, 5), and similarity window radius (here, 2). The standard deviation (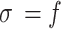 ) of noise is the acceptable value for the smoothing parameter. Figure 3 illustrates several instances of reduction of noise according to NLM filter.
) of noise is the acceptable value for the smoothing parameter. Figure 3 illustrates several instances of reduction of noise according to NLM filter.
Fig. 3.
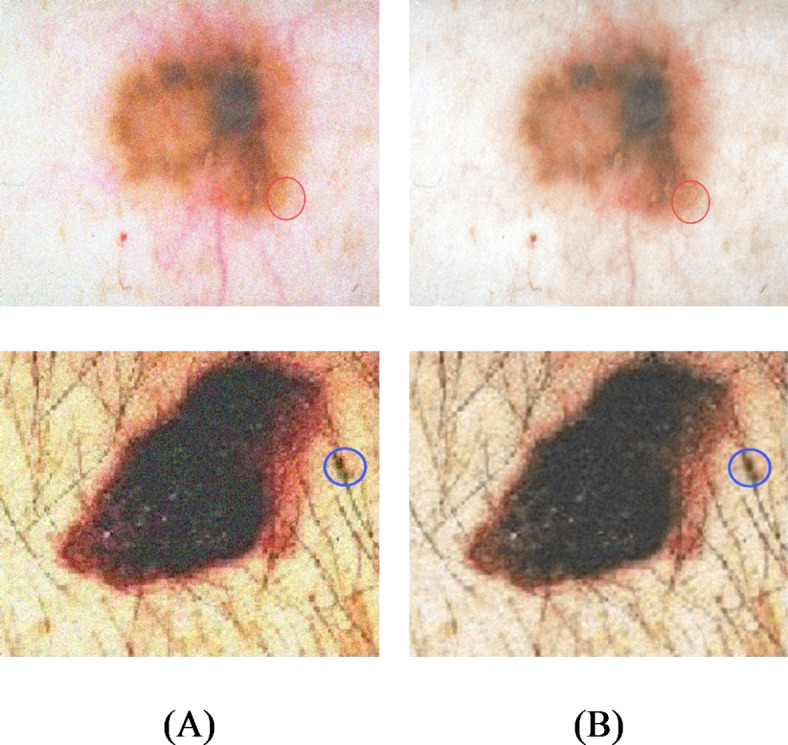
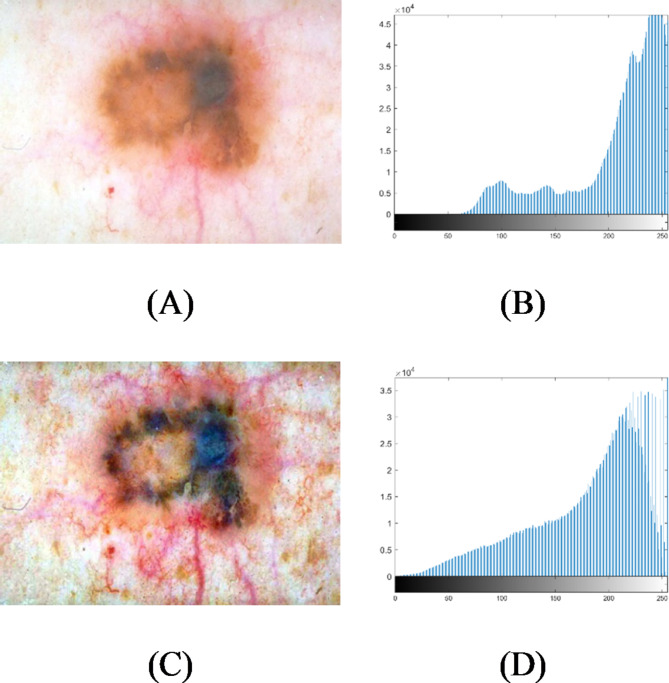
Several instances of noise reduction founded on NLM filter: (A) Input image, and (B) image after reduction of noise.
Contrast enhancement
Contrast enhancement has been considered a significant element in processing medical images. HE (Histogram Equalization) has been found to be among the most prevalent procedures to enhance contrast in digital images and is a simple and effective way to enhance contrast. Also, HE does not maintain the average brightness of the image well, so other methods have been proposed to balance the image while maintaining the brightness of the image. This paper uses another improved form of histograms enhancement, called Balancing Multi-peak histogram with retention Brightness (MPHEBP).
It is difficult to detect each peak of the histogram as long as there is a possibility of fluctuation in brightness levels, which are indistinct. Linear interpolation is applied to fill in unspecified levels of brightness, which is used by the averaging process and neighborhoods, to smooth the histogram. Sequential probability of brightness levels is averaged over the probability of the central brightness level.
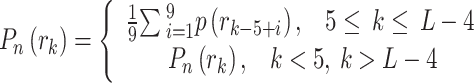 |
32 |
where, 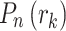 describes probability distribution function. The new probability
describes probability distribution function. The new probability 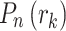 is used only in the head point of detection process.
is used only in the head point of detection process.
In order to obtain the head point at each peak (Max), the different signs between the two possible steps in the smoothed histogram are calculated, and the signal change process is used. 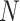 number of head points must be identified. Afterwards, histogram equalization is employed separately in any histogram peak. By assuming
number of head points must be identified. Afterwards, histogram equalization is employed separately in any histogram peak. By assuming 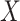 as input image, and
as input image, and 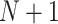 peaks, the image histogram of
peaks, the image histogram of 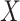 is separated to
is separated to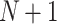 peaks, where,
peaks, where, 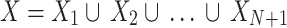 . These
. These 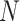 peaks of the image histogram are separated based on the breakpoint with intensity
peaks of the image histogram are separated based on the breakpoint with intensity 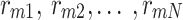 :
:
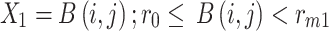 |
33 |
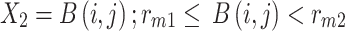 |
34 |
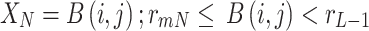 |
35 |
The intensity probability function for each histogram peak is defined as follows:
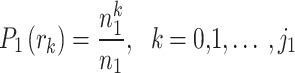 |
36 |
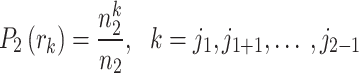 |
37 |
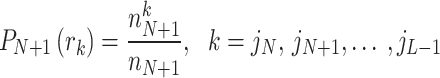 |
38 |
The cumulative intensity function is also defined for each histogram peak as follows.
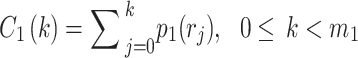 |
39 |
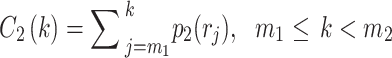 |
40 |
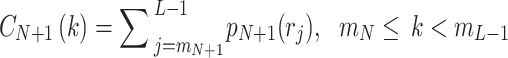 |
41 |
During the histogram equalization, the histogram of the first peak is extended in intensity between 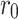 and
and 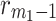 . For the
. For the 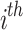 average peak, the histogram is extended from
average peak, the histogram is extended from 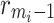 to
to 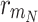 . Figure 4 shows an example of image contrast enhancement based on MPHEBP filter.
. Figure 4 shows an example of image contrast enhancement based on MPHEBP filter.
Fig. 4.
An instance of image contrast enhancement on the basis of MPHEBP filter: (A) input image, (B) histogram of (A), (C) enhanced image, and (D) histogram of (C).
Simulations and results
Database
There are several databases that may be used to validate the suggested skin cancer detection method. This study makes use of the SIIM-ISIC Melanoma database for the validation. This database is a common product of the SIIM and ISIC organizations. The SIIM (Society for Imaging Informatics in Medicine) has been found to be the main health service organization for medicinal imaging. Its goal is promulgating medicinal imaging through training, study, and development within a community that has several disciplines.
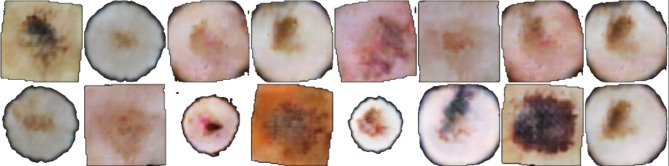
The ISIC (International Skin Imaging Collaboration), a global invention to improve melanoma recognition, has joined SIIM. The ISIC Archive has the world’s biggest collection of high-resolution dermoscopic pictures of dermal lesions. The images have been created in DICOM format that include metadata and image, allowing them to be accessed by common libraries. The dataset is considered in two formats, including JPEG and TFRecord. The photos are all in the same size (1024 × 1024). The total number of images include 33,126 “*.Jpeg” images. Figure 5 shows some of the images that were used in the study.
Fig. 5.
Some examples of the SIIM-ISIC Melanoma dataset.
The data was divided stochastically into test and training data that 80% of the data, equal to 26,500 images, was allocated for training. Moreover, 20% of the data, equal to 6,626 images, was allocated for testing data. It has been achieved by the toolbox “splitEachLabel”. This dataset collection can be achieved by the following link: https://www.kaggle.com/competitions/siim-isic-melanoma-classification.
System configuration
The method was written in the 64-bit version of MATLAB R2019b and was run on an Intel Core i7 CPU with speeds of 2.00 GHz and 2.5 GHz, 8GB of RAM, and a 64-bit operating system. For each optimization issue, the most frequent choices are population size of 30, maximum number of iterations of 200 time, and 30 independent runs.
Methodology
The input images are normalized by subtracting the mean value of the RGB from the input image to optimize the images for the network. Then, all images have been resized to 227 × 227 standard size employing “augmentedImageDatastore” code and bicubic interpolation in environment of Matlab. At last, the database has been augmented to provide bigger training set. Data augmentation for the images is done by rotating it in 0, 90, 180 and 270 degrees. Also, horizontal flipping has been applied to the images. Figure 6 displays some instances of the data augmentation findings35.
Fig. 6.
Several instances of the data augmentation findings, including (A) input image and (B) augmented image35.
The overall design of the proposed ICSA/CNN is consistent with the improved Chameleon Swarm Algorithm. At first, a crew of chameleons were defined by an order set 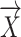 , and the components are defined by
, and the components are defined by 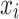 that can describe different arrangements of the hyper-parameters. Uniform distribution is used for initializing the hyper-parameters (
that can describe different arrangements of the hyper-parameters. Uniform distribution is used for initializing the hyper-parameters (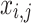 ), wherein
), wherein 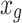 and
and 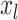 describe the global and local finest values for the hyper-parameters.
describe the global and local finest values for the hyper-parameters.
Secondly, the positions of the chameleons are updated by local data. Afterward, according to their objective values, 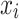 are reorganized in descending order in
are reorganized in descending order in 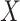 , and the set
, and the set 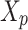 of local bests in addition to the global best
of local bests in addition to the global best 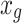 has been updated. After reaching the termination condition, the best solution has been returned. The convolution neural network includes three foremost layers of convolution, FC (fully-connected), and pooling.
has been updated. After reaching the termination condition, the best solution has been returned. The convolution neural network includes three foremost layers of convolution, FC (fully-connected), and pooling.
Each layer has its own set of hyperparameters, which are normally chosen by the user experimentally. The proposed improved chameleon swarm algorithm has been used to obtain an optimum design for the CNN. For the proposed network, three layers are set for convolution, three layers have been allocated for pooling, three layers are set for dropout, and three layers are set for ReLU. Moreover, for this investigation, 1 flatten layer and 2 dense layers have been chosen. Each of the above-mentioned layers have some hyperparameters which should be chosen appropriately to get efficient arrangement.
The network’s Kernel sizes are 2 × 2 and 6 × 6, respectively, with the lower range used to preserve fine local features and the upper range employed to save fine adjacent details. In this study, the lower and upper ranges are defined as 3 × 3 and 5 × 5, respectively.
Simple features were picked within the first layer, and sophisticated features were set in subsequent layers, as specified by the number of kernel layers. In pooling layers, pooling size is a key hyperparameter. The input attributes have been down sampled and fed on to subsequent layer when the pooling size is large enough.
Proper balance for the size of pooling layers has a substantial impact on the model, in a way that a greater value of the present attribute causes the network to overlook good details, while a little value of this feature extracts local fine grain. The pooling layer in this investigation has a size range of 3 × 3 to 5 × 5. The main parameter for dropout layers is dropout rate, and incorrect choosing of such a parameter causes overfitting. The rate of dropout with the present research has been estimated to be between 0.2 and 0.6.
The quantity of layers of pooling and convolution is limited to be between 4 and 10 to prevent from overfitting and underfitting by the layer of convolution, as well as creating repetitive features. There will be a need to a lot of trial and error, once the workable range has been defined to find the ideal network arrangement. Although, optimal CNN hyperparameters are aimed to be selected by the proposed metaheuristic-based methodology.
In this study, optimization is done on the aforementioned “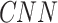 ” function by optimal selection of the following decision variables:
” function by optimal selection of the following decision variables:
For convolution (
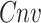 ) layer:
) layer:
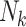 : number of kernels
: number of kernels
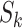 : the size of kernel
: the size of kernel
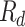 : the rate of dropout
: the rate of dropout
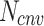 : number of convolutional layers
: number of convolutional layers
For pooling (
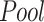 ) layer:
) layer:
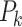 : the size of kernel
: the size of kernel
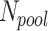 : number of pooling layers
: number of pooling layers
For dropout (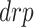 ) layer:
) layer:
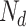 : number of dropout rates,
: number of dropout rates,
Finally, by considering the number of layers in the convolution and pooling layers (which is 3), the decision variables of the optimization will be as follows:
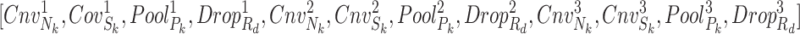 |
42 |
Therefore, the network will have the best arrangement if all decision variables have been selected suitably.
Evaluation indicators
Numerous tests have been carried to assess the efficiency of the medical imaging techniques. At first, Receiver Operating Characteristics (ROC) curve is used for analyzing the method efficiency. A receiver operating characteristic curve, is a graphical illustration that indicates how a binary classifier system’s diagnostic function switches when the discrimination threshold is altered. This study uses six different measurement indicators for analyzing the proposed method. The indicators are Accuracy (Acc), Specificity (Sp), Precision (Pr), Sensitivity (Se), Jaccard Index (JI), F1-score (FS).
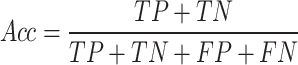 |
43 |
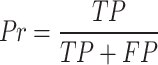 |
44 |
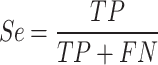 |
45 |
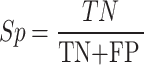 |
46 |
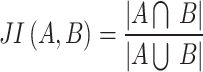 |
47 |
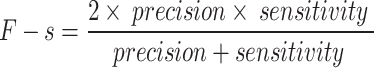 |
48 |
where, TP defines True Positive, FP describes False Positive, TN signifies True Negative, and FN specifies the False Negative.
For providing a suitable validation, the outcomes of the suggested approach are measured with several state-of-the-art published approaches, such as Blob Detection (BD)36, Combined Convolutional Neural Networks (CCNN)37, miRNAs38, hybrid Neural Network–World Cup Optimizer (NN/WCO)39, and support vector machine and a new optimization algorithm (OSVM)18.
Results
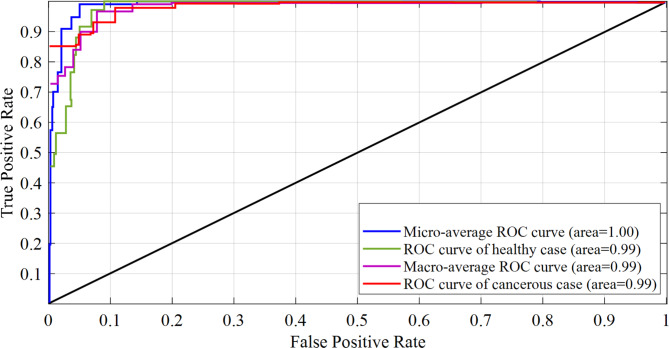
Figure 7 depicts the Receiver Operating Characteristics (ROC) curve in two kinds of cancerous and healthy. The TPR (True Positive Rate) is shown against the FPR (False Positive Rate) on the ROC curve (FPR). It measures the degree of separability across different classes to indicate the model’s diagnostic capabilities.
Fig. 7.
ROC curve in two kinds of cancerous and healthy cases.
The model’s ability to differentiate between various classes improves as the AUC (Area Under the Curve) increases. The AUC of an ideal model is 1.0, whereas that of a bad model is 0. AUC of 0.5 implies that the model is similar to guessing at random. As can be observed from Fig. 7, it can be seen that normal class has an AUC of 0.99, and cancerous class has an AUC of 0.99, with macro-average and micro-average AUC of 0.99 and 1.0, respectively. The AUC of cancerous and healthy class is 0.99 because our model predicted one erroneous positive in the case of healthy and one false negative in the case of a healthy patient.
Then, the efficacy of the recommended technique has been assessed employing the evaluation indicators explained in the previous subsection. To demonstrate the influence of the preprocessing stage, which includes noise deletion and contrast enhancement, the data have been compared before and after these changes. The numerical simulations of the approach performance evaluation without and with preprocessing have been demonstrated in Table 3.
Table 3.
Numerical simulations of the approach performance evaluation without and with preprocessing.
| Method | Acc | Pr | Se | Sp | JI | F-S |
|---|---|---|---|---|---|---|
| Method with preprocessing | 94.99 | 90.23 | 96.99 | 95.97 | 88.79 | 90.86 |
| Method without preprocessing | 88.99 | 88.99 | 95.00 | 92.31 | 95.11 | 87.85 |
It can be witnessed from Table 3 that the approach with and without preprocessing has 9.14 and 12.15 error, where, 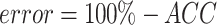 . This shows how using preprocessing technique can enhance the accuracy of the system. Also, the priority of the suggested technique based on the other terms can be proved based on Table results.
. This shows how using preprocessing technique can enhance the accuracy of the system. Also, the priority of the suggested technique based on the other terms can be proved based on Table results.
In the following, the efficiency of the suggested approach has been measured by several established indicators that are explained before. Table 4 presents the comparative assessment between the developed method and various baseline techniques applied to the SIIM-ISIC Melanoma dataset.
Table 4.
Comparative assessment between the developed method and various baseline techniques applied to the SIIM-ISIC Melanoma dataset.
| Method | Acc | Pr | Se | Sp | JI | F-S |
|---|---|---|---|---|---|---|
| Proposed method | 94.99 | 90.23 | 96.99 | 95.97 | 90.23 | 90.86 |
| BD 36 | 76.99 | 79.99 | 87.00 | 82.98 | 80.90 | 84.52 |
| miRNAs 38 | 81.97 | 76.98 | 90.01 | 84.16 | 84.52 | 86.15 |
| OSVM 18 | 87.99 | 83.98 | 90.23 | 86.15 | 88.90 | 87.99 |
| NN/WCO 39 | 91.65 | 83.99 | 92.37 | 90.23 | 88.79 | 90.23 |
| CCNN 37 | 94.97 | 85.73 | 93.58 | 92.31 | 92.31 | 92.34 |
Table 4 shows that the proposed methodology, with a lowest error rate of 5.01% and a highest accuracy of 94.99%, has been found to be the best regarding skin cancer detection. Furthermore, the proposed technique could achieve the specificity value of 95.97%, which indicated its rate of true negative as the highest one clarifies its capability for correctly recognition of healthy pixels. The suggested technique’s better aptitude in diagnosing rate of genuine positive, i.e., appropriate recognition of cancerous pixels, has been depicted by the high-level view of the Sensitivity (96.99%). The recommended technique’s great precision of 95.98% illustrated its advanced likelihood for the diagnosed images, whereas the Jaccard Index’s 90.23% value illustrated its better ability for diversity and similarity of sample set.
K-Fold cross-validation
For conducting a more thorough assessment of the method efficiency, k-fold cross-validation has also been employed to enhance the accuracy and reliability of the results. K-fold cross-validation is a method used to measure the performance of a machine learning model by dividing the dataset into k segments, training the model on k-1 segments, and evaluating it on the remaining segment40. For this analysis, 5-fold cross-validation has been implemented. The results have been presented in Table 5.
Table 5.
K-Fold Cross-Validation Results.
| Fold | Accuracy | Precision | Sensitivity | Specificity | Jaccard Index | F1-Score |
|---|---|---|---|---|---|---|
| 1 | 94.21 | 90.15 | 96.42 | 95.65 | 89.45 | 90.71 |
| 2 | 94.59 | 90.65 | 96.67 | 95.83 | 90.11 | 91.01 |
| 3 | 94.01 | 89.83 | 96.21 | 95.45 | 88.91 | 90.31 |
| 4 | 94.41 | 90.41 | 96.51 | 95.71 | 89.81 | 90.91 |
| 5 | 94.81 | 91.01 | 96.83 | 96.01 | 90.51 | 91.31 |
| Average | 94.41 | 90.41 | 96.528 | 95.73 | 89.758 | 90.85 |
The results from the 5-fold cross-validation indicated that the proposed method achieved high levels of accuracy, precision, sensitivity, specificity, Jaccard Index, and F1-Score. The average metrics revealed that the current approach achieved an accuracy value of 94.40%, a precision value of 90.41%, a sensitivity value of 96.53%, a specificity value of 95.73%, a Jaccard Index value of 89.76%, and an F1-Score value of 90.85%.
Conclusions
Melanoma is one of the most universal diseases of skin cancer. Quick detection of melanoma can greatly decrease the risk of death from this fatal skin cancer. It is extremely beneficial and valuable to provide a strategy that aids in the early detection of melanoma. Within the current research, an algorithm was selected that aided in the diagnosis of melanoma by extracting and classifying relevant information from dermoscopic images. The accurate demarcation between the lesion and the field was accomplished before extracting the required features. At present, the size of the cancer in dermoscopy is determined manually by the physicians, which is wasteful when the size of the data is large. Cancer segmentation or uneven areas of dermoscopy image may be valuable within clinical cure and cancer study. It requires a very long time for radiologists to correctly identify tumors, although it is ideal. An automatic approach was suggested and tested for ascertaining abnormal region of the skin in a dermoscopy image. The current system used a deep learning-based optimization pipeline approach to diagnose cancers in dermoscopy images. Following preprocessing of the input raw images by hair removal for eliminating the artifacts, noise deletion, and contrast enhancement, the images were fed into an optimal CNN for the ultimate recognition. To obtain the best efficiency, a new upgraded metaheuristic, called Improved chameleon swarm algorithm, was designed and used. The designed diagnosis system was then verified by applying it to the SIIM-ISIC Melanoma dataset, and the outcomes were contrasted with some other published procedures, including Blob Detection (BD), Combined Convolutional Neural Networks (CCNN), miRNAs, hybrid Neural Network–World Cup Optimizer (NN/WCO), and Support Vector Machine and a new optimization algorithm (OSVM). Final outcomes displayed the prominence of the suggested technique in optimal melanoma diagnosis from the dermoscopic images against the other advanced methods.
Acknowledgements
Science and Technology Projects Foundation of Guangzhou City (grant nos. 202102080594 and 202201011802). Research project of Traditional Chinese Medicine Bureau of Guangdong Province(grant nos. 20241179). Science and Technology project of traditional Chinese medicine and integrated traditional Chinese and Western medicine in Guangzhou (20242A010040).
Author contributions
Weiqi Wu,Liuyan Wen,Shaoping Yuan,Xiuyi Lu, Juan Yang and Asad Rezaei sofla wrote the main manuscript text and prepared figures. All authors reviewed the manuscript.
Data availability
All data generated or analysed during this study are included in this published article.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Weiqi Wu and Liuyan Wen are co-first authors.
Contributor Information
Xiuyi Lu, Email: 714373606@qq.com.
Juan Yang, Email: yjuan0623@163.com.
Asad Rezaei sofla, Email: asadrezaeisofla@gmail.com.
References
- 1.Garg, S. & Jindal, B. <ArticleTitle Language=“En”>Skin lesion segmentation using k-mean and optimized fire fly algorithm. Multimedia Tools Appl.80, 7397–7410 (2021). [Google Scholar]
- 2.Ranjbarzadeh, R. et al. Nerve optic segmentation in CT images using a deep learning model and a texture descriptor. Complex. Intell. Syst. 8, 1–15 (2022).
- 3.Yang, Y. & Razmjooy, N. Early detection of brain tumors: Harnessing the power of GRU networks and hybrid dwarf mongoose optimization algorithm. Biomed. Signal Process. Control. 91, 106093 (2024). [Google Scholar]
- 4.Garg, S. & Balkrishan, J. Skin lesion segmentation in dermoscopy imagery. Int. Arab. J. Inf. Technol.19, 29–37 (2022). [Google Scholar]
- 5.Kapravchuk, V., Briko, A., Kobelev, A., Hammoud, A. & Shchukin, S. An Approach to Using Electrical Impedance Myography Signal Sensors to Assess Morphofunctional Changes in Tissue during Muscle Contraction. Biosensors. 14, 76 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Razmjooy, N. et al. Computer-Aided Diagnosis of Skin Cancer: A Review. Curr. Med. Imaging 16 (2020). [DOI] [PubMed]
- 7.Cai, W. et al. Optimal bidding and offering strategies of compressed air energy storage: A hybrid robust-stochastic approach. Renew. Energy. 143, 1–8 (2019). [Google Scholar]
- 8.Ebrahimian, H., Barmayoon, S., Mohammadi, M. & Ghadimi, N. The price prediction for the energy market based on a new method. Economic Research-Ekonomska Istraživanja. 31, 313–337 (2018). [Google Scholar]
- 9.Fan, X. et al. High voltage gain DC/DC converter using coupled inductor and VM techniques. IEEE Access.8, 131975–131987 (2020). [Google Scholar]
- 10.Jindal, B. & Garg, S. FIFE: fast and indented feature extractor for medical imaging based on shape features. Multimedia tools Appl.82, 6053–6069 (2023). [Google Scholar]
- 11.Garg, S. & Jindal, B. F. D. L. M. An enhanced feature based deep learning model for skin lesion detection. Multimedia Tools Appl.83, 36115–36127 (2024). [Google Scholar]
- 12.Ghiasi, M., Ghadimi, N. & Ahmadinia, E. An analytical methodology for reliability assessment and failure analysis in distributed power system. SN Appl. Sci.1, 44 (2019). [Google Scholar]
- 13.Gollou, A. R. & Ghadimi, N. A new feature selection and hybrid forecast engine for day-ahead price forecasting of electricity markets. J. Intell. Fuzzy Syst.32, 4031–4045 (2017). [Google Scholar]
- 14.Zghal, N. S. & Derbel, N. Melanoma skin cancer detection based on image processing. Curr. Med. Imaging. 16, 50–58 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Salah, B., Alshraideh, M., Beidas, R. & Hayajneh, F. Skin cancer recognition by using a neuro-fuzzy system. Cancer Inform.10, S5950 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roffman, D., Hart, G., Girardi, M., Ko, C. J. & Deng, J. Predicting non-melanoma skin cancer via a multi-parameterized artificial neural network. Sci. Rep.8, 1–7 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dorj, U. O., Lee, K. K., Choi, J. Y. & Lee, M. The skin cancer classification using deep convolutional neural network. Multimedia Tools Appl.77, 9909–9924 (2018). [Google Scholar]
- 18.Li, M., Han, C. & Fahim, F. Skin cancer diagnosis based on support vector machine and a new optimization algorithm. J. Med. Imaging Health Inf.10, 356–363 (2020). [Google Scholar]
- 19.Liu, Z. et al. A generalized deep learning model for heart failure diagnosis using dynamic and static ultrasound. J. Translational Intern. Med.11, 138–144 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu, Y., Liu, L., Yang, L., Hao, L. & Bao, Y. Measuring distance using ultra-wideband radio technology enhanced by extreme gradient boosting decision tree (XGBoost). Autom. Constr.126, 103678 (2021). [Google Scholar]
- 21.Guo, Z., Xu, L., Si, Y. & Razmjooy, N. Novel computer-aided lung cancer detection based on convolutional neural network‐based and feature‐based classifiers using metaheuristics. Int. J. Imaging Syst. Technol.10.1002/ima.22608 (2021). [Google Scholar]
- 22.Darwish, A., Ezzat, D. & Hassanien, A. E. An optimized model based on convolutional neural networks and orthogonal learning particle swarm optimization algorithm for plant diseases diagnosis. Swarm Evol. Comput.52, 100616 (2020). [Google Scholar]
- 23.Nguyen, T., Nguyen, G. & Nguyen, B. M. EO-CNN: an enhanced CNN model trained by equilibrium optimization for traffic transportation prediction. Procedia Comput. Sci.176, 800–809 (2020). [Google Scholar]
- 24.Ayub, N., Aurangzeb, K., Awais, M. & Ali, U. in IEEE 23rd International Multitopic Conference (INMIC). 1–6 (IEEE). (2020).
- 25.Fan, X. et al. Multi-objective optimization for the proper selection of the best heat pump technology in a fuel cell-heat pump micro-CHP system. Energy Rep.6, 325–335 (2020). [Google Scholar]
- 26.Tizhoosh, H. R. In International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06) 695–701 (IEEE).
- 27.Cuevas, E., Fausto, F. & González, A. In New Advancements in Swarm Algorithms: Operators and Applications139–159 (Springer, 2020).
- 28.Yazdani, M. & Jolai, F. Lion optimization algorithm (LOA): A nature-inspired metaheuristic algorithm. J. Comput. Des. Eng.3, 24–36 (2016). [Google Scholar]
- 29.Biedrzycki, R. in 2017 IEEE Congress on Evolutionary Computation (CEC). 1489–1494 (IEEE).
- 30.Hadi, A. A., Mohamed, A. W. & Jambi, K. M. In Heuristics for Optimization and Learning103–121 (Springer, 2021).
- 31.Braik, M. S. Chameleon Swarm Algorithm: A bio-inspired optimizer for solving engineering design problems. Expert Syst. Appl.174, 114685 (2021). [Google Scholar]
- 32.Hansen, N. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers 2389–2396.
- 33.Wu, G., Mallipeddi, R. & Suganthan, P. N. Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization. National University of Defense Technology, Changsha, Hunan, PR China and Kyungpook National University, Daegu, South Korea and Nanyang Technological University, Singapore, Technical Report (2017).
- 34.Yaroslavsky, L. P. Digital Picture Processing: An IntroductionVol. 9 (Springer Science & Business Media, 2012).
- 35.Ha, Q., Liu, B. & Liu, F. Identifying melanoma images using efficientnet ensemble: Winning solution to the siim-isic melanoma classification challenge. 11arXiv preprint. arXiv: 2010.05351 (2020).
- 36.Jain, S. & Pise, N. Computer aided melanoma skin cancer detection using image processing. Procedia Comput. Sci.48, 735–740 (2015). [Google Scholar]
- 37.Tschandl, P. et al. Expert-level diagnosis of nonpigmented skin cancer by combined convolutional neural networks. JAMA dermatology. 155, 58–65 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Neagu, M., Constantin, C., Cretoiu, S. M. & Zurac, S. miRNAs in the Diagnosis and Prognosis of Skin Cancer. Front. Cell. Dev. Biology. 8, 71 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Razmjooy, N., Sheykhahmad, F. R. & Ghadimi, N. A hybrid neural network–world cup optimization algorithm for melanoma detection. Open Med.13, 9–16 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Liu, Y. & Bao, Y. Review on automated condition assessment of pipelines with machine learning. Adv. Eng. Inform.53, 101687 (2022). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analysed during this study are included in this published article.