Dependent censoring bias assessment using inverse probability of censoring weights: Type 2 diabetes mellitus risk in patients initiating bisoprolol versus other antihypertensives in a Clinical Practice Research Datalink cohort study

Abstract

Dependent censoring involves a preferential attrition of a subgroup of interest; occurring in survival analysis, it may impact interpretation by introducing a selection bias. To assess the potential bias in a comparison of bisoprolol to other antihypertensives in terms of Type 2 diabetes mellitus (T2DM) incidence, inverse probability of censoring weights (IPCW) was used. It was further used to contextualize results obtained through competing risks analysis. Two estimands were considered to assess T2DM incidence while accounting for deviations from the initial antihypertensive monotherapy (DFM). A hypothetical estimand using IPCW, treating DFM as censoring, was interpreted together with a ‘while-on-treatment’ estimand, treating DFM as a competing risk. We illustrated our application with a cohort study based on Clinical Practice Research Datalink (CPRD) including 267,352 patients with newly diagnosed arterial hypertension between 2000 and 2017, initiating antihypertensive monotherapy among bisoprolol, other beta-blockers, renin-angiotensin system drugs (ACEi/ARB), diuretics and calcium-channel blockers. A mild dependent censoring process was hypothesized, leading to slight overestimation of T2DM incidence. Although subject to some limitations, a nonsignificant trend toward an excess of risk associated with ACEi/ARB was yielded consistently by IPCW and competing risks analyses. Conversely, in comparisons of bisoprolol versus either diuretics, other beta-blockers or calcium channel blockers, no significant differences or critical dependent censoring impact were found. Concurrent use of complementary estimands allowed formulating a refined interpretation of our findings: though not significant, the trend toward an excess of T2DM risk associated with a ACEi/ARB monotherapy compared with bisoprolol is likely not originating only from the minor dependent censoring. Reassessing identical estimands in other cohorts would provide insights to corroborate or refute this result.

In survival analysis, censoring refers to a lack of information concerning the effective survival time of a subject; in other words, an obstacle precluding the observation of the event of interest [1]. When occurring randomly in any subgroup of interest it is then qualified as independent censoring. Dependent censoring involves a preferential attrition of a subgroup of interest, driven for instance by a link between the event of interest and censoring criterion. This process might give rise to a selection bias [2].

Dependent censoring was suspected in a study aimed to compare the risk of Type 2 diabetes mellitus (T2DM) in patients who initiated antihypertensive monotherapy [3]. There is controversy over the significance of T2DM that develops during treatment with antihypertensives. On the one hand, diuretics and β-blockers were shown to increase the risk of T2DM in some studies [4–6]. On the other hand, evidence from two other studies have highlighted an increase of risk with diuretics, but not with β-blockers [7,8]. To answer this question, we designed an active-comparator new-user cohorts, where patients were censored at any deviation from their initial antihypertensive monotherapy treatment (abbreviated DFM), in other words, either discontinuation, addition or switch.

We proposed a new user and active comparator design to mitigate time confounding bias [9]. In clinical practice, patients will initiate a first line monotherapy. Then be moved to a combination therapy if not sufficiently controlled [10]. However, the risk of diabetes was assumed to be independent of the line of therapy used.

Furthermore, it was assumed that censoring may occur preponderantly in patients with an adverse cardiovascular profile as physician may alter the treatment to strengthen the preventive treatment or cure a cardiovascular event [11]. Conversely, patients at low cardiovascular risk may see their treatment discontinued. Theses hypotheses were assumed considering that arterial hypertension and T2DM are risk factors for one another: the former is a risk factor for T2DM in the pre-diabetic state while the latter doubles the risk of cardiovascular disease [12,13]. Formally, Tsiatis A. [14] shows that dependent censoring cannot be demonstrated as it requires independence between competing risks. Our conjecture based on clinical knowledge could have been completed by tests proposed by some authors in the literature [15,16].

Modification of the initial antihypertensive monotherapy being a factor that may impact interpretation of the T2DM incidence, it then qualifies as an intercurrent event, in the sense of the ICH E9 addendum on estimands [17]. We proposed two estimands strategies to account for patients that discontinue monotherapy (e.g., discontinuation, switch to another class, combination therapy…). First, competitive risks models may be considered to deal with such intercurrent events as they compel to formulate a joint interpretation of clinical and competing events; it yields an ‘on-treatment’ effect with discontinuation being considered as a competing risk. As an alternative, the inverse probability of censoring weights (IPCW) [18] can also constitute a suitable countermeasure to mitigate dependent censoring. Weights, computed as the inverse probability of remaining uncensored can then be supplied to a time-dependent survival model to obtain an unbiased estimation. IPCW then yields a ‘hypothetical’ estimand, i.e., the T2DM incidence estimated in a virtual population where censoring would not occur.

We hereafter present a clinical application of dependent censoring assessment through IPCW and an analysis of the T2DM risk associated with the different antihypertensive medications carried out through the two described methods.

Materials & methods

Motivating example

A non-interventional study, active-comparator new-user cohorts, based on routinely collected data from the British Clinical Practice Research Datalink (CPRD) was used as a motivating example. Patients with newly diagnosed arterial hypertension and initiating an antihypertensive treatment in monotherapy between 2000 and 2017 constituted the study population. Full inclusion and exclusion criteria are described elsewhere [3]. Furthermore, for T2DM risk estimation, patients were excluded if presenting with diabetes at baseline. Bisoprolol treatment group was compared pairwise against four other therapeutic classes: angiotensin conversion enzyme inhibitors (ACEi) bundled with angiotensin receptor blockers (ARB), diuretics (including loop, thiazidics and potassium sparing), calcium-channel blockers (CCB) and other beta-blockers (OBB). For each comparison 1:4 matching using propensity score was computed on baseline variables (no longitudinal variables; see details described in parent paper [3]). Patients were followed from the index date (initiation of monotherapy) to the earliest event among: T2DM or deviation from initial monotherapy (switch to another antihypertensive drug, or addition of one to the index treatment, discontinuation of the index treatment), patient's death, transfer out date, or end of the study period (31 December 2018). T2DM was defined via either diagnosis or prescription of a non-insulin antidiabetic medication. Our assumption was that T2DM might be impacted by dependent censoring.

Application of our example to the estimands

Deviations from the initial monotherapy (DFM) treatment scheme are likely to occur not at random and thus qualify as intercurrent events that may impact outcome estimation. They were treated either as a competing event or as a censoring event in the statistical analyses. In our motivating example, hazard ratios represent treatment effects assed over 16 years, with bisoprolol as reference.

Two different estimands were devised for T2DM: a ‘while on treatment’ strategy estimand and a ‘hypothetical’ strategy estimand.

In the first case, deviations from monotherapy (intercurrent event) or death were treated as a competing event. Competing risks survival analyses were carried out with Cox proportional hazards model and Fine & Gray proportional subdistribution hazards model [19]; cause-specific and subdistribution hazard ratios were reported to summarize the incidence of T2DM in patients effectively being treated, while taking into account that they may discontinue their treatment first.

In the second case, for the ‘hypothetical’ strategy estimand, deviations from monotherapy were treated as a censoring event (intercurrent event); the estimand is then the T2DM incidence estimated in a hypothetical population in which, contrary to the facts, everybody would stay on their initial treatment. The effect of time-varying confounders that may generate dependent censoring was controlled through IPCW. This idea behind IPCW is to compensate for censored subjects by giving higher weight to uncensored subjects with similar characteristics to the ones who are censored [20]. A Bonferroni correction (α = 0.0125) was used to account for the fact that four comparisons were performed.

Inverse probability of censoring weight

Censoring process modeling

Weights used in IPCW require the determination of the probability of remaining uncensored for every subjects at each event occurrence throughout the follow-up.

A three-step procedure aimed at modeling the censoring process through iterative fitting of Cox models. Both baseline and time-dependent variables, with less than 80% of missing values, were eligible as explanatory variables.

First step intended to identify variables not associated with the outcome and thus unlikely to generate dependent censoring. Univariate Cox models for T2DM fitted on the entire cohort were used for this purpose; variables displaying a p-value superior to 0.3 were dismissed.

Second step aimed at classifying available variables into three categories, using clinical relevance (expert opinion) and univariate Cox models, fitted in each treatment group from the entire cohort.

Third and final step consisted of fitting multivariate Cox models for censoring, separately for each treatment groups from the entire cohort. Variable selection was carried out with a stepwise AIC procedure, constrained by aforementioned variable classification: ‘essential’ variables were mandatory, ‘common’ were available for all treatment groups, ‘other’ were available only for some groups. Further details are available in Supplementary materials. Model's standard error was estimated using the ‘Hubert-White’ robust estimator [21,22].

Weights computation

Throughout the entire follow-up, for each patient, probabilities of remaining uncensored were computed from previously fitted multivariate Cox models, at each occurrence of either an outcome or a censoring event. To limit excessive variability, the weights were stabilized by multiplying by the unadjusted probability of remaining uncensored at each event or censoring time. Those were obtained using an empty Cox model, fitted individually for each treatment group. Increasing truncations (1st, 5th, 10th percentiles) were applied to mitigate excessive variance of the weights.

Time-dependent IPCW-weighted Cox models

T2DM risks were estimated in matched samples for each treatment group: propensity score was used to match bisoprolol patients against patients treated by another therapeutic class.

Time-dependent IPCW-weighted Cox models for T2DM were fitted in each matched dataset with treatment as the only explanatory variable.

Schoenfeld residuals were inspected to detect any departure from the proportional hazards assumption for all models. All computation were performed using R [23] 3.6.2 with minimal dependencies, including packages data.table 1.13.0 and survival 3.1–12. Of note, for reproducibility purposes, code is available in Supplementary materials. It notably includes: steps to break down the cohort in long format while accounting for each and every T2DM and censoring event; steps to compute probability of remaining uncensored for each patient at any event occurrence.

Results

A total of 1640 (77.6%) bisoprolol patients were matched to 6560 other β-blocker patients; 1929 (91.2%) to 7716 ACEi/ARB patients; 1881 (89.0%) to 7524 CCB patients; and 1804 (85.3%) to 7216 diuretic patients. After matching, patients presented similar baseline characteristics, with baseline covariates including in the PS showing a good balance (SMD ≤0.1). Median follow-up in the bisoprolol cohort was 8.3 months, while the mean follow-time was 23.3 months. Concerning the comparative cohorts, the median follow-up ranged from 4.6 months for the diuretic cohort to 14.7 months for the ACEi/ARB cohort. Similarly, on average, the diuretic cohort had the shorter follow-up (mean 19.5 months) and the ACEi/ARB the longest (mean 30.5 months). In the overall cohort, 204 deaths (0.09% of included patients) were observed before the end of the follow-up. Lost to follow-up is considered minimal: in the UK, patients are followed over a long time by their general practitioners who is the primary care contact person. In CPRD, the average duration of follow is of 5.1 years [24]. Description of the cohort prior and after matching is presented in parent paper [3].

Inverse probability of censoring weights

Model selection

Glycated hemoglobin and heart rate were dismissed on grounds of high percentage of missing value (>80%). Handling of missing is described in Appendix 1, Section A.1.2.1. No variable was rejected on grounds of nonsignificant association with T2DM. Some known relations were retrieved, e.g., the protective effect of alcohol against diabetes. Expected demographic and clinical variables were retained: age at baseline, sex, BMI at baseline, systolic blood pressure (time dependent), onset of dyslipidemia (time-dependent variable); core variables used to model censoring also included: alcohol misuse at baseline, use of platelet aggregation inhibitor at baseline, glomerular filtration rate at baseline. No strong departure from proportional hazards assumption was identified after inspection of Schoenfeld residuals during model selection process.

Weights distribution & performance

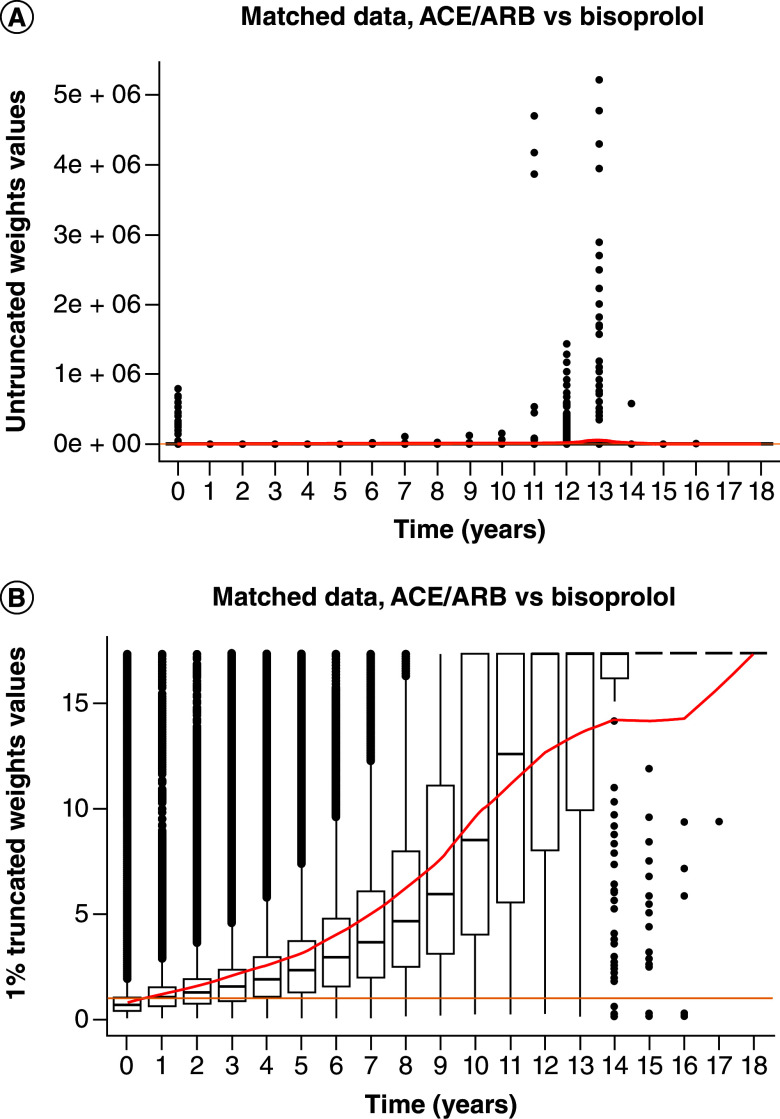
The weights behaved identically in all treatment groups (Supplementary materials). Hereinafter, only the comparison between ACEi/ARB and bisoprolol is presented. Without truncation, weights reached extreme values especially after 10 years (Figure 2A). The 1% truncation (Figure 1B) allowed to cut off extreme values and keep weights mean inferior to 10 for the first 10 years; greater truncations did not seem to provide a substantial benefit in terms of expected values of the weights – (Table 1).

Figure 2. . Weights distribution (angiotensin conversion enzyme/angiotensin receptor blocker vs bisoprolol matched data).

In red: weight's mean; in orange: y = 1. (A) Untruncated weights; (B) 1% truncation; mean departure from one is indicative of inverse probability of censoring weight assumptions violations.

Figure 1. . Cohort design.

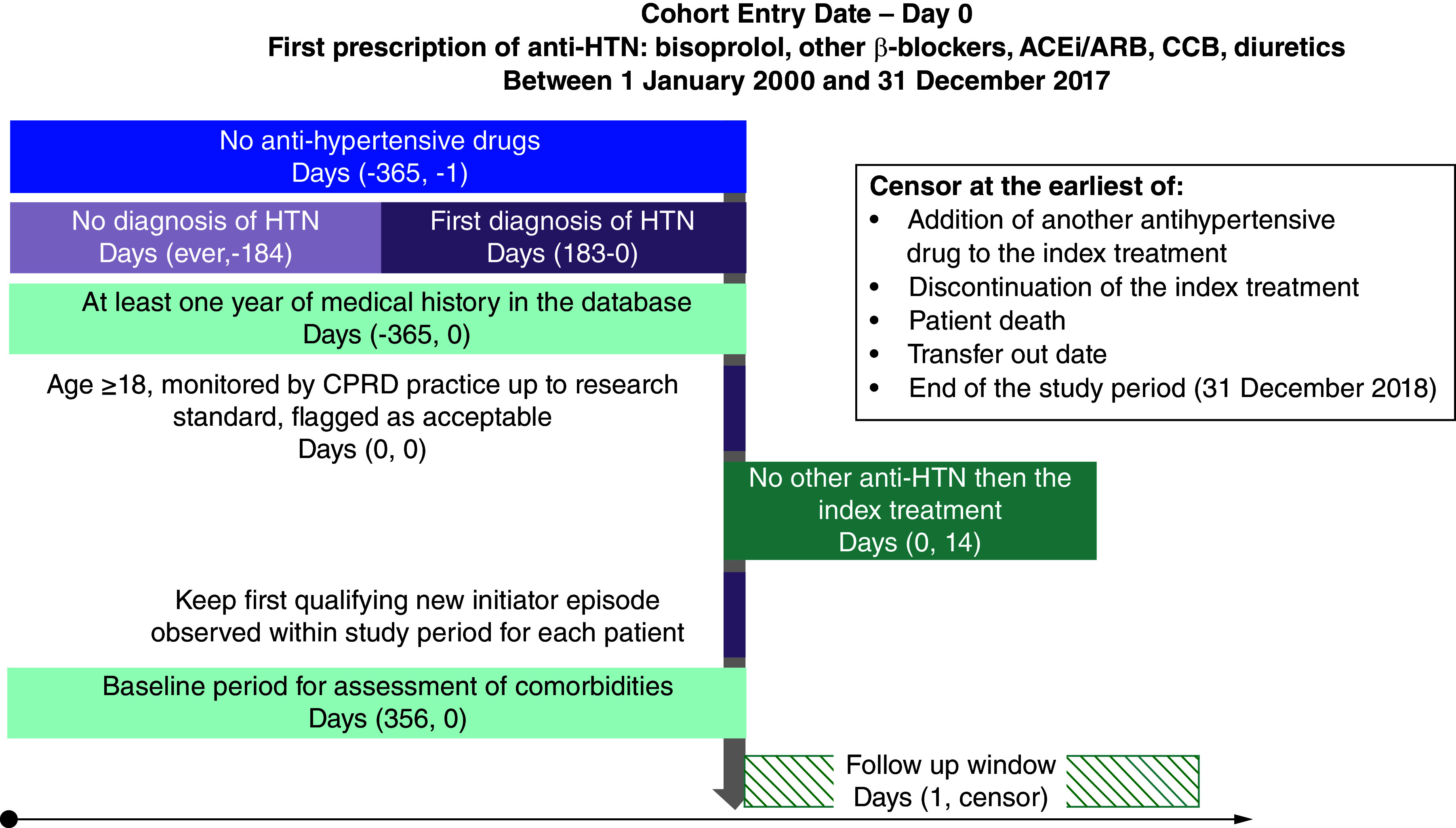
ACEi: Angiotensin conversion enzyme inhibitor; ARB: Angiotensin receptor blocker; CCB: Calcium-channel blockers; CPRD: Clinical Practice Research Datalink; HTN: Hypertension.

Table 1. . Overall weight means in ACE/ARB matched data.

Weights	Mean (ACE/ARB matched group)
Untruncated	54.42
1% truncation	1.49
5% truncation	1.23
10% truncation	1.12

ACE: Angiotensin conversion enzyme; ARB: Angiotensin receptor blocker.

Kaplan–Meier curves: magnitude of dependent censoring bias

Weights were first used to plot weighted Kaplan–Meier curves. (Figure 2). For all groups and during early follow-up, untruncated weights KM curves appear atop the unweighted KM curves, suggesting a modest overestimation of the T2DM incidence in the latter case. Effect is persistent beyond 5 years (∼1800 days) for ACEi/ARB, CCB and OBB while it fades off for diuretics and bisoprolol. Other curves are available in Supplementary materials.

Approximately 50% of patients are censored within the first 2 years of follow-up. The decreasing number of patients led to large confidence intervals after 5 years, especially for untruncated weights. Furthermore, abrupt breaks observed several times are most likely the result of the worsening stability of weights along time and primarily affect the untruncated weights' curves. Assessing the effect of IPCW from KM curves ought to consider this heterogeneous distribution of censoring events.

Weighted Cox PH models

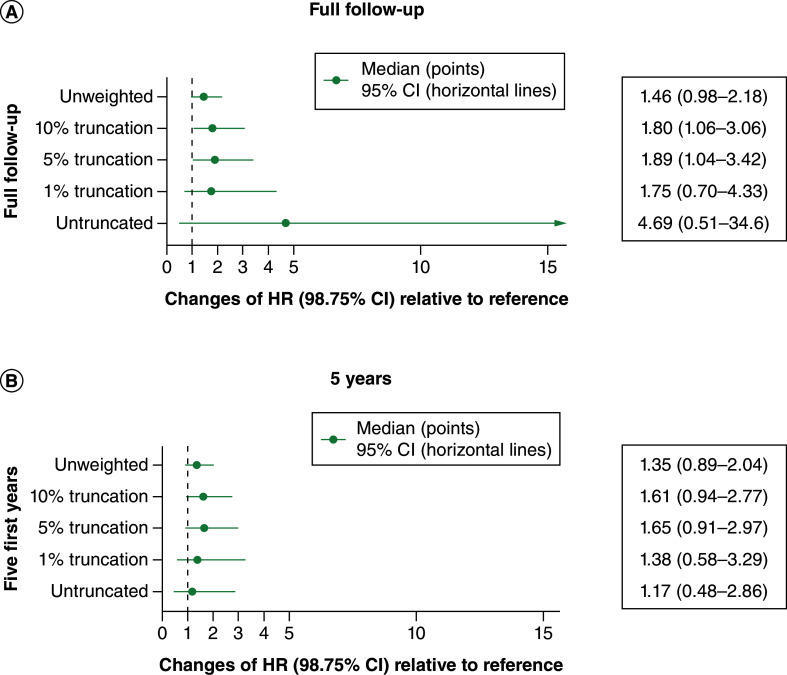
The high variance of untruncated and 1%-truncated weights resulted in large confidence intervals around HRs (Figure 4A). In ACEi/ARB versus bisoprolol comparison, a trend toward an excess of T2DM risk was observed. Even though the untruncated weights provide an asymptotically unbiased estimation, its large CI (0.51; 34.60) hindered drawing direct conclusions. Truncated weights did provide comparable HR point estimates around 1.8 versus 1.46 for unweighted model with their respective CI having similar range. Schoenfeld residuals displayed a slightly increasing T2DM risk associated with ACE/ARB, when compared with bisoprolol. This departure from proportional hazards, although minor, rises as truncation increases.

Figure 4. . Hazard ratios for angiotensin conversion enzyme inhibitor/angiotensin receptor blocker matched data.

(A) Full follow-up. (B) First 5 years.

CI: Confidence interval; HR: Hazard ratio.

Considering weights' performance and Kaplan–Meier curves, additional Cox models were fitted on a restricted period of time. While the trend toward an excess of risk associated with ACE/ARB is already recorded at 5 years, no significant differences is observed (Figure 3B).

Figure 3. . Inverse probability of censoring weight Kaplan–Meier curves comparing angiotensin conversion enzyme/angiotensin receptor blocker to bisoprolol.

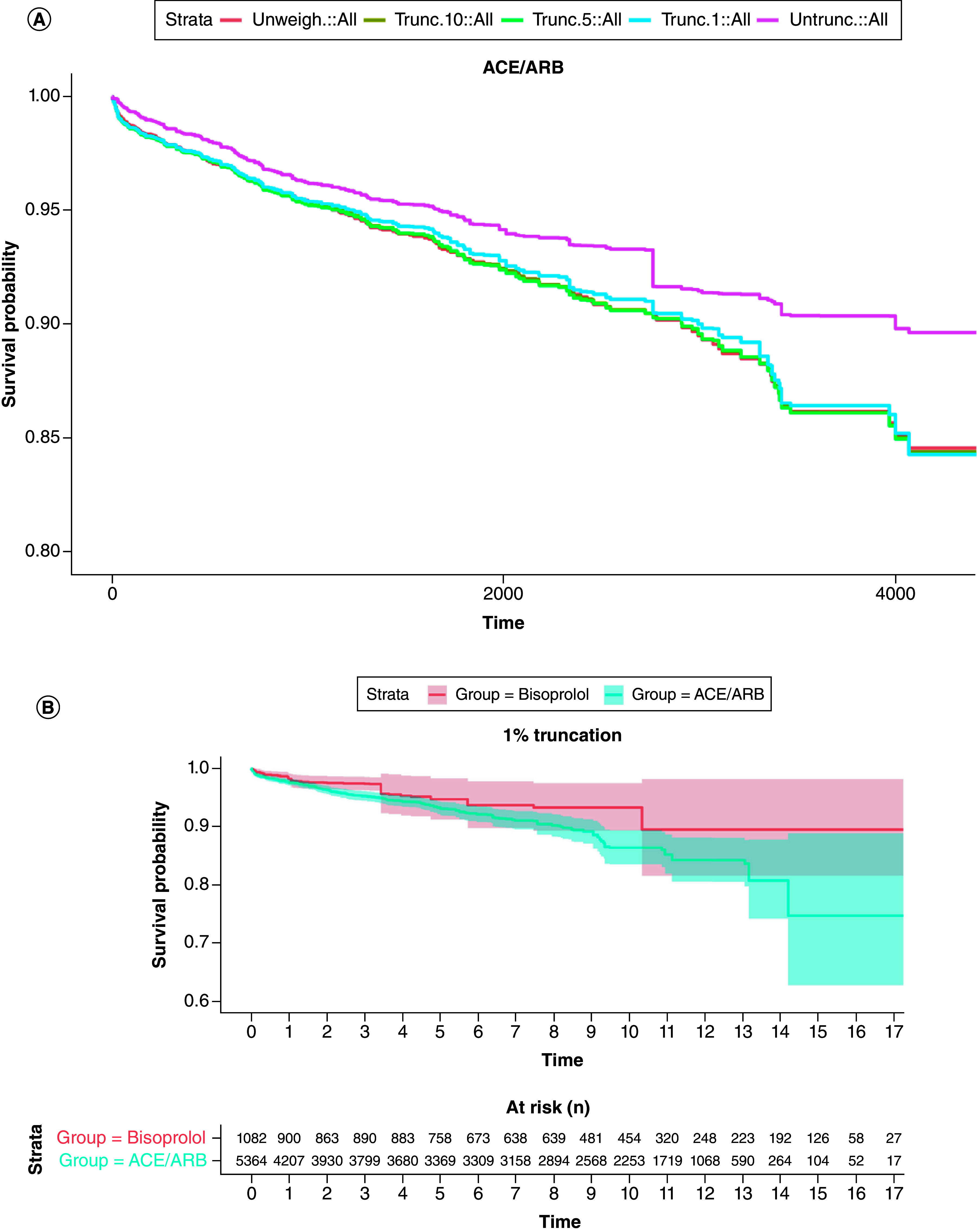
(A) Inverse probability of censoring weight (IPCW) Kaplan–Meier curves, with different weights' truncations, first 10 years of follow-up; untruncated weights (purple) provide the greatest mitigation of censoring, when compared with unweighted Cox model (x-axis unit is days; y-axis cropped at 0.8). (B) 1% truncated IPCW weighted Kaplan–Meier curves comparing bisoprolol and ACEi/ARB, numbers at risks described are similar for other IPCW curves.

ACE: Angiotensin conversion enzyme; ARB: Angiotensin receptor blocker.

Competing risk analysis (‘while-on-treatment’ estimand)

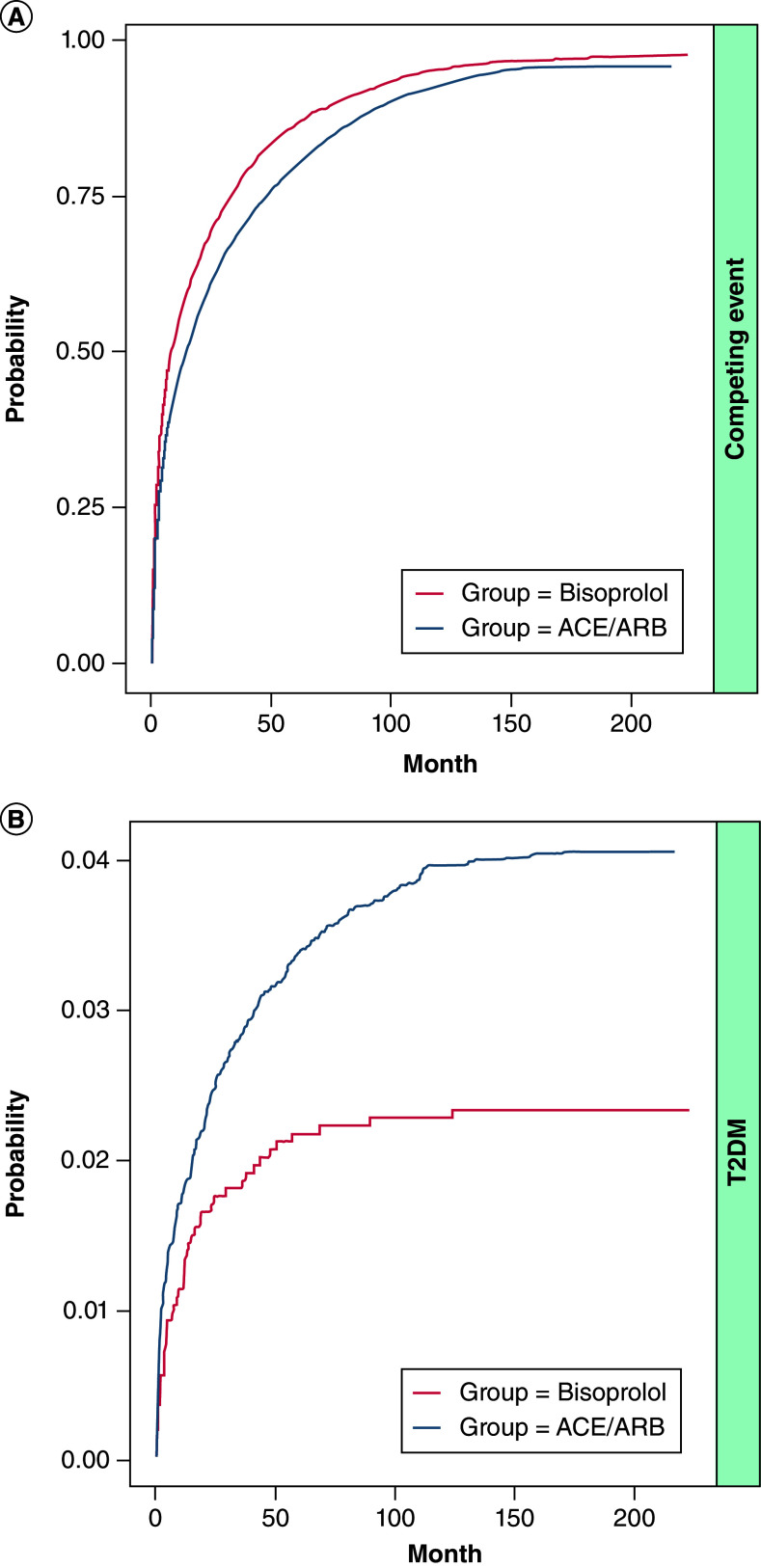
The ACE/ARB treatment group was associated with a higher probability of T2DM compared with bisoprolol (Table 2): the statistically significant subdistribution hazard ratio (SHR) confirmed the clear separation of CIFs (SHR[98.75%CI] = 1.75 [1.18;2.61]). A similar effect, albeit nonsignificant, was displayed by the cause specific hazard ratio (CSH[98.75%CI] = 1.46[0.98;2.18]). Concerning the competing event: deviations from monotherapy and deaths were combined together. The ACE/ARB treatment group was at lower risk of censoring as illustrated by nearly identical CSH and SHR (0.82[0.77;0.88] and 0.80[0.75;0.86], resp.); associated CIFs (Figure 5) confirmed the lower incidence, with the slight lag displayed by the ACE/ARB curve.

Table 2. . Competing risks results ACE/ARB versus bisoprolol.

Model	Estimator	Event	HR (98.75% CI)
Cox	CSH	T2DM	1.46 (0.98, 2.18)
		DFM	0.82 (0.77, 0.88)
Fine & Gray	SHR	T2DM	1.75 (1.18, 2.61)
		DFM	0.80 (0.75, 0.86)

CI: Confidence interval; CSH: Cause-specific hazard; DFM: Deviation from monotherapy; HR: Hazard ratio; SHR: Subdistribution hazard ratio; T2DM: Type 2 diabetes mellitus.

Figure 5. . Cumulative incidence functions.

(A) Deviation from monotherapy. (B) Type 2 diabetes.

ACE: Angiotensin conversion enzyme; ARB: Angiotensin receptor blocker; T2DM: Type 2 diabetes mellitus.

Discussion

Interpretation

A consistent effect was found in all groups: weighted KM curves showed slightly reduced incidence of T2DM compared with the unweighted curve. This suggests that a moderate dependent censoring bias may be at work, suggesting that individuals being censored were slightly less likely to develop T2DM. The ‘hypothetical’ estimand yielded by IPCW identifies a trend toward an excess of T2DM linked to ACEi/ARB.

This finding is in line with the ‘while-on-treatment’ estimand yielded by the competing risks analysis which consistently identifies the same trend, while also highlighting that patients treated by ACEi/ARB tend to a have a longer exposure to their treatment. In both analyses, no differences in terms of T2DM were to be found when comparing bisoprolol to either CCI, diuretics, or other beta-blockers.

These two strategies used their own estimators. While a censoring event merely prevents us from observing the outcome, a competing event precludes the outcome from occurring [25].

The ‘hypothetical’ estimand assesses a counterfactual risk, meaning a risk under the hypothetical scenario in which no patients would discontinue. It requires causal identification assumptions to link patients on treatment to patients discontinuing treatment (exchangeability, consistency, positivity) [18,26]. The ‘while on treatment’ estimand, using competing risks framework, rely on different assumptions. The framework assumes that there are multiple types of events that could potentially occur, and these events compete with each other; censoring must be non-informative [19].

In our example, while both estimands have distinct definition and construction, their estimates likewise yield a trend toward a moderately increased risk of T2DM either when considering a population of patient staying ‘on-treatment’ or a ‘hypothetical’ population of patients whom treatment would never change over 16 years. However, these findings are subject to several limitations.

A trend toward a moderately increased risk of T2DM either when considering a population of patient staying ‘on-treatment’ or a ‘hypothetical’ population of patients whom treatment would never change over 16 years. However, these findings are subject to several limitations.

Limitations

Weights construction

In our context, even though BMI and blood pressure have a valuable informational input, models could not include glycated hemoglobin on grounds of data missingness. As this is an important predictor of T2DM [13] it may result in residual confounding and prevent optimal censoring modeling. In particular, cardiovascular comorbidities were highly predictive of censoring in all groups and may have proved even more informational as time-to-event covariates. Use of directed acyclic graphs [27] (DAGs) beforehand could have proven useful to direct an even better choice of variable. However, as noted by Cole & Hernán [26], reducing confounding by feeding models with a high number of variables comes at the cost of a higher risk of positivity violations, especially if continuous variables are used. In our case, only BMI was thus kept as a continuous variable owing its paramount importance in T2DM and cardiovascular disease development. A bootstrap estimator for diagnosing departure from experimental treatment assignment assumption in IPTW – analog to the positivity assumption of IPCW – have been previously proposed [28,29]. An adaptation to IPCW may provide a valuable tool to assess violation occurrence and provide enhancement to weight modeling. However, the implementation seems not overly trivial and possibly requires high computational resources. Furthermore, it does not seem to address positivity violations occurring in a longitudinal context.

No validation of Cox models was carried out to ascertain prediction accuracy; an external validation or using remaining unmatched patients of the cohort might have support the reliability of the censoring modeling.

Weights performances

After 5 years, a progressive departure from the expected value 1 is consistently observed, with weights taking extreme values after 10 years of follow-up. This happens in all treatment groups and is related to the decreasing number of patients after 2-years of follow-up (mean FU = 1 year; median FU = 2 years). Applying truncations in order to restore a suitable behavior comes with a bias-variance tradeoff. Untruncated weights are (asymptotically) unbiased and are thus providing the best correction of dependent censoring [15]. Hence, an increasing truncation entails a lesser correction of the selection bias: the narrower variability comes at the price of a weaker correction of dependent censoring.

Other limitations

Beyond IPCW caveats, other phenomena may affect the results. All weighted Cox models suffer from a departure from the proportional hazards assumption as shown by Schoenfeld residuals: ACE/ARB diabetes risk is slightly increasing over time while bisoprolol's is not. This effect is more pronounced in unweighted Cox model and 10% and 5% truncated weights than in untruncated and 1% truncated weights.

Furthermore, some limitations can be applied to both estimands. First, the initial balance between treatment groups established through baseline propensity score matching may dispel over time and it is likely that some confounding may reappear after, for instance, 10 years of follow-up. An additional, hypothetical, source of ambiguity might be linked to the composite nature of the ‘deviation of monotherapy’ event: discontinuation, switch and ‘additional prescription’ may each be uniquely associated with T2DM or explanatory variables. Hence, melting them as one unidimensional event might lead to inaccuracy in the modeling of censoring. For instance, it can be supposed that elderly (>80 years) are more likely to discontinue treatments than to be prescribed with another medicine: association between each modality and the explanatory variable (age) may have different distributions. Although providing more precision, taking into account three separate events would first come at the cost of another complexity layer to interpret competing risk model and would secondly induce an additional and challenging implementation burden.

Hence, this study yields conflicting results in light of the previous knowledge from the medical literature [4–6,11,30]. Cause for this discrepancy remains unclear. The study design and the statistical expedients together with the large sample size and number of variables, are providing a reasonable degree of trust in the mitigation of confounding and of potential others bias. For instance, indication and protopathic bias are unlikely given the longitudinal design combined with the 1 year of exposure washout ensuring new users recruitment.

Conclusion

This study illustrates the benefit of using different estimands yielding complementary interpretations of results and strengthening clinical conclusions. IPCW results are consistent with findings of the competing risks analysis, which also show a lengthier treatment exposure in this latter group. IPCW analysis identified a modest dependent censoring, mainly affecting healthy patients in the ACEi/ARB group; a trend toward an excess of T2DM associated risk seems associated with ACEi/ARB exposure, when compared with bisoprolol. This finding concerning the ACEi/ARB comparison is nevertheless discordant with previous literature and calls for further investigations.

Summary points

• Design: an active-comparator new-user cohorts of patients initiating hypertensive treatments in monotherapy.

• Outcome: Type 2 diabetes mellitus.

• Potential bias: dependent censoring when patients discontinued monotherapy.

• Two estimands strategies to address this potential bias.

• First ‘on-treatment’ estimand, via competitive risks models with discontinuation being considered as a competing risk.

• Second ‘hypothetical’ estimand via inverse probability of censoring weights.

• Results were consistent between the two estimands.

• No significant differences in the risk of diabetes were found between bisoprolol and either diuretics, other beta-blockers or calcium-channel blockers. A nonsignificant trend toward an excess of risk with angiotensin conversion enzyme inhibitor/angiotensin receptor blocker was observed.