Abstract
Background
In May 2024, a chickenpox outbreak was reported at Xiasha Primary School located in Nanshan District, Shenzhen City, China, with a total of 12 cases identified. Despite thorough on-site investigations, the source of infection remained undetected. The purpose of our study was to infer the timing and duration of the infectious period of the initial case using modeling techniques, thereby deducing the identity of the source.
Methods
We conducted an individual contact survey within the class affected by the epidemic and utilized an agent-based model (ABM) to estimate the key parameters related to the timing of the infectious source’s emergence and the duration of its infectiousness. The point estimates derived from the ABM served as prior information for a subsequent Bayesian analysis, which in turn provided the posterior distribution for these parameters.
Results
Our models suggested the infection source entered the classroom around April 24th (95% credible interval: April 22nd to April 26th), with an infectious period of approximately two days. Based on these findings, we should aim to detect students who may have been absent due to atypical chickenpox symptoms during this period and closely examine teachers who were present for two consecutive days for any indication of potential infection.
Conclusion
This study demonstrates the efficacy of combining contact surveys with mathematical modeling for outbreak source tracing, offering a novel approach to supplement field epidemiological surveys.
Clinical trial number
Not applicable.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12879-024-10127-3.
Keywords: Chickenpox outbreak, Source tracing, Agent-based model, Bayesian analysis
Background
Chickenpox, an acutely infectious illness, is caused by the varicella-zoster virus (VZV). Its hallmark manifestation is an eruptive rash that evolves into intensely itchy, vesicular lesions, which subsequently crust over [1]. However, following the recommendation and routine use of the chickenpox vaccine, there has been a significant increase in cases that exhibit an atypical presentation of the disease, posing difficulties in confirming a clinical diagnosis [2]. While chickenpox is commonly viewed as a benign childhood ailment, it can lead to severe complications, including pneumonia, encephalitis, cerebellar ataxia, and in rare cases, it can be fatal [1, 3]. Chickenpox is transmitted mainly through airborne respiratory droplets and direct contact with skin lesions, which is highly contagious, leading to a persistent and significant global health burden [4]. In China, the disease burden from chickenpox has been on an upward trajectory in recent years. The number of reported cases has seen a dramatic rise from 327,054 in 2010 to 981,699 in 2019, indicating a threefold increase over the past decade [5]. However, it is estimated that the actual rate of chickenpox cases is significantly higher, with an underestimation rate of approximately 71% [5].
The transmission dynamics of infectious diseases like chickenpox are governed by various factors related to human activities. Key among these are the contact networks of the host population and the dynamics of human mobility [6–11]. Human mobility, especially, has a profound impact on the spread of epidemics and significantly accelerates the rate of disease transmission [12–16]. Thus, inferring the sources of infectious diseases by studying human activities is a methodologically feasible approach.
For epidemiologists, identifying the primary case in a chain of infections is vital as it helps elucidate the outbreak’s genesis, its transmission dynamics, and provides guidance on how to avert future outbreaks. However, in chickenpox outbreaks within school-like environments, identifying the initial source of infection often proves elusive. This difficulty arises partly because the spread may originate from individuals with asymptomatic infections or atypical symptoms [2, 17, 18], which are hard to identify through symptom-based screenings. Additionally, the source might be transient visitors whose brief presence leads to secondary infections within the school, but they have departed by the time of the investigation. Genetic analysis of viral populations within hosts is essential for identifying transmission clusters [19], but tracing the direction of transmission during outbreaks is complicated by the complexities of viral evolution. In recent years, researchers have developed a probabilistic model to map disease transmission [19, 20], simulating the genetic evolution of viruses between directly linked cases. Yet, the success of this method in pinpointing the primary case depends on the initial case being sampled.
When epidemiological investigations cannot identify the source of infection, employing mathematical models to infer the emergence time and duration of the infectious source in relevant settings can offer clues for tracing the infection. In May 2024, a chickenpox outbreak occurred at Xiasha Primary School in Nanshan District, Shenzhen City, China, exhibiting a clear clustering pattern. The school reported a total of 12 cases, with 10 cases in Class 6 (1) and 2 in another class. At the time of writing, the outbreak has been resolved. The investigation concluded that the 10 cases in Class 6 (1) were secondary, with disease onset within the shortest incubation period, yet the infection source remained unidentified.
This study aims to deduce the timing of the primary case’s emergence and its infectious duration to identify the source of infection. We conducted an individual contact survey in Class 6 (1) at Xiasha Primary School. Utilizing data on student interactions, we employed an agent-based model (ABM) [21, 22] to estimate the parameters associated with the infectious source’s appearance time and the duration of infectiousness. This was achieved by minimizing the discrepancy between the simulated and actual sequences of disease onset times. These initial estimates provided prior information for a Bayesian model, which then estimated the posterior distribution of the parameters. The use of these methods allowed us to account for the complexities of human interactions and the dynamics of disease transmission within the school environment. Consequently, we were able to infer the origins of the chickenpox outbreak in Class 6 (1).
Materials and methods
Basic school information
To provide a comprehensive understanding of the context in which this study was conducted, it is essential to first introduce the school where the research took place. Xia Sha Primary School, located in Xia Sha Community, Sha Tou Street, Futian District, Shenzhen, is a full-time six-year public school. It is situated at No. 88 Furong Road and covers an area of 10,538.13 square meters, housing 54 functional rooms. The school currently has 36 teaching classes with 1,568 students and a faculty of 120 members.
Chickenpox outbreak data
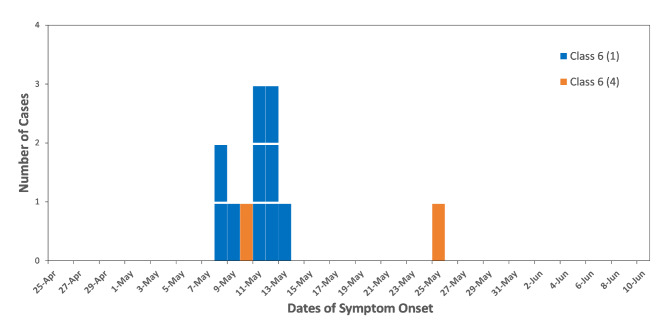
On May 13, 2024, the CDC of Futian District was notified of an outbreak at Xia Sha Primary School. Between May 8 and 12, numerous students in Class 6 (1) developed systemic rashes, suspected to be an outbreak of chickenpox. On the day of the report, the CDC team visited the school to manage the situation. They collected case registration information from the school’s medical staff and conducted individual case investigations, following the standard principles of outbreak investigation for chickenpox as recommended by the U.S. CDC [23]. This included gathering data on the onset time, clinical symptoms, and the duration of the students’ presence at school after symptom onset. Since cases were concentrated in Class 6(1), a focused case search was conducted in this class from April 24th, which is one average incubation period prior to May 8th, the day when the first secondary case developed symptoms. Despite these efforts, the initial case was not identified through symptom screening. Subsequent laboratory tests confirmed the outbreak as chickenpox. The CDC of Futian District initiated case monitoring, and the last case was reported on May 25. A total of 12 chickenpox cases were reported at Xia Sha Primary School, 10 in Class 6 (1) and 2 in Class 6 (4). The epidemic curve is depicted in Fig. 1. According to the epidemic curve, we inferred that the 10 cases in Class 6(1) were all second-generation cases, as their onset of symptoms fell within the shortest incubation period. The case in Class 6(4) on May 25th was likely a third-generation case in the entire outbreak, with the probable source of infection being the case in Class 6(4) that occurred on May 10th.
Fig. 1.
Epidemic curve of chickenpox outbreak at Xia Sha primary school
Contact investigation
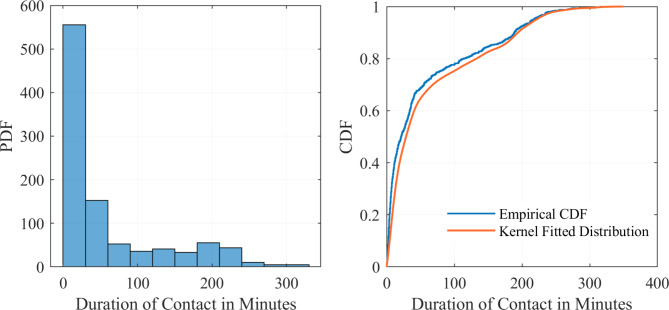
As the initial case was not identified through symptom screening, the Shenzhen CDC aimed to deduce the characteristics of the primary case through mathematical modeling. On June 7, the Shenzhen CDC conducted a supplementary investigation at Xia Sha Primary School to collect individual student contact data. All 46 students in Class 6 (1) were equipped with a contact signal receiving device based on UWB (Ultra Wide Band) wireless communication technology. This device can send and receive extremely narrow pulses at the nanosecond level to record the ID and duration of contact between individuals. The devices were set to record contacts within a 2-meter range, capturing interactions throughout the students’ school day. To clarify, we define ‘contact’ as any instance where two individuals are in proximity within a 2-meter range, reflecting the airborne transmission characteristics of respiratory viruses. After analyzing the contact data, it was found that each student interacted with other class members daily. Based on the empirical distribution of contact durations—the cumulative contact times for each unique pair of individuals—a kernel distribution was fitted. The goodness-of-fit for this distribution was then tested using a chi-square test (χ2 = 9.4326, P = 0.3983). The fitting results are illustrated in Fig. 2. The contact survey utilized in this study was specifically developed for the investigation of the chickenpox outbreak at Xiasha Primary School. The survey was tailored to detail classroom interactions, with full methodology in the Supporting Information.
Fig. 2.
Empirical and kernel fitted distributions for contact duration. The y-axis indicates the probability density function(PDF) or cumulative distribution function(CDF) associated with the contact duration values
Incubation period distribution
The incubation period for infectious diseases is often assumed to follow one of three distributions: Gamma, Lognormal, and Weibull. In this study, we utilized the Gamma distribution to model the incubation period of chickenpox. According to the U.S. Centers for Disease Control and Prevention, the shortest reported incubation period for chickenpox is 10 days, while the longest is 21 days, with an average between 14 and 16 days [23].
 |
1 |
 |
2 |
We employed the probability density function of the Gamma distribution (1) and solved a set of Eq. (2) to determine the distribution’s parameters, 
and 
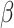. The calculated values are 28.4010 for 
and 0.5282 for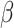 
. The Gamma (28.4010,0.5282) has an expected value (mean) of 15, with the 2.5th percentile at 10 and the 97.5th percentile at 21. These statistical characteristics closely match the incubation period data provided by the U.S. CDC.
Vaccine efficacy
The vaccination records for chickenpox among students of class 6 (1) at Xiasha Primary School were obtained during the on-site investigation conducted by the Futian CDC and verified against the Shenzhen Immunization Information Management System. Results showed that 9 students, representing 19.57% of the class, were unvaccinated, and 6 of them became ill. Among the 20 students, or 43.48%, who received a single dose of the vaccine, 4 developed chickenpox. In contrast, none of the 17 students, accounting for 36.96%, who completed the two-dose vaccination regimen reported a case. We conducted a univariate logistic regression analysis, which revealed that the odds ratio (OR) for vaccination was 0.06 (vaccinated vs. unvaccinated). This indicates a 94% decrease in the risk of chickenpox infection for vaccinated individuals within the class. The regression coefficient 
for vaccination in the logistic regression model is -2.8034, with a variance of 0.8833. Therefore, we assume that the regression coefficient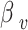 
follows a normal distribution N(-2.8034, 0.8833). In the Agent-Based Model, the vaccine’s protective effect is reflected by the OR value. However, this value is not fixed; it is derived by drawing a random value for 
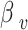from the normal distribution N(-2.8034, 0.8833) and then converting it into an OR value, calculated as 
.
Epidemic stages
The chickenpox outbreak at Xiasha Primary School, Class 6 (1), can be categorized into two distinct stages. Initially, the introduction of the infectious source into the class resulted in 10 secondary cases. In the subsequent phase, from the emergence of these secondary cases until the outbreak was contained, no tertiary cases occurred in Class 6 (1). It is important to note that during the latter stage, parameters associated with transmissibility are indistinguishable; assigning a value of zero or any negligible value to these parameters could account for the absence of tertiary cases. Consequently, this study concentrates solely on the first stage of the epidemic. The model simulates the period from the infectious source’s entry into the class to the appearance of secondary cases and estimates the timing and duration of the infectious source’s presence.
Agent-based model (ABM)
Individual status
In this model, we focus solely on the first phase of the epidemic. During this phase, individuals can be categorized into four distinct states: S (Susceptible), E (Exposed), I (Secondary Infectors), and I0 (Infection Source). I0 is capable of spreading the infection. When susceptible individuals (S) come into contact with I0, they have a certain probability of being infected, thus entering the E state. The progression from the E state to the I state hinges on the individual’s incubation period, which is determined by a random draw from the Gamma distribution mentioned in Sect. 2.4. Once I0 has passed through his/her infectious period, which is an estimated parameter within the ABM model, they cease to be contagious. Since the model does not account for the second phase of the epidemic, it does not incorporate the infectivity of I (Secondary Infectors). Additionally, considering the outbreak’s timing near the Chinese Labor Day holiday, the model takes into account the holiday and weekend factor, stipulating that contact between S and I0 can only occur on school days, while the transition from the E state to the I state is allowed at any time, including holidays and weekends.
Infection probability function
We have developed a function that correlates the infection probability with the contact time 
(the duration of interaction between S and I0 within a classroom setting), factoring in the protective effects of vaccination. Given that the probability function outputs values between 0 and 1, and we have tailored our model to increase the infection probability with contact time, the sigmoid function emerges as a logical and effective choice for our purposes [24].
 |
3 |
In formula (3), the sigmoid function is represented on the first part of the right side, with parameters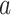 
and 
. Parameter 
signifies the infection probability when contact time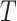 
is zero, essentially the baseline community infection rate. Drawing data from the National Notifiable Infectious Diseases Surveillance System (NNIDSS), the chickenpox incidence rate in Shenzhen city for the year 2023 is 0.00058. By calculating 
, we determine the daily community infection probability 
to be 1.6443 × 10−6, which is then assigned to 
. Parameter 
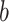, an estimated parameter in the ABM model, is associated with the transmissibility of the disease. A higher value of 
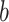, with a constant 
, indicates a faster convergence of the function value towards 1. This implies that for a given contact time 
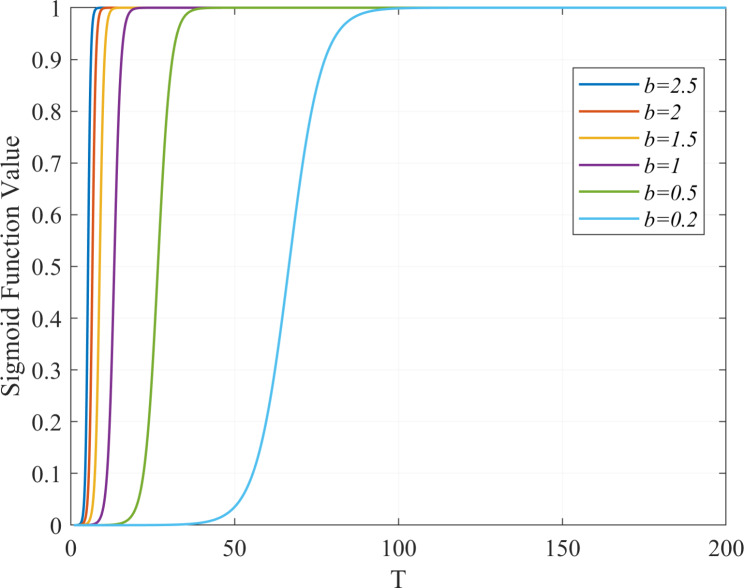
, a larger 
value results in a higher likelihood of infection for susceptible individuals (S), as depicted in Fig. 3. The 
component of formula (3) accounts for the vaccine’s protective influence as discussed in Sect. 2.5. In summary, formula (3) presents a continuous infection probability function. For vaccinated individuals, the infection probability varies continuously from 0 to 
, whereas for unvaccinated individuals, it ranges from 0 to 1.
Fig. 3.
Impact of parameter b on the sigmoid function value with parameter a fixed
Parameters estimation
In our Agent-Based Model, we have defined three key parameters essential for the simulation:
Parameter b
This is the infectivity-related parameter within the sigmoid function described in Sect. 2.7.2.
Parameter dayselapse
This parameter is related to the appearance time of the infection source. Given the first secondary case onset date of May 8th, by considering the shortest and longest incubation periods, we estimate the emergence of the infection source to be between April 17th and April 28th. The parameter represents the number of days from April 17th to the appearance of the infection source, with a range set from 0 to 11.
Parameter duraI0
This denotes the duration for which the infection source remains infectious. Based on literature, the contagious period for chickenpox generally lasts for 7 days [25–27]. Accordingly, we set the parameter to range from 0 to 7 days.
The model operates iteratively on a daily basis, thus the time within the model is discrete. Both 
and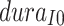 
are set as integers to reflect this discretization. We set the model’s runtime to commence from the emergence of the infection source, which is determined by the parameter 
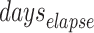, and extend it until May 21st, which is seven days after the last case in Class 6(1) was reported. The length of time the infection source remains in the classroom in our ABM simulations depends on the parameter 
. The loss function of the ABM is defined as the sum of squared residuals between the model’s predicted daily new cases and the actual values. Due to the stochastic nature of the simulation process, the same set of parameters can yield different outcomes upon repeated runs. To mitigate this, we run each parameter set 100 times and calculate the average number of daily new cases from the 100 simulated incidence sequence. We then compare the average incidence sequence with the actual values and calculate the loss. Considering the integer constraints on 
and 
within the model, we employ the surrogate optimization algorithm [28–30] to find the minimum of the loss function and the point estimates for the respective parameters.
Simulation process of ABM
Here, we briefly describe the simulation process of the Agent-Based Model. Initially, we establish a classroom with 46 individuals, 37 of whom have been vaccinated. We introduce a single source of infection within the classroom. Based on contact investigation, this individual can potentially interact with all other members of the class. The duration of these interactions is randomly assigned from the kernel distribution outlined in Sect. 2.3. The probability of infection for the contact is calculated through formula (3). Then, through a Bernoulli experiment, it is determined whether the contact is infected and enters the E (exposed) state. For those who enter the E state, the duration of the incubation period is randomly assigned according to the distribution detailed in Sect. 2.4. Once the incubation period elapses, individuals transition from the E state to the I state. This daily process is iteratively carried out, with the emergence of new infections being recorded. The simulation continues until it reaches a predetermined number of days.
Bayesian model
Due to the integer constraints on the parameters and the nature of the surrogate optimization algorithm, our Agent-Based Model estimated the point values of the corresponding parameters but did not provide confidence intervals for them. To address this limitation, we adopted a Bayesian approach for modeling. The parameter estimates from the ABM served as prior information for the Bayesian model. While the ABM simulated the entire Class 6 (1), the Bayesian model focused specifically on modeling the onset time distribution of 10 secondary cases. The basic formulation of our model is as follows:
 |
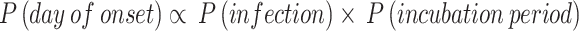4 |
In this formula, P(day of onset) represents the probability of a case developing symptoms on a given day. P(infection) is the probability of an individual becoming infected, as formulated in Eq. (3), but does not account for vaccination effects, which are present in Eq. (5) with the exclusion of the vaccine’s odds ratio.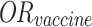 
, derived from class-wide survey data, is suitable for simulating the entire population but becomes less appropriate when modeling a specific subset of 10 cases. Applying Eq. (3) suggests that the probability of observing this particular sample of 10 cases would be less than (
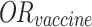)4, indicating a significantly low likelihood. Given that we know 4 vaccinated individuals did become ill, we can assume that these individuals did not benefit from the vaccine’s protective effect. 
is the probability density function (PDF) that describes the likelihood of the incubation period lasting for a given number of days.
 |
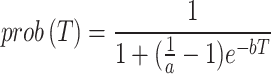5 |
Parameter estimation
The model is set with four parameters:
The time-related parameter for the appearance of the infection source,
∈(0 1). Since the infection source may appear within a time frame from April 17th to April 28th, spanning 12 days, 12×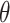
represents the number of days from April 17th to the appearance time.The duration-related parameter for the persistence of the infection source,
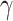∈(0 1). Given that the infectious period for chickenpox cases is 7 days [25–27], 
denotes the duration of the infection source’s presence in days. This duration is relatively short, leading us to assume that the 10 cases were infected at the same time.The daily contact time between the infection source and secondary cases,
, and 
represents the cumulative contact time in minutes between the infection source and secondary cases.The parameter related to the infection probability function,
, which is consistent with the ABM model.
Prior distribution of parameters
Since 
and 
are bounded between 0 and 1, the beta distribution is a natural choice for their prior distribution. We set the mode of the beta distribution to correspond to the converted point estimates of the ABM parameters ‘
’ and ‘
’, respectively. The prior distribution for 
is the kernel distribution described in Sect. 2.3. For the parameter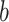 
, we assume a normal distribution with the mode (mean) as the point estimate from the ABM for the same parameter, and the variance as a reasonable estimated value.
Likelihood function
The likelihood function is as follows:
 |
6 |
The distribution of the incubation period is consistent with the Agent-Based Model, following a Gamma(28.4010,0.5282) distribution. The infection date is calculated as Infection Datetime = April17th + 12×θ + 7×γ, and incubation periodi = day of onseti - Infection Datetime. So, P(incubation periodi)=gampdf(incubation periodi, 28.4010, 0.5282).
Bayesian formula
 |
7 |
The Bayesian formula integrates four independent components. D represents the onset data of the 10 secondary cases, 
is the likelihood function, and 
is the prior distribution.
Posterior sampling
We employ the Hamiltonian Monte Carlo (HMC) method, initiating with a burn-in phase where the first 200 samples are discarded to ensure convergence to the target distribution. Subsequently, we draw 1000 samples from the posterior distribution to obtain the posterior mean, standard deviation, and quantiles such as the 2.5th, 50th (median), and 97.5th percentiles for the parameters. We also conducted model diagnostics using the Gelman-Rubin convergence statistic to assess the convergence of the Markov chains in our Hamiltonian Monte Carlo (HMC) simulations.
Simulation procedure of bayesian model
From a sample of 1000 sets of posterior parameters, we calculate the infection probability, denoted as
, using Eq. (5) for each set. Subsequently, we employ a binomial distribution Bin(10, probj) to stochastically generate the number of infectors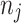 
for each set, and determine the corresponding 
through parameters
and
.We generate
incubation periods using a random draw from Gamma(28.4010,0.5282) distribution. Based on these incubation periods and the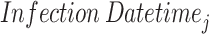 
, we ascertain the onset times for each of the 
infectors, thus obtaining the onset time series for that set of parameters.Repeat the above process (b) until we obtain the onset time series for all 1000 sets of parameters.
For the 1000 onset time series, we calculate the mean daily incidence and establish the 95% individual predictive intervals.
Results
Parameter estimation results
The ABM model’s parameter estimation yielded a result of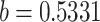 
, with 
being 8, and 
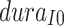being 2, suggesting that the emergence of the infection source occurred on April 25th and it remained in the classroom for 2 days. Based on the ABM’s parameter estimation results, we established the prior distributions for the Bayesian model parameters and drew 1000 posterior samples using the HMC method. The results are presented in Table 1. The Bayesian model estimated a posterior mean for 
of 0.5638, with a 95% credible interval from 0.3576 to 0.7420, indicating the emergence of the infection source on April 24th (95% credible interval: April 22nd to April 26th). The posterior mean and 95% credible interval for 
are 0.3343 (0.1084 to 0.5818), suggesting that the infection source lasted for 2.3401 days, with a 95% credible interval from 0.7588 to 4.0726 days.
Table 1.
Bayesian model parameter estimation
| Parameter | Description | Prior Distribution | Posterior Statistics | |||
|---|---|---|---|---|---|---|
| Mean | SD | P2.5 | P97.5 | |||
| θ | Related to the time of the infection source’s emergence, with the maximum density at 0.6667 (8/12) based on the value of dayselapse | Beta(2.7716,1.5905) | 0.5638 | 0.0988 | 0.3576 | 0.7420 |
|
Related to the duration of the infection source, with the maximum density at 0.2857 (2/7) based on the value of duraI0 | Beta(1.1682,2.009) | 0.3343 | 0.1294 | 0.1084 | 0.5818 |
|
Daily Contact Time Between Infection Source and Secondary Cases (minutes), following the Kernel Distribution in Sect. 2.3 |
Kernel Smoothing Function: normal Bandwidth = 7.1687 |
106.76 | 80.50 | 11.2826 | 260.8161 |
| b | Related to infectivity, with the maximum density at 0.5331 according to the same parameter in the ABM | N(0.5331,0.2) | 0.5675 | 0.1914 | 0.1784 | 0.9697 |
Model diagnostics
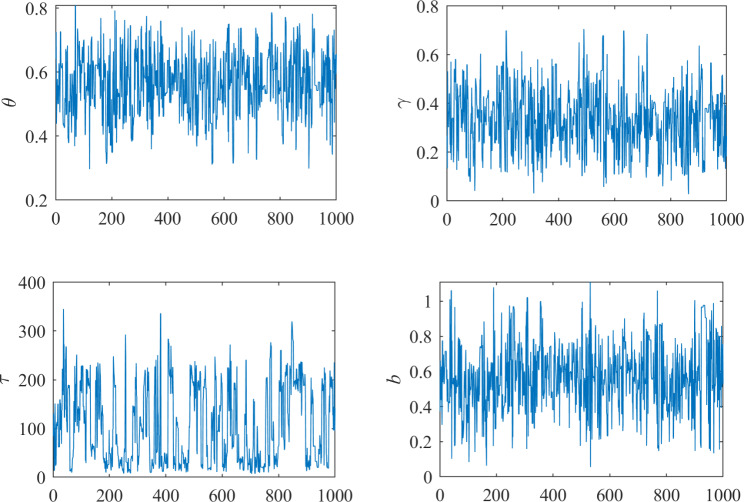
We conducted model diagnostics using the Gelman-Rubin convergence statistic for each parameter to assess the convergence of the Markov chains in our Hamiltonian Monte Carlo (HMC) simulations. The Gelman-Rubin convergence statistic(RHat) for each of the four parameters is 1, indicating that the posterior samples have converged to the target distribution, as depicted in Fig. 4.
Fig. 4.
Convergence diagnostics of Markov Chain Monte Carlo simulations
Model simulation outcomes
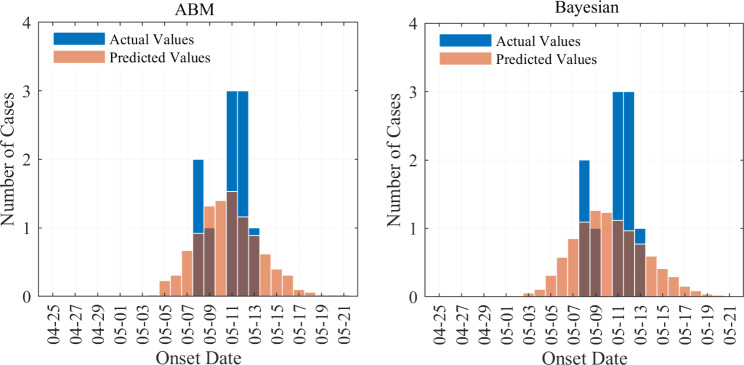
As detailed in Sect. 2.7.4 and 2.8.2, we employed both Agent-Based Modeling and Bayesian models to simulate the incidence timeline for class 6 (1). The outcomes are depicted in Fig. 5. The simulated case distributions from both methodologies are observed to cluster within the incubation phase, with a notable inclination towards a peak in the outbreak between May 8th and May 13th.
Fig. 5.
Incidence predictions by ABM and Bayesian models
Discussion
In our present research, we utilized Agent-Based Modeling and Bayesian models to deduce the origins of the chickenpox outbreak in Class 6 (1), at Xiasha Primary School. Regarding the model findings, we offer the following hypotheses concerning two specific questions.
Speculation on the identity of the infection source
Our model suggests that the infectious period of the contagion origin within the classroom was over two days. Given that chickenpox cases typically exhibit infectivity for seven days [25–27], and breakthrough infection cases for 4.5 days [25, 27], it is inferred that the source of infection in Class 6 (1) did not cease naturally but rather departed the classroom due to some cause. With the model-provided timeframe of April 22 to April 26, we should concentrate our investigation on identifying students who may have taken leave for non-specific chickenpox symptoms (atypical cases) during this period. Additionally, we should scrutinize whether any teachers who were present in the class for two consecutive days showed signs of potential infection, including herpes zoster.
Hypothesis on the lack of third-generation cases
In the course of this epidemic in Class 6(1), the primary case resulted in the infection of 10 secondary cases, yet curiously, none of these secondary cases led to the emergence of third-generation infections. This indicates a significant divergence in the transmissibility of the disease and the susceptibility of the population between the two phases. Some plausible explanations are considered: First, the initial outbreak may have significantly reduced the number of susceptible individuals, as 9 out of the class’s total were unvaccinated, with 6 falling ill. Second, the concentrated occurrence of cases in Class 6(1) from May 8th to May 13th likely heightened awareness among teachers and students, prompting the implementation of necessary protective measures such as opening windows for better ventilation and reducing contact with infected individuals, thereby exerting a certain influence on the transmissibility of the disease. Third, the model’s analysis raises the possibility that the initial case could have been a teacher, whose interactions and potential to disseminate the disease within the classroom may be distinct from those of the students.
Limitations
Primarily, our model captured only the initial phase of the epidemic in Class 6(1), which was from the introduction of the infectious source to the onset of the 10 secondary cases. When we attempted to include the second phase, spanning from the emergence of secondary cases until the outbreak was contained, and to expand our model to include the states S (Susceptible), E (Exposed), I (Infectious), Q (Quarantined), and R (Recovered), we encountered a challenge: we could not prevent the emergence of third-generation cases in Class 6(1). This led us to hypothesize that transmissibility parameters might differ between the initial and subsequent phases of the outbreak. As mentioned earlier, if we were to perform segmented simulations, the transmissibility-related parameters for the second phase would be unidentifiable due to the absence of third-generation cases in Class 6(1). Given these factors, our modeling focused exclusively on the first stage of the outbreak within this class.
Secondly, we did not consider the interactions between different classes, such as those between Class 6(1) and Class 6(4). Inter-class contact is more sporadic compared to the frequent and consistent contact within a single class, and it might require multiple repeated contact surveys to accurately reconstruct the contact patterns between specific classes. Nevertheless, we believe that omitting the 2 cases in Class 6(4) is unlikely to significantly affect the determination of the infection source, given that the outbreak initially occurred and was primarily concentrated in Class 6(1). We can be certain that the source of infection was present and lingered in Class 6(1), and therefore, by modeling the transmission within this class, we can uncover clues regarding the source of the infection.
Thirdly, environmental factors play a crucial role in the spread of infectious diseases. Including these factors in our model could potentially improve the precision of our predictions. However, we have yet to identify a viable method for measuring and quantifying the impact of environmental influences. Addressing this challenge is a priority for our upcoming research endeavors.
Conclusion
Our research exemplifies the integration of field epidemiological surveys with mathematical modeling for tracing the source of infection. Through individual contact investigations in the affected class, we deduced the timing and duration of the infectious source’s emergence, enabling further conjecture about its identity. Consequently, the integration of mathematical models provides essential supplementary insights that enhance field epidemiological studies and offer valuable information for implementing effective and efficient control measures. In the future, we aim to further refine our models by incorporating environmental factors to improve simulation accuracy and to model more complex scenarios.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
We extend our sincere gratitude to Xiasha Primary School for their invaluable support and cooperation throughout the course of this study. The school’s administration and staff demonstrated an unwavering commitment to facilitating our research, providing us with access to essential data and resources that were pivotal in the successful execution of our investigation.
Author contributions
The authors collectively contributed to the acquisition, analysis, or interpretation of data. Drafting of the manuscript was primarily conducted by Chang-Wei Liang and Qiu-Ying Lv, while critical revision for important intellectual content was performed by all authors. Statistical analysis and mathematical model constructing was undertaken by Chang-Wei Liang, Qiu-Ying Lv, Zhi-Gao Chen and Ying-Si Lai, and funding was obtained by Zhen Zhang. The final manuscript was reviewed and approved by all authors.
Funding
This study was jointly funded by the Special Foundation of Science and Technology Innovation Strategy of Guangdong Province, China (Grant No. 2020B1111340077), the Key Project of Shenzhen Science and Technology Innovation Commission (Grant No. JCYJ20210324115411030), and Natural Science Foundation of Shenzhen Municipality (Grant No. RKX20200327095612234).
Data availability
All data and mathematical model codes involved in this study are accessible from the corresponding author upon reasonable request in accordance with the Shenzhen Center for Disease Control and Prevention’s research regulations.
Declarations
Ethics approval and consent to participate
This study was conducted in accordance with the Declaration of Helsinki, reviewed and approved by the Shenzhen Center for Disease Control and Prevention Ethics Committee (SZCDCLL-[2023]028B). Informed consent was obtained from all individual participants involved in the study.
Consent for publication
There are no details on individuals reported within the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Gershon A, Breuer J, Cohen J, Cohrs R, Gilden D, Zhang Z, et al. Varicella Zoster virus infection. Nat Rev Dis Primers. 2015;1:15016. 10.1038/nrdp.2015.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dooling K, Marin M, Gershon AA. Clinical manifestations of Varicella: disease is largely forgotten, but it’s not gone. J Infect Dis. 2022;226(Supplement_1):S380–4. 10.1093/infdis/jiac390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lo Presti C, Curti C, Montana M, Bornet C, Vanelle P, et al. Chickenpox: an update. Médecine Mal Infect. 2019;49:1–8. 10.1016/j.medmal.2018.04.395. [DOI] [PubMed] [Google Scholar]
- 4.Huang J, Wu Y, Wang M, Jiang J, Zhu Y, Kumar R, et al. The global disease burden of varicella-zoster virus infection from 1990 to 2019. J Med Virol. 2022;94(6):2736–46. 10.1002/jmv.27538. [DOI] [PubMed] [Google Scholar]
- 5.Feng H, Zhang H, Ma C, Zhang HN, Yin D, Fang H. National and provincial burden of varicella disease and cost-effectiveness of childhood varicella vaccination in China from 2019 to 2049: a modelling analysis. Lancet Reg Health West Pac. 2023;32. 10.1016/j.lanwpc.2022.100639. [DOI] [PMC free article] [PubMed]
- 6.Changruenngam S, Bicout DJ, Modchang C. How the individual human mobility spatio-temporally shapes the disease transmission dynamics. Sci Rep. 2020;10. 10.1038/s41598-020-68230-9. [DOI] [PMC free article] [PubMed]
- 7.Mossong J, Hens N, Jit M, Beutels P, Auranen K, Mikolajczyk R, et al. Social contacts and mixing patterns relevant to the spread of Infectious diseases. PLoS Med. 2008;5(3):e74. 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Merler S, Ajelli M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proc Biol Sci. 2009;277(1688):557–65. 10.1098/rspb.2009.1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pardo-Araujo M, García-García D, Alonso D, Bartumeus F. Epidemic thresholds and human mobility. Sci Rep. 2023;13. 10.1038/s41598-023-38395-0. [DOI] [PMC free article] [PubMed]
- 10.Harding N, Spinney RE, Prokopenko M. Population mobility induced phase separation in SIS epidemic and social dynamics. Sci Rep. 2020;10. 10.1038/s41598-020-64183-1. [DOI] [PMC free article] [PubMed]
- 11.Ishola DA, Phin N. Could influenza transmission be reduced by restricting mass gatherings? Towards an evidence-based policy framework. J Epidemiol Glob Health. 2011;1(1):33–60. 10.1016/j.jegh.2011.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang Z, Cui A-X, Zhou T. Impact of heterogeneous human activities on epidemic spreading. Phys a. 2011;390:4543–8. 10.1016/j.physa.2011.06.068. [Google Scholar]
- 13.Meloni S, Perra N, Arenas A, Gómez S, Moreno Y, Vespignani A. Modeling human mobility responses to the large-scale spreading of infectious diseases. Sci Rep. 2011;1. 10.1038/srep00062. [DOI] [PMC free article] [PubMed]
- 14.Dalziel BD, Pourbohloul B, Ellner SP. Human mobility patterns predict divergent epidemic dynamics among cities. Proc Biol Sci. 2013;280(1759):20130763. 10.1098/rspb.2013.0763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ni S, Weng W. Impact of travel patterns on epidemic dynamics in heterogeneous spatial metapopulation networks. Phys Rev E. 2009;79(1):016111. 10.1103/PhysRevE.79.016111. [DOI] [PubMed] [Google Scholar]
- 16.Tang M, Liu Z, Li B. Epidemic spreading by objective traveling. EPL. 2009;87(1):18005. 10.1209/0295-5075/87/18005. [Google Scholar]
- 17.Dollard S, Chen M-h, Lindstrom S, Marin M, Rota P. Diagnostic and immunologic testing for Varicella in the era of high-impact varicella vaccination: an evolving problem. J Infect Dis. 2022;226(Supplement_1):S450–5. 10.1093/infdis/jiac363. [DOI] [PubMed] [Google Scholar]
- 18.Zhu YF, Li YF, Du Y, Zeng M. Epidemiological characteristics of breakthrough varicella infection during varicella outbreaks in Shanghai, 2008–2014. Epidemiol Infect. 2017;145:2129–36. 10.1017/s0950268817000772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gussler JW, Campo DS, Dimitrova Z, Skums P, Khudyakov Y. Primary case inference in viral outbreaks through analysis of intra-host variant population. BMC Bioinformatics. 2022;23:62. 10.1186/s12859-022-04585-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Longmire AG, Sims S, Rytsareva I, Campo DS, Skums P, Dimitrova Z, et al. GHOST: global hepatitis outbreak and surveillance technology. BMC Genomics. 2017;18(Suppl 10):916. 10.1186/s12864-017-4268-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Macal CM, North MJ. Tutorial on agent-based modelling and simulation. J Simul. 2017;4(3):151–62. 10.1057/jos.2010.3. [Google Scholar]
- 22.Litvinova M, Liu Q-H, Kulikov ES, Ajelli M. Reactive school closure weakens the network of social interactions and reduces the spread of influenza. Proc Natl Acad Sci U S A. 2019;116(38):13174–81. 10.1073/pnas.1821298116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.U.S. Centers for Disease Control and Prevention. Chickenpox (Varicella). Atlanta, GA: U.S. Centers for Disease Control and Prevention.2024. https://www.cdc.gov/chickenpox/index.html. Accessed 9 Sep 2024.
- 24.Dombi J, Jónás T. Generalizing the sigmoid function using continuous-valued logic. Fuzzy Set Syst. 2022;449:79–99. 10.1016/j.fss.2022.02.010. [Google Scholar]
- 25.Sharomi O, Xausa I, Nachbar R, Pillsbury M, Matthews I, Petigara T, et al. Modeling the impact of Exogenous Boosting and Universal Varicella Vaccination on the clinical and economic burden of varicella and herpes zoster in a Dynamic Population for England and Wales. Vaccines. 2022;10(9):1416–37. 10.3390/vaccines10091416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tang X, Zhao S, Chiu APY, Ma H, Xie X, Mei S, et al. Modelling the transmission and control strategies of varicella among school children in Shenzhen, China. PLoS ONE. 2017;12(5):e0177514. 10.1371/journal.pone.0177514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schuette MC, Hethcote HW. Modeling the effects of Varicella Vaccination Programs on the incidence of Chickenpox and Shingles. Bull Math Biol. 1999;61(4):1031–64. 10.1006/bulm.1999.0126. [DOI] [PubMed] [Google Scholar]
- 28.Han Z-H, Zhang K-S. Surrogate-based optimization. In: Roeva O, editor. Real-world applications of genetic algorithms. Rijeka, Croatia: InTech; 2012. pp. 344–60. 10.5772/36125. [Google Scholar]
- 29.Queipo NV, Haftka RT, Shyy W, Goel T, Vaidyanathan R, Tucker PK. Surrogate-based analysis and optimization. Prog Aerosp Sci. 2005;41:1–28. 10.1016/j.paerosci.2005.02.001. [Google Scholar]
- 30.Smith J, Doe J. Surrogate modelling for sustainable building design – A review. J Build Phys. 2019;43(2):123–40. 10.1016/s0378-7788(19)30287-7. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data and mathematical model codes involved in this study are accessible from the corresponding author upon reasonable request in accordance with the Shenzhen Center for Disease Control and Prevention’s research regulations.