Abstract
Purpose:
Current breast DCE-MRI strategies provide high sensitivity for cancer detection but are known to be insufficient to fully capture rapidly changing contrast kinetics at high spatial resolution across both breasts. Advanced acquisition and reconstruction strategies aim to improve spatial and temporal resolution and increase specificity for disease characterization. In this work, we evaluate the spatial and temporal fidelity of a modified data-driven low-rank based (MOCCO) compressed sensing reconstruction compared to compressed sensing with temporal total variation (CS-TV) with radial acquisition for high spatial-temporal breast DCE-MRI.
Methods:
Reconstruction performance was characterized using numerical simulations of a golden-angle stack-of-stars breast DCE-MRI acquisition at 5 second temporal resolution. Specifically, MOCCO was compared to CS-TV and conventional SENSE reconstructions. The temporal model for MOCCO was pre-learned over the source data whereas CS-TV was performed using a first-order temporal gradient sparsity transform.
Results:
MOCCO was able to capture rapid lesion kinetics while providing high image quality across a range of optimal regularization values. MOCCO also recovered kinetics in small lesions (1.5 mm) in line-profile analysis and error images, while g-factor maps showed relatively low and constant values with no significant artifacts. CS-TV demonstrated either recovery of high spatial resolution with reduced temporal accuracy using large regularization values, or recovery of rapid lesion kinetics with reduced image quality using low regularization values.
Conclusion:
Simulations demonstrated that MOCCO with radial acquisition provides a robust imaging technique for improving temporal fidelity while maintaining high spatial resolution and image quality in the setting of bilateral breast DCE-MRI.
Keywords: Breast, DCE-MRI, compressed sensing, dynamic imaging
Introduction
Dynamic contrast-enhanced (DCE) MRI plays an essential role in the diagnosis and staging of breast cancer1. High spatial resolution is routinely prioritized in clinical diagnostic DCE-MRI protocols to allow detection of small lesions and assessment of lesion morphology2. Historically, clinical bilateral breast MRI exams typically used multi-phase fully sampled Cartesian encoding to achieve high spatial resolution (at or below 1 × 1 mm in-plain pixel size) over the large field of view (FOV) however this allowed only limit temporal resolution (60–120 s)3. Studies have showed that a temporal resolution of 90 s or faster was sufficient to allow lesion detection and assessment prior to the occurrence of lesion washout and maximal background parenchymal enhancement that might otherwise obscure these findings in the diagnostic setting1,4. The authors also found washout-like lesion kinetics to be present in approximately 85% of cancers. However, much higher temporal resolution may enable more advanced quantitative kinetic analysis including quantitative pharmacokinetic (PK) modeling of DCE-MRI. PK modeling has shown promise in providing additional non-invasive information for differentiating benign and malignant lesions5,6 and assessing response to therapy7,8. It relies on fitting the PK model to DCE-MRI data to extract physiologic parameters, but requires very high temporal resolution (< 10 s) for the entire acquisition series to accurately do so9,10. To achieve such high levels of temporal and spatial resolution, more advanced acquisition and reconstruction approaches are needed.
Within breast DCE-MRI, the term Ultrafast Imaging has come to refer to protocols with temporal frame update times on the order of 7–9 s. Hybrid approaches combining the use of Ultrafast imaging for the first minute after contrast injection followed by four 60–80 s temporal resolution time frames have been suggested to provide improved detection of early contrast enhancement associated with malignancy.11,12 However, these approaches reduce the achievable spatial resolution, imaging FOV, or both. Further, these acquisition strategies only allow for semi-quantitative analysis due to the lack of the wash-out information. Another approach is to use an interleaved acquisition to improve both temporal and spatial resolution by alternating between frames of high temporal resolution imaging and high spatial resolution imaging during the contrast passage.13 This approach prevents the sharing of temporal data between individual images to improve temporal fidelity. However, the sequence is sensitive to timing mismatch between contrast administration and image acquisition due to the relatively short pre-contrast interval. Moreover, it may not allow for a detailed morphologic evaluation in the early enhancement phase due to the interleaved and non-continuous nature of the temporal and spatial resolution.
Undersampled Cartesian acquisitions combined with view-sharing reconstructions have been proposed more recently as another approach to achieve high spatial and temporal resolution14–18. In these methods, the undersampled high spatial frequencies are filled in using data from other time points in order to mitigate the loss of spatial resolution. However, these approaches have been shown to suffer from temporal blurring19 that may comprise evaluation of lesion features and temporal kinetics. Compressed sensing (CS) has been proposed as an alternative reconstruction strategy that exploits the availability of a sparse representation of MR images and relies on randomized k-space sampling with incoherent artifacts to produce images via nonlinear constrained reconstruction20. A sparse representation can be considered in the spatial20, temporal21, or other parametric domains, with the level of sparsity directly affecting achievable acceleration factors. Several CS-based techniques, such as k-t BLAST/k-t SENSE22, or k-t FOCUSS23, have exploited correlations in both k-space and time to reduce the scan time by factors of 6 – 1024,25. However, it is a challenge for Cartesian acquisitions to achieve higher acceleration factors. Non-Cartesian sampling schemes, such as radial or spiral, present alternative acquisition approaches that are readily amenable to use with CS techniques and can provide higher acceleration factors26.
A 3D stack-of-stars acquisition with a golden-angle radial sampling scheme can provide nearly uniform k-space coverage for any arbitrary number of projections27. However, undersampled radial acquisition results in streaking artifacts, making it a proxy for random sampling that is required by the CS theory20,28–30. A CS reconstruction using a temporal total variation (TV) sparsifying transform with undersampled golden-angle radial acquisition, referred to as iGRASP31, has been demonstrated for abdomen21 and breast DCE-MRI32. Kim et. al. demonstrated that high spatial resolution can be achieved at 5 s temporal resolution. However, the demonstrated image quality may not be achievable for different breast imaging protocols because a general transform may not result in the necessary level of sparsity for situations with complex spatial and/or kinetic features. An alternative data-driven low-rank-based method, known as MOdel Consistency COndition (MOCCO), uses temporal models estimated from the acquired data itself and thereby has the ability to adapt to varying imaging protocols and to reduce modeling error21. Preliminary results have been presented demonstrating the feasibility of MOCCO with radial acquisition for high spatial resolution breast DCE-MRI with 10 s temporal resolution33.
Although advanced acquisition and reconstruction techniques, such as view sharing and CS-based algorithms, show promise for providing high spatial and temporal resolution, additional studies are needed to characterize the performance of these approaches under a broader range of imaging conditions such as noise level, lesion size, and contrast kinetics. In practice, comparison and validation studies of new techniques for advanced acquisition and reconstruction in breast DCE-MRI are difficult to perform in patients due to the lack of a known ground truth in patient physiology and low reproducibility due to physiologic variability between patients and exams. To minimize patient dependent variation, retrospective simulations, which generate undersampled data from fully-sampled series, have been used to validate time-resolved CS reconstructions34–37. However, such approaches still lack a known ground truth to evaluate temporal fidelity. To overcome these limitations, breast digital reference objects (DROs) present an alternative strategy since they can be readily programmed to reproducibly simulate tissue features, such as lesion morphology, physiology, and MR tissue characteristics, without suffering from confounders due to MRI hardware biases or patient related factors such as positioning and motion.
In this work, we evaluate the performance of undersampled stack-of-stars radial acquisition and CS reconstruction using a DRO. Two different reconstruction algorithms, temporal TV and MOCCO, are compared for time-resolved bilateral breast DCE-MR with a goal to achieve high temporal resolution (~5 s) while maintaining required spatial resolution. To test the reconstruction performance, we carry out simulations to mimic clinical scenarios and evaluate the reconstruction performance in the spatial and temporal domains as compared with the simulated ground truth.
Theory
The MRI measurements of an image series acquired using an encoding matrix can be modeled in the matrix form as
| [1] |
In many applications, MR images or image series possess a representation in some basis that has only a relatively small number of non-zero coefficients, i.e., a sparse representation. The sparse representation can be learned and extracted from prior knowledge or assumptions about signal behavior. The CS theory guarantees that under certain conditions on the encoding matrix and sparsity level, the signal can be recovered from the undersampled data by solving the following minimization problem
| [2] |
where is the encoding matrix comprising coil sensitivity values and Fourier encoding terms, is an operator mapping the signal to the selected representation space (sparsifying transform), and is a regularization parameter providing a balance between the data consistency and the sparsity terms. Minimizing the norm promotes sparsity of the image representation, while simultaneously allowing for outlying values.
For dynamic imaging, different image pixels often have similar temporal enhancement curves. Therefore, an image series can have a sparse representation in a properly chosen basis of temporal waveforms. The compressed sensing with temporal total variation (CS-TV) regularization can be defined as
| [3] |
where is the first order temporal gradient.
When a low-resolution estimate of an image series is available (e.g. obtained from the fully sampled k-space center in radial imaging), it can be utilized to construct a tailored basis for representation of temporal behavior of different pixels in the image series. MOCCO uses such basis to construct a temporal model of the image series, which provides a sparsifying transform. The image series is then reconstructed as
| [4] |
where is the matrix constructed from elements of this basis. In this work, was learned through complex independent component analysis (ICA).38 The ICA technique assumes that each component is statistically independent from the source signals, which has been shown to be a robust method to identify key components of the perfusion series and remove unwanted image-to-image fluctuations.39
Methods
Simulations:
All simulations were performed using a modified breast DRO based on work by Bancroft et. al.40 and generated using MATLAB (Math-Works, Inc., Natick, Massachusetts, USA). The DRO was designed to include both static features derived from a standard T1 weighted breast MRI with fat saturation as well as simulated enhancing features as shown in Figure 1. Imaging simulation parameters were chosen to replicate a conventional clinical bilateral breast protocol: FOV = 340 mm × 340 mm, in-plane spatial resolution = 0.75 mm × 0.75 mm, slice thickness = 1.4 mm, flip angle (FA) = 30°, TE/TR = 2.4 ms / 4.7 ms, and matrix size = 448 × 448 × 142. Circles with diameters of 1.5 mm, 5 mm, 8 mm, and 10 mm were used to simulate lesions with circumscribed margins. The extended Tofts model41,42 was used to simulate lesion signal changes as a function of time similar to what is observed in vivo. An arterial input function curve based on the publicly available dispersion model described by Barboriak et. al. was used to generate the DCE-MRI data.43 To cover a range of different lesion types, seven lesions were simulated based on PK parameters outlined in the ACR BI-RADS Breast Magnetic Resonance Imaging44 including two malignant lesions (Ktrans>0.25 min−1 and kep>1.0 min−1), three benign lesions (Ktrans<0.25 min−1 and kep<1.0 min−1) and two intermediate lesions (Ktrans>0.25 min−1 and kep<1.0 min−1). Simulation parameters for all lesions are listed in Supporting Information Table S1.The spoiled gradient recalled echo (SPGR) signal model was then used to generate signal time curves assuming a field strength of 3 T, T1 value of breast tissue (T10 =1444 ms45), and contrast agent relaxivity of r1 = 4.9 mM −1s −1 to simulate Gd-BOPTA (gadobenate dimeglumine, Multihance, Bracco, Milan, Italy)46, and imaging flip angle (FA = 30°). Images containing both static and dynamic features were then sampled using the non-uniform fast Fourier transform (NUFFT) to simulate k-space data generated from an undersampled golden-angle radial acquisition consisting of 1024 projections × 16 coils.
Figure 1.
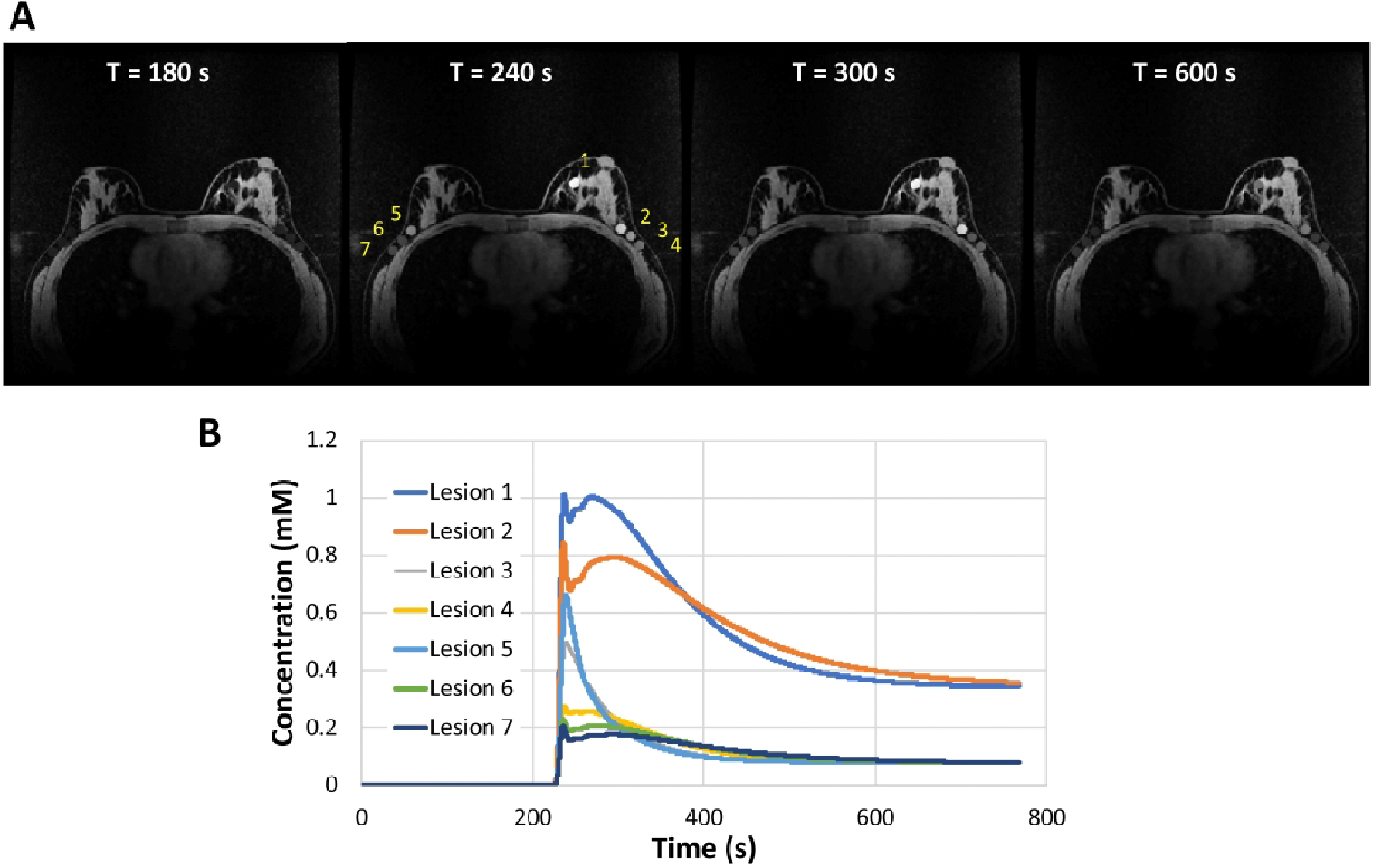
Simulations using the DRO. (A) Fully-sampled reference images at 180, 240, 300, and 600 s post contrast injection. Simulated lesions were placed in the left central/medial breast (lesion 1) as well as the left (lesions 2, 3, 4) and right axilla and axillary tail breast tissue (lesions 5, 6, 7). (B) Concentration time curves for each lesion generated from the pharmacokinetic models.
Reconstruction:
The undersampled radial data were reconstructed at 5 s temporal resolution corresponding to 8 projections per time frame (undersampling factor, R = 88) using MOCCO, CS-TV, and iterative SENSE. For the purposes of providing reference images for comparison, fully-sampled radial data consisting of 704 individual projections per time frame were generated by matching the temporal resolution of the undersampled radial images. Next, reference images were reconstructed using iterative SENSE reconstruction from fully sampled k-space data. Both MOCCO and CS-TV were implemented using iteratively re-weighted least squares minimization47. To reconstruct source data without noise added, iterations were performed until the relative norm of the k-space residual was less than a specified tolerance (10 −9) or until a maximal number of iterations (n=250) was reached. The regularization parameter () for both CS-TV and MOCCO was selected from a wide range of values (from 0.05 to 100) to minimize the normalized root-mean-square-error (nRMSE) between the reconstructed and reference image series. The optimized values for MOCCO and CS-TV were then used for all subsequent analysis.
Analysis:
Temporal curves from regions-of-interest (ROIs) placed in each lesion were measured across all image series in the time-series to evaluate the temporal fidelity of the reconstruction algorithm. The curves from the reconstructed data were compared to the original signal model. The nRMSE(%) between the reconstructed image and reference image was evaluated either within lesion ROIs or the whole image for all time points to demonstrate the reconstruction accuracy. nRMSE(%) values were reported as the percentage of the mean value of the reference images given in Equation 5,
| [5] |
where is equal to the number of pixels in the region of interest and is the number of time points. PK modeling was also performed to evaluate the temporal fidelity by assessing the ability to recover the original kinetic parameters from the temporal curves. PK modeling was performed using the ROCKETSHIP toolbox48 by fitting the extended Tofts model to the time-signal curves using the Levenberg-Marquardt algorithm. The obtained PK parameters were then compared to the PK parameters used to generate the input time curves for the simulation to determine how well the acquisition and reconstruction could recover the time curves. The input PK parameters are listed in Supporting Information Table S1.
To evaluate the spatial fidelity for varying lesion sizes, signal intensity line profiles were measured across each lesion for both reference and MOCCO images. To evaluate the performance of the MOCCO reconstruction in the presence of noise, Monte-Carlo simulations were performed to measure the noise amplification factor (g-factor, ).49 One hundred realizations of independent and identically distributed (i.i.d.) complex Gaussian noise with zero mean and standard deviation of 10% and 30% of the mean k-space magnitude were added to the k-space data resulting in 200 unique datasets (100 for each noise level). Each dataset was then reconstructed with MOCCO and SENSE. Iterations were carried out until the residual error fell below 10 −9 or a maximum number of iterations (set to 100) was reached. Additionally, 100 reconstructions were performed using fully-sampled data with additive i.i.d. Gaussian noise with the standard deviation matched to the undersampled data. The propagation of noise was estimated by calculating :
| [6] |
where and are noise variances for the undersampled and fully-sampled reconstructions, respectively, calculated across Monte-Carlo samples. The mean values from ROIs including breast tissue, axilla region, and chest wall were measured across all time frames for all reconstructions. The reconstruction bias was assessed by taking a pixel-wise mean across all Monte-Carlo samples and calculating the normalized image difference between the undersampled and the fully sampled images.
Results
Example signal intensity time curves are shown for several simulated lesions with varying enhancement patterns following iterative SENSE, CS-TV, and MOCCO reconstructions in Figure 2. Note that the displayed time interval ranges from 150 s to 400 s to allow better visualization over the points of greatest change. The complete time-curves are shown in Supporting Information figure S1. Both the CS-TV and MOCCO approaches generated temporal signal curves that were free of signal oscillations compared to iterative SENSE. The MOCCO technique was found to better represent the lesion temporal enhancement kinetics, such as rapid wash-in and wash-out in lesion 5 (Figure 2, H) as well as minor deviations within all simulated lesions in the difference image (Figure 3, I). The choice of regularization parameter in the CS-TV approach allows the user to optimize between image quality and temporal characteristics. A smaller regularization parameter () provides a relatively accurate depiction of the lesion signal intensity (Figure 2, A–D) but leads to larger residual error in the background breast tissue which is easily visible in the difference image (Figure 3, G). However the larger regularization parameter () displays overall similar image quality to the reference image (Figure 3, D) but induces temporal blurring in the measured signal time curves from the simulated lesions (Figure 2, A–D).
Figure 2.
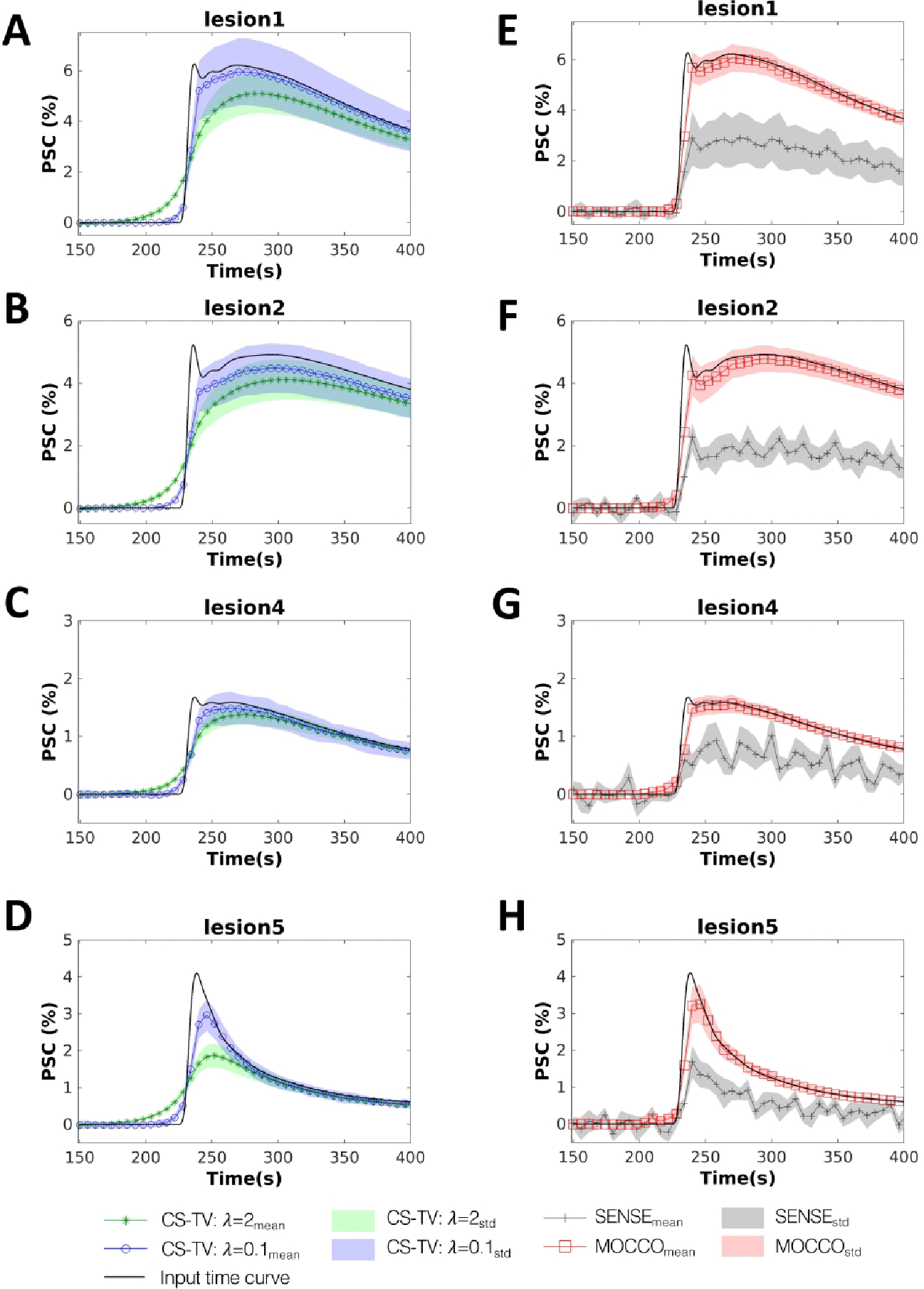
Simulated contrast agent uptake curves (displayed for a subset of time from 150 to 400 s). Mean percent signal change measured for four 8 mm lesions with varying pharmacokinetics (lesions 1, 2, 4 and 5 as defined in Figure 1) reconstructed using CS-TV with (A-D, blue circles), CS-TV with (A-D, green stars), MOCCO (E-F, red squares) and iterative SENSE (E-F, gray pluses). Standard deviations are shown with banded areas. The input time curves (“true”) used to generate the source data are plotted with dark black lines in all frames.
Figure 3.
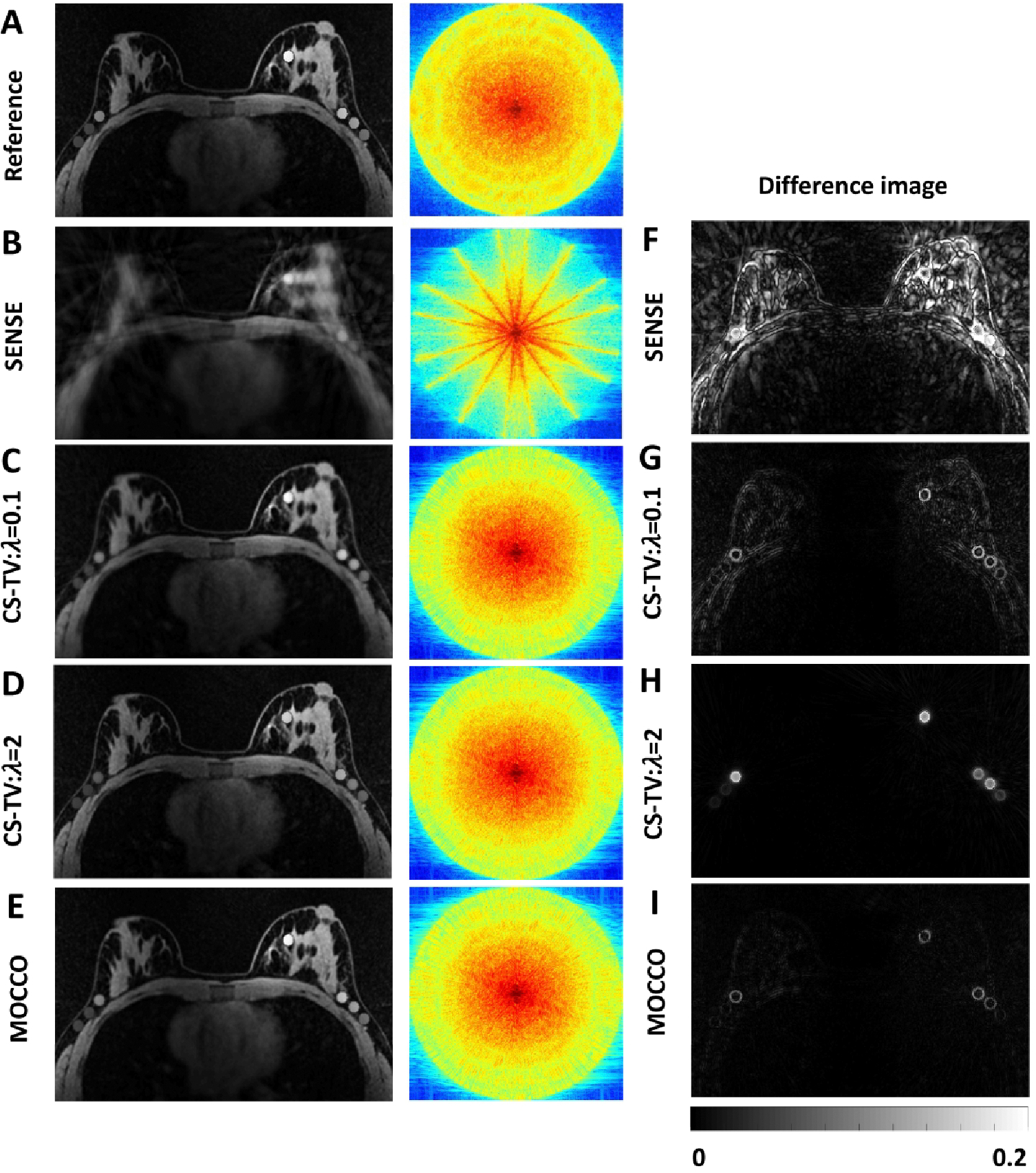
Reference image (A), reconstructed images (B-E), and corresponding difference images (F-I) all shown for 5 s temporal resolution at time = 240 s. Difference images were measured by subtracting the reconstructed images from the reference image and normalized to the maximum value of the reference image. Log scale k-space plots show how well high and low spatial frequency data were recovered.
Plots of nRMSE(%) over the entire FOV for MOCCO and CS-TV with different values for are shown in Figure 4. The corresponding reconstructed images are shown in Supporting Information Figure S2. Although the nRMSE(%) measured over the full FOV is too general to provide a precise metric for both spatial and temporal quality assessment, the plots provide a quantitative measure for the overall errors. Both methods decreased the nRMSE(%) when increasing from 0–10 for MOCCO and from 0–2 for CS-TV. The curves of the nRMSE(%) for MOCCO show a relatively stable region between , whereas CS-TV shows a narrow range of over which nRMSE(%) has been minimized. For larger regularization parameters ( for MOCCO and for CS-TV), the reconstruction was strongly dominated by the minimization of the temporal constraint, so the reconstructed images were observed to be overly smoothed and resulted in increased nRMSE(%). The images can be found in Supporting Information Figure S2 B, for , and Figure S2 C, for . Results for PK parameters obtained from MOCCO (), CS-TV ( and ), and fully-sampled reference images for 8 mm lesion size are shown in Supporting Information Table S2.
Figure 4.
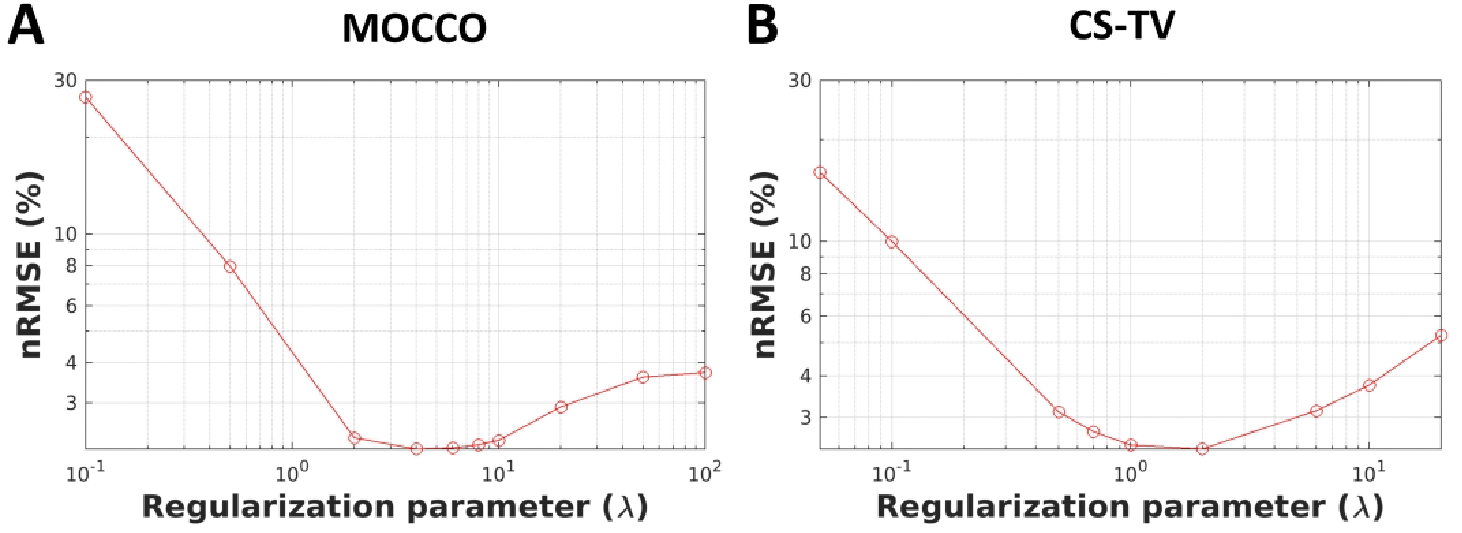
Plot of nRMSE(%) from the reconstructed images using MOCCO (A) and CS-TV (B) as a function of the regularization parameter () to indicate the reconstruction accuracy.
In order to evaluate the reconstruction accuracy of the MOCCO approach for different lesion sizes, temporal curves and the corresponding line profiles were created and are plotted with lesion sizes of 1.5 and 8 mm in Figure 5 and Figure 6. Results of all lesion sizes and complete time-curves are shown in Supporting Information figure S3 and S4. No significant error was observed in the temporal curves as a function of the decreasing lesion size. The corresponding line profiles are well matched to those measured in the fully-sampled reference images. The nRMSE(%) of all lesion time curves are summarized in Table 1 showing that the temporal error is increased for small lesion sizes (1.5 and 5 mm) with nRMSE(%) around 13–20%. For lesions larger than 8 mm, the nRMSE(%) was found to be ≤ 13% for most lesion types with the exception of lesions 3 and 5 that simulated very rapid wash-in and wash-out characteristics. Results for PK parameters obtained from fully-sampled reference images and MOCCO for varying lesion sizes are shown in Supporting Information Table S3 and Table S4, respectively.
Figure 5.
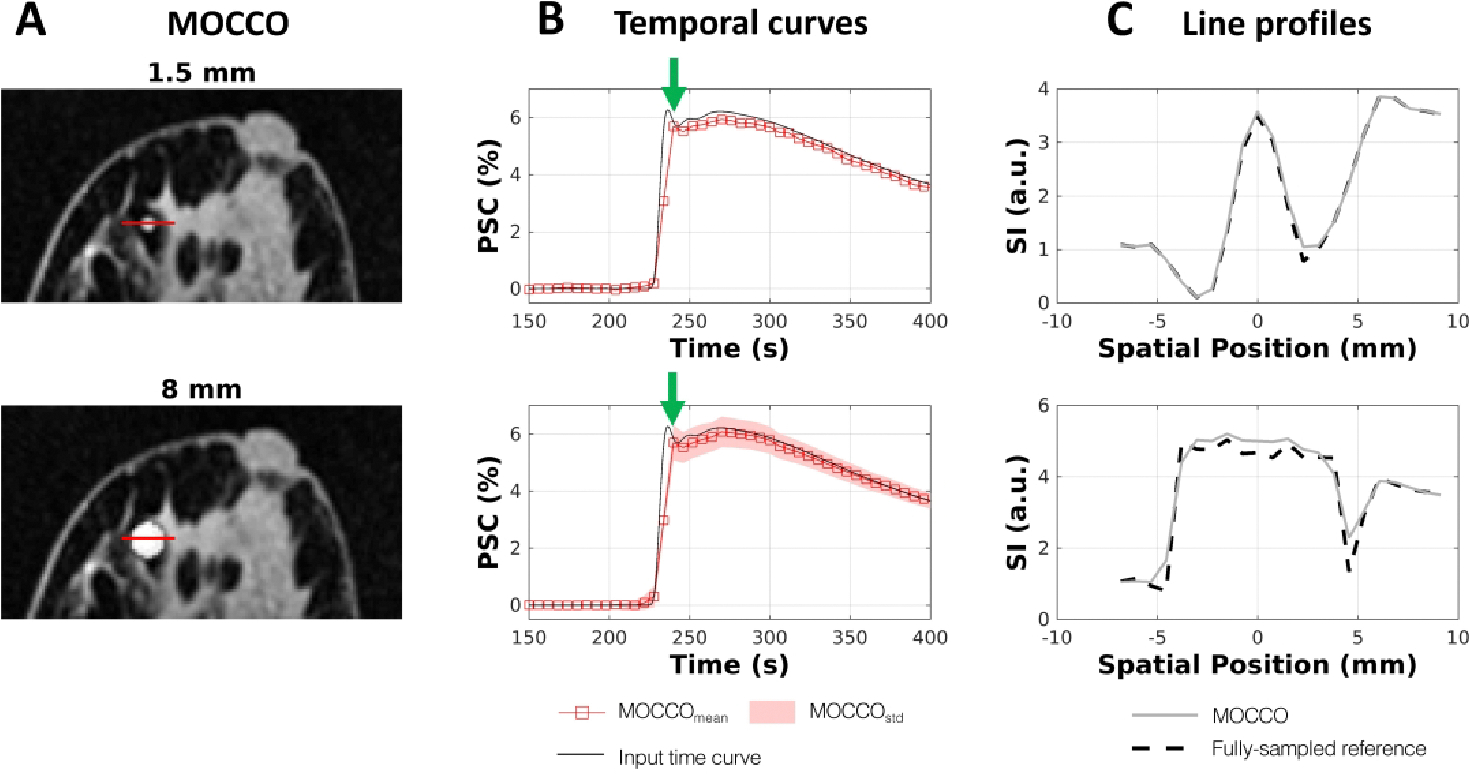
Performance of spatial and temporal fidelity for lesion 1, which has general curve shape but highest percent signal change (PSC) compared with other lesions. Example images with lesion sizes of 1.5 mm and 8 mm for matched representative time frames (A). Corresponding percent signal time curves compared to the input time curves (B). The line profiles (C) through the center of the lesion (red line in (A)) plotted for MOCCO-reconstructed (solid line) and fully-sampled reference images (dashed line) corresponding to T = 240 s (green arrows in B).
Figure 6.
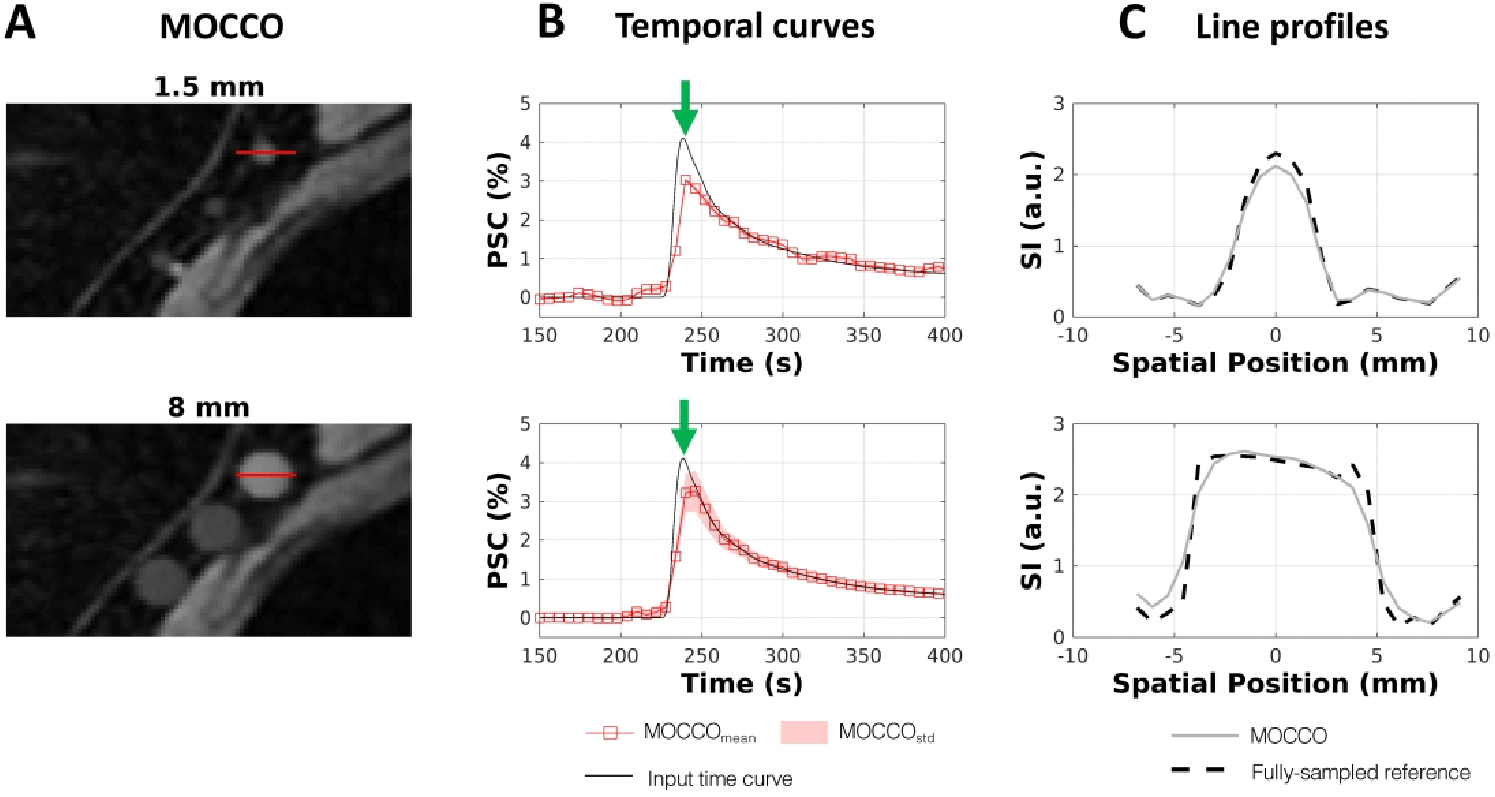
Evaluation of spatial and temporal fidelity for a lesion with sharper wash-in and wash-out contrast kinetics. Zoomed-in region at the right side of the axilla with lesions 5 – 7 is shown for MOCCO (A) at T = 240 s. Percent signal time curves evaluated for lesion 5 show modest temporal blurring at small lesion sizes (1.5 mm) (B). Line profiles shown in (C) were measured horizontally through lesion 5 as indicated by red lines in (A). The dash line profile is from the fully-sampled reference images. The solid gray profile is from the MOCCO image. Note underestimation of the signal intensity at the center of the lesion although the edges are well preserved.
Table 1.
nRMSE(%) for CS-TV: λ=0.1, CS-TV: λ=2 and MOCCO with varying lesion sizes ranging between 1.5 – 10 mm with no additional noise added.
| CS-TV | MOCCO | |||||
|---|---|---|---|---|---|---|
| Regularization parameter (λ) | Lesion size (mm) | |||||
| Lesion # | 0.1 | 2 | 10 | 8 | 5 | 1.5 |
| 1 | 22.97 | 22.79 | 11.11 | 11.24 | 12.77 | 8.40 |
| 2 | 20.03 | 22.20 | 11.69 | 11.95 | 13.08 | 11.84 |
| 3 | 22.81 | 28.72 | 16.94 | 17.00 | 19.67 | 17.47 |
| 4 | 22.15 | 19.21 | 12.78 | 12.77 | 14.31 | 11.64 |
| 5 | 27.27 | 40.58 | 21.28 | 21.46 | 25.00 | 24.01 |
| 6 | 26.52 | 19.29 | 11.95 | 12.16 | 14.04 | 13.77 |
| 7 | 28.17 | 17.60 | 11.42 | 12.04 | 14.38 | 14.43 |
Figure 7 shows the reconstructed images when different levels of noise were added to the projection source data for the iterative SENSE (Figure 7, A) and MOCCO reconstructions (Figure 7, B). For better visualization of the reconstruction error, corresponding error images are also shown in Figure 8 on the same scale. MOCCO reconstructed images were visually well matched to the reference image with only small normalized image difference (< than 0.22) located at the lesion edges (Figure 8, C and D). In contrast, iterative SENSE was not able to preserve the high spatial frequency information due to the noise in the source data (Figure 8, A and B) (with maximum normalized image difference < 0.65). The temporal curves obtained from MOCCO with noise levels of 10% and 30% of the mean signal values (Figure 7, C–F) were found to both closely match the curves from the ground truth.
Figure 7.
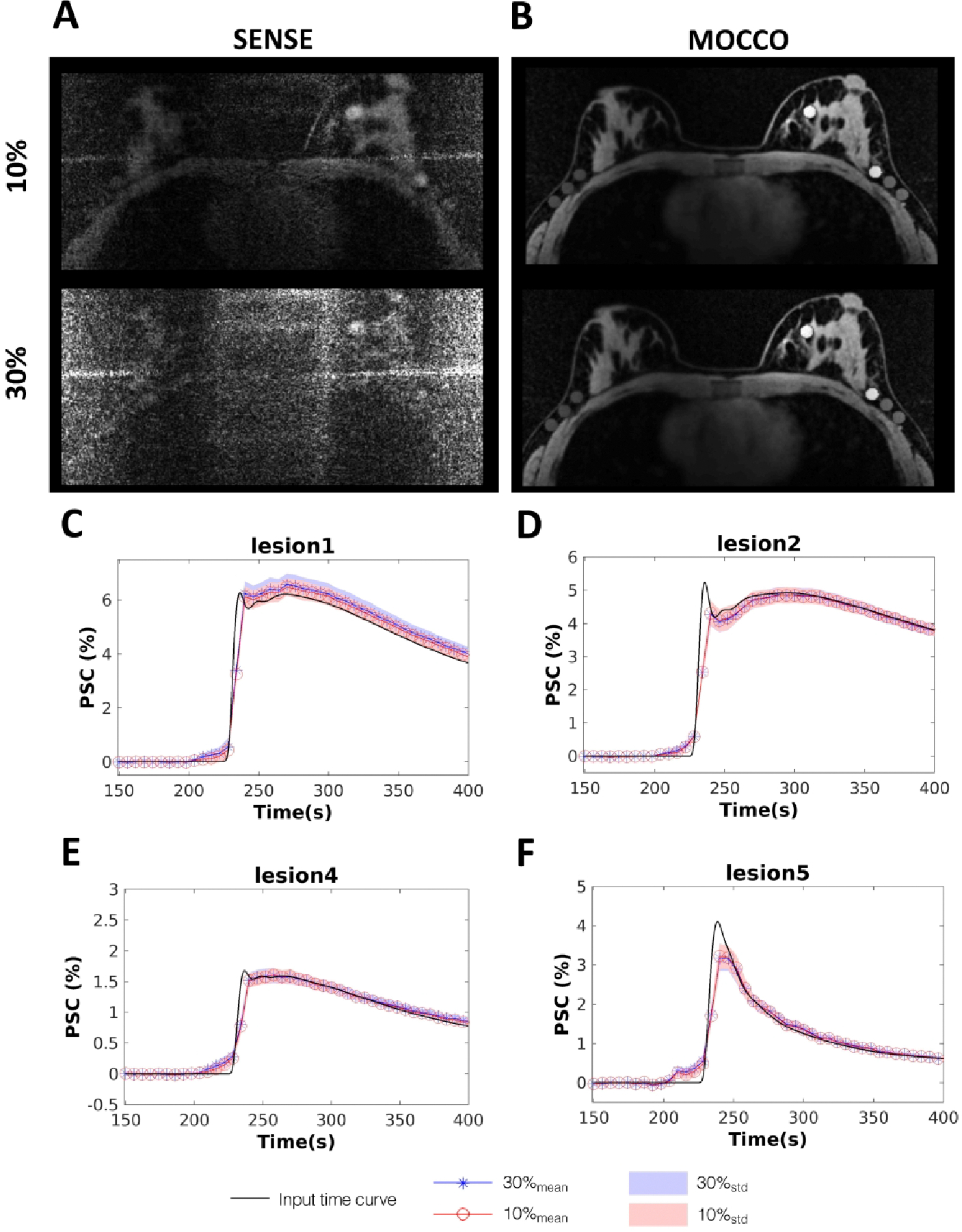
SENSE (A) and MOCCO (B) images with additive Gaussian noise equal to 10% and 30% of the mean k-space magnitude at time = 300 s. The corresponding mean percent signal change time curves of lesion 1, 2, 4 and 5 for MOCCO (C-F) with 10% (red circles) and 30% (blue stars) additive noise. Standard deviations are represented by the banded areas. The input time curve is plotted with dark black lines.
Figure 8.
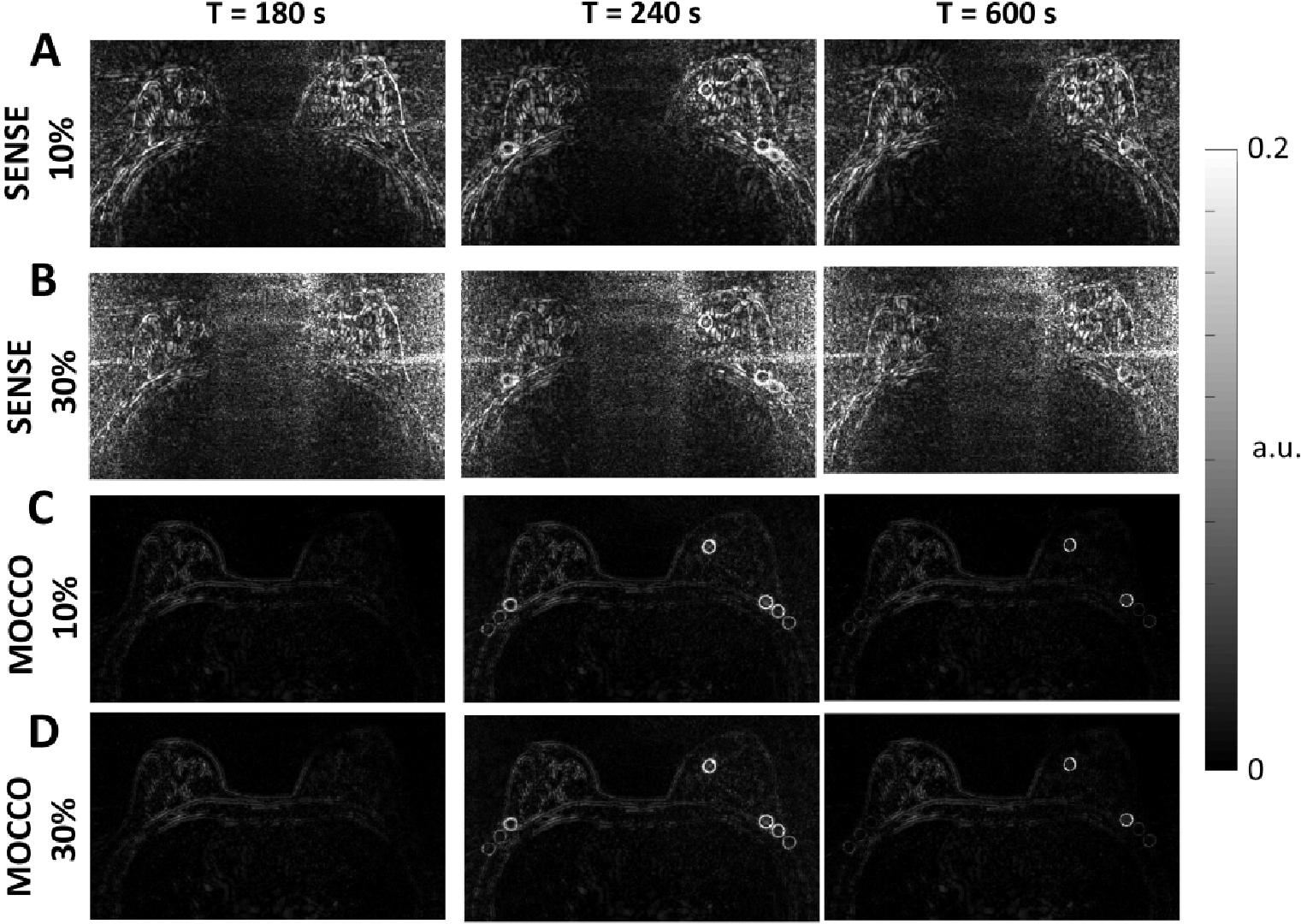
Error images measured by subtracting the reference mean images from reconstructed mean images. The mean images were averaged over the 100 Monte-Carlo iterations at t = 180, 240, and 600 s. Error images for SENSE with 10% (A) and 30% (B) noise level showed increased error with increasing noise level. Error images for MOCCO with 10% (C) and 30% noise level (D) demonstrated reduced overall error compared to SENSE.
Quantitative g-factor maps for iterative SENSE and MOCCO reconstructions with 5 s temporal resolution are shown in Figure 9. The mean gR values of the g-factor maps for iterative SENSE (Figure 9, A and B) are 1.93 and 6.28 for the 10% and 30% noise levels, respectively. MOCCO was found to greatly reduce the mean gR value to 0.06 and 0.08 for the 10% and 30% noise levels and provide less reconstruction error. The overall performance of MOCCO was found to be consistent with increasing the noise levels from 10% to 30% (Figure 9, C and D).
Figure 9.

Performance in the presence of noise with an undersampling factor R = 88 (5 s temporal resolution). SENSE reconstruction g-factor maps with 10% (A) 30% (B) noise level at t = 180, 240, and 600 s. MOCCO reconstruction g-factor maps with 10% (C) and 30% (D) noise level.
Discussion
In this work, we present a framework to achieve high spatial and temporal resolution breast DCE-MRI through a combination of golden-angle stack-of-stars radial acquisition with a data-driven low-rank based CS reconstruction (MOCCO). Numerical simulations are employed to evaluate the reconstruction accuracy under representative imaging conditions to mimic those found in vivo. The MOCCO approach is compared to another CS-based reconstruction algorithm that uses temporal total variation as a sparsity transform (CS-TV) as well as the more conventional iterative SENSE technique.
We have demonstrated that by applying basis functions generated using ICA to construct a signal-specific temporal model, reconstruction performance was improved as compared to the use of a generic sparsity transform in the form of the temporal TV approach. The TV algorithm can attain high frequency detail and ensure the same visually perceived image sharpness at larger , but at the expense of over smoothing the wash-in and wash-out time-signal slope when rapid temporal changes occurred. On the contrary, MOCCO provided a relatively robust balance between image quality and temporal fidelity across a wide range of indicating that MOCCO is less sensitive to the selection of a specific value for λ. This can be explained by the fact that the temporal TV approach efficiently sparsifies those time curves that have small first derivatives. Therefore, if the actual time course does not meet this assumption by satisfying this model, the reconstruction result may exhibit a bias that manifests in the form of smoothing of the temporal behavior. In contrast, learning the reconstruction basis functions from the source data using ICA analysis during the MOCCO reconstruction allows for the accommodation of more complex temporal behavior patterns including rapid signal changes.
Prior work has demonstrated the potential for time-resolved breast DCE to improve diagnostic specificity by evaluating correlations of morphologic features and contrast enhancement patterns for lesions ~ 1 cm 50,51. However, conventional DCE-MRI protocols are challenged in the need to encode large FOVs at both high spatial and temporal resolutions. In this study, MOCCO achieved 5 s temporal resolution with highly undersampled data while still providing high image quality for bilateral axial imaging with less than 1 mm in-plane voxel size, which meets the minimum requirement for spatial resolution by the American College of Radiology for breast DCE-MRI44.
Although iterative SENSE reconstruction for radial acquisition is becoming more common, a critical challenge for this algorithm is the tradeoff between signal-to-noise ratio (SNR) and the level of artifacts in the reconstructed images52. Literature has shown that radial sampling combined with iterative SENSE can achieve high image quality with acceleration factors between 4–1253,54 but noise amplification has been observed at higher undersampling factors where greater numbers of iterations are typically needed55. In our simulation results, iterative SENSE showed significantly higher divergence from the fully-sampled reference images at higher noise levels with R = 88 (Figure 8, B). This is in agreement with prior studies looking at the convergence behavior of iterative SENSE in the presence of low SNR and undersampled data52. The MOCCO technique was found to be less impacted by noise in the source data and provided better reconstruction accuracy as demonstrated in the Monte-Carlo simulations. Further, the MOCCO approach showed decreased g-factors (gR<0.1) compared with iterative SENSE (gR=6.28) for the larger noise level indicating limited impact of causing spatially varying noise amplitudes49,55.
The breast DRO used for this study was generated using in vivo T1 breast MRI images followed by introducing artificial tumor mimicking objects with lesion specific contrast kinetics based on a user defined pharmacokinetic model40. MR parameters for the simulation were chosen to match those from the in vivo exam to ensure that the simulated k-space data were reflective of typical in vivo data. Such a strategy has several advantages over other simulation techniques. The digital phantom provides the advantage of readily allowing simulations to model a variety of different lesion specific spatial and temporal behaviors that would be challenging to replicate using physical phantoms56. Using this numerical phantom approach, the performance of various reconstruction algorithms can be evaluated by measuring the errors in morphologic and dynamic features in reconstructed images including through directly comparing them with the ground truth used to generate the simulation. Further, PK modeling can be performed to determine how well the input PK parameters can be recovered following the simulated data acquisition and reconstruction. Examples are presented in Supporting Information Table S2 – S4. It should be noted that breast DCE-MRI presents a challenge in terms of validating novel imaging techniques due to the long clearance time of contrast agent precluding comparisons with multiple injections. Reproducibility is a further confounder due to time dependent physiological variability as well as subject motion. Digital simulations provide a critical step in the overall validation process by eliminating non-reproducible subject dependent physiological confounders for the purposes of comparisons between imaging techniques.
While the use of a realistic DRO has several advantages as a platform for initial development and validation work, the current simulation is still relatively simplistic in comparison to the complexity of the in vivo environment. Future work is needed to assess performance of the reconstruction algorithms in these more complex imaging environments such as heterogeneous lesion morphologies and enhancement patterns, non-mass enhancement, and the degree and distribution of background breast parenchymal enhancement. In this work we have assumed the data are free of motion artifacts; however, further validation is needed to characterize these algorithms in the presence of subject motion. Further, this work has aimed to better characterize the temporal fidelity of two promising CS-based approaches for breast imaging and further evaluation is needed to test the robustness and limitations of PK modeling approaches in vivo using this understanding.
Conclusions
In this paper, we compared both spatial and temporal performance of iterative SENSE, CS-TV, and MOCCO for breast DCE-MRI. We demonstrated the use of these advanced reconstructions with stack-of-stars radial acquisition for breast DCE-MRI to allow for an effective temporal resolution of 5 s. Achieving such a temporal resolution using modern MRI scanners across the large imaging volumes and slice coverage typically used in MR breast imaging allows for the acquisition of only 8 unique radial projections angles per time frame. With such high angular undersampling factors, significant streaking artifacts were observed in the iterative SENSE reconstruction. CS-TV provided the best suppression of background artifacts but showed compromised performance in terms of recovering the original temporal kinetics of the lesions. The MOCCO technique demonstrated improved temporal fidelity when matching spatial resolution and coverage from routine clinical protocols as compared with CS-TV. The results from this study demonstrate that MOCCO is less sensitive to the selection of the regularization parameter for very high undersampling factors (=88).
Supplementary Material
Acknowledgements
This project was supported by NIH-R21EB018483, NIH-R01EB027087, NIH-P30CA014520, GE Healthcare and a Research and Development Grant from the Departments of Radiology and Medical Physics, University of Wisconsin.
References
- 1.Mann RM, Cho N, Moy L. Breast MRI: State of the Art. Radiology. 2019;292(3):520–536. doi: 10.1148/radiol.2019182947 [DOI] [PubMed] [Google Scholar]
- 2.Pinker-Domenig K, Bogner W, Gruber S, et al. High resolution MRI of the breast at 3 T: which BI-RADS® descriptors are most strongly associated with the diagnosis of breast cancer? Eur Radiol. 2012;22(2):322–330. doi: 10.1007/s00330-011-2256-6 [DOI] [PubMed] [Google Scholar]
- 3.Mann RM, Kuhl CK, Kinkel K, Boetes C. Breast MRI: guidelines from the European Society of Breast Imaging. Eur Radiol. 2008;18(7):1307–1318. doi: 10.1007/s00330-008-0863-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gutierrez RL, Strigel RM, Partridge SC, et al. Dynamic Breast MRI: Does Lower Temporal Resolution Negatively Affect Clinical Kinetic Analysis? American Journal of Roentgenology. 2012;199(3):703–708. doi: 10.2214/AJR.11.7836 [DOI] [PubMed] [Google Scholar]
- 5.El Khouli RH, Macura KJ, Kamel IR, Jacobs MA, Bluemke DA. 3-T Dynamic Contrast-Enhanced MRI of the Breast: Pharmacokinetic Parameters Versus Conventional Kinetic Curve Analysis. American Journal of Roentgenology. 2011;197(6):1498–1505. doi: 10.2214/AJR.10.4665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sorace AG, Partridge SC, Li X, et al. Distinguishing benign and malignant breast tumors: preliminary comparison of kinetic modeling approaches using multi-institutional dynamic contrast-enhanced MRI data from the International Breast MR Consortium 6883 trial. JMI. 2018;5(1):011019. doi: 10.1117/1.JMI.5.1.011019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Drisis S, Metens T, Ignatiadis M, Stathopoulos K, Chao S-L, Lemort M. Quantitative DCE-MRI for prediction of pathological complete response following neoadjuvant treatment for locally advanced breast cancer: the impact of breast cancer subtypes on the diagnostic accuracy. European Radiology. 2016;26(5):1474–1484. doi: 10.1007/s00330-015-3948-0 [DOI] [PubMed] [Google Scholar]
- 8.Tudorica A, Oh KY, Chui SY-C, et al. Early Prediction and Evaluation of Breast Cancer Response to Neoadjuvant Chemotherapy Using Quantitative DCE-MRI. Translational Oncology. 2016;9(1):8–17. doi: 10.1016/j.tranon.2015.11.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Henderson E, Rutt BK, Lee T-Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magnetic Resonance Imaging. 1998;16(9):1057–1073. doi: 10.1016/S0730-725X(98)00130-1 [DOI] [PubMed] [Google Scholar]
- 10.Shukla-Dave A, Obuchowski NA, Chenevert TL, et al. Quantitative imaging biomarkers alliance (QIBA) recommendations for improved precision of DWI and DCE-MRI derived biomarkers in multicenter oncology trials. Journal of Magnetic Resonance Imaging. 2019;49(7):e101–e121. doi: 10.1002/jmri.26518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pineda FD, Medved M, Wang S, et al. Ultrafast Bilateral DCE-MRI of the Breast with Conventional Fourier Sampling: Preliminary Evaluation of Semi-quantitative Analysis. Academic Radiology. 2016;23(9):1137–1144. doi: 10.1016/j.acra.2016.04.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Abe H, Mori N, Tsuchiya K, et al. Kinetic Analysis of Benign and Malignant Breast Lesions With Ultrafast Dynamic Contrast-Enhanced MRI: Comparison With Standard Kinetic Assessment. American Journal of Roentgenology. 2016;207(5):1159–1166. doi: 10.2214/AJR.15.15957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Georgiou L, Sharma N, Broadbent DA, et al. Estimating breast tumor blood flow during neoadjuvant chemotherapy using interleaved high temporal and high spatial resolution MRI. Magnetic Resonance in Medicine. 2018;79(1):317–326. doi: 10.1002/mrm.26684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vaals JJV, Brummer ME, Dixon WT, et al. “Keyhole” method for accelerating imaging of contrast agent uptake. Journal of Magnetic Resonance Imaging. 1993;3(4):671–675. doi: 10.1002/jmri.1880030419 [DOI] [PubMed] [Google Scholar]
- 15.Jones RA, Haraldseth O, Müller TB, Rinck PA, Øksendal AN. K-space substitution: A novel dynamic imaging technique. Magnetic Resonance in Medicine. 1993;29(6):830–834. doi: 10.1002/mrm.1910290618 [DOI] [PubMed] [Google Scholar]
- 16.Mann RM, Mus RD, van Zelst J, Geppert C, Karssemeijer N, Platel B. A Novel Approach to Contrast-Enhanced Breast Magnetic Resonance Imaging for Screening: High-Resolution Ultrafast Dynamic Imaging. Investigative Radiology. 2014;49(9):579–585. doi: 10.1097/RLI.0000000000000057 [DOI] [PubMed] [Google Scholar]
- 17.Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential subsampling with cartesian ordering (DISCO): A high spatio-temporal resolution dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. Journal of Magnetic Resonance Imaging. 2012;35(6):1484–1492. doi: 10.1002/jmri.23602 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Song HK, Dougherty L. Dynamic MRI with projection reconstruction and KWIC processing for simultaneous high spatial and temporal resolution. Magnetic Resonance in Medicine. 2004;52(4):815–824. doi: 10.1002/mrm.20237 [DOI] [PubMed] [Google Scholar]
- 19.Tsao J, Kozerke S. MRI temporal acceleration techniques. Journal of Magnetic Resonance Imaging. 2012;36(3):543–560. doi: 10.1002/jmri.23640 [DOI] [PubMed] [Google Scholar]
- 20.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391 [DOI] [PubMed] [Google Scholar]
- 21.Velikina JV, Samsonov AA. Reconstruction of dynamic image series from undersampled MRI data using data-driven model consistency condition (MOCCO). Magnetic Resonance in Medicine. 2015;74(5):1279–1290. doi: 10.1002/mrm.25513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magnetic Resonance in Medicine. 2003;50(5):1031–1042. doi: 10.1002/mrm.10611 [DOI] [PubMed] [Google Scholar]
- 23.Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI. Magnetic Resonance in Medicine. 2009;61(1):103–116. doi: 10.1002/mrm.21757 [DOI] [PubMed] [Google Scholar]
- 24.Chen L, Schabel MC, DiBella EVR. Reconstruction of dynamic contrast enhanced magnetic resonance imaging of the breast with temporal constraints. Magnetic Resonance Imaging. 2010;28(5):637–645. doi: 10.1016/j.mri.2010.03.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang H, Miao Y, Zhou K, et al. Feasibility of high temporal resolution breast DCE-MRI using compressed sensing theory. Medical Physics. 2010;37(9):4971–4981. doi: 10.1118/1.3483094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Peters DC, Korosec FR, Grist TM, et al. Undersampled projection reconstruction applied to MR angiography. Magnetic Resonance in Medicine. 2000;43(1):91–101. doi: [DOI] [PubMed] [Google Scholar]
- 27.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An Optimal Radial Profile Order Based on the Golden Ratio for Time-Resolved MRI. IEEE Transactions on Medical Imaging. 2007;26(1):68–76. doi: 10.1109/TMI.2006.885337 [DOI] [PubMed] [Google Scholar]
- 28.Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magnetic Resonance in Medicine. 2007;57(6):1086–1098. doi: 10.1002/mrm.21236 [DOI] [PubMed] [Google Scholar]
- 29.Chan RW, Ramsay EA, Cheung EY, Plewes DB. The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI. Magnetic Resonance in Medicine. 2012;67(2):363–377. doi: 10.1002/mrm.23008 [DOI] [PubMed] [Google Scholar]
- 30.Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magnetic Resonance in Medicine. 2013;70(5):1263–1273. doi: 10.1002/mrm.24577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI: iGRASP: Iterative Golden-Angle RAdial Sparse Parallel MRI. Magnetic Resonance in Medicine. 2014;72(3):707–717. doi: 10.1002/mrm.24980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kim SG, Feng L, Grimm R, et al. Influence of temporal regularization and radial undersampling factor on compressed sensing reconstruction in dynamic contrast enhanced MRI of the breast: Temporal Regularization and Radial Undersampling Effects on DCE-MRI. Journal of Magnetic Resonance Imaging. 2016;43(1):261–269. doi: 10.1002/jmri.24961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang P, Velikina J, Strigel R, et al. Breast DCE-MRI using Radial Acquisition with Data-Driven Model Consistency Condition Reconstruction. In: Proceedings of the 26th Annual Meeting of ISMRM. Montreal, Canada; 2019:Abstract 1857. [Google Scholar]
- 34.Tao Y, Rilling G, Davies M, Marshall I. Carotid blood flow measurement accelerated by compressed sensing: Validation in healthy volunteers. Magnetic Resonance Imaging. 2013;31(9):1485–1491. doi: 10.1016/j.mri.2013.05.009 [DOI] [PubMed] [Google Scholar]
- 35.Chandarana H, Feng L, Block TK, et al. Free-Breathing Contrast-Enhanced Multiphase MRI of the Liver Using a Combination of Compressed Sensing, Parallel Imaging, and Golden-Angle Radial Sampling: Investigative Radiology. 2013;48(1):10–16. doi: 10.1097/RLI.0b013e318271869c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rapacchi S, Han F, Natsuaki Y, et al. High spatial and temporal resolution dynamic contrast-enhanced magnetic resonance angiography using compressed sensing with magnitude image subtraction. Magnetic Resonance in Medicine. 2014;71(5):1771–1783. doi: 10.1002/mrm.24842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Smith DS, Welch EB, Li X, et al. Quantitative effects of using compressed sensing in dynamic contrast enhanced MRI. Phys Med Biol. 2011;56(15):4933–4946. doi: 10.1088/0031-9155/56/15/018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Novey M, Adali T. On Extending the Complex FastICA Algorithm to Noncircular Sources. IEEE Transactions on Signal Processing. 2008;56(5):2148–2154. doi: 10.1109/TSP.2007.911278 [DOI] [Google Scholar]
- 39.Wollny G, Kellman P, Santos A, Ledesma-Carbayo MJ. Automatic motion compensation of free breathing acquired myocardial perfusion data by using independent component analysis. Medical Image Analysis. 2012;16(5):1015–1028. doi: 10.1016/j.media.2012.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Henze L Digital Breast Phantom for Evaluating Dynamic Accelerated Imaging Methods. In: Proceedings of the 18th ISMRM Scientific Meeting 2010. Stockholm Sweden; 2010. [Google Scholar]
- 41.Tofts PS, Brix G, Buckley DL, et al. Estimating kinetic parameters from dynamic contrast-enhanced t1-weighted MRI of a diffusable tracer: Standardized quantities and symbols. Journal of Magnetic Resonance Imaging. 1999;10(3):223–232. doi: [DOI] [PubMed] [Google Scholar]
- 42.O’Connor JPB, Jackson A, Parker GJM, Jayson GC. DCE-MRI biomarkers in the clinical evaluation of antiangiogenic and vascular disrupting agents. British Journal of Cancer. 2007;96(2):189–195. doi: 10.1038/sj.bjc.6603515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Barboriak DP, MacFall JR, Viglianti BL, Dewhirst DVM MW. Comparison of three physiologically-based pharmacokinetic models for the prediction of contrast agent distribution measured by dynamic MR imaging. Journal of Magnetic Resonance Imaging. 2008;27(6):1388–1398. doi: 10.1002/jmri.21344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Morris EA, Comstock CE, Lee CH. ACR BI-RADS® Magnetic Resonance Imaging. In: ACR BI-RADS® Atlas, Breast Imaging Reporting and Data System. In: ACR BI-RADS Breast Magnetic Resonance Imaging. American College of Radiology; 2013:18. [Google Scholar]
- 45.Rakow-Penner R, Daniel B, Yu H, Sawyer-Glover A, Glover GH. Relaxation times of breast tissue at 1.5T and 3T measured using IDEAL. Journal of Magnetic Resonance Imaging. 2006;23(1):87–91. doi: 10.1002/jmri.20469 [DOI] [PubMed] [Google Scholar]
- 46.Rohrer M, Bauer H, Mintorovitch J, Requardt M, Weinmann H-J. Comparison of Magnetic Properties of MRI Contrast Media Solutions at Different Magnetic Field Strengths: Investigative Radiology. 2005;40(11):715–724. doi: 10.1097/01.rli.0000184756.66360.d3 [DOI] [PubMed] [Google Scholar]
- 47.Bube KP, Langan RT. Hybrid ℓ1/ℓ2 minimization with applications to tomography. GEOPHYSICS. 1997;62(4):1183–1195. doi: 10.1190/1.1444219 [DOI] [Google Scholar]
- 48.Barnes SR, Ng TSC, Santa-Maria N, Montagne A, Zlokovic BV, Jacobs RE. ROCKETSHIP: a flexible and modular software tool for the planning, processing and analysis of dynamic MRI studies. BMC Med Imaging. 2015;15. doi: 10.1186/s12880-015-0062-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Breuer FA, Kannengiesser SAR, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magnetic Resonance in Medicine. 2009;62(3):739–746. doi: 10.1002/mrm.22066 [DOI] [PubMed] [Google Scholar]
- 50.Schlossbauer T, Leinsinger G, Wismuller A, et al. Classification of Small Contrast Enhancing Breast Lesions in Dynamic Magnetic Resonance Imaging Using a Combination of Morphological Criteria and Dynamic Analysis Based on Unsupervised Vector-Quantization. Investigative Radiology. 2008;43(1):56–64. doi: 10.1097/RLI.0b013e3181559932 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nagarajan MB, Huber MB, Schlossbauer T, Leinsinger G, Krol A, Wismüller A. Classification of small lesions in dynamic breast MRI: eliminating the need for precise lesion segmentation through spatio-temporal analysis of contrast enhancement. Machine Vision and Applications. 2013;24(7):1371–1381. doi: 10.1007/s00138-012-0456-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Qu P, Zhong K, Zhang B, Wang J, Shen GX. Convergence behavior of iterative SENSE reconstruction with non-Cartesian trajectories. Magnetic Resonance in Medicine. 2005;54(4):1040–1045. doi: 10.1002/mrm.20648 [DOI] [PubMed] [Google Scholar]
- 53.Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine. 2001;46(4):638–651. doi: 10.1002/mrm.1241 [DOI] [PubMed] [Google Scholar]
- 54.Boubertakh R, Prieto C, Batchelor PG, et al. Whole-heart imaging using undersampled radial phase encoding (RPE) and iterative sensitivity encoding (SENSE) reconstruction. Magnetic Resonance in Medicine. 2009;62(5):1331–1337. doi: 10.1002/mrm.22102 [DOI] [PubMed] [Google Scholar]
- 55.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999;42(5):952–962. doi: [DOI] [PubMed] [Google Scholar]
- 56.Le Y, Nickel MD, Kannengiesser S, et al. A novel framework for evaluating the image accuracy of dynamic MRI and the application on accelerated breast DCE MRI. Magn Reson Mater Phy. 2018;31(2):309–320. doi: 10.1007/s10334-017-0648-6 [DOI] [PubMed] [Google Scholar]
- 57.Litjens GJS, Heisen M, Buurman J, ter Haar Romeny BM. Pharmacokinetic models in clinical practice: What model to use for DCE-MRI of the breast? In: 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro.; 2010:185–188. doi: 10.1109/ISBI.2010.5490382 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


