Abstract
The formation of energetically favorable and metastable mineral phases within the Fe–H2O system controls the long-term mobility of iron complexes in natural aquifers and other environmentally and industrially relevant systems. The fundamental mechanism controlling the formation of these phases has remained enigmatic. We develop a general partial equilibrium model, leveraging recent synchrotron-based data on the time evolution of solid Fe(III) hydroxides along with aqueous complexes. We combine thermodynamic considerations and particle-morphology-dependent kinetic rate equations under full consideration of the aqueous phase in disequilibrium with one or more of the forming minerals. The new model predicts the rate of amorphous 2-line ferrihydrite precipitation, dissolution, and overall transformation to crystalline goethite. It is found that the precipitation of goethite (i) occurs from solution and (ii) is limited by the comparatively slow dissolution of the first forming amorphous phase 2-line ferrihydrite. A generalized transformation mechanism further illustrates that differences in the kinetics of Fe(III) precipitation are controlled by the coordination environment of the predominant Fe(III) hydrolysis product. The framework allows modeling of other iron(bearing) phases across a broad range of aqueous phase compositions.
Keywords: precipitation, iron, kinetics, pH, partial equilibrium
Short abstract
The transformation of 2-line ferrihydrite is rate-limited by its dissolution as aqueous Fe(III) across a broad range of natural and industrially relevant aqueous systems.
Introduction
Depending on the aqueous phase composition and a range of other physiochemical parameters including temperature and pH, iron may precipitate in the form of over 38 stable and metastable phases characterized to date.1 Iron (hydr)oxides are the most common form of metallic oxides in soils.2 Their formation governs the immobilization of elements of concern (EOCs) including As, Se, Mo, Ni, and 226Ra in groundwater streams,3 soil environments,4 nuclear processing facilities,5 and across a broad range of other natural and industrial aqueous systems.6−8 Iron (hydr)oxide precipitation within the pore network of cementitious materials is one of the major causes of premature structural degradation of reinforced concrete structures.9 Iron uptake by calcium silicate hydrates (C–S–H) may further reduce the ability of cement-based nuclear waste repositories to contain and safely store hazardous radionuclides.10,11 Iron (hydr)oxides are also versatile industrial products used as pigments in the production of paints and coatings,12 in wastewater treatment,13 as well as in nanotechnology,14 photovoltaic,15 and energy storage systems.16 For these reasons, detailed knowledge about the mechanism and transformation kinetics of such iron (hydr)oxides is needed to assess their stability over different time scales and conditions.
Investigations into the kinetics of iron (hydr)oxide precipitation primarily quantify the reaction rate, and thus its extent, by monitoring the molar fraction of solids formed, often assuming direct proportionality between their rate of formation and concentration.17−20 Two objections may be raised against this modeling approach. First, it is known that the formation and transformation of some iron (hydr)oxides proceeds via particle-mediated growth mechanisms,21,22 or involve metastable intermediate species19 (Figure 1a). As opposed to growth by the addition of singular atoms into an existing solid phase, as described within the framework of classical nucleation theory,23 these nonclassical growth mechanisms consist of multiple dissolution and precipitation steps and can thus not be described completely by the integrated first-order rate equation or any other semiempirical equation of the form Fe(t) = Fe0 × exp(f(t)). Second, mineral dissolution and growth rates are, among other parameters, dependent on the aqueous phase composition, the degree of supersaturation Ω, and the activity of dissolved species in disequilibrium with the solid phase(s). These parameters are generally not considered in first-order rate expressions. Moreover, due to the low solubility of iron, these parameters are significantly more difficult to obtain from an experimental point of view than the molar fraction of solid phases. In the simplest case, the irreversible formation of one ferrous (z = 2) or ferric (z = 3) iron (hydr)oxide according to the general reaction
| 1 |
is expected to depend on the Fez+ and the H+ activity. In the context of natural and industrially relevant aqueous electrolytes, the phase assemblage of iron (hydr)oxides is significantly more complex. Consider the fate of Fe2+ due to the corrosion of carbon steel in near-neutral environments.
Figure 1.

Schematic representation of the formation mechanism of crystalline iron (hydr)oxide phases from supersaturated aqueous solutions (a), together with the measured and computationally predicted aqueous iron concentration (b) and solid mole fractions (c). The initial precipitation of amorphous 2l–Fe(OH)3(s) from dissolved Fe(III) proceeds within seconds, full conversion to the stable end member α-FeOOH(s) is reached after months to years. This multistep conversion process is commonly approximated by the integrated first-order rate equation Fe(t) = Fe0 × exp(−kt), irrespective of the varying degree of supersaturation Ω and other aqueous phase parameters.
In the aqueous phase, the ferrous cation may be coordinated as FeOH+, Fe(OH)2(aq), or Fe(OH)3–, depending on the pH. These aqueous Fe(II) complexes may further oxidize, both aerobically and in the absence of oxygen, to form Fe3+ or any of the Fe(III) hydrolysis products FeOH2+, Fe(OH)2+, Fe(OH)3(aq), or Fe(OH)4–.24 The presence of carbonates, chlorides, silica, or any other anion characteristic to the aqueous environment of interest5,25−27 can lead to further complexation of the dissolved Fe(II) and Fe(III) hydrolysis products. The phase assemblage of solid iron(bearing) phases is thus in direct competition with the speciation of iron in the aqueous phase. From all of these considerations, it is evident that the mechanism fundamentally controlling the kinetics of iron (hydr)oxide formation can only be unraveled in a tightly coupled investigation of both the solid and the aqueous phase composition. Until recently, however, there was no data reported that comprehensively characterize the evolution of both the solid phases and the electrolyte composition at alkaline pH.
Recent studies28,29 reporting on the time evolution of solid Fe(III) hydroxides and complexes allow, for the first time, to model their formation mechanism in the Fe–H2O system under full consideration of the aqueous phase in disequilibrium with one or more of these minerals. On this basis, we develop a new partial equilibrium model, combining state-of-the-art thermodynamic parameters and particle-morphology-dependent kinetic rate equations. We use this model to demonstrate that the formation of goethite, a thermodynamically stable iron hydroxide, is controlled by the dissolution kinetics of amorphous 2-line ferrihydrite at alkaline pH. The proposed model simultaneously describes both the evolution of all solid and the aqueous phase constituents involved and breaks down the transformation mechanism into individual steps, thus rendering the need for various fitting parameters obsolete. All steps constituting the dissolution–crystallization pathway rely on a single kinetic rate constant. Upon considering the speciation of aqueous Fe(III) at neutral to mildly acidic pH, the transformation mechanism can be generalized to all thermodynamically stable solid Fe(III) phases, by adopting the Palandri–Kharaka kinetic formalism. Here, the overall rate of Fe(III) precipitation is limited by the intrinsic precipitation rate of the predominant hydrolyzed aqueous Fe(III) species, Fe(OH)3(aq) at circumneutral and Fe(OH)4– at alkaline pH. These observations are in line with both Stranski’s rule30 and the Ostwald step rule.31 We envision this model to be expanded to a wider range of iron-bearing phases and aqueous systems.
Results and Discussion
The Precipitation of 2-Line Ferrihydrite at Alkaline pH
Recently, we have shown that the precipitation of 2-line ferrihydrite (2l–Fe(OH)3(s)) from supersaturated alkaline stock solutions (e.g., [Fe(III)] > 10–4 M at pH = 14.0) occurs significantly more rapidly than its transformation to more stable secondary phases including hematite (α-Fe2O3(s)) and goethite (α-FeOOH(s)).28 As over 99.8% of Fe(III) in solution is coordinated as Fe(OH)4– at a pH ≥ 12,32 the precipitation of 2l–Fe(OH)3(s) at alkaline pH can be described by
| 2 |
Considering that phase growth velocity is anticipated to rise with increasing activity of Fe(OH)4– and decline as saturation conditions are approached, we formulate the rate of 2-line ferrihydrite precipitation as
| 3 |
for j = 2l–Fe(OH)3(s), ∀t (compare Supporting Information, List of symbols and notations). Correspondingly, the molar balance1 of all species i involved in the formation reaction displayed in eq 2 is
 |
4 |
To quantify the rate constant kj and reaction order wj as a function of the pH,
the progression of [Fe(OH)4–] is fitted
to the aqueous Fe(III) concentration, measured by inductively coupled
plasma optical emission spectroscopy (ICP-OES) at pH = 13.0, 13.5,
and 14.0, as published in Furcas et al.,28 within the first 60 s of equilibration time. It is assumed that
the morphology of precipitated 2-line ferrihydrite does not change
upon growth. Figure 1b displays the resultant concentration profiles at various pH values
over time. It can be recognized that the precipitation rate drastically
decreases, as the aqueous Fe(OH)4– concentration
approaches its pH-dependent solubility limit with respect to 2-line
ferrihydrite. Within the pH interval investigated, the solubility
limit of 2-line ferrihydrite increases by approximately 1 order of
magnitude per pH unit. The pH dependence of 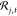 is therefore
implicitly accounted for by
the thermodynamic speciation solver. Within the error of the experimentally
measured Fe(III) concentrations, the apparent rate constant of 2l–Fe(OH)3(s) precipitation is evaluated as (kj · Aj,t) = 0.078 ± 0.010 s–1, while the reaction
order is wj = 1 with
respect to the Fe(OH)4– concentration.
is therefore
implicitly accounted for by
the thermodynamic speciation solver. Within the error of the experimentally
measured Fe(III) concentrations, the apparent rate constant of 2l–Fe(OH)3(s) precipitation is evaluated as (kj · Aj,t) = 0.078 ± 0.010 s–1, while the reaction
order is wj = 1 with
respect to the Fe(OH)4– concentration.
The here presented analysis also holds true for 2-line ferrihydrite stoichiometries other than the assumed Fe(OH)3(s). Assuming an ideal stoichiometry of Fe10O14(OH)2 in the absence of additional surface-bound water,33 the precipitation of 2-line ferrihydrite at alkaline pH proceeds according to
| 5 |
While on a molar basis, the number of protons consumed in eqs 2 and 5 per equivalent of Fe(OH)4– reacted off remains constant, it is evident that the ideal product stoichiometry reported in Michel et al.33 is significantly dryer than the assumed structural formula of Fe(OH)3, equivalent to the 2-line ferrihydrite standard reported in Furcas et al.28 As shown in Figure 2, the additional elimination of 1.4 equiv of H2O(l) per equivalent of iron does not compromise the goodness of the fitting results. In accordance with the 10-fold increase in the stoichiometric coefficient of Fe(OH)4–, the apparent rate constant of 2-line ferrihydrite precipitation decreases by a factor of 10, reaching values of (kj · Aj,t) = 0.008 ± 0.001 s–1. The reaction order remains proportional to the concentration of Fe(OH)4–.
Figure 2.
Comparison between the computationally predicted aqueous Fe(OH)4– concentrations in mol/L, assuming their stoichiometric conversion to Fe(OH)3 (shaded regions), as given by eq 2 and to the ideal stoichiometric formula Fe10O14(OH)2 reported by Michel et al.33 (circular markers), shown in eq 5.
The Transformation of 2-Line Ferrihydrite to Goethite at Alkaline pH
For aqueous Fe(III) concentrations in-between the solubility limits of 2-line ferrihydrite and goethite (e.g., 10–4 > [Fe(III)] > 10–7 M at pH = 14.0), the aqueous Fe(OH)4– concentration can increase due to the redissolution of 2l–Fe(OH)3(s) according to
| 6 |
and decrease due to the precipitation of goethite from solution
| 7 |
Phase growth may also occur via aggregation-based mechanisms, involving the formation of iron–oxygen bonds due to the elimination of water
| 8 |
Analogous to the formation of 2-line ferrihydrite (2l), the growth rate of goethite (gt) is expected to be primarily dependent on the activity of Fe(OH)4– as well as the degree of supersaturation
| 9 |
for j = α-FeOOH(s), ∀t. In contrast, the rate of 2-line ferrihydrite dissolution
| 10 |
for j = 2l–Fe(OH)3(s) and ∀t is found to be insensitive to the saturation index Ω, as the aqueous Fe(OH)4– concentration remains close to the solubility limit of 2-line ferrihydrite (Supporting Information, Figure S1a). It is instead determined by the number of moles of n2l,t. The rate of aggregation-based growth of goethite from 2-line ferrihydrite does not involve the redissolution of Fe(OH)4–, and is thus written as
| 11 |
j = 2l–Fe(OH)3(s), ∀t. Combining these rate expressions2, the molar species balances that describe the evolution of various species i involved in the dissolution (eq 6) and precipitation (eq 7) reaction are
| 12 |
Taking the initial specific surface area of 2-line ferrihydrite and goethite to be 6.0 × 105 and 1.3 × 105 m2 kg–1,34 the kinetic rate parameters of ∂ni/∂t are determined by fitting the predicted aqueous progression of [Fe(OH)4–] and the solid mole fraction xj of both phases j ∈ Γ to the experimental data collected by Furcas et al.28 It is assumed that the specific surface area As,j scales with the phase mass in accordance with the cubic root correction formula displayed in eq 31. As illustrated in Figures 1 and 3, the calculated aqueous Fe(III) concentration and the solid phase assemblage are in good agreement with their experimental counterparts within the uncertainty associated with ICP-OES measurements and the estimated surface rate constants.
Figure 3.
Combined modeling results (solid lines) considering the kinetics governing the rate of goethite formation (eq 9) and 2-line ferrihydrite dissolution (eq 10), matching the iron concentration measured by ICP-OES at pH = 14.0. Dashed lines represent the confidence intervals of the computationally predicted aqueous iron concentrations. Simulations correct for the specific surface area of both phases by applying a mass cubic root correction. Note that the computationally predicted solid molar fractions and aqueous iron concentrations are fitted to their experimental counterparts published in Furcas et al.28
In contrast to its precipitation velocity, the
rate of 2-line ferrihydrite
dissolution is correlated to the pH and proportional to the cube of
the phase mass. The rate of goethite precipitation, on the other hand,
is sensitive to the aqueous concentration of [Fe(OH)4–]4 and decreases exponentially with pH (Figure 4). For all simulations
performed, the best fits were achieved, excluding a solid–solid
transformation (k2l→gt = 0 mol
m–2 s–1). As displayed in Figure 5, the additional
consideration of an aggregation-based transformation between 2-line
ferrihydrite and goethite predicts aqueous Fe(OH)4– concentrations within the confidence interval of concentration
profiles predicted in its absence (Figure 5a). High solid–solid transformation
rate constants in the orders of 10–10 mol m–2 s–1 result in a marginally more
accurate prediction of the solid fraction at low equilibration times,
but grossly overpredict the rate of 2-line ferrihydrite conversion
in the long term (Figure 5b). Moreover, the designated initial precipitation rate of
the more soluble, amorphous precursor 2-line ferrihydrite is much
larger than the rate of goethite precipitation 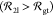 . The emerging transformation mechanism,
consisting of the rapid precipitation of 2-line ferrihydrite, followed
by its dissolution and the slow precipitation of goethite from solution,
is a multistep process of which each step is in complete agreement
with the principles of classical nucleation theory35 as well as Stranski’s rule30 and the Ostwald step rule.31
. The emerging transformation mechanism,
consisting of the rapid precipitation of 2-line ferrihydrite, followed
by its dissolution and the slow precipitation of goethite from solution,
is a multistep process of which each step is in complete agreement
with the principles of classical nucleation theory35 as well as Stranski’s rule30 and the Ostwald step rule.31
Figure 4.
Surface rate constants kj in mol–3 m–2 s–1 of two-line ferrihydrite dissolution (a) and goethite precipitation (b) as a function of pH.
Figure 5.
Predicted aqueous Fe(OH)4– concentration (a) and solid molar fraction of 2-line ferrihydrite (b) including a solid–solid transition reaction between 2-line ferrihydrite and goethite at pH = 14.0. In both panels, the dashed and dotted lines correspond to the simulation results, including a low (k2l→gt = 4 · 10–11 mol m–2 s–1) and high (k2l→gt = 4 · 10–10 mol m–2 s–1) rate of solid–solid transformation.
Even though the surface rate constant of goethite precipitation is 1023–1025 times higher than the rate of 2-line ferrihydrite dissolution, the effective reaction rates evaluated at the measured aqueous n4Fe(OH)4– and solid n32l over time are of comparable magnitude (Supporting Information, Figure S1c). At low equilibration times, the rapid decrease in nFe(OH)4– and the corresponding reduction in the degree of supersaturation with respect to goethite appear to attenuate the high precipitation rate constant. Likewise, the specific surface area of goethite reduces to about 10% of its initial value within the first 3 h of the experiment (Supporting Information, Figure S1d). Over the entire timespan investigated, the rate of 2-line ferrihydrite dissolution remains below the rate of goethite precipitation, as evidenced by the strictly monotonic decrease in the aqueous Fe(OH)4– concentration measured by ICP-OES, and can thus be considered the rate-limiting step of the transformation mechanism. It can furthermore be shown that, for a specific dependence of dnj,t/dt on the specific surface area As,j,t, the evolution of nj,t follows the progression
| 13 |
where τ = Mw,jAs,j,0kjn3j,0 in s–1. For a more detailed account of the derivation of eq 13, the reader is referred to the Supporting Information. At constant pH and sample mass, the rate of 2-line ferrihydrite dissolution is first order with respect to nj,t and the time constant of dissolution τ depends entirely on the initial sample surface area.
The Precipitation of Fe(III) at Neutral to Alkaline pH
As elucidated in the previous section, the rate of goethite precipitation is highly sensitive to the aqueous concentration of Fe(OH)4–. This association between precipitation velocity and the predominant aqueous Fe(III) hydrolysis product was documented in previous studies. Pham et al.29 established an analogous relationship between the rate of Fe(III) precipitation and the concentration of Fe(OH)3(aq) at pH = 6.0–9.5, i.e., across the predominance interval of Fe(OH)3(aq), and obtained an intrinsic precipitation rate constant of kFe(OH)3(aq) = 2.0 · 107 L mol–1 s–1. Even though Fe(III) is known to precipitate as mixtures 2-line ferrihydrite, goethite, and hematite at circumneutral pH,17,19kFe(OH)3(aq) can be compared to the transformation rates quoted in this study under the assumption that the rate of 2-line ferrihydrite dissolution is rate-limiting. The observed relationship (Figure 4) between the rate of goethite precipitation and the concentration of Fe(OH)4– at pH = 13.0–14.0, i.e., across the predominance interval of Fe(OH)4–, suggests that the precipitation rate of Fe(III) follows the solubility limit of the solid Fe(III) phase stabilized. Moreover, differences in the precipitation mechanism at acidic, neutral, and alkaline pH appear to be a consequence of the different Fe(III) coordination environments. The partial equilibrium model developed in this paper can hence be extended to any pH, provided the thermodynamic speciation solver includes the respective predominant aqueous Fe(III) species correlated with the precipitation velocity. At acidic pH beyond the range considered in Pham et al.29 and this study, Fe(III) is predominantly coordinated as the trivalent cation Fe3+ (pH = 0.0–2.8), FeOH2+ (pH = 2.8–3.9), and Fe(OH)2+ (pH = 3.9–6.4).32 In addition to the predominant Fe(III) hydrolysis products, the formation of polynuclear ferric species including Fe2(OH)4+2 and Fe3(OH)5+4 makes up a significant portion of the total aqueous molar fraction at highly alkaline pH < 2.32,36 According to the pH-dependent speciation, the total rate constant of Fe(III) precipitation
| 14 |
will be a combination of the individual rate constants of all species contributing to the solubility limit ki(Fe(III)i) and their aqueous molar fractions xFe(III)i. Depending on the crystallization conditions and the presence of other complexing ions, the overall precipitation rate may further be influenced by the formation of aqueous complexes including iron chlorides and silicates25,37,38 as well as other transformation pathways including the recrystallization of solid Fe(III) phases other than the here investigated 2-line ferrihydrite and goethite.17 Nevertheless, the total rate of Fe(III) precipitation as formulated in this section holds true, provided that (i) 2-line ferrihydrite is the solubility limiting Fe(III) phase and (ii) Fe(OH)3(aq) and Fe(OH)4– are the predominant aqueous hydrolysis complexes at pH = 6.0– 9.5 and pH = 9.5–14.0, respectively.
To enable better comparison between the rates goethite precipitation presented in this study and those computed by Pham et al.,29 various kj values have been normalized to a surface area of 1 m2, multiplied by the solubility limit of 2-line ferrihydrite at pH = 6.0–14.032 and reformulated in terms of the H+ activity instead of the pH. The here presented novel empirical fitting results and the previously obtained intrinsic rate of Fe(III) precipitation are thereby expressed in terms of the Palandri and Kharaka39 kinetic formalism, where the overall rate of transformation,
| 15 |
consists of 3 individual contributions at acidic, neutral, and alkaline pH. In eq 15, Ea stands for the activation energy in J mol–1, R denotes the ideal gas constant in J mol–1 K–1, and all other parameters have their usual meanings. Figure 6 displays the fitted overall rate of Fe(III) precipitation, dntotal/dt in mol s–1. The kinetic parameters of each contribution to the overall rate of precipitation are obtained by segregating the experimental data into an acidic (pH = 6.5–7.1), near-neutral (pH = 7.6–8.5) and basic (pH = 9.4–14.0) region and then performing a piecewise linear regression on each pH interval.
Figure 6.
Estimated Palandri–Kharaka-type precipitation rate of Fe(III) dntotal/dt in mol s–1 at neutral to alkaline pH (solid line), together with the individual mechanistic acidic, neutral and basic contributions to dntotal/dt (dashed lines), obtained via linear regression of the experimentally measured precipitation rates (symbols) at pH = 6.5–7.1, 7.6–8.5 and 9.4–14.0, respectively.
It is found that the rate constants of Fe(III) precipitation decrease from log10 k = −1.49 at acidic to log10 k = −7.80 at neutral and log10 k = −15.59 at alkaline pH. The overall transformation rate is slightly weaker correlated with aH+ at acidic pH (p = −0.857) as opposed to the basic regime (q = 0.908), though various acidic rate parameters may be subject to further revision due to the lack of data points at pH < 6.5. Irrespective of the pH, the activation energy is estimated to be Ea = 11.7 kJ mol–1. It is also remarkable that the precipitation velocity at circumneutral pH is close to the dissolution rate of goethite (log10 k = −7.94), as determined by Palandri and Kharaka.39 These findings underline the crucial role of the pH-dependent speciation of iron as a rate-limiting factor in the formation of thermodynamically stable, crystalline Fe(III) end members.
Environmental Implications
The analysis carried out in this paper demonstrates that the rate of crystalline Fe(III) (hydr)oxide formation is highly sensitive to the coordination environment of Fe(III) in the aqueous phase. At highly alkaline pH > 13, i.e., across the thermodynamic stability domain of Fe(OH)4–, precipitation occurs rapidly in the orders of 10–7 (pH = 13) to 10–4 (pH = 14) mol s–1. At neutral (pH = 7) to mildly alkaline (pH = 10) conditions, i.e., characteristic to uranium mine tailings,18 Fe(III) is predominantly coordinated as Fe(OH)3(aq). This shift in the coordination environment coincides with a reduction in the incident rate of Fe(III) (hydr)oxide formation by 2–5 orders of magnitude. It is further highlighted that the accelerated stabilization of crystalline Fe(III) end members proceeds via and is rate-limited by the dissolution of the amorphous iron hydroxide 2-line ferrihydrite. These observations have severe implications for the sequestration of contaminants including heavy metals from groundwater streams3 and hazardous radionuclides in nuclear processing facilities.5 As 2-line ferrihydrite has a strong affinity for adsorbing and coprecipitating contaminants such as heavy metals, it is expected that the accelerated rate of dissolution (Figure 4) and the strong dependency of the overall rate of crystalline Fe(III) precipitation on the H+ activity (Figure 6) enhance the mobility and bioavailability of elements of concern at alkaline conditions. A more thorough understanding of their sequestration must thus be investigated under consideration of all mechanistic steps that govern the formation of amorphous and crystalline iron (hydr)oxides, including the pH-dependent speciation of Fe(III) in the Fe–H2O system.
Methods
The formation of
from and in the presence of
can
be described by a sequence of partial
equilibrium steps. It is assumed that one or more Γ is out of
equilibrium with the remaining species and all Θ are in equilibrium
with one another. Depending on the time-dependent evolution of the
aqueous species, the rate of mineral dissolution and growth  is formulated
as a function of their bulk
thermodynamic quantities, the phase saturation index Ωj,t and the activity of various Θ the formation
of j ∈ Γ is sensitive to. Analogous
to the seeded growth modeling of other minerals including portlandite40 and calcite,41 changes
to the particle geometry are considered by correcting for changes
in the particle surface area upon each time step of the simulation.
is formulated
as a function of their bulk
thermodynamic quantities, the phase saturation index Ωj,t and the activity of various Θ the formation
of j ∈ Γ is sensitive to. Analogous
to the seeded growth modeling of other minerals including portlandite40 and calcite,41 changes
to the particle geometry are considered by correcting for changes
in the particle surface area upon each time step of the simulation.
Gibbs Free Energy Minimization
Mineralogical phase equilibria and bulk compositions were determined using the Reaktoro framework,42 utilizing a custom thermodynamic database of Fe(II) and Fe(III) complexes and solid phases previously published in Furcas et al.,32 accompanied by selected auxiliary species taken from Grenthe et al.43 and Hummel et al.44 The mineral–water interaction of Γ can be described as
| 16 |
where νi and ai are the stoichiometric coefficient and activity of species i ∈ Θ, respectively. With n(x) being the bulk composition at equilibrium and n(b) representing the initial number of atoms present, the system’s total Gibbs free energy
| 17 |
is minimized subject to the molar balance
| 18 |
where M is the component-wise matrix of atomic balance coefficients.
Calculation of the Activity Coefficients
We denote the chemical potential of each constituent of the aqueous electrolyte solution i as
| 19 |
where gi is the partial molar Gibbs free energy in J mol–1; Mw,H2O = 18.0153 g mol–1 is the molecular weight of liquid water; and nw, ni, and niw represent the total number of moles of the aqueous phase, of constituent i and of the water solvent iw.45,46 For each species, the activity coefficient γi is computed according to the extended Debye–Hückel equation in Truesdell–Jones form
| 20 |
where bγ ∼ 0.098 for NaOH,
| 21 |
| 22 |
and the effective ionic strength
| 23 |
is computed from the charge of each species zj and their respective molarity, relative to 1 kg of water.47 Considering the density ϱ0 and dielectric constant ε0 of pure water at Tr = 298.15 K and Pr = 1 bar, the Debye–Hückel limiting law parameters are Aγ ∼ 0.5114 and Bγ ∼ 0.3288.
Implementation of Mineral–Water Reaction Kinetics
Dissolution and growth kinetics are incorporated in the minimization routine via a series of partial, rather than complete equilibria, as described by Kulik and Thien.48 The number of solid species n(x)j ∈ Γ is changed based on its saturation index Ωj.49 For
| 24 |
where ηj is the dual-solution chemical potential, g°j is the standard Gibbs free energy in J mol–1, and γj is the activity coefficient of phase j. The number of moles n(x)j at time step t + Δt may be computed as
| 25 |
for
| 26 |
and
| 27 |
for
| 28 |
where Aj,t is the total particle surface area, Rj,t is the rate of phase growth in mol m–2 s–1, and ϵj is the stability criterion for phase j at time t. These series simulate the stepwise precipitation from supersaturation (log10 Ωj > 0) and dissolution in undersaturated conditions (log10 Ωj < 0). The kinetic rate laws that govern changes to the bulk elemental composition of the chemical system due to the formation and dissolution of Γ may be written as
| 29 |
∀ i ∈ Θ,
∀j ∈ Γ, ∀t, where kj is the reaction
rate constant and Ωj,t denotes the
dimensionless saturation index of species j at time t. Moreover, ai,t represents the activity of species i at time t and wi,j, pj, and qj are treated as empirical parameters. For
a specific molar volume of Vm,j in m3 mol–1, the mean orthogonal
velocity of surface propagation 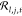 is related to the rate of phase formation
is related to the rate of phase formation  , according to
, according to
| 30 |
In these Palandri–Kharaka-type reaction rate expressions,39 the saturation index is evaluated directly from the dual-solution chemical potential of phase j, as displayed in eq 24.
Surface Area and Morphology Correction
Changes to the mineral surface area Aj are incorporated into the molar balance of each phase j ∈ Γ by two different models part of the TKinMet library of the geochemical modeling package GEM-Selektor.46,48 Consider the growth of Γ, as schematically illustrated in Figure 7.
Figure 7.
Schematic illustration
of the growth process of mineral particles
at the mean orthogonal velocity of surface propagation 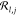 . The resultant
increase of the particle
diameter and thus particle volume Vj, surface area Aj, and mass mj causes
a reduction in specific surface area As,j and surface area per unit volume Av,j.
. The resultant
increase of the particle
diameter and thus particle volume Vj, surface area Aj, and mass mj causes
a reduction in specific surface area As,j and surface area per unit volume Av,j.
The increase of particle diameter dj at time t to 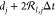 at time t + Δt at the mean orthogonal rate of surface
propagation
at time t + Δt at the mean orthogonal rate of surface
propagation  increases the particle volume Vj, surface area Aj and mass mj, while
the specific surface area As,j = Aj/mj and
the area per unit volume Av,j = Aj/Vj are expected to reduce. This
reduction can be computed from the initial specific surface area As,j,0 by the simple cubic root correction
increases the particle volume Vj, surface area Aj and mass mj, while
the specific surface area As,j = Aj/mj and
the area per unit volume Av,j = Aj/Vj are expected to reduce. This
reduction can be computed from the initial specific surface area As,j,0 by the simple cubic root correction
| 31 |
where nj,0 and nj,t represent the initial and final number of moles of phase j.48,50 The expected reduction to the surface area per unit volume can alternatively be described by
| 32 |
where all parameters have their usual meaning. The shape factor ψj in eq 32 is equivalent to the sphericity coefficient, as described by Wadell51
| 33 |
where Vj and Aj are the mean particle volume and surface area and dj = 6/(ψjAj) is the estimated particle diameter. Further, changes in morphology upon dissolution and growth are accounted for by the shape factor function, expressed as a formal power series
| 34 |
of the phase saturation index u = log10 Ωj,t.50
Data Availability Statement
The data that support the findings of this study are available within the article and its Supporting Information.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.4c06818.
Additional plots of the saturation indices of 2-line ferrihydrite and goethite, their dissolution and precipitation rates, and specific surface areas; derivation of the rate of 2-line ferrihydrite dissolution; and list of symbols and notations (PDF)
Author Contributions
F.E.F., S.M., B.L., and U.M.A. conceived the overall study; all authors contributed to the study design, analysis, and interpretation of the results. F.E.F. wrote the main draft of the manuscript, to which all authors contributed. U.M.A. was the main supervisor of the project. All authors read and approved the final manuscript.
The authors are grateful to the European Research Council (ERC) for the financial support provided for Fabio Enrico Furcas under the European Union Horizon 2020 research and innovation program (grant agreement no. 848794).
The authors declare no competing financial interest.
Footnotes
Supplementary Material
References
- Lemire R. J.; Berner U.; Musikas C.; Palmer D. A.; Taylor P.; Tochiyama O.. Chemical Thermodynamics of Iron, Part 1, Chemical Thermodynamics, 2013; Vol. 13. [Google Scholar]
- Schwertmann U. T. R. M.; Taylor R. M. Iron Oxides. Miner. Soil Environ. 1989, 1, 379–438. 10.2136/sssabookser1.2ed.c8. [DOI] [Google Scholar]
- Violante A.; Gaudio S. D.; Pigna M.; Ricciardella M.; Banerjee D. Coprecipitation of arsenate with metal oxides. 2. Nature, mineralogy, and reactivity of iron (III) precipitates. Environ. Sci. Technol. 2007, 41 (24), 8275–8280. 10.1021/es070382+. [DOI] [PubMed] [Google Scholar]
- Peak D.; Sparks D. L. Mechanisms of selenate adsorption on iron oxides and hydroxides. Environ. Sci. Technol. 2002, 36 (7), 1460–1466. 10.1021/es0156643. [DOI] [PubMed] [Google Scholar]
- Robertson J.; Hendry M. J.; Kotzer T.; Hughes K. A. Geochemistry of uranium mill tailings in the Athabasca Basin, Saskatchewan, Canada: A review. Crit. Rev. Environ. Sci. Technol. 2019, 49 (14), 1237–1293. 10.1080/10643389.2019.1571352. [DOI] [Google Scholar]
- Hering J. G.; Chen P.-Y.; Wilkie J. A.; Elimelech M.; Liang S. Arsenic removal by ferric chloride. J. AWWA 1996, 88 (4), 155–167. 10.1002/j.1551-8833.1996.tb06541.x. [DOI] [Google Scholar]
- Hering J. G.; Chen P.-Y.; Wilkie J. A.; Elimelech M. Arsenic removal from drinking water during coagulation. J. Environ. Eng. 1997, 123 (8), 800–807. 10.1061/(asce)0733-9372(1997)123:8(800). [DOI] [Google Scholar]
- Lin J.; Hu S.; Liu T.; Li F.; Peng L.; Lin Z.; Dang Z.; Liu C.; Shi Z. Coupled kinetics model for microbially mediated arsenic reduction and adsorption/desorption on iron oxides: role of arsenic desorption induced by microbes. Environ. Sci. Technol. 2019, 53 (15), 8892–8902. 10.1021/acs.est.9b00109. [DOI] [PubMed] [Google Scholar]
- Angst U. M. Challenges and opportunities in corrosion of steel in concrete. Mater. Struct. 2018, 51 (1), 4 10.1617/s11527-017-1131-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieland E.; Tits J.; Kunz D.; Dähn R. Strontium uptake by cementitious materials. Environ. Sci. Technol. 2008, 42 (2), 403–409. 10.1021/es071227y. [DOI] [PubMed] [Google Scholar]
- Tits J.; Stumpf T.; Rabung T.; Wieland E.; Fanghänel T. Uptake of Cm (III) and Eu (III) by calcium silicate hydrates: a solution chemistry and time-resolved laser fluorescence spectroscopy study. Environ. Sci. Technol. 2003, 37 (16), 3568–3573. 10.1021/es030020b. [DOI] [PubMed] [Google Scholar]
- Bozorth R. M. Structure of a protective coating of iron oxides. J. Am. Chem. Soc. 1927, 49 (4), 969–976. 10.1021/ja01403a010. [DOI] [Google Scholar]
- Xu P.; Zeng G. M.; Huang D. L.; Feng C. L.; Hu S.; Zhao M. H.; Lai C.; Wei Z.; Huang C.; Xie G. X.; Liu Z. F. Use of iron oxide nanomaterials in wastewater treatment: A review. Sci. Total Environ. 2012, 424, 1–10. 10.1016/j.scitotenv.2012.02.023. [DOI] [PubMed] [Google Scholar]
- Song G.; Chen M.; Zhang Y.; Cui L.; Qu H.; Zheng X.; Wintermark M.; Liu Z.; Rao J. Janus iron oxides@ semiconducting polymer nanoparticle tracer for cell tracking by magnetic particle imaging. Nano Lett. 2018, 18 (1), 182–189. 10.1021/acs.nanolett.7b03829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amrillah T.; Hermawan A.; Alviani V. N. Potential of iron oxides in photovoltaic technology. Cryst. Growth Des. 2023, 23 (4), 3034–3055. 10.1021/acs.cgd.3c00021. [DOI] [Google Scholar]
- Indra A.; Menezes P. W.; Sahraie N. R.; Bergmann A.; Das C.; Tallarida M.; Schmeißr D.; Strasser P.; Driess M. Unification of catalytic water oxidation and oxygen reduction reactions: amorphous beat crystalline cobalt iron oxides. J. Am. Chem. Soc. 2014, 136 (50), 17530–17536. 10.1021/ja509348t. [DOI] [PubMed] [Google Scholar]
- Schwertmann U.; Murad E. Effect of pH on the formation of goethite and hematite from ferrihydrite. Clays Clay Miner. 1983, 31 (4), 277–284. 10.1346/CCMN.1983.0310405. [DOI] [Google Scholar]
- Das S.; Hendry M. J.; Essilfie-Dughan J. Effects of adsorbed arsenate on the rate of transformation of 2-line ferrihydrite at pH 10. Environ. Sci. Technol. 2011, 45 (13), 5557–5563. 10.1021/es200107m. [DOI] [PubMed] [Google Scholar]
- Das S.; Hendry M. J.; Essilfie-Dughan J. Transformation of two-line ferrihydrite to goethite and hematite as a function of pH and temperature. Environ. Sci. Technol. 2011, 45 (1), 268–275. 10.1021/es101903y. [DOI] [PubMed] [Google Scholar]
- Grundl T.; Delwiche J. Kinetics of ferric oxyhydroxide precipitation. J. Contam. Hydrol. 1993, 14 (1), 71–87. 10.1016/0169-7722(93)90042-Q. [DOI] [Google Scholar]
- Soltis J. A.; Feinberg J. M.; Gilbert B.; Penn R. L. Phase transformation and particle-mediated growth in the formation of hematite from 2-line ferrihydrite. Cryst. Growth Des. 2016, 16 (2), 922–932. 10.1021/acs.cgd.5b01471. [DOI] [Google Scholar]
- Banfield J. F.; Welch S. A.; Zhang H.; Ebert T. T.; Penn R. L. Aggregation-based crystal growth and microstructure development in natural iron oxyhydroxide biomineralization products. Science 2000, 289 (5480), 751–754. 10.1126/science.289.5480.751. [DOI] [PubMed] [Google Scholar]
- Baumgartner J.; Dey A.; Bomans P. H. H.; Le Coadou C.; Fratzl P.; Sommerdijk N. A. J. M.; Faivre D. Nucleation and growth of magnetite from solution. Nat. Mater. 2013, 12 (4), 310–314. 10.1038/nmat3558. [DOI] [PubMed] [Google Scholar]
- Mundra S.; Tits J.; Wieland E.; Angst U. M. Aerobic and anaerobic oxidation of ferrous ions in near-neutral solutions. Chemosphere 2023, 335, 138955 10.1016/j.chemosphere.2023.138955. [DOI] [PubMed] [Google Scholar]
- Bottero J. Y.; Manceau A.; Villieras F.; Tchoubar D. Structure and mechanisms of formation of iron oxide hydroxide (chloride) polymers. Langmuir 1994, 10 (1), 316–319. 10.1021/la00013a046. [DOI] [Google Scholar]
- Rzepa G.; Pieczara G.; Gaweł A.; Tomczyk A.; Zalecki R. The influence of silicate on transformation pathways of synthetic 2-line ferrihydrite. J. Therm. Anal. Calorim. 2016, 125 (1), 407–421. 10.1007/s10973-016-5345-6. [DOI] [Google Scholar]
- Robertson J.; Hendry M. J.; Essilfie-Dughan J.; Chen J. Precipitation of aluminum and magnesium secondary minerals from uranium mill raffinate (pH 1.0–10.5) and their controls on aqueous contaminants. Appl. Geochem. 2016, 64, 30–42. 10.1016/j.apgeochem.2015.09.002. [DOI] [Google Scholar]
- Furcas F. E.; Lothenbach B.; Mundra S.; Borca C. N.; Albert C. C.; Isgor O. B.; Huthwelker T.; Angst U. M. Transformation of 2-line ferrihydrite to goethite at alkaline ph. Environ. Sci. Technol. 2023, 57, 16097–16108. 10.1021/acs.est.3c05260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham A. N.; Rose A. L.; Feitz A. J.; Waite T. D. Kinetics of Fe (III) precipitation in aqueous solutions at pH 6.0–9.5 and 25°c. Geochim. Cosmochim. Acta 2006, 70 (3), 640–650. 10.1016/j.gca.2005.10.018. [DOI] [Google Scholar]
- Blesa M. A.; Matijević E. Phase transformations of iron oxides, oxohydroxides, and hydrous oxides in aqueous media. Adv. Colloid Interface Sci. 1989, 29 (3–4), 173–221. 10.1016/0001-8686(89)80009-0. [DOI] [Google Scholar]
- Ostwald W. Studien über die Bildung und Umwandlung fester Körper: 1. Abhandlung: Übersättigung und Überkaltung. Z. Phys. Chem. 1897, 22 (1), 289–330. 10.1515/zpch-1897-2233. [DOI] [Google Scholar]
- Furcas F. E.; Lothenbach B.; Isgor O. B.; Mundra S.; Zhang Z.; Angst U. M. Solubility and speciation of iron in cementitious systems. Cem. Concr. Res. 2022, 151, 106620 10.1016/j.cemconres.2021.106620. [DOI] [Google Scholar]
- Michel F. M.; Ehm L.; Antao S. M.; Lee P. L.; Chupas P. J.; Liu G.; Strongin D. R.; Schoonen M. A. A.; Phillips B. L.; Parise J. B. The structure of ferrihydrite, a nanocrystalline material. Science 2007, 316 (5832), 1726–1729. 10.1126/science.1142525. [DOI] [PubMed] [Google Scholar]
- Schwertmann U.; Cornell R. M.. Iron Oxides in the Laboratory: Preparation and Characterization, 2nd ed.; John Wiley & Sons, 2008. [Google Scholar]
- Kashchiev D.Nucleation: Basic Theory with Applications; Elsevier, 2000. [Google Scholar]
- Zhu M.; Frandsen C.; Wallace A. F.; Legg B.; Khalid S.; Zhang H.; Mørup S.; Banfield J. F.; Waychunas G. A. Precipitation pathways for ferrihydrite formation in acidic solutions. Geochim. Cosmochim. Acta 2016, 172, 247–264. 10.1016/j.gca.2015.09.015. [DOI] [Google Scholar]
- Pokrovski G. S.; Schott J.; Farges F.; Hazemann J.-L. Iron (III)-silica interactions in aqueous solution: Insights from X-ray absorption fine structure spectroscopy. Geochim. Cosmochim. Acta 2003, 67 (19), 3559–3573. 10.1016/S0016-7037(03)00160-1. [DOI] [Google Scholar]
- Furcas F. E.; Mundra S.; Lothenbach B.; Borca C. N.; Huthwelker T.; Angst U. M. The influence of silicon on the formation and transformation of corrosion products. Cem. Concr. Res. 2024, 182, 107554 10.1016/j.cemconres.2024.107554. [DOI] [Google Scholar]
- Palandri J. L.; Kharaka Y. K.. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; Technical Report; US Geological Survey, 2004.
- Tadros M. E.; Skalny J.; Kalyoncu R. S. Kinetics of calcium hydroxide crystal growth from solution. J. Colloid Interface Sci. 1976, 55 (1), 20–24. 10.1016/0021-9797(76)90004-7. [DOI] [Google Scholar]
- Dreybrodt W.; Eisenlohr L.; Madry B.; Ringer S. Precipitation kinetics of calcite in the system CaCO3-H2O-CO2: The conversion to CO2 by the slow process H+ + HCO3– → CO2 + H2O as a rate limiting step. Geochim. Cosmochim. Acta 1997, 61 (18), 3897–3904. 10.1016/S0016-7037(97)00201-9. [DOI] [Google Scholar]
- Leal A. M. M.Reaktoro: An Open-Source Unified Framework for Modeling Chemically Reactive Systems, 2015. https://reaktoro.org (accessed Oct 05, 2024).
- Grenthe I.; Fuger J.; Konings R. J. M.; Lemire R. J.; Muller A. B.; Nguyen-Trung C.; Wanner H.. Chemical Thermodynamics of Uranium; Elsevier: Amsterdam, 1992; Vol. 1. [Google Scholar]
- Hummel W.; Berner U.; Curti E.; Pearson F. J.; Thoenen T. Nagra/PSI chemical thermodynamic data base 01/01. Radiochim. Acta 2002, 90 (9–11), 805–813. 10.1524/ract.2002.90.9-11_2002.805. [DOI] [Google Scholar]
- Wagner T.; Kulik D. A.; Hingerl F. F.; Dmytrieva S. V. GEM-Selektor geochemical modeling package: TSolMod library and data interface for multicomponent phase models. Can. Mineral. 2012, 50 (5), 1173–1195. 10.3749/canmin.50.5.1173. [DOI] [Google Scholar]
- Kulik D. A.; Wagner T.; Dmytrieva S. V.; Kosakowski G.; Hingerl F. F.; Chudnenko K. V.; Berner U. R. GEM-Selektor geochemical modeling package: revised algorithm and GEMS3K numerical kernel for coupled simulation codes. Comput. Geosci. 2013, 17 (1), 1–24. 10.1007/s10596-012-9310-6. [DOI] [Google Scholar]
- Helgeson H. C.; Kirkham D. H.; Flowers G. C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures: IV, Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5kb. Am. J. Sci. 1981, 281 (10), 1249–1516. 10.2475/ajs.281.10.1249. [DOI] [Google Scholar]
- Kulik D. A.; Thien B. M. J.. Adding Uptake Kinetics and Surface Entrapment to Geochemical Models: Code Extensions and Test Results. In 3rd Annual Workshop Proceedings, 7th EC FP–KIN, 2013; pp 127–159.
- Karpov I. K.; Chudnenko K. V.; Bychinskii V. A.; Kulik D. A.; Avchenko O. V. Minimization of Gibbs free energy in geochemical systems by convex programming. Geochem. Int. 2001, 39, 1108–1119. [Google Scholar]
- Thien B. M. J.; Kulik D. A.; Curti E. A unified approach to model uptake kinetics of trace elements in complex aqueous-solid solution systems. Appl. Geochem. 2014, 41, 135–150. 10.1016/j.apgeochem.2013.12.002. [DOI] [Google Scholar]
- Wadell H. Volume, shape, and roundness of quartz particles. J. Geol. 1935, 43 (3), 250–280. 10.1086/624298. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available within the article and its Supporting Information.









