Abstract
While operational stability has evolved to be the primary issue for the practical applications of perovskite solar cells (PSCs), the understanding of the origins of device degradation is still limited. Hysteresis is known as a unique and significant feature of PSCs. The hysteresis behavior of the current density-voltage (J–V) curves, governed by the interaction between the evolving ion-induced electric field and the carrier transport/recombination, offers rich and important information about the physical properties of the device. Herein, we propose to establish hysteresis as a diagnostic key to unveil and remedy degradation issues with device physics. With a custom-made ion-incorporated drift-diffusion simulator, we comprehensively investigate the relations between characteristic J–V hysteresis features and critical device issues such as bulk and surface defects, and low mobility of each layer in the PSCs. Ultimately, we derive a fundamental understanding and unveil the origins of the device degradation during the continuous operation of PSCs. This work therefore offers a new way to address and optimize PSC operational stability.
Subject terms: Photonic devices, Solar cells
The understanding of the origins of device degradation of perovskite solar cells remains limited. Here, the authors establish hysteresis as a diagnostic key to unveil and remedy degradation issues and investigate the relations between characteristic J-V hysteresis features and device deficiencies.
Introduction
Hysteresis behavior is a unique and significant feature of perovskite solar cells (PSCs), which is due to the slow dynamics of mobile ions inside the perovskite film1–9. It yields uncertain current density-voltage (J–V) curves of the cells depending on the voltage scan protocols. Walker et al.3 and Snaith et al.9 have analyzed this phenomenon based on the ion redistribution assumption that the ion accumulation will affect the carrier collection. Bisquert et al.10,11 proposed the surface polarization model because contact quality plays an important role in hysteresis. Tress et al.12 further experimentally confirmed the voltage-scan-rate dependent property of hysteresis and the important role of E-field on the hysteresis. Calado et al.5 modeled this process and proposed the effect of ion migration on the device measurement results other than J–V curves, and also unveiled that the J–V hysteresis are due to the ion migration and the recombination loss. Among these studies, efficient simulation for theoretical analysis shows the importance of understanding the physical processes in the device, while there are still very limited works focusing on this topic13.
The J–V characteristics of a solar cell offer rich information about device properties. For example, the defects in the contact layer can be investigated through studying the serious S-shaped J–V curves14–16. However, most measured J-V curves do not show conspicuous features like S-shape allowing the direct diagnosis of device performances. Other characterizations are used to understand the device physics, such as transient photoluminescence for detecting defects in the bulk17,18, transient photovoltage decay for recombination orders19–22, and many other kinds of spectroscopies for investigating the quality of the films23. These methods are powerful but sometimes require a combination of experimental measurement or additionally advanced characterization techniques, and the characterized results are hard to explain. Theoretical studies have been adopted to assist the experiments for understanding the device physics24–27 including carrier generation, recombination, transportation, and collection. Based on the previous studies of J–V characteristics of solar cells26,27, efficiency loss factors of solar cells have been identified, and the radiative and nonradiative recombination, series, and shunt resistances, and the quality of the contacts are described. But these works, which can diagnose the bottleneck issues (including bulk/surface recombination loss, interfacial energy alignment, and carrier mobility) of solar cells, ignore the unique and important ion migration-induced hysteresis in PSCs. Interestingly, as the hysteresis of the devices will be governed by the interaction between the ion migration and the various device deficiencies3,4,10, particularly bulk or surface recombination, J–V hysteresis features will uncover the hidden information (such as ion migration for E-field regulation, recombination and transportation) about the device. Therefore, taking into account ion migration and its influence on E-field and etc., it is desirable to quickly unveil the device physics by simply analyzing the hysteresis features.
Besides identifying the device deficiencies, the operational instability of PSCs is another barrier that prevents PSCs from commercialization4,28. Previously people have been focusing more on the long-term power conversion efficiency (PCE) loss, but it is also of great importance to understand the origins of degradation for making more stable devices. However, it is still quite challenging to in-situ characterize the degraded components or locations inside the device through experimental measurement. The examinations of J–V hysteresis could open the door for this problem. No matter what the chemical reasons are, the degradation in PSCs will present as additional efficiency loss terms like recombination centers. This fact implies that the hysteresis features of the degraded PSCs would also conceal the information about degradation.
In this work, we propose and establish an efficient custom-made drift-diffusion simulator with the capability for comprehensively studying the relationship between different J–V hysteresis features and the device deficiencies, such as the loss induced by the defects at the surface and in the bulk of perovskite, and low carrier mobility of the layers. We will study the detailed transient physical processes that will cause the hysteresis of PSCs, analyze the characteristic features of hysteresis, and unveil their influences on device performances. We will also offer a diagnosis approach to address the device intrinsic issues by assigning the hysteresis features to different device deficiencies. A group of PSCs with device deficiencies in experiments will be elucidated by our approach, and we will also extend the diagnosis to degradation issues. Two different kinds of PSCs will be diagnosed before and after the stability test, and we will discuss the origins of the degradations of each group.
Results
Theory and simulation
The mobile ion has been taken into account by incorporating the continuity equation of mobile ion into the conventional drift-diffusion model (continuity equations, Poisson’s equation) of electron and hole. The governing equations of the ion-incorporated drift-diffusion model are listed below. Equations1–4 represent the continuity equations of electron, hole, anion and cation mobile ionic carrier respectively, where Jn, Jp, Ja and Jc are the current of electron, hole, anion and cation ionic carriers; G and R denote the free carrier generation rate and recombination rate of electron and hole, respectively. Equation 5 is Poisson’s equation, considering doping (NA, ND), the positive mobile ionic carrier (c), and the negative mobile ionic carrier (a). ε0 and εr are the vacuum dielectric constant and the relative dielectric constant. Generation rate G can be uniform in the absorber for simplification, or depth-dependent, imported from optical simulation29,30. R in the modeling includes the intrinsic radiative (band to band) and defect-assisted Shockley-Read-Hall (SRH) recombination terms, whereas Auger recombination can be ignored in PSCs10.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
We assume that there is no generation nor recombination terms for mobile ions, as the total amount of mobile ions are fixed. The recombination kinetic equations include the radiative Rrad = krad (np - n2i) and SRH recombination RSRH = (np - n2i) / [τn(p + pt) + τp(n + nt)], where ni refers to the intrinsic carrier density. The capture coefficient and density of the defect are represented by the reciprocal of their product, SRH lifetime τn(p), which is intuitional and directly related to the characteristic lifetime measured in transient photoluminescence study. Trapped electron and hole densities are nt and pt, respectively, which depend on the energy levels of their trap states.
Regarding the carrier diffusion coefficients of mobile ions that are 10 orders lower than those of electrons and holes8,9,31, the ion-incorporated drift-diffusion model will be solved by the transient approach by utilizing the Gummel’s method with a modified backward-Euler finite difference scheme, which is fully implicit and stable and ensure the accurate simulation results32. Although the penetration of ions into carrier transporting layers (CTLs) or even electrodes are reported23,33,34, it is still questionable whether the ions that penetrated in CTLs can move freely and back to perovskite, then affect the device performance electrically like in the perovskite bulk. In this work, to simplify the model we assume the mobile ions will only move in the perovskite bulk region, and the interfaces between perovskite and CTLs including both the electron transporting layer (ETL) and hole transporting layer (HTL) will block their transportation. Thus, a barrier layer is set for the mobile ion in the heterojunction interface between perovskite and CTL in the model. The Scharfetter-Gummel-based finite-difference discretization form of the governing equations in the space and time domain is described in detail in Supporting Information and the computation procedure is schematically expressed in Supplementary Fig. 1. In the next section, we will perform an ion-incorporated drift-diffusion simulation to study the J–V hysteresis issues. The input parameters (Supplementary Table 1) and the energy band diagram of n-i-p PSC used for the simulation are given in the Supplementary Fig. 2.
Hysteresis characteristics
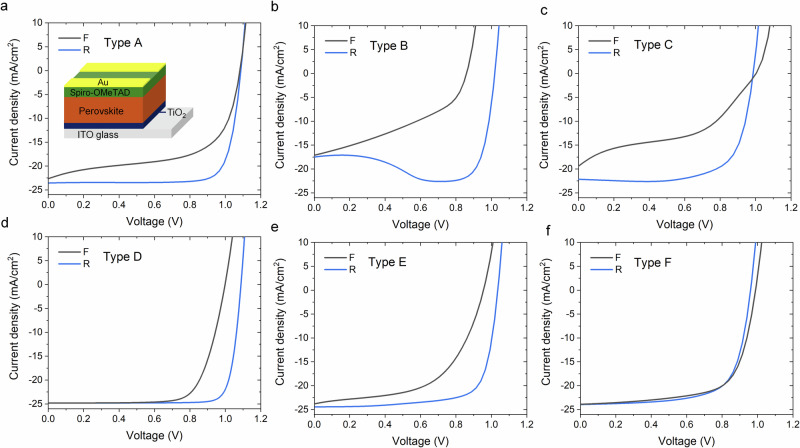
Several kinds of hysteresis features, hereafter named as hysteresis characteristics, have been summarized and distinguished from literatures3,5,8,12,34–41. Interestingly, most PSCs fabricated by different approaches, perovskite absorbers and CTLs, can be classified into those kinds of hysteresis (See Fig. 1)11. As a dynamic process relates to the E-field, ion distribution and their evolution, the hysteresis characteristics will vary with the voltage scan protocol10. For instance, too fast or too slow a scan will result in hysteresis-free J–V curves, and pre-bias of PSC before the scan will also affect the J–V characteristics. Therefore, in this section, we will discuss the hysteresis characteristics with the considerations of the voltage scan protocols usually applied in the experiments. In this section, “forward” voltage scan refers to the scan from the short-circuit state (SC state, 0 V) or negative voltage, to the voltages larger than the open-circuit state (OC state), and “reverse” voltage scan means the opposite direction. In the following paragraphs, the default voltage scanning protocol refers to the long-time pre-bias of devices at 0 V, followed by forward voltage scan (0 V to 1.3 V) and then reverse voltage scan (1.3 V to 0 V). The scanning protocol is hereafter named as “FR” scan. Revisiting the reported hysteresis characteristics, we modeled these features and shown them in Fig. 1. We reproduced all these hysteresis features, which indicated the device deficiencies such as the specific film/interface quality issues can be distinguished by just checking the hysteresis features of the devices. A detailed discussion can be given in the following sections.
Fig. 1. Simulated hysteresis characteristics.
a, b, c bulk recombination effect dependent hysteresis characteristics. d surface recombination dependent hysteresis characteristics. e, f synergetic effects induced hysteresis characteristics. “F” and “R” refer to forward and reverse voltage scans, respectively. The schematic diagram of simulated device configuration is inserted in (a).
Type A as in Fig. 1a: This kind of hysteresis shows a considerably lower photocurrent at voltages smaller than Voc in the forward scan, while the Voc of forward and reverse scan curves is similar35,36.
Type B as in Fig. 1b: The forward scan curve is like that in Type A, but the reverse scan curve shows pronounced photocurrent increment, even a current bump larger than Jsc, at the voltage close to Voc. However, this additional photocurrent will fade out when the voltage decreases towards 0 V3,12,37.
Type C as in Fig. 1c: This kind of hysteresis shows higher Voc but a dramatic drop in both photocurrent and fill factor in the forward scan3,12.
Type D as in Fig. 1d: This kind of hysteresis shows a drop in Voc in the forward scan but the same/similar Jsc and fill factor38,39.
Type E as in Fig. 1e: This kind of hysteresis shows a lower fill factor and a drop for both Voc and Jsc in forward scan36.
Type F as in Fig. 1f: This kind of hysteresis shows a cross of the forward and reverse scan curves, and similar fill factor Voc and Jsc in both forward and backward scans38,40,41.
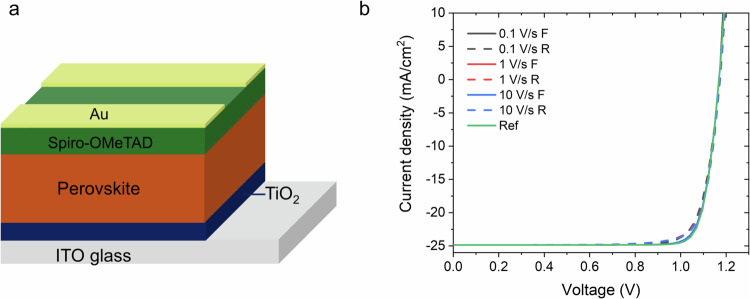
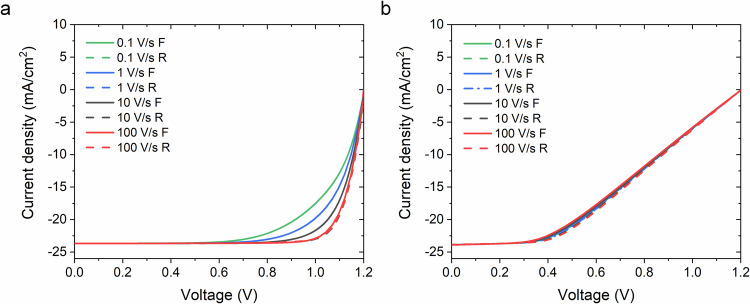
Before the discussion, we would like to point out that, only with significant non-radiative recombination inside PSCs, ion migration can induce clear hysteresis, as reported previously in Refs. 5 and 42. We have simulated a high-performance n-i-p PSC with PCE ≈ 24.7% and Voc ≈ 1.17 V43, and plotted the J–V hysteresis curves with different voltage scan rates in Fig. 2. It can be observed that in such high-performance device with minimal recombination and efficient carrier transport, the hysteresis is negligible with scan rates from 0.1 V/s to 10 V/s, and the J–V hysteresis curves are very close to the reference J–V curve without mobile ion. This result unveiled that J–V hysteresis highly depends on the device deficiencies, and conversely, also indicates the analysis of PSCs through J–V hysteresis can help to diagnose the device deficiencies.
Fig. 2. Simulated hysteresis of the high-performance PSCs with different voltage scan rates and FR protocol.
a device configuration diagram of simulated n-i-p PSC. b scan rates dependent JV characteristics of PSC, where “Ref” refers to the reference device without mobile ion.
Type A, B, C: Bulk recombination effect
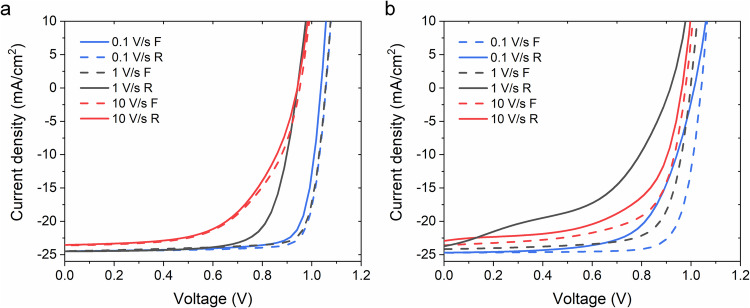
The quality of the perovskite active layer (such as intrinsic defects, and film degradations) is one of the crucial factors affecting the PSC performances30. For those non-optimized perovskite films, we assign large bulk recombination to defect-assisted SRH recombination and change the rate of recombination by varying SRH recombination lifetime τSRH (i.e., τn(p)). The case with short τSRH is considered as large recombination while long τSRH means small recombination. A long surface recombination lifetime (τSRH = 1 μs) is considered in this part of study.
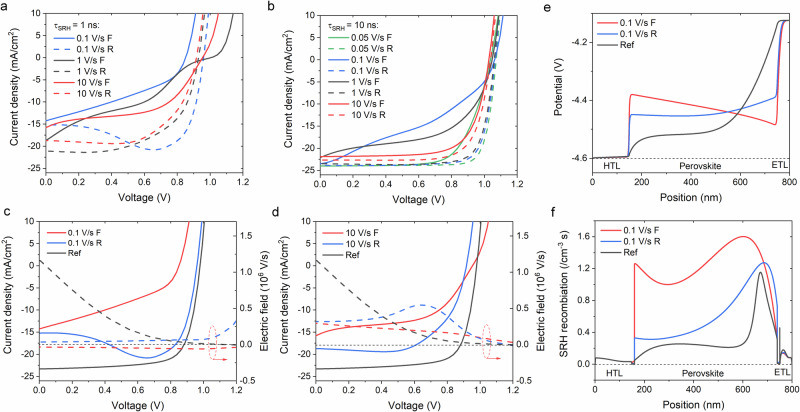
The J–V hysteresis curves with large bulk recombination under different voltage scan rates are shown in Fig. 3, which includes the cases Type A, B, and C in Fig. 1 (A: black line, 1 V/s in Fig. 3b; B: blue line, 0.1 V/s in Fig. 3a; and C: red line, 10 V/s, in Fig. 3a). In all of the cases with different scan rates, the photocurrents of the forward scan curves are always lower than those of the reverse scan curves, and the photocurrent can be improved with slower scan rate (will be discussed later). The curves (for both forward and reverse) of 10 V/s high scan rate show very pronounced resistive features, which means the extraction of photogenerated carriers in the bulk is hard. The largest hysteresis loops in Fig. 3b can be obtained by the intermediated scan rate 0.1 V/s. This hysteresis feature was previously reported and explained by the effect of rate-dependent E-field12, and our simulation study further related this feature to the specific nonradiative SRH recombination issue of the perovskite. We then studied the transient E-field changes with the sweeping voltage of different scan rates shown in Fig. 3c, d. The E-field was probed in the middle region of the perovskite bulk, i.e., 300 nm depth for the 600 nm thick perovskite, which will affect the extraction of carrier generated in the bulk most. The J–V curve and E-field of the reference device without mobile ions are also shown in Fig. 3c, d, in which ion migration is not considered but other parameters are the same.
Fig. 3. Simulated hysteresis originated from the dominated SRH recombination in perovskite bulk.
a τSRH of 1 ns and (b) 10 ns. The simulated transient E-field in the middle of perovskite bulk vs applied voltage compared with the corresponding hysteresis curves of (c) 0.1 V/s and (d) 10 V/s scan in (a). “Ref” refers to the reference device without mobile ion. e, f the position-dependent potential and bulk recombination profiles under a bias of 0.8 V, respectively.
At the starting voltage of 0 V, the potential drop from ETL to HTL will drive the cation and anion mobile ions to move out from their initial places and accumulate at the perovskite/CTL interface. This accumulation of mobile ions will continuously cancel the potential drop until the equilibrium state is reached, where the E-field in the bulk reduces to almost zero (as the red dashed curves in Fig. 3c, d) and the ion distribution becomes stable. The stabilized potential distribution at 0 V of the device with the consideration of mobile ion was compared with the reference case (without mobile ion), as shown in Fig. 3e. Afterwards, the voltage scan from the starting voltage of 0 V will break this equilibrium state as the positive voltage applied to the device decreases the potential drop. As a result, the mobile cations and anions on the HTL and ETL sides, respectively, will start to move backward to rebalance the potential. In this process, the voltage scan rate plays an important role: on the one hand, when the forward voltage scans faster than the ion redistribution, the accumulated mobile ion near CTL will contribute to a negative E-field in the bulk, which prevents the carrier extraction and causes a large bulk recombination and a reduction of photocurrent, as displayed in Fig. 3f. As the comparison of the reference case under forward scan E-fields in Fig. 3c, d, the positive E-field accelerates the carrier extraction, but the ion-induced negative E-field does not. On the other hand, the slower the voltage scan, the less mobile ions remain on the CTL sides. The consequent E-field can extract a higher photocurrent as confirmed in Fig. 3c, and the summarized plot in Fig. 3a.
For clarification, the transient potential distributions in the forward and reserve scan at the scan rate of 0.1 V/s were plotted in Fig. 3e, as well as the corresponding ion distributions were shown in Supplementary Fig. 3. When the bias voltage continues to increase and the ion to accumulate, the potential in the bulk will start to increase from HTL to ETL (see in Fig. 3e), as confirmed by the negative E-field of reference device in this regime of voltage (see in Fig. 3c). The mobile ions will be driven from HTL to ETL side, and counter-adjust the potential. When the voltage sweeps back to 0 V, as shown in Fig. 3c, the positive potential and E-field induced by the accumulation of ions near CTL benefits the carrier extraction (see in Fig. 3e), and thus the photocurrent of the reverse scan curve is larger than the forward current. The lower bulk recombination can be observed under the reverse scan, as displayed in Fig. 3f. This process also depends on the scan rate: if the voltage scans too fast and the redistribution of ions from the forward to reverse scans is negligible, the reverse-scan photocurrent will be unfavorably affected by the E-field in the bulk (see Fig. 3d). Based on Fig. 3c−f, we can conclude that the ion distribution evolution only adjusts the potential timely with the slow scan. The slow voltage scan will result in an insignificant Jsc difference between forward and reverse scans but will still exhibit a bump in the J–V curve, and the photocurrents are still lower than that of the reference device, due to the low E-field explained above.
With the understanding of the J–V characteristics under the effects of bulk recombination and ion migration, we further emphasize the important issues of the large SRH recombination on producing the different types of hysteresis characteristics in J–V curves (i.e., Type A, B and C). There is a large photocurrent loss (i.e., the quenched photogenerated carriers) that comes from the additional recombination during the slow extraction due to the serious loss term, e.g., defects in perovskite bulk. In Fig. 3a, b, we compared the J–V hysteresis curves of the devices with τSRH = 1 ns and 10 ns. With the same voltage scan rate, τSRH = 1 ns device shows more pronounced hysteresis and larger photocurrent loss for the forward scan curve (and extra photocurrent for the reverse scan curve), which indicates the role of high SRH bulk recombination. Type B and C come from the higher SRH bulk recombination (i.e., τSRH = 1 ns) with different voltage scan rates, while Type A can be attributed to a low SRH bulk recombination (i.e., τSRH = 10 ns). The SRH recombination rate distributions of the device at 0.8 V during the 0.1 V/s forward and backward scan were compared in Fig. 3f, which further implies the different recombination at the same voltage causes the current difference in hysteresis J–V characteristics. Meanwhile, the low electron and hole mobilities in the bulk region will also contribute to this process. The J–V hysteresis curves with τSRH = 10 ns but lower carrier mobilities are shown in Supplementary Fig. 4, in which a larger hysteresis is close to those in Fig. 4a can be found.
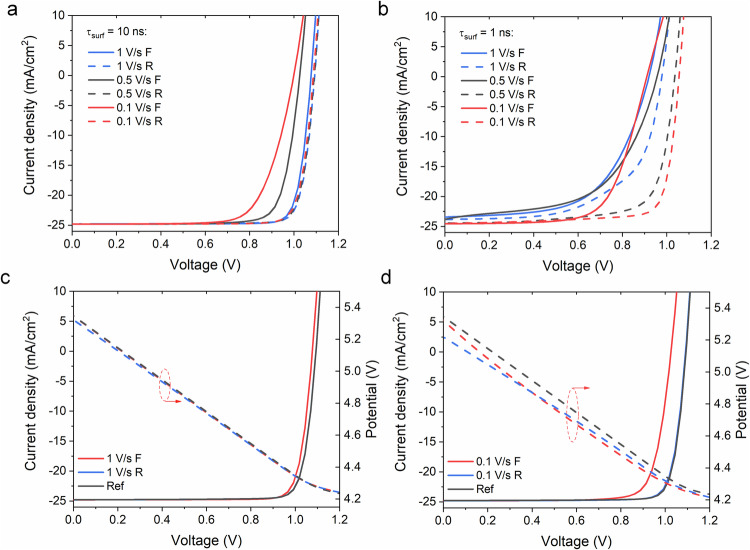
Fig. 4. Simulated hysteresis originated from the dominated surface recombination.
The interfaces recombination between perovskite and CTLs with (a) τsurf = 10 ns and (b) τsurf = 1 ns. The simulated transient E-field at perovskite/HTL interface vs applied voltage compared with the corresponding hysteresis curves of (c) 0.1 V/s and (d) 1 V/s in (a). “Ref” refers to the reference device without mobile ion.
Another example that can support the explanation above is the hysteresis obtained by different pre-bias voltages. We simulated the J–V curves based on the same modeling device in Fig. 3a, but with opposite voltage scan protocol: starting from the pre-bias at 1.3 V, sweeping from 1.3 V to 0 V, then backward, named by “RF”. The results are compared with Fig. 3a and shown in Supplementary Fig. 5. Different from Fig. 4a, the pre-bias at 1.3 V drives mobile ions to accumulate near CTL and forms the E-field beneficial to the extraction, thus largely improving photocurrent approaching the reference Jsc. The distinction between the J–V curves obtained from FR and RF protocols in Supplementary Fig. 5 also indicates the role of bulk recombination in the modeled device. The theoretical results successfully explain the experimental J–V hysteresis curves reported in our previous work44, in which the main loss in the Bi-doped device is attributed to bulk recombination coupled with low mobility, but neither surface recombination nor poor contacts.
In summary, taking the voltage scan protocol FR, we can attribute the J–V hysteresis features showing obvious photocurrent difference and even the formation of a current bump at low voltage, but no clear Voc change, i.e., Type A, B, and C, to the existence of device deficiencies in the perovskite bulk, which could be defects, others resulting in the high bulk SRH recombination and low carrier mobility. Besides, our results also suggest the study of the different scan protocols FR and RF, can also help to identify the bulk SRH recombination in the perovskite layer.
Type D: Surface recombination effect
Besides the bulk recombination related Type A, B and C hysteresis characteristics discussed above, we can ascribe Type D to the existence of large surface recombination at the interfaces between perovskite and CTLs, due to the surface defects, which are believed to be the main loss in the state-of-the-art high-efficiency PSCs. Negligible bulk recombination (e.g., τSRH = 1 μs) but high surface recombination (τsurf = 10 ns and 1 ns) was set in the simulation, and the corresponding J–V hysteresis curves are shown in Fig. 4a, b, where Type D is included. The simulation methods of surface recombination can be found in Supporting Information. Similar to the definition of τSRH, surface recombination lifetime τsurf is physically related to the reciprocal of the product of surface defect density and its capture cross-section. The higher the surface defect density, the lower τsurf.
Quite different from the bulk recombination cases, the forward and reverse scan curves do not show the large difference of photocurrent at low voltages, but obvious change in Voc. To study the effect of surface recombination, the E-field was probed at the perovskite/HTL interface, where the E-field will particularly influence surface recombination by changing the carrier transport. We plotted the transient potential as a function of sweeping voltage of 0.1 V/s and 1 V/s rates in Fig. 4c, d. With the increase of voltages, the accumulated cation ion will decrease the E-field at perovskite/HTL interface. In this condition, the lower and potential and E-field intensity at the interfaces leads to the possibility of carrier trapping by the surface defects. As shown in Fig. 4c, the potential of forward and reverse curves shows reflectively small change due to relatively few ions accumulates at the interface for a fast scan. Thus, similar JV curves under forward and reverse bias compared to reference devices (In the bulk, ions move back and forth to balance the potential; all potential drops fall at the interfaces). However, with slow scan in Fig. 4d, the Voc of forward curve is lower than the same reference voltage, while the Voc of reverse curve is much closer, which is due to the different ion induced potential in these two cases. The cation and anion ion density distributions at Voc of the cases in Fig. 4c, d are shown in Supplementary Fig. 6. The faster forward scan will remain more mobile ion near HTL and form potential barriers, which will heavily prevent the carrier transport, and increase the surface recombination loss. The slight accumulation of ions near HTL at the reverse Voc results in the comparable E-field to the reference case at the interfaces, thus the comparable Voc.
The higher surface defect density hysteresis curves (τsurf = 1 ns) are shown in Fig. 4b. Comparing to the hysteresis in Fig. 4a, the larger Voc difference between curves with the same scan rate indicates this characteristic hysteresis feature is indeed caused by surface defects but nothing else, and this explanation can be supported by experimental results that Voc difference is reduced after surface passivation45,46.
Another important phenomenon can be observed with the opposite scan protocol. For the case with pre-bias at 1.3 V and RF scan protocol, plotted in Supplementary Fig. 7a, the reverse scan curves of different rates overlap, but the Voc of forward scan curves will increase when the scan rate decreases. This simulated results well explain the experiments phenomena that where the same scan protocol was applied and similar hysteresis features were observed47. This change can also be interpreted by the transient E-field at the perovskite/HTL interfaces, shown in Supplementary Fig. 7b. With different scan rates, the E-fields at the interfaces of the reverse curves are similar at high voltages, and thus will not affect the Voc. But the scan rates do influence the E-fields when sweeping forward, which causes different forward Voc48.
In the discussion so far, surface recombination was set at the two interfaces between perovskite and CTLs simultaneously. However, surface recombination occurs at perovskite/ETL interface or perovskite/HTL interfaces only will produce the same hysteresis feature with slight Voc difference. We have simulated normal-structure PSCs (light comes from the ETL side) with a realistic optical generation profile in the perovskite (obtained from optical model31,48,49, shown in Supplementary Fig. 8) and surface recombination at different interfaces only. A significant hysteresis features were observed, as shown in Supplementary Fig. 9. Consequently, no matter the scan protocol is FR or RF, we can attribute the J-V hysteresis features showing large difference in Voc but not photocurrent, i.e., Type D, to the deficiencies exist at the perovskite surfaces, which could be due to the surface defects, and introduce large surface recombination. Meanwhile, the accumulation of the carriers at the interfaces due to the injection barriers will also boost the surface recombination, when the surface defects exist.
Low carrier mobility
We have also studied the influences of the low carrier mobility of perovskite or CTLs. In the discussion of bulk recombination, we mentioned that the low carrier mobility in the bulk region would contribute to the Type A, B and C hysteresis characteristics, here we demonstrate that the low carrier mobility will assist the non-radiative recombination. As shown in Fig. 5a, hysteresis of defect-free device (i.e., perovskite with only intrinsic radiative recombination and low carrier mobility) reveals Type A feature but weaker hysteresis. Regarding the case of CTLs with low carrier mobility, we have taken the ETL as an example. Since very low electron mobility of ETL (or low donor doping density) will introduce large additional series resistance to the device, it will convert the J–V of the device from diode type to resistance type. In this case, a lowered fill factor will be readily observed and the ion migration will only slightly influence the J–V curves (Fig. 5b), as the majority of electric potential drops in the ETL (with low carrier mobility) region but not perovskite region, and there is no substantial E-field that can drive the ion migration. Based on the fundamental assumption of the simulation that the mobile ions are blocked by the CTLs, ion migration only plays an important role in the perovskite bulk and surface region, thus cannot bend J–V curves anymore, and no hysteresis can be found, either. Because of the same reason, the problems induced by the electrodes, e.g., the diffusion of metal atom into Spiro-OMeTAD33,34, are not in the range of discussion in this work, as long as the perovskite layer and surface are not degraded by the problematic electrodes, where large recombination and resistive effect will raise.
Fig. 5. Simulated hysteresis originated from low conductivity.
a mobility of perovskite is μn(p) = 0.02 cm2/Vs and (b) mobility of ETL is μn = 210−5 cm2/Vs.
Type E, F: Synergetic effects
Moreover, the synergetic effect of bulk and surface recombination on hysteresis was also simulated and shown in Fig. 6, including higher surface recombination (Fig. 6a) and comparable bulk recombination (Fig. 6b). The hysteresis characteristics of the bulk and surface recombination, as discussed above, are mixed, where the effect of the stronger recombination mechanism will be more obvious. As a result, we can find the J–V hysteresis belongs to Type E (red line, 1 V/s in Fig. 6b) and Type F (black line, 10 V/s in Fig. 6a). Type E shows clear drops for both Voc and Jsc, which comes from the large bulk and surface recombination. Comparing the Type E curves with the red line of the same scan rate in Fig. 7a, the similar Voc and less Jsc difference of the latter one indicate the relatively low non-radiative recombination in the perovskite bulk, i.e., the higher film quality. We can also compare Type E curves with the black lines of the same scan rate in Fig. 6b, in which bulk recombination rate is the same. The larger difference of Voc of Type E points out the higher surface recombination loss and worse interfaces. Therefore, our results suggest people can quickly evaluate the importance of surface or bulk recombination in the overall losses of different devices by comparing the hysteresis features under the same scan rate and protocol. Type F, which shows a cross of forward and reverse scan curves and similar fill factors, can be attributed to the competition of bulk and surface recombination with specific scan rates using FR protocol. However, it is worth noting that the crossing hysteresis Type F can also be found in the cases of poor perovskite bulk and CTL (large bulk SRH recombination and low carrier mobility of CTL), as shown in Supplementary Fig. 10. This result indicates the crossing of J–V curves originates from the bulk recombination together with inefficient carrier extraction at the contacts, no matter it is due to surface recombination or the low carrier mobility in CTL.
Fig. 6. Simulated hysteresis originated from surface and bulk recombination.
a τSRH = 100 ns, τsurf = 10 ns and (b) τSRH = 10 ns, τsurf = 10 ns.
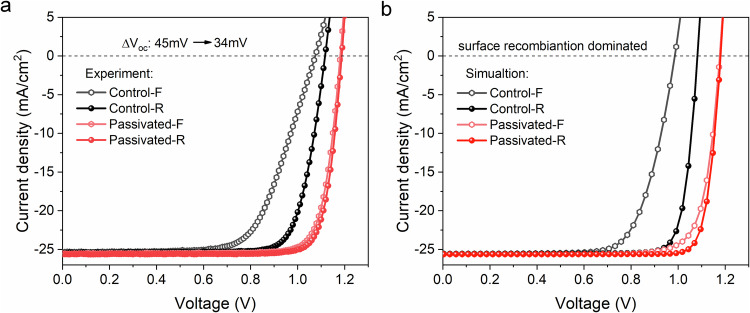
Fig. 7. Comparison of the experimental and theoretical performances of the of PSCs with a large voltage loss.
a experimental J–V hysteresis curves of the PSCs before and after the surface passivation treatment. b simulated J–V hysteresis curves of the PSCs with the same scan protocol as in experiments. The term “Control-F/R” denotes the control device under forward/reverse scan, respectively.
In summary, the hysteresis features discussed above originate from the combined effects of ion-migration-induced E-field change and the device deficiencies. Transient ion migration to ETL or HTL side will modify the E-field in the bulk and at the interfaces simultaneously, but depending on the dominated recombination, these modifications at different locations cause different kinds of the hysteresis. The change of E-field in the bulk coupled with high bulk SRH recombination and low carrier mobility in the bulk results in the discrepancies in photocurrent and the hysteresis features of Type A, B and C; and the change of E-field at the interfaces coupled with high surface recombination causes the hysteresis of Type D, in which the photovoltage Voc differs. When both of the bulk and surface recombination are pronounced, hysteresis shows Type E and F, while Type F can also be found with low carrier mobility of CTL. Therefore, slow ion migration should work with different recombination/transport mechanisms to perform the hysteresis features.
For systematic study, another more complex conditions were studied, where the surface and bulk recombination induced by defects, low conductivities in bulk and ETL were combined in the modeling devices (see Supplementary Figs. 11,12,13). The explanations of these cases can be directly extended from our discussions above as the effect of each kind of deficiencies can be mixed. The simulated hysteresis curves were plotted as indicated in Table 1 with the corresponding device deficiencies. Besides, our simulations also confirm the previous statement from Snaith et al.47 that the so-called hysteresis index (HI) does not really help with the estimation of the device performance, because there are such different kinds of hysteresis features, and each of them represents different device problems.
Table 1.
Summary of the simulated hysteresis curves of PSCs with specific device deficiencies
| Deficiencies | Bulk Rec. | Surf. Rec. | Low carrier mobility in bulk | Low carrier mobility in ETL |
|---|---|---|---|---|
| Bulk defects | Fig. 3 | |||
| Surf. defects | Fig. 6 | Fig. 4 | ||
| Low carrier mobility in bulk | Supplementary Fig. 4 | Supplementary Fig. 11 | Fig. 5a | |
| Low carrier mobility in ETL | Supplementary Fig. 10 | Supplementary Fig. 12 | Supplementary Fig. 13 | Fig. 5b |
Through the ion-incorporated simulation, we analyze the relationship between the characteristic hysteresis and the device deficiencies of the PSCs. From all the above discussions, we are ready to propose a simple diagnosis method for the deficiencies of PSCs by checking the hysteresis features of the J–V curves. While devices show features of Type A, B and C with FR protocol, or clear photocurrent difference with RF or FR scan protocols, we assign the device suffering from large SRH recombination, and also possibly low mobility of carriers in the perovskite bulk region, which should be attributed to the film quality and bulk defects. For devices with features of Type D, we can point the device experiencing large surface recombination at the interfaces due to the surface defects, which can be eliminated by surface passivation. For device featuring with Type E, which are proved to be the mixture of features belong to bulk and surface recombination, we suggest the device problems exist both in the bulk and at the interfaces. Regarding Type F, we suggest it can originate from bulk recombination together with the inefficient carrier extraction. We can also evaluate the influences of bulk or surface recombination in the devices by comparing their hysteresis curves at the same voltage scan rate with the same protocol. The diagnosis methods we obtained in this work are summarized in Table 2. Besides, more device problems as the combinations of different device deficiencies can be analyzed by comparing the J–V hysteresis as listed in Table 1.
Table 2.
Summary of diagnosis of PSCs by studying hysteresis characteristics
| Hysteresis features | Diagnosis through simulation | |
|---|---|---|
| Type | Description | |
| Type A | Large photocurrent difference only | |
| Type B | Obvious bump in reverse curve (FR protocol) | Deficiencies in the perovskite bulk (defect-assisted bulk SRH recombination, or low carrier mobility in the bulk) |
| Type C | Dramatic low FF of forward curve (FR protocol) | |
| Type A, B, C | Much larger photocurrent with RF protocol than that with FR protocol with dominated bulk recombination | |
| Type D | Obvious Voc difference only (FR/RF protocols) | Deficiencies at perovskite surface (defect-assisted surface SRH recombination) |
| Type E | Larger Voc and photocurrent of reverse curve (FR protocol) | Deficiencies in the bulk and at the surface of perovskite (defect-assisted bulk and surface SRH recombination, or low carrier mobility in the bulk) |
| Type F | Cross of forward and reverse curves, with low efficiency (FR/RF protocol, depending on scan rate) | Deficiencies in the bulk and inefficient carrier extraction (defect-assisted bulk and surface SRH recombination, and low carrier mobility in the CTL) |
| Type E, F | Relatively low FF | Low carrier mobility in the CTL/bulk results into large bulk recombination |
Discussion
Diagnosis the device physics of operation degradation
We will first study a group of PSCs with large voltage loss, and analyze their experimental J–V hysteresis curves before and after surface passivation treatment with our diagnostic method and simulation. Then we will extend our diagnosis from the problems caused during the fabrication to the issues related to degradation under continuous operation. Two different kinds of PSCs were fabricated and characterized for the stability (1 Sun illumination, room temperature, 300 h in N2). J–V hysteresis curves of them were measured and recorded before and after the degradation, and we will take these curves to deliver the diagnosis, and point out the degraded components/locations of each kind of PSCs. It is worth noting that, although the migration of ions itself does not necessarily cause unstable device, the ion-induced stability issue is still be presented and influences the degradation discussions50. Whenever there any chemical interaction will change the ion distribution and other device properties6, we can determine the different induced/additional losses induced in the degradation such as the unstable contacts or perovskite. Device simulations will be performed and compared with the experiments to support the diagnosis49. The input parameters for the simulation in this section will all be listed in Supplementary Table 2.
Case A: Device deficiencies at the surface
For studying large Voc loss of PSCs, we have fabricated p-i-n type PSCs (PTAA/PVK/PCBM:C60/ZrAcac/Ag) with obtaining additional PbI2 in the perovskite results in very low Voc of 1.08 V (forward) and 1.12 V (reverse). By passivating the perovskite/ETL surface with guanidinium iodide (GAI) treatment, Voc increases to 1.18 V (forward and reverse), as shown in Fig. 7a. Theoretically, with the given scan rate and protocol, the results agree well with the experimental ones as shown in Fig. 7b. The simulation results show that the surface recombination lifetime τsurf increases from 3 ns to 10 ns. By studying with the previous kinds of hysteresis, Type D hysteresis (as shown in Fig. 1) can match with these PSCs. As discussed previously, these PSCs is diagnosed as suffering from large surface recombination. In addition, since the Voc difference between the forward and reverse scan reduces from 45 meV to 34 meV for the PSCs without and with GAI treatment respectively, we can conclude the surface recombination is indeed passivated by GAI treatment.
Case B: Degradation in perovskite bulk
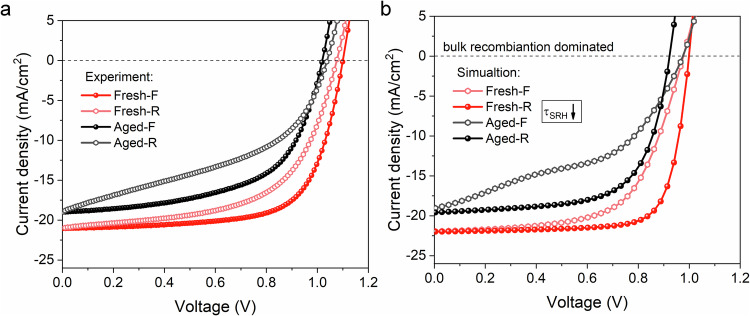
Moreover, we investigate the change of operation performances due to the degradation of bulk perovskite. The degradation diagnosis is shown in Fig. 8. We fabricated the PSCs with the structure of FTO/c-TiO2/meso-TiO2/perovskite/spiro-OMeTAD/Au. The voltage scanned from 1.2 V to 0 V, then back to 1.2 V with 0.1 V/s. Supplementary Fig. 14 shows the operational stability test results of a mesoscopic PSC with maximum power point tracking method under 1-sun illumination. The J–V hysteresis curves before and after the operational stability test are shown in Fig. 8a. The simulated J–V hysteresis is obtained as shown in Fig. 8b. The bulk SRH recombination τSRH of the theoretical results show significantly reduction from 10 ns to 0.5 ns. In this example, the hysteresis of fresh device is close to Type A and Type E, which indicates the main loss is bulk recombination, together with slight surface recombination. Differently, after the stability test, the J–V hysteresis curves of the aged devices show larger loop of photocurrent at low voltages, and there is also a Jsc loss. The discussion in Fig. 3 and Supplementary Fig. 5 leads the diagnosis of the aged devices that the perovskite bulk rather than other components degrades when the device is under continuous operation. The efficiency loss after 300 hours mainly comes from the increasing bulk SRH recombination, which may be attributed to the generation of more defects/traps due to the decomposition of bulk perovskite etc. and finally results in decreasing the operational stability. Overall, from the J–V hysteresis diagnosis, we experimentally and theoretically show that even though there are different losses (bulk and surface recombination) in the fresh device, the loss during operation will evolve. In this case, the bulk recombination will increase and dominate the loss after 300 h of operation with a serious change in J–V characteristics and device performance parameters.
Fig. 8. Comparison of the experimental and theoretical performances of PSCs suffering from degradation of perovskite bulk.
a experimental J–V hysteresis curves of the PSCs before and after 300 h’ operation test. b simulated J–V hysteresis curves of the PSCs with the same scan protocol as in experiments.
From all the experimental cases, the analysis of the J–V hysteresis can firstly offer an approach to identify the origins of the device deficiencies which will contribute to loss. The diagnosis can in-situ study with the operation test to determine the change of the losses and finally state the modification of the losses after operation and explain the original reasons. The results/diagnosis can therefore offer a guideline to address the issues of the PSCs for optimizing device performances. It is worth to note that the diagnosis of the degraded devices provides a simple and efficient way to understand the stability issues of PSCs, which can be easily combined with other characterization methods, to further unveil the device physics behind this problem.
In this work, we establish hysteresis as the diagnostic key for unveiling device physic issues and thus optimizing performances of PSCs. We first have developed a modified drift-diffusion model with the incorporation of mobile ions in PSCs, which offer us an approach to investigate the transient physical change in the device induced by the evolution of ion distribution during J–V measurement. Through examination and modeling of the typical hysteresis characteristics, we have established the connections between the hysteresis features and the specific device deficiencies existed in the experiments, including bulk or surface defects, and low carrier mobility of the layers. The theoretical studies offer a simple platform to diagnose the losses existing in the PSCs and unveil the loss mechanisms, by just analyzing the J–V hysteresis features of the device. Taking this diagnosis method, we also examine device deficiencies of various fabricated PSCs, and extend its application to the study of degradation. We have diagnosed the aged PSCs as having unstable contacts or perovskite bulk, respectively, through examining the J–V characteristics. This work can serve as an efficient tool to quickly estimate the main deficiency or degradation of the devices, and also provide a systematic understanding of hysteresis behavior of PSCs.
Methods
Device fabrication
For the CsFA based PSCs, Cs0.17FA0.83PbI3 perovskite precursor solution was dissolved in the mixed solvent of DMF and DMSO with a volume ratio of 4:1. The precursors were then filtered by 0.2 µm PTFE syringe filter before use. Patterned ITO-coated glasses were washed with detergent, deionized water, acetone, and ethanol with ultra-sonication 15 min each and dried by a nitrogen gas flow. Then the ITO glasses were ultraviolet ozone treated for 20 min. After transferring substrates into the nitrogen-filled glovebox, the PTAA solution (2 mg/ml in toluene) was spin-coated on the top of the ITO substrate at 5000 rpm for 30 s and subsequently sintered at 100 °C for 10 min. The mixed perovskite precursor was then spin-coated onto the sample at 1000 rpm for 6 s and 4000 rpm for 30 s, Then the film was annealed at 100 °C for 60 min. Thereafter, a total concentration of 20 mg mL-1 mix solution of PC61BM/C60 (weight ratio, 2:3) in dichlorobenzene was spin-coated on top of the perovskite layer at 700 rpm for 60 s and then 4000 rpm for 60 s, followed by spin-coating ZrAcac (2 mg/ml in isopropanol) at 4000 rpm. Finally, 100 nm thick Ag electrode was thermally evaporated on top of the device under a base pressure of 10-4 Pa with a device area of 0.06 cm2.
For the mesoscopic PSCs, fluoride-doped tin oxide glass substrates (FTO, 4.0 mm-thick, 10 Ω/sq, Nippon Sheet Glass) were patterned using zinc powder and concentrated hydrochloric acid (1 M). The patterned FTO was sequentially cleaned by 2 % commercial detergent (Hellmanex) water solution, deionized water, ethanol, and acetone in ultrasonic bath for 15 min, rinsed with deionized water and then dried by air blowgun. After O3/ultraviolet treatment for 15 min, the 20–40 nm compact layer TiO2 (c-TiO2) was deposited on cleaned FTO substrate by spray pyrolysis at 450 °C using a precursor solution of titanium diisopropoxide bis(acetylacetonate), 75 wt.% in isopropanol is diluted with ethanol with a volume ratio of 1:9 and addition 4% volume ratio of additional acetylacetone and oxygen as carrier gas. After cooling down to room temperature and O3/ultraviolet treatment for 15 min, the mesoporous TiO2 (mp-TiO2) was spin-coated at 4000 rpm for 20 s onto the c-TiO2 using a commercial paste (Dyesol 30 NR-D) diluted in ethanol (1:6, weight ratio) to achieve 100 to 150 nm thickness. After drying at 80 °C for 10 min, the TiO2 films were sintered by gradually raising the temperature to 450 °C, keeping it at this temperature for 30 min and cooling it to room temperature. After cooling down to 150 °C, the substrates were transferred to dry-air glovebox (relative humidity <15%) for deposition of the perovskite films. The triple-cation perovskite films were prepared by a one-step antisolvent method. Briefly, a 1.4 M mixed cation Cs0.05(MA0.1FA0.9)0.95Pb(I0.9Br0.1)3 perovskite precursor solution with 3 mol% excess of PbI2 in the mixed solvent of DMF: DMSO (4 /1; v/v) was spin-coated at 2000 rpm (acceleration of 200 rpm s−1) and 6000 rpm (acceleration of 2000 rpm s−1) for 10 and 30 s, respectively. During the last 10 s of the second spin-coating step, 200 μL of chlorobenzene antisolvent was drop-casted. The perovskite film was then dried on a hot plate at 150 °C for 10 min to form perovskite layer. A hole transport material solution containing 75 mM spiro-OMeTAD (>99.5%, Xi’an Polymer Light Technology Corp.) in chlorobenzene with 40 mM Li-TFSI (99.95%, Sigma-Aldrich) and 270 mM tBP (96%, Sigma-Aldrich) additives was dynamic spin-coated onto the substrate at 3000 rpm for 30 s. The device fabrication was completed with deposition of a gold electrode (~70 nm) by thermal evaporation.
Solar cell characterizations
Simulated AM 1.5 sunlight was generated by an Abet Class AAB AM 1.5 G solar simulator. The light intensity (100 mW cm−2) was calibrated by an ISO 17025-certified KG3-filtered silicon reference cell. The J–V curve was recorded by a Keithley 2635 source meter. UV-vis absorption spectra were obtained from a UV-vis spectrometer (Perkin Elmer Lambda 750). The external quantum efficiency (EQE) spectra were collected with a photomodulation spectroscopic setup (Enlitech QE-R).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Acknowledgements
We acknowledge the fruitful discussion with Prof. Michael Grätzel and Dr. Felix Eickemeye. This research was supported by the seed fund of University Grant Council of the University of Hong Kong (Grant# 202011159254 and 202111159113), the General Research Fund (Grant# 17211220, 17200021, 17200823, and 17310624), and the Collaborative Research Fund (Grant No. C7035-20G) from the Research Grants Council (RGC) of Hong Kong Special Administrative Region, China and the support from Innovation and Technology Fund (MRP/040/21X, and GHP/245/22SZ). X.R. acknowledges funding from National Natural Science Foundation of China (Grant No. 62171001, 61701003) and of Anhui Province (2108085MF198, 1808085QF179), also with the support of Key R&D plan of Ministry of Science and Technology (2022YFB4200901-1, 2022YFB4200903) and the University Synergy Innovation Program of Anhui Province (GXXT-2022-009). H.Z. acknowledge the funding from Shanghai Pujiang Program (22PJ1401200) and the National Natural Science Foundation of China (No. 52302229). H-L.Y. acknowledge the funding from Green Technology Fund (GTF202020164) and General Research Fund (11307323).
Author contributions
Z.S.W., W.C.H.C. conceived the idea, and Z.S.W., Y.A., X.R., and W.C.H.C. contributed to the simulation calculation and manuscript writing for the study, with H.Z. performed the experiment support, with data interpretation from Z.F.H., H.L.Y., and Z.X.H. Hysteresis model were developed by Z.S.W., Y.A., and X.R. These authors contributed equally to this work: Z.S.W., Y.A., X.R., and H.Z. W.C.H.C coordinated the work. All authors critically reviewed, edited, and approved the final version of the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data that support the plots within this paper and other finding of this study are available from the corresponding authors upon request.
Competing interests
The authors have no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Zi Shuai Wang, Yidan An, Xingang Ren, Hong Zhang.
Change history
12/3/2024
A Correction to this paper has been published: 10.1038/s41467-024-54971-y
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53162-z.
References
- 1.Tress, W. Metal halide perovskites as mixed electronic-ionic conductors: Challenges and opportunities-from hysteresis to memristivity. J. Phys. Chem. Lett.8, 3106–3114 (2017). [DOI] [PubMed] [Google Scholar]
- 2.Tress, W., Correa Baena, J. P., Saliba, M., Abate, A. & Graetzel, M. Inverted current–voltage hysteresis in mixed perovskite solar cells: polarization, energy barriers, and defect recombination. Adv. Energy Mater. 6, 1600396 (2016).
- 3.Richardson, G. et al. Can slow-moving ions explain hysteresis in the current–voltage curves of perovskite solar cells? Energy Environ. Sci.9, 1476–1485 (2016). [Google Scholar]
- 4.Ren, X., Wang, Z. S. & Choy, W. C. H. Device physics of the carrier transporting layer in planar perovskite solar cells. Adv. Opt. Mater. 7, 1900407 (2019).
- 5.Calado, P. et al. Evidence for ion migration in hybrid perovskite solar cells with minimal hysteresis. Nat. Commun.7, 13831 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yuan, Y. & Huang, J. Ion migration in organometal trihalide perovskite and its impact on photovoltaic efficiency and stability. Acc. Chem. Res.49, 286–293 (2016). [DOI] [PubMed] [Google Scholar]
- 7.Eames, C. et al. Ionic transport in hybrid lead iodide perovskite solar cells. Nat. Commun.6, 7497 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bertoluzzi, L. et al. Mobile ion concentration measurement and open-access band diagram simulation platform for halide perovskite solar cells. Joule4, 109–127 (2020). [Google Scholar]
- 9.Snaith, H. J. et al. Anomalous hysteresis in perovskite solar cells. J. Phys. Chem. Lett.5, 1511–1515 (2014). [DOI] [PubMed] [Google Scholar]
- 10.Lopez-Varo, P. et al. Device physics of hybrid perovskite solar cells: theory and experiment. Adv. Energy Mater. 8, 1702772 (2018).
- 11.Ravishankar, S. et al. Surface polarization model for the dynamic hysteresis of perovskite solar cells. J. Phys. Chem. Lett.8, 915–921 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Tress, W. et al. Understanding the rate-dependent j–v hysteresis, slow time component, and aging in ch3nh3pbi3 perovskite solar cells: The role of a compensated electric field. Energy Environ. Sci.8, 995–1004 (2015). [Google Scholar]
- 13.Courtier, N. E., Cave, J. M., Walker, A. B., Richardson, G. & Foster, J. M. Ionmonger: a free and fast planar perovskite solar cell simulator with coupled ion vacancy and charge carrier dynamics. J. Comput. Electron.18, 1435–1449 (2019). [Google Scholar]
- 14.Tress, W. & Inganäs, O. Simple experimental test to distinguish extraction and injection barriers at the electrodes of (organic) solar cells with s-shaped current–voltage characteristics. Sol. Energy Mater. Sol. Cells117, 599–603 (2013). [Google Scholar]
- 15.Saive, R. S-shaped current–voltage characteristics in solar cells: a review. IEEE J. Photovolt.9, 1477–1484 (2019). [Google Scholar]
- 16.Wagenpfahl, A., Rauh, D., Binder, M., Deibel, C. & Dyakonov, V. S-shaped current-voltage characteristics of organic solar devices. Phy. Rev. B82, 115306 (2010).
- 17.Baloch, A. A. B. et al. Analysis of photocarrier dynamics at interfaces in perovskite solar cells by time-resolved photoluminescence. J. Phys. Chem. C.122, 26805–26815 (2018). [Google Scholar]
- 18.Stolterfoht, M. et al. Voltage-dependent photoluminescence and how it correlates with the fill factor and open-circuit voltage in perovskite solar cells. ACS Energy Lett.4, 2887–2892 (2019). [Google Scholar]
- 19.Bisquert, J. & Garcia-Belmonte, G. On voltage, photovoltage, and photocurrent in bulk heterojunction organic solar cells. J. Phys. Chem. Lett.2, 1950–1964 (2011). [Google Scholar]
- 20.Chen, X., Shirai, Y., Yanagida, M. & Miyano, K. Photocarrier dynamics in perovskite-based solar cells revealed by intensity-modulated photovoltage spectroscopy. Phys. Chem. Chem. Phys.20, 17918–17926 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Maurano, A. et al. Recombination dynamics as a key determinant of open circuit voltage in organic bulk heterojunction solar cells: A comparison of four different donor polymers. Adv. Mater.22, 4987–4992 (2010). [DOI] [PubMed] [Google Scholar]
- 22.Wood, S. et al. Transient photocurrent and photovoltage mapping for characterisation of defects in organic photovoltaics. Sol. Energy Mater. Sol. Cells161, 89–95 (2017). [Google Scholar]
- 23.Jeangros, Q. et al. In situ tem analysis of organic-inorganic metal-halide perovskite solar cells under electrical bias. Nano Lett.16, 7013–7018 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Tress, W., Leo, K. & Riede, M. Optimum mobility, contact properties, and open-circuit voltage of organic solar cells: A drift-diffusion simulation study. Phy. Rev. B85, 155201 (2012).
- 25.Sha, W. E. I., Ren, X., Chen, L. & Choy, W. C. H. The efficiency limit of ch3nh3pbi3 perovskite solar cells. Appl. Phys. Lett. 106, 155201 (2015).
- 26.Ren, X., Wang, Z., Sha, W. E. I. & Choy, W. C. H. Exploring the way to approach the efficiency limit of perovskite solar cells by drift-diffusion model. ACS Photonics4, 934–942 (2017). [Google Scholar]
- 27.Sha, W. E. I. et al. Quantifying efficiency loss of perovskite solar cells by a modified detailed balance model. Adv. Energy Mater. 8, 1701586 (2017).
- 28.Petrus, M. L. et al. Capturing the sun: a review of the challenges and perspectives of perovskite solar cells. Adv. Energy Mater. 7, 1700264 (2017).
- 29.Sha, W. E. I., Choy, W. C. H., Wu, Y. & Chew, W. C. Optical and electrical study of organic solar cells with a 2d grating anode. Opt. Express20, 2572–2580 (2012). [DOI] [PubMed]
- 30.An, Y. et al. Perovskite solar cells: Optoelectronic simulation and optimization. Sol. RRL2, 1800126 (2018).
- 31.Courtier, N. E., Richardson, G. & Foster, J. M. A fast and robust numerical scheme for solving models of charge carrier transport and ion vacancy motion in perovskite solar cells. Appl. Math. Modell. 63, 329–348 (2018).
- 32.Selberherr, S. Analysis and simulation of semiconductor devices, (Springer-Verlag Wien, 1984).
- 33.Fakharuddin, A., Schmidt‐Mende, L., Garcia‐Belmonte, G., Jose, R. & Mora‐Sero, I. Interfaces in perovskite solar cells. Adv. Energy Mater. 7, 1700623 (2017).
- 34.Zhang, T., Hu, C. & Yang, S. Ion migration: a “double‐edged sword” for halide‐perovskite‐based electronic devices. Small Methods4, 1900552 (2019).
- 35.Unger, E. L. et al. Hysteresis and transient behavior in current-voltage measurements of hybrid-perovskite absorber solar cells. Energy Environ. Sci.7, 3690–3698 (2014). [Google Scholar]
- 36.Sanchez, R. S. et al. Slow dynamic processes in lead halide perovskite solar cells. Characteristic times and hysteresis. J. Phys. Chem. Lett.5, 2357–2363 (2014). [DOI] [PubMed] [Google Scholar]
- 37.Nemnes, G. A. et al. Dynamic electrical behavior of halide perovskite based solar cells. Sol. Energy Mater. Sol. Cells159, 197–203 (2017). [Google Scholar]
- 38.Chen, B., Yang, M., Priya, S. & Zhu, K. Origin of j-v hysteresis in perovskite solar cells. J. Phys. Chem. Lett.7, 905–917 (2016). [DOI] [PubMed] [Google Scholar]
- 39.Wojciechowski, K. et al. Heterojunction modification for highly efficient organic-inorganic perovskite solar cells. ACS Nano, 8, 12701–12709 (2014). [DOI] [PubMed]
- 40.Zhao, Y. et al. Thick tio2-based top electron transport layer on perovskite for highly efficient and stable solar cells. ACS Energy Lett.3, 2891–2898 (2018). [Google Scholar]
- 41.Sepalage, G. A. et al. Copper(i) iodide as hole‐conductor in planar perovskite solar cells: probing the origin of j–v hysteresis. Adv. Funct. Mater.25, 5650–5661 (2015). [Google Scholar]
- 42.Yang, C., Shan, X. & Xie, T. Insights of hysteresis behaviors in perovskite solar cells from a mixed drift-diffusion model coupled with recombination. Photonics7, 47 (2020).
- 43.Jeong, M. et al. Stable perovskite solar cells with efficiency exceeding 24.8% and 0.3-v voltage loss. Science369, 1615–1620 (2020). [DOI] [PubMed]
- 44.Yavari, M. et al. How far does the defect tolerance of lead-halide perovskites range? The example of bi impurities introducing efficient recombination centers. J. Phys. Chem. A7, 23838–23853 (2019). [Google Scholar]
- 45.Xia, J. et al. Surface passivation toward efficient and stable perovskite solar cells. Energy Environ. Mater. 6, e12296 (2022).
- 46.Zhang, P. et al. Hysteresis-free and efficient perovskite solar cells using sno2 with self-assembly l-cysteine layer. Eng. Sci.20, 180–187 (2022).
- 47.Habisreutinger, S. N., Noel, N. K. & Snaith, H. J. Hysteresis index: a figure without merit for quantifying hysteresis in perovskite solar cells. ACS Energy Lett.3, 2472–2476 (2018). [Google Scholar]
- 48.Ai, Z. et al. Physics, simulation, and experiment of perovskite solar cells with addressing hysteresis effect. Sol. RRL6, 2200606 (2022).
- 49.An, Y., Wang, C., Cao, G. & Li, X. Heterojunction perovskite solar cells: Opto-electro-thermal physics, modeling, and experiment. ACS Nano14, 9 (2020). [DOI] [PubMed] [Google Scholar]
- 50.Khenkin, M. V. et al. Consensus statement for stability assessment and reporting for perovskite photovoltaics based on isos procedures. Nat. Energy5, 35–49 (2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the plots within this paper and other finding of this study are available from the corresponding authors upon request.