On the similar spectral manifestations of protonic and hydridic hydrogen bonds despite their different origin

Abstract

Previously studied complexes with protonic and hydridic hydrogen bonds exhibit significant similarities. The present study provides a detailed investigation of the structure, stabilization, electronic properties, and spectral characteristics of protonic and hydridic hydrogen bonds using low-temperature infrared (IR) spectroscopy and computational methods. Complexes of pentafluorobenzene with ammonia (C₆F₅H⋯NH₃) and triethylgermane with trifluoroiodomethane (Et₃GeH⋯ICF₃) were analyzed using both experimental and computational tools. Additionally, 30 complexes with protonic hydrogen bonds and 30 complexes with hydridic hydrogen bonds were studied computationally. Our findings reveal that, despite the opposite atomic charges on the hydrogens in these hydrogen bonds, and consequently the opposite directions of electron transfer in protonic and hydridic hydrogen bonds, their spectral manifestations - specifically, the red shifts in the X–H stretching frequency and the increase in intensity - are remarkably similar. The study also discusses the limitations of the current IUPAC definition of hydrogen bonding in covering both types of H-bonds and suggests a way to overcome these limitations.

Understanding hydrogen-bonding is essential for many fields of natural science. Here, the authors investigate protonic and hydridic hydrogen bonds using low-temperature infrared spectroscopy and computational methods, finding that despite opposite atomic charges on the hydrogens in these hydrogen bonds their spectral manifestations are remarkably similar.

Introduction

Non-covalent interactions determine not only the physicochemical properties of molecular clusters and condensed molecular matter but also the structure and properties of larger macro- and biomacromolecules^1–4. Among the various types of non-covalent interactions, hydrogen (H)-bonding plays a key role. Understanding H-bonding is thus essential for many fields of natural science. Recognizing its importance, the IUPAC introduced a definition in 2011 that encompasses not only the standard, red-shifted H-bonding but also the blue-shifting H-bonding discovered and described at the end of the 20th century^5–7. This definition, like any other, aims to be simple and unambiguous, and for a long time, it was believed that the IUPAC definition of H-bonding met these criteria.

Previous studies^8–14, including our recent ones^15,16 have identified some ambiguities in this definition. Specifically, according to the 2011 IUPAC definition of an X-H⋯Y hydrogen bond, the hydrogen atom bears a partial positive charge because it is covalently bound to a more electronegative atom⁷. Among the 92 stable elements of the periodic table, only nine (C, N, O, F, Cl, Br, I, S, Se) are more electronegative than hydrogen, while the rest are more electropositive. These hydrogens, with partial negative charges, are called hydridic. The different character of hydrogen, depending on whether it is covalently bound to a more or less electronegative atom, results in different electronic properties, including the direction of intermolecular charge transfer (CT).

In protonic X-H…Y H-bonds, atom or group of atoms Y is an electron donor, and CT is directed from Y to X-H. In hydridic H-bonds, the situation is mostly opposite: X-H is an electron donor, and Y is an electron acceptor, meaning the CT is directed from X-H to Y. Despite the different charges on hydrogen leading to opposite directions of CT, the spectral presentations of protonic and hydridic H-bonds are very similar. In both cases, the X-H bond is elongated, the respective stretching frequency is red-shifted, and the intensity of the corresponding spectral band systematically increases. It is important to note that only changes in stretching vibration frequencies and the intensity of the respective spectral bands are observable, as changes in bond length cannot be detected in the gas phase. These features are widely used to identify the existence of H-bonds and represent a fingerprint of H-bond formation⁷.

Previously, we investigated hydridic H-bonded complexes formed by Me₃SiH and several electron acceptors both experimentally and computationally¹⁵, and hydridic H-bonded complexes formed by transition metal hydrides and several electron acceptors computationally¹⁶. However, a direct comparison of protonic and hydridic H-bonds based on both reliable experimental and calculated data is still lacking.

The aim of the present paper is to investigate experimentally (using low-temperature IR spectroscopy) and computationally the origin and consequences of changes in electron density in electron donors and acceptors during the formation of protonic and hydridic H-bonds in C₆F₅H⋯NH₃ and Et₃GeH⋯ICF₃ complexes. In the first complex, hydrogen is protonic, while in the second, it is hydridic. Electronic changes accompanying the formation of both complexes are rather small, and to prevent misinterpretation of the data obtained, we used in both cases identical and as accurate as possible experimental and computational tools.

Systems considered

For calculations of hydridic hydrogen bond complexes, we selected Me₃SiH, Me₃GeH, Me₃SnH, and Et₃GeH as electron donors. The electron acceptors chosen included molecules with p-holes (BF₃), σ-holes (BrCN, ICF₃, ICN, PCl₃, P(CN)₃, and S(CN)₂), and π-holes (C₆(CN)₃H₃, COF₂, and NO₂F). To compare these with protonic hydrogen bond complexes, we selected H-bonded complexes from a reference¹⁶ and complexes from another study^17,18 with comparable ΔE to the hydridic hydrogen-bonded ones. Specifically, we chose complexes of ammonia with acetaldehyde and nitrosomethane; ethyne with acetaldehyde and acetone; hydrogen fluoride with acetone; hydrogen chloride with methanol and phosphorine; hydrogen bromide and hydrogen iodide with dimethyl sulfoxide, N-methylacetamide, tetrahydrothiophene, tetrahydroselenophene, tetrahydrotellurophene, trimethyl phosphate, and trimethylphosphine; methanethiol with methanol and phosphorine; methanol with acetamide and methylazide; pentafluorobenzene with acetone, ammonia, nitrosomethane, and trimethylphosphine; and water with furan and nitrosomethane.

Results and discussion

IR experiments

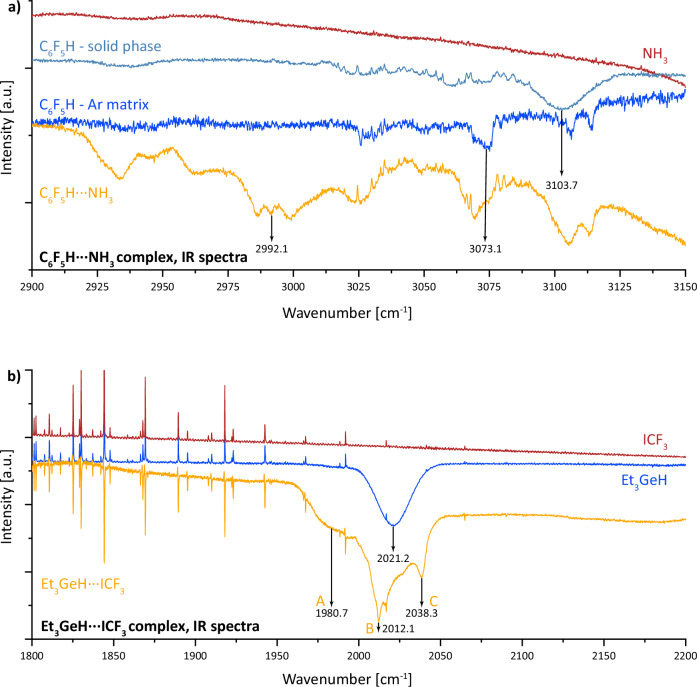
Orange spectrum in Fig. 1a, belongs to a mixture of Ar (500 parts), C₆F₅H (1 part) and NH3 (1 part by volume) obtained by supersonic expansion of this mixture on a KBr window cooled to 20 K. Comparison with this spectrum are C₆F₅H spectra measured in an argon matrix (blue) and spectrum of pure ammonia (red). In addition, the spectrum of C₆F₅H measured after direct injection of this substance onto a cooled window made of KBr material is added to the figure.

Fig. 1. Experimental Infrared spectra of investigated complexes, C₆F₅H···NH₃ and Et₃GeH···ICF₃ measured in the argon matrix.

a provides spectrum of C₆F₅H···NH₃ complex in yellow, C₆F₅H monomer in blue and NH₃ monomer in red. The C₆F₅H solid phase spectrum is also presented for the sake of comparison in light blue. b provides spectrum of Et₃GeH···ICF₃ in yellow, Et₃GeH monomer in blue and ICF₃ monomer in red. The narrow lines in the red, blue and yellow spectra depicted in panel (b) correspond to the atmospheric water absorption.

The picture shows a broad peak of C₆F₅H at 3103.7 cm⁻¹ which belongs to C₆F₅H in the solid phase in the form of ice. The spectrum of the C₆F₅H⋯NH₃ system is relatively complex and breaks down into a number of relatively broad peaks that partly belong to the complex itself, but also to individual unreacted components. It turned out that in a number of our experiments it is very important to estimate stoichiometrically the ratio (mixture) of the individual components forming the complex. It often happens that during the formation of a molecular complex, some unreacted molecules are excluded from the reaction and appear in the spectrum as individual components. The spectral lines of these unreacted molecules can easily be identified based on previously measured individual spectra. From the argon-matrix spectra we attributed the peak around 3073 cm⁻¹ to the C₆F₅H monomer, and the peak around 2992 cm⁻¹ to the C₆F₅H⋯NH₃ complex, with the resulting redshift of the C-H stretching frequency being 40.5 cm⁻¹.

Figure 1b shows the spectrum of pure Et₃GeH in an argon matrix (blue), the spectrum of pure ICF₃ in an argon matrix (red), and the spectrum of the Ar–Et₃GeH⋯ICF₃ mixture (1000:1) at 55 K (orange). The single peak around 2021.2 cm⁻¹ at the blue curve is attributed to the Ge-H stretching frequency in the isolated Et₃GeH monomer. Three peaks at 1980.7, 2012.1, and 2038.3 cm⁻¹ at the orange curve correspond to the Ge-H stretching frequencies in the A, B and C structures (Fig. S1 and the following text) of the Et₃GeH⋯ICF₃ complex. We assigned the resulting redshift of 40.5 cm⁻¹ to the hydridic hydrogen bond in the structure A, where the hydridic hydrogen from Et₃GeH interacts with the positive σ-hole on ICF₃. A redshift of 9.1 cm⁻¹ was assigned to the structure B where the CF₃ fragment from the ICF₃ molecule interacts with the ethyl groups of Et₃GeH. Lastly, a blueshift of 17.1 cm⁻¹ was assigned to the dispersion-driven structure C where iodine from ICF₃ interacts with ethyl groups of Et₃GeH. Complexes B and C are not the main interest of this study and are therefore not discussed further.

It should be noted that all spectra were measured in a cryostat freely inserted into the sample chamber of the Vertex spectrometer under atmospheric air pressure in the laboratory. For these reasons, narrow absorption lines of atmospheric water appear in the spectrum, which were then used in the pre-calibration of the individual spectra.

Calculations

Subsystems

Table S1 provides a summary of the atomic charges for all hydrogen donors (both protonic and hydridic) discussed in this paper. As expected, the X-H hydrogens in the Me₃XH (X = Si, Ge, Sn) and Et₃GeH subsystems exhibit hydridic character, whereas the hydrogens in other donors are protonic. Additionally, the data in Table S1 shows that the NBO charges, which are primarily used in the subsequent analysis, show a strong correlation with those derived from alternative methods, such as Hirshfeld or RESP.

Complexes

Structures of the C₆F₅H⋯NH₃ and Et₃GeH⋯ICF₃ complexes, which exhibit protonic and hydridic H-bonds respectively, are shown in Fig. 2. The structure, energy, and vibrational characteristics are summarized in Table 1. Table S2 shows energy and vibration characteristic of all three structures of the latter complex (cf Fig. S1). Clearly, structure A corresponds to the global minimum with binding free energy of 3.2 kcal.mol⁻¹ and only it will be considered in the forthcoming discussion. Our intention was to compare protonic and hydridic H-bonded complexes with similar stabilization energies, and Table 1 demonstrates that the present selection was successful. Both complexes exhibit comparable stability, as evidenced by their calculated interaction and binding free energies. The binding free energies of both complexes at 50 K are positive (stabilizing), indicating that both complexes will be populated at this experimental temperature. Moreover, the difference in binding free energies, with the first complex having a larger value, is attributed to entropy.

Fig. 2. Structures of protonic H-bonded C₆F₅H···NH₃ and hydridic H-bonded Et₃GeH···ICF₃ complexes optimized at MP2/aug-cc-pwCVTZ (aug-cc-pwCVTZ-PP for Ge and I) level of theory.

Interaction free energies (in kcal.mol⁻¹) are depicted in blue while the red shifts of X-H stretching frequency (in cm⁻¹) are depicted in red.

Table 1.

Interaction energy and interaction free energy, changes of the X-H stretching frequency and its intensity, population of the σ bonding and σ*antibonding orbitals and the X-H bond distance upon complex formation, and total charge at XH subsystem for complexes with hydridic and protonic H-bonds optimized at the MP2/aug-cc-pwCVTZ (aug-cc-pwCVTZ-PP for Ge and I)^a

Et3GeH···ICF3
ΔET	ΔG(50 K)	ΔνCALC	ΔνEXP	ΔICALC	Δσ(X-H)	Δσ*(X-H)	Δr(X-H)	Q(XH)b
−5.16	−3.20	−47.5	−40.5	148.8	−0.014	0.006	0.009	0.003
C6F5H···NH3
ΔET	ΔG(50 K)	ΔνCALC	ΔνEXP	ΔICALC	Δσ(X-H)	Δσ*(X-H)	Δr(X-H)	Q(XH)c
−4.42	−2.32	−76.1	−81.0	166.5	−0.007	0.033	0.005	−0.014

^aEnergies in kcal.mol⁻¹, Δν in cm⁻¹, ΔI in km.mol⁻¹, Δr in Å, Δσ, Δσ* and Q(XH) in electrons, ^b and ^c is the total charge at Et₃GeH and C₆F₅H, respectively.

The main finding of this study is related to the shift in the X-H stretching frequency, which serves as a fingerprint for H-bond formation. IR experiments on both complexes reveal significant red shifts, with the shift being slightly larger for the protonic H-bond. The calculated spectral shifts agree fairly well with the experimental values, providing evidence for the accuracy of the theoretical treatment. In addition to the shifts in stretching frequencies, the H-bond is also manifested by an increase in the intensity of the respective spectral band. Since the current experimental setup does not allow for the detection of spectral band intensity, we determined it computationally (see Table 1). The intensity increase is significant in both complexes and comparable.

The comparable changes in stretching frequencies and intensities of spectral bands upon complex formation, regardless of whether the hydrogen is protonic or hydridic, are indeed surprising. This is because systems with protonic and hydridic hydrogens exhibit different directions of charge transfer. In hydridic hydrogen systems, such as triethylgermane, the molecule acts as an electron donor, while in protonic hydrogen systems, like pentafluorobenzene, the molecule acts as an electron acceptor.

The spectral red shifts are primarily attributed to the weakening and elongation of the X-H bond upon complex formation, with the change in bond length being a key quantity. Since experimental determination of geometry changes for these complexes in the gas phase is not feasible, we are limited to computational methods. Table 1 reveals that the X-H bond was elongated in both complexes, by 0.005 and 0.009 Å, respectively. To verify these values obtained at the correlated MP2 level, we employed various computational techniques, including different DFT functionals (wB97M-V and PBE0). As shown in Table S3, all these techniques provided X-H bond elongations comparable to those listed in Table 1.

Tables S4–S7 present data for 30 protonic and 30 hydridic H-bonded complexes determined at the MP2 level with stabilization energies ranging from 3.0 to 10.9 kcal.mol⁻¹ and 3.5 to 8.0 kcal.mol⁻¹, respectively. Structures of all complexes investigated are depicted on the Figs. S2–S6. This range covers weak, medium, and strong H-bonds, and it is noteworthy that all X-H bond lengths were systematically elongated, with comparable elongation observed for both types of H-bonded complexes.

An important question arises: what is the reason for this systematic elongation of the X-H bond? To address this, we performed NBO analysis. Tables 1, 2, 3, and Tables S3–S15 confirm the well-known fact that, in protonic H-bonding, charge transfer from the electron donor is directed to the X-H σ* antibonding orbital, leading to its weakening and elongation. The X-H system thus behaves as a Lewis acid. Table 1 shows for protonic H-bond a significant increase (by 0.033 e) in electron density in the C-H σ* antibonding orbital. In contrast, for hydridic H-bond, Table 1 indicates that the largest change does not concern an increase in the Ge-H σ* antibonding orbital, but a decrease in electron density in the Ge-H σ bonding orbital (−0.014 e). The X’ – H system thus now behaves as a Lewis base. This trend is consistent across all 30 hydridic and 30 protonic H-bond complexes listed in Tables S3–S15. The NBO analysis across all these complexes unambiguously confirms that the electron density in the X-H σ* orbitals of protonic complexes systematically increase, while electron density in the X-H σ orbitals of hydridic complexes systematically decreases and we are aware of the fact that the changes in populations of σ bonding and σ* antibonding orbitals are for the complexes with hydridic H-bonds smaller. Correlation between increase in population of σ* antibonding orbitals and the respective red shift of the X-H stretching frequency in complexes with protonic H-bond given in Table 3 is closer than that between decrease in population of σ bonding orbitals and the respective red shift of the X-H stretching frequency in complexes with hydridic H-bond presented in Table 2 (0.9 and 0.7). Explanation of this fact is due to the different role of charge transfer, electrostatic, induction and dispersion energy components. In the case of protonic H-bonds the leading role of electrostatic energy is well recognized. Recently we published the paper¹⁶ where we studied different transition metal containing complexes with hydridic H-bonds. In all complexes investigated the dispersion energy represented the dominant energy components what was explained by the partial negative charge at hydridic hydrogens. The SAPT calculations performed for the present set of complexes with hydridic and protonic H-bonds (Tables 2 and 3) fully confirmed this findings. Specifically, Tables S16, S17 and S18 present SAPT(2 + 3) energy decomposition for complexes with hydridic H-bonds and in all cases the dispersion energy is more attractive than the electrostatic one. Table S19 shows the energy decomposition for complexes with protonic H-bond and in all but two complexes the electrostatic energy is clearly dominant.

Table 2.

Selected characteristics of hydridic H- bonded complexes evaluated at the MP2/aug-cc-pwCTZ (aug-cc-pwCVTZ-PP for Ge, Br, Sn, and I) level^a

Complex	Type of interaction	Δν	Δr(X-H)	Δσ(X-H)	Δσ*(X-H)
Me3SiH···BF3	SiH···B	−30.8	0.007	−0.009	0.005
Me3SiH···BrCN	SiH···Br	−46.9	0.008	−0.011	0.004
Me3SiH···C6(CN)3H3	SiH···π-hole	−7.6	0.004	−0.004	0.004
Me3SiH···COF2	SiH···π-hole	−23.9	0.005	−0.003	0.003
Me3SiH···ICF3	SiH···I	−47.1	0.005	−0.012	0.004
Me3SiH···ICN	SiH···I	−68.8	0.007	−0.018	0.006
Me3SiH···NO2F	SiH···π-hole	−20.9	0.011	−0.002	0.003
Me3SiH···PCl3	SiH···P	−31.0	0.005	−0.010	0.006
Me3SiH···P(CN)3	SiH···P	−98.2	0.005	−0.030	0.011
Me3SiH···S(CN)2	SiH···S	−58.3	0.016	−0.014	0.006
Me3GeH···BF3	GeH···B	−37.5	0.008	−0.009	0.004
Me3GeH···BrCN	GeH···Br	−42.1	0.008	−0.011	0.005
Me3GeH···C6(CN)3 H3	GeH···π-hole	−5.0	0.003	−0.005	0.005
Me3GeH···COF2	GeH···π-hole	−27.7	0.006	−0.003	0.003
Me3GeH···ICF3	GeH···I	−48.9	0.006	−0.013	0.005
Me3GeH···ICN	GeH···I	−70.9	0.009	−0.020	0.007
Me3GeH···NO2F	GeH···π-hole	−26.2	0.013	−0.002	0.003
Me3GeH···PCl3	GeH···P	−33.1	0.006	−0.015	0.008
Me3GeH···P(CN)3	GeH···P	−107.7	0.005	−0.012	0.013
Me3GeH···S(CN)2	GeH···S	−62.7	0.019	−0.015	0.006
Me3SnH···BF3	SnH···B	−39.3	0.011	−0.009	0.004
Me3SnH···BrCN	SnH···Br	−52.8	0.012	−0.013	0.004
Me3SnH···C6(CN)3 H3	SnH···π-hole	−10.1	0.005	−0.005	0.002
Me3SnH···COF2	SnH···π-hole	−22.4	0.008	−0.003	0.002
Me3SnH···ICF3	SnH···I	−52.8	0.008	−0.016	0.001
Me3SnH···ICN	SnH···I	−79.9	0.011	−0.025	0.007
Me3SnH···NO2F	SnH···π-hole	−30.3	0.018	−0.002	0.011
Me3SnH···PCl3	SnH···P	−36.9	0.008	−0.015	0.001
Me3SnH···P(CN)3	SnH···P	−121.1	0.008	−0.045	0.008
Me3SnH···S(CN)2	SnH···S	−66.5	0.027	−0.017	0.017

^aΔν in cm⁻¹, Δr in Å, Δσ and Δσ* in electrons.

Table 3.

Selected characteristics of protonic hydrogen bond complexes evaluated at the MP2/aug-cc-pwCTZ (aug-cc-pwCVTZ-PP for Se, Br, Te, and I) level^a

Complex	HB type	Δν	Δr(X-H)	Δσ(X-H)	Δσ*(X-H)
NH3···MeCHO	NH···O	−37.4	0.004	−0.001	0.006
NH3···MeNO	NH···O	−20.8	0.002	−0.001	0.003
C2H2···MeCHO	CH···O	−57.0	0.006	−0.001	0.008
C2H2···Me2CO	CH···O	−71.3	0.007	−0.002	0.010
HF···Me2CO	FH···O	−569.1	0.026	0.000	0.050
HCl···MeOH	ClH···O	−396.3	0.028	−0.002	0.043
HCl···C5H5P	ClH···P	−192.1	0.013	−0.002	0.035
HBr···Me2SO	BrH···O	−633.1	0.052	−0.006	0.078
HBr···C3H7NO	BrH···O	−457.6	0.038	−0.006	0.060
HBr···(CH2)4S	BrH···S	−721.3	0.060	−0.006	0.135
HBr···(CH2)4Se	BrH···Se	−629.1	0.051	−0.005	0.127
HBr···(CH2)4Te	BrH···Te	−556.9	0.045	−0.005	0.121
HBr···(OMe)3PO	BrH···O	−458.7	0.038	−0.005	0.055
HBr···Me3P	BrH···P	−606.3	0.048	−0.005	0.127
HI···Me2SO	IH···O	−689.0	0.067	−0.010	0.095
HI···C3H7NO	IH···O	−369.4	0.036	−0.008	0.059
HI···(CH2)4S	IH···S	−871.4	0.095	−0.012	0.193
HI···(CH2)4Se	IH···Se	−740.5	0.075	−0.009	0.172
HI···(CH2)4Te	IH···Te	−655.8	0.065	−0.009	0.164
HI···(OMe)3PO	IH···O	−389.2	0.037	−0.008	0.056
HI···Me3P	IH···P	−701.0	0.068	−0.009	0.165
MeSH···MeOH	SH···O	−19.1	0.002	−0.001	0.004
MeSH···C5H5P	SH···P	−19.9	0.002	−0.002	0.005
MeOH···C2H5NO	OH···O	−86.8	0.012	0.000	0.023
MeOH···MeN3	OH···N	−114.3	0.006	−0.002	0.011
C6F5H···Me2CO	CH···O	−55.1	0.004	−0.007	0.008
C6F5H···MeNO	CH···O	−8.3	0.001	−0.005	0.002
C6F5H···Me3P	CH···P	−69.2	0.005	−0.006	0.015
H2O···C4H4O	OH···O	−23.7	0.004	−0.001	0.005
H2O···MeNO	OH···O	−30.9	0.005	0.000	0.011

^aΔν in cm⁻¹, Δr in Å, Δσ and Δσ* in electrons.

Tables S3–S15 further demonstrate that the X-H stretching frequency for all electron donors is systematically red-shifted upon complex formation, with a corresponding increase in the intensity of the spectral band. From Tables S3–S15, it is further evident that these findings hold consistently without exception. This conclusion is crucial as it shows that the dominant changes in electron density in systems with protonic and hydridic H-bonds, upon complex formation, act in the same direction. Specifically, an increase in electron density in the antibonding orbital of protonic H-bonded complexes and a decrease in electron density in the bonding orbital of hydridic H-bonded complexes both lead to the weakening and elongation of the X-H bond and a red shift in the respective stretching frequency.

The experimental and computational analyses of C₆F₅H⋯NH₃ and Et₃GeH⋯ICF₃ complexes, which feature protonic and hydridic H-bonds revealed a surprising result: despite the opposite directions and different origin of charge transfer in protonic and hydridic hydrogen bonds, their spectral characteristics -specifically, the red shift of the X-H stretching frequency and the increase in intensity upon complex formation- are remarkably similar. Additional computational analyses performed on 30 protonic and 30 hydridic H-bonded complexes fully confirmed the above mentioned results. This observation is a key characteristic that unifies protonic and hydridic H-bonding, supporting the formulation of a new, unified definition of H-bonding.

Nomenclature

The IUPAC definition of hydrogen bonding recognizes only one type of H-bond, which we referred to earlier as the protonic H-bond. The definition does not encompass the other type, known as the hydridic H-bond, because it specifies that hydrogen in an H-bond must be covalently bound to an electronegative atom and thus bears a partial positive charge, and, further, the dominant energy term must be electrostatic. Consequently, alternative names such as “hydride bond”¹³, “charge-inverted H-bond”^8–11,19, “inverse H-bond”¹², or our term “hydridic H-bond”^15,16 are fundamentally at odds with the existing IUPAC definition.

For some, but not all, types of hydridic H-bonds studied here and elsewhere, the term “halogen bond” may be appropriate. However, it is important to note that there are complexes where hydridic hydrogen interacts with p-holes, π-holes, and various σ-holes, not exclusively those on halogens. For instance, the Et₃GeH⋯ICF₃ complex investigated in this study could be alternatively referred to as an H⋯I σ-hole halogen bonded complex. The formation of this halogen bond is accompanied by a small to negligible red shift in the I-C stretching frequency (3 cm⁻¹) and a negligible change in the intensity of the corresponding spectral band. These changes are subtle and may be difficult or impractical to detect. Conversely, when considering the complex as an H-bonded system, the red shift of the Ge-H stretching frequency (−47.5 cm⁻¹) and the significant increase in intensity (148.8 km/mol) are substantial, making their IR detection routine and straightforward. We ask the question whether it is better to use for this and similar complexes the name of halogen bond where experimental detection of the respective properties would be difficult or even impractical.

There are three potential solutions to handle the nomenclature issue:

• (i)to keep the current definition of H-bond as it is with no other action. Based on several discussions invoked by our lectures on this topic we find out this being preferred.
• (ii)To keep the current IUPAC definition and introduce a completely new term for bonds involving hydridic hydrogen. Since the term “H-bond” is already reserved for the original definition, this would require the introduction of a new term (e.g., hydride bond as suggested by Grabowski et al.¹³) which does not contain “H-bond’ in any version.
• (iii)To modify the existing 2011 IUPAC definition of hydrogen bonding to cover both protonic and hydridic H-bonds. Although it is generally not easy to make any change in definition and it requires extensive scientific discourse, the necessary modifications which we suggest are relatively easy to implement. In this connection, one of us (PH) recalls a very friendly and productive atmosphere in Pisa in 2005, where the current IUPAC definition of the H-bonding was established. This definition was triggered by the discovery that the H-bonding can be evidenced not only by a red shift of the X-H stretching frequency but also by a blue shift.

We are certainly aware that before changing the definition of hydrogen bonding considerably more data, both experimental and computational, should be collected and carefully analyzed with the aim to be more unambiguously convincing. In our first paper on hydridic H-bonding published in J. Am. Chem. Soc.¹⁵ we noted that “ any change of existing definition is difficult and cannot be rushed and required an extended, broad, and in-depth discussion within the scientific community”.

Methods

IR experiment

In our low-temperature IR experiments, we employed two different approaches (for more details, see the SI). The first approach involves the technique of direct spectral measurement of a supersonically expanded mixture of reaction intermediates on a cold substrate, referred to as the solid-phase complex (SPC) method. The second approach utilizes the technique of noble-gas matrix isolation (MI).

The procedure of low-temperature experiments was described elsewhere²⁰. The gas mixtures are deposited onto a cooled KBr substrate of the cryostat at a temperatures between 18–70 K. The relative concentrations of the products were monitored using integrated absorption intensities of the selected infrared bands. The intermediates which are parts of low temperature complex have been supersonically expand into the high vacuum (10⁻⁶ Torr) on cold 18 K substrate (minimal attainable temperature) inside of Leybold cryostat chamber. The spectra were obtained by use of the Bruker Vertex spectrometer with KBr optics, HgCdTe detector and a KBr beam splitter. The broad spectral region was cut by optical interference filters with transparency in the range of 700–5000 cm⁻¹. The KBr entry window of the spectrometer was used. The unapodized spectral resolution was 0.06 cm⁻¹. Between 30 and 100 scans, depending on the sample, were coadded so as to obtain a reasonable signal-to-noise ratio. The observed wavenumbers were calibrated using H₂O absorption rotation-vibration lines presented in the spectrum.

Matrix isolation is a well-known technique frequently used for the measurement of unstable species such as ions, radicals, and low-temperature molecular complexes in a cold matrix of noble gas (Ng). Similar to the first approach, a mixture of reaction intermediates combined with argon gas (molar ratio 1:1000) is expanded through a pulse nozzle onto the cold (20 K) KBr substrate, and the spectra are recorded using the Bruker Vertex spectrometer.

Computations

Geometries of all subsystems and complexes were optimized at the RI-MP2/aug-cc-pwCVTZ²¹ level (aug-cc-pwCVTZ-PP²² for Ge, Se, Br, Sn, Te, and I), the ωB97M-V²³/aug-cc-pwCVTZ level (aug-cc-pwCVTZ-PP for Ge, Se, Br, Sn, Te, and I), and the PBE0²⁴/def2-TZVPPD²⁵ level with an additional D4²⁶ dispersion correction. Harmonic vibration frequencies, evaluated under the rigid rotor-harmonic oscillator-ideal gas approximation, were determined at the same theoretical levels. Natural Bond Orbital (NBO) analyses were performed with the NBO7^27,28 program at the same levels as the geometry optimizations. These calculations were carried out using the ORCA 5.0.4²⁹ software and Molpro 2024.1^30,31. Hirshfeld population³² analysis was conducted using ORCA 5.0.4 with the PBE0/def2-TZVPPD method. Restricted electrostatic potential (RESP) charges³³ were calculated at the PBE0/def2-TZPPD level of theory, utilizing the Q-Chem 6.2³⁴ software package. Symmetry-adapted perturbation theory³⁵ (SAPT) were performed using the aug-cc-pwCVTZ basis set for all atoms with atomic numbers less than 32. For Ge, Se, and Br atoms, the all-electron aug-cc-pVTZ³⁶ basis set was employed due to convergence issues encountered with the aug-ccpwCVTZ-PP basis set. For Sn, Te, and I atoms, the aug-cc-pwCVTZ-PP basis set was applied. All SAPT calculations were executed using the PSI4 1.9.1³⁷ software package.

Supplementary information

Figure S1 provides three structures of the Et₃GeH···ICF₃ possessing hydridic H-bond, Figures S2–S6 provides pictures of all studied complexes. Tables S1–S15 collect charge, energy and vibration characteristics of selected complexes with protonic and hydridic H-bonds. Tables S16–S19 collects SAPT 2 + 3 results for all studied complexes.

Author contributions

M.L. performed the calculations. S.C. designed and conducted experiments. P.H. supervised the project and wrote the manuscript.

Peer review

Peer review information

Communications Chemistry thanks Shamik Chakraborty, Daniel Sethio, and Ekaterina Pas for their contribution to the peer review of this work. Peer review reports are available.

Data availability

Authors can confirm that all relevant data are included in the paper and its supplementary information files.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42004-024-01334-9.