Graph spiking neural network for advanced urban flood risk assessment

Summary

Urban flooding significantly impacts city planning and resident safety. Traditional flood risk models, divided into physical and data-driven types, face challenges like data requirements and limited scalability. To overcome these, this study developed a model combining graph convolutional network (GCN) and spiking neural network (SNN), enabling the extraction of both spatial and temporal features from diverse data sources. We built a comprehensive flood risk dataset by integrating social media reports with weather and geographical data from six Chinese cities. The proposed Graph SNN model demonstrated superior performance compared to GCN and LSTM models, achieving high accuracy (85.3%), precision (0.811), recall (0.832), and F1 score (0.821). It also exhibited higher energy efficiency, making it scalable for real-time flood prediction in various urban environments. This research advances flood risk assessment by efficiently processing heterogeneous data while reducing energy consumption, offering a sustainable solution for urban flood management.

Graphical abstract

Highlights

• •Integration of GCN and SNN in urban flood risk assessment models
• •Real-time flood risk dataset created from social media data
• •Our Graph SNN model outperforms LSTM and GCN across all evaluation metrics

Earth sciences; Computer science; Engineering

Introduction

Urban flooding is a serious disaster that affects people, destroys homes, breaks down communication, and leads to deaths around the world.¹ The 21st century’s rapid urban growth has packed more people and buildings into cities, making them more prone to floods.² Floods cause over 30% of the world’s disaster-related losses each year, and this problem is getting worse with climate change and continuous city growth.^3,4 For example, a severe flood in Beijing on July 21, 2012 resulted in over 70 fatalities and impacted 1.6 million people.⁵ More recently, Zhengzhou, China faced a catastrophic flood on July 20, 2021, which caused hundreds of deaths and an economic loss of RMB 40 billion.⁶ The intense rainfall-driven urban floods happen quickly and last a short time.

A reliable and quick urban flood risk assessment tool is vital for reducing the risk of disasters.^2,7 By accurately gauging the probability of flooding and developing efficacious mitigation strategies, these instruments occupy a pivotal role in urban planning and disaster management. The enhancement and advancement of these tools is of particular significance as the necessity for secure and sustainable urban environments intensifies. Such tools enable relevant organizations to make informed decisions promptly before or during a flood, thereby effectively protecting property and saving lives.⁷ Urban flood risk assessment tools can be divided into two main categories: those based on physical mechanisms that predict flood behavior by simulating hydrologic and hydrodynamic processes and data-driven approaches that rely on historical data and statistical models to assess flood risk.

Urban flood risk assessment tools based on physical mechanisms replicate the flooding process by numerically solving hydrodynamic equations, which can range from one-dimensional to complex three-dimensional forms.³ These tools, like SWAT,⁸ SHE,⁹ SWMM,¹⁰ and HIPIMS,¹¹ hinge on comprehensive datasets, which include initial and boundary conditions, as well as spatial details from Digital Elevation Models (DEMs), land use configurations, and hydrometeorological data such as rainfall and river flow rates.¹² For example, SWMM models simulate flooding processes by solving the hydrodynamic equations through numerical methods. In particular, SWMM models simulate surface runoff from rainfall and water flow in drainage systems by requiring information on the sewer network, rainfall events, topography, and land use. SWMM simulates the dynamic behavior of water flow in a drainage system, including the confluence, conveyance, and discharge processes, by means of one- or two-dimensional flow equations. These tools are adept at detailed flood dynamics representation, providing accurate predictions of flood impacts. However, there are significant drawbacks to consider. First, they demand extensive computational power and lengthy processing times to yield refined results.¹³ Additionally, the effectiveness of these tools hinges on the availability of high-resolution data, which is often scarce, particularly in less affluent regions.¹³ For example, consider the application of the SWMM or SWAT models in simulating a flood event in a medium-sized city. These models typically require spatial data with resolutions as fine as 30 m, temporal data in 15-min intervals, and high-resolution information, such as precipitation patterns or urban infrastructure details. The modeling process for an event using such detailed data can span from hours to days, even on current mid-to high-end computers.

Data-driven urban flood risk assessment tools analyze patterns from historical data to predict flooding events.¹⁴ Unlike tools that rely on physical mechanisms, these tools employ statistical and machine learning algorithms to identify risk factors and forecast potential flood scenarios,¹⁵ offering a potentially faster and more adaptable approach to urban flood risk assessment. With the growth of artificial intelligence, data-driven AI models have found many applications in urban flood risk assessment.¹⁶ For example, Pham employed a hybrid model of AI, including support vector machines, for flood risk assessment in Vietnam, which improved the accuracy of risk detection.¹⁷ Taromideh and colleagues applied decision tree algorithms alongside machine learning to refine flood risk assessments, resulting in more dependable evaluations.¹⁶ Lyu evaluated the use of artificial neural networks in assessing flood risks for metro systems within smart cities.¹⁸ Ye developed an AI framework using deep learning for comprehensive urban flood resilience planning, showing promise in detailed urban design and management.¹⁹ However, these models are mainly used in certain places and do not work well where there is not enough data.¹⁴ They also often lack the ability to be used in different situations and to stay reliable when conditions change. Additionally, their deep learning networks, known for being a "black box,"²⁰ often yield results that lack interpretability. When dealing with urban flood risk, where the safety of people and the protection of assets are very important, results without clear explainability are hard to accept.²¹

In urban flood risk assessment, the necessity for a tool that is both efficient and universally applicable cannot be overstated. Moreover, the complexity of urban environments demands that such a tool’s outcomes be easily interpretable to inform decision-making effectively.²² Recognizing this, we have embarked on a path by integrating the capabilities of Spiking Neural Networks (SNNs)²³ and Graph Neural Networks (GNNs).²⁴ This synergy aims to capitalize on the distinctive attributes of each network type—SNN’s bio-inspired processing mechanisms²⁵ and GNN’s robust relational data handling—to establish a model that fulfills the aforementioned requirements.²⁴ Our objective is to create a hybrid model that leverages the strengths of SNN and GNN for superior urban flood risk analysis.

SNNs are cutting-edge tools that mirror the human brain’s operation.²³ They stand out for their mode of communication, where information is relayed in quick, sharp bursts—akin to the pulse-like signals used by neurons in our brains.²⁶ This method of data transmission not only makes SNNs more intuitive and easier to interpret but also contributes to their low power consumption.²⁵ Because they transmit data in pulses rather than continuous signals, they require less energy, making them both effective and energy-efficient. And SNNs have shown great promise across various fields.²⁶ For example, Yin’s team invented an SNN learning method, which was successfully tested in Amsterdam to real-time track cyclists, walkers, and cars.²⁷ Tan’s group applied SNNs to biomedical imaging for emotion recognition, aiding medical diagnosis.²⁸ Auge’s team developed an SNN-based audio system for smart sound processing.²⁹ Xiao and colleagues used SNNs for energy-efficient language tasks like sentiment analysis.³⁰ By integrating SNNs into urban flood risk assessments, there is hope to leverage their brain-like interpretability and low energy consumption to create a more explainable and efficient model.

GNNs prove their mettle in capturing complex relationships and dependencies between varied elements.³¹ This makes them perfect for making sense of complicated city systems. Expanding on the general applicability of GNNs, a number of studies have demonstrated their versatility in urban systems.³¹ For instance, Jin and colleagues have utilized GNNs to enhance traffic management systems by predicting flow and congestion patterns, thereby optimizing urban mobility.³² Li and colleagues used GNNs to develop intelligent systems for monitoring and managing urban energy consumption, contributing to more sustainable city planning.³³ Hou and colleagues found GNNs to be instrumental in tasks such as urban region profiling, which helps to identify and classify areas based on their functions and characteristics—a significant step toward smart urban governance.³⁴ In this article, we treat small segments of different cities as nodes within a network and consider features such as elevation, building density, population density, and the like as relations within the nodes. By doing so, GNNs effectively map out the intricate connections that define an urban area’s flood risk profile. This allows for a more generalized approach to flood risk assessment that can be applied across diverse urban landscapes, enhancing the model’s usability and scalability.

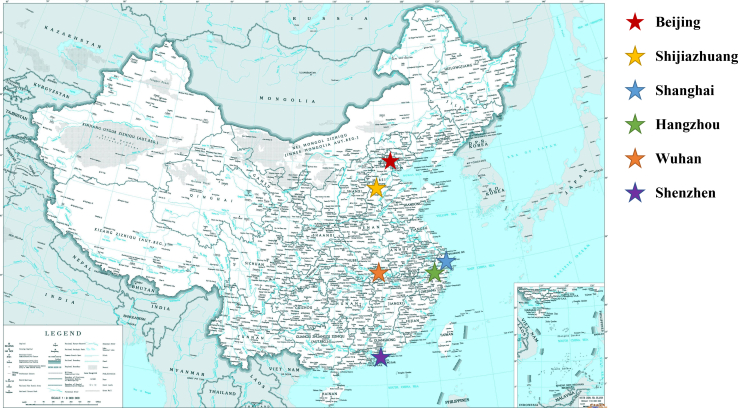
Today, city dwellers often use social media platforms such as Sina Weibo, TikTok, WeChat Space, Facebook, and Community to share information about local disasters.³⁵ This information often comes in the form of text, images, or short videos. These social media posts can provide accurate, up-to-the-minute information about local flooding. Social sensing has been used for extracting fast disaster information since 2010.³⁶ For example, Bruijn developed a database for flood records using social sensing data.³⁷ Lin employed deep learning and social data for rapid urban flood risk mapping in Zhengzhou.³⁵ In order to address the paucity of data on urban flooding, we have gathered social media data from Sina Weibo (Figure 1). The dataset includes specific details such as location, time, and severity (Figure 2). In the initial phase of data cleansing, the first step is to filter out reliable information for retention through manual verification. Secondly, outliers are processed through data processing scripts. Following the data cleansing process, the data are then matched with the rainfall amount at these locations, which has been obtained from satellite observations. In addition, we have collated data on urban building density and population distribution in order to construct a comprehensive dataset on urban flooding, which we have named the “mixed urban flood risk dataset.” In the experimental section of this article, we compared the performance of our hybrid model, comprising GNN and SNN, LSTM, and GNN, on the test set from our mixed urban flood risk dataset. The metrics included precision, recall, F1 score, and accuracy, as well as power consumption and total energy consumption of each type of hardware. The results show that our hybrid model of GNN and SNN performed best in terms of both accuracy and energy consumption metrics.

Figure 1.

The proposed methodology framework for constructing a mixed urban flood risk dataset

Figure 2.

The study area: six representative cities in China

In conclusion, the challenges posed by accelerating urbanization and climate change necessitate more advanced and resilient approaches to urban flood risk management. Our research addresses this critical need by developing a hybrid model that integrates SNN with GNN, establishing a cutting-edge framework for urban flood risk assessment (Figures 1 and 3). By harnessing the bio-inspired capabilities of SNNs for efficient, spike-based data processing and the relational strengths of GNNs for analyzing complex spatial and temporal relationships, our model significantly enhances accuracy, interpretability, and energy efficiency in flood risk analysis. One of the keys to our work is the integration of social media data into flood risk assessment frameworks. Traditional monitoring systems often suffer from data scarcity, particularly in rapidly evolving urban environments. To address this limitation, we employ social sensing to create a mixed urban flood risk dataset, incorporating real-time data from platforms such as Sina Weibo. This approach captures the immediacy and granularity of flood events, providing a rich, real-time source of information that enhances the precision and responsiveness of flood monitoring systems. The academic value of this research lies in its contribution to the fields of deep learning and urban risk management. By introducing a hybrid model that combines the neuro-inspired processing capabilities of SNN with the structural advantages of GNN, we pave the way for more robust and scalable solutions in disaster management. Furthermore, utilizing social media as a data source contributes to addressing the challenges of real-time environmental monitoring, providing valuable insights into the dynamics of urban flooding. This work enhances flood risk assessment methodologies and broadens the potential applications of energy-efficient and interpretable AI models in environmental risk management.

Figure 3.

The Graph SNN model architecture and data flow process

Results

Model performance and comparison

The evaluation of model performance is represented by confusion matrices, as illustrated in Figure 4. These matrices offer an objective view of each model’s classification precision at various risk levels: low, medium, and high. The GCN model, which specializes in graph data, demonstrated solid accuracy, especially in the low- and medium-risk categories, with scores of 0.84 and 0.79, respectively. This high performance in these categories indicates the model’s strong capability to identify and distinguish between areas with low to moderate flood risks accurately. However, the GCN model exhibited a noticeable drop in accuracy for the high-risk category, with a score of 0.62. This decline suggests that although GCNs excel in handling less extreme cases, their ability to predict high-risk situations might be compromised, potentially due to the increased complexity and variability of the data in this category. Nevertheless, its overall performance underscores the advantages of graph-based models in analyzing spatial data, particularly in scenarios where relational information is critical.

Figure 4.

Confusion matrices of different models

Each matrix visually represents the classification accuracy of the respective model at various flood risk levels: low, medium, and high.

On the other hand, the LSTM model, not inherently designed for graph data, was less effective, showing the lowest accuracy rates across all risk levels: 0.79 for low, 0.19 for medium, and 0.11 for high risk. The significant drop in accuracy from low- to medium- and high-risk categories highlights the limitations of sequential models like LSTM when applied to tasks involving spatial and graph-structured data. The model’s struggle to accurately predict higher risk levels may stem from its inability to effectively capture and utilize the complex spatial dependencies present in urban flood risk scenarios. In stark contrast, our Graph SNN model outperformed the others, achieving the highest accuracy across all risk levels, with scores of 0.88 for low risk, 0.85 for medium risk, and 0.77 for high risk. These results not only demonstrate the model’s superior capability in accurately classifying flood risks but also affirm its robustness in discerning intricate spatial connections, particularly in urban environments where flood risk factors are interdependent and nonlinear. The relatively high accuracy in the high-risk category (0.77) is particularly noteworthy, indicating that the Graph SNN model is more adept at managing the complexities associated with predicting extreme flood events. This performance further validates the effectiveness of SNNs in capturing both temporal and spatial dynamics, making them a powerful tool for urban flood risk evaluation.

Although GCN is designed to deal with spatial relationships, its performance in risk identification is not satisfactory, especially in the high-risk level, which may be attributed to the limitations of GCN in dealing with time series data, which makes it difficult to effectively capture the cumulative effect of sustained rainfall on urban flooding. The accuracy of LSTM model is generally lower in all risk levels, which may be attributed to the fact that as a time sequence model, LSTM has difficulty in resolving the complex spatial differences among different cities. In contrast, the key advantage of the Graph SNN model is its structure designed to handle complex spatiotemporal tasks. The model skillfully integrates the spatial feature learning capability of GCN and the time series processing mechanism of SNN. This combination equips Graph SNN to effectively capture the spatiotemporal dynamics of urban flooding, allowing it to perform well in practical applications.

To further the comparative analysis of the models' performance, we adopted four primary metrics: precision, recall, F1 score, and accuracy. Table 1 illustrates the distinct performances of the GCN, LSTM, and Graph SNN models as quantified by precision, recall, F1 score, and overall accuracy. The metrics reveal a clear hierarchy in model effectiveness, with the Graph SNN consistently leading across all evaluation criteria. The GCN model presents a mixed performance profile. Although its recall of 0.746 is relatively strong, indicating that it effectively identifies most flood instances, its precision of 0.763 is lower than that of the Graph SNN model. This suggests a higher rate of false positives, where the model may incorrectly classify non-flooded areas as flooded. This trade-off is reflected in its F1 score of 0.759, which, although respectable, still lags behind the Graph SNN model. The GCN model’s accuracy of 0.793, although higher than the LSTM, still falls short of the Graph SNN, highlighting its less consistent performance across different flood risk levels.

Table 1.

Evaluation metrics for performance comparison of different models

Criteria/Model	GCN	LSTM	Graph SNN
Precision	0.763	0.591	0.811
Recall	0.746	0.643	0.832
F1 score	0.759	0.598	0.821
Accuracy	0.793	0.678	0.853

In contrast, the LSTM model shows a marked deficiency in performance, particularly evident in its low precision (0.591) and recall (0.643). The model’s inability to effectively capture the spatial dependencies inherent in flood prediction tasks likely contributes to its poor metrics. This is particularly problematic in scenarios where distinguishing between flood and non-flood events is critical. The suboptimal F1 score of 0.598 reflects this imbalance, suggesting that the LSTM model may generate a higher number of false positives and false negatives, which could undermine its utility in real-world flood prediction applications. Its overall accuracy of 0.678, the lowest among the models, further underscores its limitations in this domain.

The Graph SNN model’s precision of 0.811 suggests that it excels in correctly identifying flood events with minimal false positives, an essential feature for reducing unnecessary alerts in flood prediction systems. This high precision is complemented by its recall of 0.832, indicating the model’s strong capability to detect the vast majority of actual flood instances. The combination of these metrics results in an F1 score of 0.821, demonstrating a well-balanced performance in terms of precision and recall. The overall accuracy of 0.853 further emphasizes the model’s robustness and reliability in predicting flood risks, marking it as a superior choice for practical applications in urban flood risk management.

In conclusion, our comparative analysis reveals the strengths of the GCN model in processing graph-structured data for low- and medium-risk scenarios. However, it is important to note that the model’s accuracy may be diminished in high-risk categories, potentially due to its sensitivity to certain graph features or data imbalances. Conversely, the LSTM model’s performance is consistently suboptimal, particularly in tasks that require spatial orientation. This reflects a misalignment with the model’s strengths in sequential data processing. In stark contrast, the Graph SNN model demonstrates unparalleled performance across all risk levels, exhibiting an exceptional ability to navigate complex spatial correlations, which is crucial for urban flood risk assessment. The high F1 score indicates an optimal balance between precision and recall, rendering it an optimal tool for accurate flood predictions. Consequently, the Graph SNN model emerges as the optimal choice for stakeholders and decision-makers seeking to enhance flood response strategies with informed, proactive measures.

Graph SNN leads to low power consumption and parameter efficiency

In response to the pressing need for sustainable and cost-effective surveillance systems, our study presents a comparative analysis of the energy utilization patterns across various neural network architectures. Furthermore, by integrating a comparative evaluation of parametric density, our investigation offers a comprehensive perspective on the operational efficiency characteristic of each considered model.

Table 2 presents a comparison of power consumption and model efficiency across the GCN, LSTM, and Graph SNN models. The Graph SNN model stands out due to its superior power efficiency and compactness, as evidenced by its parameter count of 1.46 million, which is notably lower than the 2.29 million parameters of the GCN model and the 2.63 million parameters of the LSTM model. This reduction in parameters suggests that the Graph SNN achieves high performance while maintaining a more streamlined architecture, which is particularly advantageous in scenarios where computational resources and memory are limited.

Table 2.

Power consumption of different models

Criteria/Model	GCN	LSTM	Graph SNN
Param (M)	2.29	2.63	1.46
RAM power (kWh)	6E-06	2E-06	4E-06
CPU power (kWh)	1E-05	2E-06	1E-06
GPU power (kWh)	6E-06	3E-06	1E-06
Energy (J)	79.2	25.2	17.6

The energy consumption data further emphasize the Graph SNN’s efficiency. Its RAM power consumption is 4E-06 kWh, significantly lower than GCN’s 6E-06 kWh, though slightly higher than LSTM’s 2E-06 kWh. However, the Graph SNN model surpasses both in CPU and GPU power consumption, using only 1E-06 kWh for each, compared to GCN’s 1E-05 kWh and 6E-06 kWh and LSTM’s 2E-06 kWh and 3E-06 kWh, respectively. These lower energy demands reflect the model’s optimized processing and resource allocation, which are critical in reducing operational costs and enhancing battery life, particularly in edge computing environments or mobile deployments. Moreover, the total energy consumption of the Graph SNN, measured at 17.6 J, is substantially lower than that of the GCN (79.2 J) and LSTM (25.2 J). This significant reduction in energy usage underscores the efficiency of the Graph SNN in practical applications, where energy conservation is crucial. The reduced power requirements also imply a smaller environmental footprint, aligning with growing demands for sustainable AI practices.

In conclusion, our Graph SNN represents a revolutionary advancement in sustainable artificial intelligence, particularly within the context of smart city frameworks. This model represents an exemplar of resource-conscious AI, integrating principles of sustainability with minimal energy requirements and compact parameterization. The Graph SNN’s modest parameter footprint, coupled with its energy-efficient design, facilitates seamless integration across a diverse array of platforms, including portable devices. The inherent energy frugality of the Graph SNN not only forecasts a promising avenue for diminishing running costs but also cements its stature as a precise, cost-efficient, and eco-friendly alternative for intricate evaluations in smart city operations. Such notable energy parsimony further enhances its appeal as a viable and eco-sustainable approach to AI in the realm of urban administration.

Discussion

The core of this research focuses on an approach to urban flood risk assessment that integrates the strengths of GNNs and SNNs. The combined model benefits from GNNs' ability to capture complex spatial relationships in urban environments and SNNs' capacity to track temporal dynamics with high energy efficiency. This dual capability contributes to a more nuanced understanding of urban flooding patterns, improving both the accuracy and interpretability of flood risk predictions.

One key feature of the Graph SNN model is its strong performance in terms of accuracy, energy efficiency, and interpretability compared to traditional models like GCN and LSTM. The experimental results show that the model performs well across key performance metrics, offering urban planners and decision-makers a reliable tool for predicting and managing flood risks. Enhanced accuracy is important for protecting lives, reducing property damage, and minimizing economic losses during flood events. Additionally, the model’s interpretability ensures that its predictions are easily understood and trusted, promoting greater acceptance among stakeholders. The energy-efficient design meets the growing demand for sustainable AI solutions, making it suitable for smart city initiatives focused on sustainable urban development.

The inclusion of social media data within the flood risk assessment framework introduces a valuable enhancement. By incorporating real-time data from platforms such as Sina Weibo, the model addresses the challenge of data scarcity in urban flood monitoring, enriching the dataset with timely and granular information. This approach improves the comprehensiveness of the dataset, covering multiple cities across China, and ensures that the data reflect real-time flood dynamics. The resulting dataset provides a more detailed analysis of urban flooding, enabling more precise risk assessments and better-informed decision-making.

Looking ahead, several directions for future work could further enhance the robustness and applicability of the model. Expanding the dataset to include additional cities would improve the model’s generalizability and adaptability, potentially increasing the accuracy of predictions in diverse urban environments. Additionally, the development of real-time data acquisition and automated cleaning techniques would streamline data processing, enhancing the timeliness and efficiency of flood risk assessments. Integrating real-time flood information into a publicly accessible platform, such as a website, could further aid in disseminating evacuation guidance and supporting city managers with real-time monitoring tools.

Moreover, incorporating multidimensional data, such as traffic patterns and infrastructure resilience, could lead to the development of a more comprehensive flood risk assessment system, offering robust support for urban planning and management. Efforts to improve the interpretability of the model will continue, with the goal of increasing its trust and acceptance among decision-makers, thereby promoting its widespread adoption in practical applications. Finally, deploying the model in real-world scenarios will be crucial for testing its utility and effectiveness in operational settings. Feedback from these real-world applications will provide valuable insights for further optimizing the model, ensuring it remains responsive to the practical needs of urban flood management and emergency response.

Limitations of the study

Despite the outstanding performance of our proposed model, there are still some limitations. First, the complexity of integrating GNNs and SNNs may present challenges related to computational requirements and implementation, particularly in resource-constrained environments. Although our model demonstrates energy efficiency and adaptability across six cities with diverse characteristics, its performance in more extreme conditions or atypical urban settings remains to be thoroughly evaluated. Additionally, the use of social media data, while offering valuable insights, may introduce biases or inaccuracies related to user behavior and engagement, potentially affecting the robustness of flood risk assessments. Moreover, although the current dataset is comprehensive, it could be further enhanced by incorporating additional variables such as infrastructure resilience and traffic patterns, which may improve the model’s predictive capabilities. Finally, although steps have been taken to improve interpretability, the complexity of the model may still present challenges in gaining full trust from stakeholders, potentially influencing its adoption in urban flood management.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dr. Zhantu Liang (liangzhantu2087@xhsysu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •Fundus photographs data reported in this paper will be shared by the lead contact upon request.
• •All original code is available in https://github.com/ZtL-sysu/Graph-SNN.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

This research was supported by the Guangdong Provincial Key Discipline Research Capacity Improvement Project on 'Artificial Intelligence Application Research Based on Medical Imaging Big Data', project number: 2022ZDJS152.

Author contributions

Z.L. (Zhantu Liang) designed the research study, performed the experiments, and wrote the manuscript. X.F. and Z.L. (Zhanhao Liang, the third author) developed the computational models and analyzed the data. J.X. contributed to the experimental design and data analysis. F.D. and T.E.N. collected and annotated the data. J.X. also oversaw the project coordination and final approval of the version to be published. All authors reviewed the manuscript.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Urban flood risk data	This paper	N/A
Code for model and network training	This paper	https://github.com/ZtL-sysu/Graph-SNN
Software and algorithms
SpikingJelly	Version 0.0.0.0.4	https://github.com/fangwei123456/spikingjelly
PyTorch Geometric	Version 2.4.0	https://pytorch-geometric.readthedocs.io/en/latest/
PyTorch	Version 1.8.1	https://pytorch.org/blog/pytorch-1.8-released/
Matplotlib	Version 3.6.3	https://matplotlib.org/3.6.3/
Python	Version 3.8.10	https://www.python.org/downloads/release/python-3810/

Experimental model and study participant details

The dataset used in this study was self-constructed and consists of 1,826 records from six cities in the study area. Each record represents a 30-meter by 30-meter grid and includes key variables such as latitude, longitude, rainfall series, elevation, building density, and population density. The dataset was categorized into three flood risk levels: low (532 data points), medium (673 data points), and high (621 data points). The data is divided into dynamic and static components: rainfall series as dynamic data, while building density and population density are static. Elevation, along with latitude and longitude, plays a critical role in constructing standardized map data and calculating weighting coefficients between nodes. This multidimensional dataset provides a comprehensive foundation for urban flood risk assessment and analysis.

The research was conducted on a Lenovo workstation with the following specifications: OS - Ubuntu 20.04.6 LTS, CPU - Intel Xeon Gold 6128 @ 3.40GHz, RAM - 128GB, GPU - RTX 2080Ti, using the PyTorch³⁸ and SpikingJelly³⁹ deep learning frameworks. The dataset was randomized using a fixed random seed to ensure consistency and avoid bias, and split into 80% for training and 20% for testing. A constant random seed (set to zero) was maintained for reproducibility. During model training, we employed techniques such as dropout to improve generalization, L2 regularization to prevent overfitting, batch normalization to stabilize training, and an adaptive learning rate to enhance performance. These strategies ensured efficient learning and prevented the model from overfitting to the training data.

In the comparative analysis, the performance of the Graph Spiking Neural Network (Graph SNN) was evaluated against a Graph Convolutional Network (GCN)⁴⁰ and a Long Short-Term Memory (LSTM) network,⁴¹ both implemented using the native functions available in PyTorch. All models used in the comparison shared a seven-layer architecture to ensure consistency. The GCN was selected to compare the management of spatial dependencies, while the LSTM network was included to assess the handling of temporal dynamics. Experimental evaluations were conducted on the test subset, providing a thorough assessment of the models across the entire dataset.

Method details

Build a mixed urban flood risk dataset

Urban flooding is an increasingly critical issue globally, and it is particularly pertinent in China due to the rapid pace of urbanization. Existing public datasets often lack detailed and accurate information on urban flood risks, which hinders researchers' ability to understand and predict flood patterns and to devise effective flood management strategies. Recognizing the necessity for a dedicated urban flood dataset, our team was motivated to assemble a comprehensive repository of data. The dataset was meticulously constructed to ensure it would be a valuable resource for analyzing flood risks in urban landscapes, facilitating the advancement of research and the development of solutions to manage and mitigate the effects of urban flooding. The Figure 1 shows how we construct a mixed urban flood risk dataset for our research.

In conducting our research, we selected six Chinese metropolises—Beijing, Shanghai, Hangzhou, Shenzhen, Wuhan, and Shijiazhuang—drawing on their geographic spread and recorded history of urban flooding. The locations of these cities are elucidated in Figure 2. They encapsulate the varied climatic, economic, and infrastructural profiles present across China, thus offering a diverse spectrum for the assessment of urban flood risk. Our selection criteria were centered around encompassing a broad latitudinal and longitudinal range, urban population densities, and different economic development stages, which would enable our model to be trained on a widely relevant dataset.

To systematically collect social data on urban flooding, we employed a dual strategy: leveraging the Sina Weibo API and utilizing data acquisition scripts. This approach enriched our dataset, capturing detailed information about the locations and times of flooding events as reported by residents. These data are essential for pinpointing flood-prone areas and analyzing the temporal patterns of urban flooding. To enhance the precision of our analysis, we developed a classification system to categorize the flooding incidents based on the observed water depth, which is fundamental for a precise analysis of the urban flooding phenomenon. The classification criteria are as follows.

• (1)Low Risk: Incidents with water depths visually estimated to be less than 2 cm, or where no flooding is observed, are classified as low-risk events.
• (2)Medium Risk: Incidents where water levels rise above the sidewalk curb or submerge half of a car’s wheel, with depths ranging from approximately 10 to 30 cm, are categorized as medium-risk events.
• (3)High Risk: Incidents with water depths exceeding 30 cm, such as those that submerge a car’s engine hood or reach above pedestrians' knees, are designated as high-risk events.

This classification facilitates a clear and logical framework for assessing the severity of urban flooding, thereby informing effective urban planning and disaster response strategies.

After collecting the data, we initiated a meticulous cleaning and preprocessing routine to ensure the dataset’s reliability and uniformity. Initially, we manually checked text-based entries against historical weather data, verifying rain events on the dates mentioned. If corresponding weather reports and related regional information corroborated these events, we retained the entries; otherwise, they were purged. For entries with images, we simply confirmed rainfall on the dates preceding the posts. Once this manual verification was complete, we proceeded to the automated cleaning phase. Data cleaning involved removing duplicates, filtering out irrelevant entries, and standardizing data formats. To ensure consistency, quantitative data was normalized, and outliers identified using the standard score:

$$\begin{array}{c}{Z}_i=\frac{\left(X_i-\mu \right)}{\sigma }\end{array}$$ (Equation 1)

where $Z_i$ represents the standardized data point, $X_i$ the original data, $\mu$ the mean of the set, and $\sigma$ its standard deviation with outliers typically classified $\text{if}\left|Z_i\right|>3$. Missing values were imputed by:

$$\begin{array}{c}{\hat{X}}_{miss}=X_{obs}+\frac{\sum \left(X_{miss,i}-X_{obs,i}\right)}{n}\end{array}$$ (Equation 2)

where ${\hat{X}}_{miss}$ signifies the imputed value, $X_{miss,i}$ the missing value, $X_{obs,i}$ observed entries, and $n$ the count of missing instances.

Then, data was organized within a 30m $\times$ 30m urban grid. Each social media data point was allocated based on geographical coordinates. This data was categorized into ‘medium’ and ‘high’ risk levels and coupled with additional information including elevation data derived from 30-meter DEM and rainfall measurements from GPM,⁴² complemented by population density to establish a comprehensive risk assessment dataset. This method resulted in a detailed classification dataset that not only documents flood events but also outlines normal urban conditions, providing a well-rounded basis for our model to discern various flood risk levels effectively.

Because very little low-risk data has been collected, to increase the robustness of our urban flood risk assessment model, we randomly generate some non-flood condition data as low-risk data. These non-flood points also included pertinent elevation and rainfall data, mirroring the flood data setup. For non-flood scenarios, we randomly allocated 40–50% of the data points for each city, ensuring a balanced dataset to avoid model bias. The random allocation determined by:

$$\begin{array}{c}{N}_{nf}=\left(0.4+r\times 0.1\right)\times N\end{array}$$ (Equation 3)

where $N_{nf}$ is the number of data points for non-flood conditions, $r$ a uniform random number between 0 and 1, and $N$ is the total number of grid cells. After determining the required non-flood points, we randomly distributed them across the city grid to obtain the location.

Transform the mixed urban flood risk dataset into a standard graphical dataset

The meticulous construction of standard graph dataset necessitates the articulation of relationships between nodes, which are integral in describing their connections. The weights of these connections are determined using a weighted average approach that effectively blends the influence of proximity and elevation factors, providing a cohesive method for predicting flood impacts across our dataset. This is accomplished by considering the physical distance $d_{ij}$ and elevation differences $\Delta h_{ij}$, with closer nodes and those within the same urban area—indicating shared flood risks—assigned a greater weight to reflect their increased likelihood of similar flood patterns. To articulate these relationships, we employed the formula:

$$\begin{array}{c}{w}_{ij}=\frac{\alpha ·d_{ij}+\beta ·\Delta h_{ij}}{\alpha +\beta }\end{array}$$ (Equation 4)

where $\alpha$ and $\beta$ are constants that quantify the relative importance of proximity and elevation differences in influencing flood patterns.

To optimize these parameters for our specific task, we utilized an intelligent optimization algorithm known as the genetic algorithm (GA).⁴³ GA operates by defining a search space for each parameter and considering each model training instance as an individual within a population. The optimization goal is to minimize the error on our test dataset, ensuring the model’s predictions closely align with observed flood extents. GA is especially suited to complex, nonlinear problems where the search for optimal parameters requires a strategy that mimics natural evolutionary processes, navigating the entire solution space and avoiding the pitfalls of simpler methods.

For our experimental setup, we initialized a GA population of 10 and iterated through 50 generations. The genetic algorithm assesses each individual’s fitness based on the model’s performance metric—specifically, its accuracy in predicting flood-affected areas. Through natural selection, crossover, and mutation, the GA refines the parameters until it converges on a set that optimizes this performance metric. By harnessing GA, we effectively determined the values of $\alpha$ and $\beta$ that most accurately encapsulate the intricate interrelations of spatial proximity, elevation, and flood risk within our urban flood risk dataset.

Graph spiking neural network (graph SNN)

To advance the understanding of urban flood risks, this study employs a methodological approach that integrates Graph Neural Networks (GNN) with Spiking Neural Networks (SNN). Specifically, we utilized the Graph Convolutional Network (GCN) from GNNs, as well as the Tempotron model⁴⁴ from SNNs. Furthermore, we meticulously constructed a comprehensive dataset tailored to the nuances of urban flooding. The following subsections detail our approach and dataset construction process.

The architecture of the Graph SNN model combines four layers of a recurrent graph convolutional network (GCN) with three tempotron layers from spiking neural networks (SNNs). As shown in Figure 3, Our Graph SNN architecture comprises three principal components: the GCN, Spike Encoder, and the SNN. Initially, the input data is processed through the GCN according to the time step, extracting the spatial information of the different nodes in a cyclical graphical convolutional fashion. This process generates a time series. Subsequently, the generated time series is input into a spiking neural network (SNN) for further in-depth data analysis, leveraging the SNN’s time-series analysis capabilities. However, as the SNN processes spike signals, it is necessary to encode the time series data in order to render it comprehensible and manageable by the SNN. This structural configuration enables our Graph SNN model to effectively integrate the spatial feature extraction capability of the GCN with the time-series analysis proficiency of the SNN. Consequently, the model’s flexibility and adaptability in handling spatiotemporal data are enhanced, enabling a profound understanding and processing of complex datasets.

GCN is structured to function iteratively, processing each temporal timestep in a systematic fashion, which is a mathematical structure consisting of a set of nodes (or vertices) and a set of edges that connect pairs of nodes. Given a graph $G=\left(V,E\right)$, where $V$ and $E$ represent the sets of nodes $V$ ($\left|V\right|=n$) and edges, respectively, we assume that each node is self-connected, such that $\left(v,v\right)\in E$. The node feature matrix $X\in R^{n\times m}$ comprises $n$ nodes, each with an $m$-dimensional feature vector, denoted by $x_v\in R^m$ for node $v$. The adjacency matrix $A$ and the degree matrix $D$, where $D_{ii}=\sum _j{A}_{ij}$, are defined accordingly. Self-loops are accounted for by setting $A$'s diagonal elements to 1. A single-layer GCN acquires immediate neighbor information via convolution. However, stacking multiple GCN layers integrates extended neighborhood data. For a single-layer GCN, the $k$-dimensional feature matrix $L^{\left(1\right)}\in R^{n\times k}$ is computed as:

$$\begin{array}{c}{L}^{\left(1\right)}=\rho \left(\tilde{A}X{W}^{\left(0\right)}\right)\end{array}$$ (Equation 5)

with $\tilde{A}=D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$ signifying the normalized symmetric adjacency matrix, $W^{\left(0\right)}\in R^{m\times k}$ as a weight matrix, and $\rho$ representing an activation function, for instance, ReLU defined as $\rho \left(x\right)=\max \left(0,x\right)$. For incorporating information from higher-order neighborhoods, we stack multiple layers of GCN:

$$\begin{array}{c}{L}^{\left(j+1\right)}=\rho \left(\tilde{A}{L}^{\left(j\right)}{W}^{\left(j\right)}\right)\end{array}$$ (Equation 6)

where $j$ indicates the layer index and $L^{\left(0\right)}=X$.

This iterative approach ensures a thorough analysis of time-dependent data. Following the complete processing of temporal sequences, the output is encoded by a Gaussian encoder⁴⁵ that specializes in temporal data, converting it into a series of spike trains. The Gaussian encoding scheme can be represented as:

$$\begin{array}{c}{S}_i\left(t\right)=\exp \left(-\frac{{\left(t-{\mu }_i\right)}^2}{2{\sigma }_i^2}\right)\end{array}$$ (Equation 7)

where $S_i\left(t\right)$ is the spike train generated for the $i$-th feature, ${\mu }_i$ is the mean firing time related to the feature value, and ${\sigma }_i$ is the standard deviation, dictating the firing time dispersion. This encoder effectively converts the values into a pattern of spikes that can represent variations over time, making it possible for the network to interpret and analyze temporal information.

Subsequently, these spike trains are input into the Tempotron layers for further refinement. Tempotron layers is designed to respond with a spike when the integrated input signals exceed a certain threshold. The firing condition of a Tempotron neuron can be defined as:

$$\begin{array}{c}V\left(t\right)=\sum _i\sum _{f}K\left(t-t_i^f\right)>\theta \end{array}$$ (Equation 8)

where $V\left(t\right)$ represents the membrane potential at time $t$, $t_i^f$ denotes the firing time of the $i$-th input spike, $K\left(t-t_i^f\right)$ is the kernel function describing the postsynaptic potential (PSP) evoked by a spike arriving at time $t_i^f$, and $\theta$ is the firing threshold.

The final output of this method resembles a score vector rather than a conventional probability distribution, as the sum of its components does not necessarily equal one. Classification is performed by identifying the highest scoring category within this output, which is then designated as the predicted classification.

Quantification and statistical analysis

We compiled a confusion matrix and calculated key metrics such as precision, recall, F1 score and accuracy. Precision calculates the accuracy of positive predictions, showing how often the model is correct when it predicts a positive outcome. Recall measures the model’s ability to find all the actual positives, indicating its thoroughness. The F1 Score combines Precision and Recall into one figure to assess the model’s overall balance between these two factors. Accuracy gives us the percentage of all predictions, both positive and negative, that the model gets right, providing an overall effectiveness measure. These metrics can be calculated as:

$$\begin{array}{c}\text{Precision}=\frac{TP}{TP+FP}\end{array}$$ (Equation 9)

$$\begin{array}{c}\text{Recall}=\frac{TP}{TP+FN}\end{array}$$ (Equation 10)

$$\begin{array}{c}\mathrm{F}1\text{Score}=2\times \frac{\text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}\end{array}$$ (Equation 11)

$$\begin{array}{c}\text{Accuracy}=\frac{TP+TN}{TP+FP+FN+TN}\end{array}$$ (Equation 12)

where $TP$ is true positives, $FP$ is false positives, $TN$ is true negatives and $FN$ is false negatives.

We assessed the energy consumption and parameter count of the Graph SNN in comparison to the GCN and LSTM models. We quantified energy consumption and parameter count using several metrics, including Parameter Count (M), RAM power (kWh), CPU power (kWh), GPU power (kWh), and Total Energy (J). For this assessment, we utilized Python libraries such as torchinfo for parameter counting and pynvml for measuring GPU power, along with system utilities like psutil for monitoring RAM and CPU power usage.

All these metrics were calculated using Python 3.8.10.

Published: September 26, 2024