Abstract
Background
Missing values in datasets present significant challenges for data analysis, particularly in the medical field where data accuracy is crucial for patient diagnosis and treatment. Although MissForest (MF) has demonstrated efficacy in imputation research and recursive feature elimination (RFE) has proven effective in feature selection, the potential for enhancing MF through RFE integration remains unexplored.
Methods
This study introduces a novel imputation method, “recursive feature elimination-MissForest” (RFE-MF), designed to enhance imputation quality by reducing the impact of irrelevant features. A comparative analysis is conducted between RFE-MF and four classical imputation methods: mean/mode, k-nearest neighbors (kNN), multiple imputation by chained equations (MICE), and MF. The comparison is carried out across ten medical datasets containing both numerical and mixed data types. Different missing data rates, ranging from 10 to 50%, are evaluated under the missing completely at random (MCAR) mechanism. The performance of each method is assessed using two evaluation metrics: normalized root mean squared error (NRMSE) and predictive fidelity criterion (PFC). Additionally, paired samples t-tests are employed to analyze the statistical significance of differences among the outcomes.
Results
The findings indicate that RFE-MF demonstrates superior performance across the majority of datasets when compared to four classical imputation methods (mean/mode, kNN, MICE, and MF). Notably, RFE-MF consistently outperforms the original MF, irrespective of variable type (numerical or categorical). Mean/mode imputation exhibits consistent performance across various scenarios. Conversely, the efficacy of kNN imputation fluctuates in relation to varying missing data rates.
Conclusion
This study demonstrates that RFE-MF holds promise as an effective imputation method for medical datasets, providing a novel approach to addressing missing data challenges in medical applications.
Keywords: Missing value imputation, MissForest, Recursive feature elimination, Feature selection, Medical datasets
Introduction
Missing values, also known as missing data, are defined as data points that are not recorded for a variable in a given observation of interest [1]. This pervasive issue spans across various domains [2–6], often arising from a combination of factors such as human and machine errors, data processing difficulties, privacy concerns, or situations where relevant information is either unavailable or unobserved [7–10]. In medical research, missing data presents significant challenges, potentially impairing downstream statistical analyses and predictive models [11, 12]. These challenges can have broad implications, influencing clinical decision-making processes and ultimately affecting the quality of patient care [10, 13]. The severity of these consequences highlights the critical need to address the missing data problem in medical research.
To mitigate these challenges, researchers have developed and implemented various missing value imputation (MVI) techniques, which aim to replace missing values with derived estimates, thereby preserving dataset integrity and utility [14–18]. In the medical domain, several traditional imputation methods have been widely employed, including mean/mode imputation [19], multiple imputation by chained equations (MICE) [20], and k-nearest neighbor (kNN) imputation [21]. While these conventional techniques offer valuable solutions in certain contexts, they are subject to innate limitations that may affect either the accuracy of the imputed data or the applicability of the method itself. For instance, mean/mode imputation, despite its simplicity, replaces missing values with the mean or mode of the observed data for a given variable [22, 23]. However, this approach disregards the inherent uncertainty in such imputations, often yielding biased or unrealistic outcomes [24, 25]. MICE, renowned for its flexibility, is frequently employed as a multiple imputation method [26, 27]. Nevertheless, MICE, along with other multiple imputation techniques, faces challenges in high-dimensional settings [28], particularly those involving interactive and nonlinear relationships among variables [26, 29]. In such scenarios, the complexity of specifying conditional models for each variable with missing data increases substantially, rendering the imputation process both intricate and computationally demanding, potentially compromising the accuracy and efficiency of MICE [4, 30]. Similarly, while kNN imputation is widely utilized for its robustness and effectiveness [9, 31], its computational complexity and sensitivity to parameter settings—such as the number of neighbors, choice of distance metrics, and imputation order—present notable limitations, constraining its practical applicability in real-world settings [32, 33].
In response to these challenges, tree-based imputation methods have emerged as promising alternatives [34]. Notably, MissForest (MF), an iterative imputation algorithm based on random forests (RF), distinguishes itself from traditional imputation methods by neither assuming normality nor requiring parameter specifications for modeling [35, 36]. Furthermore, its capacity to effectively handle mixed data types renders it particularly adept in heterogeneous data contexts [37, 38]. Consequently, MF has garnered increasing attention in the field of MVI research, attributed to its favorable performance relative to traditional imputation methods [35, 36]. Moreover, several studies have demonstrated MF’s promising efficacy within the medical domain [37, 39]. However, while effective at imputing missing data, MF lacks inherent feature selection, which is critical for reducing dimensionality and improving model interpretability, particularly in high-dimensional medical datasets.
Feature selection reduces model complexity by identifying relevant features and removing irrelevant or redundant ones [40, 41]. Recursive feature elimination (RFE), a wrapper method, is particularly effective among feature selection strategies [42, 43] and has gained considerable acclaim within the biomedical domain for its efficacy across numerous studies [44, 45]. It iteratively removes the least important features based on their impact on model performance, aiming to optimize the feature subset for better classification accuracy [46, 47]. Recently, numerous studies have shown that conducting feature selection on observed data to filter out unrepresentative features can significantly enhance the efficiency of the imputation process, as certain missing features deemed unrepresentative may not be essential for effective imputation [48–51].
While MF has gained widespread recognition in MVI research, demonstrating its efficacy across various applications [35–37, 39], efforts to further optimize and fully explore its potential remain limited. Concurrently, RFE is a well-established feature selection method known for reducing dimensionality and improving computational efficiency [44, 45, 48]. However, its use has primarily been limited to a preprocessing role, aimed at enhancing predictive models rather than directly improving imputation methods. A significant research gap exists in integrating RFE feature selection and MF imputation techniques to improve both tasks simultaneously.
To address this, we propose RFE-MF, a novel approach that combines MF with RFE to mitigate the influence of irrelevant features and enhance imputation quality. This study introduces RFE-MF and demonstrates its effectiveness using medical datasets. We perform a comparative analysis to evaluate the performance of our proposed RFE-MF method against four conventional imputation approaches—mean/mode imputation, MICE, kNN, MF—using ten medical datasets. Furthermore, we evaluate their performance on both numerical and mixed data types, with simulated missing rates ranging from 10 to 50%, addressing key practical challenges in the medical field.
The rest of this paper is organized as follows. Section 2 reviews the related literature, covering missing data mechanisms, imputation techniques, and the RFE feature selection method. In Sect. 3, we describe the proposed RFE-MF algorithm. Sections 4 and 5 present the experimental evaluation and the results, respectively. Finally, conclusions are drawn in Sect. 6.
Literature review
Missing data mechanisms
According to [52], there are three mechanisms for missing data: missing completely at random (MCAR), missing at random (MAR), and not missing at random (NMAR). These classifications are based on the relationship between the missingness of the data and the observed or unobserved values in the dataset [53].
MCAR occurs when the probability of missingness is independent of both observed and unobserved variables [54]. An illustrative example is a heart rate monitoring study where data points are missing due to equipment malfunction, such as battery failure. In this scenario, the missing data are unrelated to participants’ heart rates or any other measured variables, thus satisfying the MCAR criteria. MAR is characterized by missingness that is contingent upon observed variables but remains independent of unobserved data [54]. Consider a large-scale health survey where participants periodically report on their health status. If older individuals are more likely than younger participants to omit questions related to dietary habits, the missingness is associated with the observed variable (age) but not with the unobserved dietary information. Once age is controlled for, the missingness can be treated as random, thereby fulfilling the MAR condition. MNAR, the most complex mechanism, occurs when missingness is directly related to unobserved data, such as the value of the missing variable itself [55]. This is exemplified in longitudinal studies of depression, where participants experiencing more severe symptoms may be less inclined to complete follow-up assessments. In this instance, the likelihood of missing data correlates with the unobserved severity of depression, as those with the most pronounced symptoms are the ones most likely to be absent. This represents a case of MNAR, where the missing data are systematically linked to unobserved characteristics.
Imputation methods are predicated on specific missingness mechanisms, and deviations from these underlying assumptions may introduce bias into subsequent analyses [53]. When data adhere to the MCAR condition, results derived from various imputation techniques maintain their validity, and complete case analysis does not introduce systematic bias [56]. To evaluate the efficacy of our proposed imputation method relative to established classical techniques, we conducted a comparative analysis under the MCAR mechanism. The selection of MCAR as a fundamental basis for this comparative analysis is supported by its relatively straightforward assumptions, which provide a well-defined benchmark for assessing imputation performance. Furthermore, previous studies [14, 15] have revealed that MCAR is the most commonly used missingness mechanism in simulation studies, due to its simplicity and ease of implementation, making it an ideal starting point for evaluating imputation methods.
Missing value imputation
Current MVI strategies can be broadly classified into four main categories: single imputation, multiple imputation, machine/deep learning, and tree-based imputation [34, 50, 57, 58]. The first category comprises single imputation methods, including mean/mode imputation [19], regression imputation [59], and expectation–maximization [60]. Among these methods, mean/mode imputation replaces missing numerical values with the mean and categorical values with the most frequent value (mode), effectively using central tendencies to fill in the gaps for the corresponding variables [22, 23]. It is often favored for its simplicity and serves as a common reference technique [61]. However, despite its ease of use, these methods tend to underestimate the variance of estimates and overlook the correlations between variables, potentially resulting in biased or unrealistic outcomes [24, 25].
The second category, multiple imputation, was proposed by Rubin [62, 63], who developed a method for averaging outcomes across multiple imputed datasets. This approach diverges from single imputation methods by substituting each missing observation with multiple plausible values, thereby more accurately reflecting the inherent uncertainty associated with the imputation process [64, 65]. Among the various multiple imputation methods, MICE exhibits flexibility and robustness in managing mixed data structures by offering a full range of conditional distributions and regression-based methods [20, 29]. Its unique design, based on chained equations, enables the estimation of each variable using the model best suited to its specific distribution characteristics [66, 67]. However, MICE is not without limitations. While it imputes missing data through a series of conditional distributions, there is no guarantee that these align with the appropriate joint distribution, potentially compromising the validity and reliability of the imputed results [26]. This issue is particularly pronounced in massive, multivariable datasets, where the complexity of specifying appropriate models is exacerbated by nonlinear and interactive relationships between variables [26, 29].
The third category encompasses machine learning and/or deep learning methods such as kNN [21], support vector machine [68], clustering [69], and multi-layer perceptron [70], etc. The kNN imputation method has been widely studied for its efficacy in addressing missing data [9, 65]. It works by classifying the nearest neighbors of missing values and use those neighbors for imputation using a distance measure between instances [71]. Configuring kNN typically requires selecting an appropriate distance metric—such as Hamming, Euclidean, or Manhattan distance—and determining the optimal number of neighbors, k, to predict each missing value [9]. However, the efficacy of kNN imputation is not only critically dependent on several key parameters (i.e., the number of neighbors, and choice of distance metrics)—factors for which standardized determination methods are currently lacking [9, 72]—but it also faces a substantial limitation due to its computational complexity, particularly in high-dimensional datasets [32].
The fourth category, tree-based imputation, includes decision tree [73], RF [36], and MF [38]. Among these methods, MF employs the RF algorithm for missing data imputation, efficiently managing multivariate datasets that include both numerical and categorical variables [37, 38]. Additionally, MF requires no parameter tuning and imposes no assumptions about the underlying distribution of the data [35, 36], demonstrating its effectiveness in managing missing data, particularly in medical research [74, 75]. Despite its efficacy, MF exhibits limitations, particularly in handling high-dimensional datasets where the computational burden of iterative imputation presents a significant challenge [37, 76, 77].
RFE feature selection
Feature selection in machine learning is essential for reducing data dimensionality and constructing models that are both simplified and interpretable [40, 41]. This process identifies relevant features while eliminating irrelevant or redundant ones through various approaches, including filter, wrapper, or embedded methods [78, 79].
Among these, RFE, a wrapper selection method, has gained prominence for its ability to identify optimal feature subsets based on model performance and classification accuracy [42, 46]. RFE’s operational mechanism involves iteratively eliminating features, generating a ranking of features and candidate subsets, along with a list of accuracy values corresponding to each subset [47, 80]. This approach allows for a comprehensive evaluation of feature importance and their impact on model performance. Notably, RFE is frequently employed in conjunction with various classification algorithms, such as support vector machines [42] and RF [44], to construct more efficient classifiers. This synergistic combination enhances the overall model efficacy by focusing on the most informative features, thereby potentially improving both accuracy and interpretability in complex classification tasks while simultaneously reducing storage and computational costs [81, 82].
Proposed RFE-MF algorithm
This study integrates RFE into MF, aiming to leverage MF’s inherent capability to handle mixed data types while enhancing its utility in real-world clinical settings. By incorporating RF-RFE, the extended MF method performs both missing data imputation and feature selection, yielding more efficient and interpretable models. The details of the RF-RFE mechanism and how it complements MF in achieving both imputation and feature selection are as follows.
Suppose we have a data matrix , where n denotes the number of observations and p the number of predictors, of size . For an arbitrary variable () with missing values at certain entries, the RFE-MF algorithm divides the dataset into four distinct parts [38]:
Observed values of : These are the entries in that are not missing, denoted by .
Missing values of : These are the variables other than for which the corresponding observations in are not missing, denoted by .
Other variables with complete observations: These are the variables other than with observations, denoted by .
Other variables with missing observations: These represent the variables other than , corresponding to the rows has missing values. These variables with observations are denoted as .
Figure 1 presents the pseudo-code of the proposed RFE-MF algorithm, which consists of six steps: (1) initial imputation, (2) iterative imputation, (3) feature selection, (4) model fitting, (5) convergence, and (6) outputting the final imputed dataset.
Fig. 1.
The proposed RFE-MF algorithm
In Step 1, the variables in are sorted by the number of missing values in each , starting with the variable that has the fewest missing values. Initially, all missing values in the dataset are imputed using simple strategies: the mean for numerical variables and the mode for categorical variables. In Step 2, the RFE-MF algorithm iteratively updates the imputed dataset. Specifically, given a previously imputed dataset (denoted as ) and a stopping criterion , Step 2 generates a new imputed dataset (denoted as ) until the imputed values stabilize. The stopping criterion will be discussed in later paragraphs.
In each iteration, Steps 3–5 are executed. Let k denote the vector of sorted indices of variables in . For each in k, Step 3 begins by applying the RF-RFE procedure, RF-RFE(), to perform feature selection using the response variable and the predictors , resulting in (i.e., the important predictors selected by RF-RFE).
The Procedure RF-RFE () facilitates the elimination of irrelevant or redundant features through an iterative process to optimize model performance. Initially, a random forest model is trained using the full set of predictors, , to predict the response variable, . After the model is trained, the importance of each predictor is evaluated and ranked based on its contribution to the model's accuracy. In each iteration, the algorithm removes a certain number of the least important predictors and retrains the random forest model with the reduced subset. This process is repeated, with the model’s performance being evaluated and the remaining predictors ranked after each iteration. The goal is to identify the subset of predictors that results in the best model performance. Once the optimal set of predictors is determined, it is returned as the final list of important features, .
In Step 4, a random forest model is trained using and . The missing values are then predicted by applying the trained RF model to in . The imputed matrix is continually updated for all variables listed in k, ultimately yielding .
In Step 5, convergence is checked by comparing the imputed values from the current iteration (i.e., ) with those from the previous iteration (). Convergence is defined as when the difference between and in the current iteration exceeds the difference between them in the previous iteration. Once the imputed data matrix has converged, the stopping criterion is met, and the algorithm return from the current iteration as the final result (Step 6).
Similar to MF, the proposed RFE-MF method can impute values for both numerical and categorical variables. To assess convergence in RFE-MF, the difference for the set of numerical variables is defined as:
| 1 |
Similarly, the difference for the set of categorical variables is defined as:
| 2 |
where is an indicator function that equals 1 when the newly and previously imputed values differ, and #NA is the number of missing values in the categorical variables.
Experimental evaluation
Dataset source
We assessed RFE-MF on ten medical datasets from the UCI repository of machine learning databases [83] and Kaggle.1These datasets included numerical and mixed data types. See Table 1 for dataset descriptions.
Table 1.
Medical datasets used for experimental analysis
| Data type | Dataset | Year | Instances | Features |
|---|---|---|---|---|
| Numerical | Parkinson Disease Detection | 2020 | 195 | 22 |
| Mehmet Diabetes | 2020 | 768 | 8 | |
| Prostate Cancer | 2018 | 100 | 8 | |
| Lower Back Pain Symptoms | 2016 | 310 | 12 | |
| Liver Disorders | 1990 | 345 | 7 | |
| Mixed | Pre-processed Stroke | 2021 | 5109 | 11 |
| Heart Failure Prediction | 2020 | 299 | 12 | |
| Early-Stage Diabetes Risk Prediction | 2020 | 520 | 16 | |
| Indian Liver Patient Records | 2017 | 583 | 10 | |
| Contraceptive Method Choice | 1997 | 1473 | 9 |
Experimental setup
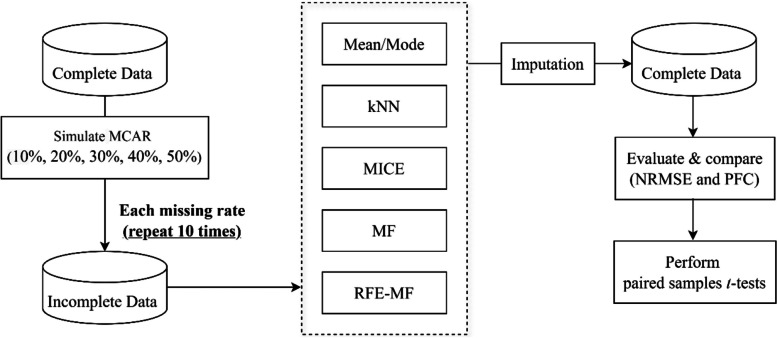
The experimental process, illustrated in Fig. 2, begins with simulating ten complete datasets using the MCAR mechanism, across five missing rates: 10%, 20%, 30%, 40%, and 50%. For each missing rate, the simulation is repeated ten times to generate incomplete datasets. Five imputation methods, including mean/mode, kNN, MICE, MF, and RFE-MF, are then applied to impute the missing values. The imputation quality is assessed using two metrics: normalized root mean squared error (NRMSE) for numerical variables and the proportion of falsely classified entries (PFC) for categorical variables. To compare the performance of each imputation method against RFE-MF, paired samples t-tests are conducted, utilizing results from ten repetitions of the simulated tests.
Fig. 2.
The experimental process
In addition to standard mean/mode imputation, kNN imputation was applied with k = 5. MICE was used to generate five multiple imputed datasets, with a threshold of 1 to address multicollinearity. MF parameters were optimized following recommendations from [38], employing 10 iterations and 100 forests. The proposed RFE-MF used the RF-RFE algorithm with enhanced resampling over 10 cross-validation iterations. The number of forests for predicting missing values matched those in MF, though only 3 iterations were found sufficient after experimentation. All methods were implemented in R, and categorical variables were preprocessed using label encoding.
Evaluation metrics
The performance for numerical variables is evaluated using NRMSE, as proposed by [84], defined as:
| 3 |
where is the imputed data matrix and is the complete data matrix. "Mean" and "var" are shorthand notations for the empirical mean and variance, computed over the numerical missing values.
For categorical variables, PFC is used as the evaluation metric, defined as:
| 4 |
where is the true value, is the imputed value, and #NA is the number of missing values in the categorical variables. In both cases, better performance results in values closer to 0, while poorer performance approaches a value of 1.
Experimental results
Results of numerical datasets
The NRMSE results for numerical data and the paired t-test for the differences in population means are presented in Table 2. In the Parkinson Disease Detection dataset, at a 10% missing rate, MF performs optimally with an NRMSE of 0.342. However, the difference between MF (0.342) and our proposed RFE-MF (0.343) is negligible. Notably, the discrepancy increases slightly at the 20%, 40%, and 50% missing rates. Interestingly, at a 30% missing rate, RFE-MF marginally outperforms MF (NRMSE = 0.310 vs. 0.312). In the Mehmet Diabetes dataset, RFE-MF achieves the lowest NRMSE (0.627) at a 10% missing rate, followed by MF (0.641) and kNN (0.694), a trend that persists across all missing rates up to 50%. In the Prostate Cancer dataset, mean/mode imputation performs poorly at a 10% missing rate but stabilizes as missing rates increase. Conversely, kNN’s performance deteriorates as missing rates rise, with MICE exhibiting a similar trend but with slightly better performance than kNN. MF and RFE-MF alternate as the top-performing methods. In the Lower Back Pain Symptoms dataset, RFE-MF consistently outperforms all other methods across every level of missingness. Similarly, in the Liver Disorders dataset, RFE-MF consistently delivers the best results.
Table 2.
NRMSE and paired t-test results for numerical datasets across five imputation methods
| Dataset | Imputation method | Missing Rates | Mean | t | p | ||||
|---|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | |||||
| Parkinson Disease Detection | Me/Mo | 0.419 | 0.390 | 0.387 | 0.392 | 0.394 | 0.396 | 12.725 | < 0.001*** |
| kNN | 0.411 | 0.391 | 0.402 | 0.409 | 0.411 | 0.405 | 16.392 | < 0.001*** | |
| MICE | 0.506 | 0.469 | 0.485 | 0.471 | 0.498 | 0.485 | 15.961 | < 0.001*** | |
| MF | 0.342 | 0.313 | 0.312 | 0.338 | 0.341 | 0.329 | -2.234 | 0.0301** | |
| RFE-MF | 0.343 | 0.322 | 0.310 | 0.342 | 0.353 | 0.334 | |||
| Mehmet Diabetes | Me/Mo | 0.810 | 0.841 | 0.819 | 0.814 | 0.815 | 0.850 | 12.184 | < 0.001*** |
| kNN | 0.694 | 0.732 | 0.768 | 0.787 | 0.796 | 0.755 | 9.466 | < 0.001*** | |
| MICE | 0.910 | 0.897 | 0.928 | 0.969 | 0.989 | 0.939 | 16.745 | < 0.001*** | |
| MF | 0.641 | 0.672 | 0.713 | 0.752 | 0.763 | 0.708 | 5.182 | < 0.001*** | |
| RFE-MF | 0.627 | 0.662 | 0.698 | 0.739 | 0.750 | 0.695 | |||
| Prostate Cancer | Me/Mo | 0.418 | 0.478 | 0.433 | 0.454 | 0.451 | 0.447 | 15.683 | < 0.001*** |
| kNN | 0.340 | 0.415 | 0.408 | 0.466 | 0.459 | 0.418 | 16.898 | < 0.001*** | |
| MICE | 0.246 | 0.267 | 0.351 | 0.401 | 0.416 | 0.336 | 4.076 | < 0.001*** | |
| MF | 0.191 | 0.255 | 0.284 | 0.351 | 0.348 | 0.286 | 0.611 | 0.544 | |
| RFE-MF | 0.180 | 0.260 | 0.281 | 0.341 | 0.356 | 0.284 | |||
| Lower Back Pain Symptoms | Me/Mo | 0.397 | 0.473 | 0.474 | 0.462 | 0.438 | 0.449 | 27.984 | < 0.001*** |
| kNN | 0.370 | 0.453 | 0.477 | 0.478 | 0.462 | 0.448 | 33.971 | < 0.001*** | |
| MICE | 0.396 | 0.477 | 0.461 | 0.455 | 0.469 | 0.452 | 18.625 | < 0.001*** | |
| MF | 0.280 | 0.369 | 0.384 | 0.371 | 0.371 | 0.355 | 5.074 | < 0.001*** | |
| RFE-MF | 0.275 | 0.365 | 0.381 | 0.369 | 0.365 | 0.351 | |||
| Liver Disorders | Me/Mo | 0.579 | 0.595 | 0.575 | 0.579 | 0.583 | 0.582 | 13.906 | < 0.001*** |
| kNN | 0.521 | 0.568 | 0.546 | 0.542 | 0.566 | 0.585 | 11.781 | < 0.001*** | |
| MICE | 0.648 | 0.695 | 0.653 | 0.677 | 0.699 | 0.674 | 15.501 | < 0.001*** | |
| MF | 0.500 | 0.542 | 0.502 | 0.511 | 0.546 | 0.520 | 4.933 | < 0.001*** | |
| RFE-MF | 0.489 | 0.529 | 0.493 | 0.497 | 0.529 | 0.507 | |||
The optimal values across five simulated missing rates and their mean value for the different medical datasets are highlighted in bold
Me/Mo mean/mode imputation, kNN k-nearest neighbor imputation, MICE multiple imputation by chained equations, MF MissForest, RFE-MF recursive feature elimination-MissForest. Significant differences at the 99% and 99.9% levels are indicated by ** and ***, respectively
Regarding the paired t-tests results, RFE-MF consistently demonstrates the lowest means values across four datasets: Mehmet Diabetes, Prostate Cancer, Lower Back Pain Symptoms, and Liver Disorders, with all p-values < 0.001*** (except for the difference between RFE-MF and MF in the Prostate Cancer dataset, which is not statistically significant). Conversely, in the Parkinson Disease Detection dataset, MF yields superior results compared to RFE-MF, with a p-value of 0.030**, indicating a statistically significant difference in favor of MF.
Results of mixed datasets
The results of the NRMSE and PFC for both numerical and categorical variables, along with the paired t-test for the difference in population means, are presented in Table 3. In terms of the NRMSE metric, in the Heart Failure Prediction dataset, RFE-MF slightly outperforms MF, although the mean/mode imputation method exhibits the best performance. Similar trends are observed in the PFC metric, with RFE-MF closely trailing MF at a 10% missing rate. To better understand the efficacy of the mean/mode imputation method in this dataset, we analyzed the statistical characteristics of each variable under complete conditions and various simulated missing rates. The findings suggest that the dataset's characteristics favor the mean/mode imputation method, as the continuous variables closely approximate their complete-condition mean values, while the mode values for categorical variables consistently align with the complete data.
Table 3.
NRMSE, PFC results, and paired t-test results for mixed datasets across five imputation methods
| Dataset | Imputation method | NRMSE | PFC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Missing Rates | Mean | t | p | Missing Rates | Mean | t | p | ||||||||||
| 10% | 20% | 30% | 40% | 50% | 10% | 20% | 30% | 40% | 50% | ||||||||
| Heart Failure Prediction | Me/Mo | 0.354 | 0.402 | 0.356 | 0.376 | 0.369 | 0.371 | -14.085 | < 0.001*** | 0.374 | 0.377 | 0.372 | 0.378 | 0.368 | 0.374 | 9.001 | < 0.001*** |
| kNN | 0.370 | 0.429 | 0.387 | 0.404 | 0.396 | 0.397 | -2.097 | 0.0411** | 0.422 | 0.430 | 0.420 | 0.440 | 0.439 | 0.430 | -6.006 | < 0.001*** | |
| MICE | 0.546 | 0.568 | 0.519 | 0.514 | 0.530 | 0.536 | -14.085 | < 0.001*** | 0.429 | 0.422 | 0.442 | 0.445 | 0.457 | 0.439 | -7.129 | < 0.001*** | |
| MF | 0.375 | 0.424 | 0.384 | 0.405 | 0.415 | 0.401 | -5.071 | < 0.001*** | 0.408 | 0.407 | 0.406 | 0.426 | 0.423 | 0.414 | -1.504 | 0.139 | |
| RFE-MF | 0.366 | 0.406 | 0.378 | 0.400 | 0.403 | 0.391 | 0.415 | 0.404 | 0.395 | 0.418 | 0.415 | 0.409 | |||||
| Pre-processed Stroke | Me/Mo | 0.571 | 0.570 | 0.570 | 0.572 | 0.573 | 0.571 | 12.995 | < 0.001*** | 0.316 | 0.324 | 0.320 | 0.320 | 0.319 | 0.320 | 19.581 | < 0.001*** |
| kNN | 0.574 | 0.588 | 0.602 | 0.608 | 0.628 | 0.600 | 36.539 | < 0.001*** | 0.302 | 0.310 | 0.316 | 0.321 | 0.330 | 0.316 | 36.158 | < 0.001*** | |
| MICE | 0.691 | 0.709 | 0.709 | 0.718 | 0.721 | 0.710 | 57.120 | < 0.001*** | 0.339 | 0.341 | 0.346 | 0.347 | 0.356 | 0.346 | 50.703 | < 0.001*** | |
| MF | 0.503 | 0.514 | 0.538 | 0.562 | 0.585 | 0.540 | 8.847 | < 0.001*** | 0.297 | 0.306 | 0.309 | 0.315 | 0.324 | 0.310 | 30.866 | < 0.001*** | |
| RFE-MF | 0.496 | 0.508 | 0.528 | 0.547 | 0.558 | 0.527 | 0.279 | 0.287 | 0.293 | 0.296 | 0.303 | 0.291 | |||||
| Early-Stage Diabetes Risk Prediction | Me/Mo | 1.004 | 1.003 | 1.002 | 1.000 | 1.000 | 1.002 | 13.232 | < 0.001*** | 0.386 | 0.391 | 0.391 | 0.388 | 0.386 | 0.388 | 20.971 | < 0.001*** |
| kNN | 0.850 | 0.899 | 0.943 | 1.009 | 1.011 | 0.942 | 15.062 | < 0.001*** | 0.172 | 0.210 | 0.248 | 0.284 | 0.306 | 0.244 | 17.691 | < 0.001*** | |
| MICE | 1.229 | 1.197 | 1.215 | 1.211 | 1.256 | 1.222 | 24.680 | < 0.001*** | 0.318 | 0.331 | 0.339 | 0.352 | 0.367 | 0.341 | 21.197 | < 0.001*** | |
| MF | 0.703 | 0.741 | 0.797 | 0.900 | 0.950 | 0.818 | 0.425 | 0.673 | 0.118 | 0.167 | 0.208 | 0.253 | 0.289 | 0.207 | 5.819 | < 0.001*** | |
| RFE-MF | 0.711 | 0.743 | 0.813 | 0.879 | 0.932 | 0.816 | 0.110 | 0.157 | 0.202 | 0.245 | 0.282 | 0.199 | |||||
| Indian Liver Patient Records | Me/Mo | 0.773 | 0.862 | 0.860 | 0.863 | 0.865 | 0.845 | 15.627 | < 0.001*** | 0.247 | 0.244 | 0.239 | 0.237 | 0.251 | 0.243 | -3.083 | 0.0034** |
| kNN | 0.737 | 0.829 | 0.851 | 0.858 | 0.864 | 0.828 | 15.616 | < 0.001*** | 0.276 | 0.301 | 0.293 | 0.292 | 0.292 | 0.291 | 6.581 | < 0.001*** | |
| MICE | 1.185 | 0.933 | 0.960 | 0.957 | 0.977 | 1.002 | 8.674 | < 0.001*** | 0.335 | 0.348 | 0.354 | 0.363 | 0.373 | 0.355 | 12.688 | < 0.001*** | |
| MF | 0.619 | 0.676 | 0.718 | 0.726 | 0.824 | 0.713 | 3.497 | 0.001** | 0.245 | 0.256 | 0.263 | 0.284 | 0.288 | 0.267 | 2.455 | 0.0177* | |
| RFE-MF | 0.606 | 0.663 | 0.704 | 0.714 | 0.788 | 0.695 | 0.257 | 0.247 | 0.255 | 0.257 | 0.266 | 0.256 | |||||
| Contraceptive Method Choice | Me/Mo | 0.383 | 0.386 | 0.387 | 0.386 | 0.384 | 0.385 | 13.099 | < 0.001*** | 0.370 | 0.374 | 0.369 | 0.372 | 0.373 | 0.372 | 7.983 | < 0.001*** |
| kNN | 0.371 | 0.392 | 0.405 | 0.416 | 0.417 | 0.400 | 27.304 | < 0.001*** | 0.365 | 0.378 | 0.379 | 0.395 | 0.403 | 0.384 | 22.883 | < 0.001*** | |
| MICE | 0.426 | 0.434 | 0.453 | 0.470 | 0.482 | 0.453 | 52.507 | < 0.001*** | 0.411 | 0.413 | 0.418 | 0.425 | 0.438 | 0.421 | 41.197 | < 0.001*** | |
| MF | 0.325 | 0.339 | 0.362 | 0.383 | 0.398 | 0.361 | 13.035 | < 0.001*** | 0.385 | 0.391 | 0.393 | 0.400 | 0.405 | 0.395 | 25.186 | < 0.001*** | |
| RFE-MF | 0.314 | 0.324 | 0.343 | 0.358 | 0.370 | 0.342 | 0.338 | 0.344 | 0.349 | 0.365 | 0.376 | 0.354 | |||||
The optimal values across five simulated missing rates and their mean value for the different medical datasets are highlighted in bold
Me/Mo mean/mode imputation, kNN k-nearest neighbor imputation, MICE multiple imputation by chained equations, MF MissForest, RFE-MF recursive feature elimination-MissForest. Significant differences at the 95%, 99%, and 99.9% levels are indicated by *, **, and ***, respectively
In the Pre-processed Stroke dataset, RFE-MF consistently performs best across both the NRMSE and PFC metrics, followed by MF, while kNN’s performance declines with increasing missing rates. In the Early-Stage Diabetes Risk Prediction dataset, MF excels in NRMSE at missing rates between 10 and 30%, whereas RFE-MF performs slightly better at missing rates between 40 and 50%. RFE-MF consistently outperforms the PFC metric. In the Indian Liver Patient Records dataset, RFE-MF consistently outperforms MF in NRMSE across all missing rates. The mean/mode imputation method shows optimal PFC performance, with RFE-MF trailing MF slightly only at a 10% missing rate. In the Contraceptive Method Choice dataset, RFE-MF exhibits the best NRMSE performance across all missing rates. RFE-MF consistently outperforms in PFC, except for being slightly surpassed by mean/mode imputation method at a 50% missing rate.
Regarding the paired t-tests for NRMSE, RFE-MF performs optimally across four datasets: Pre-processed Stroke, Early-Stage Diabetes Risk Prediction, Indian Liver Patient Records, and Contraceptive Method Choice, with statistically significant results. However, in the Early-Stage Diabetes Risk Prediction dataset, the difference between RFE-MF and MF is not statistically significant. In the Heart Failure Prediction dataset, mean/mode imputation method exhibits the best performance, with RFE-MF slightly trailing behind. Similar trends are observed in the paired t-tests for PFC, where RFE-MF performs optimally across most datasets. However, in the Heart Failure Prediction and the Indian Liver Patient Records datasets, the mean/mode imputation method outperforms RFE-MF.
In summary, as shown in Table 4, the results highlight the effectiveness of the proposed RFE-MF method in handling missing values across the selected datasets. In the experimental evaluation of 10 medical datasets, RFE-MF achieved the top rank in seven datasets, while securing the second rank in the remaining three. These findings confirm that RFE-MF outperforms the other four classical imputation methods, demonstrating its suitability for medical datasets.
Table 4.
The rankings of five imputation methods across all datasets
| Data type | Dataset | Metric | Me/Mo | kNN | MICE | MF | RFE-MF |
|---|---|---|---|---|---|---|---|
| Numerical | Parkinson Disease Detection | NRMSE | 3 | 4 | 5 | 1 | 2 |
| Mehmet Diabetes | NRMSE | 4 | 3 | 5 | 2 | 1 | |
| Prostate Cancer | NRMSE | 5 | 4 | 3 | 2 | 1 | |
| Lower Back Pain Symptoms | NRMSE | 4 | 3 | 5 | 2 | 1 | |
| Liver Disorders | NRMSE | 3 | 4 | 5 | 2 | 1 | |
| Mixed | Heart Failure Prediction | NRMSE | 1 | 3 | 5 | 4 | 2 |
| PFC | 1 | 4 | 5 | 3 | 2 | ||
| Pre-processed Stroke | NRMSE | 3 | 4 | 5 | 2 | 1 | |
| PFC | 2 | 4 | 5 | 3 | 1 | ||
| Early-Stage Diabetes Risk Prediction | NRMSE | 4 | 3 | 5 | 2 | 1 | |
| PFC | 5 | 3 | 4 | 2 | 1 | ||
| Indian Liver Patient Records | NRMSE | 4 | 3 | 5 | 2 | 1 | |
| PFC | 1 | 4 | 5 | 3 | 2 | ||
| Contraceptive Method Choice | NRMSE | 3 | 4 | 5 | 2 | 1 | |
| PFC | 2 | 3 | 5 | 4 | 1 | ||
| Total scores | 45 | 53 | 72 | 36 | 19 | ||
| Overall ranking | 3 | 4 | 5 | 2 | 1 | ||
Me/Mo mean/mode imputation, kNN k-nearest neighbor imputation, MICE multiple imputation by chained equations, MF MissForest, RFE-MF recursive feature elimination-MissForest, NRMSE normalized root-mean-square error, PFC proportion of falsely classified samples
Conclusions
In this study, the proposed RFE-MF exhibits superior performance across the majority of medical datasets compared to four classical imputation methods (mean/mode imputation, kNN, MICE, and MF), underscoring its efficacy in MVI tasks. Notably, RFE-MF consistently outperforms the original MF, regardless of variable type (numerical or categorical), indicating the effectiveness of our integrated approach in improving imputation quality for datasets with mixed characteristics. Additionally, the results highlight the sensitivity of kNN imputation to varying missing rates, whereas mean/mode imputation maintains consistent performance across all missing data rates, depending on the dataset's characteristics. Our proposed RFE-MF demonstrates potential for practical applications, offering a valuable imputation technique for healthcare data analysis and the development of predictive models. Furthermore, this study emphasizes the importance of considering data type and missingness rate when selecting imputation techniques, as these factors significantly impact the performance of different methods.
This study acknowledges several limitations. Firstly, certain parameters, such as the k value in kNN imputation method and the number of iterations for MICE, were not optimized. Default hyperparameter values were employed for MF, indicating a need for further investigation into parameter tuning. Secondly, while this study focuses on RF-RFE, future research could explore the integration of other feature selection methods with MF, potentially uncovering novel synergies and enhancing imputation performance. Nevertheless, the current selection of RF-RFE is justified by the limitations of alternative methods. For instance, genetic algorithms [85] often face issues of high computational cost for fitness calculation [86], especially when dealing with high-dimensional datasets prevalent in medical research. Finally, it is crucial to note that the analyses and conclusions presented in this study are predicated on the assumption of MCAR data. Future research should explore the performance of these methods under different missing data mechanisms, including MAR and MNAR, to enhance the generalizability and applicability of the findings across various scenarios in medical research.
Acknowledgements
This research was supported in part by the Ministry of Science and Technology (grant number MOST 111-2410-H-008-026-MY2) and the National Science and Technology Council (grant number NSTC 113-2410-H-008-054).
Authors’ contributions
All authors had full access to all of the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Study concept and design: YHH and TYL. Acquisition of data: YCL. Analysis and interpretation of data: YHH, RYW, and YCL. Drafting of the manuscript: All authors. Critical revision of the manuscript for important intellectual content: All authors. Study supervision: YHH.
Funding
The authors report no funding.
Data availability
The datasets generated and/or analyzed during the current study are available in the UCI Machine Learning Repository (https://archive.ics.uci.edu/datasets) and Kaggle (https://www.kaggle.com/).
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Little RJ, Rubin DB. Statistical analysis with missing data. 3rd ed. Hoboken, NJ: John Wiley & Sons; 2019. [Google Scholar]
- 2.Arriagada P, Karelovic B, Link O. Automatic gap-filling of daily streamflow time series in data-scarce regions using a machine learning algorithm. J Hydrol. 2021;598:126454. 10.1016/j.jhydrol.2021.126454. [Google Scholar]
- 3.Berkelmans GF, Read SH, Gudbjörnsdottir S, Wild SH, Franzen S, Van Der Graaf Y, Eliasson B, Visseren FL, Paynter NP, Dorresteijn JA. Population median imputation was noninferior to complex approaches for imputing missing values in cardiovascular prediction models in clinical practice. J Clin Epidemiol. 2022;145:70–80. 10.1016/j.jclinepi.2022.01.011. [DOI] [PubMed] [Google Scholar]
- 4.Hegde H, Shimpi N, Panny A, Glurich I, Christie P, Acharya A. MICE vs PPCA: missing data imputation in healthcare. Inform Med Unlocked. 2019;17:100275. 10.1016/j.imu.2019.100275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lan Q, Xu X, Ma H, Li G. Multivariable data imputation for the analysis of incomplete credit data. Expert Syst Appl. 2020;141:112926. 10.1016/j.eswa.2019.112926. [Google Scholar]
- 6.Zhang S, Gong L, Zeng Q, Li W, Xiao F, Lei J. Imputation of gps coordinate time series using missforest. Remote Sens. 2021;13(12):2312. 10.3390/rs13122312. [Google Scholar]
- 7.Austin PC, White IR, Lee DS, van Buuren S. Missing data in clinical research: a tutorial on multiple imputation. Can J Cardiol. 2021;37(9):1322–31. 10.1016/j.cjca.2020.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cheng C-H, Chang J-R, Huang H-H. A novel weighted distance threshold method for handling medical missing values. Comput Biol Med. 2020;122:103824. 10.1016/j.compbiomed.2020.103824. [DOI] [PubMed] [Google Scholar]
- 9.Emmanuel T, Maupong T, Mpoeleng D, Semong T, Mphago B, Tabona O. A survey on missing data in machine learning. J Big Data. 2021;8(1):140. 10.1186/s40537-021-00516-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pedersen AB, Mikkelsen EM, Cronin-Fenton D, Kristensen NR, Pham TM, Pedersen L, Petersen I. Missing data and multiple imputation in clinical epidemiological research. Clin Epidemiol. 2017;9:157–66. 10.2147/CLEP.S129785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Viñas R, Azevedo T, Gamazon ER, Liò P. Deep learning enables fast and accurate imputation of gene expression. Front Genet. 2021;12:624128. 10.3389/fgene.2021.624128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Molenberghs G, Kenward M. Missing data in clinical studies. Chichester, UK: John Wiley & Sons; 2007. [Google Scholar]
- 13.Jakobsen JC, Gluud C, Wetterslev J, Winkel P. When and how should multiple imputation be used for handling missing data in randomised clinical trials–a practical guide with flowcharts. BMC Med Res Methodol. 2017;17:1–10. 10.1186/s12874-017-0442-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin W-C, Tsai C-F. Missing value imputation: a review and analysis of the literature (2006–2017). Artif Intell Rev. 2020;53:1487–509. 10.1007/s10462-019-09709-4. [Google Scholar]
- 15.Donders ART, Van Der Heijden GJ, Stijnen T, Moons KG. A gentle introduction to imputation of missing values. J Clin Epidemiol. 2006;59(10):1087–91. 10.1016/j.jclinepi.2006.01.014. [DOI] [PubMed] [Google Scholar]
- 16.Afkanpour M, Hosseinzadeh E, Tabesh H. Identify the most appropriate imputation method for handling missing values in clinical structured datasets: a systematic review. BMC Med Res Methodol. 2024;24(1):188. 10.1186/s12874-024-02310-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu X, Xia L, Zhang Q, Wu S, Wu M, Liu H. The ability of different imputation methods for missing values in mental measurement questionnaires. BMC Med Res Methodol. 2020;20:1–9. 10.1186/s12874-020-00932-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tsiampalis T, Panagiotakos D. Methodological issues of the electronic health records’ use in the context of epidemiological investigations, in light of missing data: a review of the recent literature. BMC Med Res Methodol. 2023;23(1):180. 10.1186/s12874-023-02004-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Grzymala-Busse JW, Grzymala-Busse WJ. Handling missing attribute values. In: Maimon O, Rokach L, editors. Data mining and knowledge discovery handbook. Boston, MA: Springer; 2010. p. 33–51. [Google Scholar]
- 20.Van Buuren S, Groothuis-Oudshoorn K. MICE: multivariate imputation by chained equations in R. J Stat Softw. 2011;45:1–67. 10.18637/jss.v045.i03. [Google Scholar]
- 21.Batista GE, Monard MC. An analysis of four missing data treatment methods for supervised learning. Appl Artif Intell. 2003;17(5–6):519–33. 10.1080/713827181. [Google Scholar]
- 22.Sim J, Lee JS, Kwon O. Missing values and optimal selection of an imputation method and classification algorithm to improve the accuracy of ubiquitous computing applications. Math Probl Eng. 2015;2015(1):538613. 10.1155/2015/538613. [Google Scholar]
- 23.Farhangfar A, Kurgan L, Dy J. Impact of imputation of missing values on classification error for discrete data. Pattern Recognit. 2008;41(12):3692–705. 10.1016/j.patcog.2008.05.019. [Google Scholar]
- 24.Carroll OU, Morris TP, Keogh RH. How are missing data in covariates handled in observational time-to-event studies in oncology? a systematic review. BMC Med Res Methodol. 2020;20:1–15. 10.1186/s12874-020-01018-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Van Buuren S. Flexible imputation of missing data. 2nd ed. Boca Raton: CRC Press; 2018. [Google Scholar]
- 26.Burgette LF, Reiter JP. Multiple imputation for missing data via sequential regression trees. Am J Epidemiol. 2010;172(9):1070–6. 10.1093/aje/kwq260. [DOI] [PubMed] [Google Scholar]
- 27.Costantini E, Lang KM, Sijtsma K, Reeskens T. Solving the many-variables problem in MICE with principal component regression. Behav Res Methods. 2024;56(3):1715–37. 10.3758/s13428-023-02117-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Alharthi AM, Lee MH, Algamal ZY. Improving penalized logistic regression model with missing values in high-dimensional data. Int J Online Biomed Eng. 2022;18(2). 10.3991/ijoe.v18i02.25047.
- 29.Azur MJ, Stuart EA, Frangakis C, Leaf PJ. Multiple imputation by chained equations: what is it and how does it work? Int J Methods Psychiatr Res. 2011;20(1):40–9. 10.1002/mpr.329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Khan SI, Hoque ASML. SICE: an improved missing data imputation technique. J Big Data. 2020;7(1):37. 10.1186/s40537-020-00313-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Beretta L, Santaniello A. Nearest neighbor imputation algorithms: a critical evaluation. BMC Med Inform Decis Mak. 2016;16:197–208. 10.1186/s12911-016-0318-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fan M, Peng X, Niu X, Cui T, He Q. Missing data imputation, prediction, and feature selection in diagnosis of vaginal prolapse. BMC Med Res Methodol. 2023;23(1):259. 10.1186/s12874-023-02079-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sachan S, Almaghrabi F, Yang J-B, Xu D-L. Evidential reasoning for preprocessing uncertain categorical data for trustworthy decisions: an application on healthcare and finance. Expert Syst Appl. 2021;185:115597. 10.1016/j.eswa.2021.115597. [Google Scholar]
- 34.Valdiviezo HC, Van Aelst S. Tree-based prediction on incomplete data using imputation or surrogate decisions. Inf Sci. 2015;311:163–81. 10.1016/j.ins.2015.03.018. [Google Scholar]
- 35.Ramosaj B, Pauly M. Predicting missing values: a comparative study on non-parametric approaches for imputation. Comput Stat. 2019;34(4):1741–64. 10.1007/s00180-019-00900-3. [Google Scholar]
- 36.Tang F, Ishwaran H. Random forest missing data algorithms. Stat Anal Data Min. 2017;10(6):363–77. 10.1002/sam.11348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hong S, Lynn HS. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med Res Methodol. 2020;20:1–12. 10.1186/s12874-020-01080-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stekhoven DJ, Bühlmann P. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics. 2012;28(1):112–8. 10.1093/bioinformatics/btr597. [DOI] [PubMed] [Google Scholar]
- 39.Shadbahr T, Roberts M, Stanczuk J, Gilbey J, Teare P, Dittmer S, Thorpe M, Torné RV, Sala E, Lió P. The impact of imputation quality on machine learning classifiers for datasets with missing values. Commun Med. 2023;3(1):139. 10.1038/s43856-023-00356-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dhal P, Azad C. A comprehensive survey on feature selection in the various fields of machine learning. Appl Intell. 2022;52(4):4543–81. 10.1007/s10489-021-02550-9. [Google Scholar]
- 41.Li J, Cheng K, Wang S, Morstatter F, Trevino RP, Tang J, Liu H. Feature selection: a data perspective. ACM Comput Surv. 2017;50(6):1–45. 10.1145/3136625. [Google Scholar]
- 42.Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Mach Learn. 2002;46:389–422. 10.1023/A:1012487302797. [Google Scholar]
- 43.Gregorutti B, Michel B, Saint-Pierre P. Correlation and variable importance in random forests. Stat Comput. 2017;27:659–78. 10.1007/s11222-016-9646-1. [Google Scholar]
- 44.Chen Q, Meng Z, Liu X, Jin Q, Su R. Decision variants for the automatic determination of optimal feature subset in RF-RFE. Genes. 2018;9(6):301. 10.3390/genes9060301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Su R, Liu X, Wei L. MinE-RFE: determine the optimal subset from RFE by minimizing the subset-accuracy–defined energy. Brief Bioinform. 2020;21(2):687–98. 10.1093/bib/bbz021. [DOI] [PubMed] [Google Scholar]
- 46.Liu W, Wang J. Recursive elimination–election algorithms for wrapper feature selection. Appl Soft Comput. 2021;113. 10.1016/j.asoc.2021.107956.
- 47.Darst BF, Malecki KC, Engelman CD. Using recursive feature elimination in random forest to account for correlated variables in high dimensional data. BMC Genet. 2018;19:1–6. 10.1186/s12863-018-0633-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu C-H, Tsai C-F, Sue K-L, Huang M-W. The feature selection effect on missing value imputation of medical datasets. Appl Sci. 2020;10(7):2344. 10.3390/app10072344. [Google Scholar]
- 49.Tran CT, Zhang M, Andreae P, Xue B, Bui LT. Improving performance of classification on incomplete data using feature selection and clustering. Appl Soft Comput. 2018;73:848–61. 10.1016/j.asoc.2018.09.026. [Google Scholar]
- 50.Awawdeh S, Faris H, Hiary H. EvoImputer: an evolutionary approach for missing data imputation and feature selection in the context of supervised learning. Knowl Based Syst. 2022;236:107734. 10.1016/j.knosys.2021.107734. [Google Scholar]
- 51.Sefidian AM, Daneshpour N. Missing value imputation using a novel grey based fuzzy c-means, mutual information based feature selection, and regression model. Expert Syst Appl. 2019;115:68–94. 10.1016/j.eswa.2018.07.057. [Google Scholar]
- 52.Rubin DB. Inference and missing data. Biometrika. 1976;63(3):581–92. 10.1093/biomet/63.3.581. [Google Scholar]
- 53.Beaulieu-Jones BK, Lavage DR, Snyder JW, Moore JH, Pendergrass SA, Bauer CR. Characterizing and managing missing structured data in electronic health records: data analysis. JMIR Med Inform. 2018;6(1):e8960. 10.2196/medinform.8960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sterne JA, White IR, Carlin JB, Spratt M, Royston P, Kenward MG, Wood AM, Carpenter JR. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009;338:b2393. 10.1136/bmj.b2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Council NR. The prevention and treatment of missing data in clinical trials. Washington, DC: The National Academies Press; 2010. [PubMed] [Google Scholar]
- 56.Jamshidian M, Jalal SJ, Jansen C. MissMech: an R package for testing homoscedasticity, multivariate normality, and missing completely at random (MCAR). J Stat Softw. 2014;56(6):1–31. 10.18637/jss.v056.i06. [Google Scholar]
- 57.Fazakis N, Kostopoulos G, Kotsiantis S, Mporas I. Iterative robust semi-supervised missing data imputation. IEEE Access. 2020;8:90555–69. 10.1109/ACCESS.2020.2994033. [Google Scholar]
- 58.D’Ambrosio A, Aria M, Siciliano R. Accurate tree-based missing data imputation and data fusion within the statistical learning paradigm. J Classif. 2012;29:227–58. 10.1007/s00357-012-9108-1. [Google Scholar]
- 59.Song Q, Shepperd M. Missing data imputation techniques. Int J Bus Intell Data Min. 2007;2(3):261–91. 10.1504/IJBIDM.2007.015485. [Google Scholar]
- 60.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B Stat Method. 1977;39(1):1–22. 10.1111/j.2517-6161.1977.tb01600.x. [Google Scholar]
- 61.Jerez JM, Molina I, García-Laencina PJ, Alba E, Ribelles N, Martín M, Franco L. Missing data imputation using statistical and machine learning methods in a real breast cancer problem. Artif Intell Med. 2010;50(2):105–15. 10.1016/j.artmed.2010.05.002. [DOI] [PubMed] [Google Scholar]
- 62.Rubin DB, Multiple imputations in sample surveys: a phenomenological Bayesian approach to nonresponse. In: Proceedings of the survey research methods section, 1978; p. 20–34.
- 63.Rubin DB. Multiple imputation for nonresponse in surveys. Hoboken, NJ: John Wiley & Sons; 2004. [Google Scholar]
- 64.Sun Y, Li J, Xu Y, Zhang T, Wang X. Deep learning versus conventional methods for missing data imputation: a review and comparative study. Expert Syst Appl. 2023;227:120201. 10.1016/j.eswa.2023.120201. [Google Scholar]
- 65.Jadhav A, Pramod D, Ramanathan K. Comparison of performance of data imputation methods for numeric dataset. Appl Artif Intell. 2019;33(10):913–33. 10.1080/08839514.2019.1637138. [Google Scholar]
- 66.Jolani S, Debray TP, Koffijberg H, van Buuren S, Moons KG. Imputation of systematically missing predictors in an individual participant data meta-analysis: a generalized approach using MICE. Stat Med. 2015;34(11):1841–63. 10.1002/sim.6451. [DOI] [PubMed] [Google Scholar]
- 67.Mera-Gaona M, Neumann U, Vargas-Canas R, López DM. Evaluating the impact of multivariate imputation by MICE in feature selection. PLoS ONE. 2021;16(7):e0254720. 10.1371/journal.pone.0261739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mallinson H, Gammerman A. Imputation using support vector machines. Department of Computer Science: Royal Holloway, University of London, Egham, UK; 2003. [Google Scholar]
- 69.Zhang S, Zhang J, Zhu X, Qin Y, Zhang C. Missing value imputation based on data clustering. In: Gavrilova ML, Tan CJK, editors. Transactions on computational science I. Berlin: Springer; 2008. p. 128–38. [Google Scholar]
- 70.Gupta A, Lam MS. Estimating missing values using neural networks. J Oper Res Soc. 1996;47(2):229–38. 10.1057/jors.1996.21. [Google Scholar]
- 71.Zhang S. Nearest neighbor selection for iteratively kNN imputation. J Syst Softw. 2012;85(11):2541–52. 10.1016/j.jss.2012.05.073. [Google Scholar]
- 72.Maillo J, Ramírez S, Triguero I, Herrera F. kNN-IS: an Iterative Spark-based design of the k-Nearest Neighbors classifier for big data. Knowl Based Syst. 2017;117:3–15. 10.1016/j.knosys.2016.06.012. [Google Scholar]
- 73.Twala B. An empirical comparison of techniques for handling incomplete data using decision trees. Appl Artif Intell. 2009;23(5):373–405. 10.1080/08839510902872223. [Google Scholar]
- 74.Tiwaskar S, Rashid M, Gokhale P. Impact of machine learning-based imputation techniques on medical datasets: a comparative analysis. Multimed Tools Appl. 2024. 10.1007/s11042-024-19103-0. [Google Scholar]
- 75.Aracri F, Bianco MG, Quattrone A, Sarica A. Imputation of missing clinical, cognitive and neuroimaging data of dementia using missForest, a random forest-based algorithm. In: 2023 IEEE 36th International Symposium on Computer-Based Medical Systems (CBMS). New York: IEEE; 2023. p. 684-688.
- 76.Dong W, Fong DYT, Yoon JS, Wan EYF, Bedford LE, Tang EHM, Lam CLK. Generative adversarial networks for imputing missing data for big data clinical research. BMC Med Res Methodol. 2021;21:1–10. 10.1186/s12874-021-01272-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Miao X, Wu Y, Chen L, Gao Y, Yin J. An experimental survey of missing data imputation algorithms. IEEE Trans Knowl Data Eng. 2022;35(7):6630–50. 10.1109/TKDE.2022.3186498. [Google Scholar]
- 78.Remeseiro B, Bolon-Canedo V. A review of feature selection methods in medical applications. Comput Biol Med. 2019;112:103375. 10.1016/j.compbiomed.2019.103375. [DOI] [PubMed] [Google Scholar]
- 79.Saeys Y, Inza I, Larranaga P. A review of feature selection techniques in bioinformatics. Bioinformatics. 2007;23(19):2507–17. 10.1093/bioinformatics/btm344. [DOI] [PubMed] [Google Scholar]
- 80.Jeon H, Oh S. Hybrid-recursive feature elimination for efficient feature selection. Appl Sci. 2020;10(9):3211. 10.3390/app10093211. [Google Scholar]
- 81.Duan K-B, Rajapakse JC, Wang H, Azuaje F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans Nanotechnol. 2005;4(3):228–34. 10.1109/TNB.2005.853657. [DOI] [PubMed] [Google Scholar]
- 82.Shen K-Q, Ong C-J, Li X-P, Hui Z, Wilder-Smith EP. A feature selection method for multilevel mental fatigue EEG classification. IEEE Trans Biomed Eng. 2007;54(7):1231–7. 10.1109/TBME.2007.890733. [DOI] [PubMed] [Google Scholar]
- 83.Blake CL. UCI repository of machine learning databases. 1998. Available from: https://archive.ics.uci.edu/. Accessed 8 May 2024.
- 84.Oba S, Sato MA, Takemasa I, Monden M, Matsubara KI, Ishii S. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics. 2003;19(16):2088–96. 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- 85.D’Angelo G, Palmieri F. GGA: a modified genetic algorithm with gradient-based local search for solving constrained optimization problems. Inf Sci. 2021;547:136–62. 10.1016/j.ins.2020.08.040. [Google Scholar]
- 86.Lobato F, Sales C, Araujo I, Tadaiesky V, Dias L, Ramos L, Santana A. Multi-objective genetic algorithm for missing data imputation. Pattern Recognit Lett. 2015;68:126–31. 10.1016/j.patrec.2015.08.023. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the UCI Machine Learning Repository (https://archive.ics.uci.edu/datasets) and Kaggle (https://www.kaggle.com/).