Abstract
Dynamic Ca2+ signaling is crucial for cell survival and death, and Ca2+ imaging approaches are commonly used to study and measure cellular Ca2+ patterns within cells. However, the presence of image noise from instrumentation and experimentation protocols can impede the accurate extraction of Ca2+ signals. Removing noise from Ca2+ Spatio-Temporal Maps (STMaps) is essential for precisely analyzing Ca2+ datasets. Current methods for denoising STMaps can be time-consuming and subjective and rely mainly on image processing protocols. To address this, we developed CalDenoise, an automated software that employs robust image processing and deep learning models to remove noise and enhance Ca2+ signals in STMaps effectively. CalDenoise integrates four pipelines capable of efficiently removing salt-and-pepper, impulsive, and periodic noise and detecting and removing background noise. Comprising both an image-processing-based pipeline and three generative-adversarial-network-based (GAN) deep learning models, CalDenoise proficiently removes complex noise patterns. The software features adjustable parameters to enhance accuracy and is integrated into a user-friendly graphical interface for easy access and streamlined usage.
CalDenoise can serve as a robust platform for denoising complex dynamic fluorescence signal images across diverse cell types, including Ca2+, voltage, ions, and pH signals.
Keywords: Deep learning, Ca2+ imaging analysis, Image denoising, Generative adversarial networks
Graphical abstract

Highlights
-
•
CalDenoise is a software that enhance Ca2+ signals by eliminating background noise.
-
•
The software offers a combination of one image-processing pipeline and three deep learning models.
-
•
Effectively mitigates various noise types, including salt-and-pepper, impulsive, and periodic noises.
-
•
It enhances the accurate extraction of Ca2+ event parameters.
-
•
The models minimize user error and provide flexible calibration settings, allowing for efficient and precise denoising.
We developed CalDenoise, a software designed to automate the denoising of Ca2+ Spatio-Temporal Maps (STMaps) to quantify cellular Ca2+ patterns. The software comprises an image-processing-based pipeline and three generative-adversarial-network-based deep learning models capable of removing various types of noise patterns.
1. Introduction
Calcium signaling is a vital cellular mechanism that influences a wide range of physiological responses and functions [1,2]. Ca2+ imaging is a broadly utilized technique in medical and biological research, aiding in the study of various cell types, including neurons, smooth muscle cells, and pacemaker interstitial cells, as well as their functions. Cellular Ca2+ signals display complex firing patterns with distinct spatial and temporal properties. These signals can manifest as Ca2+ waves that propagate within or between cells, lasting from a few seconds to several minutes [[3], [4], [5], [6], [7], [8], [9]]. or are stochastic, short-lived signals that occur within milliseconds range [[10], [11], [12], [13]]. Recent developments in Ca2+ imaging methods and optogenetic techniques have made it possible to achieve resolution at the subcellular level, providing new insights into the complex nature of Ca2+ signaling dynamics within cells. These innovations have led to the generation of vast datasets that demand thorough and efficient analysis. While the hardware for capturing cellular Ca2+ signals has evolved significantly, the development of analytical tools to process these signals has lagged behind. Many existing analysis methods struggle to effectively manage the extensive data produced by modern Ca2+ imaging technologies.
Most Ca2+ imaging systems, such as confocal, light-sheet microscopy, two-photon, or wide-field, are capable of capturing Ca2+ signals, but the images often contain varying levels of noise. This noise typically originates from several system hardware sources: 1) Camera-specific noise, such as gain, dark current noise, and photon shot noise, 2) fluctuations in the light source, such as instability in mercury or xenon arc lamps, tungsten-halogen lamps, or LEDs, as well as variations in laser power, and 3) mechanical vibrations within the system.
Signal noise poses a significant challenge in biological imaging research, with tissue fluorescence imaging facing specific issues related to sample noise. Sources of sample noise include autofluorescence, especially when imaging collagen due to its natural autofluorescent properties that overlap with fluorescent dyes; contamination from dyes or sensors and bleed-through between channels can also introduce fluorescence noise. To minimize fluorescence noise and obtain accurate and reliable images it is important to carefully select imaging parameters, optimize sample preparation techniques, and use appropriate controls to account for any potential sources of noise. However, noise present in Ca2+ imaging experiments can become superimposed with the collected Ca2+ signal datasets, potentially leading to significant inaccuracies during signal extraction and interpretation. As a result, noise reduction is a critical step in analyzing Ca2+ imaging data.
One common technique for analyzing and quantifying Ca2+ signals is the use of spatio-temporal maps (STMaps). These maps represent intracellular Ca2+ signals by plotting them as a function of space and time, providing an effective way to quantify complex Ca2+ signaling patterns [5,[14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26]]. Through Ca2+ STMaps analysis, various parameters such as event duration, spatial propagation, frequency, angle, and intensity of Ca2+ signals can be measured and analyzed [[27], [28], [29], [30], [31]].
Effectively removing signal noise from the dynamics of the Ca2+ sensor is essential for accurately resolving Ca2+ signals and processing information from STMaps. Various prepossessing and denoising approaches for Ca2+ imaging data have been employed, including image averaging protocols and kernel-based smoothing [[32], [33], [34], [35]]. Ca2+ Image averaging is a method that is easy to understand and implement, but it requires a substantial number of images, often difficult to acquire due to photobleaching resulting from prolonged exposure times. Another technique, principal components analysis (PCA), is utilized for reducing noise in image data and extracting cellular signals by simplifying their dimensions [36]. This method identifies and removes dimensions that primarily capture signal noise, but it may also inadvertently discard important information related to Ca2+ transient signals and responses to stimuli. A similar PCA-based technique has been employed in neuroimaging to enhance weaker neuronal signals by filtering out background noise in maps of neuronal activity. This method effectively combines traditional difference analysis with principal components analysis. In this approach, the activity map is created by projecting the standard difference onto a basis formed by the principal components that exhibit the highest statistical relevance, while also ensuring that the PCA components exceed a specific correlation threshold with the stimulus distribution [37].
Specific applications also utilize image denoising techniques, such as Fourier analysis, which is effective for morphological imaging of brain activity in response to cyclic stimulation. This method enables signal extraction at the excitation frequency while filtering out activity at other irrelevant frequencies [[38], [39], [40]]. Additionally, another approach uses matrix decomposition to denoise image sequences by taking advantage of the inherent characteristics of the data [41].
The advent of deep learning has led to significant advancements in the accuracy and efficiency of denoising algorithms, largely relying on GPU-powered computation. Significantly, the U-Net architecture and its variants have surpassed traditional machine learning and image processing techniques, establishing themselves as leading solutions for medical image denoising tasks [[42], [43], [44]]. This architecture functions similarly to an auto-encoder and consists of encoder and decoder modules, featuring multiple convolutional layers for both down-sampling and up-sampling. An essential feature of the U-Net architecture is the incorporation of skip connections linking the encoder and decoder, which ensures the retention of high-resolution feature data. The U-Net architecture has found successful application across various imaging techniques, including Computed Tomography (CT), Magnetic Resonance Imaging (MRI) and digital pathology [43]. Additionally, a newer deep learning method known as Generative Adversarial Networks (GANs) employs a generator to create denoised images while using a discriminator to assess whether the generated image matches the true data distribution [45]. Despite the popularity of deep learning models, their potential for denoising Ca2+ imaging tasks has not yet been explored. Previous denoising methods typically relied on basic background subtraction, leading to the loss of critical information regarding Ca2+ signals and event details. Ca2+ STMaps often contain a specific type of periodic noise; typically, periodic noise in images is attributed to system noise and in spinning disk confocal microscopes, this pattern arises from the rotation of the confocal head disks. Factors such as disk speed, laser alignment and imperfections in the microlenses on these disks contribute to the formation of this periodic noise pattern.
Existing denoising techniques lack specific components designed to eliminate periodic and sensor noise. To address this critical issue, we introduce a denoising software that utilizes innovative image-processing techniques alongside three new architectures based on GANs. These techniques successfully filter out noise and enhance Ca2+ signals in STMaps, supporting more accurate measurement and analysis of Ca2+ activity. Our proposed image-processing method imposes minimal computational demands, making it suitable for handling large datasets. Furthermore, the GAN architectures leverage GPU acceleration for rapid inference. The overall system includes several hyperparameters that can be adjusted to optimize noise removal from Ca2+ signals. Additionally, the parameters of the denoising image-processing modules can be combined in various ways to produce a range of denoised maps of Ca2+signals.
In this study, our denoising software was used to effectively reduce noise and enhance Ca2+ signals, resulting in a notable improvement in the signal-to-noise ratio. The objective of this research is to enhance the detection of Ca2+ events through machine learning techniques that automatically identify and remove inherent noise in Ca2+ maps, optimizing the analysis of these signals. We monitored and obtained Ca2+ signals from two different interstitial cell types in the murine colon: submucosal interstitial cells of Cajal (ICC-SM) and intramuscular interstitial cells of Cajal (ICC-IM) [25,46]. Typically, ICC-SM is responsible for generating pacemaker activity in the colon, whereas ICC-IM facilitates neurotransmission [15,[47], [48], [49], [50], [51], [52], [53]]. Each ICC type displays unique Ca2+ firing patterns, with ICC-IM exhibiting stochastic firing and ICC-SM demonstrating rhythmic firing [9,52]. Our denoising method was illustrated using ICC Ca2+ STMaps, highlighting the accuracy and effectiveness of our model in enhancing Ca2+ signals and reduce image noise.
2. Results
2.1. Calcium signal denoising using image processing and generative adversarial networks architectures
Our Calcium Denoising software, CalDenoise, was developed using an image processing module and three state-of-the-art GANs. It includes several innovative components that allow for effective and reliable denoising of subcellular signals which are described below.
2.1.1. Ca2+ signal datasets
We utilized datasets from Ca2+ STMaps imaged from mice expressing a GCaMP Ca2+ sensor in Kit-positive gastrointestinal pacemaker ICCs. These datasets contain subcellular Ca2+ signals, which exhibited a range of event patterns, from stochastic to rhythmic, often accompanied by background noise. Within our dataset, signals displayed diverse and complex Ca2+ signal patterns. To visualize these dynamic Ca2+ signals we generated STMaps which are 2D maps created by reslicing an X-Y-Z section in a movie or image stack. However, these STMaps inherently contain noise and conventional background subtraction and smoothing techniques are not effective in eliminating this noise. To accurately analyze the Ca2+ imaging data and other fluorescent dynamic signals present in the STMaps, it is crucial to remove image noise in order to properly define and segment different signal events. Therefore, we developed a novel deep-learning approach based on GANs architecture which achieves highly accurate denoising of Ca2+ STMaps. The software consists of four denoising modules as discussed in the following sections.
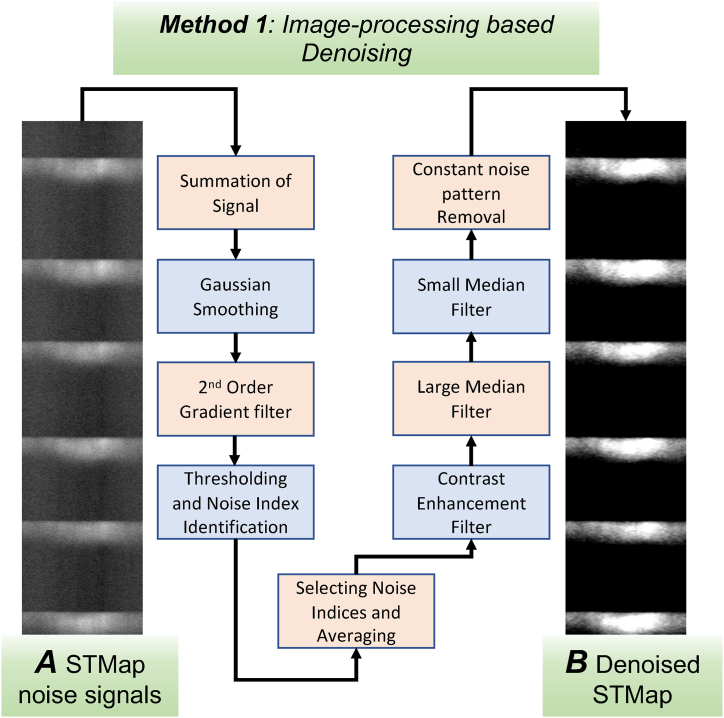
2.1.2. Denoising of calcium signal maps using image-processing approach
Ca2+ signals in colonic ICC-SM were captured using a spinning-disk confocal system (Fig. 1A and B) and pacemaking rhythmic Ca2+ transients were recorded and analyzed using STMaps (Fig. 1C and D). STMaps allow the visualization and quantification of both the temporal and spatial characteristics of Ca2+ events, along with their intensities, represented through color coding (Fig. 1D). However, while STMap analysis provides an efficient way to quantify Ca2+ imaging data, it is prone to several issues, such as artifacts, noise from salt-and-pepper patterns, and impulse noise like light streaks (Fig. 1C–F). These anomalies can interfere with accurate signal extraction.
Fig. 1.
Background signal noise in Ca2+ spatio-temporal maps (STMaps).
A Representative image of ICC-SM from colonic tissues of a Kit-iCre-GCaMP6f mouse. B Fluorescence Ca2+ intensity image (color-coded), where blue-black represents low fluorescence levels and red-orange represents high Ca2+ fluorescence. The pink outline defines the region of interest (ROI) for generating the Ca2+ STMap. C Representative raw STMap constructed from a single ROI (ICC-SM) indicated in B, plotting Ca2+ signals in 2 dimensions as a function of time. D STMap of Ca2+ signals in ICC-SM (Color-coded), with the red box highlighting a user-defined ROI for averaging background noise. E Representative image of background subtraction noise removal method of Ca2+ STMap and additional gaussian filter was applied for signal smoothing F. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Traditional techniques, such as background subtraction and Gaussian smoothing filters, are typically applied to reduce noise in STMaps. Unfortunately, these methods are not capable of completely eliminating noise without also distorting or reducing the original Ca2+ signal (Fig. 1E and F). To address these challenges, we propose a novel preprocessing and denoising pipeline for STMap analysis. This image-processing denoising approach effectively minimizes artifacts and noise without significantly compromising the integrity of the original Ca2+ signals, offering a more refined and accurate method for analyzing Ca2+ imaging data.
2.1.3. Calcium signal extraction using Gaussian kernel and Laplacian momentum
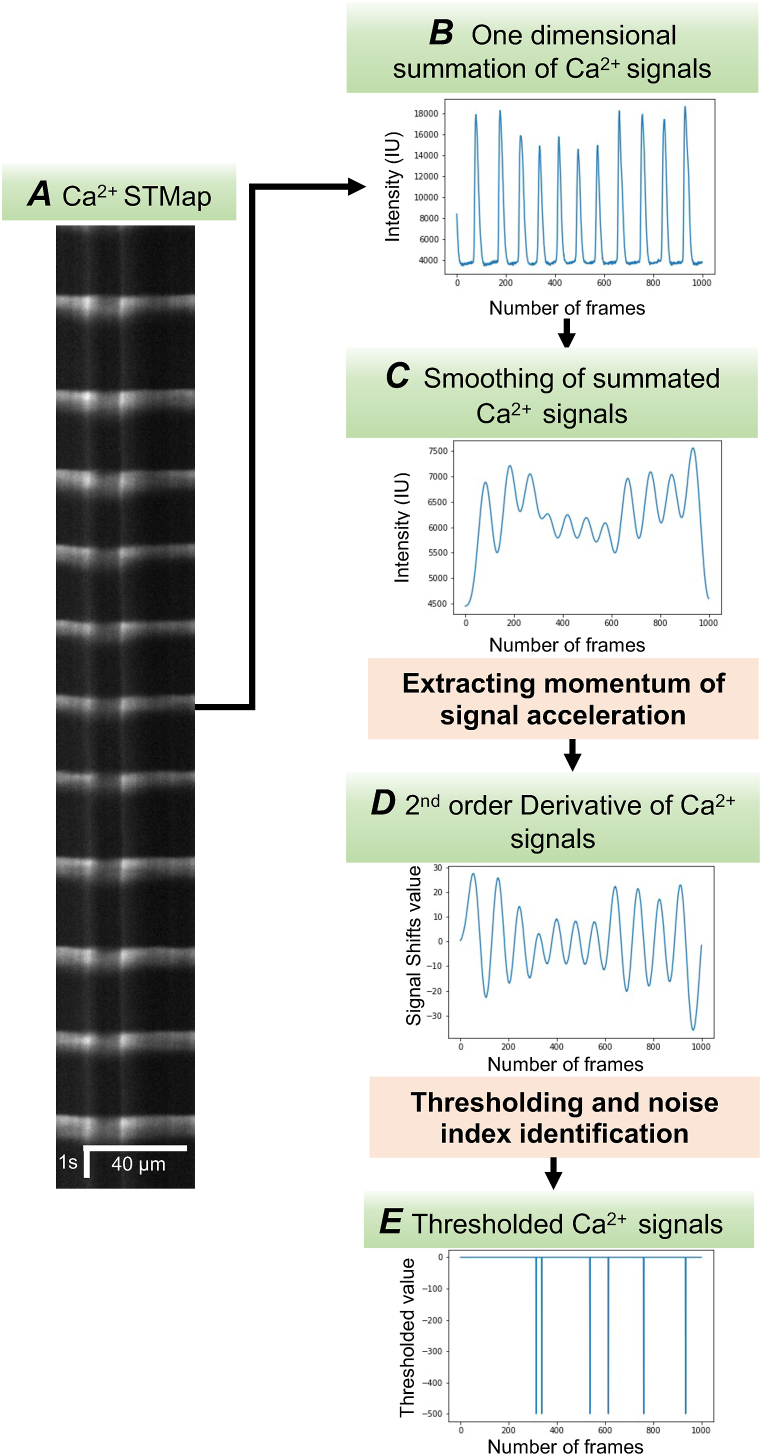
We adopted a mathematical approach to define noise, moving away from the conventional image denoising techniques that typically depend on heavy filtering and thresholding. The process begins By aggregating the Ca2+ signal values across the X-axis from an individual STMap, This process converts the image data into a one dimensional (1D) cumulative signal (Fig. 2 A&B). This transformation condenses the information, enabling a more computationally efficient analysis of the Ca2+ signals. Based on this summated signal, we developed two key equations that describe the behavior of the Ca2+ signals as given in Eq. (1) and Eq. (2). Q represents the STMap, where we sum all the values in the i-th row into an intermediate value, Ti as shown in Eq. (2), repeating this summation for each row of Q results in the final 1D signal, T (Fig. 2 B).
| (1) |
| (2) |
Fig. 2.
Momentum extraction and thresholding for noise indices of STMap Ca2+ signals.
A Representative image of Ca2+ Spatio-temporal map (STMap) of ICC-SM. B The Ca2+ signals are transformed into one-dimensional data points by summing the intensity signals over the Y-axis of the STMap. C Plot of the STMap signal after applying a Gaussian convolution filter, using a kernel size of 3, to smooth the data. D A second-order derivative is applied to the one-dimensional signal to detect signal peaks and extract momentum by identifying zero crossings in the STMap. E One-dimensional plot of the ICC-SM Ca2+ STMap after applying thresholding techniques to locate and define noise indices and signal plateaus.
Our STMaps clearly reveal that the Ca2+ signals in ICC-SM exhibit oscillatory behavior, with non-uniform changes in frequency (Fig. 2 B). Once the 2-dimensional Ca2+ STMap data was converted into a 1-dimensional data (1D), we applied a Gaussian filter to create a more consistent and smooth signal (Fig. 2C). The degree of smoothing is controlled by the parameter sigma (σ), which is user-adjustable to accommodate different datasets. To further refine this process, we formulated two key equations Eq. (3) and Eq. (4). In the default configuration, the sigma value is determined by dividing the length of the 1D signal by 40. In Equation (3), the Gaussian filter is denoted as G(u) for 1D signal with the sigma value serving as a variable parameter. Equation (4) presents a 1D convolution operation performed on the input signal T(x) which was derived from Eq. (2), to generate a uniform and smoothed Ca2+ signal V(x). It is important to note that convolution, in this case, is a nonlinear process. To ensure proper execution, the signal is padded by 2 prior to applying the convolution, which utilizes a filter size of 3. This padding helps to maintain the integrity of the signal at the boundaries while smoothing it effectively.
| (3) |
| (4) |
To effectively remove noise from STMaps, it is crucial to properly isolate the start and end points of the Ca2+ transient signal. This step is essential for eliminating background noise and reducing the overall noise level to zero. We utilized a combination of the Laplacian filter and thresholding techniques to accomplish this. We began by applying the Laplacian filter, specifically a 2nd order derivative, to the filtered 1D Ca2+ signal to detect zero-crossings that correspond to changes in the Ca2+ signal. These zero-crossings form plateaus that indicate noise indices, which can then be used to filter out noise from the original image (Fig. 2 D). In STMaps, variations in Ca2+ signals frequently manifest as vertical line impulses (Fig. 2 B&C). To capture this, we formulated an equation to model the signal using Eq. (5), Where V(x) represents the filtered signal obtained from the previous step in Equation (4) and (nabla) represents the discrete Laplacian operation applied to the 1D signal V(x). The result is K(x), a1D signal in which the impulses are highlighted as zero-crossings (Fig. 2 E).
To accurately identify noise indices and signal spikes, We applied a thresholding algorithm to the Ca2+ signal, governed by a conditional Equation (6). In this process, the 1D signal with impulses, denoted as Z(x), is transformed to Z(x) = -j, based on the following rule: if K(x) is smaller than predefined t. otherwise, Z(x) is set to zero. Z(x), as noted in (Fig. 2 E). The default value of j=−500.
2.1.4. Background noise identification and removal
Once the Ca2+ signals and their start and end points have been established, we identify background noise by mapping the plateau indices from the 1D signal to the summated signal. These plateau indices are used to define areas of image noise, allowing for targeted noise subtraction. To achieve this, a window of size 10 is created, ranging from and , where x represents the plateau index (Fig. 3 A). This window is used to calculate the image noise. If the window extends beyond the boundaries of the 2nd dimension, the window is adjusted to fit within the available range.
Fig. 3.
Mapping and removal of background noise in Ca2+ STMaps.
A One-dimensional plot extracted from the ICC-SM Ca2+ STMap, with noise indices mapped and marked by red squares. B Representative image of raw Ca2+ STMap of ICC-SM. (C) Ca2+ STMap after subtracting the average noise indices defined in A. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
After identifying the plateau regions associated with noise, we proceed to calculate the average noise values within these corresponding indices from Eq (1). This total is then divided by the size of the 2nd dimension of the original image to obtain the average noise value for that region.
The calculated average, adjusted by a bias parameter (θ), is subtracted from the raw image to produce the denoised result. Furthermore, the bias parameter (θ) can be customized by the user as a hyperparameter, with a default value of 0.
| (7) |
| (8) |
| (9) |
In this method, W represents the noise window, and n is the window size. By default, n is set to 10, unless the lower bound is below zero or the upper bound exceeds the limits of the 2nd dimension of the raw image, as described in Eq. (7). In Eq. (8), The average noise value is then calculated by summing all the values within the noise window, and dividing this sum by the window size (Fig. 4A). Next, the calculated average is adjusted by adding a bias , which has a default value of 0. This result is then subtracted from the entire original image (Fig. 3B) and Eq (9). The final outcome of this operation is a denoised STMap (Fig. 3C).
Fig. 4.
Calcium signal refinement and noise suppression in STMaps.
A Representative image of denoised Ca2+ STMap showing Ca2+ events in ICC-SM. B Denoised Ca2+ STMap after gradient based denoising. C Image of Ca2+ STMap after applying a contrast enhancement filter to the STMap in A. D A large median filter was applied to the Ca2+ STMap. E Representative image of Ca2+ STMap created by subtracting the median-filtered STMap in D from the contrast-enhanced STMap in C, to reduce salt-and-pepper noise. The process can be repeated as needed to achieve the desired level of signal enhancement. F Final ICC-SM Ca2+ STMap after applying a small median filter. The scale bar in A represents 2 s (y-axis) and 40 μm (x-axis) and applies to all panels B-F.
2.1.5. Calcium maps noise suppression and contrast enhancement
The final stage of the STMap denoising workflow using the imaging processing module emphasizes the reduction of remaining noise while enhancing the clarity and strength of the Ca2+ signals within the STMap. In the case of ICC-SM, a type of pacemaker cell in the colon, this workflow effectively highlights the complex nature of different Ca2+ signals and demonstrates the effectiveness of the denoising software and its modules in Ca2+ signal analysis (Fig. 4). This denoising process involves several key steps, including the application of a contrast enhancement filter to improve the clarity of the STMap (Fig. 4A and B). Additionally, a large median filter is applied to create a blurred version of the STMap, reducing the impact of outliers and suppressing patterns of salt-and-pepper noise (Fig. 4C and D). From the resulting STMap, pixels with zero values are mapped back into the original image coordinates, which further suppresses noise in the original STMap (Fig. 4E). This process may be repeated as necessary to reach optimal denoising levels. Additionally, a small median filter was applied to denoise the ICC-SM Ca2+ STMap (Fig. 4F). This approach has demonstrated equal effectiveness when utilized to ICC-IM STMaps, which display a stochastic and spatially localized firing pattern rather than the oscillatory pattern observed in ICC-SM. The complete denoising workflow, along with all noise suppression and signal enhancement protocols for the STMap Ca2+ signals, is described through the following equations.
| (10) |
| (11) |
| (12) |
In this step, we apply a contrast enhancement operation Eq. (10) on the denoised STMap (Fig. 5, Fig. 6), denoted as , which results in a contrast-stretched image (Fig. 4 B). Following this, a median filter Eq. (11) with a size of 15 is applied, producing the output (Fig. 5, Fig. 6). The output effectively suppresses noise in the raw Ca2+ STMap by eliminating salt and pepper noise outliers (zero pixel values) while preserving the signals in STMaps, as demonstrated in Eq. (12).
Fig. 5.
Image processing method for STMap denoising.
A Representative raw STMap of ICC-SM Ca2+ signals. B Denoised STMap of Ca2+ signals in ICC-SM using the image-processing generated method. C Overview of the image-processing-based denoising model developed for STMaps.
Fig. 6.
Key components for generators and discriminators
The denoising generative adversarial network (GAN) architecture comprises several key units: A Downsampling unit, B Upsampling unit, C Attention unit, D Residual generator unit, and E Residual discriminator unit. Here, K represents kernel size, S denotes stride, and D refers to the dilation rate. The “+” symbol indicates element-wise summation of features along the depth axis.
The procedure involving the application of the median filter and noise suppression (Eq. (11) and Eq. (12)) is repeated n times, where n is a user-defined hyperparameter, set to 1 by default. In the final step, a median filter size, is employed to create the denoised STMap (Fig. 4 E). The complete workflow for this image-processing-based denoising of STMaps is summarized and visualized in Fig. 5.
3. Denoising of calcium signals using generative adversarial network (GAN)
Our proposed GAN is detailed in this section and includes descriptions of the building blocks incorporated within the architecture. We also integrated a machine learning approach into the second denoising module of the software to automatically remove noise more efficiently. While the training strategies differ across the three deep learning modules used in the software, their internal architecture and underlying semantics remain consistent.
3.1. GAN-based generator architecture for STMap denoising
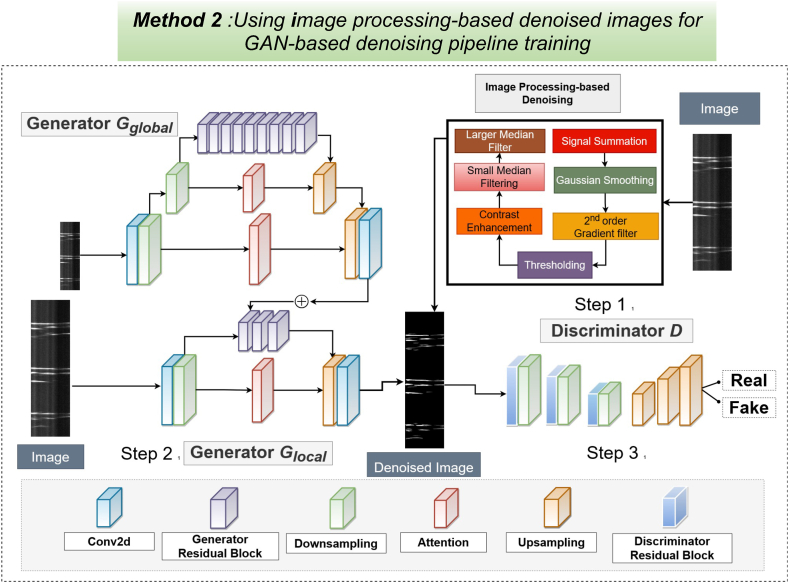
To produce fine-grained denoised STMap images as seen in Fig. 7, Fig. 8, Fig. 9, the proposed GAN architecture employs two generators, each constructed with unique building blocks tailored to specific denoising tasks. This dual-generator strategy has proven highly effective for image denoising, as each generator focuses on different aspects of the process, working in tandem to enhance overall image quality.
Fig. 7.
GAN-based denoising of STMaps with image-processed ground truth.
The denoising generative adversarial network (GAN) pipeline consists of two generators Gglobal, Glocal, and one discriminator D. Step 1. Raw and raw (noisy) Ca2+ STMaps are processed through an image-processing-based denoising pipeline to create ground-truth denoised STMaps. Step 2. The global generator, Gglobal, processes smaller noisy Ca2+ STMaps, producing coarsely denoised outputs. Simultaneously, the local generator takes larger noisy Ca2+ STMaps and generates finely denoised STMaps. Step3. The discriminator then takes both the raw noisy Ca2+ STMaps and the generated denoised STMaps as input and produces a probability map, indicating whether the input pairs are real or generated (fake). The discriminator employs auto-encoders to produce pixel-wise predictions, determining if each pixel is real or fake.
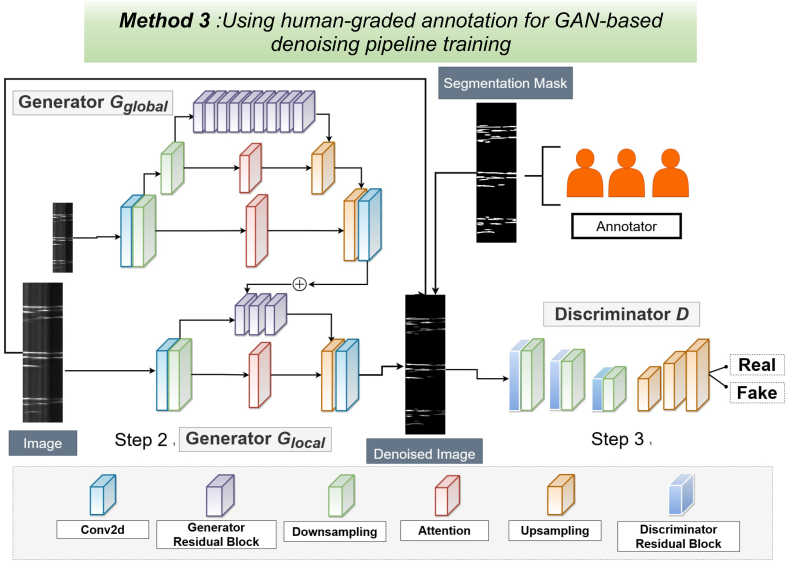
Fig. 8.
GAN-based denoising of STMaps with human-annotation ground truth.
The denoising generative adversarial network (GAN) model, consists of two generators Gglobal, Glocal, and one discriminator D. Step 1. The raw Ca2+ STMaps are segmented using human annotations to generate ground-truth denoised maps. Step 2. The global generator (Gglobal) processes smaller noisy Ca2+ STMaps to produce coarsely denoised outputs, while the local generator (Glocal) handles larger noisy Ca2+ STMaps to create finely denoised results.
Step3. The discriminator then takes both original noisy and denoised Ca2+ STMaps as input, generating a probability map that determines whether the pairs are real or fake. The discriminator uses auto-encoders for pixel-wise outputs, deciding the authenticity of each pixel.
Fig. 9.
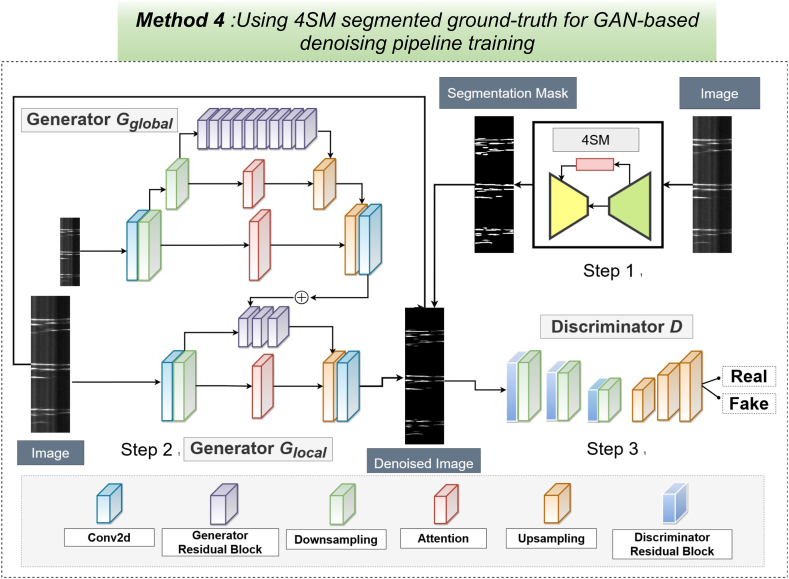
GAN-based denoising of STMaps with 4SM model ground truth.
The denoising generative adversarial network (GAN), consists of two generators Gglobal, Glocal, and one discriminator D. Step 1. The raw Ca2+ STMaps are segmented using the 4SM segmentation model to create ground-truth denoised images. Step 2. The global generator (Gglobal) processes smaller noisy Ca2+ STMaps, producing coarsely denoised outputs, while the local generator handles larger noisy Ca2+ STMaps outputting finely denoised STMaps. Step3. The discriminator takes both original noisy and denoised Ca2+ STMaps and denoised Ca2+ STMaps as input, producing a probability map that indicates whether the pairs are real or generated (fake). The discriminator utilizes auto-encoders to generate pixel-wise outputs, determining the authenticity of each pixel.
The integration of two specialized generators, Glocal and Gglobal, for local and global patch denoising has yielded impressive results in image refinement (Fig. 9). The Glocal generator focuses on extracting detailed patch-level information, essential for clarifying fine-grained boundaries and reducing periodic noise. On the other hand, the Gglobal generator targets broad-spectrum disturbances such as salt-and-pepper and other visually significant noise types. Both generators employ downsampling and upsampling within their residual convolution blocks to enhance processing efficiency.
Additionally, an attention block is incorporated to more accurately capture and enhance fine features crucial for denoising subcellular boundaries (Fig. 6). Glocal processes images at a resolution of 64x64x1, maintaining this resolution in its output, whereas Gglobal works with images at a reduced resolution of 32x32x1 and similarly outputs images at this resolution. Gglobal also generates a feature vector of size 32x32x64, which is integrated into Glocal through a skip connection, enhancing the depth and quality of the denoising process. Further details on each component will be provided in subsequent sections.
3.2. Optimized GAN downsampling and upsampling modules
Traditional non-learnable downsampling and upsampling techniques can result in the loss of crucial spatial features and disrupt the propagation of core information. To address this, we propose two new innovative blocks for both upsampling and downsampling, designed to retain and learn essential feature information for precise denoising through learnable convolution layers (Fig. 6 A&B). These innovative upsampling and downsampling blocks are integral to both the generators and discriminators in our GAN architecture. While the downsampling block is employed in both generators and discriminators, the upsampling block is exclusively used within the generators to produce feature maps and generate the final output.
The downsampling unit block includes a convolutional layer, that integrated and followed by Batch Normalization [54], and activated using a Leaky-ReLU layer (Fig. 6 A). In contrast, the upsampling unit block is constructed with a transposed convolution layer, similarly followed by Batch Normalization [54], and a Leaky ReLU activation layer (Fig. 6 B). This architecture ensures that both upsampling and downsampling can efficiently capture and maintain key spatial features throughout the denoising process.
The downsampling unit is utilized twice after successive residual blocks in both generator models. The upsampling unit block is applied within Gglobal to produce feature outputs that maintain the original spatial dimensions. In Glocal, it is used once to reconstruct the output at its original spatial resolution. We apply a kernel size of K=3 and a stride of S=2 to both convolution and transposed convolution layers, maintaining a balanced transformation of the feature maps.
3.3. Optimized residual convolution units
Our architecture incorporates two unique residual blocks: one designed specifically for the generator and the other for the discriminator. A typical residual block consists of two sequential convolution layers and a skip connection that merges the input feature tensor with the resulting output. However, regular convolution layers tend to be less computationally efficient compared to separable convolutions [55]. The key difference is that separable convolution divides the process into depth-wise and point-wise convolution layers, optimizing the retention of both the spatial and depth of signal information. To further enhance feature acquisition, recent studies indicate that merging separable convolution layers with dilation enhances performance [56]. Building on this concept, we designed the generator's residual unit to better preserve depth and spatial information by employing separable convolution, followed by batch normalization and Leaky ReLU activation. This configuration decreases the computational overhead and ensures efficient memory utilization. (Fig. 6 D). Additionally, we incorporate reflection padding before each separable convolution to reuse the values at the borders, padding the input with plausible data.
Through extensive experimentation, we discovered that a wider receptive field captures adjacent, visually significant features more effectively. To achieve this, we enhanced our residual unit by incorporating two branches of separable convolution layers, each utilizing distinct dilation rates: one with a dilation rate of D=1 and the other with D=2 (Fig. 6 D). Each separable convolution layer employs a kernel size of K=3 and a stride of S=1, with reflection padding applied before and batch normalization along with Leaky ReLU activation applied afterward. The final output is generated by combining the skip connection from the input with the outputs of both branches.
A comparable method was used to design a customized residual block specifically for the discriminator. This residual block also features two branches of separable convolution layers, followed by batch normalization and Leaky ReLU activation. In the case of the discriminator, both branches use separable convolutions with a kernel size of K=3 and stride S=1, ensuring effective processing while maintaining computational efficiency.
3.4. Enhanced attention unit components
Repetitive upsampling and downsampling operations often result in the loss of critical spatial information, weakening the model's ability to preserve finer details [57,58]. To overcome this limitation, we introduce an enhanced Attention Unit (Fig. 6C). These attention units act as skip connections, allowing feature information from the lower encoder blocks of the network to be fused with the upper decoder blocks. Each attention unit is composed of two consecutive residual units that include convolution, Batch Normalization, and Leaky ReLU layers. To enhance training speed and stability, Batch Normalization is used to re-centering and re-scaling inputs, while Leaky ReLU helps mitigate the vanishing gradient problem [59]. In this unit, we use a kernel size of K=3 and a stride of S=1. The first skip connection combines the input with the output of the first residual block, while the second skip connection performs element-wise addition between the input and the output of the final residual block. Gglobal incorporates two attention units, positioned after the downsampling blocks and added successively to the two upsampling blocks. In contrast, Glocal uses a single attention unit between its downsampling and upsampling blocks.
3.5. Enhanced discriminator architecture for STMap denoising
In our denoising GAN framework, we utilize a single discriminator for Glocal (Fig. 7, Fig. 8, Fig. 9). Traditionally, GAN discriminators consist of only an encoder, producing small spatial feature outputs to differentiate between real and synthesized images [[60], [61], [62]]. These outputs typically represent patches of the original image, which is why these models are often referred to as Patch-GANs [62]. To improve upon this approach, we introduce a decoder, transforming the discriminator into an auto-encoder designed for pixel-level predictions. This enables the model to determine the authenticity of each individual pixel, rather than just image patches, providing more detailed and fine-grained information to enhance the denoising process for our STMap images. The discriminator processes STMap inputs with a resolution of 64x64x1, generating feature maps of the same size. Each point in the resulting feature map corresponds to a value within the range of −1 to +1, where −1 represents a real pixel and +1 indicates a synthesized or adversarial pixel. This pixel-level distinction allows for more precise detection of noise and artifacts, enabling finer control over the denoising process and enhancing the model's ability to differentiate between real and generated data.
3.6. Adversarial objective function
In our GAN architecture, we implemented an adversarial training loss function to estimate the probability of errors and reduce both training and testing inaccuracies. To achieve this, we used a multi-hinge loss for both the discriminator and generator architectures [58,63], as expressed in Eq. (1) and Eq. (2), respectively. To ensure consistency, we normalized all noisy Ca2+ STMaps along with their respective ground-truth denoised versions to the range of [−1,1]. In Eq. (3), we combine the outputs of Equations (1), (2)), applying as a weight multiplier for , as we prioritize the generator's performance over the discriminator to achieve higher quality denoised STMaps.
| (1) |
| (2) |
| (3) |
In the first step (Equation (1)), the discriminator was initially trained on original noisy Ca2+ STMaps, denoted as x, and their corresponding real denoised STMaps, denoted as x’, represented by D (x, x’). It was then retrained on real noisy Ca2+ STMaps, x, paired with synthesized denoised STMaps, G(x) represented as D (x, G(x)).
The discriminator, D, underwent several iterations of batch-wise training using randomly sampled data. Once the discriminator was trained, the global generator (Gglobal) was trained while the weights of D remained frozen. Similarly, the local generator (Glocal) was trained on a batch of randomly sampled noisy STMaps, with the discriminator's weights also frozen during this process. The generators employed the mean squared error loss, as shown in Eq. (2). To ensure that the generated STMaps accurately replicate realistic representations of denoised Ca2+ signals. Additionally, we incorporated a discriminator feature loss component, similar to that described in Ref. [62], and formalized in Eq. (5).
| (4) |
| (5) |
In this context, represents the mean squared loss for a real denoised STMap, x’, given a generated denoised STMap, G(x), where ||⋅|| denotes the absolute value. The loss function for both Gglobal and Glocal was employed to ensure that the model produces high-quality denoised STMaps at two different scales. Next, Eq. (6) was estimated first by extracting features from the intermediate layers of the discriminator, first by inputting the real denoised STMaps and then the synthesized denoised STMaps in sequence. M denotes the number of feature layers extracted from the discriminator. Dn (x, x’) refers to the intermediate features obtained from the discriminator with a real image as the input, and Dn (x, G(x)) pertains to the features extracted when a synthesized image is input.
Finally, the overarching objective for the architecture was established by integrating Eq. (3), Eq. (4), and Eq. (5), as detailed in Eq. (6).
| (6) |
In this context, , and represent the loss weightings applied to their respective losses. These weightings determine the emphasis placed on different components of the network during training. For our GAN-based models, higher importance is placed on and and thus, which is why larger values are chosen for these parameters.
3.7. Image-processing outputs for GAN model training
In our first deep learning GAN-based method, as the ground truth for training, we employed denoised STMaps generated from our improved image-processing protocols described earlier. The overall training architecture and approach are depicted in Fig. 7. In Step 1, the relevant parameters are selected for the image-processing method to denoise the Ca2+ STMap. In Step 2, the Glocal and Gglobal generators take multi-scale of raw and noisy STMaps as input and use the denoised STMaps as ground truth for training. Finally, in Step 3, the discriminator processes pairs of real noisy and denoised STMaps, followed by pairs of real raw and noisy STMaps and generated denoised STMaps, to differentiate between authentic and generated images. It is important to highlight that Gglobal generates only a feature vector, which is then element-wise added to one of the intermediate layers of Glocal. During the testing phase, only the generators are used to synthesize denoised STMaps, while the discriminators are excluded from the process.
3.8. Human-annotated segmentation for GAN model training
Our second GAN-based training method, utilizes a manually annotated segmentation mask created by a human to generate a denoised Ca2+ STMap, which is used as the ground truth as shown in (Fig. 8).
In Step 1, a human annotator is tasked with creating a binary segmentation mask that isolates the Ca2+ events in the STMap and separates them from the background. This binary mask is then applied to the noisy STMap, effectively removing all background noise while preserving the foreground. In Step 2, the generators are trained on the noisy STMaps using the manually segmented denoised STMap as the ground truth. Finally, in Step 3, the discriminators are used to differentiate between real and synthesized STMap pairs, ensuring that the model learns to produce high-quality, denoised outputs.
3.9. Deep segmentation model integration for GAN-based denoising
The third GAN-based model utilizes a pre-trained segmentation architecture called the Spatiotemporal Subcellular Signal Segmentation Model (4SM), specifically designed for segmenting Ca2+ events in STMaps. 4SM is a GAN architecture optimized for this task, as described in a previous study [64]. In Step 1, the model segments noisy STMaps to create the denoised ground-truth STMaps, as illustrated in (Fig. 9). In Step 2, the Glocal and Gglobal are trained using pairs of raw (noisy) and denoised STMaps. Finally, in Step 3, the discriminator is employed to differentiate between real and synthesized STMap pairs, ensuring the model's capability to generate high-quality denoised images.
4. Performance assessment of denoising architectures
4.1. Training dataset for denoising GAN models
We optimized our GAN model training using STMaps generated from a diverse set of imaging sequences: 12 Ca2+ STMaps derived from ICC-SM and 12 STMaps derived from ICC-IM, captured at various resolutions. To enhance the dataset, we created overlapping 64x64 crops from these images, utilizing a stride of 8 to maximize the use of available data.
For evaluation purposes, the test dataset was assembled from STMaps originating from 6 ICC-SM and 5 ICC-IM videos, providing a robust basis for assessing model performance. The training set contained 37,408 cropped images from ICC-IM and 12,980 cropped images from ICC-SM. The test set included 15,458 cropped images for ICC-IM and 6962 for ICC-SM. Both the noisy and denoised images were collected in grayscale format.
To train the GAN architectures, we employed a leave-one-out cross-validation approach, dividing the dataset into five folds. The training was performed on four folds, with the remaining fold used for validation. Each of the five model versions was tested on the test dataset, and the most accurate version was selected as the primary model. The results for each of our GAN-based techniques are presented in Table 1, Table 2.
Table 1.
Quantitative Results for ICC-SM (Rhythmic) test images for denoising.
| Denoising Models | SSIM | PSNR |
|---|---|---|
| Image-Process Denoising | 25.49 % | 21.49 |
| GAN-denoising | 61.72 % | 22.95 |
| Segmentation GAN-denoising | 88.75 % | 24.64 |
| 4SM GAN-denoising | 84.97 % | 23.20 |
Table 2.
Comparative Results for ICC-IM (Stochastic) test images for denoising.
| Denoising Models | SSIM | PSNR |
|---|---|---|
| Image-Process Denoising | 27.45 % | 21.67 |
| GAN-denoising | 59.64 % | 24.92 |
| Segmentation GAN-denoising | 91.98 % | 26.96 |
| 4SM GAN-denoising | 92.74 % | 25.88 |
4.2. Tuning parameters for GAN training
For hyper-parameter selection, we set , and (as described in Eq. (6)). We employed the Adam optimizer [65], with a learning rate of , and . The model was trained using a batch size of over 150 epochs. Depending on the dataset type: either ICC-IM (stochastic) or ICC-SM (rhythmic) the training process on an NVIDIA V100 GPU took approximately 14–18 h to complete.
4.3. Denoising models evaluation
To assess the effectiveness of our models, we evaluated and compared them to a state-of-the-art deep learning-based auto-encoder model known as U-Net [42]. The U-Net architecture utilizes an encoder-decoder structure with convolutional filters to capture spatial information, progressively downsampling and upsampling to extract multi-depth features. U-Net has been widely adopted across various biomedical imaging applications due to its powerful feature-learning capabilities [[66], [67], [68]].
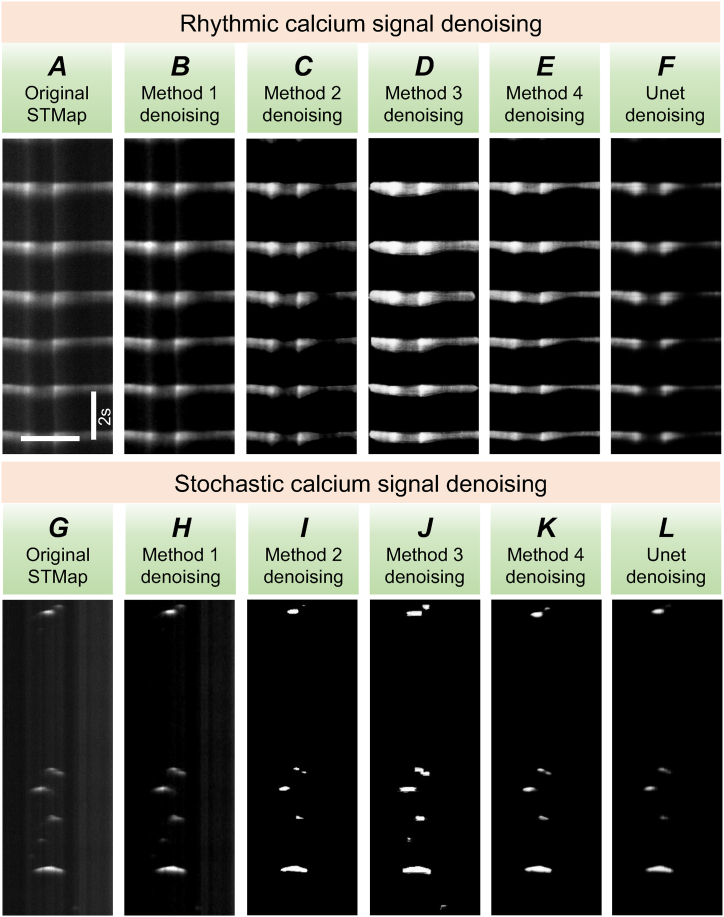
In Fig. 10A–F, we provide a detailed comparison between predictions from our innovative denoising GAN architectures and U-Net. Our segmentation-based GAN architecture consistently produced superior denoised Ca2+ STMaps for ICC-SM, achieving 88 % similarity to the ground truth (GT). In contrast, U-Net struggled to define clear boundaries for Ca2+ signals and was unable to effectively remove background noise, positioning our segmentation-based GAN as the more optimal model among the five evaluated.
Fig. 10.
Comparing denoising methods for stochastic and rhythmic Ca2+ signals.
A Representative image of raw STMap of Ca2+ signals in ICC-SM. B Denoised output from the image-processing-based method. C Denoised output from the image-processing-based GAN trained method. D Denoised output from the segmentation-based GAN trained method. E Denoised output from the 4SM-based GAN trained method. F Denoised output from U-Net method. The scale bars in A represent x = 2 s and y =10 μm. G Representative raw STMap of Ca2+ signals in ICC-IM. H-L Corresponding denoised outputs from the same image-processing pipelines: image-processing (method 1, H), image-processing-based GAN (method 2, I), segmentation-based GAN (method 3, J), 4SM-based GAN (method 4, K), and U-Net denoising (L), respectively. The scale bars in A also apply to G.
In the case of Ca2+ STMaps generated from ICC-IM, the 4SM-segmentation GAN-based model outperformed all other models, achieving 92.74 % structural similarity, as depicted in Fig. 10. In comparison, U-Net achieved only 59.99 % similarity, highlighting the superior performance of our model in retaining structural details.
To quantitatively evaluate the denoising performance of Ca2+ STMaps, we employed two key metrics: 1) Structural Similarity Index Measure (SSIM), a standard metric used to assess image quality degradation by measuring perceptual similarity. 2) Peak Signal-to-Noise Ratio (PSNR), which evaluates the quality of the reconstructed images.
We present the 5-fold cross-validated results for our models, evaluated in terms of SSIM and PSNR, in Table 1, Table 2, Table 3. For ICC-SM, the segmentation-based GAN was our top performer, achieving 88.75 % structural similarity and a PSNR of 24.64 (Table 1). For ICC-IM, the 4SM-based GAN demonstrated superior performance, with a structural similarity of 92.74 % and a PSNR of 25.88 (Table 2). Additionally, we compared the 4SM-segmentation model against U-Net, and the results in Table 3 show that the 4SM model significantly outperformed U-Net in both SSIM and PSNR metrics. Finally, we analyzed the strengths and weaknesses of each denoising approach, comparing them in terms of speed and accuracy, as outlined in Table 4.
Table 3.
Comparative Results between U-Net and our best GAN-based denoising pipeline.
| Denoising Models | SSIM | PSNR |
|---|---|---|
| U-Net (ICC-SM) | 61.31 % | 21.67 |
| U-Net (ICC-IM) | 59.99 % | 23.92 |
| 4SM GAN-denoising (ICC-SM) | 84.97 % | 23.20 |
| 4SM GAN-denoising (ICC-IM) | 92.74 % | 25.88 |
Table 4.
Advantages and disadvantages of each of the denoising approaches.
| Technique | Inference Speed (second) | Training with Annotated Masks | Manual Parameter Tuning |
Hardware | SSIM (ICC-SM) | SSIM (ICC-IM) |
|---|---|---|---|---|---|---|
| Image-processing Based | 0.09 | No | Required | CPU | 25.49 % | 27.45 % |
| GAN-denoising | 0.1 | No | Not required | GPU | 61.72 % | 59.64 % |
| Segmentation GAN-denoising | 0.1 | Yes | Not required | GPU | 88.75 % | 91.98 % |
| 4SM GAN-denoising | 0.1 | No | Not required | GPU | 84.97 % | 92.74 % |
5. Graphical user interface for CalDenoise denoising pipelines
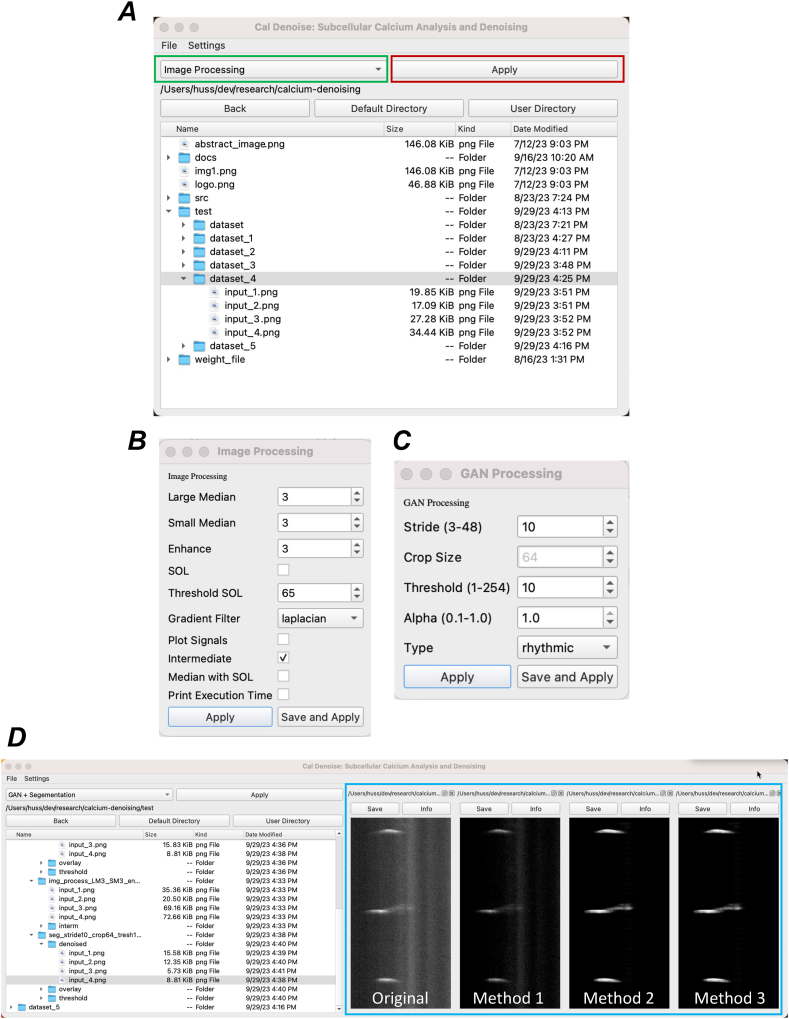
To simplify the use of the denoising modules for STMaps and enhance user experience, we developed a graphical user interface (GUI) for CalDenoise, our Python-based tool designed for efficient denoising of subcellular Ca2+ fluorescent signals. The GUI was built using PyQt, an open-source Python library. One of the key advantages of PyQt is that it allowed us to create a user-friendly interface without the need for additional frameworks. Moreover, the software is platform-independent and can run on any operating system that supports Python.
The CalDenoise interface offers four distinct denoising methods, all of which are accessible via an intuitive GUI (Fig. 11). Users can batch process datasets for faster denoising and can easily upload input images using drag-and-drop functionality. The interface provides a real-time display of the denoising results, allowing users to adjust the degree of denoising by selecting from the four methods available (Fig. 11A). Additionally, all denoising parameters are fully customizable, giving users granular control over the process (Fig. 11B and C).
Fig. 11.
Features of CalDenoise interface
A Representative view of the CalDenoise interface, showing user-controlled denoising model selection (green box) and model settings (red box). B&C Each denoising model provides a parameter selection window, allowing users to input their preferred settings. D The interface displays the original and denoised STMaps (blue box), helping users compare results from different denoising models and adjust settings accordingly. A comparison of STMap denoising outputs from various CalDenoise models is also shown in D. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Once the denoising is complete, the denoised maps can be compared, saved, and exported for further analysis and interpretation, all within the tool itself (Fig. 11D).
6. Discussion
Ca2+ signaling is a major aspect of cell survival and death. Technological advancements in Ca2+ indicators, biosensors and imaging instruments provide exceptional spatial and temporal resolution for imaging cellular Ca2+ signals. However, extracting Ca2+ dynamics data is laborious and time-consuming due to the complexity and variability of Ca2+ signal patterns across cell types. STMaps are a common method to analyze Ca2+ transients but their effectiveness is hindered by suboptimal instrumentation and experimental noise. Challenges currently exist to effectively remove imaging noise and analyze STMaps in a fast, accurate, and standardized method. Previous denoising protocols for Ca2+ images and STMaps mostly relied on subjective background subtraction methods to define noise pixel ROIs and many of these protocols ignored the dynamic and nonuniform nature of image noise all together. The present study focuses on STMap noise removal in an effective, uniform, dynamic, fast, and unbiased method to enhance Ca2+ signals and achieve more accurate Ca2+ signal detection and quantification. Here, we've proposed four automated image-processing and deep learning based denoising modules for a STMap analysis pipeline to help researchers carry out essential denoising of Ca2+ STMaps swiftly and with little overhead for computation. The proposed model is very fast with the average inference time for image-processing to final output is 80–90 ms (ms). In contrast, the deep learning model's output is around 100–120 ms (ms) per single image crop. This efficient computation time includes all the denoising filter and noise model mapping and computation associated with each step. The method also can be used for batch processing of images, a feature within the software that enables the simultaneous processing of multiple image files rather than handling single images one at a time. This approach improves efficiency by allowing batch image processing and is particularly useful when working with large datasets. Our image-processing pipeline can also generate filtered images to enable user evaluation and adjustment of the denoising degree at each given step. Summation of Ca2+ signals over time is a method commonly used for finding peaks of active signals in Ca2+ imaging [34,35,69,70]. In our approach, we utilize the signal peak function to allow identification of noise indices and the denoising module which incorporates a zero-crossings function, commonly used for edge detection methods [[71], [72], [73]], to define the noise indices and active signal indices for proper denoising of Ca2+ STMaps. This process allows effective and accurate separation of noise indices from the active signal and ensures that only noise was discriminated rather than active signals.
Fluorescent signal photobleaching is a common issue in Ca2+ imaging that causes the average signal intensity to decrease over time, affecting both noise and active signal indices. Therefore, the background noise index must be defined from the noise indices. In the image processing denoising module the average noise index was selected from the noise plateau signal's highest pixel values which was shown to effectively remove salt and pepper or random telegraph noise while minimizing background noise. In addition, the image-processing denoising module includes a contrast enhancement filter to improve the active Ca2+ signal. Multiple consecutive median filters were employed to ensure removal of salt and pepper or random telegraph noise from STMaps. To preserve active signals that may be disrupted by applying the filters to the resulting images, we used inverse mapping in the pipeline before applying each filter.
In typical image background subtraction methods, a region of interest (ROI) with the appearance of a noisy background is manually selected by the user. The task involves averaging the pixel intensity of that area and subtracting or dividing the selected pixel values from the entire image. While this method can remove salt and pepper noise to some degree, it is ineffective against impulsive noise and constant background noise that may have higher pixel intensity than the actual signal. Furthermore, these methods are subjective and lack consistency as user judgment may vary. Other background noise removal methods have been employed in imaging preprocessing, such as Fourier analysis [[38], [39], [40]], PCA [36,37] and Matrix decomposition [41]. Although these techniques can reduce image noise, they can also cause image signal degradation, miss certain signal frequencies, and allow for the persistent presence of noise and artifacts.
Distinguishing between signal and noise within cells is complex. Non-dynamic signals, along with low-intensity or diffuse fluorescence, can make it challenging to identify true dynamic signals. Additionally, noise from external sources or artifacts can further obscure cellular signals and affect the clarity of dynamic signal detection. Our approach primarily focused on enhancing intracellular dynamic signals, though we recognize that basal fluorescence and non-dynamic signals may also be affected by the software. While our method effectively isolates dynamic signals, it may still influence basal fluorescence to some extent.
The U-Net architecture has become a prevalent standard for medical image denoising tasks due to recent advancements in deep learning [[42], [43], [44]]. It has shown success in various applications including digital pathology, dermatoscopy, MRI, and CT images [43]. However, the proposed 3 novel GAN architecture-based denoising pipelines surpassed U-Net's denoising capabilities by providing more accurate denoising and enhanced Ca2+ signals in STMaps with higher qualitative and quantitative metrics. Additionally, our model's parameter count is only 3.34 million, which is 10-times less than that of U-Net. In our proposed machine learning approach we established three different ground truths. The first approach used an image-processing-based technique as the ground truth for training and the other two approaches employed segmentation mask-based noise removal with human annotation and a GAN-based model, respectively. To evaluate the results, we used structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR) to assess structural similarity and signal quality between the original and denoised signals. Additionally, ground truths enhanced dynamic signal extraction by primarily focusing on dynamic and non-dynamic signals which reduced basal background fluorescence and improved overall signal analysis.
7. Conclusions
Our novel denoising techniques leverage various deep learning and image processing approaches to deliver an automated, swift, and precise STMap denoising protocol for a wide range of Ca2+ imaging. This effectively eliminates a variety of noise types that STMaps are prone to including background, impulsive, sensor, periodic, and low-frequency noise. Given that these types of signal noise can hinder the Ca2+ data extraction from STMaps, it is crucial to integrate such a module in the Ca2+ imaging analysis and data retrieval pipelines.
8. Limitations of the study
This study introduces a novel solution for efficiently and accurately removing image noise from dynamic cellular Ca2+ and fluorescent signals. However, for optimal performance and speed, our software relies on more recent GPU technology, which can be expensive and may restrict accessibility. It's important to note that this limitation is not unique to CalDenoise, as most deep learning architectures rely on GPU-based computations. Consequently, the software's utilization in commonly used image analysis tools like Image J is limited. Despite these constraints, the CalDenoise software offers rapid and precise noise removal for cellular fluorescent signals facilitating seamless signal analysis. To improve the robustness and accuracy of image processing algorithms, software enhancement and development are required to incorporate a wider range of image noise modalities. This is essential for effectively handling the diverse noise patterns that may exist in various image datasets.
9. STAR★Methods
9.1. Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: Organisms/strains | ||
| GCaMP6f-floxed mice (B6; 129S-Gt(ROSA)26Sortm95.1(CAG-GCaMP6f)Hze/J) | Jackson Laboratories | Strain #:024105 RRID:IMSR_JAX:024105 |
| Kit-Cre mice (c-Kit+/Cre−ERT2) | Provided by Dr. Dieter Saur | https://doi.org/10.1113/JP271699 |
| Software and algorithms | ||
| Fiji, version 2.0.0-rc-69/1.52 | NIH | https://fiji.sc/ |
| 4SM, Subcellular Fluorescence Analysis Software | GitHub |
https://doi.org/10.1016/j.isci.2022.104277; https://github.com/SharifAmit/CalciumGAN/tree/main |
| STMapAuto, Ca2+ Analysis plugin | GitHub | https://doi.org/10.1016/j.ceca.2020.102260 |
10. Method details
10.1. Experimental model and subject details
10.1.1. Animals
GCaMP6f mice (B6.129S-Gt(ROSA)26Sortm38(CAG-GCaMP3)Hze/J) and their control counterparts (C57BL/6) were obtained from Jackson Laboratories (Bar Harbor, MN, USA). These were crossed with Kit-iCre mice (c-Kit+/Cre−ERT2), from Dr. Dieter Saur (Technical University Munich, Munich, Germany). Tamoxifen was administered at 6–8 weeks of age, as previously described [13].
10.1.2. Tissue preparation
Segments of the colon, each 2 cm long, were excised from Kit-iCre-GCaMP6f mice and placed in Krebs-Ringer bicarbonate solution (KRB) following established protocols [13]. Each segment was longitudinally opened along the mesenteric border, and contents were gently rinsed off. Selective dissection was used to separate either the mucosal or the muscular layers. The prepared tissue samples, either submucosa or muscle, were then stretched out and secured onto Sylgard-lined dishes.
10.1.3. Calcium imaging
Colonic sheets were perfused with 37 °C KRB solution and were equilibrated for a period of 1 h, as previously described [13,28]. A spinning-disk confocal microscope (CSU-W1 spinning disk; Yokogawa Electric Corporation) was used for all Ca2+ imaging experiments. The confocal head is connected to a Nikon Eclipse FN1 microscope equipped with a 40x 0.8 NA CFI Fluor lens (Nikon instruments INC, NY, USA). Laser at 488 nm wavelength was directed using a Borealis system (ANDOR Technology, Belfast, UK). EMCCD Camera (Andor iXon Ultra; ANDOR Technology, Belfast, UK) was used to capture the GCaMP6f emission. Images were acquired at 33 frames per second using MetaMorph software (Molecular Devices INC, CA, USA).
10.1.4. Calcium event analysis
Analysis of Ca2+ activity in ICC was performed as previously described [13,28]. Briefly, movies of Ca2+ activity in ICC (30 s long) were converted to a stack of tagged image file format (TIFF) images and imported into custom software (Volumetry G8.a) for analysis. The whole-cell ROIs were used to generate STMaps of Ca2+ activity in individual ICC.
10.1.5. Download and installation of software
For successful software operation, the system should have 1) a GPU-enabled system with CUDA version 10.0+ installed and 2) Anaconda, a Python package and environment management tool, installed. The code can be downloaded from the following GitHub repository: https://github.com/SharifAmit/CalDenoise. Once downloaded, please follow the instructions in the README.md file for installing and running the denoising program.
Data and code availability
The original software “CalDenoise” is an open-source and publicly available from.
Github: https://github.com/SharifAmit/CalDenoise.
Further information necessary for reanalyze the data reported in this paper can be obtained from the lead contact upon request.
CRediT authorship contribution statement
Sharif Amit Kamran: Writing – review & editing, Writing – original draft, Validation, Software, Investigation, Formal analysis, Data curation, Conceptualization. Hussein Moghnieh: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Methodology, Formal analysis, Data curation. Khondker Fariha Hossain: Validation, Formal analysis. Allison Bartlett: Writing – original draft, Visualization, Data curation. Alireza Tavakkoli: Writing – review & editing, Validation, Supervision, Resources, Conceptualization. Bernard T. Drumm: Writing – review & editing, Writing – original draft, Visualization, Validation. Kenton M. Sanders: Writing – review & editing, Funding acquisition, Conceptualization. Salah A. Baker: Writing – review & editing, Writing – original draft, Visualization, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Data curation, Conceptualization.
11. Materials availability
The software code developed in this study has been uploaded to GitHub: https://github.com/SharifAmit/CalDenoise.
All relevant data are provided within the main text.
Ethics statement
All procedures followed the NIH Guide for the Care and Use of Laboratory Animals and were approved by the University of Nevada, Reno's IACUC (Protocol ID: 21-02-1131-1).
Funding
This project was supported by R01 DK-120759 from the National Institute of Diabetes and digestive and Kidney (NIDDK).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to thank the Computational Modeling and Analysis core supported by the NIH (P30-GM145646) and Nevada Bridge to AI-enabled Scientific & Engineering Computing (NvBAISEC) supported by the NSF (OAC-2201599) for their computer services.
Data and materials availability
All data are available in the main text and the codes are available from repository: https://github.com/SharifAmit/CalDenoise.
References
- 1.Berridge M.J., Lipp P., Bootman M.D. The versatility and universality of calcium signalling. Nat. Rev. Mol. Cell Biol. 2000;1:11–21. doi: 10.1038/35036035. [DOI] [PubMed] [Google Scholar]
- 2.Sanders K.M., Drumm B.T., Cobine C.A., Baker S.A. Ca. Physiol. Rev. 2024;104:329–398. doi: 10.1152/physrev.00036.2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Straub S.V., Giovannucci D.R., Yule D.I. Calcium wave propagation in pancreatic acinar cells: functional interaction of inositol 1, 4, 5-trisphosphate receptors, ryanodine receptors, and mitochondria. J. Gen. Physiol. 2000;116:547–560. doi: 10.1085/jgp.116.4.547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hennig G.W., Spencer N.J., Jokela‐willis S., Bayguinov P.O., Lee H.t., Ritchie L.A., Ward S.M., Smith T.K., Sanders K.M. ICC‐MY coordinate smooth muscle electrical and mechanical activity in the murine small intestine. Neuro Gastroenterol. Motil. 2010;22:e138–e151. doi: 10.1111/j.1365-2982.2009.01448.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheng H., Lederer M.R., Lederer W., Cannell M. Calcium sparks and [Ca2+] i waves in cardiac myocytes. Am. J. Physiol. Cell Physiol. 1996;270:C148–C159. doi: 10.1152/ajpcell.1996.270.1.C148. [DOI] [PubMed] [Google Scholar]
- 6.Boittin F.X., Macrez N., Halet G., Mironneau J. Norepinephrine-induced Ca(2+) waves depend on InsP(3) and ryanodine receptor activation in vascular myocytes. Am. J. Physiol. 1999;277:C139–C151. doi: 10.1152/ajpcell.1999.277.1.C139. [DOI] [PubMed] [Google Scholar]
- 7.Baker S.A., Hennig G.W., Salter A.K., Kurahashi M., Ward S.M., Sanders K.M. Distribution and Ca2+ signalling of fibroblast‐like (PDGFRα+) cells in the murine gastric fundus. J. Physiol. 2013;591:6193–6208. doi: 10.1113/jphysiol.2013.264747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Berridge M.J., Lipp P., Bootman M. Calcium signalling. Curr. Biol. : CB. 1999;9:R157–R159. doi: 10.1016/s0960-9822(99)80101-8. [DOI] [PubMed] [Google Scholar]
- 9.Drumm B.T., Cobine C.A., Baker S.A. Insights on gastrointestinal motility through the use of optogenetic sensors and actuators. J. Physiol. 2022;600:3031–3052. doi: 10.1113/JP281930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bootman M.D., Berridge M.J. The elemental principles of calcium signaling. Cell. 1995;83:675–678. doi: 10.1016/0092-8674(95)90179-5. [DOI] [PubMed] [Google Scholar]
- 11.Jaggar J.H., Porter V.A., Lederer W.J., Nelson M.T. Calcium sparks in smooth muscle. Am J Physiol Cell Physiol. 2000;278:C235–C256. doi: 10.1152/ajpcell.2000.278.2.C235. [DOI] [PubMed] [Google Scholar]
- 12.Parker I., Choi J., Yao Y. Elementary events of InsP3-induced Ca2+ liberation in Xenopus oocytes: hot spots, puffs and blips. Cell Calcium. 1996;20:105–121. doi: 10.1016/s0143-4160(96)90100-1. [DOI] [PubMed] [Google Scholar]
- 13.Baker S.A., Drumm B.T., Saur D., Hennig G.W., Ward S.M., Sanders K.M. Spontaneous Ca(2+) transients in interstitial cells of Cajal located within the deep muscular plexus of the murine small intestine. J. Physiol. 2016;594:3317–3338. doi: 10.1113/JP271699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roome C.J., Kuhn B. Simultaneous dendritic voltage and calcium imaging and somatic recording from Purkinje neurons in awake mice. Nat. Commun. 2018;9:3388. doi: 10.1038/s41467-018-05900-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee H.T., Hennig G.W., Park K.J., Bayguinov P.O., Ward S.M., Sanders K.M., Smith T.K. Heterogeneities in ICC Ca2+ activity within canine large intestine. Gastroenterology. 2009;136:2226–2236. doi: 10.1053/j.gastro.2009.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Drumm B.T., Hennig G.W., Baker S.A., Sanders K.M. Applications of spatio-temporal mapping and particle analysis techniques to quantify intracellular Ca2+ signaling in situ. J. Vis. Exp. 2019 doi: 10.3791/58989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Colman M.A., Pinali C., Trafford A.W., Zhang H., Kitmitto A. A computational model of spatio-temporal cardiac intracellular calcium handling with realistic structure and spatial flux distribution from sarcoplasmic reticulum and t-tubule reconstructions. PLoS Comput. Biol. 2017;13 doi: 10.1371/journal.pcbi.1005714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Waadt R., Krebs M., Kudla J., Schumacher K. Multiparameter imaging of calcium and abscisic acid and high-resolution quantitative calcium measurements using R-GECO1-mTurquoise in Arabidopsis. New Phytol. 2017;216:303–320. doi: 10.1111/nph.14706. [DOI] [PubMed] [Google Scholar]
- 19.Park K.J., Hennig G.W., Lee H.T., Spencer N.J., Ward S.M., Smith T.K., Sanders K.M. Spatial and temporal mapping of pacemaker activity in interstitial cells of Cajal in mouse ileum in situ. Am J Physiol Cell Physiol. 2006;290:C1411–C1427. doi: 10.1152/ajpcell.00447.2005. [DOI] [PubMed] [Google Scholar]
- 20.Dargan S.L., Schwaller B., Parker I. Spatiotemporal patterning of IP3-mediated Ca2+ signals in Xenopus oocytes by Ca2+-binding proteins. J. Physiol. 2004;556:447–461. doi: 10.1113/jphysiol.2003.059204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cobine C.A., Hannigan K.I., McMahon M., Ni Bhraonain E.P., Baker S.A., Keef K.D. Rhythmic calcium transients in smooth muscle cells of the mouse internal anal sphincter. Neuro Gastroenterol. Motil. 2020;32 doi: 10.1111/nmo.13746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bolton T.B., Gordienko D.V. Confocal imaging of calcium release events in single smooth muscle cells. Acta Physiol. Scand. 1998;164:567–575. doi: 10.1046/j.1365-201X.1998.00464.x. [DOI] [PubMed] [Google Scholar]
- 23.Baker S.A., Drumm B.T., Skowronek K.E., Rembetski B.E., Peri L.E., Hennig G.W., Perrino B.A., Sanders K.M. Excitatory neuronal responses of Ca(2+) transients in interstitial cells of cajal in the small intestine. eNeuro. 2018;5 doi: 10.1523/ENEURO.0080-18.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Leigh W.A., Del Valle G., Kamran S.A., Drumm B.T., Tavakkoli A., Sanders K.M., Baker S.A. A high throughput machine-learning driven analysis of Ca. Cell Calcium. 2020;91 doi: 10.1016/j.ceca.2020.102260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Baker S.A., Hwang S.J., Blair P.J., Sireika C., Wei L., Ro S., Ward S.M., Sanders K.M. Ca(2+) transients in ICC-MY define the basis for the dominance of the corpus in gastric pacemaking. Cell Calcium. 2021;99 doi: 10.1016/j.ceca.2021.102472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Baker S.A., Drumm B.T., Skowronek K.E., Rembetski B.E., Peri L.E., Hennig G.W., Perrino B.A., Sanders K.M. Excitatory neuronal responses of Ca+2 transients in interstitial cells of cajal in the small intestine. eNeuro. 2018 doi: 10.1523/ENEURO.0080-18.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Drumm B.T., Sergeant G.P., Hollywood M.A., Thornbury K.D., McHale N.G., Harvey B.J. The role of cAMP dependent protein kinase in modulating spontaneous intracellular Ca(2)(+) waves in interstitial cells of Cajal from the rabbit urethra. Cell Calcium. 2014;56:181–187. doi: 10.1016/j.ceca.2014.07.002. [DOI] [PubMed] [Google Scholar]
- 28.Baker S.A., Drumm B.T., Cobine C.A., Keef K.D., Sanders K.M. Inhibitory neural regulation of the Ca (2+) transients in intramuscular interstitial cells of cajal in the small intestine. Front. Physiol. 2018;9:328. doi: 10.3389/fphys.2018.00328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sergeant G.P., Johnston L., McHale N.G., Thornbury K.D., Hollywood M.A. Activation of the cGMP/PKG pathway inhibits electrical activity in rabbit urethral interstitial cells of Cajal by reducing the spatial spread of Ca2+ waves. J. Physiol. 2006;574:167–181. doi: 10.1113/jphysiol.2006.108621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sancho M., Bradley E., Garcia-Pascual A., Triguero D., Thornbury K.D., Hollywood M.A., Sergeant G.P. Involvement of cyclic nucleotide-gated channels in spontaneous activity generated in isolated interstitial cells of Cajal from the rabbit urethra. Eur. J. Pharmacol. 2017;814:216–225. doi: 10.1016/j.ejphar.2017.08.020. [DOI] [PubMed] [Google Scholar]
- 31.Fedigan S., Bradley E., Webb T., Large R.J., Hollywood M.A., Thornbury K.D., McHale N.G., Sergeant G.P. Effects of new-generation TMEM16A inhibitors on calcium-activated chloride currents in rabbit urethral interstitial cells of Cajal. Pflugers Arch. 2017;469:1443–1455. doi: 10.1007/s00424-017-2028-5. [DOI] [PubMed] [Google Scholar]
- 32.Schummers J., Yu H., Sur M. Tuned responses of astrocytes and their influence on hemodynamic signals in the visual cortex. Science. 2008;320:1638–1643. doi: 10.1126/science.1156120. [DOI] [PubMed] [Google Scholar]
- 33.Martinez L.M., Alonso J.M., Reid R.C., Hirsch J.A. Laminar processing of stimulus orientation in cat visual cortex. J. Physiol. 2002;540:321–333. doi: 10.1113/jphysiol.2001.012776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kerr J.N., Greenberg D., Helmchen F. Imaging input and output of neocortical networks in vivo. Proc Natl Acad Sci U S A. 2005;102:14063–14068. doi: 10.1073/pnas.0506029102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Basole A., White L.E., Fitzpatrick D. Mapping multiple features in the population response of visual cortex. Nature. 2003;423:986–990. doi: 10.1038/nature01721. [DOI] [PubMed] [Google Scholar]
- 36.Mukamel E.A., Nimmerjahn A., Schnitzer M.J. Automated analysis of cellular signals from large-scale calcium imaging data. Neuron. 2009;63:747–760. doi: 10.1016/j.neuron.2009.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gabbay M., Brennan C., Kaplan E., Sirovich L. A principal components-based method for the detection of neuronal activity maps: application to optical imaging. Neuroimage. 2000;11:313–325. doi: 10.1006/nimg.2000.0547. [DOI] [PubMed] [Google Scholar]
- 38.Mrsic-Flogel T., Hübener M., Bonhoeffer T. Brain mapping: new wave optical imaging. Curr. Biol. 2003;13:R778–R780. doi: 10.1016/j.cub.2003.09.022. [DOI] [PubMed] [Google Scholar]
- 39.Kalatsky V.A., Stryker M.P. New paradigm for optical imaging: temporally encoded maps of intrinsic signal. Neuron. 2003;38:529–545. doi: 10.1016/s0896-6273(03)00286-1. [DOI] [PubMed] [Google Scholar]
- 40.Sornborger A., Sailstad C., Kaplan E., Sirovich L. Spatiotemporal analysis of optical imaging data. Neuroimage. 2003;18:610–621. doi: 10.1016/s1053-8119(02)00045-9. [DOI] [PubMed] [Google Scholar]
- 41.Li Q., Qi L., Bi G., Li W. 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP) IEEE; 2014. Denoising for bio-image sequences via matrix decomposition; pp. 515–519. [Google Scholar]
- 42.Ronneberger O., Fischer P., Brox T. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2015. U-net: convolutional networks for biomedical image segmentation; pp. 234–241. [Google Scholar]
- 43.Nasrin S., Alom M.Z., Burada R., Taha T.M., Asari V.K. 2019 IEEE National Aerospace and Electronics Conference (NAECON) IEEE; 2019. Medical image denoising with recurrent residual u-net (r2u-net) base auto-encoder; pp. 345–350. [Google Scholar]
- 44.Heinrich M.P., Stille M., Buzug T.M. Residual U-net convolutional neural network architecture for low-dose CT denoising, Current Directions in Biomedical. Engineering. 2018;4:297–300. [Google Scholar]
- 45.Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. Generative adversarial networks. Commun. ACM. 2020;63:139–144. [Google Scholar]
- 46.Baker S.A., Leigh W.A., Del Valle G., De Yturriaga I.F., Ward S.M., Cobine C.A., Drumm B.T., Sanders K.M. Ca(2+) signaling driving pacemaker activity in submucosal interstitial cells of Cajal in the murine colon. Elife. 2021;10 doi: 10.7554/eLife.64099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yoneda S., Fukui H., Takaki M. Pacemaker activity from submucosal interstitial cells of Cajal drives high-frequency and low-amplitude circular muscle contractions in the mouse proximal colon. Neuro Gastroenterol. Motil. 2004;16:621–627. doi: 10.1111/j.1365-2982.2004.00546.x. [DOI] [PubMed] [Google Scholar]
- 48.Lies B., Gil V., Groneberg D., Seidler B., Saur D., Wischmeyer E., Jimenez M., Friebe A. Interstitial cells of Cajal mediate nitrergic inhibitory neurotransmission in the murine gastrointestinal tract. Am. J. Physiol. Gastrointest. Liver Physiol. 2014;307:G98–G106. doi: 10.1152/ajpgi.00082.2014. [DOI] [PubMed] [Google Scholar]
- 49.Drumm B.T., Hwang S.J., Baker S.A., Ward S.M., Sanders K.M. Ca(2+) signalling behaviours of intramuscular interstitial cells of Cajal in the murine colon. J. Physiol. 2019;597:3587–3617. doi: 10.1113/JP278036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sanders K.M., Kito Y., Hwang S.J., Ward S.M. Regulation of gastrointestinal smooth muscle function by interstitial cells. Physiology. 2016;31:316–326. doi: 10.1152/physiol.00006.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Drumm B.T., Rembetski B.E., Huynh K., Nizar A., Baker S.A., Sanders K.M. Excitatory cholinergic responses in mouse colon intramuscular interstitial cells of Cajal are due to enhanced Ca. FASEB J. 2020 doi: 10.1096/fj.202000672R. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sanders K.M., Drumm B.T., Cobine C.A., Baker, Ca S.A. Physiol. Rev. 2023 doi: 10.1152/physrev.00036.2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sanders K.M., Santana L.F., Baker S.A. Interstitial cells of Cajal - pacemakers of the gastrointestinal tract. J. Physiol. 2023 doi: 10.1113/JP284745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ioffe S., Szegedy C. International Conference on Machine Learning. PMLR; 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift; pp. 448–456. [Google Scholar]
- 55.Chollet F. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017. Xception: deep learning with depthwise separable convolutions; pp. 1251–1258. [Google Scholar]
- 56.Kamran S.A., Tavakkoli A., Zuckerbrod S.L. 2020 IEEE International Conference on Image Processing (ICIP) IEEE; 2020. Improving robustness using joint attention network for detecting retinal degeneration from optical coherence tomography images; pp. 2476–2480. [Google Scholar]
- 57.Chen X., Xu C., Yang X., Tao D. Proceedings of the European Conference on Computer Vision. ECCV); 2018. Attention-gan for object transfiguration in wild images; pp. 164–180. [Google Scholar]
- 58.Zhang H., Goodfellow I., Metaxas D., Odena A. International Conference on Machine Learning. PMLR; 2019. Self-attention generative adversarial networks; pp. 7354–7363. [Google Scholar]
- 59.Maas A.L., Hannun A.Y., Ng A.Y. Rectifier nonlinearities improve neural network acoustic models. Proc. icml, Citeseer. 2013:3. [Google Scholar]
- 60.Park K.-B., Choi S.H., Lee J.Y., gan M. Retinal blood vessel segmentation by balancing losses through stacked deep fully convolutional networks. IEEE Access. 2020;8:146308–146322. [Google Scholar]
- 61.Choi Y., Uh Y., Yoo J., Ha J.-W. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020. Stargan v2: diverse image synthesis for multiple domains; pp. 8188–8197. [Google Scholar]
- 62.Wang T.-C., Liu M.-Y., Zhu J.-Y., Tao A., Kautz J., Catanzaro B. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018. High-resolution image synthesis and semantic manipulation with conditional gans; pp. 8798–8807. [Google Scholar]
- 63.Lim J.H., Ye J.C. arXiv Preprint arXiv:1705.02894. 2017. Geometric gan. [Google Scholar]
- 64.Kamran S.A., Hossain K.F., Moghnieh H., Riar S., Bartlett A., Tavakkoli A., Sanders K.M., Baker S.A. New open-source software for subcellular segmentation and analysis of spatiotemporal fluorescence signals using deep learning. iScience. 2022;25 doi: 10.1016/j.isci.2022.104277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kingma D.P., Ba J. arXiv Preprint arXiv:1412.6980. 2014. Adam: a method for stochastic optimization. [Google Scholar]
- 66.Alom M.Z., Hasan M., Yakopcic C., Taha T.M., Asari V.K. 2018. Recurrent Residual Convolutional Neural Network Based on U-Net (R2u-net) for Medical Image Segmentation. arXiv preprint arXiv:1802.06955. [Google Scholar]
- 67.Alom M.Z., Yakopcic C., Hasan M., Taha T.M., Asari V.K. Recurrent residual U-Net for medical image segmentation. Journal of Medical Imaging. 2019;6 doi: 10.1117/1.JMI.6.1.014006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zhuang J. 2018. LadderNet: Multi-Path Networks Based on U-Net for Medical Image Segmentation. arXiv preprint arXiv:1810.07810. [Google Scholar]
- 69.Malik W.Q., Schummers J., Sur M., Brown E.N. Denoising two-photon calcium imaging data. PLoS One. 2011;6 doi: 10.1371/journal.pone.0020490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Giovannucci A., Friedrich J., Kaufman M., Churchland A., Chklovskii D., Paninski L., Pnevmatikakis E.A. Onacid: online analysis of calcium imaging data in real time. Adv. Neural Inf. Process. Syst. 2017:2381–2391. [Google Scholar]
- 71.Laligant O., Truchetet F. A nonlinear derivative scheme applied to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 2008;32:242–257. doi: 10.1109/TPAMI.2008.282. [DOI] [PubMed] [Google Scholar]
- 72.Haralick R.M. Digital step edges from zero crossing of second directional derivatives. IEEE Trans. Pattern Anal. Mach. Intell. 1984;6:58–68. doi: 10.1109/tpami.1984.4767475. [DOI] [PubMed] [Google Scholar]
- 73.Ding L., Goshtasby A. On the Canny edge detector. Pattern Recogn. 2001;34:721–725. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The original software “CalDenoise” is an open-source and publicly available from.
Github: https://github.com/SharifAmit/CalDenoise.
Further information necessary for reanalyze the data reported in this paper can be obtained from the lead contact upon request.
All data are available in the main text and the codes are available from repository: https://github.com/SharifAmit/CalDenoise.