Abstract
Numerical models are increasingly used for noninvasive diagnosis and treatment planning in coronary artery disease, where service-based technologies have proven successful in identifying hemodynamically significant and hence potentially dangerous vascular anomalies. Despite recent progress towards clinical adoption, many results in the field are still based on a deterministic characterization of blood flow, with no quantitative assessment of the variability of simulation outputs due to uncertainty from multiple sources. In this study, we focus on parameters that are essential to construct accurate patient-specific representations of the coronary circulation, such as aortic pressure waveform and intramyocardial pressure, and quantify how their uncertainty affects clinically relevant model outputs. We construct a deformable model of the left coronary artery subject to a prescribed inlet pressure and with open-loop outlet boundary conditions, treating fluid-structure interaction through an arbitrary-Lagrangian-Eulerian framework. Random input uncertainty is estimated directly from repeated clinical measurements from intracoronary catheterization and complemented by literature data. We also achieve significant computational cost reductions in uncertainty propagation thanks to multifidelity Monte Carlo estimators of the outputs of interest, leveraging the ability to generate, at practically no cost, one- and zero-dimensional low-fidelity representations of left coronary artery flow, with appropriate boundary conditions. The results demonstrate how the use of multifidelity control variate estimators leads to significant reductions in variance and accuracy improvements with respect to traditional Monte Carlo. In particular, the combination of three-dimensional hemodynamics simulations and zero-dimensional lumped parameter network models produces the best results, with only a negligible (less than 1%) computational overhead.
Keywords: cardiovascular simulation, multi-fidelity framework, coronary artery hemodynamics, uncertainty quantification
1. INTRODUCTION
Cardiovascular disease poses a significant burden on the lives of millions of people worldwide, with projected total costs estimated by the American Heart Association of over 1 trillion dollars by 2035 [1]. As the standard of care improves through continued research and innovation, virtual hemodynamic representations have been proposed as a noninvasive, image-based approach to complement clinical diagnostics, assess patient risk, aid in clinical decision-making, and facilitate treatment planning. Use of numerical models in clinical diagnosis for specific pathologies has also been extensively tested and supported by clinical studies [2–4]. The complexity of these models has substantially increased in recent years, transitioning from idealized and patient-agnostic concepts to patient-specific models constructed through a complex pipeline which includes image acquisition and segmentation, application of physiologically sound boundary conditions, specification of heterogeneous wall material properties, and accurate solution of the governing equations on high-performance computing platforms [5,6]. Our cardiovascular simulation methods have been extensively validated against in vitro data [7–9], and have been applied to clinical decision making including noninvasive assessment of fractional flow reserve (FFR) [10], new surgical designs for congenital heart disease [11], risk assessment in coronary artery bypass surgery [12], thrombotic risk stratification in Kawasaki disease [13], design of ventricular assist devices [14], study of cerebral and aortic aneurysms [15], stent design and placement [16,17], and many others.
Although the realism of simulation tools has improved in recent years, the predictions provided through these tools are essentially deterministic in most of the literature. Most cardiovascular simulations ignore impact of variability due to uncertainty in input parameters on simulation outcomes. In our view, this shortcoming can be overcome through the establishment of strict guidelines and effective methods to assess the impact of uncertainty on simulation predictions, particularly for model-as-a-device technologies used in the clinic. In particular, there is a need for methods that can increase efficiency of uncertainty quantification to make it tractable for full-scale patient-specific problems. Common sources of uncertainty relate to basic hemodynamic metrics (e.g., heart rate or blood pressure), echocardiography measures (stroke volume, ejection fraction, cardiac output, acceleration times) and invasive cardiac catheterization data (cardiac pressures or intravascular ultrasound velocities). Inter-patient variability from population studies as well as intra-patient variability from repeated measurements, can also be useful in complementing information on uncertainty.
After characterizing the input variability, output statistics are determined by uncertainty propagation through a computationally expensive three-dimensional cardiovascular model. This step can easily become prohibitive, particularly for models with large discretizations, models that account for fluid-structure interaction [18], or include physiologic boundary conditions [19], possibly assimilated from available clinical data under uncertainty [20,21]. Several studies in the literature have investigated the effects of parametric uncertainty in the context of coronary artery disease, for example, considering one-dimensional hemodynamic models and the effect of variability in constitutive model parameters [22], arterial wall stiffness, inlet velocity [23], combined boundary conditions and material properties [24], physiologic and anatomic parameters that impact the predictions of FFR [25] resistance and pressure [26], and assessment of global sensitivity. In most of these studies, uncertainty propagation is performed using spectral stochastic approaches based on generalized polynomial chaos expansion [27], multielement [28] or multiresolution [29–31] approaches, probabilistic tessellations [32], compressive sampling and LASSO [33,34] and others. While offering significant computational savings when the problem at hand has a smooth stochastic response under a moderate dimensionality, these methods suffer significantly from the increase in computational complexity of handling tensor product basis in high dimensions.
Acceleration, more precisely variance reduction, in Monte Carlo sampling has been widely discussed in the literature but, more recently, new multifidelity Monte Carlo estimators are increasingly appearing in applications (see a recent review in [35]). In this study, we focus on approximate control variate estimators [36]. The basic idea is to shift the computational cost from the solution of an expensive high-fidelity model to that of a family of inexpensive low-fidelity surrogates, with the only requirement for high- and low-fidelity models being that they are sufficiently correlated (Fig. 1). In other words, the low-fidelity models do not necessarily need to be an exact approximation of higher-fidelity models, as long as they are correlated. Our group has recently demonstrated the efficiency of such estimators on fully pulsatile simulations using healthy and diseased cardiovascular geometries [37], but further applications of multifidelity approach research remains to be conducted in cardiovascular simulations. In this study, we focus on a vascular submodel with boundary conditions that are specifically designed to capture coronary physiology [38,39]. We aim to quantify the variability of clinically relevant model outputs, based on uncertainty in input parameters that are often subjectively chosen by the analyst. The following original contributions are discussed in this paper:
Random input uncertainty is informed directly through repeated measurements from intracoronary chatheterization. To the authors’ knowledge, this is one of the few studies where clinical data collection is designed to provide sufficient data so that uncertain random inputs can be statistically characterized.
We focus on the most important parameters, whose characterization is essential for accurately simulating the coronary arterial circulation in specific patients. For example, the intramyocardial pressure and its time derivative are difficult to determine in practice, and often assumed equal to the left ventricular pressure.
Coronary boundary conditions have been implemented for all model fidelities, in particular for one- and zero-dimensional flow solvers.
We demonstrate the effectiveness of multifidelity approaches in models incorporating wall deformation with the arbitrary-Lagrangian-Eulerian (ALE) framework.
The paper is organized as follows. Section 2 presents the formulation for the three-, one-, and zero-dimensional hemodynamic solvers used to analyze the coronary circulation and discusses the boundary conditions used to mimic the coronary physiology. This is followed by a discussion of approximate control variate estimators and their variance in Section 3. Section 4 focuses on the random inputs and their representation in terms of a random combination of time-varying modes. We also identify the quantities of interest, the computational cost needed for their determination, and the correlations across different model fidelities. Variance reduction and accuracy for the selected Monte Carlo estimators are analyzed in Section 5 and finally, in Section 6, we summarize our findings, discuss limitations, and briefly outline future work.
FIG. 1:
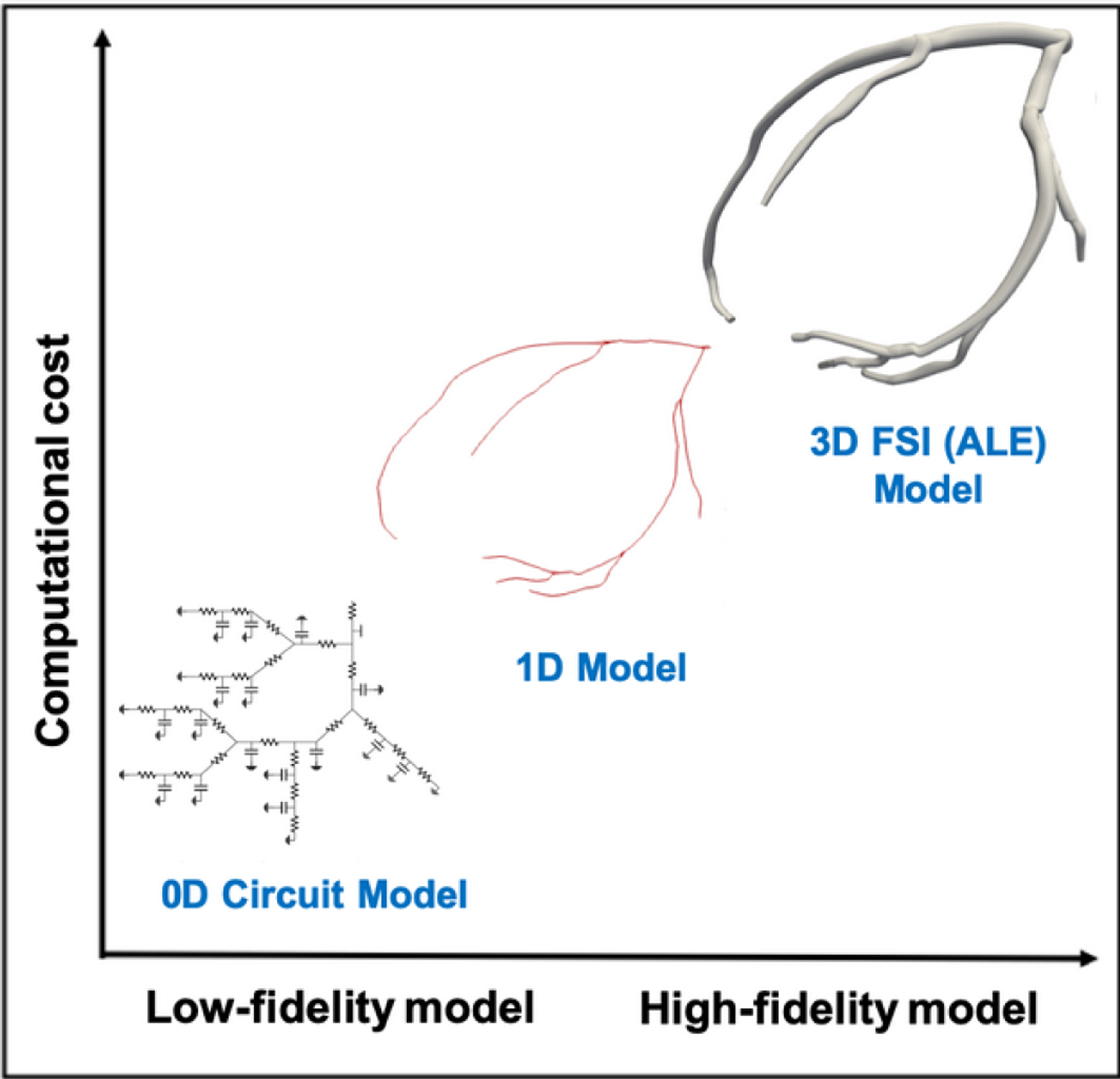
Computational cost versus fidelity for the three hemodynamic models utilized in this study
2. MULTIDIMENSIONAL MODELS FOR THE CORONARY CIRCULATION
2.1. Three-Dimensional Left Coronary Model
A three-dimensional anatomic model of the left coronary artery was constructed from computed tomography clinical images using SimVascular [40]. Outlet boundary conditions are specified through a lumped parameter network (LPN) representation of the downstream circulation whose parameters are tuned to match multiple clinical targets (stroke volume, ejection fraction, pressure, etc.) and found to reproduce physiologically admissible responses [20,41]. Interaction between fluid and structure is simulated through arbitrary Lagrangian-Eulerian (ALE) coupling provided through the SimVascular svFSI solver, which implements a variational multiscale finite element method with second-order implicit generalized- time integration [42,43]. The incompressible Navier-Stokes equations in ALE form are
| (1) |
where , and are fluid density, velocity vector, and body force in the fluid domain . Blood is assumed as a Newtonian fluid, for which , with viscosity , pressure , and is the fluid velocity relative to the mesh. Additionally, in the solid domain , we solve the equilibrium equations
| (2) |
where and denote the density and stress tensor in the solid, respectively. The spatial discretization is based on the variational multiscale finite element method [41–43] and P1–P1 (linear and continuous) elements with colocated nodal velocity and pressure unknowns, while a Saint Venant-Kirchhoff hyperelastic constitutive model is used for the solid wall. For a complete formulation of the above equations in weak form and the resulting algebraic system, the interested reader is referred to [41,43]. Linear system solutions are computed using the Trilinos library [44], developed at Sandia National Laboratory and coupled with the SimVascular svFSI solver. We use either the Biconjugate gradient iterative linear solver with incomplete LU preconditioner or the generalized minimum residual with a diagonal preconditioner. These combinations were shown to be optimal for cardiovascular simulations with deformable walls in our prior work [41]. The computational mesh for the coronary artery lumen was informed by a preliminary convergence study [45] and contains 567,373 tetrahedral elements. The wall mesh consists of 373,435 tetrahedral elements, with three elements through the thickness, which is regarded as appropriate due to the prevalent membrane deformations.
2.2. One-Dimensional Left Coronary Model
The formulation of the one-dimensional hemodynamics solver used in this study, and available through the SimVascular project, is adapted from Hughes and Lubliner [46], with details discussed in [47–49]. Blood is assumed Newtonian, flowing in the axial direction of an ideal cylindrical branch, the pressure is assumed constant over the entire vessel cross section, and no-slip boundary conditions are applied at the lumen.
Conservation of mass and momentum are formulated by integrating the incompressible Navier-Stokes equations over the cross section of a deformable cylindrical domain as
| (3) |
Here the solution variables are the vessel cross-sectional area and blood flow rate ; other parameters are the density , external force , kinematic viscosity , and velocity profile parameters and defined as
| (4) |
where is a general velocity profile function given in the form with average velocity and radius . A linear constitutive equation is given by
| (5) |
where is the Young’s modulus of the vascular tissue, the wall thickness, and and the undeformed inner radius and area, respectively. Our in-house 1D solver combines a stabilized finite element discretization in space and a discontinuous Galerkin approach in time; the nonlinear algebraic system is solved using modified Newton iterations, while pressure and cross-sectional area continuity at the joints between two segments is enforced through Lagrange multipliers. Location and properties of joints, segments, boundary conditions, data tables, initial conditions, and solver parameters are specified through a text input file. Input flow and pressure waveforms are prescribed through time/frequency data tables, while supported boundary conditions include pressure, area, flow, resistance (steady or time-varying), pressure wave, RCR, coronary, impedance, and admittance. Further details can be found in [47].
2.3. Zero-Dimensional Left Coronary Model
Our simplest low-fidelity representation consists of a lumped parameter network, an equivalent circuit layout formulated by hydrodynamic analogy, with flow rate and pressure as the main unknowns. Each circuit element is associated with an algebraic or differential equation, so that
| (6) |
Resistors, capacitors, and inductors are used to represent viscous dissipation in vessels through friction at the endothelium, vascular tissue compliance, and blood inertia, respectively. A Poiseuille flow assumption is used to determine the model parameters for these circuit elements [50],
| (7) |
where is the dynamic viscosity, is the vessel length, is the vessel radius, is the elastic modulus, is the wall thickness, and is the blood density. An in-house automated 0D solver is used in this study, designed to formulate arbitrary circuit layouts from the integration of simple templates, such as capacitors, inductors, resistors, junctions, pressure sources, flow sources, and diodes. Each template is connected via edges and junctions with user-specified connectivity among the templates. The equations are then automatically assembled in a system of differential-algebraic equations,
| (8) |
which is solved numerically. The above equation is discretized in time and integrated in time using an implicit, generalized- scheme.
2.4. LPN Boundary Conditions at the Coronary Arteries
Specialized boundary conditions are applied in this study to three-, one-, and zero-dimensional model fidelities, to better capture the physiology of coronary blood flow [51]. In this context, it is well known how the contraction of the cardiac muscle during systole impedes the flow in the coronaries, which instead reaches its maximum following diastolic relaxation. In other words, a typical coronary flow waveform is out of phase with the aortic pressure. To mimic this behavior, a special coronary boundary condition has been proposed in the literature [51], consisting of an RCRCR circuit connected to an intramyocardial pressure generator. Coronary boundary conditions [51,52] are applied to the left coronary artery (LCA) outlets, formulated through the ordinary differential equations
| (9) |
| (10) |
where and are the proximal and distal pressures, and are the proximal and distal capacitances, and and are the resistances, respectively (Fig. 2). Note that the same rate of intramyocardial pressure is used for all outlets. In the 3D model, the above equations are integrated in time using a fourth-order Runge-Kutta explicit scheme, while the pressure at the 3D model outlet is computed as and coupled to the three-dimensional model solution at each time step [53]. In the 1D model, algebraic equations of the coronary circuit are instead implemented as discussed in [51], whereas the compartment containing the coronary boundary conditions simply extends the 0D circuit network and these two are solved in a monolithic fashion.
FIG. 2:
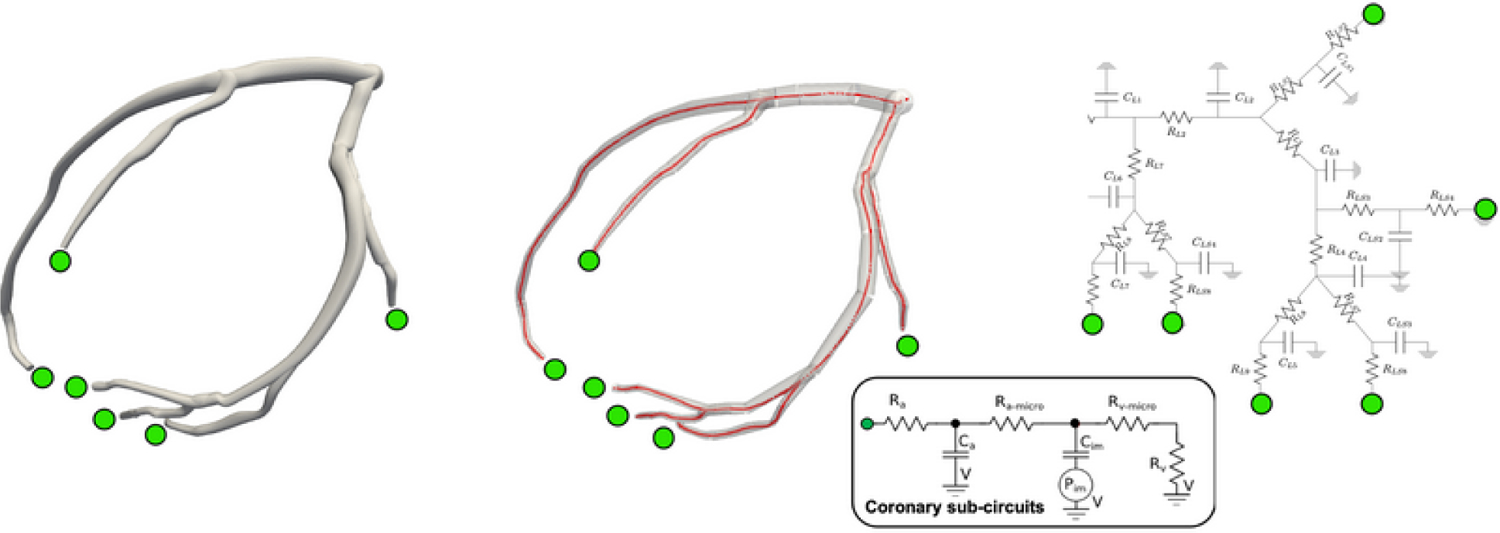
Numerical models with coronary boundary conditions at the outlets. Three-dimensional model with deformable walls (left), one-dimensional model (center), and zero-dimensional lumped parameter network model (right).
The total coronary resistance was computed by assigning 4% of the cardiac output to the coronary arteries [54] and vessel resistances were distributed among outlets following a morphometric relation associating flow rates with vessel diameters, . An empirically derived morphometry exponent has been suggested in [55, 56]; for the coronary circulation, a previous uncertainty quantification study found only negligible difference in the simulation results with ranging between 2.4 and 2.8 [45]. Approximating the diameter with the square root of the area , the resistance of a distal branch, is computed as
| (11) |
while the capacitances are instead distributed proportional to the outlet area [52].
2.5. Agreement between Low- and High-Fidelity Model Outputs
Low-fidelity one-dimensional models were extracted from the three-dimensional segmentation using a newly developed plug-in in SimVascular [57] that automatically creates one-dimensional solver input files, containing the appropriate inlet and outlet boundary conditions. Similarly, low-fidelity zero-dimensional models were generated through a separate set of conversion tools from one-dimensional model segments. The agreement between low-fidelity and three-dimensional model outputs was found to be excellent under both resistance-capacitance-resistance circuit (RCR) and coronary outlet boundary conditions as shown in Fig. 3 for selected flow and pressure quantities of interest.
FIG. 3:
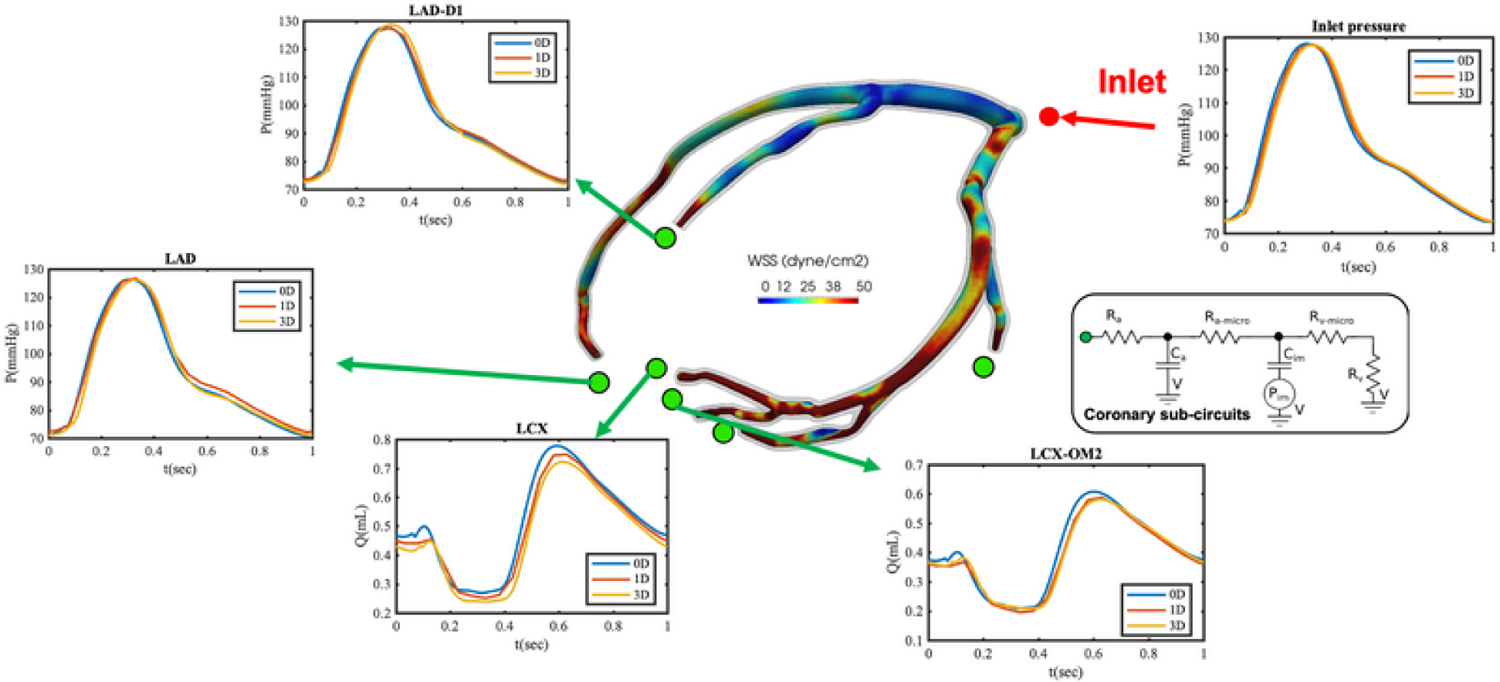
Three-, one-, and zero-dimensional model results with pulsatile inlet pressure and coronary outlet boundary condition
3. MULTIFIDELITY MONTE CARLO UNCERTAINTY PROPAGATION
Consider a complete probability space where is a set of elementary events, is a Borel -algebra of , and a probability measure assuming values in [0,1] over events in . Model inputs are represented though the random vector , with components (for -dimensional random variable) having marginals and joint probability density . Space and time are denoted by and , respectively. In this study, we focus on the forward problem in uncertainty quantification, , (through its mean or variance , where, for a given realization of the random inputs, is determined through the numerical solution of a high-fidelity model. For simplicity, in what follows we assume space and time to be fixed, leading to .
The Monte Carlo estimator of the expected value of based on realizations is defined as
| (12) |
The variance can be reduced by either increasing its denominator or reducing its numerator. The former can be achieved through stratified or low-discrepancy sampling sequences, such as latin hypercube or quasi Monte Carlo sampling (QMC), which offer a more uniform coverage of the random input range , and have been shown to improve the convergence rate of MC estimators up to . In this study, we use Sobol’ [58] QMC sequences, as shown in Fig. 4.
FIG. 4:
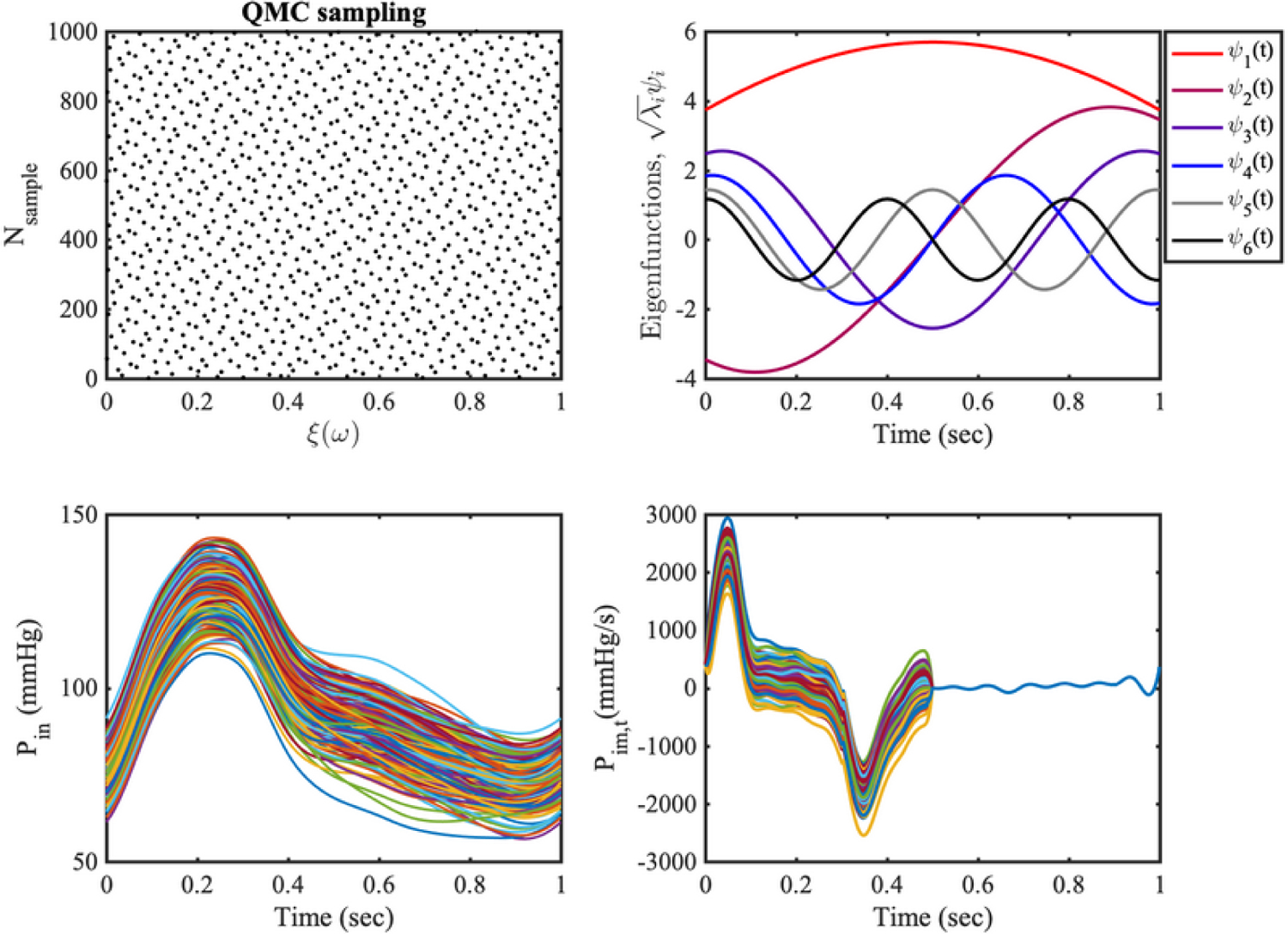
Stochastic modeling of the random inputs. (a) 1000 samples from a quasi Monte Carlo Sobol’ sequence. (b) Six largest eigenfunctions of the exponential covariance kernel. (c) 200 inlet pressure realizations from the Karhunen-Loève (K–L) expansion (17). (d) 200 realizations for the intramyocardial pressure time-derivative.
Alternatively, reduction in the numerator can be achieved by introducing approximate control variate Monte Carlo estimators, which combine contributions from two different model fidelities (low-fidelity LF and high-fidelity HF, respectively). The Monte Carlo estimator for the high-fidelity model is replaced by which embeds a correction based on the LF model [59,60]
| (13) |
where , and the additional LF realizations are used to estimate as . Similarly to the MC estimator, is unbiased with variance
| (14) |
Thus, the regression coefficient that minimizes (14) can be determined as
| (15) |
where is Pearson’s correlation coefficient between the LF and HF estimators. Substituting the optimal from Eq. (15) into Eq. (14), leads to
| (16) |
Expression (16) suggests how a sufficiently large correlation between HF and LF models is the main determinant of variance reduction and, since approximate control variate estimators are always superior to their vanilla Monte Carlo counterpart.
4. INPUT AND OUTPUT UNCERTAINTIES
In an effort to focus our attention on relevant random inputs, essential for the physiological admissibility of the coronary outputs of interest, we consider two uncertain input parameters in the modeling of the coronary circulation model. The first random input parameter is the left coronary artery inlet pressure waveform imposed at the inlet of the left coronary model, Pin, whose intra-patient variability is determined from repeated clinical data acquired in vivo through cardiac catheterization [45]. The second random input parameter is the time derivative of the intramyocardial pressure in the LPN model for coronary circulation, Pim,t, imposed at the outlets of the model, whose variability is instead assumed. In our study we assumed these two parameters are independent and then conducted two separate propagation studies.
4.1. Karhunen-Loève Representation of the Random Inputs
We approximate the left coronary pressure waveform, Pin, with a wide-sense stationary Gaussian process in time with exponential covariance, , where , and are two arbitrary time points, is the correlation length, and the process variance [61]. Under these circumstances, for a sufficiently large truncation level , such a process admits the representation
| (17) |
where is a collection of independent standard Gaussian random variables and are the eigenvalues and eigenvectors of the covariance kernel , respectively ([62]). A satisfactory approximation of is obtained using only the eigenmodes associated with the four largest eigenvalues , when the correlation length is chosen to . In other words, is modeled with the K-L expansion with four terms in the truncated expansion. We select based on the decay rate of the eigenvalue spectrum of the exponential covariance function. Specifically, the largest eigenvalue spectra compared to the first eigenvalue, , are , and decays to less than 5 percent after the first four modes . For , the process standard deviation is set equal to 7% of the mean, as per repeated pressure measurements from cardiac catheterization in six patients [45]. Samples from are obtained by projecting the four-dimensional Sobol’ sequence in Fig. 4(a) through the inverse cumulative distribution function of a multivariate Gaussian. Results are illustrated in Fig. 4. A collection of eigenfunctions from the selected covariance kernel is shown in Fig. 4(b), while Fig. 4(c) contains an ensemble of inlet pressure realizations from Eq. (17).
Due to the significant challenge of measuring the intramyocardial pressure, Pim, in vivo, the left ventricular pressure and its time derivative are often used as a viable replacement [12,20,24,52]. This is clearly an approximation, whose effect on the simulation results is rarely discussed in the literature, despite the key importance of intramyocardial pressure in defining the diastolic character of coronary flow. This may relate to the use of open-loop boundary conditions with prescribed coronary flow in many studies. Here, rather than a flow, we prescribe an inlet pressure and additionally model the uncertain intramyocardial pressure time derivative Pim,t as a stochastic process in time. is modeled with the K–L expansion with four terms in the truncated expansion. We perturbed a baseline intramyocardial pressure time derivative [20] using a zero-mean Gaussian process having standard deviation equal to , with the heart cycle duration [Fig. 4(d)].
4.2. Quantities of Interest
We focused on three hemodynamic quantities of interest (QoIs), flow rate, and pressure at each outlet ), and branch wall shear stress (WSS). In more detail, the shear stress was averaged over one heart cycle in time and over the vessel circumference in space so that
| (18) |
where is the spatial distance along the vessel branch centerline, and is the lumen circumference at the branch cross section. Finally, we averaged along the centerlines of each vessel branch to obtain a single averaged value for WSS. For zero-dimensional models, the wall shear stress is determined based on Poiseuille flow conditions on an ideal vessel with circular cross section of radius ,
| (19) |
where is the instantaneous flow rate, the dynamic viscosity, and the vessel radii are based on a one-dimensional model anatomy.
4.3. Computational Cost
Outputs for each model fidelity were computed using a fixed number of input parameter realizations. Specifically, we solved a total of 400 high-fidelity (HF) cardiovascular model instances in parallel using 48 cores for each HF simulation, either through the Comet cluster available through a XSEDE allocation, or using resources from the Center for Research Computing at the University of Notre Dame. All simulations were performed over four cardiac cycles, the first half consisting of QMC realizations of the inlet pressure Pin, and the remaining 200 with stochastic intramyocardial pressure Pim. One- and zero-dimensional models were solved 1000 and 10,000 times, respectively, for each random input. Relative and cumulative simulation costs are reported in Tables 1 and 2, respectively.
TABLE 1:
Absolute and relative simulation costs for all three model fidelities. The simulation cost is reported in CPU times, in which computing times from all processors are summed
| Solver | Cost (one simulation) | Effective cost (one simulation) |
|---|---|---|
| 3D | 1775 hrs | 1 |
| 1D | 8.5 mins | 7.98 × 10−5 |
| 0D | 5 secs | 7.82 × 10−7 |
TABLE 2:
Effective cost and associated number of model evaluations for high-fidelity Monte Carlo and multifidelity estimators
| Method | Effective cost (percentage to QMC) | No. 3D simulations | No. 1D simulations | No. 0D simulations |
|---|---|---|---|---|
| QMC | 100% | 200 | 0 | 0 |
| MF-1D | 108.13% | 200 | 1000 | 0 |
| MF-0D | 100.78% | 200 | 0 | 10,000 |
4.4. Correlations of High- and Low-Fidelity Models
Following the discussion on approximate control variate Monte Carlo estimators in Section 3, it should be clear how the correlations among high- and low-fidelity model outputs are the main determinant of variance reduction. We observe very large average Pearson correlations across all QoIs and all coronary branches, as reported in Tables 3 and 4. Once again we would like to emphasize that a high correlation between model outputs does not necessarily imply a close agreement between high- and low-fidelity QoIs, as shown in Fig. 5.
TABLE 3:
High- to low-fidelity model correlations under inlet pressure waveform uncertainty. LCx—left circumflex artery, OM—obtuse marginal, LAD—left anterior descending artery, D—diagonal branch of the LAD
| QoI | Pressure | Flow | WSS | |||
|---|---|---|---|---|---|---|
| Branch | 3D-1D | 3D-0D | 3D-1D | 3D-0D | 3D-1D | 3D-0D |
| LCx | 0.9756 | 0.9999 | 0.9388 | 0.9999 | 0.9353 | 0.9997 |
| LCx-OM1 | 0.9756 | 0.9999 | 0.9281 | 0.9999 | 0.9092 | 0.9998 |
| LCx-OM2 | 0.9753 | 0.9999 | 0.9360 | 0.9999 | 0.9292 | 0.9997 |
| LCx-OM3 | 0.9758 | 0.9999 | 0.9315 | 0.9999 | 0.9234 | 0.9999 |
| LAD | 0.9758 | 0.9999 | 0.9420 | 0.9999 | 0.9077 | 0.9995 |
| LAD-D1 | 0.9716 | 0.9959 | 0.9295 | 0.9999 | 0.9040 | 0.9998 |
TABLE 4:
High- to low-fidelity model correlations under intramyocardial pressure uncertainty
| QoI | Pressure | Flow | WSS | |||
|---|---|---|---|---|---|---|
| Branch | 3D-1D | 3D-0D | 3D-1D | 3D-0D | 3D-1D | 3D-0D |
| LCX | 0.9886 | 0.9960 | 0.9857 | 0.9999 | 0.9864 | 0.9969 |
| LCX-OM1 | 0.9909 | 0.9942 | 0.9911 | 0.9999 | 0.9913 | 0.9984 |
| LCX-OM2 | 0.9888 | 0.9949 | 0.9872 | 0.9999 | 0.9877 | 0.9972 |
| LCX-OM3 | 0.9894 | 0.9968 | 0.9902 | 0.9999 | 0.9904 | 0.9984 |
| LAD | 0.9822 | 0.9999 | 0.9829 | 0.9999 | 0.9831 | 0.9944 |
| LAD-D1 | 0.9207 | 0.9297 | 0.9905 | 0.9999 | 0.9906 | 0.9984 |
FIG. 5:
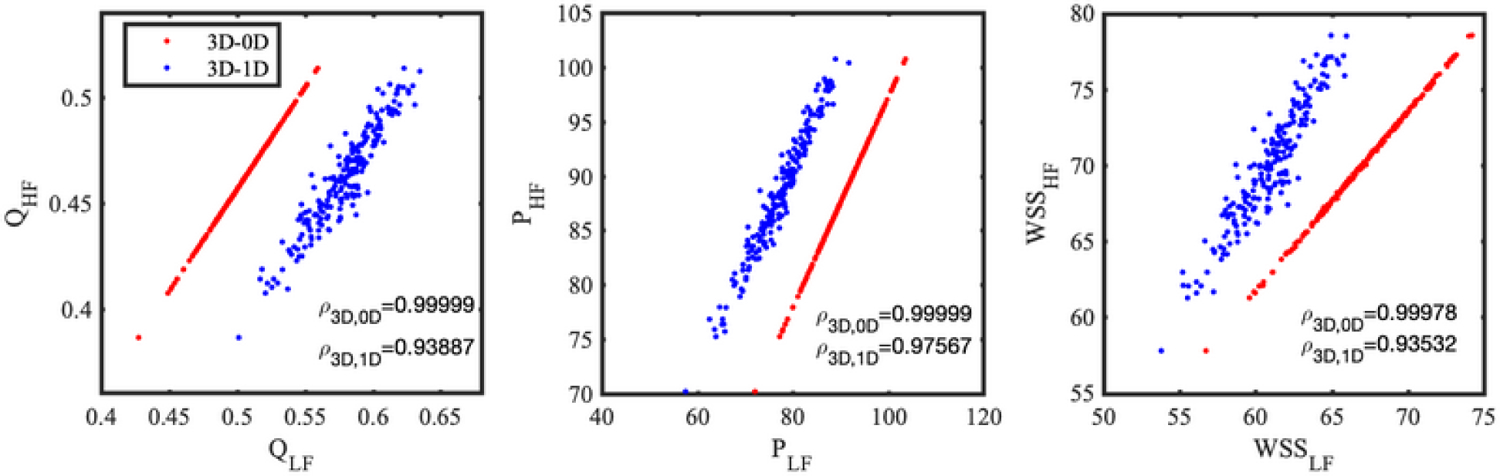
Low- versus high-fidelity model outputs at LCx branch and Pearson correlations under intramyocardial pressure uncertainty
5. UNCERTAINTY PROPAGATION RESULTS
5.1. Uncertainty in the Inlet Pressure Waveform
To provide a preliminary idea of how the variability in inlet pressure waveform affects the model outputs, we first performed 200 realizations from the zero-dimensional model in Fig. 6, and observed similar results as in previous studies from our research group [45]. Next, we compared the variance reduction obtained for QoIs in six left coronary artery branches resulting from vanilla Monte Carlo sampling and approximate control variate estimators with one-(CV-1D) and zero-dimensional (CV-0D) low-fidelity models, respectively (Fig. 7). From a pilot run consisting of 200, 1000, and 10,000 model evaluations, the CV-1D estimator reduces the variance by a factor of 3–4, while an order of magnitude reduction is achievable using the CV-OD estimator.
FIG. 6:
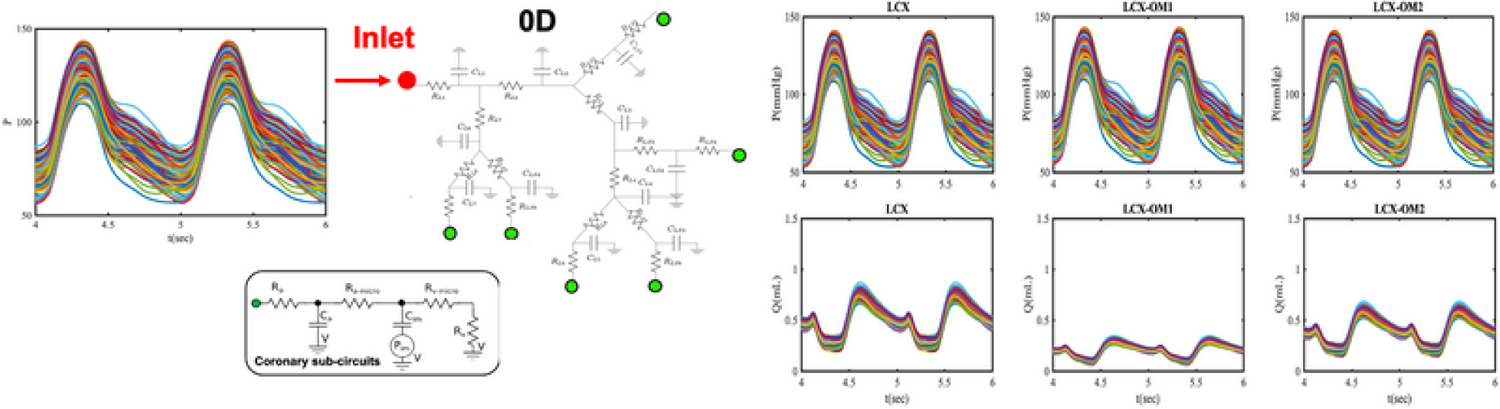
Schematic workflow showing how the uncertainty in the inlet pressure waveform is propagated through a zero-dimensional left coronary artery model, specifically for outlet pressure and flow QoIs in LCx branches
FIG. 7:
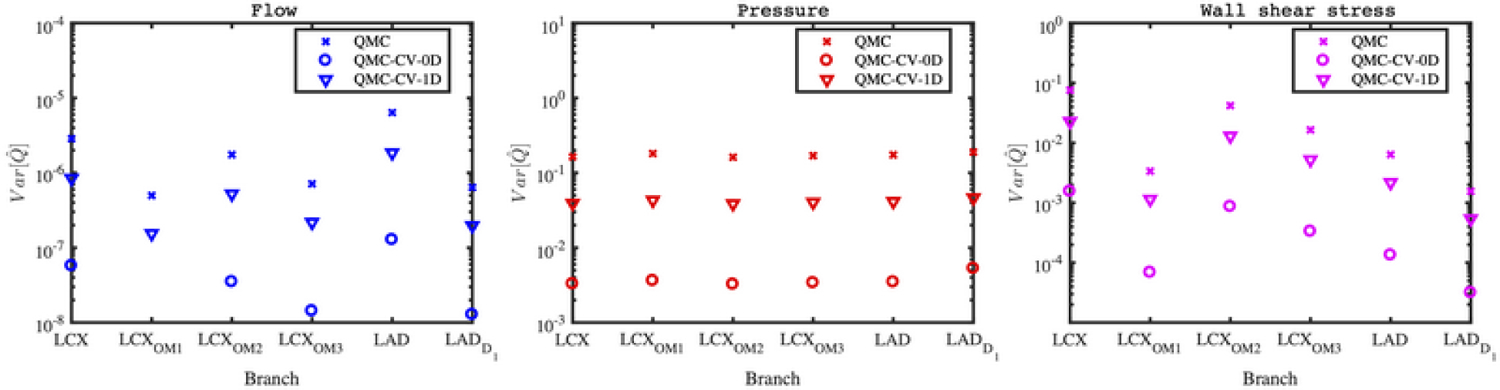
Variance reduction for QMC and approximate control variate estimators
We use the normalized confidence interval of a generic estimator as six times the coefficient of variation in accordance with previous literature [37,63],
| (20) |
The amplitude of (i.e., three standard deviations) confidence interval normalized by the mean corresponds to the 99.7% confidence interval normalized by the expected value. Smaller values of indicate a higher level of confidence in the estimates from . The of QMC, CV-1D, and CV-0D estimators is shown in Fig. 8 for all relevant QoIs. Similar to previous results, reductions in of one order of magnitude result from the CV-0D estimator. Finally, we note that the discussion above is equally valid for pressure/flow and for wall shear stress QoIs.
FIG. 8:
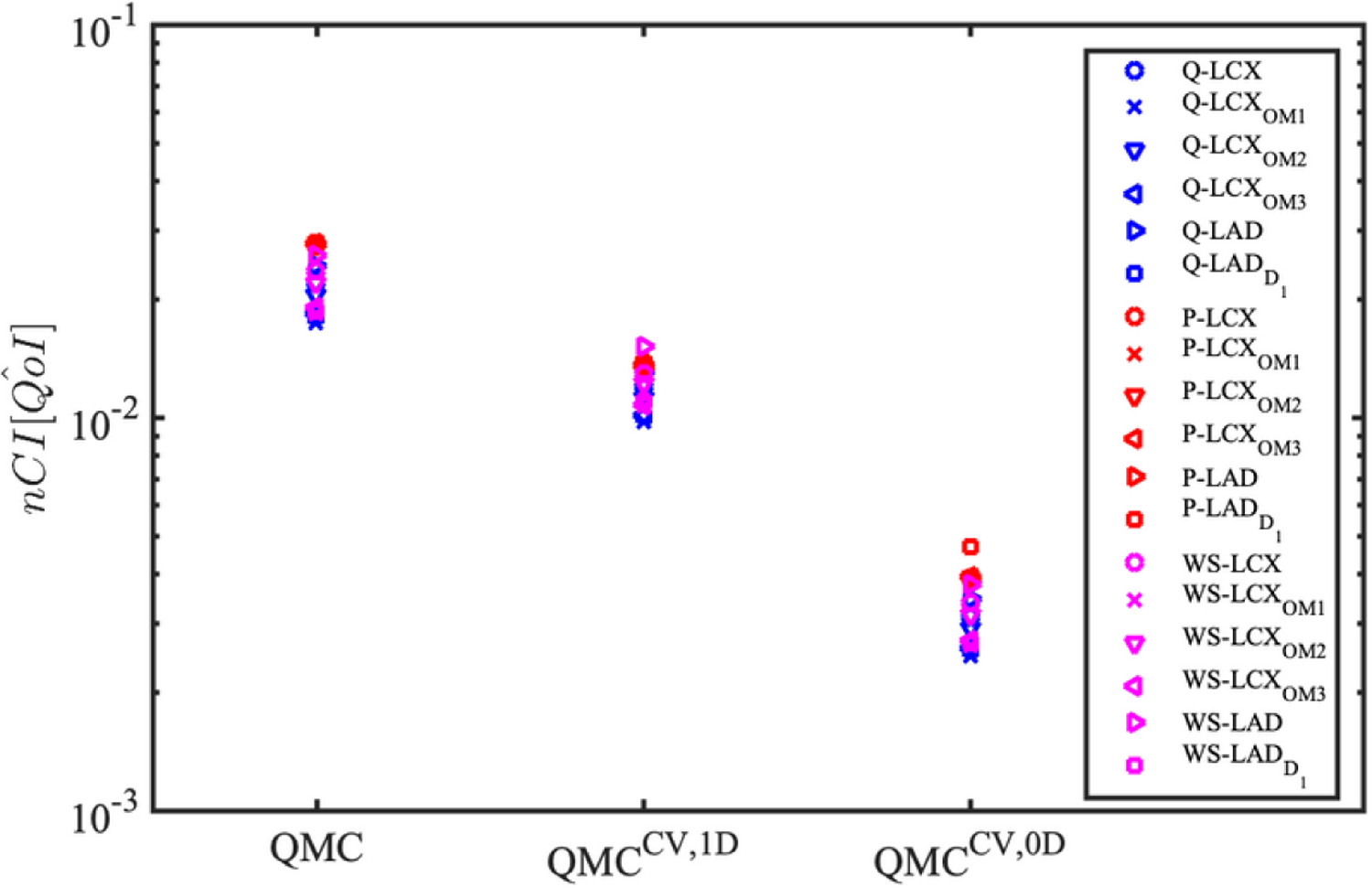
Improvements in normalized confidence interval from approximate control variate estimators under the inlet pressure uncertainty
5.2. Uncertainty in the Intramyocardial Pressure Time-Derivative
Variability in the intramyocardial pressure time derivative significantly affects outlet flow and time-averaged wall shear stress uniformly across all branches (~ 30% variation [45]), leaving the pressure almost unaltered, as shown in Fig. 9. Variance reduction for QMC and multifidelity estimators is quantified in Fig. 10, while their is shown in Fig. 11.
FIG. 9:
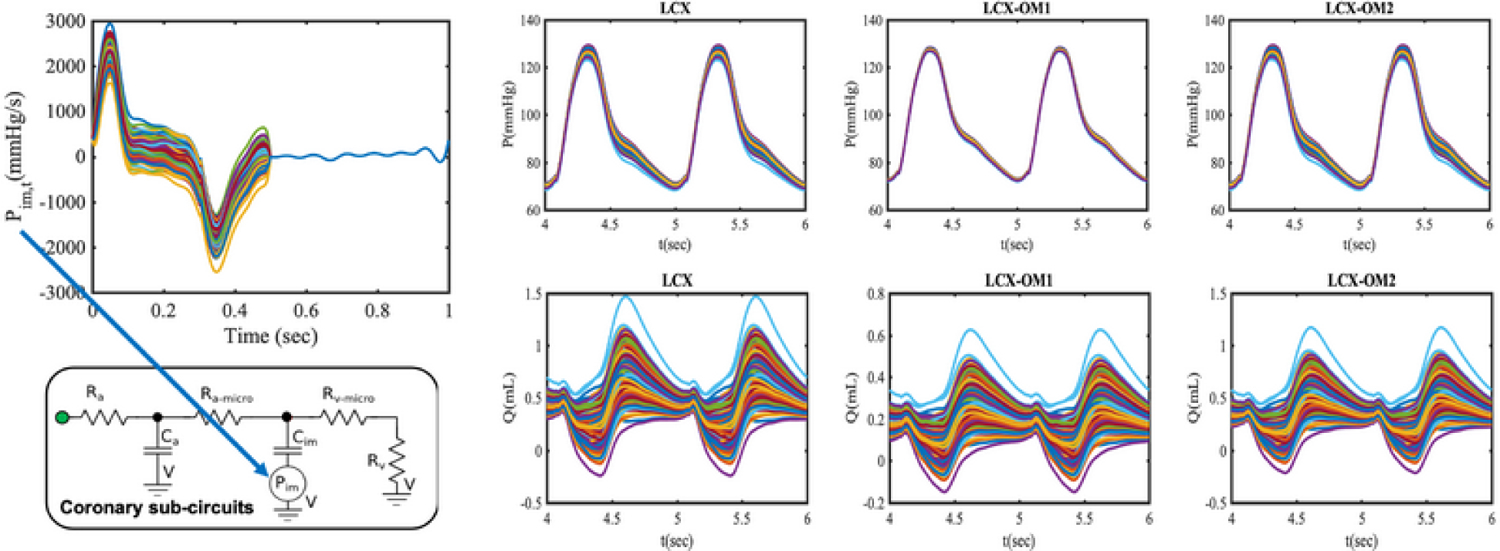
Ensemble of model outputs for the zero-dimensional model of the left coronary circulation under intramyocardial pressure uncertainty
FIG. 10:
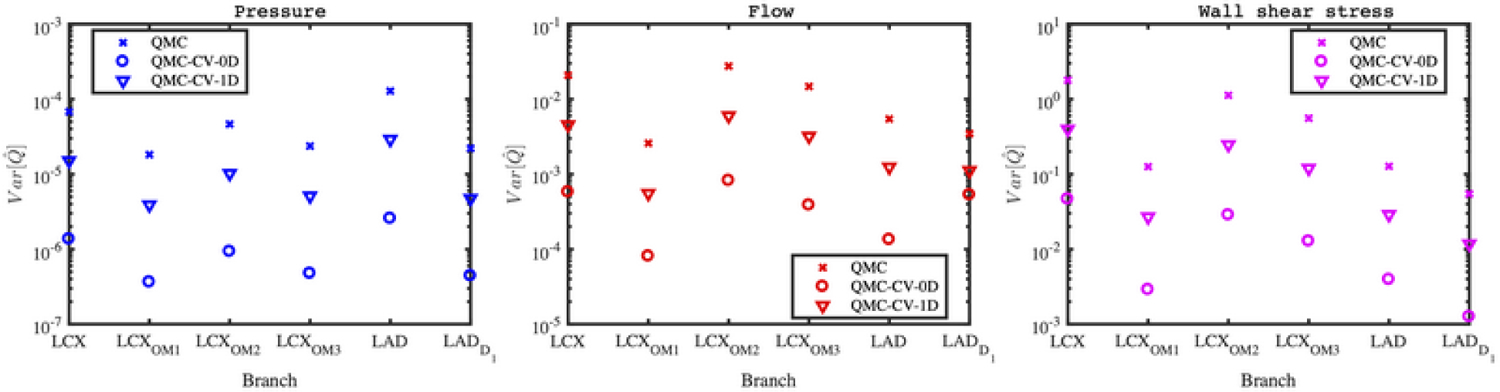
Variance reduction from approximate control variate estimators under intramyocardial pressure uncertainty
FIG. 11:
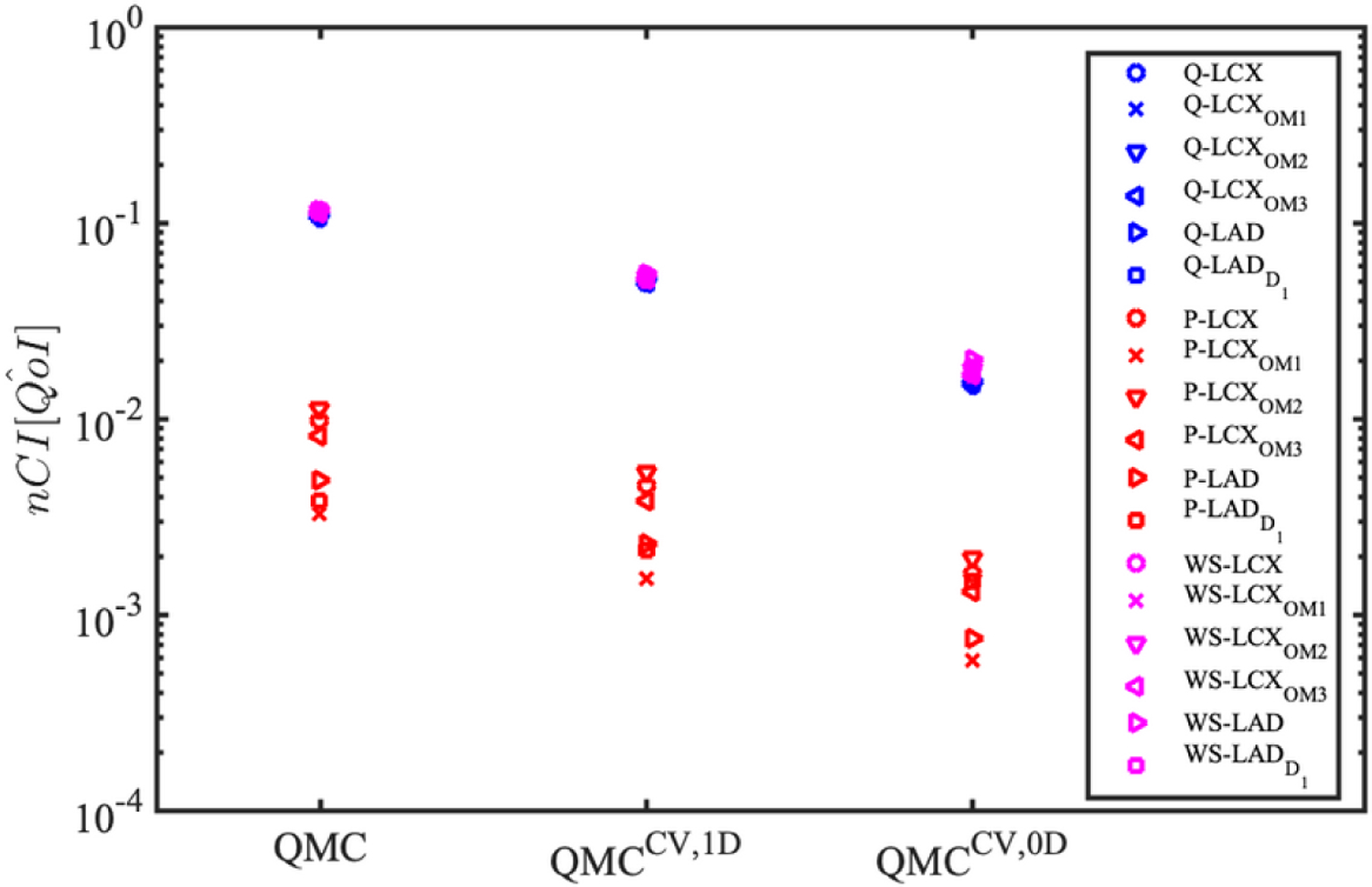
Improvements in from approximate control variate estimators under intramyocardial pressure rate uncertainty
Similarly to the findings in the previous section, both variance reduction and are greatly improved by the multifidelity estimators with superior performance of CV-0D. This is due to the Pearson correlations being very high over all the QoIs for this latter estimator and the larger number of zero-dimensional simulations (10,000 for each input uncertainty) included in the pilot run. This suggests zero-dimensional models to be particularly well suited for low-fidelity or reduced-order representations of the coronary subcirculation due to their almost negligible computational cost and highly correlated QoIs. Finally, we observe how outlet pressure variability due to intramyocardial pressure uncertainty is limited if compared to flow or wall shear stress QoIs. This justifies the clustering of results in Fig. 11.
We evaluate the performance of the multifidelity UQ using extrapolation of the computing cost in terms of the equivalent high-fidelity model runs. We first set a range of targeted and estimate the computational cost to achieve the target by extrapolation using Eqs. (12) and (16). Specifically, the number of equivalent high-fidelity runs, , is computed as
| (21) |
where and are the computational cost and and are the number of simulations of high- and low-fidelity models, respectively. We set a target of 0.2, 0.1, 0.05, 0.025, 0.01, and 0.005, and extrapolate the cost of the simulation to reduce using the variance reduction rule in Eq. (12), in which the variance is reduced by the inverse of the number of simulations.
In Fig. 12, we summarize the extrapolated computational cost to achieve a targeted of the Monte Carlo estimator. The multifidelity Monte Carlo (MFMC) methods dramatically reduce the computational cost for providing accurate estimators of Monte Carlo, especially for MF with the 0D models.
FIG. 12:
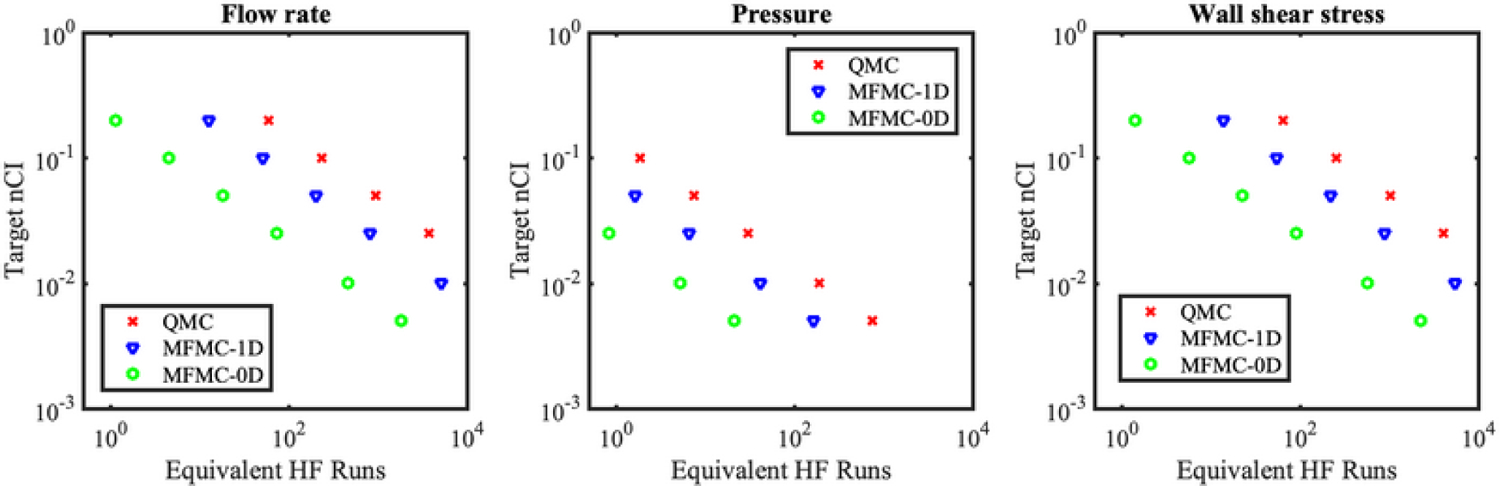
Extrapolated equivalent high-fidelity model costs for target for MC, MFMC with 1D model, and MFMC with 0D model. QoI are at the LCX branch when the intramyocardial pressure is perturbed
6. DISCUSSION
Recent advances in model-based diagnostics of coronary artery disease have demonstrated how models can be successfully integrated in clinical routines, but have raised questions related to their robustness, in light of possible uncertainty or ignorance associated with their input parameters. In this study, we focused on two clinically relevant parameters, the inlet pressure for coronary circulation subnetworks, and the intramyocardial pressure time derivative. Stochastic processes in time are used to inject uncertainty in these parameters, leading to a representation by a finite collection of independent random variables following Karhunen-Loève expansion. Inlet pressure waveform uncertainty is directly estimated from repeated measurements obtained during cardiac catheterization in six patients [45], while variability in intramyocardial pressure is assumed equal to 10% of its maximum systolic rate.
We have quantified the variance in model output expectations for a three-dimensional multiscale cardiovascular model with deformable walls, ALE fluid-structure interaction, and conforming fluid and wall mesh interfaces. We also generated computationally inexpensive one- and zero-dimensional low-fidelity representations from three-dimensional segmentation, using a recently developed pipeline in SimVascular. Coronary boundary conditions were also implemented for all low-fidelity formulations and thoroughly validated against three-dimensional simulation results. Despite a common misconception that UQ analysis can easily become computationally intractable for large cardiovascular models containing millions of degrees of freedom, we were able to characterize confidence in expectations of clinically relevant quantities of interest under a fixed computational budget of approximately 200 high-fidelity model runs.
This is possible thanks to the high correlations between high- and low-fidelity outputs, even if these outputs are not necessarily in perfect agreement with each other, or in other words low-fidelity QoIs do not need in general to be close to their high-fidelity counterpart. Our results highlight how CV-1D estimators of mean pressure, flow, and wall shear stress have variance which is reduced by a factor of 3–4 with respect to QMC estimators, with accuracy improvements of the same order. CV-0D estimators show superior performance with improvements up to one order of magnitude and total simulation cost equal to less than 1% with respect to high-fidelity three-dimensional models. The computational cost savings using extrapolation of the current results shows that one can save one or two orders of magnitude compared to high-fidelity model evaluations alone to achieve a targeted by using the multifidelity framework.
Estimator variance and are computed, in this study, from a pilot run consisting of a fixed number of simulations selected a priori. A better approach would be to adaptively refine the number of simulations needed to achieve a certain variance reduction or to satisfy a certain computational budget from a small initial pilot run. This will be easily achieved through a software interface between SimVascular and the Dakota UQ software platform (developed at Sandia National Laboratory), currently under development [37].
The high correlations between high- and low-fidelity models obtained in this study can be attributed to the fact that the current quantities of interest are spatially averaged global variables, and that the current cardiovascular model does not involve complex flows (e.g., flow recirculation or turbulence) or abrupt changes in the geometry (e.g., bifurcation, valve, or stenosis). We note that the 3D-1D approach cannot be replaced by 3D-0D when quantities of interest include local variations of wall shear stress, atheroprone area, and wall deformations, as those are not obtainable from the 0D modeling.
We remark that the MFMC approach provides many advantages over nonintrusive stochastic collocation methods, which were generally regarded as an accurate choice for uncertainty propagation. In our previous work [45], we demonstrated that the convergence of QMC method provided similar performance against the stochastic collocation methods. However, MFMC can reduce variance by orders of magnitude at only a small fraction of the cost of one HF additional, while the next step refinement of stochastic collocation requires on the order of tens to hundreds of HF simulations, since it requires a discrete increase in samples for refinements. The stochastic collocation method also has other shortcomings against the MC approach, for example, nonconvergent behavior for discontinuous response surfaces.
Future work will extend the present results for high-dimensional, arbitrarily distributed, and correlated random inputs. There are multiple sources of uncertainty in cardiovascular simulations, including boundary conditions, material properties, and geometry that should be combined in future studies to offer a complete picture of uncertainty in predictions. The effects of these uncertainty sources used to be studied independently. In more realistic cases these uncertainty sources may be correlated. By reducing the computational cost, the multifidelity framework will be exploited to study the effect of multiple sources.
ACKNOWLEDGMENTS
This work was supported by a NIH grant (NIH NIBIB R01-EB018302), NSF SSI grants 1663671 and 1339824, and NSF CDS&E CBET 1508794. This work used the Extreme Science and Engineering Discovery Environment (XSEDE) [64], which is supported by National Science Foundation grant number ACI-1548562 and computational resources from the Centre for Research Computing at the University of Notre Dame. The authors would like to thank Aekaansh Verma, and Jonathan Pham for many the fruitful discussions on multifidelity estimators, LPN custom solvers, and high-performance computing resources. We also acknowledge support from the open source SimVascular project at www.simvascular.org.
REFERENCES
- 1.Benjamin E, Virani S, Callaway C, Chamberlain A, Chang A, Cheng S, Chiuve S, Cushman M, Delling F, and Deo R, Heart Disease and Stroke Statistics-2018 Update: A Report from the American Heart Association., Circulation, 137(12):e67, 2018. [DOI] [PubMed] [Google Scholar]
- 2.Koo B, Erglis A, Doh J, Daniels D, Jegere S, Kim H, Dunning A, DeFrance T, Lansky A, Leipsic J, and Min J, Diagnosis of Ischemia-Causing Coronary Stenoses by Noninvasive Fractional Flow Reserve Computed from Coronary Computed Tomographic Angiograms: Results from the Prospective Multicenter DISCOVER-FLOW (Diagnosis of Ischemia-Causing Stenoses Obtained via Noninvasive Fractional Flow Reserve) Study, J. Am. Coll. Cardiol, 58(19):1989–1997, 2011. [DOI] [PubMed] [Google Scholar]
- 3.Min J, Leipsic J, Pencina M, Berman D, Koo B, Van Mieghem C, Erglis A, Lin F, Dunning A, Apruzzese P, Budoff M, Cole JH, Jaffer F, Leon M, Malpeso J, Mancini G, Park S, Schwartz R, Shaw L, and Mauri L, Diagnostic Accuracy of Fractional Flow Reserve from Anatomic CT Angiography, JAMA, 308(12):1237–1245, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nørgaard B, Leipsic J, Gaur S, Seneviratne S, Ko B, Ito H, Jensen J, Mauri L, De Bruyne B, Bezerra H, Osawa K, Marwan M, Naber C, Erglis A, Park S, Christiansen E, Kaltoft A, Lassen J, Bøtker H, and Achenbach S, Diagnostic Performance of Noninvasive Fractional Flow Reserve Derived from Coronary Computed Tomography Angiography in Suspected Coronary Artery Disease: The NXT Trial (Analysis of Coronary Blood Flow Using CT Angiography: Next Steps), J. Am. Coll. Cardiol, 63(12):1145–1155, 2014. [DOI] [PubMed] [Google Scholar]
- 5.Marsden A, Optimization in Cardiovascular Modeling, Ann. Rev. Fluid Mech, 46:519–546, 2014. [Google Scholar]
- 6.Marsden A and Esmaily-Moghadam M, Multiscale Modeling of Cardiovascular Flows for Clinical Decision Support, Appl. Mech. Rev, 67:030804, 2015. [Google Scholar]
- 7.Kung E, Les A, Figueroa A, Medina F, Arcautre K, Wicker R, McConnell M, and Taylor C, In Vitro Validation of Finite Element Analysis of Blood Flow in Deformable Models, Ann. Biomed. Eng, 39(7):1947–1960, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kung E, Kahn A, Burns J, and Marsden A, In Vitro Validation of Patient-Specific Hemodynamic Simulations in Coronary Aneurysms Caused by Kawasaki Disease, Cardiovasc. Eng. Technol, 5(2):189–201, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Steinman D, Hoi Y, Fahy P, Morris L, Walsh MT, Aristokleous N, Anayiotos AS, Papaharilaou Y, Arzani A, Shadden SC, and Berg P, Variability of Computational Fluid Dynamics Solutions for Pressure and Flow in a Giant Aneurysm: The ASME 2012 Summer Bioengineering Conference CFD Challenge, J. Biomech. Eng, 135(2):1–13, 2013. [DOI] [PubMed] [Google Scholar]
- 10.Taylor C, Fonte T, and Min J, Computational Fluid Dynamics Applied to Cardiac Computed Tomography for Noninvasive Quantification of Fractional Flow Reserve: Scientific Basis, J. Am. Coll. Cardiol, 61(22):2233–2241, 2013. [DOI] [PubMed] [Google Scholar]
- 11.Yang W, Feinstein J, and Marsden A, Constrained Optimization of an Idealized Y-Shaped Baffle for the Fontan Surgery at Rest and Exercise, Comput. Methods Appl. Mech. Engi, 199(33–36):2135–2149, 2010. [Google Scholar]
- 12.Bangalore Ramachandra A, Kahn A, and Marsden A, Patient-Specific Simulations Reveal Significant Differences in Mechanical Stimuli in Venous and Arterial Coronary Grafts, J. Cardiov. Transl. Res, 9(4):279–290, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grande Gutierrez N, Shirinsky O, Gagarina N, Lyskina G, Fukazawa R, Ogawa S, Burns J, Marsden A, and Kahn A, Assessment of Coronary Artery Aneurysms Caused by Kawasaki Disease Using Transluminal Attenuation Gradient Analysis of Computerized Tomography Angiograms, Am. J. Cardiol, 120:556–562, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Long C, Marsden A, and Bazilevs Y, Shape Optimization of Pulsatile Ventricular Assist Devices Using FSI to Minimize Thrombotic Risk, Comput. Mech, 54:921–932, 2014. [Google Scholar]
- 15.Humphrey JD and Taylor C, Intracranial and Abdominal Aortic Aneurysms: Similarities, Differences, and Need for a New Class of Computational Models, Ann. Rev. Biomed. Eng, 10:221–246, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Migliavacca F, Petrini L, Colombo M, Auricchio F, and Pietrabissa R, Mechanical Behavior of Coronary Stents Investigated through the Finite Element Method, J. Biomech, 35(6):803–811, 2002. [DOI] [PubMed] [Google Scholar]
- 17.Gundert T, Marsden A, Yang W, Marks D, and LaDisa JJ, Identification of Hemodynamically Optimal Coronary Stent Designs based on Vessel Caliber, IEEE Trans. Biomed. Eng, 58(7):1992–2002, 2012. [DOI] [PubMed] [Google Scholar]
- 18.Figueroa C, Vignon-Clementel I, Jansen K, Hughes T, and Taylor C, A Coupled Momentum Method for Modeling Blood Flow in Three-Dimensional Deformable Arteries, Comput. Methods Appl. Mech. Eng, 195(41–43):5685–5706, 2006. [Google Scholar]
- 19.Esmaily-Moghadam M, Hsia T, and Marsden A, A Non-Discrete Method for Computation of Residence Time in Fluid Mechanics Simulations, Phys. Fluids, 25(11):110802, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tran J, Schiavazzi D, Bangalore Ramachandra A, Kahn A, and Marsden A, Automated Tuning for Parameter Identification and Uncertainty Quantification in Multi-Scale Coronary Simulations, Comput. Fluids, 142:128–138, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schiavazzi D, Baretta A, Pennati G, Hsia T, and Marsden A, Patient-Specific Parameter Estimation in Single-Ventricle Lumped Circulation Models under Uncertainty, Int. J. Numer. Methods Biomed. Eng, 33(3):e02799, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xiu D and Sherwin S, Parametric Uncertainty Analysis of Pulse Wave Propagation in a Model of a Human Arterial Network, J. Comput. Phys, 226:1385–1407, 2007. [Google Scholar]
- 23.Brault A, Dumas L, and Lucor D, Uncertainty Quantification of Inflow Boundary Condition and Proximal Arterial Stiffness-Coupled Effect on Pulse Wave Propagation in a Vascular Network, Int. J. Numer. Methods Biomed. Eng, 33:e2859, 2017. [DOI] [PubMed] [Google Scholar]
- 24.Tran J, Schiavazzi D, Kahn A, and Marsden A, Uncertainty Quantification of Simulated Biomechanical Stimuli in Coronary Artery Bypass Grafts, Comput. Methods Appl. Mech. Eng, 345:402–428, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yin M, Yazdani A, and Karniadakis G, One-Dimensional Modeling of Fractional Flow Reserve in Coronary Artery Disease: Uncertainty Quantification and Bayesian Optimization, Comput. Methods Appl. Mech. Eng, 353:66–85, 2019. [Google Scholar]
- 26.Chen P, Quarteroni A, and Rozza G, Simulation-Based Uncertainty Quantification of Human Arterial Network Hemodynamics, Int. J. Numer. Methods Biomed. Eng, 29:698–721, 2013. [DOI] [PubMed] [Google Scholar]
- 27.Xiu D and Karniadakis G, The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations, SIAM J. Sci. Comput, 24(2):619–644, 2002. [Google Scholar]
- 28.Wan X and Karniadakis G, An Adaptive Multi-Element Generalized Polynomial Chaos Method for Stochastic Differential Equations, J. Comput. Phys, 209(2):617–642, 2005. [Google Scholar]
- 29.Le Matre O, Najm H, Ghanem R, and Knio O, Multi-Resolution Analysis of Wiener-Type Uncertainty Propagation Schemes, J. Comput. Phys, 197(2):502–531, 2004. [Google Scholar]
- 30.Schiavazzi D, Doostan A, and Iaccarino G, Sparse Multiresolution Regression for Uncertainty Propagation, Int. J. Uncertainty Quantif, 4(4):303–331, 2014. [Google Scholar]
- 31.Schiavazzi D, Doostan A, Iaccarino G, and Marsden A, A Generalized Multi-Resolution Expansion for Uncertainty Propagation with Application to Cardiovascular Modeling, Comput. Methods Appl. Mech. Eng, 314:196–221, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Witteveen J and Iaccarino G, Simplex Stochastic Collocation with Random Sampling and Extrapolation for Nonhypercube Probability Spaces, SIAM J. Sci. Comput, 34(2):A814–A838, 2012. [Google Scholar]
- 33.Doostan A and Owhadi H, A Non-Adapted Sparse Approximation of PDEs with Stochastic Inputs, J. Comput. Phys, 230(8):3015–3034, 2011. [Google Scholar]
- 34.Blatman G and Sudret B, Adaptive Sparse Polynomial Chaos Expansion based on Least Angle Regression, J. Comput. Phys, 230(6):2345–2367, 2011. [Google Scholar]
- 35.Peherstorfer B, Willcox K, and Gunzburger M, Survey of Multifidelity Methods in Uncertainty Propagation, Inference, and Optimization, SIAM Rev., 60(3):550–591, 2018. [Google Scholar]
- 36.Gorodetsky A, Geraci G, Eldred M, and Jakeman J, A Generalized Framework for Approximate Control Variates, Stat. Comput, arXiv:1811.04988, 2018. [Google Scholar]
- 37.Fleeter C, Geraci G, Schiavazzi D, Kahn A, and Marsden A, Multilevel and Multifidelity Uncertainty Quantification for Cardiovascular Hemodynamics, Comput. Methods Appl. Mech. Eng, 365:113030, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kim H, Vignon-Clementel I, Coogan J, Figueroa C, Jansen K, and Taylor C, Patient-Specific Modeling of Blood Flow and Pressure in Human Coronary Arteries, Ann. Biomed. Eng, 38(10):3195–3209, 2010. [DOI] [PubMed] [Google Scholar]
- 39.Sankaran S, Moghadam M, Kahn A, Tseng E, Guccione J, and Marsden A, Patient-Specific Multiscale Modeling of Blood Flow for Coronary Artery Bypass Graft Surgery, Ann. Biomed. Eng, 40(10):2228–2242, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Updegrove A, Wilson N, Merkow J, Lan H, Marsden A, and Shadden S, SimVascular: An Open Source Pipeline for Cardiovascular Simulation, Ann. Biomed. Eng, 45(3):525–541, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Seo J, Schiavazzi D, and Marsden A, Performance of Preconditioned Iterative Linear Solvers for Cardiovascular Simulations in Rigid and Deformable Vessels, Comput. Mech, 64:717–739, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bazilevs Y, Calo V, Cottrell J, Hughes T, Reali A, and Scovazzi G, Variational Multiscale Residual-Based Turbulence Modeling for Large Eddy Simulation of Incompressible Flows, Comput. Methods Appl. Mech. Eng, 197:173–201, 2007. [Google Scholar]
- 43.Esmaily-Moghadam M, Bazilevs Y, and Marsden A, A Bi-Partitioned Iterative Algorithm for Solving Linear Systems Arising from Incompressible Flow Problems, Comput. Methods Appl. Mech. Eng, 286:40–62, 2015. [Google Scholar]
- 44.Heroux M, Bartlett R, Howle V, Hoekstra R, Hu J, Kolda T, Lehoucq R, Long K, Pawlowski R, Phipps E, Salinger A, Thornquist H, Tuminaro R, Willenbring J, Williams A, and Stanley K, An Overview of the Trilinos Project, ACM Trans. Math. Software, 31(3):397–423, 2005. [Google Scholar]
- 45.Seo J, Schiavazzi DE, Kahn AM, and Marsden AL, The Effects of Clinically-Derived Parametric Data Uncertainty in Patientspecific Coronary Simulations with Deformable Walls, Int. J. Numer. Methods Biomed. Eng, 36:e3351, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hughes T and Lubliner J, On the One-Dimensional Theory of Blood Flow in the Larger Vessels, Math. Biosci, 18:161–170, 1973. [Google Scholar]
- 47.Wan J, Steele B, Spicer SA, Strohband S, Feijo GR, Hughes TJ, and Taylor CA, A One-Dimensional Finite Element Method for Simulation-Based Medical Planning for Cardiovascular Disease, Comput. Methods Biomech. Biomed. Eng, 5:195–206, 2002. [DOI] [PubMed] [Google Scholar]
- 48.Vignon I and Taylor C, Outflow Boundary Conditions for One-Dimensional Finite Element Modeling of Blood Flow and Pressure Waves in Arteries, Wave Motion, 39:361–374, 2004. [Google Scholar]
- 49.Vignon I, A Coupled Multidomain Method for Computational Modeling of Blood Flow, PhD, Stanford University, 2006. [Google Scholar]
- 50.Milisic V and Quarteroni A, Analysis of Lumped Parameter Models for Blood Flow Simulations and Their Relation with 1D Models, ESAIM: Math. Modell. Numer. Anal, 38:613–632, 2004. [Google Scholar]
- 51.Kim H, Vignon-Clementel I, Figueroa C, LaDisa J, Jansen K, Feinstein J, and Taylor C, On Coupling a Lumped Parameter Heart Model and a Three-Dimensional Finite Element Aorta Model, Ann. Biomed. Eng, 37(11):2153–2169, 2009. [DOI] [PubMed] [Google Scholar]
- 52.Sankaran S, Esmaily-Moghadam M, Kahn A, Tseng E, Guccione J, and Marsden A, Patient-Specific Multiscale Modeling of Blood Flow for Coronary Artery Bypass Graft Surgery, Ann. Biomed. Eng, 40(10):2228–2242, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Esmaily Moghadam M, Vignon-Clementel I, Figliola R, and Marsden A, A Modular Numerical Method for Implicit 0D/3D Coupling in Cardiovascular Finite Element Simulations, J. Comput. Phys, 244:63–79, 2013. [Google Scholar]
- 54.Bogren H, Klipstein R, Firmin D, Mohiaddin R, Underwood S, Rees R, and Longmore D, Quantitation of Antegrade and Retrograde Blood Flow in the Human Aorta by Magnetic Resonance Velocity Mapping, Am. Heart J, 117(6):1214–1222, 1989. [DOI] [PubMed] [Google Scholar]
- 55.Zhou Y, Kassab G, and Molloi S, On the Design of the Coronary Arterial Tree: A Generalization of Murray’s Law, Phys. Med. Biol, 44(12):2929, 1999. [DOI] [PubMed] [Google Scholar]
- 56.Changizi M and Cherniak C, Modeling the Large-Scale Geometry of Human Coronary Arteries, Can. J. Physiol. Pharmacol, 78:603–611, 2000. [PubMed] [Google Scholar]
- 57.Lan H, Updegrove A, Wilson N, Maher G, Shadden S, and Marsden A, A Re-Engineered Software Interface and Workflow for the Open-Source SimVascular Cardiovascular Modeling Package, J. Biomech. Eng, 140:024501, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sobol I, Uniformly Distributed Sequences with an Additional Uniform Property, USSR Comput. Math. Math. Phys, 16:236–242, 1976. [Google Scholar]
- 59.Pasupathy R, Schmeiser BW, Taaffe MR, and Wang J, Control-Variate Estimation Using Estimated Control Means, IIE Trans., 1044:381–385, 2012. [Google Scholar]
- 60.Ng L and Willcox K, Multifidelity Approaches for Optimization under Uncertainty, Int. J. Numer. Methods Eng, 100:746–772, 2014. [Google Scholar]
- 61.Ghanem R and Spanos P, Stochastic Finite Elements: A Spectral Approach, New York: Springer, 2003. [Google Scholar]
- 62.Le Maitre O, Reagan M, Najm H, Ghanem R, and Knio O, A Atochastic Projection Method for Fluid Flow II. Random Process, J. Comput. Phys, 181:9–44, 2002. [Google Scholar]
- 63.Geraci G, Eldred M, and Iaccarino G, A Multifidelity Control Variate Approach for the Multilevel Monte Carlo Technique, Center Turbul. Res. Ann. Res. Briefs, 2015:169–181, 2015. [Google Scholar]
- 64.Towns J, Cockerill T, Dahan M, Foster I, Gaither K, Grimshaw A, Hazlewood V, Lathrop S, Lifka D, Peterson G, Roskies R, Scott J, and Wilkins-Diehr N, XSEDE: Accelerating Scientific Discovery, Comput. Sci. Eng, 16(5):62–74, 2014. [Google Scholar]


