Toxicity Adaptive Lists Design: A Practical Design for Phase I Drug Combination Trials in Oncology

Abstract

PURPOSE

We introduce a novel algorithmic approach to design phase I trials for oncology drug combinations.

METHODS

Our proposed Toxicity Adaptive Lists Design (TALE) is straightforward to implement, requiring the prespecification of a small number of parameters that define rules governing dose escalation, de-escalation, or reassessment of previously explored dose levels. These rules effectively regulate dose exploration and control the number of toxicities. A key feature of TALE is the possibility of simultaneous assignment of multiple-dose combinations that are deemed safe by previously accrued data.

RESULTS

A numerical study shows that TALE shares comparable operative characteristics, in terms of identification of the maximum tolerated dose (MTD), to alternative approaches such as the Bayesian optimal interval design, the COPULA, the product of independent beta probabilities escalation, and the continual reassessment method for partial ordering designs while reducing the risk of overdosing patients.

CONCLUSION

The proposed TALE design provides a favorable balance between maintaining patient safety and accurately identifying the MTD. To facilitate the use of TALE, we provide a user-friendly R Shiny application and an R package for computing relevant operating characteristics, such as the risk of assigning highly toxic dose combinations.

INTRODUCTION

Phase I clinical trials typically aim to identify the maximum tolerated dose (MTD) of a therapy. In oncology, the therapy often combines two or more agents or drugs that can be administered at different dose levels (DLs).¹ Simple, efficient, and practical phase I trial designs are needed to identify safe and effective dose combinations and to assess their toxicity (Fig 1). These designs need to be simple to describe and implement. Additionally, they must control the risk of severe toxicities during the study while generating data that allow investigators to estimate the relationship between DLs of the therapy and toxicities.

FIG 1.

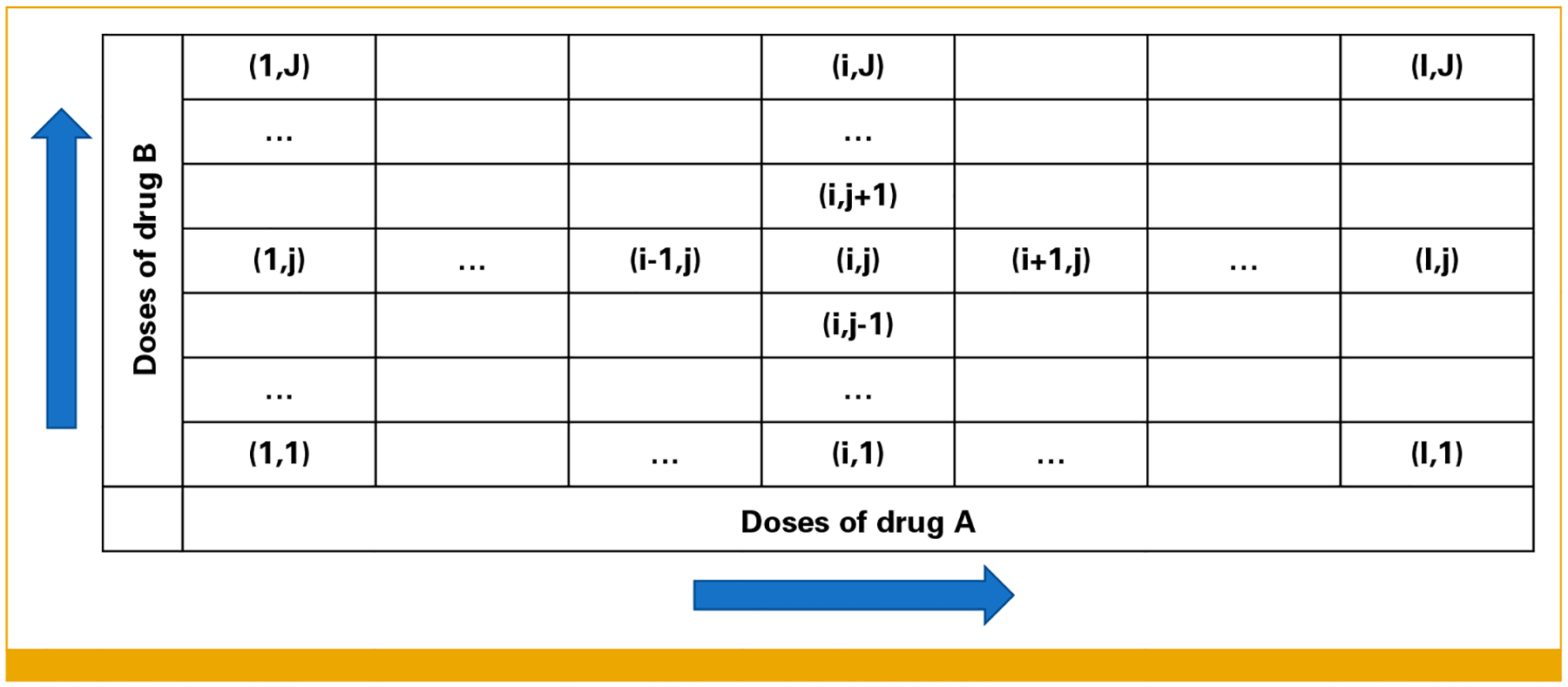
Example of a grid in which DLs of drug A (rows) and drug B (columns) are organized. Doses for drug A are increasing from left to right and for drug B from bottom to top. DLs, dose levels.

There are several phase I trial designs for drug combinations. Some convert the study of dose combinations into a series of single-drug subtrials, often requiring a large sample size. In each subtrial, the goal is to identify the MTD of one drug while keeping the other drug at a fixed dose. Others investigate combinations of DLs from a prespecified grid of doses. Designs can be broadly classified as algorithm-based and model-based.² Algorithm-based methods, such as the 3 + 3 design and extensions,^3–6 are commonly used for their simplicity but might have suboptimal operating characteristics. Model-based designs use parametric models to describe the relationship between DLs and toxicities and can incorporate data from previous studies on single drugs.^7–21 We also mention model-assisted designs that follow easy-to-interpret rules for sequential decision making, which in turn are selected using dose-toxicity models. Notable examples include the Bayesian optimal interval (BOIN) design,²² the modified toxicity probability interval design,^23,24 and the Keyboard design.⁴ Comprehensive comparisons of model-based and model-assisted designs for drug combinations have been previously published.^1,8,25–27

Previous studies comparing phase I trial designs suggest that model-based designs tend to outperform algorithm-based designs.^2,3,8,9 However, stakeholders (eg, sponsors and investigators) might perceive model-based designs as black boxes because the criteria underlying the decisions to escalate and de-escalate DLs can be difficult to interpret.^3–5 Additionally, they require sequential inference on the relation between DLs and toxicities and rely on parametric models whose assumptions might be violated.^1,26

We introduce an algorithm-based approach for phase I drug combination trials: the Toxicity Adaptive Lists Design (TALE). TALE is a multistage design that, at each stage, defines a list of explorable DLs of the combination therapy. DLs are included in the list only if lower doses have been previously explored and the available data suggest acceptable toxicity rates in the study population. The sequential rules defining the study design control the risk of assigning patients to toxic DLs and generate data for rapid characterization of the relationship between DLs and toxicities. A distinctive feature of TALE is that patients enrolled during a phase of the study might be assigned to multiple DLs. When patients’ accrual is sufficiently rapid, this can lead to a considerable reduction in the trial duration compared with other phase I designs that assign a single cohort per phase. Moreover, simultaneous exploration of DLs tends to reduce the number of times the data are analyzed for sequential decision making during the study.

TALE is straightforward to interpret and practical to implement. We illustrate TALE operating characteristics and discuss comparisons with more complex model-based and model-assisted designs.

A Phase I Study of PK and ATR Inhibitors

We used TALE in a recent phase I clinical trial (Clinical-Trials.gov identifier: NCT05687136; CTEP 10527). In this study, we explore the combination of two anticancer drugs: the DNA-PK inhibitor peposertib (M3814) and the ATR inhibitor tuvusertib (M1774). DNA-PK and ATR are critical proteins involved in DNA repair and in the cellular response to replicative stress. In preclinical models, the combination demonstrates synergistic lethality to cancer cells dependent on the ATR pathway, such as those with mutations in ATM or those with a high degree of replicative stress.²⁸ Both agents have been studied as monotherapies and in combinations with other agents; however, this is the first trial evaluating this specific combination. It will start accruing patients in 2024.

The same strategy is being used in a phase I trial combining gemcitabine with the ATR inhibitor elimusertib (Clinical-Trials.gov identifier: NCT04616534; CTEP 10403).

TALE Design

We consider a design to investigate the toxicity of the combination of two drugs, A and B. The design components are defined in the Data Supplement. DLs for the drugs are included in a grid and labeled as (i, j), where i and j represent the DLs of drugs A and B, respectively (Fig 1). TALE proceeds in stages, and at each stage k, a cohort of n (eg, 3) patients is assigned to each DL in an explorable list. Initially (stage I), the list includes only the lowest dose in the grid. It is then updated sequentially after each stage on the basis of the observed number of dose-limiting toxicities (DLTs) and a set of prespecified rules (Figs 2A and 2B). The trial ends when a sample size of N patients is reached or the list of explorable DLs is empty.

FIG 2.

Illustration of how the list of explorable DLs for the TALE design is updated throughout the trial. The figure includes two components (A and B) to summarize the available data up to stage k and two more components (C and D) translating available data into the decision of which DLs will be assigned during the next stage (k+1). The set L_k includes all the (i, j) dose combinations assigned during the k-th stage. For example, L₃ = {(1, 3), (2, 1)} indicates that during the third stage, two distinct dose combinations are explored (1, 3) and (2, 1). DLs, dose levels; TALE, Toxicity Adaptive Lists Design.

A maximum of n_max patients can be assigned to a DL. We indicate with p_ij the observed toxicity rate at DL (i, j), that is:

$$p_{ij}=\frac{\text{number}\text{of}\text{DLT}\text{at}\left(i,j\right)}{\text{number}\text{of}\text{patients}\text{enrolled}\text{at}\left(i,j\right)}.$$

After the k-th stage, the p_ij rates are updated, and TALE identifies the list L_{k + 1} of explorable DLs for the next stage. The list is obtained comparing the values of p_ij with prespecified parameters, λ_e, λ_d, and λ_r (Fig 2B), which categorize the observed toxicity rate of a DL (i, j):

1. p_ij ≤ λ_e low toxicity.

2. λ_e < p_ij ≤ λ_d intermediate-low toxicity.

3. λ_d < p_ij ≤ λ_r intermediate toxicity.

4. p_ij ≥ λ_r high toxicity.

Figure 2B associates colors with toxicity levels: green for low toxicity, blue for intermediate-low toxicity, orange for intermediate toxicity, and red for high toxicity. Thresholds λ_e, λ_d, and λ_r are trial-specific (possible values are in the Data Supplement, Table S1). The use of the three parameters, λ_e, λ_d, and λ_r, provides flexibility in defining how many toxicity events suggest escalation, de-escalation, and revisiting of the DLs. TALE can, however, be simplified by choosing the escalation parameters (λ_e) and letting λ_d = cλ_e and λ_r = cλ_d for some c > 0. For example, one can choose λ_e = 0.16 and c = 1.6 corresponding to (λ_e, λ_d, λ_e) = (0.16, 0.272, 0.4624), which, for n_max = 3, defines the same decisions as the vector (λ_e, λ_d, λ_e) = (0.16, 0.24, 0.45) in the Data Supplement (Table S1).

Next, TALE provides the definition of L_{k + 1}, that is, which DLs can be explored in the stage k + 1. As summarized in Figures 2C and 2D, previous data from the explored doses trigger specific actions: escalation, de-escalation, stay, and reconsider.

Figure 2 provides a complete description of how the available data are sequentially translated into decisions for the subsequent stage of the trial. The figure includes two components (boxes A and B) to summarize the available data up to stage k and two more components (boxes C and D) translating available data into the decision of which DLs will be assigned during the next stage (k + 1).

A DL (i, j) can enter in L_k only if safety is suggested by lower adjacent neighbors that are the DLs (i − 1, j) and (i, j − 1). Figure 2C contains a scheme that uses four questions to determine whether a DL can enter in L_{k + 1} on the basis of the available data.

After the list L_{k + 1} has been created (Fig 2C), some DLs are excluded (Fig 2D). We remove (1) overly toxic DLs, (2) DLs with n_max previously assigned patients (low uncertainty), and (3) DLs defined by lower or identical doses for both agents as other combinations in the list of explorable DLs. In successive stages, some DLs could be re-explored. A DL with an intermediate toxicity rate at completion of the k-th stage does not continue to enroll patients in the (k + 1)-th stage, but it might be revisited later in the study (Fig 2C). TALE can be described in three steps:

1. For the first stage k = 1, the list of explorable DLs L₁ includes only the lowest DL (1, 1).

2. During the k-th stage of the trial, the design assigns a cohort of n patients to each DL in L_k. After the k-th stage, the toxicity rates p_ij are updated, on the basis of the available data, and a new list of explorable DLs L_{k + 1} is provided (Figs 2C and 2D).

3. The trial completes the enrollment when the maximum sample size N is reached or if the list of explorable DLs L_{k + 1} for the next stage is empty.

In the final stage, the sample size N could be insufficient to investigate all DLs in L_{k + 1}. For example, with N = 30 and a cohort size of three patients, after the enrollment of 27 patients during the initial k stages, the data might indicate two explorable DLs for the (k + 1)-th stage. Two cohorts require six patients, but only 30–27 = 3 patients can be enrolled. In this case, the remaining three patients are assigned to one of the explorable DLs, giving priority to the DL with the lowest number of enrolled patients. When patient accrual is completed, the MTD is estimated via isotonic regression.²⁹

Example of TALE Trial

Figure 3 provides a stylized example to illustrate the rules governing the escalation and de-escalation decisions in TALE. This example illustrates how the escalation and de-escalation rules work and does not refer to a specific clinical context. Both drugs A and B have three DLs, and the trial can enroll up to N = 30 patients in cohorts of n = 3 patients. The design parameters are λ_e = 0.16, λ_d = 0.24, and λ_r = 0.45. The Data Supplement (Table S2) indicates the number of DLTs during the course of the study that dictate escalation (Q1 in Fig 2C) and de-escalation (Q4 in Fig 2C) decisions for the subsequent stage of the trial. The maximum number of patients that can be assigned to a single DL is set at n_max = 9. The trial results are illustrated in Figure 3, and the key events are as follows:

1. Stage I: Three patients receive DL (1, 1) and 0/3 DLTs are reported. Escalation to DLs (1, 2) and (2, 1) is allowed.

2. Stage II: Two cohorts of patients are assigned to DLs (1, 2) and (2, 1). At DL (1, 2), 0/3 patients experience DLTs; therefore, escalation to DL (1, 3) is allowed. At DL (2, 1), 1/3 patients experience a DLT; therefore, de-escalation to DL (1, 1) is suggested. However, DL (1, 1) will not be explored in stage III since (1, 3) is in the list of explorable DLs.

3. Stage III: A cohort receives DL (1, 3) and 1/3 patients experience a DLT; therefore, de-escalation to DL (1, 2) is suggested. Moreover, revisit is allowed at DL (2, 1) since p₂₁ ≤ λ_r, which re-enters the list of explorable DLs.

4. Stage IV: Two cohorts of patients are assigned to DLs (1, 2) and (2, 1). For both levels, 0/3 patients experience DLTs. In total, 1/6 patients assigned to DL (2, 1) experience a DLT and stay/continue assigning patients to this DL is suggested. At DL (1, 2), 0/6 patients experience DLTs and escalation to DL (1, 3) is allowed.

5. Stage V: Two cohorts of patients are assigned to DLs (1, 3) and (2, 1). For both DLs, 0/3 patients experience DLTs. On the basis of these outcomes, escalation is allowed to DLs (2, 2) and (3, 1) and stay/continue at DL (1, 3) is suggested.

6. Stage VI: Three cohorts of patients are assigned to each of the DLs (1, 3), (2, 2), (3, 1). At DL (1, 3) and (2, 2) 1/3 patients experience a DLT, whereas at DL (1, 3) 2/9 patients experience DLTs. The maximum sample size is reached, and the trial stops.

FIG 3.

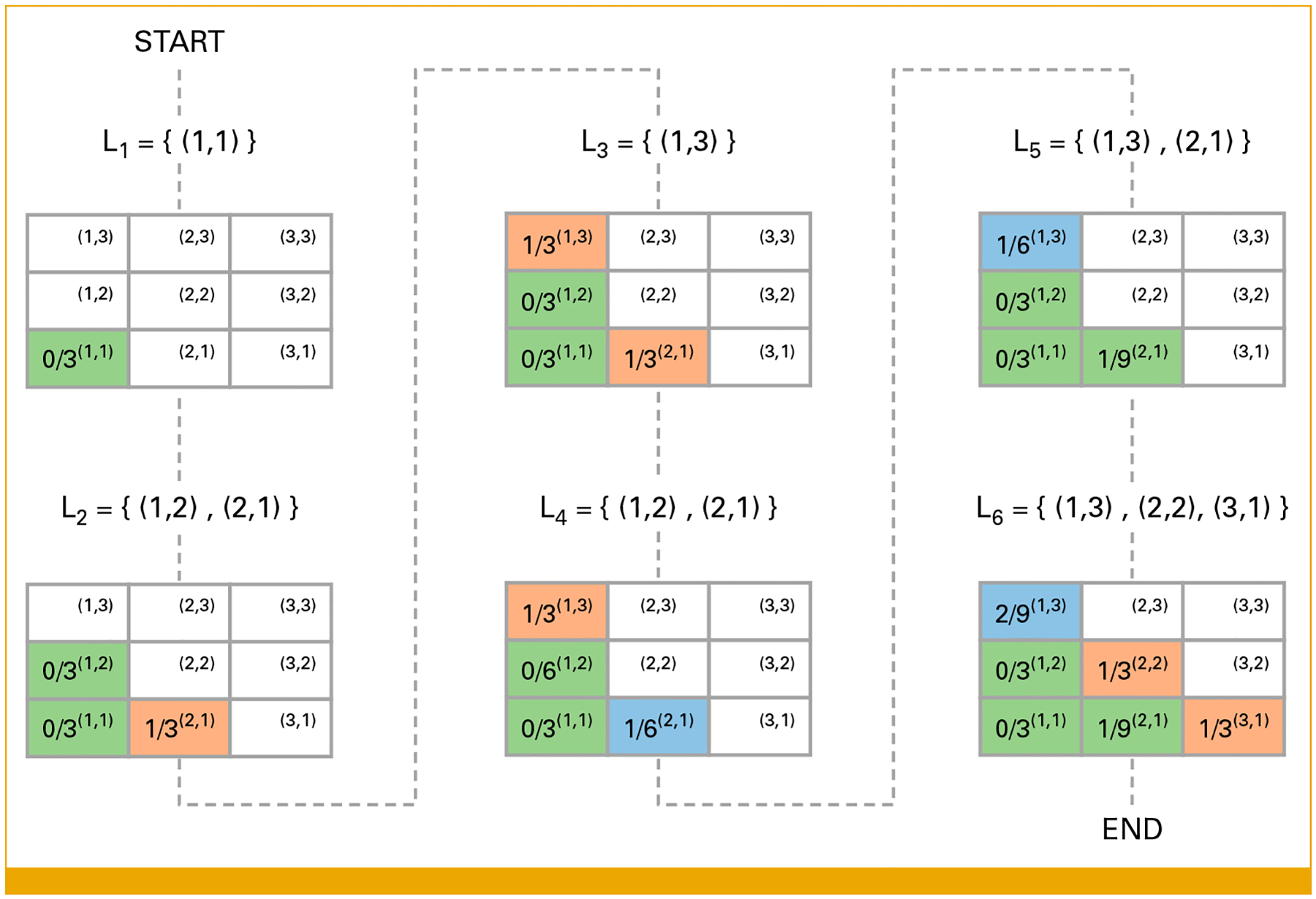
A hypothetical phase I clinical trial using the TALE design. Each table represents a stage of the trial, and the number in each cell represents the number of DLTs/number of enrolled patients. The set L_k includes all dose combinations that are assigned at stage k. DLTs, dose-limiting toxicities; TALE, Toxicity Adaptive Lists Design.

Numerical Study

We compare TALE, the dual-agent BOIN,²² the model-based COPULA,¹⁴ the continual reassessment method for partial ordering (POCRM),^21,30 and the product of independent beta probabilities escalation (PIPE)¹⁵ designs across eight simulation scenarios (Table 1). Each scenario considers five DLs for drugs A and B, resulting in 25 combinations. The maximum sample size is N = 42 patients, enrolled in 14 cohorts of n = 3 patients. For each scenario and design, we simulate 1,000 independent trials.

TABLE 1.

Toxicity Scenarios for Two-Drug Combinations

Drug A
Level	1	2	3	4	5
Drug B	Scenario 1
5	0.32	0.37	0.42	0.43	0.46
4	0.27	0.33	0.37	0.40	0.43
3	0.24	0.29	0.34	0.37	0.42
2	0.20	0.23	0.29	0.33	0.37
1	0.11	0.20	0.24	0.28	0.32
Drug B	Scenario 2
5	0.26	0.32	0.38	0.41	0.46
4	0.24	0.27	0.34	0.38	0.41
3	0.20	0.24	0.29	0.34	0.38
2	0.12	0.20	0.22	0.29	0.32
1	0.09	0.13	0.20	0.23	0.26
Drug B	Scenario 3
5	0.12	0.15	0.22	0.40	0.42
4	0.12	0.15	0.20	0.35	0.42
3	0.10	0.12	0.18	0.33	0.40
2	0.10	0.12	0.15	0.26	0.27
1	0.00	0.10	0.10	0.20	0.22
Drug B	Scenario 4
5	0.23	0.33	0.35	0.46	0.48
4	0.13	0.23	0.34	0.36	0.43
3	0.05	0.20	0.27	0.34	0.35
2	0.02	0.05	0.08	0.27	0.33
1	0.00	0.01	0.02	0.10	0.30
Drug B	Scenario 5
5	0.29	0.53	0.60	0.61	0.92
4	0.20	0.39	0.45	0.57	0.79
3	0.04	0.14	0.15	0.18	0.32
2	0.03	0.09	0.13	0.15	0.23
1	0.02	0.02	0.05	0.09	0.13
Drug B	Scenario 6
5	0.21	0.45	0.77	0.87	0.99
4	0.08	0.35	0.48	0.83	0.97
3	0.07	0.31	0.46	0.82	0.97
2	0.04	0.08	0.20	0.51	0.94
1	0.02	0.06	0.15	0.17	0.93
Drug B	Scenario 7
5	0.39	0.49	0.53	0.55	0.58
4	0.20	0.40	0.44	0.45	0.56
3	0.19	0.33	0.42	0.44	0.54
2	0.02	0.20	0.31	0.33	0.43
1	0.01	0.06	0.20	0.32	0.32
Drug B	Scenario 8
5	0.36	0.50	0.56	0.58	0.58
4	0.20	0.32	0.34	0.48	0.58
3	0.05	0.24	0.27	0.40	0.55
2	0.03	0.20	0.23	0.26	0.46
1	0	0.07	0.17	0.20	0.34

NOTE. The MTDs at 0.20 are in bold.

Abbreviation: MTDs, maximum tolerated doses.

In scenarios 1 and 2, drugs A and B share similar toxicity effects; the toxicity probability increases approximately symmetrically with drugs A and B. In scenarios 3 and 4, the toxicity probability increases markedly with the DL of drug A, whereas the toxicity effects of drug B are less pronounced. Scenarios 5–8 are randomly generated using the algorithm provided by Liu et al.²⁷

We use the following parameters for the designs:

1. TALE: We set n_max = 9, λ_e = 0.16, λ_d = 0.24, and λ_r = 0.45; see the Data Supplement (Table S2) for the corresponding numbers of DLTs. TALE uses isotonic regression and selects the highest DL with an estimated MTD below 0.2.

2. BOIN: We follow the recommendations of Lin and Yin.²² The trial stops if the number of patients assigned to a single DL reaches nine patients, and the data suggest staying at the same DL.

3. COPULA: This approach requires specifying prior probabilities of observing a DLT when drugs A and B are administered separately. In our numerical study, drugs A and B share the same single-agent probability of DLT (0, 0.05, 0.10, 0.15, 0.20, for DLs 1, …, 5). The dose escalation and de-escalation thresholds are set (default parameters) at 0.8 and 0.45, respectively.

4. POCRM: We use the default design settings with three equally probable partial orderings.^21,30 The trial stops when nine patients are assigned to the same DL.

5. PIPE: We set the safety threshold at 0.8 and prior medians equal to the target toxicity rate. Other parameters are set to their default.¹⁵

We consider the following metrics to compare trial designs:

1. The percentage of simulations a design selects an MTD with a toxicity rate of 0.2.

2. The percentage of simulations a design selects an MTD with a toxicity rate in (0.16, 0.24), a symmetric interval around the target toxicity.

3. The percentage of patients allocated at a DL with a toxicity rate of 0.

4. The average number of toxicities per trial.

5. The percentage of overdose assignments, that is, the percentage of patients receiving dose combinations with toxicity probability higher than 0.3.

6. The percentage of underdose assignment, that is, the percentage of patients receiving combinations with toxicity probability equal to or below 0.12.

Metrics a-c focus on the MTD selection accuracy, whereas metrics d-f focus on the number of toxicities during the trial.

RESULTS

Accuracy Metrics (a, b, and c)

No design outperforms the others across all scenarios and metrics (Figs 4A and 4B). COPULA performs particularly well in scenario 2, where it selects the true MTD with a frequency of 45.2% simulated trials compared with 29.8% of BOIN, 34.7% of TALE, 26.4% of PIPE, and 31% of POCRM. With metric b, PIPE has the highest accuracy in scenario 3 (30.2%) and COPULA in scenarios 2 and 4 (56.3% and 37.8%, respectively), whereas TALE has a high accuracy in scenario 1 (45.9%). COPULA allocates a higher percentage of patients at the MTDs compared with the other designs in most scenarios (Fig 4C). However, in scenario 5, it has the lowest allocation rate at 2.8%. On average, COPULA has 27.5% of the enrolled patients treated at the MTDs, against 26.9% of BOIN, 27.6% of TALE, 24.9% of POCRM, and 18.6% of PIPE. In scenario 3, TALE shows a smaller percentage of allocation around the true MTD (metric b) than the competitor designs. At the same time, the percentage of accurate selection of the MTD (metric a) and the number of patients allocated to the MTD (metric c) are closer to the other designs. This behavior can be explained by the structure of the toxicity matrix defined in Table 1, having most of the lower adjacent neighbors of the MTDs outside the interval (0.16, 0.24) considered by metric b.

FIG 4.

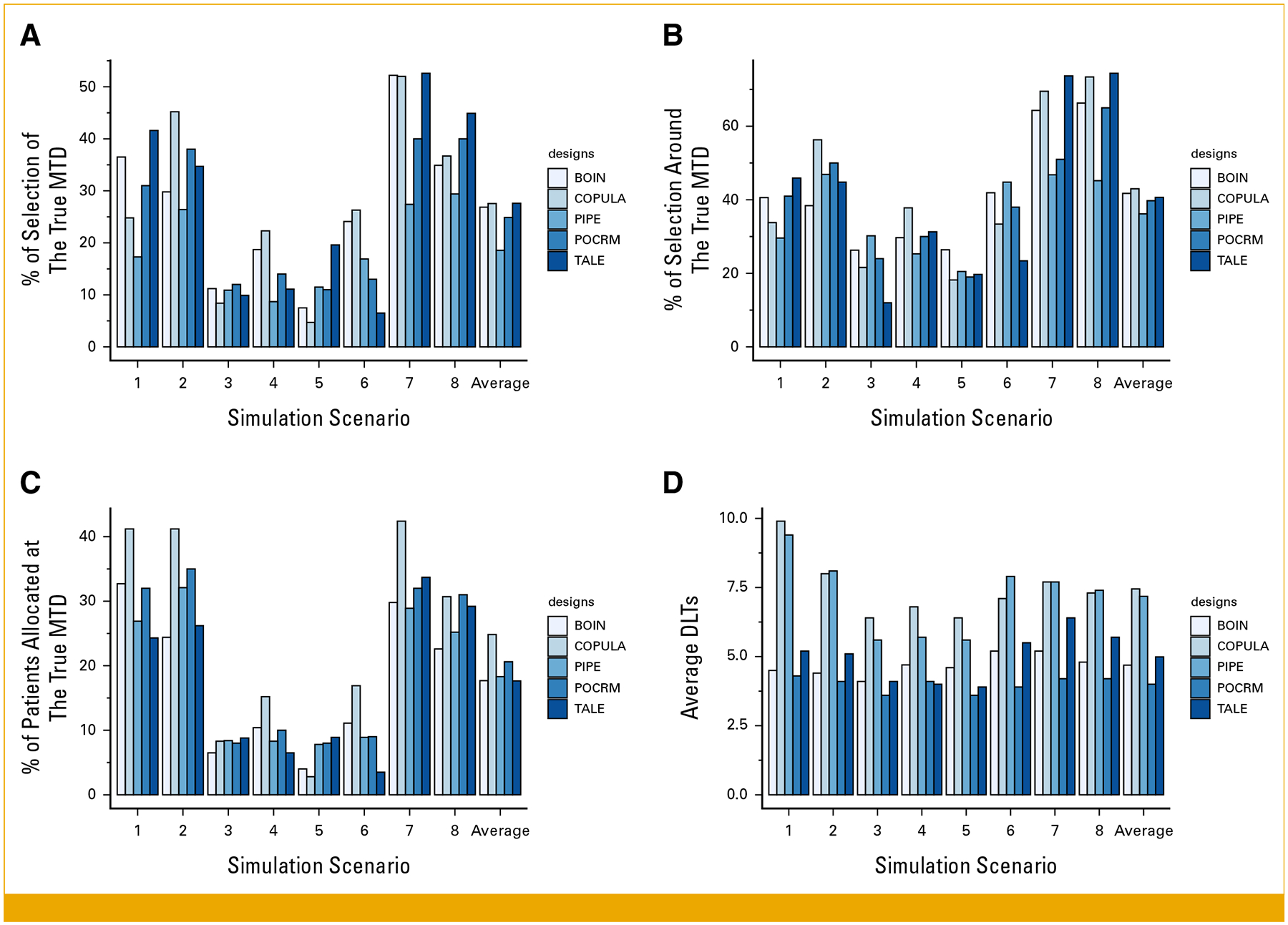
Comparison of the proposed TALE design and existing model-based or model-assisted methods. We focus on metrics a-d evaluated in scenarios 1–8. BOIN, Bayesian optimal interval design; DLTs, dose-limiting toxicities; MTD, maximum tolerated dose; PIPE, product of independent beta probabilities escalation; POCRM, continual reassessment method for partial ordering; TALE, Toxicity Adaptive Lists Design.

Toxicity Metrics (d, e, and f)

On average, COPULA and PIPE produce 3 DLTs more than BOIN, TALE, and POCRM (Fig 4D). Table 2 shows that TALE results in fewer overdose assignments (4.8% on average) than COPULA (10.8%), BOIN (11.6%), POCRM (6%), and PIPE (8.3%). In most scenarios, COPULA has the lowest percentage of patients assigned to a dose lower than 0.12 (Table 2). In scenarios 5, 6, and 7, the lowest percentage of patients assigned to a dose lower than 0.12 is provided by BOIN (14.1% of patients underdosed in scenario 5), PIPE (46.5% of patients underdosed in scenario 7), and POCRM (15% of patients underdosed in scenario 7). On average, TALE results in approximately 44% of patients being assigned to a dose with toxicity probability below 0.12, compared with 39% using BOIN, 27% with COPULA, and 32% with POCRM and PIPE.

TABLE 2.

Comparison of the TALE With Existing Model-Based and Model-Assisted Methods in Terms of the Percentage of Overdose Assignment and Percentage of Underdose Assignment (metrics e and f)

Scenario	1	2	3	4	5	6	7	8	Average
Percentage of overdose assignment
TALE	1.5	0.05	0	5.2	1.5	9.8	14.3	6.3	4.8
BOIN	4.8	2.8	4.7	12.7	11.8	22.1	24.4	9.5	11.6
COPULA	9.3	2.4	3.8	11.2	12.4	21.4	19	6.7	10.8
POCRM	5	0	1	11	6	13	5	7	6
PIPE	6.8	0.8	1.5	8.6	6.6	22.8	7.8	11.7	8.3
Percentage of underdose assignment
TALE	15.2	12.0	54.8	70.1	65.6	60	34	42.7	44.3
BOIN	33.3	37.1	44.9	52.9	14.1	53.2	37.2	40	39.1
COPULA	1.9	0.24	30.0	45.9	36.2	47.6	25	28.3	26.9
POCRM	19	12	40	47	45	49	15	30	32.1
PIPE	15.7	11.4	37.7	53.9	46.2	46.5	16.5	31.7	32.4

Abbreviations: BOIN, Bayesian optimal interval design; PIPE, product of independent beta probabilities escalation; POCRM, continual reassessment method for partial ordering; TALE, Toxicity Adaptive Lists Design.

The five designs show comparable operative characteristics in terms of accurate identification of the MTDs. TALE tends to reduce the number of DLTs and the number of patients that are assigned to DLs with toxicity above 0.3. Also, TALE allows for multiple cohorts of patients to be assigned to DLs at the same time, potentially reducing the duration of the trial.

Practical Implementation (software)

An R Shiny application³¹ that allows users to select design parameters, conduct simulation studies, and compute relevant operative characteristics is available at TALE design.³² We also provide an R package³³ at GitHub.³⁴

DISCUSSION

We introduced TALE, an algorithm-based design for oncology phase I drug combination. TALE is straightforward to implement and uses escalation and de-escalation rules that account for patients’ safety. It is extremely adaptable: one can define the size of cohorts, the target DLT rate of MTDs, the maximum number of patients treated at each DL, and the parameters that control the dose escalation and de-escalation processes. A key feature of TALE is exploring multiple DLs simultaneously, ultimately reducing the duration of the trial.

TALE categorizes DL toxicity levels using a color scale from green to red (Fig 2). From our experience (Clinical-Trials.gov identifiers: NCT05687136 and NCT04616534), these easy-to-understand categories clarify how sequential decisions are made during the trial on the basis of available data for stakeholders such as clinicians and protocol reviewers.

Our software lets users select the design parameters with simulation studies. Notably, choosing λ_d = λ_r removes the intermediate-low category. The software lets users explore different configurations of the design parameters and summarize the operating characteristics across plausible scenarios. Selecting the design parameters should account for relevant operating characteristics and other context-specific considerations. For example, users should examine the comprehensive list of data configurations that make a DL (i, j) explorable for the next stage. Importantly, TALE simplifies this task because the set of data configurations that make DL (i, j) explorable is defined only by p_ij and the toxicity rates at the neighbor DLs (Fig 2).

TALE also has some limitations. Simultaneous exploration of multiple DLs might be problematic in settings with a slow patient accrual rate. We also mention the restricted number of simulation scenarios that are illustrated for ease of presentation.

Previous studies suggested that model-based or assisted designs tend to outperform algorithm-based designs,^2,7–9 especially in terms of MTD selection accuracy. However, in our simulations, TALE demonstrated a similar accuracy in selecting MTDs as the other designs with a reduced number of patients exposed to toxic DLs.

Importantly, TALE reduces the assignment of toxic DLs and the occurrence of DLTs, resulting in an improved balance between patient safety and MTD identification accuracy and providing an attractive option for the statistical design of phase I oncology combination studies.

CONTEXT.

Key Objective

To propose a novel algorithmic approach to design phase I clinical trials for drug combinations: the Toxicity Adaptive Lists Design (TALE).

Knowledge Generated

TALE controls patients’ assignment to toxic combinations and adverse events related to therapy, providing a good balance between patient safety and accurate assessment of candidate dose levels (DLs).

Relevance

TALE is simple to implement and can simultaneously explore multiple DLs. In settings where patients’ accrual is sufficiently rapid, this translates into a shorter duration of the phase I trial compared with popular designs that explore only a single DL at the time. The design proceeds in stages, and to simplify decision making, it categorizes both DLs and toxicity rates into four groups on the basis of the observed data. At each stage of the trial, these categories are used to make decisions following an intuitive scheme.