Unveiling nodeless unconventional superconductivity proximate to honeycomb-vacancy ordering in the Ir-Sb binary system

Abstract

Vacancies in solid-state physics are underexplored in materials with strong electron-electron correlations. Recent research on the Ir-Sb binary system revealed an extended buckled-honeycomb vacancy (BHV) order. Superconductivity arises by suppressing BHV ordering through high-pressure growth with excess Ir atoms or Rh substitution, yet the superconducting pairing nature remains unknown. To explore this, we conducted muon spin rotation experiments on Ir_1−δSb (synthesized at 5.5 GPa, T_c = 4.2 K) and ambient pressure synthesized optimally Rh-doped Ir_1−xRh_xSb (x=0.3, T_c = 2.7 K). The exponential temperature dependence of the superfluid density suggests a fully gapped superconducting state exists in both samples. The ratio of T_c to the superfluid density resembles that of unconventional superconductors. A significant increase in the superfluid density in the high-pressure synthesized sample correlates with T_c, indicating that unconventional superconductivity is intrinsic to the Ir-Sb binary system. These findings, along with the dome-shaped phase diagram, highlight IrSb as the first unconventional superconducting parent phase with ordered vacancies, requiring further theoretical investigations.

Vacancies or defects are structural features of the crystal lattice that can be used to engineer the physical properties of a solid-state system, and have played an important role in the investigation of quantum materials. Here, the authors apply muon spin rotation to explore the suppression of vacancy ordering in Rh-doped Ir_1−xRh_xSb and discuss the potential presence of unconventional superconductivity in the system.

Introduction

Vacancies and defects play crucial roles in the properties of materials, and their significance is evident in various classes of materials, including transition metal dichalcogenides (TMDs)^1–5, Fe-based superconductors^6–9 and cuprate high-temperature superconductors^10–12. In transition metal dichalcogenides like MoS₂ or WSe₂, vacancies and defects can significantly influence electronic and optical properties¹. For instance, point defects such as sulfur or selenium vacancies can introduce localized states into the band gap, affecting the materials conductivity and optical absorption. Defects can serve as active sites for chemical reactions and play a role in catalysis². Defects in TMDs can also induce magnetism and lead to interesting magnetic properties^3–5.

Several studies have investigated the impact of vacancy ordering in different iron-based superconductors^6,7. For example, in iron chalcogenide superconductors such as FeSe, the ordering of selenium vacancies has been observed to influence the electronic structure and can lead to novel phenomena, including the emergence of superconductivity⁸. Understanding and controlling the role that vacancies and defects play in materials is therefore essential for tailoring their properties for specific applications. Researchers often explore the effects of defects to harness their potential benefits or mitigate undesirable consequences in various materials systems, ranging from electronics and catalysis to energy storage and superconductivity.

In this context, scientists have uncovered a distinct type of vacancy ordering in the Ir-Sb binary system Ir₁₆Sb₁₈, manifesting as an extended buckled-honeycomb vacancy (BHV) order^13,14. The system Ir₁₆Sb₁₈ has been identified as the first superconducting parent phase known to exhibit ordered vacancies. The emergence of superconductivity in Ir-Sb is closely linked to the suppression of the BHV ordering. This suppression is achieved through two distinct methods: high-pressure growth of Ir_1−δSb involving the squeezing of additional Ir atoms into the vacancies, and isovalent Rh substitution Ir_1−xRh_xSb. These interventions disrupt the ordered vacancy structure, paving the way for superconductivity. However, while the connection between vacancy ordering and superconductivity is established, the exact nature of the superconducting pairing in this system remains an intriguing aspect which has not yet been fully explored.

The comprehensive exploration of superconductivity at the microscopic level in the bulk of Ir_1−δSb and optimally doped Ir_1−xRh_xSb (x = 0.3) is therefore essential, requiring both experimental and theoretical investigations. In this context, our focus is on muon spin rotation/relaxation/resonance (μSR) measurements of the magnetic penetration depth, λ in these superconductors^15,16. This parameter is fundamental to understanding superconductivity, as it is directly related to the superfluid density, n_s through the expression, 1/λ² = μ₀e²n_s/m^* (where m^* is the effective mass). The temperature dependence of λ is particularly sensitive to the structure of the superconducting gap^15,17. Moreover, zero-field μSR proves to be a powerful tool for detecting a spontaneous magnetic field arising from time-reversal symmetry (TRS) breaking in exotic superconductors^18–21. This is particularly noteworthy as internal magnetic fields as small as 0.1 G can be detected in measurements without the application of external magnetic fields. These investigations aim to unveil the intricate details of the superconducting state in Ir_1−δSb and Ir_1−xRh_xSb, and contribute to our broader understanding of unconventional superconductivity in these materials.

We report on the fully gapped and time-reversal invariant superconducting state in the bulk of Ir_1−δSb and Ir_0.7Rh_0.3Sb. The fully gapped nature suggests a well-defined energy structure in the superconducting state, while time-reversal invariance emphasizes the preservation of fundamental symmetries in the superconducting order parameter. The zero-temperature limit of the penetration depth was evaluated to be approximately 319(7) nm and 639(10) nm for Ir_1−δSb and Ir_0.7Rh_0.3Sb, respectively. The T_c/${\lambda }_{eff}^{-2}$ ratio was found to be comparable to that of unconventional superconductors. The relatively high critical temperature (T_c) despite a small carrier density raises the intriguing possibility of an unconventional pairing mechanism in Ir-Sb binary superconductors. This observation opens avenues for further investigation into the underlying physics of superconductivity in these materials, potentially revealing mechanisms that contribute to their unique superconducting properties.

Results and discussion

The investigation into the possible magnetism, both static and fluctuating, in Ir_1−δSb and Ir_1−xRh_xSb with x = 0.3 involved zero-field muon spin relaxation (ZF-μSR) experiments conducted both above and below the critical temperature, T_c. Figure 1a and b illustrate that, down to 1.7 K, no evidence of either static or fluctuating magnetism was detected in the ZF time spectra. The ZF-μSR spectra can be well described by the Gaussian Kubo-Toyabe (GKT) depolarization function²²:

$$A_{ZF}^{\mathrm{GKT}}\left(t\right)=A_0\left(\frac{1}{3}+\frac{2}{3}\left(1-{\mathrm{\Delta }}_{ZF}^2{t}^2\right)\exp \left[-\frac{{\mathrm{\Delta }}_{ZF}^2{t}^2}{2}\right]\right)$$ 1

Here, Δ/γ_μ is the width of the local field distribution due to the presence of the dense system of nuclear moments. γ_μ = 0.085 μs⁻¹G⁻¹ is the muon gyromagnetic ratio. The inset of Fig. 1a shows the temperature evolution of Δ, which shows no enhancement across T_c. The initial asymmetry was also found to be temperature independent and remained constant throughout the analysis. The absence of any change in the ZF-μSR relaxation rate across T_c suggests the lack of spontaneous magnetic fields associated with a time-reversal symmetry (TRS) breaking pairing state in Ir_1−δSb and Ir_1−xRh_xSb with x = 0.3.

Fig. 1. Zero-field (ZF) μSR time spectra.

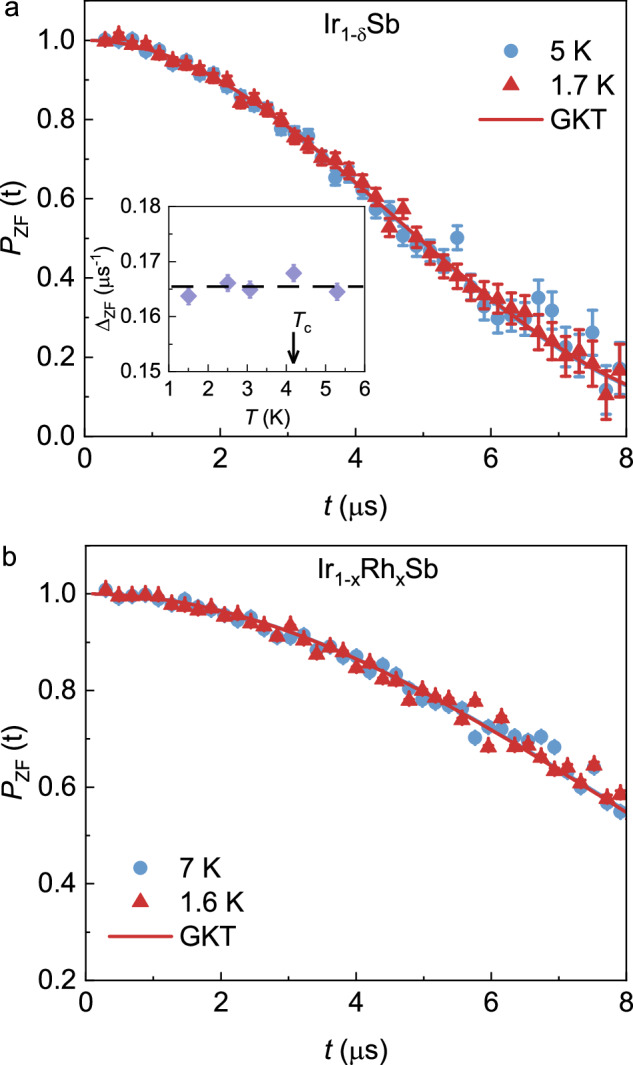
Time evolution of zero-field muon spin polarization P_ZF(t) = $A_{ZF}^{\mathrm{GKT}}\left(t\right)/A_0$, measured above and below T_c for Ir_1−δSb (a), synthesized at 5.5 GPa and for Ir_1−xRh_xSb with x = 0.3 (b). Error bars are the standard error of means (s.e.m.) in about 10⁶ events. The error of each bin count n is given by the standard deviation (s.d.) of n. The errors of each bin in P_ZF(t) are then calculated by standard error (s.e.) propagation. The solid lines represent fits to the data by means of equation (1). The inset in panel a displays the temperature dependence of the zero-field muon spin relaxation rate Δ_ZF across T_c ≃ 4.0 K.

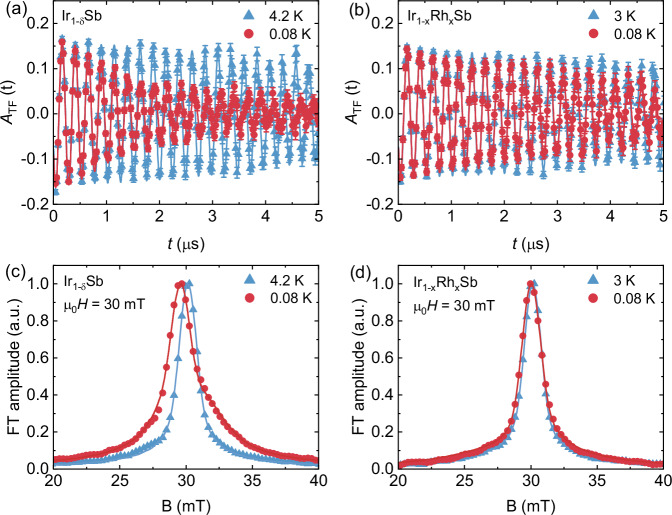
Figure 2a, b depicts the TF-μSR time spectra for Ir_1−δSb and Ir_0.7Rh_0.3Sb, respectively. These measurements were conducted in an applied magnetic field of 30 mT, both above (4 K) and below (0.08 K) the superconducting transition temperature, T_c. The measurements for Ir_0.7Rh_0.3Sb were also conducted under an applied magnetic field of 10 mT. The data were collected after field-cooling the sample from above T_C. The applied field was selected based on the criterion B_c1<B ≪ B_c2. Under this condition, a well-ordered Abrikosov vortex lattice is formed. The zero-temperature limits of B_c1 and B_c2 of Ir_1−δSb synthesized at 5.5 GPa are determined to be 28 mT and 1.19 T, respectively¹³. Consequently, the calculated Ginzburg-Landau parameter κ is estimated to be κ ≃ 6.2. For Ir_0.7Rh_0.3Sb, the zero-temperature limits of B_c1 and B_c2 are determined to be 8 mT and 0.9 T, respectively¹³. These values confirm the suitability of our applied magnetic field. Above T_c the oscillations show a small relaxation due to the random local fields from the nuclear magnetic moments. At 0.08 K, the relaxation rate increases due to the formation of a flux-line lattice (FLL) in the superconducting state, resulting in a nonuniform local field distribution. It is noteworthy that the rise in relaxation rate in the superconducting state is more pronounced in Ir_1−δSb compared to Ir_0.7Rh_0.3Sb. This distinction is further evident in the Fourier transforms (see Fig. 2c, d) of the μSR time spectra, highlighting a significant broadening of the signal in the superconducting state for Ir_1−δSb, whilst the spectra are almost identical above and below T_c in Ir_0.7Rh_0.3Sb.

Fig. 2. Transverse-field (TF) μSR time spectra and the corresponding Fourier transforms.

μSR time spectra are obtained above and below T_c in the applied magnetic field of 30 mT (after field cooling the sample from above T_c) for Ir_1−δSb, synthesized at 5.5 GPa, (a) and Ir_1−xRh_xSb with x = 0.3 (b). The corresponding Fourier transforms are shown in panel c for Ir_1−δSb, synthesized at 5.5 GPa and in panel d for Ir_1−xRh_xSb with x = 0.3. Error bars are the s.e.m. in about 10⁶ events. The error of each bin count n is given by the s.d. of n. The errors of each bin in A(t) are then calculated by s.e. propagation. The solid lines in a and b represent fits to the data by means of Eq. (2). The solid lines in c and d are the Fourier transforms of the fitted time spectra.

As denoted by the solid lines in Fig. 2a, c, TF-μSR data were analyzed using the following functional form²³:

$$A_{T{F}_s}\left(t\right)={\sum }_{i=1}^2{A}_{s,i}{e}^{\left[-\frac{\left({\sigma }_{sc,i}^2+{\sigma }_{nm}^2\right)t^2}{2}\right]}\cos \left({\gamma }_{\mu }{B}_{int,s,i}t+\phi \right).$$ 2

The field distribution in the superconducting state of the sample Ir_1−δSb synthesized at 5.5 GPa exhibits a noticeable broadening with an asymmetric line shape, as anticipated in the vortex state (see Fig. 2c). As a result, a two-component expression was utilized to accurately represent this broad and asymmetric field distribution. Conversely, the field distribution for the sample Ir_0.7Rh_0.3Sb (see Fig. 2d) in the superconducting state displays a significantly narrower width compared to Ir_1−δSb and can be adequately represented by a single-component Gaussian. In Eq. (2), A_s,i, B_int,s,i and σ_sc,i are the the initial asymmetry, the internal magnetic field at the muon site and the superconducting relaxation rates of the i-th component. σ_nm characterizes the damping due to the nuclear magnetic dipolar contribution. Since the relaxation rate remains nearly unchanged above T_c upon the application of a magnetic field, this indicates the absence of field-induced magnetism, with only nuclear magnetic moments contributing to the normal state muon depolarization rate. During the analysis σ_nm was assumed to be constant over the entire temperature range and was fixed to the value obtained above T_c. In order to extract the superconducting muon spin depolarization rate σ_sc (the second moment of the field distribution) and B_int,s (the first moment of the field distribution) from the two-component fit we used the same procedure as described in ref. ²⁴.

In Fig. 3a, σ_sc is plotted against temperature for both Ir_1−δSb, synthesized at 5.5 GPa (at μ₀H = 0.03 T), and for Ir_0.7Rh_0.3Sb (at μ₀H = 0.01 T and 0.03 T). Below T_c, the relaxation rate σ_sc begins to increase from zero due to the formation of the flux-line lattice (FLL) and saturates at low temperatures. The temperature dependence of σ_sc reflects the topology of the superconducting gap and is consistent with the presence of a single superconducting gap on the Fermi surface of these materials, as we show below. The absolute value of σ_sc is five times smaller for Ir_0.7Rh_0.3Sb compared to Ir_1−δSb, indicating a lower superfluid density for the Rh-doped sample. Below T_c, a large diamagnetic shift of B_int,s experienced by the muons is observed in both samples. In Fig. 3b, the temperature dependence of the diamagnetic shift ΔB_dia = B_int,s,SC - B_int,s,NS is plotted, where B_int,s,SC represents the internal field measured in the superconducting state, and B_int,s,NS is the internal field measured in the normal state at 5 K. This diamagnetic shift indicates the bulk nature of superconductivity and rules out the possibility of field-induced magnetism in these superconductors.

Fig. 3. Superconducting muon spin depolarization rate σ_sc and the field shift.

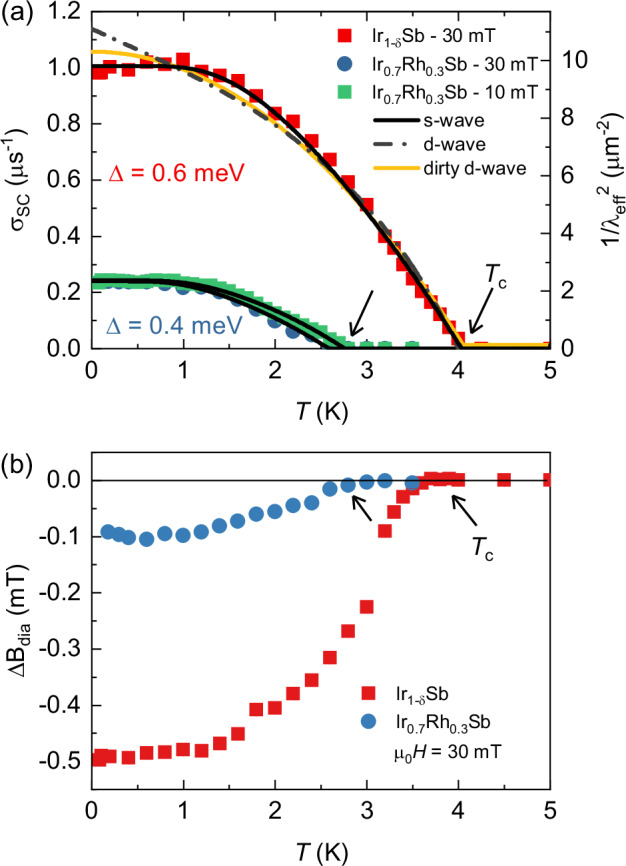
a Temperature dependence of the superconducting muon spin depolarization rate, σ_sc (left y-axis), and ${\lambda }_{\mathrm{eff}}^{-2}$ (right y-axis) measured in an applied magnetic fields of μ₀H = 10 mT and 30 mT for Ir_1−δSb, synthesized at 5.5 GPa and Ir_1−xRh_xSb with x = 0.3. b Temperature dependence of the difference between the internal field μ₀H_SC measured in the SC state and the one measured in the normal state μ₀H_NS at T = 5 K for Ir_1−δSb and Ir_1−xRh_xSb. The error bars represent the standard deviation of the fit parameters.

To perform a quantitative analysis, it is important to note that the London magnetic penetration depth, λ(T) is directly related to the measured relaxation rate in the superconducting state, σ_sc. The triangular FLL relationship is described by the equation²⁵:

$$\frac{{\sigma }_{sc}^2\left(T\right)}{{\gamma }_{\mu }^2}=0.00371\frac{{\mathrm{\Phi }}_0^2}{{\lambda }^4\left(T\right)},$$ 3

where Φ₀ = 2.068 × 10⁻¹⁵ Wb is the magnetic-flux quantum. Equation (3) is applicable only when the separation between vortices is smaller than λ. In this particular scenario, as per the London model, σ_sc becomes field-independent²⁵.

To explore the superconducting gap structure of Ir_1−δSb and Ir_0.7Rh_0.3Sb, we conducted an analysis of the temperature dependence of the magnetic penetration depth, λ(T), directly linked to the superconducting gap. The behavior of λ(T) can be characterized within the local (London) approximation (λ ≫ ξ) using the following expression^23,26:

$$\frac{{\lambda }^{-2}\left(T,{\mathrm{\Delta }}_{0,i}\right)}{{\lambda }^{-2}\left(0,{\mathrm{\Delta }}_{0,i}\right)}=1+\frac{1}{\pi }{\int }_0^{2\pi }{\int }_{\mathrm{\Delta }\left(T,\phi \right)}^{\infty }\left(\frac{\partial f}{\partial E}\right)\frac{EdEd\phi }{\sqrt{E^2-{\mathrm{\Delta }}_i{\left(T,\phi \right)}^2}},$$ 4

where $f={\left[1+\exp \left(E/k_{\mathrm{B}}T\right)\right]}^{-1}$ is the Fermi function, φ is the angle along the Fermi surface, and Δ_i(T, φ) = Δ_0,iΓ(T/T_c)g(φ) (Δ_0,i is the maximum gap value at T = 0). The temperature dependence of the gap is approximated by the expression $\mathrm{\Gamma }\left(T/T_{\mathrm{c}}\right)=\tanh \left\{1.82{\left[1.018\left(T_{\mathrm{c}}/T-1\right)\right]}^{0.51}\right\}$²⁷. while g(φ) describes the angular dependence of the gap and it is replaced by 1 for an s-wave gap, [1+acos(4φ)/(1+a)] for an anisotropic s-wave gap and $\mid \cos \left(2\phi \right)\mid$ for a d-wave gap²⁸.

In Fig. 3a, the experimentally obtained ${\lambda }_{eff}^{-2}$(T) dependence is most accurately described by a momentum-independent s-wave model with a gap value of Δ = 0.6(1) meV and T_c = 4.1(1) K for Ir_1−δSb, and a gap value of Δ = 0.4(1) meV and T_c = 2.7(2)K for Ir_0.7Rh_0.3Sb. The d-wave and p-wave gap symmetries were also considered but were found to be inconsistent with the data (illustrated by the dashed line in Fig. 3a). Particularly, these models struggle to account for the very weak temperature dependence of λ(T) at low temperatures. We note that the (p_x + ip_y) pairing symmetry is also characterized by the full gap in 2D systems and should also saturate at low temperatures. However, the possibility of p_x + ip_y pairing is excluded by the absence of a TRS breaking state. It should also be noted, though, that saturation of the muon depolarization rate at low temperatures can arise even in a nodal d-wave^29–34 superconductor, but in the dirty limit. In this case a power law $\left[1-{\left(\frac{T}{T_c}\right)}^2\right]$ temperature dependence was proposed theoretically³⁵. We tested this function but deemed it inconsistent with the data (see Fig. 3a). Therefore, our analysis shows that a nodeless or fully gapped state is the most plausible bulk superconducting pairing state for Ir_1−δSb and Ir_0.7Rh_0.3Sb. Our specific heat results down to 300 mK for Ir_1−δSb, synthesized at 5.5 GPa (see Fig. 4), measured on the same sample used for muon spin rotation experiments, show saturation at low temperatures and a large jump at T_c, providing the confirmation for bulk nodeless superconductivity.

Fig. 4. Specific heat.

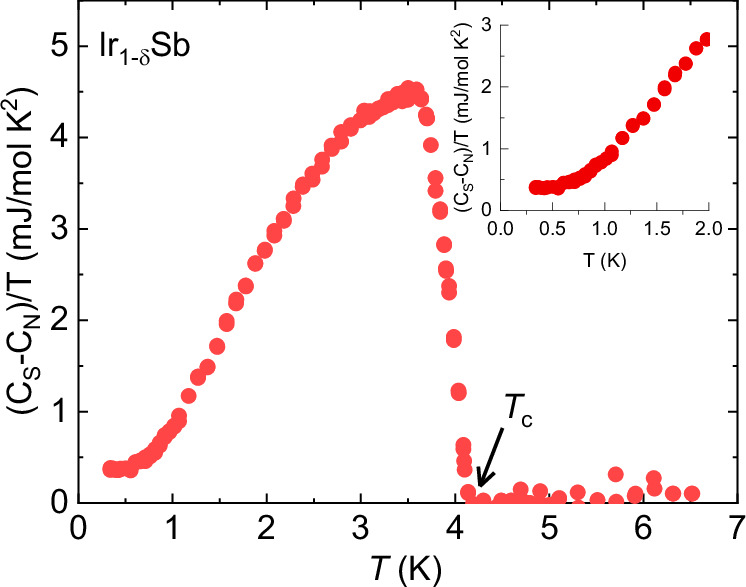
Temperature evolution of the electronic part of specific heat for the Ir_1−δSb, synthesized at 5.5 GPa. The inset shows a zoomed-out version of the low-temperature points, clearly displaying the saturation.

The estimated ratio of the superconducting gap to T_c, (2Δ/k_BT_c), is approximately 3.4, aligning with the BCS (Bardeen-Cooper-Schrieffer) expectation¹⁵. However, it’s crucial to acknowledge that a similar ratio can also be anticipated within a Bose-Einstein Condensation (BEC)-like framework. Importantly, the ratio 2Δ/k_BT_c, on its own, does not effectively distinguish between BCS or BEC condensation scenarios. Further insights are required to differentiate between these two possibilities and elucidate the nature of the superconducting state in the studied materials. What distinguishes between BCS and BEC superconductivity is a key parameter: the ratio of the superconducting critical temperature to the superfluid density. This ratio, T_c/n_s, plays a crucial role in characterizing the nature of the superconducting state in different materials. In a simplified interpretation of the BEC to BCS crossover, the T_c/n_s ratio serves as a critical parameter. Systems characterized by a small T_c/n_s (with a large superfluid density, n_s) are often considered to reside on the “BCS” side of the crossover. Conversely, systems with a large T_c/n_s (exhibiting a small superfluid density, n_s) are expected to be on the BEC side. Moreover, the correlation between T_c and the superfluid density is anticipated to be significant primarily on the BEC side of the crossover. As one moves from the BCS limit to the BEC limit in the crossover, the nature of the pairing mechanism evolves, transitioning from Cooper pairs formed through electron-phonon interactions (BCS) to a more Bose-Einstein condensation-like scenario involving preformed pairs.

The observation of a correlation between T_c and the superfluid density (${\lambda }_{eff}^{-2}$) was first noted in hole-doped cuprates back in 1988–89^36,37, extending later to include electron-doped cuprates³⁸. This intriguing relationship has been investigated across various superconducting systems. Guguchia and collaborators demonstrated that this linear correlation is an intrinsic feature in superconductors such as transition metal dichalcogenides^15,39 and kagome-lattice superconductors^20,40,41. The ratio T_c/${\lambda }_{eff}^{-2}$ in these systems tends to be lower than that observed in hole-doped cuprates (see Fig. 5). To contextualize the superconductors Ir_1−δSb and Ir_0.7Rh_0.3Sb within this framework, Fig. 5 illustrates the critical temperature plotted against the superfluid density. For Ir_0.7Rh_0.3Sb, the estimated ratio T_c/${\lambda }_{eff}^{-2}$ is approximately 1 (K/μm⁻²), closely resembling electron-doped cuprates known for their correlated superconductivity. In the case of Ir_1−δSb, the ratio is reduced to 0.4 (K/μm⁻²) but remains notably distant from conventional BCS superconductors. Intriguingly, it aligns nearly perfectly with the trend line occupied by charge density wave superconductors like 2H-NbSe₂, 4H-NbSe₂, LaRu₃Si₂, as well as the Weyl-superconductor T_d-MoTe₂¹⁵. This finding strongly suggests an unconventional pairing mechanism in Ir_1−δSb and Ir_0.7Rh_0.3Sb, characterized by a low density of Cooper pairs. It is beyond the scope of this work to comment on the microscopic origin of the similarity between Ir-Sb and other superconductors.

Fig. 5. Hallmark feature of unconventional superconductivity.

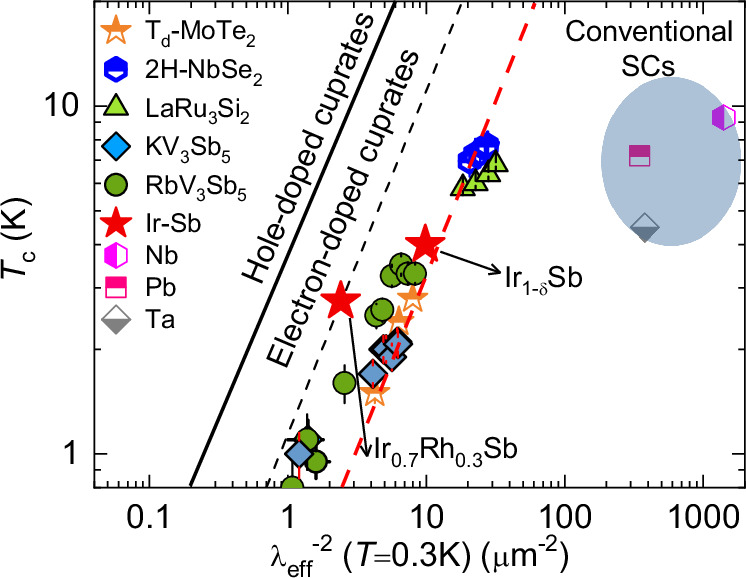
Plot of T_c versus ${\lambda }_{\mathrm{eff}}^{-2}\left(0\right)$ on a logarithmic scale obtained from μSR experiments for Ir_1−δSb, synthesized at 5.5 GPa and Ir_0.7Rh_0.3Sb. The data for the kagome-lattice superconductors KV₃Sb₅^20,21,41, RbV₃Sb₅⁴¹, and LaRu₃Si₂⁴⁶ are also included. The dashed red line represents the relationship obtained for the layered transition metal dichalcogenide superconductors, T_d-MoTe₂ and 2H-NbSe₂ by Guguchia et al.^39,40. The relationship observed for cuprates is shown^36,38 as well as the points for various conventional superconductors.

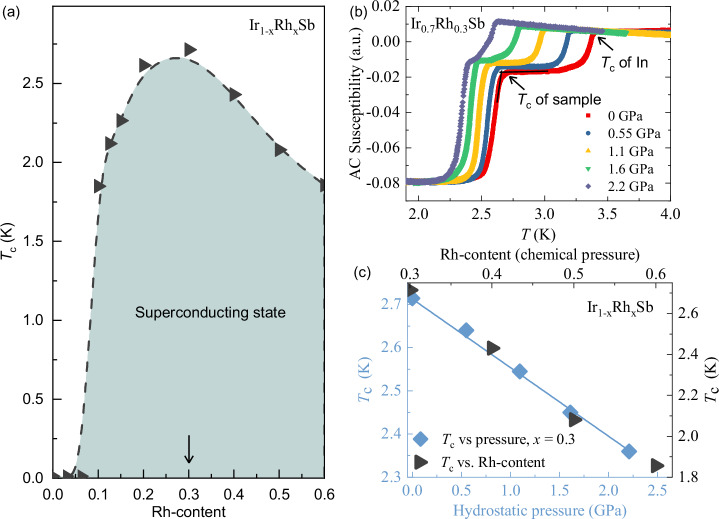
Another unconventional feature in the superconducting phase diagram of Ir_1−xRh_xSb is a dome-shaped dependence of T_c (see Fig. 6a). This pattern is characterized by an optimal T_c value occurring at x = 0.3, followed by a reduction as the Rh concentration deviates from this optimal point. The isovalent Rh substitution on the Ir site in IrSb, without introducing additional holes or electrons, creates a condition often termed “chemical pressure”. Typically, chemical substitution introduces disorder effects, potentially influencing T_c. To discern the intrinsic nature of this dome shape, a cleaner external parameter is essential. For example, hydrostatic pressure introduces fewer disorder effects compared to isovalent chemical substitutions ("chemical pressure”). For this reason, we explored the impact on T_c in the optimally Rh-doped, Ir_0.7Rh_0.3Sb with hydrostatic pressure, spanning a range up to p = 2.2 GPa. As shown in Fig. 6b, c, the observed trend revealed a linear decrease in T_c with increasing pressure. This behavior qualitatively mirrors the effect of Rh doping. The figure is intended to illustrate the linear suppression of T_c by both hydrostatic pressure and Rh content. In the manuscript, we do not provide a quantitative relationship between hydrostatic pressure and the chemical pressure induced by Rh content. Our main point is that this finding suggests the impact of both external hydrostatic pressure and chemical modifications is consistent in the Ir_0.7Rh_0.3Sb system. This underscores that the reduction in T_c beyond x = 0.3, resulting in a dome-shaped dependence, is primarily due to chemical pressure rather than disorder.

Fig. 6. Chemical and hydrostatic pressure effects on superconductivity in Ir_1−xRh_xSb.

a The superconducting critical temperature vs Rh-content, showing a dome-shaped SC phase diagram (adapted from ref. ¹³). The arrow indicates the sample with x = 0.3, which was measured under hydrostatic pressure. b The temperature dependence of AC susceptibility, measured at various hydrostatic pressures, ranging up to 2.21 GPa. c The superconducting critical temperature as a function of hydrostatic pressure and the Rh-content ("chemical pressure'') in the range between x = 0.3 and 0.6. The intention of this figure is to qualitatively illustrate the linear suppression of T_c both by hydrostatic pressure and Rh-content.

Conclusions

In summary, our study provides a microscopic exploration of superconductivity in Ir_1−δSb (synthesized at 5.5 GPa with T_c = 4.2 K) and optimally Rh-doped Ir_0.7Rh_0.3Sb (T_c = 2.7 K) in close proximity to vacancy ordering, employing a bulk sensitive local probe. Specifically, we investigated the zero-temperature magnetic penetration depth ${\lambda }_{eff}\left(0\right)$ and the temperature dependence of ${\lambda }_{eff}^{-2}$ through μSR experiments. The superfluid density in both systems aligns with a scenario of a complete gap. Intriguingly, the T_c/${\lambda }_{eff}^{-2}$ ratio is comparable to that of high-temperature unconventional superconductors, suggesting the unconventional nature of superconductivity in Ir-Sb binary superconductors. Additionally, the μSR experiments, serving as an extremely sensitive magnetic probe, do not exhibit evidence of spontaneous magnetic fields, which would be expected for a time-reversal-symmetry-breaking state in the bulk of the superconductor. Consequently, our results categorize Ir_1−δSb and Ir_0.7Rh_0.3Sb as unconventional, time-reversal-invariant, and fully gapped bulk superconductors. We further demonstrate the similarity between the effects of chemical pressure, induced by isovalent Rh substitution, and hydrostatic pressure on the superconducting critical temperature in Ir_0.7Rh_0.3Sb. This highlights that the observed dome-shaped dependence of T_c is not merely a consequence of disorder effects introduced by chemical substitution but is rooted in the intrinsic properties of the material. These results offer valuable insights into the underlying mechanisms governing the materials behavior. A more comprehensive analysis requires consideration of various factors, including the specific pairing mechanisms and the role of interactions in the superconducting state.

Methods

Sample growth and characterization

The details of the synthesis of the polycrystalline samples of Ir_1−δSb and Ir_0.7Rh_0.3Sb are reported elsewhere^13,14.

Sample characterization

A comprehensive characterization of the δ parameter was conducted in our previous publication¹³. Using an electron probe microanalyzer (EPMA), we determined the Ir deficiency in the Ir_1−δSb series, observing that the filling rate increased gradually with higher synthesis pressure. At 5.5 GPa, the δ was approximately 4%. The characterization of the basic physical properties (magnetic susceptibility, electrical resistivity, and heat capacity) for Ir_1−δSb at various synthesized external pressures and Ir_1−xRh_xSb samples is also detailed in the same publication¹³. Samples from the same batch were used in the current investigation.

Experimental details

Zero field (ZF) and transverse field (TF) μSR experiments were performed on the GPS (πM3 beamline)⁴², and high-field HAL-9500 instruments (πE3 beamline)⁴³, equipped with BlueFors vacuum-loaded cryogen-free dilution refrigerator (DR), at the Swiss Muon Source (SμS) at the Paul Scherrer Institute, in Villigen, Switzerland. Zero field is dynamically obtained (compensation better than 30 mG) by a newly installed automatic compensation device⁴². When performing measurements in zero-field the geomagnetic field or any stray fields are tabulated and automatically compensated by the automatic compensation device. The μSR time spectra were analyzed using the free software package MUSRFIT²³. AC susceptibility experiments under pressure were carried out using double wall piston-cylinder type of cell made of MP35N/MP35N material generate pressures up to 2.3 GPa^40,44,45. A small indium plate was placed together with the sample in the pressure cell filled with the Daphne oil. The pressure was estimated by tracking the SC transition of a indium plate by AC susceptibility.

Author contributions

Z.G. conceived and supervised the project. Sample Growth: Y.T. and H.H. μSR experiments, data analysis and corresponding discussions: V.S., J.N.G., D.D., C.M.III., S.S.I., R.K., H.L., and Z.G. Specific heat experiments and corresponding discussions: V.S., S.S., M.M., M.B., and Z.G. Figure development and writing of the paper: Z.G., and V.S., with contributions from all authors. All authors discussed the results, interpretation and conclusion.

Peer review

Peer review information

Communications Physics thanks James Annett and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

All relevant data are available from the authors. Alternatively, the data can be accessed through the data base at the following link http://musruser.psi.ch/cgi-bin/SearchDB.cgiusing the following details: 1. Area: HAL. Year: 2020. Run from 0107 to 0198 and from from 0294 to 0356. 2. Area: GPS. Year: 2020. Run from 0014 to 0037. Year: 2024. Run from 2004 to 2008.

Competing interests

The authors declare no competing interests.