Comprehensive comparative evaluation of the eight pediatric estimated glomerular filtration rate equations in a large Korean pediatric patient cohort

Abstract

Introduction

Although estimated glomerular filtration rate (eGFR) are continuously developed for pediatric population, impact of height measurement is often neglected due to variable dynamic growth changes in children. This study aimed to compare differential impacts of eGFR values calculated by six equations that do not use height information.

Materials and methods

3503 Korean pediatric patients with creatinine/cystatin C assay-based laboratory results from 2008 to 2021 were analyzed for clinical course using a total of 8113 laboratory test results. Baseline eGFR was calculated by eight different equations including two widely used equations incorporating height parameter. Along with the agreement of CKD (chronic kidney disease) stage categorization by different equations, clinical outcome of incident CKD diagnosis in 13 years of study period were compared.

Results

Among a total of 28 pairwise comparisons among eight equations, only 4 combinations of comparisons revealed optimal P15 values (≥80 % concordance), with FAS-age equation being both concordant with two equations using height parameter. Clustering of eight equations by incident CKD diagnosis in subsequent tests also highlighted FAS-age as candidate equation within the same cluster with Schwartz-bedside and FAS-height equations. When the equation values were classified into Kidney Disease Improving Global Outcomes (KDIGO) CKD stages, the distribution patterns for stage 1 and 5 were significantly different among eGFR equations. FAS-age equation revealed the highest agreement with Schwartz-bedside and FAS-height equations that incorporate the height data.

Conclusions

The eGFR equation type should be considered to establish the eGFR intervals for CKD stage classification, particularly in the pediatric patient population. Cautious interpretation is required for eGFR value along with clinical context.

1. Introduction

The estimated glomerular filtration rate (eGFR) equation is a good alternative for situations where gold standard glomerular filtration rate (GFR) measurements are not available [1]. As an important laboratory-based estimation for clinical decision making parameter, the clinical utility of eGFR has been widely investigated in various clinical scenarios especially focusing on the adult population [2,3]. For pediatric population, the gold standard GFR measurements are invasive and expensive to use universally, although GFR is the best indicator of renal function in children [4]. As an alternative, eGFR is widely used in the clinical practice, and the 2012 Kidney Disease Improving Global Outcomes (KDIGO) guideline recommends equation for children with chronic kidney disease (CKD) using updated bedside Schwartz equation and 1B equation. However, the 1B equation requires additional blood urea nitrogen (BUN) results [5].

Among various eGFR equations for pediatric population, the updated bedside Schwartz equation requires height information compared to the Chronic Kidney Disease-Epidemiology Collaboration (CKD-EPI) and Modification of Diet in Renal Disease (MDRD) equations commonly used in adults [6]. However, obtaining accurate height information from growing children according to standard anthropometric methodologies is often not feasible in real-world clinical practice. Accordingly, CKD-EPI equation and MDRD equation were reported to be utilized more frequently in clinical laboratories than the updated bedside Schwartz equation [7]. There is also an equation using cystatin C in the pediatric eGFR equation that does not require height information [8], but many clinical laboratories encounter obstacles while testing cystatin C due to relatively expensive cost of serum cystatin C measurement, along with a lack of standardization of the cystatin C laboratory assays. In attempt to overcome these difficulties, equations that do not require height information have been also developed, such as full age spectrum (FAS) equations [9], but they are not yet commonly used. In addition, previous evaluation data of these equations in Korean children are limited [10].

Although the measured GFR (mGFR) is theoretically recommended as the reference standard, different types of eGFR equations developed for pediatric population impute the choice of specific equation to clinicians and laboratory physicians. Currently, most of widely adopted pediatric eGFR equations have been primarily developed based on data from children in the United States and Europe, therefore data from Asian children are not adequately represented [11]. Additionally, it has been reported in several previous studies that muscle mass and renal creatinine secretion vary depending on the race [[12], [13], [14]]. Therefore, there is a need to evaluate whether various eGFR equations developed for pediatric populations are suitable for Korean children.

In this study, we aimed to evaluate the degree of agreement between different eGFR equations, including the height-independent eGFR equation and the updated bedside Schwartz equation, using real-world clinical data in a large cohort of Korean pediatric patient population.

2. Materials and Methods

2.1. Study population

The study population was defined as Korean patients aged 1- to 18-year-old who underwent both creatinine and cystatin C tests at Severance Hospital from November 1st, 2008 to October 31st, 2021. Patients with spina bifida or muscular dystrophy, who are likely to be affected by muscle mass change, were excluded. In addition, patients with height information indicating clerical errors (i.e. less than 30 cm) were excluded. Finally, 8113 test results performed in a total of 3503 patients were included in the analysis.

2.2. Measurements of serum creatinine and cystatin C concentrations

Serum creatinine was measured by compensated Jaffe method on Hitachi 7600 platform (Daichi, Tokyo, Japan) for the period 1 (before May 2019) and on Atellica CH platform (Siemens, Erlangen, Germany) for the period 2 (after May 2019). Serum cystatin C was measured by immunoturbidimetric assay on Cobas e601 platform (Roche Diagnostics GmbH, Mannheim, Germany) for the period 1 (before May 2019) and on Cobas c702 platform (Roche) for the period 2 (after May 2019). Atellica CH platform was equipped with Crea_2 reagent and CH CHEM Calibrator, which is traceable to both NIST SRM 967 and IDMS method. As for Hitachi 7600, duplicate comparison tests were performed with 40 random patient samples to ensure that the platform has sufficient correlation with Atellica CH platform. The reagent for cystatin C measurement, Tina-quant Cystatin C Gen.2 (Roche), is traceable to the international calibrator standard ERM-DA471/IFCC, and was calibrated to 6-point curve using C.F.A.S. cystatin C calibrator (Roche).

During both periods with different assay measurement platforms for serum creatinine and cystatin C measurements, internal quality control of both analytes in the laboratory was comprehensively performed and showed excellent analytical performances.

2.3. Application of eGFR equations

A total of 8 eGFR equations designed for pediatric population were included in this study (Table 1): Schwartz-bedside [15], Schwartz-cysC [8], FAS-age [9], FAS-height [16], FAS-cysC [17], FAS-combi [17], Berg [18], CAPA [19]. Among these equations used, the equations that require height information are Schwartz-bedside and FAS-height.

Table 1.

eGFR equations evaluated in this study.

Schwartzbedside	eGFR = k × L/SCr in which k is 0.413, L represents height in cm, and SCr is expressed in mg/dL
SchwartzcysC	eGFR = 70.69 × (cysC−0.931)
FASage	eGFR = 107.3∕(SCr/Qage), in which Qage = 0.21 + 0.057 × Age − 0.0075 × Age2 + 0.00064 × Age3 − 0.000016 × Age4 for males and Qage = 0.23 + 0.034 × Age − 0.0018 × Age2 + 0.00017 × Age3 − 0.0000051 × Age4 for females
FASheight	eGFR = 107.3∕(SCr/Qheight), in which Qheight = 3.94 − 13.4 × L + 17.6 × L2− 9.84 × L3+ 2.04 × L4, in which L represents height in meters for males and females
FAScysC	eGFR = 107.3/(cysC/QcysC), with QcysC 0.82
FAScombi	eGFR = 107.3/(α × (SCr/Qage) + (1 − α) × (cysC/QcysC)), with QcysC 0.82 and α set at 0.5. Qage: 0.21 + 0.057 × Age −0.0075 × Age2 + 0.00064 × Age3 − 0.000016 × Age4 for males 0.23 + 0.034 × Age − 0.0018 × Age2 + 0.00017 × Age3 − 0.0000051 × Age4 for females
Berg	eGFR = 91 × cysC−1.213
CAPA	eGFR = 130 × (cysC−1.069) × (age−0.117) − 7

Serum creatinine (SCr in mg/dL, if not specified otherwise. Serum cystatin C (cysC) in mg/L. Height (L) in meter (m), weight in kg, and age in year. FAS full age spectrum, CAPA Caucasian, Asian, pediatric, and adult.

2.4. Statistical analysis

For the comparative evaluation among eGFR values calculated by 8 different equations, Pearson correlation coefficient (r) was calculated for each combination of two equations. Slope and intercept analyzed by Passing-Bablok regression with 95 % confidence interval (CI) along with Pearson correlation coefficients were examined.

Statistically significant differences between two equations from a combination of 28 comparisons were calculated using a paired sample t-test. The statistical significance threshold was set to P < 0.05 with Bonferroni correction for multiple comparisons. Additionally, grouping by the KDIGO CKD stages was applied to calculate the categorical agreement between eGFR values calculated by different equations. The agreement rates between two equations were determined using kappa statistics. Furthermore, P15 and P30 values were calculated for 28 pairwise comparisons referring to the percentage of the total sample who had an eGFR values within 15 % and 30 % of their presumably reference eGFR, which was proved to be useful for diagnostic accuracy evaluation for eGFR equations. For relatedness comparison of eight eGFR equations for diagnosis of incident CKD, which was defined as consecutive eGFR values lower than 60 ml/min/1.73 m² in a longitudinal follow-up evaluation, K-means clustering analysis were performed using discordant eGFR results among eight equations.

All data were analyzed using Analyse-it (Analyse-it Software Ltd., Leeds, UK), Microsoft Excel 2016 (Microsoft, Redmond, WA), R studio software, and SPSS 25 (SPSS, Chicago, IL, USA).

3. Results

3.1. Basic characteristics of study participants and laboratory results

A total of 3503 pediatric patients were enrolled in this study, among which 42 % were female (Table 2). Median (1st–3rd quartile) age was 8.2 years (3.8–13.6). Median height and weight were 125.0 cm (99.0–155.0) and 26.0 kg (15.5–47.0), respectively. A total of 4619 samples from 2026 men and 3494 samples from 1477 women were included in the investigation (Supplementary Fig. 1). 2046 patients had multiple laboratory tests including both creatinine and cystatin C which were performed during a 13-year study period. The median interval of the shortest follow-up period between two laboratory test performed in 2046 patients was 35 days.

Table 2.

Demographics of the study population with laboratory result distribution of study samples.

	Total	Male	Female
Number of patients	3503	2026	1477
Age, years	8.2 (3.8–13.6)	7.7 (3.5–13.7)	8.6 (4.4–13.5)
Height, cm	125.0 (99.0–155.0)	123.0 (96.6–162.0)	126.9 (102.0–150.0)
Weight, kg	26.0 (15.5–47.0)	25.0 (15.1–51.0)	26.5 (16.0–43.1)
Number of samples	8113	4619	3494
Serum creatinine, mg/dL	0.49 (0.35–0.80)	0.50 (0.34–0.82)	0.49 (0.35–0.76)
Serum cystatin C mg/L	0.97 (0.82–1.37)	0.97 (0.83–1.31)	0.96 (0.80–1.49)

3.2. Comparative evaluation of 8 eGFR equations

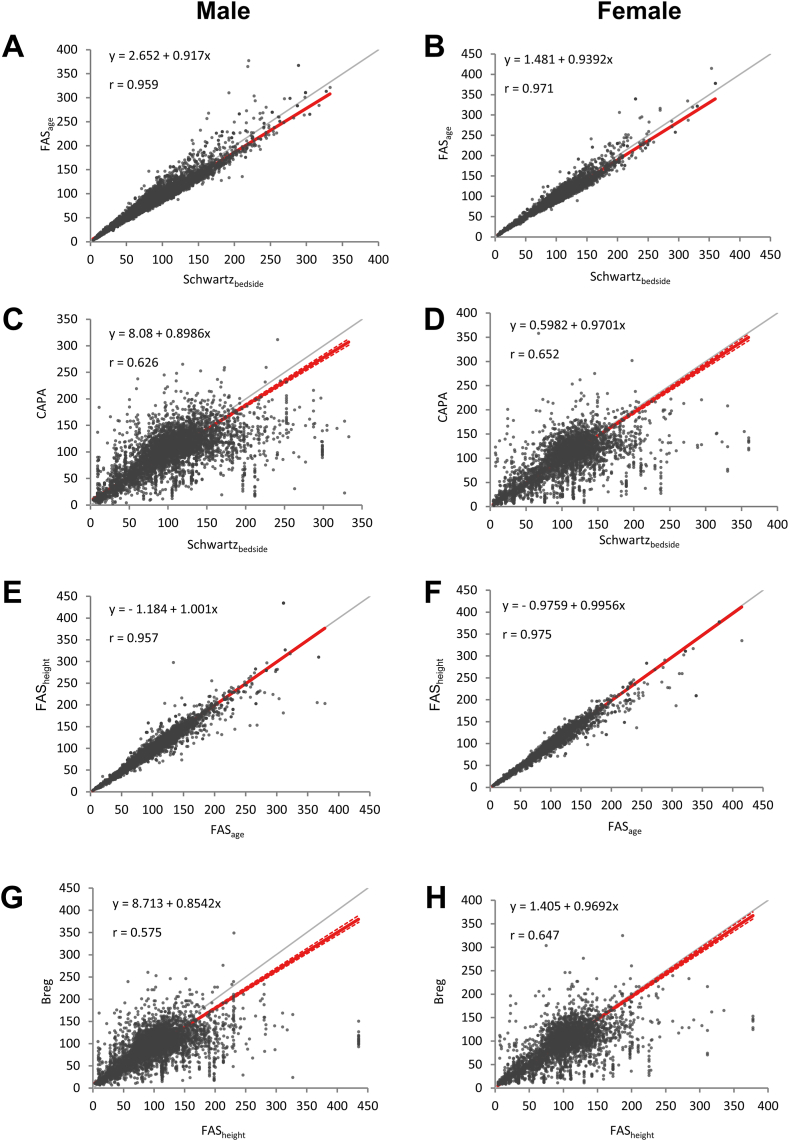
When comparison between a total of 28 pairwise combinations among the 8 eGFR equations was performed (Table 3), the range of slope and R values ranged between (0.4538–2.076) and (0.536–1.000), respectively. In the comparison between Schwartz-bedside and FAS-height, which are two equations using height information, good correlations were observed with R values of 0.961 for boys and 0.991 for girls. Compared with Schwartz-bedside and FAS-height, the equation without height information showing the best slope of the regression model to 1 was FAS-age. The slope of regression model between Schwartz-bedside and FAS-age was 0.92 (r = 0.959) for boys and 0.94 (r = 0.971) for girls, and between FAS-height and FAS-age was 1.00 (r = 0.958) for boys and 1.00 (r = 0.975) for girls. Furthermore, subgroup analyses according to age groups in both genders also presented equivalent comparability of FAS-age when compared with Schwarz-bedside and FAS-height (Supplementary Tables 1 and 2).

Table 3.

Comparison between the eight eGFR equations.

	Schwartzbedside	SchwartzcysC	FASage	FASheight	FAScysC	FAScombi	Berg	CAPA
Male
Schwartzbedside	–
SchwartzcysC	y = 23.63 + 0.4538x r = 0.643	–
FASage	y = 2.652 + 0.917x r = 0.959	y = - 47.12 + 2.076x r = 0.600	–
FASheight	y = 1.652 + 0.9211x r = 0.961	y = - 46.79 + 2.059x r = 0.583	y = - 1.184 + 1.001x r = 0.957	–
FAScysC	y = 23.28 + 0.6286x r = 0.641	y = - 6.364 + 1.337x r = 1.000	y = 21.35 + 0.6726x r = 0.599	y = 21.76 + 0.6766x r = 0.582	–
FAScombi	y = 16.76 + 0.7282x r = 0.878	y = - 11.23 + 1.463x r = 0.893	y = 14.31 + 0.7883x r = 0.868	y = 14.89 + 0.7863x r = 0.833	y = - 3.21 + 1.085x r = 0.890	–
Berg	y = 10.92 + 0.791x r = 0.635	y = - 26.82 + 1.677x r = 0.996	y = 8.201 + 0.8517x r = 0.594	y = 8.713 + 0.8542x r = 0.575	y = - 17.98 + 1.244x r = 0.998	y = - 11.65 + 1.126x r = 0.884	–
CAPA	y = 8.082 + 0.8986x r = 0.626	y = - 26.97 + 1.777x r = 0.965	y = 5.077 + 0.9641x r = 0.541	y = 6.092 + 0.9665x r = 0.536	y = - 16.11 + 1.357x r = 0.916	y = - 11.67 + 1.287x r = 0.800	y = 0.2994 + 1.096x r = 0.912	–
Female
Schwartzbedside	–
SchwartzcysC	y = 15.92 + 0.5277x r = 0.673	–
FASage	y = 1.481 + 0.9392x r = 0.971	y = - 27.21 + 1.785x r = 0.621	–
FASheight	y = 0.555 + 0.9358x r = 0.991	y = - 27.23 + 1.766x r = 0.658	y = - 0.9759 + 0.9956x r = 0.975	–
FAScysC	y = 13.73 + 0.723x r = 0.671	y = - 6.134 + 1.335x r = 1.000	y = 12.59 + 0.7719x r = 0.619	y = 13.2 + 0.7791x r = 0.656	–
FAScombi	y = 10.31 + 0.7907x r = 0.881	y = - 7.081 + 1.394x r = 0.915	y = 8.893 + 0.8457x r = 0.854	y = 9.906 + 8481x r = 0.873	y = - 1.154 + 1.049x r = 0.909	–
Berg	y = 2.217 + 0.8967x r = 0.662	y = - 25.7 + 1.668x r = 0.996	y = 0.6752 + 0.9608x r = 0.611	y = 1.405 + 0.9692x r = 0.647	y = - 17.58 + 1.244x r = 0.998	y = - 13.03 + 1.159x r = 0.902	–
CAPA	y = 0.5982 + 0.9701x r = 0.652	y = - 20.99 + 1.679x r = 0.975	y = - 1.354 + 1.033x r = 0.574	y = - 0.2141 + 1.042x r = 0.625	y = - 13.6 + 1.271x r = 0.949	y = - 12.81 + 1.243x r = 0.849	y = - 0.7514 + 1.052x r = 0.946	–

CAPA and Berg also showed the slope of the regression model close to 1, in comparison with Schwartz-bedside and FAS-height; their regression slopes were similar to FAS-age, but there were differences in Pearson correlation coefficients (Fig. 1). Finally, the results were corrected for multiple repeated measurements per patient to demonstrate similar correlations (Supplementary Fig. 2).

Fig. 1.

Correlation between various equations in different genders.

Compared to Schwartz-cysC, FAS-cysC, Berg, CAPA equations using Cystatin C and FAS-combi equation using creatinine and cystatin C, there was a high degree of agreement between equations using creatinine, but not between equations using cystatin C (Table 3). The eGFR value of the equation using cystatin C was always lower than that of the equation using creatinine. Compared with Schwartz-bedside, the highest degree of agreement among the eGFR values of the cystatin C-based equation was CAPA and the lowest was Schwartz-cysC.

Apart from various equations above, there are other candidate equations proposed recently, including the cystatin C-based equation from Schwartz group updated in 2021 [20]. When we have compared the FAS-age equation to the 2021 version of cystatin C-based Schwartz equation, good correlation between two equations were observed (Supplementary Fig. 3).

3.3. Clinical impact of different eGFR equation values on CKD stage classifications

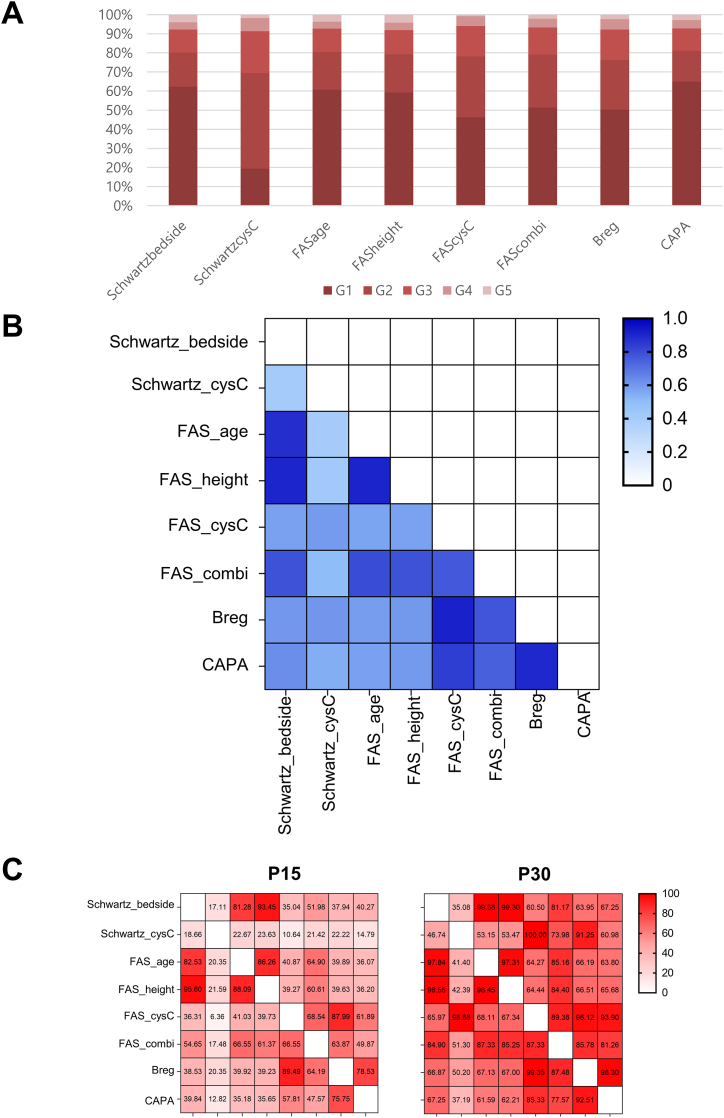
When the values of the eGFR equations were classified into KDIGO CKD stages, Schwartz-cysC showed a tendency to calculate the eGFR value low (Fig. 2A). Interestingly, Schwartz-bedside, FAS-age, and FAS-height equations presented similar distribution trends for 5 stage distributions among the study population. Additionally, Schwartz-CysC presented the largest proportion of stage G2, accounting for 41 %.

Fig. 2.

(A) Classification of the values of the eGFR equations according to the KDIGO CKD stages. (B) Agreement analysis among 8 equations using kappa statistics. (C) Percent agreement results by P15 and P30 values calculated in a total of 28 comparison pairs.

According to agreement analysis results, two clusters of similar eGFR equations were detected with kappa values over 0.8 (Fig. 2B); cluster 1 with FAS-age, FAS-height, Schwartz-bedside, and cluster 2 with FAS-cysC, Berg, CAPA. P15 and P30 values among 28 pair comparison also presented highest agreement percentages among Schwartz-bedside, FAS-age, and FAS-height equations (Fig. 2C).

3.4. Dynamic changes of different eGFR equation values in pediatric patients

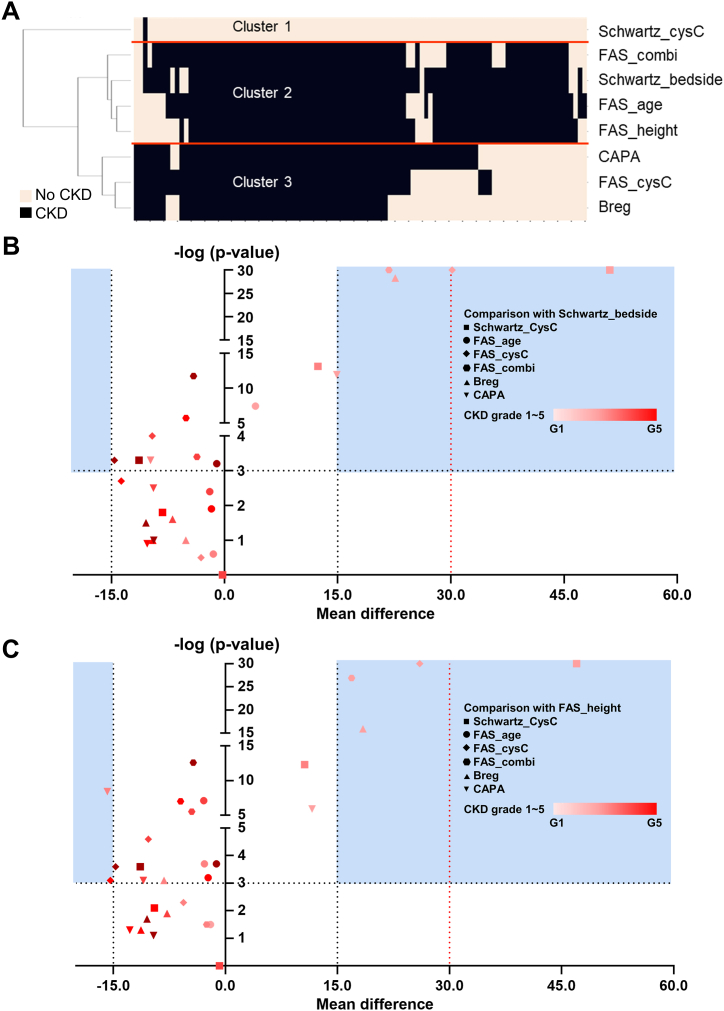
To evaluate real-world clinical impact in a setting of follow-up monitoring by eGFR values, dynamic changes of eGFR values in the same patients were separately analyzed to evaluate the performance of incident CKD detection, which was defined as two consecutive eGFR values below 60 mL/min/1.73 m² within two months. Subgroup clustering analysis using 100 patients with at least one discrepant results revealed 3 major clusters among 8 eGFR equations: cluster 1 with Schwartz-cysC; cluster 2 with Schwartz-bedside, FAS-height, FAS-age, and FAS-combi; cluster 3 with FAS-cysC, Berg, and CAPA (Fig. 3A). Notably, FAS-age and FAS-combi equations presented closest association with equations incorporating height information (i.e. Schwartz-bedside and FAS-height).

Fig. 3.

Comparative analysis of 8 eGFR equations using clustering analysis (A) and volcano plot analysis (B, C) (A) Dendrogram analysis by incident CKD detection (i.e. two consecutive eGFR <60 mL/min/1.73 m² within two months). by individual equations. (B) Pairwise comparison of eGFR values calculated by each equation against Schwartz_bedside as the reference values using paired T-test. X axis represents the mean differences of eGFR calculated values between the corresponding equation and the Schwartz-bedside. Y axis represents the –log(p-value) derived from paired T-test between the corresponding equation and the Schwartz-bedside. P-value <0.001 corresponds to –log(p-value) > 3.0 as the cut-off value for statistical significance interpretation. (C) Pairwise comparison of eGFR values calculated by each equation against FAS_height as the reference values using paired T-test. X axis represents the mean differences of eGFR calculated values between the corresponding equation and the FAS-height. Y axis represents the –log(p-value) derived from paired T-test between the corresponding equation and the Schwartz-bedside. P-value <0.001 corresponds to –log(p-value) > 3.0 as the cut-off value for statistical significance interpretation.

Furthermore, eGFR values in discrepant incident CKD diagnosis patients were compared in a pairwise comparison with putative reference values by Schwartz-bedside and FAS-height according to CKD stages, since two equations incorporate height information as clinically relevant parameter. Although lower CKD stages presented largest mean differences in all equations, FAS-age results showed least mean differences with negative biases (Fig. 3B and C).

4. Discussion

Pediatricians confront various obstacles when attempting to utilize GFR as a standard in clinical setting. Renal inulin clearance is the gold standard for GFR measurement, but repeated urine sampling is more difficult in children. In addition, repeated use of radioisotopes is not ideal in children [1]. eGFR is used as an alternative, but the recommended equation for children, the updated bedside Schwartz, incorporates height value which dramatically changes as children grow and may not be measured together with the blood test. There may also be a possibility of a clerical error if the results are entered manually. In clinical laboratories in Korea, CKD-EPI and MDRD equations are being reported more frequently as pediatric eGFR equations rather than updated bedside Schwartz equations due to limitations in accurate height information acquisition [7]. However, the eGFR values of the CKD-EPI and MDRD equations are neither reliable nor accurate in children [21].

In this study, we aimed to identify the best alternative equation in the absence of height information through comprehensive comparison between various eGFR equations in Korean pediatric patient population using a large retrospective cohort. As expected, the agreement between the Schwartz-bedside and FAS-height equations, which are equations using height information, showed a higher degree of agreement than the comparison between other equations, confirming that height information is indeed an important parameter for the accurate calculation of eGFR especially in pediatric population. Interestingly, FAS-age presented the highest agreement with both Schwartz-bedside and FAS-height among equations using clinical parameters other than height.

There have been previous studies comparing the values of Schwartz-bedside and FAS-height equations with mGFR, but it is unclear which of the two equations is more accurate. In a study of pediatric cancer patients, the FAS-height equation was superior to the Schwartz-bedside equation [10]. Other studies have shown that the Schwartz-bedside equation is better in children with renal disease and the FAS-height equation is better in healthy children, as the formulas were originally designed in according populations [22].

Interestingly, this study also revealed differential results calculated by creatinine and cystatin C in pediatric patient population, which was also investigated in adult CKD and cancer patients [23,24]. When compared to the creatinine-based equation, the eGFR values of the cystatin C-based equation were lower in all equations, although there were differences in bias degrees. When the eGFR value is obtained with the cystatin C-based equation, it is highly recommended to pay attention to the possibility that it might be underestimated compared to mGFR. For the gender effect studied in this study, the degree of agreement between the eGFR equations was higher in girls than in boys. Since the serum creatinine and cystatin C are differentially affected by sex [[25], [26], [27]], high degree of agreement between the eGFR equations is possibly explained in girls.

As the distributions of eGFR values by various equations are different especially when five CKD stage classification according to KDIGO guideline was applied, it is important for clinicians to cautiously decide the appropriate eGFR equation when setting the reference range and apply CKD stage classification in target population. One of the diagnostic criteria for CKD, which involves the persistence of structural or functional abnormalities in the kidneys for more than three months, is a GFR less than 60 mL/min/1.73 m² [28]. As a result of comparing various eGFR equations, there were differences in the diagnosis of CKD among the equations. This suggests that the choice of eGFR equation can have an impact on the diagnosis and treatment of patients, depending on which equation is used. Notably, the rate of CKD diagnosis was higher in the creatinine-based equations compared to cystatin C-based equations.

When comparing the Schwartz-bedside equation and the FAS-height equation, which use height and creatinine information, with other equations, the FAS-age and FAS-combined equations exhibited minimal differences in values with high significance. It is likely that these two equations, which are based on creatinine values and were developed by the same researchers as the FAS-height equation, share similarities based on the developmental background. On the other hand, according to a recent study that compared six eGFR equations with mGFR in a group of children, discrepancies were found in all the equations, and the need for equation improvement was suggested, particularly in children who presented normal renal function [29]. These previous findings are consistent with our results, where it was observed that in the same equation, the significance was lower and the differences in values were larger as the stage of CKD decreased. This result highlights that biases due to eGFR equation differences are also affected by studied population, especially when normal and patient pediatric population are separately investigated.

The limitations of this study was absence of mGFR value directly measured through an extrinsic substance. Although two pediatric eGFR equations incorporating the height information were regarded as presumable reference equations, the accuracy of the Schwartz-bedside and FAS-height equations using height information was difficult to evaluate in this study. Another shortcoming of this study is that the serum creatinine level had to be measured by compensated Jaffe assay, which has been demonstrated to be an inferior method than enzymatic assays in pediatric populations.

In conclusion, the FAS-age equation could be considered as an alternative in the Korean children without height information since the FAS-age equation revealed the highest agreement with Schwartz-bedside and FAS-height equations. Compared to the creatinine-based equation, the cystatin C-based equations present a lower value, suggesting the cautious interpretation of the eGFR value may be required along with clinical context.

CRediT authorship contribution statement

Jeongyun Bae: Writing – original draft, Visualization, Software, Formal analysis, Data curation. Hanmil Jang: Writing – review & editing, Visualization, Validation, Formal analysis, Conceptualization. Jaehyeok Jang: Methodology, Investigation. Kwang Seob Lee: Visualization, Validation, Software. Hyein Kang: Validation, Supervision, Resources. John Hoon Rim: Writing – review & editing, Supervision, Project administration, Funding acquisition, Formal analysis, Conceptualization. Jong-Baeck Lim: Validation, Supervision, Project administration, Conceptualization.

Data availability statement

Data will be made available on request. In other words, the data that support the findings of this study are available on request to the corresponding author, JHR. The original data can be provided after the approval of the Ethics Committee of Yonsei University College of Medicine.

Ethical approval statement

This study was conducted according to the Declaration of Helsinki and was approved by the Institutional Review Board of Yonsei University Health System (IRB no. 4-2021-1388). The written informed consent was waivered as the study meets all following requirements.

• 1)The risk of participants does not exceed the minimum level of risk, as this study only utilizes the remnant serum samples after routine test procedures.
• 2)The written informed consent waiver does not infringe on participants' right and welfare; this study followed strict procedures of anonymizing information of each sample.
• 3)The study cannot be practically conducted without written informed consent waiver.
• 4)If requested, the participant will be provided with additional information related to the study.
• 5)The study is not controlled by MFDS/US-FDA regulations.

Funding

This research was supported by a grant of the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health and Welfare, Republic of Korea (grant number: HI22C103500).

Declaration of competing interest

Authors declare no conflict of interest.

Appendix A. Supplementary data

The following is the supplementary data related to this article: