Abstract
Identification of the breathing cycle forms the basis of any breath-by-breath gas exchange analysis. Classically, the breathing cycle is defined as the time interval between the beginning of two consecutive inspiration phases. Based on this definition, several research groups have developed algorithms designed to estimate the volume and rate of gas transferred across the alveolar membrane (“alveolar gas exchange”); however, most algorithms require measurement of lung volume at the beginning of the ith breath (VLi−1; i.e., the end-expiratory lung volume of the preceding ith breath). The main limitation of these algorithms is that direct measurement of VLi−1 is challenging and often unavailable. Two solutions avoid the requirement to measure VLi−1 by redefining the breathing cycle. One method defines the breathing cycle as the time between two equal fractional concentrations of lung expired oxygen (Fo2) (or carbon dioxide; Fco2), typically in the alveolar phase, whereas the other uses the time between equal values of the Fo2/Fn2 (or Fco2/Fn2) ratios [i.e., the ratio of fractional concentrations of lung expired O2 (or CO2) and nitrogen (N2)]. Thus, these methods identify the breathing cycle by analyzing the gas fraction traces rather than the gas flow signal. In this review, we define the traditional approach and two alternative definitions of the human breathing cycle and present the rationale for redefining this term. We also explore the strengths and limitations of the available approaches and provide implications for future studies.
Keywords: cardiopulmonary exercise testing, gas exchange, gas exchange kinetics, lung gas stores, respiratory cycle
INTRODUCTION
Identification of the breathing cycle forms the basis of the quantitative analysis of alveolar breath-by-breath (B-by-B) gas exchange (1, 2). Classically, the breathing cycle is identified by analyzing the gas flow signal from a flowmeter, where the zero-crossing points represent the transition between inspiratory and expiratory phases, and vice versa. The gas flow, together with the gas fractions, is generally collected at the mouth and used to estimate alveolar gas exchange on a B-by-B basis. However, accurate and reliable estimation of gas transfer across the alveolar membrane (V̇o2A and V̇co2A) requires changes in B-by-B lung gas stores to be known (2).
Several research groups have developed algorithms and methods to estimate the B-by-B alveolar gas exchange; however, most algorithms require knowledge of the absolute lung volume at the beginning of the ith breath (VLi−1; i.e., the end-expiratory lung volume of the preceding ith breath) (3–8). Because of the technical complexity of measuring VLi−1, it is generally estimated rather than measured directly (9, 10). However, different values of VLi−1 lead to different B-by-B alveolar gas exchange estimations (11). In addition, VLi−1 is not stable during exercise (7, 12) and is affected by body position (13) and exercise modality (e.g., walking, running, and cycling) (14). Therefore, the validity of these techniques depends largely on the validity of the VLi-1 measurement.
Grønlund (15) conceived an ingenious solution to overcome the issues related to the determination of VLi−1; however, this solution required redefining the breathing cycle. In Grønlund’s algorithm, a single breathing cycle is identified between two points on successive, but not necessarily consecutive, breaths with the same fractional concentration (or partial pressure) of lung O2 (or CO2) occurring typically in the alveolar phase (Fo2 or Fco2). Intrabreath integration of gas flow and concentration fractions is performed between these two points, allowing the estimation of alveolar gas exchange without the need for VLi−1 measurement (see Different Definitions of the Breathing Cycle in the B-By-B Gas Exchange Analysis for further details). A modification of this technique has been proposed by Cettolo and Francescato (16) that also eliminates the need to measure VLi−1, but uses a different redefinition of the breathing cycle. This algorithm (16) defines the breathing cycle as the time interval elapsed between two successive, but not necessarily consecutive, breaths with the same fractional concentration of lung O2/N2 (or CO2/N2) ratio, typically in the alveolar phase (Fo2/Fn2 or Fco2/Fn2). Therefore, these two techniques use gas fractional concentration signals instead of gas flow signals to define the breathing cycle (Table 1).
Table 1.
General definition of breathing cycle (in the time domain) when using classic (VLi−1-based algorithms), Grønlund, and Cettolo and Francescato algorithms to estimate alveolar gas transfer
|
VLi−1-Based Algorithms |
VLi−1-Independent Algorithms |
||
|---|---|---|---|
| Classic Approach | G Algorithm | CF Algorithm | |
| Definition of breathing cycle (in time domain) | Time interval between the beginning of two consecutive inspiration phases | Time interval between two equal values of Fo2 (or Fco2) on successive, but not necessarily consecutive, expiration phases, typically in the alveolar phase | Time interval between two equal values of Fo2/Fn2 (or Fco2/Fn2) on successive, but not necessarily consecutive, expiration phases, typically in the alveolar phase |
| Signal(s) used to identify the breathing cycle | Flow signal | Fo2, Fco2, and Fn2 | Fo2, Fco2, and Fn2 |
| Variables required to obtain alveolar gas transfer | Flow signal, Fo2, Fco2, Fn2, and VLi−1 | Flow signal, Fo2, Fco2, and Fn2 | Flow signal, Fo2, Fco2, and Fn2 |
VLi-1, end-expiratory lung volume of the preceding breath; G, Grønlund algorithm; CF, Cettolo and Francescato algorithm; Fo2, fractional oxygen concentration; Fco2, fractional carbon dioxide concentration; Fn2, fractional nitrogen concentration.
This review presents the current definitions of the human breathing cycle and provides the rationale behind the use of alternative definitions, which arises from the need to estimate alveolar gas exchange. A brief description of gas exchange measurements at the mouth level is provided to facilitate the understanding of different alveolar corrections [more in-depth information on mouth measurements can be found elsewhere (1, 2, 4, 17–19)]. Moreover, we summarize the main limitations of applying one technique over another and present implications for future research. We have focused our review on definitions of the breathing cycle using B-by-B open-circuit systems that measure the inspired and expired gas flows and volumes. Historical perspectives of the development of B-by-B gas exchange analysis, including details of the equipment, measurements, and volume and gas corrections, are available elsewhere (1, 2, 4, 17–25).
CLASSICAL DEFINITION OF THE BREATHING CYCLE FOR B-BY-B GAS EXCHANGE ANALYSIS
Remarkable developments in real-time B-by-B open-circuit systems during the second half of the 20th century made it possible to quantify the inspired and expired gas volumes in real time (1, 18, 20). The breathing cycle was identified based on these techniques and used to quantify external respiration (i.e., exchange of O2 and CO2 between the alveoli and pulmonary capillary) on a B-by-B basis.
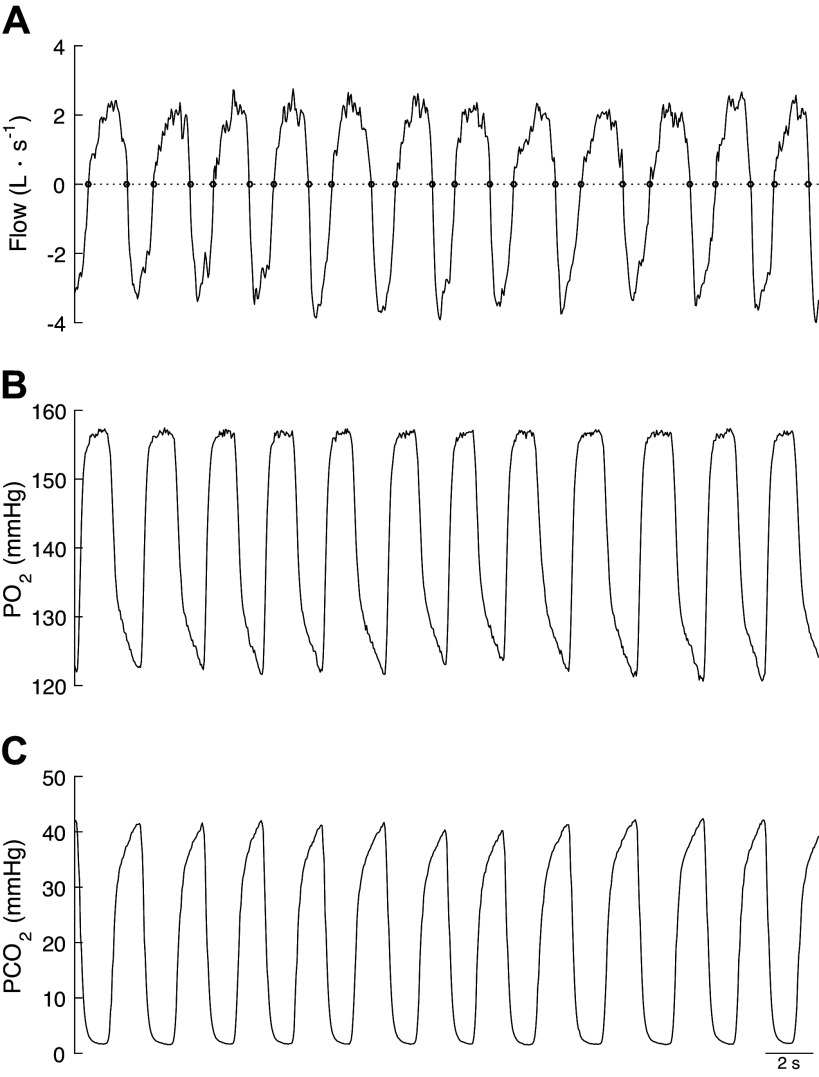
In general, a cycle can be defined as a series of incidences of the same condition that are repeated over time. Accordingly, the breathing cycle can be defined as the time interval between two equal incidences (i.e., inspiration or expiration phases). Convention defines “a breath” as the time interval between the beginning of two consecutive inspiration phases (Fig. 1).
Figure 1.
Gas flow (A), partial pressure of oxygen (B), and partial pressure of carbon dioxide (C) during a series of breaths performed at a moderate exercise intensity in healthy-trained individual. Top also depicts the zero-crossing points (open circle) identified using the MATLAB function “find_cross.m” (26).
The first step in identifying the breathing cycle is to detect the beginning and end of each inspiration and expiration phase. This requires analysis of the gas flow signal () from the flow meter. Theoretically, zero-crossing points of the flow signals can be used to identify the start and end of each inspiration and expiration phase, as the sign of the flow signal changes with inhalation and exhalation (Fig. 1). However, the flow signal, being a digitalized signal, rarely presents an absolute zero value. Therefore, the nearest points to zero in the flow signal are generally used in B-by-B gas exchange analysis to provide a reasonable estimation of the transition points between inspiration and expiration, and vice versa (12).
Determining the beginning and end of each inspiration and expiration phase enables the estimation of the inspiratory and expiratory volumes. The volume of the inspired (Vin) and expired (Vex) gas is determined by integrating the flow signal during the inspiration and expiration phases of the ith breath, respectively.
| (1) |
| (2) |
where and are the time instants at which the inspiration phase begins and ends for the breath i, respectively, whereas and are the time instants at which the expiration phase begins and ends for the ith breath, respectively. The total time (tTOT) over the ith breath can be defined as , where and are the expiratory and inspiratory times, respectively.
It is then possible to derive other important ventilatory-based variables over a breathing cycle, such as tidal volume (), breathing rate (), expired flow (V̇e), and inspired flow (V̇i) from , , , and (commonly expressed in L·min−1 for V̇e and V̇i, breaths·min−1 for , and L for ) (see Refs. 1, 4, 17, and 25 for the relevant equations).
Several commercial automated B-by-B systems do not compute (and the associated ) directly. Instead, these variables are estimated using the nitrogen balance approach: [i.e., the so-called Haldane’s correction; reviewed in Ward (1)], where is the mixed fraction of nitrogen (N2) during the expiration phase, and is the inspired N2 fractional concentration.
| (3) |
As B-by-B systems generally also do not measure the N2 fraction directly, and as there is only a negligible quantity of other inert gases in the inspired air, Fn2 is commonly estimated as follows: Fn2 = 1 – (Fo2 + Fco2). Accordingly, for breath i can be determined as follows:
| (4) |
However, this Haldane correction is intrinsically flawed when applied to B-by-B gas exchange analysis, as it assumes constancy in the lung N2 stores, which, over the duration of a single breathing cycle, occurs only when the respiratory exchange ratio (RER = V̇co2/V̇o2) is equal to 1 and consecutive end-expiratory lung volumes are precisely equal (2). Fluctuations in the end-expiratory lung volume at rest (27) and during exercise (7) cause subsequent changes in the fractional composition of the lung gas. Therefore, to facilitate accurate alveolar gas exchange measurement, should be measured directly.
Identifying the beginning and end of the inspiration and expiration phases of breath i also enables quantification of the volumes of the inspired and expired gas. The total volume of O2 and CO2 exchanged at the mouth over the ith breath (Vo2iM and Vco2iM, respectively) is determined by the difference between their inspired and expired volumes.
| (5) |
| (6) |
where and are the instantaneous O2 fractions in the inspired and expired gas of breath i, respectively, and and are the instantaneous CO2 fractions in the inspired and expired gas over the ith breath, respectively. Therefore, the intrabreath integration of flow and gas tensions is performed over the inspiration and expiration phases of breath i, from which the volumes of O2 and CO2 exchanged at the mouth during a single breathing cycle are obtained [Fig. 1 depicts gas flow (A), and O2 and CO2 gas tension traces (B and C, respectively) used to perform the intra-breath integration].
Some studies have shown that the use of Vo2M instead of Vo2A amplifies the intrinsic B-by-B variability in O2 exchange (2, 5–7, 10, 12). Similar results were expected for the difference between the B-by-B variability of Vco2M and Vco2A, although the B-by-B variability for the alveolar CO2 exchange could be greater than for O2 exchange (5). In contrast, the average values of Vo2M and Vco2M during steady-state conditions can be considered an unbiased average of the alveolar gas exchange (i.e., Vo2A and Vco2A) (7, 10, 12). However, the differences between external gas exchange measured at the mouth and that between the alveolar space and pulmonary capillary can be substantial during the work rate transition phases (4, 28), as neither Eqs. 5 nor 6 consider the changes in the volumes of each gas stored in the lung. Therefore, distinguishing between gas exchange at the mouth and the alveoli under these conditions is of paramount importance.
Several approaches designed to estimate Vo2A and Vco2A from measurements of gas volumes exchanged at the mouth have been proposed [for a complete review, please see Capelli et al. (2)]. Each of these approaches derives from the pioneering work of Auchincloss et al. (3). The alveolar-capillary gas transfer over breath i differs from the transfer measured at the mouth by the changes in the lung gas stores over the same breath:
| (7) |
| (8) |
where and represent the changes in the volumes of O2 and CO2 stored in the lung, respectively. The net transfer of O2 or CO2 at the alveolar level approaches that value measured at the mouth only when metabolism is in a steady-state condition and consecutive end-expiratory lung volumes are precisely equal. However, and are rarely zero when considering a single breathing cycle, and therefore, changes in the lung gas stores must be considered for valid estimation of alveolar-capillary gas transfer over the ith breath (i.e., and ) (2).
Changes in lung gas stores depend on the changes in the lung volume and alveolar gas fractions (1–3):
| (9) |
| (10) |
where VLi−1 is the end-expiratory lung volume of the preceding ith breath; and are the alveolar fractions of O2 and CO2 of the preceding breath (i.e., i − 1), respectively; and are the alveolar fractions of O2 and CO2 in the current breath i, respectively; and △VLi is the change in the lung volume occurring over breath i. Therefore, the changes in the lung gas stores depend mainly on two factors: 1) changes in the overall alveolar gas fractions of O2 and CO2 between the beginning and the end of breath i (i.e., the first term on the right-hand side of Eqs. 9 and 10, and , respectively), and 2) the changes in lung volume (i.e., the second term on the right-hand side of Eqs. 9 and 10, △VLi).
△VLi can be determined by assuming no alveolus-to-capillary N2 exchange (i.e., ; where and are the amounts of N2 exchanged at the alveolus and mouth levels, respectively, and is the change in the volume of N2 in the lung over a breathing cycle). By substituting into Eq. 9 (i.e., ), △VLi can be determined as follows:
| (11) |
where the amount of N2 exchanged at the mouth level over the breath i (i.e., ) can be determined as follows:
| (12) |
Beaver et al. (4) proposed an alternative approach to determine :
| (13) |
where and account for the water vapor pressure in the inspired and expired volumes, respectively, and and are alveolar fractions of O2 and CO2 of the breath i and preceding one (i.e., i − 1). This approach presents some advantages. First, can be expressed in terms of measured quantities, which is convenient from a computational perspective. Second, compared with Eq. 11, the Beaver et al.’s approach is less prone to estimation errors when the inspired gas fractions are transiently changed. For instance, when the inspired Fn2 changes significantly, which may occur when manipulating inspired gas fractions (e.g., supplemental oxygen), the terms and in Eq. 11 are large and nearly the same in magnitude during a transient period. This will expose Eq. 11 to a higher error sensitivity and, in some cases, it cannot be used (4).
The only quantity that remains to be determined is VLi−1, which is not directly measurable using Eqs. 9, 10, 11, and 13. Therefore, a predetermined value for VLi−1 must be chosen. In their pioneering work, Auchincloss et al. (3) proposed setting VLi−1 equal to the functional residual capacity (FRC) of the subject (hereinafter referred to as the A algorithm). Other research groups made the same assumptions, in which FRC was either directly determined before exercise (4, 7, 10) or indirectly estimated using predictive equations (29).
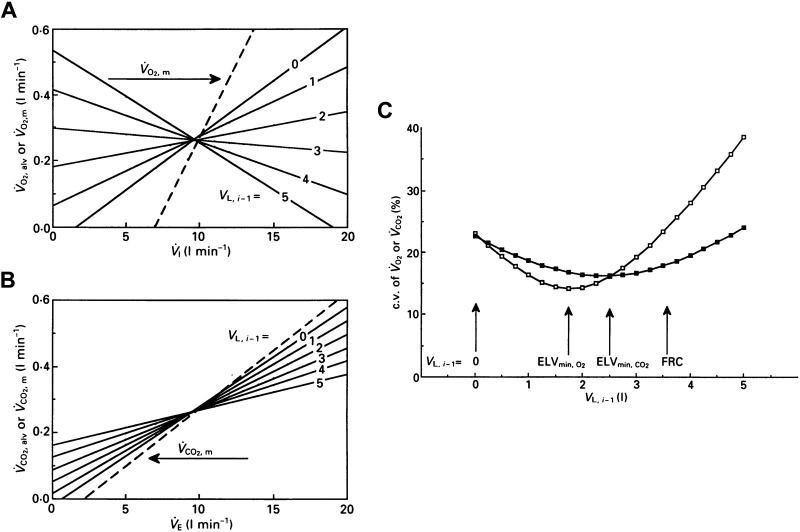
Wessel et al. (30) suggested that, as the quantity (and ) is likely to be rather small, the term can be neglected; thus, VLi−1 can be assumed to equal 0 L. However, this approach was subsequently questioned by di Prampero and Lafortuna (11) who demonstrated that setting VLi−1 equal to 0 changes the alveolar gas exchange measure. Moreover, they also showed that selecting different values of VLi−1 leads to a change in the B-by-B estimation and variability of and (Fig. 2) (11).
Figure 2.
Single breath alveolar V̇o2 (A) and V̇co2 (B) exchange as a function of ventilation computed on the same breath (continuous lines). V̇o2M/V̇o2A versus V̇I (A) and V̇co2M/V̇co2A vs. V̇E (B). Continuous lines (calculated on 100 breaths) depict differences from the expected value in alveolar gas exchange when using different VLi−1 values (from 0 to 5 L) in Eqs. 7 and 8. The dashed line depicts gas exchange at mouth (V̇o2M in A and V̇co2M in B). C: variability of alveolar V̇o2 (open square) and V̇co2 (filled square) expressed as coefficient of variation (c.v., %), as a function of different VLi−1 values. VLi−1 value, which gives the lowest computed V̇o2A and V̇co2A variability, is indicated by vertical arrows and ELVmin (effective lung volume; i.e., ELVmin,O2 and ELVmin,CO2, respectively). Functional residual capacity (FRC) indicates when VLi−1 = FRC. Modified with permission from di Prampero and Lafortuna (11).
Swanson (6) proposed an alternative approach based on the assumption that most of the B-by-B gas exchange variability at the mouth level is the result of B-by-B changes in lung gas stores. Swanson proposed selecting VLi−1 as the lung volume that yields the lowest B-by-B variability in gas exchange (6). He defined this volume as the “effective lung volume,” which represents the end-expiratory lung volume that “effectively” participates in alveolar gas exchange (a practical example of the “effective lung volume” is shown in Fig. 2C). Swanson’s approach yields a lower B-by-B and variability compared with that of the A algorithm (5), which might be particularly useful for detecting time-based events in gas exchange (such as the gas exchange threshold). Nevertheless, this technique has some limitations. As the effective lung volume can only be calculated a posteriori, this method does not allow for real-time monitoring of gas exchange. Moreover, when applied to the rest-exercise transition, this technique assumes a deterministic variation of FRC as a function of time, which is a questionable assumption (2). In addition, B-by-B variability in gas exchange are a result of both physiological events, such as rhythmic changes in pulmonary capillary blood flow with the breathing and cardiac cycles and the consequence of computational artifacts. di Prampero and Lafortuna (11) pointed out that it is difficult to distinguish between these effects and stressed the notion that a valid alveolar gas exchange measure largely relies on the validity of VLi−1 assessment on a B-by-B basis (11).
Busso and Robbins (5) suggested yet another alternative, which is also based on minimizing B-by-B variability in gas exchange; data suggest that it provides the lowest B-by-B and variability (5). They proposed that VLi−1 = FRC and assumed that the “true” change in alveolar end-expiratory gas fraction (i.e., and/or ) lies between 0 and the change in end-tidal gas fraction (i.e., and/or ), implying that the “true” alveolar O2 and CO2 exchange is compromised within those obtained using Wessel’s and Auchincloss’s approach. Using a nine-compartment, nonhomogeneous, tidally ventilated, and constantly perfused lung model that reproduces a realistic breathing pattern, Busso and Robbins elegantly tested the validity of this method (5). Although appealing, this method presents similar limitations to that of Swanson, primarily that the requirements for a posteriori processing prevents real-time monitoring of gas exchange. A detailed review on different VLi−1-based algorithms designed to estimate B-by-B alveolar gas exchange can be found elsewhere (1, 2). However, a central tenet and limitation of these flow-based approaches is measurement of VLi−1 that, as described above, is methodologically challenging and often unavailable.
Notably, the development of techniques based on optical reflectance motion analysis (i.e., optoelectronic plethysmography, OEP) has enabled the accurate estimation of lung volumes at any point of the breathing cycle and, in turn, the determination of changes in VLi−1 for each breath (7, 12, 28, 31, 32). However, when using OEP-based techniques, independent estimation of the vital capacity (VC) and FRC is still required to estimate and (7). Using this technique, Aliverti et al. (7) showed that VLi−1 changes between the onset and end of exercise, suggesting that the use of a constant value for VLi−1 would likely introduce an estimation error in the alveolar gas exchange computation. Despite its robustness, this technique is not free from limitations. For instance, the overall volume changes of the chest wall measured by OEP-based techniques can include blood volume shifts inside and outside of the thorax compartment, which could introduce an estimation error when assessing changes in VLi−1 (33, 34). This technique is certainly appealing; however, its application is demanding, time-consuming, and requires measures of VC and FRC, which represent the primary limitation of this approach.
DIFFERENT DEFINITIONS OF THE BREATHING CYCLE IN THE B-BY-B GAS EXCHANGE ANALYSIS
To circumvent the issues related to measurements of VLi−1, Grønlund (15) proposed a radically different solution; however, this requires the breathing cycle to be redefined. Rather than performing the integration of flow and gas fraction signals within the inspiration and expiration phases, it is performed between two successive expirations with equal Fo2 (or Fco2) values, typically in the alveolar phase (Fig. 3); the important point to note is that these equal Fo2 (or Fco2) values do not necessarily occur in consecutive breaths, or necessarily at a common time or lung volume during a subsequent breathing cycle (Fig. 4A). Thus, Grønlund defined a single breathing cycle as the time interval between two equal points of Fo2 (or Fco2) on successive expirations, i.e., , where t1 and t2 are the time instants with two equal Fo2 values. By Grønlund’s definition, the time interval between t1 and t2 represents the total time of a given breathing cycle, where t1 is the start and t2 is the end of a cycle, which can be (and commonly is) different from the time interval between the beginning of two consecutive inspiration phases (i.e., the conventional breathing cycle). Grønlund’s astute solution makes the term in Eq. 9 equal to 0; thus, VLi−1 can be omitted from the computation. Therefore, according to Grønlund’s algorithm (hereinafter referred to as the G algorithm), the volume of O2 exchanged at the alveolar level over breath i is reduced to:
| (14) |
Figure 3.
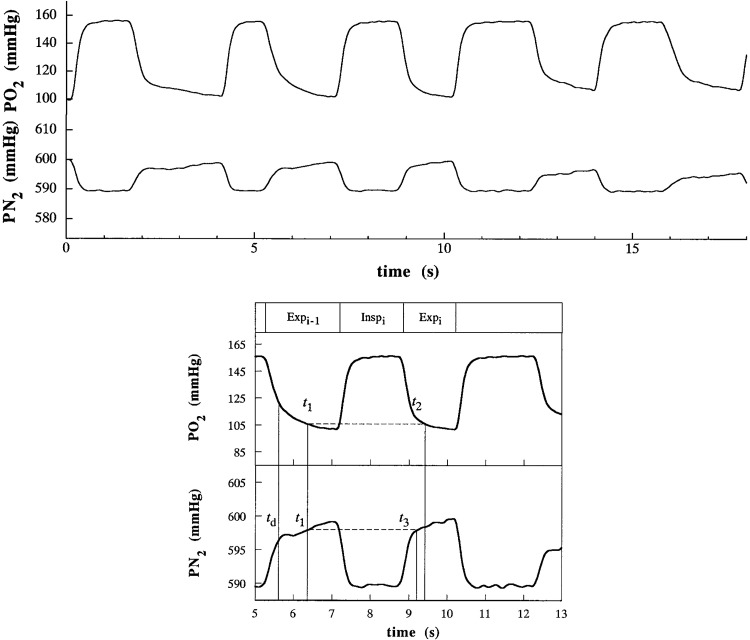
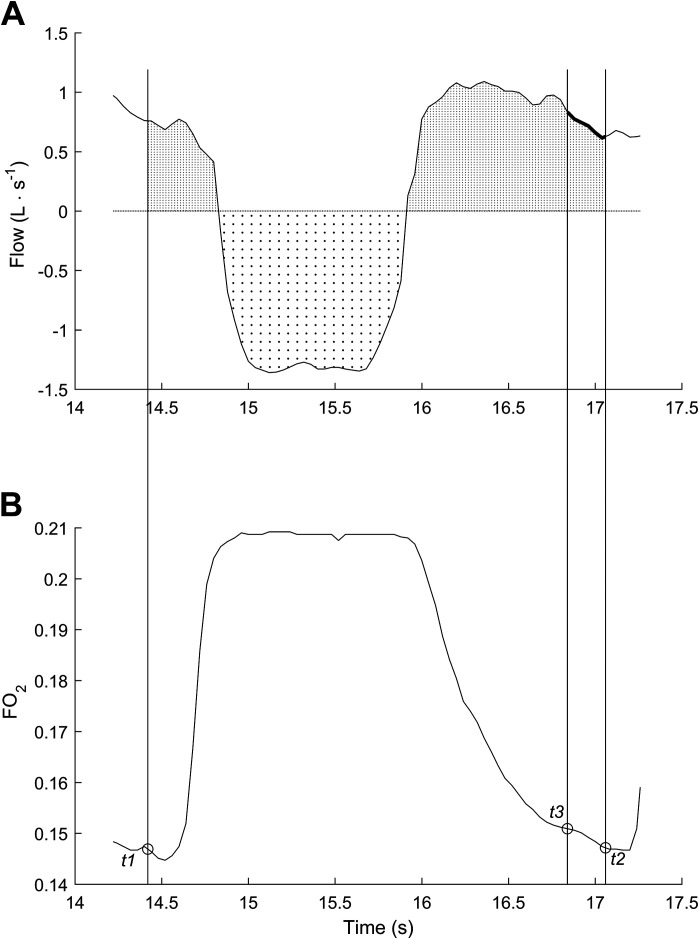
Partial pressure of O2 and N2 in mmHg (Po2 and Pn2, respectively) (top). The same data over the 5th and the 13th second (bottom). Expi-1, Inspi, and Expi refer to the conventional expiration phase of the breath i-1, inspiration phase of the breath i, and expiration phase breath i. td indicates the time after which the estimated dead space gas volume is fully expired. The reference value t1 is chosen according to specific criteria [see text and Capelli et al. (10) for further details], whereas t2 and t3 are chosen to yield Po2 and Pn2 equal to t1, respectively. The breathing cycle is defined as the time elapsing between t1 and t2. Modified with permission from Capelli et al. (10).
Figure 4.
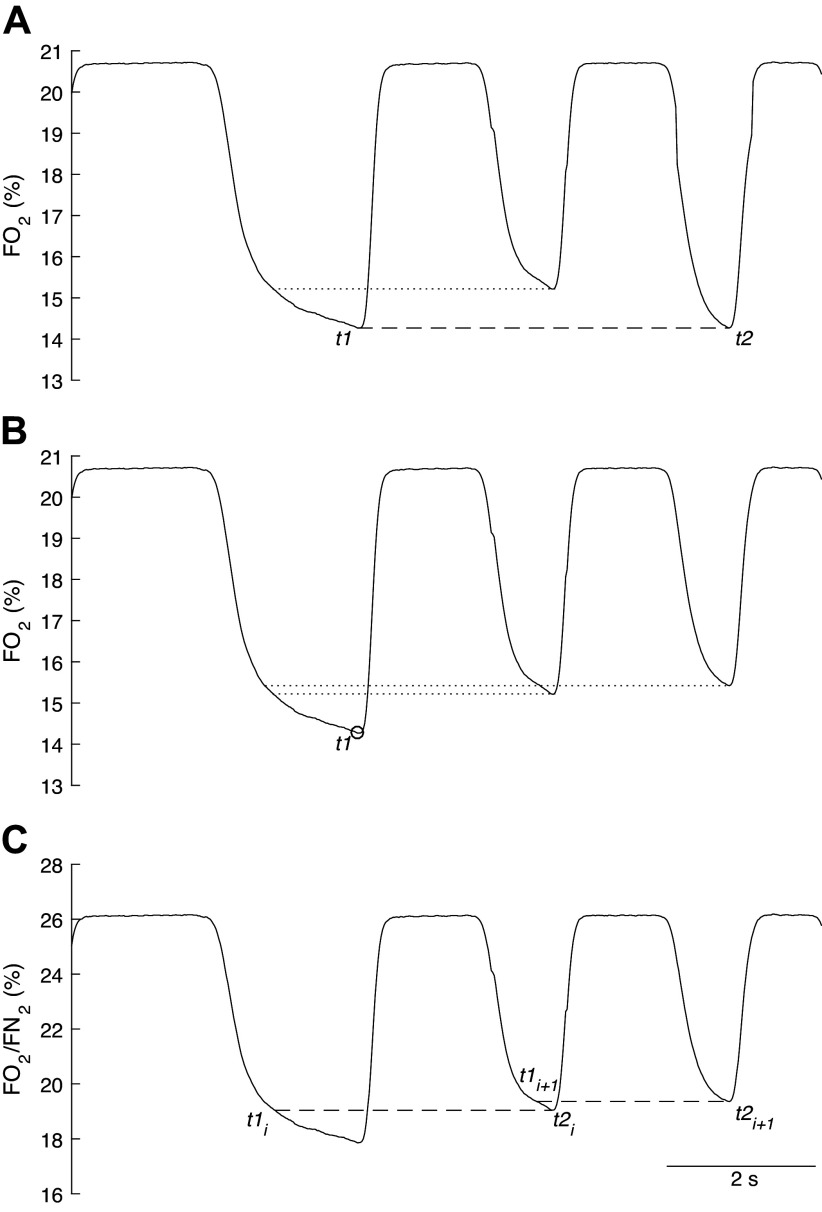
A: a particular case where a given Fo2 reference value at the time instant t1 does not meet any Fo2 value on the successive expiration to satisfy the condition , but during which a value equal to is then met during the subsequent expiration. This results in an integration of gas and flow data over a longer time interval. Horizontal dotted line shows that the latest Fo2 value pertaining to the second expiration that coincides with the first Fo2 value would allow the identification of a breathing cycle using the G algorithm. B: effect of hyperventilation on Fo2 (O2 fractional concentration in %) during three successive expirations. There are no Fo2 reference values at time instant t1 that are met on two consecutive expirations, making the identification of a breathing cycle using the G algorithm impossible. C: so-called “independent breath” algorithm, which allows the identification of two breathing cycles (t1i − t2i and t1i+1 − t2i+1) during hyperventilation. Fo2/Fn2 ratio (ratio of O2 and N2 fractions in %). Here, the summed duration of two successive breaths is larger than the summed duration of two conventional breaths defined by the beginning of two consecutive inspiration phases, i.e., consecutive breaths overlap. See text for further details.
To note, only the variables marked with (t1) are constant values for the considered breath i [i.e., and , the fraction of O2 and N2 at the time instant t1], whereas the others change over time (i.e., , , Fo2, Fn2, which are variables varying over time). As originally pointed out by Grønlund (15), Eq. 14 is very similar to that proposed earlier by Beaver et al. (i.e., Eq. A9 in Ref. 4), with the substantial difference of how a single breathing cycle is identified.
Accordingly, Eqs. 7 and 14 can be rewritten as follows:
| (15) |
where
| (16) |
The second term on the right-hand side of Eq. 15 accounts for the lung gas storage, where ΔVLi can be determined from N2 balance (Eq. 16). corresponds to the N2 gas fraction at t1 and is used as a reference value for identifying Fn2 at t3 [], such that (Fig. 3). Therefore, t3 is identified using the Fn2 signal, which satisfies the condition . Thus, Eq. 11 can be reduced to Eq. 16, which represents the changes in the alveolar volume occurring over the ith breath. If t3 does not temporally coincide with t2, volume correction must be applied (Figs. 3 and 6), a correction that assumes a negligible gas exchange from t2i to t3i with a RER = 1. Notably, straightforward modifications, which are not described here for simplicity, make it possible to obtain Vco2A [e.g., applying Eq. 8, inverting the subtraction of the inspired and expired volumes from () to () and considering the Fco2 instead of the Fo2 trace].
Figure 6.
A single breathing cycle identified using the Grønlund’s algorithm, where t1 and t2 represent the beginning and the end of one breath. A: gas flow at the mouth. Expiration occurs during positive deflections of the flow signal, whereas the inspiration occurs during negative deflections of the flow signal. B: fractional O2 concentration. Soft dotted area represents the inspired gas volume, while the heavy dotted area corresponds to the expired gas volume. Thick line represents the gas flow occurring between t3 and t2 (i.e., the volume correction for Eq. 16). Some ventilatory-based variables estimated over t1 and t2 are as following: Vex = 0.9 L STPD (VT = 1.2 L BTPS), Vin = 1.03 L STPD, V̇E = 23 L·min−1 STPD, V̇I = 24 L·min−1 STPD. Alveolar net transfer of oxygen uptake occurring over t1 and t2 is equal to V̇o2A = 1.09 L·min−1 STPD. Time elapsing between t1 and t2 (i.e., tTOT, which is the total time of the considered breath) is equal to 2.54 s. Corresponding breathing frequency is 24 breaths·min−1. BTPS, body temperature, ambient pressure, and saturated water vapor; STPD, standard temperature and barometric pressure, dry.
Therefore, according to the G algorithm (15) the intrabreath interval time of breath i is defined as the time interval between two points on successive expirations in which the lung O2 fractional concentration is the same, i.e., (Fig. 3). Generally, t1 is selected within the second half of the first expiration after the dead space has fully expired (10, 35), where the condition is satisfied (Figs. 3 and 4) (10, 35). As the condition can be met several times within breath i, and selecting different t1-t2 couples may lead to different VO2A and VCO2A (15), it is also necessary to determine which t1 and t2 should be chosen. Capelli et al. (10) proposed a robust technique to identify t1-t2-t3, which enables the reliable measurement of VO2A [see Capelli et al. (10) for further details].
The condition may not be satisfied between two consecutive breaths. In such cases, the subsequent expiration phase (i.e., following two standard breathing cycles after the ith breath) can be used to satisfy the condition , which results in integration over a longer time interval (Fig. 4A) (10, 35). Although unlikely, a given reference value at t1 may not be attained at t2 over a long series of breaths, which would result in losing the breath considered (Fig. 4B) (see Capelli et al. for further details) (10). This may occur during hyperventilation, where tachypnea increases the slope of the alveolar partial pressure of expired O2 (and CO2) (36) (see Limitations, Methodological Considerations, and Future Directions for further details).
The use of the G algorithm presents some advantages over the use of other VLi−1-dependent algorithms, especially when attempting to characterize the B-by-B alveolar gas exchange kinetics during the transition to or from different work rates. For instance, di Prampero and Lafortuna (11) showed that the A algorithm is likely to be exposed to an estimation error of the duration of V̇O2A phase I during the rest-exercise transition, and the magnitude of this error is highly dependent on the accuracy of VLi−1. They also showed that assuming VLi−1 equal to 0 (i.e., Wessel et al.’s approach; 30) causes wide variability in the estimation of the duration of phase 1 compared with assuming VLi−1 equals FRC. This instability might be due to the failure of the assumption that VLi−1 = 0 completely account for changes in lung gas stores (11). Moreover, by comparing the G and A algorithms at the onset of exercise in the moderate-intensity domain, Cautero et al. (35) demonstrated that the time constant of phase 2 V̇o2A kinetics (τ2) obtained when using the A algorithm was systematically greater than that obtained with the G algorithm (34.3 ± 9.18 s vs. 45.0 ± 10.66 s, respectively). Notably, the authors found a positive correlation between τ2 and , suggesting that choosing greater VLi−1 values lead to a systematic increase in V̇O2 τ2. Indeed, increases in VLi−1 amplifies the contribution of (see Eq. 9) and (see Eq. 11) in the V̇o2A computation, which results in V̇o2A kinetic distortions [see Cautero et al. (35) and Capelli et al. (2) for further details]. Therefore, the use of the G algorithm can help prevent distortions caused by inaccuracy in the estimation or measurement of . However, we note that the “true” alveolar V̇o2 (and V̇co2) kinetics are unknown. It may be possible to use simulations of gas flow traces with different kinetic features to elucidate which algorithm provides the most realistic response kinetic estimation (see Limitations, Methodological Considerations, and Future Directions for further details).
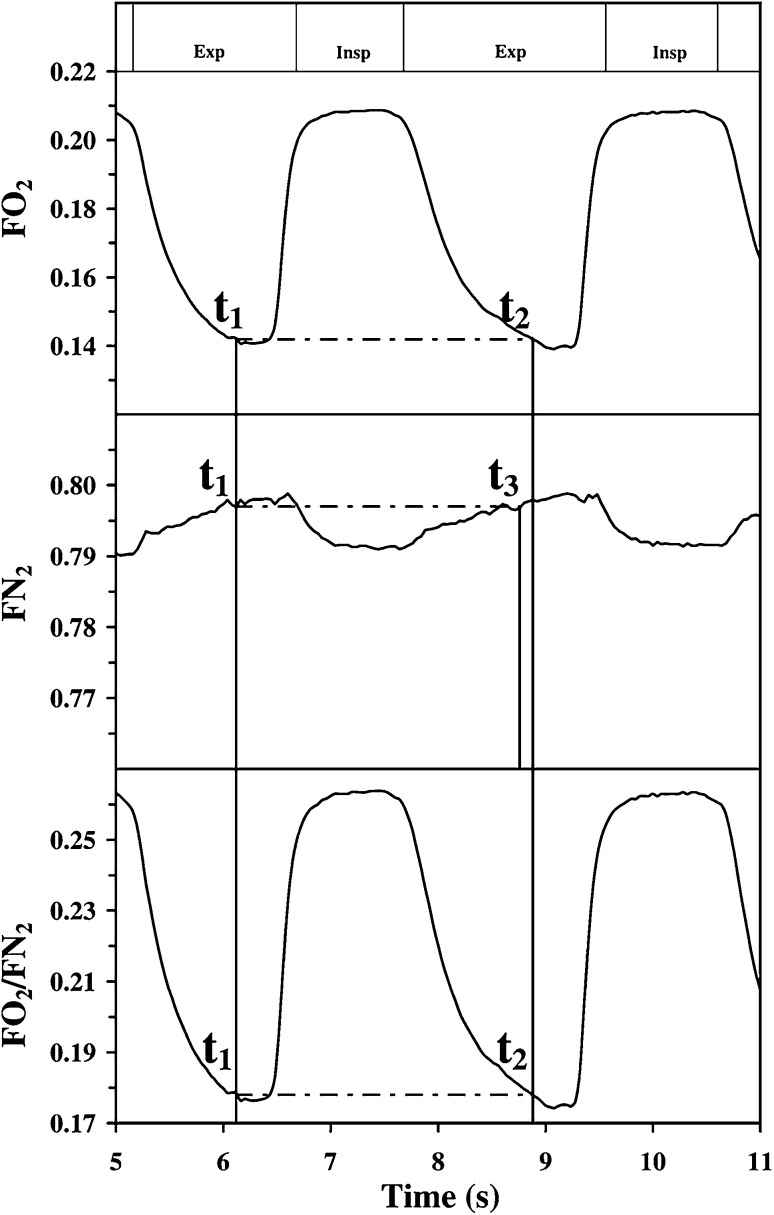
Cettolo and Francescato (16) recently proposed an alternative algorithm designed to measure alveolar gas exchange, which also circumvents the requirement to assess VLi−1 by redefining the breathing cycle. Rather than considering the intrabreath interval time using the condition , the start and the end of each breath i are defined by satisfying the condition , typically in the alveolar phase (Fig. 5) (where t1 and t2 conceptually have the same meaning as t1 and t2 in Eq. 14; see below for further details). Similar to the G algorithm, this condition makes the term of Eq. 9 equal to 0, allowing to be omitted from the computation. Thus, the breathing cycle can be defined as the time interval between two equal values of on successive, but not necessarily consecutive, expiration phases.
Figure 5.
Comparison of Grønlund’s and Cettolo and Francescato’s algorithms. Top and middle: method introduced by Grønlund, which is also described in Fig. 3. Bottom: method introduced by Cettolo and Francescato (16). For the Cettolo and Francescato’s method, the reference value t1 is chosen accordingly to specific criteria [see text and Cettolo and Francescato (16) for details], whereas t2 is chosen to yield Fo2/Fn2 equal to t1. The breathing cycle is defined as the period elapsing between t1 and t2. Modified with permission from Cettolo and Francescato (16).
Cettolo and Francescato (16) reorganized Eq. 7, which is essentially the method proposed by Auchincloss et al. (3).
| (17) |
Considering the condition , Eq. 17 reduces to
| (18) |
Equation 18 is a simplified version of Eq. 15; straightforward modifications, which will not be described here, make it possible to also obtain alveolar CO2 exchange. Notably, although t1 and t2 in Eq. 18 have the same conceptual meanings as t1 and t2 in Eqs. 14 and 15, they are defined differently [i.e., ] (16) (Figs. 3 and 5).
Equation 18 presents several advantages from a computational perspective. For instance, the Cettolo and Francescato algorithm (hereinafter referred to as the CF algorithm) does not require the definition of t3, which must be determined when using the G algorithm (Fig. 5). Moreover, identifying the breathing cycle using the Fo2/Fn2 and Fco2/Fn2 ratio traces may help identify outlier breaths. The Fn2 trace generally shows greater noise and signal distortion compared with the Fo2/Fn2 and Fco2/Fn2 ratio traces, which may affect the identification of t1-t2-t3 (not present in the CF algorithm). Furthermore, the Fo2/Fn2 and Fco2/Fn2 ratio traces have signal amplitudes that are greater than that of Fn2 alone, which may reduce variability associated with trace detection in real time (16, 37). Nevertheless, the advantage of using Fo2/Fn2 and/or Fco2/Fn2 ratio traces, instead of Fo2 and Fn2 and/or Fco2 and Fn2, is yet to be determined by independent research groups under different exercise conditions and/or using different modalities (see Limitations, Methodological Considerations, and Future Directions for further details).
There are also limited data directly comparing the G and CF algorithms; thus, whether one algorithm can outperform the other is unclear. Some data suggest no differences in the alveolar B-by-B gas exchange estimation between the two algorithms; however, the comparison was performed over a limited range of V̇o2, V̇co2, and ventilatory rates (16). Notably, the CF algorithm was only recently introduced; hence, there are limited data showing its validity in assessing B-by-B alveolar gas exchange compared with the G algorithm (16, 37–40). Therefore, further investigations are warranted to better understand whether substantial differences exist between these algorithms, and which more accurately measures the true physiologic response.
LIMITATIONS, METHODOLOGICAL CONSIDERATIONS, AND FUTURE DIRECTIONS
Using the G or CF algorithms has the undoubted advantage of removing the need to measure VLi−1, which is appealing from a practical perspective. However, redefining the breathing cycle for the B-by-B gas exchange analysis may present some limitations. First, as previously highlighted (1, 41), these techniques would benefit from validation conducted by independent research groups under different conditions. For instance, it would be of great interest to test these algorithms together, under different environmental conditions (e.g., hypoxia, hyperoxia), exercise modalities (e.g., running, cycling, walking), with different populations (e.g., patients with cardiovascular and lung diseases and athletes), body positions (e.g., supine and upright posture), or work rate protocols (e.g., square-wave, sinusoidal-wave, ramp- and step-incremental tests). Specifically, comparisons made under conditions where lung volumes, lung gas stores, and/or ventilation-perfusion relationships are expected to vary would help to identify the algorithm that best characterizes the true physiological response.
Second, Whipp et al. (41) pointed out that Grønlund’s approach may provide a different breath duration under specific conditions, such as during the transition from rest to exercise, compared with that of the conventional flow-based approach. As the slope of the alveolar partial pressure of expired O2 (and CO2) increases at the onset of exercise and during continued exercise (36), a particular intrabreath Fo2 reference value at t1 might be reached earlier during the expiration phase at t2, which in turn would result in a shorter estimated breath duration, and differentially alter the durations of inspiratory and/or expiratory time (such as in tin/tex or tin/tTOT) (41). The same concern applies to the CF algorithm (16), although specific aspects of this algorithm may help mitigate this concern (see below) (37, 39). However, no study has investigated the potential differences in breath duration among different algorithms; therefore, further investigations are required.
Whipp et al. (41) also stated that during acute hyperventilation, due to the large increment of the entire (or fall in ), a given intrabreath Fo2 reference value at t1 (or Fco2) may not match any Fo2 (or Fco2) value at t2 in the expired phase, resulting in the potential loss of breath detection using the G algorithm (Fig. 4B). This may negatively affect the analysis of gas exchange kinetics during the transition phases. Modifications in the CF algorithms may help reduce the influence of large changes in Fo2/Fn2 (or Fco2/Fn2) on the identification of the breathing cycle (37, 39). Cettolo and Francescato (37, 39) have recently implemented a technique in which each breathing cycle is identified without considering the end time point of the preceding cycle and the start time point of the following one (i.e., the so-called “independent breath” algorithm). Therefore, each breathing cycle has its own t1 and t2, where t1 of the breath i + 1 does not necessarily correspond to t2 of the breath i (i.e., noncontiguity in time of the breathing cycles, Fig. 4C). This would increase the possibility of identifying the breathing cycle during outlying breaths (e.g., atypically large or small breaths such as a sigh or a pant) and reduce the negative effects of hyperventilation on the identification of the breathing cycle and gas exchange estimation (37, 39). Although some promising findings have already been reported (37–40), utilization of this approach would benefit from further validation by independent research groups under different exercise conditions. Moreover, the impact of hyperventilation on gas exchange kinetics estimation when using the G algorithm remains to be systematically determined.
Concerns have been raised regarding how ventilatory-based variables are computed using the G and CF algorithms (1). Information is lacking regarding the inspired and expired volumes, which are needed to estimate other important variables such as V̇E, V̇I, the ventilatory equivalents for O2 and CO2 (i.e., V̇E/V̇o2 and V̇E/V̇co2, respectively), and inspiratory and expiratory time. However, it is worth noting that several (if not all) ventilatory-based variables can be determined using these approaches. The intrabreath integration of the positive flow signal values between t1 and t2 can provide the expired volume (i.e., Vex), which can be used to derive other variables (such as V̇E and VT) (Fig. 6). Likewise, the intrabreath integration of negative values can provide the inspired volume (i.e., Vin), which in turn would enable the estimation of V̇I (Fig. 6). This procedure would also theoretically enable the estimation of BR, where tTOT corresponds to the time elapsing between t1 and t2 (Fig. 6). Inspiratory and expiratory times are also computable in the G and CF algorithms, although their physiological meaning is questionable, as they do not refer to the start and end of a conventional inspiration and expiration phases, which are commonly used to gain insights into the mechanisms involved in the control of the transition phase between inspiration and expiration, or vice-versa (42–44). However, although these ventilatory-based variables are computable using the G and CF algorithms, they have not been reported in published works. It is currently unclear whether these algorithms would provide a reasonable estimation of ventilatory-based variables. Evaluation of variability and irregularity of ventilatory-based variables during cardiopulmonary exercise testing (CPET) has the potential to detect underlying breathing pattern disorders (45, 46). For instance, Bansal et al. (47) showed that a V̇e approximate entropy (i.e., a measure of V̇E variability) > 0.88 conferred sensitivity and specificity to detect breathing pattern disorder of 70% and 80%, respectively. Whether this ventilatory-based information, computed using VLi−1-independent algorithms, provides the same valuable information is currently unknown. Further study is recommended to demonstrate that all CPET variables can be precisely and accurately derived.
Similarly, quantitative analysis of ventilatory and gas exchange kinetics during exercise is commonly used to understand underlying metabolic and ventilatory control mechanisms (41, 48) and are modified in patients with chronic disease (49, 50). This is particularly true for the investigation of the control mechanisms of V̇E, where analysis of V̇E and V̇co2A kinetics can provide important physiological information (51–55).
Analysis of other ventilatory-based variables can also provide useful information for athletes and populations with chronic disease (55–57). For instance, V̇E/V̇o2 and V̇E/V̇co2 responses can be used to noninvasively identify the gas exchange threshold (58, 59) and for diagnostic and prognostic stratification (56, 60). Therefore, identifying the most appropriate and reliable way to quantify ventilatory-based variables is of paramount importance.
The impact of lung gas store changes on B-by-B alveolar O2 and CO2 exchange rates during progressive exercise (i.e., step-wise or ramp-incremental work-rate protocols) has received less attention compared with the responses occurring during square-wave work-rate protocols (reviewed in Ref. 2). As progressive exercise is commonly used in research and clinical evaluation, it is of paramount importance to understand whether the dynamic changes in the alveolar gas stores affect the B-by-B gas exchange and their derived variables (such as gas exchange threshold and the ventilatory equivalent for O2 and CO2). Indeed, the use of V̇o2A and V̇co2A instead of V̇o2M and V̇co2M was shown to increase the B-by-B signal-to-noise ratio and reduce B-by-B variability (4, 7, 10–12), thereby potentially improving discrimination of time-based events in gas exchange. However, there are no studies exploring the effect of using different algorithms on threshold detection.
Mathematical simulations and mechanical gas exchange simulation systems may be used to assess the validity of different alveolar corrections on the measurements of gas exchange and kinetics. As previously mentioned, the “real” alveolar gas exchange kinetics is unknown. Although speculative, simulating gas flow traces with different known kinetics could potentially help to compare different algorithms to identify the algorithm that provides the most accurate kinetic estimates. On the other hand, the use of mechanical gas exchange simulation systems could be used to assess the validity of alveolar gas exchange measures during steady-state conditions and in the presence of an aberrant single breath (40). The application of these techniques seems feasible (5, 40, 61), but the paucity of studies using these approaches means that further investigation is needed.
As V̇o2A and V̇co2A can be obtained using different reference values at t1, t2, or t3 (depending on the algorithm used – G or CF), a given breathing cycle obtained for V̇o2A is not temporally aligned with that for V̇co2A. Moreover, tin, tex and tTOT may not necessarily have the same durations when computed by these different algorithms. Therefore, a temporal misalignment on a B-by-B basis between V̇o2A and V̇co2A, although small, can occur. This issue can be partially overcome by interpolation and extrapolation. Second-by-second interpolation and extrapolation (rather than B-by-B) of data are commonly used in postprocessing when investigating gas exchange kinetics of actual (51, 62, 63) and simulated data (52, 64). Although, again, the implications for altering the standard reporting format for research and clinical gas exchange and ventilatory variables are yet to be determined. Moreover, interpolation/extrapolation techniques might alter the data, especially during the rest-exercise transition period, potentially affecting the physiological interpretation.
Until recently, G and CF algorithms have typically only been applied to raw gas flow and gas concentration recordings postprocessing. That is, they have not been used to provide a real-time B-by-B measure of gas exchange. However, the use of the CF algorithm in real-time data analysis is feasible (37). The CF algorithm can identify t1 and t2 within every single breath in real time as data are collected (37). Thus, similar to what occurs during the classical real-time analysis of gas exchange, the integration of flow and gas fractions can be performed independently in a single breath (the so-called “independent breath”), allowing real-time data visualization (37, 39). Although not yet tested, this modification could theoretically be implemented in the G algorithm. Further studies are required to identify the most efficient technical solution to implement these algorithms in automated real-time B-by-B systems.
A CALL TO ACTION
Data show the clear advantages of using V̇o2A/V̇co2A instead of V̇o2M/V̇co2M in B-by-B gas exchange analysis. However, the requirement for substantial validation work that confirms the advantage of VLi−1-independent algorithms to determine not only alveolar gas exchange but also ventilatory-based variables is prohibitive to making use of these routines. For example, it is still unclear which alveolar correction better reflects alveolar-to-capillary gas exchange, especially under the diverse range of conditions commonly observed in research and clinical CPET laboratories. In addition, the lack of open access to these algorithms for routine application is a key barrier limiting the use of alveolar corrections. We are unaware of any automated commercial system that has implemented an algorithm to measure B-by-B alveolar gas exchange. This is despite literature that shows the advantages of using V̇o2A/V̇co2A instead of V̇o2M/V̇co2M to increase signal-to-noise and reduce distortions in gas exchange responses during exercise. Therefore, given 1) the introduction of the algorithm by Auchincloss et al. in 1966 (3), 2) the development of several solutions aimed at optimizing the estimation of alveolar gas exchange (2, 39), and 3) the large number of studies showing the importance of differentiating between V̇o2M/V̇co2M and V̇o2A/V̇co2A (2, 4–6, 10, 16, 28, 35, 38, 39, 65), it is surprising that manufacturers have not progressed past conventional B-by-B algorithms and developed commercial systems that provide alveolar gas exchange analysis alongside standard measurements. This would not only increase signal-to-noise to provide improved characterization of clinically important variables from an exercise test but also enable implementation of the most suitable algorithm for a given purpose, satisfying a wide range of different needs in health and chronic disease. Incorporating different algorithms into commercial systems would advance the reach of these techniques and facilitate the progression of our knowledge on their validity and applicability under different exercise conditions.
Perspectives and Significance
Although fundamental concerns have been raised in using alternative algorithms that change the definition of the breathing cycle, their benefit for increasing accuracy and precision of alveolar gas exchange measurement is appealing and promising. Nevertheless, the paucity of data describing the physiological meaning of several ventilatory-based variables when using these alternative algorithms requires further investigation. In addition, further validation studies are required to assess these methods and their implementation in real-time for online analysis. This is essential to understand which algorithm best characterizes the “true” physiological response in both clinical and research settings.
GLOSSARY
- BTPS
Body temperature, ambient pressure, and saturated water vapor
- CPET
Cardiopulmonary exercise testing
- CO2
Carbon dioxide
- , , ,
Alveolar gas concentrations
- , , ,
Mixed expired fractional gas concentration
- , ,
Fractional gas concentration in expirate
- ,
End-tidal gas fraction
- , , ,
Fractional gas concentration in inspirate
Fractional N2 concentration at the time instant t3
- , ,
Fractional gas concentration
- , ,
Fractional gas concentration at the time instant t1
- , ,
Fractional gas concentration at the time instant t2
- FRC
Functional residual capacity
- i-1
Preceding breath
- N2
Nitrogen
- OEP
Optoelectronic plethysmography
- O2
Oxygen
- RER
Respiratory exchange ratio
- STPD
Standard temperature and barometric pressure, dry
- , ,
Time interval of a breath, inspiratory time interval, expiratory time interval
- V̇
Gas flow
- VC
Vital capacity
- V̇e, V̇i
Expired flow rate, inspired flow rate
- V̇e/V̇o2, V̇e/V̇co2
Ventilatory equivalents for O2 and CO2, respectively
- V̇in, V̇ex
Flow rate during inspiration and expiration, respectively
- Vin, Vex
Inspired volume, expired volume
- VLi
end-expiratory lung volume of the ith breath
- VLi– 1
end-expiratory lung volume of the preceding breath
- V̇o2A, V̇co2A, V̇n2A
Alveolar-to-capillary gas exchange rate
- Vo2A, Vco2A
Alveolar-to-capillary gas exchange volume
- , ,
Pulmonary gas exchange volume
- V̇o2M, V̇co2M
Pulmonary gas exchange rate
- VT, BR
Tidal volume, breathing rate
- ΔVLi
Changes in lung volume during breath interval
- ΔVo2S, ΔVco2S, ΔVn2S
Changes in lung gas content during breath interval
- τ2
Time constant of phase II gas kinetic
GRANTS
H. B. Rossiter is supported by National Institutes of Health Grants R01HL151452, R01HL153460, P50HD098593, and R01DK122767) and by the Tobacco Related Disease Research Program (T31IP1666).
DISCLOSURES
H. B. Rossiter reports consulting fees from Omniox Inc. and is involved in contracted clinical research with Boehringer Ingelheim, GlaxoSmithKline, Novartis, AstraZeneca, Astellas, United Therapeutics, Genentech, and Regeneron. He is a visiting Professor at the University of Leeds, UK. R. Casaburi is involved in contracted research with United Therapeutics, Genentech, and Regeneron. He is an advisory board member for Inogen and Abbott and a speaker bureau member for GlaxoSmithKline. C. Ferguson is involved in contracted clinical research with United Therapeutics, Genentech, and Regeneron. She is a visiting Associate Professor at the University of Leeds, UK. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.
AUTHOR CONTRIBUTIONS
M.G., C.G., W.W.S., H.B.R., R.C., C.F., and C.C. conceived and designed research; M.G., C.G., W.W.S., H.B.R., R.C., C.F., and C.C. interpreted results of experiments; M.G., C.G., W.W.S., H.B.R., R.C., C.F., and C.C. prepared figures; M.G. drafted manuscript; M.G., C.G., W.W.S., H.B.R., R.C., C.F., and C.C. edited and revised manuscript; M.G., C.G., W.W.S., H.B.R., R.C., C.F., and C.C. approved final version of manuscript.
ACKNOWLEDGMENTS
The authors are grateful to Prof. Pietro Enrico di Prampero for critically reading the manuscript and providing valuable comments and suggestions.
REFERENCES
- 1. Ward SA. Open-circuit respirometry: real-time, laboratory-based systems. Eur J Appl Physiol 118: 875–898, 2018. doi: 10.1007/s00421-018-3860-9. [DOI] [PubMed] [Google Scholar]
- 2. Capelli C, Cautero M, Pogliaghi S. Algorithms, modelling and VO2 kinetics. Eur J Appl Physiol 111: 331–342, 2011. [Erratum in Eur J Appl Physiol 111: 343, 2011]. doi: 10.1007/s00421-010-1396-8. [DOI] [PubMed] [Google Scholar]
- 3. Auchincloss JH Jr, Gilbert R, Baule GH. Effect of ventilation on oxygen transfer during early exercise. J Appl Physiol 21: 810–818, 1966. doi: 10.1152/jappl.1966.21.3.810. [DOI] [PubMed] [Google Scholar]
- 4. Beaver WL, Lamarra N, Wasserman K. Breath-by-breath measurement of true alveolar gas exchange. J Appl Physiol Respir Environ Exerc Physiol 51: 1662–1675, 1981. doi: 10.1152/jappl.1981.51.6.1662. [DOI] [PubMed] [Google Scholar]
- 5. Busso T, Robbins PA. Evaluation of estimates of alveolar gas exchange by using a tidally ventilated nonhomogenous lung model. J Appl Physiol (1985) 82: 1963–1971, 1997. doi: 10.1152/jappl.1997.82.6.1963. [DOI] [PubMed] [Google Scholar]
- 6. Swanson GD. Breath-to-breath considerations for gas exchange kinetics. In: Exercise, Bioenergetics and Gas Exchange, edited by Cerretelli P, Whipp BJ.. Amsterdam: Elsevier/North-Holland, 1980, p. 211–222. [Google Scholar]
- 7. Aliverti A, Kayser B, Macklem PT. Breath-by-breath assessment of alveolar gas stores and exchange. J Appl Physiol (1985) 96: 1464–1469, 2004. doi: 10.1152/japplphysiol.01198.2003. [DOI] [PubMed] [Google Scholar]
- 8. Giezendanner D, Cerretelli P, Di Prampero PE. Breath-by-breath alveolar gas exchange. J Appl Physiol Respir Environ Exerc Physiol 55: 583–590, 1983. doi: 10.1152/jappl.1983.55.2.583. [DOI] [PubMed] [Google Scholar]
- 9. Lumb AB. Nunn’s Applied Respiratory Physiology. Amsterdam: Elsevier Health Sciences, 2020. [Google Scholar]
- 10. Capelli C, Cautero M, di Prampero PE. New perspectives in breath-by-breath determination of alveolar gas exchange in humans. Pflugers Arch 441: 566–577, 2001. doi: 10.1007/s004240000429. [DOI] [PubMed] [Google Scholar]
- 11. di Prampero PE, Lafortuna CL. Breath-by-breath estimate of alveolar gas transfer variability in man at rest and during exercise. J Physiol 415: 459–475, 1989. doi: 10.1113/jphysiol.1989.sp017731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Wüst RCI, Aliverti A, Capelli C, Kayser B. Breath-by-breath changes of lung oxygen stores at rest and during exercise in humans. Respir Physiol Neurobiol 164: 291–299, 2008. doi: 10.1016/j.resp.2008.06.002. [DOI] [PubMed] [Google Scholar]
- 13. Lumb AB, Nunn JF. Respiratory function and ribcage contribution to ventilation in body positions commonly used during anesthesia. Anesth Analg 73: 422–426, 1991. doi: 10.1213/00000539-199110000-00010. [DOI] [PubMed] [Google Scholar]
- 14. Henke KG, Sharratt M, Pegelow D, Dempsey JA. Regulation of end-expiratory lung volume during exercise. J Appl Physiol (1985) 64: 135–146, 1988. doi: 10.1152/jappl.1988.64.1.135. [DOI] [PubMed] [Google Scholar]
- 15. Grønlund J. A new method for breath-to-breath determination of oxygen flux across the alveolar membrane. Eur J Appl Physiol Occup Physiol 52: 167–172, 1984. doi: 10.1007/bf00433387. [DOI] [PubMed] [Google Scholar]
- 16. Cettolo V, Francescato MP. Assessment of breath-by-breath alveolar gas exchange: an alternative view of the respiratory cycle. Eur J Appl Physiol 115: 1897–1904, 2015. doi: 10.1007/s00421-015-3169-x. [DOI] [PubMed] [Google Scholar]
- 17. Beaver WL, Wasserman K, Whipp BJ. On-line computer analysis and breath-by-breath graphical display of exercise function tests. J Appl Physiol 34: 128–132, 1973. doi: 10.1152/jappl.1973.34.1.128. [DOI] [PubMed] [Google Scholar]
- 18. Macfarlane DJ. Automated metabolic gas analysis systems. Sports Med 31: 841–861, 2001. doi: 10.2165/00007256-200131120-00002. [DOI] [PubMed] [Google Scholar]
- 19. Beaver WL. Water vapor corrections in oxygen consumption calculations. J Appl Physiol 35: 928–931, 1973. doi: 10.1152/jappl.1973.35.6.928. [DOI] [PubMed] [Google Scholar]
- 20. Macfarlane DJ. Open-circuit respirometry: a historical review of portable gas analysis systems. Eur J Appl Physiol 117: 2369–2386, 2017. doi: 10.1007/s00421-017-3716-8. [DOI] [PubMed] [Google Scholar]
- 21. Porszasz J, Stringer W, Casaburi R. Equipment, measurements and quality control. Eur Respir Monogr 80: 59–81, 2018. [Google Scholar]
- 22. Bradley PW, Younes M. Relation between respiratory valve dead space and tidal volume. J Appl Physiol Respir Environ Exerc Physiol 49: 528–532, 1980. doi: 10.1152/jappl.1980.49.3.528. [DOI] [PubMed] [Google Scholar]
- 23. Garcia-Tabar I, Eclache JP, Aramendi JF, Gorostiaga EM. Gas analyzer’s drift leads to systematic error in maximal oxygen uptake and maximal respiratory exchange ratio determination. Front Physiol 6: 308, 2015. doi: 10.3389/fphys.2015.00308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Porszasz J, Blonshine S, Cao R, Paden HA, Casaburi R, Rossiter HB. Biological quality control for cardiopulmonary exercise testing in multicenter clinical trials. BMC Pulm Med 16: 13, 2016. doi: 10.1186/s12890-016-0174-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Sietsema KE, Stringer WW, Sue DY, Ward SA. Wasserman & Whipp’s Principles of Exercise Testing and Interpretation: Including Pathophysiology and Clinical Applications. UK: Wolters Kluwer Health, 2020. [Google Scholar]
- 26. Feldman PM. find_cross.m, version 2.1 (Online). https://www.mathworks.com/matlabcentral/fileexchange/24063-find_cross-m-version-2-1 [2022 Apr 23].
- 27. Hlastala MP, Wranne B, Lenfant CJ. Cyclical variations in FRC and other respiratory variables in resting man. J Appl Physiol 34: 670–676, 1973. doi: 10.1152/jappl.1973.34.5.670. [DOI] [PubMed] [Google Scholar]
- 28. Aliverti A, Kayser B, Cautero M, Dellacà RL, di Prampero PE, Capelli C. Pulmonary V˙O2 kinetics at the onset of exercise is faster when actual changes in alveolar O2 stores are considered. Respir Physiol Neurobiol 169: 78–82, 2009. doi: 10.1016/j.resp.2009.08.012. [DOI] [PubMed] [Google Scholar]
- 29. Brambilla I, Pizzamiglio R. ABC dei test di Funzionalità Respiratoria (ABC of Respiratory Function Testing). Milan: Masson, 1979. [Google Scholar]
- 30. Wessel HU, Stout RL, Bastanier CK, Paul MH. Breath-by-breath variation of FRC: effect on VO2 and VCO2 measured at the mouth. J Appl Physiol Respir Environ Exerc Physiol 46: 1122–1126, 1979. doi: 10.1152/jappl.1979.46.6.1122. [DOI] [PubMed] [Google Scholar]
- 31. Cala SJ, Kenyon CM, Ferrigno G, Carnevali P, Aliverti A, Pedotti A, Macklem PT, Rochester DF. Chest wall and lung volume estimation by optical reflectance motion analysis. J Appl Physiol (1985) 81: 2680–2689, 1996. doi: 10.1152/jappl.1996.81.6.2680. [DOI] [PubMed] [Google Scholar]
- 32. LoMauro A, Colli A, Colombo L, Aliverti A. Breathing patterns recognition: a functional data analysis approach. Comput Methods Programs Biomed 217: 106670, 2022. doi: 10.1016/j.cmpb.2022.106670. [DOI] [PubMed] [Google Scholar]
- 33. Aliverti A, Pedotti A. Opto-electronic plethysmography. Monaldi Arch Chest Dis 59: 12–16, 2003. [PubMed] [Google Scholar]
- 34. Iandelli I, Aliverti A, Kayser B, Dellacà R, Cala SJ, Duranti R, Kelly S, Scano G, Sliwinski P, Yan S, Macklem PT, Pedotti A. Determinants of exercise performance in normal men with externally imposed expiratory flow limitation. J Appl Physiol (1985) 92: 1943–1952, 2002. doi: 10.1152/japplphysiol.00393.2000. [DOI] [PubMed] [Google Scholar]
- 35. Cautero M, Beltrami AP, di Prampero PE, Capelli C. Breath-by-breath alveolar oxygen transfer at the onset of step exercise in humans: methodological implications. Eur J Appl Physiol 88: 203–213, 2002. doi: 10.1007/s00421-002-0671-8. [DOI] [PubMed] [Google Scholar]
- 36. Steinacker JM, Dehnert C, Whipp BJ. Effect of exercise intensity on the changes in alveolar slopes of carbon dioxide and oxygen expiratory profiles in humans. Eur J Appl Physiol 85: 56–61, 2001. doi: 10.1007/s004210100422. [DOI] [PubMed] [Google Scholar]
- 37. Cettolo V, Francescato MP. Assessing breath-by-breath alveolar gas exchange: is the contiguity in time of breaths mandatory? Eur J Appl Physiol 118: 1119–1130, 2018. doi: 10.1007/s00421-018-3842-y. [DOI] [PubMed] [Google Scholar]
- 38. Koschate J, Cettolo V, Hoffmann U, Francescato MP. Breath-by-breath oxygen uptake during running: Effects of different calculation algorithms. Exp Physiol 104: 1829–1840, 2019. [Erratum in Exp Physiol 105: 919, 2020]. doi: 10.1113/EP087916. [DOI] [PubMed] [Google Scholar]
- 39. Francescato MP, Cettolo V. The “independent breath” algorithm: assessment of oxygen uptake during exercise. Eur J Appl Physiol 119: 495–508, 2019. doi: 10.1007/s00421-018-4046-1. [DOI] [PubMed] [Google Scholar]
- 40. Francescato MP, Thieschäfer L, Cettolo V, Hoffmann U. Comparison of different breath-by-breath gas exchange algorithms using a gas exchange simulation system. Respir Physiol Neurobiol 266: 171–178, 2019. doi: 10.1016/j.resp.2019.04.009. [DOI] [PubMed] [Google Scholar]
- 41. Whipp BJ, Ward SA, Rossiter HB. Pulmonary O2 uptake during exercise: conflating muscular and cardiovascular responses. Med Sci Sports Exerc 37: 1574–1585, 2005. doi: 10.1249/01.mss.0000177476.63356.22. [DOI] [PubMed] [Google Scholar]
- 42. Roux SG, Garcia S, Bertrand B, Cenier T, Vigouroux M, Buonviso N, Litaudon P. Respiratory cycle as time basis: an improved method for averaging olfactory neural events. J Neurosci Methods 152: 173–178, 2006. doi: 10.1016/j.jneumeth.2005.09.004. [DOI] [PubMed] [Google Scholar]
- 43. Ramirez J-M, Baertsch N. Defining the rhythmogenic elements of mammalian breathing. Physiology (Bethesda) 33: 302–316, 2018. doi: 10.1152/physiol.00025.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Feldman JL. Neurophysiology of breathing in mammals. In: Handbook of Physiology. The Nervous System. Intrinsic Regulatory Systems of the Brain. Washington, DC: Wiley Online, 1986, p. 463–524. [Google Scholar]
- 45. Boulding R, Stacey R, Niven R, Fowler SJ. Dysfunctional breathing: a review of the literature and proposal for classification. Eur Respir Rev 25: 287–294, 2016. doi: 10.1183/16000617.0088-2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Ionescu MF, Mani-Babu S, Degani-Costa LH, Johnson M, Paramasivan C, Sylvester K, Fuld J. Cardiopulmonary exercise testing in the assessment of dysfunctional breathing. Front Physiol 11: 620955, 2020. doi: 10.3389/fphys.2020.620955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Bansal T, Haji GS, Rossiter HB, Polkey MI, Hull JH. Exercise ventilatory irregularity can be quantified by approximate entropy to detect breathing pattern disorder. Respir Physiol Neurobiol 255: 1–6, 2018. doi: 10.1016/j.resp.2018.05.002. [DOI] [PubMed] [Google Scholar]
- 48. Forster HV, Haouzi P, Dempsey JA. Control of breathing during exercise. Compr Physiol 2: 743–777, 2012. doi: 10.1002/cphy.c100045. [DOI] [PubMed] [Google Scholar]
- 49. Rossiter HB. Exercise: kinetic considerations for gas exchange. Compr Physiol 1: 203–244, 2011. doi: 10.1002/cphy.c090010. [DOI] [PubMed] [Google Scholar]
- 50. Ward SA. Ventilatory control in humans: constraints and limitations. Exp Physiol 92: 357–366, 2007. doi: 10.1113/expphysiol.2006.034371. [DOI] [PubMed] [Google Scholar]
- 51. Girardi M, Nicolò A, Bazzucchi I, Felici F, Sacchetti M. The effect of pedalling cadence on respiratory frequency: passive vs. active exercise of different intensities. Eur J Appl Physiol 121: 583–596, 2021. doi: 10.1007/s00421-020-04533-z. [DOI] [PubMed] [Google Scholar]
- 52. Girardi M, Gattoni C, Mauro L, Capelli C. The effects of sinusoidal linear drifts on the estimation of cardiorespiratory dynamic parameters during sinusoidal workload forcing: a simulation study. Respir Physiol Neurobiol 289: 103652, 2021. doi: 10.1016/j.resp.2021.103652. [DOI] [PubMed] [Google Scholar]
- 53. Casaburi R, Whipp BJ, Wasserman K, Koyal SN. Ventilatory and gas exchange responses to cycling with sinusoidally varying pedal rate. J Appl Physiol Respir Environ Exerc Physiol 44: 97–103, 1978. doi: 10.1152/jappl.1978.44.1.97. [DOI] [PubMed] [Google Scholar]
- 54. Casaburi R, Whipp BJ, Wasserman K, Beaver WL, Koyal SN. Ventilatory and gas exchange dynamics in response to sinusoidal work. J Appl Physiol Respir Environ Exerc Physiol 42: 300–301, 1977. doi: 10.1152/jappl.1977.42.2.300. [DOI] [PubMed] [Google Scholar]
- 55. Ward SA. Ventilation/carbon dioxide output relationships during exercise in health. Eur Respir Rev 30: 200160, 2021. doi: 10.1183/16000617.0160-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Levett DZH, Jack S, Swart M, Carlisle J, Wilson J, Snowden C, Riley M, Danjoux G, Ward SA, Older P, Grocott MPW; Perioperative Exercise Testing and Training Society (POETTS). Perioperative cardiopulmonary exercise testing (CPET): consensus clinical guidelines on indications, organization, conduct, and physiological interpretation. Br J Anaesth 120: 484–500, 2018. doi: 10.1016/j.bja.2017.10.020. [DOI] [PubMed] [Google Scholar]
- 57. Beaver WL, Wasserman K, Whipp BJ. A new method for detecting anaerobic threshold by gas exchange. J Appl Physiol (1985) 60: 2020–2027, 1986. doi: 10.1152/jappl.1986.60.6.2020. [DOI] [PubMed] [Google Scholar]
- 58. Reinhard U, Müller PH, Schmülling RM. Determination of anaerobic threshold by the ventilation equivalent in normal individuals. Respiration 38: 36–42, 1979. doi: 10.1159/000194056. [DOI] [PubMed] [Google Scholar]
- 59. Whipp BJ, Ward SA, Wasserman K. Respiratory markers of the anaerobic threshold. Adv Cardiol 35: 47–64, 1986. doi: 10.1159/000413438. [DOI] [PubMed] [Google Scholar]
- 60. Puente-Maestu L, Palange P, Casaburi R, Laveneziana P, Maltais F, Neder JA, O’Donnell DE, Onorati P, Porszasz J, Rabinovich R, Rossiter HB, Singh S, Troosters T, Ward S. Use of exercise testing in the evaluation of interventional efficacy: an official ERS statement. Eur Respir J 47: 429–460, 2016. doi: 10.1183/13993003.00745-2015. [DOI] [PubMed] [Google Scholar]
- 61. Swanson GD, Sherrill DL. A model evaluation of estimates of breath-to-breath alveolar gas exchange. J Appl Physiol Respir Environ Exerc Physiol 55: 1936–1941, 1983. doi: 10.1152/jappl.1983.55.6.1936. [DOI] [PubMed] [Google Scholar]
- 62. Cautero M, di Prampero PE, Tam E, Capelli C. Alveolar oxygen uptake kinetics with step, impulse and ramp exercise in humans. Eur J Appl Physiol 95: 474–485, 2005. doi: 10.1007/s00421-005-0038-z. [DOI] [PubMed] [Google Scholar]
- 63. Lamarra N, Whipp BJ, Ward SA, Wasserman K. Effect of interbreath fluctuations on characterizing exercise gas exchange kinetics. J Appl Physiol (1985) 62: 2003–2012, 1987. doi: 10.1152/jappl.1987.62.5.2003. [DOI] [PubMed] [Google Scholar]
- 64. Benson AP, Bowen TS, Ferguson C, Murgatroyd SR, Rossiter HB. Data collection, handling, and fitting strategies to optimize accuracy and precision of oxygen uptake kinetics estimation from breath-by-breath measurements. J Appl Physiol (1985) 123: 227–242, 2017. doi: 10.1152/japplphysiol.00988.2016. [DOI] [PubMed] [Google Scholar]
- 65. Cautero M, di Prampero PE, Capelli C. New acquisitions in the assessment of breath-by-breath alveolar gas transfer in humans. Eur J Appl Physiol 90: 231–241, 2003. doi: 10.1007/s00421-003-0951-y. [DOI] [PubMed] [Google Scholar]