A multichannel graph neural network based on multisimilarity modality hypergraph contrastive learning for predicting unknown types of cancer biomarkers

Abstract

Identifying potential cancer biomarkers is a key task in biomedical research, providing a promising avenue for the diagnosis and treatment of human tumors and cancers. In recent years, several machine learning–based RNA–disease association prediction techniques have emerged. However, they primarily focus on modeling relationships of a single type, overlooking the importance of gaining insights into molecular behaviors from a complete regulatory network perspective and discovering biomarkers of unknown types. Furthermore, effectively handling local and global topological structural information of nodes in biological molecular regulatory graphs remains a challenge to improving biomarker prediction performance. To address these limitations, we propose a multichannel graph neural network based on multisimilarity modality hypergraph contrastive learning (MML-MGNN) for predicting unknown types of cancer biomarkers. MML-MGNN leverages multisimilarity modality hypergraph contrastive learning to delve into local associations in the regulatory network, learning diverse insights into the topological structures of multiple types of similarities, and then globally modeling the multisimilarity modalities through a multichannel graph autoencoder. By combining representations obtained from local-level associations and global-level regulatory graphs, MML-MGNN can acquire molecular feature descriptors benefiting from multitype association properties and the complete regulatory network. Experimental results on predicting three different types of cancer biomarkers demonstrate the outstanding performance of MML-MGNN. Furthermore, a case study on gastric cancer underscores the outstanding ability of MML-MGNN to gain deeper insights into molecular mechanisms in regulatory networks and prominent potential in cancer biomarker prediction.

Introduction

According to the National Cancer Institute (NCI), disease biomarkers are biological molecules found in blood, other bodily fluids, or tissues, serving as indicators of normal or abnormal processes, conditions, or diseases (NCI), such as cancer. Biomarkers can be utilized for various purposes, including assessing cancer risk [1], diagnosing cancer, determining treatment and prognosis responses [2, 3], and monitoring disease progression [4]. In essence, identifying novel cancer biomarkers holds promise for advancing the understanding of cancer pathogenesis and improving cancer diagnosis and treatment [5]. However, conventional approaches to biomarker discovery are often constrained by costly resources and ethical considerations. Therefore, leveraging advanced computational methods to identify reliable candidate targets remains an essential approach for biomarker discovery in research [6].

Compelling evidence indicates that microRNAs (miRNAs) are implicated in nearly all known physiological and pathological processes, including cancer [7]. Noncoding RNAs such as circular RNAs (circRNAs) and long noncoding RNAs (lncRNAs) competitively bind to miRNAs through miRNA response elements (MREs), thereby modulating the expression of target genes and subsequently influencing biological processes, leading to the onset of diseases [8].

Given the significant biological implications of miRNAs, researchers in recent years have explored computational methods for predicting miRNA–disease associations [9]. These methods model prior knowledge from matrix factorization, network structures, and graph structures to extract representative feature descriptors of biomolecules for downstream prediction tasks [10, 11]. By preemptively identifying high-probability candidate miRNAs associated with diseases, this approach has effectively advanced related research. As investigations into competitive endogenous RNAs (ceRNAs) progress, more noncoding RNAs (ncRNAs), including circRNAs and lncRNAs, have been confirmed to participate in miRNA-related regulatory systems [12]. Consequently, there is a growing emphasis on predictive studies related to noncoding RNAs, such as circRNA–miRNA interactions [13–15], circRNA–disease associations [16–18], lncRNA–miRNA interactions [19–22], and lncRNA–disease associations [23–26]. This has established a common paradigm of modeling based on prior singular associations to infer potential molecular interactions.

In fact, while biomarker prediction methods based on singular associations have yielded exciting results and significantly advanced the modeling and analysis of associations between biological medical entities, they do have certain limitations. The primary limitation is that they model and analyze singular associations by isolating the complete regulatory network. Consequently, they may encounter challenges in effectively capturing the full regulatory information of nodes and long-distance dependencies within the network. This limitation directly results in a focus on the high predictive performance of biomarkers of specific types, overlooking the discovery of unknown types of biomarkers. Additionally, these methods also face issues related to the learning and integration of local and global topological structures.

Interestingly, the latest research has begun incorporating multiple types of molecules into association modeling. For instance, Sheng et al. supplemented information by integrating miRNA molecules into lncRNA–disease associations [21]; Wang et al. enriched the circRNA-miRNA-cancer association (CMCA) network with miRNAs in circRNA-cancer associations [27]; Zou et al. integrated eight biological entity relationships to predict potential miRNA-disease associations [28]; Zhao et al. integrated nine interactions between five biomolecules to construct a heterogeneous network HIN to predict potential lncRNA–miRNA associations [29]. This approach represents an inevitable trend as adding nodes effectively mitigates the sparsity of network construction, thereby enhancing prediction efficiency. Unfortunately, while these methods have improved the predictive efficiency of models, the added molecules fail to construct complete regulatory networks, leading to challenges in obtaining global biological regulatory interaction information for the molecules.

On the other hand, almost all biomarker prediction models are trained and predicted based on the same type of prior knowledge. This implies that in case studies examining the practicality of the models, validation of predictive results typically relies on comparing them with existing data from databases or literature. This validation method actually overly relies on the serendipity of dataset construction, making it difficult to obtain convincing results.

To address the aforementioned issues, we propose a novel multichannel graph neural network based on multisimilarity modal hypergraph contrastive learning (MML-MGNN) for predicting different types of cancer biomarkers at the graph level within local and global regulatory networks. Specifically, MML-MGNN constructs competitive endogenous RNA regulatory networks (CENA) for 72 cancers based on experimental reports and then utilizes multisimilarity modality hypergraph contrastive learning (MHCL) to deeply isolate individual molecular associations, learning diverse topological structural insights of molecules across different subassociations, and enhancing differential representations of various structures through contrastive learning (CL). Subsequently, a multichannel graph autoencoder (MCGAE) is employed to receive multimodal local insights of molecules and propagate and aggregate them in the global CENA to obtain molecular feature descriptors with both global and local insights. These descriptors can be used for downstream tasks such as predicting unknown types of biomarkers. It is noteworthy that all data in the downstream prediction task of unknown biomarker types do not participate in feature engineering. MML-MGNN demonstrates competitive performance in predicting three types of biomarkers. Furthermore, in a case study based on gastric cancer, high-probability predictions of three different biomarker types underwent differential expression analysis and expression visualization in normal and cancerous tissues. The results indicate that the predictive outcomes of MML-MGNN are supported by the literature and can predict biomarkers with significant expression differences not reported in the literature, demonstrating the practical value of the proposed method.

Materials and methods

Datasets and materials

In this study, we constructed cancer-related CENA based on reports from existing research. Specifically, the circRNA–miRNA–cancer regulatory network data were sourced from the CircR2Cancer database [30], a manually curated circRNA–cancer association database. The latest version contains 1439 experimentally supported positive samples between 1135 circRNAs and 82 types of cancer. We focused on cancer associations mediated by circRNA–miRNA interactions, ultimately retaining 648 circRNA–cancer associations, 753 circRNA–miRNA associations, and 731 miRNA–cancer associations. The circRNA–miRNA–cancer association dataset was constructed based on our previous research [27], and the 753 circRNA–miRNA associations (CMI-753) dataset is one of the commonly used datasets in the field of circRNA–miRNA interaction prediction.

The lncRNA–miRNA–cancer regulatory network data were obtained from the lncRNAdisease3.0 database [31]. In the latest version, we selected 308 experimentally supported lncRNA–miRNA associations, 732 miRNA–cancer associations, and 1066 lncRNA–cancer associations.

The miRNA–target gene associations were extracted from the miRTarBase database [32]. Among 1 048 576 miRNA–target gene associations, we chose positive samples with experimental support from two or more sources, resulting in 5330 miRNA–target gene associations.

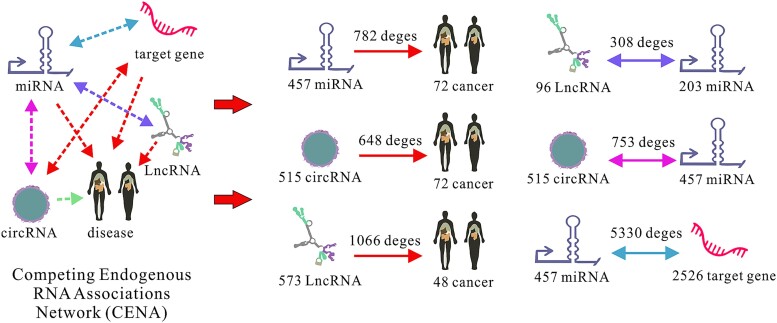
Given the biological process by which various types of RNA (circRNA, lncRNA, mRNA) competitively bind to miRNAs, we utilized miRNAs as intermediate nodes within different subnetworks to construct the CENA. Specifically, nodes targeting the same miRNA were connected to form a comprehensive regulatory network. By integrating the circRNA–miRNA–cancer regulatory network, the lncRNA–miRNA–cancer regulatory network, and the miRNA–target gene associations, we ultimately obtained a competing endogenous RNA network that includes 72 types of cancer, 515 circRNAs, 568 miRNAs, 573 lncRNAs, and 2526 target genes.

The detailed statistical information of the CENA is presented in Table 1. To visually illustrate the construction of various types of regulatory associations within CENA, we have provided a visualization in Fig. 1. This dataset will be used for downstream training and prediction tasks.

Table 1.

The detailed information of the CENA.

Dataset	Edges	miRNA	circRNA	lncRNA	Disease	Gene	Database
MCA	782	457	Non	Non	72	Non	Data integration
CCA	648	Non	515	Non	72	Non	circR2Cancer
LCA	1066	Non	Non	573	48	Non	lncRNAdisease3.0
LMI	308	203	Non	96	Non	Non	lncRNAdisease3.0
CMI	753	457	515	Non	Non	Non	circR2Cancer
MGA	5330	457	Non	Non	Non	2526	miRTarBase
CENA	8887	568	515	573	72	2526	Data integration

Figure 1.

The visualization explanation of CENA.

Multichannel graph neural network based on multisimilarity modal hypergraph contrastive learning

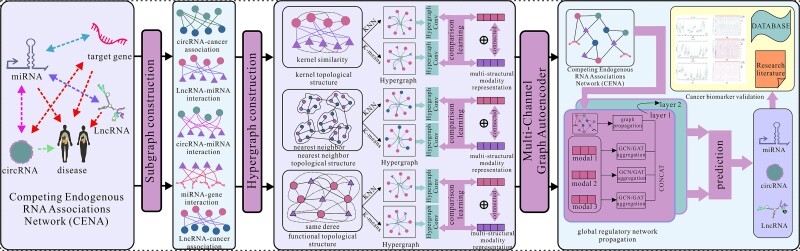
The architecture of MML-MGNN is illustrated in Fig. 2. MML-MGNN learns molecular representations by considering the multisimilarity topological structural modalities of isolated subgraphs in CENA and multifeature propagation in the complete CENA and then identifies potential unknown biomarkers in an end-to-end manner.

Figure 2.

The architecture of MML-MGNN.

Multisimilarity modal

Extracting a comprehensive topological representation of nodes in graph-level tasks remains a major challenge in current research. This is because graph-structured data typically exhibit high complexity and diversity and lacks a fixed topology; the arrangement of nodes and the connections between edges are dynamic and irregular. Consequently, when extracting topological representations of nodes, models must possess the ability to capture both local and global structural information, understanding not only the relationships between neighboring nodes but also the overall structure of the entire graph. At the same time, graph representation learning must balance preserving topological information with avoiding information overload and redundancy. This requires that the model effectively leverage the structural information of the graph while filtering out irrelevant or secondary information. Inspired by multistructural feature extraction in molecular networks [33, 34], we construct comprehensive topological representations of nodes within subgraphs through the incorporation of multisimilarity structures.

In detail, for each independent subgraph, we construct three types of topological similarities for nodes: kernel topological similarity, nearest-neighbor topological similarity, and functional topological similarity. Kernel topological similarity represents the centrality of a node in the graph and its degree of tight connection with other key nodes. It reflects the node’s importance in the global network and helps identify pivotal nodes, revealing their dominant roles in the overall topological structure. Nearest-neighbor topological similarity primarily captures the local structural relationships between a node and its neighboring nodes. By analyzing the local neighborhood around the node, we can understand its position and role within its immediate environment. Functional topological similarity, on the other hand, focuses on the functional roles that a node plays in the network, beyond its mere structural location. This similarity measures the performance similarity of nodes in specific regulatory processes or functional tasks, making it highly relevant to systems with molecular networks.

By integrating these three different types of topological similarities, we can comprehensively capture the multidimensional structural information of nodes within a subgraph, thereby obtaining a more refined topological representation. This multisimilarity structure integration enhances performance in graph-level tasks, enabling models to better adapt to complex network structures. The obtained multisimilarity structural topology will be utilized for further hypergraph construction and hypergraph comparison learning.

Based on the assumption of functional similarity in molecules, i.e. molecules with the same targets may exhibit similar functions, we constructed molecular kernel topology using the adjacency matrix of the subgraph. Taking the miRNA–cancer subgraph as an example, we used the adjacency matrix MC to store the associations between 568 miRNAs and 72 cancers, with MC_ij set to 1 when there is a positive relationship between miRNA i and cancer j and 0 otherwise. The calculation of miRNA Gaussian kernel similarity is as follows:

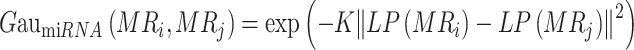(1)

where MR_i and MR_j represent miRNA i and j, respectively, and K is a variable parameter controlling the bandwidth of the Gaussian similarity:

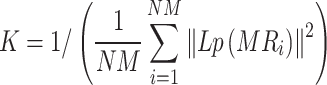(2)

Similarly, the calculation of Gaussian kernel similarity for the cancer is as follows:

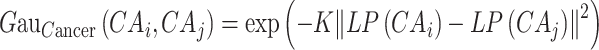(3)

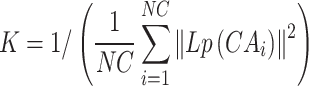(4)

The calculation of miRNA sigmoid kernel similarity is as follows:

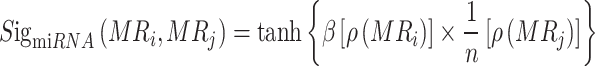(5)

Similarly, the calculation of cancer sigmoid kernel similarity is as follows:

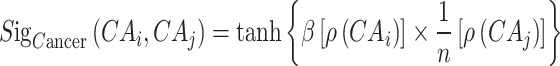(6)

We organically integrate different kernel similarity measures using the following formula:

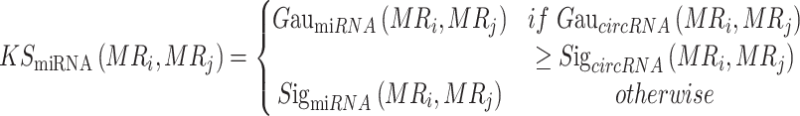(7)

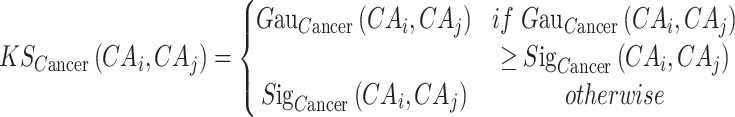(8)

For the molecular similarity of the nearest-neighbor topological structure in the subgraph, we employ a random walk approach [35] to explore the neighbor set of nodes and calculate the neighborhood representation of node MR_i:

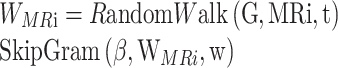(9)

where t represents the maximum extent of random walk, and w represents the size of the predicted context window.

Considering that the nearest-neighbor structure cannot simultaneously capture nodes with similar functions but distant distances, we introduce functional topological structure as a supplement [36]. The functional topological structure is based on the assumption that if nodes have the same degree, they are structurally similar, and, if the neighbors of nodes have the same degree, the nodes are assumed to have higher structural similarity. The functional topological structure utilizes a hierarchical structure to calculate the structural similarity of nodes. When considering the C-hop neighborhood between nodes i and j, the distance d is calculated as:

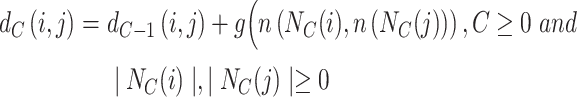(10)

where n represents the ordered sequence of C-order neighboring nodes of node n, N represents the set of C-order neighboring nodes, and g is the distance based on the order sequence. By combining a biased random walk strategy and employing skip-gram [37] training for context, the functional topological structure representation of nodes is ultimately obtained.

Multisimilarity modality hypergraph contrastive learning

In this study, we introduce an MHCL module for learning node multistructural modalities to gain insights into the high-order regulatory correlations within subnetworks. Within the multisimilarity structural modality construction module, we calculate the node kernel topological structure similarity matrix KX, the nearest neighbor topological structure similarity matrix KN, and the functional topological structure similarity matrix KS within the subgraph, respectively. For each structural modality, we use K-nearest neighbors (KNNs) and K-means to construct node-relevant hypergraph matrices HX from the subgraph and then employ hypergraph neural networks to learn embeddings representing different perspectives of each modality. Furthermore, to obtain differentiated insights into embeddings from different perspectives, we incorporate contrastive learning to enforce differential learning of representations from the two perspectives, thereby enhancing insights into the distinct features of molecules.

Taking KX as an example, we initially utilize the Euclidean distance to compute the KNNs of each node in the kernel topological structure, where k is an optional parameter, to establish the node neighbor set, known as a hyperedge. The K-means method randomly selects central nodes of the matrix, calculates the Euclidean distance between each node and this center, and categorizes nodes with closer distances into a subset, i.e. a hyperedge. We represent the hyperedge matrix HX using the hypergraph construction approach:

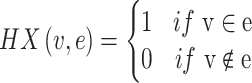(11)

V represents the vertex set of the hypergraph; E denotes the set of hyperedges in the hypergraph, where each hyperedge e is a subset of the vertex set V, representing nodes that are closer in distance to the central node.

We utilize spectral graph convolution on the hypergraph to encode higher-order relationships in the hyperedge matrix HX. Regarding the hyperedge matrix HX, the core representation of hyperedge convolution is as follows:

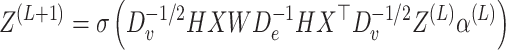(12)

where Z^(L) denotes the aggregated information of the hypergraph over L layers. α represents the hyperedge weight, initialized as an identity matrix, indicating that the weight of each hyperedge is equal. D_e and D_v stand for the degree matrices of hyperedges and vertices, respectively. The degrees of vertex n and hyperedge e are defined as follows:

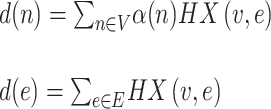(13)

To enhance the diversity and uniformity of node representations in different views of vertices and hypergraph matrices in hypergraph spectral convolution, we introduce a contrastive learning approach to learn node contrastive representations by optimizing the contrastive loss between positive and negative representations.

In detail, for the same node n, we construct two hypergraphs using KNN and K-means, respectively, to explore comprehensive representations of nodes in regulatory networks. For node n, we aim for the representations BN_n learned in the KNN view and BM_n learned in the K-means view to be more similar; thus, BN_n and BM_n are treated as positive representations. For different node representations within the same view, we expect the representation of node n to exhibit significant differences from the representations of other nodes k. Similarly, for different nodes in different views, the representation of node n should demonstrate significant differences from the representations of other nodes k. Therefore, node representations within the same view and node representations in different views are considered as two types of negative representations. To achieve the above objectives, we define the training objective as follows:

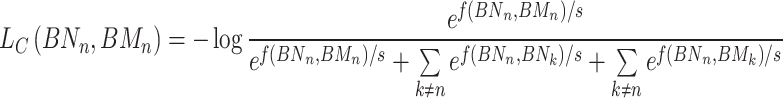(14)

where s is a temperature parameter, and f(BN, BM) = c(l(BN), l(BM)), where c denotes cosine similarity and l represents nonlinear projection.

For the miRNA node set, the contrastive loss of the KNN hypergraph can be defined as follows:

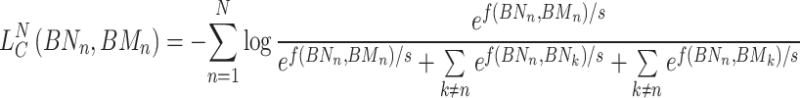(15)

Similarly, the contrastive loss of the K-means hypergraph is defined as:

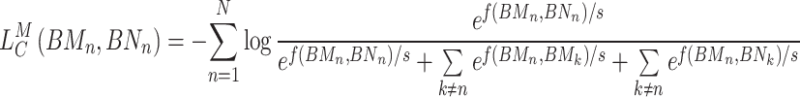(16)

The overall contrastive loss for miRNA can be calculated as:

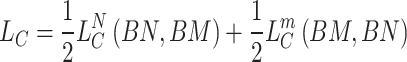(17)

For all molecule sets, we conduct hypergraph contrastive learning on three structural modalities to obtain the structural representations of nodes. Subsequently, these representations are fully connected, and the node’s multistructural modality representation in the subgraph is obtained through an output using a single linear layer.

Multichannel graph autoencoder

MML-MGNN obtains the three structural modality representations of each molecule in the subgraph through MHCL, which represents the local connectivity insights of molecules in the regulatory network. To obtain a comprehensive regulatory network insight of molecules, we construct an MCGAE to propagate and aggregate the multi-structural modality features of molecules in the to obtain nodal feature descriptors benefiting from both local and global perspectives.

The MCGAE consists of three parts: the encoding layer, the hidden layer, and the output layer. The encoding layer takes the three features of nodes as inputs from the undirected graph G, corresponding to the three structural modality representations of nodes and the global CENA. Subsequently, the input multichannel features are mapped to the hidden layer for global network feature aggregation. For each modality representation channel, we provide two propagation layers for feature aggregation: graph convolutional neural network layer and graph attention mechanism layer.

For the input features X_k (k = 3₎ of nodes and the global network graph structure G, the graph convolutional layer aggregates the input features through the following formula:

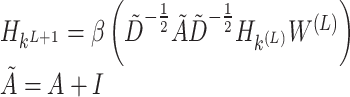(18)

where H_k⁽⁰⁾ is the input feature matrix of the k-th channel, A represents the adjacency matrix of graph G, and I is a diagonal matrix representing the self-connections of nodes. W^(L) is the weight matrix of the L-th layer, and 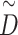is the degree matrix of .

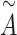The graph attention aggregation layer can be computed as:

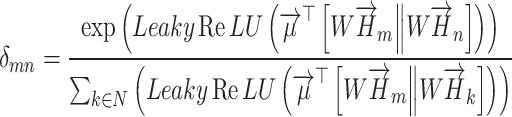(19)

where H is the input feature matrix of the k-th channel, and W^(L) is the weight matrix of the L-th layer.

For each channel of input features in each layer, the feature propagation layers are optional. Through feature propagation in the global graph, we ultimately obtain three types of global representations, denoted as X.

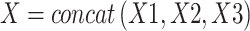(20)

where X1, X2, and X3 represent the structural modal outputs in three channels. We then output X through a decoding layer constructed by a linear transformation layer to obtain the final feature descriptors of nodes.

In the MML-MGNN model, we define the target association prediction task as a binary classification problem. To prevent potential label leakage during feature engineering, all target associations of the same type are excluded from the feature engineering process and reserved solely for downstream prediction tasks. The feature descriptor X, serving as the sole feature for each node, is input into an advanced classifier for training (this study uses Catboost classifier [38] as an advanced classifier to support downstream tasks), which is then used to predict target associations.

Results

Evaluation criteria

In this study, we introduce comprehensive evaluation metrics to assess the predictive performance of MML-MGNN. Specifically, during the model training process, we treat the target associations as the validation set. For each cancer biomarker prediction task, all associations of that type are excluded from network modeling and feature engineering. Subsequently, we feed the molecular features and validation set into advanced classifiers for five-fold cross-validation (5-fold CV).

The detailed process and evaluation criteria of 5-fold CV are shown in the supplementary materials.

Cancer biomarker prediction

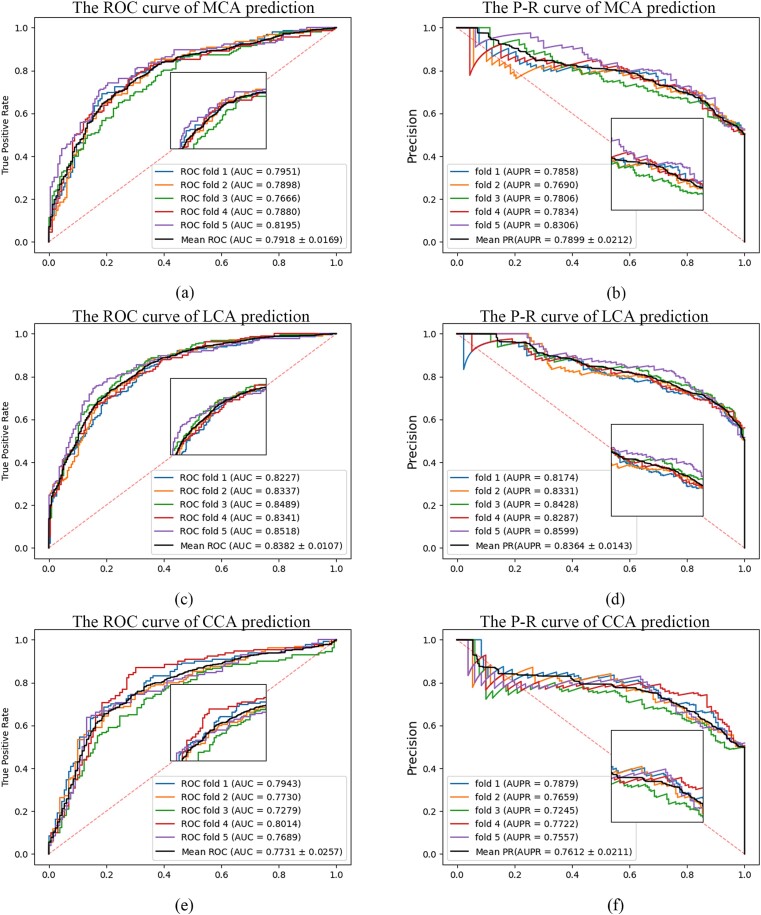
In this section, we perform predictions on tasks involving unknown types of cancer biomarkers (prediction types not included in the feature engineering process). Specifically, we predict three types of cancer biomarkers: miRNA, circRNA, and lncRNA, to validate the predictive capabilities of the proposed method. The objective results of the 5-fold CV are objectively documented in Table 2. Additionally, the Receiver Operating Characteristic (ROC) curve and Precision–Recall (P-R) curve are illustrated in Fig. 3.

Table 2.

The prediction result of the three types of cancer biomarkers.

MCA	Acc	Prec.	Rec.	F1-score	AUC	AUPR
1	0.7412	0.7420	0.7413	0.7410	0.7951	0.7858
2	0.7125	0.7128	0.7124	0.7123	0.7898	0.7690
3	0.6965	0.6969	0.6966	0.6964	0.7666	0.7806
4	0.7284	0.7284	0.7284	0.7284	0.7880	0.7834
5	0.7436	0.7485	0.7436	0.7423	0.8195	0.8306
Mean	0.7244	0.7257	0.7244	0.7241	0.7918	0.7899
std	0.0178	0.0189	0.0178	0.0176	0.0169	0.0212
LCA	Acc	Prec.	Rec.	F1-score	AUC	AUPR
1	0.7400	0.7409	0.7400	0.7398	0.8227	0.8174
2	0.7518	0.7523	0.7518	0.7516	0.8337	0.8331
3	0.7676	0.7681	0.7676	0.7675	0.8489	0.8428
4	0.7488	0.7498	0.7488	0.7486	0.8341	0.8287
5	0.7934	0.7966	0.7934	0.7929	0.8518	0.8599
Mean	0.7603	0.7615	0.7603	0.7601	0.8382	0.8364
std	0.0188	0.0196	0.0188	0.0187	0.0107	0.0143
CCA	Acc	Prec.	Rec.	F1-score	AUC	AUPR
1	0.7231	0.7236	0.7231	0.7229	0.7943	0.7879
2	0.7143	0.7162	0.7145	0.7138	0.7730	0.7659
3	0.6911	0.694	0.6909	0.6898	0.7279	0.7245
4	0.7490	0.7490	0.7490	0.7490	0.8014	0.7722
5	0.7336	0.7377	0.7338	0.7326	0.7689	0.7557
Mean	0.7222	0.7241	0.7222	0.7216	0.7731	0.7612
std	0.0194	0.0189	0.0194	0.0197	0.0257	0.0211

Figure 3.

The ROC and P-R curves of MML-MGNN [(a) and (b) are the ROC and PR curves of MML-MGNN in MCA prediction; (c) and (d) are the ROC and PR curves of MML-MGNN in LCA prediction; and (e) and (f) are MML-MGNN ROC and PR curves in CCA prediction].

As shown in Table 2 and Fig. 3, the average Acc, Prec, Rec, F1, Area Under the ROC Curve (AUC), and Area Under the P-R Curve (AUPR) of MML-MGNN in the prediction of miRNA markers of cancer were 0.7244, 0.7257, 0.7245, 0.7241, 0.7918, and 0.7899, respectively, and in the prediction of lncRNA, the average Acc, Prec, Rec, F1, AUC, and AUPR were 0.7603, 0.7615, 0.7603, 0.7601, 0.8382, and 0.8364, respectively. In the prediction of marker circRNA, the average Acc, Prec, Rec, F1, AUC, and AUPR were 0.7222, 0.7241, 0.7223, 0.7216, 0.7731, and 0.7612, respectively. The above results show that MML-MGNN can effectively predict three different types of cancer biomarkers, and all of them have >75% AUC. Excellent results show that MML-MGNN is a powerful method for predicting different types of biomarkers of cancer.

Optimal feature aggregation method

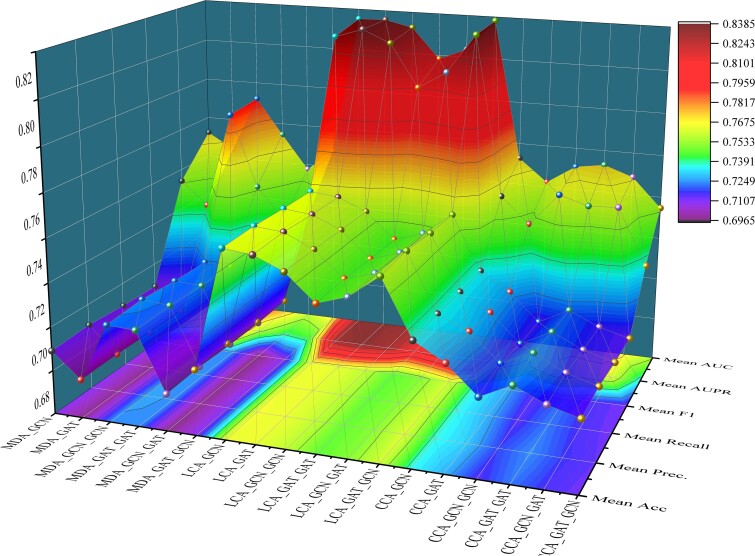
MML-MGNN leverages hypergraph contrastive learning and multichannel graph autoencoder learning in CENA to elucidate the local and global regulatory correlations of nodes. To better accommodate the propagation of node features in the global network and mitigate excessive smoothing, we incorporate various aggregation layer combinations in the multichannel graph autoencoder module, including single-layer GCN, single-layer GAT, two-layer GCN, two-layer GAT, GCN + GAT, and GAT + GCN. In this section, we conduct experiments with different aggregation layers for predicting three cancer biomarkers, aiming to tailor propagation methods that enhance predictive performance specific to different tasks. Experimental results are presented in Table 3 and Fig. 4.

Table 3.

Predictive performance using different aggregation layer combinations.

MCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
GCN	0.7091 ± 0.02	0.7102 ± 0.02	0.7091 ± 0.02	0.7087 ± 0.02	0.7722 ± 0.02	0.7542 ± 0.03
GAT	0.6976 ± 0.02	0.6980 ± 0.02	0.6976 ± 0.02	0.6975 ± 0.02	0.7645 ± 0.01	0.7431 ± 0.02
GCN_GCN	0.7244 ± 0.02	0.7257 ± 0.02	0.7245 ± 0.02	0.7241 ± 0.02	0.7918 ± 0.02	0.7899 ± 0.02
GAT_GAT	0.7238 ± 0.01	0.7245 ± 0.01	0.7238 ± 0.01	0.7236 ± 0.01	0.7744 ± 0.02	0.7550 ± 0.03
GCN_GAT	0.6969 ± 0.02	0.6976 ± 0.02	0.6969 ± 0.02	0.6967 ± 0.02	0.7576 ± 0.02	0.7395 ± 0.03
GAT_GCN	0.7097 ± 0.01	0.7103 ± 0.01	0.7097 ± 0.01	0.7095 ± 0.01	0.7682 ± 0.01	0.7439 ± 0.01
LCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
GCN	0.7645 ± 0.02	0.7651 ± 0.02	0.7645 ± 0.02	0.7644 ± 0.02	0.8353 ± 0.01	0.8315 ± 0.01
GAT	0.7631 ± 0.01	0.7639 ± 0.01	0.7631 ± 0.01	0.7630 ± 0.01	0.8356 ± 0.02	0.8357 ± 0.01
GCN_GCN	0.7575 ± 0.02	0.7577 ± 0.02	0.7575 ± 0.02	0.7575 ± 0.02	0.8326 ± 0.01	0.8300 ± 0.01
GAT_GAT	0.7457 ± 0.03	0.7463 ± 0.03	0.7457 ± 0.03	0.7456 ± 0.03	0.8183 ± 0.02	0.8101 ± 0.03
GCN_GAT	0.7500 ± 0.02	0.7503 ± 0.02	0.7500 ± 0.02	0.7499 ± 0.02	0.8237 ± 0.01	0.8182 ± 0.01
GAT_GCN	0.7603 ± 0.02	0.7615 ± 0.02	0.7603 ± 0.02	0.7601 ± 0.02	0.8382 ± 0.01	0.8364 ± 0.01
CCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
GCN	0.7353 ± 0.01	0.7358 ± 0.01	0.7353 ± 0.01	0.7352 ± 0.01	0.7728 ± 0.01	0.7619 ± 0.02
GAT	0.7276 ± 0.03	0.7299 ± 0.03	0.7276 ± 0.03	0.7269 ± 0.03	0.7622 ± 0.03	0.7499 ± 0.03
GCN_GCN	0.7153 ± 0.02	0.7178 ± 0.03	0.7152 ± 0.02	0.7144 ± 0.02	0.7710 ± 0.02	0.7652 ± 0.04
GAT_GAT	0.7222 ± 0.02	0.7241 ± 0.02	0.7223 ± 0.02	0.7216 ± 0.02	0.7731 ± 0.03	0.7612 ± 0.02
GCN_GAT	0.7160 ± 0.03	0.7173 ± 0.03	0.7159 ± 0.03	0.7154 ± 0.03	0.7684 ± 0.04	0.7619 ± 0.03
GAT_GCN	0.7122 ± 0.03	0.7134 ± 0.03	0.7122 ± 0.03	0.7118 ± 0.03	0.7547 ± 0.02	0.7358 ± 0.02

Figure 4.

Predictive performance using different aggregation layer combinations.

Table 3 and Fig. 4 demonstrate that different aggregation layer combinations achieve optimal predictive performance for various prediction tasks. Moreover, within the same prediction task, different aggregation layer combinations also exhibit notable performance variations. These results underscore the necessity of adopting tailored propagation methods for multitask prediction approaches, highlighting one of MML-MGNN’s strengths. For predicting cancer biomarker miRNA, the GCN + GCN propagation method achieves the best predictive performance with average AUC and AUPR values of 0.7918 and 0.7899, respectively. In contrast, for cancer biomarker lncRNA prediction, the GAT + GCN propagation method yields superior performance, with average AUC and AUPR values of 0.8382 and 0.8364, respectively. Regarding cancer biomarker circRNA prediction tasks, the GAT_GAT and GCN_CGN propagation methods achieve the best average AUC and AUPR values, specifically 0.7731 and 0.7652. Through customized propagation methods, MML-MGNN efficiently enables targeted predictions for different types of cancer biomarkers, demonstrating high adaptability.

Optimal multichannel fusion method

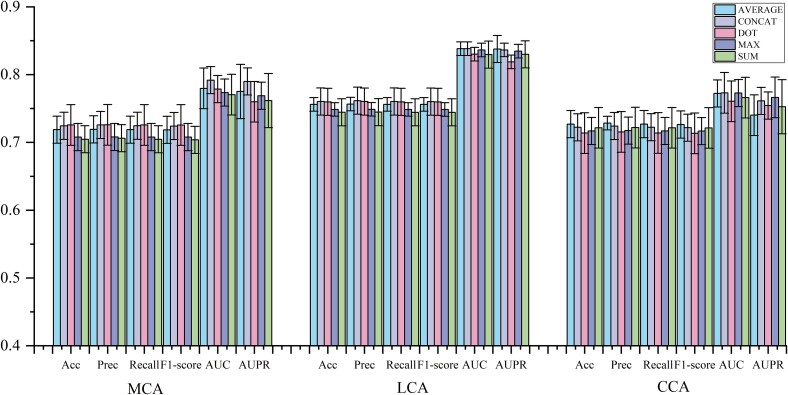
MML-MGNN employs hypergraph-contrastive learning to learn the regulate local singular associations within the network, acquiring diverse structural modalities of node insights. This approach yields three distinctive representations for each node, emphasizing the multimodal nature of node characteristics. By constructing an MCGAE capable of capturing these diverse structural modalities and facilitating global propagation, we focus on determining the optimal method for multichannel feature fusion. Specifically, we explore fusion techniques such as average, concat, dot, max, and sum across three modal channels. Furthermore, we conduct fusion tests on these channels within the context of three biomarker prediction tasks to ascertain the most effective fusion strategy. Experimental outcomes are documented in Table 4 and Fig. 5.

Table 4.

Predictive performance using different channel fusion methods.

MCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
AVERAGE	0.7187 ± 0.02	0.7192 ± 0.02	0.7187 ± 0.02	0.7185 ± 0.02	0.7796 ± 0.03	0.7751 ± 0.04
CONCAT	0.7244 ± 0.02	0.7257 ± 0.02	0.7245 ± 0.02	0.7241 ± 0.02	0.7918 ± 0.02	0.7899 ± 0.02
DOT	0.7257 ± 0.03	0.7259 ± 0.03	0.7257 ± 0.03	0.7256 ± 0.03	0.7786 ± 0.02	0.7599 ± 0.03
MAX	0.7078 ± 0.02	0.7079 ± 0.02	0.7078 ± 0.02	0.7078 ± 0.02	0.7735 ± 0.02	0.7688 ± 0.02
SUM	0.7046 ± 0.02	0.7061 ± 0.02	0.7046 ± 0.02	0.7037 ± 0.02	0.7704 ± 0.03	0.7616 ± 0.04
LCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
AVERAGE	0.7561 ± 0.01	0.7565 ± 0.01	0.7561 ± 0.01	0.7560 ± 0.01	0.8382 ± 0.01	0.8377 ± 0.02
CONCAT	0.7603 ± 0.02	0.7615 ± 0.02	0.7603 ± 0.02	0.7601 ± 0.02	0.8382 ± 0.01	0.8364 ± 0.01
DOT	0.7598 ± 0.02	0.7602 ± 0.02	0.7598 ± 0.02	0.7598 ± 0.02	0.8301 ± 0.01	0.8188 ± 0.01
MAX	0.7486 ± 0.01	0.7488 ± 0.01	0.7486 ± 0.01	0.7485 ± 0.01	0.8363 ± 0.01	0.8346 ± 0.01
SUM	0.7444 ± 0.02	0.7446 ± 0.02	0.7443 ± 0.02	0.7443 ± 0.02	0.8295 ± 0.02	0.8299 ± 0.02
CCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
AVERAGE	0.7269 ± 0.02	0.7284 ± 0.01	0.7269 ± 0.02	0.7263 ± 0.02	0.7722 ± 0.02	0.7402 ± 0.03
CONCAT	0.7222 ± 0.02	0.7241 ± 0.02	0.7223 ± 0.02	0.7216 ± 0.02	0.7731 ± 0.03	0.7612 ± 0.02
DOT	0.7137 ± 0.03	0.7154 ± 0.03	0.7138 ± 0.03	0.7133 ± 0.03	0.7606 ± 0.03	0.7543 ± 0.02
MAX	0.7168 ± 0.02	0.7174 ± 0.02	0.7168 ± 0.02	0.7166 ± 0.02	0.7728 ± 0.02	0.7663 ± 0.03
SUM	0.7215 ± 0.03	0.7218 ± 0.03	0.7215 ± 0.03	0.7213 ± 0.03	0.7660 ± 0.03	0.7526 ± 0.04

Figure 5.

Predictive performance using different channel fusion methods.

The data in Table 4 and Fig. 5 show that among the five channel fusion methods, CONCAT has achieved obvious advantages in three different prediction tasks. Among them, the highest AUC and AUPR were achieved in the prediction of biomarker miRNA, and the highest AUC values were achieved in the prediction of marker lncRNA and circRNA, respectively. This may be because the CONCAT method increases the feature dimension, so it shows a higher advantage in the training and prediction of downstream classifiers. It is worth noting that the other four different fusion methods also achieved expressive prediction performance, showing that the model has a high generalization ability.

Model robustness testing

In this study, we proposed a method MML-MGNN that can predict multiple unknown types of cancer markers. We experimentally verified the prediction performance of MML-MGNN and determined the optimal training parameters. In addition to focusing on the prediction performance of the model, the robustness and generalization of the model in the prediction task are also important references for judging the prediction ability of the model. Therefore, we conduct model robustness testing in this section. Specifically, we randomly interfere with the input node feature matrix by adding random noise and perform model training and prediction. Feature interference is controlled by the interference factor k, which represents the percentage degree of interference. The factor of 0.05 is commonly used for feature perturbation. Additionally, we amplify this factor by 2-fold (0.1) and 10-fold (0.5) to conduct comprehensive robustness testing, aiming to observe the model’s prediction performance under different values of k. The experimental results are recorded in Table 5.

Table 5.

Predictive performance using different k values for robustness.

MCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
0.05	0.7225 ± 0.02	0.7237 ± 0.02	0.7225 ± 0.02	0.7221 ± 0.02	0.7793 ± 0.02	0.7688 ± 0.02
0.1	0.7033 ± 0.01	0.7035 ± 0.01	0.7033 ± 0.01	0.7033 ± 0.01	0.7603 ± 0.01	0.7320 ± 0.01
0.5	0.6963 ± 0.01	0.6972 ± 0.01	0.6964 ± 0.01	0.6960 ± 0.01	0.7568 ± 0.03	0.7258 ± 0.06
Non	0.7244 ± 0.02	0.7257 ± 0.02	0.7245 ± 0.02	0.7241 ± 0.02	0.7918 ± 0.02	0.7899 ± 0.02
Std	0.012	0.0124	0.0121	0.0120	0.0143	0.0264
LCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
0.05	0.7669 ± 0.02	0.7672 ± 0.02	0.7669 ± 0.02	0.7668 ± 0.02	0.8371 ± 0.01	0.8293 ± 0.01
0.1	0.7683 ± 0.02	0.7688 ± 0.02	0.7683 ± 0.02	0.7682 ± 0.02	0.8367 ± 0.02	0.8201 ± 0.02
0.5	0.7373 ± 0.03	0.7379 ± 0.03	0.7373 ± 0.03	0.7372 ± 0.03	0.8181 ± 0.02	0.8146 ± 0.02
Non	0.7603 ± 0.02	0.7615 ± 0.02	0.7603 ± 0.02	0.7601 ± 0.02	0.8382 ± 0.01	0.8364 ± 0.01
Std	0.0124	0.0124	0.0124	0.0124	0.008	0.008
CCA	Acc.	Prec.	Rec.	F1.	AUC	AUPR
0.05	0.7238 ± 0.01	0.7272 ± 0.01	0.7239 ± 0.01	0.7227 ± 0.02	0.7737 ± 0.02	0.7630 ± 0.02
0.1	0.7377 ± 0.02	0.7391 ± 0.01	0.7377 ± 0.02	0.7372 ± 0.02	0.7801 ± 0.02	0.7578 ± 0.02
0.5	0.7330 ± 0.02	0.7346 ± 0.02	0.7331 ± 0.02	0.7325 ± 0.02	0.7668 ± 0.02	0.7443 ± 0.03
Non	0.7222 ± 0.02	0.7241 ± 0.02	0.7223 ± 0.02	0.7216 ± 0.02	0.7731 ± 0.03	0.7612 ± 0.02
Std	0.0064	0.0059	0.0064	0.0066	0.0047	0.0073

The results in Table 5 show that feature perturbation at varying levels has a slight impact on prediction performance across the three prediction tasks. As the percentage of feature perturbation increases, the model exhibits different degrees of performance degradation in predicting the three cancer biomarkers. This effect is more evident in the MCA and LCA tasks, where performance decreases incrementally with increasing perturbation levels. The decline is relatively minor with 0.05 and 0.1 perturbations but more pronounced with 0.5 perturbations. However, overall, the standard deviations of AUC for the three tasks are 0.0143, 0.008, and 0.0047, respectively, and the standard deviations of AUPR are 0.0264, 0.008, and 0.0073, respectively. This indicates that despite varying degrees of feature perturbation, the model’s performance remains stable, demonstrating high robustness. Additionally, in the CCA prediction task, the model performance improved under 0.05 and 0.1 feature perturbations. This improvement may be attributed to the introduction of a moderate amount of noise during training, which could enhance the model’s robustness and generalization, thereby boosting its performance. Overall, the results of the feature perturbation experiment strongly indicate that MML-MGNN exhibits high robustness and generalization ability.

Comparison with state-of-the-art models

In this section, we compare our proposed method, MML-MGNN, with existing state-of-the-art (SOTA) models across multiple prediction tasks to validate its superior performance. Specifically, we evaluate MML-MGNN against SOTA models on cancer-related circRNA biomarker prediction and introduce two independent datasets, CMI-9905 and CMI-9589, for a comprehensive assessment. To the best of our knowledge, MML-MGNN is one of the few methods capable of modeling CNEA, and thus, there is a lack of models that can be directly compared. We incorporate the core methodologies of representative prediction models into the MML-MGNN framework and validate our approach using three independent standard datasets.

In existing studies, the core of SOTA models involves constructing biomedical molecular entity association networks or graphs and utilizing advanced network or graph algorithms to capture behavioral association features of molecules for downstream tasks. The capturing of behavioral features can be broadly categorized into two main types. The first type is based on graph neural networks, focusing on node feature propagation and aggregation. For instance, the GCNCMI model employs graph convolutional networks (GCNs) for node feature propagation [39]; KS-CMI integrates signed graph convolutional neural networks to aggregate features in molecular social networks [27]; WSCD utilizes graph representation via recursive eigenvector propagation (GraRep) to capture multihop behavioral features between nodes [40]. The second type of approach centers on preserving structural information within molecular association networks for downstream prediction and relationship reconstruction tasks. For example, JSNDCMI proposes a multistructural feature extraction framework in molecular networks to extract behavioral features of molecules [41]; KGDCMI employs higher-order embedding preservation to extract high-order structural information of nodes in the network for downstream prediction tasks [13]; and BGF-CMAP combines large-scale information network embedding (LINE) and graph factorization (GF) to capture network structural learning and obtain low-dimensional representations of nodes [42].

In this study, we use graph convolutional neural networks, signed graph convolutional neural networks, GraRep, multistructure feature extraction framework, high-order embedding preservation, LINE, and GF to replace the feature extraction module in MML-MGNN and build GCN, SGCN, WSCD, JSND, KGD, BGFLINE, and BGFGF models for prediction tasks. In order to ensure the fairness of the comparison, we apply the feature extraction methods of these models to three independent prediction tasks and use the same prediction method for comparison.

In the prediction of circRNA–cancer associations (CCAs), we adopt the same training paradigm as in our study, where all circRNA–cancer associations are excluded from feature engineering. The bar charts depicting the evaluation metrics for model comparison are shown in Fig. S1. The box plots for evaluation metrics derived from 5-fold CV are presented in Fig. S2. The average ROC and P-R curves for the models are displayed in Fig. S3. The data distribution of prediction scores is illustrated in Fig. S4.

Fig. S1 shows that in the CCA prediction task, MML-MGNN outperforms SOTA models across four evaluation metrics: ACC, precision, recall, and F1 score, with improvements of 0.0355, 0.0409, 0.0077, and 0.0334, respectively. Fig. S2 presents box plots from 5-fold cross-validation, indicating that MML-MGNN achieves stable standard deviations across all metrics. Fig. S3 shows that MML-MGNN exceeds SOTA models in both AUC and AUPR, with enhancements of 0.0233 and 0.007, respectively, and exhibits lower SDs. Fig. S4 visualizes the distribution of prediction scores, indicating that MML-MGNN effectively distinguishes between positive and negative samples, while SOTA models’ scores tend to concentrate between 0.4 and 0.7, struggling to clearly differentiate samples. This highlights two advantages of MML-MGNN: first, it leverages latent node features through hypergraph learning, demonstrating significant advantages in tasks with long-range associations, especially when feature engineering does not involve target prediction types. Second, the incorporation of contrastive learning further enhances the benefits of hypergraph learning, resulting in higher sample discrimination and improved predictive performance.

In the predictive analysis based on the CMI-9905 dataset, we employed a 5-fold CV for prediction. Additionally, for models incorporating molecular attribute features, we utilized singular value decomposition as the node's initial feature. The evaluation metrics of model comparison are presented in Fig. S5 as a bar chart, the evaluation metrics of 5-fold CV are illustrated in Fig. S6 as a box plot, the average ROC and P-R curves of the models are shown in Fig. S7, and the distribution of prediction scores is depicted in Fig. S8.

Fig. S5 illustrates that MML-MGNN achieves superior prediction results across all four evaluation metrics: ACC, Precision, Recall, and F1. MML-MGNN outperforms the second-best model by 0.012, 0.0312, and 0.0104 in ACC, Precision, and F1, respectively. However, in the Recall metric, MML-MGNN slightly lags behind the second-best model by 0.0032. Fig. S6 demonstrates that MML-MGNN maintains a consistently low SD across all evaluation metrics in five-fold experiments, indicating its robust stability. Fig. S7 depicts that MML-MGNN attains the highest average ROC and P-R curves, outperforming the second-best model by 0.0233 and 0.0185, respectively, with the lowest SDs. These observations unequivocally affirm the superior performance and stability of MML-MGNN. Further analysis through the distribution of model prediction scores, as shown in Fig. S8, reveals that MML-MGNN’s predictions are predominantly clustered in the intervals of 0–0.1 and 0.9–1, with the fewest predictions within the less discriminative range of 0.4–0.6. This underscores MML-MGNN’s remarkable capability in effectively distinguishing between positive and negative samples, highlighting the notable advantages of contrastive learning in differentiating between positive and negative samples.

In comparison to the GCN model, which exhibits a slightly higher Recall, the GCN model demonstrates a lower count in the most discriminative intervals of 0–0.1 and 0.9–1 but captures a higher number of samples in the moderately discriminative ranges of 0.2–0.4 and 0.6–0.9. This discrepancy is influenced by the distinct task objectives and the core objectives of the corresponding algorithms. Specifically, MML-MGNN aims to extract molecular interaction information within complex biological regulatory networks. Therefore, it exhibits a higher advantage in scenarios involving numerous molecular types and extended association distances. The CMI-9905 dataset, composed of two types of molecules, with fewer long-range associations, benefits GCN models that employ short-range adjacency matrices for graph modeling. These models capture molecular behavioral features more effectively, albeit with fewer high-prediction-score samples. Thus, GCN models capture a higher number of positive samples in less discriminative intervals, leading to an elevated Recall. However, this approach may introduce a higher rate of false-positive samples, consequently reducing Precision.

To further validate the conclusions drawn from the CCA and CMI-9905 prediction tasks, we introduce the CMI-9589 dataset for an independent prediction task. As one of the most widely used datasets in the field of CMI prediction, CMI-9589 boasts a higher average node degree, indicating that it is denser and possesses longer-range associations compared to CMI-9905. The prediction methodology for CMI-9589 remains the same as that for CMI-9905. The evaluation metrics for model comparison are presented in a bar chart in Fig. S9. Fig. S10 illustrates the evaluation metrics of 5-fold CV using a box plot. The average ROC and P-R curves of the models are shown in Fig. S11, and the distribution of prediction scores is depicted in Fig. S12.

Fig. S9 demonstrates that MML-MGNN outperforms the SOTA models across all four evaluation metrics, exceeding the second-best model by 0.0335, 0.0232, 0.0213, and 0.0392, respectively. The results in Fig. S10 indicate that MML-MGNN achieves a stable SD across all evaluation metrics during the five-fold experiments, reflecting its robust stability. The average ROC and P-R curves shown in Fig. S11 reveal that MML-MGNN attains the highest average AUC and AUPR, outpacing the second-best model by 0.0306 and 0.0254, respectively, thereby substantiating the superior performance and generalizability of MML-MGNN.

In the distribution of model prediction scores depicted in Fig. S12, the prediction distribution exhibits a pattern similar to that observed in the CMI-9905 dataset. Specifically, MML-MGNN’s prediction scores are predominantly concentrated in the intervals of 0–0.1 and 0.9–1, with fewer samples in the less discriminative range of 0.4–0.6. The GCN model shows a lower count in the most discriminative intervals, 0–0.1 and 0.9–1, but captures a higher number of samples in the moderately discriminative intervals of 0.2–0.4 and 0.6–0.9. This finding corroborates our analysis from the CMI-9905 prediction task. Different from CMI-9905, since the CMI-9589 dataset has fewer molecules and longer association behaviors, the number of positive samples captured by MML-MGNN in the 0.9–1 interval is much higher than the positive samples captured by GCN in the interval with lower discrimination, so the recall of MML-MGNN is higher than that of GCN. For the SGCN model, which captures the highest number of samples in the 0–0.1 interval, the performance in predicting positive samples is notably inferior, with the number of negative samples far surpassing that of positive samples. This indicates that the model generates an excessive number of false negatives. Consequently, the model exhibits suboptimal performance and demonstrates poor stability.

Overall, the comparative results with SOTA models unequivocally demonstrate the superior and competitive performance of MML-MGNN in predicting biomarkers of unknown cancer types.

Case study on cancer marker prediction

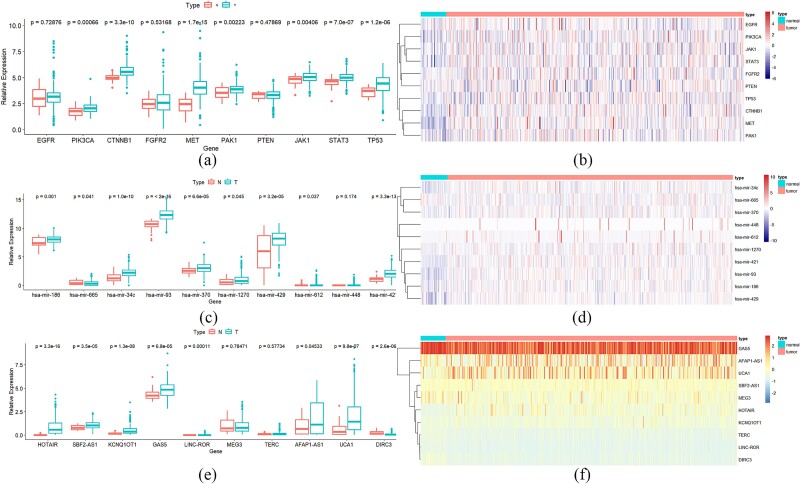
To validate the practicality of MML-MGNN in predicting different types of cancer biomarkers, we conducted a study focusing on the prediction of gastric cancer biomarkers, encompassing target genes, miRNAs, and lncRNAs. The study was designed to assess MML-MGNN’s capability in biomarker discovery through differential expression analysis and by referencing existing literature. Specifically, we employed the MML-MGNN to predict high-probability candidates for the three types of gastric cancer biomarkers. Subsequently, we downloaded gastric cancer and normal tissue samples from the Cancer Genome Atlas [43] for differential expression analysis. In this analysis, we classified normal and primary tumor tissues and calculated the differential expression value (P) for the high-probability candidates. It was deemed that when P < .05, there was a statistically significant difference between the two groups. To further confirm the differential expression of the cancer biomarkers, we generated a visual heatmap to illustrate the expression potential of the cancer biomarkers across different types of tissues. The experimental results are documented in Fig. 6 and Table 6.

Figure 6.

The analysis of differential expression and expression heatmap for the three biomarkers in gastric cancer [(a), (c), and (e) represent the differential expression analysis results of genes, miRNAs, and lncRNAs in cancer tissue and adjacent tissue; (b), (d), and (f) represent the gene expression heatmaps of genes, miRNAs, and lncRNAs in cancer tissue and adjacent tissue].

Table 6.

Examination results of three cancer markers predicted by MML-MGNN in existing studies.

Num	Gene	Cancer type	Evidence	Differential expression
1	EGFR	Gastric cancer	PMID: 34618022	N
2	PIK3CA	Gastric cancer	PMID: 31908498	Y
3	CTNNB1	Gastric cancer	PMID: 31889902	Y
4	FGFR2	Gastric cancer	PMID: 34307360	N
5	MET	Gastric cancer	Unconfirmed	Y
6	PAK1	Gastric cancer	PMID: 36636079	Y
7	PTEN	Gastric cancer	PMID: 36636064	N
8	JAK1	Gastric cancer	PMID: 36483041	Y
9	STAT3	Gastric cancer	PMID: 36483041	Y
10	TP53	Gastric cancer	PMID: 36477655	Y
Num	miRNA	Cancer type	Evidence
1	Has-mir-34c	Gastric cancer	PMID: 36316351	Y
2	Has-mir-370	Gastric cancer	PMID: 35957833	Y
3	Has-mir-612	Gastric cancer	PMID: 35581633	Y
4	Has-mir-448	Gastric cancer	PMID: 35528235	N
5	Has-mir-665	Gastric cancer	PMID: 35322746	Y
6	Has-mir-93	Gastric cancer	PMID: 35183057	Y
7	Has-mir-1270	Gastric cancer	PMID: 34986743	Y
8	Has-mir-429	Gastric cancer	PMID: 34976174	Y
9	Has-mir-421	Gastric cancer	PMID: 34938121	Y
10	Has-mir-186	Gastric cancer	PMID: 34900056	Y
Num	lncRNA	Cancer type	Evidence
1	SBF2-AS1	Gastric cancer	PMID: 36549764	Y
2	GAS5	Gastric cancer	PMID: 36316351	Y
3	LINC-ROR	Gastric cancer	PMID: 36299522	Y
4	MEG3	Gastric cancer	PMID: 36299522	N
5	TERC	Gastric cancer	PMID: 36267723	N
6	AFAP1-AS1	Gastric cancer	PMID: 36164273	Y
7	UCA1	Gastric cancer	PMID: 35949302	Y
8	DIRC3	Gastric cancer	PMID: 35949302	Y
9	HOTAIR	Gastric cancer	PMID: 35949302	Y
10	KCNQ1OT1	Gastric cancer	PMID: 35910231	Y

The data from Fig. 6 and Table 6 indicate that, among the 10 high-probability target gene biomarkers predicted by MML-MGNN, seven genes exhibit significant expression differences across various tissue types. This finding is further corroborated by the heatmap of target gene expression, which clearly demonstrates differential expression across multiple tissues. Additionally, 9 out of the 10 candidate target genes have been validated by existing literature, underscoring the efficacy of MML-MGNN in identifying potential biomarkers and effectively excluding low-expression data and tissue-specific interference. This capability is particularly evident in the miRNA and lncRNA expression analysis results.

In the current analysis, technical limitations associated with probes often hinder the effective detection of low-expression biomarkers. However, MML-MGNN shows a marked advantage in predicting these low-expression biomarkers. While Figures c and e indicate that nine miRNAs and eight lncRNAs exhibit significant expression differences, these differences are less pronounced in the differential expression heatmap. Nevertheless, MML-MGNN successfully predicted the existence of these biomarkers, with its predictions validated by existing literature, further highlighting the model’s substantial advantages and utility in processing low-expression biomarker data. Thus, MML-MGNN not only demonstrates high efficacy in target gene prediction but also excels in filtering out interference from low-expression data and handling tissue-specific influences. These strengths position MML-MGNN as a reliable method for identifying candidate biomarkers in related research.

Discussion

Cancer diagnosis, treatment, and prognosis have long been focal points of biomedical research. Identification of cancer biomarkers offers promising avenues for advancing cancer-related studies. With the evolution of machine learning methods, computational approaches can efficiently sift through vast datasets to uncover potential high-probability biomarker candidates, thus saving time, manpower, and resources in wet lab experiments.

However, constrained by reductionism and machine learning limitations, existing research typically employs task modeling through isolated regulatory networks with target associations, leading to an overemphasis on high-performance requirements within a single association. This approach has achieved advanced prediction results and has effectively promoted progress in related fields. Nonetheless, focusing excessively on modeling and predicting single associations has the drawback of overlooking the overall associations in regulatory networks and the discovery of unknown types of biomarkers.

As research progresses, researchers have begun attempting to construct large heterogeneous networks to enrich the molecular interaction information within single association networks, achieving promising results. Despite these advancements, the fundamental objective remains to address sparsity in network modeling, with the incorporated molecules failing to construct a complete regulatory network. Consequently, existing research still lacks comprehensive graph-level modeling and node interaction information extraction within complete regulatory networks. Moreover, current computational models generally validate their practical utility by comparing their prediction results with existing research data and literature. However, the potential for label leakage and the fortuitous nature of data construction render this validation approach less convincing.

To address this situation, we propose a method called MML-MGNN, capable of predicting multitype cancer biomarkers, and construct the cancer-related CENA. MML-MGNN leverages hypergraph contrastive learning to obtain multimodal local insights of nodes within individual associations and then propagates molecular features globally through a multichannel graph neural network, effectively capturing both local and global regulatory behaviors of molecules. We tested our method on the prediction tasks of three types of biomarkers: miRNA, lncRNA, and circRNA, achieving robust performance. In comparative studies with existing research, MML-MGNN demonstrated competitive performance. Notably, target prediction associations do not participate in the feature engineering process, enabling MML-MGNN to efficiently predict unknown association types.

To further validate the practical utility of our computational model, we introduce a case study approach with high reference value. Specifically, our model predicts high-probability potential biomarker candidates for the gastric cancer. We then conduct differential expression analysis of these biomarkers in cancerous versus adjacent normal tissues, constructing an expression matrix. By examining whether the biomarkers show significant differential expression between cancer and normal tissues and combining this with preliminary observations from the expression matrix, we identify potential candidates. Finally, we verify whether these candidates have the potential as disease biomarkers through comparison with existing literature and databases. This approach effectively addresses the challenge of performance validation for the model in real-world scenarios.

While the results are indeed exciting, there remains room for improvement. Firstly, the data used for CENA construction, though supported by experiments, are sparse due to the difficulty in collection, which poses challenges for modeling and prediction. Additionally, the absence of molecular attribute features, including RNA sequences and descriptions, limits multi-modal feature processing. Despite these limitations, the first modeling and prediction tasks for CENA have yielded surprising results, providing a reference example for future research. We hope to continuously improve the biomarker data and related algorithms in subsequent studies to enhance the model’s predictive performance and efficiency in biomarker discovery.

Key Points

• A novel multi-channel graph neural network based on multisimilar modal hypergraph contrastive learning (MHCL) is proposed for predicting different types of cancer biomarkers at the graph level of local and global regulatory networks.

• Deeply separate individual molecular associations using multisimilarity MHCL and learn different topological insights of molecules in different subassociations.

• A multichannel graph autoencoder is employed to receive multimodal local insights of molecules and propagate and aggregate them in a global competitive endogenous RNA regulatory network to obtain molecular feature descriptors with global and local insights.

• It can predict biomarkers with significant expression differences and be verified by literature, which has a high practical value.

Author contributions

X.-F.W., H.L., W.Y.: conceptualization, methodology, software. H.L., W.Y., R.-C.G., Z.-H.Y.: resources and data curation. X.-F.W., S.N., X-.P.X., Q.-X.Y.: validation. All authors contributed to the manuscript revision and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No.62072212), the Jilin Provincial Scientific and Technological Development Program (No.20230201065GX, 20240101364JC) and the Jilin Provincial Key Laboratory of Big Data Intelligent Cognition (No.YDZJ202402075CXJD).

Data availability

The data and source code can be found at https://github.com/1axin/MML-MGNN.