Is stochastic thermodynamics the key to understanding the energy costs of computation?

Abstract

The relationship between the thermodynamic and computational properties of physical systems has been a major theoretical interest since at least the 19th century. It has also become of increasing practical importance over the last half-century as the energetic cost of digital devices has exploded. Importantly, real-world computers obey multiple physical constraints on how they work, which affects their thermodynamic properties. Moreover, many of these constraints apply to both naturally occurring computers, like brains or Eukaryotic cells, and digital systems. Most obviously, all such systems must finish their computation quickly, using as few degrees of freedom as possible. This means that they operate far from thermal equilibrium. Furthermore, many computers, both digital and biological, are modular, hierarchical systems with strong constraints on the connectivity among their subsystems. Yet another example is that to simplify their design, digital computers are required to be periodic processes governed by a global clock. None of these constraints were considered in 20th-century analyses of the thermodynamics of computation. The new field of stochastic thermodynamics provides formal tools for analyzing systems subject to all of these constraints. We argue here that these tools may help us understand at a far deeper level just how the fundamental thermodynamic properties of physical systems are related to the computation they perform.

Information technology accounted for roughly 6 to 10% of world electricity usage in 2018, resulting in a greater carbon footprint than all civil aviation (1, 2). This demand for computational power is only expected to grow, increasing energy costs to society and the environment. Unsurprisingly, reducing energy requirements has become a central concern for the engineering of computers (3).

How does all of this energy usage depend on the details of how the computation is physically implemented, as well as the computational problem itself? The relationship between the unavoidable energetic costs of carrying out a computation in a physical system and the details of that computation is a deep issue that has been of concern in the physics community for close to two centuries (4, 5). For a long time, it was thought that a lower limit on this cost is given by the original version of Landauer’s bound (6). This stated that the “thermodynamic cost” of erasing a bit in a physical system was always $k_{B}Tln2$, where $k_B$ is Boltzmann’s constant, and $T$ is the temperature of the system.

The modern, fully formal version of this bound applies to any physical system that evolves for a fixed period while in contact with one or more thermal reservoirs. Like all of statistical physics, this modern version of the bound involves the change in the probability distribution over the states of a physical system during its evolution. Specifically, the bound says that the sum over the reservoirs, of the net energy flow of energy to those reservoirs divided by that reservoir’s temperature, is lower-bounded by the drop in Shannon entropy of the system.

Unfortunately, Landauer’s bound is almost useless for analyzing real-world computers. The problem is that the bound is only saturated when there are no constraints on the processes that can be used to implement the computation, i.e. when we can consider any process whatsoever to achieve the desired change in Shannon entropy. However, real-world computers are almost all subject to constraints on the processes they can use. Such constraints invariably mean that the process must have nonzero “irreversible entropy production (EP),” which is an energetic cost over and above the cost demanded by Landauer’s bound.

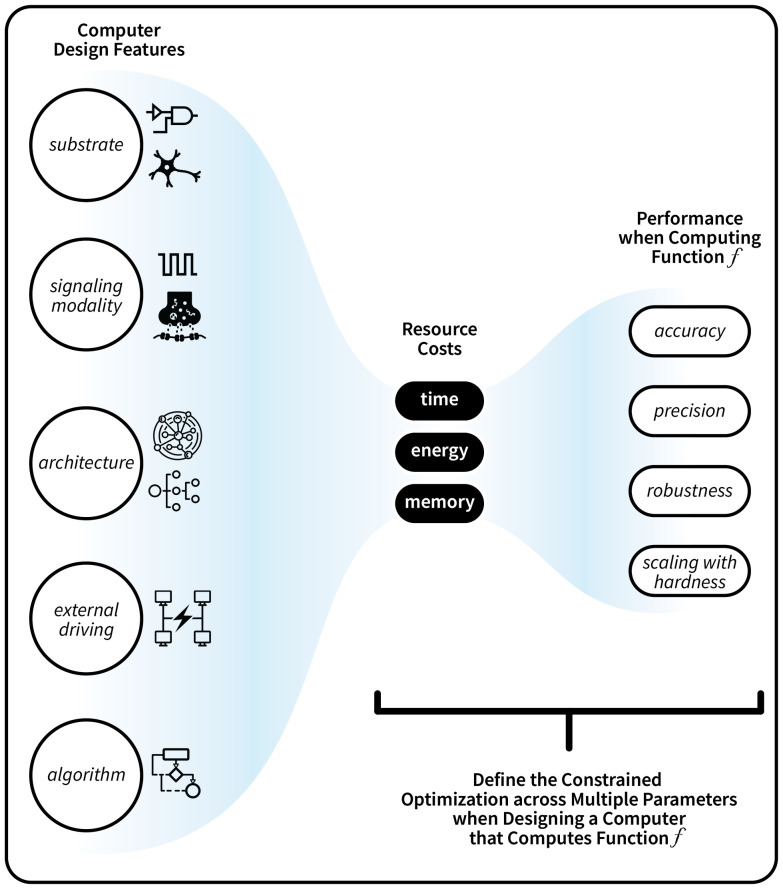
For example, almost all real-world computations must finish in some given, finite time. The thermodynamic speed limit theorems (SLTs) provide nonzero lower bounds on the EP, which increases as the required time shrinks. Furthermore, almost all digital computers run in a periodic process, where an electronic clock on the chip is used to ensure that the exact same process is used to implement each iteration of any desired computation. However, as described below, any periodic process has a nonzero EP. Finally, consider two separate bits that are erased in parallel. Each such bit eraser, considered by itself, achieves Landauer’s bound. However, suppose that the initial states of the bits are statistically coupled. In this case, even though each bit-eraser considered by itself is thermodynamically reversible, the joint system of the two bits is not thermodynamically reversible. The map between a computer’s design features and performance is shown in Fig. 1.

Fig. 1.

The mapping between the design features of a computer and its performance when computing a function is mediated by its resource costs.

The general theory underlying these examples is a set of revolutionary recent advances in nonequilibrium statistical physics, often called stochastic thermodynamics (7–10). This exploding field provides precisely the tools required to analyze the thermodynamics of far-from-equilibrium systems—like computers. The implications of stochastic thermodynamics for running computers are just starting to be explored.

These extra unavoidable costs mean Landauer’s bound is far below the actual energy costs of computers.^* This has been verified in numerous investigations of detailed physical models of computers, like complimentary metal-oxide semiconductor (CMOS)-based electronic circuits (11, 12), as well as biological systems like brains (13). These investigations also reveal deep relationships between the thermodynamics of different kinds of physical systems that we characterize as “performing computation.” For example, ribosomes perform simple decoding computations at an energy cost within an order of magnitude of Landauer’s bound (14). In contrast, typical artificial computers can only reach within multiple orders of magnitude of Landauer’s bound (15).

Are there fundamental reasons for the yawning gap between the energetic efficiency of the computers we build and those found in nature? If so, can they be at least partially circumvented? Why do even biological computers require so much more energy than the minimum given by Landauer’s bound, in light of the fact that energy use is one of the most important fitness costs in biological evolution?

We argue below that the time is ripe to use stochastic thermodynamics to investigate the relationship between i) the energy usage of physical computational systems, ii) their other performance metrics [e.g., their “space” and “time” complexity, in the sense of those terms investigated in computer science (CS) theory], and iii) constraints on the allowed physical processes in those computers. Such investigations can potentially generate breakthroughs in the design of artificial computers that expend less energy. They may also reveal insights into the relationship between artificial and biological computers.

For experts in stochastic thermodynamics, these investigations provide new kinds of dynamical systems to analyze (namely, those that implement computational machines). For CS theorists, they provide new kinds of resource costs to analyze (namely, those grounded in statistical physics). For scientists as a whole community, they may provide important new insights into physical systems of many types.

1. Background

The term “computation” is semiformally used in many fields (16–19). It is also sometimes called “information processing” in this literature. The common thread uniting the various approaches is that a physical system is “computing” if its dynamics modifies the distribution over the variables of the system, with some subset of those variables identified as “information-bearing degrees of freedom (IBDF).” [Sometimes certain subsets of these IBDF are referred to as input, output, or temporary data variables (6, 20).]

Unfortunately, neither the term “information processing” nor the term “computation” is ever defined in this literature in a way that is both formal and broadly applicable. More precisely, there is no consensus on how to define precisely what computation an arbitrary given dynamic system does.^† At present, the only universal agreement of how to define “computation” is that whatever else computation is, it includes the digital systems analyzed in CS theory as special cases. In addition, these are the computational systems that have received the most attention in the stochastic thermodynamics community. In light of this, we focus on the digital systems considered in CS theory in this perspective.^‡

To begin, in the next subsection, we present some relevant background on CS theory. After that, we present some background on stochastic thermodynamics.

1.1. Theoretical Computer Science.

Much of theoretical CS is concerned with the minimal resources needed to solve computational problems with some abstractly defined computational machine (23–25). Each such computational machine is a generic model of any entity that computes (transforms an input into an output). There is a set of one or more natural “resource costs” for all commonly studied computational machines. One of the core concerns of CS theory is how the minimal resource costs required to solve a given computational problem on a given computational machine depend on the size of the instance of the problem. In the rest of this subsection, we elaborate on this high-level description of CS theory, underscoring why it is of central importance in designing real computers.

An important example of a computational machine is the Turing machine (TM) (26). This is an abstract, nonphysical device that scans back and forth over one or more “tapes” containing infinite sequences of bits. The input to the TM (e.g., a list of integers to be sorted) specifies the initial string on a tape. The output (e.g., the sorted version of that list of integers) is given by the bit string on a tape of the TM when the TM enters a special “halt state.” TMs have a natural notion of a resource cost involving “time” (the number of operations the TM runs before completing a computation) and a resource cost involving “space” (the number of tape cells used by the TM to complete the computation).

Another frequently studied computational machine is a Boolean circuit (24), which is a directed acyclic graph (DAG) where each node implements a Boolean operation (a “gate”). The full graph executes a Boolean function by mapping the input bit string (written onto the bits at the roots of the DAG) through the intermediate gates to an output bit string (sequence of bits produced at the leaves of the DAG). Natural resource costs for Boolean circuits include the total number of gates and the maximal number of directed links from any input node to any output node. These roughly correspond to the time cost and space cost, respectively.

Another set of computational models is designed for investigating distributed sets of interacting computers, e.g., multiple (perhaps very many) computers connected in a network. Associated costs include the total number of asynchronous messages sent among the computers and the number of “rounds” of communication required by the system.

In CS theory, a “computational problem” that a computational machine may be tasked with is defined as a set of instances of that problem that must be solved. For example, one of the most important computational problems is integer sorting (24). Each instance of this problem is specified by a list of integers, and the associated solution is that set of integers sorted into ascending order.

A well-studied issue is how the worst-case number of iterations required by a TM to sort a list of $n$ integers scales with $n$. In particular, the class $\text{P}$ is the set of all computational problems that can be solved using a TM that is guaranteed to halt on an instance of size $n$ “in polynomial time,” i.e., within a number of iterations that is a polynomial function of $n$. The class $\text{NP}$ is instead the set of computational problems such that a solution to the problem can be verified by a TM in polynomial time. One of the deepest open questions in mathematics and theoretical CS is whether $\text{P}=\text{NP}$.

The main reason for analyzing any of the resource costs formalized in CS theory is that those costs approximate important operating costs that arise when solving computational problems on real physical systems like digital computers. For example, consider a problem that requires a TM to undergo a number of steps, which is roughly exponential as a function of the input size. This problem will also require exponentially many operations as a function of the input size to run on a real, digital computer.^§

Most previous investigations in CS theory have ignored a primary resource cost of any real computer—the energy it uses to run. One notable exception is an attempt to formalize the energy complexity of algorithms (27). Unfortunately, the study uses Landauer’s bound to guide their investigations, which leads to the misunderstanding of the thermodynamic costs of far-off equilibrium systems that we discussed in the Introduction. In hindsight, this is not surprising. Only recently have physicists had the framework (stochastic thermodynamics) to calculate energy usage of out-of-equilibrium systems, and so provide computer scientists with the theoretical tools to explore how energy scales with the size of a problem.

Note that computational complexity theory analyzes how the resource costs of computational problems scale with the size of the (instance of the) problem (24). Typically, these analyses concern worst-case resource costs, mostly due to mathematical tractability. However, other types of costs, including “average-case complexity”, “derandomization” or “hardness amplification” are also studied (24). Most importantly, though, many real computation tasks do not typically operate on worst-case inputs but rather on a set of many different inputs with different occurring frequencies. By calculating the average quantities over the set of all possible inputs, we can more accurately estimate the performance of an algorithm when repeatedly used to perform a computation on many possible inputs.

Accordingly, all information theory considers systems with stochastic inputs (28). Similarly, statistical physics involves distributions, including stochastic thermodynamics. This is illustrated in the following subsection.

1.2. Statistical Physics.

Throughout the 20th century, the thermodynamics of computation focused on questions of whether an intelligent being could violate the second law of thermodynamics through measurement and feedback (4, 5) and erasure (6, 20) of single bits. Although modern approaches have resolved the paradoxes brought up by these systems (29–31), they retain wide resonance throughout the physics community and have remained a focus of investigation (32, 33), mostly due to mathematical tractability.

Statistical physics, which analyzes the behavior resulting from large collections of components, offers a potential pathway to widen the prior focus to more complex systems. Most of the research in statistical physics through the end of the 20th century considered systems modeled to be at (a perhaps local) thermodynamic equilibrium. These systems are either static, undergoing quasi-static evolution, or undergoing some first-order perturbation around such evolution, as, for example, they are in a local equilibrium that evolves quasistatically (i.e., infinitely slowly). Thus, they cannot complete a computation in finite time.

Accordingly, analyzing real computers requires extending equilibrium statistical physics to concern systems with many nonhomogeneous degrees of freedom evolving quickly while far from thermodynamic equilibrium. Over the past two decades, stochastic thermodynamics, an important development in the study of nonequilibrium systems, has provided a framework for addressing this need in both theoretical computer science and the physics of computation (7, 8).

Stochastic thermodynamics is the extension of thermodynamics which allows us to analyze heat, work, and entropy at the level of individual trajectories generated in a physical system that is evolving arbitrarily quickly while arbitrarily far from thermal equilibrium (7). For a brief introduction to stochastic thermodynamics, see ref. 8 and see refs. 9 and 10 for textbook-length introductions. For a physical system that is evolving while coupled to $N$ thermal reservoirs at temperatures $T_i$, the entropy production can be expressed as

$$\begin{array}{c}\hfill \sigma =\mathrm{\Delta }S+{\displaystyle \sum _{i=1}^N}\frac{Q_i}{k_B{T}_i}.\end{array}$$ [1]

In this formula, $\mathrm{\Delta }S$ is the change in entropy between the probability distributions of the input and output states and $Q_i$ is the heat flow out of the system to the heat reservoir $i$. The second law of thermodynamics states that $\sigma \ge 0$, no matter what physical process transpires.

Crucially for the analysis of computers, all of this holds whether we consider an entire computer (e.g., a modern digital computer) or subsystems of that computer (e.g., individual gates on a circuit, or individual circuits in a digital computer). It also holds no matter how long the time interval we are considering, e.g., a single cycle of a clock in a synchronous computer, or the time for the computer to complete an entire run of calculating the output given by running an algorithm on an input.

To illustrate Eq. 1, consider a physical system performing a computation task (e.g., sorting a list of inputs). Suppose we define a probability distribution over possible inputs and a particular algorithm for the task. For sorting, this would be the joint distribution over input lists. With these specifications, the joint distribution of input, intermediate, and output variables is fixed, and so is the entropy change $\mathrm{\Delta }$S. Applying the nonnegativity of EP to Eq. 1 gives the “generalized Landauer bound,” which states that total entropy flow cannot be less than the entropy change $\sum _i\frac{Q_i}{k_B{T}_i}\ge -\mathrm{\Delta }S$

Note, that the term $\mathrm{\Delta }S$ in the generalized Landauer bound can be quite small. Indeed, in many models of biological computational systems like those that occur inside cells, the system is in a steady state—so there is no change in entropy in time. Similarly, consider a clocked, Boolean circuit of depth $L$ that is run repeatedly, with IID inputs. In both cases, $\mathrm{\Delta }S=0$.

However, even when the change in entropy is strictly positive, the generalized Landauer bound is a tiny fraction of the heat generated by running the process in real-world computers. This is due to the fact that the factors of $k_B{T}_i$ in Eq. 1 are so small compared to the heat flow generated in real-world computers. Moreover, the difference between the heat flow and the change in entropy of a computer depends on the details of the physical system implementing that computer. [For example, they depend on whether a given sorting algorithm is implemented on a system that uses CMOS technology (34) or something else.] Since Eq. 1 is an exact equality, the total EP will vary with the details of the physical process.

Consequently, relying solely on the Landauer bound misses the effect of the large, EP in real computations, which often dominates the total thermodynamic cost. Even biological computers that are far more energetically efficient than our current artificial ones (14, 35) only come within an order of magnitude or two of the generalized Landauer bound. So, Eq. 1 tells us that almost all the dissipated heat (energy cost) of actual computers comes from the EP.

As technology continues to improve, the minimum achievable EP—subject to constraints on the materials involved and other restrictions on the physical process—may rapidly become the primary limitation on the energy costs of real computers. However, it is now known that essentially any constraint results in strictly positive EP (36, 37). In the rest of this section, we discuss some important special cases.

As a first example, one possible source of EP in computation is the mismatch cost (38, 39). Write the initial distribution over states of a system that minimizes EP as $q_0$.^¶ We denote by $\sigma (q_0)$ the EP corresponding to a computational process starting with the distribution $q_0$. The EP $\sigma (p_0)$ associated with the same process starting at another distribution $p_0$ can be expressed as (38)

$$\begin{array}{c}\hfill \sigma (p_0)=\sigma (q_0)+D(p_0||q_0)-D(p_f||q_f),\end{array}$$ [2]

where $p_f$ and $q_f$ are the final distributions in the process started at $p_0$ and $q_0$, respectively, and $D(p||q)=\sum _{x}p(x)ln\frac{p(x)}{q(x)}$ denotes the Kullback–Leibler (KL) divergence. The difference $D(p_0||q_0)-D(p_f||q_f)$ is called the mismatch cost. Importantly, the formula for mismatch cost is very general, applicable to classical systems, quantum systems, and even systems undergoing non-Markovian dynamics.

Note that the difference between the initial and final KL divergences is always nonnegative by the data processing inequality for KL divergence. So even if the process is thermodynamically reversible for some $q_0$, the system generates a positive EP when initialized at any other initial distribution. We cannot optimize the system’s EP for all possible $p_0$. Therefore, if $p_0\ne q_0$, EP must be positive.

Mismatch cost is not the only source of EP. EP is also unavoidable when there are constraints on the overall dynamics. To illustrate these, in the rest of this paper we will restrict attention to the case where the state space of the system is digitized into a countable number of values, e.g., due to coarse-graining or due to quantum mechanical effects.^# Given this restriction, then as described above, under certain technical conditions, if a computation has to be performed within a certain time interval $\tau$ [here, $\tau$ describes physical (clock) time], the EP is lower bounded (41) by the SLT:

$$\begin{array}{c}\hfill \sigma (\tau )\ge \frac{{\left({\sum }_x|p_0(x)-p_{\tau }(x)|\right)}^2}{2A_{\text{tot}}(\tau )}.\end{array}$$ [3]

The numerator is the square of the distance between the initial ($p_0$) and final ($p_{\tau }$) distributions. The term $A_{\text{tot}}(\tau )$ in the denominator is the total activity, which is the average number of physical state transitions^‖ that occur during the computational process. Thus, the SLT states that the minimum EP increases as the process speeds up.

Another contribution to the EP arises if we need statistical precision in the dynamics of our computer. Fix some observable, real-valued function of state transitions $x^{\prime }\to x$ that is antisymmetric under the interchange of the two states. The current $J$ associated with such an “increment function” for a full trajectory is the value of the observable summed over all state transitions in that trajectory. Examples of currents include the total transport of a molecular motor and the total heat flow down a thermal gradient. As another example, we can define the current through a transistor as the difference between the input state and the output state. In general, the more statistically precise the value of the current, the more heat has to be dissipated. Intuitively, when the precision of digital computation is higher, the switching transistors require higher steepness of flanks and more precise rectangular voltage curves, which require increased energy consumption.

Write $⟨J(t)⟩$ for the expected current over all trajectories in the time period $[0,t]$, and write $\text{Var}(J(t))$ for the variance of $J$. The ratio of those two quantities is called the (statistical) “precision” of the process. A quickly growing set of thermodynamic uncertainty relations (TUR) (42–44) is being derived that lower bound the statistical precision in terms of the EP generated by the underlying system. The historically first TUR applies in the special case that the system is in a nonequilibrium steady state (NESS):

$$\begin{array}{c}\hfill \sigma (\tau )\ge \frac{2{⟨J(\tau )⟩}^2}{\text{Var}(J(\tau ))}.\end{array}$$ [4]

This TUR says that the minimum EP in a computational process increases as the precision of any current of the process increases, assuming the system is in a NESS.

Many of these theoretical predictions of stochastic thermodynamics have been experimentally validated; see, e.g., refs. 45, 46, 47. In addition, important generalizations of these results have been recently found, including extended versions of the TURs (48–50), and stronger SLTs (51–54). Other results of stochastic thermodynamics promising for the thermodynamics of computers include the fluctuation theorems (55–58), the kinetic uncertainty relations (59), and the thermodynamic correlation inequality (60).

2. Integrating Computer Science and Statistical Physics

2.1. Previous Work.

Before discussing how to integrate CS theory and statistical physics, we comment on earlier work. As described in the previous section, real-world computers operate far from equilibrium and cannot be analyzed with equilibrium statistical physics. Before the advent of stochastic thermodynamics, physicists were forced to try to do precisely this since the primary tool they had was the equilibrium statistical physics. This resulted in some confusion in the literature.

In particular, there was some confusion in earlier literature about the relation between logical (ir)reversibility and thermodynamic (ir)reversibility. The difference is that logical reversibility is about the dynamics over a state space (specifically, it must be injective). In contrast, thermodynamic reversibility (i.e., zero EP) is about the associated dynamics of distributions over that state space. These two types of (ir)reversibility are, in fact, completely independent properties of a physical process (29, 61).

A related confusion arose regarding the consideration of computations performed in a logically reversible manner. In that case, it is at least possible that a single run of the computation can be performed without any thermodynamic cost (e.g., refs. 27 and 62). However, the complete cycle of computation, from generation of the input to computation of the output back to generation of a new input, overwriting the original input, results in unavoidable thermodynamic costs. (See section XI in ref. 61.)

While real-world computers cannot be directly analyzed as systems described by equilibrium statistical physics, there has been some important work applying mathematical techniques of equilibrium statistical physics to investigate CS theory problems without considering the underlying dynamics of a computer designed to solve those problems. For example, a recent study (63) presents a random language model, establishing the statistical physics of generative grammars. Furthermore, statistical physics increased attention to inference methods (see, e.g., ref. 64 for a recent review) and deep learning (65). Statistical physics models, such as the Ising model or the hard-core lattice gas model, have also permeated the design of Markov Chain Monte Carlo algorithms in CS (66), and more recently have been applied to swarm robotics systems (67).

Additionally, results from the statistical physics of disordered systems can help us understand how the difficulty of solving a randomly generated computational problem depends on the distribution generating those problems (68). Consider the example of a $k$-SAT (Boolean satisfiability) problem, the example of a NP-complete problem. (69). The goal of this problem is to determine whether there is an assignment to a set of $K$ Boolean variables that can simultaneously satisfy $N$ Boolean clauses (logical OR of $K$ variables or their negations). Random instances of $k$-SAT are typically easy for a broad range of values of $\alpha =N/K$. However, for a fixed $k$, existing algorithms for solving $k$-SAT display a discontinuous phase transition in their efficiency as $\alpha$ increases (25).

Note, though, that these are all applications of statistical physics techniques to computer science. They do not address the issue of the thermodynamic costs associated with physically implementing that computation. In the rest of this section, we review some preliminary work on precisely this issue, and discuss how the unavoidable constraints faced by real computers contribute to their energy costs.

2.2. Stochastic Thermodynamics of Detailed Models of Artificial Computers.

Recently, researchers have started to use stochastic thermodynamics to study concrete models of circuits. These studies analyze the behavior of small, linear circuits whose operational voltages are low enough that thermal fluctuations affect their behavior. Early theoretical endeavors used stochastic thermodynamics to characterize the fluctuations in the injected and dissipated energies of resistors (70), nanoscopic circuits (71), and generic electrical conductors (72). Other recent work has analyzed more complex, time-dependent RLC circuits (73). There has also been experimental work on information engines (74) constructed with single-electron circuits (quantum dots, tunnel junctions, etc.) (75, 76) as well as physical implementations of Maxwell’s demon (77) and the Szilard engine (78).

In the past few years, in light of rapidly shrinking transistor size, researchers have also started to use stochastic thermodynamics to study the effect of noise in nonlinear electronic circuits, such as CMOS technology (11, 12), in which each gate operates in its subthreshold regime. A recent article (79) goes a step further and studies how different thermodynamic uncertainty relations constrain the efficiency of electronic devices as: an inverter, a memory, and an oscillator. Stochastic thermodynamics has proven useful enough in analyzing electronic circuits that it is starting to be used in the engineering community to model and optimize the operation of low-power electronic devices (80).

As electronic advances near the thermal fluctuation limit, interest in stochastic computing has resurged. Current computers, being deterministic, incur energy costs to prevent thermal fluctuations from affecting logical states and computations. However, many computational tasks actually use stochasticity. In those cases, deterministic computers rely on complicated algorithms to produce pseudorandom numbers. This situation is somewhat paradoxical, wasting energy unnecessarily avoiding stochasticity in the first place only to produce it artificially later. A more efficient alternative, known as stochastic computing, controls intrinsic thermal fluctuations instead of avoiding them to solve problems requiring stochasticity. Such circuits employ probabilistic bits (p-bits), which output $0$ with a probability $p$ and output $1$ with a probability $1-p$.

Some novel work has demonstrated the use of magnetic tunnel junctions to create probabilistic bits (81–83). Interestingly, (11) presented the design of a p-bit that uses only conventional CMOS gates operating in the subthreshold regime. Such a CMOS p-bit has not yet been built, but this study shows how stochastic thermodynamics can be used to analyze new computing paradigms that exploit, rather than fight, thermal noise.

Apart from aplication in stochastic algorithms (e.g., Monte Carlo methods), the main advantage of stochastic computing is that, by incorporating tunable p-bits into conventional logic, many tasks can be efficiently formulated as stochastic optimization problems that can be solved by Gibbs sampling (85). This might allow us to solve a broad set of optimization problems in a way that computes both solutions and their associated uncertainties together (82, 84).

2.3. Stochastic Thermodynamics of Abstract Artificial Computers.

The optimization of key performance metrics also increases energy dissipation. For example, minimizing computational noise (i.e., having high accuracy in the map from a computation’s inputs to its outputs) is a central concern for all computational systems. However, in general, reducing such noise also increases energy dissipation.

As reviewed in Section 1.1, the study of computational complexity aims to analyze computing costs with various abstract computational machines. The simplest nontrivial example is the deterministic finite automaton (DFA). DFAs process input strings sequentially, updating a computational state within a finite state space according to the previous state and the next input symbol.

Since the computational update of a DFA is the same at each iteration, it is natural to assume that any physical process implementing a DFA will also be the same at each iteration. (In fact, there is always such periodicity of the underlying physical process in any clocked, synchronous implementation of a computational machine—precisely the type of computer always used in modern digital systems.) In ref. 86, a strictly positive lower bound was derived on the total mismatch cost of running a DFA this way. The reason for this bound is that the distribution of the system at the start of each iteration, $p_0$ from Eq. 2, evolves with the computation, whereas $q_0$ must remain constant; hence, it is not identical. This phenomenon illustrates a general law: Whenever any physical system repeats the exact same underlying physical process on a system that is not at (periodic) stationary state, each repetition of the process will undoubtedly generate EP. This is true no matter what the details of the physical process are (86, 87). This law applies to all modern digital computers operating synchronously and governed by an electronic clock.

Consider, for example, a DFA designed to recognize input strings consisting of the letters $a$ and $b$, with no more than two $b$’s in a row. This case is investigated in ref. 86, where it was found that the resultant per-iteration mismatch cost has highly nontrivial iteration dependence—dependence that has yet to be explained. Among their other findings, the paper also showed how to split the regular languages into two separate classes, defined by (lower bounds on) the “mismatch cost complexity” of those languages.

Another recent study investigated properties of the total EP (not just mismatch cost) generated by DFAs using the inclusive Hamiltonian approach of stochastic thermodynamics (88). The inclusive Hamiltonian approach allows the system of interest to operate deterministically, as is the case for many computational complexity theory models. In applying this approach, the authors showed that the minimal DFA for a given language is also the DFA that incurs the minimum EP of any DFA implementing that language.

Aside from Boolean circuits, almost all of CS theory concerns computers that run for a number of iterations that vary depending on the input to that computer. Unfortunately, stochastic thermodynamics typically concerns physical processes that finish at fixed times; it does not apply when the “stopping time” of the process varies.

However, recent research has extended stochastic thermodynamics to apply to processes with random stopping times (89–92). Preliminary work is investigating the application of these extensions of stochastic thermodynamics to computational systems (87). As an example, we now know that the irreversible entropy produced when a DFA processes a randomly generated bit string obeys a modified “fluctuation theorem” (8, 57, 58),

$$\begin{array}{c}\hfill \int dsP(s)e^{-\sigma (x(s))-\delta (x(s))}=1.\end{array}$$ [5]

In this expression, $P(s)$ is the distribution over input strings to the DFA, and $x(s)$ is the resultant sequence of states of the DFA up to the time that it halts. The $\delta (x)$ term captures the effects of the constraints on the physical process that implements the computation, e.g., that the process be periodic (as it is in digital computers). This explicitly demonstrates how considering such constraints can lead to strengthened versions of the second law—and that these strengthened versions are particularly relevant for investigating computational systems.

In general, different algorithms can implement the same computation, whether the algorithm is represented by a pseudocode, as a program written in assembly code, or as a computational machine from the Chomsky hierarchy [e.g., a finite-state automaton or push-down automaton (23)].

Moreover, the EP generated by physically implementing an algorithm depends more than just on the details of that algorithm. It also depends on the statistical coupling of the states of the other logical variables at the time of the state transition. Consequently, the constraints embodied in the specific algorithm used to implement a given computation contribute to the overall energy costs of implementing the computation with that algorithm. These costs are higher energy costs that arise due to the constraints on the precise physical system that implements that algorithm—see refs. 61, 86, 88, and 93, 94, 95 for some preliminary work concerning the stochastic thermodynamics of such algorithms. Also, recent work has derived the minimal EP generated by any communication systems—one of the major sources of heat in modern, real-world computers that have multiple components communicating with one another (96).

2.4. Stochastic Thermodynamics of Biological Computers.

Just as artificial systems consume energy to perform computations and process information, so do living systems (97). Perhaps the first example of the connections between biological information processing, energy consumption, and irreversible dynamics was kinetic proofreading (98, 99). In protein synthesis, the genetic code is read with an error rate on the order of ${10}^4$, an accuracy far higher than can be achieved through any one-step reversible process. However, by inputting energy to generate irreversible steps, Hopfield showed that kinetic proofreading can achieve the accuracy observed in nature (98), a theoretical prediction that has been verified experimentally in multiple settings (100–103).

Stochastic thermodynamics provides a consistent mathematical framework for investigating the energetic costs of biological computations. At the foundation of all biological processes are complex networks of chemical reactions. Using stochastic thermodynamics, one can derive the energy expended and entropy produced by these chemical reaction networks (104, 105).

At a larger scale, cells must perform computations to respond to environmental cues. A simple example, first considered by Berg and Purcell, is the ability of cells to determine the concentration of chemicals in the surrounding (106). It is now understood that learning about the environment requires breaking detailed balance and consuming energy, with greater learning requiring greater energy consumption (107). After the information is gathered, it must be transferred between spatially separated components, which can consume a substantial fraction of the cellular energy budget (108). The problems of cellular sensing and information transfer have received significant focus in the statistical mechanics of living systems, revealing the thermodynamic costs of simple biological computations (97, 109–111).

At an even larger scale, groups of cells (particularly in the brain) must communicate to sense, represent, and process information (112). To execute these functions, the human brain consumes 20% of our metabolic output despite only accounting for 2% of the body’s mass (13, 16, 113, 114). Understanding how groups of neurons represent and transmit information while minimizing energy consumption remains a foundational question in neuroscience (115). Recent advances in stochastic thermodynamics have revealed that the irreversibility of neurons in the retina depends critically on the visual stimulus (116). At the whole–brain level in humans, recent studies have suggested that irreversibility and broken detailed balance may reflect increases in cognitive processing and consciousness (117, 118). Yet despite this progress, research at the intersection of stochastic thermodynamics and biology has only begun to scratch the surface of an ultimate understanding of the energetic and thermodynamic costs of computations in living systems.

3. Open Research Topics

As discussed in Section 1.1, to date, CS theory has considered the scaling properties of resource costs other than energy in various kinds of computational systems. Stochastic thermodynamics opens the possibility of integrating the energetic resource costs of computer systems in these analyses. A fascinating—and potentially practically very important—future research program is to investigate the scaling properties of the trade-off between the energy cost of computation and the kinds of computational resource cost traditionally investigated in CS theory.

Concretely, at present, we have a very limited understanding of why thermodynamic costs in both natural and artificial computers are many orders of magnitude above the minimum possible. The reason for this must lie in the physical constraints that apply to how both artificial and natural computers can operate. To start to investigate those constraints, we need to consider the minimal thermodynamic costs of broad kinds of physical computers rather than the very abstract “computational machines” considered in CS theory.

For example, computational systems can be modeled as networks of distributed computational units that communicate with each other in limited ways. However, we do not know how the properties of a network affect its energy cost when used to implement a computation. To help guide our investigation, we can consider the properties that have been considered before in the literature. In particular, computer scientists (119, 120), neuroscientists (121), network scientists (122, 123), political scientists (124), roboticists (125), and biologists (126, 127) alike have repeatedly identified two key features of network topology to the versatility, robustness, and efficiency of resource utilization in large, distributed computational systems: modularity and hierarchy.

Modularity refers to the property that a network can be divided into a set of discontinuous modules, such that each module’s intraconnectivity (number of edges among its own nodes) is much higher than would be expected in a random graph with the same number of edges. Conversely, its interconnectivity (number of edges between its nodes and the nodes of other modules) is much lower (122).

Hierarchy refers to the property that subsystems can be grouped into partially ordered “levels,” as in a tree-like network. Several definitions of the hierarchy have been proposed in the literature, e.g., refs. 120 and 128. Both modularity and hierarchy are posited to reduce the cost of establishing long-range correlations in systems of increasing size and complexity. It is known that modularity in a system’s architecture increases EP (95, 129), even though it is often useful for robustness (125, 126). However, very little is known beyond this about how the detailed architectural constraints—how each component’s state is allowed to affect the dynamics of other components—give rise to EP. The very structure of hierarchical, modular systems leads to additional energy dissipation, e.g., due to mismatch cost (86, 87). Currently, nothing is known about how the benefits of such networks connecting computer components balance with their thermodynamic costs.

Another important open issue arises from the fact that in both real-world artificial computers and real-world biological computers, communication costs—transferring information, from point to point, rather than transforming information. Formally speaking, communication is a very specific computational process, typically involving encoders and decoders on both sides of a (noisy) communication channel. Focusing on just the channel. that is a system that consists of an “input” subsystem and an “output” subsystem, and the computation is copying the state of the input subsystem to that of the output subsystem. Despite its major importance in real-world computers, applying stochastic thermodynamics to analyze the EP of communication systems—and potentially help design such systems—is still in its infancy (96, 130).

Wireless sensor networks (WSNs) are distributed computing systems that often have lightweight nodes made of single-chip microcomputers. WSNs typically manage many diverse sensors and communicate with one another via a wireless link to collectively detect, analyze, summarize, or react to phenomena that their sensors encounter. As they are usually battery-powered or run off of limited scavenged energy and share common RF channels, much of the effort in WSN systems involves reducing consumed energy. So far, these efforts have involved minimizing communications and processor load, dynamic information routing, and deciding what information to transmit from a given node (131). Stochastic thermodynamics can help reduce energy costs by modifying macroscopic parameters beyond the energy flowing through single gates.

Stochastic thermodynamics also has the potential to analyze certain nonconventional forms of computation. For example, one potentially promising application of stochastic thermodynamics to computation is in the growing sphere of molecular computation, including DNA (17, 132) and small molecule computation (133–135). In these forms of computation, molecular concentrations are used to encode information, and reactions among molecules are used to compute. Given that molecules are distributed throughout a solution, molecular computation is an inherently distributed form of computation that has the potential to involve many separate, parallel operations. Stochastic thermodynamics has been previously applied to model reaction networks (105), but much remains to be learned about the thermodynamic limits of molecular computation and how close they can be approached by selection of molecular species and tuning of their reactions.

As another example, stochastic thermodynamics might be a fruitful way to analyze alternative computational systems, such as stochastic computing. Finally, a major motivation of neuromorphic computing is reducing the energetic costs of communication among the components of a computer (136). However, to date, stochastic thermodynamics has not been used to help design such computers.

4. Conclusion

The energetic cost of computation is a long-standing, deep theoretical concern in fields ranging from statistical physics to computer science and biology. It has also recently become a major topic in the fight to reduce society’s energy costs.

Although CS theory has mostly focused on computational resource costs regarding accuracy, time, and memory consumption, energetic costs are another important cost that has barely been considered in the CS theory community. Until quite recently, most of the research regarding the thermodynamics of computation has focused either on systems in equilibrium or archetypal examples of small systems, including only basic operations such as bit erasure.

In this paper, we argue that the recent results of stochastic thermodynamics can provide a mathematical framework for quantifying the energetic costs of realistic (both artificial and biological) computational devices. This may provide major benefits for the design of future artificial computers. It may also provide important new insights into the biological computers. Finally, by combining CS theory with the theoretical tools of stochastic thermodynamics, we may uncover important new insights into the mathematical nature of all physical systems that perform computation in our universe.

Data, Materials, and Software Availability

There are no data underlying this work.