Abstract

The solubility of hydrophobic solutes increases dramatically with the temperature when hydrotropes are added to water. In this paper, the mechanism of this well-known observation will be explained via statistical thermodynamics through (i) enhanced enthalpy-hydrotrope number correlation locally (around the solute) that promotes the temperature dependence and (ii) hydrotrope self-association in the bulk solution that suppresses the temperature dependence. The contribution from (i), demonstrated to be dominant for urea as a hydrotrope, signifies the weakening of interaction energies around the solute (local) than in the bulk that accompanies incoming hydrotrope molecules. Thus, studying hydrotropic solubilization along the temperature and hydrotrope concentration provides complementary information on the local-bulk difference: the local accumulation of hydrotropes around the solute, driven by the enhanced local hydrotrope self-association, is also accompanied by the overall local weakening of energetic interactions, reflecting the fluctuational nature of hydrotrope association and the mediating role of water molecules.
1. Introduction
Hydrotropes have been employed in a range of industrial applications because of their significant ability to increase the solubility of hydrophobic solutes.1−6 However, their solubilization mechanism had long remained a mystery until a clarification from the statistical thermodynamic fluctuation theory (Figure 1):7−10 hydrotropic solubilization is driven by solute-hydrotrope association, which overcomes inefficiency caused by hydrotrope-hydrotrope association in the bulk phase.7−10 Moreover, the enhanced local hydrotrope self-association (around the solute) drives an onset of solubilization.11−14 However, all these mechanistic insights from statistical thermodynamics, supported also by 1H NMR.,15 were restricted to isothermal conditions.
Figure 1.

A schematic representation of hydrotropy according to the statistical thermodynamic fluctuation theory. (a) A typical solubility isotherm (i.e., the hydrotrope concentration dependence of solute solubility) identifying the two important regions in yellow (commonly referred to as the “minimum hydrotrope concentration”, with its mechanism illustrated in (b)) and purple (in (c)). (b) Around the minimum hydrotrope concentration, the hydrotrope-hydrotrope association is enhanced around the solute (local, compared to the bulk), driving the onset of solubilization (cf. the yellow region in (a)), which is a schematic summary of insights from the statistical thermodynamic fluctuation theory.10−12 The solute, water, and hydrotrope molecules are color-coded with red, blue, and orange, respectively, schematically representing stronger local hydrotrope association. (c) A steady increase in solubility is driven by the preferential interaction of hydrotropes around the solute; with the hydrotrope-hydrotrope association not as prominent as in (b), as has been represented schematically by comparable hydrotrope self-association between local and the bulk.
Solubility can usually be increased by raising the temperature.16,17 This “heat-solubilization” (as it will be referred to, with notable exceptions, e.g., small hydrophobic gases or salts) has been exploited routinely.16,17 Adding hydrotropes can further enhance heat solubilization (Figure 2a).18−23 Why, then, do hydrotropes enhance heat solubilization? According to the classical hypothesis, solubilization is caused by hydrotrope self-aggregation in the bulk aqueous solution.2−4,24 However, hydrotrope self-aggregation decreases with the temperature,18,25,26 while solubilization increases with the temperature20,21 (with a rare exception, as far as we know, of riboflavin solubility data in aqueous nicotinamide18), leading to a contradiction. Our statistical thermodynamic fluctuation theory, in its present form, is restricted to isothermal conditions, thereby incapable of explaining hydrotrope-intensification of heat-solubilization.22,23 Thus, how hydrotropes enhance heat-solubilization remains unexplained.
Figure 2.

(a) Temperature-dependence of hydrotropy, illustrated by the solubilization of methyl benzoate (solute, abbreviated by MB) by urea (hydrotrope), at 303 K (blue squares), 313 K (green diamonds), 323 K (orange triangles), and 333 K (red squares), using the experimental data reported by Senthil et al.54 (b) Calculation of the entropy of transfer, Δs*u, from pure water to saturated solubility (c2 = 2.8–3.0 M) from the gradient of −Δμ*u = RT ln cu/c0u (c0u: solubility in water, cu: solubility at saturation) against T, which yields a positive entropy of transfer, Δs*u = 58.9 J mol–1 K–1.
Our goal is twofold:
-
1.
to explain how hydrotropes intensify heat solubilization; and
-
2.
how (1) can shed light on the local-bulk difference of the solution structure.
To achieve this goal, we generalize our statistical thermodynamic fluctuation theory, restricted to isothermal conditions, to incorporate the temperature effects. Our specific objectives are
-
1.
to identify the local-bulk difference of hydrotrope number-enthalpy correlation as the driving force for the intensification of heat-solubilization by hydrotropes;
-
2.
to show that 1 signifies the local weakening of interaction energies caused by hydrotrope-solute association;
-
3.
to clarify that hydrotrope-solute and hydrotrope-hydrotrope associations, the driving forces for solubilization, are nonstatic and water-mediated.
By achieving these objectives, we will be able to re-examine the traditional view on “water structure”, e.g., “urea as a structure breaker”,27 based chiefly on the entropy of transfer (Figure 2b). We will show how the classical view is related more intimately to the intensification of heat-solubilization, rather than to isothermal solubilization as has originally been intended.
2. Theory and Methods
2.1. Fluctuation Theory for Temperature-Dependent Solubility
Our goal is to clarify why heat-solubilization (i.e., solubility increase under raised temperatures) is promoted by hydrotropes added to the solution. To achieve this goal, we set up our system: a solvent mixture consisting of water (species 1) and hydrotrope (species 2), into which solute (species u) is dissolved in dilution. (In our cooperative solubilization theory, restriction to solutes in dilution was removed;10 this restriction was reinstated in this paper for mathematical simplicity necessitated by the temperature derivatives.) We adopt a partially open ensemble, {T, P, N1, μ2}, closed to water and open to hydrotrope molecules. (Note that T, P, Ni, and μi denote the temperature, pressure, number, and chemical potential of species i, respectively.) According to the Gibbs phase rule,28 the degrees of freedom are F = 2 – 1 + 2 = 3. Keeping the pressure constant reduces the degrees of freedom to 2, leaving us two independent variables (i.e., T and hydrotrope concentration).
Our first objective is to formulate heat-solubilization and the influence of hydrotrope concentration thereupon. To this end, we start with the statistical thermodynamic expression for the solvation free energy of the solute,
| 1 |
where k is the Boltzmann constant and Y(T, P, N1, μ2) and Yu(T, P, N1, μ2) denote the partition functions of the partially open ensemble, {T, P, N1, μ2} and {u: T, P, N1, μ2}, respectively, where the latter refers to an inhomogeneous ensemble with a solute molecule fixed at the origin.11 To link μ*u to solubilization, we introduce the solubilization ratio, cu/cou, via the solubility in aqueous hydrotrope solution (cu) and that in pure water (cou). The solubilization ratio is related to Δμ*u, i.e., the transfer free energy of a solute from pure water to aqueous hydrotrope solution (i.e., the difference in solvation free energy of a solute between hydrotrope solution and pure water), via
| 2 |
where β = 1/kT has been introduced for shorthand. (In Appendix A, we
have shown that the signatures of hydrotropy, summarized in Figure 1, manifest even when
the logarithmic form of the isotherm (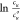 ) cannot be captured by the Setschenow
equation.)
) cannot be captured by the Setschenow
equation.)
According to chemical thermodynamics, the temperature dependence of ln(cu/cou) is central for comparing heat solubilization with and without the hydrotrope, via
 |
3a |
where Δh*u is the enthalpy of transfer, defined as
 |
3b |
where the subscript m2 signifies “under constant hydrotrope molality”, via m2 = N2/(N1M1), where M1 is the molar mass of water. Note that Δh*u is a local thermodynamic quantity whose spatial contribution (from the microscopic solution structure) diminishes at a large distance from the fixed solute (see refs (29,30) in which the locality of thermodynamics has been defined and introduced, alongside the examples of nonlocal thermodynamic quantities). For this reason, we have employed isobaric ensembles throughout this paper which conforms to the experimental condition under which solubility measurements have been performed, instead of the grand canonical ensemble adopted as the generalization of the Kirkwood-Buff theory.31−34
However, in the {T, P, N1, μ2} and {u: T, P, N1, μ2} ensembles, hydrotrope fugacity, λ2 = eβμ2, rather than m2, is the natural measure of hydrotrope concentration. (Note that λ2 is related closely to hydrotrope activity, a2, hence to the molality m2, as will be clarified in Section 2.2.) Carrying out the β-derivative under constant λ2 yields
| 4 |
where ΔH = H – Ho is the difference in enthalpy between hydrotrope solution and pure water (see Appendix B for derivation. Note that Ho is already an ensemble average in the system of pure water, hence is not subjected to the ensemble averaging operations in eq 4). Thus, under constant λ2, the local-bulk difference in average ΔH is the quantity responsible for the heat-solubilization difference between the presence and absence of hydrotropes. (In Section 2.2, ⟨ΔH⟩u – ⟨ΔH⟩ and Δh*u are shown to be close in values.)
How effective a hydrotrope is in enhancing heat solubilization can be quantified by the gradient of ⟨ΔH⟩u – ⟨ΔH⟩ with respect to hydrotrope concentration. Our goal is to evaluate this derivative while linking it to statistical thermodynamic quantities that convey a clear physical meaning. This goal can be achieved by taking λ2 as the variable. Differentiating eq 4 with respect to λ2 under constant β, we obtain (see Appendix B):
 |
5 |
Following the discussion in Appendix B, the λ2-derivative in eq 5 can be rewritten as the lna2-derivative (where a2 is hydrotrope activity), as
 |
6 |
Converting the variable from lna2 to hydrotrope concentration is straightforward with the use of hydrotrope molality, m2, through a well-known result from the Kirkwood-Buff theory of binary mixtures (see eq 21 of ref (35)),
| 7a |
where C2 = N2/N1 = M1m2,13,36−39 with M1 being the molecular weight of water. Note that eq 7a is applicable to bulk solutions without the solute, as well as in the presence of the solute under phase equilibrium at arbitrary concentration.10 In the following, we consider the solute at infinite dilution, for which eq 7a for the bulk solution will be employed. N22 is the excess number of hydrotropes around a probe hydrotrope, as the measure of bulk phase self-association, defined as
| 7b |
 |
7c |
Thus, eq 7c is the central result of this paper, from which the hydrotrope effect on heat-solubilization will be made clearer through its simplification in Section 2.2.
The simplicity in the form of eq 7c comes from the isobaric, partially open ensembles adopted for the local and bulk systems and the inhomogeneous solvation theory for the local system. Previously, local fluctuations have been formulated chiefly in the grand canonical (open isochoric) ensemble in extending the Kirkwood-Buff theory of number–number correlation to incorporate number-energy correlations.31−34 The advantage of partially open ensembles has been recognized for their ease in connecting experiments to theory,39−43 which is often cumbersome for the approaches founded on the grand canonical ensembles.40 In addition, the inhomogeneous solvation theory, in its ability to treat a fixed solute as an external field, is not only suitable for local thermodynamics but also for simplifying complex expressions involving ternary correlations (e.g., solute-hydrotrope-hydrotrope) to the conditional binary (e.g., hydrotrope-hydrotrope in the presence of the solute).41−46 For these reasons, we have adopted the partially open ensembles and inhomogeneous solvation theory for interpretive clarity, which will be demonstrated in Section 3.
2.2. Simplification for Experimental Data Analysis
Our goal is to simplify eq 7c to clarify how hydrotropes intensify heat-solubilization. To this end, we will rewrite eq 7c to be in better conformity with experimental practice.
2.2.1. Equivalence of the Enthalpies of Transfer from the Fluctuation Theory and Chemical Thermodynamics
Here, we show that the two β-derivatives, eqs 3b (constant m2) and 4 (constant λ2), are close in value to one another, such that
| 8a |
so that the enthalpy of transfer, Δh*u, commonly used in solvation thermodynamics,47 can be adopted for the fluctuation theory. To this end, the following relationship, derived in Appendix C, will play a key role:
| 8b |
where c2 is the molarity of the hydrotrope, h2 is the partial molar enthalpy of the hydrotrope, and Gui is the Kirkwood-Buff integral between solute (u) and species i. (We emphasize that eq 8b, while involving the Kirkwood-Buff integrals defined in the grand canonical ensemble, is connected to the enthalpy of solvation in the isobaric ensemble.) The order-of-magnitude analysis of c2(Gu2 – Gu1)h2 in eq 8b, carried out in Appendix C, shows that this term makes a minor contribution to urea as a hydrotrope. Consequently, eq 6 can be simplified as
| 9 |
Note, in eq 9, that constant T is equivalent
to constant β. We emphasize that eq 9 is an approximation specific for urea as
a hydrotrope, subject to the negligibility of c2(Gu2 – Gu1)h2 in eq 8b. If this
term is not negligible for a hydrotrope-solute combination, eq 8b must be used to evaluate 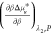 , required for our general result (eq 7c), from Δh*u and c2(Gu2 – Gu1)h2, both
of which can be evaluated when a full set of experimental data is
available (Appendix C).
, required for our general result (eq 7c), from Δh*u and c2(Gu2 – Gu1)h2, both
of which can be evaluated when a full set of experimental data is
available (Appendix C).
2.2.2. Calculating Enthalpy of Transfer from Solubility Data
Calculating the enthalpy of transfer, Δh*u, from solubility data via eq 3 can be facilitated significantly by establishing
 |
10 |
Since the molality m2, by definition, is independent of the temperature, establishing eq 10 is equivalent to the negligible temperature-dependence of molarity c2 for aqueous hydrotrope solutions within the temperature range covered by the solubility data. Note that eq 10 is valid for solutes with low solubility for which c2 is not affected by cu, i.e., the presence of the solute in the solution. This paper focuses on urea as a hydrotrope, which offers a rare combination of available density and activity data48,49 covering the entire range of concentrations and temperature range for the solubility data,19,50−54 in contrast to the severe limitations of data availability for other hydrotropes. As shown in Figure 3, the molarity-molality relationship shows no temperature variation between 298 to 333 K, which justifies eq 10. (This justification is underscored by another route via thermal expansion as demonstrated in Appendix D.) Thus, Δh*u can be evaluated via eq 10 directly from the experimental solubility data reported at a regular c2 interval, as demonstrated by Figure 4 for the solubility data of methyl benzoate (MB).54
Figure 3.

Molarity-molality relationship, based on the experimental density data of aqueous urea solutions at 298 K (blue circles), 323 K (orange triangles), and 333 K (red squares) at 1 atm published by Makarov and Egorov,49 which shows little temperature dependence. The dotted line is the fitting equation at 303 K (based on the density data at 298 and 303 K), m2 = 0.996c2 + 0.0544c22, used throughout this work.
Figure 4.

1/T-dependence of −R ln cu (cu: the solubilities of MB in aqueous urea solutions) for the calculation of the enthalpy of transfer, Δh*u, via eq 10. Shown here are the sample data fitting at 0 molal (black circles), 0.51 molal (purple asterisks), 1.05 molal (blue circles), 1.62 molal (green diamonds), 2.21 molal (red squares), and 3.48 molal (orange triangles), with the corresponding linear regression. The calculated Δh*u will be presented in Figures 5 and 6.
In addition to MB, we have used the published solubility data of p-Aminobenzoic Acid (AB),50 butyl acetate (BA),19 benzyl benzoate (BB),51 butyl stearate (BS),52 and ethylbenzene (EB),53 all at 303, 313, 323 and 333 K between 0 and 3 M urea as the hydrotrope, whose results will be presented in Section 3.
3. Results and Discussion
3.1. Hydrotrope Effect on Heat-Solubilization
Our goal is to clarify why hydrotropes promote heat-solubilization.
To this end, we begin by summarizing our achievements in Section 2. First, the enthalpy
of transfer, Δh*u, characterizes the heat-solubilization
difference between hydrotrope solution and pure water, which can be
obtained via eq 10,
namely the temperature dependence of 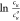 , in which the constant molality condition
can be approximated by constant molarity (see eq 10). According to eq 3a, a positive Δh*u is responsible for enhanced heat-solubilization in the presence
of hydrotropes. Second, how heat-solubilization changes with increasing
hydrotrope concentration can be captured by,
, in which the constant molality condition
can be approximated by constant molarity (see eq 10). According to eq 3a, a positive Δh*u is responsible for enhanced heat-solubilization in the presence
of hydrotropes. Second, how heat-solubilization changes with increasing
hydrotrope concentration can be captured by,
 |
11a |
which can be derived by combining eqs 3a, 7c, and 10. On the left-hand side of eq 11a, the symmetry of partial differentiation yields
 |
11b |
which states the equivalence between “the hydrotrope effect on heat-solubilization” (the left-hand side) and “the temperature effect on hydrotrope-solubilization” (the right-hand side).
According to eq 11a, our central result, the enhancement of
heat solubilization by hydrotropes is caused by the competition between
the two contributions. The first contribution is ⟨δHδN2⟩u – ⟨δHδN2⟩ (normalized by m2, the hydrotrope molality) drives up  ; a positive (⟨δHδN2⟩u – ⟨δHδN2⟩)/m2 signifies the
increased correlation between the number of hydrotropes and the enthalpy
when the solute is present. The second contribution is the hydrotrope
self-association in the bulk, quantified by N22 (i.e., the excess number of hydrotrope around a probe hydrotrope),
which lowers heat-solubilization, acting similarly to how hydrotrope
self-association in the bulk decreases the solubilization efficiency
of the hydrotrope.7,8
; a positive (⟨δHδN2⟩u – ⟨δHδN2⟩)/m2 signifies the
increased correlation between the number of hydrotropes and the enthalpy
when the solute is present. The second contribution is the hydrotrope
self-association in the bulk, quantified by N22 (i.e., the excess number of hydrotrope around a probe hydrotrope),
which lowers heat-solubilization, acting similarly to how hydrotrope
self-association in the bulk decreases the solubilization efficiency
of the hydrotrope.7,8
With this preparation, here
we analyze experimental data. First,
we show how Δh*u changes with hydrotrope
concentration based on experimental solubility data (Figure 5). According to the procedures outlined in Section 2.2, we observe the increase
of Δh*u with m2 at lower m2 (generally corresponds to
the first half of sigmoidal solubility curves) and saturation of Δh*u at higher m2 (in Figure 5). Thus, we obtain
a positive 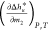 at lower m2 and
at lower m2 and  at higher m2. The gradient,
at higher m2. The gradient, 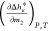 , can be attributed solely to (⟨δHδN2⟩u – ⟨δHδN2⟩)/m2 in eq 11a, because N22 + 1 ≃ 1 for urea, due to its well-known property
of forming a near-ideal mixture with water.7,8
, can be attributed solely to (⟨δHδN2⟩u – ⟨δHδN2⟩)/m2 in eq 11a, because N22 + 1 ≃ 1 for urea, due to its well-known property
of forming a near-ideal mixture with water.7,8
Figure 5.

Hydrotrope concentration (m2: molality) dependence of Δh*u, the enthalpy of transfer from pure water to aqueous urea solution for the solutes BA (magenta crosses), AB (red squares), BB (violet xs), EB (orange triangles), MB (green diamonds), and BS (blue circles).
At lower urea concentration, a positive (⟨δHδN2⟩u – ⟨δHδN2⟩)/m2 signifies a stronger correlation around the solute (⟨δHδN2⟩u) between hydrotrope accumulation (δN2 > 0) and weakened interaction (δH > 0) than in the bulk (⟨δHδN2⟩). Note that H is the sum of all the interaction energies, not only between hydrotrope molecules but also between hydrotrope and water as well as water and water. Thus, the enhancement of heat-solubilization by hydrotropes has been attributed to the weakening of interaction energy by hydrotropes coming into the solute’s locality more prominently so than in the bulk. We emphasize that the weakening of interaction energy is not contradictory to the accumulation of hydrotropes around the solute and the enhancement of hydrotrope-hydrotrope association (Figure 1b), both of which are essentially the potential of mean force interactions. In Section 3.2, we will synthesize the insights from enthalpy-number and number–number correlations to clarify the nature of hydrotrope associations.
For hydrotropes with stronger bulk-phase self-aggregation, N22 + 1 is larger than 1.7,8 Since N22 + 1 is in the denominator of eq 11a, it contributes to attenuate the hydrotrope effect on heat solubilization. Thus, the self-association of hydrotrope in the bulk phase counteracts not only isothermal solubilization (which is driven by preferential solute-hydrotrope interaction)7,8 but also the enhancement of heat solubilization (which is driven by the local strengthening of number-enthalpy correlation).
3.2. Comparison to the Classical View
The accumulated hydrotropes around the solute, responsible for solubilization, also weaken the interaction energy in the locality of the solute, as shown in Section 3.1. Such a role of urea in the vicinity of the solute is analogous to “urea as a structure breaker”27 from the classical view, i.e., how urea weakens the hydrophobic effect by breaking the hydrogen bond network of water responsible for the hydrophobic effect. Such a view, however, has also been subjected to questioning from spectroscopy,55 from the mixing ideality of urea and water,56 as well as from direct simulations of the distribution functions of water and urea molecules and their statistical thermodynamic link to the solvation free energies.57,58 Note that the classical view, despite its aim to elucidate the solvation free energy, was unwittingly referring to the role of urea on the temperature dependence of solubility because of its focus on the (delicate) balance of entropy and enthalpy, rather than the clearly observed dependence of the enthalpy on the hydrotrope concentration.
3.2.1. Classical View
Using simplified models, the classical view aimed to understand the origin of solubilization (i.e., Δμ*u = Δh*u – TΔs*u < 0) based on its entropic contribution −TΔs*u.27,59 We emphasize that Δ here refers to “aqueous solubilizer solution minus pure water”. Structure breaking leads to Δs*u > 0 (i.e., a more positive solvation entropy in aqueous solubilizer solution than in water), hence to a negative −TΔs*u,27 which is consistent with Figure 6. However, the difficulty of this approach is well-known: solubilization (Δμ*u < 0) is a small difference between the two large contributions, Δh*u and TΔs*u, as shown in Figure 6. Indeed, structure breaking also leads to a positive Δh*u through weakened intermolecular interaction energies, which is a well-known phenomenon, referred to as the entropy-enthalpy compensation.59,60 Thus, the classical view of solubilization remains speculative unless we understand why the contribution from −TΔs*u is (slightly) greater than Δh*u. Such an approach remains challenging because Δs*u involves complex expressions arising from multiple-body intermolecular correlations even in the absence of the hydrotropes.30,61,62
Figure 6.

Transfer free energy Δμ*u (black circles), directly related to solubilization via Δμ*u = −RT ln (cu/cou), is a small difference between the compensating transfer enthalpy Δh*u (blue triangles) and entropy −TΔs*u (red squares). Δμ*u of AB in aqueous urea solutions were calculated from the solubility data reported by Senthil et al. at 303 K.54 Δh*u was calculated in the method described in Figure 4.
3.2.2. Fluctuation Theory
Unlike the classical
view, our fluctuation theory is founded on the exact, model-free relationships
derived from the principles of statistical thermodynamics. First, isothermal solubilization by adding hydrotropes (i.e., the
decreasing Δμ*u with hydrotrope concentration, 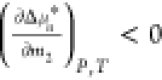 ) was attributed to preferential solute-hydrotrope
interaction,7−9 whose onset around the minimum hydrotrope concentration
originates from the enhanced hydrotrope-hydrotrope association around
the solute.10−12 Such a conclusion is free from the conundrum encountered
by splitting Δμ*u into Δh*u and TΔs*u as adopted by the classical view. Second, the structure-breaking
(i.e., weakened local interaction energies or the number-enthalpy
correlation) by hydrotrope was linked to the competition between ⟨δHδN2⟩u – ⟨δHδN2⟩ and N22, which drives the signature of the hydrotrope effect on heat-solubilization
(see eq 11a). This
conclusion is different from the speculative link between “structure
breaking” and Δμ*u according to the classical view
and would be a way to define “structure breaking” in
a manner directly relatable to the thermodynamics of solubilization.
) was attributed to preferential solute-hydrotrope
interaction,7−9 whose onset around the minimum hydrotrope concentration
originates from the enhanced hydrotrope-hydrotrope association around
the solute.10−12 Such a conclusion is free from the conundrum encountered
by splitting Δμ*u into Δh*u and TΔs*u as adopted by the classical view. Second, the structure-breaking
(i.e., weakened local interaction energies or the number-enthalpy
correlation) by hydrotrope was linked to the competition between ⟨δHδN2⟩u – ⟨δHδN2⟩ and N22, which drives the signature of the hydrotrope effect on heat-solubilization
(see eq 11a). This
conclusion is different from the speculative link between “structure
breaking” and Δμ*u according to the classical view
and would be a way to define “structure breaking” in
a manner directly relatable to the thermodynamics of solubilization.
Thus, the fluctuation theory has shown that the local structure breaking by hydrotropes is the cause of their ability to enhance heat-solubilization.
3.3. Local versus Bulk Behavior of Hydrotropes
We have identified the three signatures of hydrotropy and their respective microscopic mechanisms. The signatures are
- A.
-
B.
The isothermal onset of solubilization by hydrotropes at the minimum hydrotrope concentration (Figure 1a, yellow highlighted region);10−12 and
-
C.
Enhancement of heat-solubilization by hydrotropes (Figures 2 and 7a).
Figure 7.

A schematic representation of local hydrotrope association. (a) A typical hydrotrope concentration dependence of the enthalpy of transfer, Δh*u, in which the important region is highlighted in yellow. (b) The local hydrotrope-solute and hydrotrope-hydrotrope association around the solute (left) is accompanied by more unfavorable energetic interactions than in the bulk (right), as represented schematically by the reduced number and strength of intermolecular bonds (represented by yellow lines with different lengths and thickness) that contribute to lower the interaction energy.
The mechanisms underlying A–C are
-
1.
The dominance of solute-hydrotrope association over bulk hydrotrope-hydrotrope association (Figure 1b);7−9
-
2.
Enhancement of hydrotrope association locally than in the bulk (Figure 1b);10−12 and
-
3.
Interaction energy being weaker locally than in the bulk (Figure 7b).
Since they refer to different thermodynamic functions and conditions, their insights are complementary to one another.
Here, we show that synthesizing A–C will lead to a clearer understanding of hydrotropy on a microscopic scale: local (=around the solute) hydrotrope accumulation is accompanied also by a local weakening of overall interaction energy (i.e., local structure breaking). Such a statement would be counterintuitive if “interaction” simply meant the formation of the dimers, trimers, and clusters of hydrotropes. Indeed, “structure breaking” is accompanied by solute-hydrotrope and local hydrotrope-hydrotrope associations (1–3), as shown schematically in Figure 7b. However, 1–3 can be rationalized by understanding hydrotrope-solute and hydrotrope-hydrotrope interactions as the potentials of mean force (Figure 7b), that, by definition, are mediated by water.63 In this framework, enhanced self-association of hydrotrope around the solute is not contradictory to the weakening of energetic interactions around the solute, as depicted schematically by Figure 7b, since the former reflects the free energy that includes the energetic and entropic contributions. We emphasize that the potential of mean force is founded on the molecular distribution function63 that can capture the statistical distribution of fluctuating, nonstatic hydrotrope molecules around the solute, instead of hypothesizing hydrotrope clusters with well-defined stoichiometry.
Thus, synthesizing hydrotropy along concentration and temperature axes has led to an elucidation that hydrotrope accumulation and local self-association enhancement are far from static and stoichiometric. Such a fluctuating nature of the hydrotrope around the solute is responsible for the strong temperature dependence of hydrotropic solubilization. (Note that “fluctuation” here is thermodynamic, arising from the existence of broad ensembles of structures in the ensemble, rather than kinetic fluctuations in time.)
4. Conclusions
Hydrotropes often enhance the heat-solubilization of solutes.18−23 To elucidate the origin of this well-known and well-exploited yet hitherto unexplained experimental observation, we extended our statistical thermodynamic fluctuation theory of hydrotropy7−12 to incorporate the temperature effects (by taking advantage of the formal simplicity afforded by the inhomogeneous solvation theory41−46 and partially open ensembles39−43 as an alternative approach to the extension of the Kirkwood-Buff theory.31−34). The hydrotrope enhancement of heat-solubilization is strengthened by (i) enhanced hydrotrope number-enthalpy correlation around the solute and weakened by (ii) hydrotrope self-association in the bulk solution.
The enhanced hydrotrope number-enthalpy correlation around the solute can be interpreted as the local “structure breaking”. This novel insight, based on a rigorous statistical thermodynamic theory, is different from the classical speculations about a link between “structure breaking” and solubilization.27 Instead, local structure breaking by hydrotropes intensifies heat-solubilization, as has been clarified by the statistical thermodynamic fluctuation theory (eq 11a).
Thus, studying solubilization along the hydrotrope concentration and the temperature axes leads to a clarification of the local behavior of hydrotropes. Both the hydrotrope-solute association (as the driving force for solubilization)7−9 and the locally enhanced hydrotrope-hydrotrope association (cause for the onset of solubilization at the minimum hydrotrope concentration)10−12 weaken the local interaction energy, as shown by the local-bulk difference in number-enthalpy correlation. This clarifies the fluctuating, nonstatic, and water-mediated nature of local hydrotrope associations, which are responsible for the enhanced heat-solubilization by hydrotropes.
Acknowledgments
We thank Steven Abbott for critical comments on the manuscript and encouragement and João Coutinho, Dinis Abranches, Jack Domenech, and Joe Hurd for stimulating discussions. S.S. acknowledges the travel fund from the Steven Abbott TCNF Ltd. N.M. is grateful to the Fugaku Supercomputer Project (Nos. JPMXP1020230325 and JPMXP1020230327) and the Data-Driven Material Research Project (No. JPMXP1122714694) from the Ministry of Education, Culture, Sports, Science, and Technology and to Maruho Collaborative Project for Theoretical Pharmaceutics.
Appendix A: A Non-Setschenow Behavior of Hydrotropy
The signature of hydrotropy, i.e., the sigmoidal functional shape of the solubility isotherm with the “minimum hydrotrope concentration” and saturation, has commonly been described using the plot of solubility against hydrotrope concentration (Figure 1). In contrast, the Setschenow equation,
| A1 |
has been commonly used to
quantify solubility via the Setschenow constant, kS, based on the logarithmic plot of solubilization against
the hydrotrope concentration. However, our example for hydrotropy,
i.e., the solubilization of MB in aqueous urea solutions (Figure 2a), cannot be captured
by the Setschenow constant; Figure 8 demonstrates a nonlinear dependence of 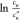 on c2, showing
that the sudden onset of solubilization at the “minimum hydrotrope
concentration” and saturating solubilization are not the artifacts
of adopting cu for solubility
isotherms.
on c2, showing
that the sudden onset of solubilization at the “minimum hydrotrope
concentration” and saturating solubilization are not the artifacts
of adopting cu for solubility
isotherms.
Figure 8.

Replotting the solubility isotherm of MB in aqueous urea solutions (Figure 2a) as the logarithmic solubilization (ln(cu/cou)) of MB against urea concentration (c2), which exhibits a nonlinear behavior that cannot be captured by the Setschenow equation (eq A1) and preserves the signatures of hydrotropy summarized in Figure 1a (i.e., the minimum hydrotrope concentration and saturation).
Appendix B: Fluctuation Theory
First, we derive eq 4, starting from eq 1. To do so, we start with the expressions of the partially open partition functions, i.e.,
| B1a |
| B1b |
where Q and Qu are the canonical partition functions and λ2, the fugacity of hydrotrope, is defined as λ2 = eβμ2. Carrying out the β-derivative of eq 1, we arrive at
| B2 |
where ⟨H⟩u and ⟨H⟩ are the enthalpies of the inhomogeneous and homogeneous systems, respectively, defined as
| B3a |
| B3b |
With the above preparation, now we derive eq 4. To do so, we note that eq B2 is valid for all hydrotrope concentrations. Consequently, subtracting the pure water version of eq B2 yields
| B4 |
where Ho is the enthalpy in pure water. Introducing ΔH = H – Ho yields eq 4.
Second we derive eq 5. To do so, it is useful to note that
| B5 |
Carrying out a μ2-differentiation of eq B3a, we obtain
| B6 |
Evaluating the derivative of eq B3b similarly, while noting that Ho does not depend on μ2, we obtain
| B7 |
Finally, we derive eq 6 from eq 5 through a variable conversion from λ2 to a2, by remembering the, λ2 = eβμ2. Taking advantage of the constant β in eq B7 (eq 5), such that
| B8 |
Using βdμ2 = d ln a2 = da2/a2, we obtain
| B9 |
Appendix C: Relating Constant Fugacity to Constant Mole Ratio
Here, we demonstrate the accuracy of
| C1 |
via an order-of-magnitude analysis using experimental data. In this Appendix, all the partial differentiations are done at constant pressure, and the pressure P as a fixed parameter will be omitted in the expressions for the partial derivatives. Noting that the constant λ2 is equivalent to constant βμ2 because of λ2 = eβμ2, we start with the following change of variables
| C2a |
which can be simplified (under constant β, which is equivalent to constant T) as
 |
C2b |
Using the following well-known results from the Kirkwood-Buff theory24 and chemical thermodynamics,
 |
C2c |
where h2 is the partial molar enthalpy of the hydrotrope. Combining eqs C2b and C2c yields
| C3a |
which, via eqs 2 and 3b (and noting, again, that constant λ2 is equivalent to constant βμ2), can be rewritten as
| C3b |
To establish the accuracy of eq C1, we need to demonstrate that c2(Gu2 – Gu1)h2 in eq C3b makes a minor contribution compared to other terms. Since c2(Gu2 – Gu1) has been reported for aqueous hydrotrope solutions, here we focus on the remaining factor, h2. Using the molality-based activity coefficient, γ2, h2 can be evaluated via
 |
C4 |
With the above preparation, now we carry out an order-of-magnitude analysis on c2(Gu2 – Gu1)h2 in eq C3b, by taking urea as an example hydrotrope, because of its common use as a hydrotrope for which all the physical properties data necessary for our analysis is available. First, at the peak of Gu2 – Gu1 with respect to its c2 dependence, most sharply for ethylbenzene (EB)8 with Gu2 – Gu1 ≃ 2.5 dm3 mol–1 at c2 ≃ 0.6 mol dm–3, c2(Gu2 – Gu1) ≃ 1.5. Second, h2, evaluated via the temperature-dependence of the molality-based activity coefficient of urea, γ2, at the urea concentration of 0.5 molal (close to the c2(Gu2 – Gu1) peak) between 10 and 40 °C yields h2 = −0.35 kJ mol–1 (Figure 9). Combining all above leads to an estimation of c2(Gu2 – Gu1)h2 ≃ −0.53 kJ mol–1, which is minor compared to Δh*u ∼ 10 kJ mol–1 (see Figure 5) in the same hydrotrope concentration region. This approximation is still valid at higher hydrotrope concentrations where (Gu2 – Gu1) significantly decreases in magnitude while Δh*u increases to ∼18 kJ mol–1. Thus, we have justified eq C1.
Figure 9.

Partial molar enthalpy of urea, h2, can be calculated from the 1/T-dependence of lnγ2 (where γ2 is in the molal concentration basis). The experimental data for 0.5 and 1.0 molal urea solutions (taken from Stokes48), in blue circles and red squares, have been fitted with lnγ2 = −42.7T–1 + 0.102 (blue solid line) and lnγ2 = −79.9T–1 + 0.190 (red solid line), yielding (via eq C4 in Appendix C) h2 = −0.35 and −0.66 kJ mol–1 for 0.5 and 1.0 molal, respectively.
We emphasize that the limited availability of thermodynamic
data
has restricted our analysis to choose urea as the sole example of
hydrotrope in this paper. When the approximation (eq C1) breaks down,  required for the fluctuation theory can
be calculated via eq C3b, through a direct evaluation of (i) Δh*u from the temperature-dependent solubility data (eq 3a), (ii) h2 from the temperature-dependent activity data (eq C4), and (iii) c2(Gu2 – Gu1) from the Kirkwood-Buff
theory based on a combination of the solubility and activity data.64
required for the fluctuation theory can
be calculated via eq C3b, through a direct evaluation of (i) Δh*u from the temperature-dependent solubility data (eq 3a), (ii) h2 from the temperature-dependent activity data (eq C4), and (iii) c2(Gu2 – Gu1) from the Kirkwood-Buff
theory based on a combination of the solubility and activity data.64
Appendix D: Use of Hydrotrope Molarity in Data Analysis
Here, we show that the effect of thermal expansion on hydrotrope is quite negligible, hence the constant molality condition, required by chemical thermodynamics, can be approximated by constant hydrotrope molarity. When the temperature rises by ΔT, the relative change of molarity, induced by the thermal expansion of the solution, can be expressed as
| D1 |
where αV is the thermal expansion coefficient of the aqueous hydrotrope solution. Here, we carry out the order-of-magnitude estimation, using αV by that of pure water. At 318 K (which is right in the middle of the temperature range, 303–333 K, of the solubility data by Nagendra Gandhi and co-workers), αV = 4.22 × 10–4 K–1 as reported by Kell.65 (Note that αV of aqueous urea solutions are also in the order of αV ∼ 10–4 K–1.) Taking the temperature interval ΔT = 30 K, the relative change of molarity is estimated as
| D2 |
Thus, the constant m2 (hydrotrope molality) condition, required by chemical thermodynamics, can be approximated by a constant c2 condition.
The authors declare no competing financial interest.
References
- Neuberg C. Hydrotropie. Biochem. Z. 1912, 76, 107–176. [Google Scholar]
- Friberg S. E. Hydrotropes. Curr. Opin. Colloid Interface Sci. 1997, 2 (5), 490–494. 10.1016/S1359-0294(97)80096-9. [DOI] [Google Scholar]
- Hodgdon T. K.; Kaler E. W. Hydrotropic Solutions. Curr. Opin. Colloid Interface Sci. 2007, 12 (3), 121–128. 10.1016/j.cocis.2007.06.004. [DOI] [Google Scholar]
- Kunz W.; Holmberg K.; Zemb T. Hydrotropes. Curr. Opin. Colloid Interface Sci. 2016, 22, 99–107. 10.1016/j.cocis.2016.03.005. [DOI] [Google Scholar]
- Patel A. D.; Desai M. A. Aggregation Behavior and Thermodynamic Studies of Hydrotropes: A Review. Tenside Surfactants Deterg. 2020, 57 (3), 192–202. 10.3139/113.110686. [DOI] [Google Scholar]
- Patel A. D.; Desai M. A. Progress in the Field of Hydrotropy: Mechanism, Applications and Green Concepts. Rev. Chem. Eng. 2023, 39 (4), 601–630. 10.1515/revce-2021-0012. [DOI] [Google Scholar]
- Booth J. J.; Abbott S.; Shimizu S. Mechanism of Hydrophobic Drug Solubilization by Small Molecule Hydrotropes. J. Phys. Chem. B 2012, 116 (51), 14915–14921. 10.1021/jp309819r. [DOI] [PubMed] [Google Scholar]
- Booth J. J.; Omar M.; Abbott S.; Shimizu S. Hydrotrope Accumulation around the Drug: The Driving Force for Solubilization and Minimum Hydrotrope Concentration for Nicotinamide and Urea. Phys. Chem. Chem. Phys. 2015, 17 (12), 8028–8037. 10.1039/C4CP05414H. [DOI] [PubMed] [Google Scholar]
- Abbott S.; Booth J. J.; Shimizu S. Practical Molecular Thermodynamics for Greener Solution Chemistry. Green Chem. 2017, 19 (1), 68–75. 10.1039/C6GC03002E. [DOI] [Google Scholar]
- Shimizu S.; Matubayasi N. Cooperativity in Micellar Solubilization. Phys. Chem. Chem. Phys. 2021, 23 (14), 8705–8716. 10.1039/D0CP06479C. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. Hydrotropy: Monomer-Micelle Equilibrium and Minimum Hydrotrope Concentration. J. Phys. Chem. B 2014, 118, 10515–10524. 10.1021/jp505869m. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. The Origin of Cooperative Solubilisation by Hydrotropes. Phys. Chem. Chem. Phys. 2016, 18 (36), 25621–25628. 10.1039/C6CP04823D. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. Hydrotropy and Scattering: Pre-Ouzo as an Extended near-Spinodal Region. Phys. Chem. Chem. Phys. 2017, 19 (39), 26734–26742. 10.1039/C7CP04990K. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. Synergistic Solvation as the Enhancement of Local Mixing. J. Phys. Chem. B 2024, 128 (23), 5713–5726. 10.1021/acs.jpcb.4c01582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abranches D. O.; Benfica J.; Soares B. P.; Leal-Duaso A.; Sintra T. E.; Pires E.; Pinho S. P.; Shimizu S.; Coutinho J. A. P. Unveiling the Mechanism of Hydrotropy: Evidence for Water-Mediated Aggregation of Hydrotropes around the Solute. Chem. Commun. 2020, 56 (52), 7143–7146. 10.1039/D0CC03217D. [DOI] [PubMed] [Google Scholar]
- Yalkowsky S. H.; He Y.; Jain P.. Handbook of Aqueous Solubility Data, 2nd ed.; CRC Press: Boca Raton, FL, 2010. [Google Scholar]
- Hansen C. M.Hansen Solubility Parameters: A User’s Handbook; CRC Press: Boca Raton, FL, 2007. [Google Scholar]
- Coffman R. E.; Kildsig D. O. Hydrotropic Solubilization - Mechanistic Studies. Pharm. Res. 1996, 13 (10), 1460–1463. 10.1023/A:1016011125302. [DOI] [PubMed] [Google Scholar]
- Nagendra Gandhi N.; Dharmendira Kumar M.; Sathyamurthy N. Effect of Hydrotropes on Solubility and Mass-Transfer Coefficient of Butyl Acetate. J. Chem. Eng. Data 1998, 43 (5), 695–699. 10.1021/je970212k. [DOI] [Google Scholar]
- Jayakumar K. K.; Gandhi N. N. Enhancement of Solubility and Mass Transfer Coefficient of Salicylic Acid through Hydrotropy. Int. J. Chem. Anal. Sci. 2012, 3 (4), 1348–1352. 10.1631/jzus.A0820516. [DOI] [Google Scholar]
- Marimuthu C.; Jayakumar C.; Gandhi N. N. A Study on Hydrotropy—Petroleum and Petrochemical Products. Pet. Sci. Technol. 2011, 29 (4), 337–348. 10.1080/10916460903330106. [DOI] [Google Scholar]
- Kim J. Y.; Kim S.; Papp M.; Park K.; Pinal R. Hydrotropic Solubilization of Poorly Water-Soluble Drugs. J. Pharm. Sci. 2010, 99 (9), 3953–3965. 10.1002/jps.22241. [DOI] [PubMed] [Google Scholar]
- Beig A.; Lindley D.; Miller J. M.; Agbaria R.; Dahan A. Hydrotropic Solubilization of Lipophilic Drugs for Oral Delivery: The Effects of Urea and Nicotinamide on Carbamazepine Solubility-Permeability Interplay. Front. Pharmacol. 2016, 7, 379. 10.3389/fphar.2016.00379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimizu S. Formulating Rationally via Statistical Thermodynamics. Curr. Opin. Colloid Interface Sci. 2020, 48, 53–64. 10.1016/j.cocis.2020.03.008. [DOI] [Google Scholar]
- Kopecký F.; Vojteková M.; Bednářová-Hyttnerová M. Osmometric Study of Self-Association of Nicotinamide and Isonicotinic Acid Hydrazide in Aqueous Solutions at 40 °C and the Freezing Point. Collect. Czechoslov. Chem. Commun. 1978, 43 (1), 37–46. 10.1135/cccc19780037. [DOI] [Google Scholar]
- Stokes R. Osmotic Coefficients of Concentrated Aqueous Urea Solutions from Freezing-Point Measurements. J. Phys. Chem. 1966, 70 (4), 1199–1203. 10.1021/j100876a038. [DOI] [PubMed] [Google Scholar]
- Frank H. S.; Franks F. Structural Approach to the Solvent Power of Water for Hydrocarbons; Urea as a Structure Breaker. J. Chem. Phys. 1968, 48 (10), 4746–4757. 10.1063/1.1668057. [DOI] [Google Scholar]
- Prigogine I.; Defay R.. Thermodynamique Chimique; Desoer: Liege, 1950; 70–73. [Google Scholar]
- Matubayasi N.; Reed L. H.; Levy R. M. Thermodynamics of the Hydration Shell. 1. Excess Energy of a Hydrophobic Solute. J. Phys. Chem. 1994, 98 (41), 10640–10649. 10.1021/j100092a040. [DOI] [Google Scholar]
- Matubayasi N.; Gallicchio E.; Levy R. M. On the Local and Nonlocal Components of Solvation Thermodynamics and Their Relation to Solvation Shell Models. J. Chem. Phys. 1998, 109 (12), 4864–4872. 10.1063/1.477097. [DOI] [Google Scholar]
- Buff F. P.; Brout R. Molecular Formulation of Thermodynamic Functions Encountered in Solution Theory. J. Chem. Phys. 1955, 23 (3), 458–465. 10.1063/1.1742010. [DOI] [Google Scholar]
- Ploetz E. A.; Smith P. E. Local Fluctuations in Solution Mixtures. J. Chem. Phys. 2011, 135 (4), 044506 10.1063/1.3615718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ploetz E. A.; Smith P. E. Local Fluctuations in Solution: Theory and Applications. Adv. Chem. Phys. 2013, 153, 311–372. 10.1002/9781118571767.ch4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ploetz E. A.; Smith P. E. Particle and Energy Pair and Triplet Correlations in Liquids and Liquid Mixtures from Experiment and Simulation. J. Phys. Chem. B 2015, 119, 7761–7777. 10.1021/acs.jpcb.5b00741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. Intensive Nature of Fluctuations: Reconceptualizing Kirkwood-Buff Theory via Elementary Algebra. J. Mol. Liq. 2020, 318, 114225 10.1016/j.molliq.2020.114225. [DOI] [Google Scholar]
- Nishikawa K. Simple Relationship between the Kirkwood-Buff Parameters and the Fluctuations in the Particle Number and Concentration Obtained by Small-Angle X-Ray Scattering: Application to Tert-Butyl Alcohol and Water Mixtures. Chem. Phys. Lett. 1986, 132 (1), 50–54. 10.1016/0009-2614(86)80692-3. [DOI] [Google Scholar]
- Hayashi H.; Nishikawa K.; Iijima T. Easy Derivation of the Formula Relating the Fluctuations of a Binary System to the X-Ray Scattering Intensity Extrapolated to s = 0. J. Appl. Crystallogr. 1990, 23 (2), 134–135. 10.1107/S0021889889012331. [DOI] [Google Scholar]
- Gazzillo D. Stability of Fluids with More than Two Components I. General Thermodynamic Theory and Concentration-Concentration Structure Factor. Mol. Phys. 1994, 83 (6), 1171–1190. 10.1080/00268979500100221. [DOI] [Google Scholar]
- Shimizu S.; Matubayasi N. Statistical Thermodynamic Foundation for Mesoscale Aggregation in Ternary Mixtures. Phys. Chem. Chem. Phys. 2018, 20, 13777–13784. 10.1039/C8CP01207E. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Matubayasi N. Ensemble Transformation in the Fluctuation Theory. Physica A 2022, 585, 126430 10.1016/j.physa.2021.126430. [DOI] [Google Scholar]
- Percus J. K. Approximation Methods in Classical Statistical Mechanics. Phys. Rev. Lett. 1962, 8 (11), 462–463. 10.1103/PhysRevLett.8.462. [DOI] [Google Scholar]
- Henderson D.Fundamentals of Inhomogeneous Fluids; Marcel Dekker: New York, 1992; 1–22. [Google Scholar]
- Hansen J. P.; McDonald I. R.. Theory of Simple Liquids: With Applications to Soft Matter: Fourth ed.. In Theory of Simple Liquids: With Applications to Soft Matter: Fourth ed.; Academic Press: Amsterdam, 2013; 203–264. [Google Scholar]
- Lazaridis T. Inhomogeneous Fluid Approach to Solvation Thermodynamics. 1. Theory. J. Phys. Chem. B 1998, 102 (18), 3531–3541. 10.1021/jp9723574. [DOI] [Google Scholar]
- Lazaridis T. Inhomogeneous Fluid Approach to Solvation Thermodynamics. 2. Applications to Simple Fluids. J. Phys. Chem. B 1998, 102 (18), 3542–3550. 10.1021/jp972358w. [DOI] [Google Scholar]
- Levy R. M.; Cui D.; Zhang B. W.; Matubayasi N. Relationship between Solvation Thermodynamics from IST and DFT Perspectives. J. Phys. Chem. B 2017, 121 (15), 3825–3841. 10.1021/acs.jpcb.6b12889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Naim A.Solvation Thermodynamics; Plenum: New York, 1987. [Google Scholar]
- Stokes R. Thermodynamics of Aqueous Urea Solutions. Aust. J. Chem. 1967, 20 (10), 2087. 10.1071/CH9672087. [DOI] [Google Scholar]
- Makarov D. M.; Egorov G. I. Density and Volumetric Properties of the Aqueous Solutions of Urea at Temperatures from T = (278 to 333) K and Pressures up to 100 MPa. J. Chem. Thermodyn. 2018, 120, 164–173. 10.1016/j.jct.2018.01.024. [DOI] [Google Scholar]
- Thenesh Kumar S.; Nagendra Gandhi N. A Study on the Properties of Hydrotrope Solutions for the Enhancement of Solubility of P-Aminobenzoic Acid Through Hydrotropy. Int. J. Pharm. Pharm. Sci. 2012, 4, 324–330. [Google Scholar]
- Meyyappan N.; Gandhi N. N. Effect of Hydrotropes on the Solubility and Mass Transfer Coefficient of Benzyl Benzoate in Water. J. Chem. Eng. Data 2005, 50 (3), 796–800. 10.1021/je049756u. [DOI] [Google Scholar]
- Sampath Kumar V.; Jayakumar C.; Raja C.; Nagendra Gandhi N. Hydrotropic Aggregation Behavior of Butyl Stearate. Chem. Mater. Eng. 2013, 1 (1), 1–7. 10.13189/cme.2013.010101. [DOI] [Google Scholar]
- Morais A. B.; Jayakumar C.; Gandhi N. N. Hydrotropic Effect and Thermodynamic Analysis on the Solubility and Mass Transfer Coefficient Enhancement of Ethylbenzene. Korean J. Chem. Eng. 2013, 30 (4), 925–930. 10.1007/s11814-012-0213-y. [DOI] [Google Scholar]
- Senthil N.; Jayakumar C.; Gandhi N. Effect of Hydrotropes on Solubility and Mass Transfer Coefficient of Methyl Benzoate. Mod. Appl. Sci. 2009, 3 (3), 101–111. 10.5539/mas.v3n3p101. [DOI] [Google Scholar]
- Rezus Y. L. A.; Bakker H. J. Effect of Urea on the Structural Dynamics of Water. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (49), 18417–18420. 10.1073/pnas.0606538103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funkner S.; Havenith M.; Schwaab G. Urea, a Structure Breaker? Answers from THz Absorption Spectroscopy. J. Phys. Chem. B 2012, 116 (45), 13374–13380. 10.1021/jp308699w. [DOI] [PubMed] [Google Scholar]
- Canchi D. R.; García A. E. Cosolvent Effects on Protein Stability. Annu. Rev. Phys. Chem. 2013, 64, 273–293. 10.1146/annurev-physchem-040412-110156. [DOI] [PubMed] [Google Scholar]
- Horinek D.; Netz R. R. Can Simulations Quantitatively Predict Peptide Transfer Free Energies to Urea Solutions? Thermodynamic Concepts and Force Field Limitations. J. Phys. Chem. A 2011, 115 (23), 6125–6136. 10.1021/jp1110086. [DOI] [PubMed] [Google Scholar]
- Blokzijl W.; Engberts J. B. F. N. Hydrophobic Effects. Opinions and Facts. Angew. Chem., Int. Ed. Engl. 1993, 32 (11), 1545–1579. 10.1002/anie.199315451. [DOI] [Google Scholar]
- Southall N. T.; Dill K. A.; Haymet A. D. J. A View of the Hydrophobic Effect. J. Phys. Chem. B 2002, 106, 521–533. 10.1021/jp015514e. [DOI] [Google Scholar]
- Lazaridis T.; Paulaitis M. E. Entropy of Hydrophobic Hydration: A New Statistical Mechanical Formulation. J. Phys. Chem. 1992, 96 (9), 3847–3855. 10.1021/j100188a051. [DOI] [Google Scholar]
- Lazaridis T.; Paulaitis M. E. Simulation Studies of the Hydration Entropy of Simple, Hydrophobic Solutes. J. Phys. Chem. 1994, 98 (2), 635–642. 10.1021/j100053a044. [DOI] [Google Scholar]
- Naito H.; Sumi T.; Koga K. How Do Water-Mediated Interactions and Osmotic Second Virial Coe Ffi Cients Vary with Particle Size ?. Faraday Discuss. 2024, 249, 440–452. 10.1039/D3FD00104K. [DOI] [PubMed] [Google Scholar]
- Shimizu S.; Booth J. J.; Abbott S. Hydrotropy: Binding Models vs. Statistical Thermodynamics. Phys. Chem. Chem. Phys. 2013, 15 (47), 20625–20632. 10.1039/c3cp53791a. [DOI] [PubMed] [Google Scholar]
- Kell G. S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0° to 150°C. J. Chem. Eng. Data 1975, 20 (1), 97–105. [Google Scholar]


