Abstract
Cardiovascular MRI (CMRI) is a non-invasive imaging technique adopted for assessing the blood circulatory system’s structure and function. Precise image segmentation is required to measure cardiac parameters and diagnose abnormalities through CMRI data. Because of anatomical heterogeneity and image variations, cardiac image segmentation is a challenging task. Quantification of cardiac parameters requires high-performance segmentation of the left ventricle (LV), right ventricle (RV), and left ventricle myocardium from the background. The first proposed solution here is to manually segment the regions, which is a time-consuming and error-prone procedure. In this context, many semi- or fully automatic solutions have been proposed recently, among which deep learning-based methods have revealed high performance in segmenting regions in CMRI data. In this study, a self-adaptive multi attention (SMA) module is introduced to adaptively leverage multiple attention mechanisms for better segmentation. The convolutional-based position and channel attention mechanisms with a patch tokenization-based vision transformer (ViT)-based attention mechanism in a hybrid and end-to-end manner are integrated into the SMA. The CNN- and ViT-based attentions mine the short- and long-range dependencies for more precise segmentation. The SMA module is applied in an encoder-decoder structure with a ResNet50 backbone named CardSegNet. Furthermore, a deep supervision method with multi-loss functions is introduced to the CardSegNet optimizer to reduce overfitting and enhance the model’s performance. The proposed model is validated on the ACDC2017 (n=100), M&Ms (n=321), and a local dataset (n=22) using the 10-fold cross-validation method with promising segmentation results, demonstrating its outperformance versus its counterparts.
Keywords: Cardiac magnetic resonance imaging, Deep learning, Hybrid attention mechanism, Image segmentation, Vision transformer
1. Introduction
Cardiovascular diseases (CVDs) is a general term applied to defining diseases related to the heart and vessels, like coronary artery disease, valvular heart disease, and congenital heart disease (Lum and Tsiouris, 2020). According to the WHO, CVDs have been and still are the primary cause of death in recent years, with almost 31.8 % attributed to cardiovascular disease in the last decade (von von von Knobelsdorff-Brenkenhoff et al., 2017). CVD is one of the chronic non-communicable diseases with a prevalence of over 12 % (Topol and Califf, 2007). Next to physical examinations and blood tests, there are many non-invasive tests like computed tomography (CT) scans, cardiac magnetic resonance imaging (CMRI), electrocardiograms (ECG), echocardiograms, and exercise stress test (or ergospirometry) reports that can be run to diagnose CVDs. The CMRI is one of the safest and most effective imaging techniques for the heart, even during pregnancy, because it is free of radiation (Lum and Tsiouris, 2020). In cardiovascular diseases, this technique has a key impact on evidence-based diagnostic and therapeutic pathways (von von von Knobelsdorff-Brenkenhoff et al., 2017). A precise image segmentation step is required to assess the structure and function of the cardiovascular system through CMRI data, which enables clinicians to measure local and global cardiac parameters for more accurate diagnosis, treatment, and surgical planning. Segmentation of the LV, RV, and LVM in CMRI is challenging due to anatomical heterogeneity, image quality restrictions like similarity in image intensities of the heart chambers, and motional aberrations at acquisition time. The precision of segmentation directly influences the CVDs’ diagnosis. Manual segmentation of cardiac images can be beneficial in some cases, while the diagnostic procedure cycles due to the subjective, time-consuming, and expert-level nature of the process can be protracted with no satisfying accuracy. Consequently, computer-aided diagnostic systems based on AI can be adopted to automate the segmentation process and assist cardiologists in reducing diagnostic errors, is a must in cardiac function analysis (Topol and Califf, 2007). There exist many image processing and machine learning techniques that seek to analyze cardiac regions automatically and accurately (Zhao et al., 2022), and a briefing of the relevant literature is presented in Section ↱II. Despite recent advances, accurate cardiac segmentation in CMRI remains challenging due to the distinctions in cardiac structures, variations in size and shape, heart axes orientation due to the disease, low-contrast boundaries of heart regions, and the presence of motional artifacts. Due to the organ’s dynamic nature, these obstacles prevent accurate segmentation.
The following is a brief summary of our most significant technological contributions to this work:
A novel self-adaptive multi-attention (SMA) module is developed and introduced for image representation in deep learning models, capturing key information in multi-range dependencies simultaneously. It leverages the strengths of both convolutional neural networks (CNN)-based and vision transformers (ViT)-based attentions in the processing scale. The SMA module applies pixel-group attention to input tensors using a hybrid attention mechanism that considers local-global interdependencies. With the least number of trainable parameters, this module automatically weighs and highlights local and global information provided by CNN-based (Fu et al., 2019) and ViT-based (Lee et al., 2021) attentions in an end-to-end and adaptive manner, thereby enhancing the performance of the attention process. By learning multi-semantic, contextually representative features in addition to efficient local representations, the SMA module significantly improves the overall model’s representation capability.
CardSegNet model, a new U-shaped deep learning structure with a ResNet50 (He et al., 2016) backbone, is introduced and assessed for heart region segmentation in CMRI analysis. The enhancement of visual features at multiple scales in both the encoding and decoding paths of the model, facilitated by the proposed SMA attention mechanism, is projected to enhance the local and global modeling proficiencies of CardSegNet, leading to a more accurate and robust performance.
A deep supervision learning (DSL) (Reis et al., 2021; Peng and Wang, 2021) scheme based on multiple combined loss functions is proposed to optimize the CardSegNet model. The model output is converged into the target through multiple scale-dependent penalties and a mixed loss function superposition technique to alleviate the imbalanced samples due to the high proportion of non-desired regions in CMR images. It also leverages a curvature-based loss function to direct the model toward the closed contour of the heart regions.
A new local CMRI dataset, is collected and will be accessible upon academic requests by researchers in the field. The dataset, called Rajaie CMRI dataset, was obtained from Tehran’s Shahid Rajaie Hospital, Iran between 2022 and 2023. This dataset represents a valuable resource for academic research, offering scholars access to locally sourced data for further study and analysis.
Extensive experiments and ablation studies conducted on the ACDC 2017 (Zheng et al., 2018), M&Ms-2 (Campello et al., 2021), and Rajaie CMRI datasets provide evidence of the effectiveness of the proposed framework and technological contributions. CardSegNet, with comparable results, outperforms other baselines and state-of-the-art deep learning (DL) methods in the CMRI data segmentation task. It demonstrates acceptable inference performance and execution time.
The structure of the paper is organized as follows: The related works are reviewed in Sec. ↱II; material and method are expressed in Sec. ↱III; the experimental study and results are presented in Sec. ↱IV; the findings are discussed in Sec. ↱V; and finally the study is concluded in Sec. ↱VI.
2. Related work
The automatic analysis of cardiac data is influenced by the rapid development of machine learning techniques and DL during the last few decades. Research groups from all over the world constantly compete on challenging CMRI topics. To extract both local and global parameters of the heart in CMRIs, the greatest technical challenge that developers face is maintaining synchronicity across multiple range dependencies. The primary issue with DL networks is that their training requires a large quantity of data. To address this issue, several techniques, like image data augmentation, regularization methods, and transfer learning, are proposed for the limited dataset analysis. The recent studies on the CMRI segmentation problem based on dataset, model, cross-validation (CV), assessments, and results are tabulated in Table 1. The details of the winners of the ACDC 2017 challenge and the recently developed methods (Isensee et al., 2017; Khened et al., 2017; Zotti et al., 2018; Bernard et al., 2018) are expressed in this table. The contributions of the listed studies are summarized as follows: (I) U-Net (Graves et al., 2021), TransU-Net (Chen et al., 2021a), nn-TransU-Net (Zhao et al., 2022), FCN (Khened et al., 2017), VAE (Painchaud et al., 2020), U-Net++ (Le et al., 2022), Deeplabv3 (Chen et al., 2017), Seg-Net (Yan et al., 2022), and GridNet (Zotti et al., 2018) are the most widely adopted DL architectures for medical image segmentation. The U-shape model is a common deep learning architecture for medical image segmentation among previous approaches examined for the CMRI segmentation problem. (II) Some researchers have introduced new modules that prevent overfitting and/or enable DL models to converge in a more efficient and precise manner (Wang et al., 2022). (III) Introduced new or mixed loss functions and penalty terms are among the contributions in this context (Shi et al., 2021; Zhou et al., 2021). (IV) The attention mechanism is viewed in two distinct manners: CNN-based and transformer-based, respectively (Niu et al., 2021; Guo et al., 2022). Due to their inherent character as convolutional processes, CNN attentions extract local and short-range dependency information from the image, while vanilla transformers primarily extract global data to model long-range dependency. Self-attention (Guo et al., 2022), co-attention and hierarchical mechanisms (Niu et al., 2021), bilinear attention (Guo et al., 2022), attention-over-attention (Niu et al., 2021), and coordinated attention processes (Chen et al., 2022) are frequently applied to improve the attention mechanisms performance. According to (Zhao et al., 2022), self-attention modules are developed to demonstrate the benefits of spatial and/or channel attention in enhancing different image analysis tasks. As to segmentation and attention mechanisms for medical images, SCA Net (Shan and Yan, 2021) is among the first models to incorporate spatial and channel attentions.
Table 1.
Review of the Last Segmentation Methodologies and Winners of the ACDC 2017 Challenge.
| Reference | Dataset |
Model |
CV Method | Reported Result (%)* (LVC, RVC, LVM, Mean) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset Name | Sample Size (trains/tests) | Class Size | Pre processing | Data Augment. | Crop-Resize | Localizer | Base Model | Attention mechanism | Additional data | Loss Function (s) | Ex. Classifier | ||||||
|
| |||||||||||||||||
| Isensee et al. 2017 (Isensee et al., 2017) | ACDC-17 | 100/50 | 4 | - | ✓ | - | - | 3D U-Net + 2D U-Net | - | - | C+D | - | 5-fold | 94.5, 90.8, 90.5, 91.9 | |||
| Khened et al. 2017 (Khened et al., 2017) | ACDC-17 | 100/50 | 4 | ✓ | ✓ | - | ✓ | Densely FCN | - | ✓ | D | RF | H.O (90 %) | 94.1, 90.7, 89.4, 91.3 | |||
| Zotti et al. 2018 (Zotti et al., 2018) | ACDC-17 | 100/50 | 4 | - | - | - | - | Grid net | - | - | C | - | H.O (75 %) | 93.8, 91.0, 89.4, 91.4 | |||
| Painchaud et al. 2020 (Painchaud et al., 2020) | ACDC-17 | 100/50 | 4 | - | ✓ | - | - | VAE | - | ✓ | KL loss | - | 10-fold | 93.6, 90.9, 88.9, 91.1 | |||
| Shi et al. 2021 (Shi et al., 2021) | ACDC-17 LV-09 RV-12 |
100 /50 130/20 80/10 |
4 4 4 |
✓ | - | - | ✓ | MIFNet | PAM | - | D | - | 4-fold | Mean: 97.2 Mean: 96.1 Mean: 89.6 |
|||
| Zhou et al. 2021 (Zhou et al., 2021) | ACDC-17 | 100/50 | 4 | ✓ | ✓ | - | - | nnFormer | Multi-head self-attention | - | MSE | - | H.O (70 %) | Mean: 92.1 | |||
| Chen et al. 2022 (Chen et al., 2022) | ACDC-17 2018 ASC |
100/50 50 |
4 5 |
✓ | - | - | - | Multiresolution Aggregation Transformer U-Net |
Coordinate attention (CA) | - | C+D | - | H.O (70 %) | Mean: 92.0 Mean: 92.1 |
|||
| Galazis et al. 2021 (Galazis et al., 2021) | ACDC-17 | 100/50 | 4 | ✓ | ✓ | - | ✓ | Tempera: Spatial Transformer Feature Pyramid |
PAM | ✓ | D | - | H.O (90 %) | Mean: 92.1 | |||
| Fu et al. 2022 (Fu et al., 2022) | ACDC-17 Synapse |
100/50 50 |
4 8 |
✓ | - | ✓ | - | TF-U-Net | - | - | C | - | H.O (80 %) | Mean: 91.7 Mean: 85.5 |
|||
| D. Li et al. 2022 (Li et al., 2022a) | ACDC-17 | 100/50 | 4 | ✓ | ✓ | ✓ | - | U-Net | PAM CAM |
- | C+D | - | H.O (80 %) | RV: 89.1 | |||
| Y. Li et al. 2022 (Li et al., 2022b) | ACDC-17 | 100/50 | 4 | ✓ | - | - | - | ViT Decoder | Window Attention Unsampled |
- | MSE | - | H.O (80 %) | Mean: 92.1 | |||
| Galea et al. 2021 (Galea et al., 2021) | 2018 ASC |
50 | 5 | ✓ | ✓ | - | - | U-Net + DeepLabV3+ | - | - | MSE | - | H.O (80 %) | Mean: 92.1 | |||
| Garcia-Cabrera et al. 2023 (Garcia-Cabrera et al., 2023) | ACDC-17 | 100/50 | 4 | - | ✓ | - | - | U-Net (ImageNet) | - | - | MSE | - | H.O (80 %) | Mean:96.6 | |||
| Płotka et al. 2023 (Grzeszczyk et al., 2023) | ACDC-17 | 100/50 | 4 | - | - | - | - | Swin Transformer/U-Net | Shifted-window multi-head | - | C+D | - | 5-fold | Mean:87.1 | |||
| Liu et al. 2023 (Liu et al., 2023) | ACDC-17 | 100/50 | 4 | - | - | - | - | Successive subspace learning | - | - | MSE | - | 5-fold | Mean:95.0 | |||
| J.M.Harana et al. 2021 (Mariscal-Harana et al., 2021) | ACDC-17 M&Ms-2 Local (NHS) |
100/50 360 (321 MRI) 4228 |
4 | ✓ | - | - | - | 2D U-Net | - | - | C+D | - | 5-fold | 87.8, 81.7, 79.1, 82.9 83.8, 80.7, 82.2, 82.2 90.1, 82.1, 78.9, 83.7 |
|||
| A.K. Yasmina et al. 2023 (Al Khalil et al., 2023) | M&Ms-2 | 360 (200 annotated) | 4 | - | ✓ | - | - | Conditional GAN | Post processing | - | D+H | - | 5-fold | 95.9, 90.7, 93.8, 93.4 | |||
| C. Galazis et al. 2023 (Galazis et al., 2021) | M&Ms-2 | 360 (200 annotated) | 4 | ✓ | ✓ | ✓ | ✓ | Tempera | Post processing | - | F+D | - | H.O (93 %) | Mean: 83.6 | |||
| Gao et al. 2022 (Gao and Zhuang, 2022) | M&MS-2 | 360 (200 annotated) | 4 | ✓ | ✓ | - | ✓ | U-Net+ ViT | Self-attention | - | C+D | - | H.O (80 %) | Mean: 88.1 | |||
| Habijan et al. 2021 (Habijan et al., 2021) | MM-WHS | 100/40 | 7 | ✓ | ✓ | - | - | VAE and FM-Pre- ResNet | - | - | D, L2, KL | - | 10-fold | Mean: 89.5 | |||
| Yang et al. 2022 (Yang et al., 2022a) | Synapse | 50 | 8 | ✓ | - | - | - | Encoder-Decoder | Fuzzy | - | - | - | H.O (80 %) | Mean: 85.5 | |||
| Pereira et al. 2020 (Pereira et al., 2020) | MICCAI 2019 | 1120 +56 | 4 | - | - | - | ✓ | U-Net | - | - | MAE | - | 5-fold | Mean: 94.2 | |||
ACDC-17: Automated Cardiac Diagnosis Challenge dataset, ACC: Accuracy, C: Cross-Entropy Loss, CAM: Channel Attention Module, D: Dice Loss, H: Hausdorff Distance, H.O: Hold Out, KL: Kullback-Leibler Divergence, L2: L2 norm, LV: Left Ventricle, LV-09: Sunnybrook Cardiac dataset, Myo: Myocardium, PAM: Position Attention Module, RF: Random Forest, ROI: Region of Interest, RV: Right Ventricle, RV-12: MICCAI 2012 Right Ventricle Segmentation Challenge dataset, VAE: Variational Autoencoder.
The results are reported based on CMRI analyses like LV, RV, Myo, and Overall mean, respectively. Here, class size indicates the segmented heart regions count plus the background.
ViT is extensively utilized by the vision community for computer vision problems (Khan et al., 2022; Dosovitskiy et al., 2020). There exist several distinct categories of transformer-based attention studies: (I) In the ViT (Dosovitskiy et al., 2020) and PVT (Wang et al., 2021) models, information extraction is applied predominantly to capture long-range dependencies for data modeling purposes. With the main disadvantage of not presenting local features perfectly. (II) The Swin (Liu et al., 2021) model is designed to extract local features by applying the self-attention mechanism in transformers. (III) There exist a few additional ViT structures, like Twins (Chu et al., 2021), ViL (Zhang et al., 2021), RegionViT (Chen et al., 2021b), and shifted patch marker (Lee et al., 2022), that simultaneously acquire local and global representations. A spatial feature pyramid transformer applied in image segmentation is Tempera (Galazis et al., 2021) in this category. (IV) The combination of local and global attentions is applied in TransU-Net (Chen et al., 2021a) and its affiliations (like nn-TransU-Net (Zhao et al., 2022) and Ds-TransU-Net (Lin et al., 2022)) for enhanced data representation. Although in the aforementioned techniques, the TransU-Net model family applies the proper attention combinations, to the best knowledge of the researchers here, the effects of adaptive attention fusion techniques are not assessed or applied to the CMRI data segmentation field. Motivated by attention fusion models, an attempt is made here to combine CNN and transformer-based attention processes in a new, end-to-end attention block. To extract multi-range dependencies through a new paradigm, the proposed attention fusion module, SMA, adaptively combines CNN-based (spatial, channel) and ViT-based attention mechanisms at different scales. To prevent overfitting and improve and generalize the model segmentation performance, the DSL and multiple loss functions are applied here.
3. Material and method
This section introduces the dataset and pre-processing pipeline used in this work. The SMA module and this newly proposed model are then presented and formulated. The DSL scheme, the proposed weighted objective function, and the learning strategy are later described.
3.1. Dataset
In this study, three different CMRI datasets were utilized to design and evaluate our proposed method. The first dataset, ACDC 2017 (Zheng et al., 2018), is a publicly available dataset of CMRI scans that was released as part of the Automated Cardiac Diagnosis Challenge (ACDC) at the Medical Image Computing and Computer-Assisted Intervention (MICCAI) conference in 2017. The second dataset, M&Ms-2 (Campello et al., 2021) (Multi-Disease, Multi-View, and Multi-Center), is another publicly available dataset that focuses on cardiac imaging, specifically MRI. It contains images from various imaging centers and vendors. The third dataset is the Rajaie CMRI dataset, which is a local dataset obtained from the Shahid Rajaie Research Centre at Tehran University of Medical Sciences in Iran. This dataset was collected and annotated under the supervision of Dr. H. Pour Aliakbar and Dr. F. Tabesh. A summary of the research datasets is provided in Table 2.
Table 2.
Summary of the Research Cardiac MRI Datasets.
| Dataset | Scanner | No. Case | No. Images | No. Frames | No. Slices per Case | Lables | Categories | Image Sizes (pixels) |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| ACDC-17 | Siemens Area 1.5 T, and Trio Tim 3.0 T | 100 Tr 50 Te |
1902 | 2 (ED,ES) | SA 8–10 | LV, Myo, RV | 4 Groups | 154×224–428×512 |
| M&Ms - 2 | Siemens, Philipps, GE, and Canon | 200 Tr 160 Te |
1440 (720 SA) |
2 (ED,ES) | SA 9–13 LA 1 |
LV, Myo, RV | 4 Groups | 196×240–512×512 |
| Rajaie CMRI Dataset | Siemens MAGNETOM Avanto eco 1.5 T | 22 | 6087 (4785 SA) | 25 (Full Cardiac Cycle) | SA 7–11 LA 0–4 |
LV, Myo | Not Classified | 144×156 and 280×204 |
ED: End-diastolic, ES: End-systolic, Tr:Train, Te:Test.
3.2. CardSegNet
The proposed framework, CardSegNet, for CMRI data segmentation is shown in Fig. 1. It is based on the U-Net model, with four stages of transformation in the contraction and expansion paths. The CardSegNet comprises seven key components: (1) a pre-processing block, (2) a pre-stage block, (3) encoder units, (4) adaptive attention modules, (5) decoder units, (6) an output block, and (7) a post-processing block.
Fig. 1.
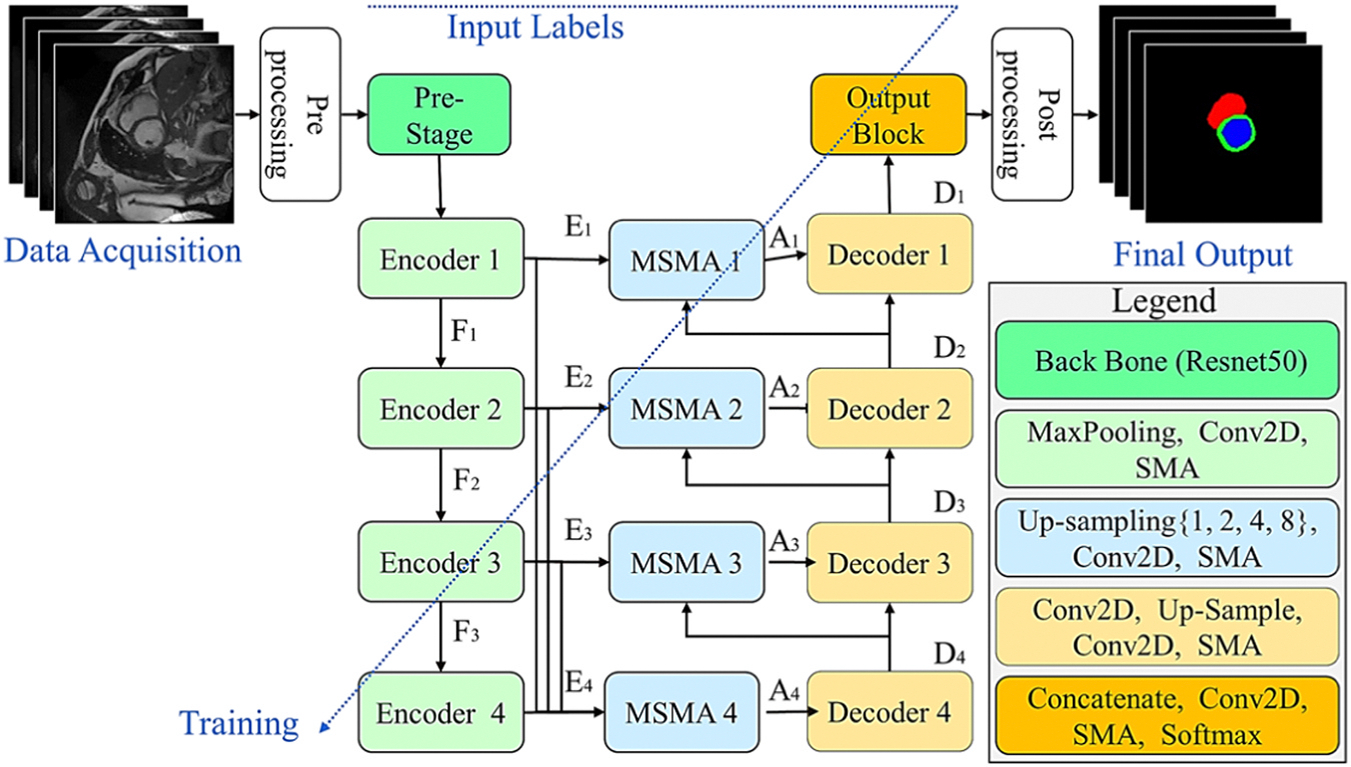
The proposed CardSegNet architecture for CMRI segmentation.
The workflow of CardSegNet commences with an image pre-processing block to standardize the input CMRI data and conduct a quality control check to ensure the inclusion of the entire heart region in the input image. This is followed by the extraction of powerful and informative features using the pre-trained Resnet50 at the pre-stage block. Subsequently, more efficient feature maps are learned through encoder units operating at various depths and scales to enhance feature representation learning. The embedded adaptive attention modules (i.e., SMA in decoder/encoder/output blocks, and multi-scale SMA (MSMA) in skip-connections) enhance attention across different data dependency ranges by dynamically adapting during training based on the specific characteristics of the data representation at the given scale within the operating node. This dynamic adjustment of attention enables the model to focus on relevant features, leading to improved performance in segmentation tasks. The decoder units then up-sample and refine the abstracted representations learned by the encoders. Utilizing attention-based skip connections, they efficiently preserve key spatial information that may have been lost during the encoding and down-sampling process. Subsequently, the output block generates a multi-channel output for the multiclass segmentation task, where each channel corresponds to a heart region, and each pixel in a channel represents the probability of belonging to the corresponding class. Finally, the post-processing block refines and validates the segmentation results produced by the output block, ensuring their accuracy and meaningfulness. To achieve this, a pipeline of morphological transformations, boundary refinement, and label assignment operations is performed.
The model integrates a joint loss function explicated in Section C to enhance overall performance, employing an adaptive deep supervision learning scheme for the refinement of lower-level network layers during the model’s optimization.
The details of the processing blocks and units are presented in the following:
3.2.1. Pre-processing block
First, all image slices are scaled to 128×128 pixels. To avoid the intensity variation effects of different types of scanners, the voxel intensities of the dataset samples are then normalized by applying the min-max normalization method, which transforms the input slice into the according to Eq. (1):
| (1) |
where and are the maximum and minimum of the image, respectively.
In the research datasets, there are some CMRI slices that do not intersect with the heart region during the acquisition time. These slices may not provide a clear view of the heart, especially those located far from the apex. For example, there are 61 slices without any heart region in the ACDC CMRI dataset. To address this issue, the YOLOv7 model (Wang et al., 2023) is employed. The YOLOv7 model is fine-tuned to determine whether a given CMR scan includes at least one complete heart region. Initially, the CMR images and segmentation masks for a given dataset are automatically annotated with bounding boxes to indicate the location and extent of the regions of interest (ROIs). The largest bounding box is then selected to indicate the presence of an ROI in the input image, aligning with YOLO’s object detection requirements. Images without bounding box annotation are processed by the YOLO network with black mask targets. As part of the proposed CardSegNet framework, the YOLO model is trained and evaluated using the k-fold CV method. In each iteration of the k-fold CV method, all training cardiac images and their detection annotations, including CMR images with or without any heart region, are input to the YOLO network for optimization. The CMR images identified by the YOLO model as containing any heart region are subsequently forwarded to the segmentation sub-network for further analysis. In cases where the YOLO model’s output is empty, indicating that the given image does not contain any heart region, a zero mask (pure background) is utilized to represent the final segmentation output predicted by the overall framework.
3.2.2. Pre-stage block
The pre-stage block aims to efficiently extract feature patterns from the given image data. It incorporates a Resnet50 (He et al., 2016) backbone with pre-trained weights on ImageNet data, enabling downscaling operations on CMR images to obtain feature representations at various resolutions. The use of the pre-trained backbone in the proposed deep structure is motivated by the rich and generalizable features learned from the extensive ImageNet dataset. Leveraging the Resnet50 model as a backbone can significantly enhance the performance of our deep model by transferring knowledge and feature representations. This approach reduces the need for a large training sample size, training from scratch with randomly initialized weights, and can lead to improved convergence and generalization on specific tasks and datasets.
In this work, the backbone network is imported, and the last blocks of the pre-trained model are trimmed (Kora et al., 2021). The sampling step is eliminated, and the dilated convolutions are applied instead in the final two blocks of ResNet50, forming an output feature map tensor with half the spatial size of the input image, where more details are preserved without adding extra parameters.
3.2.3. Encoder units
Each encoder unit in the proposed CardSegNet comprises two Conv2D-BN-ReLU layers with a 3×3 kernel block, followed by a 2×2 max pooling operation and the subsequent SMA module. The inclusion of maximum pooling operations serves to abstract data information and reduce model complexity. The incorporation of SMA modules in the encoder units at different scales is driven by their advantageous ability to dynamically adjust attention across various parts of the data representation, allowing the model to focus on pertinent features. The adaptability of SMA modules contributes to capturing multi-range dependencies and amplifying the model’s capability to represent intricate relationships within the input data, particularly beneficial during the encoding phase of the deep structure.
3.2.4. Adaptive attention modules
3.2.4.1. SMA module.
In this study, the novel SMA module is introduced for adaptive integration of both CNN-based and ViT-based attentions in our UNet-based structure, offering a compelling approach to leverage the strengths of both attention mechanisms. This combination allows for the exploitation of CNN’s robust feature extraction capabilities, complemented by ViT’s proficiency in capturing long-range dependencies and global context. The proposed hybrid attention approach has demonstrated potential to enhance representation learning in our structure. The adaptability and tunability of this combined approach at different processing scales highlight its flexibility and capacity to adjust attention mechanisms based on specific characteristics and requirements at various levels of data representation. This adaptability empowers the model to effectively capture both local and global features, thereby enhancing its performance across diverse scales and contexts.
The proposed SMA block employs CNN-based attentions, including the channel attention mechanism (CAM) and the position attention mechanism (PAM) (Fu et al., 2019), as well as a patch-based ViT attention sub-module, comprising the shift-patch tokenization (SPT) and locality self-attention (LSA) (Lee et al., 2021), to serve as local, regional, and global attention-based feature extractors. The SMA module adaptively uses the self-attention and multi-head attention mechanisms, which enable the processing pipeline to refine the resulting features for better modeling of multi-range data dependency. The SMA module structure is shown in Fig. 2 and the output of SMA module, , can be yielded through Eq. (2) for the given input tensor :
| (2) |
here , and are trainable parameters optimized in the learning phase of the overall model.
Fig. 2.
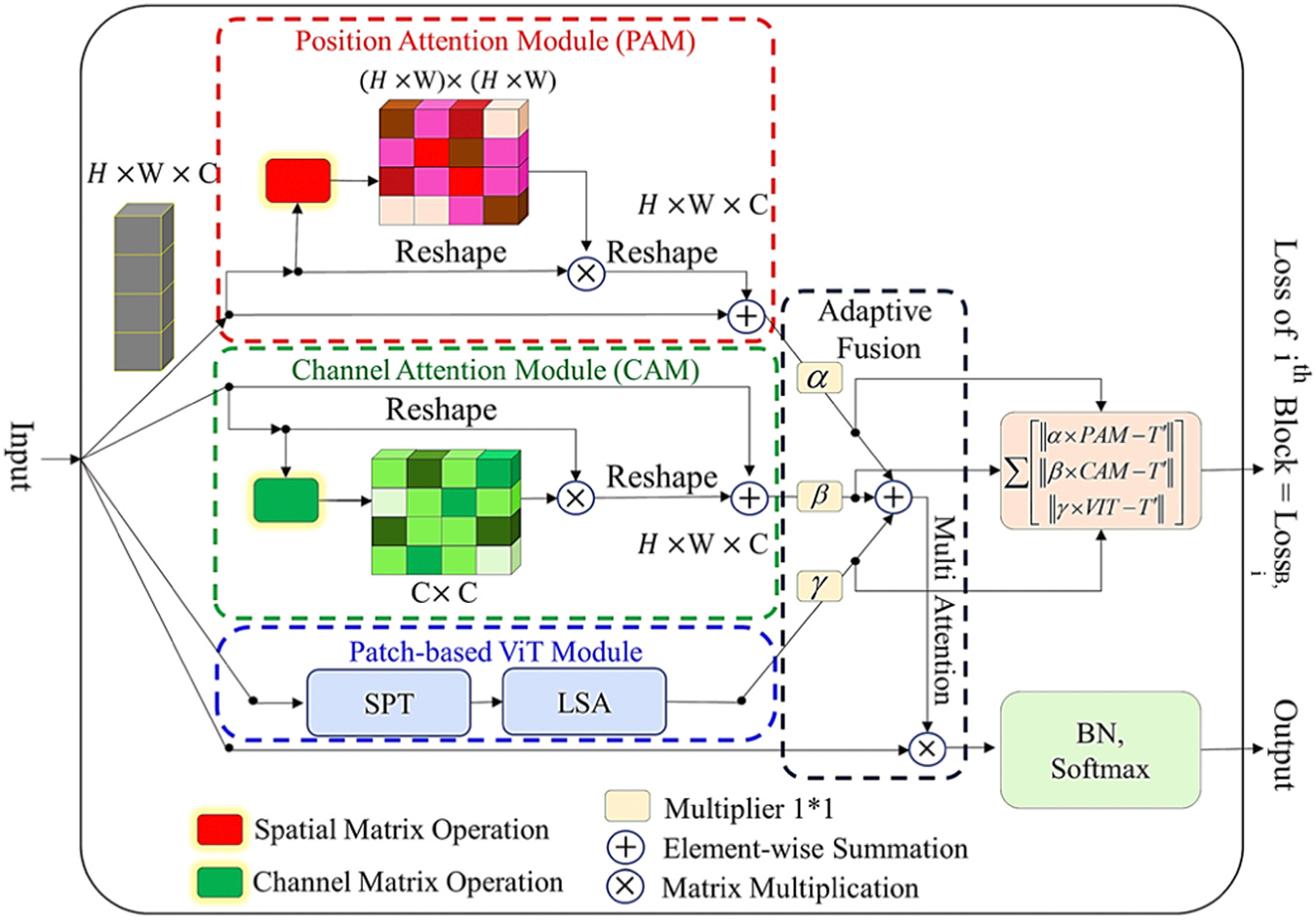
The proposed SMA block for multi-range data dependency modeling.
The PAM and CAM attention processes are employed in our SMA module, as proposed in (Fu et al., 2019; Rasti et al., 2022). The patch-based ViT attention sub-module adopts SPT which allows for the enhancement of spatial information for visual markers and the mitigation of the low receptive field issue in ViTs. The data processing steps for the SPT module begin with a given image, which is then shifted in diagonal directions. These shifted images are concatenated with the original image, and many image patches are extracted from the concatenated tensor. The SPT and LSA are the two techniques applicable in training a ViT on small datasets and effectively solve the lack of locality inductive bias while enabling the ViT to learn from scratch even on small datasets (Lee et al., 2021). These exist as generic and effective add-on modules, easily applicable in different ViTs. The SPT transforms that generate patch features and visual tokens from the input are shown in Fig. 3. Applying the patch partition as a standard ViT, SPT embeds visual labels sequentially through patch flattening, layer normalization, and linear projection.
Fig. 3.
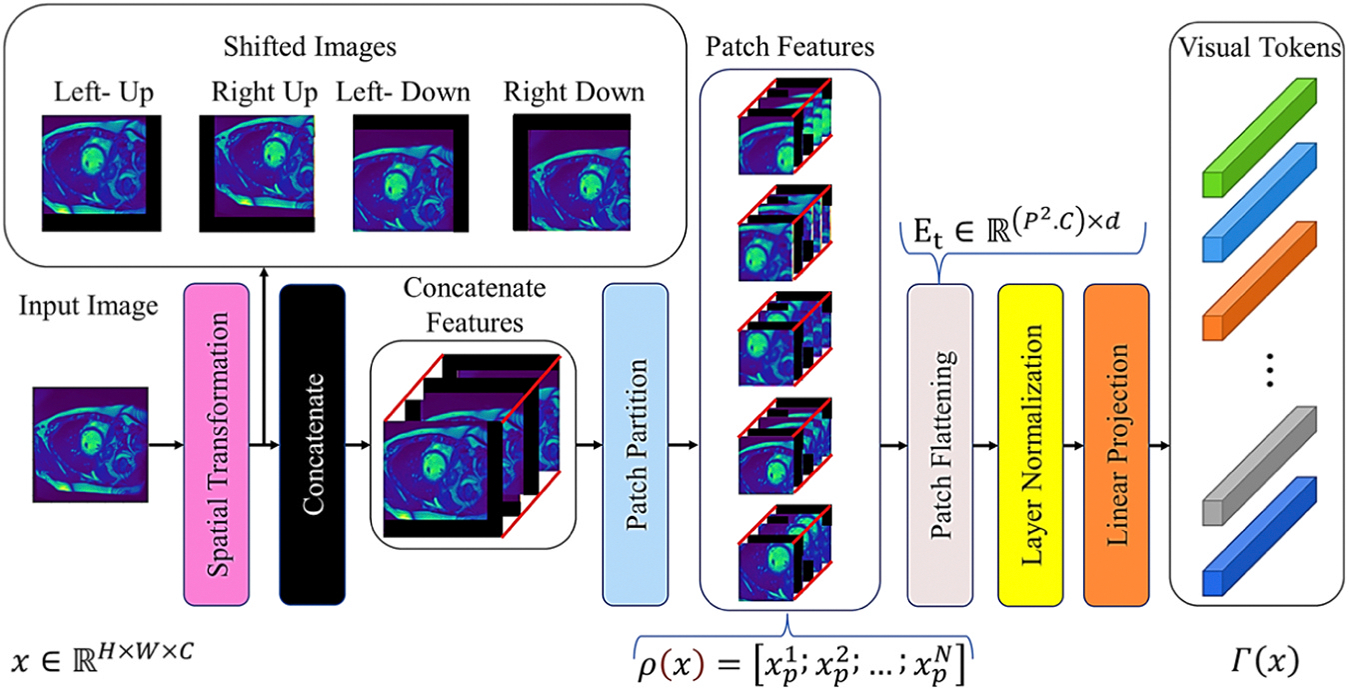
The architecture of shift-patch tokenization (SPT): It applies spatial transformers and patch partitioning to create patch features and convert them into visual tokens.
Assume the input image as , where , and are the image’s height, width, and channel, respectively. The SPT module first partitions the input image into non-overlapping patches and then, flattens them to produce a vector sequence . This process is expressed through Eq. (3):
| (3) |
where is i-th flatten vector of input. The patch size and the patch count are and , respectively.
To linearly project each vector into the hidden dimensional space, the transformer encoder of the SPT is applied to generate the patch embedding through Eq. (4):
| (4) |
where is the trainable linear projection of tokens (embedding matrix) in the transformer model, and is the third dimension of the encoder.
In a ViT pipeline, the input images are first proportioned into patches and then linearly projected into tokens (), which refer to the applied visual affine transformation on images. Tokenization determines the visual tokens’ receptive fields, with no change in their count after tokenization in the encoder of VIT; therefore, the receptive field cannot be altered there. The tokenization of standard ViT is similar to the non-overlapping convolutional layer operation with the same kernel and stride, expressed through Eq. (5) (Lee et al., 2021):
| (5) |
where and are the tokenization and transformer encoder receptive field sizes, and the convolutional layer stride and kernel size are and . In this case, because the transformer encoder does not modify the receptive field, and equals the kernel and the ViT patch size. LSA is implemented because the efficacy of these tokens must be enhanced to improve outcomes. LSA is a readily adaptable add-on module for different ViTs, and as shown in Fig. 4, temperature scaling can be applied to control the output distribution smoothness (Lee et al., 2021). LSA mainly improves the distribution of attention scores by learning the attention parameter of the Softmax activation function. The self-labeled relations are removed through the diagonal masks, which assure the suppression of the diagonal components of the similarity matrix calculated by the query and the key. This masking relatively increases attention scores between different markers, making the attention score distribution clearer, thus increasing the local induction bias by LSA while the localizing the ViT focus.
Fig. 4.
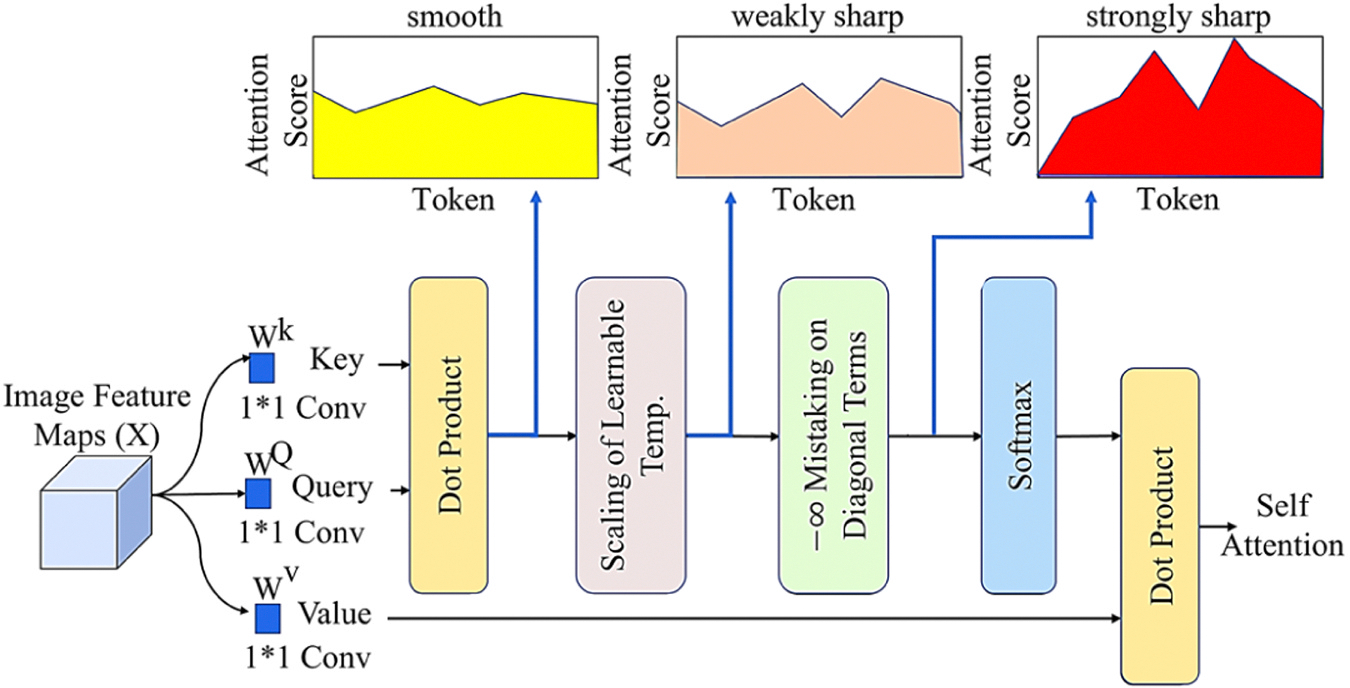
Architecture of the LSA to increase attention scores distribution.
The advantage of these self-attention sequences versus others is that they determine which patches are likely to come together in an image. Transformers explicitly mimic sequence interactions for structured prediction challenges through self-attention, the layers of which update sequence components by applying the global input sequence data. This is accomplished by creating three learnable weight matrices for the Queries (), Keys (), and Values (), where . The input sequence is projected onto these weight matrices through Eq. (6) (Lee et al., 2021):
| (6) |
where , and is the output of the self-attention layer. To obtain query, key, and value, general ViTs apply a learnable linear projection to each token in their self-attention process to generate the similarity matrix, , where the semantic relation between tokens is shown by the dot product operation of query and key. R’s diagonal and off-diagonal components express self- and inter-token relations in Eq. (7), respectively:
| (7) |
where, and are the learnable linear projections for query, value, and key. The query and key dimensions are and . The attention score matrix is obtained after dividing R into the square root of the key dimension and applying the Softmax function. Self-attention is computed based on the dot product of the attention score matrix and its value through Eq. (8):
| (8) |
As observed in Fig. 2, a SMA block loss term is computed based on the difference between each attention process’s rescaled output and the given ground truth. In each path, the error value of the module predicted mask is computed subject to the final target () through Eq. (9):
| (9) |
where and is the ground truth tensor, reshaped to match the dimensions of the block’s input. The coefficients of and of attention in each layer are subjected to a positive condition. The function is applied to convert these coefficients into positive values. The local losses of the multi-attention block are utilized in the optimization process to maintain the sub-attention output portions close to the designated regions on the image mask target.
3.2.4.2. MSMA module.
This block is designed to efficiently perform a multiscale attention-oriented feature learning and fusion process. Its mechanism empowers the model to enhance feature representation by integrating and emphasizing features derived from diverse levels of semantic representation. It leverages feature maps procured from various encoders and/or decoders with disparate resolutions, facilitating the identification of essential image patterns across both short and long dependencies. As shown in Fig. 5, different inputs, which may be encoder- or decoder-based and undergo a dimension reduction step in accordance with the processing scale, contribute to the integration of multi-range dependency information in the decoders. The cross-attention method generates the outcome of the applied attention mechanism (based on SMA), combines it with the residual signal, and passes it to the decoder block.
Fig. 5.
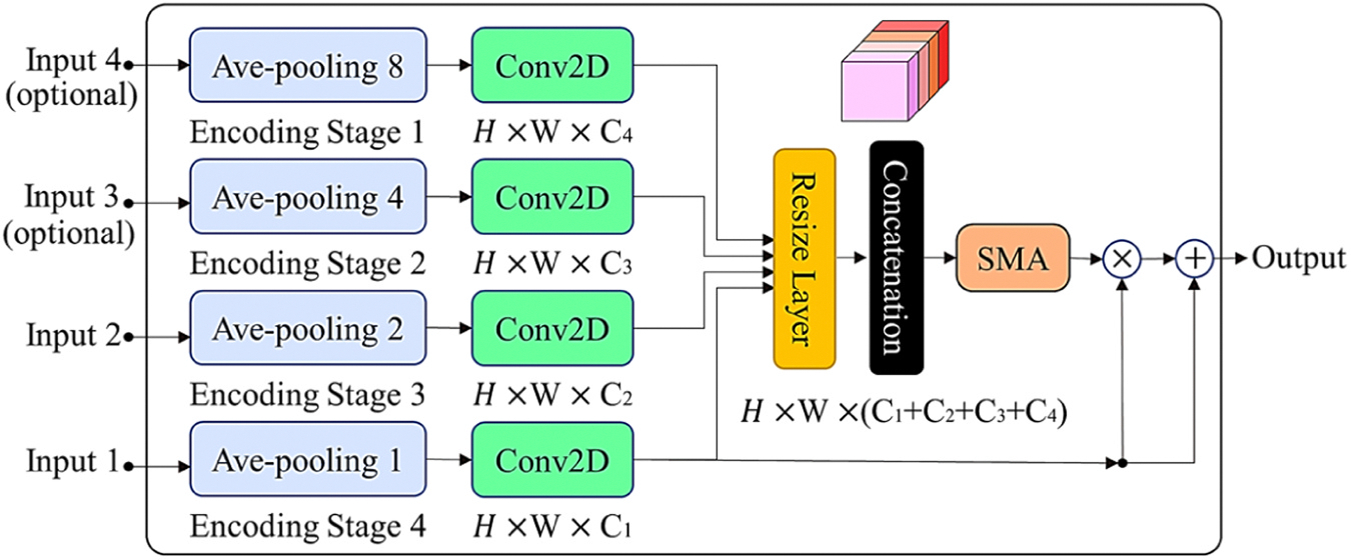
MSMA block: multi-scale block of the self-adaptive multi attention module with two required inputs and two optional inputs.
3.2.5. Decoder units
In deep learning models, the primary utilization of decoder units is for the restoration of spatial information. The generation of output by reconstructing information from encoded representations, a key role in segmentation task, is facilitated by the process in decoder blocks. In the structure proposed in this study, an attention-based decoder unit is employed at different scales, enabling the network to obtain longer range dependencies on the smallest resolution of activation maps, leading to improved results with a minimal increase in model complexity. As displayed in Fig. 1, CardSegNet comprises four decoder units, each composed of a Conv2DTranspose layer with a 2×2 transpose convolution, three Conv2D blocks with 3×3 kernel sizes, Batch Normalization (BN), and ReLU layers, followed by the SMA block for feature enhancement. The decoding of the encoded image data and the location of features, while maintaining the spatial resolution of the input, are tasks performed by the decoder units. The preservation and enhancement of spatial information, lost in the contracting path, is aided by the MSMA-based skip connections from the contracting path, thereby assisting the decoder layers in accurately locating the features.
3.2.6. Output block
A multi-channel output for the multiclass segmentation task is generated by the model output block, with each channel corresponding to a heart region in the CMRI data. Each pixel in a channel represents the probability of belonging to the corresponding class. This is achieved using a Conv2D with a 1×1 kernel size, the SMA block, and a Softmax layer with four nodes.
3.2.7. Post-processing block
Post-processing in deep learning models is used for refining and interpreting raw predictions, enhancing model outputs, and ensuring they align with specific task requirements or application objectives. Fig. 6 illustrates the post-processing procedures used in this study.
Fig. 6.

The post-processing block consists of two steps for inter- and intra-region refinement. First, the input mask tensor undergoes modifications based on the anatomical prior information of LV, RV, and Mayo regions. This is achieved by adhering to the relationships among the region masks, resulting in a refined mask tensor referred to as the Refined Mask. Second, the mask obtained in step (1) is further refined by exploring and taking into account the intra-region neighborhood based on pixel connectivity operations. This leads to the generation of the final output mask.
The first step leverages the image’s prior information to further improve the segmentation results through the following rules and constraints: (1) RV, LV, and LV∪Myo are assumed to have non-rigid solid forms. So, pixels originating from the exterior region cannot be positioned within the layers. (2) The LV and RV are kept separated; any pixel gap between them should be filled by Myo pixels. (3) If the RV is present, it is connected to the Myo region. If Myo region does not exist for given predicted mask, the RV should be removed. (4) If the Myo exists, it should be directly connected to the LV region. If LV region does not exist, Myo region should be removed. (5) The edges of each region are assumed to be smooth. So, a 5×5 Gaussian kernel followed by an adaptive threshold-based image binarization is used. In the second step, eight additional sets of neighboring pixels are generated for each pixel, inspired from the pixel connectivity loss function (Yang et al., 2022b; Yang and Farsiu, 2023). This concept is operationalized by establishing nine distinct regions, as depicted in Fig. 7. Following this, a post-refinement step based on mathematical transformations is utilized to improve the mask’s quality and yield the final refined mask. The pixel groups in Fig. 7 can contribute to mask refinement through various methods. After experimenting with different techniques on train subsets, Eq. (10) was derived using a trial-and-error approach, which resulted in improved results for our analysis.
| (10) |
where represents the approximate value of the pixel , the “” is the statistical function that mathematically returns the value with the highest frequency in a given set of data, and indicates the kth neighboring region as illustrated in Fig. 7.
Fig. 7.
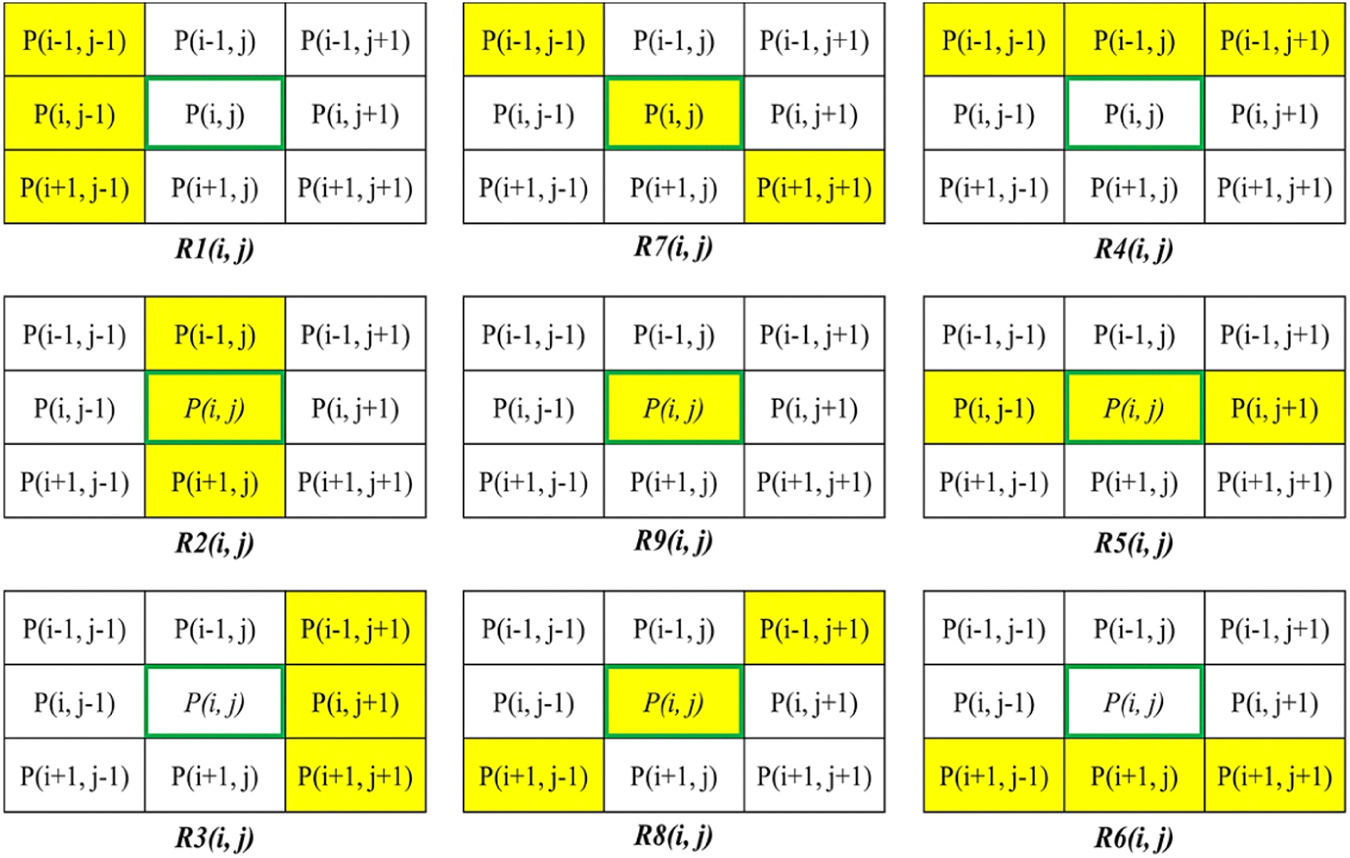
This figure demonstrates the pixel neighborhoods definition by the pixel connectivity function. It defines nine distinct and directional neighborhoods for a candidate mask pixel. The yellow-labeled pixel neighborhoods are denoted as .
3.3. Learning schema: an empirical prospective
In this paper, an adaptive deep supervision learning scheme is integrated into the optimization method by conducting intermediate supervision of local errors at various stages of the model. The DSL scheme aims to address the issue of gradient vanishing and to effectively facilitate the flow of information through the model during training. Through the DSL scheme, the network is prone to acquire more meaningful and representative features at various levels, resulting in enhanced performance in our multi-class image segmentation task. This is achieved in this work by introducing auxiliary output to the intermediate encoder and decoder units of the network.
Each unit is supervised through the inclusion of a compound loss function, which calculates a weighted sum of five distinct losses where the combination coefficients are adjusted through an empirical method. MSE, L1-L2, dSSIM, IoU and Curvature losses are considered for this purpose as they are subsequently introduced. MSE is used for pixel-wise precision and overall reconstruction improvement, L1-L2 regularization helps prevent overfitting and enhances the model’s generalization, dSSIM preserves fine details and textures for global and local perceptual quality, IoU encourages the model to focus more accurately on the location and size of objects in the image by penalizing false positives and false negatives, and Curvature loss enhances segmentation shape accuracy by encouraging smoother and less abrupt boundaries.
Furthermore, to provide additional supervision for the performance of the SMA-based attention modules at different scales, LossSMA (according to Eq. (9)) is incorporated into the overall loss function during the optimization process. This approach promotes the acquisition of more representative features yielded by better attention processes at multiple levels of the network, thereby enhancing the model’s performance.
The loss functions are defined as follows:
- MSE Loss: The mean square error (MSE) is used to construct the loss function between and in Eq. (11), where and are the predicted mask and ground truth images, respectively. It is recommended to apply MSE to detect differences at the image pixel level.
(11) - L1-L2 Regularization Loss: The regularization loss is expressed through Eq. (12) where a term is added to the loss function and is proportional to the absolute value of the magnitude of the weights or parameters of the model to avoid overfitting.
here, the hyperparameters and control the strengths of L1 (Lasso) and L2 (Ridge) regularization terms, respectively, and are both set to 0.01. P represents the number of trainable weights in our model.(12) - dSSIM Loss: The structural dissimilarity metric (dSSIM) loss function is represented by the following equation, which compares the structural differences between the and . The and are applied as constant variables and are set to 2.55 and 7.65 empirically, respectively (Graves et al., 2021).
(13) - IoU Loss: The intersection over union (IOU) loss is defined according to Eq. (14). The IoU measures the similarity between a ground truth image and a prediction image by calculating the pixel count in the intersection set divided by the pixel count in the union set excluding the intersection region (Zhou et al., 2019):
where is the area of all pixels of the predicted mask and is the area of all pixels of the ground truth.(14) - Curvature Loss: In a general context, curvature loss is a loss function used to quantify the degree of deviation from straightness or flatness in a curve or surface, as indicated by Eq. (15) (Xing et al., 2022).
where is a two-dimensional image, while and are the derivatives along the x- and y-axes, respectively. For ease of calculation, is estimated as , an estimation of the curvature function, and it is calculated through the Euler theorem and Eq. (16) (Xing et al., 2022).(15)
where is the convolution operation and is a 2D image. Curvature loss is then expressed through Eq. (17):(16)
where is the total pixel count, and are the curvature estimation of the predicted image and the ground truth, respectively, and is a minor constant applied to stabilize the computation. This function improves the contour detection accuracy when the edge value in the predicted image increases.(17) - The Proposed Weighted Objective Function: The proposed overall loss function which incorporates the adaptive DSL method is calculated through Eq. (18):
where is the loss coefficient vector and is calculated according to a normalization method in which, at the beginning of model optimization, all losses should contribute equally to the overall loss. The loss component vector, denoted as , comprises the following components, respectively: MSE (), Regularization (), dSSIM , IoU , and Curvature losses. The last term in the equation, LossSMA,i, is the local attention loss of the ith SMA module in the model.(18)
The error analysis conducted across diverse losses at the initial epoch in the ACDC dataset training process during the first iteration of the k-fold CV method resulted in the incorporation of normalized coefficients: , and . The loss coefficients are consistently used throughout the model implementations in this study.
4. Experimental study and results
4.1. Evaluation metrics
The following evaluation measures are utilized to calculate the segmentation performance of different methods in this study.
The dice similarity coefficient (DSC) is employed to assess the similarity between CMR images and ground truths, and it can be expressed as shown in Eq. (19), where the segmentation result and ground truth are denoted by and , respectively (Li et al., 2022a; Zou et al., 2004).
| (19) |
In this equation, a value of 0 indicates zero overlap between the ground truth and the derived segmentation result, while a value of 1 indicates complete overlap between the ground truth and segmentation result in both the foreground and background.
The pixel accuracy, utilized for pixel-wise classification performance, is defined through Eq. (20):
| (20) |
here, the , and are the true positive and false positive pixels and the true negative and false negative pixel counts, respectively. It is the true positive pixels percentage of all pixels in an image, providing an overall assessment of prediction.
The Precision metric is also considered to measure the predicted positive pixels’ accuracy and Recall metric measures positive predictions’ completeness, defined in Eq. (21) and Eq. (22), respectively.
| (21) |
| (22) |
4.2. Validation method
In this study, the evaluation of DL models’ performance is conducted using an unbiased k-fold CV method. This method entails dividing the dataset into K equal parts, or folds, and training the model K times, with each iteration utilizing a different fold as the test set and the remaining folds as the training set. Data partitioning is performed at the case level, and the final performance metrics are subsequently calculated by averaging the results at the test slice level. This technique is particularly useful for small datasets where the risk of overfitting is high, as it allows for a more reliable estimate of the model’s performance. Additionally, by using all the data for training and testing, this method provides an unbiased assessment of the DL model’s ability to generalize to unseen data. The 10-fold CV method is selected for reporting the results of the baseline and ablation studies. The newly proposed method is also compared to those of other state-of-the-art techniques where the hold out (H.O), or 5-fold CV methods are adopted.
4.3. Study design
Baseline Study: The segmentation performance of the proposed model is compared with that of the common image segmentation CNN models, like U-Net (Graves et al., 2021), Deeplabv3+ (Chen et al., 2017), U-Net++ (Le et al., 2022), nnU-Net (Isensee et al., 2021), and CE-Net (Gu et al., 2019). All the models are trained by applying the same configuration to assure fairness in the evaluation stages. On the ACDC 2017 test dataset, the segmentation sample results of the baseline and CardSegNet methods are shown in Fig. 8. The first column shows input images that were chosen randomly from the test dataset. The second column is the corresponding image ground truths, in which the red, green, and blue masks are the RV, the myocardium, and the LV, respectively. The U-Net, U-Net++, DeeplabV3, nnU-Net, and CE-net models’ performance is compared to our proposed method in particular.
State-of-the-art Analysis: The state-of-the-art CMRI segmentation techniques and the winners of the ACDC 2017 and M&M-2 challenges are compared with the proposed model based on dice, recall, f1-score, and precision in this section. The evaluation methods and preprocessing pipelines used in the original studies were meticulously taken into account for a fair comparison. The segmentation results for the ACDC 2017 and M&M-2 datasets are compared in Table 4.
Ablation Study: This investigation is conducted to gain a greater understanding of the impact of the model components for the one-training fold on the 10-fold CV. In the initial phase, the impact of CNN’s backbone is evaluated.
Fig. 8.

Comparison of different DL method segmentation results: visualization using five baseline models (U-Net, U-Net++, Deeplabv3, nnU-Net, CE-Net) and CardSegNet over a sample subset of ACDC2017 test dataset. Red, green, and blue regions are the right ventricle (RV), myocardium, and left ventricle (LV) areas, respectively.
Table 4.
State-Of-The-Art Performance Evaluation Over Study Dataset.
| Dataset | Reference | Method |
Reported Ave-Dice Result (%) | Our Ave-Dice Result (%)* | |||
|---|---|---|---|---|---|---|---|
| Pre-processing | Main Model | Post-processing | CV Method | ||||
|
| |||||||
| ACDC 2017 | Zhao et al. 2022 (Zhao et al., 2022) | Image Cropping | nn-TransU-Net | nn-TransU-Net Post Processing Block | 5-fold CV | 93.6±0.6 | 95.2±0.7 |
| Chen et al. 2021 (Chen et al., 2021a) | - | TransU-Net | - | 5-fold CV | 89.7±0.8 | 95.2±0.7 | |
| Painchaud et al. 2020 (Painchaud et al., 2020) | Data Augmentation | VAE | Anatomical VAE Post-Processing | 10-fold CV | 91.1±1.3 | 95.3±0.6 | |
| Shi et al. 2021 (Shi et al., 2021) | Data Enhancement and Normalization | MIFNet | - | H.O (80 %) | 97.2 | 96.3 | |
| Zhou et al. 2021 (Zhou et al., 2021) | - | nnFormer | - | H.O (70 %) | 92.1 | 94.8 | |
| Galazis et al. 2021 (Galazis et al., 2021) | - | Tempera | Largest Connected Region as RV +Median Filter | H.O (90 %) | 92.1 | 95.3±0.6 | |
| Pereira et al. 2020 (Pereira et al., 2020) | Image Localization | CNN | - | 5-fold CV | 94.2±0.7 | 95.2±0.7 | |
| Yang et al. 2022 (Yang et al., 2022a) | - | FA-SegNet | - | H.O (80 %) | 92.4 | 96.1 | |
| M&Ms-2 | C. Galazis et al. 2023 (Galazis et al., 2021) | Data Augmentation | Tempera | Largest Connected Region as RV +Median Filter | H.O (93 %) | 83.6 | 96.8 |
| J.M.Harana et al. 2022 (Mariscal-Harana et al., 2021) | Data Enhancement | 2D U-Net | - | 5-fold CV | 82.2±1.2 | 95.2±0.7 | |
| A.K. Yasmina et al. 2023 (Al Khalil et al., 2023) | Data Augmentation | U-Net + cGAN | Retaining The Largest Region per Class | 5-fold CV | 93.4±0.9 | 95.2±0.7 | |
| Gao et al. 2022 (Gao and Zhuang, 2022) | Data Augmentation | U-Net+ ViT and Self-attention | Multi-View Rule Base Post-Processing Using LA On SA Images | H.O (80 %) | 88.12 | 95.2 | |
To make a fair comparison between existing models and the proposed model, since the authors do not explicitly present the train and test data indices in the H.O-based validations, the data partitioning and CardSegNet optimization steps are repeated five times based on the H.O percentage of train-test data splitting, and the average test result is computed and reported accordingly.
The effect of the attention fusion-mechanism is then evaluated further. In this study, attention options include PAM, CAM, and ViT modules, as well as none. The impact of the proposed loss function is subsequently investigated. During training, the same dataset index is applied to each experiment. Table 5 presents the cross-validated results of the ablation study. Moreover, to evaluate the impact of the YOLO component on the overall segmentation outcomes, an additional assessment was carried out on the CardSegNet framework’s performance using the ACDC dataset. This evaluation involved excluding the YOLO component from the pre-processing block. The segmentation results revealed Dice scores of 93.4 %, 93.7 %, and 93.2 % for LV, RV, and Myo, respectively. These findings indicate that the utilization of the YOLO component enhances the overall dice score by approximately 1.9 % on average on the ACDC dataset.
-
SMA Fusion Coefficients Analysis: In SMA attention modules, the fusion coefficients of , and for the model’s layers are adaptively optimized during the train phase. Fig. 10 depicts the trend of the coefficient values changing throughout the optimization process. In the figure, the adaptive coefficients for the PAM (i.e., ), CAM (i.e., ), and ViT (i.e., ) attention processes are marked in red, green, and blue, respectively.
In Fig. 11, the optimized coefficients for each CardSegNet processing block are further depicted.
Complementary Evaluation: To assess the performance of CardSegNet on multi-center and multi-scanner CMRI datasets with varying scanning protocols, the Rajaie CMRI dataset, in addition to the M&M-2 dataset, was employed. The Rajaie CMRI dataset includes images from all phases of the cardiac cycle. In this experimental evaluation, the model was retrained from scratch and assessed using the 10-fold cross-validation method, ensuring the reliability of the model’s performance. The outcomes of this experiment are presented in Table 6.
Table 5.
Ablation Study Cross-Validated Results: Impact Assessment of Backbone, Attention, and Losses based on Dice Metric.
| CardSegNet Configuration |
Dice Performance |
||||||
|---|---|---|---|---|---|---|---|
| Backbone | Attention Fusion | Post-Processing | Loss | LV (%) | Myo (%) | RV (%) | Overall (%) |
|
| |||||||
| None | None | ✕ | MSE | 80.6±2.6 | 72.7±1.5 | 74.7±1.3 | 77.4±1.8 |
| ✕ | Combined | 82.6±1.2 | 76.0±0.8 | 77.1±0.6 | 79.5±1.0 | ||
| PAM+CAM | ✕ | MSE | 84.6±1.3 | 79.4±1.8 | 79. 4±0.8 | 82.1±1.4 | |
| ✕ | Combined | 86.7±1.5 | 83.0±0.8 | 81.8±0.4 | 84.9±0.9 | ||
| ViT | ✕ | MSE | 88.2±1.3 | 85.8±0.5 | 83.6±1.6 | 86.6±1.1 | |
| ✕ | Combined | 88.8±0.6 | 86.8±1.2 | 84.3±0.7 | 87.4±0.8 | ||
| PAM+CAM+ViT | ✕ | MSE | 91.9±0.7 | 88.6±1.1 | 85.5±0.9 | 89.6±0.9 | |
| ✕ | Combined | 92.1±1.3 | 91.5±0.7 | 87.9±1.0 | 90.5±1.1 | ||
| ✓ | Combined | 92.4±0.7 | 91.9±0.9 | 91.1±1.2 | 92.0±0.8 | ||
| ResNet50 | None | ✕ | MSE | 87.0±1.3 | 81.9±1.6 | 87.1±1.2 | 83.2±1.3 |
| ✕ | Combined | 89.3±1.4 | 84.4±1.3 | 84.2±1.4 | 85.5±1.3 | ||
| PAM+CAM | ✕ | MSE | 91.3±0.8 | 87.5±0.8 | 86.1±0.9 | 88.2±0.8 | |
| ✕ | Combined | 91.7±1.5 | 89.7±0.5 | 88.5±1.1 | 89.4±1.0 | ||
| ViT | ✕ | MSE | 93.4±0.6 | 92.2±0.7 | 90.1±0.7 | 91.3±0.8 | |
| ✕ | Combined | 93.9±1.5 | 93.2±1.4 | 90.7±0.8 | 92.3±1.1 | ||
| PAM+CAM+ViT * | ✕ | MSE | 94.4±1.2 | 94.2±0.5 | 92.0±0.7 | 93.6±0.8 | |
| ✕ | Combined | 94.8±0.7 | 94.4±1.3 | 94.7±0.5 | 94.6±0.8 | ||
| ✓ | Combined | 95.5±0.6 | 95.2±0.9 | 95.3±0.8 | 95.3±0.7 | ||
The comparison of results for the MSE, MSE+Regularization, dSSIM, IoU, Curvature, and Combined losses on ResNet50+PAM+CAM+ViT+no post-processing demonstrates overall Dice performance scores of 93.6 %, 93.8 %, 92.5 %, 94.0 %, 92.3 %, and 94.6 %, respectively. These findings serve as an indication of the validity of the proposed combined loss function’s contribution.
Fig. 10.
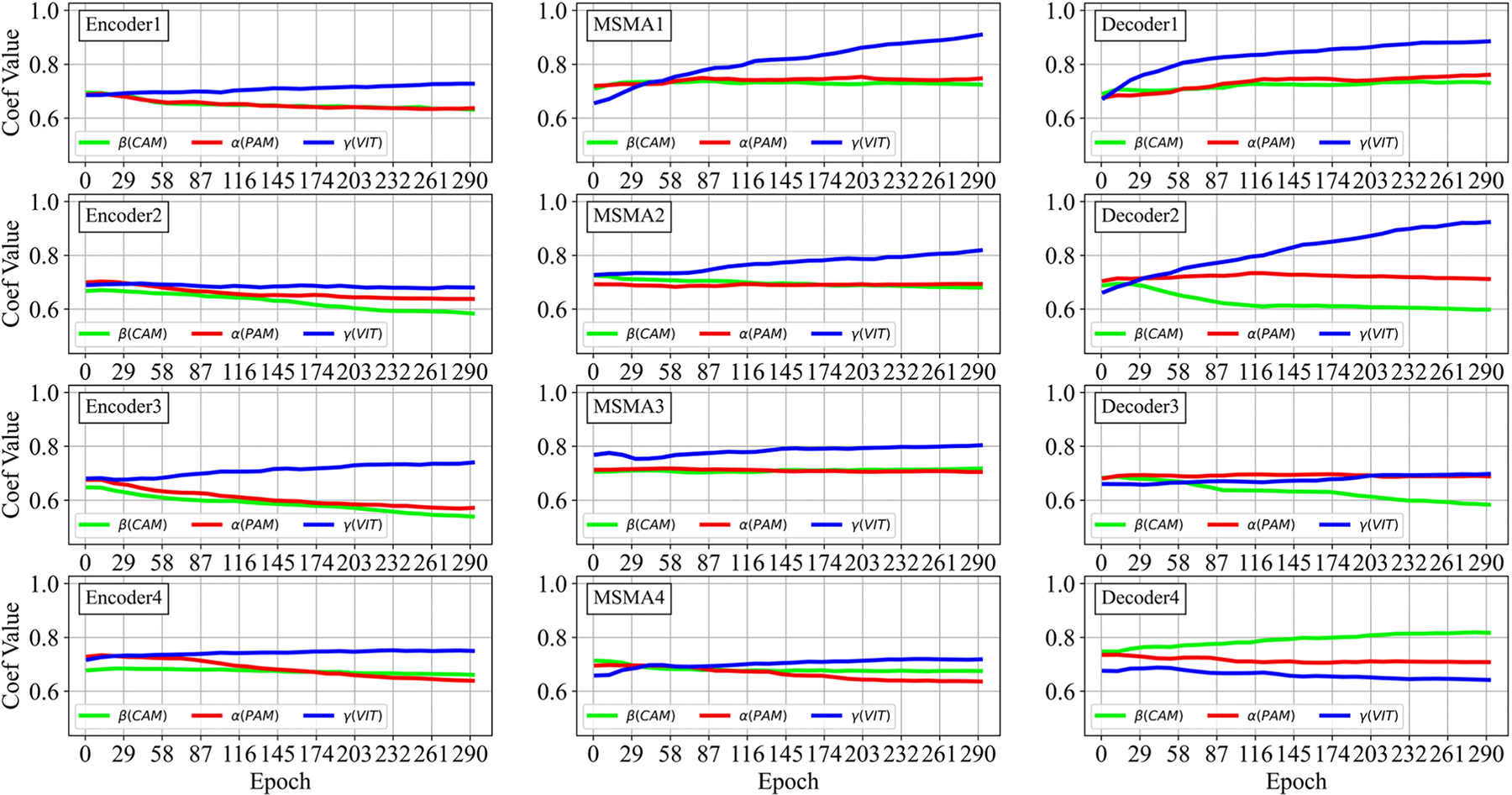
Training trends for the SMA modules coefficients of and in different processing blocks in the CardSegNet model.
Fig. 11.
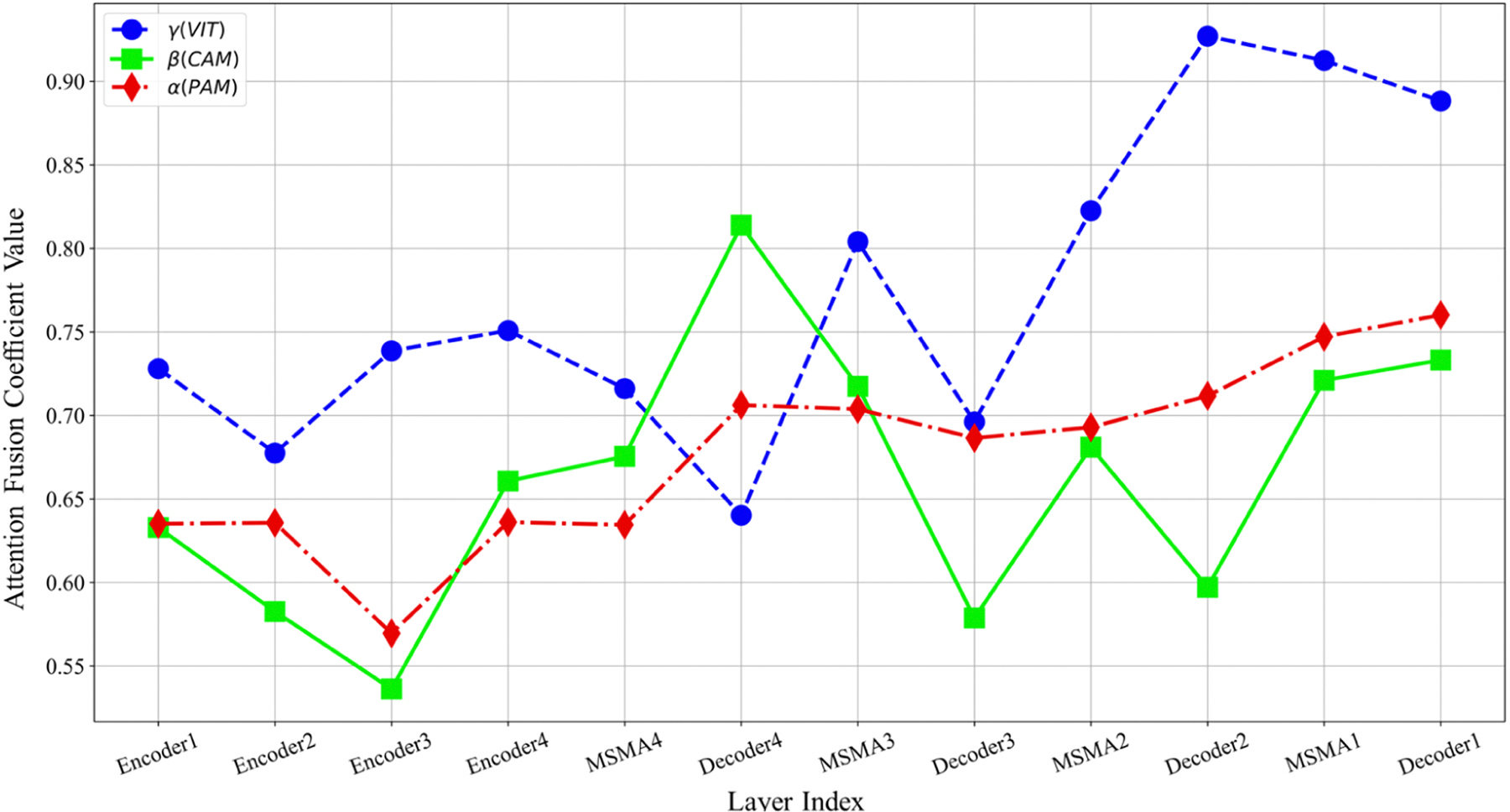
Optimized coefficients of and in the processing block.
Table 6.
Assessment of CardSegNet Framework Segmentation Dice Performance on M&M-2 and Local Datasets Using 10-Fold Cross-Validation.
| Dataset | Label | Cardiac Slices |
Mean | Overall Dataset | ||
|---|---|---|---|---|---|---|
| Base | Middle | Apex | ||||
|
| ||||||
| M&M-2 | LV | 95.1±0.3 | 96.5±0.5 | 94.3±0.9 | 95.3±0.6 | 95.4±0.6 |
| Myo | 95.4±0.7 | 97.8±0.8 | 95.1±1.1 | 96.1±0.8 | ||
| RV | 94.6±0.4 | 95.9±0.4 | 93.9±0.8 | 94.8±0.5 | ||
| Rajaie CMRI Dataset* | LV | 95.4±0.7 | 96.8±0.6 | 94.6±0.9 | 95.3±0.7 | 94.5±0.7 |
| Myo | 93.1±0.7 | 94.4±0.5 | 92.4±0.8 | 96.1±0.6 | ||
Although images of the long axis were also available in our local database, only images of the short axis were utilized for the comparison purpose. "Base," "Middle," and "Apex" labels were assigned to the top 30 %, subsequent 40 %, and remaining 30 % of CMR slices, respectively.
4.4. Training Detail
Implementation Detail: The experiments are performed on a system with an Intel Core i7@2.6 GHz, an NVIDIA GeForce GTX 1080Ti GPU, and 32 GB of RAM. The software environment specifications are Keras 3.7.2, CUDA 10.1, and cuDNN 7.6.5.
Training Protocol: The Adam optimizer with an initial learning rate of 1e-03 and a batch size of 4 is used as the optimization algorithm for training deep learning models (Kingma and Ba, 2014). A learning rate adjustment strategy is also considered based on where epoch is the current Epoch, Max Epoch is the maximum epoch count equal to 300 epochs, and Power = 0.5 controls the rate of decay. Furthermore, in the training phase, label smoothing and dropout regularization techniques are used. In each processing layer (in both the encoder and decoder blocks for the CardSegNet model), to prevent overfitting, a value of 0.2 and label smoothing with a value of are applied.
5. Discussion
5.1. Qualitative assessment
The segmentation results of three random samples for the proposed CardSegNet on the ACDC 2017 test dataset, along with a comparison to the five high-performance baseline networks, are shown in Fig. 8. The competing models, U-Net (third column from the left) and U-Net++ (fourth column from the left), lack myocardium mask continuity. The third row shows our method detects the boundary of RV and LV better than nnU-Net, CE-Net, and DeeplabV3. As a result, CardSegNet outperforms nnU-Net, CE-Net, and DeeplabV3. The visual performance of the proposed model is further assessed by evaluating random sample images from M&M-2 and Rajaie CMRI datasets in Fig. 9. The qualitative analysis demonstrates the model’s adaptability to various scanner vendors and scanning protocols. Moreover, Fig. 10 shows that the ViT coefficients in SMA modules are generally increased during the training, except for Decoder 4, which means that while the CNN-based attention mechanisms have their impact on information fusion in the model blocks, the patch-based ViT received greater attention than PAM and CAM in several blocks. As shown in the figure, increases in the latent space, indicating that CAM extracts more efficient features from the MSMA 3, MSMA 4, and Decoder 4 blocks. The CardSegNet’s Encoder 1, Encoder 2, Decoder 1, and Decoder 2 have higher γ values than the deeper levels. Because the applied ViT attention is based on shifted patch tokenization, it can extract regional and global features more efficiently than the PAM process, resulting in a decrease in α impact. Fig. 10 indicates that there exists no linear relation among the coeffects as the index of the layer increases. As observed in Fig. 11, (PAM), (CAM), and (ViT) play different functions at processing scales by receiving appropriate attention coefficient values to improve the model’s capacity for better representation.
Fig. 9.
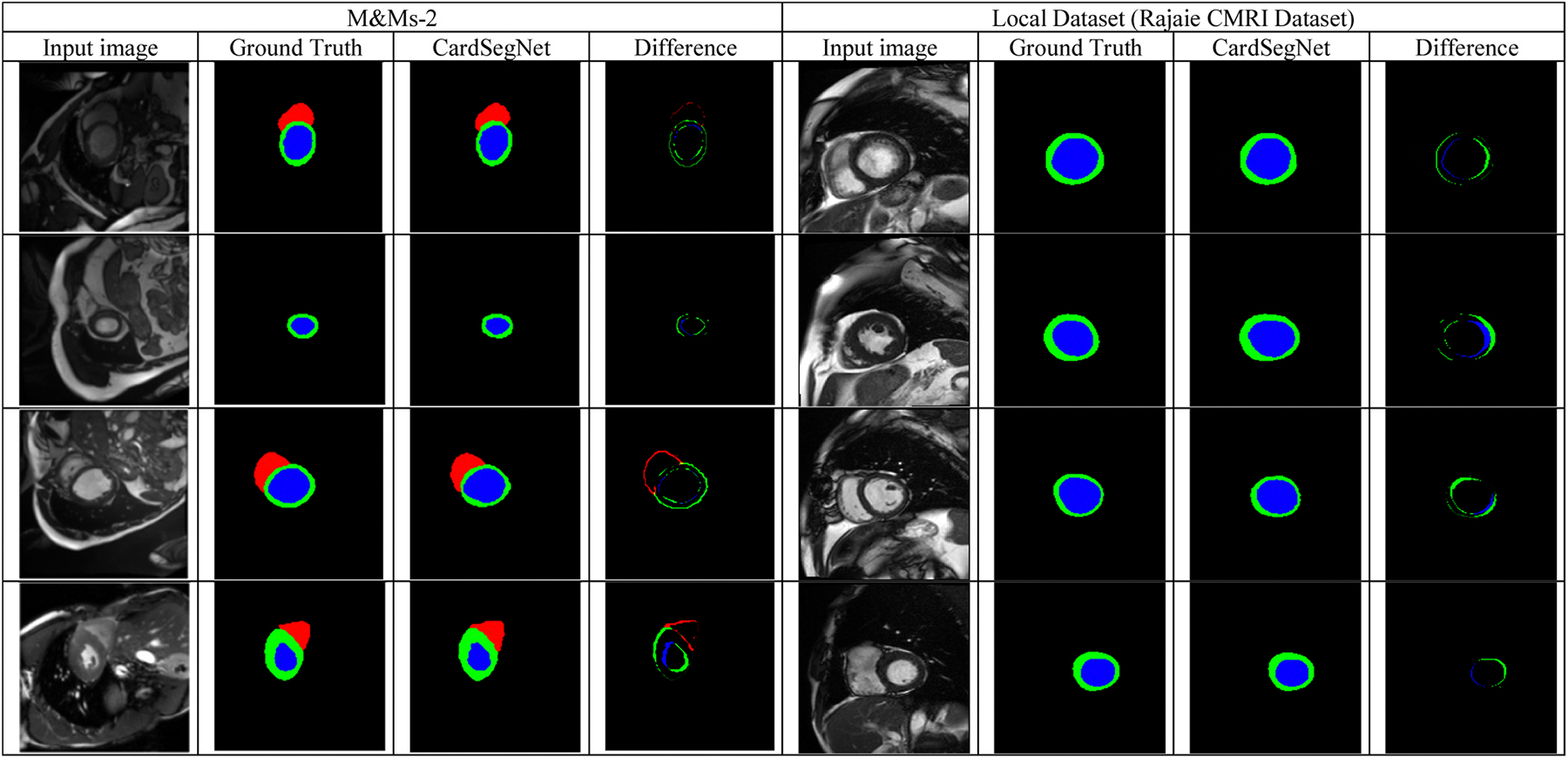
CardSegNet performance evaluation on random test samples from the M&M-2 and Rajaie CMRI datasets. The figure displays input images and their corresponding ground truth, the network’s output, and the pixel difference between the network’s output mask and the ground truth.
5.2. Quantitative evaluation
The CardSegNet model undergoes a quantitative comparison with several baseline models, and Table 3 presents the comparison results. CardSegNet attains the top scores, with Dice at 94.6 %, Recall at 95.6 %, Accuracy at 95.2 %, and Precision at 94.7 %. The statistical significance of the DSC performance improvement for the proposed CardSegNet model, in comparison to Deeplabv3 and nnU-Net (the best performing baselines in terms of DSC metric), was assessed using the Wilcoxon signed-rank test. The results showed that all improvements in DSC for CardSegNet, compared to the other methods, are statistically significant (p<0.05) for LV, Myo, RV, and average segmentation performance. For a reliable comparison based on the state-of-the-art study, the Dice results are tabulated in Table 4. The CardSegNet performance is promising against the recent SOTA. Shi et al.’s results (Shi et al., 2021) on ACDC 2017 (Dice score: 97.2 % with H.O. 80 %) slightly exceed the average CardSegNet dice performance by less than 1 %. This difference is due to the fact that Shi’s model evaluation method cannot be reproduced precisely because the train and test data indices are not explicitly presented by the authors. In CardSegNet optimization using the five repetitions of the H.O. (80 %) method, there is a best test dice value of 98.1 %, which is higher than Shi’s model performance.
Table 3.
Performance comparison of U-Net, U-Net++, Deeplab v3, Nn-U-Net CE-Net, and the proposed CardSegNet (Average ± std).
| Method | PP | Segmentation Metrics |
Complexity |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dice (%) |
Recall (%) |
Accuracy (%) |
Precision (%) |
ATT (S) | TP (M) | ||||||||||||||
| LV | Myo | RV | Ave. | LV | Myo | RV | Ave. | LV | Myo | RV | Ave. | LV | Myo | RV | Ave. | ||||
|
| |||||||||||||||||||
| U-Net, 2017 (Khened et al., 2017) | ✕ | 84.3±0.8 | 85.7±0.9 | 85.3±0.6 | 85.1±0.8 | 85.8±0.7 | 87.1±0.8 | 86.9±0.6 | 86.6±0.7 | 75.8±0.8 | 77.0±1.1 | 76.7±0.8 | 76.5±0.9 | 77.5±0.6 | 78.7±0.9 | 78.4±0.8 | 78.2±0.6 | 0.6 | 3.89 |
| ✓ | 84.9±0.9 | 86.8±1.0 | 87.2±0.5 | 86.3±0.8 | 86.0±0.7 | 88.2±0.6 | 87.6±0.5 | 87.3±0.6 | 79.6±0.7 | 76.6±1.0 | 77.3±0.7 | 77.8±0.8 | 77.1±0.5 | 80.5±1.0 | 80.7±0.9 | 79.4±0.8 | 3.4 | ||
| CE-Net, 2019 (Gu et al., 2019) | ✕ | 89.9±0.6 | 91.4±0.5 | 91.1±0.4 | 90.8±0.5 | 90.8±0.6 | 92.3±0.8 | 92.0±0.7 | 91.7±0.7 | 91.8±0.6 | 93.3±0.8 | 93.0±0.6 | 92.7±0.6 | 91.5±0.4 | 93.0±0.5 | 92.7±0.3 | 92.4±0.4 | 1.6 | 39.44 |
| ✓ | 90.1±0.5 | 92.2±0.6 | 91.6±0.3 | 91.2±0.4 | 91.1±0.6 | 93.4±0.6 | 92.7±0.5 | 92.3±0.5 | 92.9±0.6 | 93.9±0.7 | 93.5±0.5 | 93.4±0.6 | 91.4±0.3 | 93.7±0.3 | 93.1±0.1 | 92.7±0.2 | 4.4 | ||
| U-Net++, 2021 (Graves et al., 2021) | ✕ | 89.6±0.5 | 91.1±0.8 | 90.8±0.6 | 90.5±0.6 | 90.3±0.8 | 91.8±0.8 | 91.5±0.5 | 91.2±0.7 | 87.9±0.8 | 89.2±1.2 | 89.0±1.0 | 88.7±1.1 | 90.2±1.3 | 91.6±1.6 | 91.2±1.2 | 91.0±1.3 | 0.9 | 4.87 |
| ✓ | 90.0±0.5 | 91.9±0.7 | 90.9±0.6 | 90.9±0.6 | 90.8±0.8 | 92.7±0.6 | 92.5±0.5 | 92.0±0.6 | 89.5±0.7 | 89.3±1.0 | 90.1±1.1 | 89.6±0.9 | 90.1±1.2 | 92.2±1.5 | 91.4±1.1 | 91.2±1.2 | 3.8 | ||
| Deeplab v3, 2021 (Chen et al., 2021a) | ✕ | 90.8±0.8 | 92.2±1.1 | 91.8±0.7 | 91.6±0.9 | 91.8±0.7 | 93.3±0.9 | 93.0±0.6 | 92.7±0.7 | 90.9±0.6 | 92.3±0.6 | 91.9±0.4 | 91.7±0.5 | 91.5±0.8 | 92.9±1.1 | 92.5±0.5 | 92.3±0.8 | 1.1 | 11.85 |
| ✓ | 92.0±0.7 | 93.1±1.0 | 92.5±0.6 | 92.5±0.7 | 92.1±0.7 | 93.4±0.7 | 93.7±0.5 | 93.1±0.6 | 90.8±0.7 | 92.2±0.4 | 92.5±0.3 | 91.8±0.4 | 91.9±0.7 | 93.5±0.9 | 92.4±0.4 | 92.6±0.6 | 4.0 | ||
| nnU-Net, 2021 (Isensee et al., 2021) | ✕ | 91.9±0.4 | 93.4±0.5 | 93.1±0.3 | 92.8±0.4 | 92.2±0.8 | 93.7±0.8 | 93.4±0.6 | 93.1±0.8 | 92.6±0.7 | 94.1±0.8 | 93.8±0.7 | 93.5±0.7 | 92.0±0.6 | 93.5±1.2 | 93.2±0.7 | 92.9±0.8 | 1.1 | 52.11 |
| ✓ | 92.2±0.5 | 94.0±0.4 | 93.4±0.1 | 93.2±0.3 | 92.8±0.7 | 93.9±0.8 | 94.0±0.6 | 93.6±0.7 | 93.0±0.7 | 94.4±0.6 | 93.7±0.6 | 93.7±0.6 | 92.8±0.6 | 93.8±1.3 | 93.2±0.7 | 93.3±0.8 | 3.9 | ||
| CardSegNet | ✕ | 94.8±0.7 | 94.4±1.3 | 94.7±0.5 | 94.6±0.8 | 94.7±0.6 | 96.2±0.8 | 95.9±0.5 | 95.6±0.6 | 94.3±0.7 | 95.8±1.0 | 95.5±0.8 | 95.2±0.8 | 93.8±0.6 | 95.4±0.9 | 94.9±0.6 | 94.7±0.7 | 3.7 | 17.6 |
| ✓ | 95.5±0.6 | 95.2±0.9 | 95.3±0.8 | 95.3±0.6 | 95.8±0.5 | 97.3±0.6 | 97.0±0.5 | 96.7±0.5 | 95.3±0.9 | 96.8±0.9 | 96.5±0.7 | 96.2±0.9 | 96.7±0.6 | 98.2±0.9 | 97.9±0.8 | 95.6±0.8 | 6.6 | ||
PP: Post processing; ATT: Average test time per slice (CPU-tested: Intel Core i7@2.6 GHz); TP: Trainable parameters; S: Seconds; M: Million parameters.
CardSegNet leverages PAM, CAM, and ViT attention, similar to TransU-Net (Chen et al., 2021a). The transformer encoder in TransU-Net consists of multi-head self-attention and multi-layer perceptron blocks. In this newly proposed SMA module, in addition to applying the above attentions, the pure ViT is modified into patched-based ViT. In addition, the coefficients of PAM, CAM, and ViT attentions are optimized in an adaptive manner to facilitate and control information fusion through SMA. As observed in Table 4, CardSegNet’s Ave-Dice performance is greater than that of nn-TransU-Net and TransU-Net by more than 1.6 % and 5.5 %, respectively.
The quantitative analysis for the oblation study, according to Table 5, indicates the direct effect of the proposed combined loss function, attention module, pre-train backbone, and post-processing step on segmentation results. The experimental findings support the effectiveness of the proposed hybrid CNN-Transformer-based attention module and model. The SMA and CardSegNet enable adaptively capturing both local and global contextual information in the given CMR image, which is advantageous for more precise segmentation. Short-to-middle-range and middle-to-long-range dependency modeling in an image would be effectively handled by the CNN- and ViT-based components, respectively. In order to significantly highlight local and global structures for more accurate segmentation performance, the , and values are adaptively optimized at each processing block and scale to capture cross-pixel, cross-channel, and cross-patch dependencies. During the optimization process for a given SMA block, the positional attention sub-module adaptively aggregates features at each position through a weighted sum of the features at all positions. Simultaneously, the channel attention sub-module highlights interdependent channel maps by selectively combining similar features across all channel maps, recognizing that similar features are relevant regardless of their distances. Additionally, the patch-based ViT sub-module facilitates attention by explicitly learning visual representations through cross-patch information interactions. This approach to processing feature patches enables the analysis of visual feature dependencies over short and long distances, resulting in the generation of a global receptive field. Consequently, the model can focus on different parts of the input tensor and comprehend their interrelationships, which is particularly significant for image analysis tasks. This capability is important for medical images since they often contain highly complicated structures.
The performance outcomes presented in Table 6 provide evidence of the adaptability of the proposed CardSegNet framework on the M&M-2 and Rajaie CMRI datasets, which were obtained using different CMR scanner vendors and scanning protocols. The model produced acceptable results on both. These findings suggest that the CardSegNet has the potential to be a versatile tool for analyzing cardiac MRI data from various sources. Based on the findings presented in Table 5, the incorporation of image post-processing results in an approximate 0.7 % enhancement in the overall segmentation performance.
The proposed model has limitations, mainly concerning its training time complexity, despite achieving acceptable testing times of less than 0.9 and 6.5 seconds per slice frame tested on the GPU and CPU, respectively. Although CardSegNet has attempted to minimize the number of module parameters, the DL network built on the Transformer+CNN structure has relatively high parameters overall. The parameter reduction consideration still has room for improvement.
In the present work, we employed the image of the heart in the direction of the short-axis (SA). Experiments show that the accuracy of heart segmentation will be enhanced by incorporating other long-axes (LA), such as 2ch, 3ch, and 4ch, to the input of the model, further feeding the SA images to more efficiently handle the complex shapes, variable intensity, and unclear boundaries of the cardiac structures. By transferring information from one view to another or by combining them in a spatio-temporal framework, our model will be able to take advantage of the complementary information from both views and reduce the ambiguity in the segmentation, and there is room for further improvement. In future research, we will address these issues to develop the model and make it more efficient in real clinical situations.
6. Conclusion
In this paper, a hybrid deep learning framework was presented for CMRI data segmentation. A novel adaptive attention fusion module was designed and applied in the proposed CardSegNet to assist the overall model in efficiently extracting multi-range dependencies by leveraging the capabilities of pixel-, channel-, and patch-based ViT attentions. In order to improve CMRI segmentation, a deep supervision method and a joint loss function were also incorporated into the optimization of the proposed model. Based on an end-to-end training procedure, this model employs all the mechanisms in an adaptive fashion design.
To verify the effectiveness of our proposed method, this model was trained and evaluated on two publicly available datasets ACDC 2017, M&Ms-2, and also on the local Rajaie CMRI dataset. The average Dice scores for LV, Myocardium, and RV segmentation using CardSegNet on ACDC 2017 were 95.2 %, 95.5 %, and 95.3 %, respectively. These results were 95.3 %, 96.1 %, and 94.8 % for LV, Myocardium, and RV segmentation on M&Ms-2. For the Rajaie CMRI datasets, CardSegNet obtained average Dice scores of 95.3 % and 96.1 % for LV and Myocardium segmentation in both end-diastolic and end-systolic frames, respectively.
CardSegNet is advantageous to cardiologists for rapid and reliable automated segmentation of the heart region in cardiac MRI data analysis in order to measure cardiac parameters and diagnose anomalies.
Acknowledgment
This research was supported by the Isfahan University of Medical Sciences, Isfahan, Iran (Grant no. 3400806 with IRCT no; IR.MUI. REC.1400.067). The authors would like to acknowledge the services provided by the institution.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
CRediT authorship contribution statement
Hamid Sanei: Validation, Investigation, Data curation, Conceptualization. Hamidreza Pour Aliakbar: Conceptualization, Data curation, Investigation, Resources, Validation. Hossein Yousefi Banaem: Conceptualization. Faezeh Tabesh: Conceptualization, Data curation, Validation. Saeed Kermani: Funding acquisition, Data curation, Project administration, Resources, Supervision, Validation. Hamed Aghapanah: Writing – original draft, Visualization, Software, Investigation, Formal analysis, Data curation. Reza Rasti: Writing – review & editing, Writing – original draft, Supervision, Project administration, Methodology. William Paul Segars: Resources, Conceptualization.
Data availability
Data will be made available on request.
References
- Lum M, Tsiouris AJ, 2020. MRI safety considerations during pregnancy. Clin. Imaging vol. 62, 69–75. [DOI] [PubMed] [Google Scholar]
- von Knobelsdorff-Brenkenhoff F, Pilz G, Schulz-Menger J, 2017. Representation of cardiovascular magnetic resonance in the AHA/ACC guidelines. J. Cardiovasc. Magn. Reson. vol. 19 (1), 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Topol EJ, Califf RM, 2007. Textbook of Cardiovascular Medicine. Lippincott Williams & Wilkins. [Google Scholar]
- Zhao L, Zhou D, Jin X, Zhu W, 2022. nn-TransUNet: an automatic deep learning pipeline for heart MRI segmentation. Life vol. 12 (10), 1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu J, Liu J, Tian H, Li Y, Bao Y, Fang Z, Lu H, 2019. Dual attention network for scene segmentation,” in Proceedings of. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. 3146–3154. [Google Scholar]
- Lee SH, Lee S, and Song BC, “Vision Transformer for Small-size Datasets,” ArXiv preprint arXiv:2112.13492, 2021. [Google Scholar]
- He K, Zhang X, Ren S, and Sun J, “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778. [Google Scholar]
- Reis S, Seibold C, Freytag A, Rodner E, and Stiefelhagen R, “Every Annotation Counts: Multi-label Deep Supervision for Medical Image Segmentation,” 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 9527–9537, 2021. [Google Scholar]
- Peng J, Wang Y, 2021. “Medical image segmentation with limited supervision: a review of deep network models. IEEE Access vol. 9, 36827–36851. [Google Scholar]
- Zheng Q, Delingette H, Duchateau N, Ayache N, 2018. “3-D consistent and robust segmentation of cardiac images by deep learning with spatial propagation. IEEE Trans. Med. Imaging vol. 37 (9), 2137–2148. [DOI] [PubMed] [Google Scholar]
- Campello VM, Gkontra P, Izquierdo C, Martín-Isla C, Sojoudi A, Full PM, Maier-Hein K, Zhang Y, He Z, Ma J, Parreño M, Albiol A, Kong F, Shadden SC, Acero JC, Sundaresan V, Saber M, Elattar M, Li H, Menze B, Khader F, Haarburger C, Scannell CM, Veta M, Carscadden A, Punithakumar K, Liu X, Tsaftaris SA, Huang X, Yang X, Li L, Zhuang X, Viladés D, Descalzo ML, Guala A, Mura LL, Friedrich MG, Garg R, Lebel J, Henriques F, Karakas M, Çavus E, Petersen SE, Escalera S, Seguí S, Rodríguez-Palomares JF, Lekadir K, 2021. “Multi-centre, multi-vendor and multi-disease cardiac segmentation: the M&Ms challenge. IEEE Trans. Med. Imaging vol. 40 (12), 3543–3554. [DOI] [PubMed] [Google Scholar]
- Isensee F, Jaeger PF, Full PM, Wolf I, Engelhardt S, and Maier-Hein KH, “Automatic cardiac disease assessment on cine-MRI via time-series segmentation and domain specific features,” in International Workshop on Statistical Atlases and Computational Models of the Heart, 2017, pp. 120–129. [Google Scholar]
- Khened M, Alex V, and Krishnamurthi G, “Densely connected fully convolutional network for short-axis cardiac cine MR image segmentation and heart diagnosis using random forest,” in International Workshop on Statistical Atlases and Computational Models of the Heart, 2017, pp. 140–151. [Google Scholar]
- Zotti C, Luo Z, Humbert O, Lalande A, Jodoin PM, 2018. “GridNet with Automatic Shape Prior Registration for Automatic Mri Cardiac Segmentation,”. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 10663. LNCS, pp. 73–81. [Google Scholar]
- Bernard O, Lalande A, Zotti C, Al E, 2018. “Deep learning techniques for automatic MRI cardiac multi-structures segmentation and diagnosis: is the problem solved? IEEE Trans. Med. Imaging vol. 37 (11), 2514–2525. [DOI] [PubMed] [Google Scholar]
- Graves CV, Moreno RA, Rebelo MFS, Bordignom A, Nomura CH, and Gutierrez MA, “Cardiac motion estimation using pyramid, warping, and cost volume neural network,” in Medical Imaging 2021: Biomedical Applications in Molecular, Structural, and Functional Imaging, 2021, vol. 11600, p. 116000X. [Google Scholar]
- Chen J, Lu Y, Yu Q, Luo X, Adeli E, Wang Y, Lu L, Yuille AL, and Zhou Y, “Transunet: Transformers make strong encoders for medical image segmentation,” ArXiv preprint arXiv:2102.04306, 2021a. [Google Scholar]
- Painchaud N, Skandarani Y, Judge T, Bernard O, Lalande A, Jodoin P-M, 2020. “Cardiac segmentation with strong anatomical guarantees. IEEE Trans. Med. Imaging vol. 39 (11), 3703–3713. [DOI] [PubMed] [Google Scholar]
- Le D-H, Le N-M, Le K-H, Pham V-T, and Tran T-T, “DR-Unet++: An Approach for Left Ventricle Segmentation from Magnetic Resonance Images,” in 2022 6th International Conference on Green Technology and Sustainable Development (GTSD), 2022, pp. 1048–1052. [Google Scholar]
- Chen L-C, Papandreou G, Kokkinos I, Murphy K, Yuille AL, 2017. Deeplab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. vol. 40 (4), 834–848. [DOI] [PubMed] [Google Scholar]
- Yan Z, Su Y, Sun H, Yu H, Ma W, Chi H, Cao H, Chang Q, 2022. “SegNet-based left ventricular MRI segmentation for the diagnosis of cardiac hypertrophy and myocardial infarction. Comput. Methods Prog. Biomed. vol. 227, 107197. [DOI] [PubMed] [Google Scholar]
- Wang Z, Peng Y, Li D, Guo Y, Zhang B, 2022. MMNet: a multi-scale deep learning network for the left ventricular segmentation of cardiac MRI images. Appl. Intell. vol. 52 (5), 5225–5240. [Google Scholar]
- Shi J, Ye Y, Zhu D, Su L, Huang Y, Huang J, 2021. “Automatic segmentation of cardiac magnetic resonance images based on multi-input fusion network. Comput. Methods Prog. Biomed. vol. 209, 106323. [DOI] [PubMed] [Google Scholar]
- Zhou H-Y, Guo J, Zhang Y, Yu L, Wang L, and Yu Y, “nnformer: Interleaved transformer for volumetric segmentation,” ArXiv preprint arXiv:2109.03201, 2021. [Google Scholar]
- Niu Z, Zhong G, Yu H, 2021. A review on the attention mechanism of deep learning. Neurocomputing vol. 452, 48–62. [Google Scholar]
- Guo M-H, Xu T-X, Liu J-J, Liu Z-N, Jiang P-T, Mu T-J, Zhang S-H, Martin RR, Cheng M-M, Hu S-M, 2022. Attention mechanisms in computer vision: a survey. Comput. Vis. Media vol. 8 (3), 331–368. [Google Scholar]
- Chen S, Qiu C, Yang W, Zhang Z, 2022. Multiresolution aggregation transformer UNet based on multiscale input and coordinate attention for medical image segmentation. Sensors vol. 22 (10), 3820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shan T, Yan J, 2021. “SCA-Net: a spatial and channel attention network for medical image segmentation. IEEE Access vol. 9, 160926–160937. [Google Scholar]
- Khan S, Naseer M, Hayat M, Zamir SW, Khan FS, Shah M, 2022. Transformers in vision: a survey. ACM Comput. Surv. vol. 54 (10s), 1–41. [Google Scholar]
- Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, Dehghani M, Minderer M, Heigold G, and Gelly S, “An image is worth 16×16 words: Transformers for image recognition at scale,” ArXiv preprint arXiv:2010.11929, 2020. [Google Scholar]
- Wang W, Xie E, Li X, Fan D-P, Song K, Liang D, Lu T, Luo P, and Shao L, “Pyramid vision transformer: A versatile backbone for dense prediction without convolutions,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 568–578. [Google Scholar]
- Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, Lin S, and Guo B, “Swin transformer: Hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 10012–10022. [Google Scholar]
- Chu X, Tian Z, Wang Y, Zhang B, Ren H, Wei X, Xia H, Shen C, 2021. Twins: revisiting the design of spatial attention in vision transformers. Adv. Neural Inf. Process. Syst. vol. 34, 9355–9366. [Google Scholar]
- Zhang P, Dai X, Yang J, Xiao B, Yuan L, Zhang L, and Gao J, “Multi-scale vision longformer: A new vision transformer for high-resolution image encoding,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 2998–3008. [Google Scholar]
- Chen C-F, Panda R, and Fan Q, “Regionvit: Regional-to-local attention for vision transformers,” ArXiv preprint arXiv:2106.02689, 2021b. [Google Scholar]
- Lee SSSS, Lee SSSS, Song BC, 2022. “Improving vision transformers to learn small-size dataset from scratch. IEEE Access. [Google Scholar]
- Galazis C, Wu H, Li Z, Petri C, Bharath AA, and Varela M, “Tempera: Spatial Transformer Feature Pyramid Network for Cardiac MRI Segmentation,” in International Workshop on Statistical Atlases and Computational Models of the Heart, 2021, pp. 268–276. [Google Scholar]
- Lin A, Chen B, Xu J, Zhang Z, Lu G, Zhang D, 2022. Ds-transunet: dual swin transformer u-net for medical image segmentation. IEEE Trans. Instrum. Meas. vol. 71, 1–15. [Google Scholar]
- Fu Z, Zhang J, Luo R, Sun Y, Deng D, Xia L, 2022. “TF-Unet: an automatic cardiac MRI image segmentation method. Math. Biosci. Eng. vol. 19 (5), 5207–5222. [DOI] [PubMed] [Google Scholar]
- Li D, Peng Y, Guo Y, Sun J, 2022a. MFAUNet: multiscale feature attentive U-Net for cardiac MRI structural segmentation,”. IET Image Process. vol. 16 (4), 1227–1242. [Google Scholar]
- Li Y, Cai W, Gao Y, Li C, and Hu X, “More than encoder: Introducing transformer decoder to upsample,” in 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 2022b, pp. 1597–1602. [Google Scholar]
- Galea R-R, Diosan L, Andreica A, Popa L, Manole S, Bálint Z, 2021. Region-of-interest-based cardiac image segmentation with deep learning. Appl. Sci. vol. 11 (4), 1965. [Google Scholar]
- Garcia-Cabrera C, Arazo E, Curran KM, O’Connor NE, and McGuinness K, “Cardiac Segmentation Using Transfer Learning Under Respiratory Motion Artifacts,” in Statistical Atlases and Computational Models of the Heart. Regular and CMRxMotion Challenge Papers: 13th International Workshop, STACOM 2022, Held in Conjunction with MICCAI 2022, Singapore, September 18, 2022, Revised Selected Papers, 2023, pp. 392–398. [Google Scholar]
- Grzeszczyk MK, Płotka S, and Sitek A, “Multi-task Swin Transformer for Motion Artifacts Classification and Cardiac Magnetic Resonance Image Segmentation,” in Statistical Atlases and Computational Models of the Heart. Regular and CMRxMotion Challenge Papers: 13th International Workshop, STACOM 2022, Held in Conjunction with MICCAI 2022, Singapore, September 18, 2022, Revised Selected Papers, 2023, pp. 409–417. [Google Scholar]
- Liu X, Xing F, Gaggin HK, Kuo C-CJ, El Fakhri G, and Woo J, “Successive Subspace Learning for Cardiac Disease Classification with Two-phase Deformation Fields from Cine MRI,” ArXiv preprint arXiv:2301.08959, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mariscal-Harana J, Kifle N, Razavi R, King AP, Ruijsink B, and Puyol-Antón E, “Improved AI-based segmentation of apical and basal slices from clinical cine CMR,” in International Workshop on Statistical Atlases and Computational Models of the Heart, 2021, pp. 84–92. [Google Scholar]
- Al Khalil Y, Amirrajab S, Lorenz C, Weese J, Pluim J, Breeuwer M, 2023. Reducing segmentation failures in cardiac MRI via late feature fusion and GAN-based augmentation. Comput. Biol. Med. vol. 161, 106973. [DOI] [PubMed] [Google Scholar]
- Gao Z and Zhuang X, “Consistency based co-segmentation for multi-view cardiac MRI using vision transformer,” in Statistical Atlases and Computational Models of the Heart. Multi-Disease, Multi-View, and Multi-Center Right Ventricular Segmentation in Cardiac MRI Challenge: 12th International Workshop, STACOM 2021, Held in Conjunction with MICCAI 2021, Strasbourg, Fra, 2022, pp. 306–314. [Google Scholar]
- Habijan M, Galić I, Leventić H, Romić K, 2021. Whole Heart Segmentation Using 3D FM-Pre-ResNet encoder–decoder based architecture with variational autoencoder regularization. Appl. Sci. vol. 11 (9), 3912. [Google Scholar]
- Yang R, Yu J, Yin J, Liu K, Xu S, 2022a. An FA-segnet image segmentation model based on fuzzy attention and its application in cardiac MRI segmentation. Int. J. Comput. Intell. Syst. vol. 15 (1), 1–10. [Google Scholar]
- Pereira RF, Rebelo MS, Moreno RA, Marco AG, Lima DM, Arruda MAFF, Krieger JEJE, and Gutierrez MA, “Fully Automated Quantification of Cardiac Indices from Cine MRI Using a Combination of Convolution Neural Networks,” in 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), 2020, vol. 2020-July, pp. 1221–1224. [DOI] [PubMed] [Google Scholar]
- Wang C-Y, Bochkovskiy A, and Liao H-YM, “YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 7464–7475. [Google Scholar]
- Kora P, Ooi CP, Faust O, Raghavendra U, Gudigar A, Chan WY, Meenakshi K, Swaraja K, Plawiak P, Acharya UR, 2021. Transfer learning techniques for medical image analysis: a review. Biocybern. Biomed. Eng. [Google Scholar]
- Rasti R, Biglari A, Rezapourian M, Yang Z, Farsiu S, 2022. “RetiFluidNet: a self-adaptive and multi-attention deep convolutional network for retinal OCT fluid segmentation. IEEE Trans. Med. Imaging vol. 42 (5), 1413–1423. [DOI] [PubMed] [Google Scholar]
- Yang Z, Soltanian-Zadeh S, Farsiu S, 2022b. “BiconNet: an edge-preserved connectivity-based approach for salient object detection. Pattern Recognit. vol. 121, 108231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z and Farsiu S, “Directional Connectivity-based Segmentation of Medical Images,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 11525–11535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Zhang Q, Zhang B, Chen X, 2019. TongueNet: a precise and fast tongue segmentation system using U-net with a morphological processing layer. Appl. Sci. vol. 9 (15). [Google Scholar]
- Xing G, Chen L, Wang H, Zhang J, Sun D, Xu F, Lei J, Xu X, 2022. Multi-scale pathological fluid segmentation in OCT with a novel curvature loss in convolutional neural network. IEEE Trans. Med. Imaging. [DOI] [PubMed] [Google Scholar]
- Zou KH, Warfield SK, Bharatha A, Tempany CMC, Kaus MR, Haker SJ, Wells III WM, Jolesz FA, Kikinis R, 2004. Statistical validation of image segmentation quality based on a spatial overlap index1: scientific reports,”. Acad. Radiol. vol. 11 (2), 178–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH, 2021. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods vol. 18 (2), 203–211. [DOI] [PubMed] [Google Scholar]
- Gu Z, Cheng J, Fu H, Zhou K, Hao H, Zhao Y, Zhang T, Gao S, Liu J, 2019. “CE-Net: context encoder network for 2D medical image segmentation. IEEE Trans. Med. Imaging vol. 38 (10), 2281–2292. [DOI] [PubMed] [Google Scholar]
- Kingma D and Ba J, “Adam: A method for stochastic optimization,” ArXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.


