Modelling the temporal trajectories of human milk components

Abstract

Background

This paper demonstrates how available data can be explored and utilized to conclude generic patterns in the temporal changes in Human Milk (HM) composition.

Methods

The temporal trajectories of selected human milk components (HMC-s) were described, in the first four months postpartum, by a primary model consisting of two phases: a short linear phase in the colostrum, triggered by the parturition; and a longer second phase, where the concentration of the component converges to a steady state. The model was fitted to data available in a recently published database of temporal HMC trajectories both at the levels of individual molecules (such as specific fatty acid, oligosaccharide, and mineral molecules) and molecule-groups (such as total protein, total fat).

Results

The properties of the trajectories suggest that experimental designs should follow non-equidistant sampling times, with increasingly longer time intervals after the first week postpartum. A selected parameter, the final stationary level, of the primary model was then studied as a function of geographical location (secondary modelling).

Conclusions

We found that the total variation of the concentration of specific HMC-s is dominantly due to the inherent biological differences between individual mothers and to less extent to the geographical location.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12884-024-06896-z.

Background

Exclusive breastfeeding is recommended during the first six months of life for the infants’ optimal growth and development, with continued breastfeeding for up to 2 years and beyond, together with the timely introduction of adequate complementary foods [1]. Human Milk (HM) and breastfeeding mediates a special bond between the mother-infant dyad and helps the newborn with normal growth, maturation, and development in the early period of life [2–4].^. In the short term, HM reduces the risk of morbidity and mortality from diarrhoea and lower respiratory tract infections, while, in the long-term, it is linked with higher IQ and prevention of metabolic syndromes [5]. It provides a unique source of nutritive and non-nutritive bioactive components, tailor-made by each mother, to meet the nutritional needs of her growing infant [6, 7].

In recent years, extensive research efforts [8–13] have been made to better characterize HM and to explore the factors that may affect human milk components (HMC-s), such as maternal diet (affected by geographical location and lifestyle), parity, mode of delivery, gestational age at birth, lactation stage, use of medication or nutritional supplements, gender of the infant, health status, and methodological factors related to milk sampling, handling, storage and analysis [6, 14].^.Despite these efforts, a mechanistic understanding of the dynamic system that mother and child form via HM [6, 15], is still missing. One of the reasons is the lack of longitudinal data on HMC [6, 15], especially from individual mothers. In fact, according to our best knowledge, no numerical or statistical assessment has been yet made about the sources (let alone their ranking) of the heterogeneity of HM composition. The data generation and collection, the statistical and modelling methods and the interpretation of the results rarely focus on the dynamic nature of the mother-milk-infant system. In their seminal review, Shenhav & Azad [15] have attributed this knowledge gap to the neglecting of the temporal evolution of HMC-s and, most importantly, to the lack of appropriate mathematical models that could identify patterns in the data, ultimately linking them to infant health outcomes.

A database called MilkyBase has been developed by Pacza et al. [16], to help resolve these difficulties. It serves as a recommended template that is especially suitable for dynamic modelling. By and large, that database, as well as this article, follow the recommendations of Shenhav & Azad [15], who also advocated dynamic modelling to advance HM research.

Mathematical modelling is key to understanding the temporal behaviour of HMC-s. Dynamic modelling has greater predictive power than what can be gained from simple statistical analyses. While the focus of a statistical analysis is to describe and visualize complex observations, the primary aim of dynamic modelling is to understand and predict the temporal evolution of a system, where both the explanatory and the response variables can change with time. Dynamic models are commonly differential equations describing the interactions between selected variables and their temporal rates. However, the answer to the question “what variables and what interactions” is not always straightforward and needs a sort of “omitting the unnecessary” [17], where “what is unnecessary” results from a consensus between practitioners and scientists of related fields. The resultant model must be a compromise between (i) resolution (i.e. details) of the acquired data; (ii) identifiability (i.e. we should be able to estimate the model parameters from observations); and (iii) applicability (i.e. the identified model should be implementable in predictive software, to aid decision making).

Reducing the complexity of this process is a major task. Fitting a set of differential equations to data can be challenging, therefore explicit algebraic functions are preferred. Besides, certain parameters (for example biochemical rates) may have higher priority than others, for example if they have strong relationships with mechanistic interpretation and/or their numerical domain is well-known. Other parameters, like the one(s) expressing the effect of history, forming the initial values for the model, may be stochastic, depending on unknown factors.

These aspects lead us to an approach that became a standard procedure, for example in predictive microbiology, in the last three decades [18].

• Acquire longitudinal concentration measurements (i.e. temporal trajectories) of HM components, preferably from many individual mothers, in a defined interval (say over the first 120 days of the infant), during which the conditions are well-known and at least approximately constant.

• Establish a class of mathematical functions that is generic enough to represent the acquired temporal trajectories. This is called the primary model; its parameters can be estimated by fitting the model to observed data.

• Model the effect of factors, such as geography, or mother / infant conditions, on the parameters of the above primary model (and not on the measured individual points). This is called the secondary model.

• Use the combination of the primary and secondary models to generate predictions and validate them on independent datasets. Use the results for example, for optimal experimental designs.

• Determine the expected sources of the variabilities and uncertainties. Rank them to prioritize new research topics in innovation and clinical practice.

The terminology “primary / secondary” modelling were coined in the 90-s, when predictive microbiology [18] was going through a stage not dissimilar to what currently HM research is experiencing; to make sense of the large amount of data requires predictive modelling. Accordingly, we suggest that a predictive HM model should be built in two steps: (i) identify primary models to describe the temporal trajectories of the studied HMC-s; (ii) determine how the parameters of the primary models depend on factors other than time.

Our objective is to demonstrate these steps using a publicly available database and make a case to invest more efforts in modelling as a cost-effective means to evaluate HMC data and to advance HM research.

Results

Primary model

To get ideas for the structure of possible primary models, we needed detailed data on the temporal variation of HMC-s, measured for individual mothers. John et al. [19] published such a dataset on the total protein of HM; it has also been deposited in MilkyBase [20].

Figure 1a shows such individual protein trajectories for those four mothers who provided more than 10 samples during at least 30-days within 120 days postpartum. Observations suggest that the individual trajectories are smooth curves: all of them decrease linearly, and one of them converges, while decreasing, to a steady state. Ideally, we should collect such trajectories for a large number of individual mothers, but such datasets are rare.

Fig. 1.

HM protein trajectories based on John et al.[19]. Figure 1a shows the protein concentration, as a function of time, from those four mothers, who gave at least 10 samples in a post-partum interval spanning over at least one month. The thin red line is a pure saturation model fitted to mother M256, who gave the most samples, in time points spanning over the four-month-long observation time. Figure 1b shows all the 545 pooled measurements (blue dots) coming from 177 mothers. Red thick line: pure saturation curve fitted to all points

We can safely assume that, even if an individual trajectory is linearly decreasing in the observation interval, later it will tail off (if nothing else, towards zero). Therefore, all the four individual trajectories can be described by monotonous, convergent mathematical functions, such as the pure saturation model (see 4. Material and Methods), noting that the (close-to-) linear trajectories have (close-to-) zero exponential convergence rates.

Figure 1b shows the total protein concentrations, as a function of postpartum time, measured for individual mothers. As 545 measurements were made for 177 mothers, the average number of samples donated by one mother was around 3. From these, one cannot expect to identify the individual trajectories, but the average concentrations, as a function of time, can be well fitted by the above pure saturation model. As the rate of the exponential convergence here is based on a population, we call it population convergence rate as opposed to the individual convergence rate for a HMC of an individual mother.

It is important to see that, because of the non-linear model, the population convergence rate is not the arithmetical average of the individual rates, but a function of their distribution. However, as Fig. 1b demonstrates, the pure saturation function is still a good model for their typical (average) behaviour.

The regression results, when fitting all the points in Fig. 1b, can be interpreted as follows: The rate of the exponential convergence is 0.031/day, which is equivalent to ca 22 days “half-time”; i.e. the remaining distance to the final level halves in every ca. 3 weeks. The relative error of the rate estimate is 15%.The standard error of fit is 1.5 g/L while the final saturation level was estimated as 9.7 ± 0.19 g/L. Considering that the cohort of this study (healthy young women from Texas) was as homogeneous as can reasonably be expected, the results (and the R² = 0.42 value) show, what Fig. 1a also demonstrates, that the total variation in the protein concentration is primarily due to the inherent biological differences between individual mothers and to less extent due to the temporal variation. Note that while the former (cross-sectional) variation is inevitably stochastic, the latter (longitudinal) variation for an individual mother is well described by our deterministic pure saturation model.

Figure 2 shows the trajectories of the total HM protein concentrations from a set of MilkyBase records where the cohort was from the EU. The data points placed on one trajectory are average protein concentrations derived from the cohort. Whenever, from the publication, we could deduce the standard deviation generated by the individuals of the cohort, it was between 1 and 2 g/L, which confirms the result of John et al. [19] (Fig. 1b), for which the standard error of fit, i.e. the cross-sectional standard deviation, is ca 1.5 g/L. For inhomogeneous populations (randomly including Caesarean section, pre-term birth, etc., as the data behind the publications in Fig. 2 indicate), the expected error obviously must be much bigger; the cross-sectional deviation is around. 5 g/L. This is confirmed by Samuel et al. [14], reporting on standard deviations around 4.8 g/L, on average, for the HM protein concentrations generated by multicentred, longitudinal cohort living in the EU. In other words: the difference between the protein concentrations of two randomly chosen mother’s milk, at the same time after birth, would be highly likely 3–4 times bigger than the difference between the protein concentrations of two random samples, one colostrum and one mature, from the same mother.

Fig. 2.

Nineteen temporal trajectories of total protein concentration in HM, published in seven papers and stored in the MilkyBase [20] database. The measurements were made in various EU countries and birth conditions. The data points are average concentrations, typically from > 10 mothers. Conditions like gestation age, delivery method, geographical location, etc. all contributed to the total variation. The pure saturation model, with three parameters, was used to fit the trajectories. Legend: the key that MilkyBase [20] uses for the records, where the trajectories are stored

When developing primary models to describe the temporal trajectories formed by the concentrations of HMC, ideally, we should acquire high resolution longitudinal data for the studied components, preferably from individual mothers. We have seen that the pure saturation model is flexible enough to fit protein trajectories at both individual and population level. The model has three parameters; the initial and the final concentration (to where the trajectory converges), and the rate of this exponential convergence.

Figure 1 demonstrates that the fit of the pure saturation model at population level is robust (all the three parameters were estimated by less than 20% relative error), though some individual trajectories were linear (at least in the observed interval), while others showed a pronounced curvature. Analogously, it would be important to know whether a pattern recognized for a group of molecules like proteins, fatty acids, oligosaccharides, minerals, vitamins, is equally valid for the individual molecules of that group. Data are available for such specific molecules, too, though rarely for individual mothers. Samuel et al. [14] reported on the population trajectories of selected molecules (Figs. 3–4). The data represented averages, derived from large cohorts, therefore had small standard errors. Some of the trajectories followed the pure saturation model but some did so only after a rapidly changing initial period.

Fig. 3.

Our two-phase primary model can well be used to describe the concentration trajectory of fatty acid molecules as well as minerals studied by Samuel et al. [14]. As the paper investigated the effect of delivery mode, we overlayed the corresponding trajectory-pairs on one plot. The suffix “_csr” denotes Caesarean section

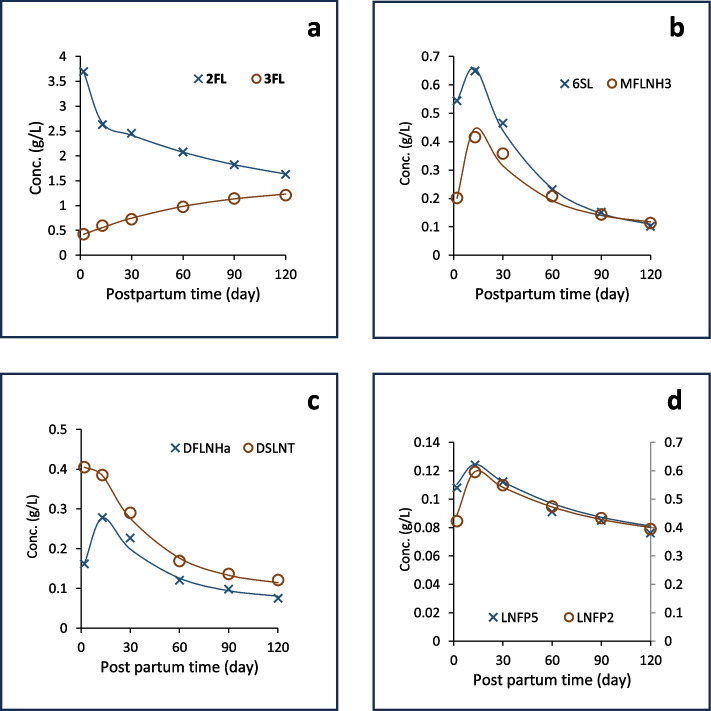
Fig. 4.

Measured temporal trajectories of various HM oligosaccharides described by our two-phase primary model. The data are from Samuel et al. [7]. 2FL: 2’-Fucosyllactose; 3FL: 3’-Fucosyllactose; 6SL: 6′-Sialyllactose; MFLNH3: Monofucosyllacto-N-hexaose-III; DFLNHa: Difucosyllacto-N-hexaose-a; DSLNT: Disialyllacto-N-tetraose; LNFP5: Lacto-N-fucoPentaose-V; LNFP2: Lacto-N-fucoPentaose-II. The latter component is measured on the secondary vertical axis, on the right-hand side

Very few data are available to vindicate this pre-saturation initial phase. The only such records in MilkyBase [20] were from Liu et al. [21]. The dataset convincingly demonstrated (see Fig. 5) that the total fatty acid concentration linearly increased in the colostrum before the trajectory entered the second, the pure saturation phase. The average of the fitted slopes, in this initial phase) was 3.5 g/L/day, with ca 12% relative standard error. As a rule of thumb, we can say that the fat content ca. doubled during the first 6 days.

Fig. 5.

Fast linear increase of the total fatty acid concentration in the colostrum, in five Chinese cities, as reported by Liu et al. [21]

Therefore, for a generic model, we assume an initial, linear “take-off” period prior to the saturation model. We call this as two-phase saturation model, with five parameters, as opposed to the pure saturation model, with three parameters (i.e. no initial linear phase; see Material and Methods). If the two phases have the same trend, the initial phase can well be embedded in the pure saturation model. However, the existence of the initial linear phase is surely a good assumption if the two phases have different trends. A physiological (mechanistic) explanation for the two phases may be that for some molecules, a sudden change in their production (or excretion) is triggered by the parturition; then the process converges to an autonomous system, the pure saturation.

Unfortunately, the existence of the initial phase can only be shown on datasets having at least two samples from the colostrum and such datasets are scarce.

For demonstration, we fitted all the data found in Samuel et al. [7, 14] (Figs. 3–4). A single-phase three-parameter saturation model was fitted to the post-colostrum data by non-linear regression, then the only point from the colostrum was combined with the fitted value at the first post-colostrum point. This way, the slope defined by the first two points demonstrates a bound for the slope of the initial linear phase.

The two-phase model could explain all the population trajectories of the molecules Samuel et al. [7, 14] published. The a-c plots on Fig. 3 show the population trajectories of three fatty acid molecules that fast increase to their final concentration levels. The d-e plots show a decreasing trend all along, where the initial linear phase could be embedded in the subsequent pure saturation model. The f–h plots start with a linear increase, followed by a decreasing trajectory converging exponentially to a final level. The i-k plots show similar good fits for minerals, just as the plots in Fig. 4 do, for oligosaccharides.

Figure 3 demonstrates the example when comparison is made between trajectories (i.e. on the parameters of the primary model), to see the effect of delivery mode. As described in the introduction, this leads us to secondary modelling.

Secondary model

Recall that primary models describe temporal trajectories of HMC-s in more-or-less constant conditions, while secondary models are about the effect of those conditions on the parameters of the primary model. The main reason why the two kinds of models should not be merged is mechanistic: it is the rate, with time, how a component changes (not their level directly), that is determined by the conditions. To reduce complexity, it is the parameter set of the primary model, that can be used as a replacement for the whole temporal trajectory. In what follows, we make comparisons, how a secondary parameter, the final concentration level, is affected by the geographical location. We take extra care, by putting down the plus/minus standard errors in the fitted curves, to indicate the confidence in our findings.

Geographical differences

The total fat concentration did not change significantly, post-colostrum, for either the Texas cohort of John et al. [19] (35 ± 7 g/L) or for the EU cohort of Samuel et al. [14] (40 ± 15 g/L). For the Chinese cohort of Liu et al. [21], the total post-colostrum fat also remained between 25 and 30 g/L until the 42nd day. Wu et al. [22] confirmed thus when finding that that the fat concentration in mature HM was around 25 g/L in their Chinese cohort. These publications are all digitized in MilkyBase [20], in such a way that the geographical region is one of the explanatory variables, while the temporal trajectories of various HM components represent dynamic responses.

We took the two-phase saturation curves fitted to the data of Samuel et al. [14] as a reference for comparison. The reason for this was that here the authors collected the samples at about the same times for individual mothers and the published concentrations are the averages of large samples, therefore their standard errors are small. Figure 6, created from MilkyBase [20], summarizes the difference between the HM fat concentrations produced by EU and Chinese cohorts. The typical (average) fat concentration for the EU cohort is 25–30% higher than that for the Chinese cohort, all along the observation time.

Fig. 6.

HM total fat concentration trajectories derived from MilkyBase [20] records on EU and Chinese cohorts. Black continuous line: Our generic model fitted to the EU-cohort data of Samuel et al. [14] (black crosses), which were the averages of large (N > 100) samples at each time point. Green broken line: the same primary model fitted to other EU-cohort data (green squares); these are averages from smaller (10 < N < 50) samples, from 9 other publications. Red broken line: two-phase saturation model (with an initial linear increase in the colostrum, as this was significant here) fitted to similar data from China, based on 4 publications. The rate of exponential convergence was fixed as 0.2/day for all the fitted curves

The base model (black continuous line in Fig. 6) fits average fat concentrations, each of which was produced by hundreds of mothers at about the same time. The standard deviation of the original measurements is 10–20 g/L (as shown by the tables of Samuel et al. [14]), so the errors of the points fitted are less than 1 g/L. Notice that they follow a smooth pattern, even if the individual trajectories are more stochastic, as seen in Fig. 2, though for proteins. The reason for the small error of the average is that the size of the cohort compensates for the big, ca 15 g/L standard deviations of the raw data caused by the individual mothers’ biological differences. Ordinary ANOVA confirmed (though it is visible from the plot, too) that that this is significantly higher than the variation caused by the geographical location, i.e. whether the cohort was from EU or China.

The other EU data shown in Fig. 6 are averages of smaller (10 < N < 50) cohorts, from 9 independent publications. The fitted model is close to our reference model fitted to the data of Samuel et al. [14]: the fat concentration increases from 22.2 g/L, measured on day 1, to 37.2 g/L towards the end of the four-month-long observation time. Indeed, these values are 19 and 40 g/L, respectively, for our reference model. The estimates for these parameters are even further away, 15 and 30 g/L, respectively, for the data derived from Chinese cohorts. The standard error of fit for the EU cohorts is 6.3 g/L, while it is 4 g/L for the Chinese cohorts. These are, of course, much bigger than the standard errors of the data of Samuel et al. [14], but this is understandable, considering that the latter ones are averages generated by much bigger cohorts. In the first case, when 9 independent publications provided the data, heterogeneity comes not only from the randomized (otherwise healthy individuals) cohort, but also from known and studied factors, e.g. mother’s diet, delivery mode, infant’s gender, measurements methods, etc., as described in the publications producing the data).

Therefore, similarly to the proteins, also for the fat content, the variation coming from cross-sectional differences is bigger than either the longitudinal or geography-generated variation (at least regarding EU and China).

Figure 6 shows that, in agreement with Wu et al. [22], the fat concentration in Chinese cohorts is lower than in EU cohorts all along the 120 days of the observation interval. The question is whether this difference also holds for the individual fatty acid molecules. This can be answered by using molecule-specific data from the MilkyBase [20] database.

The most abundant fatty acid molecules are the oleic (C18:1n-9) and linoleic (C18:2n-6) acids, their sum providing more than half of the total fatty acid content of HM. Figure 7 shows the data available from MilkyBase [20] for oleic (Fig. 7a) and the linoleic acid (Fig. 7b), respectively. As can be seen, the concentrations from the Chinese cohorts tend to have lower level of oleic acid than EU cohorts do, but the situation is the opposite with linoleic acid, especially in the first two weeks.

Fig. 7.

The trajectories of oleic acid (C18:1 n-9; Fig. 7a) and linoleic acid (C18:2 n-6; Fig. 7b), in the first 120 days of HM. Legend and symbols are as in Fig. 6. The averages of the data from Samuel et al. [14] are confirmed by the averages of other EU data, but the latter have much bigger standard errors than what the fit to the data from Chinese cohorts indicates

In MilkyBase [20], data are also available for eicosadienoic acid (C20:2n-6) and docosahexaenoic acid (DHA; C22:6n-3). Figure 8 shows that, in case of the first one, the concentrations from Chinese cohorts tend to be higher than those from EU cohorts, while the case is the opposite for DHA. Therefore, the geography-generated differences in the total fatty acid concentrations does not necessarily show the same patterns when individual fatty acid molecules are compared.

Fig. 8.

The concentration of eicosadienoic acid (C20:2n-6 – Fig. 8a) and docosahexaenoic acid (DHA; C22:6 n-3 – Fig. 8b) in the first 120 days. Legend and symbols are as in Fig. 6. The fit to independent EU data is close to the fit to the data of Samuel et al. [14], in both cases. An initial linear phase could not be identified on Fig. 8a, because of the lack data from the colostrum. The data provided by Chinese cohorts were scattered around their mean so that no trend could be established. For DHA, the initial linear phase was significant for both geographical regions

Discussion

Typically, when the amount of data in a scientific discipline becomes sufficient, predictive modelling becomes a useful tool to make the field more predictive, not only descriptive. While HM research may be in its figurative “infancy”, there is a noticeable need to exploit the data for predictions. Such efforts have proven successful in other disciplines such as in biotechnology and food microbiology [18, 23].

Here we used predictive modelling to characterize the temporal trajectories of HM components. We found that, for measured concentrations in the observed intervals, the time points should span at least 30 days, with at least 4–5 but preferably > 10 points within the studied time range. While such datasets are scarce in the literature, we can certainly make use of their derived averages and standard deviations within the studied cohorts. On the other hand, for a predictive model, it would be desirable to identify the inherent statistical distributions of biological conditions within the cohorts. As a rule of thumb, minimum 30–40 individuals would be necessary to identify such distributions.

A generic consequence of our primary models is that time points for sampling should not be equidistant but rather samples should be taken more frequently when the nonlinearity of the trajectory is expected to be high. For example, a good sampling time set could look like 1, 3, 6, 14, 30, 60 days, reflecting the idea that the same amount of data should be collected from the colostrum, transitional and mature stages of the first 4 months, even though the length of these stages is increasing. The concentration of the studied molecule between months 2 and 4 can be predicted with high confidence from the data before 2 months, as the latter ones are in the convergent saturation phase of the primary model.

The component trajectories were shown to follow the saturation model, possibly preceded by a short linear phase in the colostrum. We used final saturation level, as a parameter of the primary model, to demonstrate the geography-generated effect on HMC-s. For example, the total fatty acid concentration in the HM provided by Chinese cohorts tended to be lower than the level provided by EU cohorts, which agreed with other authors’ findings [21, 22]. We found that this difference is not proportionally passed to individual fatty acid molecules, but some tend to be present at an even higher concentration in samples from Chinese than in samples from EU cohorts.

A point to mention is the frequently misused concept of statistical significance. Our primary model fitted to [time, concentration] data can be used to predict the average concentrations at other time points. The measured averages have smaller standard errors with increasing cohort size, while the standard deviation of the sample of course does not change. If such averages of new measurements (for example in a different country) are consistently above or below the previously predicted curve, possibly by a small margin only, then the difference between the two trajectories formed by the respective averages can be statistically significant even if this magnitude is negligible compared, for example, to the standard deviation of individual measurements, which is the “noise” of the data collection. So, it is possible that the difference between the two groups is statistically significant (i.e. that it is not by accident and the difference can be stated with confidence), but numerically insignificant (negligible) compared to the difference caused by other factors. A good example for this is in Fig. 4. The effect of delivery mode is statistically significant (detectable), although its magnitude is insignificant compared to the longitudinal variation.

Conceiving the molecules of HM as the manifestation of certain set of maternal genes, correlations between the parameters of the temporal trajectories of those molecules may help understand the mother’s regulatory network. For example, those molecules, for which an initial sudden change preceding the saturation curve could be identified, may be produced by genes activated during parturition. Studying such mechanisms belongs to systems biology of individual mothers’ genome that may lead to personalized nutrition strategies.

As we pointed out, via our primary-secondary modelling approach, the biological variation generated by individuals is greater than that generated by geographical differences. In other words, the difference between the concentrations of a specific HMC produced by two randomly chosen individual mothers from a homogeneous population is likely to be greater than the average difference generated by geographical effects. Therefore, predicting HM composition as a function of individual mothers would benefit HM research more than predicting the effect of geography or postpartum time. It is to be added that, while precision nutrition (individually beneficial by having quantitative information on the relation between an individual, food consumption and phenotype) or personalized nutrition (suited to each individual by using information on individual characteristics) may be a long-term aim, a less ambitious stratified nutrition suited to each group by grouping individuals with shared physiological characteristics (e.g. BMI ranges, dietary patterns etc.) may offer a first start to the application of predictive nutrition.

As predictive research in HM needs to grow from its stage of infancy, it is important to emphasize several desirable requirements, including (i) good quality longitudinal data on HM components; (ii) appropriate sampling methods and that the samples are collected according to optimal experimental designs; (iii) standardization of HM collection methodologies across studies; and (iv) good quality metadata to link the HM components with relevant health outcomes.

Our work is a first attempt to use mathematical modelling to propose novel approaches that can help HM research become more predictive then descriptive. Predictions, even if just rudimentary, represent great benefits for making decisions on experimental design and data interpretation, as well as on selecting research and innovation fields for resource allocation.

Material and Methods

Data

A recently published HM component database, MilkyBase [20], used for model estimation and validation in this paper, has been constructed with the aim of mathematical modelling. One record consists of explanatory and response variables (fields). The first group refers to those factors that affect the HMC-s, which belong to the second group, the response fields. Both groups allow a temporal trajectory to be represented by a single entry, namely a pointer referring to a table that contains a [t_i, y_i] observed/estimated value set, identifying the trajectory. Therefore, both the explanatory conditions and the HMC responses can contain dynamic entries, i.e. temporal trajectories. They are described by time-dependent primary models while secondary models describe how the parameters of the primary model depend on explanatory variables other than time.

The above ontology makes it easy to replace the trajectories by the primary parameters. The detailed technical description of the database is available as referenced in the paper [16].

It is important to see that, when populating MilkyBase [20], the aim was to record large amounts of data from publications, regardless of either their objectives, or the studied molecules or selected cohorts. Therefore, publications with large tables, possibly in a Supplement, were prioritized when populating the database. It is unlikely that the omission of publications with small datasets would have introduced bias in the modelling. Developing MilkyBase [16] was not a kind of “data mining”, rather a prototype for a user-friendly data digitization, advanced enough for mathematical modelling. In this paper, we showed what can be implied from the data available in MilkyBase [20].

Mathematical modelling

Our primary model was developed as follows: The focus interval was the first four months. During this time, the y(t) concentration of a HMC was assumed to follow a two-phase model. In the first, initial phase (colostrum), the HMC concentration changed with time in a linear fashion, followed by an exponentially convergent saturation phase:

$$y\left(t\right)=\begin{array}{c}{y}_0+a·t\hfill \\ y_{\lambda }·e^{-r·(t-\mathrm{\lambda })}+y_{\text{End}}(1-e^{-r·\left(t,-,\mathrm{\lambda }\right)})\hfill \end{array}\begin{array}{c}(0\le t\le \mathrm{\lambda })\hfill \\ (t>\mathrm{\lambda })\hfill \end{array}$$

where y_λ = y₀ + a·λ, r ≥ 0, λ ≥ 0.

That is, during the first phase (colostrum: t < λ), the HMC production rapidly changes from an initial level, y₀, at a rate, a. Then, the system enters an autonomous phase, where the concentration exponentially converges to a stationary level. The initial parameters, y₀ and a, as well as those of the second phase, r, and the final concentration level y_End depend on various factors, primarily on some characteristics of the mother.

The second, convergent phase is called the saturation model. The name has been used mainly for situation when the response value increases with time; however, for the sake of simplicity, we use it for the mirror image, too.

Figure 9 shows three examples for this generic primary model. In this case, the HMC decreases in the post-colostrum period (the increasing versions can be obtained by mirroring). For all the curves, r = 0.07/day was used for the saturation rate, λ = 6 days for the length of the initial phase (colostrum), while a > 0 for the lowest two curves and a < 0 for the top curve, as the slope of the initial linear phase. The lowest curve is hardly different from the r = 0 case, which would produce a bi-phasic function: linear change in the colostrum, followed by a constant (y_End) HM concentration. The upper curve is hardly different from the λ = 0, a = 0 case, which would represent the single-phase pure saturation model, with three parameters. Note that the end of the first phase was fixed as λ = 6.

Fig. 9.

Examples for our generic, two-phase saturation model. Broken line: initial phase (colostrum). Continuous line: second (saturation) phase. The alternative of the λ = 0 case (when the parameter a becomes per se insignificant) is λ = 6, with either a < 0, a = 0, or a > 0. Similarly, significance test may show that r can be taken as zero, implying y₀ + aλ = y_End

F-test decided whether the full two-phase model with four parameters (y₀, a, r, y_End) were needed to describe a dataset, or any of the parameters could be a fixed value, to decrease the dimension of the model. Note that value set of λ was considered binary: it is either 6 (default) or 0. In the latter case, the first phase is embedded in the saturation model, and the result is a single-phase, pure saturation model, with three-parameters. Again, F-test decided if the single-phase pure saturation model was sufficient to fit a particular dataset or the λ = 6 case was significant with a slope a.

Similarly, F-test was used to decide whether one or two of the parameters can be considered identical, for a pair of datasets (e.g. a pair of trajectories, showing the effects of delivery mode; – see Fig. 4).

The secondary model could be used to quantify the effect of various factors, mother history and other characteristics on the fitted parameters (e.g. y_End) of the primary model. The non-linear regression algorithm was built in a bespoke Microsoft Excel Add-In, written in Visual Basic, implementing the standard Levenberg–Marquardt method. The Data Analysis Add-In of Excel was used to carry out linear regression and ANOVA procedures, with 5% significance level.

Conclusions

Lots of data are available on the molecular composition of Human Milk, still it would be a very difficult to predict this composition for a specific mother at a specified time after giving birth. The more this would be important as a deviation from the prediction could be used as a marker for any disorder in the milk production.

Here we use a database of published data to show that the pattern how the concentration of a Human Milk component changes with time, for an individual mother, is predictable by mathematical means, assuming that the maternal conditions are stable. This pattern is highly non-linear and can be divided into phases that justify the traditional colostrum – transitional – mature division. The ideal trajectory for an individual mother’s milk composition undergoes a fast change in the first week, but then it gradually takes up a trajectory that is typical of saturation processes, converging to a steady state at a slow but exponential rate.

Cross-sectional studies cannot confirm this pattern as the random variability of personal (genetics and diet) characteristics are bigger than the one caused by time or other (like geographic or diet) conditions.

Abbreviations

HM

Human Milk

HMC

human milk component

Authors’ contributions

J.B. conceptualized the study, developed the mathematical model, coordinated the data acquisition and validation efforts, largely wrote, and edited the manuscript. T.P performed the data acquisition and validation, formal analysis and visualization of data, contributed to the writing and editing up of the manuscript. M.L.M performed the data acquisition and validation, contributed to the data visualization, and to the writing up of the manuscript. T.M.S., S.K.T. contributed to the conceptualization of the study and to the writing up of the manuscript. All authors reviewed and approved the manuscript.

Authors information

M.L.M. has been supported by the Stipendium Hungaricum Scholarship Programme of the Ministry of Foreign Affairs and Trade of Hungary, via the Tempus Public Foundation.

Funding

József Baranyi received funds from Société des Produits Nestlé SA for this work.

Data availability

The data on which this study is based are available on 10.6084/m9.figshare.c.6160191.v1.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

T.M.S and S.K.T are employees of Société des Produits Nestlé SA. The other authors declare no competing interests.