Enhancing mathematical learning outcomes through a low-cost single-channel BCI system

Abstract

This study investigates the effectiveness of a Low-Cost Single-Channel BCI system in improving mathematical learning outcomes, self-efficacy, and alpha power in university students. Eighty participants were randomly assigned to either a BCI group receiving real-time neurofeedback based on alpha rhythms or a sham feedback group. Results showed that the BCI group had significantly higher mathematical performance, self-efficacy, and alpha power compared to the sham feedback group. Mathematics performance, alpha wave intensity, and self-efficacy showed significant positive correlations after training, indicating that neurofeedback training may have promoted their interaction and integration. These findings demonstrate the potential of BCI technology in enhancing mathematical learning outcomes and highlight the importance of considering pre-test performance and self-efficacy in predicting learning outcomes, with implications for personalized learning interventions and the integration of BCI technology in educational settings.

Introduction

Mathematical learning is a complex cognitive process that involves the coordination of multiple brain regions and is influenced by various cognitive and affective factors, such as working memory, attention, problem-solving, executive control, and emotional motivation^1–3. Previous research has shown that mathematical learning not only requires basic numerical abilities, such as “number sense”^4,5 and symbolic skills⁴, but also involves language skills, spatial skills, working memory, and executive functions^6,7.

Math anxiety, which refers to a debilitating negative emotional response to mathematical tasks, can impact mathematical performance through its effects on working memory, symbolic-numerical processing, and directly⁸. Studies have also shown that in numerical tasks, personal salience and reward stimuli better engage the affective-motivational systems anchored in the amygdala and ventral striatum, and the learning and memory systems anchored in the medial temporal lobes, with increased hippocampal responses mediating the relationship between positive attitude and effective problem-solving⁹.

Many researchers have made efforts to improve mathematical performance. Some have used digital educational games to train children’s math performance, but they only showed better results in number line estimation and did not significantly impact other aspects, post-test performance, or math anxiety¹⁰. Other studies have evaluated the effects of math anxiety reduction training on math performance, finding that while such training helps reduce anxiety levels, it does not significantly impact math scores. Furthermore, strategy training for overcoming math anxiety shows complex effects on math achievementy¹¹. Researchers have also observed immediate improvements in math performance after working memory training, with the enhancement persisting over time. The same study found that the group receiving concurrent metacognitive strategy training improved more than the group receiving only working memory training¹². Spatial training has also been found to be an effective means of improving math understanding and achievement¹³. However, all these methods require management by trained professionals. In contrast, we sought to find a low-cost approach to enhancing mathematical performance.

Brain-computer interface (BCI) technology has emerged as a promising approach to enhance learning and cognitive abilities by providing real-time feedback or stimulation based on brain activity¹⁴. Previous studies have applied BCI technology to various domains of learning, such as language¹⁵, memory¹⁶, and executive functions¹⁷. However, few studies have explored the potential of BCI technology, particularly alpha rhythm neurofeedback training, in improving mathematical learning outcomes. While our study focuses on alpha oscillations due to their strong associations with cognitive functions critical for learning, such as attention and working memory, it is important to acknowledge that other brain oscillations, such as theta and gamma rhythms, have also been implicated in learning and memory processes^18,19.

Gamma band oscillations (around 40 Hz) in the visual cortex were detected and modulated using a source-based BCI, demonstrating the potential for manipulating fast oscillatory activity with high specificity²⁰. Delta phase-amplitude coupling with alpha oscillations was observed in individuals who showed better performance on a knowledge generation task, suggesting that these oscillatory dynamics work together to encode and represent new knowledge with respect to reactivated prior knowledge²¹. This study aims to fill this research gap by investigating whether a low-cost single-channel BCI system providing alpha rhythm neurofeedback can enhance algebra learning performance, self-efficacy, and alpha power in university students.

One of the main challenges of applying BCI technology in educational settings is the cost and complexity of the equipment. Most BCI systems require expensive hardware, invasive surgery, or multiple electrodes. Invasive electrodes have significant disadvantages due to the risk of surgery and gradual degradation of signal recording²², making them difficult to use in large-scale or long-term educational settings. Furthermore, most BCI systems are designed for specific tasks or paradigms, and the complexity and structure of BCI technology applications in different fields vary. Most BCI applications follow a standard structure and system¹⁴, which limits their generalizability and portability in real-world learning scenarios.

In this study, we propose a novel Low-Cost Single-Channel BCI system that can enhance mathematical learning outcomes by providing neurofeedback based on alpha rhythms. Recent studies have demonstrated the causal role of alpha oscillations in top-down (endogenous) attention²³, and significant results in improving cognitive function in healthy subjects through auditory-induced alpha waves have been achieved²⁴. Other studies have supported the causal link between alpha oscillations and working memory maintenance²⁵, with researchers evoking or enhancing alpha waves to improve working memory levels^26,27.

We hypothesize that by promoting attentional focus, reducing anxiety, and enhancing working memory, an increase in alpha power can also improve mathematical learning outcomes. To test this hypothesis, we conducted a randomized controlled experiment on 80 university students learning algebra concepts on an online platform. Half of the participants received real-time neurofeedback from the BCI system, while the other half received sham feedback. We measured their mathematical performance, self-efficacy, and alpha power before and after the intervention. We expected the BCI group to have significantly higher mathematical performance and self-efficacy compared to the sham feedback group. Additionally, we anticipated the BCI group to exhibit higher alpha power in the prefrontal regions involved in mathematical cognition.

Results

The results showed a significant interaction effect between Measure Time (Pre-test & Post-test) and Group (BCI & Sham) on mathematical performance (F (1,78) = 8.941, p = 0.004, η²_p = 0.103). The BCI group had significantly higher mathematical performance than the sham feedback group on the post-test (p_bonf < 0.001), but there was no significant difference between the two groups on the pre-test (Fig. 1).

Fig. 1. Comparison of pre-test and post-test mathematical performance scores between BCI and control groups.

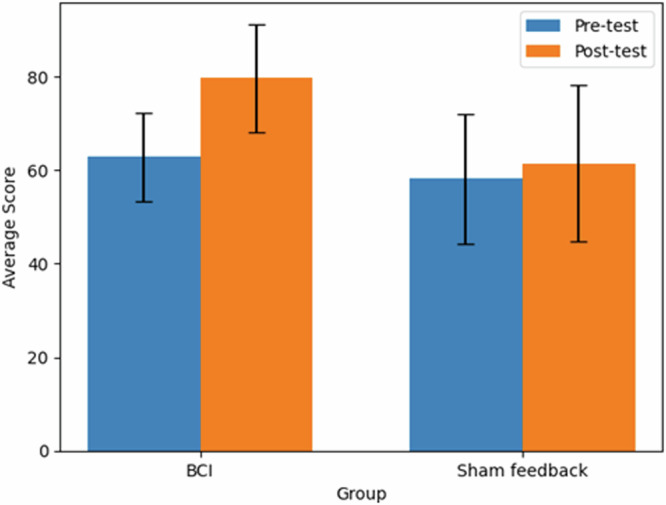
The bar graph illustrates the average mathematical performance scores for both the BCI neurofeedback group and the sham feedback control group, comparing pre-test, and post-test results. Blue bars represent pre-test scores, while orange bars show post-test scores for each group. Error bars indicate the standard error of the mean. The BCI group demonstrated a notable increase in performance from pre-test to post-test, whereas the control group showed minimal change. This visual representation suggests that the BCI neurofeedback intervention may have had a positive impact on mathematical performance, though statistical significance (p < 0.05) should be noted when interpreting these results.

The results also showed a significant interaction effect between Measure (Pre-test & Post-test) and Group (BCI & Sham) on self-efficacy (F(1,78) = 10.076, p = 0.002, η²_p = 0.114). The BCI group had significantly higher self-efficacy than the sham feedback group on the post-test (p_bonf < 0.001), but there was no significant difference between the two groups on the pre-test (Fig. 2).

Fig. 2. Pre-test and post-test self-efficacy scores comparison between BCI and control groups.

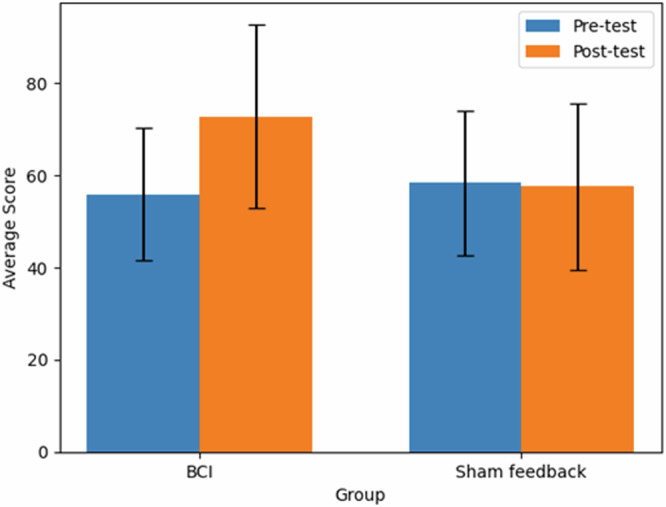
The bar graph presents the average self-efficacy scores for both the BCI neurofeedback group and the sham feedback control group before and after the intervention. Blue bars indicate pre-test scores, while orange bars represent post-test scores for each group. Error bars show the standard error of the mean. The BCI group exhibited a notable increase in self-efficacy from pre-test to post-test, whereas the control group’s scores remained relatively stable. This visual comparison suggests that the BCI neurofeedback intervention may have positively influenced participants’ self-efficacy in mathematics, with the statistical significance (p < 0.05) supporting this observation. The graph allows for a clear comparison of the intervention’s effects on self-efficacy between the two groups.

The results showed a significant interaction effect between Measure (Pre-test & Post-test) and Group (BCI & Sham) on alpha power (F(1,78) = 13.735, p < 0.001, η²_p = 0.150). The BCI group had significantly higher alpha power than the sham feedback group on the post-test (p_bonf < 0.001), but there was no significant difference between the two groups on the pre-test (Fig. 3).

Fig. 3. Comparison of frontal lobe alpha power between BCI and control groups pre- and post-intervention.

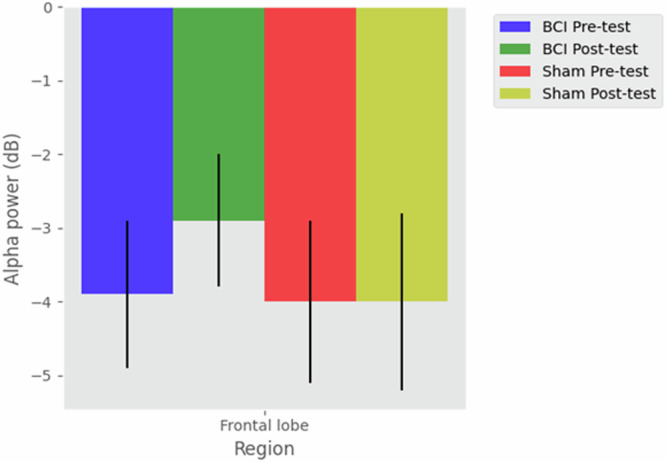
The bar graph displays the relative mean alpha power (in dB) measured from the frontal lobe region for both the BCI neurofeedback group and the sham feedback control group before and after the intervention. Blue and red bars represent pre-test measurements for the BCI and sham groups respectively, while green and yellow bars show post-test measurements. Error bars indicate the standard error of the mean. The BCI group exhibited a notable increase in alpha power from pre-test to post-test, whereas the control group showed minimal change. This visual representation suggests that the BCI neurofeedback intervention may have effectively increased alpha power in the frontal lobe, a finding supported by statistical significance (p < 0.05). The graph provides a clear comparison of the intervention’s effects on brain activity between the two groups, highlighting the potential neurophysiological impact of BCI-assisted learning.

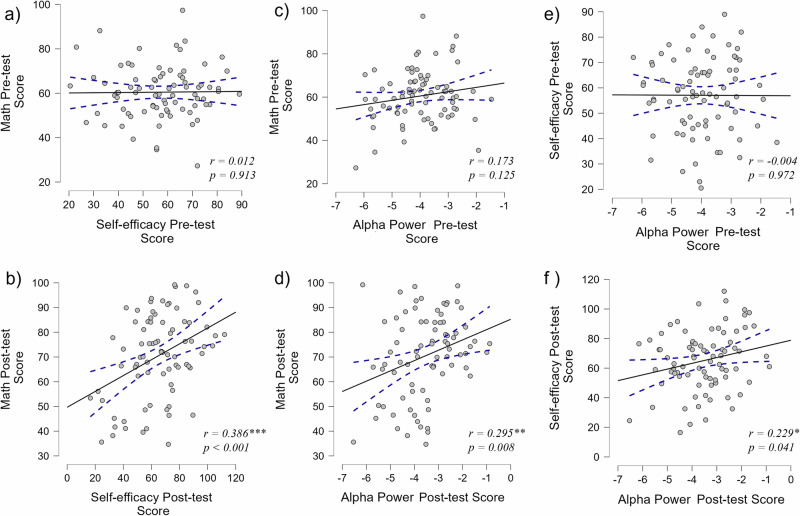
A Pearson correlation analysis was conducted to examine the relationship between participants’ mathematical performance, alpha power, and self-efficacy at both pre-test and post-test stages (Fig. 4). The results revealed no significant correlations between math scores, alpha power, and self-efficacy at pre-test (math scores & alpha power: r = 0.173, p = 0.125; math scores & self-efficacy: r = 0.012, p = 0.913; alpha power & self-efficacy: r = −0.004, p = 0.972). However, significant positive correlations emerged at post-test between math scores and alpha power (r = 0.295, p = 0.008), math scores and self-efficacy (r = 0.386, p < 0.001), as well as alpha power and self-efficacy (r = 0.229, p = 0.041).

Fig. 4. Relationship dynamics between mathematical performance, alpha power, and self-efficacy before and after BCI intervention.

This multi-panel figure presents scatter plots illustrating the correlations between mathematical performance, alpha power, and self-efficacy measures at pre-test (top row) and post-test (bottom row). Each plot includes individual data points, a linear regression line, and confidence intervals. The correlations and their statistical significance are reported for each relationship: (a) Pre-test math scores vs. pre-test self-efficacy: no significant correlation (r = 0.012, p = 0.913); (b) Post-test math scores vs. post-test self-efficacy: Significant positive correlation (r = 0.386, p < 0.001); (c) Pre-test math scores vs. pre-test alpha power: no significant correlation (r = 0.173, p = 0.125); (d) Post-test math scores vs. post-test alpha power: Significant positive correlation (r = 0.295, p = 0.008); (e) Pre-test self-efficacy vs. pre-test alpha power: No significant correlation (r = −0.004, p = 0.972); (f) Post-test self-efficacy vs. post-test alpha power: Significant positive correlation (r = 0.229, p = 0.041); The contrast between pre-test and post-test results suggests that the BCI intervention may have facilitated the integration of cognitive (math performance), affective (self-efficacy), and neural (alpha power) factors, as evidenced by the emergence of significant positive correlations in all three relationships after the intervention.

The random forest regression model was trained using 51 samples, validated using 13 samples, and tested on 16 samples (Fig. 5). The model achieved a validation MSE of 0.584 and a test MSE of 0.671. The model used 14 trees and considered one feature per split. The out-of-bag (OOB) error was 0.940.

Fig. 5. Comparison of predicted and observed mathematical performance scores using Random Forest Regression.

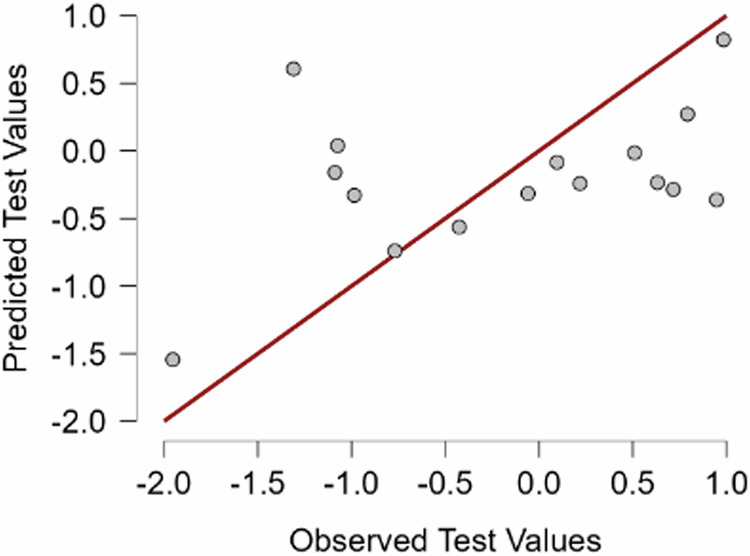
The scatter plot displays the relationship between predicted and observed mathematical performance scores derived from a Random Forest Regression model. The x-axis represents the observed test values, while the y-axis shows the predicted test values. Each gray dot represents an individual data point, corresponding to a participant’s actual score and the model’s prediction for that score. The red diagonal line indicates perfect prediction, where predicted values would exactly match observed values. The proximity of the data points to this line provides a visual indication of the model’s predictive accuracy. Points falling close to the line suggest accurate predictions, while those farther away represent larger discrepancies between predicted and actual scores. This visualization allows for an assessment of the Random Forest model’s performance in predicting mathematical achievement based on the study’s variables, offering insights into the potential effectiveness of using machine learning techniques to forecast educational outcomes in the context of BCI-assisted learning.

The model achieved an MSE of 0.671, a root mean squared error (RMSE) of 0.819, a mean absolute error (MAE) of 0.654, a mean absolute percentage error (MAPE) of 118.25%, and a correlation coefficient (R) of 0.187.

The feature importance analysis revealed that pre-test mathematical performance had the highest mean decrease in accuracy (0.226) and total increase in node purity (11.591), followed by pre-test self-efficacy (0.112 and 6.601, respectively).

Discussion

The present study investigated the effectiveness of a low-cost single-channel BCI system in enhancing mathematical learning outcomes by providing neurofeedback based on alpha oscillations recorded from the prefrontal cortex. Our results showed significant interaction effects between Measure (Pre-test & Post-test) and Group (BCI & Sham) on mathematical performance, self-efficacy, and alpha power. While there were no differences between the BCI and sham feedback groups at pre-test, the BCI group demonstrated significant improvements in all three outcomes at post-test compared to the sham feedback group. These findings support our hypotheses that alpha neurofeedback can improve attentional control, enhance working memory capacity, and reduce math anxiety, leading to better learning outcomes.

The higher alpha power observed in the prefrontal cortex of the BCI group suggests that our neurofeedback training specifically targeted the brain regions involved in cognitive control and emotional regulation. By enhancing alpha oscillations in the prefrontal cortex, our BCI system may have facilitated the recruitment of cognitive control mechanisms and the downregulation of negative emotions, leading to improved mathematical performance and reduced math anxiety. These findings are consistent with previous studies demonstrating the modulation of neural oscillations during learning interventions. For instance, Pi found that higher theta and alpha power were associated with more effective learning strategies, such as self-explanation and teaching others²⁸. The consistency between our results and prior research supports the role of alpha oscillations in enhancing cognitive functions and learning outcomes, providing further evidence for the potential of BCI neurofeedback as an educational intervention. When researchers tested the effectiveness of three learning strategies (self-interpretation, learning by teaching, and passive viewing), higher EEG θ and αpower was used as one of the criteria for more effective strategies.

The finding that the BCI group had significantly higher self-efficacy than the sham feedback group highlights the importance of considering affective factors in mathematical learning. By providing real-time feedback on their brain activity and teaching them to modulate it through mental strategies, our BCI system may have increased participants’ sense of agency and control over their learning process, leading to higher self-efficacy and motivation.

The significant interaction effects between Measure and Group on mathematical performance, self-efficacy, and alpha power, along with the predictive power of the random forest regression model, highlight the importance of considering individual differences in cognitive and affective factors when designing personalized learning interventions. These findings have important implications for the development of accessible and scalable BCI technologies that can be integrated with online learning platforms to support students’ academic success and well-being in STEM fields.

The additional behavior-brain correlation analyses provide valuable insights into the interplay between cognitive, affective, and neural factors in mathematical learning and the potential mechanisms underlying the effectiveness of neurofeedback training. The significant positive correlations observed at post-test suggest that the neurofeedback training may have facilitated the interaction and integration of mathematical ability, alpha wave levels, and self-efficacy. The positive correlation between math scores and alpha power supports the role of alpha waves in cognitive functions such as attention and working memory, while the correlation between math scores and self-efficacy highlights the importance of self-efficacy in learning outcomes. The correlation between alpha power and self-efficacy suggests that the effects of neurofeedback training may extend beyond the cognitive domain and positively influence emotional regulation and self-perception.

One of the main strengths of our study is the use of a low-cost and easy-to-use BCI system that can be readily integrated with online learning platforms. By employing a single-channel EEG headset with a dry electrode, our system offers a highly accessible and scalable solution for large-scale implementation in educational settings. This is particularly relevant given the growing demand for personalized learning interventions and the increasing adoption of online and remote learning formats^29,30. Our findings demonstrate the potential of BCI technology in enhancing mathematical learning outcomes in an ecologically valid and cost-effective manner, paving the way for its widespread application in real-world educational contexts.

Comparing our findings with other neurofeedback studies employing various imaging modalities, such as fMRI³¹ and MEG³², reveals the unique advantages of our low-cost, portable EEG-based neurofeedback system. While fMRI and MEG-based neurofeedback provides high spatial resolution and can target specific brain regions, these methods are expensive, time-consuming, and require specialized facilities, limiting their accessibility and scalability. In contrast, our single-channel, wireless EEG system offers high ecological validity, as it can be easily implemented in classrooms and other real-world settings. The portable and cost-effective nature of our approach makes it particularly promising for widespread applications in education and future large-scale studies investigating the effectiveness of neurofeedback interventions in authentic learning environments.

However, our study also has some limitations that should be addressed in future research. First, while we tested our BCI system on university students learning algebra concepts using an online platform, future studies should investigate its effectiveness in other mathematical domains, age groups, and learning environments. Second, long-term follow-up studies with larger sample sizes are needed to determine the sustainability and generalizability of the neurofeedback training effects. Third, future research should explore the use of more comprehensive cognitive, affective, and demographic variables to develop predictive models of mathematical learning outcomes. We acknowledge that individual differences in cognitive abilities, prior knowledge, and learning styles may have influenced the effectiveness of the neurofeedback training. Future research could employ mixed linear effect models to better account for these individuals confounds and provide a more nuanced understanding of the factors contributing to the success of BCI-based interventions in mathematical learning.

Despite these limitations, our study makes a significant contribution to the field of mathematical learning and BCI neurofeedback by demonstrating the potential of a low-cost and accessible BCI system in enhancing cognitive and affective aspects of learning. Our findings have important implications for the development of personalized learning interventions that adapt to students’ individual needs and preferences, particularly in the context of online and remote learning. By integrating BCI technology with online learning platforms and using machine learning techniques to predict learning outcomes, our approach can facilitate the delivery of targeted and effective neurofeedback training to large numbers of students, promoting their academic success and well-being in STEM fields.

In conclusion, our study demonstrates the effectiveness of a low-cost single-channel BCI system in enhancing mathematical learning outcomes by modulating alpha oscillations in the prefrontal cortex. The significant interaction effects between Measure and Group on mathematical performance, self-efficacy, and alpha power, along with the predictive power of the random forest regression model, highlight the importance of considering individual differences in cognitive and affective factors when designing personalized learning interventions. These findings have important implications for the development of accessible and scalable BCI technologies that can be integrated with online learning platforms to support students’ academic success and well-being in STEM fields. Future research should investigate the long-term effects and underlying mechanisms of alpha neurofeedback training in diverse educational contexts, as well as explore the use of advanced machine learning techniques for optimizing learning outcomes based on individual characteristics. Future investigations could also consider the potential of modulating other oscillations through BCI neurofeedback and their interactions with alpha rhythms in the context of varying learning.

Methods

Participants

Eighty university students (40 males, 40 females) with a mean age of 20.5 years (SD = 1.2) participated in the study. The participants were first-year undergraduate students majoring in science-related disciplines. They were randomly assigned to either the BCI group (n = 40) or the control group (n = 40). The participants were recruited from Shanxi Normal University. All participants were right-handed and had normal or corrected-to-normal vision. The study was approved by the Ethics Committee of Shanxi Normal University, and all participants provided written informed consent prior to the experiment.

Materials

Mathematics Performance Questionnaire used in this study was designed to assess participants’ mathematical problem-solving abilities in the domain of algebra. The tasks consisted of 20 algebra problems that required participants to apply various algebraic concepts and techniques, such as simplifying expressions, solving equations, and graphing functions. The problems were presented in a multiple-choice format, with four possible answers for each question. Participants were instructed to select the correct answer within a time limit of 2 minutes per problem. The difficulty level of the problems was adjusted based on participants’ performance in the pre-test, ensuring an appropriate level of challenge throughout the learning phase.

The 20 algebra problems were selected from a pool of problems developed by two experienced mathematics teachers and validated through a pilot study with 30 university students. The problems covered a range of difficulty levels and were designed to assess participants’ understanding of key algebra concepts, such as linear equations, quadratic functions, and systems of equations. A sample problem (Eq. (1)) is provided below:

$$\genfrac{}{}{0ex}{}{″}{}Solveforx:3\left(x+2\right)-2\left(x-1\right)=5x-3\genfrac{}{}{0ex}{}{″}{}$$ 1

The complete list of algebra problems can be found in the supplementary materials (Supplementary Note 1).

The Self-Efficacy Questionnaire was adapted from previous research³³. The Self-Efficacy Questionnaire used in this study was adapted from the General Self-Efficacy Scale (GSE) developed by Schwarzer and Jerusalem. The GSE is a 10-item scale designed to assess a general sense of perceived self-efficacy, with the aim of predicting coping with daily hassles and adaptation after experiencing stressful life events.

Procedure

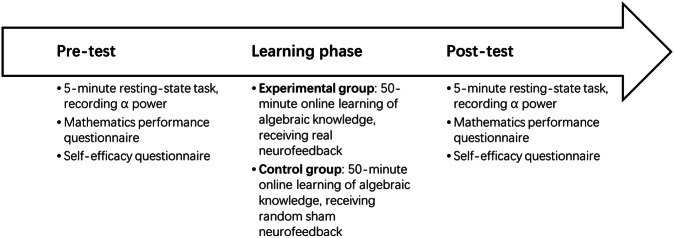
The study consisted of three phases: pre-test, learning intervention (Learning phase), and post-test. Figure 6 illustrates the schematic of the experimental procedure.

Fig. 6. Experimental design for assessing the impact of BCI-assisted learning on mathematics performance and self-efficacy.

The experiment followed a three-phase structure: pre-test, learning intervention (Learning phase), and post-test. In the pre-test phase, all participants completed initial assessments of their mathematics performance and self-efficacy. The learning phase involved random assignment to either a BCI group receiving real-time neurofeedback or a control group receiving sham feedback during a 50-minute online algebra session. The post-test phase repeated the initial assessments to measure changes resulting from the intervention.

Prior to the experimental tests, participants’ learning ability was assessed using the Mathematics Performance Questionnaire, while the Self-Efficacy Questionnaire measured participants’ confidence in their ability to learn and solve mathematical problems. The pre-test scores on these questionnaires were used to evaluate participants’ baseline mathematical abilities and self-beliefs.

In the pre-test phase, all participants completed a demographic questionnaire, the Mathematics Performance Questionnaire, and the Self-Efficacy Questionnaire. The FP1 electrode was positioned according to the international 10-20 system. To locate the FP1 position, we first identified the nasion and inion points and measured 10% of the distance between these two points. From the nasion, we measured this 10% distance upwards and marked the position.

The neurofeedback training consisted of a 5-minute baseline recording, followed by 6 training blocks of 5 minutes each, with 1-minute breaks between blocks. During the training blocks, participants were instructed to focus on the visual feedback provided by the BCI system, which reflected their real-time alpha power. The feedback was presented in the form of a bar on the screen, with the bar’s size and color changing based on the participant’s alpha power. Participants were taught mental strategies to increase their alpha power, such as deep breathing, positive imagery, and focused attention.

In the intervention phase, the BCI group received real-time neurofeedback while learning algebra concepts on the online learning platform (Khan Academy) for 50 min in a quiet room. The neurofeedback software provided visual and auditory feedback to the participants, indicating the level of their alpha power. The control group received sham feedback that was not based on their brain activity.

In the post-test phase, all participants completed the same measures as in the pre-test phase, except the neurofeedback training.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. The study was approved by the Ethics Committee of Shanxi Normal University (Approval Number: 2024-0304).

EEG data acquisition and preprocessing

The BCI system consisted of a single-channel Mind Wave headset (NeuroSky, Inc.) with a dry electrode placed on the Fp1 position. The headset sampled brain activity at a rate of 128 Hz. The neurofeedback software was developed using the MATLAB software platform.

The EEG data was analyzed using a sliding window approach to provide real-time neurofeedback during the mathematical learning task. The continuous EEG data was segmented into 5-second windows with a 50% overlap. For each window, the following steps were performed: (1) Preprocessing: The EEG data was filtered using a 4th order Butterworth bandpass filter (0.5–30 Hz) to remove low-frequency drift and high-frequency noise. Extreme values (outliers with amplitudes exceeding ±100 μV) were identified and replaced with the median value within each window. (2) Power Spectral Density (PSD) Estimation: The PSD of each window was computed using Welch’s method with a Hamming window and a 50% overlap. The PSD provided a measure of the power distribution across different frequency bands. (3) Alpha Power Calculation: The alpha power was obtained by averaging the PSD values within the alpha frequency range (8–12 Hz).

The calculated alpha power for each 5-second window was used to provide real-time neurofeedback to the participants. The neurofeedback was presented visually using a bar graph, where the height of the bar represented the relative change in alpha power compared to a baseline value. The color of the bar was modulated based on the percent change in alpha power, with red indicating an increase and green indicating a decrease. The baseline value was updated every minute to account for temporal changes in alpha power throughout the learning session (Supplementary Fig. 1).

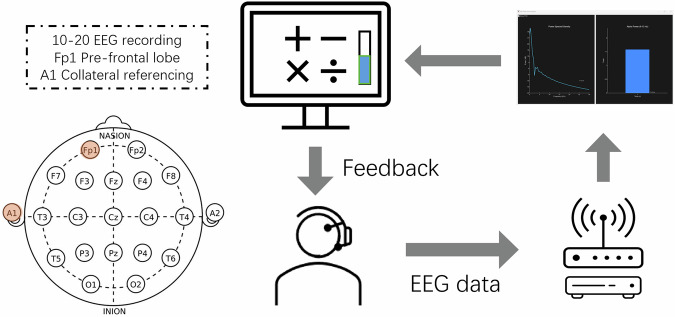
By continuously updating the alpha power bar graph every 5 s, participants received real-time feedback on their brain activity during the mathematical learning task. This neurofeedback aimed to enhance participants’ awareness of their cognitive states and potentially facilitate the learning process. Figure 7 shows a schematic diagram of the BCI system used in the study.

Fig. 7. EEG-based BCI system configuration for neurofeedback during mathematical learning.

The BCI system employed a single-channel EEG setup recording from the Fp1 position (prefrontal lobe) with A1 as the reference electrode, as illustrated in the 10-20 EEG electrode placement diagram. Real-time processing of the EEG signal focused on extracting alpha power, which was then used to generate visual neurofeedback displayed to participants during the algebra learning session. The feedback consisted of two graphs: a time-series plot of alpha power and a bar graph showing current alpha levels, enabling participants to monitor and potentially modulate their brain activity while engaged in mathematical problem-solving.

Relative alpha power in resting state for pre- and post-test was calculated by dividing the absolute power in the alpha frequency range (8-12 Hz) by the baseline. This approach helps to minimize inter-individual differences in EEG signal amplitude, better reflects the contribution of alpha oscillations to the overall EEG activity, and controls for baseline differences among participants³⁴.

Data analysis

The Repeated Measures ANOVAs were used to examine the effects of Measure (Pre-test & Post-test) and Group (BCI & Sham) on their mathematical performance, self-efficacy, and alpha power.

Additionally, a random forest regression model was used to predict post-test mathematical performance based on pre-test scores and self-efficacy. The dataset was split into a training set (n = 51), a validation set (n = 13), and a test set (n = 16). The model was trained using the training set, and hyperparameters were tuned using the validation set. The final model performance was evaluated on the test set. The random forest regression model was implemented using the scikit-learn library in Python. The model was trained using 100 trees and a maximum depth of 5. The mean squared error (MSE) was used as the performance metric for model evaluation.

A Pearson correlation analysis was conducted to examine the relationship between participants’ mathematical performance and alpha power changes from pre-test to post-test.

Author contributions

H.Z. and L.X. conceptualized and designed the study, supervised data collection, and wrote the original draft of the manuscript. Y.J. contributed to the study design, collected the data, and assisted with data analysis. X.S. contributed to the interpretation of the results and critically reviewed and edited the manuscript. All authors have read and approved the final version of the manuscript.

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Code availability

The MATLAB scripts for real-time EEG analysis, focusing on Alpha power, and a sham stimuli generator for control experiments are available on the Open Science Framework (OSF) platform at https://osf.io/pt75k.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41539-024-00277-z.