Abstract
Organic molecular crystals constitute a class of materials of critical importance in numerous industries. Despite the ubiquity of these systems, our ability to predict molecular crystal structures starting only from a two-dimensional diagram of the constituent compound(s) remains a significant challenge. Most structure-prediction protocols require a customized interatomic interaction model on which the quality of the results can depend sensitively. To overcome this problem, we introduce a new topological approach to molecular crystal structure prediction. The approach posits that in a stable structure, molecules are oriented such that principal axes and normal ring plane vectors are aligned with specific crystallographic directions and that heavy atoms occupy positions that correspond to minima of a set of geometric order parameters. By minimizing an objective function that encodes these orientations and atomic positions, and filtering based on the vdW free volume and intermolecular close contact distributions derived from the Cambridge Structural Database, stable structures and polymorphs for a given crystal can be predicted entirely mathematically without reliance on an interaction model.
Subject terms: Computational methods, Applied mathematics, Chemistry
Reliable prediction of the organic molecular crystal structures is critical across numerous industries yet remains a significant challenge. Here, the authors develop a mathematical workflow based on topological concepts that reduces solution time to mere hours.
Introduction
Organic molecular crystal structure prediction (CSP) is an active field of critical importance in numerous industries that include pharmaceuticals1, contact insecticides2–4 and other agrochemicals, semiconductors5,6, and high-energy materials7,8. Experimental determination of molecular crystal structures can be both costly and time-consuming, especially if a compound can potentially crystallize into multiple stable or metastable polymorphs. For this reason, CSP protocols based entirely on computational, theoretical, or mathematical approaches are poised to impact this field in a significant way, a fact that has been highlighted in the range and performance of various methods in the six blind structure prediction tests carried out by the Cambridge Crystal Data Centre (CCDC)9–14. These reports also make clear that the CSP problem remains a significant challenge.
Early efforts to derive molecular crystal structures and understand packing motifs based solely on mathematical principles date back to the 1950s15. Roughly a decade later, J. J. Burckhardt suggested that possible arrangements of points in crystallographic cells should be derivable using mathematical reasoning alone16. Burckhardt’s vision has never been fully realized; in fact, most current CSP approaches require a model of the interatomic interactions. This model must be of sufficient accuracy to distinguish and correctly rank structures whose lattice energies might differ by less than ~4 kJ/mol17. Recent studies have revealed that in more than 50% of structures in the CCDC, energy differences between pairs of polymorphs are smaller than ~2 kJ/mol, while only about 5% have energy differences larger than ~7 kJ/mol18. Universal force fields are generally unable to resolve such small differences, rendering them unreliable for computational CSP. Consequently, it becomes necessary to generate a system-specific model of high accuracy for each structure-prediction problem, which is often the most time-consuming step in a CSP workflow, consuming the majority of the total time to solution14. Machine learning approaches are beginning to impact the CSP problem19, but precision remains elusive in these schemes. Machine learning/data-based topological structure generators have proven successful to generate reasonable molecular structures but they still rely on costly density functional theory (DFT) methods to generate optimized structures20. A mathematically driven CSP protocol enabling prediction of molecular structures based on efficient procedures other than direct evaluation of interatomic interactions or construction of learning models would remove the necessity of computing lattice energies or performing model training and, consequently, simplify and accelerate the CSP process while also eliminating model bias and bringing a universality to and new modalities for understanding molecular CSP. In previous work21, we showed that a combined mathematical/energy-driven approach could be used to map the locations of water molecules in crystal hydrates given a dry framework.
Simply stated, the CSP problem amounts to a determination of the cell geometry, the number of asymmetric units (Z), the number of components in the asymmetric unit , and the coordinates of all atoms in the unit cell. For a given monomer conformation, determining atomic coordinates is equivalent to finding the molecular center-of-mass location, the internal conformation, and the orientation of each molecule. Alternatively, one can specify the crystallographic space group and the location, conformation, and orientation of one molecule, the “reference” molecule in the unit cell. For a fixed molecular conformation, the CSP problem amounts to specifying 13 total parameters, which include the cell lengths (a, b, c) and angles (α, β, γ), the center-of-mass position of the reference molecule (X, Y, Z), its orientation, expressed as a unit vector along an orientation axis, a single rotation angle (ω) about this axis, and one of the 230 space groups. In addition, if the molecule has ν internal conformational degrees of freedom, then the total number of parameters to determine is 13 + ν.
In this work, we take a major step forward by showing that a purely mathematical approach is possible for bottom-up CSP. By analyzing geometric and physical descriptors, we derive governing principles for the arrangement of molecules in a crystal lattice. While we focus on and crystals in this article, the principles introduced also apply to structures. These principles allow for the prediction of stable structures and polymorphs without relying on interatomic interaction models. We validate the approach through tests on several well-known molecular crystals, demonstrating its efficiency and broad applicability in CSP.
Results
Topological CSP principles
The governing principles of our topological approach, which we have named CrystalMath, were derived from a careful examination of a database of more than 260,000 organic molecular crystal structures in the Cambridge Structural Database (CSD)22 containing C, H, N, O, S, F, Cl, Br and I atoms. The fact that a set of such general principles can be derived gives us a new framework for understanding how molecules pack into three-dimensional crystal structures. The first principle of CrystalMath, obtained from our analysis, states that the principal axes of molecular inertial tensors about mass centers are orthogonal to crystallographic (Miller) planes determined by searching over neighboring cells to the unit cell. Recall that the 3 × 3 inertial tensor of a reference molecule having M atoms with atomic coordinates , where λ = 1, …, M, and the (1) superscript indicates the reference molecule in the unit cell, is
| 1 |
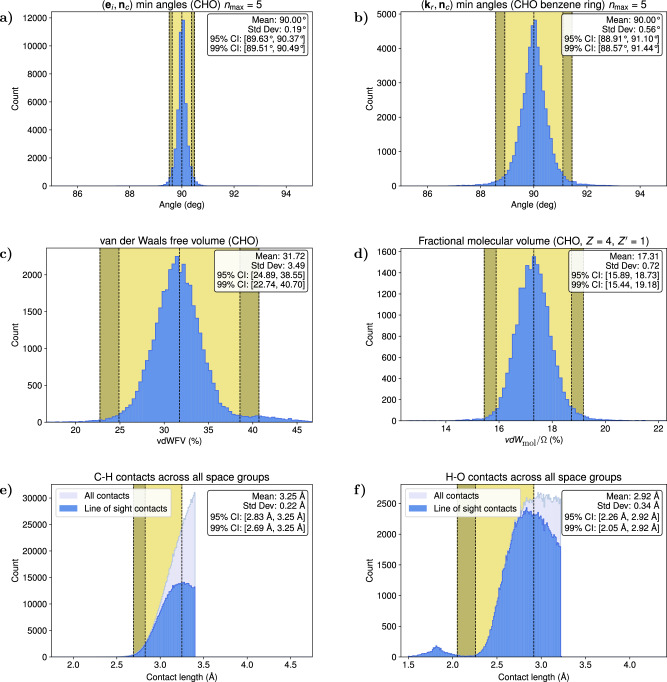
The eigenvectors of Iij are denoted ei. Crystallographic planes are represented here by an integer vector nc = (nu, nv, nw), where , with nunvnw = 0 and at least one of the components equal to . Figure 1(a) shows the distribution of angles between the principal axes and crystallographic planes for from nearly 37,000 structures composed of C, H, and O atoms in the database (distributions for additional values are provided in the Supporting Information (SI)). If are vectors in fractional coordinates that define a crystallographic plane orthogonal to the eigenvector ei, then the orthogonality conditions are and , where H is the (upper triangular) cell matrix
| 2 |
with Ω being the volume of the unit cell. In addition, the three eigenvectors must be mutually orthogonal, ei ⋅ ej = 0. These nine conditions are sufficient to determine a unit cell geometry and orientation of the reference molecule for a given nc. The number of possible crystallographic directions is quite large, e.g., if , it is around 1.6 billion from which pools of structures could be randomly drawn. As we expect considerable redundancy among this large set of possible structures, even relatively small random pools should contain realizable structures, which would be found repeatedly across multiple random pools. Alternatively, one could generate all 1.6 billion structures once and retain them in a database for all subsequent applications.
Fig. 1. Statistical distributions for all structures in the Cambridge Structural Database (CSD) composed of C, H and O atoms.
a Distributions of the minimum angle formed by the vectors ei and nc for . The 95% and 99% confidence intervals are within 3 degrees, suggesting a restriction in the orientation of the inertial eigenvectors related to the vector set nc. b Distributions of the minimum angle formed by the vectors kr, defined to be perpendicular to the average plane of the benzene rings, and nc for . c The van der Waals (vdW) free volume as a fraction of the unit cell volume. d The molecular van der Waals volume (vdW)mol as a fraction of the unit cell volume Ω for crystals with four molecules in the unit cell (Z = 4). e, f Distributions of the lengths of the C–H and O–H close contacts for contact length l ≤ (sum of vdW radii + 0.5)Å. The close contacts are characterized as line-of-sight contacts, for which the position vector connecting the two atoms does not intersect the vdW sphere of a third atom. The peak of the distribution for the line-of-sight contacts provide the optimal separation between the two atoms forming the contact. The distribution for the C–H contacts is characteristic of all contacts involving at least one C atom while the O–H distribution is characteristic of the contacts between a hydrogen and a highly electronegative atom. The presence of intermolecular hydrogen bonding creates a secondary peak characteristic of the optimal hydrogen bond length affecting the connectivity of neighboring molecules in the unit cell. Source data are provided as a Source Data file.
As a corollary to this first principle, a second principle of CrystalMath states that normal vectors kr, r = 1, …, nr to nr chemically rigid subgraphs in a molecular graph, such as rings, fused rings, and so forth, are orthogonal to crystallographic planes, i.e., and . Figure 1(b) shows the distribution of angles between kr and the crystallographic directions for the 37,000 structures described above.
For a given crystal system, the aforementioned orthogonality equations can be solved to provide the 6 cell parameters (a, b, c, α, β, γ) as well as the molecular orientation in terms of a rotation axis and a rotation angle ω. As shown in the SI, the system of equations allows one of the parameters to be set a priori, reducing the rank of the system to 5. For example, we may choose the length a of cell vector a to be 1.0 (in arbitrarily chosen units). Given this choice, in order to specify an explicit form of the orthogonality equations, we introduce the column vectors
| 3 |
where For orthorhombic (α = β = γ = 90°) and for monoclinic (β ≠ 90°) unit cells, the orthogonality equations result in the systems of matrix-vector equations
| 4 |
where
| 5 |
For triclinic cells, a solution is generated by proposing two different eigenvector sets for each pair of fragments in the reference molecule, which yields the system of equations
| 6 |
where
| 7 |
where σi, τij refers to the set w and to the set and
| 8 |
For each cell geometry (a, b, c, α, β, γ), we generate an expression for the eigenvectors w in the physical coordinate system, by applying the transformation ei = ciTTwi, where ci a normalization constant and T = H−1. The rotation axis is then and the rotation angle for the molecule is
| 9 |
A pool of structures resulting from the application of principles 1 and 2 subject to the aforementioned orthogonality conditions is obtained using Eqs. (4), (6), (9) for the three different types of crystal systems.
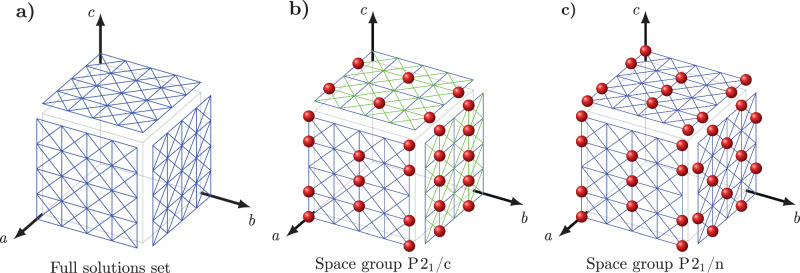
The third principle of CrystalMath provides the most restrictive constraint on candidate structures. It states that certain atomic positions in a stable molecular crystal lie at the zeroes of a set of three-dimensional shape functions or order parameters. These functions are defined in terms of the generators Gk of a crystallographic space group. Let , k = 1, …, Z be the symmetry related fractional coordinates of atom λ in the unit cell, i.e., . Denoting the shape functions as Ξκ, where κ is a multicomponent index, the third rule of CrystalMath is expressed as
| 10 |
where is the average of the Z positions . Eq. (10) can be re-expressed in terms of physical coordinates and cell parameters using the transformation . The choice of the shape functions for Eq. (10) is critical. Although various choices might be suitable, we have identified the so-called Zernike order parameters (ZOPs)23,24, which are constructed from a set of basis functions , for their predictive capability. The shape functions constructed from the ZOPs are
| 11 |
where Yℓm(θ, ϕ) is a spherical harmonic, and the radial polynomial, Rnℓ(r), is given by
| 12 |
and is particular to the ZOPs (additional details of ZOPs are provided in the SI). The full set of solutions of Eq. (10) particularized to the ZOPs are shown in Fig. 2 for the P21/c and P21/n space groups. Mathematical details of the solution of Eq. (10) in the P21/c space are shown in Section 1 of the SI. In the CrystalMath protocol, among the solutions of Eq. (10), those of greatest utility are planes in crystallographic coordinates, which, in the most common space groups, take the form A ⋅ s = kZZP/4, where the components of the vector A are −1, 0, or 1, with A ≠ 0, AuAvAw = 0, s = (u, v, w) and . These conditions generate nine unique vectors A. If these planar solutions for s are denoted si, for a given vector A, then the placement of atoms on these planes also means that separations between corresponding pairs of atoms in the reference molecule along directions perpendicular to these planes must equal kZZP/(4|δsi,i+1|), where |δsi,i+1| is the distance between neighboring planar solutions of Eq. (10) for the ZOPs. For the most common space groups, .
Fig. 2. Illustrations of the solutions of equation (10) for the Zernike order parameters.
a The full set of solutions of equation for select space groups. The figure shows the intersections between the set of planes forming the solutions to Eq. (10) for the ZOPs and the faces of the unit cell. In general, the solutions are either planes parallel to the faces of the unit cell or parallel to the diagonals of the unit cell. b, c Projections of the high density regions (red spheres) on the faces of the unit cell in fractional coordinates as generated from the analysis of the molecular positions of the organic molecular crystal structures in the P21/c and P21/n space groups with one molecule in the asymmetric unit (). The green lines correspond to solutions missing from the specific space group. For all space groups, the high-density regions are found on a zero Zernike position (ZZP) or on the intersection between two or three ZZPs. There are clear differences in the positions of the high-density regions among the different space groups, indicating that the geometry of the unit cell and, more specifically, the symmetry in each space group is correlated with the arrangements of the molecules.
The CrystalMath protocol
A CrystalMath CSP prediction consists of a series of steps that can be executed in just a few hours on a standard desktop or laptop computer: (1) Following principle 1, a random sampling of possible crystallographic directions is used to propose sets of principal axes of the inertial tensors of each rigid fragment in a molecule. (2) For each set of axes wi, a possible cell geometry and molecular orientation are generated by solving Eqs. (4), (6) and (9). Triclinic cells are generated using pairs of sets of axes . This process generates an initial pool of cell geometries and orientations for the fragments of the reference molecule. It is worth mentioning that, up to this stage, the proposed solutions do not depend on the precise chemical structure of the molecule and can be used for any compound. (3) Flexible molecules comprised of Nf fragments are generated by combining Nf orientations corresponding to similar cell geometries that are averaged. The internal fragment geometries are obtained by a database generated by averaging geometries of rigid fragments in the CSD database. Possible conformations are generated by joining the fragments at their common atoms, and then filtered for unnatural intramolecular close contacts. (4) Base structures are generated by placing the molecule in a specific conformation at the origin of a generic P1 unit cell, which is then scaled to the desired volume via
| 13 |
where Vmol is the vdW volume of the asymmetric unit, f(Vmol/Ω) is the distribution of the ratio Vmol/Ω in the database, shown in Fig. 1(d), and Vs = [0.95, 1, 1.05] is a volume coefficient to allow 5% deviations from the volume corresponding to the peak of the distribution to account for thermal effects. Z is the number of molecules in the unit cell for a target space group. (5) Each base structure is transformed into a set of complete structures for each target space group by optimizing the position of the reference molecule to achieve maximal adherence to the zeroes of the ZOPs (ZZPs) using the objective functions
| 14 |
and
| 15 |
where , M\{H} is the number of non-hydrogen atoms in the reference molecule and χλ the Mulliken electronegativity of atom λ. In eq. (14), is the vector connecting any two non-hydrogen atoms. The two objective functions have the respective effect of translating the molecule in the unit cell so that the quantity is as close as possible to kZZP/4δsi,i+1 for an optimal choice of atoms for each vector Aκ and aligning the non-hydrogen atoms in the molecule as closely as possible to the ZZPs described by an optimal choice of vector A for each atom. In carrying out this step, preference is given to atoms having the highest electropositivity or electronegativity, through χλ. For , the aforementioned process generates partial structures with one molecule in the asymmetric unit (see next paragraph). Structures with high combined cost value and/or unnatural intermolecular close contacts are discarded.
An intermolecular close contact is characterized as unnatural if the distance between a pair of atoms (X1, X2) satisfies the condition dc(X1, X2) < dc,0(X1, X2) − dtol, where dc,0(X1, X2) is the peak of the distribution (Fig. 1(e, f)) and dtol is a tolerance, which in this stage, is set equal to 2 ⋅ dCI where dCI ≃ 0.5 Å is the 95% confidence interval of the optimal contact distributions for all vdW pairs in the CSD database. This filter allows the formation of strong close contacts that can be subsequently optimized but prevents the formation of unreasonably strong close contacts. (6) Complete structures are generated by combining partial structures with similar or identical geometries in the same space group. The molecules in the partial structures are combined to generate the asymmetric unit while the cell geometry is averaged. (7) From the remaining pool, the structures are optimized such that close contacts adhere to optimal values obtained from an analysis of the CSD using the objective function
| 16 |
where the “ICC" subscript stands for intermolecular close contacts and Ncc is the number of close contacts associated with the reference molecule. This step can be regarded as a simple ersatz for energy minimization. A more precise filter for the close contacts is applied by checking the distribution of the contacts in the cell. The contact lengths in the database follow a normal distribution with σ ≃ 0.25 Å. Since the volume selection of the unit cell is based on the vdW volume of the molecule according to eq. (13), realistic low volume structures generated by the algorithm may exhibit lower contact lengths. To allow the generation of such structures, we found that the distribution needs to be slightly wider, i.e.,σ = 0.3 Å. Such a distribution requires that 68% and 95% of the contacts have lengths within σ and 2σ from the peak of the optimal contact distributions. For the structures in the final pool, a final filter is applied to discard structures with . Depending on the number of structures in the final pool, this limit can be increased or decreased to add or remove structures from the pool of accepted structures. The resulting structures are clustered based on their packing similarity using the COMPACK algorithm25,26. As the vdWFV is an excellent measure of effective crystal packing, for each cluster, the structure with the lowest vdWFV is selected. The clustered structures are ranked based on their vdWFV and the function CICC. Mathematical details of the protocol are provided in Section 2 of the SI. In the examples to be presented next, when structures have multiple polymorphs, the topological ranking is evaluated against an energy ranking in order to benchmark the topological ranking procedure. Energies of structures are calculated using the Filippini-Gavezzotti intermolecular potential implemented in the CSD Python API package.
Rigid CSP of aspirin polymorphs
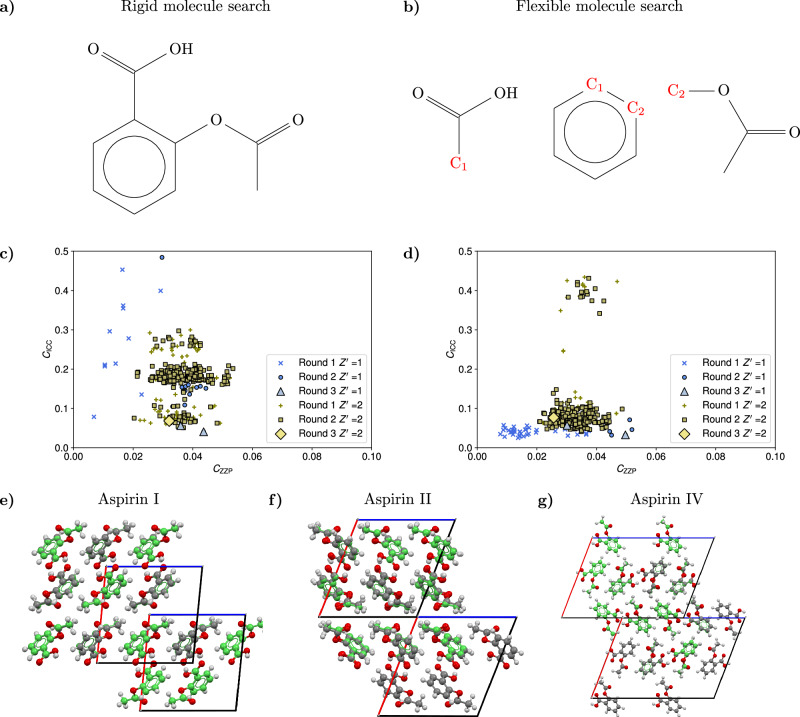
As a first test of the CrystalMath protocol, we predict the most stable polymorphs of aspirin (C9H8O4) by conducting a rigid-molecule search. We begin the search by sampling a set of 100,000 of principal inertial axes frames for the molecule, ensuring coverage of the distribution and generating the same number of scaled cell geometries and orientations in the triclinic, monoclinic, and orthorhombic systems. The cell geometries are clustered and scaled to the desired volumes for Z ∈ [1, 2, 4, 8] corresponding to the 20 most common space groups and . The aspirin molecule is placed at the origin of the generated unit cells. For the purposes of this simple search, the geometry of the molecule is determined from the existing known aspirin structures. An initial check for unnatural close contacts between the reference molecule and its periodic images discards the majority of structures from the pool, generating in total ~79,000 base structures. Complete structures are generated by placing the conformers in the selected cell geometries and minimizing the objective functions , to find optimal positions for the molecules. The process generates a total of 970 complete and ~26,000 partial structures in the 20 most common space groups. Complete structures are generated by combining pairs of partial structures (see previous paragraph) having almost identical unit cell geometries in the same space group and filtering them for unnatural close contacts. The process generates ~4700 complete structures. The total set of structures is optimized and filtered for close contacts using the distribution method with σ = 0.3 Å. After a final clustering and vdWFV filtering, two structures are found in the final pool, corresponding to the known experimental aspirin polymorphs I () and IV () with respective RMSD20 values equal to 0.122 Å for aspirin I and 0.281 Å for aspirin IV27,28. By expanding the maximum allowed vdWFV to , a third structure is added to the pool, corresponding to the experimental aspirin II polymorph with RMSD20 = 0.237 Å. A figure detailing the structure generation and filtering of the structures is shown in the SI Section 4. Low vdWFW structures that were discarded during the filtering process are provided as Supplementary Data. The landscape for the cost function CZZP against CICC is shown in Fig. 3(c). Additional landscapes for the cost functions against the vdWFV are provided in the SI. The total computation time was ~30 h on a midrange laptop. The vdWFVs of the predicted structures I, II, IV are, respectively, 27.37%, 32.32%, 28.36% and all in the P21/c space group. The vdWFV ranking for the predicted structures is consistent with the reported vdWFV of each of the experimental structures (vdWFVI < vdWFVIV < vdWFVII). The CICC ranking for the predicted structures is slightly different from the vdWFV ranking (CICC,I < CICC,II < CICC,IV). A lattice energy calculation with the CSD Python API package reveals that EI < EII < EIV, consistent with the contacts cost function ranking. As a further examination of the accuracy of the cost function ranking scheme, we performed additional single-point DFT PBE0+MBD energy calculations for the three structures in the final pool. The structure ranking is consistent for all the schemes, demonstrating the accuracy of the close-contact ranking scheme. Details for the energy and CICC rankings are provided in Table 1.
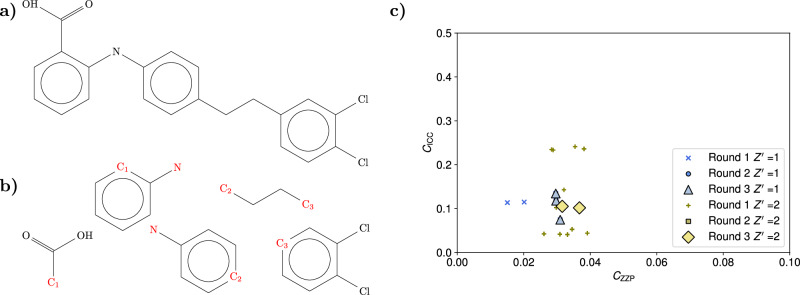
Fig. 3. Details of the crystal structure search for the aspirin molecule.
a Diagram of the complete aspirin molecule used in the rigid molecule search. b Diagram of the three rigid fragments used for the flexible molecule search of the aspirin structures. For triplets of similar unit cell geometries, the fragments are joined at the common C atoms C1, C2 (shown in red) to generate the possible conformations. c, d Scatter plots of the cost function CICC against the cost function CZZP for the three different rounds of filtering in the search for the aspirin structures. Round 1 includes all the acceptable structures with close adherence to the zero Zernike polynomial (ZZP) positions, round 2 includes structures optimized for close contacts, and round 3 contains the final accepted structures, subject to van der Waals free volume (vdWFV) and contact length constraints. High vdWFV structures were excluded from the plot. The differences in the landscapes are explained by the fact that for a given inertial eigenvector set, the orientation of the aspirin molecule in the rigid search is different from the orientation in the fragment based approach even if the conformations are similar. In addition, the rigid search conformation is not a perfect match for any flexible conformation used in the flexible search and, as a result, the structures with a rigid conformation exhibit a different adherence to the ZZPs and different contact distributions. e, f, g Overlays of the three predicted structures with the respective experimental aspirin structures, which are displayed in green. After the application of all the topological filters, only three structures are found for each search corresponding to the known aspirin I, aspirin II, and aspirin IV polymorphs, showing the agreement in the final predictions of the two searches. Source data are provided as a Source Data file.
Table 1.
Comparison of the experimental energy , the predicted energy Ecalc, the PBE0+MBD DFT relative energy ΔEDFT and the predicted cost function CICC rankings for the aspirin and target XXIII polymorphs identified in the searches
| Polymorph | Ecalc | ΔEDFT | vdWFVcalc | CICC | ||
|---|---|---|---|---|---|---|
| Aspirin rigid search | ||||||
| Aspirin I | –124.50 | 28.14 | –117.80 | 0.00 | 27.37 | 0.0901 |
| Aspirin II | –116.60 | 30.25 | –105.00 | 5.62 | 32.32 | 0.1167 |
| Aspirin IV | –109.90 | 30.08 | –73.00 | 19.69 | 28.36 | 0.1364 |
| Aspirin flexible search | ||||||
| Aspirin I | –124.50 | 28.14 | –116.80 | 0.00 | 26.78 | 0.0655 |
| Aspirin II | –116.60 | 30.25 | –109.10 | 3.75 | 33.19 | 0.1137 |
| Aspirin IV | –109.90 | 30.08 | –94.00 | 20.08 | 28.06 | 0.1535 |
| ROY flexible search | ||||||
| ON | –166.30 | 24.01 | –151.90 | 15.19 | 27.82 | 0.0491 |
| ON* | –157.22 | 24.01 | –130.40 | 15.56 | 33.76 | 0.0549 |
| ON* | –157.22 | 24.01 | –133.20 | 15.44 | 33.53 | 0.0497 |
| OP | –160.10 | 23.52 | –137.10 | 9.60 | 33.04 | 0.0478 |
| ORP | –154.70 | 30.73 | –148.40 | 0.00 | 28.24 | 0.0397 |
| PO13 | –164.50 | 28.20 | –152.10 | 22.12 | 28.43 | 0.0433 |
| PO13* | –160.60 | 28.20 | –138.40 | 22.24 | 28.98 | 0.0557 |
| R | –156.70 | 30.28 | –129.60 | 20.30 | 28.65 | 0.0884 |
| Y | –173.80 | 23.67 | –151.90 | 2.06 | 28.28 | 0.0476 |
| Y19 | –161.10 | 29.77 | –155.30 | 23.34 | 28.03 | 0.0503 |
| Y19* | –161.10 | 29.77 | –131.90 | 24.07 | 33.55 | 0.0617 |
| YN | –147.00 | 32.01 | –127.10 | 9.12 | 34.41 | 0.0398 |
| YT04 | –158.90 | 28.97 | –151.30 | 6.56 | 27.85 | 0.0417 |
| YT04* | –158.90 | 28.97 | –119.80 | 7.41 | 33.86 | 0.0638 |
| X1 | − | − | –132.80 | 4.01 | 34.44 | 0.0506 |
| X2 | − | − | –131.00 | 26.62 | 33.43 | 0.0543 |
| X3 | − | − | –128.00 | 3.37 | 34.07 | 0.0535 |
| X4 | − | − | –124.40 | 30.79 | 34.37 | 0.0420 |
| X5 | − | − | –113.90 | 20.06 | 34.50 | 0.0684 |
| Target XXIII flexible search | ||||||
| Polymorph I | –191.9 | 34.83 | –184.80 | 0.00 | 31.27 | 0.1179 |
| Polymorph II | –211.9 | 32.96 | –176.60 | 42.53 | 31.25 | 0.0745 |
| Polymorph III | –212.9 | 32.50 | –173.90 | 4.71 | 37.85 | 0.1051 |
| Polymorph IV | –201.0 | 35.50 | –176.60 | 10.23 | 37.80 | 0.1344 |
| Polymorph V | –197.9 | 34.58 | –187.90 | 102.91 | 31.46 | 0.1017 |
The experimental vs the predicted van der Waals free volumes (vdWFV) are also presented for reference.
Flexible CSP of aspirin polymorphs
We next demonstrate that CrystalMath can be applied to a flexible molecule using the fragment approach described earlier. As a first test case, we repeat the search for the three known aspirin polymorphs by treating the molecule as flexible. We consider three rigid fragments, one comprised of the atoms found in the hydroxyl group, on comprised of the atoms in the benzene ring, and one comprising of the remaining atoms, as shown in Fig. 3(b). The flexible search is performed by using the same initial pool of inertial eigenvector sets employed in the rigid search. After the clustering process following the generation of cell geometries and molecular orientations, we were able to identify ~18,000 groups of three or more similar unit cell geometries and different molecular orientations for the three fragments. We construct the aspirin conformers by assigning orientations from each group to the three molecular fragments and joining them at their common atom. A filter is applied to discard conformers with unphysical intramolecular close contacts. The process generates ~10,500 base structures. Complete structures are generated by placing the conformers in the selected cell geometries and continuing the protocol used for the rigid molecules. The optimization of the molecular positions generated 49 and 233 structures. The close contact optimization and filtering process discards the majority of structures such that only six and two structures pass the topological filters. After the final clustering and vdWFV check, two and one structures are accepted in the P21/c space group, corresponding to the three known aspirin polymorphs with RMSD20 values equal to 0.115 Å for aspirin I, 0.217 Å for aspirin II and 0.179 Å for aspirin IV. Low vdWFW structures that were discarded during the filtering process are provided as Supplementary Data. The landscape for the cost function CZZP against CICC is shown in Fig. 3(d). Additional landscapes for the cost functions against the vdWFV are provided in the SI. The complete computation time was ~6 h on a midrange laptop, considerably shorter than that of the rigid search owing to the fact that the flexible search discards unnatural conformations in their respective unit cells in the initial stages of the search. The vdWFVs of the predicted structures I, II, IV are, respectively, 26.78%, 33.19%, 28.06%, and are again consistent with the vdWFV ranking for the experimental structures. The CICC ranking for the predicted structures is in again consistent with both the experimental energy ranking and DFT-D3 energy ranking (Table 1).
CSP of the CCDC blind test target XXII compound
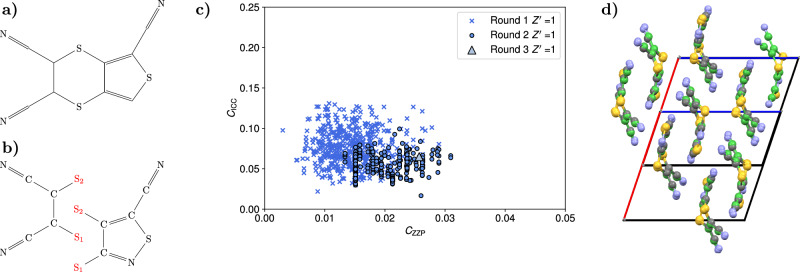
A second test of CrystalMath was performed on the rigid target XXII molecule (C8N4S3) from the 6th CCDC blind structure prediction competition. This molecule is known to have a puckered conformation, as reported in ref. 14, determined from a Density Functional Theory optimization. However, here we demonstrate how our approach can be used to determine both the conformation and crystal structure of the molecule, by treating it as a flexible compound with two rigid fragments shown in Fig. 4(b). Following the same protocol as for the flexible aspirin search, conformations are constructed from the initial pool by joining the two fragments to their two common atoms, generating a total of ~9500 base structures. The optimization of the molecular positions and close contacts generates, respectively, 815 and 372 structures. After the final clustering and vdWFV check, only one structure is accepted which is a match to the known experimental structure 14,29 in the P21/c space group, with an RMSD20 equal to 0.240 Å. Low vdW structures that were discarded during the filtering process are provided as Supplementary Data. The landscape for the cost function CZZP against CICC is shown in Fig. 4(c). Additional landscapes for the cost functions against the vdWFV are provided in the SI. The computation time for the search was ~4.5 h on a midrange laptop.
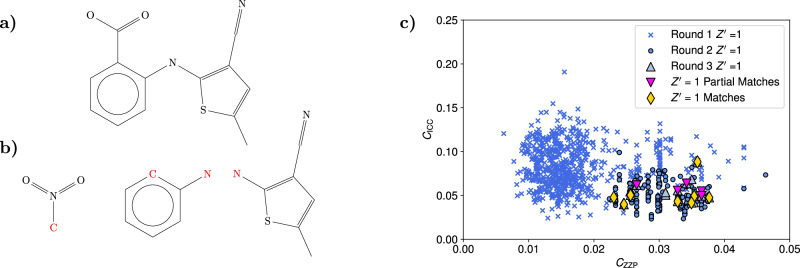
Fig. 4. Details of the crystal structure search for the target XXII compound.
a Diagram of the target XXII compound. b Diagram of the two fragments used to generate the puckered target XXII molecule. The two fragments are joined to their common atoms S1 and S2. c Scatter plot of the cost function CICC against the cost function CZZP for the accepted structures in each of the three different rounds of filtering in the search for the target XXII structures. High van der Waals free volume structures were excluded from the plot. d Overlay of the single predicted structure against the known experimental structure of the target XXII molecule, which are displayed in green. Source data are provided as a Source Data file.
CSP of the CCDC blind test target XXIII compound
As a third test of CrystalMath, we performed a search for the 5 known polymorphs of the target XXIII molecule (C21H17Cl2NO2), also from the 6th blind structure prediction competition. The target XXIII compound is a flexible molecule with three rotatable bonds (see Fig. 5(a)). Three of the known polymorphs have while the other two known polymorphs are structures. This particular molecule proved challenging in the CSP competition, as none of the participating groups was able to identify all of the polymorphs. One of the participating teams was able to predict all of the polymorphs, but none found all of the structures. For the structures, a fragmented-based approach was employed using five fragments, which are indicated in Fig. 5(b). When combining a large number of fragments, only a few conformations can be generated without intramolecular overlap between the fragments. To increase the number of candidate conformations, we increased the number of inertial eigenvectors from 100,000 used in the aspirin and Target XXII searches to 200,000. From a pool of 282 base structures, we were able to generate five and 107 structures optimized for molecular positions by minimizing the cost function (15). After the close contact optimization and filtering, three and two structures were accepted in the final pool. When compared to the known target XXIII polymorphs, the three structures correspond to polymorphs I, II, IV in the P21/c, and P21/n space groups with RMSD20 equal to 0.226 Å, 0.485 Å and 0.324 Å, respectively, while the structures correspond to the two experimental structures in the space group with RMSD20 values equal to 0.537 Å and 0.233 Å, respectively. Low vdWFW structures that were discarded during the filtering process are provided as Supplementary Data. The landscape for the cost function CZZP against CICC is shown in Fig. 5(c). Additional landscapes for the cost functions against the vdWFV and overlays between the predicted and experimental structures are provided in the SI. The complete computation time was ~32 h on a midrange laptop. Overlays of the predicted structures are provided in SI Section 5. The vdWFVs of the predicted structures range between 30.4% and 36.2%, which is similar to the range of the known experimental polymorphs (30.4%–34.1%). In contrast to the energy ranking of aspirin structures, the correlation between the cost function CICC values, the lattice energy of the predicted structures, and the lattice energy of the experimental structures is low. A potential explanation is the limited accuracy of the force field in describing halogen contacts and/or the relatively low correlation between the lattice energy and the CICC function. The DFT energy differences are in line with experimental measurements, confirming that polymorph I is the most stable polymorph at 257 K30. However, the energy differences between the polymorphs are relatively high and the correlation between the energy differences and the cost function rankings are again low. We believe that the main reasons behind these findings is related to the rigid cell optimization approach we currently use, which does not allow the unit cell geometry to be altered for full optimization of the atomic positions and close contacts. Future work will include methodology for removing this restriction, as described below.
Fig. 5. Details of the crystal structure search for the target XXIII compound.
a Diagram of the target XXIII compound. b Diagram of the five fragments used to generate the target XXIII molecule. c Scatter plot of the cost function CICC against cost function CZZP for the accepted structures in each of the three different rounds of filtering in the search for the polymorphs. After clustering the structures surviving the third filtering round, 5 structures are found corresponding to the 5 known polymorphs of target XXIII. The high number of fragments in the molecule allow only a small number of physically meaningful conformations to be generated in the initial step, reducing significantly the number of structures generated at each stage. Overlays for the predicted structures are provided in Section 5 of the SI. High van der Waals free volume structures were excluded from the plot. Source data are provided as a Source Data file.
CSP of the ROY polymorphs
As a final test case for CrystalMath, which challenges the ability of the protocol to predict the crystal structures of compounds exhibiting high degree of polymorphism, we performed a search for the 10 known polymorphs of the molecule ROY, (C12H9N3O2S)31–36 so named for the colors (red, orange, yellow) of the different ROY crystals. ROY is a flexible compound that possesses three rigid fragments connected through two rotatable bonds (see Fig. 6(a, b)). Different conformers correspond to different polymorphs, which have different geometries and space-group symmetries. A fragment-based search was initialized from the same pool of 200,000 eigenvectors as for the target XXIII case. Optimization of molecular positions to ZZPs of the ~8700 base structures generated 2704 viable candidates, and when these are filtered for close contacts, 765 complete structures are generated. By setting the maximum allowed vdW free volume to , four structures are found in the final pool, corresponding to the PO13, Y19, ON polymorphs in the P21/c space group and Y polymorph in the P21/n space group, with RMSD20 values from the experimental structures are, respectively, 0.217 Å, 0.187 Å, 0.167 Å and 0.171 Å. By expanding the maximum allowed vdW free volume to , 15 additional structures are added to the pool. These include five additional polymorphs: R and YN in the space group, ORP in the Pbca space group, and OP and YT04 in the P21/n space group. The respective RMSD20 values from experiment are 0.162 Å, 0.289 Å, 0.201 Å, 0.250 Å, 0.101 Å. Overlays of the predicted and experimental structures for these nine matches are provided in the SI Section 6. From the remaining structures, five are partial matches for the ON, YT04, PO13 and Y19 polymorphs, with 11/20–16/20 molecules aligned to the respective experimental structures in a similarity check, while the remaining five are new unique structures. The landscape for the cost function CZZP against CICC is shown in Fig. 6(c). The total computation time for the search was ~10 h on a midrange laptop.
Fig. 6. Details of the crystal structure search for the ROY compound.
a Diagram of the ROY compound. b Diagram of the three fragments used to generate the ROY molecule. c Scatter plot of the cost function CICC against cost function CZZP for the accepted structures in each of the three different rounds of filtering in the search for the polymorphs. When clustering the structures surviving the third filtering round, 19 structures are found. 9 of them are matching 9 of the 10 known ROY polymorphs, 5 are partial matches to experimental structures and additional 5 are unique structures. Overlays for the predicted structures are provided in Section 6 of the SI. High van der Waals free volume structures were excluded from the plot. Source data are provided as a Source Data file.
For the matches of polymorphs ON, Y, R, ORP, YT04, PO13 and Y19, the vdWFV of the predicted structures is in the range 27.82%–28.97%. The matches for the OP, YN polymorphs have a vdWFV in the range 33.14%–34.41%. The vdWFV for partial matches range between 28.99% and 33.86% while the vdWFV for the five new structures is above 33.49%. Given the polymorphic propensity of the ROY molecule, it is possible that some of the five structures that are not a match to known experimental structures may correspond to currently unidentified ROY polymorphs. For the polymorphs for which we identified both perfect and partial matches, the CICC values are always lower for the perfect matches than for the partial matches. With the exception of X1, all the new structures exhibit higher CICC values compared to the experimental matches, except for the polymorph R.
The DFT-D3 energy ranking in the case of the predicted ROY structures demonstrates low correlation to the calculated CICC values. The ORP polymorph is found to rank 1st in both ranking schemes, while the Y polymorph, which is experimentally known to be the most stable, ranks 6th in the cost function ranking scheme and 2nd in the DFT-D3 energy calculation. However, it is reported that common DFT models fail to accurately predict the correct energy ranking of ROY structures37. Consequently, it is not possible to obtain reliable results concerning the accuracy of the cost function ranking.
Although we were not able to find the tenth polymorph among the 200,000 eigenvector sets chosen for the search, additional eigenvector sets from the total pool of ~1.6 billion possibilities could be selected to search not only for this remaining polymorph but also for the polymorphs not considered in this search. Given the large redundancy among these eigenvector sets, it is expected that these and the nine polymorphs already identified would show up multiple times among different subsets of the complete set of eigenvectors. Such a search and detailed analysis of the frequency of polymorph occurrence among different pools will be the subject of future work on this and other molecular crystal systems.
Discussion
The examples presented above demonstrate that a mathematical approach, including some simple physical concepts, is feasible as an efficient generator of organic molecular crystal structures. However, it is important to ask if known organic molecular crystal structures largely adhere to the principles presented in this work. If so, it would indicate that the rules of Crystal Math represent a new framework for understanding molecular packing in three-dimensional crystal structures. To test this, we examined the complete set of organic molecular crystal structures containing C, H, N, O, F, Cl, Br, I, and S atoms with molecular weight ≤500 in the most common space groups available in the CSD22. From this set, we obtained distributions of the molecular center-of-mass positions, molecular orientations in terms of the angles formed by the vector pairs (ei, nc) and (kr, nc), the atomic separations, the atomic connectivity, and unit cell geometry. The analysis can be refined based on the atomic composition of the crystal. Resulting distributions for selected crystal compositions and space groups are shown in Fig. 1 (the remaining distributions are provided in the SI, Section 3). The center-of-mass distributions in the selected space groups (Fig. 2(b, c)) clearly show that there are preferred locations of molecules in the unit cell, and that these locations correspond to the solutions of Eq. (10) with the order parameters chosen to be the Zernike parameters in Eq. (11) (the full set of solutions for different space groups are provided in the SI, Section 3). The orientational distributions (Fig. 1(a, b)) similarly show that the molecules clearly prefer specific orientations such that the inertia eigenvectors and normal ring plane vectors are nearly perpendicular to the set of vectors nc. In addition, the analysis of the atomic separations revealed that ~99% of the structures have atomic pairs involving at least one highly electropositive/electronegative atom separated by k/(4|δsi,i+1|), k = 0, ± 1, …, ± 4 along the crystallographic directions si (Table 2).
Table 2.
Percentage of the atomic pairs involving at least one atom with high electropositivity or electronegativity, separated by a distance kZZP/(4|δsi|), (kZZP = 0, ± 1, …, ± 4) along the nine possible crystallographic directions si, for all the structures composed of C, H, O atoms
| A | (%) | A | (%) | A | (%) |
|---|---|---|---|---|---|
| (1, 0, 0) | 99.00 | (1, 1, 0) | 98.96 | (1, −1, 0) | 98.91 |
| (0, 1, 0) | 99.14 | (1, 0, 1) | 98.92 | (1, 0, −1) | 99.09 |
| (0, 0, 1) | 99.07 | (0, 1, 1) | 99.15 | (0, 1, −1) | 98.88 |
The analysis of the unit cell geometry reveals a strong correlation between the unit cell volume, the molecular volume, and the vdW free volume (Fig. 1(c, d)). The proximity of neighboring molecules can be expressed using the intermolecular atomic separations, which are measured by the length of the close contacts. The optimal contact distances depend on the molecular composition and the atomic species forming short contacts (Fig. 1(e, f)). For most pairs, the distributions are quite similar, as in the case of C–H contacts (Fig. 1(e)). However, if a short contact can form a hydrogen bond, as in the case of the O–H pairs, the distribution exhibits a secondary peak characteristic of the hydrogen bond length affecting the connectivity of the molecules by allowing shorter contacts to form (Fig. 1(f)). These distributions provide the criteria referred to earlier in the structure selection phase of the algorithm. The analysis performed here demonstrates the close adherence of known organic molecular crystal structures to the topological principles introduced above.
The notion that a purely mathematical theory for molecular crystal structures can be predictive and that a structure generation algorithm operating within the principles of the theory can be constructed opens an entirely new paradigm for reliably predicting and understanding these structures with minimal resources and investment of computational time. We believe we have established the proof of this concept. The next phase of development will involve incorporating greater molecular flexibility and the functionality to treat more complex structures and co-crystals. In both cases, the approach would be similar to the search for flexible structures: each molecule in the asymmetric unit could be treated as a separate entity that can be decomposed into rigid fragments if these entities are flexible. A unit cell can be constructed by identifying unit cell geometries that are nearly identical for all fragments and placing the fragments in the unit cell in ways that are consistent with the topological connectivity rules applied in our protocol. Although the combination of the vdWFV and CICC objective functions appears adequate to distinguish valid structures from false candidates and provides a sufficient ranking of the predicted structures, there is room for improvement for increasing the correlation between the cost function and the lattice energy of the structures. An enhanced flexible unit cell contact optimization is currently under development and will include terms for the cell parameters (a, b, c, α, β, γ) in a modified form of the close-contact cost function, currently given by Eq. (16). The new form of this function will be determined through a careful analysis of the CSD database and the requirement of maintaining consistency with the CrystalMath principles.
Supplementary information
Description of Additional Supplementary Files
Source data
Acknowledgements
This work was supported by the National Science Foundation grant nos. CHE-1955381 and DMR-2118890.
Author contributions
Nikolaos Galanakis (ORCID: 0000-0002-1134-2335) and Mark E. Tuckerman (ORCID: 0000-0003-2194-9955) conceived and designed the study. Nikolaos Galanakis performed the computational experiments, analyzed the data, and drafted the manuscript. Mark E. Tuckerman contributed to the writing and revision of the manuscript. All authors gave final approval for the version to be published.
Peer review
Peer review information
Nature Communications thanks Graeme Day, Sarah Price and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
All data presented in the manuscript and crystallographic information files (CIFs) of low vdW free volume structures discarded during CrystalMath runs are available as supporting information. Source data are provided with this paper.
Code availability
CrystalMath software38 can be downloaded from https://github.com/nigalanakis/Crystal_Math10.5281/zenodo.13641003.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Nikolaos Galanakis, Email: ng1807@nyu.edu.
Mark E. Tuckerman, Email: mark.tuckerman@nyu.edu
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53596-5.
References
- 1.Price, S. L. The computational prediction of pharmaceutical crystal structures and polymorphism. Adv. Drug Deliv. Rev.56, 301 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Yang, J. X. et al. Inverse correlation between lethality and thermodynamic stability of contact insecticide polymorphs. Cryst. Growth Des.19, 1839–1844 (2019). [Google Scholar]
- 3.Zhu, X. L. et al. Manipulating solid forms of contact insecticides for infectious disease prevention. J. Am. Chem. Soc.141, 16858–16864 (2019). [DOI] [PubMed] [Google Scholar]
- 4.Yang, J. X. et al. A deltamethrin crystal polymorph for more effective malaria control. Proc. Natl. Acad. Sci. USA117, 26633–26638 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jurchescu, O. D. et al. Effects of polymorphism on charge transport in organic semiconductors. Phys. Rev. B80, 085201 (2009). [Google Scholar]
- 6.Yang, J. et al. Large-scale computational screening of molecular organic semiconductors using crystal structure prediction. Chem. Mater.30, 4361 (2018). [Google Scholar]
- 7.Podeszwa, R., Rice, B. M. & Szalewicz, K. Crystal structure prediction for cyclotrimethylene trinitramine (RDX) from first principles. Phys. Chem. Chem. Phys.11, 5512 (2009). [DOI] [PubMed] [Google Scholar]
- 8.Szalewicz, K. Determination of structure and properties of molecular crystals from first principles. Acc. Chem. Res.47, 3266 (2014). [DOI] [PubMed] [Google Scholar]
- 9.Lommerse, J. P. M. et al. A test of crystal structure prediction of small organic molecules. Acta Cryst.B56, 697–714 (2000). [DOI] [PubMed] [Google Scholar]
- 10.Motherwell, W. D. S. et al. Crystal structure prediction of small organic molecules: a second blind test. Acta Cryst.B58, 647–661 (2002). [DOI] [PubMed] [Google Scholar]
- 11.Day, G. M. et al. A third blind test of crystal structure prediction. Acta Cryst.B61, 511–527 (2005). [DOI] [PubMed] [Google Scholar]
- 12.Day, G. M. et al. Significant progress in predicting the crystal structures of small organic molecules - a report on the fourth blind test. Acta Cryst.B65, 535–551 (2009). [DOI] [PubMed] [Google Scholar]
- 13.Bardwell, D. A. et al. Towards crystal structure prediction of complex organic compounds - a report on the fifth blind test. Acta Cryst.B67, 535–551 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Reilly, A. M. et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Cryst.B72, 439–459 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pepinsky, R. Crystal engineering - new concept in crystallography. Phys. Rev.100, 971–972 (1955). [Google Scholar]
- 16.Burckhardt, J. J. Zur Geschichte der Entdeckung der 230 Raumgruppen. Arch. Hist. Exact Sci.4, 235–246 (1967). [Google Scholar]
- 17.Price, S. L.& Brandenburg, J. G. “Molecular crystal structure prediction” in Non-Covalent Interactions in Quantum Chemistry and Physics (eds A. O. De La Roza, G. A. Di Labio) (Elsevier, 2017).
- 18.Nyman, D. & Day, G. M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm17, 5154–5165 (2015). [Google Scholar]
- 19.Kilgour, M., Rogal, J. & Tuckerman, M. E. Geometric deep learning for molecular crystal structure prediction. J. Chem. Theor. Comput.19, 4743–4756 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tom, R. et al. Genarris 2.0: a random structure generator for molecular crystals. Comput. Phys. Commun.250, 107170 (2020). [Google Scholar]
- 21.Hong, R. S., Mattei, A., Sheikh, A. Y. & Tuckerman, M. E. A data-driven and topological mapping approach for the a priori prediction of stable molecular crystalline hydrates. Proc. Natl. Acad. Sci. USA119, e2204414119 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Groom, C. R., Bruno, I. J., Lightfoot, M. P. & Ward, S. C. The Cambridge structural database. Acta Cryst.B72, 171–179 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Novotni, M. & Klein, R. 3D Zernike descriptors for content-based shape retrieval. Comput. Aided Des.36, 1047–1062 (2003). [Google Scholar]
- 24.Khotanzad, M. & Hong, Y. H. Invariant image recognition by Zernike moments. IEEE Trans. Pattern Anal. Mach. Intel.12, 489–497 (2002). [Google Scholar]
- 25.Chisholm, J. & Motherwell, S. COMPACK: a program for identifying crystal structure similarity using distances. J. Appl. Cryst.38, 228–231 (2005). [Google Scholar]
- 26.Wilson, C. C. Interesting proton behaviour in molecular structures. Variable temperature neutron diffraction and ab initio study of acetylsalicylic acid: characterising librational motions and comparing protons in different hydrogen bonding potentials. Acta Cryst.B72, 171–179 (2016). [Google Scholar]
- 27.Wheatley, P. J. The crystal and molecular structure of aspirin. J. Chem. Soc.0, 6036–6048 (1964). [Google Scholar]
- 28.Visweshar, P. et al. The predictable elusive form II of Aspirin. J. Am. Chem. Soc.127, 16802–16803 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Horton, P. N.& Grossel, M. C. CSD Communication (2016).
- 30.Samas, B. et al. Five Degrees of Separation: Characterization and Temperature Stability Profiles for the Polymorphs of PD-0118057 (Molecule XXIII). Cryst. Growth Des.21, 4435–4444 (2021)
- 31.Harty, E. L. et al. Reversible piezochromism in a molecular wine-rack. Chem. Commun.51, 10608–10611 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Yu, L. et al. Thermochemistry and conformational polymorphism of a hexamorphic crystal system. J. Am. Chem. Soc.122, 585–591 (2000). [Google Scholar]
- 33.Levesque, A., Maris, T. & Wuest, J. D. ROY reclaims its crown: new ways to increase polymorphic diversity. J. Am. Chem. Soc.142, 11873–11883 (2020). [DOI] [PubMed] [Google Scholar]
- 34.Chen, S., Guzei, I. A. & Yu, L. New polymorphs of ROY and new record for coexisting polymorphs of solved structures. J. Am. Chem. Soc.127, 9881–9885 (2005). [DOI] [PubMed] [Google Scholar]
- 35.Gushurst, K. S. et al. The PO13 crystal structure of ROY. CrystEngComm,21, 1363–1368 (2019). [Google Scholar]
- 36.Tyler, A. R. et al. Encapsulated nanodroplet crystallization of organic-soluble small molecules. Chem6, 1755–1765 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Beran, G. J. O. et al. How many more polymorphs of ROY remain undiscovered. Chem. Sci.13, 1288–1297 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Galanakis, N., & Tuckerman, M. E. Rapid prediction of molecular crystal structures using simple topological and physical descriptors, CrystalMath, 10.5281/zenodo.13641003 (2024).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of Additional Supplementary Files
Data Availability Statement
All data presented in the manuscript and crystallographic information files (CIFs) of low vdW free volume structures discarded during CrystalMath runs are available as supporting information. Source data are provided with this paper.
CrystalMath software38 can be downloaded from https://github.com/nigalanakis/Crystal_Math10.5281/zenodo.13641003.