Rectified activity-dependent population plasticity implicates cortical adaptation for memory and cognitive functions

Abstract

Cortical network undergoes rewiring everyday due to learning and memory events. To investigate the trends of population adaptation in neocortex overtime, we record cellular activity of large-scale cortical populations in response to neutral environments and conditioned contexts and identify a general intrinsic cortical adaptation mechanism, naming rectified activity-dependent population plasticity (RAPP). Comparing each adjacent day, the previously activated neurons reduce activity, but remain with residual potentiation, and increase population variability in proportion to their activity during previous recall trials. RAPP predicts both the decay of context-induced activity patterns and the emergence of sparse memory traces. Simulation analysis reveal that the local inhibitory connections might account for the residual potentiation in RAPP. Intriguingly, introducing the RAPP phenomenon in the artificial neural network show promising improvement in small sample size pattern recognition tasks. Thus, RAPP represents a phenomenon of cortical adaptation, contributing to the emergence of long-lasting memory and high cognitive functions.

RAPP phenomenon describes a formula to measure intrinsic adaptation of neuronal population activity, which carries features of both the homeostasis regulation of the original state and the distilling of sparse memory traces in neocortex.

Introduction

The brain is dynamic and plastic^1,2. One excellent example is sensory adaptation. In auditory or visual cortex and many other areas of the neocortex, neural responses to the same stimulus during repeated exposure, typically become smaller and smaller with the passing of time. Memories, on the other hand, reflect the stability of the brain, where the responses to some stimuli are robust and long-lasting³. Other processes, such as extinction and reconsolidation, add more dynamics into the neuronal responses. Synaptic plasticity is fundamental underlying both the sensory adaption⁴ and the formation of consolidated memories and their reconsolidation^5–7. At cellular level, memory trace neurons (neural engrams), representing new memories⁸, emerge in hippocampus, amygdala⁹, and neocortex^10,11. While memory trace neurons are activated upon learning^12,13, some memory traces appear inactivated overtime^14,15 and a few memory trace neurons in neocortex are engaged in long-term memory^16–18. It is unclear if such cellular changes and adaptation are following specific regulation. In this study, we asked whether the adaptation of cellular activities at large scale in neocortex is modulated, instead of randomized, and whether such adaptation might underlie some aspects of sustained and long-lasting memories.

In the biological nervous system, homeostasis is a strong trend to reset neuronal activity level back to their set points, after perturbation. For example, at cellular level and synaptic level, studies have uncovered an adaptive phenomenon that the neuronal firing rates return to the set point during a constantly changing environment due to the homeostatic synaptic scaling, both in neuron cultures¹⁹, and in neocortex of mice^20,21. Such homeostasis regulation could contribute to the dynamics of memory traces. Although the homeostasis regulation described aspects of adaptation in some neurons by electrophysiological recording, the quantitative survey of adaptation in a much larger population requires a high-throughput method.

Immediate early gene expression is positively correlated with the neuronal activation²² and is used to label memory traces under many conditions^17,23–25. Florescent proteins driven by immediate early gene promoter allows quantitively measuring neural activity-related signals in a relatively large population in vivo^17,24,26. Here, we used Egr1 gene transgenic mice to monitor the neural activities. The task-induced-signal increase of Egr1-EGFP about 1–2 h after the stimuli is positively correlated with the induced neural activity. While in the neurons with high spontaneous activity (post-stimulus period), fluorescent intensities of Egr1-EGFP are positively correlated with their sustained basal activities²⁶. As the Egr1-EGFP signal is suitable for large scale recording, we monitored the adaptation of cortical population activity of awake mice by quantitative in vivo imaging in Egr1-EGFP mice. During contextual fear conditioning training, the changes of signal reflect the sensory and memory induced neuronal activity. At the resting state in their homecage, alterations of signals in each neuron might reflect the network adaptation.

Although there could exist different activity-induced plasticity rules for different subtypes of neurons, we found evidence of a general principle for the population level adaptation of neurons in cortical networks, through rectified activity-dependent population plasticity (RAPP). The linear rectified function (ReLU), as the activation function of neurons, has been widely used in artificial neuronal network to introduce sparsity^27,28. In this study, the observed rectified linear correlation of neuronal population plasticity predicted the homeostatic adaptation of population activity, as well as the emergence of sparse memory traces in neocortex. Hippocampus reinstated the population activation pattern, against adaptation. Model simulation indicates two factors mainly account for the RAPP phenomenon: the preserved local inhibitory connections, instead of excitatory connections, and activation-engaged alteration of cellular excitability. Interestingly, the RAPP rule embedded learning algorithm in deep convolutional neural network (CNN) achieved significant improvement over the state-of-art training algorithms in pattern recognition task with small sample size. These findings suggest a phenomenon of regulated population adaptation to form sparse long-lasting memory traces in a constantly changing network in the mammalian neocortex.

Results

We measured the cellular activity of local circuits in neocortex in EGR1-EGFP mice¹⁷. EGR1 is an immediate early gene, the expression of which is induced by neural activation and it is critical for long-term memory formation²². Neurons that selectively express the immediate early gene during memory encoding are present as memory traces or neural engrams in different brain areas, including hippocampus, amygdala, and neocortex^9,25,26,29. In the Egr1-EGFP reporter mice, the florescent intensity changes in each neuron were positively correlated with the spiking rate over several hours in neural cultures (Supplementary Fig. 1) and in the brain induced by a behavioral task^17,26,30. The induced increase of signals is positively correlated with the accumulative summation of task-induced calcium events and spontaneous neural activity in absence of sensory inputs²⁶. Cellular Egr1-EGFP Signals are segmented using a CNN-based algorithm (supplemental materials) and the 3D volumes were aligned to its original signal on day 1 in pixel precision as previously described^17,26,30. We imaged cellular signals 1–1.5 h after each training trial or homecage condition in a systematic manner for multiple cortical areas of the same mouse, including visual cortex (VIS), primary somatosensory cortex (SSp), motor cortex (MO) and retrosplenial cortex (RSP). All EGR1⁺ neurons recorded from layer 1 through layer 6 within the same volume (Fig. 1A). Here, we only used cortical layer 2–3 neurons data in the analysis to focus on the adaptation of memory-related populational changes^17,31.

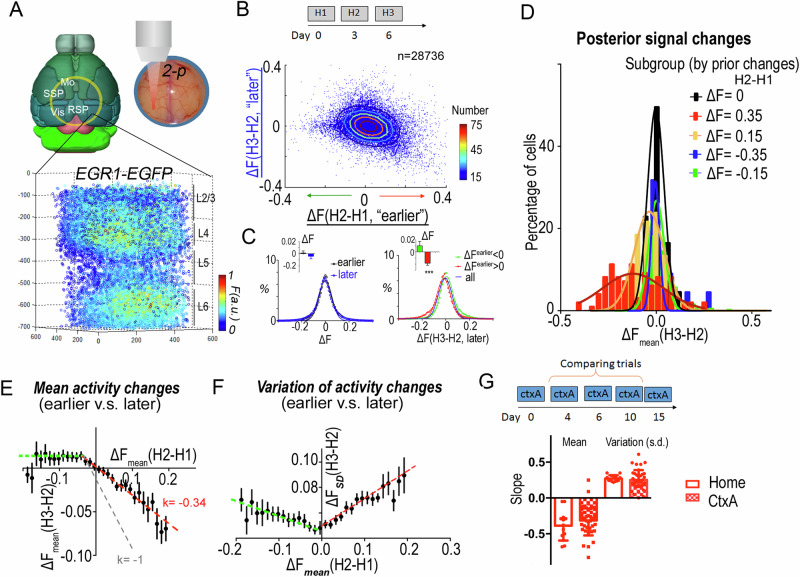
Fig. 1. EGR1-EGFP signals reveal activity-dependent population plasticity in mouse neocortex.

A Recording of neuronal activity in neocortex of EGR1-EGFP mouse by 2-photon microscopy. Signals were collected 1–1.5 h after each trial. Layers were determined by the morphology and density of cells. B Activity change correlation between the earlier versus later trials in the homecage environment (H2-H1 vs. H3-H2) for cortical layer 2/3 neurons. Color-coded contour lines plot the gradient of normal distribution. 10 areas of layer 2/3 neurons were recorded (total n(neurons) = 28,736). C Population changes of signal. Fitting with Gaussian distribution curve. Inserts are mean changes of each population (n(mouse) = 8). ***, one sample t-test, deviated from 0. D Distribution of posterior population activity in different subgroups of neurons in B. The subgroups are divided according to prior activity changes. E, F The rectified linear correlation of each subgroup between prior and posterior changes in activity (E), or standard deviation (F). Error bar reflects data from multiple individuals (n = 18 mice). G The population plasticity in trials of a neutral context (CtxA). Slopes of the population plasticity in the activated neuron population (red line in E, F) in the neocortex for homecage trials and CtxA trials (n = 13 mice for homecage, n = 36 mice for CtxA). Error bars, s.e.m.

Rectified linear correlation between prior and posterior population activity changes

To quantify the populational adaptation in neocortex, we recorded mice in three trials for the highly habituated homecage environment. Under the condition without trained stimuli, the spontaneous activity levels of neurons are correlated with their Egr1-EGFP signal intensities²⁶. In this case, we were wondering if any random events induced perturbation in the brain (between two homecage trials) will leave traces for long time. If the events are trivial and random, leaving no impacts on the following days, the changes of cellular activities between adjacent trails should be anticorrelated with a slope around −1. If the events have long-enduring impact, terming as a memory phenomenon, the changes of cellular activity between trials should be higher than −1.

We pooled the cellular signals across 10 areas (n = 28,736) of the same mice from layer 2/3³² and plotted the correlation of the activity change of each neuron between the earlier and later trials (Fig. 1B). Importantly, the population density plot of this data showed an asymmetric distribution, different from a two-dimensional Gaussian. While the total averages of signal variations, in the earlier as well as later trials, were not significantly different from zero (p = 0.747, p = 0.337, respectively; two-tailed one sample t-test) (Fig. 1C), the means of signal variations in the previously enhanced neurons, but not in the previously repressed neurons, were significantly different from zero (p = 0.0009, p = 0.211, respectively, two-tailed one sample t-test). This asymmetry in the activity changes of previously repressed and enhanced neurons implied that population signal variations between the prior and the posterior trials were not random, but specifically modulated.

In order to identify the source of this modulation, we divided recorded neurons into subpopulations according to their activity changes in earlier trials. The subpopulation with increased signals in the earlier trials (day 3–day 0) showed activity-dependent reductions in average signal strength and an increase in the population activity variability (standard deviation) in the later trials (day 6–day 3; Fig. 1D). This systematic adaptation was not present in the subpopulation with reduced signals in earlier trials, which just changed its activity stochastically in the later trials. The highly activated neuron population (ΔF = 0.35 ± 0.01, n = 97) showed a much wider distribution of signal changes as well as stronger reduction of mean signals than the less strongly activated neuron population (ΔF = 0.15 ± 0.01, n = 1953).

To characterize these observations more systematically, layer 2/3 neurons from one visual volume were divided into subgroups (n > 200 neurons in each subgroup) according to their signal changes in the earlier trials. The cortical population activity showed a clear, rectified linear correlation between the signal changes in consecutive trials, such that populations with increased signals in the earlier trials had reduced activity in the later trials. The amplitude of the signal reduction in the later trial was linearly correlated with the signal increase in the prior trial (r² = 0.96, Supplementary Fig. 2A). By contrast, neuronal subgroups with decreased signals in the earlier trials subsequently showed a general activity increase by a small constant (Supplementary Fig. 2A). Such a rectified linear correlation was consistently observed in all of the individual cortical volumes (slope = −0.34 ± 0.03, b = −0.001 ± 0.002, for ΔF_prior > −0.05; slope = −0.002 ± 0.057, b = 0.013 ± 0.006 for ΔF_prior < −0.05, Fig. 1E). As the slope is far from −1, where the activated ones return to its original set point as predicted by homeostasis adaptation, this result (k = −0.34) suggests a long-lasting impact is observed in the neocortex, implicating memory in the network.

In addition to the average signal strength, the signal variation in each subpopulation also showed a rectified linear correlation with the signal changes in the earlier trials. Interestingly, we found for subgroups with increased signal in earlier trials, the standard deviation was increased linearly in the posterior trials, proportional to the mean signal increase in the prior trials (r² = 0.95, Supplementary Fig. 2B). This increase in signal variation (Fig. 1F) was in contrast to the expected situation in which the noise is proportional to the signal strength, as here averaged cellular signals decreased in the later trials (Fig. 1E). This rectified linear correlation was consistently observed in all individual volumes (Fig. 1F, slope = 0.21 ± 0.03, intercept = 0.050 ± 0.003 for ΔF_pre > −0.05; slope = −0.07 ± 0.04, intercept = 0.050 ± 0.005 for ΔF_pre < −0.05).

Taken together, we found that while adaptation was observed that neurons activated in the earlier trials tended to reduce their activity in the later trials, residue potentiation of the engaged population were remained in the cortical network, implicating memory. At the same time, those activated neurons also showed high population variability, adding a stochastic component to the activity of this population (Supplementary Fig. 3). On the other hand, neurons with reduced activity in prior trials showed a tendency to increase their signal in posterior trials by a constant amount (i.e., independent of their prior activity level, slope is non-zero, p = 0.97, F = 0.0014, linear reg.). It is noticed that this phenomenon of population adaptation might also be interpreted as the combination of homeostasis regulation and random walk process. In addition, it is less likely that this phenomenon was a result of orthogonal sensory inputs in two homecage trials. Because, if the observed population adaptation is due to the input of orthogonal sensory signals, then the population of neurons activated on the 6th day should be different from the population activated on the 3rd day (orthogonal), causing the neurons activated on the 3rd day to return to their baseline state on the 6th day as they were on the 0th day, thus producing a slope of −1 in the population neuronal response. As a prove of notion that distinct sensory stimuli result in −1 slope, we performed a context A and context B comparing experiment and found that the distinct sensory inputs yield a −0.8 slope (Supplementary Fig. 4), significantly lower than that recorded in homecage trials (−0.3).

These rectified linear correlations of population changes between later and earlier trials were observed not only in the homecage trials, but also in trials where the animals explored a neutral context (for context-activated subpopulations, the slope for the amplitude is −0.31 ± 0.03, and the slope for the standard deviation 0.25 ± 0.03, Fig. 1G and Supplementary Fig. 5).

In summary, plasticity based on rectified linear correlations between prior and posterior population activity changes was consistently observed in the layer 2/3 of mouse neocortex. Although neural activities were adaptive and variable between days, their population activities appear to be regulated by an intrinsic property of the cortical network, which can be formulated and described as the RAPP phenomenon.

Dynamics of cortical responses predicted by the RAPP phenomenon

The activity-dependent population plasticity rule comprehensively predicted the dynamics of cortical responses. When the network was repeatedly exposed to neutral inputs (CtxA) or inputs without new information (homecage), the empirical constants of the population plasticity rule determined the global dynamics of the network at each step of the evolution of the population activity (Fig. 2A). Numerical simulation of this dynamical system, starting from an initial, Gaussian-distributed population activity (skewed in the evolution), demonstrated two features of cortical activity patterns, representation adaptation and generation of long-lasting memory traces. First, the model predicted that the characteristic activity patterns of the whole population fade over time (Fig. 2B). Second, the numerical simulation of such population adaptation rules suggested that sparse individual neurons might show long-lasting activities, appearing as the memory trace-like neuron (Fig. 2C). While subpopulations with increased activity reduced their activity and increased the population variation, a small portion of the activated neurons continuously increased their activity in the next round, becoming neurons with persistent, high activity. Due to the linear correlations both in amplitude and signal variation, the same proportion of neurons as activated in the pre-prior trial increased their activity in the posterior trial (Supplementary Fig. 3). Thereby, the size of the activated subpopulation arising from the originally active population decayed by a power law, achieving a sparse, yet high-activity (robust) representation of the original activity patterns. Thus, the RAPP phenomenon generated and distilled sparse and long-lasting cortical memory traces.

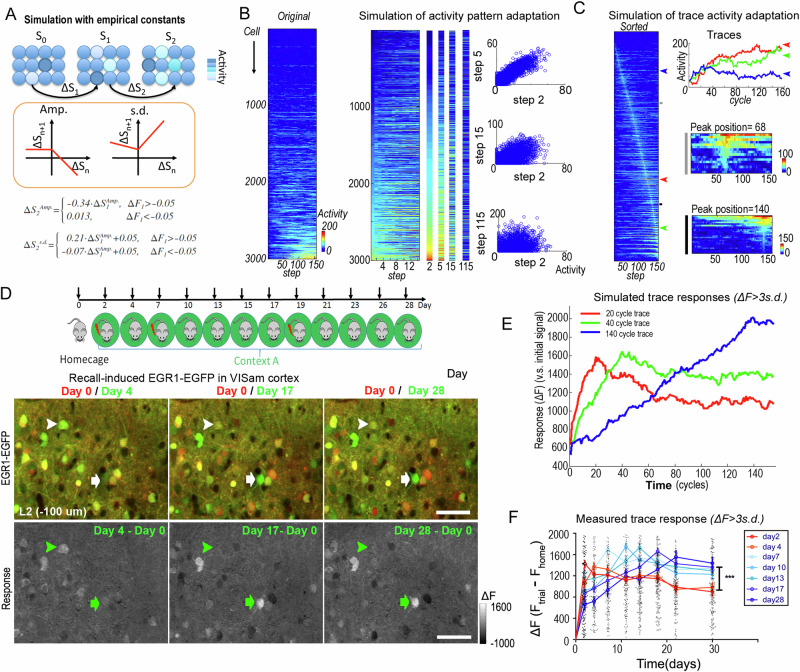
Fig. 2. The RAPP rule predicts the decay of activity patterns and the emergence of long-lasting memory traces.

A Illustration of the rectified activity-dependent population plasticity (RAPP) and the empirical parameters describe it (Amp & s.d.). S, population response state; Amp., amplitude, the mean response of the subgroup; s.d., standard deviation of the subgroup. B, C Simulation of population dynamics in neocortex. A Gaussian-distributed pattern was seeded in the first step. Activity changes from one step to the next were determined by the empirical parameters. (B) Pattern decay. Rows indicate the same neuron; columns indicate sequential steps. The left activity map was plotted by the deviation of each neuron (smallest deviation at top); the right activity map was sorted according to the signal intensity in the first step. Representative patterns in steps were enlarged in separated columns. Scatter plots show the decay of patterns by loss of correlation over increasing time steps. C Dynamics of individual neurons in adaptation. The right activity map was sorted according to the position of the peak activity step for each neuron. Small panels show the enlarged sector indicated as the gray and black bars. D–F Dynamics of cortical memory traces. D Mice were subjected to several trials of contextual fear conditioning training or memory recall over one month. Representative images of EGR1-EGFP signal in recent and early recall trials in visual cortex. Red, EGFP signal in homecage trial of day 0; Green, EGFP signal in context A recall trials. Arrowheads indicate the trace neuron of day 4 and arrows indicate the trace neurons of day 17. Scale bar, 40 μm. E, F Simulated activities of individual neurons (for details see “Methods” section) (E) and recorded memory trace responses over 30 days (F). Neurons counted as traces are the most active neurons on the referenced day (ΔF over 3x of standard deviation). In the simulation (E), neurons counted as traces are the most active neurons on the referenced cycle (ΔF over 3 x of standard deviation, on 20th, 40th, and 140th round of updating). Simulated activities in those three cell populations are shown. Early phase, day 2–4 traces vs. later phase, day 7–28 traces: n > 80 memory trace neurons from 6 mice for each group; ***p < 0.001, two-way ANOVA. Error bars, s.e.m.

Observation of biological memory traces in mouse neocortex as predicted by RAPP

In mouse neocortex, intense (ΔF over 2.8 folds of standard deviation), but sparse neuronal activity (in less than 1% of the population) has been observed as stimulus-related “memory traces”¹⁷. We trained the mice for three blocks of contextual fear conditioning training and imaged their cortical Egr1-EGFP signals one hour after training and 1.5 h recall trials. Repeated anesthetization processes every other day did not alter animal performance in memory retrieval trials (Supplementary Fig. 6). Mice showed stable freezing behavior from day 4 to day 28 (Supplementary Fig. 7). Consistent with the predictions of the RAPP rule, when the mice were imaged in CtxA for one month, memory traces were identified in different neurons (Fig. 2D) in early and late trials. Some strongly activated neurons in early trials reduced their activities in later recall trials. In contrast, some weakly activated neurons in the early phase significantly increased their activities later on.

Furthermore, the simulation work also predicted that the responses of the trace neurons are dynamic. Traces activated in early trials decay fast and traces emerging in the later trials decay slowly (Fig. 2E). The empirically observed biological responses in the brain confirmed this prediction (Fig. 2F). Thereby, the quantitative formula of cortical adaptation as the RAPP phenomenon perfectly predicts the emergence and the dynamics of the long-lasting memory traces in layer 2/3 of neocortex.

The slope of population adaptation in RAPP is modulated by hippocampus-dependent memory

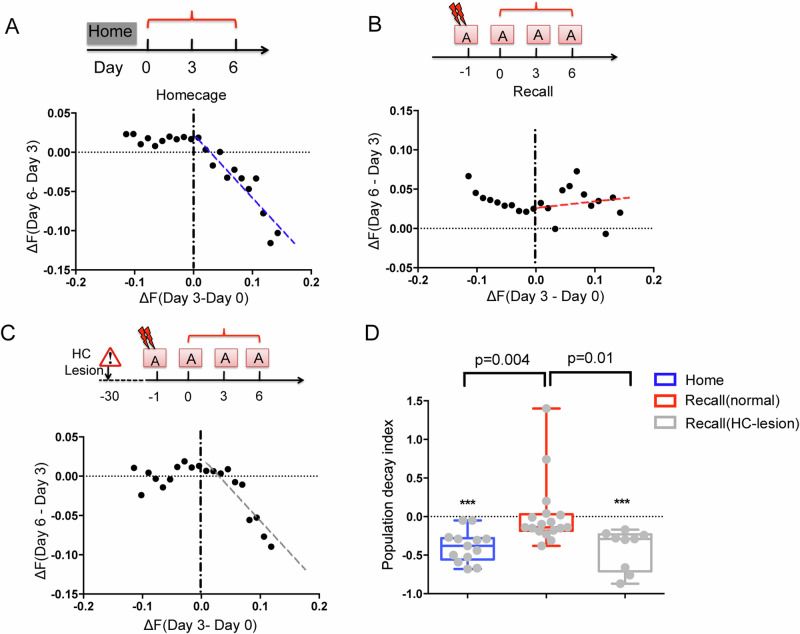
It has been reported that the hippocampus reinstates the cortical representation during memory recall³³. Thus, we wondered if hippocampal input might reverse the effect of populational adaptation. To address this question, mice were trained for a contextual fear conditioning task (using a mild electric footshock) in context A on day 1, followed by recall tests in the same context for 3 trials. While the population activity showed a rectified linear correlation (slope = −0.4) between the early and later testing in the homecage trials (Fig. 3A), indicating a general decay of the activated ensemble on day 3, it produced no significant adaptation (slope > 0) in the conditioned context (Fig. 3B). Interestingly, in hippocampus damaged mice, the population activity showed strong adaptation (slope < 0) in the conditioned context (Fig. 3C, D). Such a hippocampus-induced reversal of populational activity adaptation appears to reinstate the cortical activity patterns, preventing it from adaptation. Consistent with is observation, previous studies have shown that activities of cortical memory traces are engaged by hippocampus-regulated cortical γ-synchrony³⁴. Thereby, the slope in the RAPP phenomenon appears as the result of two factors: the homeostatic adaptation reset the network to its original state and the hippocampus-dependent memory signal reinstate the perturbation in each day.

Fig. 3. The hippocampus reverses cortical population adaptation in the conditioned context.

A–C Example of cortical population plasticity in the visual cortex, in homecage (A), or conditioned context in normal mice (B) or animals with HC lesion (C). Each dot shows the mean changes of signal intensity in a neuron subgroup. D The decay slope (as the dashed lines in A–C) of the activated neurons between the prior and the posterior section. n = 13 mice for home; 9 for HC-lesion; 17 for normal recall. Error bars, s.e.m.

Functional distinct cortical areas show different adaptation rate in RAPP

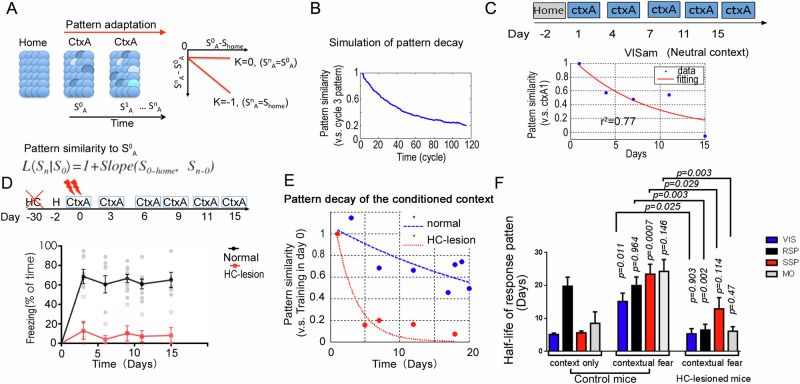
As hippocampus-dependent memory signals might be variable in distinct cortical areas, we were wondering if the population adaptation described as RAPP are region specific. To this end, we presented the mice in a neutral context for several days to observed the context associated population adaptation. RAPP predicts the decay of cortical populational response in a time-dependent manner (Fig. 2B). To quantify the pattern changes, we calculated the slope parameter α of the CtxA-activated cellular Egr1-EGFP signal (compared to homecage) versus the alterations of recall signals (compared to the first CtxA trial) for the mean activity values of all the CtxA-activated subgroups (Fig. 4A). Thereby, signal reductions in highly activated neuron subgroups in CtxA imposed stronger influence on the general activity pattern of CtxA than the reduction in less activated subgroups. Model simulation based on the RAPP demonstrated a putative time-dependent decay of the populational activation pattern (Fig. 4B). We then experimentally measured the pattern decay in mouse visual cortex. The subjects were placed in box A for 5 repeated trials. The representation pattern (relative to day 1 in CtxA) in layer 2/3 neurons of visual cortex indeed showed a trial-to-trial decay across two weeks, with a half-life around 5 days (Fig. 4C).

Fig. 4. Hippocampus reinstates cortical representation pattern in multiple areas of neocortex for the conditioned context.

A, B Simulation of the pattern similarity decay using the empirical parameters of the population plasticity. A Gaussian-distributed activity pattern was used as the initial seed. The pattern in the third cycle was treated as the initial representation. α, is the slope parameter. C Representative example of pattern similarity decay after repeated CtxA exposure in VIS cortex of mice. The mouse explored the box A for 3 min each day. Data was fitted with an exponential curve (red). D Freezing in box A after contextual fear conditioning in hippocampus-lesion group (n = 5 mice) and normal group (n = 9 mice), Two-way ANOVA test, group p < 0.0001. E Representative example of population activity pattern decay in the VISam of normal mice (Blue) and HC-lesion mice (Red). F Quantifications of the half-life for the pattern decay in each recorded areas of normal mice (Control) and HC-lesion mice. Context only group, n = 6 mice; contextual fear group, normal, n = 9 mice; HC-lesion, n = 5 mice. Multiple cortices were recorded from one mouse. The roof of half-life was set to 40 days. Error bars, s.e.m.

To ask if the decay of population activation patterns is regulated by hippocampus, we performed a hippocampus-dependent fear memory task. As the hippocampus reverses the population adaptation in neocortex, the decay of response patterns would be attenuated in the conditioned context. The hippocampus was critical for the recall of contextual fear memory and was engaged by conditioned context^33,35–37. In the experiment, normal mice, but not hippocampal damaged mice (HC-lesion), showed freezing upon repeated exposure to the conditioned box (CtxA) (Fig. 4D). Consistently, in HC-lesion mice, the representation pattern decayed much faster than that in the normal mice in the visual cortex (Fig. 4E).

At last, we measured population activation pattern decay in distinct cortical areas, including visual cortex, retrosplenial cortex, somatosensory and motor cortices. Interestingly, higher order cortices, such as the retrosplenial cortex, showed a slower decay of the activation pattern than the early sensory cortices for the neutral context (Fig. 4F). But in the contextual fear memory task, all of the recorded areas showed slow decay (Fig. 4F). Furthermore, in the hippocampus-lesioned mice, the pattern decay rate for the conditioned context were similar to those in the neural context in VIS, SSp and Mo of normal mice. Interestingly, retrosplenial cortex showed significant faster decay in the HPC lesioned mice than that in the normal mice, suggesting this region might receive inputs from hippocampus both in the neural context and the conditioned context. These observations implicated differential cortical adaptation dynamics at distinct regions are mainly due to inputs from hippocampus (Fig. 4F).

Simulation reveals contributions of both local inhibitory connections and learning modulated neural excitability in shaping RAPP

Long-term memory is consolidated in neocortex, the process of which is mediated by hippocampus. Then, the long-term memory could be retrieved independent of hippocampus^5,38. The question is how the cortical network modified it properties to store the information from hippocampus. As the observed RAPP phenomenon demonstrates the hippocampus reinstates the cortical signals against homeostatic adaptation, similar to the consolidation process, we wanted to simulate the parameters of RAPP by manipulating synapses in an artificial cortical network. We would ask if the synaptic plasticity in cortical network is able to hold on to the RAPP parameter (k > −1) without external influence (i.e. from hippocampus).

Under this hypothesis, we considered the RAPP parameter in homecage conditions to avoid strong and direct influences from sensory-related activation, as well as from hippocampus-related activation. In habituated homecage condition, the Egr1-EGFP signal is mainly correlated with spontaneous activities so that the alterations of population activities are mainly due to the network rewiring.

For the simulation model, we considered on the artificial neural network with inhibitory connections and excitatory connections on excitable neurons (n = 5000) with 20% of inhibitory neurons and 80% of excitatory neurons. The model was adapted from Ref. ³⁹, and its parameters were modified by referring to the Refs. ^40,41. And the random inputs to the network were used to simulate the habituated homecage conditions to generate this RAPP adaptive responses. Connections between neurons were rewired randomly across days (for details see Methods section).

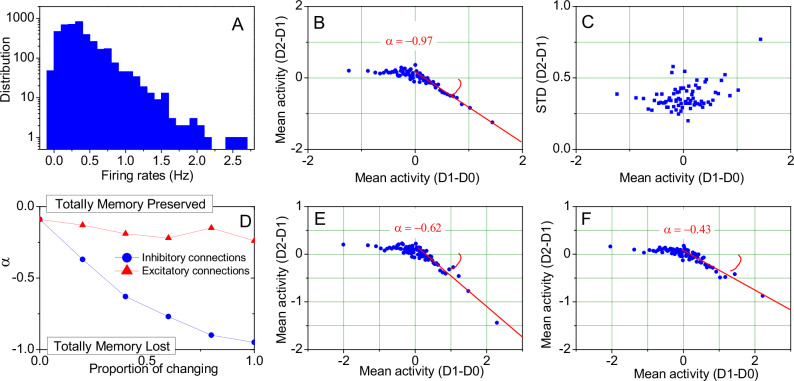
Computational modeling reveals that the rectified linear adaptation of the neural activity of memory traces can be directly accounted for by correlated and long-tail distributed neuronal activities (Fig. 5A). In layers II-III of cortical networks, the balance of Excitation/Inhibition (E/I) as an intrinsic cortical property skews the neural activity distributions to have a long tail^42,43, which then results in a rectified linear correlation (Fig. 5B, C). Due to the total rewiring of connections, the slope is around −1, indicating the total loss of the memory. We found this model can qualitatively account for those observations in a very wide range of parameters, not only limited to the parameters we demonstrated.

Fig. 5. Simulation results of the E/I balanced network.

A Long-tail distribution of firing rates of all excitatory neurons of the balanced network. B, C Mean activity and standard deviation of the rectified linear adaptation of the neural activity of memory traces based on different network realizations on day D1 and day D2 (excitatory neurons are identical). D Dependence of the slope parameter α on a partial change of connections, showing greater sensitivity to the rewiring of inhibitory connections. E Rectified linear neuronal adaptation with 40% common inhibitory connections on day D1 and day D2 (excitatory neurons are identical). F Further refinement of neural engram encoding as shown in panel (E) by learning of firing threshold potentials at the single cell level.

In order to modify the network to mimic the slope in RAPP to reverse homeostatic adaptation and encode memories, we tried to preserve parts of the network connections. Interestingly, the modeling results show that alteration of inhibitory connections more strongly affect the adaptation rate than excitatory ones (Fig. 5D). When all of the inhibitory connections remained stable, rewiring of the excitatory connections did not alter the slope in RAPP (Fig. 5D, red line). This simulation suggests the regulation of inhibitory neurons would be essential to adjust the population adaptation and to keep the memory components in neocortex. Giving inhibitory neurons play a major role in local oscillatory activities⁴⁴, the simulation was consistent with the biological evidences that regulation of the cortical-cortical oscillation synchrony is essential for cortical memory storage³⁴, even in the hippocampus damaged animals. In addition, this simulation also provides the potential for encoding and recalling multiple memories in a single balanced network (see Methods for details). Further simulations show that learning of the firing threshold at the single cell level can further reduce the adaptation to gain stronger memory component by the network (cf. parameter α in Fig. 5E, F). Thereby, simulations on the cortical RAPP phenomenon implicates the situation of memory system consolidation where the hippocampus strongly alters the adaptation rate of neocortex via remodeling local inhibitory circuits.

Discussion

The plasticity of the neocortex and hippocampus for memory storage has been widely recognized^5,45,46, implying the existence of persistent stimulus-related memory traces in the brain. Our studies indicated that the adaptation of network activity patterns is a fundamental intrinsic property of the neocortex and appears as a characteristic activity-dependent population plasticity phenomenon. The populational activity adaption in RAPP results in the decay of activity patterns overtime. In the same time, sparse neuronal outliners emerge and are distilled as long-lasting memory traces due to the increased variability in the engaged population and the residual potentiation on top of hemostatic adaptation. Although the response in each neuron appears stochastic, RAPP directed adaptation of population responses in neocortex implicates the emergence of long-term memory.

Previous studies have shown the causal role of the immediate-early-gene-labeled cells in retrosplenial cortex and hippocampus as sparse memory traces for the storage and recall of memories^25,47. While the hippocampal activity reinstates the cortical memories³³, cortical engram activity is modulated by hippocampus for memory encoding and retrieval³⁴. The population plasticity rule ensures the generation of long-lasting memory traces in the plastic brain, by strengthening the activity of just a few trace neurons. At the same time, the RAPP rule also implies that the activity of the majority of memory-related cortical neurons goes through time-dependent adaptation.

Adaptation is the intrinsic property of the brain, as it has been shown in homeostasis regulation^20,21. While the populational adaptation can be characterized as the RAPP phenomenon, it is still unknow how it is generated. While neurons receive balanced excitatory inputs and inhibitory inputs⁴⁸, increased activity could promote synaptic facilitation either in inhibitory or in excitatory connections in a random manner, thereby increasing the population variability. Furthermore, the occurrence of inhibitory connections may be higher than that of excitatory connections^49–51. Consistently, simulations using spiking neural network model demonstrated that the modification on inhibitory connections provides the much stronger contributions to the network adaptation than the excitatory connections (Fig. 5D). Similar to this finding, memory encoding and retrieval in neocortex are regulated by oscillatory activities³⁴, whereas local inhibitory neurons play critical role in modulating the oscillatory activity⁴⁴.

One interesting question will be if RAPP-imbedded learning algorithm in the artificial neural network (CNN) showed better performance? With the finding of RAPP in the cortical network, we studied whether this RAPP will contribute to the efficient learning of the brain. To answer this question, we implanted the RAPP rule into the backpropagation algorithm in a deep-learning network for handwritten digit recognition. We adopt a well-described CNN structure provided by Schott et al. ⁵² used in recognition task of handwritten digits (MINST Database). There are 4 convolutional layers with kernel sizes = [3–5] and channel numbers = [20,70,256,10] in the CNN model.

All subsequent comparisons of optimizers are performed on this network. The idea is to use the RAPP as an adaptive module for the momentum of each round of backpropagation step (Supplementary Fig. 8A). With this RAPP module of momentum, the gradient descend steps will introduce the adaptation and memory components for each movement to identify the optimal weights toward zero error (Supplementary Fig. 8B). The “Adam” optimizer is a state-of-art learning algorithm⁵³ for this task to achieve high accuracy and fast training speed. We used “Adam” optimizer as a reference to test the effects of RAPP module. To ask if the cortical adaptation rules will help with small-sample size problem, we trained the DNNs for the MINST recognition task with only 50/100/500 samples and then tested their recognition accuracy in 10000 samples. The minibatch size for training is also set to 2 for 50/100 samples and 4 for 500 samples to fit for the small sample size task.

To make a fair comparison between each optimizer, we chose the parameters to get the best accuracy as the benchmark parameters for each one (See Methods for details). While the learning speed is adjusted in “Adam” to improve the best accuracy, RAPP converge considerably faster than Adam in the case of small sample size (50 or 100 samples) (Supplementary Fig. 8C). Importantly, the final recognition accuracy of DNN trained with RAPP module achieves the best score, comparing to the baseline without optimizer (p = 0.031, 0.00095 in 50, 100 samples, paired Student’s t test, Supplementary Fig. 8D). However, RAPP rule manifests a clear disadvantage both in terms of performance when given training samples with a big size (500). We speculate the improvement by RAPP module is mainly due to the momentum factor that keeps the residual impact of each sample, rather than normalizing them. To confirm it, we set the variation in RAPP to 0, leaving no trace memory of those samples, the model did not result in good performance. Thereby, RAPP module might help to improve learning in current CNN, in condition of vary small sample size.

Population plasticity is an intrinsic property of dynamic neural networks. We postulate that such population dynamics are essential for both the flexibility and the long-lasting nature of memories in the brain. The decay of population responses might largely reduce the redundancy of sensory representations⁵⁴, leaving sparse traces of highly active neurons to efficiently represent the information¹. For example, the population representation of neurons in VISam for a novel environment gradually adapts to selective responses in a few trace neurons¹⁷. Thus, our studies revealed a fundamental rule of cortical dynamics and suggested its role in the adaptation of cortical representations and learning.

Methods

In vivo imaging

Mouse strain: BAC-EGR-1-EGFP (Tg(Egr1-EGFP)GO90Gsat/Mmucd, from Gensat project, distributed from Jackson Laboratories). Animal care was in accordance with the Institutional guidelines of Tsinghua University and ShanghaiTech University. All animals were maintained in the Tsinghua University animal research facility. The Laboratory Animal Facility at the Tsinghua University is accredited by Association for Assessment and Accreditation of Laboratory Animal Care International (AAALAC), and protocols are approved by the Institutional Animal Care and Use Committee (IACUC). Mice were housed in groups of 3–5 on a standard 12-h light/12-h dark cycle, and all behavioral experiments were performed during the light cycle. We have complied with all relevant ethical regulations for animal use. 3–5 months old mice received cranial window implantation as previously described¹⁷; recording began 1 month later. To avoid unexpected damage to the cranial window, mice were single housed. To implant the cranial window, the animal was immobilized in custom-built stage-mounted ear bars and a nosepiece, similar to a stereotaxic apparatus. A 1.5 cm incision was made between the ears, and the scalp was reflected to expose the skull. One circular craniotomy (6–7 mm diameter) was made using a high-speed drill and a dissecting microscope for gross visualization. A glass-made coverslip was attached to the skull. For surgeries and observations, mice were anesthetized with 1.5% isoflurane. EGFP fluorescent intensity (FI) was imaged with an Olympus Fluoview 1200MPE with pre-chirp optics and a fast AOM mounted on an Olympus BX61WI upright microscope, coupled with a 2 mm working distance, 25x water immersion lens (numerical aperture, 1.05). A mode-locked titanium/sapphire laser (MaiTai HP DeepSee-OL, Spectra-Physics, Fremont, CA) generated two-photon excitation at 920 nm, and three photomultiplier tubes including two GaAsP equipped with cooling features (Hamamatsu, Ichinocho, Japan) collected emitted light in the range of 380–480, 500–540, and 560–650 nm. The output power of the laser was maintained at 1.56 W, and power reaching the mouse brain ranged from 7.8 to 12.5 mW. For each cortical volume, the laser power was consistent during time-lapse images under multi-tasks. The depth effect of the 2-p microscope was calibrated by adjusting the PMT voltage, calibrated for the mouse line with universally expressed EGFP. To facilitate localization of cortical volumes from section to section, Dextran Texas Red (Dex Red; 70,000 molecular weight; Invitrogen) was injected into a lateral tail vein to create a fluorescent angiogram, as previously described⁵⁵.

Imaging data analysis and quantification

The multi-photon images were subjected to 3-D motion detection using a custom-made algorithm. In brief, we choose the positions of cells detected by classifiers, which were trained through a Support Vector Machine (SVM), as key alignment points of the recorded cortical volume. Then the least square rule was used to estimate the transformation matrix and a Scale Invariant Feature Transform (SIFT) algorithm was used as the descriptor of those key points to perform the motion correction in 3-D space. The stack images were further quantified with Matlab (MathWorks, Natick, MA). The 3D volume view was created using Image-J (NIH). The center position of each detected neuron was determined automatically through a deep neural network-based recognition algorithm and further validated manually. The EGFP intensity in each cell for each trial was quantified around the cell center as the averaged intensity in a 12×12×9 μm voxel. Data analysis was performed by custom-written code in Matlab. Imaging data were segregated using the algorithms developed in the lab¹⁷ and manually corrected to detect each neuron. Typically, 9000–14,000 EGR1⁺ neurons were quantified in a cortical volume (509x509x800μm, layer I-VI). The automated 3-D align and segmentation software is available upon request from the corresponding author. The EGFP signal in each volume at each trial was normalized by the maximum signals of the top 50 neurons in each volume.

Hippocampal lesions

Mice were anesthetized with 2% isoflurane and placed into a stereotaxic frame. A midline incision was made on the scalp, the skin was reflected and the skull overlying the targeted region was removed. Injections of NMDA (10 mg/ml, dissolved in 0.01 m PBS) were given using a 2ul Hamilton syringe (AP, −2.2; ML, −2; DV, −2.5). Injections of 0.25 μl were given over a 2.5 min delivery period. Behavior assessments of the subject for seizure and mobility abnormality were performed immediately after surgery to determine the effect of hippocampal lesions. The mice were allowed to recover for 1 week before receiving the cranial window implantation.

Contextual fear conditioning and neutral context exploration trials (Context A)

Context-dependent fear conditioning in context A. Context A is a cylinder box with white walls and grid floor. The box was wiped out with alcohol to generate an olfactory stimulus. Training consisted of a 3 min exposure of animals to the conditioning box (Multi-conditioning system, TSE system) followed by a foot shock (2 sec, 0.8 mA, constant current). For intensive training, the same procedure is performed for 3 times. The memory test was performed 24 h later by re-exposing the mice for 3 min to the conditioning context. The results were validated by the automatic freezing counting in the TSE system. We also measured freezing by human observer. Freezing, defined as a lack of movement except for heart beat and respiration associated with a crouching posture, was recorded every 10 sec by two trained observers (one was unaware of the experimental conditions) during a 3 min period (a total of 18 sampling intervals). The number of observations indicating freezing obtained as the mean of both observers was expressed as a percentage of the total number of observations. For the retrieval trial, the mouse was placed in the chamber for 3 min. In each recall section, mice were tested for 3 min in the chamber and returned to their homecage, then, 1.5 h later, they were subjected to two-photon imaging. For the long-term memory task (Fig. 2), a foot shock was delivered immediate after the recall section on day 7 and day 19 to reinforce the fear memory. For the control experiment, mice were trained in conditioning context and returned to homecage. Mice were anesthetized with 1.5% isoflurane for one hour to perform a mock section of observation on day 3 and day 6 and a recall section was performed on day 8.

Behavioral analysis

All animal behaviors in the contexts were recored and analyzed using the computerized TSE Multi Conditioning System 2.0 (TSE 2.0). The location of mouse was detected by the horizontal and depth infrared photobeams. Analysis parameters used in the software were defined as follows. Grooming > 3 s, freezing > 1000 ms, activity > 3.0 cm/s.

Neuronal culture and stimulation

Embryonic cortices (E17) of EGR1-GFP BAC transgenic mice (Genesat Project) were isolated using standard procedures and triturated with trypsin/DNAse digestion. Cortical neurons were plated at a density of 10,000 cells per well in black/clear bottom plates coated with the poly-D-lysine (Costar) in the neurobasal medium (1.6% B27, 2% glutamax, 1% pen/strep, and 5% heat-inactivated fetal calf serum) and in the neurobasal medium without serum 24 h later. Under these culture conditions, the percentage of glia was estimated to be in the range of 5–25. The optogenetic method was used to perform the light-induced stimulation. pLenti-CaMKIIa-hChR2-mCherry-WPRE was a gift from Dr. Deisseroth^56,57. ChR2-mCherry vector was transfected in the cultures. An array of LED lamps (~480 nm, 3.0–3.2 v, 1000–1200mcd/lamp, 25 mW) was placed 10 cm above the culture dish. LED lamps were controlled by the SCM control electric circuit (single chip micyoco, specifically, AT89S52 and AT89C52). Light pulses were given at 5 ms per pulse. The cultured neurons were transfected at DIV4 and stimulated at DIV7. After the transfection, neurons were kept in a dark box. Cells were harvested and subjected to RT-qPCR at the indicated time points immediate after LED pulses. Total RNA was extracted from cells or tissues with TRIzol (Invitrogen) using the manufacturer’s protocol. 1ug of total RNA was reverse transcribed by TransScript One-Step gDNA Removal and cDNA Synthesis SuperMix (Transgene), using Oligo(dT)₁₅ for mRNA and random primer for nascent RNA. Quantitative PCR was performed with SYBR-Green-based reagents (SsoFast^TM EvaGreen supermix; Bio-Rad), using a CFX96 real-time PCR Detection system (Bio-Rad).

Statistics and reproducibility

Data were represented as mean ± s.e.m. Box or violin plots were represented as the mean, interquartile range and the minimum and maximum. Column values are tested if the values come from a Gaussian distribution via D’Agostino & Pearson omnibus normality test. Statistical significance was determined by unpaired or paired two-tailed Student’s t test, one or two-way ANOVA. *P < 0.05; **P < 0.01; ***P < 0.001; ****P < 0.0001. Quantitative displays were produced using GraphPad Prism version 6 (GraphPad software, SanDiego California USA) and Matlab (Mathworks, Natick, MA, USA). Data is available upon request.

Data processing and simulation

The pattern similarity (Fig. 4) was calculated as slope + 1, where the slope was determined by the linear regression of activity changes to the learning trial (the reference trial) in each neuron and the task-induced activity in the reference trial (v.s. the homecage trial). The slope for the activity pattern identical to the learning trial was 0, resulting in a similarity pattern of 1. For each volume, neurons were grouped in multiple subgroups, according to the intensity of task-induced activity in the reference trials. More than 200 neurons were considered in each subgroup. Only the activated neurons in the reference trial were considered. The means of signals for each subgroup were used for the linear regression to reduce the noises.

Trace neurons were defined as those neurons with induced activity (ΔF, v.s. homecage) higher than 3 folds of standard deviation in the layer 2/3 population of the reference day.

For the simulation, 3,000 neurons with Gaussian-distributed activities were used as seed. A random perturbation, using Gaussian-distributed noise, was imposed on the second trial with 8% of variation. In the following trials, the system was updated according to the empirical constants of the population plasticity rules, as summarized in Figs. 1 and S2. Activities of each neuron are determined according to RAPP rule by adding an alternation amplitude component as ΔS₂^Amp and a random variation component determined by ΔS₂^s.d.. Thus, we define the adaption is following normal distributed random number under this given conditions. That means:

$$R\left(x\right)~N\left(\mu \left(x\right),\sigma {\left(x\right)}^2\right),$$

when

$$\mu \left(x\right)=\mathrm{\Delta }{\mathrm{S}}^{\mathrm{A}\mathrm{mp}}$$

$$\sigma \left(x\right)={\mathrm{\Delta }\mathrm{S}}^{\mathrm{s}.\mathrm{d}.}$$

Where

$${\mathrm{\Delta }\mathrm{S}}_2^{Amp}=\left\{\begin{array}{c}\hfill -0.34\times {\mathrm{\Delta }\mathrm{S}}_1^{Amp},\mathrm{\Delta }{F}_1>-0.05\hfill \\ \hfill 0.013,{\mathrm{\Delta }F}_1<-0.05\hfill \end{array}\right)$$

$${\mathrm{\Delta }\mathrm{S}}_2^{s.d.}=\left\{\begin{array}{c}\hfill 0.21\times {\mathrm{\Delta }\mathrm{S}}_1^{Amp}+0.05,\mathrm{\Delta }{F}_1>-0.05\hfill \\ \hfill -0.07\times {\mathrm{\Delta }\mathrm{S}}_1^{Amp}+0.05,{\mathrm{\Delta }F}_1<-0.05\hfill \end{array}\right)$$

In the next round, the signal is updated accordingly. In this way, the trace neuron responses and the representation pattern decay in the simulated system were quantified in the same way as the experimentally measured activities in mouse neocortex.

Excitation-inhibition (E-I) balanced network model and data analysis

While using artificial models to explain the mechanisms underlying RAPP, in order to match the experimental procedures, data in the model simulations were analyzed in the same way.

Data were firstly sorted according the activity changes from the default state (on day D0 in home cage) to the first exploration of the event (on day D1), labeled as Activity (D1-D0). A moving window of the size $n_{win}$ was used to group the neuron in terms of sorted activities and we calculated the averaged activities within this group, labeled as Mean activity (D1-D0). The step of the moving window was $n_{dropout}$, meaning that for each step we dropped out the $n_{dropout}$ data points with the smallest values of Activity (D1-D0), and brought the next $n_{dropout}$ points into the group, to calculate the next value of Mean activity (D1-D0). At the meantime, we calculated within each group the mean values of the change of the neural activities from day D1 to day D2 when the animal explored the repeated event, labeled as Mean activity (D2-D1) and the standard deviation of those changes, labeled as STD (D2-1).

To fully match the experimental procedures, we also focused on the dependence of Mean activity (D2-D1) on Mean activity (D1-D0), as well as the dependence of STD (D2-D1) on Mean activity (D1-D0). Specifically, after using the linear least squares to fit the data, we denoted the slope as α.

Without loss of generality, we simulated a representative integrate-and-fire models. Specially, the he model was adapted from Ref. ³⁹, The qualitative properties of the model are in fact robust in a very wide range of system parameters, and we particularly modified the parameters referring to the Refs. ^40,41, in order to make the model also quantitatively plausible.

The dynamics of the membrane potential V of each neuron is described by

$${\tau }_{inh,ex}\frac{dV}{dt}=\left(V_{rest}-V\right)+g_{ex}\left(E_{ex}-V\right)+g_{inh}\left(E_{inh}-V\right)$$

where ${\tau }_{inh,ex}$ describes the time scale of the neuron in inhibitory or excitatory populations. Specifically, ${\tau }_{inh}$= 20 ms for inhibitory neurons, and ${\tau }_{ex}$= 10 ms for excitatory neurons. Whenever the membrane potential of a neuron crosses a spiking threshold $V_{th}$, an action potential is generated and the membrane potential is reset to the resting potential $V_{rest}$= −60mV. Reversal potentials of synapses for excitatory and inhibitory neurons are $E_{ex}$ = 0 mV and $E_{inh}$ = −80mV, respectively. $V_{th}$ equals to a baseline value $V_{th0}$ plus a temporal fluctuation $V_{thf}$. $V_{thf}$ uniformly distribute between −2.5 mV and 2.5 mV. $g_{ex}$ and $g_{inh}$ are the positive and negative dimensionless synaptic conductance, and their evolutions exponentially decay with

$${\tau }_{se}\frac{d{g}_{ex}}{dt}=-g_{ex}$$

and

$${\tau }_{si}\frac{d{g}_{inh}}{dt}=-g_{inh}$$

When a neurons fires, appropriate dimensionless synaptic conductance of its postsynaptic targets is increased as $g_{ex,inh}\to g_{ex,inh}+\delta g$. The value of $\delta g$, depends on the excitatory or inhibitory properties of both the presynaptic and postsynaptic neurons. Specifically, we used $\delta g=0.2$ if both the pre- and postsynaptic neurons are excitatory, $\delta g=0.46$ if the presynaptic neuron is excitatory and postsynaptic neuron is inhibitory, $\delta g=3.05$ if the other way around, and $\delta g=3$ if both the pre- and postsynaptic neurons are inhibitory, to ensure the system located in the balanced region and have proper firing rates. The refractory period for all the neurons is a constant, and fixed as 2.5 ms. Time step for simulation is fixed as 0.05 ms. For each time step, a random input is injected with a small probability $p_{input}$, and the neurons which will receive external input are randomly selected each time from the excitatory population, of the number which is uniformly distribute between zero and $N_{inputmax}$. When one neuron receives external input, the same operation is taken as the neuron receives the excitatory inputs on the network, i.e. $g_{ex}\to g_{ex}+\delta g$, and the value of $\delta g$ is the same as the one with both pre- and postsynaptic neurons are excitatory, namely $\delta g=0.2$. We totally simulate n = 5000 neurons randomly located on a $L\times L$ 2-dimentional plane. The proportion of inhibitory neurons is fixed as 20%, and the excitatory neurons is 80%.

It is easy to set up an E.-I. balance model with such connection properties and connective strength parameters. In order to demonstrate that the results are parameters robust, we used different sets of parameters in this work. For example, it can be that ${\tau }_{se}$ = 20 ms and ${\tau }_{si}$ = 5 ms, and regarding the input, $p_{input}=3\%$ and $N_{inputmax}=4$, by using which the model does not have macroscopic rhythm, and when we used ${\tau }_{se}$ = 10 ms, ${\tau }_{si}$ = 5 ms, $p_{input}=2\%$ and $N_{inputmax}=40$, the macroscopic dynamics is oscillatory in alpha band. In this step, we do not aim to set up any intrinsic particular difference among neurons, so that we fix $V_{th0}$ identically as −50mV for all the neurons.

1000 excitatory neurons uniformly and randomly connect their postsynaptic targets with a proportion $\mu ={\mu }_0=8\%$. The other 3000 excitatory neurons and all the 1000 inhibitory neurons only connect locally to their postsynaptic targets, with the probability

$$\mu =\frac{{\mu }_0}{2\pi r_0}{e}^{-\frac{r^2}{2r_0}}$$

Where $r$ is its distance to the potentially postsynaptic target, and $r_0=0.12L$. Periodic boundary condition is used.

Memory encoding indicates the change of system parameters. In theory, there could be various ways of changing the parameters to enable the network to encode memories, out of which, we used two examples to demonstrate the memories can always be embedded in RAPP. First, we preserved parts of the network connections and randomly rewired others. Second, we enabled single cells to learn the firing threshold on day D2 based on the neural activities on day D1. Specifically, we first calculated the average, the maximum and the minimum firing rates of all excitatory neurons on day D0, labeled as ${\mathrm{\rho }}_{\mathrm{mean}}$, ${\mathrm{\rho }}_{\max }$, and ${\mathrm{\rho }}_{\min }$, respectively, and defined the range of the firing threshold sampling pool as [$V_{th\_\min S}$, $V_{th\_\max S}$,]. The firing threshold on day D2 of the neuron which had the firing rate ρ on day D1 was then defined as

$$V_{th}=\left\{\begin{array}{c}\hfill V_{th0}-\eta \left(V_{th\_\max S}-V_{th0}\right)\frac{\left(\rho -{\mathrm{\rho }}_{\mathrm{mean}}\right)}{\left({\mathrm{\rho }}_{\max }-{\mathrm{\rho }}_{\mathrm{mean}}\right)},if\rho >{\mathrm{\rho }}_{\mathrm{mean}}\hfill \\ \hfill V_{th0}+\eta \left(V_{th0}-V_{th\_\min S}\right)\frac{\left({\mathrm{\rho }}_{\mathrm{mean}-}\rho \right)}{\left({\mathrm{\rho }}_{\mathrm{mean}}-{\mathrm{\rho }}_{\min }\right)},if\rho \le {\mathrm{\rho }}_{\mathrm{mean}}\hfill \end{array}\right),$$

where $\eta$ is a random number uniformly distributed between 0 and 1.

Encoding and recall of two memories in a single network

Even with the same statistical property, one can always generate different networks realizations by sampling connections from the fixed distribution. In this part, different network realizations with the same statistical property were used to mimic how the cortical network morphologies encoded different environments, and the recalling processes were mimicked by injecting additional excitatory inputs to target inhibitory populations.

We selected two network realizations NB and NC corresponding to two environments B and C where the animal is supposed to remember specific contexts (NB and NC encoded the whole information of environments B and C), and arbitrarily selected another two network realizations N0 and N1 (without any information of the environments B or C). N0 was supposed to correspond to the default environment (home cage), and parts of the connections of N1 were used to design the target network realization NX, which was supposed to encode the memories of environments B and C simultaneously. To this end, NX was set to have all the excitatory connections from N1, i.e. totally different compared to NB and NC, but its connections originated from the first 400 inhibitory neurons (40%) which were the same as for NB (which we labeled as inhibitory population InB), and connections from the next 400 inhibitory neurons (40%) were the same as for NC (inhibitory population InC). The connections from the remaining 200 inhibitory neurons are the same as N1, i.e. different compared to NB or NC. In the simulation of mimicking a recalling process, named SB-Recall, we still gave additional excitatory inputs to inhibitory population InB of network realization NX, and in another recalling simulation, we gave additional excitatory inputs to the inhibitory population InC.

Deep convolutional neural network (CNN) model with RAPP rule

According to the learning rule that we discovered in neocortex during memory coding (Fig. 1B), we tried to find a way to apply those parameters provided by biological data of EGR1-EGFP signals. As the accumulative neural activity changes reflect the alternations of connections, we estimate the adaption of connections according to the EGR1-EGFP data. Firstly, we obtain an adaptation parameter (R(x)) for every step of learning. From the mean activity changes of earlier and later, we assume that the key parameters $x$ of the network in the neocortex obey a similar distribution $R\left(x\right)$. According to the adaptation of EGR1-EGFP signal (Fig. 1E, F), we define that the adaptation of data is normally distributed under the given conditions. That means:

$$R\left(x\right)~N\left(\mu \left(x\right),\sigma {\left(x\right)}^2\right),$$

when

$$\mu \left(x\right)=\left\{\begin{array}{c}\hfill 0.017,x<-0.05;\hfill \\ \hfill -0.34x,x\ge -0.05.\hfill \end{array}\right)$$

$$\sigma \left(x\right)=\left\{\begin{array}{c}\hfill -0.07x+0.05,x<0;\hfill \\ \hfill 0.21x+0.05,x\ge 0.\hfill \end{array}\right)$$

Considering that the connections between neuron nodes in CNN should obey a certain law, we set it to obey the distribution $R\left(x\right)$. To test the RAPP rule on few-shot tasks, we adopt a well-described CNN structure used in recognition task on MNIST dataset. For 5/10 samples per category, the training batch size is set to 2 and the training batch size is set to 4 for 50 samples per category. For the original backpropagation optimizer, the CNN are trained with the learning rate of 0.01, 0.015, and 0.05 for 50, 100, and 500 training samples. For the Adam optimizer, the CNN are trained with the learning rate of 10⁻⁵, 5 × 10⁻⁶ and 0.0002 for 50, 100, and 500 training samples. For the RAPP optimizer, the CNN are trained with the learning rate of 0.01, 0.015, and 0.05 for 50, 100, and 500 training samples. During learning, for each step of error-driven connection modification (Δw_i (t+1)), we add a component of momentum following the RAPP rule, setting as the following:

$$\Delta w_i\left(t+1\right)=lr\cdot \left(\frac{\partial f\left(t+1\right)}{\partial w_i}+c\left(t\right)\cdot R\left(\Delta w_i\left(t\right)\right)\right).$$

Here $f\left(t\right)$ is the whole CNN network, $lr$ is the learning rate and $t$ is the number of training batches. In addition, we set a decay factor, the memory component weight $c\left(t\right)$, is set as the following:

$$c\left(t\right)=\frac{2}{{\left(t/w1+1\right)}^p}.$$

For the RAPP optimizer, the CNN are trained with the $w1$ of 150, 300, and 5 for 50, 100, and 500 training samples. The $p$ is set to 1, 1, and 0.8 for 50, 100, and 500 training samples. According to the training set with few samples are sometimes not representative enough, we will restart the training if the final accuracy is lower than 50% on the training set. When the training samples are expanded to 500, the RAPP optimizer shows a disadvantage in terms of accuracy so we just choose a set of parameters to show the result. On the other cases, the parameters are set to get the best accuracy for each optimizer. In each experiment, the original net and the training dataset is consistent across three different optimizers. The small sample training set is randomly picked in the regular training set consist of 50,000 samples when the test set is the regular test set with 10000 samples. We repeat 36, 74, and 34 experiments for 50, 100, and 500 training samples and show the mean accuracy in supplemental Fig. 8.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Detailed automatic signal processing methodology

Automated cell detection

In the least square method, we should know in advance some corresponding points that are at the same position after image transformation. Generally, these key points can be chosen from corner points, rotationally invariable points and so on. For our particular problem, locations of cells can be naturally used as key points.

Since the deep convolution neural network (CNN) showed outstanding performance in diverse image processing applications in recent years, we trained a convolution neural network classifier to detect cells, with parameters as shown in Table 1. By using sliding windows of different scales in a single frame of a 3-D image, we extracted candidate 2-D patches, rescaled them to a uniform size (17*17 pixel), which is suitable for our data) and identified them through the CNN classifier. To speed up the process, we also trained a simple linear classifier that showed a high recall rate for the training dataset, to select candidates for the CNN model. By observing that the center of a cell patch is brighter than the surroundings, while non-cell patches in this frame do not have this property, we extracted the mean gray value of each row and each column as the feature used in the linear classifier. Due to the sliding windows approach, we typically obtained more than one location for a cell. Therefore, we calculated the simple connected regions with an 8-connected neighborhood in a frame and merged centers in different frames in a small domain.

Table 1.

Structure of our CNN model

	type	input-size	kernel-size	channel	stride
1	Input image	17 × 17 × 1	–	–	–
2	Convolution	17 × 17 × 1	3 × 3	10	1 (pad=1)
3	Max-pooling	17 × 17 × 10	3 × 3	10	2 (pad=0)
4	Non-linear	8 × 8 × 10	–	10	–
5	Normalization	8 × 8 × 10	5 × 5	10	–
6	Convolution	8 × 8 × 10	3 × 3	20	1 (pad=1)
7	Max-pooling	8 × 8 × 20	2 × 2	20	2 (pad=0)
8	Non-linear	4 × 4 × 20	–	20	–
9	Normalization	4 × 4 × 20	5 × 5	20	–
10	Full-connection	320 × 1	–	80	–
11	Non-linear	80 × 1	–	80	–
12	Full-connection	80 × 1	–	2	–
13	Soft-max	2 × 1	–	2	–

Automated image registration

For the convenience of comparison and tracking, we developed an algorithm to automatically warp one 3-D image into another.

Under the assumption that an affine transformation would work well (which indeed proved to be very effective), our algorithm followed the typical framework of image registration with the least square rule, and some modification was made to adapt to the given problem:

1. Locate cells that appear in the two 3-D images I1 and I2 in each image frame and employ them as key anchor points.

2. Extract SIFT features at key points to represent these points and find pairs of key points that should be at the same position after interpolation.

3. Calculate the transformation matrix used in the XY coordinate plane with the conclusion of least square method and warp I1 with the obtained matrix.

4. Apply the operation in step 3 successively on the YZ, XZ coordinate plane

5. Repeat step 1–4 until convergence, which means that I1 changes little after interpolation.

We can see from the above that there are mainly two stages in our algorithm—finding the key points and interpolation. In the first stage, for finding the key points used in the second stage, a classifier is trained in advance to determine whether a small patch is constructed by a cell or not. Then in the second stage, a standard least square method is used on a 2-D plane. This approach is inspired by the idea that an affine transformation in 3-D space can be equally divided into three affine transformations in the subspace of XY, XZ, and YZ planes. These two stages will be explained in the next two sections.

Cell detection

In the least square method, we should know in advance some corresponding points that are at the same position after transformation. Generally, these key points can be chosen from corner points, rotationally invariable points and so on. For our special problem, locations of cells can naturally be used as key points.

By observing a single frame of a 3-D image, we noticed that cell patches have the property that the center of this patch is significantly brighter than surroundings while non-cell patches in this frame do not have this property. In view of this observation, the feature we used in classification was the mean gray value of each row and each column. Then values near the middle of each row (column) will be bigger than sides. For example, if the size of a patch is 15*15, then we can get a 30-dimensional vector as feature in which the first 15 dimensions represent the mean gray value of each row and the last 15 dimensions represent the mean gray value of each column. For different sizes of patches, we can respectively train classifiers or rescale them to a uniform size, and only one classifier is needed.

The classifier is trained with a Support Vector Machine (SVM). It is worth pointing out that we do not need high precision in this step as these locations are served as key points in interpolation, instead of investigating the cells themselves. Therefore, the parameters and threshold can be chosen loosely to make sure more key points are found. And in experiments, patches with a size of 15 × 15 proved appropriate for our data.

Warping and interpolation

After the stage of cell detection, we obtain two sets C1, C2 that contain locations of cells in I1 and I2. Before interpolation, we need to match coordinates in C1 and C2. A natural idea is matching each point in C1 to the nearest point in C2 under the Euclidean metric. However, for regions that have high density of cells, we can easily find that points matched by this way cannot guarantee the right one, as the distance between several matches may be close. If we just refuse matching for this case, obviously, much information is lost. Considering this aspect, we draw on SIFT feature while matching. SIFT is a powerful descriptor in the field of image processing. By comparing the similarity of SIFT feature in C1 and C2, we can obtain pairs of points we need in interpolation. The toolbox of Vl_feat[1] is used while extracting SIFT feature and matching. Besides, we also restrict the distance between pairs of points matched cannot bigger than the threshold set artificially.

Theoretically, using the pairs of key points, a standard process of interpolation can be carried out to achieve our goal [2]. However, as 3-D interpolation is fairly time-consuming, we make some modification to this process and divide the 3-D interpolation into three 2-D interpolations. In 3-D space, any affine transformation can be equally replaced by three successively affine transformations in three orthometric 2-D planes. In the frame of axes, we choose XY plane, YZ plane and XZ plane for convenience. Then each interpolation in 2-D plane can be executed following the step in [2].

Besides, our method is an iterative algorithm. It will stop if the image changes little after one iteration. This is measured by the Frobenius distance between the transformation matrix and identity matrix which means no change is made after interpolation. [1] http://www.vlfeat.org/overview/sift.html [2] http://en.wikipedia.org/wiki/Scale-invariant_feature_transform.

Author contributions

J.-S.G. designed the project. H.X. designed and performed the experiments and data analysis. KY. L. performed the MINST test with the RAPP rule. D.L. Performed the simulation of the RAPP rule in the local inhibitory-excitatory balanced network. C.-S.Z. designed the 3-D motion correction algorithm. C.H. supervised the balanced network modeling part and helped finalization of the manuscript. The manuscript was written by J.-S.G., H.X. and commented by all the authors.

Peer review

Peer review information

Communications Biology thanks Francesco P. Battaglia and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Benjamin Bessieres.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. The source data behind the graphs in the paper (supplementary Data 1).

Code availability

Program codes of both the simulation and CNN RAPP module is available via the following link: https://www.myqnapcloud.cn/smartshare/74he137i7p84o28qu6x85y70_e795j94li22n21830vs3878223dbhgig.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42003-024-07186-2.