Abstract
The two-dimensional (2D) hexagonal group IV–V family has attracted significant attention due to their unique properties and potential applications in electronics, spintronics, and photocatalysis. In this study, we report the discovery of a stable tetragonal allotrope, termed the Td4 phase, of 2D IV–V monolayers through a structural search utilizing an adaptive genetic algorithm. We investigate the geometric structures, structural stabilities, and band structures of the Td4-phase 2D IV–V monolayers (where IV = Si, Ge, Sn; V = P, As, Sb) based on the first-principles calculations. All the investigated 2D IV–V monolayers are dynamically and thermodynamically stable, and exhibit metallic behavior in their pristine form. Furthermore, we investigate the effects of surface hydrogenation on the electronic structures of these monolayers. Except for the hydrogenated GeSb monolayer, the remaining 2D IV–V monolayers turn into indirect semiconductors, with band gap values ranging from 0.15 to 1.12 eV. This work expands the known structural motifs within the 2D group IV–V family and contributes to the ongoing exploration of low-dimensional materials.
Structural prediction of a stable tetragonal Td4 phase of 2D group IV–V monolayers.
1. Introduction
In recent years, the development of electronic devices has moved rapidly in the direction of miniaturized and portable devices, triggering an explosion of interest in low-dimensional materials.1–4 Research in two-dimensional materials, especially two-dimensional honeycomb structure materials, was inspired by the spectacular success of graphene. Due to the unique symmetry of the honeycomb structure, graphene-like two dimensional monolayers manifest a variety of novel electronic properties. In addition to graphene,5 atomically thin films of group IV elements, i.e., silicene,6 germanene,6 and stanene7 have also been predicted to be quantum spin Hall insulators. For group V elements, Sb and As monolayers with buckled honeycomb structures, namely antimonene and arsenene,8 are wide-band-gap semiconductors at their equilibrium lattice constants and can be turned into quantum spin Hall insulators via tensile strains.9 Pristine Sb and Bi monolayer honeycomb structures with planar geometry are reported to be topological crystalline insulators10 while chemically-modified planar Sb and Bi monolayers are predicted to be quantum anomalous Hall insulators.11
In addition to elemental monolayers, single-layer honeycomb lattices of group IV–V compounds have attracted significant attention in recent years. These 2D group IV–V monolayers exhibit three hexagonal allotropes designated as α, α′, and β phases, respectively. The α and α′ phase in the P6̄m2 space group exhibit mirror symmetry, while the β phase in the P3̄m1 space group possesses inversion symmetry.12,13 The difference between the α′ and α′ phase lies in their stacking sequence. In the α phase, the four sublayers are stacked in the IV–V–V–IV sequence, whereas in the α′ phase, they are arranged in the V–IV–IV–V sequence.14 Although these hexagonal phases are close to each other in formation energies, the α phase is energetically more favorable for most 2D group IV–V monolayers. Over the past decade, significant efforts have been dedicated to exploring and tuning the electronic, optical, photocatalytic, and thermoelectric properties of 2D group IV–V monolayers. These investigations have demonstrated that hexagonal 2D group IV–V monolayers possess favorable band gaps and band edge positions for photocatalytic applications,15,16 exceptional power factor for thermoelectric devices,17 and notable spin-valley splitting14 or hidden Rashba effects18 for spintronic applications.
Nevertheless, the hexagonal motif is not the only possible building block of 2D group IV–V monolayers with 1 : 1 stoichiometry. Ashton et al. proposed that 2D group IV–V monolayers can adopt a stable monoclinic Cm phase, which is the 2D derivative of layered bulk structures of SiP,19 and is characterized by buckled IV–V pentagons and hexagons. For 2D group IV–V monolayers (where IV = Si, Ge, Sn, Pb and V = As, Sb, Bi), the Cm phase is more stable compared to the α phase. To date, several C2/m phase 2D IV–V (IV = Si, Ge; V = P, As) monolayers were successfully exfoliated from their bulk counterparts.20 Xu et al. theoretically designed a tetragonal allotrope of 2D IVBi (IV = Si, Ge, Sn) monolayers and proved that these structures are dynamically and thermodynamically stable. This tetragonal phase features alternating square and octagonal rings and exhibit semiconducting behavior with band gaps ranging from 0.062 to 0.226 eV.21
Considering the diverse structural motifs present in 2D monolayers with 1 : 1 stoichiometry, it is reasonable to speculate that novel stable or metastable allotropes are likely to exist within the 2D group IV–V family. Motivated by previous discoveries of allotropes of 2D group IV–V monolayers, we performed a structural search on 2D IV–V monolayers using adaptive generic algorithm and found a new stable tetragonal allotrope (termed Td4 phase) of 2D IV–V monolayers. We report from the first-principles calculations the geometric structures, structural stabilities, and band structures of the Td4 phase of 2D IV–V monolayers. All the 2D IV–V (IV = Si, Ge, Sn; V = P, As, Sb) monolayers exbibit metallic behaviors. We also investigated the surface hydrogenation effect on the electronic structures of the 2D IV–V monolayers in the Td4 structure. Except for the hydrogenated GeSb monolayer, all the other 2D IV–V monolayers becomes indirect semiconductors with band gap values ranging from 0.15 to 1.12 eV.
2. Method
All calculations are performed based on density functional theory and the projector-augmented wave (PAW) representations22 as implemented in the Vienna ab initio Simulation Package (VASP).23,24 The exchange–correlation interaction is treated with the local density approximation (LDA). We employ a kinetic energy cutoff of 500 eV for wave functions expanded in plane wave basis and allow all atoms to relax until forces are less than 10−3 eV Å−1. A tetragonal unit cell was utilized for modeling the crystal structure and a vacuum of ∼15 Å was introduced in the out-of-plane direction in order to avoid interactions between two periodic monolayers. For Brillouin zone sampling, we generate a m × m × 1 Γ-centered grid according to the Monkhorst–Pack scheme,25 with k-point resolution of 0.025 Å−1 for relaxation and 0.01 Å−1 for self-consistent calculation. The phonon dispersions were calculated using the finite displacement approach as implemented in the PHONOPY code.26 The ab initio molecular dynamics (AIMD) simulations were carried out in the canonical ensemble with a Nosé–Hoover heat bath27 for 10 ps with a time step of 2 fs at 300 K using a 4 × 4 × 1 supercell.
3. Results and discussions
3.1. Atomic structure
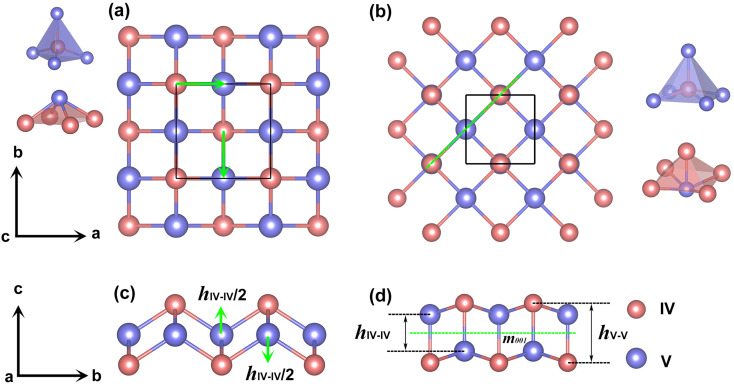
To identify low-energy 2D group IV–V monolayers, we perform an adaptive generic algorithm (AGA)28 for the structural prediction of binary IV–V compounds with fixed chemical stoichiometry of 1 : 1 under various formulas. The AGA successfully predicts two low-energy orthorhombic structures, as shown in Fig. 1. Both structures crystallize in tetragonal lattices with P4/nmm symmetry, each comprising two group IV atoms and two group V atoms within its unit cell. Fig. 1(a–d) depict the top and side views of the atomic configurations of the two tetragonal group IV–V monolayers. From the top views (Fig. 1(a) and (b)), it is evident that both structures consist of tetragonal arrangements formed by alternating group IV and V atoms. However, notable differences arise in the side views. To differentiate between the two tetragonal structures, we designate them as Td3 and Td4, respectively. The Td3 phase shares the same structure with the 2D iron monochalcogenides, as shown in Fig. 1(a) and (c). This phase features a three-atom-thick configuration from the side view, with the group IV layer sandwiched between the two group V layers, hence the designation Td3 phase. In contrast, the Td4 phase is characterized by a four-atom-thick structure from the side view, which can be considered as the stacking of two zigzag IV–V chains along the c-axis. The two zigzag chains are associated by the glide mirror operation 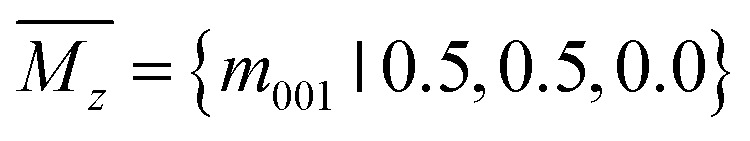 . The glide line and the mirror-invariant line are indicated by green dashed line in Fig. 1(b) and (d), respectively. The green arrows in Fig. 1(a) and (c) illustrate the structural transformation from the Td3 phase to the Td4 phase. The transition from the Td3 phase to the Td4 phase occurs when the corner group V atom is shifted by
. The glide line and the mirror-invariant line are indicated by green dashed line in Fig. 1(b) and (d), respectively. The green arrows in Fig. 1(a) and (c) illustrate the structural transformation from the Td3 phase to the Td4 phase. The transition from the Td3 phase to the Td4 phase occurs when the corner group V atom is shifted by 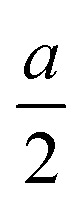 along the a-axis, the central group V atom is displaced by
along the a-axis, the central group V atom is displaced by 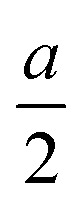 along the b-axis, and the neighboring group IV atoms are shifted by
along the b-axis, and the neighboring group IV atoms are shifted by 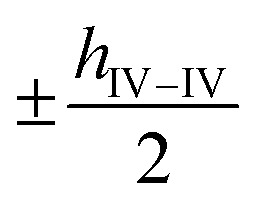 along the c-axis, respectively. Here, a represents the in-plane lattice constant, while hIV–IV denotes the vertical distance between group IV atoms as shown in Fig. 1(d).
along the c-axis, respectively. Here, a represents the in-plane lattice constant, while hIV–IV denotes the vertical distance between group IV atoms as shown in Fig. 1(d).
Fig. 1. (a and c) Top and side views of 2D group IV–V monolayers in the Td3 phase, (b and d) corresponding ones for the Td4 phase. The group IV- and V-atom centered polyhedrons are shown in the left panel of (a) for the Td3 phase, and shown in the right panel of (b) for the Td4 phase. The green arrows in (a and c) illustrate the transformation from the Td3 phase to the Td4 phase. The green dashed lines in (b) and (d) indicate the glide line and the mirror plane respectively.
The Td3 and Td4 phases also differ in their coordination numbers. In the Td3 phase, each IV(V) atom is bonded to four V(IV) atoms, as shown in the left panel of Fig. 1(a). In contrast, in the Td4 phase, each IV(V) atom is bonded to five V(IV) atom. The group IV- or V-atom centered polyhedrons are shown in the right panel of Fig. 1(b). As a result, the Td4 phase is energetically more favorable than the Td3 phase. Therefore, we will focus our discussion on the Td4 phase in the following context. It is noteworthy that several theoretically designed 2D transition metal carbides,29,30 transition metal borides,31 and transition metal pnictides32–35 crystalize in the same Td4 structure.
Table 1 tabulates the optimized structural parameters of 2D group IV–V monolayers in the Td4 phase. The equilibrium lattice constants (a), in-plane and out-of-plane bond lengths of the IV–V bond (dIV–Vab and dIV–Vc), and the vertical distances between V–V atoms (hV–V) all increase monotonically as the atomic radius of the group IV and V atoms increases. While the vertical distances between IV–IV atoms (hIV–IV) increases with the row number of the group IV atom, it fluctuates only within 0.1 Å for compounds with the same IV atom but different V atom.
Structural parameters and cohesive energies of 2D IV–V monolayers in Td4 phase. The optimized lattice constant (a), in-plane IV–V bond lengths (dIV–Vab), out-of-plane IV–V bond lengths (dIV–Vc), vertical distance of IV–IV atoms (hIV–IV), vertical distance of V–V atoms (hV–V), and cohesive energies (Ec) calculated at the LDA functional.
| System | a (Å) | d IV–V ab (Å) | d IV–V c (Å) | h IV–IV (Å) | h V–V (Å) | E c (eV per atom) |
|---|---|---|---|---|---|---|
| SiP | 3.380 | 2.420 | 2.337 | 1.955 | 2.720 | −5.874 |
| SiAs | 3.550 | 2.438 | 2.569 | 1.892 | 2.983 | −5.437 |
| SiSb | 3.811 | 2.783 | 2.635 | 1.942 | 3.328 | −4.990 |
| GeP | 3.530 | 2.530 | 2.434 | 2.023 | 2.845 | −5.402 |
| GeAs | 3.670 | 2.650 | 2.538 | 2.000 | 3.074 | −5.093 |
| GeSb | 3.899 | 2.848 | 2.708 | 1.933 | 3.423 | −4.746 |
| SnP | 3.811 | 2.718 | 2.651 | 2.297 | 3.005 | −5.117 |
| SnAs | 3.928 | 2.823 | 2.740 | 2.237 | 3.244 | −4.865 |
| SnSb | 4.162 | 3.016 | 2.911 | 2.254 | 3.567 | −4.625 |
3.2. Structure stabilities
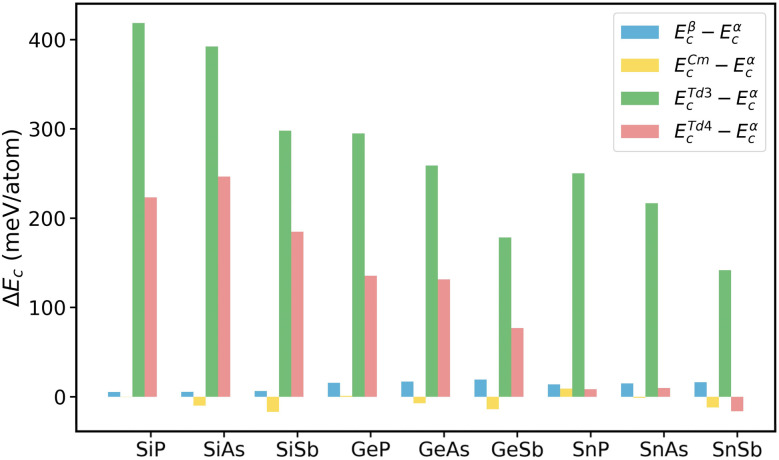
To assess the energetic stability of the tetragonal structures of 2D group IV–V monolayers, we calculate their cohesive energies (Ec) and compare them with the ones of the α phase. The cohesive energy of single-layer group IV–V is determined as,
| Ec = E[IVnVn] − n × EIVatom − n × EVatom | 1 |
where E[IVnVn] denotes the total energies of single-layer group IV–V, n is the number of group IV or V atoms in the unit cell, EIVatom and EVatom are energies of the isolated atoms of group IV and group V, respectively. As listed in Table 1, the cohesive energies of 2D IV–V monolayers are all negative, implying that they are stable in energy. Fig. 2 depicts the differences in cohesive energies (ΔEc) of the Td3 and Td4 phases with respect to the α phase. To ensure the reliability of our calculations, we also include ΔEc for the β and Cm phase. Our results show that Cm phase is more stable than α phase for IV = As and Sb, which is consistent with previous findings.19 It is observed that ΔEc of Td3 and Td4 phases decrease with the increasing atomic number of group IV or group V elements. For the SnSb monolayer, ΔETd4c becomes negative and is more negative than ΔECmc, indicating that the Td4 is energetically more favorable than both the α and Cm phases. Consequently, the Td4 phase emerges as the lowest-energy configuration for 2D SnSb. The results further indicate that the Td4 phase is energetically more favorable than the Td3 phase by an energy difference of 100 to 240 meV per atom for the 2D group IV–V (IV = Si, Ge, Sn; V = P, As, Sb) monolayers. Therefore, we will focus our discussions on the Td4 phase in the subsequent sections.
Fig. 2. Cohesive energy differences of β-, Cm-, Td3-, and Td4-phase group IV–V (X = Si, Ge, Sn; Y = P, As, Sb) monolayers with respect to α phase.
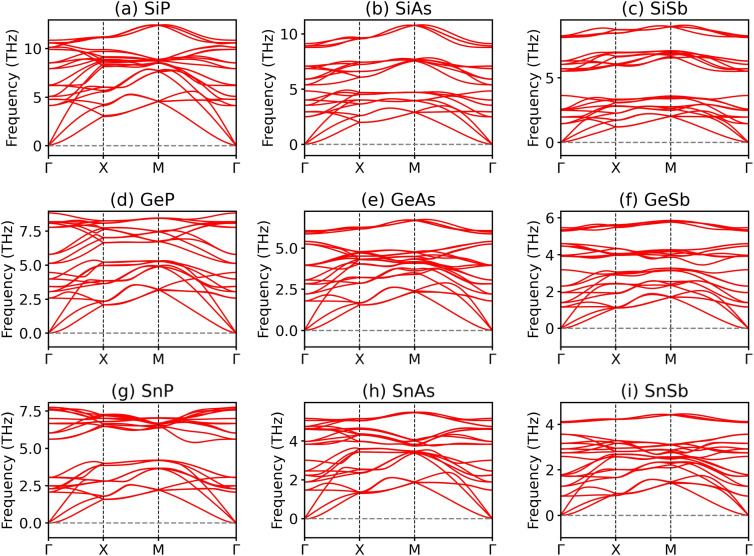
We further investigate the dynamical stabilities of the 2D group IV–V monolayers by performing phonon dispersion calculations. As illustrated in Fig. 3, all the 2D group IV–V monolayers examined in this study exhibit no imaginary frequencies throughout the entire Brillouin zone, indicating that the Td4-phase group IV–V monolayers are dynamically stable. The thermodynamical stabilities of the Td4-phase 2D group IV–V monolayers are also confirmed by the AIMD simulations. As depicted in Fig. S1,† none of the 2D group IV–V monolayers exhibits appreciable distortions after heating at 300 K for 10 ps. Additionally, the total energies of these monolayers exhibit only minor oscillations around their respective average values, suggesting that all the 9 group IV–V monolayers are thermodynamically stable at room temperature. We also examine the structural stabilities of the Td4-phase group IV–V monolayers under lattice distortions by calculating the elastic constants, which are evaluated from the second partial derivative of strain energy with respect to strain as implemented in VASPKIT code.36 For the Td4-phase group IV–V monolayers with tetragonal symmetry, there are three independent elastic constants C11, C12, and C66, which should satisfy the Born–Huang criteria as C66 > 0 and |C11| > C12 to guarantee the mechanical stabilities of the group IV–V monolayers. The elastic constants as tabulated in Table 2 show that all the 2D group IV–V monolayers are mechanical stable except for the GeSb and SnAs monolayers.
Fig. 3. (a–i) Phonon dispersions of 2D group IV–V (X = Si, Ge, Sn; Y = P, As, Sb) monolayers in the Td4 structure.
Mechanical properties of 2D IV–V monolayers in the Td4 structure. The units of elastic constants (C11, C12, and C66) are in N m−1.
| System | C 11 | C 12 | C 66 | Stability |
|---|---|---|---|---|
| SiP | 81.30 | 66.57 | 57.41 | Stable |
| SiAs | 97.34 | 59.18 | 56.88 | Stable |
| SiSb | 78.86 | 43.05 | 46.39 | Stable |
| GeP | 115.65 | 44.18 | 54.90 | Stable |
| GeAs | 62.43 | 61.58 | 35.68 | Stable |
| GeSb | 37.68 | 37.68 | 32.89 | Unstable |
| SnP | 99.72 | 37.54 | 45.79 | Stable |
| SnAs | 68.31 | 74.71 | 49.20 | Unstable |
| SnSb | 75.21 | 35.17 | 44.503 | Stable |
3.3. Electronic structures
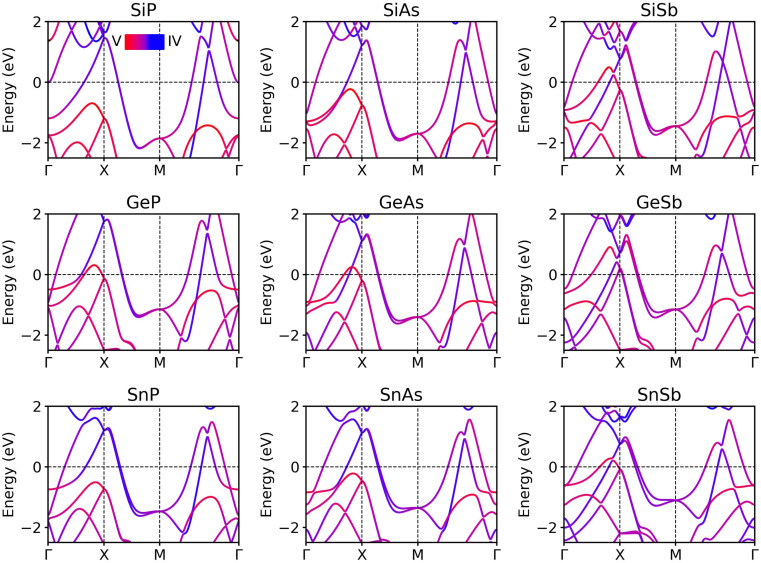
The electronic band structures of stable group IV–V monolayers are illustrated in Fig. 4. Given that the 2D group IV–V binaries studied in this work contain heavy elements, the spin–orbit coupling (SOC) effect may significantly influence their electronic structures; thus, we incorporate SOC interactions in our band structure calculations. As shown in Fig. 4, all monolayers exhibit metallic properties. Due to their isoelectronic and isostructural nature, these monolayers share similar band structure profiles. Notably, the SOC effect prominently affects the bands crossing the Fermi level along the high-symmetry X–M line. For lighter elements, such as SiP, the two bands remain degenerate. However, as the atomic mass of the constituent element increases, the bands split due to the SOC effect, a phenomenon particularly evident in the SnSb monolayer, which exhibits the strongest SOC interaction among the 9 monolayers. The elemental and orbital-resolved density of states (DOS) as presented in Fig. S2† reveal that the energy bands near the Fermi level are dominated by the hybridization of px,y orbitals of both the IV and V elements and s orbital of IV element.
Fig. 4. Elemental projected band structures of stable group IV–V monolayers in the Td4 structure calculated at the LDA functional level with SOC. The red and blue lines indicate the contributions from group V and group IV atoms, respectively. The purple lines signify a combined contribution from both group V and group IV atoms.
3.4. Hydrogenation
Surface functionalization constitutes an effective method to modulate the electronic structures of 2D materials. We decorated IV elements with hydrogen atoms to create chemically new materials of H-IV–V monolayers. The optimized atomic structures of the hydrogenated group IV–V monolayers are shown in Fig. S3.† Initially, the hydrogen atoms are positioned directly above or below the group IV atoms, with the upper-layer group IV(V) atoms aligned directly above the lower-layer group V(IV) atoms from a top view. The atomic structures of 2D H–SiP, H–SiAs, H-GeP, H–SnP, and H–SnSb exhibit minimal changes after full relaxation. However, for 2D H–SiSb, H-GeAs, H-GeSb, and H–SnAs, the upper-layer group IV(V) atoms shift away from their corresponding lower-layer group V(IV) atoms, resulting in the formation of distorted IV–V hexagonal rings within the same layer. To investigate the impact of hydrogenation on the thermodynamic stability of 2D group IV–V monolayers, we performed AIMD simulations for 2D hydrogenated group IV–V monolayers at 300 K. As shown in Fig. S4,† the total energies of the 2D H–SiSb, H-GeAs, and H–SnAs monolayers fluctuate within a narrow energy range, and their final structures exhibit only minor distortions after being heated at 300 K for 10 ps. This suggests that the 2D SiSb, GeAs, and SnAs monolayers remain thermodynamically stable at room temperature upon hydrogenation. In contrast, the 2D H–SiP, H–SiSb, H-GeP, H-GeSb, H–SnP, and H–SnSb monolayers display significant structural distortions, indicating that they are thermodynamically unstable.
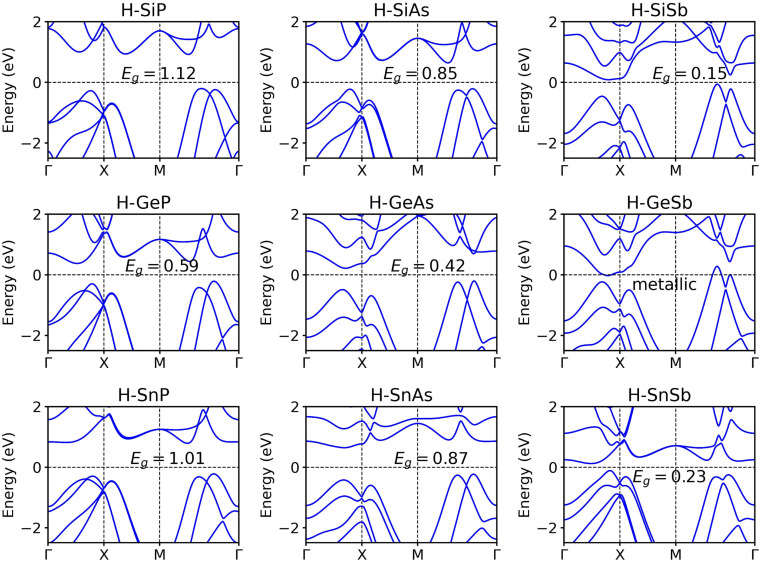
Band structure calculations, as depicted in Fig. 5, reveal that, with the exception of the hydrogenated GeSb monolayer—which retains its metallic character—all other hydrogenated IV–V monolayers exhibit fully gapped electronic structures, with indirect band gap values ranging from 0.15 eV for hydrogenated SiSb to 1.12 eV for the hydrogenated SiP monolayer. Notably, for 2D hydrogenated IV–V monolayers that share the same constituent IV element, the band gaps decrease with increasing atomic mass of group V element. Conversely, when considering 2D hydrogenated IV–V monolayers composed of the same V element, no clear correlation emerges between the band gap values and the atomic mass of the group IV atom. The LDA functional is known to underestimate the band gaps of semiconductors. To better describe the band gaps, we also apply the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional37,38 to calculate the electronic structures of the 2D hydrogenated IV–V monolayers. As depicted in Fig. S5,† the HSE functional yield larger band gap values with respect to the LDA functional. For instance, the band gap of H–SiP is calculated to be 1.12 eV at the LDA level, whereas it increases to 1.56 eV when applying the HSE06 functional. To elucidate the impact of hydrogenation on the electronic structure of the 2D group IV–V monolayers, we present in Fig. S6† the orbital-projected DOS for both the SiP monolayer and its hydrogenated counterpart. The observed hybridization between the s orbital of the hydrogen atom and the p orbitals of the IV atoms leads to the opening of a band gap in the hydrogenated IV–V monolayers.
Fig. 5. Band structures of hydrogenated group IV–V monolayers in the Td4 structure calculated with the LDA functional with SOC.
4. Conclusions
To summarize, we have proposed a novel tetragonal phase of group IV–V monolayers (IV = Si, Ge, Sn; IV = P, As, Sb) with the aid of adaptive generic algorithm. We have proved the energetical, dynamical, and thermodynamical stabilities of these monolayers by the total energy calculations, phonon dispersion calculation, and AIMD simulations. All the 9 group IV–V monolayers exhibit metallic behavior with the inclusion of SOC effect. After decoration of hydrogen on the IV atoms of the group IV–V monolayers, all the H-IV–V monolayers becomes indirect semiconductor with band gap values ranging from 0.15 to 1.12 eV. Our studies expand the family of the group IV–V monolayers.
Data availability
We confirm that the data supporting the finding of this study are available within the main article.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
Work at Jimei University was supported by the National Natural Science Foundation of China No. 52071156, the Natural Science Foundation of Xiamen, China (3502Z202372015) and the Research Foundation of Jimei University (ZQ2024086, ZQ2023013). Work at Xiamen University was supported by the Fundamental Research Funds for the Central Universities (Grant No. 20720210023). Shaorong Fang and Tianfu Wu from the Information and Network Center of Xiamen University are acknowledged for their help with GPU computing.
Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06623e
References
- Fiori G. Bonaccorso F. Iannaccone G. Palacios T. Neumaier D. Seabaugh A. Banerjee S. K. Colombo L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014;9:768–779. doi: 10.1038/nnano.2014.207. [DOI] [PubMed] [Google Scholar]
- Zhang P. P. Wang F. X. Yu M. H. Zhuang X. D. Feng X. L. Two-dimensional materials for miniaturized energy storage devices: from individual devices to smart integrated systems. Chem. Soc. Rev. 2018;47:7426–7451. doi: 10.1039/C8CS00561C. [DOI] [PubMed] [Google Scholar]
- Das S. Sebastian A. Pop E. McClellan C. J. Franklin A. D. Grasser T. Knobloch T. Illarionov Y. Penumatcha A. V. Appenzeller J. et al., Transistors based on two-dimensional materials for future integrated circuits. Nat. Electron. 2021;4:786–799. doi: 10.1038/s41928-021-00670-1. [DOI] [Google Scholar]
- Zhang H. Z. X. K. Wei X. F. Zhang Y. Z. Zhang Z. Zhang Y. Two-dimensional transition metal dichalcogenides for post-silicon electronics. Natl. Sci. Open. 2023;2:20230015. doi: 10.1360/nso/20230015. [DOI] [Google Scholar]
- Kane C. L. Mele E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005;95:226801. doi: 10.1103/PhysRevLett.95.226801. [DOI] [PubMed] [Google Scholar]
- Liu C. C. Feng W. X. Yao Y. G. Quantum Spin Hall Effect in Silicene and Two-Dimensional Germanium. Phys. Rev. Lett. 2011;107:076802. doi: 10.1103/PhysRevLett.107.076802. [DOI] [PubMed] [Google Scholar]
- Xu Y. Yan B. H. Zhang H. J. Wang J. Xu G. Tang P. Z. Duan W. H. Zhang S. C. Large-Gap Quantum Spin Hall Insulators in Tin Films. Phys. Rev. Lett. 2013;111:136804. doi: 10.1103/PhysRevLett.111.136804. [DOI] [PubMed] [Google Scholar]
- Zhang S. L. Yan Z. Li Y. F. Chen Z. F. Zeng H. B. Atomically Thin Arsenene and Antimonene: Semimetal-Semiconductor and Indirect-Direct Band-Gap Transitions. Angew. Chem., Int. Ed. 2015;54:3112–3115. doi: 10.1002/anie.201411246. [DOI] [PubMed] [Google Scholar]
- Huang Z. Q. Hsu C. H. Chuang F. C. Liu Y. T. Lin H. Su W. S. Ozolins V. Bansil A. Strain driven topological phase transitions in atomically thin films of group IV and V elements in the honeycomb structures. New J. Phys. 2014;16:105018. doi: 10.1088/1367-2630/16/10/105018. [DOI] [Google Scholar]
- Hsu C. H. Huang Z. Q. Crisostomo C. P. Yao L. Z. Chuang F. C. Liu Y. T. Wang B. K. Hsu C. H. Lee C. C. Lin H. et al., Two-dimensional Topological Crystalline Insulator Phase in Sb/Bi Planar Honeycomb with Tunable Dirac Gap. Sci. Rep. 2016;6:18993. doi: 10.1038/srep18993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin K. H. Jhi S. H. Quantum anomalous Hall and quantum spin-Hall phases in flattened Bi and Sb bilayers. Sci. Rep. 2015;5:8426. doi: 10.1038/srep08426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özdamar B. Özbal G. Çinar M. N. Sevim K. Kurt G. Kaya B. Sevinçli H. Structural, vibrational, and electronic properties of single-layer hexagonal crystals of group IV and V elements. Phys. Rev. B. 2018;98:045431. doi: 10.1103/PhysRevB.98.045431. [DOI] [Google Scholar]
- Lin J. H. Zhang H. Cheng X. L. Miyamoto Y. Single-layer group IV-V and group V-IV-III-VI semiconductors: Structural stability, electronic structures, optical properties, and photocatalysis. Phys. Rev. B. 2017;96:035438. doi: 10.1103/PhysRevB.96.035438. [DOI] [Google Scholar]
- Sheng K. Wang Z. Y. Ab Initio Discovery of Group IV-V Monolayers with Superlative Mechanical, Electronic, and Transport Properties. Cryst. Growth Des. 2024;24:6400–6412. doi: 10.1021/acs.cgd.4c00643. [DOI] [Google Scholar]
- Wu P. Zhong J. W. Ma Z. Y. Yu Y. H. Xia X. Q. Song B. W. Zhou T. Huang Y. C. Electronic, Optical, piezoelectric properties and photocatalytic water splitting performance of Two-dimensional group IV-V compounds. Appl. Surf. Sci. 2023;627:157317. doi: 10.1016/j.apsusc.2023.157317. [DOI] [Google Scholar]
- Gao X. Shen Y. Q. Ma Y. Y. Wu S. Y. Zhou Z. X. Theoretical Insights into Two-Dimensional IV-V Compounds: Photocatalysts for the Overall Water Splitting and Nanoelectronic Applications. Inorg. Chem. 2019;58:12053–12068. doi: 10.1021/acs.inorgchem.9b01255. [DOI] [PubMed] [Google Scholar]
- Bhojani A. K. Kagdada H. L. Singh D. K. Ultrahigh power factor and excellent solar efficiency in two-dimensional hexagonal group-IV-V nanomaterials. J. Appl. Phys. 2024;135:095106. doi: 10.1063/5.0189371. [DOI] [Google Scholar]
- Lee S. Kwon Y.-K. Unveiling giant hidden Rashba effects in two-dimensional Si2Bi2. npj 2D Mater. Appl. 2020;4:45. doi: 10.1038/s41699-020-00180-2. [DOI] [Google Scholar]
- Ashton M. Sinnott S. B. Hennig R. G. Computational discovery and characterization of polymorphic two-dimensional IV-V materials. Appl. Phys. Lett. 2016;109:192103. doi: 10.1063/1.4967433. [DOI] [Google Scholar]
- Barreteau C. Michon B. Besnard C. Giannini E. High-pressure melt growth and transport properties of SiP, SiAs, GeP, and GeAs 2D layered semiconductors. J. Cryst. Growth. 2016;443:75–80. doi: 10.1016/j.jcrysgro.2016.03.019. [DOI] [Google Scholar]
- Xu C. Y. Zhu M. F. Zhang J. M. Wang W. Q. Yan Y. New two-dimensional allotrope of single layer IV-V semiconductor XBi (X = Si, Ge, Sn) Comput. Mater. Sci. 2018;150:314–320. doi: 10.1016/j.commatsci.2018.04.016. [DOI] [Google Scholar]
- Kresse G. Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999;59:1758–1775. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Kresse G. Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Kresse G. Furthmüller J. Efficient of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996;6:15. doi: 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Monkhorst H. J. Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B: Solid State. 1976;13:5188. doi: 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Togo A. Oba F. Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl-type SiO at high pressures. Phys. Rev. B: Condens. Matter Mater. Phys. 2008;78:134106. doi: 10.1103/PhysRevB.78.134106. [DOI] [Google Scholar]
- Martyna G. J. Klein M. L. Tuckerman M. Nose-Hoover Chains - the Canonical Ensemble Via Continuous Dynamics. J. Chem. Phys. 1992;97:2635–2643. doi: 10.1063/1.463940. [DOI] [Google Scholar]
- Wu S. Q. Ji M. Wang C. Z. Nguyen M. C. Zhao X. Umemoto K. Wentzcovitch R. M. Ho K. M. An adaptive genetic algorithm for crystal structure prediction. J. Phys.: Condens. Matter. 2014;26:035402. doi: 10.1088/0953-8984/26/3/035402. [DOI] [PubMed] [Google Scholar]
- Fan D. Lu S. H. Guo Y. D. Hu X. J. Two-Dimensional Tetragonal Titanium Carbide: a High-Capacity and High-Rate Battery Material. J. Phys. Chem. C. 2018;122:15118–15124. doi: 10.1021/acs.jpcc.8b03425. [DOI] [Google Scholar]
- Wu Y. Y. Bo T. Zhang J. R. Lu Z. S. Wang Z. G. Li Y. H. Wang B. T. Novel two-dimensional tetragonal vanadium carbides and nitrides as promising materials for Li-ion batteries. Phys. Chem. Chem. Phys. 2019;21:19513–19520. doi: 10.1039/C9CP03954F. [DOI] [PubMed] [Google Scholar]
- Bo T. Liu P. F. Zhang J. R. Wang F. W. Wang B. T. Tetragonal and trigonal Mo2B2 monolayers: two new low-dimensional materials for Li-ion and Na-ion batteries. Phys. Chem. Chem. Phys. 2019;21:5178–5188. doi: 10.1039/C9CP00012G. [DOI] [PubMed] [Google Scholar]
- Zhang X. Zhang Z. H. Zhao X. D. Wu D. H. Zhang X. Zhou Z. Tetragonal-structured anisotropic 2D metal nitride monolayers and their halides with versatile promises in energy storage and conversion. J. Mater. Chem. A. 2017;5:2870–2875. doi: 10.1039/C6TA10980B. [DOI] [Google Scholar]
- Xuan X. Y. Wu M. H. Zhang Z. H. Guo W. L. A multiferroic vanadium phosphide monolayer with ferromagnetic half-metallicity and topological Dirac states. Nanoscale Horiz. 2022;7:192–197. doi: 10.1039/D1NH00353D. [DOI] [PubMed] [Google Scholar]
- Seksaria H. Kaur A. Singh K. De Sarkar A. Hexagonal and tetragonal ScX (X = P, As, Sb) nanosheets for optoelectronics and straintronics. Appl. Surf. Sci. 2023;615:156306. doi: 10.1016/j.apsusc.2022.156306. [DOI] [Google Scholar]
- Ma A. N. Zhang C. W. Prediction of tetragonal monolayer CuN with a quantum spin Hall state. Phys. E. 2020;124:114225. doi: 10.1016/j.physe.2020.114225. [DOI] [Google Scholar]
- Wang V. Xu N. Liu J.-C. Tang G. Geng W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021;267:108033. doi: 10.1016/j.cpc.2021.108033. [DOI] [Google Scholar]
- Heyd J. Scuseria G. E. Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003;118:8207–8215. doi: 10.1063/1.1564060. [DOI] [Google Scholar]
- Heyd J. Scuseria G. E. Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2006;124:219906. doi: 10.1063/1.2204597. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We confirm that the data supporting the finding of this study are available within the main article.