ECG-based Convolutional Neural Network in Pediatric Obstructive Sleep Apnea Diagnosis

Abstract

Obstructive sleep apnea (OSA) is a prevalent respiratory condition in children and is characterized by partial or complete obstruction of the upper airway during sleep. The respiratory events in OSA induce transient alterations of the cardiovascular system that ultimately can lead to increased cardiovascular risk in affected children. Therefore, a timely and accurate diagnosis is of utmost importance. However, polysomnography (PSG), the standard diagnostic test for pediatric OSA, is complex, uncomfortable, costly, and relatively inaccessible, particularly in low-resource environments, thereby resulting in substantial underdiagnosis. Here, we propose a novel deep-learning approach to simplify the diagnosis of pediatric OSA using raw electrocardiogram tracing (ECG). Specifically, a new convolutional neural network (CNN)-based regression model was implemented to automatically predict pediatric OSA by estimating its severity based on the apnea-hypopnea index (AHI) and deriving 4 OSA severity categories. For this purpose, overnight ECGs from 1,610 PSG recordings obtained from the Childhood Adenotonsillectomy Trial (CHAT) database were used. The database was randomly divided into approximately 60%, 20%, and 20% for training, validation, and testing, respectively. The diagnostic performance of the proposed CNN model largely outperformed the most accurate previous algorithms that relied on ECG-derived features (4-class Cohen’s kappa coefficient of 0.373 versus 0.166). Specifically, for AHI cutoff values of 1, 5, and 10 events/hour, the binary classification achieved sensitivities of 84.19%, 76.67%, and 53.66%; specificities of 46.15%, 91.39%, and 98.06%; and accuracies of 75.92%, 86.96%, and 91.97%, respectively. Therefore, pediatric OSA can be readily identified by our proposed CNN model, which provides a simpler, faster, and more accessible diagnostic test that can be implemented in clinical practice.

1. Introduction

Obstructive Sleep Apnea (OSA) is a common breathing disorder characterized by multiple episodes of partial or total upper airway obstruction during sleep, resulting in either reduction or cessation of the airflow with attendant alterations in gas exchange, and recurrent arousals fostering the occurrence of sleep fragmentation [1]. In otherwise healthy children, the prevalence of OSA ranges between 1% and 5%, affecting both sexes similarly [2]. Enlarged adenoids and tonsils are one of the major pathophysiological processes enhancing the risk of OSA occurrence [3], and the disease can impose a significant deleterious impact on the cardiovascular and central nervous systems when left untreated. Indeed, the obstructive respiratory events and accompanying manifestations (i.e., intermittent hypoxia and hypercapnia and recurrent arousals along with enhanced intrathoracic pressure swings) induce increased cardiac workload as well tachy- and brady-arrhythmias and catecholaminergic and sympathetic nervous system bursts [1,4–8]. Moreover, OSA has been linked to an elevated risk of developing cardiovascular disease during adulthood, particularly if left untreated [2,7,9,10].

OSA is routinely diagnosed using overnight polysomnography (PSG), which involves monitoring various physiological parameters, such as the electrocardiogram (ECG), oral and nasal airflow (AF), peripheral blood oxygen saturation (SpO₂), and the electroencephalogram (EEG), among others [1,2]. The signals obtained from PSG are manually analyzed by trained medical personnel to derive the apnea-hypopnea index (AHI), the standard metric used in the diagnosis of OSA [11]. AHI measures the frequency of apnea and hypopnea events per hour of sleep (e/h) and helps determine the severity of the disease [2]. However, nocturnal PSG is an uncomfortable, time-consuming, and complex test, especially in children. It requires a sleep laboratory with appropriately trained staff, and pediatric subjects have to spend the night in the hospital facility while being monitored with sensors, thus potentially disrupting their natural sleep patterns [1]. Limited availability of such facilities for children, coupled with the cost of conducting overnight PSG, leads to underdiagnosis of pediatric OSA, particularly in developing countries where resources are limited [12,13].

To simplify OSA diagnosis in children, investigators have focused on developing approaches that require a limited number of signals coupled with artificial intelligence techniques [14,15]. These proposed methodologies have mainly focused on the use of overnight SpO₂ and AF [15]. However, none of these approaches relied on cardiac signals derived from the ECG which contains a plethora of relevant information that can be used for diagnostic purposes involving both cardiorespiratory coupling and changes in heart rate frequency and variability associated with the respiratory events [2–4,7,16]. These physiological behaviors, together with the increased risk for developing cardiovascular disease, make ECG signal analysis worthy of special interest in the study of OSA [7,9,10]. Furthermore, because the ECG is one of the most widely analyzed signals in clinical practice around the world, an ECG-based application to aid in the diagnosis of OSA could be readily implementable and accessible [17–19].

Several investigative groups have focused on the analysis of cardiac information using deep learning (DL) methods, such as convolutional neural networks (CNN), recurrent neural networks (RNN), combinations of CNN and RNN, and hybrid methods to automatically detect the severity of OSA in adult patients, achieving overall robust performances [20–26]. However in children, most studies have relied on derivatives of cardiac function such as heart rate variability (HRV) or photoplethysmography (PPG), but not used the raw ECG signal [3,27–33]. These methodologies, while yielding satisfactory results, rely on existing knowledge of the effects of pediatric OSA on the ECG to extract features from different analytical approaches [34,35]. However, these approaches do not use all the information available in the ECG, which could be crucial for achieving a more thorough understanding and accurate diagnosis of the disease. Moreover, most of these previous studies relied on a feature-engineering approach, which is demanding and time-consuming due to comprehensive signal preprocessing and feature extraction [3,27–33].

To the best of our knowledge, no studies have investigated the use of raw ECG signals coupled with DL methods to explore their feasibility in the diagnosis of pediatric OSA. Such combinatorial approach is essential for two reasons: on the one hand, DL methods are gaining great interest in many fields due to a large number of existing databases [36], especially highlighting their application in the biomedical sector to help in the diagnosis and treatment of diseases [37–39]. Specifically, DL methods can handle high-dimensional data due to multiple-layer processing that allows for extracting relevant information intrinsically without exhaustive signal preprocessing [40]. On the other hand, analyzing the ECG signal could be very helpful for pediatric OSA due to associated cardiovascular risk, particularly in more severe cases [2].

Furthermore, analyzing previous studies focused on automatically detecting the severity of OSA using DL, most of them used architectures based on CNNs [20–26]. Although CNNs were originally created for image analysis [41], these networks have proven to be appropriate for time series analysis in a wide range of fields [42], especially in the domain of biomedical signal analysis [35,43,44]. CNNs contain a multi-layer architecture and their design is characterized by weight sharing, sparse connections, and pooling operations [41]. This structure allows them to identify short- and long-term patterns happening in distinct regions of the data sequences [43], with a computational efficiency that outperforms other DL models [41]. This property of CNNs can be essential in identifying patterns in the ECG signal associated with apneic events, which may manifest at different times during the night. In addition, CNNs have the ability to generate higher-level representations [41], which may allow them to learn complex patterns in prolonged segments of the ECG signal, such as heart rate fluctuations that are triggered in response to apneic events [2,7].

For these reasons, we here propose the development of a CNN-based algorithm for the classification of pediatric patients at risk of OSA based on their overnight ECG recordings that permits delineation of pediatric OSA severity according to the conventional AHI categories. This study presents two main novelties: 1) it is the first time that a DL approach is used along with raw ECG signals for the diagnosis of pediatric OSA; and 2) our approach is a new CNN-based regression model trained to aid in the diagnosis and severity estimation of pediatric OSA, in which we first estimate the number of apneic events per signal segment and then the AHI values per subject. For this purpose, we propose a data augmentation technique by dividing the whole night recordings into 10-minute segments with a 50% overlap to increase the volume of the dataset during model training. Thus, we hypothesize that a CNN-based architecture fed with the raw ECG signal can enhance and streamline the diagnosis of pediatric OSA by utilizing all relevant cardiac signal data to estimate disease severity. Accordingly, the main objective of our proposal is to evaluate a CNN-based model with the ECG signal to estimate the AHI, and accurately establish a diagnosis of OSA and its severity in pediatric patients.

2. Database and signals

The Childhood Adenotonsillectomy Trial (CHAT) database was used in this study (number of clinical trial: NCT00560859). Access to CHAT data is public upon request from the National Sleep Research Resource website (https://sleepdata.org/datasets/chat). A total of 1,610 overnight PSG recordings performed on children between the ages of 5 and 9.9 years old with suspected clinical symptoms of OSA were analyzed. Sleep studies were collected from 6 pediatric sleep centers in the United States of America (Children’s Hospital of Boston, Boston, MA; Cardinal Glennon Children’s Hospital, St. Louis, MO; Children’s Hospital of Philadelphia, Philadelphia, PA; Cincinnati Children’s Hospital, Cincinnati, OH; Montefiore Children’s Hospital, New York, NY; Rainbow Babies and Children’s Hospital, Cleveland, OH) [45]. All nocturnal PSGs were conducted following the 2007 American Academy of Sleep Medicine (AASM) recommendations [11]. Inclusion and exclusion criteria for the study can be found in previous literature [45,46]. CHAT is a randomized, controlled, single-blind, multicenter trial aimed at assessing the effectiveness of a surgical treatment for pediatric OSA. Details of the trial design, performance, and initial results obtained in the original study are explicitly documented in published reports [45,46]. Studies of nocturnal PSG were divided into three groups. Initially, the baseline cohort (451 subjects) that met the inclusion criteria, completed an initial PSG, and individuals were then randomly assigned to either early surgical adenotonsillectomy (eAT) or watchful waiting with supportive care (WWSC) [46]. In addition, the nonrandomized group (755 subjects) corresponded to individuals who did not meet the inclusion criteria conditions in the original study but had undergone an initial PSG. Finally, the follow-up group (404 subjects) comprised the subjects in the baseline group who underwent a follow-up PSG seven months after the initial PSG. Approximately half of the children in the follow-up group were treated with eAT and the other half randomly allocated to WWSC.

In this study, all recordings were randomly divided into training (60%), validation (20%) and test (20%) subsets. This partition was made so that no subject could be present in two subsets. In turn, following the recommendations from the AASM [11], all PSG recordings from CHAT included annotated data on the beginning and duration of apnea and hypopnea events. Accordingly, OSA diagnosis was established by calculating the AHI [11]. Then, pediatric OSA severity was divided into four categories based on AHI values: no OSA (AHI < 1e/h), mild OSA (1≤AHI<5 e/h), moderate OSA (5≤AHI<10 e/h), or severe OSA (AHI≥10 e/h) [11]. Table 1 presents the demographic and clinical characteristics of the subjects included in the training, validation, and test subsets.

Table 1:

Clinical and demographic features of the pediatric study subjects extracted from the CHAT dataset.

Features	Training subset	Validation subset	Test subset
Baseline subjects (n)	278 (61.64%)	88 (19,51%)	85 (18.85%)
Non-randomized subjects (n)	461 (61.06%)	157 (20.79%)	137 (18.15%)
Follow-up subjects (n)	249 (61.63%)	78 (19.31%)	77 (19.06%)
Total subjects (n)	988 (61.37%)	323 (20.06%)	299 (18.57%)
Age (years)	7.00 [2.00]	7.00 [2.00]	6.90 [2.00]
Females (n)	477 (48.28%)	164 (50.77%)	161 (53.85%)
BMI (kg/m2)	17.31 [5.92]	17.12 [6.25]	17.43 [6.04]
AHI (e/h)	2.64 [4.77]	2.45 [4.77]	2.32 [5.11]
AHI < 1 (e/h) *	212 (21.46%)	67 (20.74%)	65 (21.74%)
1≤AHI<5 (e/h) *	488 (49.39%)	167 (51.70%)	144 (48.16%%)
5≥AHI<10 (e/h) *	159(16.09%)	44 (13.62%)	49 (16.39%)
AHI ≥ 10 (e/h) *	129 (13.06%)	45 (13.93%)	41 (13.71%)
Baseline ECG segments (n)	33,402	5,350	5,059
Non-randomized ECG segments (n)	53,137	9,057	7,972
Follow-up ECG segments	29,587	4,519	4,442
Total ECG segments (n)	116,126	18,927	17,473

Data are shown as number (percentage) or median [interquartile range], depending on the feature type. BMI: body mass index; AHI: apnea-hypopnea index; e/h: apneic events per hour.

^*AHI<1 (e/h): no OSA; 1≤AHI<5 (e/h): mild OSA; 5≤AHI<10(e/h): moderate OSA; AHI≤10(e/h): severe OSA.

3. Methods

This section presents the methodology to obtain the proposed solution for predicting pediatric OSA and its severity. The workflow followed is introduced (see Figure 1), based on six principal stages: 1) ECG signals were extracted from pediatric PSG recordings; 2) A minimal preprocessing was conducted to obtain 10-minute ECG segments; 3) CHAT database was divided into training (60% of the subjects), validation (20% of the subjects), and test (20% of the subjects) subsets; 4) A regression CNN-based architecture was designed. This CNN model was trained using the preprocessed 10-minute ECG segments belonging to the training subset $\left(S_1,\dots ,S_N\right)$ as input data. $AH{I}_{cnn}$ was calculated for each subject by adding the estimated events in all segments $\left(\hat{y}\mathit{1},\dots ,{\hat{y}}_N\right)$ of a pediatric overnight recording and dividing them by the total recording time in hours. The value of this rate calculated after training with CNN underestimates the value of the actual AHI (AHI_actual) extracted from the CHAT database because the index in our initial proposal uses the total signal recording time rather than the total sleep time. To correct this tendency, we calculated the final estimated AHI (AHI_est) by implementing a support vector regression (SVR) model; 5) The validation subset was used to adjust the algorithm hyperparameters and select the optimal model; and 6) The optimal model was applied to the test data to evaluate the diagnostic ability of the CNN-based algorithm.

Figure 1:

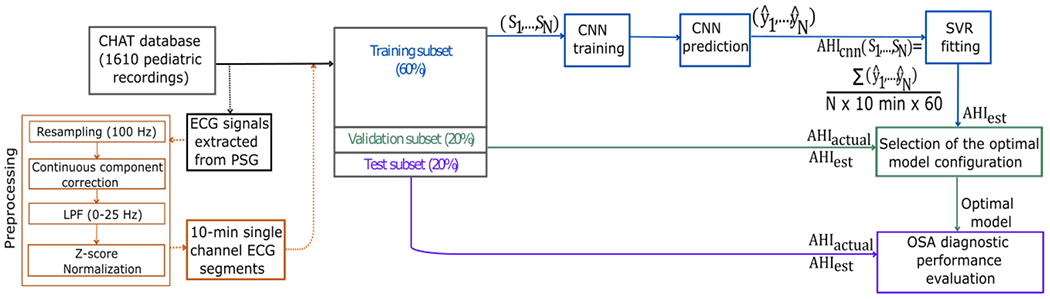
Proposed workflow for developing and validating the CNN enabling prediction of the severity of OSA in children based on their overnight raw ECG signal recordings. CHAT: Childhood Adenotonsillectomy Trial; PSG: polysomnography; ECG: LPF: low pass filter; electrocardiogram; CNN: convolutional neural network; AHI: apnea-hypopnea index; SVR: support vector regression; OSA: obstructive sleep apnea. $AH{I}_{cnn}$: rate of apnea events per subject calculated after CNN regression; $AH{I}_{\mathit{\text{actual}}}$: actual AHI extracted from CHAT database; $AH{I}_{est}$: final estimated AHI after SVR fitting. ${\mathrm{S}}_{\mathrm{N}}$: segment $\mathrm{N};{\widehat{y}}_{\mathrm{N}}$: estimation of apneic events in segment N.

3.1. ECG signal preprocessing

Following the AASM recommendations, ECG was obtained from the bipolar lead II [47]. ECG was minimally preprocessed before its use on the CNN. The raw signals were resampled at a sampling frequency of 100 Hz, which is consistent with the sampling frequencies used in prior studies [20,25,48–51]. Subsequently, the signals underwent a two-step filtering process. First, the continuous component was corrected by eliminating the signal mean within 30-second duration windows. Then, we applied a low pass filter with a pass band between 0 and 25 Hz to reduce noise, being a less restrictive approach than in previous studies which was intent on avoiding loss of important frequency components [25,50,52]. Specifically, we employed a linear-phase finite impulse response digital filter using a Hamming window to smooth out any discontinuities at the start and end of the signal [53]. After the complete records were filtered, ECG signals were divided into 10-minute segments, with a 50% overlap between segments to increase the volume of data for model training, i.e., as a data augmentation technique [54]. The final preprocessing step consisted of normalizing the amplitude of each ECG segment by extracting the mean value to the segment and dividing it by the standard deviation [55].

Finally, the determination of segment labels was performed by considering the annotations regarding the duration, beginning, and end of apneic events from CHAT annotations of the recordings [56,57]. The labels were calculated as the number of apneic events in each segment. In this way, both complete events and the proportion of incomplete events found at the edges of the segments were included as part of the target. For instance, when a single event was identified within a segment, it was labeled as 1. For segments containing a complete event along with, for example, 70% of another event (equivalent to 1.7 events), a label of 1.7 was assigned to that segment.

3.2. Design of the CNN architecture

Although CNN were initially created to deal with image data, they have been highly effective in processing time series in many fields [58], including biomedical signal processing [59]. In this work, we implemented a one-dimensional (1D) CNN-based approach since our input data responded to physiological single-channel ECG signals (see Figure 2). The network began with a data input layer containing a tensor of 60,000 samples (10-minute ECG segment) and a batch normalization (BN) layer of the input data [60]. Subsequently, the network processed the segments, which was composed of three convolutional blocks $\left(B_{C\mathit{1}-\mathit{3}}\right)$, and each of them consisting of convolutional sub-blocks $\left(N_{\mathit{\text{block}}}\right)$ with the layers described below.

Figure 2:

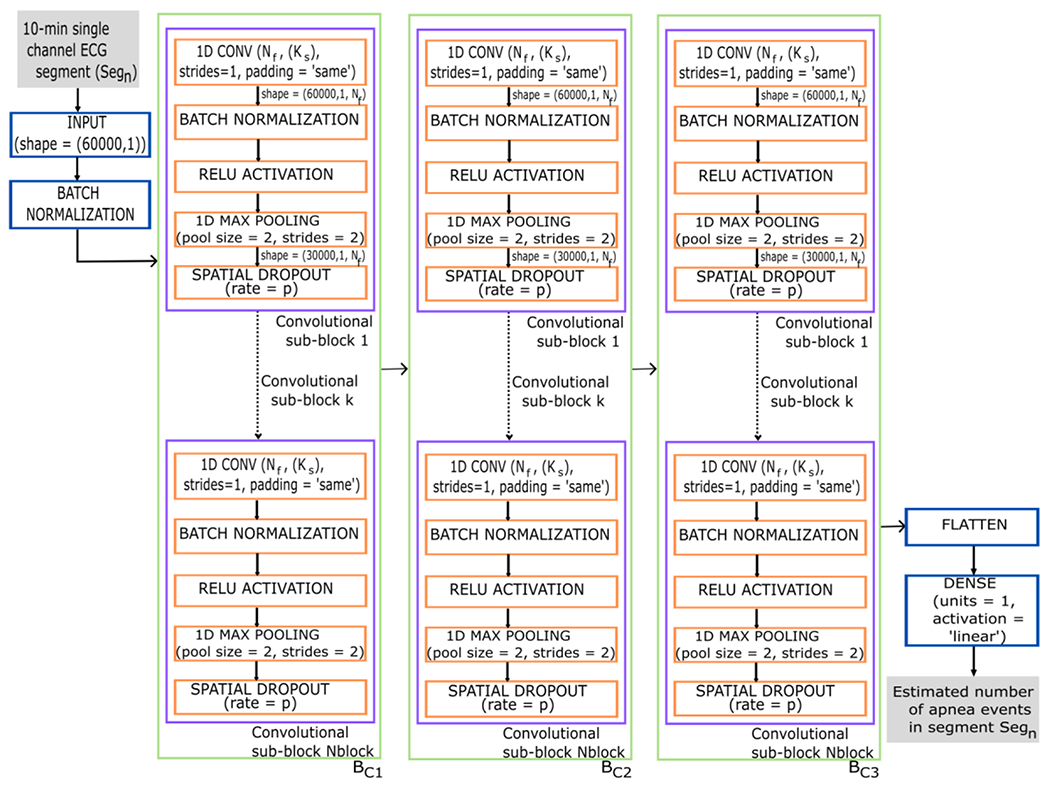
Diagram of the CNN architecture proposed in the study. The input data to the CNN are the 10-minute ECG segments and the output corresponds to the number of apnea events that the CNN estimates for each segment. 1D CONV = 1-dimensional convolutional layer; N_f = number of convolutional filters; K_s = kernel size; strides=1 in 1D CONV indicates that the stride length of the convolution is 1; padding=‘same’ in 1D CONV results in padding with zeros evenly so that the output has the same dimension as the input. RELU = rectified linear unit activation; pool size = 2 in the max pooling layer indicates that the size of the pooling window is 2; strides = 2 in the max pooling layer specifies a two-step shift of the pooling window; p = probability that each neuron is deactivated during training; N_block = number of convolutional sub-block; B_C = convolutional block 1-3. Seg_n is the number of the segment entering the network, ranging n from 1 to 116,126.

First, we incorporated a 1D convolutional layer to extract feature maps based on relevant patterns [40]. The 1D convolution operation in this layer was calculated by following the next equation [41]:

$$x_l^m[n]=\sum _{i=1}^{K_s}{w}_i^m*a_l[n-i+1]+b_i^m,$$ (1)

where $x_l^m$ is the m-th feature map and m=[1:convolutional filters ($N_f$)], $K_s$ is the kernel size, which determines the filter size, $w_i^m$ values are the weights of the convolutional filter, $a_l\left[n\right]$ are the input ECG segments, and $b_i^m$ is the bias term. The convolutional layer comprised a set of 1D filters $\left(N_f\right)$ with kernel size $K_s*1$, a step length strides = 1, and zero padding (padding= ‘same’) to obtain the output with the same dimension as the input [41]. Secondly, we integrated a BN layer to normalize the $N_f$ feature maps obtained from the previous convolutional layer [60], followed by an activation layer. This layer used the rectified linear unit activation (ReLU) function [41]:

$$f(x)=\text{max}(0,x)=\{\begin{array}{l}0,x<0\hfill \\ x,x\ge 0\hfill \end{array},$$ (2)

where x is the value of each sample in the feature map. This activation is the standard choice in DL architectures and was used to introduce nonlinearity and solve the problem of vanishing gradient during training [41]. A max-pooling layer with a window size 2 (pool size = 2) and a two-step window offset (strides = 2) was then included, which reduces the dimensionality of the input data by half while keeping the most relevant features [41]. In the last step of each sub-block, we applied regularization through a dropout layer that randomly deactivated a fraction of the neurons with probability p during training. This layer was used to prevent the network from overfitting and improve the generalization of the model. Particularly, we used spatial dropout, an approach derived from the standard dropout for CNN [61]. The conventional dropout discards individual units with a certain probability in the training process. In contrast, in the case of spatial dropout, complete feature maps are discarded to improve generalization between the different feature maps [61,62].

Finally, after the $B_{C\mathit{1}-\mathit{3}}$ configurations, we added a flattening layer to rearrange the spatial information into 1D vectors, and a densely/fully connected layer with linear activation to provide the final estimation [41]. Linear activation was selected for a regression problem to estimate apnea events by 10-minute segment as output from the proposed CNN.

The proposed CNN model was trained using the He-normal method to randomly initialize layer weights following a normal distribution [41]. We used the adaptative moment estimation (Adam) algorithm to optimize weight updates, with an initial learning rate of 0.001 [63]. Training data was presented to the network in batches of 15 samples for a maximum of 250 epochs, with randomized samples at the start of each epoch to improve convergence [41]. The loss function used to minimize the Adam algorithm in the validation subset was Huber loss with a delta parameter of $\delta =1.5$, which is robust in the presence of outliers [64]. During training, we monitored the validation loss and decreased the learning rate by a factor of 2 if there was no improvement after 10 epochs. We also used an early stop method to prevent overfitting, which stopped training after 30 epochs without a decrease in validation loss. The weights were then readjusted to the epoch in which the minimal validation loss achieved [41].

3.3. AHI estimation

As previously explained in Section 1, AHI is the standard respiratory metric for diagnosing OSA and its severity. In this study, once we obtained the predictions of the apnea and hypopnea events for each 10-minute ECG segment in the CNN, we calculated for each subject the overnight rate of events per hour of recording $\left(AH{I}_{cnn}\right)$. This was done by adding the estimated events in all segments of an overnight recording and dividing them by the total recording time in hours. It is essential to highlight that the value of this rate calculated after CNN training underestimates the value of the actual AHI $\left(AH{I}_{\text{actual }}\right)$, extracted from the CHAT database. This underestimation occurs because the rate of our initial proposal uses the total recording time of the signal rather than the total sleep time. Total recording time is typically greater than the total sleep time which is used to calculate the AHI, and which requires EEG and other signals for this purpose. To address this issue, we calculated the final estimated AHI $\left(AH{I}_{est}\right)$, through the implementation of a support vector regression (SVR) model [65]. This model is more robust than ordinary least squares when dealing with outliers. It determines the best regression function using a kernel function and minimizes the $\epsilon$-insensitive loss function. This function allows a certain degree of prediction error within a margin defined by the $\epsilon$ hyperparameter [66]. The loss function is defined as follows:

$$L(y,f(x))=\text{max}(0,|y-f(x)|-\epsilon )=\{\begin{array}{r}\hfill 0,|y-f(x)|\le \epsilon \\ \hfill |y-f(x)|-\epsilon ,|y-f(x)|\ge \epsilon \end{array},$$ (3)

where y is the actual value of the target variable, $f\left(x\right)$ is the model prediction and $\epsilon$ is the acceptable margin of error [66]. It is necessary to set a minimum value for the margin $\epsilon$, being $\epsilon \ge 0$, to delimit an area around $f\left(x\right)$ where the difference between $AH{I}_{actual}$ and $AH{I}_{\text{est }}$ does not contribute to the error. The formulation of the loss function ensures that only errors exceeding the threshold $\epsilon$ are penalized, while smaller errors do not contribute to the loss [67]. The purpose of the $\epsilon$ parameter is twofold: to control the model’s sensitivity to errors and to determine the size of the tolerance band around the regression line [66]. In this way, the loss function penalizes errors outside the tolerance band. In addition to the $\epsilon$ hyperparameter, other hyperparameters influence the SVR model optimization, such as the penalty parameter C and the $\gamma$ kernel coefficient. The C hyperparameter balances the accuracy of model predictions and complexity, determining how prediction errors are penalized. The $\gamma$ coefficient is responsible for controlling the form that the kernel function takes [65,66].

3.4. Model hyperparameter search and algorithm evaluation

To achieve optimal algorithm performance, we tuned a set of hyperparameters to minimize the generalization error of the CNN-based architecture. First, we heuristically selected the parameter $N_f$ of the convolutional layers for each block $B_{C\mathit{1}-\mathit{3}}$. We used an approach with ascending value in powers of two as the depth of the network increased: $N_f=16\left(B_{C\mathit{1}}\right),N_f=32\left(B_{C\mathit{2}}\right),N_f=64\left(B_{C\mathit{3}}\right)$. This choice was made because the deeper the layers, the more complex the characteristics that are extracted [41,68]. Subsequently, for choosing the remaining CNN hyperparameters, we implemented a more exhaustive tuning strategy using a grid search method. With this method, different combinations of hyperparameters were tested in the search space. Specifically, we searched for the following values $N_{\mathit{\text{block}}}=\{4,5\},K_s=\{7,9,17,33\}$ and dropout withp = {0.0,0.05,0.1}.

Considering the initial analyses performed, we selected this set of search hyperparameters so that the network had enough complexity to train and generalize properly. If we included smaller values in the implementation of CNN, it could not adjust sufficiently. If we increased the values, CNN took too long to train and adapted too much to the training data. In addition, the increased complexity of the network led to a computational cost not supported by the training of the CNN-based algorithm (NVIDIA GeForce RTX 2080 GPU; Keras 2.4.3 framework with TensorFlow 2.3 backend).

Then, for each of the CNN models trained with a specific combination of hyperparameters, we conducted a sequential search of three more hyperparameters in the SVR model $(\epsilon =[0.1:0.05:0.5$, C = [0:100] with logarithmic scale value search, and $\gamma =[0.01:0.01:0.1$, Ultimately, to determine the optimal hyperparameter configuration, we evaluated the performance of the CNN-based approach. This involved calculating the 4-class Cohen’s kappa coefficient $\left(k\right)$ for the subject-wise OSA severity classification (no OSA, mild, moderate, and severe OSA) in the validation subset. We selected the architecture with the highest k. Cohen’s kappa is a statistical metric used to measure agreement, particularly appropriate in classification tasks with unbalanced class distributions. Its usefulness comes from its capability to consider the likelihood of chance agreement, which reduces the bias towards the predominate class typically associated with accuracy metric [69].

3.5. Statistical analysis and figures of merit

To establish the agreement between the $AH{I}_{\mathit{\text{est}}}$ with our proposed algorithm and the $AH{I}_{\mathit{\text{actual}}}$ extracted from the CHAT database, we performed a statistical analysis. First, we calculated the intraclass correlation coefficient (ICC), which consists of a statistical measure used to evaluate the reliability or consistency of measurements made by different observers [70]. In addition to this metric, we obtained Bland-Altman plots [71] to have a more representative view of the agreement between $AH{I}_{\mathit{\text{est}}}$ and $AH{I}_{\mathit{\text{actual}}}$.

To assess the effectiveness of the proposed algorithm in diagnosing pediatric OSA, we classified subjects into four severity groups based on their estimated AHI values: AHI < 1 e/h (no OSA),1 ≤ AHI ≤ 5 e/h (mild OSA), 5 ≤ AHI < 10 e/h (moderate OSA), AHI ≥ 10 e/h (severe OSA). After establishing these categories, we calculated the confusion matrix and 4-class accuracy (Acc4) to assess the overall performance of the model across classes. Additionally, k coefficient was calculated to assess the agreement between the actual classes, i.e., the true OSA severity level of each subject, and the classes derived from the AHI predicted by the model. The importance of k should be emphasized, as it has the advantage of correcting for agreement that occurs by chance [69]. Furthermore, we calculated different merit figures for each of the OSA severity thresholds (AHI = 1,5, and 10 e/h) from the values obtained in the confusion matrix. In this way, we determined accuracy (Acc which reflects the proportion of correct predictions overall. In addition, we obtained values for sensitivity (Se) and specificity (Sp), which measure the ability of the model to detect true positives and negatives, respectively. Additionally, we used the positive predictive value (PPV) and negative predictive value (NPV) to assess the proportion of true positive and negative predictions. Moreover, we calculated positive likelihood Ratio (LR⁺) and negative likelihood Ratio (LR⁻), which provide information on how the predictions affect the probability of a positive or negative case, respectively. These metrics, in addition to giving information on crucial aspects of model performance, allow us to fully and fairly evaluate and compare the efficacy and generalizability of our model relative to previous approaches in the literature [3,29,31,72]. Finally, we calculated the 2-class kappa to assess the agreement between the actual classes and the classes predicted by the model for each AHI threshold. With this metric, we can determine at which threshold the model performs higher in terms of classification [69].

4. Results

4.1. Optimal CNN-based approach configuration

As described in Section 3.3, to select the optimal configuration of the CNN-based model, we performed an exhaustive search of different hyperparameters in the CNN network $\left(N_{\mathit{\text{block}}},K_s,p\right)$. Subsequently, sequential adjustment of the hyperparameters of the SVR model $(\epsilon ,C,\gamma )$ was performed. The training of the algorithms with each of the combinations of search values was conducted with the training subset. The evaluation was made with the validation subset, calculating the k coefficient when classifying OSA severity. Figure 3 shows the result of the CNN optimization process throughout the model training. On the one hand, the graph on the left shows how the Huber loss value decreases as the training epochs progress. In addition, it can be seen that training stopped with early stopping at epoch 155, 30 epochs after the minimum validation loss value was reached. On the other hand, the graph on the right shows how the mean absolute error obtained from the $AH{I}_{\mathit{\text{real}}}$ and $AH{I}_{cnn}$ is also decreasing in each training epoch. Figure 4 shows the boxplots (median and interquartile range) of the k values obtained in the models for each search hyperparameter. The model that obtained the highest k value (k = 0.3964) presented the CNN hyperparameters $N_{\mathit{\text{block}}}=4,p=0.1$, and $K_s=33\left(B_{C\mathit{1}}\right),17\left(B_{C\mathit{2}}\right),7\left(B_{C\mathit{3}}\right)$ (Figures 4(a), 4(b), and 4(c), respectively). To optimize the model with this configuration learning rate reached a final value of 3 × 10⁻⁵. Finally, after adjustment of the SVR regression, the optimal hyperparameters of $\epsilon =0.15,C=5.84$, and $\gamma =0.02$ were selected. Additionally, Table 1 of the supplementary material shows all the combinations of hyperparameters tested and the k results obtained in the validation subset.

Figure 3:

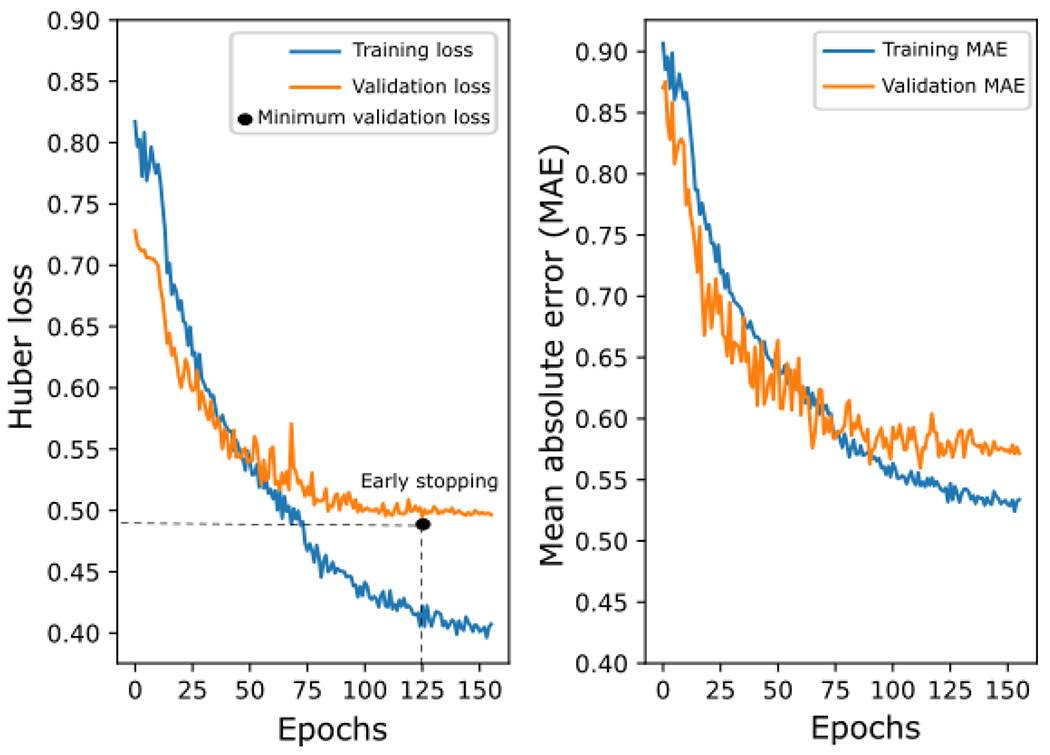
Evolution of Huber loss (left) and mean absolute error (right) in the training and validation subsets during CNN optimization as model training epochs progress. MAE: Mean absolute error.

Figure 4:

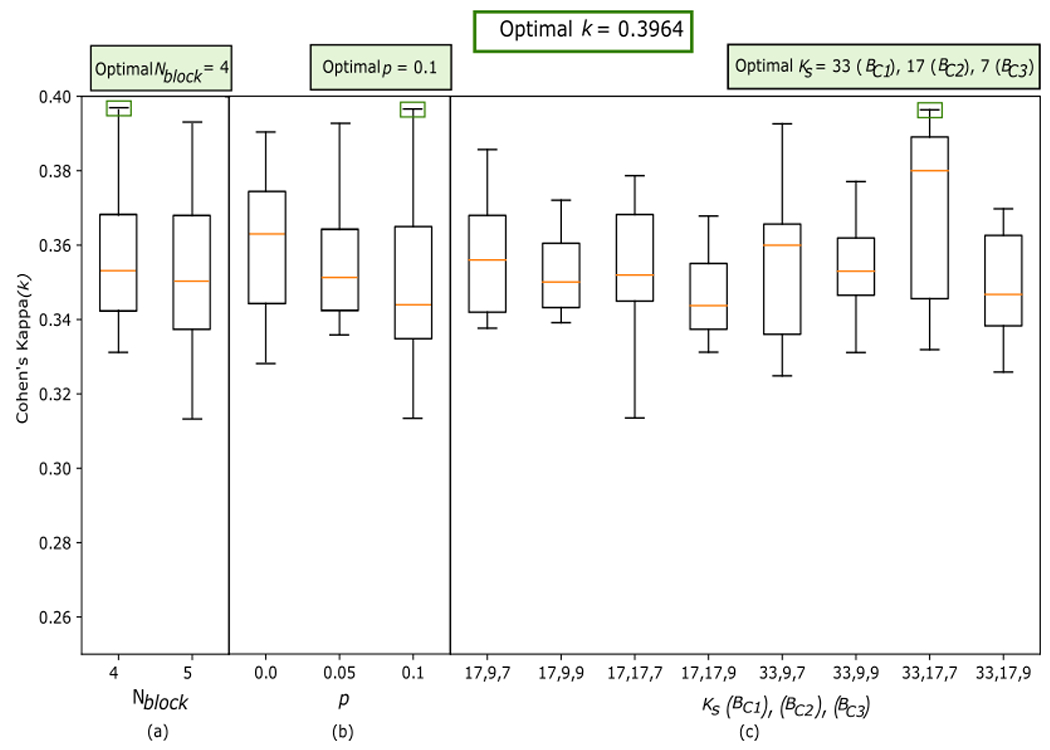
Cohen’s kappa coefficients (k) obtained in the validation subset for each model with a combination of hyperparameters. (a) k values obtained by modifying the hyperparameter N_block; (b) k values obtained by modifying the hyperparameter p; (c) k values obtained by modifying the hyperparameter K_s. N_block: convolutional sub-blocks; p: dropout; K_s: kernel size; B_C1, B_C2, B_C3: convolutional blocks 1, 2 and 3, respectively.

4.2. AHI estimation

After training the model with the training subset and establishing the optimal configuration using the validation subset, the test subset was used to estimate the $AH{I}_{\mathit{\text{est}}}$ and evaluate the performance of the CNN-based algorithm. The Bland-Altman plot was calculated to establish the similarity between the estimated final AHI of each subject in the proposed model and the AHI extracted from the PSG in the CHAT database (see Figure 5). The solid black line of the Bland-Altman plot shown in Figure 5 indicates the average difference between $AH{I}_{\mathit{\text{est}}}$ and $AH{I}_{\mathit{\text{actual}}}$. A negative value indicates that our proposed model underestimates in the test subset slightly. However, despite this underestimation, the limits of the confidence interval ([7.40, −9.40]), together with the ICC = 0.79, show that there is high agreement between $AH{I}_{\mathit{\text{est}}}$ and $AH{I}_{\mathit{\text{actual}}}$.

Figure 5:

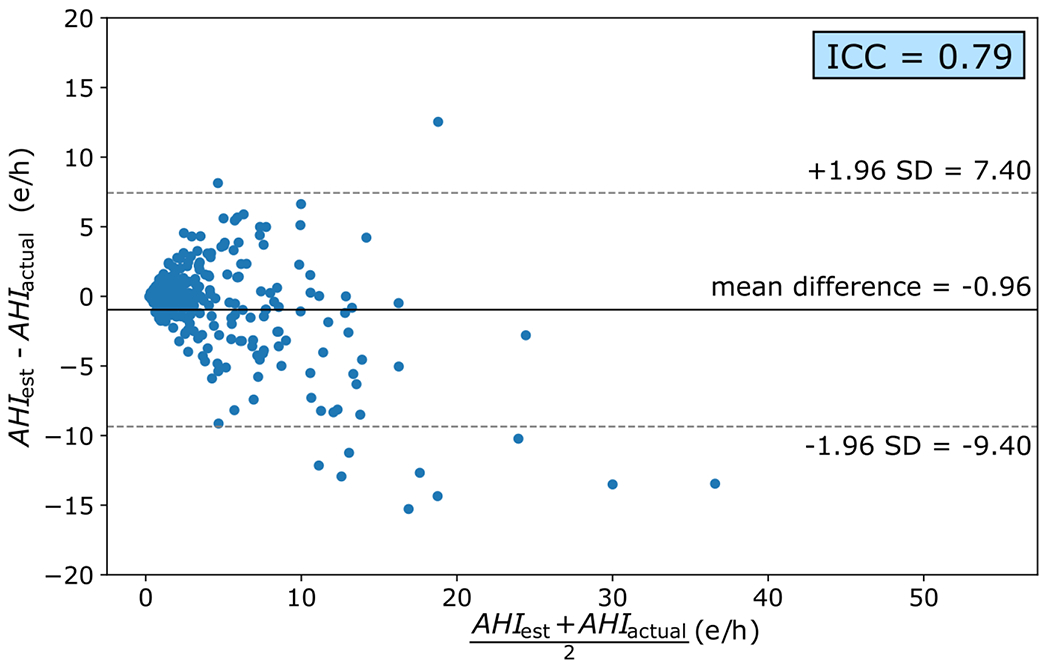
Bland-Altman plot and ICC value calculated from the AHI estimated by our model and the AHI extracted from PSG in the CHAT database. SD (standard deviation); e/h (events/hour).

4.3. Diagnostic ability of pediatric OSA

To evaluate the diagnostic ability of the model, we determined the severity of pediatric OSA after estimating the $AH{I}_{\mathit{\text{est}}}$ in the test subset. We calculated the confusion matrix, $Ac{c}_4$, and k (Figure 6). On the one hand, the cells of the confusion matrix show the proportion of subjects of the actual class assigned to each severity group. These values are associated with a cell color, indicating the performance of the model. On the other hand, the values of the number of subjects estimated in each of the four groups are shown. We observe an overestimation of the OSA severity in healthy subjects (no OSA) and an underestimation of the OSA severity in mild OSA subjects. According to the number of correctly classified subjects on the main diagonal, the performance of the model is better in subjects with mild OSA (65.28%), followed by those with moderate (55.10%), severe OSA (53.66%), and no OSA subjects (46.15%). Finally, it is important to note that all the subjects estimated with an $AH{I}_{\mathit{\text{est}}}\ge 10\mathrm{e}/\mathrm{h}$ are patients who have at least moderate OSA.

Figure 6:

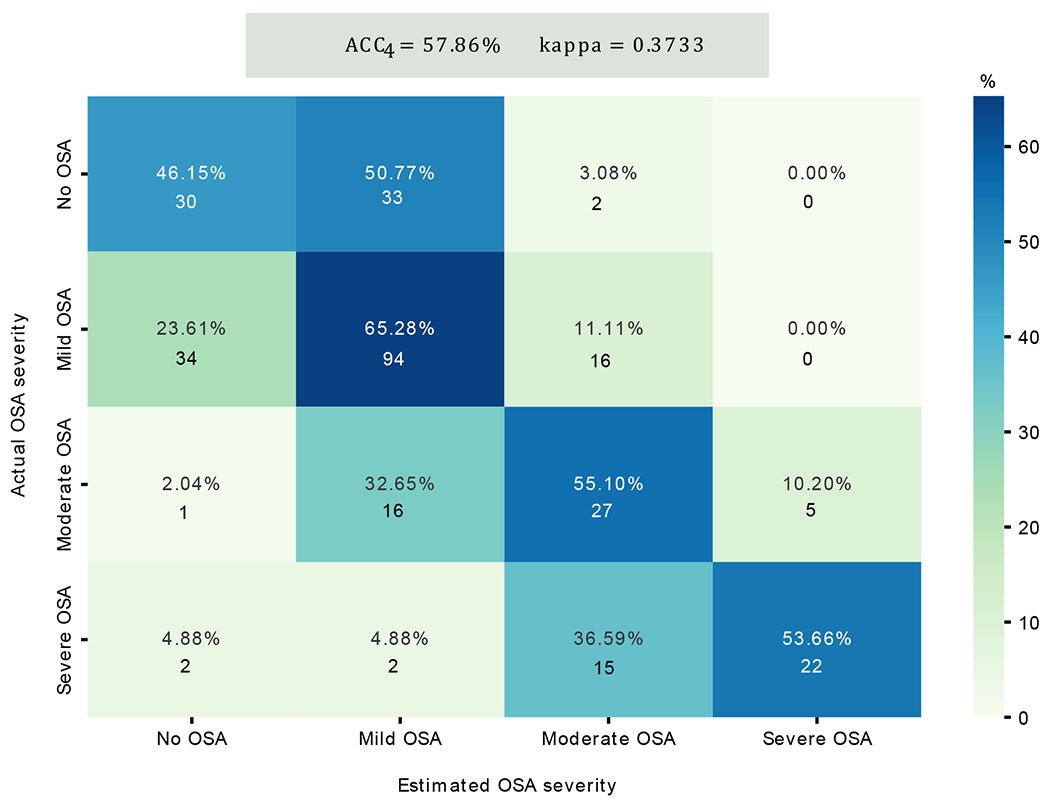
Confusion matrix of classification performance of the test subset in the four severity groups among pediatric patients. The color reference is associated with the proportion (%) of subjects of the actual class assigned in each severity group. At the top, the values of the 4-class accuracy (Acc₄) and the 4-class Cohen’s kappa coefficient (k) are shown. * No OSA: AHI<1 (e/h); Mild OSA: 1≤AHI<5 (e/h); Moderate OSA: 5≤AHI<10(e/h); Severe OSA: AHI≥10(e/h).

Table 2 presents the diagnostic performance of our pediatric OSA estimation algorithm in the three severity thresholds (AHI = 1 e/h, AHI = 5 e/h, AHI = 10 e/h). We can observe that the values of Sp are higher as the severity of OSA increases and, conversely, the values of Se decrease. The AHI threshold with the most balanced Se and Sp is 5 e/h. If we focus on the values of PPV and NPV, the highest values are obtained in 1 e/h and 10 e/h, respectively. Regarding LR values, it is essential to highlight the LR⁺ value obtained for the threshold 10 e/h (27.69), which indicates a relevant diagnostic utility for this threshold. Finally, as the severity of OSA increases, the Acc of the model is higher, with 91.97% Acc for 10 e/h. If we analyze the 2-class kappa at each threshold, we can observe that the highest value is obtained for 5 e/h (0.69). Thus, in strict terms of classification, we can state that the highest 2-class kappa results are obtained for 5 e/h. However, we consider it essential to emphasize that determining the most suitable threshold for model performance depends significantly on aligning it with the specific objectives of the clinicians using our approach. Consequently, we show various metrics to let the potential users of the model make the last decision on its application. This inherent versatility constitutes a notable advantage of our proposal.

Table 2:

Figures of merit obtained in the test subset for the evaluation of the diagnostic capacity of pediatric OSA in the AHI thresholds 1 e/h, 5 e/h, and 10 e/h. Se (sensitivity); Sp (specificity); PPV (positive predictive value), NPV (negative predictive value), LR⁺ (positive likelihood ratio), and LR⁻(negative likelihood ratio). e/h (events/hour).

Test subset
AHI threshold	Se (%)	Sp (%)	PPV (%)	NPV (%)	LR +	LR −	Acc (%)	2-class kappa
1 e/h	84.19	46.15	84.91	44.78	1.56	0.34	75.92	0.30
5 e/h	76.67	91.39	79.31	90.09	8.90	0.26	86.96	0.69
10 e/h	53.66	98.06	81.48	93.01	27.69	0.47	91.97	0.60

5. Discussion

This work evaluated a CNN-based model reliant on raw overnight ECG signals to estimate respiratory events per segment and AHI per subject for diagnosing OSA severity in pediatric patients. A CNN-based algorithm reached a moderate-to-high diagnostic performance for the thresholds of 1 e/h, 5 e/h, and 10 e/h. Results demonstrate that using single-channel ECG signal and a CNN shows an excellent potential for identifying pediatric OSA severity, thus enabling a simple, fast, objective, and accurate diagnosis. Furthermore, the diagnostic performance obtained with the proposed approach could be a valuable starting point to assess for cardiac co-morbidities, a significant risk factor in children, particularly those with severe OSA [2].

5.1. Comparison between adult and pediatric OSA

Pediatric OSA disease is a serious health problem due to its elevated prevalence and the associated morbidities it can cause [2]. As a result of the cost of PSG and the human and instrument resources required for its detection, much effort has been invested in simplifying the signals required to enable automatic OSA diagnosis in children [14]. Diagnosing pediatric OSA using a single-channel ECG signal is particularly interesting for its simplicity of recording and comfort for children. Analysis of this signal is crucial due to the relevant information it contains including potential underlying cardiovascular pathology [2,10].

In adults, some approaches have analyzed the ECG signals through DL methods. Specifically, CNN networks have been implemented for event detection and classification of OSA, achieving high performance in the OSA classification, with Acc values ranging from approximately 90% to 99% [20–23,25,26]. However, DL methods have yet to be exhaustively evaluated in conjunction with cardiac signals in children. Therefore, we developed a CNN-based model to analyze ECG signals aimed at identifying OSA in children and establishing its severity. Lower diagnostic performances emerged when compared to adults, with differences likely due to the lower AHI traditionally seen in clinical practice among children, the latter reflecting the reduced upper airway collapsible of the upper airway during childhood. As a corollary, the criteria required to establish the presence of OSA are markedly different, being substantially more restrictive for the pediatric population [1,4]. Additionally, AHI thresholds for determining the degree of severity of OSA are lower in children compared to adults (1 e/h, 5 e/h, and 10 e/h versus 5 e/h, 15 e/h, and 30 e/h, respectively) [73,74]. Another critical factor involves the differences in the kinetics of cardiac and other physiological responses during apnea episodes. Accordingly, the analysis of the ECG signals must be specifically restricted to data in children [2,10].

5.2. Configuration of CNN-based model

Regarding the architecture of the model, a regression CNN was implemented. Initially, the number of events per signal segment was estimated, and later, the AHI index per subject was calculated. This methodology had already been used in previous studies by our research group while analyzing other PSG signals such as SpO₂ or AF to identify the severity of pediatric OSA, achieving high accuracy in the classification [56,57].

During the preliminary testing runs, we trained the model with 5-minute segments to avoid any impact on the delay between apnea events and the patterns of tachycardia/bradycardia onset [7]. Later, we used 10-minute segments to train the CNN. The algorithm showed a higher k coefficient with 10-minute segments (0.3762 versus 0.3244 in the validation set), indicating that larger segment sizes have a lesser effect on inter-event delay and bradycardia/tachycardia patterns. However, if the training included segments longer than 10 minutes, there was a high computational cost. Then, once the 10-minute segments were selected, we trained the network initially with 10-minute ECG segments and then applied a 50% overlap as a data augmentation strategy. This approach served to minimize overfitting during training and to facilitate the optimal performance of the model. The highest results in terms of k in the validation subset were obtained in the CNN trained with segment overlap (0.3964 versus 0.3762 ). Therefore, we selected 10-minute segments with 50% overlap to evaluate the model on the test subset.

Concerning the selection of CNN hyperparameters, Figure 4 shows that the highest value of k was obtained with $N_{\mathit{\text{block}}}=4$, p = 0.1, and $K_s=33\left(B_{C\mathit{1}}\right),17\left(B_{C\mathit{2}}\right),7\left(B_{C\mathit{3}}\right)$. Figure 4 (a) shows that increasing the $N_{\mathit{\text{block}}}$ value and, therefore, increasing the complexity of the network, would not lead the CNN to an improvement in the capture of characteristic patterns in the ECG. Figure 4 (b) indicates that further increasing the dropout would lead to lower median values of the boxplots and lower k values for most models, as shown by the trend of interquartile ranges. From Figure 4 (c), we can extract that those models with $K_s$ of similar values obtain lower median and interquartile ranges in the boxplots. This finding highlights the importance of optimizing this hyperparameter.

5.3. Proposal of a diagnostic protocol

Regarding the confusion matrix of Figure 6, it can be observed that 96.9% of healthy children (no OSA) were estimated with an $AH{I}_{\mathit{\text{est}}}<5$ e/h (no OSA or mild OSA). In addition, of the subjects with $AH{I}_{\mathit{\text{actual}}}<5\mathrm{e}/\mathrm{h}$, 91.4% were predicted as no OSA or mild OSA. All subjects belonging to the no OSA or mild OSA class were estimated with an $AH{I}_{\mathit{\text{est}}}<10\mathrm{e}/\mathrm{h}$. Finally, of the children who were estimated with an $AH{I}_{\mathit{\text{est}}}>10\mathrm{e}/\mathrm{h}$ (severe OSA), 100% were subjects with at least moderate OSA.

Based on these results, a diagnostic protocol could be created from the developed CNN algorithm to demonstrate its clinical utility, according to the following criteria:

1. If our estimate is $AH{I}_{\mathit{\text{est}}}<1\mathrm{e}/\mathrm{h}$ (no OSA), the presence of OSA can be discarded since most of these subjects (95.5%) would have an $AH{I}_{\mathit{\text{actual}}}<5$ e/h. In these children, a follow-up evaluation of the symptoms would need to be done periodically. If the symptoms were to persist over time (i.e., 2-3 months), a determination of the need for PSG would be then made by the sleep specialist.

2. If $1\le AH{I}_{est}<5$ e/h is estimated by the algorithm, 77.2% of the subjects could have $AH{I}_{\mathit{\text{actual}}}>1$ e/h (OSA presence), so the specialist would then recommend a PSG to establish a more precise diagnosis.

3. If the model estimates $5\le AH{I}_{\mathit{\text{est}}}<10\mathrm{e}/\mathrm{h}$, the clinician would consider treatment because 96.7% of these subjects would suffer from at least mild OSA.

4. If the model estimates $AH{I}_{\mathit{\text{est}}}\ge 10\mathrm{e}/\mathrm{h}$, treatment would be established since 100% of children would have an $AH{I}_{\mathit{\text{actual}}}>5\mathrm{e}/\mathrm{h}$ (moderate OSA or severe OSA).

As a result, 51.5% of the PSG would be avoided with this screening protocol. Moreover, only 3.1% of children with an $AH{I}_{\mathit{\text{actual}}}<1$ e/h would be indicated for treatment and 3.3% with an $AH{I}_{\mathit{\text{actual}}}>5$ e/h would not be referred to PSG/treatment in the first visit to the specialist. This solution would reduce waiting lists in the hospital service, achieving a more accurate pediatric OSA diagnosis and timely treatment of the more severe cases.

5.4. Comparison with previous studies

Table 3 summarizes the diagnostic performance of previous publications that used cardiac information, but not the raw ECG signal, and where conventional machine learning (ML) techniques were applied for feature extraction. In the study by Shouldice et al. [3], the binary classification of segments (normal/apnea) and subsequent binary classification of subjects was performed using a single AHI threshold of 1 e/h. RR interval features were used to achieve Se = 85.7%, Sp = 81.8%, PPV = 85.7%, NPV = 81.8%, and Acc = 84%. Comparing the results, our approach at that threshold achieved lower values of Sp, NPV, and Acc, but similar values of Se and NPV. It is important to highlight that in their study they used only 50 total recordings and 25 for the test subset, compared to 1,610 total recordings and 299 in the test subset used in this study. Thus, we can conclude that our results are more powerful and generalizable.

Table 3:

Summary of literature publications on diagnosing pediatric OSA severity using ECG signals. The values of our study are shown in bold.

Publication	Recordings	Signal	Algorithm	Validation	AHI threshold (e/h)	Se (%)	Sp (%)	Acc (%)	PPV (%)	NPV (%)	LR+	LR−
Shouldice et al. [3]	50	RR Interval*	QD	Training/test Loo-cv	1	85.70	81.80	84.00	85.70	81.80	4.71	0.17
Gil et al. [28][29]	21	PPG*	QDA	-	>18 OSA <5 No OSA	87.50	71.40	80.00	-	-	3.05	0.17
Lázaro et al. [30]	21	PPG*	LDA	Training/test Loo-cv	>18 OSA <5 No OSA	100.00	71.40	86.70	-	-	3.5	0.00
Martin-Montero et al. [33]	1738	HRV*	LDA	Training/test	1 5 10	85.47 64.44 53.66	35.38 93.78 97.67	74.58 84.95 91.64	82.64 81.69 78.57	40.35 85.96 92.99	1.32 10.36 23.07	0.41 0.38 0.47
Martin-Montero et al. [32]	1738	HRV*	MLP	Training/test	1 5 10	76.30 62.50 66.70	38.30 84.20 91.60	63.40 81.00 89.30	70.70 40.70 44.20	45.50 92.80 96.50	1.20 4.00 7.90	0.60 0.40 0.40
Martin-Montero et al. [31]	1610	HRV*	LSBoost	Training/validation/test	1 5 10	90.76 66.67 40.00	23.40 61.17 92.03	80.07 63.18 84.12	86.26 49.66 47.37	32.35 76.16 89.53	1.18 1.72 5.02	0.39 0.54 0.65
This work	1610	ECG	CNN	Training/validation/test	1 5 10	84.19 76.67 53.66	46.15 91.39 98.06	75.92 86.96 91.97	84.91 79.31 81.48	44.78 90.09 93.01	1.56 8.09 27.69	0.34 0.26 0.47

^*Classification was performed using features extracted from these signals.

PSG (polysomnography); RR interval (interval between two R peaks); PPG (photoplethysmography); HRV( heart rate variability); PTTV (pulse transit time variability); PRV (pulse rate variability); ECG (electrocardiogram); QD (quadratic discriminant); LDA (linear discriminant analysis); MLP (multilayer perceptron); FCBF (fast correlation based filter); LSBoost (least-squares boosting); CNN (convolutional neural network); Loo-cv (leave-one-out cross-validation); e/h (events/hour); Se (sensitivity); Sp (specificity); PPV (positive predictive value), NPV (negative predictive value), LR⁺ (positive likelihood ratio); LR⁻ (negative likelihood ratio); AHI (apnea-hypopnea index); OSA (obstructive sleep apnea).

Other investigators used extracted features from the PPG signal for binary classification of pediatric OSA (AHI < 5 No OSA and AHI > 18 OSA) [28–30]. Compared to these studies, although Se was lower, our approach achieved higher Sp, LR⁺ and Acc for the most restrictive threshold of 10 e/h. Thus, we can conclude that the current methodology is preferable to correctly identifying healthy children without severe OSA. Moreover, these studies had smaller samples (50 and 21 recordings compared to 1,610 recordings), limiting the generalizability of their results.

Martín-Montero et al. [32,33] used HRV spectral characteristics in two studies to automatically classify pediatric OSA with the common AHI thresholds. In [33], the authors achieved slightly higher Se for 1 e/h (85.47% vs. 84.19%) and Sp for 5 e/h (93.78% vs. 91.39%) than our approach. However, our algorithm achieved a better balance between Se-Sp for both thresholds, resulting in higher Acc (75.95% vs. 74.58% for 1 e/h and 86.96% vs. 84.95% for 5 e/h). We also obtained better predictive accuracy for the threshold of 10 e/h for all measures, thus highlighting the ability of our algorithm to identify severe OSA cases more accurately. Compared to Martín-Montero et al. [32] who obtained slightly higher NPV values for all thresholds, our approach achieved higher Sp values, providing a better balance between NPV and Sp results. Notably, our LR⁺ value of 27.69 at the threshold of 10 e/h (versus 7.90) demonstrates the clinical utility of our algorithm in identifying children with severe OSA. Additionally, our algorithm showed higher classification measures for Se, Sp, Acc, PPV, LR⁺, and LR⁻ at the thresholds of 1 e/h and 5 e/h. This indicates the ability of this approach to distinguish between healthy children and patients with OSA and differentiate between mild and moderate pediatric OSA.

Finally, in another study, authors automatically classified pediatric OSA using features derived from HRV signal segments and a conventional ML technique [31]. This study was the most suitable to compare our results since the same study database (CHAT), number of subjects (1610), and AHI thresholds (1, 5, and10 e/h) were used. In addition, they used the same validation strategy as our proposal with three independent data subsets (training, validation, and test). Our algorithm performed better in terms of Se, Sp, Acc, PPV, NPV, LR⁺, and LR⁻ at the thresholds of 5 e/h and 10 e/h, indicating its clinical applicability in identifying the more severe cases of pediatric OSA. These findings are particularly encouraging as children with moderate to severe OSA are at increased risk of developing cardiovascular and neurocognitive morbidities, and therefore will benefit most from early diagnosis and timely treatment [10,15]. While Se value was lower at the 1 e/h threshold in this work, our Sp value was higher. In this sense, our model achieved a more balanced Se-Sp and PPV-NPV relationships, respectively. These findings indicate that the model proposed here can better identify healthy children, thereby enabling improved utilization of limited PSG resources to those patients more likely to benefit from PSG. Overall, our proposal reached higher values of k (0.372 versus 0.166) and $Ac{c}_4$ (57.86% versus 41.89%). On the one hand, the difference in the k value indicates that the model proposed in this study shows a higher level of agreement between the OSA severity degrees derived from the estimated AHI and the actual OSA severity degrees. Furthermore, it can also be concluded from these results that our model can better capture patterns and relationships in the data, resulting in predictions that are more consistent with the actual OSA severity degrees. On the other hand, the $Ac{c}_4$ results conclude that the overall performance of the proposed model on all classes is approximately 16% higher. This makes our CNN-based algorithm a more reliable diagnostic model for clinical practice.

Despite the most interesting discussion relies on comparing our results with those studies using cardiac information, different previous studies also used the CHAT database along with DL alternatives for diagnosing pediatric OSA [56,57]. They focused on the analysis of overnight SpO₂ and/or AF signals and reached promising results. However, they only used respiratory information, thus obviating possible OSA pathophysiological effects on the cardiac system, including those associated with cardiac morbidities. Moreover, Jimenez-Garcia et al. [56] showed higher technical complexity as they used the two signals for the automated diagnosis instead of a single one. On the other hand, other approaches worked with DL and cardiac information in contexts other than pediatric OSA [75], as for example the investigation of the impact of DL architectures (FC, VGGs, ResNet50, U-Net, and others) on accelerated cardiac T1 mapping, reaching U-Net the highest performance [76]. Despite all these interesting approaches, we consider that studying the ECG signal in pediatric OSA brings added value. First, there is demonstrated evidence of the lack of ECG signal analysis in the pediatric OSA context despite being an extensively studied signal in the clinical field [15]. Furthermore, the ECG contains a plethora of relevant information that can be used for diagnostic purposes, including cardiorespiratory coupling, heart rate changes, and heart rate variability associated with respiratory events [2,7,16]. Importantly, by analyzing overnight ECG the possibility of assessing cardiovascular risk in children is enabled, which is particularly relevant for severe pediatric OSA patients in which cardiovascular morbidity is a significant risk [7,10]. Finally, because the ECG is one of the most analyzed signals in clinical practice worldwide, an ECG-based application to aid in diagnosing OSA could be easily interpretable, implementable, and accessible [17–19].

Therefore, we can conclude that the application of DL-based algorithms using the raw ECG signal offers three notable advantages: 1) All the information contained in the ECG is potentially used; 2) it eliminates the need to develop specifically designed feature extraction methods; 3) it demonstrates higher diagnostic performance of pediatric OSA.

5.5. Limitations

This work has obviously several limitations that must be considered. Although we used a large sample size (1,610 PSG recordings), it would always be better to have even more recordings to perform the analysis to reach more generalized conclusions. Another limitation to consider is that all the subjects included in the CHAT database were initially suspected of having OSA, which could imply that the clinical characteristics of these subjects are more specific of OSA presence. Furthermore, all subjects in our dataset are between 5 and 9.9 years old, which prevents us from drawing conclusions beyond these age limits. Considering the characteristics of the subjects and the study signals, it is challenging to compare our results with other studies. This is because the raw ECG signal was not analyzed before in the previous existing publications of pediatric OSA [28–30,32,33]. Also, of the studies in the literature, there is only one in which the same database was used (CHAT) [31], which provides the most accurate basis for comparison. If we analyze the DL method used here, a CNN-based model network was implemented based on its suitability in the field of time series analysis and its excellent performance in previous studies in adults to diagnose OSA [20–25,35,44,49]. However, RNN/LSTM architectures could be tested to furtherly evaluate the usefulness of our proposal. Finally, there is a real limitation of DL methods in explaining the features extracted by the models that should be considered for future work.

6. Conclusions

To the best of our knowledge, this study reflects the first evaluation of a CNN-based algorithm using single-channel ECG signals to identify pediatric OSA and estimate its severity. Our findings demonstrate that this approach outperforms previous studies that used cardiac information (PPG and HRV signals) with conventional ML methods. This suggests the potential value of combining ECG signals and DL methods in pediatric OSA. Based on the diagnostic performance achieved by our approach, we suggest a diagnostic protocol that could serve as a valuable clinical tool. It would effectively reduce the need for unnecessary PSG by half, thus alleviating waiting lists in clinical facilities. In this sense, our solution could facilitate the objectivity and accuracy of pediatric OSA diagnosis, while ensuring that urgent and appropriate treatment is administered to the most severe cases. Overall, using ECG recordings and our CNN-based proposal provides a highly promising and viable alternative to PSG for diagnosing pediatric OSA.

For future works, it would always improve our study to have more recordings to perform the analysis. Moreover, it would be desirable to use other child AOS databases to assess the generalizability of the model. Additionally, a study based on screening children at risk for OSA would allow a more general population group to be analyzed. Furthermore, it would be appropriate to evaluate and compare the performance of different architectures, as has already been done in other approaches within the cardiac setting [76]. Specifically, it would be interesting to use different alternative models, such as RNN, hybrid models, or transformers, to evaluate their performance and test their diagnostic ability. Furthermore, applying explainable artificial intelligence methods may be useful for future work [77]. These approaches could provide greater clarity in interpreting the results obtained in the CNN-based model, thus enabling a better understanding of the extracted features and the relationship between apneic events and the behavior of the ECG. Finally, future development of user-friendly tools could be used to furtherly validate our proposal in a clinical environment.

Highlights.

• A CNN aimed at simplifying the diagnosis of pediatric OSA using raw ECG signals.

• First study to use this signal coupled with DL methods to diagnose pediatric OSA.

• The model outperformed previous approaches using conventional ML methods.

• A diagnostic protocol is suggested as a clinical tool, halving unnecessary PSGs.

• Accurate detection of moderate and severe OSA cases, aiding in early OSA diagnosis.