A biologically based computational model for the hypothalamic-pituitary-thyroid (HPT) axis in Xenopus laevis larvae

Abstract

A biologically based computational model was developed to describe the hypothalamic-pituitary-thyroid (HPT) axis in developing Xenopus laevis larvae. The goal of this effort was to develop a tool that can be used to better understand mechanisms of thyroid hormone-mediated metamorphosis in X. laevis and predict organismal outcomes when those mechanisms are perturbed by chemical toxicants. In this report, we describe efforts to simulate the normal biology of control organisms. The structure of the model borrows from established models of HPT axis function in mammals. Additional features specific to X. laevis account for the effects of organism growth, growth of the thyroid gland, and developmental changes in regulation of thyroid stimulating hormone (TSH) by circulating thyroid hormones (THs). Calibration was achieved by simulating observed changes in stored and circulating levels of THs during a critical developmental window (Nieuwkoop and Faber stages 54–57) that encompasses widely used in vivo chemical testing protocols. The resulting model predicts that multiple homeostatic processes, operating in concert, can act to preserve circulating levels of THs despite profound impairments in TH synthesis. Represented in the model are several biochemical processes for which there are high-throughput in vitro chemical screening assays. By linking the HPT axis model to a toxicokinetic model of chemical uptake and distribution, it may be possible to use this in vitro effects information to predict chemical effects in X. laevis larvae resulting from defined chemical exposures.

1. Introduction

Metamorphosis in anuran amphibians is primarily controlled by thyroid hormones (THs), and changes associated with this process have been studied for decades to better understand the structure and function of the vertebrate hypothalamic-pituitary-thyroid (HPT) axis [1–5]; also see Supplemental Information SI1, In-Depth Modeling Approach). Included in this body of work are numerous studies in which investigators have used inhibitors of TH synthesis to perturb the axis, resulting in delay or abolishment of metamorphic changes. More recently, interest in anuran metamorphosis has increased because of the suggestion that developing larvae can be used in a bioassay format to identify chemicals that may cause HPT axis disruption in humans [6]. Support for development of this assay derives from the known conservation of HPT axis structure-function across vertebrate species, the demonstrated responsiveness of anuran larvae to TH synthesis inhibitors, and the reduced cost of such assays relative to tests with mammals. This approach was formalized over the last two decades when the U.S. Environmental Protection Agency (EPA) and the Organization for Economic Cooperation and Development (OECD) ratified multiple standardized toxicity test guidelines that utilize a model amphibian, Xenopus laevis, to determine a subject chemical’s potential to disrupt TH-mediated metamorphic development [7–11].

Research designed to support development of these assays has been conducted by several groups [12–20]. These efforts include time-course and dose–response studies of biochemical, histological, and genetic changes elicited by different TH synthesis inhibitors including methimazole, perchlorate, ethylenethiourea, 6-propylthiouracil, and 2-mercaptobenothiazole. This work has been motivated in part by the desire to develop a shorter test, since gross morphological differences may not be manifested for up to two weeks after the start of a chemical exposure, even when TH synthesis is completely inhibited. A need also exists to discriminate among chemicals that disrupt the HPT axis by different modes of action. Recent efforts have focused on study designs that capture mechanistic linkages between early thyroid-related biochemical perturbations and apical outcomes relevant to ecological risk assessment [21].

Based on this work, it is possible to identify a temporal sequence of events that occurs when late pre- and early pro-metamorphic larvae (i.e., larvae at the marginal onset of metamorphosis) are exposed to TH synthesis inhibitors. Early changes (days 2–3 post exposure) include a decrease in the amount of thyroxine (T4), 3,5,3’-triiodothyronine (T3), monoiodotyrosine (MIT), and diiodotyrosine (DIT) stored within the thyroid gland [18,21]. Changes in thyroid gland morphology are evident after 3–5 days of treatment [14,15,18]. These changes include depletion of follicular colloid and hypertrophy of thyroid follicular cells (thyrocytes). Continued exposure results in decreased levels of circulating T3 and T4 (days 6–7; [18,21]) and glandular hyperplasia (days 6–8; [14,15,18,20]). Treatment with TH synthesis inhibitors causes changes in gene expression in pituitary tissue on a time scale of 5 to 8 days [15]. Changes in gene expression within the thyroid gland, likely resulting from a compensatory increase in the plasma concentration of thyroid stimulating hormone (TSH), occur in a similar time frame [16,19,21]. These changes include both up- and down-regulation of specific mRNA transcripts, depending on how the gene is regulated.

In addition to these in vivo research efforts, several in vitro assays have been developed to evaluate chemical effects on highly conserved biochemical processes, or “molecular targets,” associated with the HPT axis [22–27]. This work has been motivated by the need to develop alternative approaches to chemical safety evaluation that minimize animal usage in toxicity testing. Several national initiatives are using high-throughput (HTP) in vitro screening assays to identify molecular mechanisms of chemically induced biological activity and prioritize large chemical libraries for higher tiered testing [28–33]. However, in vitro bioactivity toward a molecular target is not itself predictive of organism-level adversity. A need exists for model-based tools that can be used to put these in vitro observations into a biological context.

In this paper, we describe a biologically based computational model of the HPT axis in X. laevis larvae. The study goal was to simulate normal HPT axis function in developmental stages associated with standardized in vivo chemical testing efforts. In doing so, we sought to develop a model that incorporates most of the thyroid-related molecular targets currently being evaluated using in vitro assays. A follow-up paper will illustrate how the model may be used to interpret in vivo study results and make predictions of metamorphic success based on in vitro effects information. Although the model shares features of published models for the HPT axis in mammals [34–40], its structure and parameterization are informed by biological information unique to X. laevis larvae during a critical period of thyroid-mediated metamorphosis, including histological and biochemical impacts associated with HPT axis disruption. The resulting model accurately describes the normal biology of X. laevis larvae, including stage-specific changes in circulating TSH, T4 and T3, and the accumulation of TH precursors in the developing thyroid gland.

2. Materials and methods

2.1. Modeling approach

A biologically based model for the HPT axis in X. laevis larvae was constructed as a dynamic, chemical mass-balance description (moles basis) that simulates changes in the amounts of various ions (e.g., iodide), molecules (e.g., THs), and macromolecules (e.g., thyroglobulin [Tg]) in modeled compartments over time. Represented in the model are many biochemical processes that are highly conserved among vertebrate thyroid systems. To the extent practicable, however, we sought to simplify the model structure while maintaining the dynamic behavior necessary to simulate measured biochemical profiles with reasonable accuracy. Here we describe our modeling approach in general terms. A more in-depth description of the modeling approach is provided as Supplemental Information (SI1, In-Depth Modeling Approach).

The HPT axis is primarily regulated by endocrine feedback between THs, synthesized and released from the thyroid gland, and TSH, synthesized and released from the hypothalamus-pituitary. Thyroid hormone synthesis processes in the gland are positively regulated by TSH while TSH secretion is negatively regulated by THs. The presented model represents a key window of metamorphic development in X. laevis during which TH levels are rising in the plasma to drive tissue and organ metamorphosis. This required that the model not only maintain homeostasis through various feedback mechanisms, but also include a changing setpoint for negative feedback of THs on TSH secretion.

The thyroid gland consists of many follicles, each of which contains a follicular luminal space surrounded by a single layer of thyrocytes. The overall process of TH synthesis involves active uptake of plasma iodide into the thyrocytes, Tg synthesis, organification of iodide onto Tg, and coupling of iodinated tyrosyl residues. These latter two processes are catalyzed by the enzyme thyroperoxidase (TPO). Therefore, Tg is stored in the lumen as a colloid and contains iodinated precursors of MIT, DIT, T3 and T4. Endocytosis and proteolysis of Tg in the endocytic vesicle releases MIT and DIT, which are recycled within the thyrocytes, while proteolytic release of T3 and T4 results in secretion to the plasma.

The model for X. laevis larvae consists of two compartments corresponding to the aggregated volume of thyrocytes and the remainder of the animal (Fig. 1). All model parameters and predicted state variables are given in Table 1. The units used in the model are grams (g), picomoles (pmol), milliliters (ml) and hours (h). To calculate circulating concentrations of TSH, T3, and T4, we adopted the convention of representing the whole body (henceforth referred to as the plasma compartment) as an apparent volume of distribution, referenced to biochemical concentrations in plasma. This approach is similar to that used by McLanahan et al. [40] and eliminates the need for partitioning parameters to simulate the distribution of hormones among different tissues.

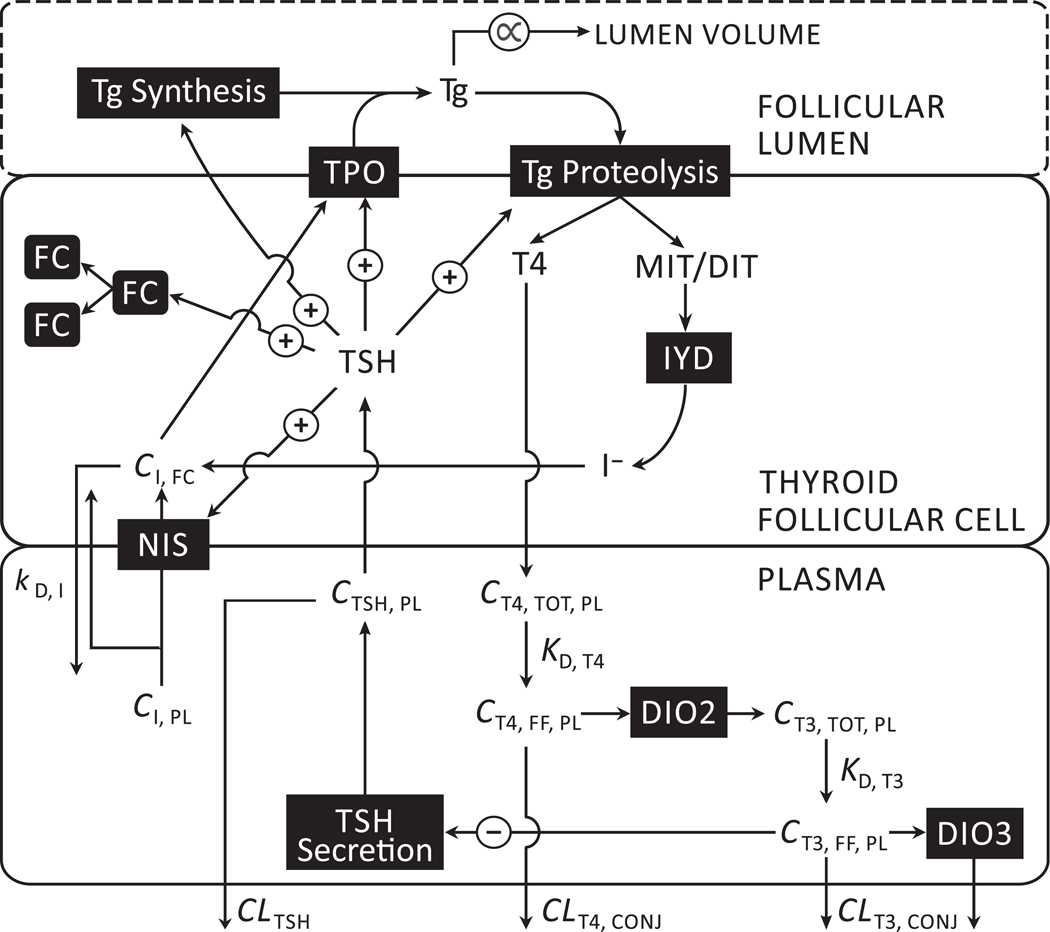
Fig. 1.

Schematic depiction of a biologically based computational model for the hypothalamic-pituitary-thyroid (HPT) axis in X. laevis larvae. Modeled compartments correspond to the aggregated volume of thyroid follicular cells and an apparent volume of blood plasma that represents the remainder of the animal. Follicular colloid (thyroglobulin), which is delineated by a dashed line, is modeled on a mass (picomoles) basis. The lumen volume of thyroid follicles is not modeled explicitly; however, changes in the mass of thyroglobulin are assumed to be proportional $(\propto )$ to changes in lumen volume. The plus signs (+) represent feed-forward effects of TSH on a variety of glandular processes. The minus sign (–) represents negative feedback of free T3 on TSH secretion. Arrows represent modeled relationships between various molecules and biochemical processes, as well as the movements of molecules into and out of modeled compartments. Abbreviations: TPO — thyroperoxidase; Tg — thyroglobulin; FC — follicular cells (thyrocytes); TSH — thyroid stimulating hormone; IYD — iodotyrosine deiodinase; NIS — sodium-iodide symporter; DIO2 — type 2 iodothyronine deiodinase; DIO3 — type 3 iodothyronine deiodinase; T3 — 3,5,3’triiodothyronine; T4 — thyroxine; MIT — monoiodotyrosine; DIT — diiodotyrosine; I⁻ — iodide; $C$ — concentration; $CL$ — plasma clearance; TOT — total; FF — free fraction; PL — plasma; CONJ — conjugation; $K_{\text{D}}$ — dissociation constant for the indicated binding interaction; $K_{\text{D}}$ — diffusion rate constant. See text for additional information on depicted relationships.

Table 1.

Starting values for model parameters and state variables used in a biologically based computational model for the hypothalamic-pituitary-thyroid (HPT) axis in X. laevis larvae.^a

Parameter	Term	Value	Source
Body growth
Starting body weight (g)	$BW$	0.28	Haselman et al. [21]; extrapolated to $t_0$
Rate of change of BW (1/h)	$R_{\text{BW}}$	0.0027	Haselman et al. [21]; fitted to measured growth data
Plasma and follicular cell iodide
Plasma concentration (pmol/ml)	$C_{\text{I},\text{PL}}$	1,000	This study (SI4)
Starting follicular cell concentration (pmol/ml)	$C_{\text{I},\text{FC}}$	20,000	$20\times C_{\text{I},\text{PL}}$
To calculate plasma concentration of TSH
Starting amount of TSH in plasma (pmol)	$A_{\text{TSH},\text{PL}}$	0.00165	Estimated from Korte et al. [41] and then optimized
Apparent volume of TSH distribution (ml/g)	$V{D}_{\text{TSH}}$	0.0554	McLanahan et al. [40]
Starting maximum rate of TSH secretion (pmol/h)	$V_{\text{MAX},\text{TSH}}$	0.325	Optimized
Rate of change of $V_{\text{MAX},\text{TSH}}$ (1/h)	$R_{V_{\text{MAX},\text{TSH}}}$	0.005	Optimized
$C_{\text{T}3,\text{FF},\text{PL}}$ resulting in half-maximal TSH secretion (pmol/ml)	$K_{\text{M},\text{TSH}}$	1.1×10−6	1/100th starting $C_{\text{T}3,\text{FF},\text{PL}}$
Starting rate of change of $K_{\text{M},\text{TSH}}$ (1/h)	$R_{K_{\text{M},\text{TSH}}}$	2.0×10−8	Optimized
Rate of change of $R_{K_{\text{M},\text{TSH}}}$ (1/h)	$R_{R_{K_{\text{M},\text{TSH}}}}$	1.0×10−9	Optimized
Plasma clearance constant (ml/h/g)	$C{L}_{\text{TSH}}$	0.11	Lemarchand-Beraud and Berthier [42]b
To calculate the aggregated volume of thyrocytes
Starting number of thyrocytes in NF stage 54 larvae	$FC{N}_{\text{TOT}}$	8,000	Haselman et al. [21]; extrapolated to $t_0$
Rate of change of thyrocyte number in controls (1/h)	$R_{\text{FCN},\text{CONT}}$	40	Optimized
Max. rate of change of TSH-mediated thyrocyte prolif. (1/h)	$R_{\text{FCN},\text{MAX}}$	700	Optimized
Average thyrocyte volume (ml)	$FCV$	1.0	This study (SI3)
Hill constant for TSH induction of gland growth (unitless)	$K_{\text{H}}$	0.6	Optimized
Hill coefficient for TSH induction of gland growth (unitless)	$n$	3.5	Optimized
To calculate intracellular iodide (see also terms that describe iodide organification and recycling of MIT and DIT)
Maximum rate of TSH-induced NIS activity (pmol/h/ml)	$V_{\text{MAX},\text{NIS}}^{\text{TSH}}$	2.55×107	Optimized
Affinity constant for TSH induction of NIS (pmol/ml)	$K_{\text{M},\text{NIS}}^{\text{TSH}}$	1.0×10−9	10x starting $C_{\text{TSH},\text{PL}}$
Affinity constant for NIS activity (pmol/ml)	$K_{\text{M},\text{NIS}}$	100,000	$100\text{x}{C}_{\text{I},\text{PL}}$
Inhibition constant for autoregulation of NIS by iodide (pmol/ml)	$K_{\text{I},\text{FC}}$	40,000	2x starting $C_{\text{I},\text{FC}}$
Rate constant for diffusion flux of iodide (ml/h/ml)	$k_{\text{D},\text{I}}$	1.1	Optimized
To calculate the rate of Tg synthesis (resulting in secretion of T4 and recycling of MIT and DIT)
Absolute maximum rate of Tg synthesis (pmol/h/ml)	$V_{\text{MAX},\text{TG},\text{SYN}}$	4400	Optimized
Affinity constant for TSH induction of Tg synthesis (pmol/ml)	$K_{\text{M},\text{TG},\text{SYN}}$	1.0	10x starting $C_{\text{TSH},\text{PL}}$
To describe the organification of iodide by TPO as MIT, DIT, and T4 iodine
Total starting amount of Tg in thyroid follicular lumen (pmol)	$A_{\text{TG},\text{TL}}$	0.4	Estimated from [21] and then optimizedc
Starting amount of organified iodine associated with Tg (pmol)	$A_{\text{I},\text{TG},\text{TL}}$	13.135	37 mol/mol iodinated Tgc
Starting amount of organified iodine associated with MIT (pmol)	$A_{\text{MIT},\text{TL}}$	0.355	1 mol/mol iodinated Tgc
Starting amount of organified iodine associated with DIT (pmol)	$A_{\text{DIT},\text{TL}}$	4.26	12 mol/mol iodinated Tgc
Starting amount of organified iodine associated with T4 (pmol)	$A_{\text{T}4,\text{TL}}$	8.52	24 mol/mol iodinated Tgc
Absolute maximum rate of TSH-induced TPO activity (pmol/h/ml)	$V_{\text{MAX},\text{TPO}}^{\text{TSH}}$	4.0×107	Optimized
Affinity constant for TSH induction of TPO (pmol/ml)	$K_{\text{M},\text{TPO}}^{\text{TSH}}$	1.0	10x starting $C_{\text{TSH},\text{PL}}$
Affinity constant for iodide incorporation into Tg via TPO	$K_{\text{M},\text{TPO}}$	2.0×106	100x starting $C_{\text{I},\text{FC}}$
To calculate the rate of Tg proteolysis
Absolute maximum rate of Tg proteolysis (pmol/h/ml)	$V_{\text{MAX},\text{TG},\text{PROT}}$	10,000	Optimized
Affinity constant for TSH induction of Tg proteolysis (pmol/ml)	$K_{\text{M},\text{TG},\text{PROT}}$	10	100x starting $C_{\text{TSH},\text{PL}}$
To calculate plasma T4 concentration
Starting total amount of T4 in plasma (pmol)	$A_{\text{T}4,\text{TOT},\text{PL}}$	0.0073	Haselman et al. [21]
Apparent volume of T4 distribution (ml/g)	$V{D}_{\text{T}4}$	0.156	McLanahan et al. [40]
Conjugative metabolism constant (ml/h/g)	$C{L}_{\text{T}4,\text{CONJ}}$	4.0	Fit to give $t_{1/2}$ of ∼2 h
Plasma protein dissociation constant (unitless)	$K_{\text{D},\text{T}4}$	0.01	Gives 1.0% free fraction
Maximum rate of T4 deiodination (pmol/h)	$V_{\text{MAX},\text{DIO}2}$	0.887	Optimized
Affinity constant for T4 deiodination (pmol/ml)	$K_{\text{M},\text{DIO2}}$	0.167	100x starting $C_{\text{T}4,\text{FF},\text{PL}}$
To calculate plasma T3 concentration
Starting total amount of T3 in plasma (pmol)	$A_{\text{T}3,\text{TOT},\text{PL}}$	0.00112	Haselman et al. [21]
Apparent volume of T3 distribution (ml/g)	$V{D}_{\text{T}3}$	0.186	McLanahan et al. [40]
Plasma clearance constant (ml/h/g)	$C{L}_{\text{T}3,\text{CON}3}$	28.3	Fit to give $t_{1/2}$ of ∼1 h
Plasma protein dissociation constant (unitless)	$K_{\text{D},\text{T}3}$	0.005	Gives 0.5% free fraction
Maximum rate of T3 deiodination (pmol/h)	$V_{\text{MAX},\text{DIO}3}$	0.58	Optimized
Affinity constant for T3 deiodination (pmol/ml)	$K_{\text{M},\text{DIO3}}$	0.011	100x starting $C_{\text{T}3,\text{FF},\text{PL}}$

^aAbbreviations: TPO — thyroperoxidase; Tg — thyroglobulin; TSH — thyroid stimulating hormone; NIS — sodium-iodide symporter; T4 — thyroxine; T3 — 3,5,3’-triiodothyronine; MIT — monoiodotyrosine; DIT — diiodotyrosine.

^bResults in plasma half-life value given by these authors for¹²⁵I-TSH in rats.

^cStarting values for Tg, MIT, DIT, and T4 were informed by measured amounts of MIT, DIT, and T4 in glands of NF 56 X. laevis tadpoles [21]; see main text for details.

Primary guidance for model development and calibration was obtained by simulating measured glandular MIT, DIT, and T4, thyrocyte numbers, and total plasma T3 and T4 concentrations in X. laevis controls from three time-course studies [21]. The goal of these studies was to link biochemical changes occurring within 10 days of exposure to a model TPO inhibitor to adverse apical outcomes such as delayed/arrested metamorphosis. The exposures were initiated with pro-metamorphic Nieuwkoop and Faber [43] stage 54 larvae. Most of the controls remaining at the conclusion of the 10-day interim biochemical assessment within each test were determined to be NF stage 56/57 animals. Additional observations from earlier studies of X. laevis tadpoles were used to inform the structure of the model and aid in the specification of starting parameter values. The model was developed and run using the ODE function of the deSolve package [44] in R [45]. Solution sets at each time point were obtained by numerical integration using the Runge–Kutta 4th order algorithm. The R script for the model is available as Supplemental Information (SI2).

2.2. Regulation of T4, T3, and TSH in plasma

The amount of T4 in the plasma compartment $\left(A_{\text{T}4,\text{TOT},\text{PL}};\text{pmol}\right)$ was simulated by constructing a mass balance (moles basis) that accounts for T4 secretion by the thyroid gland, deiodination by type 2 iodothyronine deiodinase (DIO2; forming T3), and hepatic clearance by all relevant pathways. This latter term is referred to as “conjugative metabolism” since Phase II conjugation pathways (primarily sulfation and glucuronidation) play a major role in hepatic clearance of T4 by mammals. The actual pathways for hepatic clearance of THs in amphibians are less well known. Limited data from studies of Rana catesbeiana tadpoles suggest that while conjugation plays a large role in hepatic clearance of T3, T4 may be poorly conjugated [46]. The equation that describes these processes is expressed as,

$$d{A}_{\text{T}4,\text{TOT},\text{PL}}/dt=R_{\text{T}4,\text{SEC}}-R_{\text{T}4,\text{CONJ}}-R_{\text{T}4,\text{DIO}2}$$ (1)

where $R_{\text{T}4,\text{SEC}}$ (pmol/h) is the rate of T4 secretion, $R_{\text{T}4,\text{CONJ}}$ (pmol/h) is the rate of T4 conjugation, and $R_{\text{T}4,\text{DIO}2}$ (pmol/h) is the rate of T4 deiodination/T3 production, respectively. A similar equation was used to describe changes in the amount of T3 in plasma $\left(A_{\text{T}3,\text{TOT},\text{PL}};\text{pmol}\right)$,

$$d{A}_{\text{T}3,\text{TOT},\text{PL}}/dt=R_{\text{T}4,\text{DIO}2}-R_{\text{T}3,\text{CONJ}}-R_{\text{T}3,\text{DIO}3}$$ (2)

where $R_{\text{T}3,\text{CONJ}}$ (pmol/h) is the rate of T3 conjugation and $R_{\text{T}3,\text{DIO}3}$ (pmol/h) is the rate of deiodination by type 3 iodothyronine deiodinase (DIO3). The concentrations of total T4 and T3 in the plasma compartment ($C_{\text{T}4,\text{TOT},\text{PL}}$, $C_{\text{T}3,\text{TOT},\text{PL}}$; pmol/ml) were calculated as $A_{\text{T}4,\text{TOT},\text{PL}}$ and $A_{\text{T}3,\text{TOT},\text{PL}}$ divided by the hormone’s apparent volume of distribution $\left(V{D}_{\text{T}4},V{D}_{\text{T}3};\text{ml}/\text{g}\right)$. Apparent volumes of distribution for T4 and T3 were set to values determined for rodents [40] (Table 1, see cited work for sources). Following [40], these values were then multiplied by body weight (BW; g), allowing the model to adjust for organism growth.

$$C_{\text{T}4,\text{TOT},\text{PL}}=A_{\text{T}4,\text{TOT},\text{PL}}/\left(V{D}_{\text{T}4}\cdot BW\right)$$ (3)

$$C_{\text{T}3,\text{TOT},\text{PL}}=A_{\text{T}3,\text{TOT},\text{PL}}/\left(V{D}_{\text{T}3}\cdot BW\right)$$ (4)

Studies with humans indicate that THs in plasma are >99% protein bound and that most of this binding (ca. 75%) is to thyroid binding globulin (TBG; [47]). Smaller amounts are bound to transthyretin (TTR) and albumin. Models of the HPT axis given by Kohn et al. [38] and McLanahan et al. [40] account for plasma binding to predict hepatic clearance of THs. In both models, however, inhibitory effects of THs on TSH secretion are referenced to the total T4 concentration in plasma. In the present effort, $R_{\text{T}4,\text{CONJ}}$, $R_{\text{T}3,\text{CONJ}}$, $R_{\text{T}4,\text{DIO}2}$, and $R_{\text{T}3,\text{DIO}3}$ were referenced to unbound (free) concentrations of T4 and T3 in plasma. This approach assumes that bound hormones are not bioavailable to deiodination and conjugation enzymes. In a departure from earlier modeling efforts [38,40], homeostatic inhibitory effects of THs on TSH secretion were referenced to the free concentration of T3 in plasma. Our rationale for this approach is given in Supplemental Information (SI1, In-Depth Modeling Approach).

Transthyretin appears to be the primary TH binding protein in amphibians during metamorphosis [48–50]. Transthyretin transports THs to target tissues and may participate in carrier-mediated transport of bound hormones across cell membranes. In mammals, all the major TH binding proteins have greater affinity for T4 than for T3. In contrast, amphibian TTR exhibits greater affinity for T3 than for T4 [48,49]. The fact that amphibian TTR plays a major role in binding TH is important because several studies have shown that environmental contaminants can interfere with this binding, possibly impacting the HPT axis [51–54]. Lacking basic information needed to develop a detailed description of TH binding to TTR (e.g., the concentration of TTR in plasma and its affinity for different THs), we took the simplifying approach of calculating free T4 and T3 $\left(C_{\text{T}4,\text{FF},\text{PL}},C_{\text{T}3,\text{FF},\text{PL}};\text{pmol}/\text{ml}\right)$ as the product of $C_{\text{T}4,\text{TOT},\text{PL}}$ and $C_{\text{T}3,\text{TOT},\text{PL}}$, and two hormone-specific dissociation constants ($K_{\text{D},\text{T}4},K_{\text{D},\text{T}3}$; unitless).

Deiodination of T4 by DIO2 was modeled as a saturable reaction exhibiting Michaelis–Menten kinetics,

$$R_{\text{T}4,\text{DIO}2}=V_{\text{MAX},\text{DIO}2}\cdot BW\cdot C_{\text{T}4,\text{FF},\text{PL}}/\left(K_{\text{M},\text{DIO}2}+C_{\text{T}4,\text{FF},\text{PL}}\right)$$ (5)

where $V_{\text{MAX},\text{DIO}2}$ (pmol/h/g), scaled to body weight, is the maximum rate of reaction and $K_{\text{M},\text{DIO}2}$ (pmol/ml) is the free concentration of T4 that results in half-maximal activity. Iodide concentrations in plasma were assumed to remain constant (see Section 2.5.1 and Supplemental Information, SI4). Therefore, iodide liberated by deiodination of T4 was not used as an input to the model. The T3 produced by this reaction was used, however, as the primary input to the mass-balance equation for circulating T3 (Eq. (2)).

The conversion of T3 to diiodothyronine (T2) by DIO3 was also modeled as a saturable reaction,

$$R_{\text{T}3,\text{DIO}3}=V_{\text{MAX},\text{DIO}3}\cdot BW\cdot C_{\text{T}3,\text{FF},\text{PL}}/\left(K_{\text{M},\text{DIO}3}+C_{\text{T}3,\text{FF},\text{PL}}\right)$$ (6)

where $V_{\text{MAX},\text{DIO}3}$ (pmol/h/g), scaled to body weight, is the maximum rate of reaction and $K_{\text{M},\text{DIO}3}$ (pmol/ml) is the free concentration of T3 that results in half-maximal activity. The T2 produced by this reaction was considered irrelevant to the modeling effort and is lost from the system along with the liberated iodide. Conjugation of free T4 and free T3 were modeled using first-order clearance constants $(C{L}_{\text{T}4,\text{CONJ}},C{L}_{\text{T}3,\text{CONJ}};\text{ml}/\text{h}/\text{g})$ scaled to body weight.

$$R_{\text{T}4,\text{CONJ}}=C{L}_{\text{T}4,\text{CONJ}}\cdot BW\cdot C_{\text{T}4,\text{FF},\text{PL}}$$ (7)

$$R_{\text{T}3,\text{CONJ}}=C{L}_{\text{T}3,\text{CONJ}}\cdot BW\cdot C_{\text{T}3,\text{FF},\text{PL}}$$ (8)

The T4 and T3 cleared in this manner were assumed to be lost from the system.

The plasma concentration time-course for TSH was simulated using an equation that balances TSH secretion by the pituitary gland and total plasma clearance,

$$\begin{gathered} d{A}_{\text{TSH},\text{PL}}/dt=\left(V_{\text{MAX},\text{TSH}}/\left(\left(C_{\text{T}3,\text{FF},\text{PL}}/K_{\text{M},\text{TSH}}\right)+1\right)\right) \\ -C{L}_{\text{TSH}}\cdot BW\cdot C_{\text{TSH},\text{PL}} \end{gathered}$$ (9)

where $A_{\text{TSH},\text{PL}}$ (pmol) is the amount of TSH in the plasma compartment, $V_{\text{MAX},\text{TSH}}$ is the maximal rate of TSH secretion (pmol/h), $K_{\text{M},\text{TSH}}$(pmol/ml) is equal to the $C_{\text{T}3,\text{FF},\text{PL}}$ that results in half-maximal TSH secretion, $C_{\text{TSH},\text{PL}}$(pmol/ml) is the concentration of TSH in plasma, and $C{L}_{\text{TSH}}$ (ml/h/g) is a clearance constant that describes the elimination of TSH from plasma. The total concentration of TSH in plasma ($C_{\text{TSH},\text{PL}}$; pmol/ml) was calculated at each time point as $A_{\text{TSH},\text{PL}}$ divided by the product of $V{D}_{\text{TSH}}$ and BW.

$$C_{\text{TSH},\text{PL}}=A_{\text{TSH},\text{PL}}/\left(V{D}_{\text{TSH}}\cdot BW\right)$$ (10)

Eq. (9) is similar to the relationship given by McLanahan et al. [40] for TSH kinetics in plasma but has been rearranged here to emphasize the inhibitory effect of increasing T3 concentrations on TSH secretion. An important feature of Eq. (9) is that the maximum rate of TSH secretion saturates at low levels of $C_{\text{T}3,\text{FF},\text{PL}}$. The ability of the system to compensate for a decrease in $C_{\text{T}3,\text{FF},\text{PL}}$ is therefore constrained unless the starting value of $K_{\text{M},\text{TSH}}$ is substantially lower than the starting value of $C_{\text{T}3,\text{FF},\text{PL}}$. Initially, the starting value of $K_{\text{M},\text{TSH}}$ was set equal to 1/100th the starting value of $C_{\text{T}3,\text{FF},\text{PL}}$. This results in a system that responds in a nearly proportional manner to an increase or decrease in $C_{\text{T}3,\text{FF},\text{PL}}$ across a relatively wide range of concentrations but results in a robust compensatory increase in TSH secretion at very low levels of $C_{\text{T}3,\text{FF},\text{PL}}$.

During thyroid-mediated amphibian metamorphosis, the thyroid axis exhibits a paradoxical rise in both TH and TSH concentrations. Research with X. laevis tadpoles indicates that this occurs because of an increase in the set-point for negative feedback of THs on TSH synthesis [55]. To simulate this phenomenon, the value of $K_{\text{M},\text{TSH}}$ must increase over the course of the 10-day simulation. This was accomplished by applying a rate constant $\left(R_{{\text{K}}_{\text{M},\text{TSH}}};1/\text{h}\right)$ that describes the rate of change of $K_{\text{M},\text{TSH}}$. The effect of this change is to continuously decrease the responsiveness of the system to a fixed concentration of $C_{\text{T}3,\text{FF},\text{PL}}$, thereby providing a means by which $C_{\text{TSH},\text{PL}},C_{\text{T}4,\text{TOT},\text{PL}}$ and $C_{\text{T}3,\text{TOT},\text{PL}}$ can increase over time. Finally, while the term $C_{\text{T}3,\text{FF},\text{PL}}/K_{\text{M},\text{TSH}}$ (Eq. (9)) decreases over time, the value of $V_{\text{MAX},\text{TSH}}$ must increase over time to facilitate a progressive increase in $C_{\text{TSH},\text{PL}}$. This was accomplished by applying an additional rate constant $\left(R_{{\text{V}}_{\text{MAX},\text{TSH}}};1/\text{h}\right)$ that describes the rate of change of $V_{\text{MAX},\text{TSH}}$. For information regarding the optimization of these parameters, see Supplemental Information (SI1; Model Calibration).

2.3. Thyroid gland description

The size of the thyroid gland increases during normal development of X. laevis larvae due to an increase in size of individual follicles. This increase in follicle size is due primarily to an increase in follicle cell number as well as accumulation of Tg in the luminal space [15,56]; Supplemental Information, SI3a & SI3b). For the present effort, we employed the simplifying assumption that changes in total thyrocyte volume that occur during normal development are driven entirely by changes in cell number. Further, it was assumed that changes in cell number result in proportional changes in rates of biochemical processes that occur within the thyrocytes.

The rate of change of the number of thyrocytes was calculated as the sum of rates attributable to “baseline” growth $\left(R_{\text{FCN},\text{CONT}};1/\text{h}\right)$ and growth induced by TSH $\left(R_{\text{FCN},\text{TSH}};1/\text{h}\right)$.

$$dFC{N}_{\text{TOT}}/dt=R_{\text{FCN},\text{CONT}}+R_{\text{FCN},\text{TSH}}$$ (11)

Although TSH is present at all time points in these simulations, we assumed that normal growth of the thyroid gland is only modestly dependent on TSH under control conditions. Instead, large effects of TSH on gland growth were assumed to occur only when plasma TSH concentrations increase substantially above control levels. To implement this assumption, we employed a form of the Hill equation to calculate the fractional induction in gland growth ($F_{\text{INDUC}}$; unitless, ranging from 0.0 to 1.0) induced by TSH.

$$F_{\text{INDUC}}=1/\left(1+{\left(K_{\text{H}}/C_{\text{TSH},\text{PL}}\right)}^n\right)$$ (12)

The $R_{\text{FCN},\text{TSH}}$ term was then calculated as the product of $F_{\text{INDUC}}$ and a constant $R_{\text{FCN},\text{MAX}}$, which is the limit value when $F_{\text{INDUC}}=1.0$. In this equation, the constant $K_{\text{H}}$ controls the point at which $F_{\text{INDUC}}$ begins to deviate substantially from 0.0 while the coefficient $n$ controls the slope of the linear portion of the curve. Eq. (12) predicts a sigmoid relationship between $F_{\text{INDUC}}$ and TSH. Thus, increasing levels of TSH can induce an increase in the rate of gland growth, but only to a point, thereby preventing nonsensical outcomes such as glands larger than the organism itself. As indicated previously, glandular processes are scaled directly to changes in total cell volume ($V_{\text{FC}}$; ml), which is calculated as the product of total cell number ($FC{N}_{\text{TOT}}$; cells) and a fixed standard single cell volume ($FCV$; ml).

The mass-balance for iodide within the thyrocytes is determined by NIS-mediated uptake into cells ($R_{\text{NIS}}$; pmol/h), diffusive efflux across the plasma membrane ($R_{\text{I},\text{DIF}}$; pmol/h), incorporation into Tg as MIT, DIT, and T4 iodine ($(R_{\text{TPO}}$; pmol/h), and iodotyrosine deiodinase (IYD)-mediated recycling of iodine associated with the liberation of MIT ($R_{\text{MIT},\text{REC}}$; pmol/h) and DIT ($R_{\text{DIT},\text{REC}}$; pmol/h) following proteolysis of Tg.

$$d{A}_{\text{I},\text{FC}}/dt=R_{\text{NIS}}-R_{\text{I},\text{DIF}}-R_{\text{TPO}}+R_{\text{MIT},\text{REC}}+R_{\text{DIT},\text{REC}}$$ (13)

Here the term $A_{\text{I},\text{FC}}$ (pmol) refers to the total amount of iodide within the thyrocytes. The concentration of iodide within the thyrocytes ($C_{\text{I},\text{FC}}$; pmol/ml) was calculated as $A_{\text{I},\text{FC}}$ divided by the aggregated volume of all thyrocytes $\left(V_{\text{FC}}\right)$.

The rate of iodide transport by NIS was modeled as a saturable process, where $C_{\text{I},\text{PL}}$ (pmol/ml) is the plasma iodide concentration, $V_{\text{MAX},\text{NIS}}$(pmol/h) is the maximum rate of NIS activity defined by a fixed level of TSH, and $K_{\text{M},\text{NIS}}$ (pmol/ml) is an affinity constant equal to the plasma iodide concentration $\left(C_{\text{I},\text{PL}}\right)$ that results in half-maximal NIS activity. An additional term in the denominator of this equation results in autoregulation of NIS when intracellular iodide concentrations exceed the value of an inhibition constant, $K_{\text{I},\text{FC}}$(pmol/ml).

$$R_{\text{NIS}}=V_{\text{MAX},\text{NIS}}\cdot C_{\text{I},\text{PL}}/\left(\left(K_{\text{M},\text{NIS}}+C_{\text{I},\text{PL}}\right)\cdot \left(0.5+\left(C_{\text{I},\text{FC}}/K_{\text{I},\text{FC}}\right)\right)\right)$$ (14)

The $V_{\text{MAX},\text{NIS}}$ term was calculated as a function of $C_{\text{TSH},\text{PL}}$,

$$V_{\text{MAX},\text{NIS}}=\left(V_{\text{MAX},\text{NIS}}^{\text{TSH}}\cdot C_{\text{TSH},\text{PL}}/\left(K_{\text{M},\text{NIS}}^{\text{TSH}}+C_{\text{TSH},\text{PL}}\right)\right)\cdot V_{\text{FC}}$$ (15)

where $V_{\text{MAX},\text{NIS}}^{\text{TSH}}$ (pmol/h/ml) is the maximum rate of NIS activity inducible by TSH (i.e., when $C_{\text{TSH},\text{PL}}\to \infty$) and $K_{\text{M},\text{NIS}}^{\text{TSH}}$ (pmol/ml) is the plasma TSH concentration that gives half-maximal induction of NIS protein.

Iodide diffusion across the plasma membrane was modeled as a first-order process controlled by a lumped transport parameter $\left(k_{\text{D},\text{I}};1/\text{h}\right)$,

$$R_{\text{I},\text{DIF}}=k_{\text{D},\text{I}}\left(C_{\text{I},\text{FC}}-C_{\text{I},\text{PL}}\right)\cdot V_{\text{FC}}$$ (16)

where $C_{\text{I},\text{FC}}$ (pmol/ml) is the concentration of iodide within the thyrocyte. This description assumes that the solubility of iodide in plasma is the same as that within the thyrocytes.

Endocytosis of iodinated Tg, proteolysis of iodinated Tg within the endocytic vesicle, and secretion of T4 to plasma were modeled as a lumped process controlled by a single rate constant, $R_{\text{TG},\text{PROT}}$ (pmol/h). Henceforth, we refer to this lumped process as Tg proteolysis. The rate of change of the mass of total Tg in the thyroid lumen ($A_{\text{TG},\text{TOT},\text{TL}}$; pmol) was calculated as the rate of synthesis of uniodinated Tg ($R_{\text{TG},\text{SYN}}$; pmol/h) minus $R_{\text{TG},\text{PROT}}$.

$$d{A}_{\text{TG},\text{TOT},\text{TL}}/dt=R_{\text{TG},\text{SYN}}-R_{\text{TG},\text{PROT}}$$ (17)

The term $R_{\text{TG},\text{PROT}}$ refers to the proteolysis of a standardized Tg molecule, which leads to the production of a fixed number of iodotyrosines/thyronines corresponding to a fixed ratio of MIT:DIT:T4 (see Section 2.5.3 and Supplemental Information, SI1, In-Depth Modeling Approach).

Synthesis of uniodinated Tg was described as a saturable process,

$$R_{\text{TG},\text{SYN}}=\left(V_{\text{MAX},\text{TG},\text{SYN}}\cdot C_{\text{TSH},\text{PL}}/\left(K_{\text{M},\text{TG},\text{SYN}}+C_{\text{TSH},\text{PL}}\right)\right)\cdot V_{\text{FC}}$$ (18)

where $V_{\text{MAX},\text{TG},\text{SYN}}$ (pmol/h/ml) is the maximum rate of Tg synthesis inducible by TSH and $K_{\text{M},\text{TG},\text{SYN}}$ (pmol/ml) is the plasma concentration of TSH that results in half-maximal Tg synthesis. This approach assumes that substrates for the synthesis pathway do not limit the rate of reaction. Proteolysis of Tg was described in the same manner as Tg synthesis,

$$\begin{gathered} R_{\text{TG},\text{PROT}}=\left(V_{\text{MAX},\text{TG},\text{PROT}}\cdot C_{\text{TSH},\text{PL}}/\left(K_{\text{M},\text{TG},\text{PROT}}+C_{\text{TSH},\text{PL}}\right)\right) \\ \cdot V_{\text{FC}} \end{gathered}$$ (19)

where $V_{\text{MAX},\text{TG},\text{PROT}}$ (pmol/h/ml) is the maximum rate of Tg proteolysis inducible by TSH and $K_{\text{M},\text{TG},\text{PROT}}$ (pmol/ml) is the plasma concentration of TSH that results in half-maximal Tg proteolysis.

Once iodide is taken up into thyrocytes, it passes through ion channels on the apical surface where it interacts enzymatically with TPO and Tg to produce iodinated Tg. For this effort, however, we assumed that thyrocyte iodide was directly available to TPO, thereby eliminating the need for an additional membrane transport term. The activity of TPO was calculated as

$$\begin{gathered} R_{\text{TPO}}=\left(V_{\text{MAX},\text{TPO}}\cdot C_{\text{I},\text{FC}}/\left(K_{\text{M},\text{TPO}}+C_{\text{I},\text{FC}}\right)\right) \\ \times \left(1-\left(\left(A_{\text{I},\text{TG},\text{TOT}}/A_{\text{TG},\text{TOT}}\right)/37\right)\right) \end{gathered}$$ (20)

where $C_{\text{I},\text{PL}}$ (pmol/ml) is the thyrocyte iodide concentration, $V_{\text{MAX},\text{TPO}}$ (pmol/h) is the maximum rate of TPO activity defined by a fixed level of TSH, and $K_{\text{M},\text{TPO}}$ (pmol/ml) is an affinity constant equal to the thyrocyte iodide concentration that results in half-maximal TPO activity. An additional term allows the overall iodination rate to be controlled by the amount of uniodinated Tg present (i.e., the Tg synthesis rate). As such, Tg is not treated as a classic enzyme substrate but is instead represented as a molecule that is either fully iodinated (i.e., present as colloid) or available for iodination. The benefit of this approach is that TPO activity can be calculated without having to account for changes in the volume of the luminal space, which would otherwise be expected to result in changes in the “concentration” of colloid. When Tg is 100% iodinated, the term on the far right-hand side of Eq. (20) forces the iodination rate to 0.

The term $V_{\text{MAX},\text{TPO}}$ was calculated as a function of $C_{\text{TSH},\text{PL}}$, where $V_{\text{MAX},\text{TPO}}^{\text{TSH}}$ (pmol/h/ml) is the maximum rate of TPO activity inducible by TSH (i.e., when $C_{\text{TSH},\text{PL}}\to \infty$) and $K_{\text{M},\text{TPO}}^{\text{TSH}}$ (pmol/ml) is the plasma TSH concentration that gives half-maximal induction of TPO.

$$V_{\text{MAX},\text{TPO}}=\left(V_{\text{MAX},\text{TPO}}^{\text{TSH}}\cdot C_{\text{TSH},\text{PL}}/\left(K_{\text{M},\text{TPO}}^{\text{TSH}}+C_{\text{TSH},\text{PL}}\right)\right)\cdot V_{\text{FC}}$$ (21)

With these specifications, the aggregated rate of change of total organified iodine in the follicular lumen is the difference between the rate of iodide organification and Tg proteolysis.

$$d{A}_{\text{I},\text{TG},\text{TOT}}/dt=R_{\text{TPO}}-\left(R_{\text{TG},\text{PROT}}\left(A_{\text{I},\text{TG},\text{TOT}}/A_{\text{TG},\text{TOT}}\right)\right)$$ (22)

The mass balance for iodine associated with MIT in the follicular lumen was expressed as the difference between rates of MIT formation and catabolism,

$$d{A}_{\text{I},\text{MIT}}/dt=\left(R_{\text{TPO}}\cdot (1/37)\right)-R_{\text{MIT},\text{REC}}$$ (23)

where the product term, $\left(R_{\text{TPO}}\cdot (1/37)\right)$, represents the proportion of the iodide organification rate that results in MIT formation, given that MIT contains only 1 of the 37 iodine atoms on a fully iodinated Tg molecule (see Section 2.5.3). The second term on the right side of Eq. (23) ($R_{\text{MIT},\text{REC}}$; pmol/h) represents the rate of iodine recycling (via IYD) associated with liberation of iodine from MIT following Tg proteolysis. This was assumed to be a 100% efficient process and was calculated as

$$R_{\text{MIT},\text{REC}}=R_{\text{TG},\text{PROT}}\left(A_{\text{I},\text{MIT}}/A_{\text{TG},\text{TOT}}\right)$$ (24)

The mass balance equation for iodine associated with DIT in the follicular lumen follows the same approach as that used for MIT,

$$d{A}_{\text{I},\text{DIT}}/dt=\left(R_{\text{TPO}}\cdot (12/37)\right)-R_{\text{DIT},\text{REC}}$$ (25)

with DIT constituting 12 of the 37 iodine atoms per Tg molecule. Recycling of iodine from DIT was treated the same as MIT iodine recycling and was represented as

$$R_{\text{DIT},\text{REC}}=R_{\text{TG},\text{PROT}}\left(A_{\text{I},\text{DIT}}/A_{\text{TG},\text{TOT}}\right)$$ (26)

The mass balance for iodine associated with T4 follows the same general approach used to model iodine associated with MIT and DIT. In this instance, however, the second term on the right side of Eq. (27) represents the secretion of T4 to the plasma, which was assumed to be 100% efficient.

$$d{A}_{\text{I},\text{T}4}/dt=\left(R_{\text{TPO}}\cdot (24/37)\right)-\left(R_{\text{T}4,\text{SEC}}\cdot 4\right)$$ (27)

The rate of T4 secretion ($R_{\text{T}4,\text{SEC}}$; pmol/h) to plasma is proportional to the rate of Tg proteolysis and was calculated as

$$R_{\text{T}4,\text{SEC}}=R_{\text{TG},\text{PROT}}\left(\left(A_{I,T4}/A_{\text{TG},\text{TOT}}\right)/4\right)$$ (28)

Eqs. (27) and (28) are expressed as pmol T4-associated iodine and pmol T4, respectively. Thus, conversions accounting for the 4 iodine atoms bound to each T4 molecule have been directly integrated into the equations.

2.4. Organism growth and parameter scaling

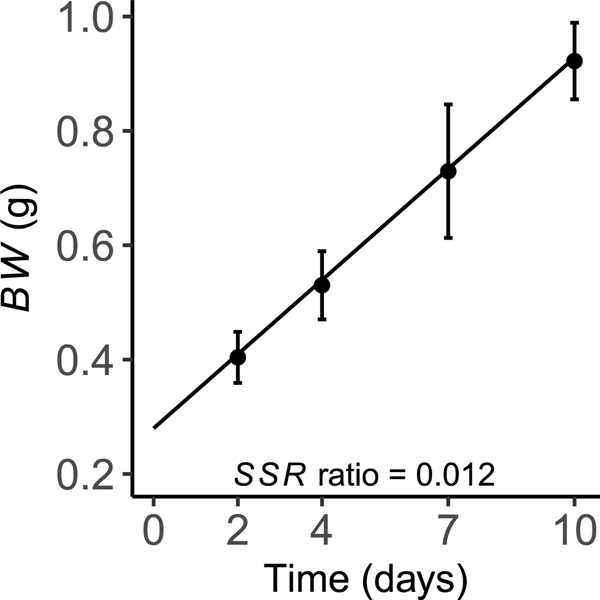
The average day 2 weight of larvae tested by Haselman et al. [21] was 0.404 g. Growth during the 10-day exposure protocol was nearly linear and resulted in an average final weight of 0.922 g. This pattern was described using a fixed growth rate constant $\left(R_{\text{BW}};1/\text{h}\right)$ that was visually fit to describe observed body weights (Fig. 2). The starting weight of test animals was determined by extrapolating back to $t_0$ using $R_{\text{BW}}$.

Fig. 2.

Model predictions of body weight (BW; solid line), plotted against control data (mean ± SD) used for model calibration. The sum of squared residual (SSR) ratio indicates the proportional contribution of the body weight endpoint to the overall model cost (see Section 3.2).

2.5. Model initialization and parameterization

2.5.1. Plasma iodide concentration

To date, plasma iodide levels during larval development have not been measured in X. laevis. Given that plasma iodide is a critical input for TH synthesis, we felt it was necessary to obtain measurements of free and bound fractions of plasma iodine in X. laevis larvae. This was accomplished by collecting plasma from three developmental stages of pro-metamorphic larvae. Additional samples were collected from X. laevis adults. We then analyzed whole and fractionated plasma using inductively coupled plasma mass spectrometry (ICP-MS) as described in the Supplemental Information (SI4). Because amphibian metamorphosis assays are conducted under controlled laboratory conditions, it is reasonable to assume that sufficient iodine is available to larvae from dietary and/or waterborne sources, and that homeostatic mechanisms maintain plasma iodide concentrations within a relatively narrow range. The measured plasma iodide data support this assumption, as free iodide levels remained relatively constant across the three prometamorphic stages. For this effort, therefore, $C_{\text{I},\text{PL}}$ was set equal to the approximate mean of the measured values (1000 pmol/ml).

2.5.2. Glandular iodide

Parameter values that define active transport of iodide into thyrocytes and its diffusive efflux back into plasma were determined by several considerations. First, NIS activity must be sufficient to support modeled synthesis of T4. This requirement substantially constrains the fitted value of $V_{\text{MAX},\text{NIS}}^{\text{TSH}}$. The affinity constant for TSH induction of NIS $\left(K_{\text{M},\text{NIS}}^{\text{TSH}}\right)$ was set equal to 10 times the starting concentration of $C_{\text{TSH},\text{PL}}$. This assignment is similar to $K_{\text{M}}$ values for other activities induced by TSH (Tg synthesis and TPO activity; see below) and results in coordinated induction of these processes. The value of $K_{\text{M},\text{NIS}}$ was set equal to 100 times the assumed concentration of plasma iodide to result in near first-order kinetics.

In mammals, active uptake of iodide by the thyroid gland results in an enrichment factor (thyrocyte iodide concentration:plasma iodide concentration) of 20- to 40-fold [57,58]. We assumed here that the starting thyrocyte iodide concentration $C_{\text{I},\text{FC}}$ was 20-fold higher than $C_{\text{I},\text{PL}}$. The need to simulate this enrichment substantially determines the value of $k_{\text{D},\text{I}}$, which tends to counterbalance uptake of iodide by NIS. Absent reliable data on iodide diffusion rates in relation to iodide uptake by NIS, the final specification of fitted values for $V_{\text{MAX},\text{NIS}}^{\text{TSH}}$ and $k_{\text{D},\text{I}}$ was driven by the assumptions that $R_{\text{NIS}}$ should normally exceed $R_{\text{I},\text{DIF}}$ and that the ratio $C_{\text{I},\text{FC}}/C_{\text{I},\text{PL}}$ should be maintained at 20 to 40 throughout normal metamorphic development. The fitting of these parameters was influenced to a much smaller degree by catabolism of MIT and DIT within the thyrocytes. When TH synthesis is inhibited, however, these recycling reactions may contribute a substantial fraction of the intracellular iodide that is organified to synthesize new TH. The extent of iodide enrichment is also impacted by an inhibitory term, $\left(0.5+\left(C_{\text{I},\text{FC}}/K_{\text{I},\text{FC}}\right)\right)$, in the denominator of Eq. (14). When $K_{\text{I},\text{FC}}$ is less than twice $C_{\text{I},\text{FC}}$ (i.e., when cellular iodide levels are high), this term imparts an inhibitory effect on $R_{\text{NIS}}$ which results in a reduction in cellular iodide and by extension production of THs (the Wolff–Chaikoff effect; [34,59,60]). To initialize the model, we made the simplifying assumption that this effect was not active at $t_0$, so $K_{\text{I},\text{FC}}$ was set to twice the starting $C_{\text{I},\text{FC}}$ to mathematically neutralize the term.

2.5.3. Iodo-species in the thyroid gland and plasma

The $K_{\text{M},\text{TPO}}$ value for incorporation of iodide into Tg was set at 100 times the starting $C_{\text{I},\text{FC}}$. As indicated earlier, the affinity constant for TSH-mediated induction of TPO $\left(K_{\text{M},\text{TPO}}^{\text{TSH}}\right)$ was set at 10 times $C_{\text{TSH},\text{PL}}$, while $V_{\text{MAX},\text{TPO}}^{\text{TSH}}$ was optimized during model calibration. In theory, one could model Tg iodination at each tyrosyl site and coupling of those tyrosyl residues to produce TH precursors. Instead, we took a much simpler data-driven approach to describe moles of organified iodine associated with a single, “fully iodinated” Tg molecule. Data obtained by Haselman et al. [21] indicate the molar ratio of MIT:DIT:T4 in thyroid glands of X. laevis larvae is, on average, 1:6:6 (measured amounts of T3 were negligible, see Supplemental Information, SI1, In-Depth Modeling Approach). Although these measurements included both Tg-associated precursors from the colloid and free MIT/DIT/T4 within the thyrocytes, we make the assumption that the majority of the measured analytes were liberated from Tg during the digestion step of the sample processing method [21]. Following on this assumption, the derived molar ratio is applied to each mole of Tg. Therefore, the iodine molar ratio associated with each of these species is 1:12:24, respectively, resulting in 37 moles of iodine per mole of Tg. Full iodination of each Tg molecule is assumed when TPO activity is >0; therefore, accumulation of partially iodinated Tg does not occur in this model system. Initially, the starting values for $A_{\text{TG},\text{TOT}}$ and $A_{\text{I},\text{MIT}}$ were set equal to each other since there is 1 mole MIT per mole Tg. However, if the starting value for $A_{\text{TG},\text{TOT}}$ does not exceed the fully iodinated pool of Tg, then $R_{\text{TPO}}$ would begin at 0, which is not optimal for model initialization. The starting value for $A_{\text{TG},\text{TOT}}$ was therefore rounded up to the nearest tenth of a picomole. This slight increase in $A_{\text{TG},\text{TOT}}$ may be seen as representing uniodinated Tg that is immediately available for iodide organification. Gland MIT data from the day 2 timepoint of Haselman et al. [21] was used as a reference point from which to extrapolate back to $t_0$ for the initialization values. Following on this approach, the starting values for $A_{\text{I},\text{DIT}}$ and $A_{\text{I},\text{T}4}$ were determined by multiplying the moles of iodine associated with each iodo-species per Tg molecule by the total moles of fully iodinated Tg at $t_0$.

The starting values of $A_{\text{T}4,\text{TOT},\text{PL}}$ and $A_{\text{T}3,\text{TOT},\text{PL}}$ were derived from mean measured values of total plasma THs ($C_{\text{T}4,\text{TOT},\text{PL}}$ and $C_{\text{T}3,\text{TOT},\text{PL}}$) in control larvae at the day 2 timepoint [21]. These values were then optimized to stabilize the feedback behavior of TSH at $t_0$ during model calibration (see Section 2.6). Initial guidance on the specification of parameters that describe T4 clearance was based on the measured amount of T4 stored in glands of NF stage 54 animals and the fact that effects of T4 synthesis inhibitors on X. laevis tadpoles become apparent only after 2–3 days of exposure [18,21]. Assuming that these inhibitors are essentially 100% effective in preventing the formation of new T4 and that T4 secretion is not rate-limiting on the system (due to upregulation by TSH), the overall rate of T4 clearance must be sufficient to substantially deplete glandular T4 in 2–3 days, resulting in reduced circulating levels of T4. Preliminary simulations indicated that rapid depletion of glandular T4 was possible only if T4 clearance rates were relatively high. The affinity constant for DIO2 $\left(K_{\text{M},\text{DIO}2}\right)$ was set at 100 times the starting $C_{\text{T}4,\text{FF},\text{PL}}$. This assignment results in near first-order kinetics under most model conditions. Initially, $V_{\text{MAX},\text{DIO}2}$ and $C{L}_{\text{T}4,\text{CONJ}}$ were set to values that resulted in target plasma T3 levels and a T4 plasma half-life of about 2 h. These terms were then optimized once $V_{\text{MAX},\text{DIO}3}$ and $C{L}_{\text{T}3,\text{CONJ}}$ were implemented (see Section 2.6 and Supplemental Information, SI1, Model Calibration). For comparison, Abrams and Larsen [61] reported the serum half-life for T4 in rats to be 12 h.

The clearance rate for plasma T3 was assumed to be even faster than that for T4 and was adjusted, along with $V_{\text{MAX},\text{DIO}3}$, to result in a half-life of approximately 1 h. Consistent with other starting assignments, the affinity constant $K_{\text{M},\text{DIO}3}$ was set at 100 times the starting $C_{\text{T}3,\text{FF},\text{PL}}$. It would have been possible to conglomerate $R_{\text{DIO}3}$ with $C{L}_{\text{T}3}$ since the products of T3 deiodination do not become inputs to any other model components; however, DIO3 has been identified as a potential toxicological target and an in vitro assay for this enzyme has been implemented for chemical screening [23,62,63]. An equation that calculates $R_{\text{DIO}3}$ was therefore added to the model.

2.5.4. Thyroglobulin synthesis and proteolysis

Eqs. (18)–(19) indicate that rates of Tg synthesis and proteolysis increase with increases in plasma TSH and gland size. If these rates are the same, the total amount of Tg in the gland will remain the same and the amount normalized to gland size will decline over time. Existing data suggest instead that the total amount of Tg stored within the gland increases during normal development. For this to occur, the rate of Tg synthesis must exceed that of Tg proteolysis under control conditions. On the other hand, research with X. laevis tadpoles suggests that exposure to TH-synthesis inhibitors may deplete the gland of colloid. For this to occur, the rate of Tg proteolysis must exceed the rate of Tg synthesis. Here we assumed that $K_{\text{M},\text{TG},\text{PROT}}$ is 10 times higher than $K_{\text{M},\text{TG},\text{SYN}}$. In relative terms, therefore, the capacity for Tg proteolysis to increase with TSH is greater than that for Tg synthesis, but the concentration of TSH required to elicit maximal Tg proteolysis is higher. These assignments result in a system that favors Tg synthesis at low TSH concentrations. As TSH levels increase, Tg proteolysis continues to increase while Tg synthesis tends to saturate. At sustained high levels of TSH these changes result in depletion of Tg. The affinity terms for Tg synthesis $\left(K_{\text{M},\text{TG},\text{SYN}}\right)$ and proteolysis $\left(K_{\text{M},\text{TG},\text{PROT}}\right)$ were set at 10 and 100 times $C_{\text{TSH},\text{PL}}$, respectively.

2.5.5. Plasma TSH

Despite repeated attempts, it has not been possible to measure plasma TSH in NF stage 54 larvae. Using an ELISA method, Korte et al. [41] determined the serum TSH concentration in NF stage 58 animals (control group) to be 15.8 ng/ml; however, all samples used to estimate this value were below the minimum level of quantification. Relative TSH levels in X. laevis pituitary glands were measured by the same authors using a Western blot method. These data suggested that pituitary TSH increases 3–4 fold between NF stages 54 and 58. Based on this information, we assumed a starting plasma TSH concentration of approximately 3 ng/ml (∼100 pM, assuming a molecular weight of 30,000). In mammals, TSH is cleared from plasma primarily by uptake into the kidney [64]. In general, reported plasma half-lives are relatively short, ranging from about 5 to 20 min [42,64,65]. Lacking any information for X. laevis, we modeled TSH elimination using a single clearance constant ($C{L}_{\text{TSH}}$; ml/hr/g) that was adjusted to achieve a plasma half-life of 15 min.

2.5.6. Thyrocyte volume and proliferation

A fluorescence-based method has been used previously to estimate thyrocyte numbers in X. laevis larvae exposed to potent thyroid disrupting chemicals [18,21]. Although this method can estimate thyrocyte numbers per gland reasonably well, the method cannot provide an estimate of thyrocyte volume, which was also needed for this modeling effort. Therefore, we undertook a second analysis of histological images generated by Grim et al. [56] to characterize X. laevis gland morphometrics and provide a basis for 2D-to-3D extrapolation of cell numbers and average thyrocyte volume. This latter approach and associated data are presented in the Supplemental Information (SI3). The histologically based analysis was in general agreement with historical fluorescence data and both approaches showed that control thyrocyte numbers change in a curvilinear manner increasing approximately 3- to 5-fold from NF stages 54 to 57.

The baseline cell proliferation rate $\left(R_{\text{FCN},\text{CONT}}\right)$ was set at 40 cells/h. This is lower than the actual control thyrocyte proliferation rate because some level of TSH stimulation is assumed to contribute to the overall proliferation rate. The value of $R_{\text{MAX},\text{TSH}}$ was set equal to 700 cells/h with the result that high levels of TSH can induce gland growth rates >10 times higher than those of control animals when $F_{\text{INDUC}}$ of Eq. (12) equals 1.0. The Hill constant $\left(K_{\text{H}}\right)$ and slope coefficient $(n)$ from Eq. (12) were optimized during model calibration to fit the calibration data set (see Section 2.6). These parameter assignments resulted in a system that is highly responsive to changes in $C_{\text{TSH},\text{PL}}$ in the concentration range from about 2 to 10 times the starting concentration of $C_{\text{TSH},\text{PL}}$.

The volume of one thyrocyte was determined from the morphometric study presented in the Supplemental Information (SI3a & SI3b). The mean total thyrocyte area across developmental stages was divided by the mean number of thyrocyte nuclei to acquire the 2D cross-sectional area per thyrocyte. Then, assuming the cells are cuboidal, the square root of the 2D area was cubed to calculate the mean volume per cell. The resulting volume was approximately 950 femtoliters per cell. For the present modeling effort, we rounded this to an average value of 1.0 × 10⁻⁹ ml per cell $(FCV)$. This figure was then multiplied by the total number of thyrocytes at each time point in the simulation to estimate the aggregated volume of all thyrocytes $\left(V_{\text{FC}}\right)$.

2.6. Model calibration

The datasets used to calibrate the model consisted of control data from three separate studies investigating how known TPO inhibitors temporally impact thyroid-related endpoints [21]. The temporal endpoints used for model calibration were growth $(BW)$, thyroid gland MIT $\left(A_{\text{MIT},\text{TL}}\right),\text{DIT}\left(A_{\text{DIT},\text{TL}}\right)$, and $\text{T4}\left(A_{\text{T}4,\text{TL}}\right)$, thyrocyte number $\left(FC{N}_{\text{TOT}}\right)$, total plasma $\text{T4}\left(C_{\text{T}4,\text{TOT},\text{PL}}\right)$, and total plasma $\text{T}3\left(C_{\text{T}3,\text{TOT},\text{PL}}\right)$. These data were collected from animals sampled at 2, 4, 7 and 10 days of exposure. Mean values calculated at each timepoint were used as targets for model calibration.

Model calibration was achieved using a stepwise approach. A detailed description of this approach is provided as Supplemental Information (SI1, Model Calibration). Initially, individual model processes were compartmentalized as a means of focusing attention on one or a small number of parameters. Model parameters and state variables that would otherwise drive dynamic behavior were held constant. Adjustments to process-specific parameters were then made to establish rough approximations of desired simulation trajectories through target values. Once each compartmentalized process roughly met the desired behavior, the components were linked so that all dynamic components and feedback became interdependent. Iterative parameter adjustments were made throughout the linkage process to hold simulation trajectories close to target values over time. Final calibration was performed on the fully interdependent model and included small adjustments to starting values for several state variables to stabilize feedback behavior at $t_0$.

Parameter values were optimized by visual fit of model simulations to control datasets. A post-hoc analysis was then performed to provide a quantitative evaluation of model performance (see Section 2.7). Although the model contains a large number of optimized parameters, the calibration process was highly constrained by the need to simulate the measured time-course for several state variables, maintain additional state variables within prescribed limits (e.g., a 20- to 40-fold enrichment of cellular iodide), and reproduce behaviors consistent with the results of chemical testing efforts (e.g., rapid depletion of glandular hormone levels when TH synthesis is abolished).

2.7. Model performance analysis

Initially, model predicted values were compared to control data [21] to determine if there were any systematic biases in endpoint estimation. For each combination $i$ of endpoints and timepoints, we took the mean $\left(Ob{s}_i\right)$ and standard deviation $\left(s{d}_i\right)$ of subsample observations. We then compared each $Ob{s}_i$ to the corresponding model predicted endpoint $\left(Mo{d}_i\right)$ by calculating residuals weighted by $s{d}_i$, using the modCost function in R package FME [66].

$$re{s}_i=\left(Mo{d}_i-Ob{s}_i\right)/s{d}_i$$ (29)

Weighting residuals by $s{d}_i$ accounts for differences in units and magnitudes across the seven endpoints [66]. In two instances, $s{d}_i$ was $0(C_{\text{T}3,\text{TOT},\text{PL}}$ at 2 and 4 days), creating undefined values of $re{s}_i$. For these cases, we replaced $s{d}_i$ with 1 (i.e., we did not weight these two residuals). This modification was important to permit comparisons of all $Mo{d}_i$ values to the corresponding $Ob{s}_i$ that were used to calibrate the model.

Next, we used modCost to calculate sums of squared residuals for each endpoint $j$,

$$SS{R}_j=\sum _{i=1}^{n_j}re{s}_i^2$$ (30)

where $n_j$ is the number of timepoints observed for endpoint $j$ (all $n_j=4$). The sum of $SS{R}_j$ across all endpoints $j$ gives the total sums of squared residuals for the model,

$$SS{R}_{TOT}=\sum _{j=1}^{n_V}SS{R}_j$$ (31)

where $n_v$ is the number of endpoint variables ($n_v=7$). The ratios $SS{R}_j/SS{R}_{TOT}$ were then calculated to quantify relative differences in each endpoint’s contribution to the total model cost, i.e., how much of the divergence between model predictions and control data was captured by a given endpoint. The R script for calculating model performance statistics is available in the Supplemental Information (SI5).

2.8. Sensitivity analysis

A local sensitivity analysis was performed by generating normalized sensitivity coefficients (NSCs) for the 33 model parameters using the method described by Clewell et al. [67],

$$NSC=((A-B)/B)/((C-D)/D)$$ (32)

where A is the model prediction resulting from a 1% change in the parameter value, B is the model prediction associated with the original value, C is the parameter value increased by 1% and D is the original parameter value. This equation is essentially equivalent to a discrete approximation of the model elasticity. Each parameter was increased by 1% in each of 33 independent analyses and the resulting model predictions for total plasma T4 and T3, thyrocyte number, and gland MIT were evaluated to determine percent deviation from the original model prediction at 2, 4, 7 and 10 days. The R script for calculating NSCs is available as Supplemental Information (SI6).

3. Results

3.1. Model calibration and simulations

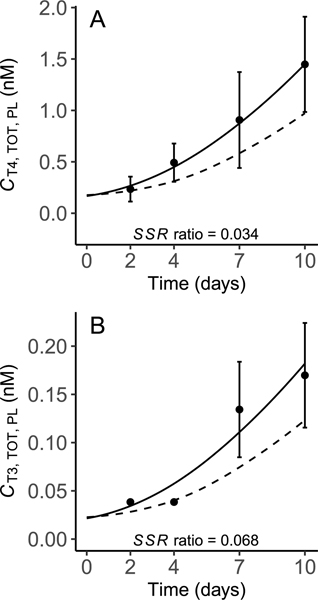
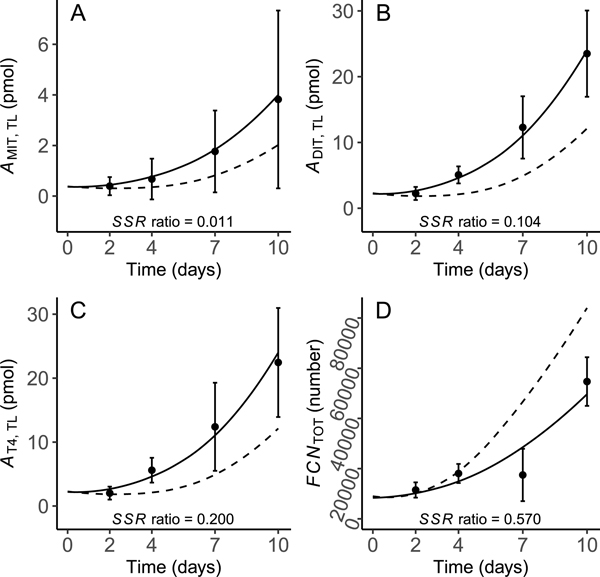
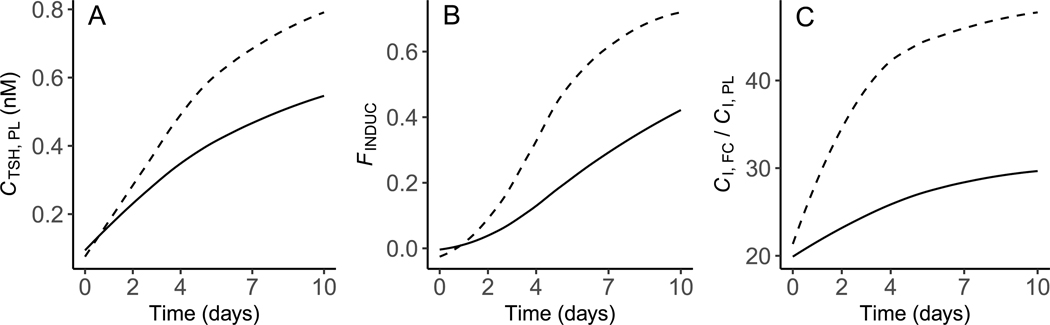
Calibration of the model to the control data from [21] resulted in 22 parameters and starting values for state variables being optimized for overall model performance, 7 of which are $V_{\text{MAX}}$ values (see Table 1 for optimized parameters). Following optimization of these terms, simulations of $C_{\text{T}4,\text{TOT},\text{PL}}$ and $C_{\text{T}3,\text{TOT},\text{PL}}$ tracked closely with the calibration dataset (Fig. 3A & B). Likewise, measured and predicted values for glandular iodo-species (MIT, DIT, T4) and thyrocyte numbers aligned reasonably well (Fig. 4A–D). The simulated concentration of TSH in plasma increased in a curvilinear manner approximately 5-fold over the 10-day simulation period (Fig. 5A), which is a larger increase than the target value of 3- to 4-fold. The ratio of the iodide concentration in thyrocytes compared to that in plasma increased over the model simulation time from 20 to approximately 30 (Fig. 5C). This finding indicates that optimized values for $V_{\text{MAX},\text{NIS}}$ and $k_{\text{D},\text{I}}$, together with the “self-regulating” Wolff–Chaikoff term, maintain the iodide enrichment factor within a reasonably narrow range. The rate of thyrocyte proliferation induced by TSH was <40% of the maximal rate of proliferation for the majority of the 10-day simulation time (Fig. 5B). This result indicates that there is a reserve proliferation capacity of approximately 60% that could come into play if TSH levels rise to compensate for reduced TH levels.

Fig. 3.

Predicted and measured total concentrations of T4 (A) and T3 (B) in plasma of X. laevis larvae. Model predictions were obtained under control conditions representing the normal biology of the organism (solid line) and when TPO activity was arbitrarily inhibited by 95% (dashed line). Solid points (mean ± SD) represent control datasets [21] used for model calibration. The sum of squared residuals (SSR) ratio indicates the proportional contribution of each endpoint to the overall model cost under control conditions. In panel B, data from days 2 and 4 were all <LLOQ so values equal to $0.5\times \text{LLOQ}$ were assigned by the authors [21]; this resulted in a $\text{SD}=0.C$ — concentration; T4 — thyroxine; T3 — 3,5,3’triiodothyronine; TOT — total; PL — plasma.

Fig. 4.

Predicted and measured precursors of MIT (A), DIT (B) and T4 (C), and follicular cell/thyrocyte numbers (D) in the thyroid gland of X. laevis larvae. Model predictions were obtained under control conditions (solid line) and when TPO activity was arbitrarily inhibited by 95% (dashed line). Solid points (mean ± SD) represent control datasets [21] used for model calibration. The sum of squared residuals (SSR) ratio indicates the proportional contribution of each endpoint to the overall model cost under control conditions. A — amount; MIT — monoiodotyrosine; DIT — diiodotyrosine; T4 — thyroxine; TL — thyroid lumen; FCN — follicular cell number; TOT — total.

Fig. 5.

Model predictions of plasma TSH (A), fractional induction of thyrocyte proliferation in the thyroid gland (B), and the ratio of the iodide concentration in thyrocytes to that in plasma (C) in X. laevis larvae. Predictions were generated under control conditions (solid line) and when TPO activity was arbitrarily inhibited by 95% (dashed line). C — concentration; TSH — thyroid stimulating hormone; PL — plasma; F — fractional; INDUC — induction; I — iodide; FC — follicular cell.

As an example, and to demonstrate the compensatory capacity of the model under circumstances of an inhibited key biochemical process, the hormone synthesis rate $\left(R_{\text{TPO}}\right)$ was arbitrarily reduced by multiplying the output of Eq. (20) by 0.05 (i.e., 95% inhibition). Several investigators have exposed X. laevis larvae to chemicals that specifically inhibit TPO [12–15,18,19,21]. This provides an opportunity to qualitatively compare modeled predictions to observed effects on circulating and stored (glandular) TH levels, thyroid gland pathology, and metamorphic development. The resulting simulations of perturbed biology are shown in Figs. 3–5 as dashed lines for comparison to simulations of control biology. Plasma T4 and T3 were reduced by <40% over the simulation time (Fig. 3A & B), while glandular MIT, DIT and T4 were all decreased by <50% (Fig. 4A–C). Evidence of compensation is clearly shown by the increased levels of plasma TSH (Fig. 5A), induction of thyrocyte proliferation (Fig. 4D & Fig. 5B), and enhanced NIS activity, as indicated by increased iodide enrichment in thyrocytes (Fig. 5C).

3.2. Model performance analysis

Model residuals were evaluated to better understand how model predictions differed from control observations for 7 endpoints (Supplemental Information, SI7). There were no trends in this dataset that would indicate the model was consistently over- or underestimating any of these state variables. Consistent with this overall match between observed and predicted endpoints, the mean across all residuals, −0.002, was close to 0. Across all endpoints, the model tended to slightly overestimate day 2 control data (mean residual = 0.187) and underestimate day 4 data (−0.234), while predictions matched control data more closely at days 7 (0.019) and 10 (0.020). Comparing endpoints, $FC{N}_{\text{TOT}}$ showed the largest discrepancy between observed and predicted values; this endpoint comprised 57% of the total model cost (3.969). Together, $C_{\text{T}4,\text{TOT},\text{PL}}$ and $C_{\text{T}3,\text{TOT},\text{PL}}$ accounted for <10% of the total model cost. The lowest contributor to total model cost (1%) was $A_{\text{MIT},\text{TL}}$. The proportional contribution of each endpoint to total model cost is provided as the SSR ratios in Figs. 2–4.

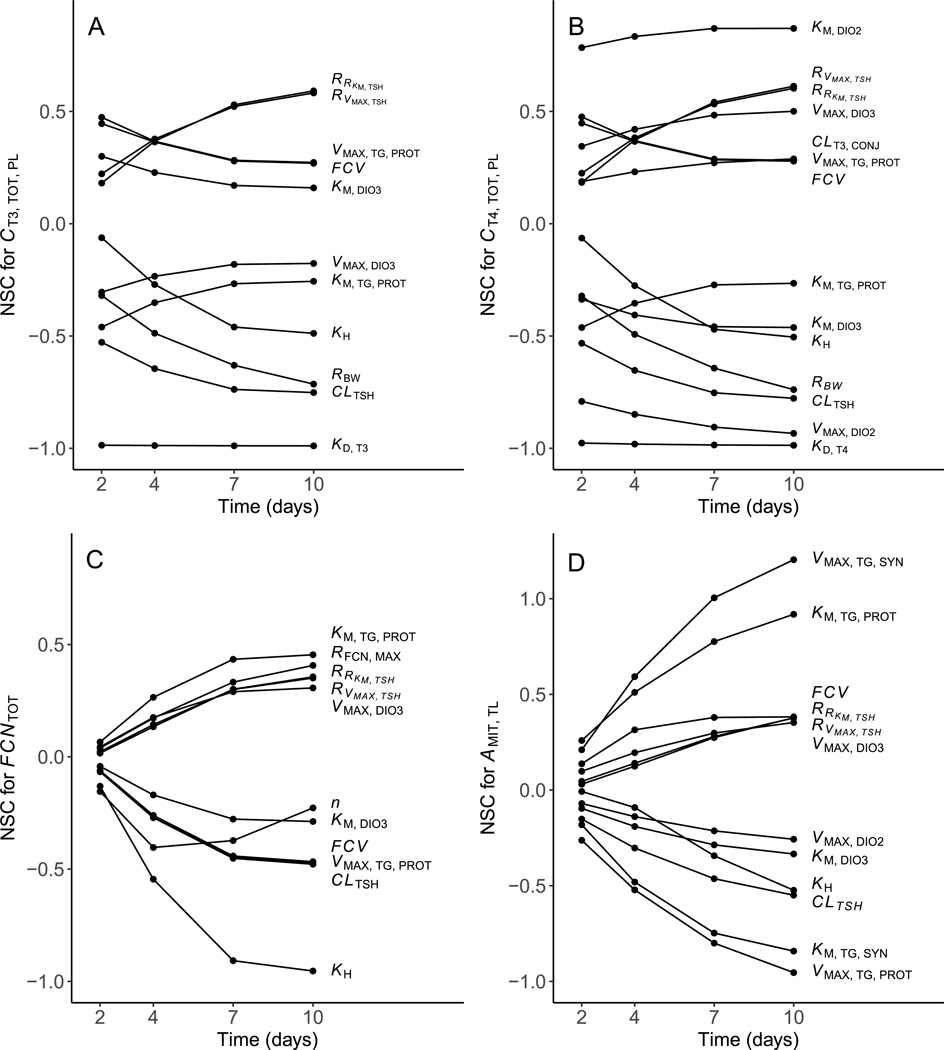
3.3. Model sensitivity analysis

A NSC $>|0.25|$ was generated at some point in the simulation for 20 of the 33 model parameters (Table 2; Fig. 6A–D); NSCs $<|0.25|$ were assumed to be of little importance. Of these 20 parameters, 9 yielded NSCs $>|0.25|$ at 1 or more timepoints across all 4 evaluated variables (total plasma T4 and T3, thyrocyte number, and gland MIT), emphasizing their global influence. The other 11 parameters yielded NSCs $>|0.25|$ at 1 or more timepoints for 1 or 2 variables. Model predictions of gland MIT were found to be highly sensitive to changes in $V_{\text{MAX},\text{TG},\text{SYN}}$, resulting in NSCs $>1.0$ at the 7- and 10-day timepoints. Relatively smaller NSCs (all $<1.0$) were generated for all other evaluated parameter and variable combinations. A general increase in model sensitivity over time to changes in various model parameters was observed for both variables related to the thyroid gland (thyrocyte number and gland MIT; Fig. 6C & D). In contrast, predictions of total plasma T4 and T3 were generally impacted to the greatest extent early in the simulation or exhibited a similar sustained level of sensitivity over time. The NSC calculated for a 1% decrease in a model parameter generally mirrored that for a 1% increase, indicating a linear response to slight parameter adjustments above or below current values (data not shown).

Table 2.

Normalized sensitivity coefficients summed across the four modeled time points (2, 4, 7, and 10 d). Positive values indicate that an increase in the selected model parameter results in an increase in the predicted state variable. Negative values indicate that an increase in the selected model parameter results in a decrease in the predicted state variable. Please see main text and Table 1 for definitions of abbreviations.

	State variable
Model parameter	$C_{\text{T}3,\text{TOT},\text{PL}}$	$C_{\text{T}4,\text{TOT},\text{PL}}$	$FC{N}_{\text{TOT}}$	$A_{\text{MIT},\text{TL}}$
Most sensitive parameters with influence on certain variable(s)
$K_{\text{D},\text{T}3}$	−3.95	–	–	–
$K_{\text{D},\text{T}4}$	–	−3.93	–	–
$V_{\text{MAX},\text{DIO}2}$	–	−3.48	–	–
$K_{\text{M},\text{DIO}2}$	–	3.36	–	–
$R_{BW}$	−2.15	−2.20	–	–
$C{L}_{\text{T}3,\text{CONJ}}$	–	0.98	–	–
$n$	–	–	−1.16	–
$R_{\text{FCN},\text{MAX}}$	–	–	0.95	–
$V_{\text{MAX},\text{TG},\text{SYN}}$	–	–	–	3.01
$K_{\text{M},\text{TG},\text{SYN}}$	–	–	–	−2.25
$V_{\text{MAX},\text{DIO}2}$	–	–	–	−0.68
Most sensitive parameters influencing all variables
$C{L}_{\text{TSH}}$	−2.66	−2.72	−1.27	−1.47
$V_{\text{MAX},\text{TG},\text{PROT}}$	1.40	1.42	−1.26	−2.54
$K_{\text{M},\text{TG},\text{PROT}}$	−1.34	−1.35	1.22	2.46
$K_{\text{H}}$	−1.28	1.31	−2.54	−0.97
$FCV$	1.36	1.38	−1.23	1.21
$R_{{\text{V}}_{\text{MAX},\text{TSH}}}$	1.70	1.74	0.82	0.84
$R_{{\text{R}}_{{\text{K}}_{\text{M}},\text{TSH}}}$	1.67	1.71	0.81	0.81
$V_{\text{MAX},\text{DIO}3}$	−0.90	1.75	0.82	0.94
$K_{\text{M},\text{DIO}3}$	0.86	−1.66	−0.78	−0.91

Fig. 6.

Normalized sensitivity coefficients (NSC) over four modeled time points (2, 4, 7, and 10 d) for: (A) total plasma T3 concentration, (B) total plasma T4 concentration, (C) total follicular cell (thyrocyte) number, and (D) the amount of MIT in the thyroid lumen. Only parameters showing NSCs $>|0.25|$ in any of the four time points are displayed. Parameters with NSCs $<|0.25|$ in all timepoints and for all variables were removed for the sake of clarity. Please see text and Table 1 for definitions of abbreviations.

To evaluate the overall sensitivity of the model to changes in different parameter values, NSCs were summed across all 4 timepoints. Model predictions of $C_{\text{T}3,\text{TOT},\text{PL}}$ and $C_{\text{T}4,\text{TOT},\text{PL}}$ exhibited a high sustained level of sensitivity to changes in $K_{\text{D},\text{T3}}$ and $K_{\text{D},\text{T}4}$, respectively (summed NSCs close to 4; Table 2 and Fig. 6A & B). Changes in $V_{\text{MAX},\text{DIO}2}$ and $K_{\text{M},\text{DIO}2}$ were also found to have a large, sustained impact on $C_{\text{T}4,\text{TOT},\text{PL}}$ (summed NSC >3.0). All other parameter and variable combinations yielded summed NSCs <3.0 (see Table 2 & Fig. 6).

4. Discussion

Thyroid hormones play a critical role in mediating amphibian metamorphosis. To date, however, computational modeling of the processes that control circulating levels of THs in a larval amphibian has not been attempted. The goal of this effort was to construct and parameterize a computational model that describes how the HPT axis in X. laevis functions during normal metamorphosis, and in doing so, provide a means to simulate effects that occur when specific components of the axis are perturbed by thyroid active chemicals. A number of computational models for the mammalian HPT axis have been provided [34–40], and the fundamental processes represented by these models are known to be well conserved across vertebrate species. Generally, however, existing models do not consider unique aspects of amphibian HPT axis function during metamorphosis, precluding direct application to meet our objectives.

The developmental window of the model represents the early pro-metamorphic period of X. laevis development (NF stage 54 larvae to NF stage 56/57 larvae). During this developmental period, the hormones (T3, T4, and TSH) that create the negative feedback archetype in thyroid endocrinology increase simultaneously in plasma. This paradox required that the affinity constant that controls TSH secretion be adjusted over time, changing the sensitivity of negative feedback by T3 on TSH. Currently, if model simulations are extended beyond 10 days, the organism continues to grow, thyrocytes continue to proliferate, iodinated Tg continues to accumulate in the gland, and plasma TH levels continue to rise. It is known, however, that once larvae reach metamorphic climax (NF stage 62), circulating TH concentrations peak and then decline to levels homeostatically maintained as juveniles and adults. To accurately model the full course of metamorphic development in X. laevis, additional events would need to be added to the model to trigger appropriate changes in parameter values. For example, when TH levels reach an upper threshold, TSH kinetic parameters could be reset to support mature negative feedback dynamics between T3 and TSH. Additional parameter changes may be required to simulate normal growth of the thyroid gland during later stages of metamorphosis as well as possible changes in processes responsible for plasma clearance of THs and TSH.

The presented model uses thyroid gland morphometry data collected in this and other studies to scale and compartmentalize physical (e.g., membrane diffusion of iodide) and biochemical (e.g., organification of iodide) processes responsible for synthesis of T4 and its secretion to plasma. Because the average size of a thyrocyte in control animals remains relatively constant throughout the modeled developmental period, we elected to aggregate the function of all cells into a single modeled unit scaled by thyrocyte number. This approach implies that all thyrocytes are equal and that all reactions occurring within each cell can be represented by the same set of relatively simple equations. It has been reported, however, that in studies with X. laevis larvae exposed to TH synthesis inhibitors, changes in gland size resulting from compensatory stimulation by TSH are due to changes in both cell number (hyperplasia) and size (hypertrophy) [13–15,17,18]. It may be necessary, therefore, to simulate both of these changes in order to model chemical effects on gland size. One example of such an approach was given by Degon et al. [34].

Model sensitivity to a fixed change in a selected input parameter varied substantially among inputs and across simulated exposure time (Table 2; Fig. 6A–D). In most cases, these findings reflect the effectiveness of homeostatic compensation for changes in a particular process. Viewed in this light, the absence of specific parameters from Table 2 and Fig. 6 (i.e., because all NSCs were $<|0.25|$ provides important information. Notable among these missing parameters are $V_{\text{MAX}}$ and $K_{\text{M}}$ terms for NIS and TPO. In other cases (e.g., for $FCV$ and $K_{\text{H}}$), large NSCs simply underscore the importance of accurately specifying a particular term. Calculated NSCs were also highly dependent on the state variable used to perform the analysis. One important cause of such differences is that individual state variables are impacted differently by changes in circulating TSH. For example, gland size $\left(FC{N}_{\text{TOT}}\right)$ increases as a simple function of baseline growth and growth induced by TSH (Eq. (11)). In contrast, the total concentration of T4 in plasma at each time point $\left(C_{\text{T}4,\text{TOT},\text{PL}}\right)$ reflects a complex interplay between several TSH-induced processes in the thyroid gland and TSH-independent clearance from plasma.

In several cases, the sensitivity of the model to changes in a particular parameter was low at 2 h and then increased progressively at later time points (e.g., the impact of changes in $K_{\text{H}}$ on $C_{\text{T}3,\text{TOT},\text{PL}}$, $C_{\text{T}4,\text{TOT},\text{PL}}$, $FC{N}_{\text{TOT}}$, and $A_{\text{MIT},\text{TL}}$; Fig. 6A–D). At first glance, this pattern suggests a change in the “trajectory” of the model simulation, resulting from a particular parameter adjustment. This simple interpretation is complicated, however, by time-dependent changes in parameters that control negative feedback of THs on TSH secretion (i.e., $K_{\text{M},\text{TSH}}$ and $V_{\text{MAX},\text{TSH}}$), as well as changes in body weight and thyroid gland size. A more detailed sensitivity analysis involving simplified versions of the model (e.g., without organism or gland growth) would be required to separate these influences. In any case, accurate specification of parameters that yield this behavior may be particularly important, given the need to correctly predict TH concentrations during the later stages of an exposure.

With regard to prioritizing future work, the parameters of special interest are those to which the model is especially sensitive and for which empirical data are lacking. Additional priority should be given to parameters that represent processes known to be impacted by chemical toxicants. For example, predictions of $C_{\text{T}3,\text{TOT},\text{PL}}$ and $C_{\text{T}4,\text{TOT},\text{PL}}$ were very sensitive to changes in $K_{\text{D},\text{T3}}$ and $K_{\text{D},\text{T}4}$, respectively (Fig. 6A & B). This is not surprising, given that modeled metabolic conversion/clearance and negative feedback are referenced to free TH concentrations. Research in mammals indicates that there are multiple TH carrier proteins in plasma that differ in terms of their relative abundance and affinity for individual THs [47]. Similar proteins exist in amphibians [48–50], but detailed information regarding their relative abundance and affinity for THs in X. laevis larvae is unavailable. The results of the sensitivity analysis suggest that research to better understand plasma binding of THs in X. laevis is warranted, both to support efforts to model the normal biology of the organism and to provide a basis for simulating the effects of chemicals that interfere with this binding [51–54]. The current model structure and described calibration process is conducive to integrating new information as it becomes available.

The compensatory behavior of the calibrated model was evaluated by simulating the effect of a 95% reduction in TPO activity. Under these circumstances, the model showed robust resistance to the perturbation given that total plasma TH levels were reduced by less than 40% throughout the 10-day simulation (Fig. 3). The results of this simulation showed that TPO inhibition results in increasing levels of plasma TSH (Fig. 5A). This increase in TSH results, in turn, in feed-forward effects on thyrocyte proliferation (Fig. 4D) as well as increased $V_{\text{MAX}}$ values for iodide transport by NIS, organification of iodide by TPO, Tg synthesis, and Tg proteolysis. Importantly, because all the processes responsible for synthesis of T4 are scaled to total thyrocyte volume, increases in thyrocyte volume and modeled $V_{\text{MAX}}$ values operate in a multiplicative manner. The overall result of this simulated behavior is a system that exhibits robust compensation for all but extreme perturbations of TH synthesis.

In vivo effects similar to those predicted by the model, including increased levels of plasma TSH, thyroid gland hyperplasia, induction of NIS, and decreased levels of circulating THs have been observed in dose–response studies with X. laevis larvae exposed to TPO inhibitors [12–15,18,19,21]. This research is part of a larger body of work that has been performed to support the use of X. laevis in a bioassay format to identify chemicals that may disrupt the HPT axis in humans [6]. The presented model provides a tool that can be used to better understand in vivo outcomes when X. laevis larvae are exposed to chemicals that inhibit the HPT axis by known or hypothesized mechanisms of action.

Additionally, high-throughput in vitro screening assays have been developed to test the relative potencies of chemicals that act on specific protein targets within the HPT axis including TPO, NIS, IYD, DIO2, DIO3, and TH binding proteins (e.g., transthyretin, thyroid binding globulin), among others. The described model contains nodes that represent most of these protein targets. It may be possible, therefore, to use the model to relate in vitro effects information to measured or predicted in vivo outcomes, and vice versa. To make this in vitro-in vivo connection it would be necessary to develop a toxicokinetic (TK) model that describes chemical uptake from water and its distribution within the organism. Because X. laevis larvae are fully aquatic, it may be possible to develop this TK model by modification of existing models for fish. Assuming that chemical effects in vitro and in vivo are caused by chemicals freely dissolved in solution, the TK model would have to account for a chemical’s bioavailability in water as well as binding at the site of action or in an appropriate surrogate tissue (e.g., blood plasma). An in vitro binding model would also be required to translate the applied in vitro dose (total concentration basis) to a freely dissolved chemical concentration. Finally, because biotransformation may substantially reduce the chemical concentration within an organism, it may be necessary to account for this activity, particularly for chemicals that are hydrophobic and would otherwise exhibit a tendency to accumulate within the organism. Empirical biotransformation data for X. laevis larvae are lacking. As a starting point, however, it may be possible to employ established Quantitative Structure-Activity (QSAR) models that predict this activity in fish [68,69].

By employing these linked models, it would be possible, in theory, to translate an in vivo aqueous exposure to a corresponding in vitro applied dose. This in vitro dose could be compared to existing in vitro dose–response information to estimate a normalized percent activity for the impaired protein. Assuming the same degree of impairment occurs in vivo, the HPT axis model could be used to simulate chemical effects on circulating levels of T4. Predicted levels of plasma T4 could then be used as an input to a probability model that links T4 levels at NF stages 56/57 to probabilities of metamorphic success/failure [21].

Alternatively, the same set of linked models could be used in “reverse”. In this case, an in vitro dose shown (using the HPT axis model) to produce an unacceptable decrease in metamorphic success/failure could be related to a corresponding in vivo exposure; that is, an exposure predicted to result in the same free chemical concentration at the site of action as that in the in vitro assay. This modeled exposure could then be used to evaluate risks associated with measured or hypothesized environmental exposures. Either analysis could be performed under the simplifying assumption of a steady-state chemical exposure. Alternatively, these linked models could be run dynamically to simulate the effects of a non-steady-state exposure. This dynamic modeling approach may be important for chemicals that accumulate in X. laevis larvae over an extended time period (>10 days).

The presented model of the HPT axis in X. laevis larvae represents decades of research assembled into a dynamic simulation tool. The model is coded using the open-source software, R, which allows access to many other computational resources and offers a barrier-free platform for continual development. As new data becomes available, those values and/or relationships can be integrated into the existing model structure and the model recalibrated. Anticipated applications for this model include ongoing research to better understand mechanisms of anuran metamorphosis, support for standardized in vivo chemical testing efforts with X. laevis larvae, and high-throughput simulation of HPT axis disruption in X. laevis larvae based on measured in vitro effects on key protein targets.

Data availability

Data and code are available from the Environmental Dataset Gateway (https://edg.epa.gov/metadata/catalog/main/home.page).