Tuning the BCS-BEC crossover of electron-hole pairing with pressure

Abstract

In graphite, a moderate magnetic field confines electrons and holes into their lowest Landau levels. In the extreme quantum limit, two insulating states with a dome-like field dependence of the their critical temperatures are induced by the magnetic field. Here, we study the evolution of the first dome (below 60 T) under hydrostatic pressure up to 1.7 GPa. With increasing pressure, the field-temperature phase boundary shifts towards higher magnetic fields, yet the maximum critical temperature remains unchanged. According to our fermiology data, pressure amplifies the density and the in-plane effective cyclotron mass of hole-like and electron-like carriers. Thanks to this information, we verify the persistent relevance of the BCS relation between the critical temperature and the density of states in the weak-coupling boundary of the dome. In contrast, the strong-coupling summit of the dome does not show any detectable change with pressure. We argue that this is because the out-of-plane BCS coherence length approaches the interplane distance that shows little change with pressure. Thus, the BCS-BEC crossover is tunable by magnetic field and pressure, but with a locked summit.

A large magnetic field induces a metal-insulator transition in graphite, which manifests as a dome in the phase diagram. Ye et al. show that this dome is an example of an electron-hole pair BCS-BEC crossover, tuneable by hydrostatic pressure with a locked summit temperature.

Introduction

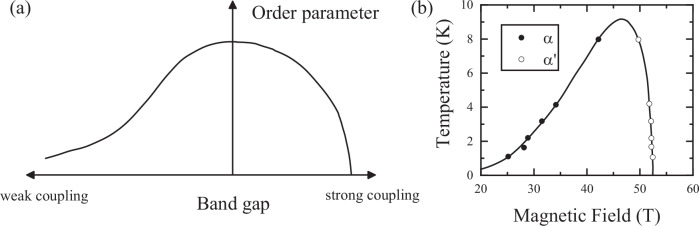
In 1961, Mott made the observation that Coulomb attraction between electrons and holes of a semi-metal can form bound pairs known as excitons¹. Knox then proposed that a sufficiently large exciton binding energy would lead to an insulating state, quite distinct from an ordinary band insulator². Later, Keldysh and Kozlov³ remarked that if the carriers are sufficiently light and not too dilute, the bosonic excitons would have a sizeable Bose-Einstein condensation (BEC) temperature. Starting from these two postulates, the early research on excitonic insulators proposed that this state of matter should be sought near a semimetal to semiconductor transition and produced a phase diagram, which we reproduce in Fig. 1a (See Fig. 3 in ref. ⁴, Fig. 1 in ref. ⁵ and Fig. 3 in ref. ⁶). In 1985, Nozières and Schmitt-Rink⁷ demonstrated that the transition between the strong-coupling limit (the BEC of composite bosons, either excitons or Cooper pairs) to the weak-coupling limit (the Bardeen-Cooper-Schrieffer or BCS) is smooth. The latter corresponds to the long tail on the left hand side of the excitonic dome in Fig. 1a.

Fig. 1. Comparing a theoretical and an experimental phase diagram.

a The theoretical phase diagram for an excitonic insulator showing the evolution of the ordering energy as a function of the band gap^4,5. The order parameter is strongest when the band gap is zero. Note the contrast between the evolution of the order parameter on the two sides of the dome. b The experimental phase diagram of graphite at high magnetic field^11,12. The insulating state resides inside a dome in the (field, temperature) plane. A second dome (starting at  ≈3 T and ending at  ≈70 T¹⁵) is not shown. Note the contrast between the gradual rise of the critical temperature to the summit of the dome and its abrupt drop afterwards.

Graphite, a semimetal with an equal density of electrons and holes (n = p ≈ 3 × 10¹⁸ cm^−3 8), suffers a phase transition at high magnetic field⁹, which has been under exploration during four decades^10–19. The experimental discovery in 1981²⁰ led to an immediate theoretical identification of this state¹⁰ as a charge density wave (CDW). Indeed, confining all carriers to their lowest Landau level opens the way to a nesting instability. This is the case of graphite in presence of a magnetic field exceeding 7.4 T^21,22. In 1998, Yaguchi and Singleton discovered that the field-induced state abruptly ends at 53 T¹¹ (see Fig. 1b). In 2013, Fauqué et al. found that the first dome is followed by a second dome¹⁵ and that the c-axis resistance shows an activated behavior in both domes. These observations challenged the CDW scenario. In 2017, Zhu et al. highlighted the similarity between the experimental (Fig. 1b) phase diagram of graphite and the theoretical (Fig. 1a) phase diagram of an excitonic insulator²³. The accumulated experimental evidence since then indicates that while the transition can be described by a BCS picture of electron-hole pairing at low field^12,16,19, the summit of the dome corresponds to the temperature at which the thermal wavelength and the interbosonic distance match¹⁸, as expected for a BEC transition²⁴.

Besides excitons^25–31, BEC has been reported for other bosonic systems, like photons^32,33, microcavity polaritons^34,35, and magnons^36–38. On the other hand, the BCS-BEC crossover^39,40, which requires tuning either distance between the bosons or the BCS correlation length, has been mainly studied in ultracold Fermi gases, thanks to the Feshbach resonance^41–48. The possibility of the existence of BEC-BCS crossover in superconductors has been proposed for cuprates³⁹, organic superconductors^49,50, iron-based superconductors^51,52, gate-controlled two-dimensional superconducting devices^53,54, interfacial superconductors^55,56, magic-angle twisted superconducting bilayer^57,58 trilayer graphene^59,60, and magnetoexcitonic condensates in heterostructure superconducting graphene⁶¹.

Here, we present a systematic study of the evolution of the phase diagram of graphite and its Fermi surface by measuring the magnetoresistance for H∥c-axis up to 60 T under hydrostatic pressure up to 1.7 GPa. We find that both the lower (low-field) and the upper (high-field) boundaries of the first dome shift to higher fields with increasing pressure. In striking contrast, the summit of the dome is insensitive to pressure. Our study of the evolution of the Fermi surface pockets with pressure demonstrates that across the lower boundary, the BCS relation between the critical temperature and the density of states (set by the degeneracy of the Landau levels) remains valid under pressure. This weak-coupling behavior is disrupted at high magnetic field, when the critical temperature approaches a ceiling set by a parameter set by BEC, which shows little variation with pressure.

Results

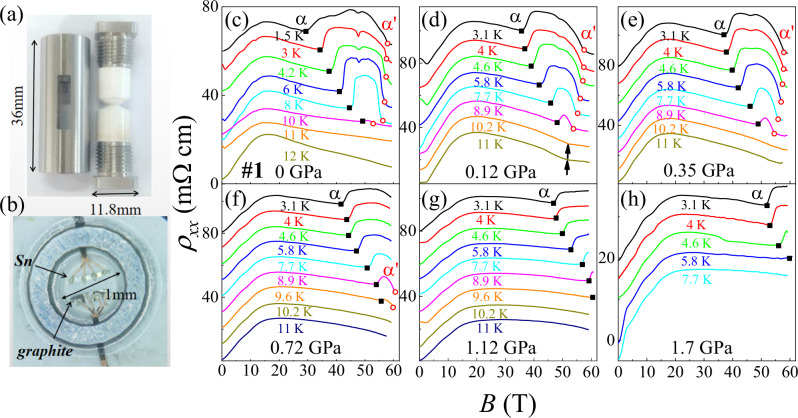
Figure 2c–h shows the field dependence of the in-plane resistivity (ρ_xx) at various temperatures for pressures of 0, 0.12, 0.35, 0.72, 1.12, and 1.7 GPa (see Supplementary Note 2 for the Hall response). Curves are shifted for clarity. At zero pressure, see Fig. 2c, ρ_xx displays a sudden increase above 20 T. This jump shifts to higher magnetic field as the temperature increases. Above 10 K, as reported previously¹², the anomaly vanishes. The onset transition and the high-field boundary, labeled α and ${\alpha }^{\prime }$, following previous authors¹², are marked by black squares and red circles, respectively. The phase between α and ${\alpha }^{\prime }$ is labeled the phase A (the first dome)^16,17. The dip structure of ρ_xx around 45 T in our small sample is the signature of the ${\beta }^{\prime }$ transition which is be observed in previous studies^11,17,62. As the pressure increases, the amplitude of the dip decreases most likely due to the decrease of the sample quality.

Fig. 2. Pressure cell and magneto resistivity results.

a Photo of the pressure cell of external diameter 11.8 mm used in the pulsed-magnet. b Photo of a Kish graphite sample in the pressure cell. The pressure was determined in situ by the superconducting temperature transition of tin. c–h Field dependence of ρ_xx up to 60 T at various temperatures and for different pressures. Curves are shifted for clarity. The onset transition (α) and the re-entrant transition (${\alpha }^{\prime }$) of the first dome are indicated with black solid squares and red empty circles. The Shubnikov-de Haas oscillations at low-field are also observed at low temperatures (see Supplementary Note 2). The α and ${\alpha }^{\prime }$ are shifting to higher field after applied pressure. Under 1.12 Gpa, the ${\alpha }^{\prime }$ shifts beyond 60 T. Note c is the data without gasket and d–h are the ones with gasket.

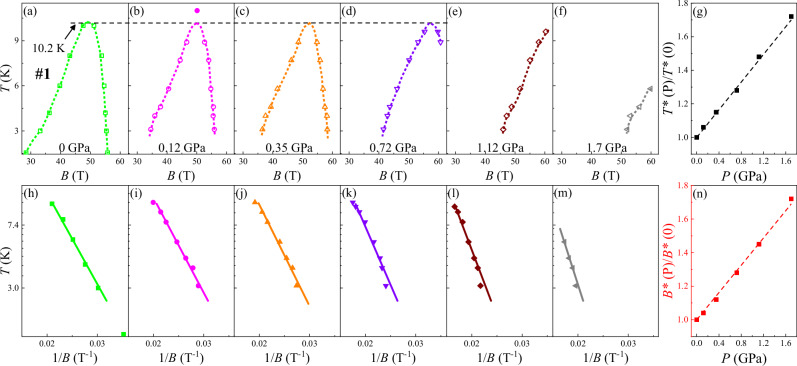
Under pressure, α, ${\alpha }^{\prime }$, and therefore the phase A, shift towards higher magnetic fields. The evolution of the T−B phase diagram with pressure is shown in Fig. 3a–f. Above 1.12 GPa, the high-field boundary ${\alpha }^{\prime }$ moves above 60 T and exits our range of measurement. In contrast, the summit of the dome remains at 10.2 K unchanged by the pressure up to 0.72 GPa (the highest detectable) as indicated by the horizontal dashed line.

Fig. 3. phase diagram of graphite under pressure.

a–f T − B phase diagrams for H∥c axis at the pressure of 0, 0.12, 0.35, 0.72, 1.12, and 1.7 GPa. The dome is shifting to higher field under hydrostatic pressure. In contrast, the summit of the dome is independent of the pressure. The two solid circles in the b show the kinks in magnetoresistance. h–m Tvs1/B at different pressure. The solid lines are a fit of the low-field boundary of phase α using Eq. (1), see the text. g, n Pressure dependence of the parameters T^* and B^* deduced from the fits.

Black arrows on Fig. 2d and solid circles in Fig. 3b indicate the kinks in ρ_xx, which survives above 10 K. A similar anomaly at ambient pressure, above the field-induced state, was detected in measurements of the sound velocity¹⁶, the out-of-plane magnetoresistance (ρ_zz)²³ and the Nernst effect¹⁸. This kink marks the field at which electron and hole Landau subbands simultaneously cross the Fermi level^18,23, creating the most favorable conditions for an electronic instability such as an exciton condensation.

In our study of graphite under pressure, we found that the α-transition shift towards high magnetic field. This is similar to what is induced by neutron irradiation^12,63,64 or by reducing thickness of graphite flakes^65,66. There is a difference, however. Neutron irradiation studies found that the re-entrance field remains unchanged, but under pressure, the re-entrance transition shifts to higher magnetic fields too. As we will discuss in the next section, this difference arises because pressure tunes the Fermi energy, whereas neutron irradiation breaks the charge neutrality by introducing ionized impurities⁶³.

Discussion

BCS regime under pressure

At ambient pressure, in the low-field boundary of the phase A, the critical temperature (T) and field (B) follows:

$$T\left(B\right)=T^{*}\exp \left(-B^{*}/B\right)$$ 1

where T^* and B^* are adjustable parameters. This formula mimics a BCS-type expression: $k_B{T}_c\left(B\right)=1.14E_F\exp \left(-\frac{1}{N\left(E_F\right)V}\right)$, where N(E_F) is the density of states (DOS) at the Fermi energy (E_F) and V is the pairing interaction^67,68. In this framework, T^* is proportional to the Fermi energy (the occupied energy width of the relevant Landau subband and can calibrate the electron and hole which can contribute to the pairing), B^* is inversely proportional to the N(E_F)V product. The change of the critical temperature with the magnetic field is due to field dependence of the DOS which increases linearly with the magnetic field, driven by the degeneracy of the Landau levels¹⁹. With increasing magnetic field, both the DOS and the critical temperature increase and approach the summit of the dome.

Figure 3h–m shows the evolution of T vs B⁻¹ with pressure. For all studied pressures, Eq. (1) is satisfied which allows a determination of T^* and B^*. At 0 GPa, we found T^* = 155 K and B^* = 129 T in good agreement with early measurements^18,62,68,69. Figure 3g, n shows the pressure dependence of T^* and B^* normalized by the ambient pressure values. Both quantities increase linearly with the pressure. Their slope is similar: a = 0.41 ± 0.02 GPa⁻¹ for T^*(P) and a = 0.4 ± 0.03 GPa⁻¹ for B^*(P).

To quantify the change of the Fermi surface induced by the pressure we studied the evolution of the Shubnikov-de Haas (SdH) oscillations in DC field up to 16 T and 1.7 GPa (see Supplementary Note 3). Figure 4a shows the evolution of the SdH frequencies (F) and the in-plane effective cyclotron mass m^* deduced from their temperature dependence. The normalized pressure dependence of the Fermi energy of electrons (E_F,e) and holes (E_F,h) are shown in Fig. 4c. The $\partial \ln m^{*}/\partial P$ and E_F increase linearly with pressure with an slope of a = 0.38 ± 0.02 GPa⁻¹ and 0.36 ± 0.04 GPa⁻¹, in good agreement with an early and comprehensive quantum oscillation analysis by Brandt (a  = 0.43 ± 0.03 GPa⁻¹)⁷⁰, see Supplementary Note 4. At the same time, the carrier density increases with the pressure according to quantum oscillations. This can also be verified by fitting the Hall resistivity with a two-band model (see the details in the Supplementary Fig. 6).

Fig. 4. Pressure dependence of the Fermi surface properties of graphite.

a Pressure dependence of the SdH frequencies (F) of the electrons (blue) and holes (red). Insert: sketch of the Fermi surface of graphite, formed by six adjacent ellipsoid pockets (electron in blue and hole in red). b Pressure dependence of the in-plane effective cyclotron mass m* of the electrons (blue) and holes (red). c Pressure dependence of the Fermi energy of the electrons (blue) and holes (red). d Sketch of the Landau-level spectrum of graphite close to the summit of the dome. The solid curves represent the conditions at ambient pressure, while the dashed curves correspond to those under pressure. On the right, the corresponding density of states is depicted.

Table 1 summarizes the amplitude of the pressure dependence of the four quantities studied: T^*(P), B^*(P), E_F(P) and $\partial \ln \left(m^{*}\right)/\partial P$ (see Supplementary Note 4). Remarkably they display the same pressure dependence. This striking observation can be linked to the pressure dependence of a single parameter (γ₂) of the Slonczewski-Weiss-McCure (SWM) tight-binding model of the band structure of graphite. This model is formed by seven energy scales (γ_i; i = 0−5 and Δ)⁷¹ that represent interactions between neighboring carbon atoms. The parameter γ₂ quantify the inter-layer coupling between the two sub-lattices. It sets the c-axis dispersion: E(k_z) = −2${\gamma }_2\sin \left(\frac{c_0{k}_z}{2}\right)$ where c₀ = 2c with c is the interlayer distance and k_z is the c-axis momentum⁶⁹. Under pressure the inter-layer coupling and γ₂ increase linearly with pressure : γ₂(P) = (1 + aP)γ₂(0) with a ranging from 0.23 to 0.43 GPa⁻¹ according to various experiments done at different temperatures^67,70. Thus, the pressure impacts T^*, which is approximately proportional to E_F, and B^*, which scales inversely with N(E_F)V if the pairing interaction V does not change significantly. Our findings suggest that the pressure-induced variation in γ₂ is not only the driving force behind the linear increase in E_F, but also in N(E_F) (as detailed in Supplementary Note 5)⁶⁷.

Table 1.

Coefficient of the linear pressure dependence of $\partial \ln m^{*}/\partial P$, T^*, B^* and E_F according to^69,70 and our study

	Methods	a (GPa−1)
Brandt et al. (1.7 GPa, 2 K)	$\partial \ln m^{*}/\partial P$	0.43 ± 0.0370
Iye et al. (1.05 GPa, <1.5 K)	T*(P) = (1 + aP)T*(0) B*(P) = (1 + aP)B*(0)	0.29 ± 0.0167 0.29 ± 0.0167
Present work (1.7 Gpa, 3–10 K)	$\partial \ln m^{*}/\partial P$ T*(P) = (1 + aP)T*(0) B*(P) = (1 + aP)B*(0) EF(P) = (1 + aP)EF(0)	0.38 ± 0.02 0.41 ± 0.03 0.4 ± 0.02 0.36 ± 0.04

BCS-BEC crossover

In contrast to the low-field boundary regime that is tuned by the pressure, the maximum critical temperature of the dome is independent of it. This result points to two distinct regimes in the dome. It was recently noticed that the summit of the dome at ambient pressure, which occurs at  ≃10 K, is close to the degeneracy temperature of excitons¹⁸. Indeed the inter-plane distance between excitons and the interplane thermal de Broglie wavelength match each other¹⁸ at this temperature, indicating that this summit corresponds to the BEC temperature. The present results imply that this critical temperature does not show any detectable shift with pressure despite the pressure-induced change of the Fermi temperature.

In order to understand why the summit of the dome is independent of the pressure, let us now put it in the context of the crossover between the BCS to BEC regime. In the weak coupling (BCS) limit, the coherence length (ξ) is much longer than the distance between e-h pairs (d), allowing the applicability of a mean-field BCS-type formula linking the critical temperature to the density of states. One can estimate ξ_∥, the coherence length along the c axis and compare it with the inter particle distance along this direction, labeled d_∥, in order to see how the system evolves from the weak limit (ξ_∥ > d_∥) to the strong limit (ξ_∥ ≃ d_∥).

Figure 5a shows the evolution of ξ_∥ with magnetic field using the BCS formula ${\xi }_{\parallel }=\frac{{\hslash }^2{k}_{F,\parallel }}{\pi m_{\parallel }^{*}{\mathrm{\Delta }}_c}=\frac{\hslash v_{F,\parallel }}{\pi {\mathrm{\Delta }}_c}$. Here, Δ_c is the energy gap measured by out-of-plane resistance measurements⁹ It increases with the magnetic field, i.e., ξ_∥ (33 T) ≃ 5 nm and ξ_∥ (25 T) ≃15 nm¹⁹. Assuming k_F,∥ to be $\approx \frac{\pi }{8c}$^19,62, allows one to extract ξ_∥ and see that its steady decrease with increasing magnetic field decelerates first and then saturates to 2c (in other words, d_∥). Thus, there is an upper bound to the critical temperature, because the coherence length cannot become shorter than the interbosonic distance.

Fig. 5. BCS-BEC crossover in graphite.

a Field dependence of ξ_∥ (black open circle points, see the text for the definition), at ambient pressure compare with the field dependence of the critical temperature (T) in red square points. The purple dashed line is the A–A interlayer distance c₀. When ξ_∥ saturates to c₀, T saturates also at its largest value. The inset shows the lattice structure of graphite. b Field dependence of ξ_∥k_F,∥ at ambient pressure compare with the inter-pair coherence length ξk_F (blue full line) at the mean-field level vs. the coupling parameter ${\left(k_F{a}_F\right)}^{-1}$. Reproduced from ref. ⁴⁰.

The product of ξ_∥ and k_F,∥ shows that the transition goes from a BCS regime, where ξ_∥k_F,∥ >> 1, to a BEC regime at the summit of the dome, where ξ_∥k_F,∥ → 1 (see Fig. 5b). This result is to be compared with the theoretical picture of the BCS-BEC crossover shown in blue in Fig. 5b. a_F is the positive scattering length⁴⁰ In the weak-coupling BCS regime⁴⁰, the inter-pair coherence length ξ decreases. In the strong-coupling BEC regime, when ${\left(k_F{a}_F\right)}^{-1}\ge 1$⁴⁰, the interaction increases further, but ξ ceases to decrease. This is consistent with our observation of the decrease in ξ_∥ followed by its saturation. Furthermore, at the BCS-BEC crossover, ξk_F shows a minimum at  ≈0.6. In the case of graphite, this corresponds to ξ = 1.53c, broadly consistent with the saturation of ξ at  ≈2c found in Fig. 5a. Consequently, the results are not only qualitatively similar (Fig. 5), but they also quantitatively align with the theoretical predictions. A discussion of the in-plane length scale is provided in the Supplementary Note 7.

How does this picture evolve with pressure? The short answer to the question is that the pressure leaves 2c almost unchanged (it changes by less than 3 % at 1 GPa⁸). Since the out-of-plane correlation length cannot become shorter than 2c, the bound to the BCS critical temperature remains identical despite the shift in the parameters. For a more comprehensive answer, one needs to quantify ξ_∥ under pressure. This requires measuring Δ_c. Let us note however, that the change in v_F,∥(P), inferred from fermiology, is small. It decreases by less than  ≈10%, as a consequence of the decrease in both the out-of-plane effective cyclotron mass and the Fermi radius (see Supplementary Note 3).

At the same time, we notice that the shift of the dome is also consistent with charge or spin density wave scenarios. However, unlike the excitonic scenario²³, where all four Landau levels are gapped, these scenarios typically involve gapping only two of the four Landau levels, which contrasts with the observed c-axis gap. Additionally, both the hole and electron Landau subbands cross the Fermi level simultaneously, enabling exciton formation at a magnetic field of 47 T as observed through Nernst effect measurements¹⁸ and in the out-of-plane resistance²³ sets constraints on the charge or spin density wave scenarios⁶².

In the BCS-BEC crossover, the hierarchy between normalized chemical potential and order parameter change, without altering the ground state and causing any phase transition⁷². The crossover is achieved by changing the ratio of the size of the pairs and the distance between the particles. Therefore, it has been argued⁷² that to drive the crossover, one can either change the particle density or the amplitude of the fermion-fermion interaction. The latter road (‘interaction driven’) is taken in the atomic gases with Feshbach resonance^41–48,72. The former road ‘density driven' was theoretically invoked for excitons decades ago⁷³, but is hard to realize experimentally. Graphite under a strong magnetic field offers an alternative. Our result shows that pairing interaction V is almost pressure-independent. It is the increase of DOS, induced by the magnetic field, that drives here the BCS-BEC crossover and not the tuning of the pairing interaction or the particle density.

Lastly, it is noteworthy that valley¹⁰ and orbital⁷⁴ degree of freedom can introduce additional complexity in the high magnetic field regime of graphite. Recently, a theoretical study by Kousa, Wei and Macdonald found that the n = 0 and n = 1 Landau levels of bilayer graphene are sensitive to the details of the particle-hole symmetry breaking and concluded that the mixing of Landau orbitals may affect the physics of bulk graphite at high magnetic fields⁷⁵. The link between two research fields, field-induced electron-hole pairing in 3D graphite and fractional quantum Hall effect in 2D graphene remains a totally unexplored territory.

In summary, we performed a study of magnetoresistance of Kish graphite up to 60 T under pressure up to 1.7 GPa. The α and ${\alpha }^{\prime }$ transitions shift to higher fields, while the summit of the dome remains at the same temperature. We argued that this observation can be understood by considering the BCS parameters of the low-field transitions and the BCS-BES crossover constraints at the summit of the dome.

Methods

The pressure cell used in this study has been developed to fit in the pulsed-field magnets of the Wuhan National High Magnetic Field Center. It is Bridgman type pressure cell adapted from the design of D. Braithwaite et al.⁷⁶. The cell body, with a diameter of 11.8 mm and a length of 36 mm, is crafted from MP35N (see Fig. 2a for a photo of the cell). The anvils are machined from ZrO₂. Daphne 7373 was used as the pressure transmitting medium (see Supplementary Note 1 for additional details regarding the pressure cell). The sample space, with a diameter of 1 mm, host a sample and a tin sample as shown on Fig. 2b. The superconducting transition temperature of the tin sample is used as an in-situ measurement of the pressure in the cell. The magnetoresistance of graphite was measured with the standard four-probe method. The electrical current was applied in-plane and the magnetic field was applied along the c-axis for all samples. The sample temperature was measured by a calibrated cernox thermometer attached to the body of the pressure cell. The unavoidable heating of the pressure cell during the pulse has been corrected through a comparison of the anomalies position with and without the gasket at ambient pressure (see Supplementary Note 1).

Author contributions

Z.Z. initiated the project. Z.Z., K.B., and B.F. directed the project. Z.Z., Y.Y., J.W., N.P., and H.Z. designed the pressure cell. Y.Y., with the help of J.W., N.P., and X.L., prepared the sample and carried out experimental work. Y.Y., Z.Z., K.B., and B.F. wrote the manuscript with the input from all authors.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

All the data and supporting materials can be made available from the corresponding authors upon request. Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54021-7.