A nearly terrestrial D/H for comet 67P/Churyumov-Gerasimenko

Abstract

Cometary comae are a mixture of gas and ice-covered dust. Processing on the surface and in the coma change the composition of ice on dust grains relative to that of the nucleus. As the ice on dust grains sublimates, the local coma composition changes. Rosetta observations of 67P/Churyumov-Gerasimenko previously reported one of the highest D/H values for a comet. However, reanalysis of more than 4000 water isotope measurements over the full mission shows that dust markedly increases local D/H. The isotope ratio measured at a distance from the nucleus where the gas is well mixed is close to terrestrial, like that of other Jupiter family comets. This lower D/H has implications for understanding comet formation and the role of comets in delivering water to Earth.

Analysis of Rosetta measurements suggests that Jupiter family comets could have delivered much of Earth’s water.

INTRODUCTION

Identifying the conditions within the protosolar nebula (PSN) at the time of planetary formation is one of the top priorities for the planetary science community (1). This is a first step toward understanding the distribution of water in the solar system, with implications for the origin of life on Earth and the potential for habitability elsewhere. One critical step to understanding this distribution is determining how the composition of icy building blocks including comets, transneptunian objects (TNOs), Centaurs, and the icy moons of the giant planets varied based on where they formed.

The isotope ratios of water in planets and remnants of planetary building blocks provide a powerful tool for mapping solar system ice composition. The ratio of deuterium to hydrogen, D/H, is especially important. Before the formation of the Sun, very low temperatures in the prestellar core allowed most volatiles to freeze out and condense onto grains. This condensation led to the formation of ices highly enriched in deuterium (2). After the Sun formed, water from these grains vaporized in the PSN and equilibrated with hydrogen. The high temperatures in the inner region of the disk led to a D/H ratio in water equal to the bulk PSN value (2). At increasing distances from the Sun, decreasing PSN temperature and density reduced the efficiency of isotopic exchange, allowing more of the initially enriched D/H to be preserved in water ice. This variability with PSN conditions allows D/H in water to serve as a tracer for planetary building block formation conditions and for the sources of water for the inner solar system.

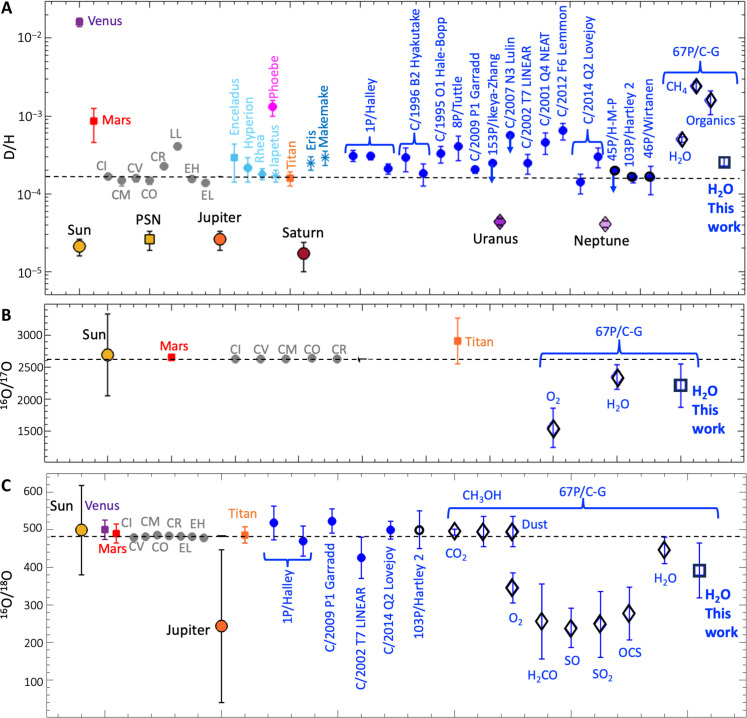
Figure 1A illustrates currently available D/H measurements throughout the solar system compared to the terrestrial Vienna standard mean ocean water (VSMOW) value (dashed line; see the Supplementary Materials and tables S1 to S3). Important constraints for the PSN include D/H in the primary form of hydrogen, H₂, and in water ice. Deuterium in the Sun is converted to ³He over time, leading to a lower D/H in the Sun today (table S1) compared to the PSN. The D/H in Jupiter’s atmosphere was used to determine the value for primordial H₂ (3). Primordial water, which varied in isotopic composition within the PSN, is best constrained through measurements made in remnants of planetary building blocks.

Fig. 1. Water isotope measurements throughout the solar system.

All measurements are compared to terrestrial VSMOW values (dashed lines). Several species have been reported for the Rosetta target comet 67P/Churyumov-Gerasimenko (67P/C-G; open black diamonds with blue error bars) and are compared to results from this work (open black squares with blue error bars). (A) Several D/H measurements are available including chondrites (gray), Saturn’s moons (cyan and orange), two TNOs (steel blue), and several Oort Cloud (blue filled) and Jupiter Family (blue with black outline) comets. (B) ¹⁶O/¹⁷O is available for the Sun, Mars, and chondrites (gray); Titan (orange); and comet 67P/C-G. (C) ¹⁶O/¹⁸O is also available for Jupiter, Venus, several Oort Cloud comets (OCCs; blue filled), and one additional Jupiter Family (blue with black outline) comet (see the Supplementary Materials and tables S1 to S3).

Many measurements are available to evaluate D/H variation in water. D/H in the terrestrial planet atmospheres is not representative of water isotopes where these planets formed. Rather, it represents a combination of water delivered to each planet during their formation directly from the PSN and after formation by impacts of asteroids and comets, followed by enhancement in deuterium resulting from escape, e.g., (4, 5). However, the exact combination of primordial water, asteroids, and comets is not fully understood. Terrestrial D/H values in chondrites and most Jupiter family comets (JFCs) have been used to argue that asteroids or JFCs are the source of Earth’s water, e.g., (6–9). However, JFCs as a source was brought into question when one of the highest D/H ratios, >3× terrestrial, was measured by Rosetta in JFC 67P/Churyumov-Gerasimenko [67P/C-G; (10)].

D/H in comets

D/H measurements from one comet to the next can vary by as much as a factor of four. Historically this variation has been interpreted to be due to different formation regions for comets. Most observations are for Oort Cloud comets (OCCs), which spent time in the Oort Cloud and are bright comets with long orbits. JFCs are fainter, originate in the Kuiper Belt and the scattered disk, and have shorter orbits. All JFCs have nearly terrestrial D/H except for 67P/C-G (6, 11, 12). Four OCCs may also have terrestrial D/H, including 153P/Ikeya-Zhang and C/2007 N3 Lulin [for which only upper limits are available; (13, 14)], and C/1996 B2 Hyakutake (12).

The final terrestrial D/H measurement in an OCC is one of two measurements for comet C/2014 Q2 Lovejoy. This is the only comet other than 67P/C-G for which multiple D/H measurements have been made, in this case, one before and one after perihelion. The pre-perihelion measurement had a terrestrial value (15), while the second measurement was enhanced like most OCCs (16). Although there are some uncertainties with the methods used for the first measurement, variations of D/H over time and space in the coma cannot be ruled out.

How dust influences the local coma composition

It is well known that ice-covered dust grains heated in the coma release volatiles that create extended sources of observed gas (17). Evidence has been found for volatiles sublimating from dust grains in remote coma observations made by Rosetta of 67P/C-G (18) with upper limits quantified by (19). Furthermore, several Rosetta Orbiter Spectrometer for Ion and Neutral Analysis [ROSINA; (20)] observations found that dust changes the locally observed composition of the coma. The comet pressure sensor confirmed that dust grains release volatiles locally into the coma (21). The ROSINA double focusing mass spectrometer (DFMS) observed HCl and HF (22) and the Rosetta time-of-flight observed CO and CO₂ (23) released from dust.

Furthermore, observational evidence of several other comets exists to suggest large differences between the D/H of water ice on dust grains compared to the bulk coma. The D/H observed in dust jets of C/1995 O1 Hale-Bopp were up to 10× larger than the main coma, suggesting that water ice on dust was greatly enhanced in deuterium (24). On the other hand, recent reviews of D/H for several hyperactive comets, or comets with strongly enhanced water production from extended sources, suggested that the D/H of hyperactive comets is terrestrial and proposed that the D/H in water on dust grains is lower than D/H in the nucleus ice (12). Because observations propose either enhanced or depleted D/H in the ice on dust grains, we look to laboratory experiments for further insights.

Experiments that explored whether differences in vapor pressures of H₂O and HDO ices at temperatures relevant to the surfaces of cometary nuclei could change D/H between the gas and ice did not show much fractionation (25, 26). However, mixing dust with ice demonstrated much larger potential for fractionation (25, 27). The gas released during sublimation of dusty ice consistently had a D/H up to a factor of ~3 lower than the bulk value, suggesting that HDO was preferentially adsorbed onto dust grains, allowing for very high D/H in the ice on the dust grains (27). Experiments with different weight percentages and grain sizes of dust showed a clear trend of increasing D/H fractionation when more surface area of the dust was available for adsorption (27). If this process is taking place on a comet nucleus, then HDO in the gas released from the nucleus could pass through layers of dust on and near the surface, preferentially adsorbing onto any exposed dust surface.

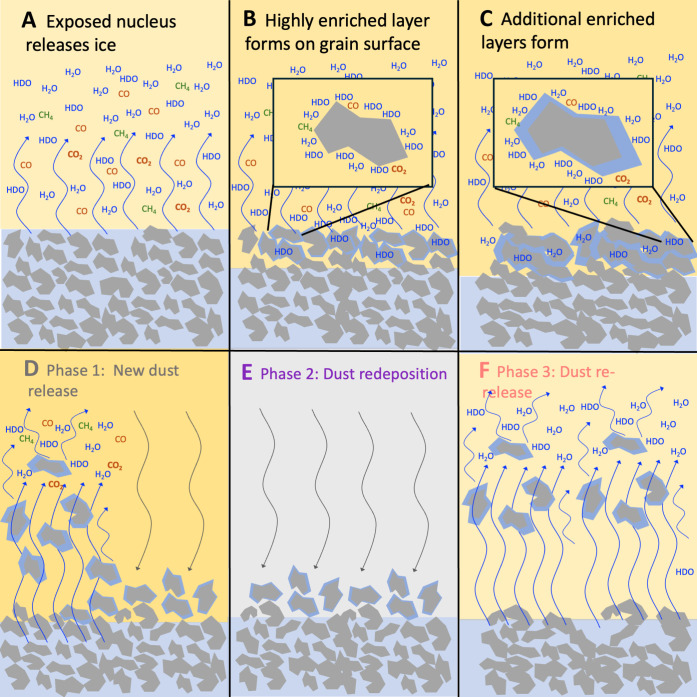
In Fig. 2, we illustrate a simple model for creating enhanced D/H in water ice on cometary dust grains. In this model, the surface of dust grains become exposed as ice sublimates from the nucleus (Fig. 2A). Because HDO adsorbs more readily to the surface of the dust grain, the ice layer directly on the grain surface would be most enriched in D/H (Fig. 2B). Water with heavy oxygen isotopes and hypervolatiles, or molecules with very low sublimation temperatures, being released from the nucleus would also adsorb onto the dust grain. Once an initial ice layer that is highly enriched in deuterium forms, lightly enriched layers may form on top of this (Fig. 2C). As the dust enters the coma (Fig. 2D) it releases enriched water, locally enriching D/H in the coma. Any hypervolatiles present will be preferentially released during this stage.

Fig. 2. A simplified model for enriching D/H on dust grains in the context of the dust cycle observed on comet 67P/C-G.

Creating enriched layers of water on dust grains begins with (A) water ice from the nucleus sublimating to expose dust surfaces. (B) HDO, hypervolatiles, and potentially H₂¹⁷O, preferentially adsorbs to the exposed surfaces creating a highly enriched near surface layer. (C) Additional slightly enriched water ice layers accumulate. (D) The dust cycle for 67P (30) begins during perihelion, or phase 1, when increasing activity releases new dust grains into the coma. These grains release hypervolatiles and the top layers of enriched water (31). (E) During both phases 1 and 2, about 20% of the dm-size dust grains are redeposited onto the surface in colder regions of the nucleus (30, 31) to be (F) reactivated during the next pre-perihelion, or phase 3. At this time, the ice on the dust grains is depleted in hypervolatiles and the most enriched layers of water ice are released.

Observed remotely, the bulk D/H for the entire coma would appear to decrease as the comet approaches perihelion because increased gas from the nucleus reduces the contribution of water adsorbed to dust (25). Furthermore, local observations of D/H will decrease with increasing distance from the comet as dust grains dry out. At some distance, the water in the coma will become fully mixed and represent a bulk value rather than local gas influenced by dust (27). Reality is more complex than this simple model, as dust grain sizes can range from micrometers to centimeter-scale chunks of ice and dust (28). Therefore, dust in a coma will be coated with ice that is a mixture of primordial ice having the same composition as the nucleus and ice enriched in D/H from interaction of HDO with exposed surfaces.

In the case of 67P/C-G, a clearly defined cycle of dust removal and redeposition creates an even more complicated picture (28–30). Choukroun et al. (30) describe the cycle as beginning during perihelion, shown in Fig. 2D as phase 1 (gray in Fig. 2). Here, the subsolar point is in the southern hemisphere and intense activity removes up to a meter of dusty material. While in the coma this “new” dust is heated, losing hypervolatiles such as CO and CO₂ (23, 28) and releasing some water ice.

Approximately 20% of the dust released during perihelion is redeposited into the colder northern hemisphere (31) during the perihelion and post-perihelion phase (30), or phase 2 (purple in Fig. 2) as shown in Fig. 2 (D and E). This “old” dust remains on the surface through aphelion and can become more enriched in HDO on surfaces exposed while in the coma. As the comet approaches the Sun again after aphelion, during phase 3 [salmon in Fig. 2; (30)], the old dust is reactivated as shown in Fig. 2F. These grains are depleted in hypervolatiles like CO and CO₂ and the water ice is highly enriched in HDO because this is the layer closest to the surface of the dust grain. These volatiles are released into the coma until the dust grains are completely dehydrated.

RESULTS

This process is best tested using observations made by DFMS. To date, no notable change in the D/H ratio has been reported over time (32) or spatially between the two lobes of the comet nucleus (33). However, these results are determined based on only 150 measurements. Rosetta orbited comet 67P/C-G for nearly 800 days providing thousands of observations covering a wide range of distances from the nucleus and from the Sun.

We re-evaluated the full mission dataset calculating D/H and oxygen isotope ratios following methods outlined in previous publications (11, 32, 34–36) using an innovative approach for separating the overlapping signals HDO and H₂¹⁷O (see Materials and Methods). The difficulty with separating these two species previously limited the number of spectra that could be evaluated, e.g., (32). We determined abundances for both species with high levels of confidence over the entire mission dataset using a Bayesian nested sampling (NS) method that explores the full probabilistic set of solutions (See Materials and Methods, figs. S1 to S4, and table S4). Using this approach, we have produced 4339 measurements of D/H and ¹⁶O/¹⁷O and 9177 of ¹⁶O/¹⁸O in water (fig. S5).

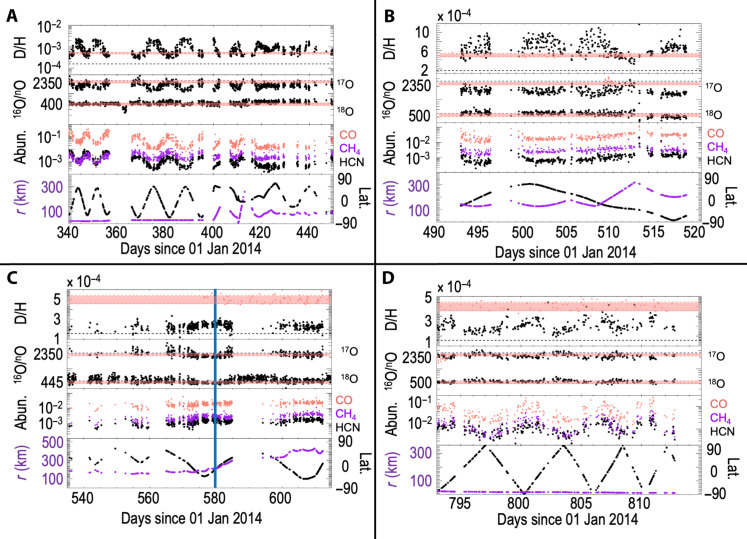
The isotope ratios for four time periods during the mission are illustrated in Fig. 3. During pre-perihelion, or phase 3 of the dust cycle, D/H and ¹⁶O/¹⁷O vary significantly with the subspacecraft latitude as shown in Fig. 3A. The observations in the southern latitudes agree well with published values [see Materials and Methods and table S5; (10, 32, 34)], but the isotope ratios are about 10× greater in the northern latitudes. This resembles the observations made for the dust jets of Hale-Bopp (24). There is also a clear correlation (see the Supplementary Materials and table S6) between the isotopes and hypervolatile abundances (shown here for CO, CH₄, and HCN), where lighter isotope ratios correlate with higher abundances in hypervolatiles. On the basis of the dust cycle illustrated in Fig. 2, old dust is being released from the northern hemisphere. The observations suggest that this dust is depleted in hypervolatiles and is emitting water that is highly enriched in HDO and H₂¹⁷O, as predicted by the enrichment stage illustrated in Fig. 2F. However, seasonal effects on the comet should be considered. The northern hemisphere was experiencing summer and released more water than the southern hemisphere, leading to a higher abundance of hypervolatiles relative to water in the south, e.g., (37).

Fig. 3. Observations of how the isotope ratios and abundances of hypervolatile species correlate with either latitude or distance at different time periods of the mission because of dust influencing the local coma composition.

The isotope ratios are compared to published values (salmon dots and shaded regions) in the top three panels. (A) Pre-perihelion at a distance of 2.1 to 2.9 AU from the Sun. (B) Pre-perihelion at a distance of 1.8 to 2.0 AU from the Sun. (C) Around perihelion (blue line) at 1.2 AU from the Sun. (D) Post-perihelion at 2.5 AU from the Sun (see the Supplementary Materials and table S6).

As the comet neared the Sun, the outgassing rate increased. Figure 3B shows that the trend with latitude decreased (see the Supplementary Materials and table S6), as expected when higher water production from the nucleus reduces the influence of enriched dust on the coma. Notably, the isotope ratios became lighter as the spacecraft moved to farther distances from the nucleus, agreeing with the prediction that D/H will decrease with increasing distance as dust dries out and has less influence on the coma. Our measurements are also in general agreement with previously published values during this time (see Materials and Methods and Table S5) (32, 34).

When the comet approached its closest point to the Sun, as indicated by the vertical blue line in Fig. 3C, D/H decreased substantially at distances beyond 120 km from the nucleus. Furthermore, this observation revealed that the variation in the D/H ratio with respect to both distance and latitude disappears (see the Supplementary Materials and table S6). This is the one time where our derived values do not match those previously published (see Materials and Methods and table S5) (32, 34). The most likely reason for this difference is that the previous study assumed a lower signal for H₂¹⁷O than we were able to determine using the more robust Bayesian NS methods.

As the comet moved away from the Sun during post-perihelion, a slight trend with latitude reappeared (see the Supplementary Materials and table S6). At this time new dust was being released from the nucleus in the southern hemisphere. The heavier ratios are in the southern hemisphere, coinciding with the greatest influence of dust. Notably, enriched D/H correlates with increased hypervolatiles, which is opposite to what would be expected from seasonal effects (37), suggesting that this is a correlation with hypervolatiles being released from new dust (see the Supplementary Materials and table S6). Our derived values in the southern hemisphere where dust is having the greatest influence agree with those previously published (see Materials and Methods and table S5) (32, 34).

Determining D/H in the nucleus

The critical value for understanding water distribution in the PSN is the bulk D/H in water ice in the nucleus. Because dust can influence D/H in a coma, it is possible that some of the spread in cometary values shown in Fig. 1A could be caused by dust influences on the coma. D/H is best measured at a sufficient distance from the nucleus that ice sublimating from dust grains is not influencing the local value and the water is well mixed. To determine the minimum distance at which the bulk nucleus D/H could be measured, we evaluated D/H as a function of distance from the nucleus. Furthermore, knowing that a dust cycle existed, we evaluated D/H as a function of distance at different stages of the orbit. The variability is shown in Fig. 4. In general, the value remained consistent during post-perihelion at distances greater than 120 km from the nucleus (fig. S7). Therefore, the D/H in water at 67P/C-G should be (2.59 ± 0.36) × 10⁻⁴. The ¹⁶O/¹⁷O and ¹⁶O/¹⁸O derived through this method, 2214 ± 340 (fig. S6 and table S8) and 392 ± 73 (fig. S6 and table S9), respectively, have similar values to those previously published but with larger uncertainties based on the variability of individual measurements. On the basis of these results, the H₂¹⁸O/H₂¹⁷O is 5.65 ± 1.36, in good agreement with the Rosetta Microwave Instrument for the Rosetta Orbiter (MIRO) determination of 5.6 ± 0.8 (19).

Fig. 4. Average and standard deviation for D/H measured during different time periods of the mission along with our final derived value compared to previous work.

Colors represent the phases of the dust cycle described earlier. Phase 1 is perihelion (gray), phase 2 is post-perihelion (purple), and phase 3 is pre-perihelion (salmon). Error bars indicate how much the D/H varies within each group (see Materials and Methods and table S7) and the dashed line corresponds to the VSMOW value.

DISCUSSION

What is most notable about this result is that the D/H can be 3 to 10 times the terrestrial value when influenced by dust, but outside of the influence of dust is only 1.2 to 1.6 times the terrestrial value. As shown in Fig. 1A, this places 67P/C-G in line with other JFCs, reopening the possibility that JFCs could have contributed a significant fraction of Earth’s water, e.g., (6).

Furthermore, a lower D/H places the formation location closer to the Sun, consistent with the fact that this comet is water-rich. Comets that are N₂- and CO-dominated, like C/2016 R2 Pan-STARRS (38, 39), would have formed farther from the Sun and would be expected to have larger D/H (40) like the value originally published for 67P/C-G (10). Our derived D/H is much smaller than the one observed in Enceladus’ plume (40). This suggests that the grains that formed 67P/C-G condensed closer to the Sun. The range of D/H ratios across comets and Saturn’s moons (41, 42) underscores the inefficiency of turbulent mixing within the PSN to eliminate local variations in D/H. The building blocks of comets and moons likely agglomerated from indigenous material within the PSN, which did not disperse over several astronomical units.

Last, the smaller D/H observed in 67P/C-G suggests that its primitive grains likely condensed within the PSN rather than originating from the interstellar medium (ISM). Icy grains originating from the ISM would exhibit D/H enrichments two orders of magnitude higher compared to the nearly terrestrial value measured in 67P/C-G (43). The condensation of cometary grains within the PSN implies that they were initially crystalline before accretion, and the possibility of their agglomeration from clathrates cannot be discounted (44–46).

MATERIALS AND METHODS

DFMS

The ROSINA DFMS (20) was a high-resolution high-sensitivity mass spectrometer that flew onboard the Rosetta spacecraft. The mass resolution, m/Δm, exceeded 3000 at 1% of the peak height, which is sufficient to separate CO from N₂ and ¹²CH from ¹³C. The sensitivity was greater than 10⁻⁵ A/mbar, which corresponds to a density of 1 cm⁻³ being measured at 0.2 counts/s. The dynamic range of DFMS was 10¹⁰ (20). The instrument measured the mass/charge of ionized neutrals in the coma of comet 67P/C-G through a combination of an electrostatic analyzer to measure the ion energy and a magnet that measures momentum, a configuration known as the Nier-Johnson geometry (47). Neutral species were first ionized using electron impact ionization. The ions passed through the instrument where they were separated according to their mass and were measured by the detector.

The detector has two rows, and the signal is spread between the two rows as illustrated in figure 6 in (48). Each pixel on the detector measures the counts as a function of mass based on the mass resolution setting for the specific measurement, creating a spectrum of summed peaks for all species within the mass range. An example for mass 19 in high resolution is illustrated in fig. S1. Each species is presented as a Gaussian-like peak and the area under the curve gives the signal for that species. Figure S1 shows how some species can overlap and create a challenge for determining individual species’ signals. Although the total signal for each species will differ between rows A and B, the relative signals of each species compared to each other should be the same for both rows.

The sensitivity of the detector could be varied by adjusting the detector gain, which is represented by the voltage difference between the front and back of the detector. The detector gain had 16 possible steps depending on the sensitivity needed for measuring the abundance of a species without saturating. As the detector aged, the gain for each gain step varied according to the values derived in (36). In addition, the gain for each pixel on the detector degraded over time requiring pixel gain corrections. The level 3 data that are publicly available and used for this analysis have been corrected for pixel gain and gain step adjustments.

Rosetta arrived within 1000 km of 67P/C-G in August 2014 when the comet was 3.6 AU from the Sun. The spacecraft remained in orbit around the comet for nearly 800 days, ending the mission by landing on the comet on 30 September 2016. The spacecraft observations cover a Sun distance range between 3.6 AU at the beginning of the mission, through perihelion at 1.2 AU and out to 3.8 AU at the end of the mission. Rosetta measurements also covered the coma at a wide range of distances from the nucleus (fig. S2).

Determining the signal of a species

The signal of a species measured by DFMS is determined by fitting a model for the signal of each species that should appear in a mass spectrum to the shape of each peak where a signal is observed. This is done using inferred fitting parameters to determine the area under the curve. Although previous publications appear to only show single Gaussians for each species [fig. S1; (10, 32)], the previously published fits were done using a double Gaussian model and the published figures show the sum of the two Gaussians.

For the ith species, the double Gaussian functional form for fitting DFMS measurements is given by

$$\text{count}{\mathrm{s}}_i=a_1\text{exp}\left[-{\left(\frac{p_i-p_0}{c_1}\right)}^2\right]+a_2\text{exp}\left[-{\left(\frac{p_i-p_0}{c_2}\right)}^2\right]$$ (1)

where a₁ and a₂ are the amplitudes of the first and second Gaussians, c₁ and c₂ are the widths of the first and second Gaussians, p₀ is the pixel zero position for the location of the integer mass on the detector, and p_i is each detector pixel value at which the Gaussian is evaluated (10, 32, 34–36). While the first Gaussian terms a₁ and c₁ are specified uniquely, the second Gaussian terms are related to the first by a₂ = 0.1 a₁ and c₂ = 3c₁, such that the second Gaussian is broader and lower amplitude than the first.

The total number of ions incident on the detector is calculated by integrating the area under the curve of the fit to the peak in the mass spectrum, which is analytic given the double Gaussian model formulation and given by (32)

$$\sqrt{\mathrm{\pi }}(a_1{c}_1+a_2{c}_2)$$ (2)

The total mass spectrum that we fit to the DFMS measurements is given by the sum of the individual species’ double Gaussians

$$F(\mathrm{\theta })=\text{total counts}={\displaystyle \sum _{i=1}^N}\text{count}{\mathrm{s}}_i$$ (3)

which we refer to as F(θ) for shorthand notation, for N different species with features included in the fit for a given mass. Since each species contributes a different term to the preceding sum (corresponding to a different peak), the total count integral is separable and can be solved individually for each species.

The pixel location of the central mass for a given species requires special attention. The pixel location of the Gaussian peak is given by relation

$$p_{\mathrm{p}}=p_0+\frac{\mathit{Dz}}{x} \mathit{\text{ln}}\left(\frac{m_{\mathrm{p}}}{m_0}\right)$$ (4)

where m_p is the mass-to-charge ratio that falls on pixel p_p, p₀ is the pixel where the commanded mass m₀ is located, x is the step width between two pixels (x = 25 μm), D is the mass dispersion factor, and z is the zoom factor (48). While m_p and x are generally known quantities, D, z, and p₀ are known to vary for different measurements and therefore may introduce errors into the calculation converting from mass to pixel and vice versa. When fitting for most species, we can reasonably assume a fixed value for these variables, but in a special case described below, we allow D, z, and p₀ to vary and fit for them between relatively tight bounds based on literature values (table S4).

Measuring water isotopes using DFMS observations

The detailed methodology for determining the water isotopes using observations from DFMS is outlined in (35). Three isotope ratios can be derived using these measurements

• D/H=HD¹⁶O/(2*H₂¹⁶O)

• ¹⁶O/¹⁸O=H₂¹⁶O/H₂¹⁸O

• ¹⁶O/¹⁷O=H₂¹⁶O/H₂¹⁷O

The isotope ratios are calculated by dividing the signal measured for one isotopolog by the signal for the other isotopolog. The most abundant isotopolog, H₂¹⁶O, is required for determining all three of the isotope ratios. It is the primary molecule that is measured at mass 18, so determining the total signal for this species in mass 18 is straightforward. We evaluated the full mission dataset, deriving the signal of H₂¹⁶O for 64,489 measurements.

The heaviest oxygen isotopolog, H₂¹⁸O, is the main peak in mass 20 and the only species in its peak. It has a fragment, ¹⁸OH, in mass 19 (fig. S1). This fragment is the only species in the second peak in mass 19 so determining the abundances of H₂¹⁸O and ¹⁸OH is also straightforward. We determined the signal for H₂¹⁸O and ¹⁸OH for 17,940 and 16,457 measurements, respectively. This species was used for determining how water is dissociated in the instrument and for evaluating the gain correction based on the measured ¹⁸OH/H₂¹⁸O (36).

The unique case of mass 19

HD¹⁶O and H₂¹⁷O are also measured in mass 19 and their peaks overlap (fig. S1). According to (10, 34–36), these are the only two species in the third peak in mass 19. However, figure 1 in (32) suggests that a third species, H₃O, is also present in this peak. No explanation is provided in the paper for why this species was introduced or should be included in the fits.

Determining the signal for multiple species that appear in a single peak is challenging. In these cases, there are correlations between the possible values of each species’ peak that can potentially bias the inferred results if only a single solution is obtained by standard nonlinear least squares optimization. To characterize the extent of these correlations and infer solutions that account for these correlations, we fit the DFMS spectra using the aforementioned forward model within a Bayesian framework designed to explore the full posterior probability density, including parameter covariances. The crux of the approach involves numerically evaluating Bayes theorem for the posterior probability of model parameters θ given observations, y

$$P(\mathrm{\theta }\mid y)=\frac{P(y\mid \mathrm{\theta }) P(\mathrm{\theta })}{P(y)}$$ (5)

where P(y∣θ) is the likelihood of the data given the model parameters, P(θ) is the prior probability of the model parameters, and P(y) is the marginal likelihood or “Bayesian evidence.” Put simply, Bayes theorem provides a statistical formalism to the process of updating one’s knowledge on a system given new data. Following typical Bayesian methods in astronomy, we evaluate the logarithm of the above equation. We define the log likelihood in terms of the standard χ² “goodness of fit” metric

$$\text{log}\left[P(\mathrm{\theta }\mid y)\right]=\text{log}L=-\frac{1}{2}{\mathrm{\chi }}^2=-\frac{1}{2}\sum {\left[\frac{y-F(\mathrm{\theta })}{\mathrm{\sigma }}\right]}^2$$ (6)

where, again, y are the measurement data, σ are the measurement errors, F(θ) is the double Gaussian forward model, and the sum runs over all pixels in the mass spectrum measurement. Given a set of model parameters θ, the forward model can be evaluated and compared to the spectrum using the log-likelihood function.

In addition to the likelihood function, the prior probability of the model parameters P(θ) or “priors” are critical to evaluating Bayes theorem. Priors encode the probability of the model parameters taking on any value before the assessment of the new measurements, y. For entirely unknown parameter values, it is common to simply bind them between two extremes beyond which they may be considered to be unphysical or unaffecting of the forward model. To implement this common approach, a uniform prior is used, which assigns equal probability to all values between the upper and lower bounds. Another common approach is to use a Gaussian prior, where probability is assigned following a normal distribution with a mean and SD informed by previous measurements or information. In this work, we use both uniform priors and Gaussian priors depending on the parameter. We chose to use Gaussian priors for parameters where uncertainties were known for them before the measurements being made. For example, the central pixel, p₀, and the uncertainty on it are provided in the data file header and the zoom factor, z, for mass 19 has been previously reported as 6.6 ± 0.2 [table 9 in (49)]. We allowed the other fitted parameters to vary broadly to allow the data to constrain their value. Table S4 lists each of our model parameters and their respective priors used for the Bayesian inference. We note the use of the log of the Gaussian width and amplitude as fitting parameters due to the orders of magnitude that each parameter can span.

There are many different approaches that can be used to solve the inverse problem (Eq. 6) for the values of the model parameters given the data. In the simplest and most common approach, one can use a nonlinear least squares optimization method to find the best-fitting model parameters. However, the propagation of errors through the forward model, from the measurement uncertainties through to the inferred model parameters, is nontrivial. This holds particularly true in the case of overlapping species that are covariant with one another and for cases with nondetections, where only an upper limit can be inferred. As a result, we implemented methods that can derive the full shape of the posterior distribution (i.e., histograms for each fitting parameter) so as to be robust to parameter covariances and non-Gaussian posteriors.

We initially opted for a Markov chain Monte Carlo sampling method; however, the degeneracy between HDO and H₃O proved to be challenging for the method to efficiently sample and, at times, led to multimodal posteriors. To mitigate this sampling issue, we implemented a NS approach (50) using the dynesty Python package (50). This method is well-suited for inverse problems with strong parameter degeneracies and multimodal posteriors. Through this approach, the information gained from each observation can be formally quantified using the Kullback-Leibler divergence between the prior probability and posterior probability density distributions. This is quantified by the natural logarithm in calculating the information, in units are referred to as “nats.” Conveniently, dynesty estimates this quantity. We find that the average information gain from a DFMS mass 19 observation is 21.0 ± 1.7 nats for row A and 22.4 ± 1.8 nats for row B. The general scaling of the information is such that the more counts that are on the ROSINA detector, the higher the information gain we are able to obtain. While this is the expected result, it indicates that our choice of model construction and parameter priors is not driving our inferences and instead our results are entirely driven by the data.

NS is a method for calculating the Bayesian evidence and posterior distribution for inference problems that are constructed in a similar manner to that described above. A thorough description of the algorithm is provided in (51, 52), but we summarize it here for completeness. The NS algorithm uses so-called “live points” to sample the entire parameter volume and, through successive iteration, converge upon the highest probability (best-fitting) regions of the parameter space. The number of live points is determined by the user, but throughout this work, we used 1000 live points for all of our fits. The approach begins by randomly drawing live points from the prior volume (the range of all possible values for each fitting parameter) and evaluating the log likelihood for each live point. Then, the code iterates using the following procedure. The resulting live points are sorted by their respective log-likelihood values and the lowest likelihood live point (i.e., the worst fit) is removed from the set. A new live point is randomly drawn from the prior, its likelihood is evaluated, and if the likelihood is higher than the discarded live point, then it joins the set of live points, otherwise a new random sample is drawn until it satisfies this criterion. By iterating through this approach, the set of live points effectively constricts upon the higher likelihood regions of the parameter volume, iterating through concentric “shells” of likelihood. This allows for a computationally efficient estimating of the Bayesian evidence, which is defined as the integral of the likelihood over the entire parameter volume, as well as an estimation of the full posterior distribution as a by-product.

Why the fits for HDO and H₂¹⁷O should not include H₃O

After fitting mass 19 with and without H₃O, we evaluated whether the presence of H₃O is demonstrated by the results and concluded based on three criteria that H₃O is not present in the signal. First, we note that fits with H₃O can be visibly good, as shown in fig. S2, but note that this opens up degeneracy between HDO and H₃O that heavily skews the subsequent results for both species. Note how the covariances and the peaks of the distributions shown in fig. S3 demonstrate that the determination of whether there is more HDO or H₃O depends on where the probability (or samples) “fall(s)” along these curving degeneracies. The entire set of results exhibits this same characteristic degeneracy, which means that the degeneracy is what dictates whether the peak is dominated by HDO or H₃O and not the physical reality of one species being more abundant than the other. This suggests that including H₃O fundamentally affects the HDO result, since the two peaks cannot be effectively separated, and which species is found to contribute more signal appears effectively random and potentially subject to systematics.

Second, the results with H₃O do not track physically with the other well-separated species that ought to be related to both HDO and H₃O, nor do they agree between rows A and B. Although the total signal in rows A and B will be different, the relative signal of one species to another should be the same on both rows. As shown in fig. S4, this is only the case when H₃O is not included in the fits suggesting that this species is probably not present in the signal.

Last, H₃O is not actually present in the coma and is theorized to form in the instrument. The ionization process of H₂O produces H⁺ as a fragment that reacts with H₂O in the instrument to form H₃O⁺. Thus, the H₃O⁺ intensity should be strongly correlated with the H₂O intensity, which it is not. Because there is no correlation, there is no clear physical evidence for H₃O to be present, while HDO does have a good physical reason to be in this signal.

Evaluating the validity of the measurements and calculating uncertainties

Although we had sufficient data to determine the water isotope ratios for more than 16,000 observations, some evaluation of the validity of these measurements was needed. When the instrument is off, water from the coma adsorbs to it and is driven off when the instrument heats up after being turned on again. We therefore excluded all observations that were made within 2 hours after the instrument was turned on following a period when the instrument was not actively taking measurements.

We only included observations where the three relevant masses were measured within 20 min of each other and excluded all observations where the angle between the instrument aperture and the nucleus was larger than 10°. We found that one mode of observation provided isotope ratios that were anomalously high compared to all other modes and excluded observations made with that mode.

Last, we evaluated the overall uncertainty in the resulting measurements and set restrictions on which observations to include. Previously published isotope ratios determined the uncertainty based on several factors: uncertainties due to the pixel gain and gain step corrections, statistical errors based on the count rates, and uncertainties in the fits. The uncertainty due to the pixel gain is estimated at 5% while the gain step is 6% (32). The common approach for determining the errors on a signal measured is to use the square root of the signal, so the magnitude of this part of the uncertainty depends on the signal itself. The error due to uncertainty in the fit for mass 19 due to the overlapping signals of HDO and H₂¹⁷O has been reported to be 25% (34). The error in the other fits is much smaller.

We used data that were already corrected for the pixel gain and gain step and propagated the reported uncertainties of 5% for pixel gain and 6% for gain step (32) into our derived values. Our Bayesian NS fitting method combines the statistical uncertainty from mass 19 with the fit error by propagating the errors numerically. This approach tends to give larger uncertainties that more accurately account for parameter covariances, which is particularly true for overlapping species. The errors in the other masses were determined based on the counting statistics.

As the final step in determining which measurements were accurate enough to include in our study, we evaluated the quality of measurements based on uncertainties. We excluded all D/H and ¹⁶O/¹⁷O observations where the uncertainty in mass 19 the fit exceeded 50%. Similarly, we excluded all ¹⁶O/¹⁸O observations where the uncertainty was greater than 50%. After selecting data based on the above conditions, we have a total of 4339 simultaneous measurements of D/H and ¹⁶O/¹⁷O in water and 9177 of ¹⁶O/¹⁸O in water (fig. S5).

Comparison of derived isotope ratios with previous published values

We compare our determinations of all three isotope ratios with those that have been published previously (Fig. 3 and fig. S5) and provide a full comparison of the individual D/H measurements and uncertainties (table S5). Note that although our uncertainties are much smaller because the method for fitting mass 19 is more accurate than previous approaches, we elected to exclude several of the data points used in previous studies because the quality of the fit to mass 19 was too poor (table S5).

In general, we can reproduce the D/H ratios published in (10) for 4 and 5 September 2014 and (34) for 3 December 2015 and 15 to 21 March 2016. Furthermore, we reproduce the ratios published in (32) for May 2015 and March 2016 but obtain a statistically significant difference in all values during August 2015, which is the period around perihelion. The only differences between our methods and the ones described in (32) are our overall method for fitting mass 19 and that we do not include H₃O in our fits. Including H₃O would further reduce the D/H, so this cannot explain the difference between our results and these published values. The only other possible explanation is if the fit to mass 19 used by (32) assumed less H₂¹⁷O during this time period than we found using the more rigorous NS methods outlined above.

Our results for ¹⁶O/¹⁷O agree with those published in (10) for 4 and 5 September 2014 and the ratios published in (36) for May 2015 and March 2016. Our results generally agree (fig. S5) with the average for the mission published in (32). Last, the values we derive for ¹⁶O/¹⁸O agree with those published in (10) for 4 and 5 September 2014 (fig. S5) and the mission average published in (36).

Determination of the best values for representing the bulk nucleus

As we showed in Results and Fig. 3, dust influences the D/H value and the amount this value varies as represented by the SD as a function of latitude when the spacecraft is near the comet and the water outgassing rates are low (Fig. 3, A and D). We also showed that the D/H value and variation as represented by the SD both decrease with increasing distance as the dust dries out showing that the influence on the local measurements is reduced (Fig. 3, B and C). We noted in Fig. 3C that the variation with distance went away after a certain distance from the nucleus had been reached. When the D/H is plotted as a function of distance and separated by pre- and post-perihelion (fig. S7), we find that the isotope ratio is relatively stable post-perihelion at distances farther than 120 km from the nucleus. These measurements are the most reliable for determining the D/H ratio of the bulk nucleus ice. The measurements of ¹⁶O/¹⁷O and ¹⁶O/¹⁸O demonstrate more scattering than the D/H. The ¹⁶O/¹⁷O follows a similar pattern to D/H with a preference for a “lighter” isotope ratio post-perihelion outside of 120 km (fig. S7). However, ¹⁶O/¹⁸O displays as much scatter in these observations as throughout the rest of the mission (fig. S7).

To determine the water isotope ratio in the bulk nucleus, we separated the 4339 D/H and ¹⁶O/¹⁷O and 9177 of ¹⁶O/¹⁸O measurements into various bins based on the phase of the dust cycle, latitude, and distance from the comet. We calculated the mean, the uncertainty of the mean based on the individual errors, the SD, and the skewness for each of the bins (tables S7 to S9). The average and SD give a mean value and an indication of the spread of values over the population. In all cases the SD is larger than the uncertainty of the mean. Because the variability provides an indication of the role of dust in the local coma measurements, we use this value for the error bars (Fig. 4 and fig. S6) and to determine the uncertainty for the derived isotope ratios. The skewness indicates whether the distribution of measurements is a normal distribution, meaning that the average is representative of the true mean, or if the distribution is skewed toward high values for a positive skewness or low values for a negative skewness.

It is first notable that the D/H varies significantly and is much larger close to the nucleus compared to far away. The spread of values is also very large except for post-perihelion outside of 120 km. The skewness indicates that measurements inside of 120 km are skewed toward higher values, suggesting that the mean does not accurately represent an average value.

Although D/H is most susceptible to variation based on the influence of dust, the oxygen isotopes are also influenced. However, the skewness indicates a nearly normal distribution for all bins, suggesting that the influence is not nearly as large for oxygen as for D/H. Most notable is the intense enrichment in the heavy isotopes ¹⁷O and ¹⁸O in the northern hemisphere during pre-perihelion at the same time as when the most extreme enrichment in D/H is also observed. This demonstrates that oxygen isotopes are also affected by dust processing on the surface.

Supplementary Materials

The PDF file includes:

Supplementary Text

Figs. S1 to S7

Tables S1 to S9

Legend for data S1

References

Other Supplementary Material for this manuscript includes the following:

Data S1