Acoustofluidic tweezers via ring resonance

Abstract

Ring resonator (RR) devices are closed-loop waveguides where waves circulate only at the resonant frequencies. They have been used in sensor technology and optical tweezers, but controlling micron-scale particles with optical RR tweezers is challenging due to insufficient force, short working distances, and photodamage. To overcome these obstacles, an acoustofluidic RR-based tweezing method is developed to manipulate micro-sized particles that can enhance particle trapping through the resonance interaction of acoustic waves with high Q factor (>3000), more than 20 times greater than traditional acoustic transducers. Particles can be precisely manipulated within the RR by adjusting the signal phase, with trapping amplified by enlarging the connected waveguide. Rapid particle mixing is achieved when particles are placed between the waveguide and RR. The signal path is strengthened by strategically positioning the RR in a two-dimensional plane. Acoustofluidic RR tweezers have immense potential for advancing applications in biosensing, mechanobiology, lab-on-a-chip, and cell-cell communication research.

An acoustofluidic RR-based tweezing method is developed for the manipulation of micron-sized particles.manipulation of micron-sized particles.

An acoustofluidic RR-based tweezing method is developed for the manipulation of micron-sized particles.manipulation of micron-sized particles.

INTRODUCTION

Ring resonator (RR) devices were conceived and developed initially as a set of waveguides in a closed loop, such that the wave can travel around the loop multiple times, similar to whispering-gallery waves. They have been extensively used in optics to filter, amplify, or delay signals of specified wavelengths (1). Since their development, RRs have commonly been implemented as circular resonators, where light or sound waves can be confined near the resonator boundary with minimal energy loss. Leveraging the strong light confinement in RRs, optical RR sensors and tweezers have been developed for manipulating particles down to the atomic scale (2–3). Optical RR sensors and tweezers use high Q factor resonators that enable strong confinement and enhancement of the optical field, creating a highly localized and intense electromagnetic field at the resonator boundary (4–6). This intense field gradient exerts optical forces capable of trapping and manipulating particles, allowing for precise manipulation at the atomic and molecular scales (7). However, controlling micron-sized particles using optical RR tweezers remains challenging due to limitations such as insufficient forces (ranging from piconewtons to nanonewtons), short working distances (in the nanoscale), and issues related to light-induced heating and photodamage.

Alternatively, acoustic tweezers have been developed to precisely manipulate particles across seven orders of magnitude, including trapping 5-nm particles and achieving three-dimensional (3D) translation and rotation of millimeter-sized organisms within fluids (8–13). In contrast with other micromanipulation technologies, acoustic tweezers offer distinct advantages, such as their noncontact nature, biocompatibility, and dynamic reconfigurability (14–24). Hence, this technology has found diverse and substantial applications in medical diagnostics (25, 26), bioanalytical chemistry (10, 27–33), and materials science (34–37). Despite their unique advantages, in most acoustic tweezers devices, a strong input power is necessary to generate sufficient force. However, this strong input power can cause several difficulties, including unwanted heat generation, bubble formation, cavitation, transducer overload, and the need for high-performance (and thus expensive) transducers. By introducing high Q resonances, it is possible to achieve strong wave-particle interactions with moderate power input. In essence, this means the field is only strong where it must be, minimizing these problems.

In this work, we introduce acoustofluidic RR tweezers with a high Q factor (>3000, more than 20 times larger than that of traditional acoustic transducers). This approach enables power-efficient manipulation of micron-sized particles with a large working distance—on the millimeter scale—and a wavelength approximately 173 times larger than the smallest particle controlled in the system. In particular, we use a high Q factor acoustic RR and adjust the phase of input signals to transport and precisely manipulate microparticles. Notably, the particle trapping effect is amplified through RR-induced pumping. Our experiments demonstrate effective particle mixing using acoustic RR, which could drive advancements in applications such as bioparticle mixing, sensing, and cell-cell interaction studies. We believe that the presented acoustofluidic RR tweezers have far-reaching interdisciplinary implications spanning biology, chemistry, engineering, and medicine because of their capacity for noncontact, label-free, biocompatible, and precise manipulation of cells and particles.

RESULTS

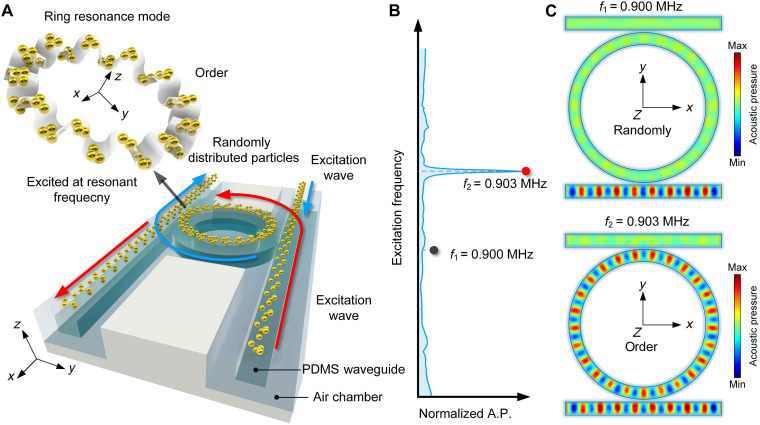
The RR-based acoustofluidic tweezers consist of two straight rectangular waveguides and an RR, illustrated in light green in Fig. 1A. The waves come from opposing directions (the red and blue wave arrows in Fig. 1A) and propagate inside the waveguide and interact in the RR (38–43) to create a predesigned mode shape parallel to the z direction. Upon energy input, the particles on the system’s surface transition from random to an ordered distribution structured by the pressure mode, as depicted in Fig. 1A RR. This creates an acoustic tweezer-trapping effect. To provide more details of the design, Fig. 1B presents the acoustic response on the ring, which shows a resonant frequency of 0.903 MHz. The RR appeared only when the applied frequency was equal to that obtained from the eigenvalue natural frequency of the governing equation of an acoustic wave in the ring. With nonresonant input at 0.9 MHz, the wave still can propagate in the rectangular waveguide, while barely any energy propagates in the ring shown in Fig. 1C. The geometric and material details of the simulation, conducted with COMSOL Multiphysics software, are provided in table S1. Owing to the principles outlined in the RR theory about the ring shape (Supplementary Text) (1), the resonant frequency is determined exclusively by the RR and is given below

$$f_{\mathrm{m}}=\frac{C_{\mathrm{w}}m}{2\mathrm{\pi }{r}_{\mathrm{w}}} \text{with} (m=1,2,\dots ,N,N\in \mathbb{Z})$$

where m denotes the number of periods on the mode shape, c_w signifies the phase acoustic velocity in polydimethylsiloxane (PDMS) (12), r_w represents the radius of the RR, and f_m corresponds to a resonant frequency. Upon extracting a cross section from the simulation results, Supplementary Text of the simulation setup and additional simulated results illustrate the acoustic field distribution, demonstrating that the acoustic field inside the water layer is constrained to the waveguide region. This phenomenon results in the trapping of particles on the RR inside the fluid chamber on the PDMS surface of both the waveguide and the RR.

Fig. 1. Acoustofluidic tweezers via ring resonance.

(A) Schematic diagram shows the positioning on both sides of the PDMS waveguide, inducing clockwise (CW) and counterclockwise (CCW) resonances in the RR due to the red and blue input signals, respectively. The particles, which are initially randomly distributed throughout the channel, will be transformed to an ordered state by ring resonance mode in the RR, enabling particle patterning. (B) Nonresonant and resonant frequencies of the RR are marked at f₁ = 0.9 MHz and f₂ = 0.903 MHz, respectively. (C) Acoustic field distribution at 0.9 MHz (nonresonant mode) and 0.903 MHz (resonant mode). A.P., acoustic pressure.

RR-based acoustofluidic tweezers for particle manipulation

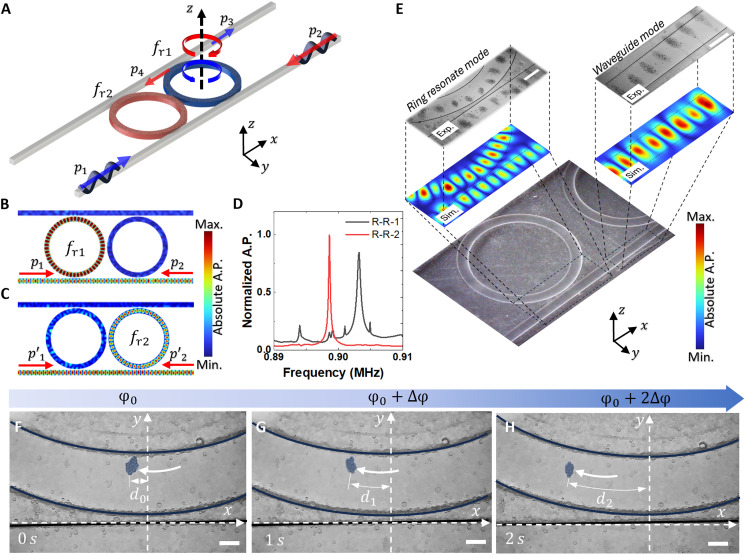
A schematic of our concept is illustrated in Fig. 2. The multiple PDMS rings feature subtle geometric variations and are designed to sustain distinct resonant frequencies. This design choice empowers the RR-based acoustofluidic tweezers to operate efficiently across various specific frequencies. Aligning the RRs in a single line allows for a consistent ring diameter, and altering the height allows for adjustments in the resonance frequency. In this context, two rings with resonant frequencies f_r1 = 0.903 MHz and f_r2 = 0.899 MHz are examined to address the proposed objectives. As shown in Fig. 2A, input signals, p₁ and p₂, generating clockwise (CW) and counterclockwise (CCW) RRs, respectively, are applied from two sides of the waveguide. Simultaneously, the pumping signal, p₃, is generated on another waveguide aligned with the RR. The corresponding simulation results in Fig. 2 (B and C) demonstrate that, with different input signals at slightly different frequencies, distinct resonant modes with standing waves are generated in the ring, while the other ring maintains a consistent silence. For a comparative analysis of the energy in these two distinct scenarios, the normalized acoustic responses on the two rings are illustrated in Fig. 2D. The peaks with high Q (>3000) in the graphs denote the resonant frequencies of their respective RRs.

Fig. 2. Particle trapping via acoustofluidic RR tweezers.

(A) Bottom schematic diagram shows the simulation and the experimental setup to create the standing acoustic wave inside of the RR and waveguide by two directly opposite input signals p₁ and p₂. The signal will be pumping with signals p₃ and p₄. (B and C) Simulation results show the standing wave in the RR and waveguide created by two directly opposing input signals p₁ and p₂ with frequency f_r1 and f_r2 for the first and second ring, respectively. (D) Blue and red lines show the normalized acoustic pressure inside of the first and second ring, respectively. (E) Simulation illustrates the acoustic field within the waveguide and RR, resulting from the acoustic radiation force within the standing wave field. This force leads to the trapping of particles within the ring, where they remain positioned at locations of maximal signal strength. From (F) to (H), the phase for the signal p₁ will be varied from p₁(φ₀) to p₁(φ₀ + 2∆φ) with step ∆φ, thus the particles inside of the RR will also move within its guideway. Scale bars, 300 μm.

The acoustic waveguide and RR have the capability to generate a standing wave on their surfaces and manipulate particles. To fulfill this purpose, a frequency of f_r1 = 0.903 MHz has been selected for the subsequent simulation and experiment. When operating in the resonant mode, the simulation results (Fig. 2E) align closely with experimental findings. This alignment illustrates the effective capture and arrangement of PDMS particles (50 to 100 μm) into the mode shape of the ring system. The influence of the wave RR affects the acoustic mode inside the waveguide, leading to an asymmetric field in some regions of the waveguide. As a result, particle trapping in the waveguide may aggregate outside of the waveguide at the asymmetric mode location of the waveguide. Furthermore, the proposed design demonstrates the ability to manipulate particles on the ring’s surface by controlling the phase of the input signal. When varying the phase (Fig. 2, F to H), the signal p₁ undergoes continual changes from p₁(φ₀ = −π) to p₁(φ₀ + 2∆φ) in increments of ∆φ = π. The phase of the signal φ and the displacement distance of the particle have the relation of φ = k_rd, where k_r is the wavenumber inside of the RR around 4550 rad•m⁻¹. Here the original phase and displacement are set as φ₀ and d₀, the phase change from φ₀ to φ₀ + ∆φ, where ∆φ = π, the distance of the particle becomes d₁ = d₀ + ∆φ/k_r and d₂ = d₀ + 2∆φ/k_r, with the displacement increment of ∆φ/k_r around 0.69 mm. Correspondingly, particles within the RR move along their designated guideway, showing the precision of the manipulation technique (44). By using this approach, we can capture and manipulate a substantial quantity of particles on the RR’s surface while also maintaining the capabilities for a precise manipulation of even a small number of particles. This level of control extends across a broad size range (from 5 to 100 μm using PDMS particles; Supplementary Text).

Particle mixing in the waveguide and RR

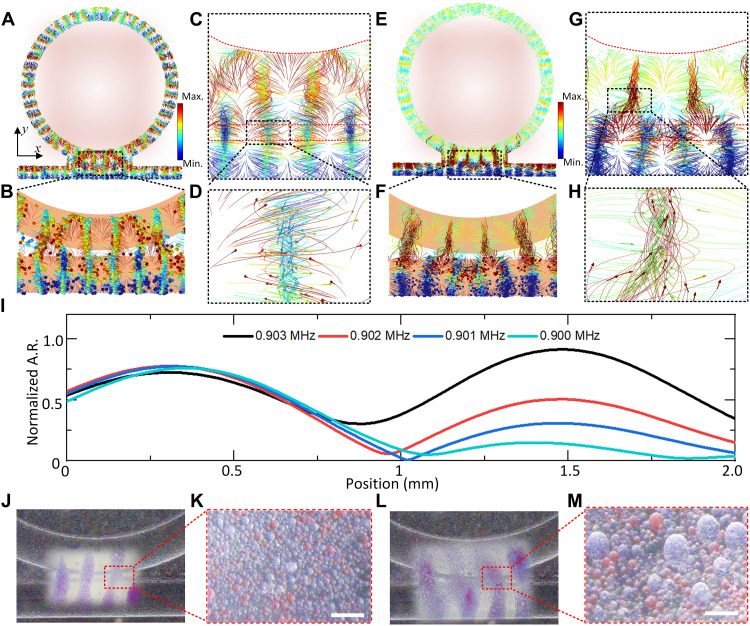
In this section, we leverage the RR effect to address particle mixing for both uniform-sized and polydisperse particles. As shown in Fig. 3 (A and B), two distinctively colored particles are trapped in the waveguide, with red particles arranged on the ring and blue particles on the rectangular waveguide. By manipulating the phase and frequency of the input signal, a shift in the RR shape occurs, resulting in the CW and CCW mixing of the red and blue particles, as illustrated in Fig. 3 (C and D). The particle trajectories indicate that the particles are influenced by the acoustic field and rotate along the center of the motion field. For particles of different sizes, frequency manipulation in a specific direction organizes the smaller red particles near the ring region, while larger blue particles are positioned in the waveguide (Fig. 3, E and F). This orchestrated movement leads to the mixing of particles of two distinct sizes in the interaction region of the ring and waveguide, as observed in Fig. 3 (G and H). During this process, the frequency increases from 0.9 to 0.903 MHz (Fig. 3I). As shown in the movie S1, when the incoming wave is not at the resonant frequency, a standing wave appears in the waveguide, trapping particles there. As the frequency approaches the resonant frequency, a strong standing resonance forms in the ring, trapping particles in the ring. In addition, some particles from the waveguide attach to the RR due to the difference in acoustic radiation force. Once the frequency surpasses the resonance frequency, some particles in the ring lose control and return to the waveguide. The acoustic response in the waveguide (around the 0.5-mm position) remains unchanged, while the acoustic response in the ring increases, causing particles to move from the waveguide into the ring. Further experimental demonstrations for mixing similar-sized particles and different-sized particles are shown in Fig. 3 (J to M), respectively. Consequently, the designed RR-based acoustofluidic tweezers exhibit particle mixing capabilities, offering potential applications in areas such as biosensing and drug delivery.

Fig. 3. Particles mixing between RR and waveguide.

(A and B) Simulation results show a similar size of particle trapping and mixing, with red particles on the ring and blue particles on the waveguide. (C and D) Simulation results show the mixing mechanism and performance. (E and F) Simulation results show the small red particle on the ring and the large blue particle on the waveguide trapping and mixing. (G and H) Simulation results show the mixing mechanism and performance. (I) Normalized acoustic response on the surface of the structure with the cut line near the center boundary of the ring (position, 1.5 mm) and waveguide (position, 0.5 mm). (J) Blue particle and red particles are controlled by the waveguide and RR, and (K) the magnified particle is controlled with mixed particles. (L) Large blue particle and small red particles are controlled by the waveguide and RR, and (M) the magnified particle is controlled with mixed particles. Scale bars, 100 μm.

Signal enhancement in RR with multiwaveguide

The Q factor, a pivotal metric in evaluating RR or whispering gallery mode systems (2–5), serves as a measure of signal quality (7). A higher Q factor signifies superior performance. In the realm of acoustic tweezers, where field intensity is often contingent on pairs of input signals (10), the design of a device with an elevated Q factor becomes imperative for optimizing acoustic tweezer functionality. To address this challenge, a novel configuration featuring multiple waveguides converging on a central RR has been conceptualized, as presented in Fig. 4.

Fig. 4. Three waveguides with one-RR configuration for signal amplification via RR.

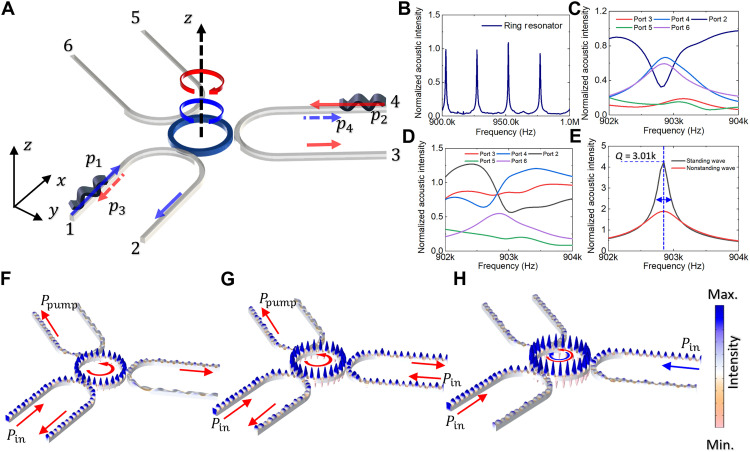
The schematic diagram in (A) shows the simulation and the experimental setup to create the standing acoustic wave inside of the RR and waveguide by two directly opposite input signals p₁ and p₂. The signal will be pumping with signals p₃ and p₄ where a standing wave will be created by CCW and CW modes in the RR. (B) Black lines show the normalized acoustic signal inside the center RR. The transmission in ports 2 to 6 is shown in (C) to (E). (F) Simulation result shows the one input signal p_in with two pumping outputs p_pump with designed three waveguides with one RR, the mode in the RR is CCW mode. (G) Simulation result shows the two same input signals p_in with one pumping output p_pump; the mode in the RR is CCW mode. (H) Simulation result shows the two different input signals that create the CCW mode and CW mode in the RR, respectively.

In the arrangement illustrated in Fig. 4A, signals injected through ports 1 and 4 navigate through ports 2 and 3, respectively. The ensuing propagation of the input signals in both CW and CCW directions within the RR creates a standing wave field in both the ring and a segment of the waveguide. Dynamically varying the input frequency from 0.9 to 1 MHz reveals resonance peaks, displayed in Fig. 4B. Upon exclusive input from port 1, the output mirrors that of ports 4 and 6, owing to the dominance of the CW RRs mode. Similarly, when signals from both ports 1 and 4 are used, the output signals in ports 2 and 3 exhibit a noteworthy resemblance. A detailed exploration of the Q factor, as depicted in Fig. 4E, underscores that the combined strength of the two input signals is twice as potent as that of a sole input signal, achieving a high of 3010. The interplay of acoustic fields is shown in Fig. 4 (F to H), depicting the input signal, double input with the same direction, and double input with opposite directions. As the input to the waveguide increases, the acoustic resonant amplitude within the waveguide intensifies. With each increase in intensity, p_i, inside the waveguide, the addition of an extra waveguide with an acoustic input of Np_i results in the resonant intensity in the RR increasing proportionally to Np_r. This trend is demonstrated in Fig. 4 (F and G), where the system is shown with three waveguides. This supports the assertion that the incorporation of multiple inputs effectively heightens the signal quality within the confines of the RR. The proposed multiwaveguide design thus emerges as a promising avenue for advancing the capabilities of acoustic tweezers, holding great potential for applications in precision manipulation and bioengineering, such as in cell sorting and manipulation.

DISCUSSION

In this work, we have studied the synergy between ring resonance physics and acoustic tweezers for particle manipulation. The creation of acoustofluidic RR-based tweezers with a high Q factor has yielded promising outcomes, addressing the constraints posed by optical tweezers in precise control of micron-sized particles. Through meticulous experimental validation, the RR-based acoustofluidic tweezers have demonstrated their effectiveness and utility, highlighting efficient microparticle manipulation. The strategic establishment of a standing wave pattern along the RR ring path and the incorporation of acoustic lenses have played pivotal roles in achieving successful particle mixing at pressure antinodes.

Looking forward, the implications of this study suggest a transformative trajectory for acoustic tweezers, positioning them as versatile tools for intricate particle manipulation. By introducing high Q resonances, strong wave-particle interactions can be achieved with moderate power input. This ensures that the field is strong only where necessary, thereby minimizing issues such as heat generation, bubble formation, cavitation, transducer overload, and the need for high-performance transducers. The prospect of biosensing applications, coupled with the ability to orchestrate controlled interactions at the cellular level, underscores the profound impact this technology can have in various scientific domains. The safety of living cells is a critical consideration in any acoustic manipulation system (45–48). In our study, the acoustic pressure applied within the acoustic RR was carefully controlled and calibrated to ensure it remained within a safe range for biological samples. The pressure levels at the top of the RR are below the known threshold for cell damage, which is typically around 1 MPa. While high Q factor systems can generate higher energy densities, they also offer the advantage of frequency selectivity, allowing the system to operate at the target frequency with lower voltage input. This feature ensures that, even in potential biomedical applications, the high Q factor system will not harm cells, as the acoustic pressure is regulated by the input source. The system can be fine-tuned to maintain acoustic pressure below the threshold for inducing cell damage, making it safe for future applications involving living cells. As innovation in acoustofluidic RR-based tweezer technology expands, continued investigations and refinements are essential. These efforts will not only serve as a foundation for future advancements in this dynamic field but will also pave the way for the application of acoustofluidic RR-based tweezers in biomedical research, unlocking possibilities in contact-free particle manipulation.

MATERIALS AND METHODS

Fabrication and setup of RR-based acoustofluidic tweezers

The detailed experimental setup is shown in Supplementary Text. Briefly, the acoustic wave was generated by commercial piezo transducers and then focused, by PDMS-focus-lens, into the RR-based acoustofluidic tweezer device. Here, The RR-based acoustofluidic tweezer device functioned by fabricating microscale PDMS structures to achieve wave control and particle manipulation. The platform was placed in a water tank for better wave-conduction performance. A camera (Amsocpe, MU1603-CK) set on a stereomicroscope (Amsocpe, SM-3 T-54S-5 M) was used to record the manipulation process.

RR-based acoustofluidic tweezers device is fabricated with a standard process of curing PDMS on 3D-printed molds. First, all casting molds were made by a 3D printer (Formlab 3B+) with clear resin (V4). After this, they are washed for 15 min in Form Wash, which contains isopropyl alcohol (VWR chemicals), and dried for 15 min in Form Cure. We highlight these two steps because they help clean the surface impurities and peel the PDMS from the mold. Second, the PDMS base (Sylgard 184 Elastomer Kit, USA) and curing agent (Dow Corning, USA) were mixed with a ratio of 10:1. This mixture was then degassed in a vacuum chamber for 30 min to remove bubbles. At last, the liquid PDMS was poured into the 3D-printed mold for the RR-based acoustofluidic tweezers and cured at 65°C for at least 2 hours. Next, the PDMS structure were peeled from the mold and shaped for experimental use. The ultrasound focus lens was fabricated using a process similar to the one described above.

Piezo transducers (STEMINC, SMPL20W15T21R111) with thickness mode vibration were used to generate acoustic waves. Two transducers were placed parallel to both sides of the RR-based acoustofluidic tweezers device. Here, a sinusoidal signal (1 MHz) is generated by a dual-channel function generator (Tektronix, catalog no. AFG3102C) and amplified by power amplifiers (Amplifier Research, catalog no. 30W1000B).

Numerical and analytical simulations

Numerical simulations of RR-based acoustofluidic tweezers are performed using the commercial finite element method (FEM) modeling and analysis software COMSOL Multiphysics. The simulation details can be found in Supplementary Text. Analytical simulations are performed using the Gor’kow potential fields.

Sample preparation

We made PDMS microparticles by emulsifying PDMS in nonionic surfactant. Briefly, the same PDMS base and curing agent we described before are mixed and vacuumed for matrix material. Here, differently colored ink can be mixed with it for visual marking. Then, 1 ml PDMS was pipetted into 50 ml 5% sodium dodecylbenzenesulfonate. Emulsified particles were cured by continuously agitating for 3 hours while heated at 35°C. Particle size was controlled and uniformed by sieving the liquid and then resuspending in deionized water.

Supplementary Materials

The PDF file includes:

Supplementary Text

Figs. S1 to S18

Table S1

Legend for movie S1

Other Supplementary Material for this manuscript includes the following:

Movie S1