Why computed protein folding landscapes are sensitive to the water model

Abstract

We investigate the effect of solvent models on the computed thermodynamics of protein folding. Atomistic folding simulations of a fast-folding mini-protein CLN025 were employed to compare two commonly used explicit solvent water models, TIP3P and TIP4P/Ew, and one implicit solvent (AMBER generalized Born) model. Although all three solvent models correctly identify the same native folded state (RMSD = 1.5 ± 0.1Å relative to the experimental structure), the corresponding free energy landscapes vary drastically between water models: almost an order-of-magnitude difference is seen in the predicted fraction of the unfolded state between the two explicit solvent models, with even larger differences between the implicit and the explicit models. Quantitative arguments are presented for why the sensitivity is expected to hold for other proteins, as well as for other conformational transitions involving large changes in solvent exposed areas such as protein-ligand binding. Comparing protein–solvent and solvent–solvent contributions to the folding energy between different water models, water–water electrostatic interactions are identified as the largest contributor to the differences in the predicted folding energy, which helps explain the strong sensitivity of the folding landscape to subtle details of the water model. For the two explicit solvent models, differences in water model parameters also result in the average number of water molecules surrounding the protein being noticeably different. Water models that poorly reproduce certain bulk properties of liquid water such as self-diffusion are likely to misrepresent water–water interactions – we argue that within a pairwise additive energy function this error can not, in general, be compensated by an adjustment to the solute–solute and solute–solvent parts of the energy.

Introduction

Understanding the details of the protein folding mechanism is critical for many problems, such as designing novel proteins¹ and developing treatments for diseases caused by the misfolding of proteins.² Free energy landscapes from atomistic Molecular Dynamics (MD) simulations are widely used to characterize the folding pathway and quantify the forces that determine the folding process.^3-5 The accuracy of the MD free energy landscape depends upon (a) the ability to sample a fully representative fraction of the conformation space, in proportion to its Boltzmann distribution – the sampling problem,⁶ and (b) the accuracy of the force-field itself, including its solvent component.⁷ Today, even a single MD trajectory can be long enough to often provide a representative sampling,⁸ at least for small, fast folding proteins.⁹ Several methods have been developed to improve conformation space sampling well beyond the single trajectory limits.^10-17 However, the better sampling and longer simulation times have brought to the fore many accuracy problems with modern force-fields.

In particular, several recent studies point towards significant discrepancies in simulation outcomes based on several widely used explicit water models,¹⁸ qualitatively wrong results in many important types of atomistic MD simulations based on such water models,^19,20 and hence the need for improved water models.^7,21 Below are several examples of the significant sensitivity of the simulation outcomes to water model in protein folding, which is the main focus here. The conformational preference of the unfolded GB1 $\beta$-hairpin was found to be sensitive to the water model used (mTIP3P vs. TIP4P with CHARMM22), while the folded state was relatively insensitive to it.^22-24 The thermodynamics of flexible regions of the chignolin $\beta$-hairpin and the EK $\alpha$-helix differed significantly depending on water model.²⁵ It is not completely unexpected that using a water model different from the one used in the original parametrization of the gas-phase force-field may introduce inconsistencies in protein-water interactions: historically, most protein force-field parameters were optimized in conjunction with specific water models. For example, AMBER force fields based on the Cornell 1994 charge scheme were originally parameterized with TIP3P,²⁶ CHARMM22 was parameterized with a modified version of TIP3P (mTIP3P),^27,28 OPLS force fields based on the Jorgensen 1988 scheme were parameterized with TIP4P,²⁹ and GROMOS 53A6 was parameterized with SPC.³⁰ The strength of this specific “coupling” between the force-field and its “preferred” water model is expected to vary significantly between force-fields, e.g. expected to be stronger for CHARMM compared to AMBER. Completely uncoupling the effects of the gas-phase and the solvent parts is difficult. On the other hand, most of the widely used water models have been developed to best reproduce water properties,⁷ agnostic of any specific gas-phase force-field. In practical simulations, different water models are often used with the same gas-phase force-field. It is therefore important to attempt to estimate, and understand, the influence of the water model alone on outcomes of biomolecular simulations.

The aim of this study is to re-assess the influence of the solvent component of force-field, i.e. water model, on protein folding simulations, and, perhaps more importantly, to understand the origin of the sensitivity of the computed landscapes to the choice of the solvent model. Our goal is to first provide a very detailed quantitative analysis based on one protein used extensively in the past, then examine implications of our findings to other proteins, other types of conformational transitions, and for force-field development.

Methods

To study the effect of different water models on the thermodynamics of protein folding, we generated three folding trajectories of a mini-protein CLN025,³¹ each trajectory being at least one microseconds long. CLN025 is a fast-folding 166 atom mini-protein, which is a more stable version of chignolin.³² CLN025 is well characterized and has been frequently used in computational studies of protein folding^9,17,31-37

We employed three commonly used solvent models: the 3-point TIP3P³⁸ water model, the 4-point TIP4P/Ew³⁹ water model, and the OBC (AMBER igb5) variant of the implicit solvent generalized Born (GB) model.⁴⁰

Choice of water models.

A large variety of solvent models is currently available for atomistic simulations.⁷ The performance of these models vary depending on the system and conditions being modeled; none of these models are consistently superior for all systems and conditions.^{19,21,22,24,34,36,37,41-45} The main goal of this work is to understand the general reason for why outcomes of certain simulations, such as prediction of protein folding landscape, are so sensitive to the water model used. We believe that the question is best addressed with the most generic water models that have been widely used for a relatively long time – models that were not optimized to perform best for a specific class of systems. Since our focus here is on the explicit water models, we believe that TIP3P and TIP4P-Ew are good (though not the only possible) choices by the above criteria. Likewise, we chose GB-OBC implicit solvent model, developed in 2004⁴⁰ as an example of a “general-purpose” GB model available in most major modeling packages. Newer GB models, such as GBNeck2, have since become available to improve the realism of protein folding simulations.^35,46 A brief comparison of the two GB models in the context of CLN025 folding landscape is presented in Fig. S1.

Simulation protocol

The experimental structure for CLN025 was protonated using H++, a web server for pK prediction and structure preparation,⁴⁷ at a pH of 6.5. For explicit solvent simulations, the structure was solvated in a truncated octahedral water box extending 10 Å from the solute. Counterions were added to the water box to neutralize the system while approximating a salt concentration of 0.145 M. The tleap utility in Amber was used to add the counterions. The utility addes ions in a 1–4 Å shell around the protein using a Coulombic potential on a grid. The ions are positioned to try and minimize electrostatic energy calculated using a distance-dependent dielectric. The procedure is not guaranteed to globally minimize electrostatic energy. We used ion parameters that were specifically optimized for TIP3P and TIP4P/Ew⁴⁸ respectively. Amber ff10^49,50 gas-phase force field was used for both implicit- and explicit-solvent simulations, unless otherwise noted. This gas-phase force-field has been widely used with all of the water models studied here.

The GPU implementation of Amber 12 MD software package with the SPFP precision model⁵¹ was used for all the MD simulations, unless otherwise stated. The particle mesh Ewald (PME) method⁵² with constant-volume periodic boundary condition was used for explicit-solvent simulations, while for the implicit-solvent simulations we employed OBC variant⁴⁰ (igb5) of the generalized Born (GB) approximation.

The simulation protocol consisted of five stages: minimization, heating, two stages of restrained equilibration, and unrestrained production run at the experimental melting temperature of the protein (340K ). First, the structure was relaxed with 2000 steps of conjugate-gradient energy minimization, with solute atoms restrained to the initial structure by a harmonic restraining potential with the force constant of 5 kcal/mol/Ų. Next, the system was heated to 340 K over 600 ps, with a restraint force constant of 1 kcal/mol/Ų. The system was then equilibrated for 2 ns with a restraint force constant of 0.1 kcal/mol/Ų, followed by another 2 ns with a restraint force constant of 0.01 kcal/mol/Ų. All restraints were removed for the 1 microsecond production stage. The simulation time step was 2 fs. A direct space cutoff of 8 Å was used for all stages of the PME simulations. No cutoff was used for the calculation of GB pairwise interactions, but a “smooth cutoff” of 15 Å was used for the calculation of the effective Born radii.⁵³ Langevin dynamics⁵⁴ with random seed was used for temperature regulation with a collision frequency of $\gamma$ = 0.01 ps⁻¹ – the use of low $\gamma$ in GB was shown to speed-up conformational search relative to protein folding by about an order of magnitude.¹⁷ The random seed ensures that separate simulations follow distinct and independent trajectories, as shown in Figure S3. The Shake algorithm⁵⁵ was used to constrain covalently bound hydrogen atoms. For the analyses presented below, snapshots from the MD trajectory were saved every 10 ps. Default values were used for all other simulation parameters.

Calculation of the free energy landscape

Conformational space was partitioned into bins of 0.2 Å RMSD relative to the experimental structure. The free energy for the conformations represented by each of these bins was then calculated as $\Delta G=-kT\text{ln}(prob(x))$, where $k$ is the Boltzmann constant, $T$ is the temperature, and $prob(x)$ is the probability of conformations in bin $x$ for each simulation.

We follow Ref¹⁷ and define the folded and unfolded states as structures with backbone RMSD values of < 1.5 Å and > 4.5 Å, respectively, consistent with the location of the folded and unfolded basins of the free energy landscape, Figure 1. The basin between these two states represents a compact misfolded state,³⁴ not seen in experiment.³¹

Figure 1:

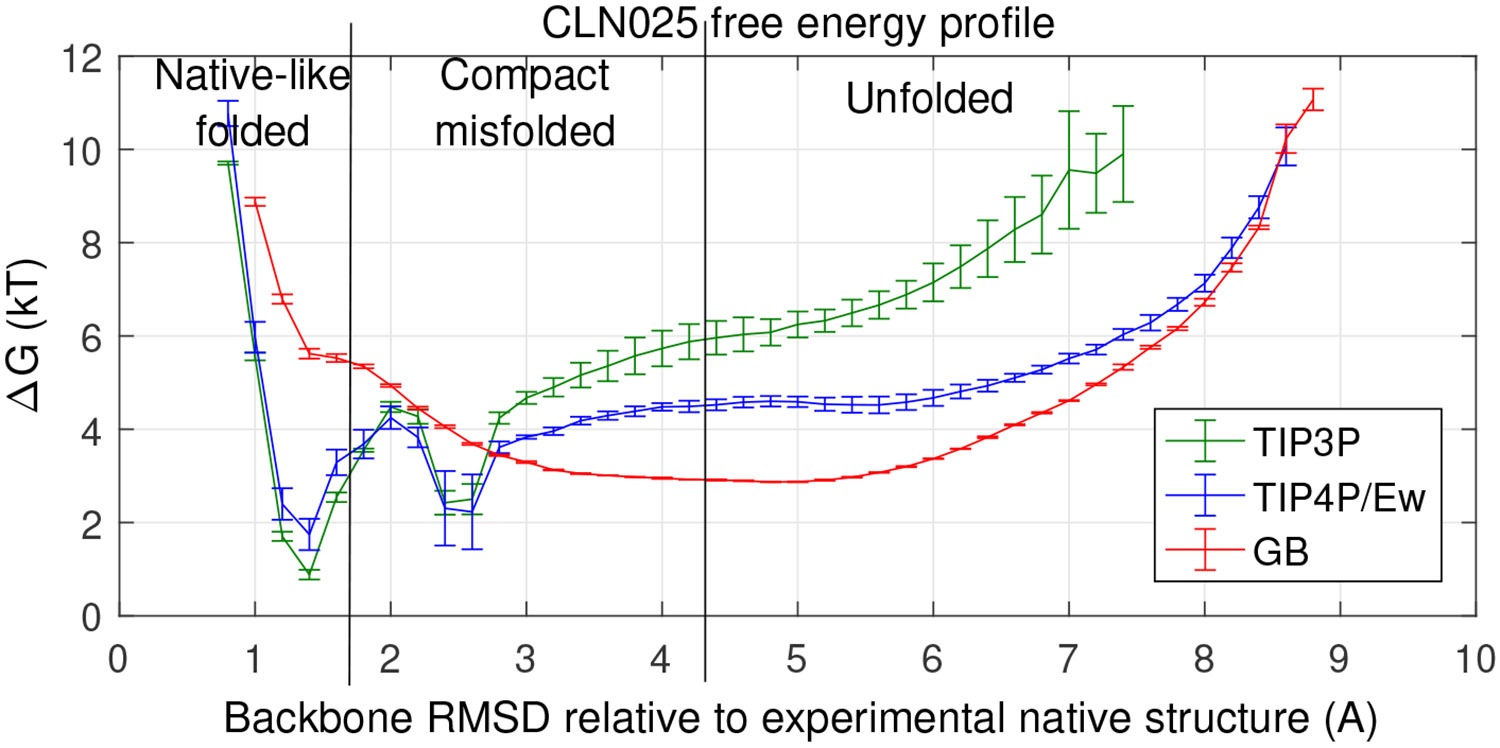
Computed folding free energy profiles of CLN025 mini-protein at its experimental melting temperature (340K) for three different solvent models shown in the inset. Error bars represent standard error of the mean from three sets of > 1 μs simulations for each solvent model. Connecting lines shown to guide the eye.

Energy decomposition protocol

To decompose the contribution of individual energy components we follow a protocol similar to the one used by Fenley et. al.⁵⁶ The protocol used here consists of four steps:

1. Select a compact and an extended state structure, loosely representative of folded and unfolded conformations

2. Generate two ensembles of solvent conformations, one each around the representative folded and unfolded protein conformations. To generate these two solvent ensembles we run MD simulations with the protein restrained to the representative compact and extended states.

3. Remove appropriate solute/solvent components from the generated ensembles to partition them into the four configurations shown in Figure 2. The partitioning is used to decompose interaction energies into protein-protein, solvent-solvent, water-water, and protein-solvent interactions, as described below

4. Calculate the energy components for each of the configurations, for each of the snapshots along the (restrained) MD trajectories.

Figure 2:

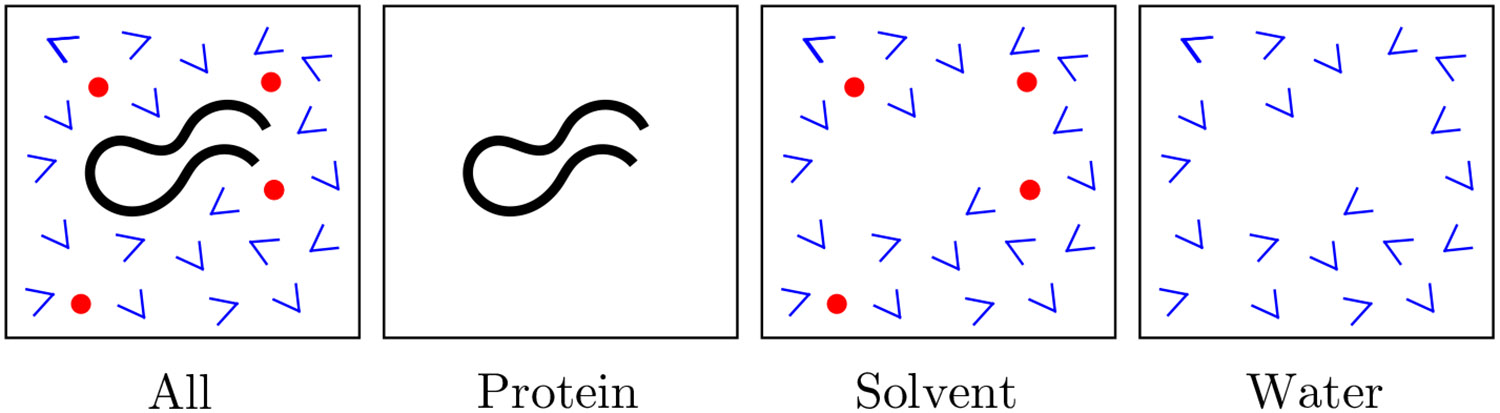
Partitioning of the snapshots from the restrained MD simulation. The protein is shown in black, water in blue, and ions in red.

Following is a more detailed description.

(1) For the compact and extended states, two snapshots were randomly selected from the unrestrained simulations described above. One representing a compact state with backbone RMSD = 1.5 Å relative to the experimental structure, and the other representing an extended state with backbone RMSD = 7.5 Å relative to the experimental structure. These structures were used as proxies for the folded and unfolded states, respectively, when calculating folding energy. (2) The two structures were then solvated using each of the two explicit solvent water models. To ensure that energies calculated from these structures in the presence of solvent could be compared on the same footing, we used the same box size (octahedral box with edge length of 49.48 Å) and the same number of water molecules (2482), for both structures and both water model used. This was achieved by first creating a pdb file for the two representative structures, including the solvent atoms. The number of water molecules in the two representative pdb file were made the same by removing excess water molecules from the pdb file with the larger number of water molecules. The Hydrogen atoms associated with all the water molecules were also removed. The topology/parameter and coordinate files for each of the water models, were then generated from these pdb files, using Amber’s leap software tool.⁵⁷ We then ran approximately 150 ns simulations of these two structures, with 1 kcal/mol/Ų restraints applied to the protein (restrained simulation). The restrained simulation provides reasonable sampling of water configurations while allowing small conformational changes in the protein to avoid any potential bias towards any one water model. (3) Snapshots from the restrained simulation were taken every 10 ps. Each snapshot was partitioned into the four configurations shown in Figure 2 using the cpptraj software in AmberTools.⁵⁸ (4) A single point energy calculation was performed on each configuration from each snapshot, to calculate the long-range electrostatic, van der Waals, and bonding energy terms for each configuration. For the purpose of our analysis the energy contribution of the restraints used in the simulations were included in the bonding energy term. The energy terms were then averaged over all the snapshots, excluding the first 10 ns.

Let $E_l^u$ represent the contribution of energy components, where $u$ represents the compact or extended state, and $l$ represents the type of interaction, i.e. protein-protein, solvent-solvent, protein-solvent, etc. The values for $E$, $E_{prot-prot}$, $E_{solv-solv}$, and $E_{wat-wat}$ correspond to the energy calculation for the four configurations in Figure 2, respectively. The values for the other components are calculated as follows:

$$E_{prot-solv}=E-E_{prot-prot}-E_{solv-solv}$$ (1)

$$E_{ion-solv}=E_{solv-solv}-E_{wat-wat}$$ (2)

The net folding energy is then calculated as $\Delta E=E^{compact}-E^{extended}$. Throughout this work, we use the same definition for “$\Delta$” of any quantity of interest – to represent the change associated with the conformational transition e.g. protein folding.

Estimation of solvent free energy components

The solvation free energy $G_{solvation}$ of a given protein conformation can be partitioned into the solute-solute and protein-solvent contributions as $G_{solvation}\approx G_{solv-solv}+E_{prot-solv}$, where $G_{solv-solv}$ includes both the change in the energy of intrasolvent interactions upon solvation as well as the associated changes in solvent entropy due to solvent the rearrangements. Here and in what follows we ignore the difference between Gibbs and Helmholtz free energy for the processes of interest. For the protein folding process, $\Delta G_{solvation}=G_{solvation}(folded)-G_{solvation}(unfolded)$, and similarly for its components. Thus,

$$\Delta G_{solv-solv}\approx \Delta G_{solvation}-\Delta E_{prot-solv}$$ (3)

Within the linear response approximation⁵⁹ $\Delta E_{prot-solv}\approx 2\Delta G_{solvation}$. From this, and from Eq. 3 it follows that

$$\Delta G_{solv-solv}\approx -\frac{1}{2}\Delta E_{prot-solv}$$ (4)

and

$$\Delta G_{solv-solv}\approx -\Delta G_{solvation}$$ (5)

Within the implicit solvent model used in this work, $G_{solvation}$ can be easily estimated for any representative conformation. The explicit solvent values of $\Delta G_{solv-solv}$ listed in Table 2 are estimated via Eq. 4 from $\Delta E_{prot-solv}$ values in Table 3. The GB $\Delta G_{solv-solv}$ in Table 2 is obtained from the calculated $G_{solvation}$ and Eq. 5.

Table 2:

Estimated contribution from solvent-solvent interactions to folding free energy $\Delta G$ (kcal/mol) of CLN025 mini-protein at its melting temperature. See Methods for details of the calculation.

Free energy (kcal/mol)	TIP3P	TIP4P/Ew	GB
$\Delta G$ (based on the distribution in Table 1)	−2.2 ± 0.1	−0.67 ± 0.3	+2.0 ± 0.1
$\Delta G_{solv-solv}$	−103.2 ± 1.2	−108.2 ± 1.5	−95 ± 0.1

Table 3:

Decomposition of the average energy difference between randomly selected compact and extended structures of CLN025 mini-protein. $\Delta E=E_{compact}-E_{extended}$ (kcal/mol). Standard error of the mean is shown next to each of the values. Here $\Delta \Delta E=\Delta E(TIP4P∕Ew)-\Delta E(TIP3P)$. The small difference, < 1 kcal/mol, in $\Delta E$ for protein-protein interactions is the consequence of the finite strength of positional restraints used in the simulation, and is not relevant to the following discussion.

Interaction	$\Delta E$ (kcal/mol)
	TIP3P	TIP4P/Ew	$\Delta \Delta E$
Solvent-Solvent
Water-Water	−68.9 ± 1.3	−35.2 ± 1.5	+33.7 ± 2.0
Ion-Solvent	−18.8 ± 1.5	−38.8 ± 1.8	−20.0 ± 2.3
Protein-Solvent	+206.5 ± 1.2	+216.5 ± 1.5	+ 10.0 ± 1.9
Protein-Protein	−120.1 ± 0.1	−119.7 ± 0.1	+0.4 ± 0.1
Total	−1.3 ± 0.9	+22.8 ± +1.1	+24.1 ± 1.4

Ensembles of protein-A and apomyoglobin

The generation of the conformational ensembles of protein-A (PDB ID: 1BDD, residues 10 through 55) are described in detail in Ref.⁴⁰ Briefly, the native state ensemble is represented by 50 consecutive snapshots from an implicit solvent simulation at 300K; the unfolded state, also represented by 50 snapshots, was prepared by heating the protein to 450 K also in the implicit solvent. The protonation state of the protein corresponds to neutral pH. The solvation energy of each snapshot is estimated using standard numerical PB methodology as detailed in Ref.⁴⁰

The conformational ensembles of apomyoglobin is described in Ref.⁶⁰ Briefly, both states are obtained from an explicit solvent trajectory that describes acid unfolding of amomyo-globin an pH=2. The native state ensemble is represented by 50 snapshots from the very beginning of the trajectory, while the unfolded sate corresponds to the end. The charge state of each snapshot was reset to correspond to neutral pH. The solvation energy of each snapshot is estimated using standard numerical PB methodology as detailed in Ref.⁶⁰ The effective Born radii are estimated using “GB-neck” flavor of the GB model.⁶¹ The reported 15 % increase of the effective Born radii in going from the near-native to the unfolded state is an average over all the protein atoms and the snapshots of the corresponding state.

Results and Discussion

In what follows we study folding landscape of a mini-protein CLN025, with the goal of understanding why subtle changes in the solvent model have such a profound effect on the folding thermodynamics. We follow several previous computational works^9,17,31-36 and choose CLN025 because it is arguably the smallest protein that exhibits simple two-state folding at time scales of microseconds, currently accessible to fully atomistic MD simulations. To observe multiple folding-refolding transitions and to have both states well represented, three one microsecond long simulations for each of the three water models were performed at the experimental melting temperature of the protein.³¹ The use of random seeds for Langevin dynamics ensures distinct and independent trajectories as shown in Fig. S3. The relatively small standard errors (average of 0.04 kcal/mol for GB, 0.35 kcal/mol for TIP3P, and 0.20 kcal/mol for TIP4P/Ew) suggest that the simulations are long enough to adequately sample conformation space, producing a free energy landscape that can be used to reliably estimate free energy.

All three water models can identify the native-like conformation

Protein native states have been shown to be robust across a range of solvent conditions.^62-64 So, it is not surprising that the native state for CLN025 is robust across the solvent models considered here, i.e. all three solvent models correctly identify the near native folded state, Figure 1. The lowest free energy state is at root mean squared difference (RMSD) = 1.4 Å, relative to the crystal structure. Note that the free energy for structures with RMSD < 1.4 Å is higher even though these structures are more similar to the crystal structure than the structures with RMSD = 1.4 Å. Our explanation is as follows. The RMSD is calculated relative to the compact native state determined by X-ray crystallography. Generally, one can still not expect a modern force-field to reproduce the exact X-ray reference in most cases, for at least two reasons. First, force-fields are imperfect. Second, crystal structures may not exactly represent the relaxed conformation in solution. In our simulations, the protein conformations are sampled well down to about 0.8 Å RMSD from the reference (see Fig. S4), which suggests that the sharp rise in the free energy to the left of the minimum at 1.4 Å , Figure 1, is most likely due to a combination of these issues, rather than to a drastic lack of sampling of the near-native conformations. In the case of the implicit solvent simulation with the specific GB model used, the near-native folded state of CLN025 is not as distinctly identifiable from the folding landscape as it is in the explicit solvent simulations (shoulder vs. distinct minimum). However, in the case of CLN025, its near-native folded state can be easily predicted in the implicit solvent as the lowest potential energy conformation,¹⁷ Fig. S1. The key point is that the near-native compact structures are similar for all the water models used, and their deviation from the correct native state is reasonably small.

Folding landscapes are very sensitive to the water model

In contract to the native state, the free energy landscapes, Figure 1, show clear differences between the solvent models considered here. These free energy differences correspond to the significantly different distributions of folded vs. unfolded structures, as summarized in Table 1. (Note that it is the difference between the effects of the solvent models that is of interest to us here, rather than the over-all agreement with experiment, which also depends strongly on the gas-phase part of the total energy.)

Table 1:

Distribution of folded, misfolded and unfolded states for the three water models and from experiment.³¹ Representative structures from these states are shown in Fig. 3. Standard error of the mean is shown alongside calculated values.

	% Native-like	% Compact misfolded	% Unfolded
TIP3P	72.0 ± 6.8	26.3 ± 6.3	1.7 ± 0.5
TIP4P/Ew	37.8 ± 12.4	49.6 ± 14.0	12.6 ± 1.6
GB	1.7 ± 0.1	47.9 ± 0.2	50.4 ± 0.3
Experiment	50	0	50

Consistent with findings from several other studies,^22-25 we conclude that the choice of water model has a significant effect on the predicted protein thermodynamics.

While the difference in the landscape between two very different types of water models, implicit and explicit, may not be completely unexpected, the large differences between the landscape obtained with two commonly used, very similar water models of the same type is puzzling. To understand its origins, we begin our analysis with singling out the solvent-solvent interaction component of the total $\Delta G$ of folding, for each type of water model used here, see Methods for details. In principle, such a decomposition should be based on reasonably large ensembles of conformations representing folded and unfolded states of the protein; however, that would be computationally prohibitive for the explicit solvent. To make computations feasible, in what follows we approximate the folded and unfolded ensembles by two randomly selected structures from the simulation, loosely representative of the folded and unfolded states respectively, Fig. 3.

Figure 3:

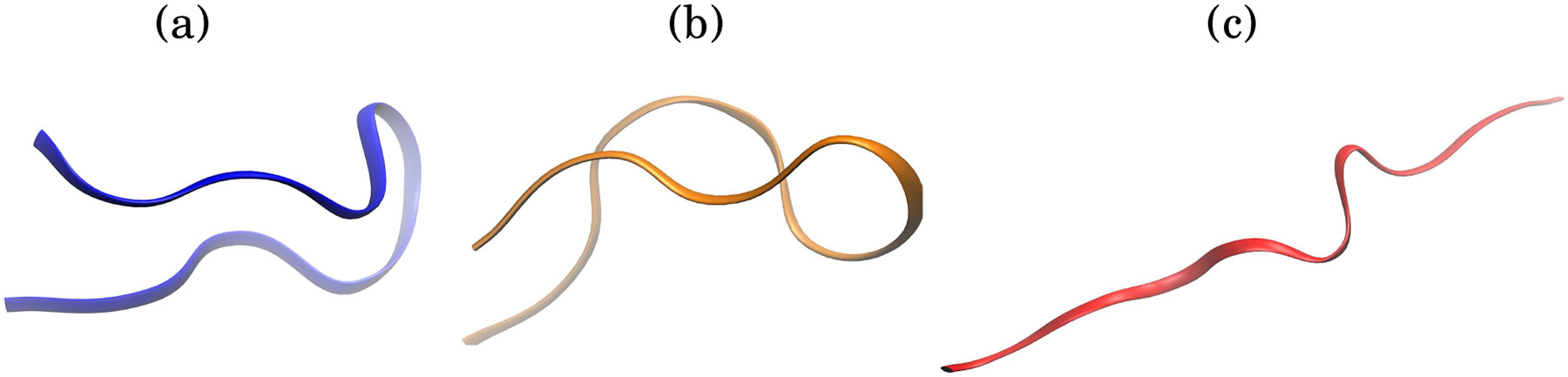
Representative structures from simulation of CLN025. (a) Compact native-like structure with RMSD = 1.5 Å. (b) Compact mis-folded structure with RMSD = 2.5 Å. (c) Extended conformation of CLN025 with RMSD = 7.3 Å. The RMSD is computed relative to the experimental structure. The representative compact native-like and extended conformations were used for the analysis presented here.

The resulting estimates, for both the explicit and implicit solvents studied here, are shown in Table 2. The total $\Delta G$ estimates in this table quantify the qualitative conclusion already made from Figure 1 – that the computed folding free energy is very sensitive to the solvent model. Note that the experimental free energy of CLN025 is near 1 kcal/mol at room temperature, while predictions by the different water models differ by as much as 4 kcal/mol; even for the two explicit solvent models, the difference is relatively large, almost 2 kcal/mol. Perhaps unexpectedly, the solvent-solvent contributions differ substantially between the solvent models, Table 2: 5 kcal/mol for the two explicit solvents, and 13 kcal/mol when the explicit and implicit solvents are compared. The immediate conclusion is that the effect of the water model, as quantified by the difference between $\Delta G_{solv-solv}$ estimates from different solvent models, is larger than stability of the protein. The conclusion is robust to the choice of representative snapshots or the specifics of the approach used to estimate $\Delta G_{solv-solv}$, see the SI. Thus, our first conclusion is that solvent-solvent interactions contribute significantly to the sensitivity of computed folding landscapes to solvent model. Therefore, accurate treatment of solvent, in of itself, is important for correctly reproducing experimental protein thermodynamics by atomistic MD simulations.

To further investigate the role of solvent-solvent interactions in the sensitivity of folding landscapes, we perform a different, and a more detailed and quantitative analysis of the folding energy breakdown, now focusing on the contributions to the folding energy (enthalpy).

Water-water electrostatics is the largest contributor to differences in folding energy

To compare the contribution of the individual energy components to the folding energy (enthalpy) for the two explicit solvent models, we randomly selected two representative folded and extended state structures from the simulation, (Fig. 3). The following analysis shows that the largest contribution to the difference in folding energy between the two explicit solvent models, is from water-water electrostatic interactions. These results are robust to the use of alternate folded and extended state structures. Figures S6 and S7 show that for two alternate sets of folded and extended state structures, water-water electrostatic energy is the largest contributor to the difference in folding enthalpy between the TIP3P and TIP4P/Ew water models.

Folding energies $\Delta E$ were estimated from fully solvated, restrained MD simulations of these two structures as described in Methods. We also obtained a breakdown of $\Delta E$ by individual contributions from solvent-solvent, protein-solvent and (gas-phase) protein-protein interactions, Table 3. For each of these interactions, Figure 4 shows a further break down of contributions to $\Delta E$ by type of interaction, i.e. electrostatics, van der Waals and bonded.

Figure 4:

Decomposition of average energy difference $\Delta E=E_{compact}-E_{extended}$ (kcal/mol), between the compact and extended states respectively of CLN025 mini-protein. Standard error of the mean range from 0.1 to 2.0 kcal/mol, making them too small to be visible in the scale of this figure. Therefore, the standard error values are listed in Table S4. The standard errors for the total values (d) are included in Table 3 as well

As with the free energy landscape, we see clear differences between the effects of the two explicit water models, Table 3. The total potential energy (enthalpy) favors the extended state in the case of TIP4P/Ew ($\Delta E=+23$ kcal/mol), while favoring the compact state in the case of TIP3P ($\Delta E=-1$ kcal/mol). It is worth noting that the experimentally measured folding enthalpy of this protein is −11.3 kcal/mol.³¹ Although the value(s) of $\Delta E$ calculated by our procedure for the two individual snapshots expectedly differ from the experimental folding enthalpy, which characterizes conformational ensembles, it is reassuring that the experimental and calculated values are of the same order of magnitude, especially considering the magnitude of the energies of the individual computed energy components (> 10⁴ kcal/mol) that are subtracted to obtain the $\Delta E$ estimate.

Again, the unexpected result is that the largest contribution to differences in computed $\Delta E$ of folding, as a function of the solvent used, comes from water-water interactions (Table 3, Figure 4(d)). Further breakdown shows that the difference is primarily due to long-range electrostatics(Figure 4(a)), and to a lesser extent to van der Waals interactions (Figure 4(b)). In this case, bonded interaction have little effect on folding energy (Figure 4(c)). The dominance of the electrostatic contribution is, perhaps, not so unexpected given the critical importance of electrostatic interactions for water structure and properties in general.^18,44,65-67 Protein-solvent electrostatic interactions tend to destabilize the compact conformation, Figure 4(a), while the other electrostatic interactions tend to stabilize the compact conformation; which is what we expect to see since protein-protein hydrogen bonds stabilize the compact structure and protein-solvent hydrogen bonds stabilize the extended structure.

The contribution of ion-solvent interactions to $\Delta E$ of folding also varies by water model, although to a smaller extent ($\Delta \Delta E_{ion-solv}=\sim 20\text{kcal}∕\text{mol}$) compared to water-water interactions ($\Delta \Delta E_{wat-wat}=\sim 30\text{kcal}∕\text{mol}$), for the compact and extended structures considered here (Table 3). Since the largest contribution to this difference is electrostatic in nature (Figure 4), the differences in charge distribution between the water models are most likely responsible for the corresponding differences in ion-solvent interaction energy.

The magnitude of the contribution of protein-solvent interactions to $\Delta E$ also varies by water model, although to a smaller extent ($\Delta \Delta E_{prot-solv}=\sim 10\text{kcal}∕\text{mol}$) than both water-water ($\Delta \Delta E_{wat-wat}=\sim 30\text{kcal}∕\text{mol}$) and ion-solvent ($\Delta \Delta E_{ion-solv}=\sim 20\text{kcal}∕\text{mol}$) interactions (Table 3). Again, the differences are primarily electrostatic in nature (Figure 4).

Analysis of additional randomly selected protein structures from the two “ends” of CLN025 folding landscape, Figure 1, also shows similar trends with significant differences in $\Delta E$ for the two water models, primarily due to water-water electrostatic interactions (see SI).

Why the thermodynamics of protein folding is sensitive to the solvent model

The key question at this point is why protein folding free energy, and hence the folding landscape, can be expected to be sensitive to details of the solvent model used, in general?

The gist of our argument, presented in detail below, is as follows. First, we show that $\Delta G_{solv-solv}$ contributes directly to the $\Delta G$ of folding, on the same footing with protein-protein interactions. Next, we demonstrate that, for the folding process in general, $\Delta G_{solv-solv}$ is large (see Fig. 5 ); more specifically, $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \gg 1$. Based on the above we argue that differences between water models, which translate into differences between computed $\Delta G_{solv-solv}$, will have a noticeable effect on the folding free energy.

Figure 5:

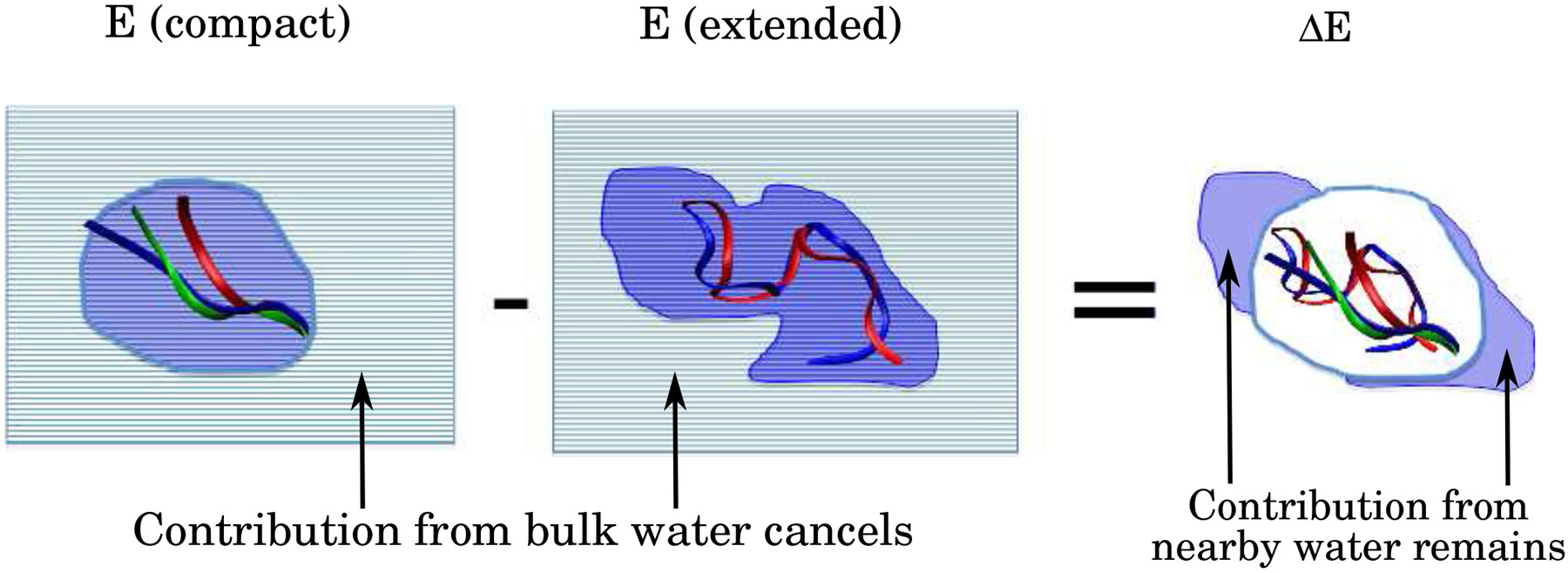
Contributions of solvent-solvent interactions to thermodynamics of conformational transitions, e.g. protein folding, that involve large changes in solvent exposure. Interaction with the solute affects water molecules, and their interactions, in the vicinity of the solute. The contribution of bulk water or water near solute regions that do not change solvent exposure upon the transition (grey) cancels or nearly cancels in the free energy of the transition. In contrast, the contribution from water molecules near solute regions of significantly altered solvent exposure (blue) remains, and depends on the water model.

We begin by deriving an equation that explicitly connects $\Delta G$ of folding with $\Delta G_{solv-solv}$. We start with $\Delta G=\Delta H-T\Delta S$, in which solvent effects are present implicitly in both terms, and approximate $\Delta H-T\Delta S\approx \Delta E_{prot-prot}+\Delta G_{solvation}-{T\Delta S}_{prot}^{conf}$ where $\Delta G_{solvation}$ is the change in the solvation free energy $G_{solvation}$ of the protein during the folding process, and ${\Delta S}_{prot}^{conf}$ is the loss of the protein’s configurational entropy. Note that within this decomposition, ⁶⁰ all of the solvent effects, including the entropy of the solute-induced solvent rearrangement, and the screening of the protein-protein electrostatic interactions, are encoded in $G_{solvation}$, as is standard within the implicit solvent theory.^53,68,69 Within the linear response approximation (Eq. 5) $\Delta G_{solvation}\approx -\Delta G_{solv-solv}$, leading to:

$$\Delta G\approx \Delta E_{prot-prot}-\Delta G_{solv-solv}-T\Delta S_{prot}^{conf}$$ (6)

The importance of Eq. 6 for our argument is that it shows explicitly that the entire $\Delta G_{solv-solv}$, and not just a fraction of it, contributes directly to the folding free energy, unopposed by any other contribution from the solvent. (Within the linear response we can make a similar argument for the importance of $\Delta E_{prot-solv}$; we chose to focus on $\Delta G_{solv-solv}$ to emphasize the pure solvent contribution, which is not obvious). A quick test for CLN025 below confirms that for the purpose of comparing magnitudes of the individual contributions to the folding free energy, the above equation is a decent approximation to $\Delta G$ of folding. Using the values of $\Delta E_{prot-prot}$ and $\Delta G_{solv-solv}$ from Tables 3 and 2 respectively, and $T\Delta S_{prot}\approx -13$ kcal/mol at 300K based on a 4.2 cal/mol-K⁻¹ estimate of per residue conformational entropy loss upon folding,⁷⁰ we arrive at $\Delta G\approx -120+103+13=-4$ kcal/mol, which is of the same order as the experimental folding free energy (~ 1 kcal/mol) of CLN025 at room temperature.

To see qualitatively why $\mid \Delta G_{solv-solv}\mid$ in Eq. 6 is expected to be large in general, note that the distribution, and, hence, interactions of water molecules near the protein are affected significantly by the conformational changes during protein folding.^71,72 In the CLN025 example, 20 more water molecules are found in the immediate vicinity (with 3 Š) of the protein in the extended state compared to the compact, Figure 6. The difference in the distribution of water molecules can also be quantified by the solvent accessible surface area (SASA). The SASA is 1018 Ų for the folded state and 1389 Ų for the unfolded state. Thus, the resulting solvent-solvent contributions to the total energy of the system do not cancel out when the interactions corresponding to the total $\Delta G$ from the unfolded state are subtracted from those for the folded state, Figure 5. For any two-state transition that involves large changes in solvent exposure, the volume of the solvent where there is no cancellation of solvent-solvent contributions from the two very different states of compaction is expected to be large, leading to large $\Delta G_{solv-solv}$ or $\Delta E_{solv-solv}$. Indeed, as we have already seen for our CLN025 example, solvent-solvent interactions contribute significantly to the folding free energy of our example protein. In fact, for this protein, one can verify explicitly that indeed $\mid \frac{\Delta E_{solv-solv}}{\Delta G}\mid \sim 100$, $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \sim 100$ at room temperature, which implies that even small changes in solvent parameters affecting the magnitude of the solvent-solvent interactions can have a large effect on the relatively much smaller folding free energy $\Delta G$. Below we present a quantitative argument for why $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \gg 1$ is a general result for this type of conformational transition.

Figure 6:

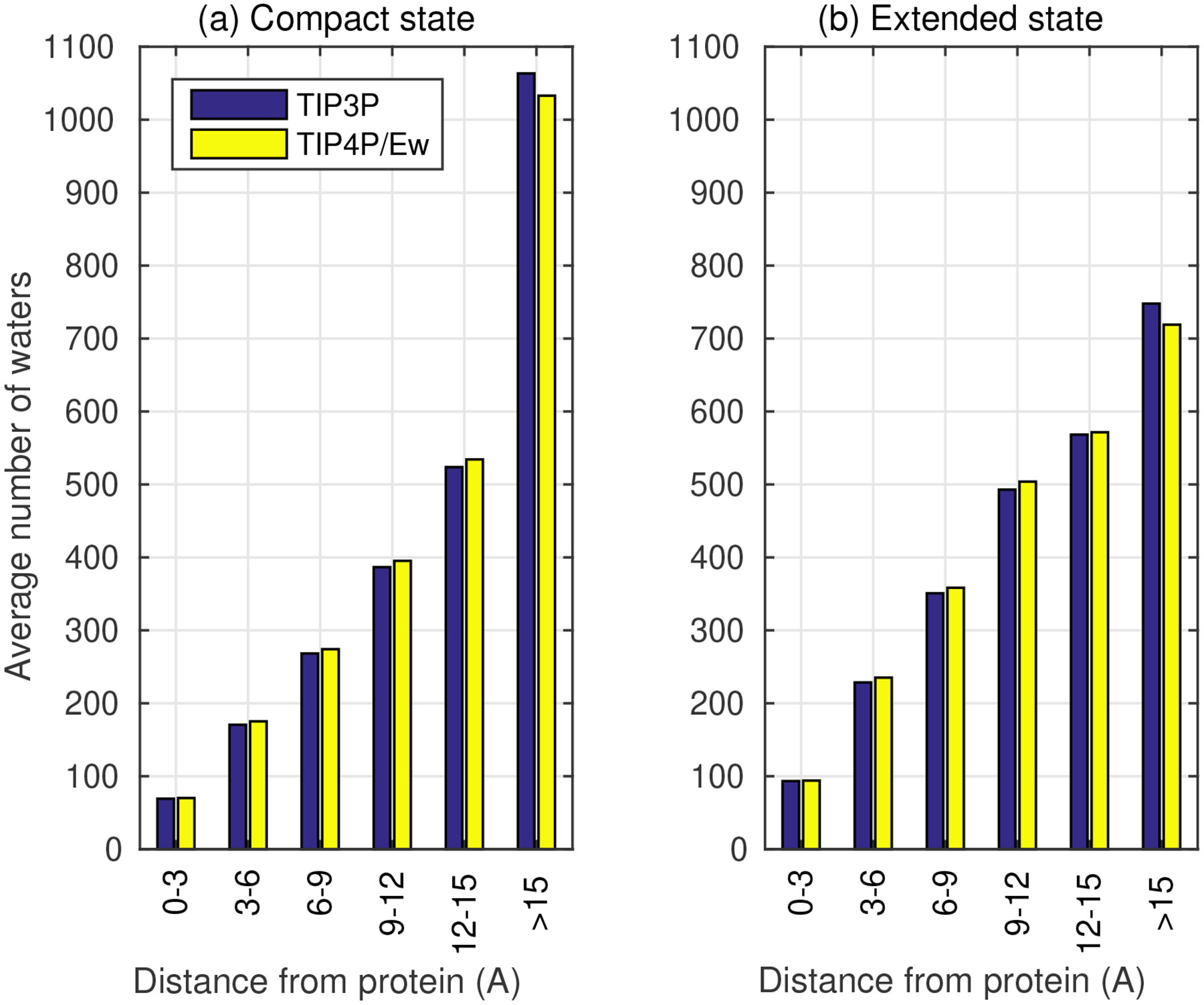
Average number of water molecules surrounding CLN025 protein in the simulation box for (a) compact native-like conformation, and (b) extended conformation. The total number of water molecules in the box is the same for both water models and protein conformations.

First, we determine how $\Delta G_{solv-solv}$ scales with the number of residues in the protein $N$, based on the known solvation energies of nonzwitterionic single amino acid side chain mimics.⁴¹ For the sixteen net neutral side-chains, the corresponding $G_{solvation}$ ranges from about −10 to −30 kcal/mol, and from −60 to −80 kcal/mol for the four charged ones. Let us assume an averaged value of $G_{solvation}\sim -30$ kcal/mol per group, and make a conservative assumption that upon protein folding the average degree of an amino-acid desolvation increases by ~ 15 % (see Methods). Thus, for a protein of $N$ residues the change of solvation energy upon folding $\Delta G_{solvation}\sim -4.5\ast N$ kcal/mol, leading, via Eq. 5 to

$$\Delta G_{solv-solv}\sim 4.5\ast N[kcal∕mol]$$ (7)

Now we note that for small and medium-size single domain proteins, the folding free energy can be approximated⁷³ as being directly proportional to the number of residues:

$$\Delta G\sim -0.1\ast N[kcal∕mol],$$ (8)

where we choose the proportionality constant to approximate $\Delta G\sim 1$ kcal/mol for the 10-residue CLN025.

From the above, and Eq 7, we conclude that, for the protein folding process in general,

$$\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \sim 45.$$ (9)

We test Eqs. 7, 8 and 9 for three dissimilar proteins for which the appropriate data is readily available to us from this or previously published work. For our CLN025 example, the very approximate estimate of $\Delta G_{solv-solv}$ based on Eq. 7 is only about 50 % off the presumably more accurate atomistic results shown in Table 2. In fact, for TIP4P/Ew water model $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \sim 45$. For a much larger, $N=153$ residue apomyoglobin at neutral pH, Eq. 7 yields $\Delta G_{solv-solv}\sim -700$ kcal/mol, which is not too far from a −1000 kcal/mol estimate based on a simulated atomistic unfolding trajectory, see Methods. For 46-residue, 3-helix domain of protein A, Eq. 7 gives $\Delta G_{solv-solv}\sim 200$ kcal/mol, compared to −143 kcal/mol based on an actual simulated trajectory. For apomyoglobin and protein-A, experimental $\Delta G$ of folding are −13 and −5 kcal/mol respectively, compared to −15.3 and −4.6 kcal/mol from Eq. 8. Using experimental $\Delta G$ and atomistic $\Delta G_{solv-solv}$ values for these two proteins leads to $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \sim 50$ and $\mid \frac{\Delta G_{solv-solv}}{\Delta G}\mid \sim 40$ respectively, which are close to the general result of Eq. 9. Thus, indeed, the solvent-solvent contribution to the folding free energy is much larger than the quantity itself.

The relatively large difference between water models in their contribution to folding free energy is ultimately due to the cumulative effect of the subtle differences^74,75 in the parameters of the different water models. For example, TIP3P has a much smaller quadrupole moment (1.72DÅ) compared with that of TIP4P/Ew (2.16DÅ).⁷⁵ The quadrupole moment of water is known to have a strong effect on the directionality of water-water interactions as well as the liquid water structure seen in simulations.⁶⁵ Due to lack of correct multiple moments, water-water interactions are much weaker in TIP3P resulting in a smaller heat of vaporization, a faster self-diffusion (250% error relative to experimental value), and a larger dielectric environment for TIP3P compared with TIP4P/Ew.⁷⁵ Such differences in water model parameters (e.g. multipole moments) and bulk properties manifest themselves in differences in properties of water distribution around the protein. For example, Figure 6 shows the effect of the water model on the distribution of water around CLN025 protein: the use of TIP4P/Ew instead of TIP3P results in 1 to 10 more water molecules in each of the 3Å thick water shells surrounding the protein. Note that the effect for the 2nd and 3rd shells is amplified by the increase in the shell volume. This is consistent with a previous finding¹⁸ showing that the average number of hydrogen bonds formed between solute and solvent in simulation of protein-ligand complexes is significantly higher for TIP4P/Ew compared with TIP3P, leading to a larger electrostatic solvation free energy when TIP4P/Ew is used.

The above arguments are not specific to protein folding: other transitions characterized by significant changes in solvent exposure between the solute states will have the same property with respect to significance of the solvent-solvent contribution to the over-all thermodynamics of the process. This observation likely explains the recently noted sensitivity^42,75 of protein-ligand binding to the water model used. In fact, the similarity of the underlying physics between protein folding and protein ligand binding (e.g. with the total number of residues replaced by the number of residues at the binding interface) suggests that even our quantitative estimate in Eq. 9 may not be too far off the mark for protein-ligand binding. The qualitative conclusion of strong sensitivity of the transition to water model may also be true for some other types of transitions which do not involve large differences of solvent exposure: for example, a significant charge transfer within the protein can have a large effect on $\Delta G_{solv-solv}$. In particular, protonation state change of a single amino-acid may result is tens of kcal/mol change of the solvation free energy,⁷⁶ leading to equally large $\mid \Delta G_{solv-solv}\mid$ that contributes to the $\Delta G$ of the transition.

Implications to force-field development

Most current force-fields use additive potentials⁷⁷ in which the total energy $E(\overrightarrow{p},\overrightarrow{w})$ of the solvated system is given by the sum of contributions from the solute-solute, solute-solvent and solvent-solvent degrees of freedom $\overrightarrow{p}$ and $\overrightarrow{w}$

$$E=E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})+E_{solv-solv}(\overrightarrow{w}).$$ (10)

Since the solute dynamics can be completely determined from its PMF⁶⁹

$$W(\overrightarrow{p})=-kTln\frac{{\sum }_{\overrightarrow{w}}exp(-[E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})+E_{solv-solv}(\overrightarrow{w})]∕kT)}{{\sum }_{\overrightarrow{w}}exp(-E_{solv-solv}(\overrightarrow{w})∕kT)}$$ (11)

via the average force $\frac{\partial W}{\partial \overrightarrow{p}}$, one can argue that if one is only interested in the solute, it may not matter if $E_{solv-solv}(\overrightarrow{w})$, and hence properties of the pure solvent, are incorrect for as long as the resulting $W(\overrightarrow{p})$ is correct (up to a constant, so that $\frac{\partial W}{\partial \overrightarrow{p}}$ is correct). An argument is then often made that an error $\delta (\overrightarrow{w})$ in $E_{solv-solv}(\overrightarrow{w})$, $E_{solv-solv}(\overrightarrow{w})=E_{solv-solv}^{true}(\overrightarrow{w})+\delta (\overrightarrow{w})$ can be compensated by a re-parametrization of $E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})$ part of the total energy. Formally, such an error compensation can indeed be accomplished by subtracting $\delta (\overrightarrow{w})$ from $E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})$, which restores the correct solute PMF in Eq. 11. However, a simple example below demonstrates that this type of error cancellation can not, in general, hold exactly for atomistic pairwise additive force-fields, which are most commonly used. Consider a perfectly spherically symmetric solute, Figure 7, and two water configurations around it.

Figure 7:

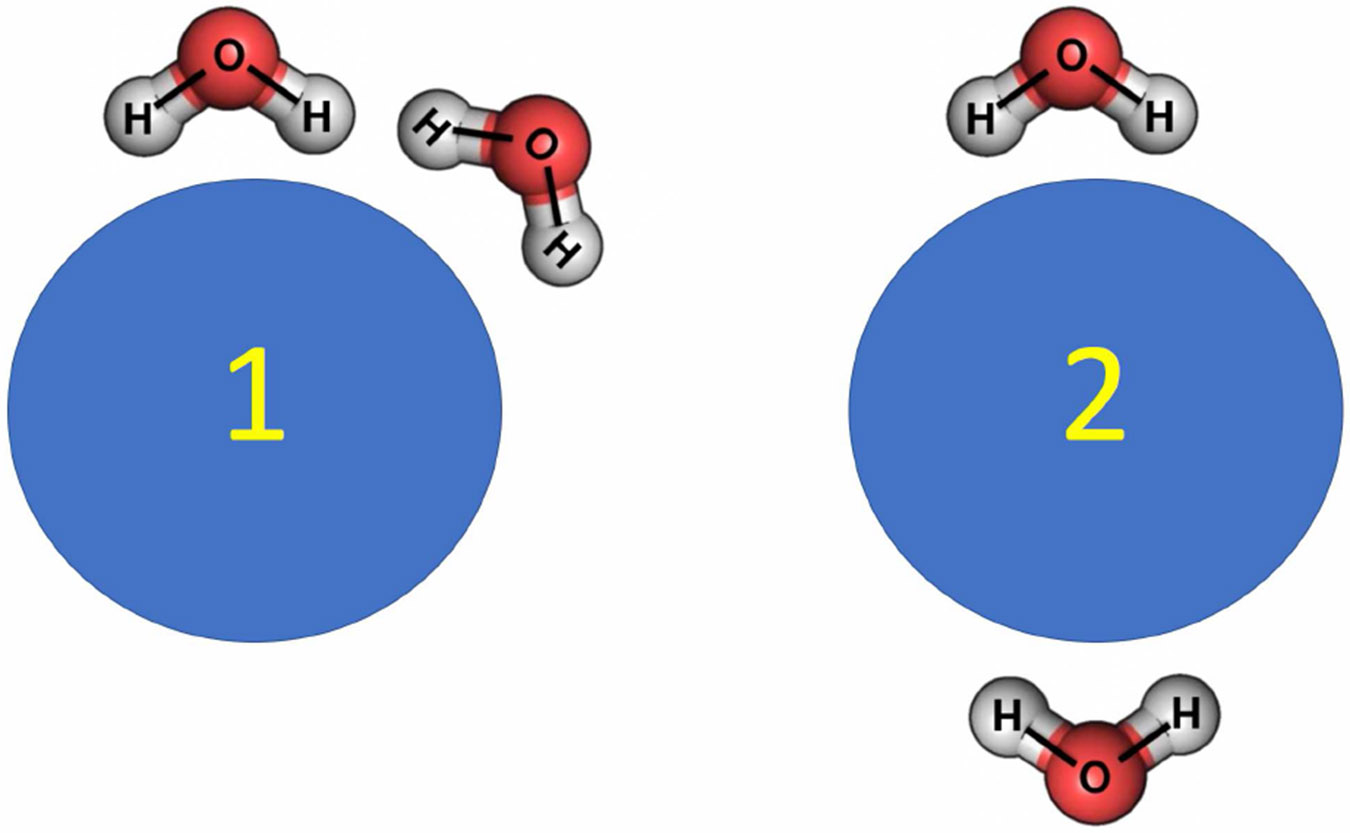
An example where an error in water-water interactions can not be canceled exactly by adjusting the solute-solute and water-solute parts of the pairwise additive energy function. Water-solute pairwise interactions are identical in configurations 1 and 2 due to solute symmetry, while the water-water interactions, and hence the error, are not identical.

For configuration “2”, the two water molecules are interacting weakly, so the corresponding error $\delta (\overrightarrow{w})$ is small, while for configuration “1” both the interaction and $\delta (\overrightarrow{w})$ are large. However, the value of $E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})$ is the same in both configurations due to symmetry – for a pairwise potential both $E_{prot-prot}(\overrightarrow{p})$ and $E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})$ are independent of the mutual position of the two water molecules in Figure 7. If the number of adjustable parameters in $E_{prot-prot}(\overrightarrow{p})+E_{prot-solv}(\overrightarrow{p},\overrightarrow{w})$ is equal to the number of the solute degrees of freedom, one can still technically match the PMF or its derivatives to the correct values at a single training conformation of the solute – the resulting parametrization may be a good approximation to reality in the vicinity of the training conformation, but its accuracy can deteriorate far away from the training conformation. In reality, force-field development is a much more nuanced process, but the gist of the above argument remains the same: compensating for errors in solvent-solvent interactions by parametrizing the solute-solute and solute-solvent parts of the total energy has its limitations. These limitations may explain why the widely used TIP3P⁷⁸ water model generally works well for proteins in their near-native conformations,^9,28 while failing for extended states,²⁰ apparently regardless of the underlying gas-phase force-field. This water model is characterized^74,75 by ~ 140 % error in the self-diffusion coefficient, meaning that hydrogen bonding water-water interactions are also incorrect.⁷⁹ A clever re-balancing of protein-protein and protein-solvent parts of the total energy can improve outcomes of practical simulations,⁸⁰ but without an accurate water model the approach has its limitations.

Conclusions

Free energy profiles computed from atomistic simulations are limited in their accuracy due to two major challenges: adequate sampling of configuration space, and the accuracy of force field parameters. In this study we focus on the accuracy of the solvent part of force-fields, commonly approximated by classical (rigid point charge) water models. We explore the thermodynamics of protein folding for a fast-folding 10-residue mini-protein using two different explicit water models, TIP3P and TIP4P/Ew, and also an implicit model, the generalized Born (GB) model.

Multiple independent microsecond long simulations show that the free energy profile for these three solvent models are clearly different, even though all three models correctly identify the native-like folded state ( the two explicit models also identify a stable misfolded state not seen in experiment). Differences between solvent models manifest themselves the most for non-compact states, resulting in differences between the computed free energy profiles that are larger than the protein stability itself. Clearly the choice of water model is critical when it comes to computing folding free energy landscapes.

To understand why water models matter so much for the free energy profiles, we decomposed the total folding free energy into the solvent-solvent, solvent-protein and protein-protein contributions. For the explicit solvents, the energy (enthalpy) component was further decomposed by the type of interaction: long-range electrostatics, van der Waals, and bonded interactions. Surprisingly, the largest difference in contribution to the folding free energy between the different water models stems from water-water interactions. Perhaps not so surprisingly, long-range electrostatic interactions contribute the most to the difference.

We have argued, quantitatively and in general, that contribution from solvent-solvent interactions to the total protein folding free energy is much larger than the folding free energy itself. Thus, even subtle differences in parameters of water models, which are likely to affect the strength of water-water interactions, can have a large effect on the folding landscape. In the case of TIP3P and TIP4P/Ew, these parameter differences also manifest themselves as differences in the number of water molecules surrounding the protein. We have provided arguments for why the same sensitivity of the thermodynamics to water model may be expected in other type of conformational transitions that involve large changes in the degree of solvent exposure of the solute, e.g. in protein-ligand binding.

In addition, many of the older water models widely used to optimize protein force fields poorly reproduce bulk properties of water.^75,81 We have shown explicitly that, within pairwise-additive force-fields, most widely used, one can not rely on error cancellation between solute-solute, solute-solvent and solvent-solvent contributions to fully compensate for errors inherent in the solvent model. The argument brings to the fore the importance of using accurate water models in force-field parametrization efforts.

In practice, there is no perfect water model; while one wants to minimize the amount of error cancellation between the different parts of the force-field, some of it is probably inevitable for the foreseeable future. In this respect we notice that force field parameters are continuously being optimized to match protein thermodynamics from experiment. These optimizations are often performed based on simulations of small peptides or amino acid analogs.^{30,49,50,82-84} However, the number of water molecules in the immediate vicinity of the protein (water shell) can vary significantly, depending on protein conformation. Therefore, force-field parameters based on small peptides or amino acid analogs with limited conformational diversity, may not be representative of the much larger conformation space sampled by proteins and, hence, the associated water shells. This limitation may translate into a limitation of the force-field optimization approach since, as we have shown here, water-water interactions can contribute significantly to protein thermodynamics.