Complexity AF score as a novel marker of atrial fibrillation instability

Abstract

Atrial fibrillation (AF) is a heart disease affecting millions of Americans. Clinicians evaluate AF-related risk by assessing the temporal pattern, variation, and severity of AF episodes through AF burden (AFB). However, existing prognostic tools based on these metrics are suboptimal, as they do not account for electrical complexity of AF signals. This study introduced Electrical Burden (EB) as a new marker to assess electrical instability and complexity of AF. We also developed a Complexity AF score that incorporates AFB, EB, and Poincaré analysis to assess the severity of AF. Electrocardiogram (ECG) from 50 AF patients in the Long-term AF database were analyzed. EB was calculated using four metrics and combined with AFB and Poincaré metrics to derive the Complexity AF score for each patient. Our results show that AFB, EB, and Poincaré metrics are independent markers, each describing different aspects of AF complexity. The Complexity AF score effectively distinguished between terminated (2.82 ± 1.29, 17 patients) and non-terminated AF groups (4 ± 1.46, 33 patients) (p-value < 0.05). This study emphasizes the importance of EB and Poincaré analysis as an indicator of electrical complexity of AF and highlights the utility of the Complexity AF score in accurately characterizing and stratifying AF to guide management.

Introduction

Atrial Fibrillation (AF) is a common cardiac arrhythmia in the United States that significantly increases the risk of stroke and can lead to other fatal heart disease. By 2050, it is estimated that 6–12 million people in the United States will have AF¹.

Clinically, AF is categorized into paroxysmal, persistent, long-standing persistent, and permanent AF². AF typically begins as paroxysmal episodes but can progress to more advanced forms that do not resolve spontaneously³. As AF progresses, the risk of cardiovascular complications and worsened symptoms increases^4,5. Early identification and appropriate management of AF progression are crucial for improving patient outcomes and treatment strategies. However, most data and analysis on AF and AF progression are gathered with intermittent and short rhythm monitoring, providing limited information on the total burden and the temporal pattern of AF^2,6,7.

Various metrics have been developed to quantify the complexity and severity of AF by assessing its presence in electrocardiograms (ECGs), including AF burden (AFB). In a review by Lin et al.⁸, different definitions of AFB are described, such as the duration of the longest AF episode and the total number of AF episodes during a monitoring period. Typically, AFB is calculated as the percentage of time that a patient is in AF^9,10, but it does not account for any information regarding complexity of the AF ECG signal. Therefore, current AFB metrics are somewhat limited in their ability to guide therapeutic decisions regarding AF management and predicting stroke risk and mortality^11,12.

Poincaré plot analysis has previously been used as a metric for identifying the severity of cardiac disease using ECG traces¹³ by measuring the temporal variability in a consecutive series of heartbeats regulated by the sympathetic and parasympathetic components of the autonomic nervous system¹⁴. Previous studies have examined the nonlinear dynamics of the heart rate to assess the risk of mortality and ischemic strokes in patients with AF^15–18 by analyzing the shape of the Poincaré plot¹⁹ and determining the SD1/SD2 ratio derived from the corresponding ECG trace²⁰. However, Poincaré analysis has not been clinically validated to determine its effectiveness as risk predictor¹³.

At present, several prognostic scores are available to identify patients at risk of developing sustained forms of AF. Many prognostic scores incorporate question-based scales for risk assessment, such as the University of Toronto AF Severity Scale (AFSS)²¹ and the Canadian Cardiovascular Society Severity of AF (CCS-SAF)^22,23, which determine frequency, duration, and severity of AF episodes for risk stratification. However, these scores may be challenging to use in everyday clinical practice, due to the qualitative nature of patient responses. Other risk assessments such as the HATCH score² and Framingham-AF²⁴ incorporate quantitative metrics only. However, none of the existing risk assessment scores include electrical complexity of ECGs signals during AF.

This study aims to improve the effectiveness of AF therapy by developing a Complexity AF score based on the intrinsic complexity of ECG signals recorded during AF. This study first introduces the concept of Electrical Burden (EB) as a novel marker of electrical instability of AF signals. The study also aims to develop a Complexity AF score that incorporates AFB, EB, and Poincaré analysis metrics. The scores are tested in the terminated and non-terminated AF group for verification.

Results

AFB, $<\mathit{E}\mathit{B}>$, Poincaré analysis, and complexity AF score for four representative patients

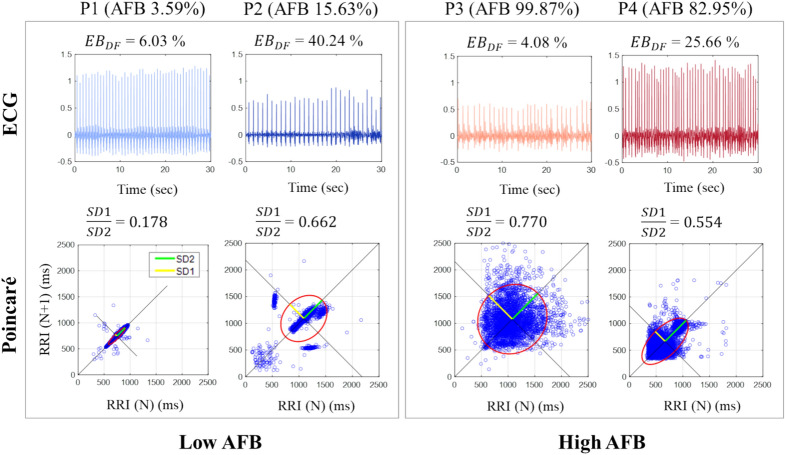
Figure 1 shows 30-s ECG traces for four representative patients labeled P1 to P4, with Low AFB (Patients P1 and P2, blue ECGs, left box) and High AFB (Patients P3 and P4, red ECGs, right box). The other metrics, ${\mathit{EB}}_{\mathit{DF}}$, and SD1/SD2 are also shown for reference for these patients. The top row of Fig. 1 shows that ${\mathit{EB}}_{\mathit{DF}}$ values do not correlate consistently with AFB levels. Indeed, both low AFB and high AFB patients show varying ${\mathit{EB}}_{\mathit{DF}}$ values: ${\mathit{EB}}_{\mathit{DF}}$ = 6.03% & 40.24%, and ${\mathit{EB}}_{\mathit{DF}}$ = 4.08% & 25.66%, respectively. Similarly, the Poincaré plots in Fig. 1 (bottom row) demonstrate that the SD1/SD2 (P1: 0.1778, P2: 0.6623, P3: 0.7703; P4: 0.5538) also do not consistently correlated with low and high AFB levels. In addition, patterns in Poincaré analysis are different: P1 has a torpedo pattern, P2 has a complex pattern, and P3 and P4 have a fan pattern, with P4 possibly showing some complex attributes as well, as described in Woo et al.¹⁹. These observations underscore that the electrical instability of the AF signal (${\mathit{EB}}_{\mathit{DF}}$) and the variability in RR intervals (SD1/SD2) highlight different aspects of the complexity of AF signals compared to the AFB metric.

Fig. 1.

(Top) Randomly selected 30-s ECG traces of four representative patients P1–P4 with Low ABF (P1, P2, left box) and High AFB (P3, P4, right box) with corresponding values of ${\mathit{EB}}_{\mathit{DF}}$. (Bottom) Poincaré plots for these patients with corresponding values of SD1/SD2. AFB atrial fibrillation burden, DF dominant frequency, ${\mathit{EB}}_{\mathit{DF}}$ EB values derived from DF approach.

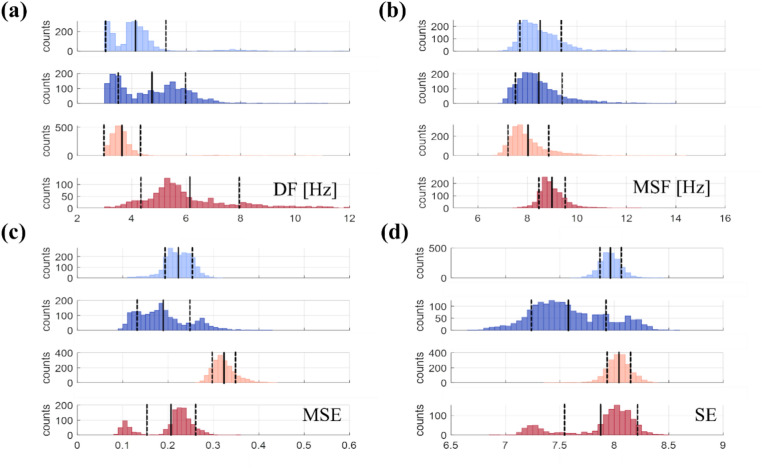
Figure 2 provides further insights into $\mathit{EB}$ by displaying histograms of four nonlinear AF complexity metrics used to calculate $\mathit{EB}$ for the same patients as in Fig. 1: Dominant Frequency (DF), Multiscale Frequency (MSF), Multiscale Entropy (MSE), and Shannon Entropy (SE). These metrics are shown over a 20-h period for P1 and P2 patients with Low AFB (blue) and P3 and P4 patients with High AFB (red). The number of values outside one standard deviation (SD, dashed vertical lines) visually indicates $\mathit{EB}$ (see Eq. 2).

Fig. 2.

Histograms illustrating the distributions of (a) DF, (b) MSF, (c) MSE, and (d) SE values over a 20-h duration for Low AFB (patients P1–P2, blues) and High AFB (patients P3–P4, reds). To assess ${\mathit{EB}}_{[appr]}$ for DF, MSF, MSE, and SE approaches, one needs to determine the ratio of values that are located outside one standard deviation (SD, dashed vertical line) in the overall distribution. The black vertical lines denote the means of the distribution. AFB atrial fibrillation burden, EB electrical burden, [appr] approaches, DF dominant frequency, MSF multi-scale frequency, MSE multi-scale entropy, SE Shannon entropy.

From the Fig. 2, it is evident that $\mathit{EB}$ values across different approaches are not linked to the amount of AFB. Figure 2a,b display DF and MSF, which are frequency-domain approaches, showing slightly right-skewed distributions with long tails on the right side. Figure 2c,d illustrate MSE and SE, which are entropy-based approaches, featuring wider distributions for patients P2 and P4 and bimodal shapes for P4, in contrast to narrower distributions for patients P1 and P3. These observations emphasize that there is no clear distinction between $\mathit{EB}$ in Low (blue) and High AFB (red), indicating the complementary roles of AFB and EB in characterizing ECG signals.

To further study the correlation between AFB, various EB metrics, and Poincaré metrics, we calculated their correlation for entire cohort of 50 patients. Figure S1 in Supplementary Information shows that no significant correlations were observed among all metrics in the cohort of n = 50 patients. Together, Figs. 1 and 2 emphasize the multifaceted nature of AF and support the rationale for using a composite score to comprehensively capture its complexity.

Complexity AF score calculation

The Complexity AF scores based on AFB, ${\mathit{EB}}_{[appr]}$, and Poincaré analysis for individual patients (P1-P4) are presented in Table 1. First, each patient’s 20-h ECG recordings were categorized into Low (L), Medium (M), and High (H) AFB groups. Subsequently, we calculated ${\mathit{EB}}_{[appr]}$ for each patient (see Eq. 2) and categorized the resulting averaged $\mathit{EB}$ values, $<EB>$, into L, M, and H groups (see Eq. 3). For ${\mathit{EB}}_{[appr]}$ calculation, each ECG trace was analyzed into 2400 30-s segments per patient. Then, we calculated Poincaré metrics, specifically the SD1/SD2 and its standard deviation (STD). These average values, called $<Poincar\acute{e}>$, were categorized into L, M, and H groups (see Eq. 4, Table 2). Finally, the Complexity AF score was calculated by summing up the AFB, $<EB>$, and $<Poincar\acute{e}>$ scores, resulting in a score ranging from 0 to 6. Following this procedure in Table 1, patients P1 and P2, both classified as Low AFB, have Complexity AF scores of 2 and 3, respectively. On the other hand, patients P3 and P4, both classified as High AFB, have Complexity AF scores of 5 and 6, respectively.

Table 1.

Complexity AF scores for the four representative patients, combining $\mathit{AFB}$, $<EB>$, and $<Poincar\acute{e}>$ Scores.

Patient ID	AFB			$<EB>$			$<Poincar\acute{e}>$			Complexity AF score
	Value [%]	Label	Score	Value	Label	Score	Value	Label	Score
P1	3.59	L	0	2H	M	1	1 H	M	1	2
P2	15.63	L	0	4H	H	2	1 H	M	1	3
P3	99.87	H	2	2H	M	1	2 H	H	2	5
P4	82.95	H	2	3H	H	2	2 H	H	2	6

Patient ID	${\mathit{EB}}_{\mathit{DF}}$		${\mathit{EB}}_{\mathit{MSF}}$		${\mathit{EB}}_{\mathit{MSE}}$		${\mathit{EB}}_{\mathit{SE}}$		$<EB>$
	Value [%]	Label	Value [%]	Label	Value [%]	Label	Value [%]	Label	Value	Label	Score
P1	6.03	L	24.63	L	28.16	H	28.21	H	2H	M	1
P2	40.24	H	25.06	H	36.24	H	32.29	H	4H	H	2
P3	4.08	L	21.47	L	29.15	H	27.85	H	2H	M	1
P4	25.66	H	21.16	L	29.14	H	26.51	H	3H	H	2

Patient ID	$SD1/SD2$		$\mathit{STD}$		$<Poincar\acute{e}>$
	Value	Label	Value	Label	Value	Label	Score
P1	0.1778	L	0.1859	H	1 H	M	1
P2	0.6623	H	0.2862	L	1 H	M	1
P3	0.7703	H	0.0663	H	2 H	H	2
P4	0.5538	H	0.1977	H	2 H	H	2

$<EB>$ an averaged EB from four different approaches (Eqs. 2, 3); $<Poincar\acute{e}>$ an averaged Poincaré metrics from SD1/SD2 and STD (Eq. 4).

AFB atrial fibrillation burden, EB electrical burden, L low, M medium, H high, DF dominant frequency, MSF multi-scale frequency, MSE multi-scale entropy, SE Shannon entropy.

Table 2.

Categorizations and methodology for complexity AF score calculation.

Category	AFB [%]	AFB Score
AFB
L	$\le 20\%$	0
M	$20\%-80\%$	1
H	$>80\%$	2

Category	No. of high EB	$<EB>$score
$<EB>$
L	$<2H{\mathit{EB}}_{[appr]}$	0	${\mathit{EB}}_{[appr]}=\left\{\begin{array}{c}L,\le 25\%\\ H,>25\%\end{array}\right)$
M	$=2H{\mathit{EB}}_{[appr]}$	1
H	$>2H{\mathit{EB}}_{[appr]}$	2

Category	No. of high $Poincar\acute{e}$	< Poincaré > score
$<Poincar\acute{e}>$
L	$<1H$	0	$\frac{SD1}{SD2}=\left\{\begin{array}{c}L,\le 0.5\\ H,>0.5\end{array}\right)$
M	$=1H$	1	$STDof\left(\frac{SD1}{SD2}\right)=\left\{\begin{array}{c}L,\ge 0.2\\ H,<0.2\end{array}\right)$
H	$>1H$	2

$<EB>$ an averaged EB from four different approaches (Eqs. 2, 3); $<Poincar\acute{e}>$ an averaged Poincaré metrics from SD1/SD2 and STD (Eq. 4).

AFB atrial fibrillation burden, EB electrical burden, L low, M medium, H high, DF dominant frequency, MSF multi-scale frequency, MSE multi-scale entropy, SE Shannon entropy.

Complexity AF score for the entire database

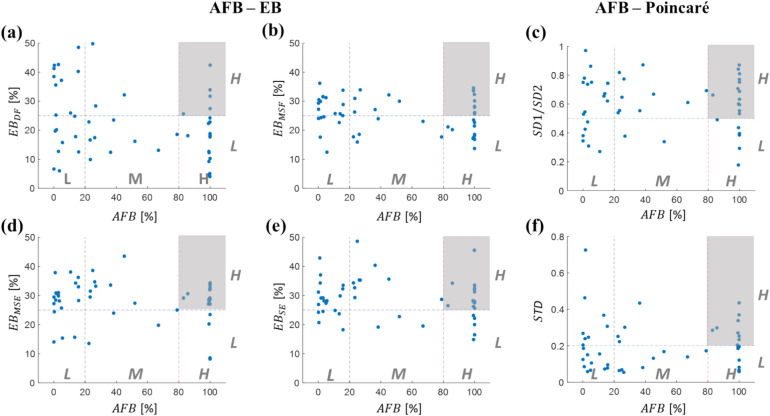
In Fig. 3, the relationship between AFB and each of the four $\mathit{EB}$ values (Panels a, b, d, e) are depicted, alongside the relationship between AFB and each Poincaré metrics (Panels c, f), based on data from n = 50 patients. Each patient is represented as a blue circle in the scatter plots, with AFB and individual EB metrics categorized into Low (L), Medium (M), and High (H) groups. The complexity of AF signals varies significantly among patients in terms of AFB and ${\mathit{EB}}_{[appr]}$. Patients with L AFB and L ${\mathit{EB}}_{[appr]}$ are at a lower risk of developing complex AF, as both complexity metrics of AF signals are classified as L in this group. Conversely, shaded areas in scatter plots, representing H AFB and H ${\mathit{EB}}_{[appr]}$, are associated with potentially high-risk patients exhibiting unstable ECG signals. Similarly, the scatter plots for the Poincaré metrics SD1/SD2 and STD illustrate that the shaded areas, representing H AFB and H values of these metrics, are linked to potentially high-risk patients with unstable ECG signals.

Fig. 3.

Relationship between AFB, EB, and Poincaré metrics. AFB-${\mathit{EB}}_{[appr]}$ scatter plots for (a) DF, (b) MSF, (d) MSE, and (e) SE (n = 50 patients, blue circles). The high-risk area exhibiting H AFB and H ${\mathit{EB}}_{[appr]}$ is shaded in grey. AFB-$Poincar\acute{e}\text{parameter}$ scatter plots for (c) SD1/SD2, (f) its standard deviation of SD1/SD2 (STD). The high-risk area exhibiting H AFB and H Poincaré metric is also shaded in grey. AFB atrial fibrillation burden, EB electrical burden, L low, M medium, H high, DF dominant frequency, MSF multi-scale frequency, MSE multi-scale entropy, SE Shannon entropy.

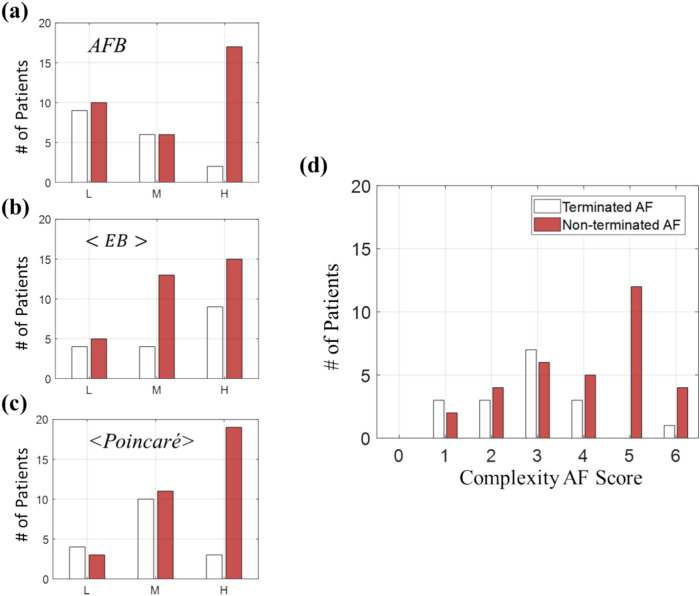
In Fig. 4, we compared Complexity AF scores between two groups of patients: Terminated AF (n = 17) and Non-terminated AF (n = 33). The analysis was conducted on a total of n = 50 AF patients, and we separately reviewed the distributions of AFB, $<EB>$, and $<Poincar\acute{e}>$, as well as Complexity AF score. Figure 4a–c demonstrate that using either AFB, $<EB>$, and $<Poincar\acute{e}>$ separately to differentiate between terminated and non-terminated AF groups did not yield optimal results. However, better outcomes were achieved when the Complexity AF score which incorporates all three metrics, was utilized, as depicted in Fig. 4d. The lower peak with a smaller Complexity AF score corresponds to the Terminated AF group (average Complexity AF score of 2.82 ± 1.29), indicating a lower complexity of the ECG signal compared to the Non-terminated AF group (average Complexity AF score of 4 ± 1.46). The differences in the distributions of the Complexity AF score between the two groups were statistically significant, as demonstrated by a two-sample Kolmogorov–Smirnov test (p-value = 0.0259, see Fig. S2 in Supplementary Information). These results underscore the significance of considering AFB, $<EB>$, and $<Poincar\acute{e}>$ together for an accurate assessment of AF complexity. Nevertheless, these findings warrant further investigations with a larger cohort to better explore these trends.

Fig. 4.

Comparison of complexity AF scores between terminated and non-terminated AF groups. (a–c) Individual $\mathit{AFB}$, $<EB>$, and $Poincar\acute{e}$ metrics used to differentiate between terminated (n = 17, white) and non-terminated AF group (n = 33, red). (d) The Complexity AF score, integrating all three metrics. Statistical significance between terminated and non-terminated group distributions is indicated by a Kolmogorov–Smirnov test (p-value = 0.0259). AFB atrial fibrillation burden; $<EB>$ an averaged EB from four different approaches (Eqs. 2, 3); $<Poincar\acute{e}>$ an averaged Poincaré metrics SD1/SD2 and STD (Eq. 4).

Discussion

The primary objective of this study was to develop the Complexity AF score using ECG signals collected during AF episodes to enhance the efficacy of guiding therapeutic decisions and identifying high-risk AF patients prone to stroke and other complications. The study introduces the concept of EB for assessing electrical instability in AF signals. By incorporating AFB, EB, and Poincaré analysis into the Complexity AF score, we provide a multidimensional assessment of AF complexity that surpasses traditional single-parameter evaluations, offering a deeper understanding and more reliable predictive capability for AF.

The main findings of the study are: (1) there is a lack of correlation between AFB, $<EB>$, and $<Poincar\acute{e}>$ metrics in the Complexity AF score, suggesting that they capture different aspects of AF complexity; (2) Using AFB, $<EB>$, and $<Poincar\acute{e}>$, we can identify high-risk patients (H AFB and H $<EB>$, H AFB and H $<Poincar\acute{e}>$), as well as low-risk patients (L AFB and L $<EB>$, L AFB and L $<Poincar\acute{e}>$), suggesting that the Complexity AF score has a higher potential for targeted treatment strategies for AF patients; (3) Complexity AF score can be used to discriminate between Terminated and Non-terminated AF groups, indicating distinct complexities in AF between the two patient groups.

Incorporating AFB, EB, and Poincaré analysis in the Complexity AF score provides valuable insights into the temporal and electrical instability of AF signals. AFB reflects the frequency or duration of AF episodes; EB assesses the variation and distribution of AF signals’ electrical properties over time; and Poincaré analysis provides both short-term and long-term variability metrics of the ECG signals. Combining these metrics give clinicians and researchers a more comprehensive understanding of AF complexity, aiding in identifying high-risk patients who may benefit from more intensive monitoring or therapeutic interventions, or be used in predicting response to AF ablation.

In this study, we linked the Complexity AF score to the types of AF (Terminated and Non-terminated AF). However, further evaluation is required in the context of AF ablation outcomes to determine its potential role as an indicator. While clinical prediction rules like CHADS₂ and CHA₂DS₂-VASc Scores for Stroke Risk Assessment in AF provide valuable information to clinicians^25,26, they may not specifically account for the electrical instability of the atria. Incorporating electrical instability into a new scoring system can provide a more comprehensive assessment of AF complexity beyond conventional risk scores, aiding in predicting the likelihood of treatment success, such as AF ablation outcomes.

Various techniques have been explored to assess the complexity of AF electrical signals. Several studies in our lab have demonstrated the efficacy of complexity metrics, such as MSF, time-delayed embedding dimension, and MSE, in differentiating between normal sinus rhythm (NSR) and AF^27–29. However, these methodologies primarily scrutinize the intrinsic complexity of AF over short-term periods, typically ranging from 10 seconds to couples of minutes. With the advent of wearable long-term ECG monitoring, analyzing physiological patterns in AF patients over multiple days or events (such as AF ablation) has become possible. To address this, we introduced the concept of EB, which captures electrical perturbations in ECGs over time, demonstrating their dynamic variations across different levels of AFB.

The advancements in long-term ECG monitoring underscore the importance of analyzing data over prolonged periods, preferably seven days or more, as per the standard classification for AF persistence³⁰. This extended monitoring duration offers a deeper understanding of AF dynamics and provides valuable information for accurate diagnosis and effective treatment of AF patients^31,32. Therefore, establishing various analysis methods that consider AFB, EB, and Poincaré aspects in long-term ECG monitoring holds the potential to advance the management of AF patients.

This study has a few limitations. First, we need to determine the best duration for ECG analysis over the long term. While the 20-h duration was chosen to balance the need for sufficient data and practical considerations of patient recordings for a 50-cohort patients’ data, it is important to recognize its limitations. Standardizing the duration to 20 h, while effective for consistency, may not fully capture variations in AF complexity over different periods. Additionally, patients may exhibit significant variability in their AF patterns beyond the 20-h window, potentially affecting the robustness of our scoring system.

Second, we need to consider the optimal threshold for each metric, including AFB, EB, and Poincaré analysis. To classify low and high categories, we established specific thresholds in AFB, EB, and Poincaré analysis. The selection of the 25% threshold for EB classification was somewhat arbitrary due to the diverse range of values produced by the four EB methods, which ranged from 0 to 50%. Despite efforts to explore systematic changes in the threshold, no clear patterns emerged from the different EB distributions (see Fig. S3 in Supplementary Information). To ensure consistency and simplicity across the EB methods, we decided to use the 25% threshold. While we recognize the arbitrary nature of this threshold, it was chosen to facilitate comparison and interpretation across the different EB methods within our dataset. We acknowledge that this threshold is not necessarily optimal and can be refined in future studies. Future research with different patient cohorts or variations in EB methodologies may require adjustments to this threshold.

In conclusion, this study highlights the significance of EB as a marker of electrical instability in AF signals. The Complexity AF score, which combines AFB, EB, and Poincaré analysis, proves to be a promising indicator for comprehensively assessing the AF complexity and severity. By accounting for AFB, EB, and Poincaré metrics, this scoring system enhances differentiation between terminated and non-terminated AF patient groups. It serves as a valuable and comprehensive tool for accurately characterizing and stratifying risk in AF management. The integration of these three facets of AF complexity assessment marks a significant advancement in the field, providing clinicians and researchers with essential tools to better understand AF, guide therapeutic decisions effectively, and predict stroke risk and mortality in AF patients.

Methods

Physionet long-term AF DATABASE

The study utilized publicly available ECG traces of patients with paroxysmal and sustained AF from the long-term AF (LTAF) database in Physionet^33,34. Our focus was on capturing the complexity and variability of long-term AF episodes by analyzing at least 20 h of ECG recordings per patient. We selected 50 patients based on balanced representation (19 with low AFB, 19 with high AFB, and 12 with medium AFB) and data quality (AF episodes longer than 1 minute and ECG recordings longer than 20 hours) to ensure a robust and comprehensive analysis. 34 patients were excluded: 27 due to data quality issues (7 had ECG recordings < 20 h, 1 had AF episodes < 1 min, and 19 had monitoring issues), and 4 to balance low and high AFB groups. Standardizing to a 20-h interval facilitated consistency and fair comparison. We used continuous segments of at least 20 h, starting 20 s after the beginning of the recording, to avoid noise and distortion. For n = 50 patients, the duration of each recording varied but was typically 24 to 25 h (23.87 ± 1.56 h, median: 24 h). The raw ECG signals were sampled at 128 Hz and filtered via a bandpass of 0.5–40 Hz to remove baseline wander and other noise. All 50 patients were categorized into terminated AF (n = 17) and non-terminated AF (n = 33) groups based on whether the AF episodes of at least 1-min durations terminated spontaneously. The database used in this study includes annotations for beat types and rhythm changes, with a specific focus on Sinus (N), Afib (AF), and AF termination (T). However, this database did not provide any information about possible diseases. All the analysis was performed on the single-lead ECG recordings using custom-written MATLAB scripts (MathWorks, Inc., Natick, MA) and Python.

AF burden (AFB)

The database contains annotations for both the total recording time and the duration of AF episodes within each recording. AFB for each ECG recording was determined by calculating the percentage of time when a patient has AF episodes as defined by the formula⁸:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${AFB= \frac{total \ duration \ of \ AF \ rhythm}{total \ duration \ of \ recording} \times 100.}$$\end{document} 1

Following preprocessing, the total duration of recording for all patients was standardized to 20 h. Based on the AFB values derived from Eq. 1, AFB ranged from 0.05 to 99.99% (48.79% ± 42.24, median: 31.56%). Patients were categorized into the following groups: Low AFB (L, ≤ 20%, 19 patients), High AFB (H, > 80%, 19 patients), and Medium AFB (M, 20% < AFB ≤ 80 %, 12 patients). We employed thresholds of 20% and 80% to categorize patients into low, medium, and high groups. These thresholds were selected by analyzing the distribution of AFB values to ensure a balanced representation of patients on each side of the threshold (see Fig. S3 in Supplementary Information).

Electrical burden (EB)

In this study, we introduce a novel concept of EB, which measures the degree of electrical instability of AF. To quantify EB, the total recording duration for all patients was standardized to 20 h to ensure consistency and facilitate fair comparison between the patients. This interval was chosen to include as many patient recordings as possible while capturing the complexity of signals during AF. We identified the longest continuous segment of at least 20 h from each patient’s ECG recording, representative of a full day’s observation, ensuring maximum data utilization without interruptions. The start time was aligned to a common reference point, typically beginning 20 s after the start of the recording session, to avoid initial noise and distortion.

Various AF complexity metrics, including DF, MSF, MSE, and SE (described in Table S1 of Supplementary Information), were computed for each 30-s interval, resulting in 2400 segments. DF and MSF were determined in the frequency domain, and MSE and SE characterized the unpredictability of a signal by estimating its tendency to repeat itself in long and short sequences. Subsequently, the percentage of signals deviating beyond one standard deviation (SD) from the distribution of an AF complexity metric, measured through the different approaches (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$[appr]$$\end{document}), was calculated as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{[appr]}= \frac{count(\left|\left[appr\right] values-mean\left(\left[appr\right] values\right)\right|>SD([appr] values))}{N([appr] values)}\times 100.$$\end{document} 2

Here, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$N([appr] values)$$\end{document} denotes the total number of estimated values for each approach, which is 2400. By capturing the number of outliers in AF complexity metrics (numerator), \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{[appr]}$$\end{document} can represent different levels of ECG instability based on the specific approach used. Therefore, it reflects frequency-based, statistical-based, and information-based complexity of ECG signals during AF.

In this study, there are four EB values derived using different approaches in Eq. 2, i.e., \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{DF}$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{MSF}$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{MSE}$$\end{document}, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{SE}$$\end{document}. Each EB value is classified as either Low (L, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{[appr]}$$\end{document} ≤ 25%) or High (H, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{[appr]}$$\end{document} > 25%), indicating either low or high complexity and instability of the signal. The 25% threshold for EB was selected to maintain consistency and simplicity across the diverse range of values produced by the four EB methods (0% to 50%). Despite exploring systematic changes, no clear patterns emerged from the different EB distributions (see Supplementary Information Fig. S3). To ensure an equal contribution from EB and AFB, the averaged EB (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>$$\end{document}) is classified as L, M, or H based on the number of High \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${EB}_{[appr]}$$\end{document} as follows (see \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>$$\end{document} categorization in Table 2):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>= \left\{\begin{array}{c} L , \ <2 \ any \ high \ {EB}_{[appr]}\\ M, \ =2 \ any \ high \ {EB}_{[appr]}\\ H, \ >2 \ any \ high \ {EB}_{[appr]}\end{array}\right..$$\end{document} 3

Poincaré analysis

To perform Poincaré analysis, R-peaks on the ECG traces were identified using the Pan Tompkins algorithm³⁵. From 1 hour ECG recordings, Poincaré plots were created to model a two-dimensional correlation between successive RR intervals (RRI), in which each interval was plotted as a function of the previous one (RRI(N), RRI(N+1)). The spatial distribution of all RR interval points was then fitted to an ellipse shape, with the center of the ellipse being the average RR interval. From the Poincaré plots, the following metrics were calculated: SD1 (the ellipse width, which measures short-term heart rate variability (HRV)³⁶), SD2 (the ellipse length measures both short- and long-term HRV³⁶) and the ratio SD1/SD2, which represents the relationship between short to long intervals variation³⁷, indicating how much randomness will appear in the HRV³⁸. Extreme values of the SD1/SD2 ratio, either too high or too low, have been correlated with illness²⁰.

SD1, SD2 and SD1/SD2 were computed for 1 h ECG segments and averaged for the entire 20 h ECG trace for each patient. Fig. S4 in Supplementary Information illustrates the distribution of the SD1/SD2 over a period of 20 h across patients with Low AFB (0.6208 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\pm$$\end{document} 0.3177), Medium AFB (0.7863 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\pm$$\end{document} 0.3342), and High AFB (0.9073 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\pm$$\end{document} 0.1120). The mean SD1/SD2 over 20 h and its standard deviation (STD) for each patient were used as Poincaré metrics in this study. To examine the threshold of the SD1/SD2 metrics, all the values in the High AFB group are at least above 0.5, and their fluctuations are much smaller than those of the other two groups. Therefore, we have set thresholds for SD1/SD2 of 0.5 and STD of 0.2. These threshold values were computed for each 1-h interval to quantify these two metrics, resulting in 20 segments.

The SD1/SD2 parameter is classified as either Low (L, SD1/SD2 ≤ 0.5) or High (H, SD1/SD2 > 0.5), and STD is classified as either Low (L, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$STD$$\end{document}\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\ge$$\end{document} 0.2) or High (H, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$STD$$\end{document}\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<$$\end{document} 0.2). To ensure an equal contribution from other metrics AFB and EB, the averaged Poincaré (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<Poincar\acute{e} >$$\end{document}) is classified as L, M, or H based on the number of High Poincaré metrics as follows in Eq. 4 and see Poincaré categorization in Table 2. Individual formulas of Poincaré analysis (SD1, SD2, SD1/SD2) can be found in Supplementary Information Table S1.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<Poincar\acute{e} >= \left\{\begin{array}{c} L , \ <1 \ high \ in \ SD1/SD2 \ or \ STD\\ M, \ =1 \ high \ in \ SD1/SD2 \ or \ STD\\ H, \ >1 \ high \ in \ SD1/SD2 \ or \ STD\end{array}\right..$$\end{document} 4

Complexity AF score

Our study proposes the Complexity AF score, which integrates AFB (Eq. 1), \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>$$\end{document} derived from AF signals (Eq. 3), and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<Poincar\acute{e} >$$\end{document} (Eq. 4). Table 2 outlines the categorizations for AFB, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>$$\end{document}, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<Poincar\acute{e} >$$\end{document}, detailing our methodology for calculating these scores. A Complexity AF score of zero (0) most likely indicates sinus rhythm. We first analyze the distributions of AFB, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<EB>$$\end{document}, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$<Poincar\acute{e} >$$\end{document} separately, and then demonstrate the effectiveness of the Complexity AF score across a cohort of n = 50 AF patients. Additionally, we illustrate its capability to differentiate between patients with terminated AF (n = 17 patients) and non-terminated AF (n = 33 patients) groups.

Author contributions

J.L. contributed to the study idea and design, conducted the entire ECG analysis, analyzed the results, and wrote the first and subsequent drafts. A.J.B. conducted Poincaré analysis, wrote the corresponding part of subsequent drafts, and revised the manuscript. H.R. reviewed the manuscript and contributed to the study by providing clinical insights. E.G.T. contributed to the study idea and design, supervised the analysis, analyzed the results, and revised and edited the manuscript. All authors have read and approved the final version of the paper.

Data availability

The datasets generated and/or analyzed during the current study are available online from the Physionet database, Long-term AF database, https://physionet.org/content/ltafdb/1.0.0/.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-76611-7.