Non-linear elasticity, earthquake triggering and seasonal hydrological forcing along the Irpinia fault, Southern Italy

Abstract

Pump-probe experiments investigate the strain sensitivity of crustal elastic properties, showing nonlinear variations during the strain cycle. In the laboratory, pre-seismic reductions in seismic velocity indicate that asperity contacts within the fault zone begin to fail before the macroscopic frictional sliding. The recognition of such effects in natural seismic-cycles has been challenging. Here we exploit seasonal hydrological strains, performing a natural analogue to a quasi-static laboratory pump-probe experiment to investigate the nonlinear strain sensitivity of crustal rocks and its role in seismic failure along the tectonically-active Irpinia Fault System (Southern Italy). By comparing 14-years-long series of spring discharge, strain, seismic velocity variations and earthquakes rate, we find that seismicity peaks during maximum hydrological forcing and minimum seismic velocity. Seasonal strains of ~10⁻⁶ are required for both earthquake triggering and significant nonlinearity effects arising from modulus reduction. We suggest that, for faults in a critical state, cyclical softening may lead to failure and seasonal seismicity.

Through the exploitation of a seasonal hydrological deformation to probe the elastic properties of the crust, the authors here explain variations of seismic waves velocity and triggering of earthquakes in terms of nonlinear elasticity.

Introduction

While linear elasticity is widely employed in Earth science applications¹, the heterogenous nature of geomaterials makes them to behave in a non-linear way, as it can be revealed by variations in elastic modulus², hysteresis³, slow dynamics⁴, when rocks are subjected to strain perturbations⁵. Pump-probe experiments are nowadays widely used to quantify the non-linear behavior of rocks in laboratory^2,5–7 and provide fundamental insights about the relationships between non-linear elastic parameters and physical properties of materials, such as damage^7,8 or presence and amount of fluids^9–11, among others^2,6,12–15. All these variables have a key role in controlling the seismic cycle^16,17 and the physics of earthquakes nucleation^18,19. It has been suggested that progressive loading produces distributed microcracks that at some stage begin to coalesce onto a volumetric region of concentrated damage that, when a critical level is exceeded, experiences instability that leads to rupture¹⁷. In laboratory²⁰ accelerated fault creep causes elastic moduli (and seismic velocity) reductions during the preparatory phase preceding failure, as asperity contacts begin to fail before macroscopic frictional sliding. This can be also related to rock damage. A temporary reduction in the fault core modulus could induce fault slip for a fault already near failure¹⁸. It is thus crucial to assess the non-linear response of crustal rocks by investigating behaviors associated with stress, pore pressure, permeability, material failure, and rock damage in the Earth in the same way as in laboratory^2,20–22. The advent of ambient noise seismology²³ offers to scientists the possibility to develop ad-hoc pump-probe experiments, measuring in-situ the velocity changes (δv/v) from estimates of the Green’s function²³ (the probe), excited by (the pump) natural (mainly tidal strains^12,24) or man-made strain. These studies revealed significant non-linearity for shallow crustal rocks¹³, enhanced in complex settings such as fault systems^8,25 and volcanic regions^9,13.

Following previous works on non-linearity^8,12,24, β represents the second order, quadratic, coefficient of the stress-strain elastic relationship⁵:

$$\sigma =M\left[\epsilon +\beta {\epsilon }^2+f\left(\epsilon ,\stackrel{°}{\epsilon }\right)\right]$$ 1

where σ is the stress, M is the elastic modulus, ε is the strain and f indicates the hysteretic components dependent on strain and strain rate. The strain sensitivity β^5,24 of seismogenic rocks can be estimated through a quantitative comparison of strain ε vs δv/v curves^5,24:

$$\frac{\delta v}{v}=\alpha +\beta \epsilon$$ 2

where α is an offset.

A value of β different from zero indicates non-linearity^13,26 and increases with the degree of the material damage and density of cracks⁷. Negative values of the strain sensitivity β have been interpreted in terms of decrease (increase) of seismic velocities under dilatational (contractional) strain operated by opening (closing)²⁷ of preexisting cracks in the crust¹³.

In this study we perform a 14-years long-term analysis based on a natural analog of a pump-probe experiment to assess the non-linear behavior of the seismogenic volume in the Irpinia Fault Zone (IFZ, Fig. 1), which hosted the largest (Ms 6.9) instrumentally recorded earthquake in Italy²⁸. Here we measured δv/v induced by annual strain variations originating from recharging groundwater in karst aquifers^29,30, that significantly extends the temporal tidal forcing employed in previous works^14,24. We show that hydrological processes induce nearly periodic, anisotropic fluctuations of horizontal strain^31,32 (which we used as a pump) associated with seasonal modulation of seismicity. We employ ambient seismic noise correlation²³ to track the temporal evolution of δv/v in two sites (MCRV and CAFE, Fig. 1; see “Methods”), representative of the variable hydrological forcing conditions, that we used as the probe to measure the non-linear elastic response of crustal rocks to strain fluctuations. Our analysis reveals a negative value for β in agreement with previous natural^12,13,24 and laboratory experiments^2,7,21, related to seasonal cycling of material damage along the IFZ and associated with seasonal modulation of seismicity. Our results highlight the dependence of seasonal seismicity on the non-linear rock behavior, which calls to improve our understanding of the role of elastic non-linearity and its effect on frictional properties in controlling the triggering of earthquakes along major seismogenic faults^8,33–40.

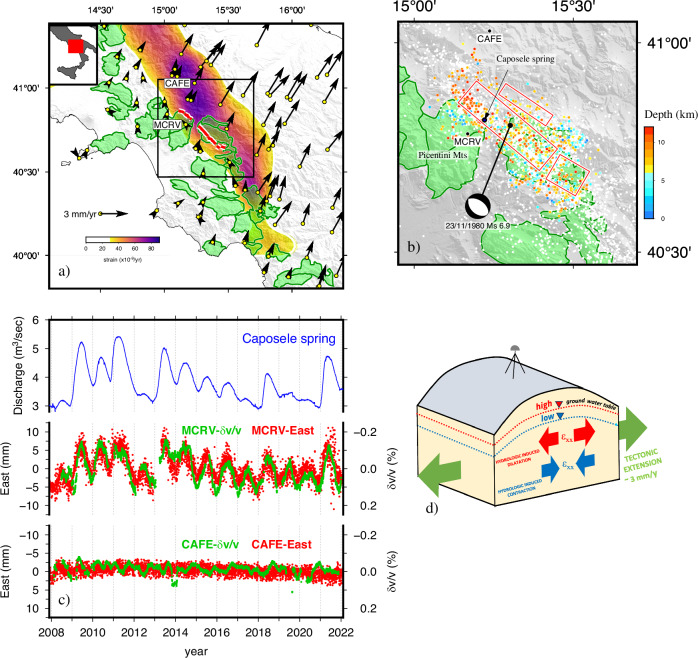
Fig. 1. Summary of observations.

a Map of the study area. Global Positioning System velocities in a Tyrrhenian reference frame⁴³. The trace of Irpinia⁷⁰ is shown in red. Carbonate rocks are represented with green overlays. Background color-coding shows the secular tectonic strain rate (second invariant of the strain rate tensor). The inset shows the location of the study area in Italy. b Enlarged map (area enclosed by the black line in a) showing 2008–2022 seismicity from the Irpinia Seismic Network. Colored dots represent the considered declustered seismicity within the first 12 km of depth and above the completeness magnitude, white dots represent other not-considered seismic events. Global Centroid Moment Tensor focal solution and surface projections of the three faults²⁸ responsible for Ms 6.9, 1980 Irpinia earthquake with its focal mechanism; green patches enclose shallow carbonates rocks; c Time series of hydrological, seismological and geodetic observations. The upper panel shows the discharge measured at Caposele spring. Lower panels show velocity variations (green circles, inverted sign) for coda waves time lapse using empirical Green’s functions reconstructed by autocorrelation of seismic noise recorded at MCRV and CAFE in the frequency band of 0.5‐ to 1‐Hz (blue dots) together with East components of displacement at the same stations (red circles); d conceptual model of the modulation of crustal deformation induced by variable hydraulic head in karst aquifers. ε_xx indicates the horizontal strain in the ENE-WSW direction.

Results

Hydrological forcing and variations of seismic velocity and strain

The Caposele spring²⁹ provides a unique, 100-years-long, hydrological dataset of discharge (average ~4 m³/s) from the karst aquifer of the Picentini Mountains (Fig. 1) hosted in extensively fractured, 2–3 km-thick, allochthonous, Mesozoic carbonates⁴¹. As no man-made modifications occur in its catchment, this spring is strictly controlled by climate trends²⁹ and is regionally-representative of the variations of hydrological forcing operated by the karst aquifers with maximum/minimum recharge in May-July and November-January, respectively^29,30. To investigate the effects of hydrological forcing on crustal elastic properties, we calculated the velocity variations δv/v from 14 years (January 2008-December 2021) of seismic data recorded at MCRV and CAFE stations (Fig. 1). Both sites (with co-located seismic and GPS receivers) are located within the tectonically deforming belt along the Apennines (Fig. 1a) but at variable distances from the IFZ and the karst aquifer. The recent microseismicity (local magnitude −0.4 ≤ M_L ≤ 3.7) occurring in the investigated region is characterized by normal fault mechanism⁴², in agreement with the regional strain field⁴³ and the geometry and slip of the faults involved in the Ms 6.9, 1980 Irpinia earthquake²⁸. We used ambient noise correlations from single station measurements to apply the Coda Wave interferometry method²³ (CWI, see Methods) in a time-lapse of 10–50 s after zero time (ballistic waves arrival time). The time series of δv/v (Fig. 1c) at MCRV reveal up to ~0.2% velocity variations which closely tracks the evolution of spring discharge and the GPS horizontal displacement (Fig. 1c). At MCRV we found that peaks of eastward displacement, which correspond to a transient, recoverable dilatational strain in the shallow crust across the karst aquifer^31,32, are correlated with negative peaks in the velocity of seismic waves, similarly to observations in other Apenninic regions^25,44. The opposite occurs for negative Eastward displacements with contractional strains and significant increase of seismic velocities. At CAFE, located outside the karst aquifer region but inside the actively-deforming tectonic belt (Fig. 1a), we observe an order of magnitude smaller fractional seismic velocity change (~0.03%), and a GPS time series insensitive to seasonal variations, which document the absence of any relevant hydrological forcing. The seasonal velocity variations observed at MCRV are higher than those observed in other regions in the same tectonic environment^25,44 and comparable to those occurring in volcanic regions^9,45, where pronounced seasonal velocity variations⁹ are similarly detected, and where the presence of large amount of preexisting microcracks can be a common condition.

To assess the depth at which seismic velocity variations occur, we computed the depth sensitivity of surface waves⁴⁶ for a local 1D velocity model⁴⁷. The sensitivity of surface wave (see Methods) in the analyzed frequency band (0.5–1.0 Hz²⁵,) is concentrated in the first few kilometers of the crust (depth < 1.5 km, see Fig. S1), which include the thickness of highly-permeable, fractured carbonate rocks⁴¹ forming the karst aquifer. However, the theoretical depth sensitivity of the scattered body waves, computed as in ref. ²⁵ considering a 3D sensitivity kernel formulation⁴⁸ (see “Methods”), shows that the kernel is sensitive to a deeper volume in the crust than for surface waves (Fig. S1). The uncertainty in the nature of scattered waves challenges a precise attribution of the velocity variations observed at MCRV, which could be related to both the shallow highly-permeable, fractured carbonate rocks and the deeper seismogenic volume. Improving the reliability of sensitivity kernels is crucial to address and solve the depth resolution problem⁴⁹. Additionally, independent information is provided by time-dependent P and S wave tomographic models, with poorer intensity and temporal sensitivity but higher spatial resolution. These analyses show significant temporal variations of Vp/Vs ratio below 6 km depth correlated with hydrological forcing⁵⁰ supporting the hypothesis of significant nonlinear effects at similar depths.

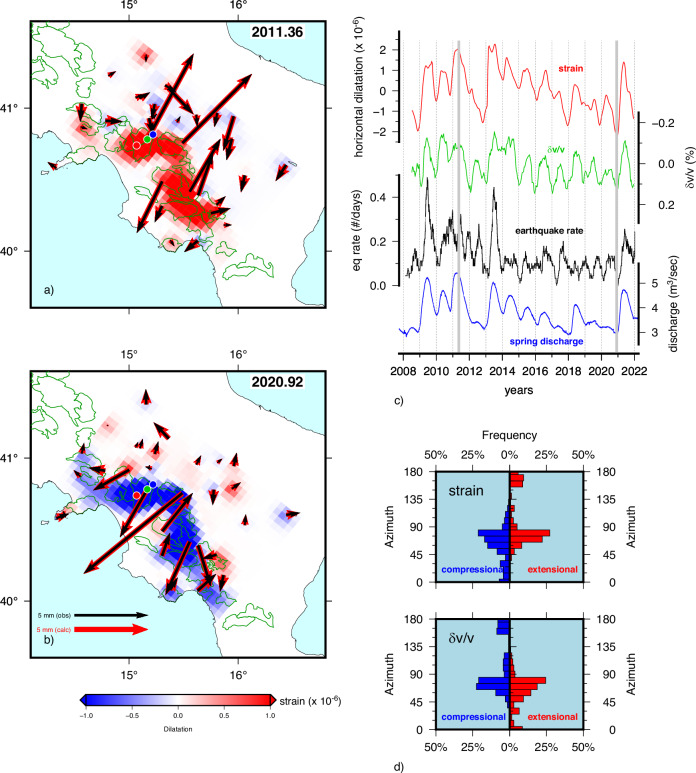
We estimated the strain variations (positive extensional strain) induced by the hydrological cycle (Fig. 2), by computing a 14 years-long time series of horizontal strain, that we modeled with a 3.5 km-thick layer of elementary cuboid sources⁵¹ in the IFZ area (similar approach as in ref. ³², see “Methods”). To remove the long-term tectonic component and mitigate the temporal high-frequency noise and daily scatter, raw GPS time series have been initially detrended and low-pass filtered using a Gaussian filter (full-width 180 days). Two snapshots illustrating the regional NNE-SSW extension during wet periods and contraction in dry periods are reported in Fig. 2a, b, respectively, while the horizontal dilatational strain at MCRV is reported in Fig. 2c. The δv/v follows the evolution of strain, with positive δv/v for contractional strains and negative δv/v associated with extension (Fig. 2c), consistent with previous natural^12,24,52 and laboratory experiments^2,21,27. We remark that in the two episodes (Fig. 2a, b) the displacement at MCRV is oriented respectively NE (Fig. 2a) and SW (Fig. 2b), suggesting that the horizontal dilatation induced by hydrological forcing occurs along a single axis during both the recharge/discharge phases. Figure 2d represents the frequency of the compressional (left) and extensional (right) axis azimuth, coupled with the sign of the temporally coincident strain (top) and velocity variations (bottom) series. In particular, the frequency of the compressional (extensional) axis is counted when the dilatation is negative (positive). During summer, when strain is positive (red color), the extensional axis is oriented mostly W-NW, while during winter, when strain is negative (blue color), a similar orientation is shown by the compressive axis. The same happens when looking at velocity variations; during summer (winter) the velocity changes are negative (positive) and the extensional (compressional) axis is oriented mostly W-NW. We attribute the uniaxial strain fluctuation to an anisotropic poroelastic response⁵³ of the crust due to hydrological forcing³² (hydraulic head ∆h in karst aquifers). The horizontal strain ε_xx in the ENE-WSW direction (taken here as the x axis, see Supplementary Material for the complete derivation) can thus be expressed as:

$${\epsilon }_{xx}=\frac{\alpha {\rho }_{w}g\mathrm{\Delta }h}{\frac{E\nu }{\left(1+\nu \right)\left(1-2\nu \right)}}$$ 3

where α is the Biot’s coefficient, ρ_w is water density, g is the gravity acceleration, E is the Young’s modulus and ν is the Poisson’s coefficient. We test the validity of our model considering a realistic water table variation ∆h = 20–40 m³² and a reasonable range of upper crust poroelastic parameters for carbonate rocks ($E=60-80GPa$, $\nu =0.2-0.3$, $\alpha =0.6-0.8$⁵⁴;). We estimate a strain variation in the order of $2-10\times {10}^{-6}$, whose lower bound is consistent with the range of observed non-tectonic strain variations within the decade-long time series (Fig.2c).

Fig. 2. Deformation, Seismic velocity changes and hydrological forcing.

a, b Maps of distributed hydrological strain with calculated/observed GPS displacements. The complete, continuous strain evolution is shown in Supplementary Movie 1. The two frames display opposite conditions of groundwater recharge in karst aquifers (shown as green lines) and opposite dilatational patterns. Red, green, and blue circles in (a) indicate data points where series of dilatational strain, velocity variations, and spring discharge (shown in (c)) have been respectively calculated. c Time series of dilatational strain (red) calculated at MCRV compared with the co-located velocity variations (green), earthquake rate (black), and Caposele spring discharge (blue); d frequency of the azimuth of compressional axis (left) and extensional axis (right) coupled with the sign of the synchronized scalar of the strain (top panel) and velocity changes (bottom panel).

Non-linear elasticity

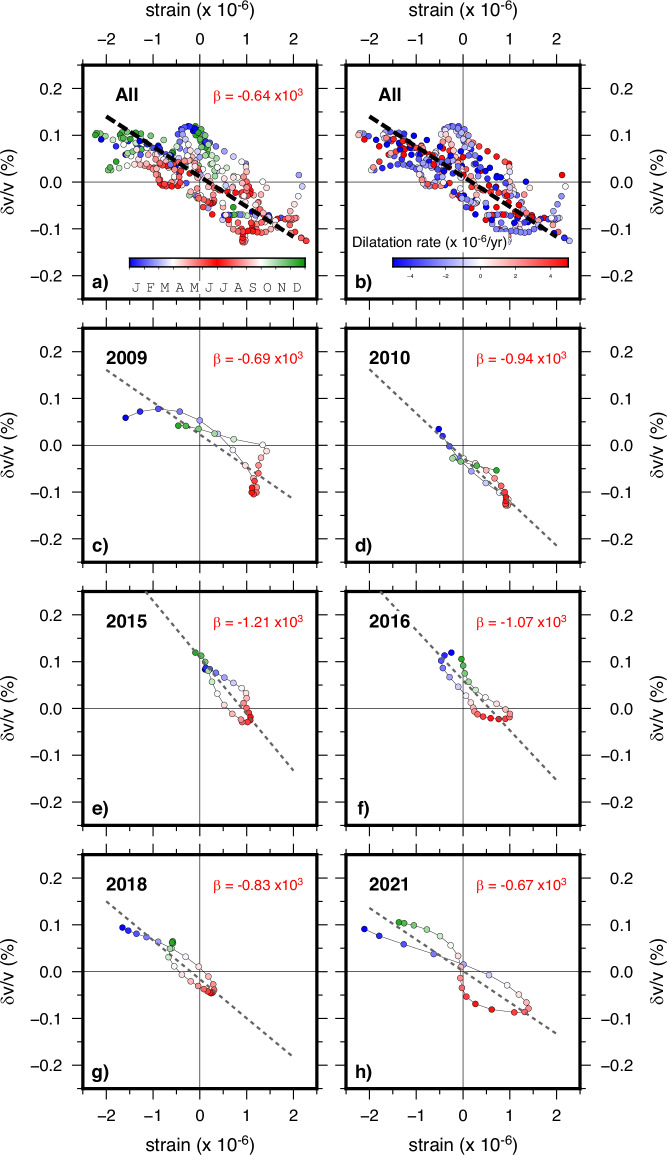
The observations summarized in Fig. 2, together with our simplified poroelastic model, suggest a strong coupling between δv/v and strain in saturated crustal rocks. The oscillatory change in velocity with strain (Fig. 2) is similar to observations in laboratory-scale experiments^2,21, and can be exploited to study the nonlinear elastic response of crustal rocks following equation [2]. A comparison between δv/v and strain values (Fig. 3a) shows a general inverse relationship (β = −0.64 × 10⁻³) indicating that, on average, seismic waves are slower when rocks are extended during maximum hydrological forcing (May-July), that when compressed during minimum hydrological forcing (December-January). This mechanism is consistent with the opening and closing of cracks and pores^6,13,52 with increasing stiffness of their internal contacts during compression²⁷.

Fig. 3. Strain sensitivity analysis of seismic velocity variations.

a seismic velocity variations (δv/v) plotted against dilatational strain, color-coded for annual phase (capital letters in the colorbar indicate each month). The black dashed line shows the best-fit regression line whose slope (β) represents the strain sensitivity of velocity variations. b same as (a) but color-coded for dilatational rate. c–h specific annual cycles (year labeled on top left) color-coded for annual phase.

The observed sensitivity β aligns with the values observed in previous works (−1 × 10³–10⁵)^12,13,24. We also observe a complex, non-unique correspondence between velocity variations and strain, attributed to the superposition of seasonal and multiyear forcing cycles³¹. This superposition results in annual trajectories with similar slopes but different cycle means along the δv/v axis (Fig. 3c–h). Additional information on the strain-rate dependency of seismic velocity variations can be inferred from the hysteretic behavior of δv/v and strains^3,8. For annual cycles defining closed or semi-closed loops (Fig. 3c–h), we observe prevalent clockwise loops but no evidence that seismic velocities are systematically higher during extension (Fig. 3b). We also do not observe a dependency of the cycles pattern upon strain magnitude.

It has been suggested³ that the mechanism controlling quadratic nonlinearity (i.e., β) is distinct from the mechanisms controlling additional nonlinear parameters (i.e., average softening and hysteresis). This distinction^3,26 may depend on the primary deformation mode across the interfaces (cracks or pores) within the bond system. Longitudinal deformation perpendicular to cracks or low-aspect ratio pores would control β, whereas shear deformation across the interfaces being responsible for average softening and hysteresis.

Possible factors arising from the calculation of strain that may affect the estimation of β are two folds. The first is the spacing of geodetic stations (tens of kilometers), larger than the dimension of the karst aquifer (Fig. 1), likely providing a lower boundary on the estimated strain. The second is the use of surface measurements of strain as representative of the actual values at depths (likely to be lower) where seismic velocity changes occur. These two factors, which cannot be easily quantified, have opposite effects and will probably affect the value of β but not its sign.

Seismicity modulation

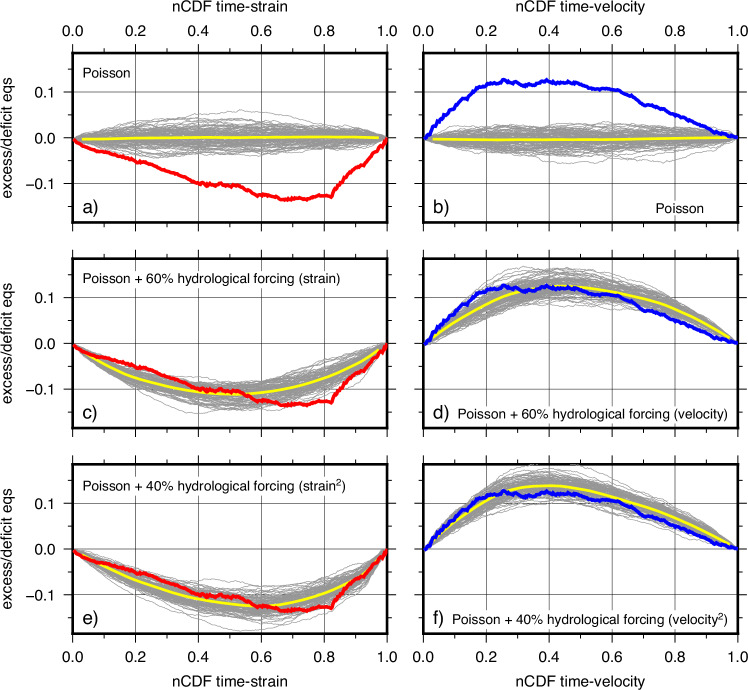
It has been previously reported that seismicity along the IFZ is modulated at seasonal and multiannual time scales by hydrological forcing from the karst aquifers³². The low values of estimated hydrologically-induced stress variations³², corresponding to the observed seismicity modulation, suggest a critical state of stress for the faults within the actively deforming area, as observed in other actively-deforming regions where seismicity is triggered by small stress changes⁵⁵. To investigate the relation between rock properties modulated by the hydrological forcing (strain and seismic velocity variations) and earthquake nucleation we declustered the seismic catalog along the IFZ (color-coded circles in Fig.1 c) and calculated the daily seismicity rates within 90-days moving windows (see Methods). This modulation is clearly displayed in the multiyear time series of Fig. 2c (where all the different observables have been resampled and synchronized at a 0.04-year step), showing in-phase peaks of seismicity rate, δv/v, strain and spring discharge. We also observe that the three largest peaks of seismicity rates in 2009, 2013 and 2021 (Fig. 2c), correspond to large seasonal increments in spring discharge (>2 m³/s) and dilatational strain (>1 × 10⁻⁶). We test the relationship between background seismicity and hydrological forcing (expressed as variations of dilatational strain or seismic velocity), following the approach of ref. ⁵⁶ using a modified quantile-quantile plot (QQP). QQP tests for a specific relationship between hydrological forcing and seismicity rate rather than simply asking the question if earthquake occurrence is correlated with such forcing. In our case we plot the normalized cumulative fraction of earthquake rates that occurs at or below a given level of strain or seismic velocity against the normalized cumulative fraction of time that is spent at or below the same given level. To facilitate interpretation, we follow ref. ⁵⁶ and modify the QQP plots to show excess or deficit of earthquakes by removing the 1:1 trend line. In the case of no correlation between the earthquake rate and hydrological forcing (either the strain or velocity variations), we expect to see a horizontal line because the fraction of earthquakes below a given level should be equivalent to the fraction of time spent at or below that level. If a point falls below the horizontal line, then there is a deficit of earthquakes up to the corresponding value compared with what is expected for time spent up to the corresponding value. If the point falls above, the opposite is true, which means we have an excess of earthquakes. We found (red lines in Fig. 4a) a deficit of earthquakes for low values of the strain compared to the case in which there would be no correlation with the strain (e.g., in the case of a Poisson process). This indicates that seismicity and hydrologically-related strains are correlated with each other. Moreover, the curve is slightly skewed to the right (Fig. 4a), showing that seismicity rate responds non-linearly to increasing strains explaining also the large response of seismicity to the largest strain increase in 2009, 2013 and 2021. As expected, the same analysis with velocity variations (Fig. 4b), shows an opposite behavior and an excess of earthquakes during low values of seismic velocity. Therefore, earthquakes occurrence and velocity variations are anti-correlated. In this second case, the curve is also skewed to the left (Fig. 4b), showing that seismicity rate also responds non-linearly to increasing velocity variations. The gray lines shown in Fig. 4a, b display 100 random permutations of the observed catalog which are cloudily disposed around the horizontal line showing that, when the catalog is randomized, no correlation is present with either strain (Fig. 4a) or seismic velocity variations (Fig. 4b). By comparing the observed seismicity rate with synthetic rate histories containing both random and hydrological components, we could estimate the level of hydrological forcing in the real catalog (see Methods). Figure 4(c–f) shows that the observed nCDFs of the observed seismicity require ~40% contribution of hydrological forcing and an increasing effect of strain or seismic velocity variation to reproduce the observed skewness, i.e., a non-linear influence of strain or seismic velocity variations on the seismicity rate.

Fig. 4. Modified quantile-quantile plots (QQP) to test correlation of seismicity rate with strain and seismic velocity variations.

The vertical axis is a measure of excess or deficit of earthquakes at a given level of strain (in red, plots a, c, e) or velocity (in blue, plots b, d, f) based on the amount of time spent at or below that level. The horizontal axis is the normalized Cumulative Density Function (nCDF) of time-strain (or time-velocity). Gray lines show synthetic realizations (mean shown in yellow) with variable contribution and increasing effect of hydrological forcing.

Discussion

We measured hydrologically-modulated velocity changes δv/v in the order of ~0.2% near the karst aquifers close to IFZ. Those variations are one order of magnitude smaller (~0.03%) at around 25 km distance, where the amplitudes of horizontal transient displacements are negligible too (Fig. 1c). Our primary observation shows that velocity is systematically slower during extension and higher during compressional strains resulting in a seasonally-controlled variation of the state of rock damage. Variations of elastic properties and their non-linear sensitivity to strain arise from the stiffness modification of the grain and fracture contacts. We thus propose that seasonal variations induce a weakening/healing process that cyclically affects the crust along the IFZ. The process we observe seems to be reversible, with a restoration of the initial conditions (and of the elastic properties), like a fault healing process⁵⁷ by which the crust retrieves its original characteristics prior to the new damage episode. Geodetic strain allows us to precisely track the mechanism underlying the velocity variations, which is the cyclical crack opening/closing of NW-SE-oriented crack system in the direction of the regional direction of minimum horizontal stress.

We observe that significant non-linear seasonal variations of elastic properties of the crust along the IFZ are statistically correlated with earthquakes rate. We propose a model in which hydrological deformations promote earthquake failure by a mechanism involving dynamic nonlinear elasticity²². Seasonal variations of elastic properties cause a weakening that triggers the observed micro-seismicity, alternated to a healing process as the strain amplitudes decrease and seismic wave velocity increases with frictional contacts ageing²⁰. In terms of frictional contacts, we may also interpret triggering as the onset of sliding of the faults, resulting from an abrupt decrease in the shear strength of the fault gouge by softening of frictional contacts. Necessary physical characteristics for this triggering mechanism require a weak fault in a critical state and dynamic strain amplitudes greater than about 10⁻⁶¹⁸, regardless of their frequency content⁵⁸. Both requirements are satisfied along the IFZ where active tectonic strain is likely to keep faults close to failure and hydrological forcing provides sufficient oscillatory strains. For the recent background micro seismicity, no significant localization along the segments responsible for the 1980 Ms 6.9 earthquake is observed⁵⁹ suggesting that a diffused triggering mechanism in the volume interested by hydrological forcing and resulting nonlinear reduction of elastic properties is more likely than an accelerated aseismic slip along major fault zones.

Laboratory experiments²² show that modulus reduction increases progressively as the effective stress is reduced, implying that the system’s elastic nonlinearity is strongly sensitive to increase in pore pressure. In agreement with the observed depth distribution of seismicity (Fig. S1), the deeper parts of the crust, where pore pressure may be greater than hydrostatic, may thus be more sensitive to hydrological forcing with respect to the shallow crust where extensive fracturing maintains a hydrostatic profile. The observed relationship between seismicity triggering and modulus reduction (Fig. 4e, f) also agrees with laboratory experiments¹⁸ showing the existence of an approximate strain threshold above which significant elastic nonlinearity is observed and earthquakes are easily triggered. Thus, our study suggests that the elastic nonlinearity of fault cores close to a critical state plays a major role in earthquake triggering and offers an alternative perspective beyond models based solely on the evolution of pore pressure or Coulomb stress. We speculate that regional weakening of active fault zones, over time scales relevant for earthquake nucleation, may also increase the likelihood of higher-magnitude ruptures on large fault systems.

Methods

Velocity changes from Coda Wave Interferometry

We computed the three-component (ZZ, EE, NN) autocorrelation using continuous seismic data recorded at the MCRV station located in the IFZ area, in Southern Italy (Fig. 1a). The considered time window for this study is from January 2008 to December 2021. We rejected daily traces if they don’t contain more than 20 h of data available and to reduce transient signals, we carried out a one‐bit normalization.

We measured the velocity variations using the stretching technique⁶⁰, which provides stable measurements²⁵, by stacking 90 days using an 89-day overlap of correlations. The stack of the autocorrelation over the full-time period was used as the reference signal to compute relative velocity variations. This operation was performed for each component in the coda wave window starting at 10 s from the arrival of ballistic waves and with a duration of 40 s. The choice of this window allows to resolve changes of δv/v in the shallow crust²⁵. Velocity variations of the three components are, then, combined weighting with squared correlation coefficients estimated after stretching. We then select the velocity variations with correlation coefficients above 0.85.

In Fig. 1c we represent the comparison of the seismic velocity variation for the stations MCRV and CAFE, this latter being outside the carbonates and characterized by much smaller variations (around 34% compared to MCRV), demonstrating that the response of crust around MCRV is very peculiar and associated with the local characteristics of the complex IFZ.

Depth sensitivity kernels

We computed the depth sensitivity of surface waves (Fig. S1c, d) as in ref. ⁴⁶ for a local velocity model⁴⁷ and for the frequency band 0.5–1.0 Hz at which we computed the velocity variations. This frequency band has been selected as it is the optimal band used in the Apennines to have a good temporal resolution with high quality correlation while limiting the number of stacked days^25,44,61. For autocorrelations, the better outcomes are observed for frequencies exceeding 0.5 Hz⁶², because in Southern Europe seasonal variations in the distribution of noise sources reduce the quality of the correlations and thus limit time dependent analysis⁶³, while frequencies higher than 1 Hz are too much contaminated by anthropogenic noise. We also computed the theoretical depth sensitivity of the scattered body waves (Fig. S1e) as in ref. ²⁵, considering a 3D sensitivity kernel formulation⁴⁸. We solved for the body wave depth sensitivity normalized to 30 km depth with each layer 1 km thick layer²⁵. In our case we considered a coda time lapse 30 s, representative of the time window 10–50 s, and two free path (10,100 km) as reference.

Horizontal strain

Continuous surface displacements have been measured by permanent GPS stations of the RING network (http://ring.gm.ingv.it). For our analysis, we considered the time series of horizontal components corrected for the long-term tectonic trend and instrumental offset from January 2008 through December 2021 obtained following the procedure outlined in ref. ³². We calculate the time-dependent horizontal strain rate tensor at the surface by modeling the observed displacement with elementary cuboid sources extending to a depth of 3.5 km⁵¹ following the approach described in ref. ³². The use of this modeling approach (fully described in ref. ⁵¹) to calculate the horizontal components of the “hydrological” strain rate field is required by the need to regularize the sparse density coverage of the GPS stations and incorporate the geometry of the karst aquifers. The second invariant of the horizontal long-term, tectonic strain rate field shown in Fig. 1a, has been obtained from the secular GPS velocity field of ref. ⁶⁴ and using the VISR code⁶⁵ to calculate a regular grid of the horizontal strain rate tensor.

Seismicity and syntethic catalogs

IFZ is monitored since 2007 by the Irpinia Near Fault Observatory (INFO), which includes the Irpinia Seismic Network (ISNet, http://isnet.unina.it, network code IX), composed of a total of 31 co-located tri-axial strong motion accelerometers and three-components short period or broad-band seismometers and 8 INGV seismic stations (https://eida.ingv.it/it/, virtual network _NFOIRPINA, network code IV). The period analyzed in the present study ranges from January 2008 through December 2021. The original data set consisted of 1898 events with local magnitude −0.4 ≤ M_L ≤ 3.7, and the seismicity is mostly concentrated at depths between 8 and 12 km (Fig. 1c, S1). To avoid biases associated to aftershocks, we declustered the earthquake catalog using the approach described in ref. ⁶⁶, and its windowing technique, where a scan of the catalog within distance and time is performed with spatiotemporal windows as a function of the magnitude⁶⁶. In this procedure, the first shock is not necessarily the largest shock in the sequence; thus, a small foreshock is the first event of an aftershock sequence. If a largest shock occurs in the series, this enlarges the window beyond the value used for the first shock⁶⁶. Since the recorded seismicity may be affected by the detection capability of the network, we select events shallower than 12 km with magnitude above the minimum magnitude of completeness (M_C), i.e., the magnitude above which the network is assumed to reliably record all the events occurring in the region of interest, estimated at M_L 1.1 for ISNet⁶⁷. Then we computed the seismicity rate as the number of earthquakes occurring in 90-days moving windows. We also tested the sensitivity of the seismicity rate to the parameters of the windowing technique⁶⁶ used for the declustering and we found that seismicity rate is not changed at all by varying the windows used (Fig. S2, Supplementary Materials). We constructed the synthetic catalogs starting from the observed number of events occurring in the considered time interval and considering this number as resulting from the sum of an homogeneous Poisson process and a nonhomogeneous hydrological forcing. The nonhomogeneous contribution has been produced using the inversion method⁶⁸ which involves firstly obtaining the cumulative distribution for the variable to be sampled (strain or seismic velocity). Cumulative distribution functions of the strain and seismic velocity variations (simple or squared to consider the case of linear and non-linear effects, respectively) are calculated from the respective time series and rearranged to give an expression for the variable of interest (strain or seismic velocity) in terms of its probability. The variable can then be sampled by inserting uniform random values between 0 and 1 into this expression for each event contributing to the nonhomogeneous part of the synthetic catalog. The same approach has been used to calculate the homogeneous Poissonian contribution to the synthetic catalogs randomly sampling the cumulative function of the exponential distribution which controls the distribution of time intervals between successive independent events in a Poisson process⁶⁸. Synthetic seismicity rate histories (90-days moving windows) are then computed from the synthetic catalogs.

Author contributions

S.T., P.P., and N.D. conceived the methodology and wrote the first draft of the manuscript. S.T., P.P., N.D., G.F., and M.V. contributed to data preparation and analysis and to the interpretation of results. G.V. provided data of the Caposele spring. A.Z. contributed to the interpretation of results. All authors revised the final draft of the manuscript.

Peer review

Peer review information

Nature Communications thanks Andrew Delorey and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The seismic catalog can be downloaded at http://isnet.unina.it. Velocimetric continuous data are available at https://eida.ingv.it/it/. Raw GPS data (rinex files) are available at http://ring.gm.ingv.it. The time series of the discharge of Caposele spring has been provided by Approvviggionamento Idrico (DIRAP), Acquedotto Pugliese, S.p.a., Bari. The dataset of seismic velocity changes, geodetic strain, and seismicity rate, generated during the current study, is available from the corresponding author on reasonable request. Analysis was made using MATLAB (release 2023a, https://www.mathworks.com/products/matlab.html) and Python (https://www.python.org/). Correspondence and material requests should be addressed to S.T. at the following address: stefania.tarantino@ingv.it.

Code availability

This study was performed using the Python package Obspy and uses workflows provided in ref. ²⁵ and ref. ³² for velocity variations measurement and strain computation respectively.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-54094-4.