Abstract

This study presents an effective method for the quantification of nitric acid (0.1–9 M) and the temperature (20–60 °C) through optimal experimental design, chemometrics, and Raman spectroscopy. Raman spectroscopy can be deployed using fiber-optic cables in hot cell environments to support processing operations in the nuclear field and industry. Chemical operations frequently use nitric acid and operate at nonambient temperatures either by design or by circumstance. Examples of Raman spectroscopy for the quantification of nitric acid with applications in the industrial field are profuse. However, the effect of temperature on quantification is often ignored and should be considered in real-world scenarios. Statistical design of experiments was used to build training sets for partial least-squares regression and support vector regression (SVR) models. The SVR model with a nonlinear kernel outperformed the top partial least-squares models with respect to temperature and resulted in percent root-mean-square error of prediction of 1.8% and 2.3% for nitric acid and temperature, respectively. The D-optimal design strategy decreased the sampling time by 75% compared to a more traditional seven-level full factorial option. The new method advances chemometric applications within and beyond the nuclear field and industry.
1. Introduction
The field of used nuclear fuel recycling has a distinct need for fast, accurate, and online analysis of actinides, fission products, and acid concentrations.1,2 Offline methods are time-consuming, require frequent maintenance or calibration, are too bulky to be used within hot cells, and have sensitive electronics that typically cannot withstand high radiation fields. Online monitoring can help users operating large-scale nuclear fuel recycling schemes via increased safety (lower radiation dose to workers), quicker data acquisition, deployment within hot cells, safeguards and materials accountability, and other similar benefits.1−3 Optical spectroscopy techniques, such as Raman spectroscopy, can be deployed remotely to provide elemental and molecular information on processing streams to support used nuclear fuel recycling operations.4−9 Dissolution, solvent extraction, uranyl nitrate hexahydrate cocrystallization, and routine operations demand that temperature is accounted for to ensure robust monitoring applications.10−13 These optical spectroscopy techniques also support various industrial and chemical operations by indicating temperature, concentration, and pKa/pH values of acids.14−19
Nitric acid, although typically reported as a strong acid, behaves like a weak acid when present in concentrations greater than 10–2 M and does not fully dissociate (<99.9%).20 As acidity and temperature of the medium increase, less dissociation of nitric acid occurs.20,21 Therefore, the dissociation constant varies based on environmental conditions, thereby affecting the solution composition (i.e., H+, NO3–, HNO3).22 Yet, the temperature variable is either overlooked in many proof-of-principle studies, or instead physicochemical measurements (e.g., pH, temperature, and conductivity) are incorporated in hierarchical models requiring additional probes (e.g., thermocouples).1,4,14−17,23,24 The effects of temperature on nitric acid, the corresponding Raman spectra, and resulting chemometric models are not well-studied.25,26 The research community would benefit from experimentally and statistically determining the influence of dynamic temperature levels on the accuracy and validity of nitric acid measurements by Raman spectroscopy and developing a way to systematically account for temperature changes.
Supervised chemometric models, such as partial least-squares regression (PLSR), are well-suited for handling colinear and confounding spectral features encountered in complex systems with changing temperature.2,4,17,19,23−25 Another supervised method, support vector regression (SVR), is a type of support vector machine useful for both linear and nonlinear regression tasks using various kernel functions. PLSR and SVR models are used for predictions and are built with training sets that cover the anticipated conditions (i.e., concentrations and temperature). Few studies have investigated whether any benefit is gained from using traditional multivariate full factorial (FF) designs, which require intensive sample preparation and analyses, in comparison with more modern D-optimal designs that are useful for minimizing sample set size needed to train a model for temperature predictions.27−29 The temperature response is inherently nonlinear and covarying,6,23 and the number of samples needed to train a model and the type of model needed to account for such features have not been established.
This work aims to answer three key questions: (1) Can Raman spectroscopy be leveraged to simultaneously measure the temperature and nitric acid concentration? (2) How many temperature levels are needed to account for spectral nonlinearity in a multivariate regression model for robust temperature predictions, and (3) can a nonlinear SVR model outperform a linear PLSR model? This work addresses a major gap in the current literature and provides a valuable method for robust nitric acid measurements by Raman spectroscopy in systems with dynamic temperature.
2. Methods and Materials
2.1. General Materials
All chemicals were commercially obtained (ACS grade) and used as received, unless otherwise stated. Concentrated nitric acid (70%) was purchased from Sigma-Aldrich. All solutions were prepared by using deionized water with a resistivity of 18.2 MΩ·cm. Samples were prepared gravimetrically using a Mettler Toledo model XS204 balance with an accuracy of ±0.0001 g in volumetric glassware.
2.2. Raman Spectroscopy
An iHR320 imaging spectrometer (Horiba Scientific) with a resolution of approximately 3 cm–1, equipped with a Synapse 2048 × 512 charge-coupled device, was used to collect Stokes–Raman spectra with a 1200 grooves per millimeter grating. A 532 nm laser (Cobolt Samba 150) was operated at 100 mW and connected to a general-purpose Raman probe (Spectra Solution Inc.) using a 2 m, 105 μm core diameter multimode fiber. Quartz sample cuvettes were placed in a Quantum Northwest qpod 2e temperature-controlled cuvette holder (Avantes) with an accuracy of 0.05 °C. Sample temperature was confirmed with a waterproof dip thermometer (VWR) for several samples to benchmark the time required to reach a steady temperature. Spectra were collected in triplicate using a 1 s integration time and the average of four accumulations from 500 to 3849 cm–1. For each sample, spectra were collected at room temperature (∼23.0 °C) and the target temperatures, after being allowed to equilibrate for about 5 min at each level.
2.3. Data Analysis
The Vektor Direktor (v2.0) software package from the KAX Group was used for PLSR, SVR, and preprocessing. Four latent variables (LVs) were used in each PLS model as the points marking the last significant decrease in root-mean-square error (RMSE). PLSR models were built by using a NIPALS algorithm describing either one Y variable (PLS1) or more than one Y variable (PLS2). PLSR is a linear function that iteratively finds the structure in X (i.e., spectra) that is most predictive for Y (i.e., concentrations). A linear function cannot always account for complex systems. SVR is a machine learning algorithm that employs linear or nonlinear kernel functions to map from the original space to a higher-dimensional feature space. Two types of SVR models are available in Vektor Direktor: epsilon-SVR (i.e., type 1) and nu-SVR (i.e., type 2). Consistent values for epsilon (ε) and γ were selected toward the center of the heat map in regions where the cross-validation (CV) error was minimal. Moderate γ parameters were selected to avoid overfitting (large γ) or underfitting (small γ). The ε parameter describes the boundaries of the fitting regression line or residuals. Each method is based on a unique approach to minimize the error function. Linear, 2D, and 3D polynomial lines and a radial basis kernel were evaluated. Results from models built with a 3D polynomial line provided the best statistics.
Predictive models were built by using a standard normal variate (SNV) transformation. SNV removes scatter effects from spectra and centers and scales each spectrum using only the data from that spectrum. A Savitzky–Golay derivative was used to compute the first derivative of the spectra. A range of adjacent variables and polynomial orders were evaluated. Trimming the data to only include regions with important peaks, X loadings, or regression coefficients did not improve the regression models.
2.4. Design of Experiments
The training set concentration matrices were created using Stat-Ease Design-Expert (version 22.0.5) by Stat-Ease. Two multivariate models were created: the more commonly used D-optimal model and a more traditional seven-level split-plot or FF model (72 = 49 samples). Extra temperature levels (total of 10) were acquired to determine whether a seven-level model provided an adequate representation of complex temperature effects in the Raman spectra (Table S1). Arbitrary values from 0 to 1 were used to generate the design, and it was scaled to the analyte variables to cover nitric acid concentrations from 0.1 to 9 M and temperatures of 20–60 °C. A random number generator in Microsoft Excel was used to generate the external validation set of 25 unique nitric acid concentrations and temperature levels within the design space. The D-optimal design contained six required model points and an additional six lack-of-fit points to achieve a fraction design space (FDS) of 0.99. FDS was calculated by mean error type, δ = 2, σ = 1, and α = 0.05. These results indicate good prediction capability over the factor range. The variable δ describes the maximum acceptable half-width (i.e., margin of error), σ is an estimate of the standard deviation, and α is the significance level used in the statistical analysis. The D-optimal design samples, selected using a quadratic process model, is shown in Table 1. Raman spectra for the D-optimal set are shown in Figure S1.
Table 1. D-Optimal Design Selected Samples with Space Type and Build Type.
| sample | nitric acid concentration (M) | temperature (°C) | space type | build type |
|---|---|---|---|---|
| 1 | 9.00 | 20.0 | vertex | model |
| 2 | 0.10 | 20.0 | vertex | model |
| 3 | 5.13 | 37.4 | interior | model |
| 4 | 0.10 | 48.0 | edge | model |
| 5 | 6.02 | 53.4 | interior | lack of fit |
| 6 | 8.11 | 33.0 | interior | lack of fit |
| 7 | 4.55 | 20.0 | center edge | lack of fit |
| 8 | 9.00 | 46.2 | edge | lack of fit |
| 9 | 2.77 | 60.0 | edge | model |
| 10 | 9.00 | 60.0 | vertex | model |
| 11 | 3.04 | 46.8 | interior | lack of fit |
| 12 | 1.88 | 32.8 | interior | lack of fit |
2.5. Statistical Comparison
PLSR models were evaluated by using calibration, CV, and validation (i.e., prediction) metrics. RMSE of the calibration (RMSEC) and the RMSE of the CV (RMSECV) are important when evaluating model performance. Prediction statistics often include RMSE of the prediction (RMSEP), percent RMSE of the prediction (RMSEP %), bias, and standard error of prediction (SEP). RMSEs for the calibration, CV, and validation were calculated using eq 1
| 1 |
where  is the predicted concentration, yi is the measured concentration,
and n is the number of samples. The RMSEP % value
was calculated by dividing the RMSEP by the median Y matrix values
using eq 2.
is the predicted concentration, yi is the measured concentration,
and n is the number of samples. The RMSEP % value
was calculated by dividing the RMSEP by the median Y matrix values
using eq 2.
| 2 |
where  represents the median value of each reference
value to ease comparisons. RMSE values are reported in analyte units.
SEP and bias values are important to consider, especially when minimizing
the training set size. SEP is corrected for bias, whereas bias values
lie either systematically above or below the regression line. Bias
values close to zero indicate a random distribution along the regression
line. Values of RMSEP % ≤ 10% indicate acceptable performance,
and values of RMSEP % ≤ 5% indicate strong performance.5 A Tukey–Kramer method was used for the
pairwise comparison of RMSEPs for PLSR and SVR models built using
different designs and described in detail in the Supporting Information.28
represents the median value of each reference
value to ease comparisons. RMSE values are reported in analyte units.
SEP and bias values are important to consider, especially when minimizing
the training set size. SEP is corrected for bias, whereas bias values
lie either systematically above or below the regression line. Bias
values close to zero indicate a random distribution along the regression
line. Values of RMSEP % ≤ 10% indicate acceptable performance,
and values of RMSEP % ≤ 5% indicate strong performance.5 A Tukey–Kramer method was used for the
pairwise comparison of RMSEPs for PLSR and SVR models built using
different designs and described in detail in the Supporting Information.28
3. Results and Discussion
3.1. Raman Spectra
Raman spectra corresponding to changes in the nitric acid concentration and sample temperatures are shown in Figure 1. The wide range of nitric acid levels (0.1–9 M) resulted in multiple species (NO3–, H+, and HNO3) with concentration-dependent features.30,31 The primary nitrate bands occurred near 1048 cm–1 (ν1 symmetric) and 716 cm–1 (ν4 in-plane deformation), and other peaks related to associated HNO3 molecules at elevated HNO3 concentrations were also identified [e.g., 968 cm–1 (ν6) and 1305 cm–1 (ν3 asymmetric)]. Figure 1a represents the Raman band changes resulting from the nitric acid concentration, and Figure 1b indicates the Raman shift caused by changes in temperature. Figure 1 showcases the variation in spectra owing to the change in nitric acid concentration, while also highlighting the normally overlooked variation in spectra owing to the temperature. The nitrate symmetric stretching peak near 1048 cm–1 decreased in intensity and slightly red-shifted with increasing temperature, and the shape of the Raman water band near 2800–3800 cm–1 gradually changed. The broad Raman water band corresponds to the combined symmetric and asymmetric stretching vibrations of the OH bonds. The band shifts around a temperature-induced isosbestic point near 3520 cm–1 related to the proportion of hydrogen-bonded and nonbonded OH valences in clusters of hydrogen-bonded H2O molecules.8,16 Hydrogen-bonded OH valences refer to OH bonds that are directly involved in hydrogen bonding with neighboring water molecules. Hydrogen bonds constantly form between clusters of water molecules, which means that water molecules can shift back and forth between hydrogen-bonded and nonbonded OH groups.
Figure 1.
Raman spectra: (a) 0.1–9.0 M nitric acid samples at room temperature with SNV pretreatment and (b) 4.5 M nitric acid with varying temperatures 20–60 °C.
As the nitric acid molarity increased, the water band (2800–3800 cm–1) intensity decreased and shifted toward higher frequencies (Figure 1a). This shift has been seen in previous studies.2,10,32−34 At the same time, the primary nitrate and nitric bands near 1048 cm–1 (ν1 symmetric), 1305 cm–1 (ν3 asymmetric), and 716 cm–1 (ν4 in-plane deformation) became sharper and more pronounced. This trend has also been shown in previous literature.12,35,36 Temperature-induced variation, although not as pronounced, is also present in the ν1 symmetric band (∼1048 cm–1) and the water band (2800–3800 cm–1). In this case, as temperature increases, the water band shifts toward higher frequencies while the nitric acid band shifts toward lower frequencies and loses intensity, which has been observed in previous literature as well.26,30
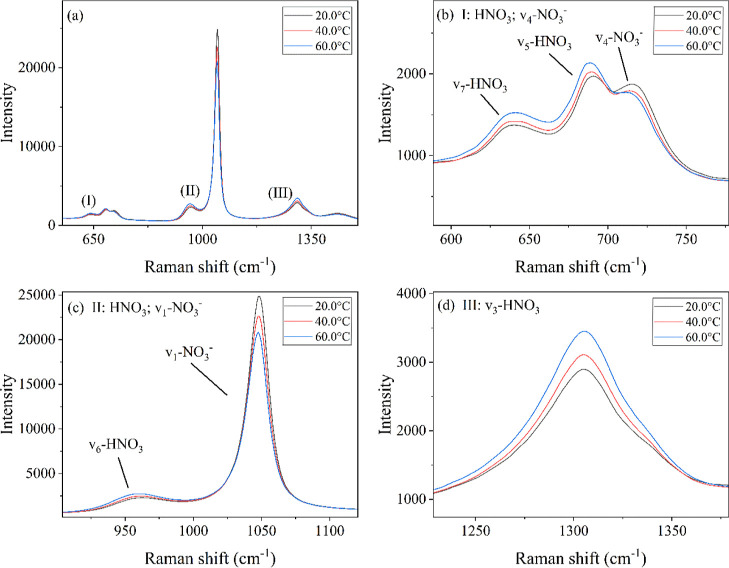
Elevated temperatures affect the dissociation constant of nitric acid and thus the resulting Raman spectra. Figure 2 shows the Raman spectra of a 9.0 M nitric acid sample: (a) represents the spectra with points of interest labeled; (b) represents the Raman shift variation of the 638 cm–1 (ν7) and 688 cm–1 (ν5) nitric acid peaks and the 716 cm–1 (ν4 in-plane deformation) nitrate peak, (c) represents the Raman shift of the 958 cm–1 (ν6) nitric acid peak and the 1048 cm–1 (ν1 symmetric) nitrate peak, and (d) represents the Raman shift of the 1305 cm–1 (ν3 asymmetric) nitric acid peak. The figure includes 20, 40, and 60 °C as representative temperature points to showcase the general trends that were present. These variations highlight the covarying relationship of several nitric acid bands with increasing temperature.
Figure 2.
(a) Raman spectra of 9.0 M nitric acid, (b) Raman shift focused on the 638 cm–1 (ν7) and 688 cm–1 (ν5) nitric acid peaks and the 716 cm–1 (ν4 in-plane deformation) nitrate peak, (c) Raman shift focused on the 958 cm–1 (ν6) nitric acid peak and the 1047 cm–1 (ν1 symmetric) nitrate peak, and (d) Raman shift focused on the 1305 cm–1 (ν3 asymmetric) nitric acid peak, with 20, 40, and 60 °C as representative temperature points.
Figure 2b reveals three peaks of interest: the two HNO3 peaks at 638 and 688 cm–1 (ν7 and ν5, respectively) and the NO3– peak at 716 cm–1 (ν4). As the temperature increased from 20 to 60 °C, the nitric acid peak intensities increased, whereas the nitrate peak decreased to a lower intensity. Likewise, in Figure 2c, including the 958 cm–1 (ν6) HNO3 peak and the 1048 cm–1 (ν1) NO3– peak, and in Figure 2d, including the 1305 cm–1 (ν3) HNO3 peak, the same trend was observed. This inverse relationship between the nitric acid and nitrate peaks supports the scientific literature regarding the decrease in the dissociation constant of nitric acid based on both high molarities and temperatures26,30,31 These observations from Figure 2 can be explained by a decrease in the dissociation constant, or an increase in the pKa, of nitric acid with increased temperature.26 Because the temperature and nitric acid concentration both affect the spectra in overlapping regions, both variables must be accounted for when building high-fidelity multivariate models.
3.2. Designed Training Sets
This study used design parameters that represent temperatures and nitric acid concentrations found within uranyl nitrate hexahydrate recrystallizations.10−12 Training set size and composition are important in chemometric model development, and the designed experiments provide a robust and user-friendly option for selecting sample sets within a statistical framework. The primary goal of a designed approach is generating a balanced sample distribution in the design space to ensure adequate coverage throughout, including vertex, edge, and interior locations. Two experimental designs (i.e., FF and D-optimal) were used to select sample concentrations and temperature levels within the same two-factor space. FF models provide a more sequential approach that typically requires more experimental analysis time because many more samples are needed compared with the D-optimal counterpart.29 A seven-level split-plot or FF design resulted in 49 samples, and the D-optimal design resulted in just 12 samples. The designed sample concentrations and temperatures used in the calibration model are showcased in Figure 3, along with 25 points randomly generated for the validation set. Randomly chosen validation samples offered good variation of temperature levels and concentrations to evaluate model prediction performance.
Figure 3.

Locations of the D-optimal, FF, and validation samples within a two-variable design space.
Requiring the least number of samples, the points chosen by the D-optimal multivariate model spread throughout this design space and allow for a broad overview of the effects of temperature and nitric acid concentration on the spectra with a minimum number of samples.1,2,9,23 Optimal design strategies are typically more efficient and amenable to incorporating many additional factors in future work to account for even more complex systems [e.g., uranium(VI), fission products, and corrosion products].7 An optimal design approach has been applied to the selection of concentration matrices in numerous studies. However, temperature levels may not necessarily be treated the same as concentration levels. Because of the inherent nonlinear spectral response to temperature, additional levels may be required to accurately estimate the response over the entire design space, and the FDS assumption of 0.99 by using a quadratic process model may not provide sufficient coverage. Instead, a higher-order model (e.g., cubic) with additional terms may be required to describe the temperature response and better capture the potential curvature in the spectral response.
3.3. Partial Least Squares Regression
Multivariate PLSR models were created using spectra generated from the seven-level FF and D-optimal designs separately. The prediction performance of each model was evaluated by predicting the 25-sample external validation set. The performance of each model was evaluated primarily by RMSEP, which represents the average variation between the predicted and reference values. Other important metrics included SEP and bias values. RMSEP values represent the approximate ± error associated with predictions, and a lower RMSEP indicates a more reliable, accurate multivariate model.24 RMSE values have the same units as the response variables. As the values for nitric acid concentration and temperature have different units, the RMSEP % is discussed for ease of understanding.
An initial test compared the prediction performance of a PLS1 model built with four LVs and FF nitric acid levels at room temperature (seven samples). This model was used to predict the randomly selected validation set collected at room temperature (25 samples) and the specified temperature levels (25 samples). The RMSEP % value for the PLS1 FF model predicting room temperature samples was 1.7%, and it was much higher, at 8.6% for the samples at disparate temperatures (data not shown here). This result confirms that changing the temperature levels creates a significant source of deviation in model predictions. However, the PLSR model that did not include temperature levels still predicted nitric acid with reasonable accuracy (i.e., below 10%), suggesting that the model had some predictive power. The test confirmed that the sample temperature affects the validity of multivariate model predictions.
Next, PLS2 models were built for nitric acid and temperature using the D-optimal and FF (seven-level) training sets. PLS2 models can correlate spectral features to analyte concentrations using two separate Y variables. The PLSR model metrics of the seven-level FF PLS2 model are showcased in Figure 4. Figure 4a represents the RMSE against LVs and highlights the optimal number of LVs (four). Figure 4b showcases the regression coefficients against the X-variable [Raman shift (cm–1)]. Figure 4c represents the explained Y-variance against the LVs for both the D-optimal (concentration and temperature prediction) and seven-level FF model (concentration and temperature predicting). Finally, Figure 4d indicates the X-loadings against the X-variable (cm–1) for LV-1, LV-2, and LV-3.
Figure 4.
PLSR model metrics of (a) RMSE against LVs, where the box indicates the optimal number of LVs, (b) regression coefficients against the X-variable (cm–1), (c) explained Y-variance against the LVs, and (d) X-loadings against the X-variable (cm–1).
The last notable decrease in RMSECV occurred at four LVs, which suggests that four LVs should be included in the PLS2 model. This result was consistent for both the D-optimal and FF (seven-level) sets. Including four LVs is reasonable considering the complexity of this system, which describes coexisting species including H+, NO3–, HNO3, H2O, OH, and ion pairing.37−39 Regression coefficients describe how each X-variable is weighted when predicting each Y-response. The regression coefficients were reasonably smooth and gave importance to realistic features in the spectra that are consistent with a quality model. The explained Y-variance plot was compared with the X-loadings to confirm whether the model discerned realistic features in the spectra. The profiles of the X-loadings looked like the original spectra, while accentuating the variables that provide the most important sources of information. With four LVs, 99.98% of the variation in Y was explained. The first LV described 95.7% of the Y-variance for nitric acid, and the loading gave importance to features related to nitric acid. The second LV described 94.2% of the Y-variance for temperature. The second X-loading gave importance to the HNO3 peaks near 638 and 688 cm–1 (ν7 and ν5, respectively), 958 cm–1 (ν6), and the 1305 cm–1 (ν3) HNO3 peak. The water band shapes in the first and second X-loadings were consistent with the HNO3 and temperature features, respectively. The third LV likely described some variation for both nitric acid and temperature by providing adjustments that account for the convolution of HNO3 and temperature-related peaks. Trimming the PLS1 and PLS2 models to include only the regions with significant (i.e., nonzero) loadings and regression coefficients marginally improved RMSEP % (Figure 4).
The results of the PLS2 analysis of the D-optimal and seven-level FF designs and spectra are presented via RMSEC, RMSECV, RMSEP, RMSEP %, SEP, and bias and are shown in Table 2. The RMSEC values for nitric acid were similar; however, the RMSECV values for the D-optimal model were higher. Excluding one sample at a time during cross validation increased the RMSECV, which suggests that the training set was minimized effectively. The RMSEP, SEP, and bias values for the D-optimal model were nearly identical to those of the seven-level FF model for nitric acid shown in Table 2. The RMSEP % and bias of the D-optimal nitric acid model performed much like those of the seven-level FF model: RMSEP % values were 1.8% and 1.9%, respectively. Although two additional nitric acid levels were included in the D-optimal design, far fewer temperature levels were included. The RMSEC and RMSECV values for the D-optimal set were higher than those for the seven-level FF set, suggesting that the seven-level FF set model was more robust for temperature. However, the RMSEP % temperature values for the D-optimal and seven-level FF models were 6.9 and 7.3%, respectively. This result emphasizes why RMSECV values are only an estimate of the prediction performance of the model when approaching the minimum number of samples in the training set and why the D-optimal PLSR model (12 samples) performed as well as the seven-level FF PLSR model (49 samples). The RMSEP values for the D-optimal model are remarkable, especially considering the 75% shorter amount of time required to collect the spectral data.
Table 2. PLS2 Model Calibration and Validation Metrics for D-Optimal and Seven-Level FF Designsa.
| PLS2 metrics | D-optimal | seven-level FF |
|---|---|---|
| LVs | 4 | 4 |
| Calibration Statistics | ||
| RMSEC (HNO3) | 0.092 | 0.086 |
| RMSECV (HNO3) | 0.19 | 0.090 |
| RMSEC (temp.) | 1.7 | 1.05 |
| RMSECV (temp.) | 4 | 1.36 |
| Validation Statistics | ||
| RMSEP (HNO3) | 0.078 | 0.085 |
| RMSEP % (HNO3) | 1.8 | 1.9 |
| SEP (HNO3) | 0.079 | 0.068 |
| bias (HNO3) | –0.011 | –0.053 |
| RMSEP (temp.) | 1.38 | 1.46 |
| RMSEP % (temp.) | 6.9 | 7.3 |
| SEP (temp.) | 1.32 | 1.42 |
| bias (temp.) | –0.48 | 0.45 |
Aside from RMSEP %, HNO3 values are in mol/L and Temp. in °C.
3.4. Support Vector Regression
PLSR is one of the most traditional supervised regression methods and has been applied to modeling Raman spectra in nitric acid systems.40 However, modeling temperature in this system is challenging, and PLSR did not achieve the desired RMSEP % level of <5% for temperature. Therefore, support vector machines were evaluated for modeling the nonlinear and covarying spectral features to determine whether a nonlinear model would outperform the linear PLSR approach. SVR has advantages over PLSR, in that is it less prone to overfitting, can handle outliers well, and models nonlinear features.29 However, it requires careful parameter selection for ε and γ values and often larger data sets. However, few works have evaluated the effect of minimized training sets on SVR performance. If SVR provides a better prediction performance than PLSR but requires many additional samples, then PLSR could still provide a better option in certain circumstances.
SVR models were built for the D-optimal and seven-level FF sets for comparison. Parity plots for the D-optimal and seven-level FF models predicting HNO3 and the temperature are shown in Figure 5. Parity plots are useful for comparing sample predictions relative to the reference values. Samples falling close to the 1:1 line represent accurate predictions. The RMSEP, SEP, and bias values for the D-optimal model were slightly higher than those for the seven-level FF model for nitric acid concentration shown in Figure 5a,b. Although two additional nitric acid levels were included in the D-optimal design, far fewer temperature levels were included. The effect of this discrepancy is visible in the RMSEP, SEP, and bias for temperature prediction between the D-optimal model compared to the seven-level FF model (Figure 5c,d). The D-optimal and seven-level FF RMSEP % values for temperature were 5.6% and 2.3%, respectively. This result suggests that the D-optimal model had reduced prediction performance for temperature compared with the seven-level FF. Therefore, unlike PLSR, SVR performs better when incorporating more temperature levels in the training set, resulting in improved prediction performance and meeting the target RMSEP % of <5% and an error of approximately ±0.5 °C.
Figure 5.
SVR parity plots of (a) D-optimal model predicting nitric acid, (b) seven-level FF multivariate model predicting nitric acid, (c) D-optimal model predicting temperature, and (d) seven-level FF multivariate model predicting temperature.
Additionally, the biases of the D-optimal models for nitric acid concentration and temperature prediction were ∼4 and ∼7 times as high as the seven-level FF models, respectively. This result indicates that when utilizing SVR, although the D-optimal model still has reasonable predictive power for nitric acid and temperature, the much smaller calibration set size is prone to bias. However, when minimizing the sample set size is crucial, the D-optimal approach could provide adequate predictive power for the intended purpose. Overall, by comparing the RMSEP, RMSEP %, SEP, and bias values for the SVR D-optimal and FF models, the SVR seven-level FF model more accurately predicted both the concentration and temperature with less bias, variation, and uncertainty.
The different prediction metrics for the PLSR and SVR models (Figure 4 and Table 2, respectively) were then statistically tested via Tukey–Kramer analysis. The full list of comparisons performed is shown in Table 3. The Tukey–Kramer pairwise method was used to confirm whether any statistical differences existed between the PLSR models (D-optimal vs seven-level FF), between the SVR models (D-optimal vs seven-level FF), and between the PLSR and SVR methodologies. Statistical significance via Tukey–Kramer analysis was decided by the 95% confidence interval for the difference in bias between two models and the SEP ratio of the two models; if the difference in bias contained 0 and the SEP ratio contained 1, then the models were considered statistically similar.28 The confidence intervals are shown in Figure S2. The statistical differences were based primarily on differences in bias because the SEP confidence interval always contained 1 (Figure S2).
Table 3. Total Model Comparisons Performed via Statistical Methodologies where M Indicates HNO3 Concentration, and T Indicates Temperature.
| Tukey–Kramer statistical comparisons | RMSEP % values | statistical significance |
|---|---|---|
| PLSR D-Opt (M) vs PLSR 7-L (M) | 1.8 vs 1.9 | yes |
| PLSR D-Opt (T) vs PLSR 7-L (T) | 6.9 vs 7.3 | no |
| SVR D-Opt (M) vs SVR 7-L (M) | 2.1 vs 1.8 | no |
| SVR D-Opt (T) vs SVR 7-L (T) | 5.6 vs 2.3 | yes |
| PLSR D-Opt (M) vs SVR D-Opt (M) | 1.8 vs 2.1 | yes |
| PLSR D-Opt (M) vs SVR 7-L (M) | 1.8 vs 1.8 | yes |
| PLSR 7-L (M) vs SVR D-Opt (M) | 1.9 vs 2.1 | yes |
| PLSR 7-L (M) vs SVR 7-L (M) | 1.9 vs 1.8 | yes |
| PLSR D-Opt (T) vs SVR D-Opt (T) | 6.9 vs 5.6 | no |
| PLSR D-Opt (T) vs SVR 7-L (T) | 6.9 vs 2.3 | yes |
| PLSR 7-L (T) vs SVR D-Opt (T) | 7.3 vs 5.6 | yes |
| PLSR 7-L (T) vs SVR 7-L (T) | 7.3 vs 2.3 | yes |
Each comparison listed in Table 3 was statistically significant, except for the comparisons of PLSR D-Opt (T) vs PLSR 7-L (T), SVR D-Opt (M) vs SVR 7-L (M), and PLSR D-Opt (T) vs SVR D-Opt (T). The PLSR D-optimal models outperformed PLSR seven-level models in terms of nitric acid and temperature prediction. SVR seven-level models outperformed SVR D-optimal (T) models in predicting temperature but had no statistically significant difference with predicting nitric acid concentration. The SVR seven-level models outperformed the PLSR seven-level models on both nitric acid and temperature prediction, whereas the SVR D-optimal model, although not statistically different with respect to nitric acid concentration prediction, outperformed the PLSR D-optimal model for temperature predictions. The PLSR methodology yielded equal or slightly better RMSEP % scores for all D-optimal and seven-level comparisons of nitric acid concentration prediction except for the PLSR and SVR seven-level model comparison (see Table 3). However, the opposite trend occurred regarding temperature. In every instance, the SVR models vastly outperformed the PLSR models with respect to temperature prediction, except for the instance of no statistical difference between the PLSR and SVR D-optimal models (Table 3). The RMSEP % values of some PLSR models were 300% higher than those of the corresponding SVR models for temperature prediction. PLSR models, specifically the PLSR D-optimal model, outperformed other models for nitric acid concentration, whereas the SVR models, specifically SVR seven-level FF model, were better for predicting temperature.
3.5. Sample Set Size and Statistics
A total of 10 temperature levels were acquired to evaluate how the sample set size influences predictions for nitric acid and temperature (Table S1). Although the initial hypothesis assumed that seven levels were sufficient to describe the nonlinear temperature response, experimental confirmation was required to determine how many samples were needed to model nonlinearity in the spectral response caused by temperature. SVR models were built with varying samples (21–70) in the training set. The set with 70 samples corresponded to 10 temperatures at each of the 7 nitric acid concentrations. A temperature level was excluded at each level until just 3 temperature levels were applied to the 7 nitric acid concentrations for a total of 21 samples.
The RMSECV, RMSEP, and bias were evaluated versus the number of temperature levels in the training set for nitric acid and temperature. If the RMSECV and RMSEP were relatively balanced, within approximately a factor of 2, then the model was considered robust, provided the bias was also reasonably low. For nitric acid SVR models, the RMSECV and RMSEP increased from 0.068 to 0.11 and from 0.078 to 0.086, respectively, and the bias remained nearly constant. The slight increase in RMSE values indicated that a full seven-level FF model for temperature levels is not necessary to maintain robust nitric acid predictions (<2% RMSEP %). A three-level design provides enough variation in the data set to build a sufficiently robust SVR model for nitric acid.
The RMSECV, RMSEP, and bias % values for temperature predictions by the SVR model are shown in Figure 6. The value bias % was calculated by dividing by the median Y value and converting it to percent. With a decreasing number of temperature levels in the model below seven levels, the RMSECV, RMSEP, and bias % values for the temperature increased substantially. By contrast, increasing the number of temperature levels beyond 7 levels, did not significantly improve the RMSCV, RMSEP, or bias. Thus, if temperature predictions are important, then including seven temperature levels in the calibration set for each nitric acid level is likely necessary. The number of levels required to build a robust regression model may increase with a wider temperature range.
Figure 6.

RMSEC and RMSECV values for temperature predictions with varying temperature levels in the FF calibration set for SVR models. The dashed box corresponds to the number of samples for balanced prediction performance.
Although several works have evaluated techniques for monitoring water temperature by Raman spectroscopy, few have extended the approach to more complex media (e.g., acid).26,31−36 The prediction performance for temperature in nitric acid solutions was comparable to previous works focused only on predicting water temperature, despite significant multicollinearity between the nitric acid and temperature spectral responses, owing to changes in pKa. Even if temperature is not included in the training set, PLSR and SVR regression models still have some predictive power. To maintain robust nitric acid prediction performance, using three temperature levels per sample, or the D-optimal approach, is effective. A similar number of samples is also sufficient for satisfactory temperature estimates. However, if additional highly accurate temperature predictions are required for a given process with respect to temperature, then as many as seven temperature levels from 20 to 60 °C and a nonlinear SVR modeling strategy are needed. The findings presented here will be leveraged in systems with additional metal nitrates (e.g., uranyl nitrate) and pursued in future work.7,41
4. Conclusions
The multicollinearity in Raman spectra corresponding to nitric acid concentrations (0.1–9 M) and temperature (20–60 °C) was successfully modeled by PLSR and SVR. Determining how to efficiently build and evaluate PLSR and SVR models with dynamic temperature levels in acidic systems will benefit numerous applications. The range of nitric acid concentrations and temperature levels is highly relevant to nuclear fuel cycle reprocessing and other industrial applications. PLSR and SVR models were able to account for covarying and overlapping spectral features caused by changes in the HNO3 dissociation constant at elevated temperatures, which varied the proportions of HNO3 and dissociated ions H+ and NO3–. The D-optimal PLSR approach matched the prediction performance for nitric acid compared with a seven-level FF model to achieve a 75% reduction in sample set size and slightly outperformed the D-optimal SVR model. The seven-level FF nonlinear SVR model outperformed PLSR models for temperature and achieved strong RMSEP % values for both nitric acid (1.8%) and temperature (2.3%). Fewer temperature levels were required to maintain robust nitric acid predictions. The designed approach in this work can be extended or augmented in future work to include additional variables that may be encountered in complex systems with even greater complexity [e.g., uranium(VI), corrosion products, and fission products]. The analytical method developed here goes beyond the nuclear field and can be applied in remote settings to determine the nitric acid concentration and solution temperature from Raman spectra with high accuracy.
Acknowledgments
This work used resources at the Radiochemical Engineering Development Center operated by the US Department of Energy’s Oak Ridge National Laboratory. This work was supported in part by the US Department of Energy Office of Science, Office of Workforce Development for Teachers and Scientists under the Science Undergraduate Laboratory Internships Program at Oak Ridge National Laboratory, administered by the Oak Ridge Institute for Science and Education.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c08219.
Extended discussion on error propagation, statistical comparisons, multielement, and training sets (PDF)
Author Contributions
The manuscript was written using contributions of all authors. All authors have given approval to the final version of the manuscript.
Funding for this work was provided by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists (WDTS) under the Science Undergraduate Laboratory Internships Program (SULI) program at Oak Ridge National Laboratory, administered by the Oak Ridge Institute for Science and Education, which supported D.V.R., and the Advanced Research Projects Agency–Energy under contract DE-AC05-00OR22725, which supported L.R.S., J.D.E, and L.H.D, and under Award Number DE-AR0001689, which supported J.D.B. The information, data, or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under contract DE-AC05-00OR22725 and Award Number DE-AR0001689. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
The authors declare no competing financial interest.
Supplementary Material
References
- Nee K.; Bryan S. A.; Levitskaia T. G.; Kuo J. W.-J.; Nilsson M. Combinations of NIR, Raman spectroscopy and physicochemical measurements for improved monitoring of solvent extraction processes using hierarchical multivariate analysis models. Anal. Chim. Acta 2018, 1006, 10–21. 10.1016/j.aca.2017.12.019. [DOI] [PubMed] [Google Scholar]
- Bryan S. A.; Levitskaia T. G.; Johnsen A. M.; Orton C. R.; Peterson J. M. Spectroscopic monitoring of spent nuclear fuel reprocessing streams: an evaluation of spent fuel solutions via Raman, visible, and near-infrared spectroscopy. Radiochim. Acta 2011, 99, 563–572. 10.1524/ract.2011.1865. [DOI] [Google Scholar]
- McFarlan C.; Nordon A.; Sarsfield M.; Taylor R.; Chen H. Comparison of Raman and mid-infrared spectroscopy for quantification of nitric acid in PUREX-relevant mixtures. Prog. Nucl. Energy 2023, 165, 104898. 10.1016/j.pnucene.2023.104898. [DOI] [Google Scholar]
- Sadergaski L.; Einkauf J. D.; Delmau L. H.; Burns J. D. Leveraging Design of Experiments to Build Chemometric Models for the Quantification of Uranium(VI) and HNO3 by Raman Spectroscopy. Front. Nucl. Eng. 2024, 3, 1411840. 10.3389/fnuen.2024.1411840. [DOI] [Google Scholar]
- Andrews H. B.; Sadergaski L. R. Leveraging visible and near-infrared spectroelectrochemistry to calibrate a robust model for Vanadium(IV/V) in varying nitric acid and temperature levels. Talanta 2023, 259, 124554. 10.1016/j.talanta.2023.124554. [DOI] [PubMed] [Google Scholar]
- Sadergaski L. R.; Andrews H. B. Simultaneous quantification of uranium(VI), samarium, nitric acid, and temperature with combined ensemble learning, laser fluorescence, and Raman scattering for real-time monitoring. Analyst 2022, 147, 4014–4025. 10.1039/D2AN00998F. [DOI] [PubMed] [Google Scholar]
- Sadergaski L. R.; Andrews H. B.; Wilson B. A. Comparing Sensor Fusion and Multimodal Chemometric Models for Monitoring U(VI) in Complex Environments Representative of Irradiated Nuclear Fuel. Anal. Chem. 2024, 96, 1759–1766. 10.1021/acs.analchem.3c04911. [DOI] [PubMed] [Google Scholar]
- Sadergaski L. R.; Toney G. K.; Delmau L. H.; Myhre K. G. Chemometrics and Experimental Design for the Quantification of Nitrate Salts in Nitric Acid: Near-Infrared Spectroscopy Absorption Analysis. Appl. Spectrosc. 2021, 75 (9), 1155–1167. 10.1177/0003702820987281. [DOI] [PubMed] [Google Scholar]
- Casella A. J.; Levitskaia T. G.; Peterson J. M.; Bryan S. A. Water O-H Stretching Raman Signature for Strong Acid Monitoring via Multivariate Analysis. Anal. Chem. 2013, 85, 4120–4128. 10.1021/ac4001628. [DOI] [PubMed] [Google Scholar]
- Burns J. D.; Moyer B. A. Group Hexavalent Actinide Separations: A New Approach to Used Nuclear Fuel Recycling. Inorg. Chem. 2016, 55 (17), 8913–8919. 10.1021/acs.inorgchem.6b01430. [DOI] [PubMed] [Google Scholar]
- Burns J. D.; Moyer B. A. Uranyl nitrate hexahydrate solubility in nitric acid and its crystallization selectivity in the presence of nitrate salts. J. Clean. Prod. 2018, 172, 867–871. 10.1016/j.jclepro.2017.10.258. [DOI] [Google Scholar]
- Einkauf J. D.; Burns J. D. Recovery of Oxidized Actinides, Np(VI), Pu(VI), and Am(VI), from Cocrystallized Uranyl Nitrate Hexahydrate: A Single Technology Approach to Used Nuclear Fuel Recycling. Ind. Eng. Chem. Res. 2020, 59 (10), 4756–4761. 10.1021/acs.iecr.0c00381. [DOI] [Google Scholar]
- Chikazawa T.; Kikuchi T.; Shibata A.; Koyama T.; Homma S. Batch Crystallization of Uranyl Nitrate. J. Nucl. Sci. Technol. 2008, 45 (6), 582–587. 10.1080/18811248.2008.9711882. [DOI] [Google Scholar]
- Shin C.; Kim J.; Kim J.; Kim H.; Lee H.; Mohapatra D.; Ahn J.; Ahn J.; Bae W. Recovery of nitric acid from waste etching solution using solvent extraction. J. Hazard. Mater. 2009, 163, 729–734. 10.1016/j.jhazmat.2008.07.019. [DOI] [PubMed] [Google Scholar]
- Bell K.; Geist A.; McLachlan F.; Modolo G.; Taylor R.; Wilden A. Nitric acid extraction into TODGA. Procedia Chem. 2012, 7, 152–159. 10.1016/j.proche.2012.10.026. [DOI] [Google Scholar]
- Frost V. J.; Molt K. Analysis of aqueous solutions by near-infrared spectrometry (NIRS) III. Binary mixtures of inorganic salts in water. J. Mol. Struct. 1997, 410–411, 573–579. 10.1016/S0022-2860(96)09707-4. [DOI] [Google Scholar]
- Xi S.; Zhang X.; Luan Z.; Du Z.; Li L.; Wang B.; Cao L.; Lian C.; Yan J. A Direct Quantitative Raman Method for the Measurement of Dissolved Bisulfate in Acid-Sulfate Fluids. Appl. Spectrosc. 2018, 72 (8), 1234–1243. 10.1177/0003702818773117. [DOI] [PubMed] [Google Scholar]
- Tomikawa K.; Kanno H. Raman Study of Sulfuric Acid at Low Temperatures. J. Phys. Chem. A 1998, 102, 6082–6088. 10.1021/jp980904v. [DOI] [Google Scholar]
- Lund Myhre C. E.; Christensen D. H.; Nicolaisen F. M.; Nielsen C. J. Spectroscopic Study of Aqueous H2SO4 at Different Temperatures and Compositions: Variations in Dissociation and Optical Properties. J. Phys. Chem. A 2003, 107, 1979–1991. 10.1021/jp026576n. [DOI] [Google Scholar]
- Ziouane Y.; Leturcq G. New Modeling of Nitric Acid Dissociation Function of Acidity and Temperature. ACS Omega 2018, 3 (6), 6566–6576. 10.1021/acsomega.8b00302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levanov A. V.; Isaikina O. Ya.; Lunin V. V. Dissociation Constant of Nitric Acid. Russ. J. Phys. Chem. 2017, 91 (7), 1221–1228. 10.1134/S0036024417070196. [DOI] [Google Scholar]
- Langner T.; Retig A.; Acker J. Raman spectroscopic determination of the degree of dissociation of nitric acid in binary and ternary mixtures with HF and H2SiF6. J. Raman Spectrosc. 2020, 51, 366–372. 10.1002/jrs.5769. [DOI] [Google Scholar]
- Sadergaski L. R.; Irvine S. B.; Andrews H. B. Partial Least Squares, Experimental Design, and Near Infrared Spectrophotometry for the Remote Quantification of Nitric Acid Concentration and Temperature. Molecules 2023, 28 (7), 3224. 10.3390/molecules28073224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews H. B.; Sadergaski L. R.; Cary S. K. Pursuit of the Ultimate Regression Model for Samarium (III), Europium (III), and LiCl Using Laser-Induced Fluorescence, Design of Experiments, and a Genetic Algorithm for Feature Selection. ACS Omega 2023, 8, 2281–2290. 10.1021/acsomega.2c06610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang G.; Lee K.; Park H.; Lee J.; Jung Y.; Kim K.; Son B.; Park H. Quantitative analysis of mixed hydrofluoric and nitric acids using Raman spectroscopy with partial least squares regression. Talanta 2010, 81, 1413–1417. 10.1016/j.talanta.2010.02.045. [DOI] [PubMed] [Google Scholar]
- Lund Myhre C. E.; Grothe H.; Gola A. A.; Nielsen C. J. Optical Constants of HNO3/H2O and H2SO4/HNO3/H2O at Low Temperatures in the Infrared Region. J. Phys. Chem. A 2005, 109, 7166–7171. 10.1021/jp0508406. [DOI] [PubMed] [Google Scholar]
- Sadergaski L. R.; Andrews H. B.; Rai D. II; Anagnostopoulos V. A. Comparing Designed Training Sets to Optimize Multivariate Regression Models for Pr, Nd, and Nitric Acid Using Spectrophotometry. Appl. Spectrosc. Practica. 2024, 2 (1), 1–12. 10.1177/27551857241243083. [DOI] [Google Scholar]
- Bondi R. W. Jr; Igne B.; Drennen J. K. III; Anderson C. A. Effect of Experimental Design on the Prediction Performance of Calibration Models Based on Near-Infrared Spectroscopy for Pharmaceutical Applications. Appl. Spectrosc. 2012, 66 (12), 1442–1453. 10.1366/12-06689. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Perez R.; Vogt M.; Bajorath J. Influence of varying training set composition and size on support vector machine-based prediction of active compounds. J. Chem. Inf. Model. 2017, 57, 710–716. 10.1021/acs.jcim.7b00088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aksenenko V. M.; Murav’ev N. S.; Taranenko G. S. Raman-Scattering Study of Nitric-Acid Solutions. J. Appl. Spectrosc. 1986, 44, 70–72. 10.1007/bf00658324. [DOI] [Google Scholar]
- Edwards H. G. M.; Fawcett V. Quantitative Raman spectroscopic studies of nitronium ion concentrations in mixtures of sulphuric and nitric acids. J. Mol. Struct. 1994, 326, 131–143. 10.1016/0022-2860(94)85013-5. [DOI] [Google Scholar]
- Pershin S. M.; Grishin M. Ya.; Lednev V. N.; Garnov S. V.; Bukin V. V.; Chizhov P. A.; Khodasevich I. A.; Oshurko V. B. Quantification of distortion of the water OH-band using picosecond Raman spectroscopy. Laser Phys. Lett. 2018, 15, 035701. 10.1088/1612-202X/aa9321. [DOI] [Google Scholar]
- Sun Q. The Raman OH stretching bands of liquid water. Vib. Spectrosc. 2009, 51, 213–217. 10.1016/j.vibspec.2009.05.002. [DOI] [Google Scholar]
- Hu Q.; Lu X.; Lu W.; Chen Y.; Liu H. An extensive study on Raman spectra of water from 253 to 753 K at 30 MPa: A new insight into structure of water. J. Mol. Spectrosc. 2013, 292, 23–27. 10.1016/j.jms.2013.09.006. [DOI] [Google Scholar]
- Wu X.; Lu W.; Ou W.; Caumon M.; Dubessy J. Temperature and salinity effects on the Raman scattering cross section of the water OH-stretching vibration band in NaCl aqueous solutions from 0 to 300°C. J. Raman Spectrosc. 2017, 48, 314–322. 10.1002/jrs.5039. [DOI] [Google Scholar]
- Lednev V. N.; Grishin M. Ya.; Pershin S. M.; Bunkin A. F. Quantifying Raman OH-band spectra for remote water temperature measurements. Opt. Lett. 2016, 41 (20), 4625–4628. 10.1364/ol.41.004625. [DOI] [PubMed] [Google Scholar]
- Lewis N. H. C.; Fournier J. A.; Carpenter W. B.; Tokmakoff A. Direct Observation of Ion Pairing in Aqueous Nitric Acid Using 2D Infrared Spectroscopy. J. Phys. Chem. B 2019, 123, 225–238. 10.1021/acs.jpcb.8b10019. [DOI] [PubMed] [Google Scholar]
- Fournier J. A.; Carpenter W.; Marco L. D.; Tokmakoff A. Interplay of Ion-Water and Water-Water Interactions within the Hydration Shells of Nitrate and Carbonate Directly Proved with 2D IR Spectroscopy. J. Am. Chem. Soc. 2016, 138, 9634–9645. 10.1021/jacs.6b05122. [DOI] [PubMed] [Google Scholar]
- Heine N.; Kratz E. G.; Bergmann R.; Schofield D.; Asmis K. R.; Jordan K. D.; McCoy A. B. Vibrational Spectroscopy of the Water-Nitrate Complex in the O-H Stretching Region. J. Phys. Chem. A 2014, 118, 8188–8197. 10.1021/jp500964j. [DOI] [PubMed] [Google Scholar]
- Nelson G. L.; Lines A. M.; Casella A. J.; Bello J. M.; Bryan S. A. Development and testing of a novel micro-Raman probe and application of calibration method for the quantitative analysis of microfluidic nitric acid streams. Analyst 2018, 143, 1188–1196. 10.1039/C7AN01761H. [DOI] [PubMed] [Google Scholar]
- Lines A. M.; Nelson G. L.; Casella A. J.; Bello J. M.; Clark S. B.; Bryan S. A. Multivariate Analysis to Quantify Species in the Presence of Direct Interferents: Micro-Raman Analysis of HNO3 in Microfluidic Devices. Anal. Chem. 2018, 90, 2548–2554. 10.1021/acs.analchem.7b03833. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.