Ultra-wide-angle peripheral refraction using a laser-scanning instrument

Abstract

We compared the peripheral refractive measurements of a recently proposed laser-scanning instrument with an established peripheral refractor. Two-dimensional refractive maps were obtained using both instruments for 18 young subjects with differing values of central refraction. The comparison shows a strong correlation between devices in the overlapping measurement area, with the new device extending the range of the explored retinal area to a 100-degree-diameter circular patch, compared to the 60°x35° rectangular area of the older peripheral refractor. Larger refractive maps exhibit trends that cannot be easily predicted from narrower scans. These results demonstrate that the new instrument can be a useful tool for assessing wide-angle peripheral optical data in the human eye.

1. Introduction

Peripheral vision strongly affects the ability to perform everyday tasks, such as driving [1] and walking [2]. It acquires even more importance for subjects with pathologies that hinder central vision [3] for whom peripheral aberration correction can improve their quality of life [4]. Despite this, the study of peripheral optics was not a very hot research topic until its potential link to myopia progression was proposed [5–8]. Due to the high prevalence of myopia [9] and its relationship with several blind-threatening diseases [10], there is great interest in the mechanisms underlying its progression and prevention.

Animal studies have shown the impact of non-foveal vision in eye growth [11–13] and have served as the basis for myopia control lenses with altered optical quality in the periphery [14,15]. However, the role of peripheral refraction as a risk predictor for myopia and high myopia is still a matter of debate. While earlier studies in humans have presented the relationship between relative peripheral hyperopia and myopia development [16,17] as a promising predictive tool, more recent studies focused on the horizontal field have concluded that this trend could be a consequence rather than a cause of myopia [5,18,19]. The situation may be different for the vertical meridian, as ocular size and peripheral refraction have been found to change differently in the horizontal and vertical dimensions depending on central refraction [20,21]. Studies in children have also found a correlation between refraction in the superior part of the retina and myopia development [22], which could be used as a risk assessment tool for early prevention of myopia progression. Another important limitation of previous studies is the range of eccentricities covered by the measurements [23]. The handful of studies producing two-dimensional refractive maps have been limited to a maximum eccentricity of 30 degrees [8,24]. However, some eyes exhibit peripheral refractive trends that can only be seen at larger angles [25,26].

Whether the vertical meridian or larger eccentricities are relevant to myopia progression is still an open question waiting for additional clinical research. The scarcity of two-dimensional longitudinal studies on wide-angle peripheral refraction stems from the absence of convenient instrumentation. While there are multiple tools to measure refraction [23], most of them require fixational changes to measure in the periphery. Hartmann-Shack devices have been shown to perform similarly to other autorefractors [27] while being able to provide fast refractive measurements and high-order aberration information. Although external fixations allow peripheral refractive measurements to be made [28], they are slow and bothersome, and thus impractical for obtaining large-field and high-sampling refraction maps.

A solution to this problem was the introduction of mechanical rotations of a Hartmann-Shack measurement arm while maintaining central fixation [29,30]. Although these devices provide significant improvements, they are still limited to sampling specific meridians or require external fixations for two-dimensional mapping. To overcome these shortcomings, Fernandez et al. [31] recently presented a novel ultra-wide-angle, optically-based laser scanning peripheral refractor (UPER) capable of producing, in a few seconds, a two-dimensional high-resolution refraction map for a 50-degree-diameter field, which could be further extended up to 100° by using additional fixations.

While some measurements with UPER in real eyes were presented as proof-of-concept, the aim of this work was to validate the instrument by performing a thorough comparison with another previously used apparatus, the rotation-based refractor (VPR) developed by Jaeken et al. [29]. This device has been previously compared with fixation-based Hartmann-Shack measurements [29], other photorefractors [32], and has been widely used in several clinical studies [22,24,33,34]. In addition, we assessed the importance of the extended range of UPER to obtain peripheral refractive trends that are not easily predicted with narrower scans.

2. Methods

2.1. Instrument descriptions

While detailed descriptions of UPER and VPR can be found in Refs. [31] and [29], respectively, we provide here a brief overview of both systems (shown in Fig. 1), focusing on the technical aspects that could lead to potential differences in their measurements.

Fig. 1.

Left: VPR with the external vertical fixation arrangement. Right: UPER prototype.

VPR combines a motorized sensing arm with a metallic mirror and a dichroic mirror, both of which are static and long enough to accommodate the full scan range while allowing an open view of the background for fixation purposes. The measurement laser operates at a 780-nm wavelength, and a Hartmann-Shack wavefront sensor obtains the aberrations of the eye. A pupil camera allows the clinician to position the subject at the rotation point of the motorized arm, where the images for all scanning angles can be captured. The main protocol of the device consists of four consecutive scans that are averaged to obtain the peripheral refraction in a 60-degree horizontal meridian in steps of 1°. Ten vertical fixations (see Fig. 1, left panel) consisting of cross-shaped lights were introduced every 4° to extend the measurement to a 60°x36° range.

UPER core measurement protocol obtains peripheral refraction in a two-dimensional 50-degree-diameter region with sampling steps of 5°. The scanning angle of an 850-nm measurement laser-beam is controlled by a steering mirror and conjugated to the pupil plane through a 5-lens eyepiece. After reflection in the retina, light is de-scanned by the mirror to reach a Hartmann-Shack wavefront sensor.

The subject’s fixation is created by multiplexing the measurement laser in time, which is visible as a red dot. Therefore, the instrument creates intervals where the actual measurements are taking place that alternate with fast and small movements that create a fixation target for the subject in the shape of a small circle. This fixation can be set at any point in the 50-degree diameter region, effectively allowing the combination of multiple scans with different fixations to increase the measurement range up to a 100-degree diameter region.

An additional advantage of using a small-aperture laser for fixation is the extended depth of focus, which allows reliable fixation, even for highly myopic subjects. Conversely, this fixation scheme has the disadvantage of making the instrument a closed-view system. Without additional visual cues and with a fixation that is similarly focused across a wide defocus range, subjects may experience different levels of accommodation for each individual scan. The instrument compensates for this by shifting the measured defocus of the new scan to match the average of the overlapping region for previous fixations. Finally, subject positioning is achieved with a double pupil camera setup that allows for precise positioning in the x-, y-, and z-directions.

The algorithm to estimate refractive errors from wavefront data is the same in both instruments. Spherical equivalent, M, and Jackson’s cross-cylinders, J0 and J45, are calculated from the second order Zernike coefficients determined over a 3-mm-diameter pupil.

2.2. Measurement protocol

Eighteen subjects (mean age: 32 ± 3 years) with different values of central refraction were recruited following the tenets of the Helsinki Declaration and adhered to the ethical protocols approved by Aier Academy of Ophthalmology (Changsha, China). Peripheral maps for each component of refraction (M, J0, and J45) of their right eyes were measured using both the UPER and VPR devices.

UPER measurement protocol consisted of obtaining a composite map formed by 13 scans with different fixations, eight of them in the horizontal and vertical meridians at 15° and 25° (up, down, nasal, and temporal), another four in the ±45° diagonals at 21°, and the central fixation. This scheme results in a retinal section of 100° diameter.

As mentioned in the previous section, the measurement range of VPR was extended from a 60-degree horizontal meridian to a 60°x36° region using external vertical fixations in 4-degree steps. This sampling step in the vertical direction was a requirement for other ongoing longitudinal studies. Consequently, the sampling schemes were not homogeneous between devices, and a direct comparison between maps in the overlapping region was not possible for the vertical meridians. Instead, each UPER row of values was compared to its nearest VPR line in the vertical direction if the difference was 0° (perfect match) or 1°, and with the mean between the two closest scans if they were at the same distance. In other words, UPER data for 5°, 10°, 15°, and 20° in the vertical direction were compared to VPR data for 4°, mean between 8° and 12°, 16°, and 20°, respectively.

On the other hand, considering the 5° sampling step in UPER, horizontal matching would simply require the selection of VPR data for eccentricities in multiples of 5°. However, we took advantage of the increased sampling scheme in VPR to implement a protocol for outlier rejection, which is not built-in in the software package of this older device as it is in the more modern UPER. These outliers were usually caused by corneal reflections that could produce erroneous results that the instrument did not eliminate and would therefore affect the comparison between devices. The first step of this outlier rejection protocol consisted of detecting and discarding VPR data points differing by more than 2 D from the median in a 2° horizontal neighborhood (5 points, including the central one). Rejected points were replaced by one of their closest neighbors (1° apart) that passed the same rejection criteria (discounting previously rejected data points) or one of their 2°-neighbors if none did. If no valid data point was found at this juncture, that location was left blank.

Additionally, once the 5°-spaced VPR-based retinal map was obtained, the second step of the outlier rejection protocol consisted of discarding data points differing by more than 1 D from the median value in its closest two-dimensional neighborhood (four points in a plus sign, the central one excluded). This additional step was necessary since it was not uncommon for corneal reflections to appear in the ranges of 5° to 10°, sometimes producing similar but erroneous results in the 5-point neighborhood used in the previous step.

2.3. Data analysis

The relative spherical equivalent, M, and the astigmatism components, J0 and J45, of the refraction maps were analyzed to study the correlation between both devices.

The peripheral refractive maps produced by both instruments were compared in the overlapping region, constrained by the smaller measurement range of VPR. The intraclass correlation coefficient (ICC) was obtained for each subject individually as well as for the entire dataset. In particular, we used the ICC(3,1) coefficient, as the two-way mixed model best fits the comparison between two specific instruments. Additionally, we calculated the mean absolute difference between each pair of maps to obtain a metric of absolute agreement between the devices.

To assess the potential importance of measuring in a wider retinal region, the capability of the spherical equivalent in a smaller section of the retina to predict the far periphery has been studied. To this end, we performed a fit to a second-order ellipsoidal function of UPER retinal maps in a smaller inner region (angles at or closer than 25° to fovea). This shape was chosen as it has been shown to accurately describe larger sections of the retina [5].

The ellipsoidal function had the form:

$$M_{fit}(x,y)=\frac{{(x-x_0)}^2}{R_x^2}+\frac{{(y-y_0)}^2}{R_y^2}+c$$ (1)

Where M is the spherical equivalent, R_x and R_y are the semidiameters along the x and y axes, respectively, x₀ and y₀ are the central coordinates of the ellipsoid, and c is the spherical equivalent at the central position. Then, the root mean square errors between the fit and the actual data values from UPER were calculated both inside the fitting region and in the outer region, defined as the angles outside the inner region. The former is related to the goodness of the fitting, while the latter provides insight into the capability of smaller refraction maps to predict refraction in the far periphery.

In addition, we obtained the mean difference between the fit and actual measurements in different sections of the far periphery. These sections were the upper, bottom, temporal, and nasal far regions, defined as the corresponding quadrants separated by two 45° meridians that were also outside of the inner region. For each zone, the standard deviation of the mean difference was calculated across subjects. While the root mean square error provides an estimate of how well the fitted form predicts the values in the periphery, the standard deviation better represents the variability in the trends found in each region.

3. Results

3.1. Comparison of refraction maps

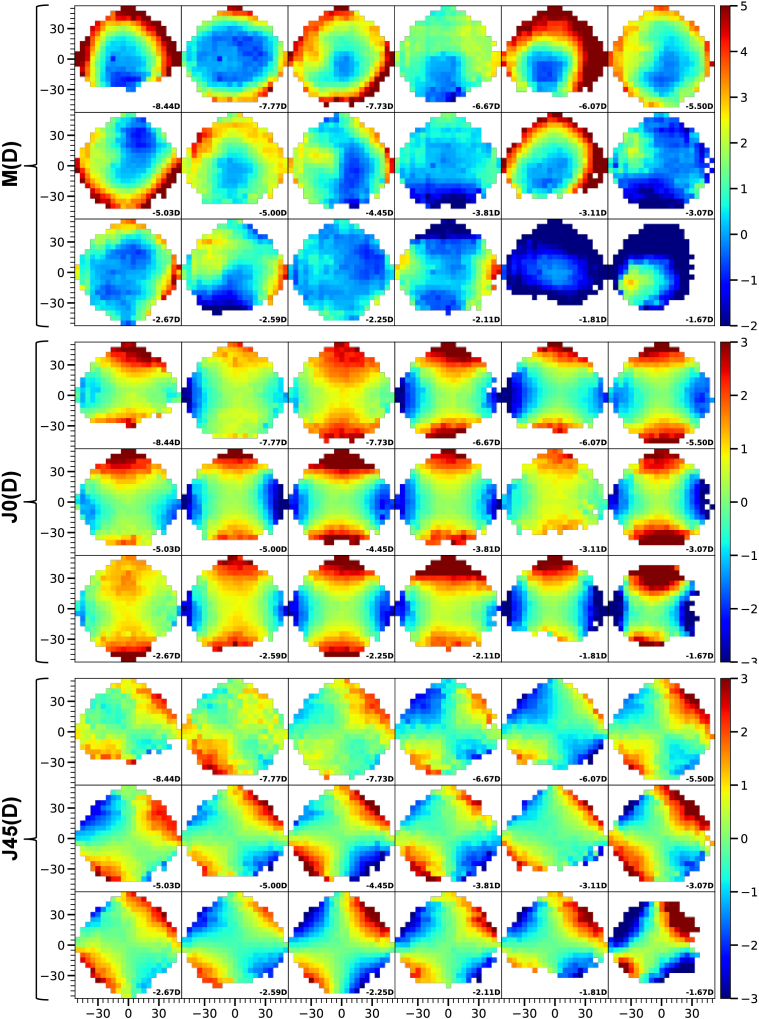
The peripheral maps of M, J0, and J45, measured with UPER for the 18 subjects are shown in Fig. 2. They are sorted from left to right and top to bottom by ascending central spherical equivalent value (i.e., from higher to milder myopia), as shown in the bottom right corner of each map. The instrument automatically created the full 100° map by combining data from the 13 individual fixations used during the measurement procedure. This process takes 9.44 minutes on average, with the longest measurements being 30 and 19 minutes, while the rest lasted between 5 and 10 minutes.

Fig. 2.

Relative spherical equivalent M (top), J0 (center), and J45 (bottom) for the right eye of 18 subjects measured with UPER. Positive and negative X and Y axis represent temporal, nasal, superior and inferior locations of the retina in degrees, respectively. The color bar is shown in diopters, and the central spherical equivalent value as measured by UPER is shown in the bottom right corner of each map.

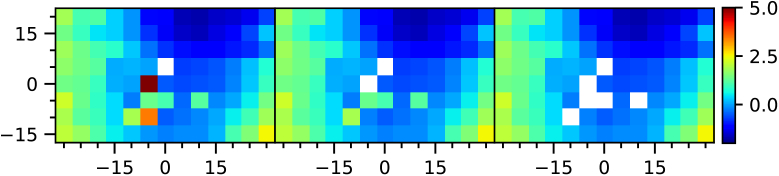
An example of the outlier removal protocol applied to VPR data, which is necessary for intraclass correlation analysis, is shown in Fig. 3. The average number of outliers removed was three per scan, with some subjects presenting no outliers while others had up to eight, which significantly affected the correlation calculation.

Fig. 3.

Example of outlier discarding protocol in VPR. Left panel: Original data, where some points are missing due to poor image quality. Central panel: Results after horizontal neighborhood comparison (first step). Right panel: Results after 2-D neighborhood comparison (final step). Axes and color bar follow the same notation as in Fig. 2.

Figure 4 shows the central 60°x35° excerpt of UPER maps side by side with the results from VPR for each subject, showing similar trends and overall values for all subjects. When comparing the values for the central refraction between instruments, we obtained that UPER results were 1.00 ± 0.53D more myopic on average. This was probably due to its nature as a closed-view system inducing the subjects to accommodate to some extent, which is less of an issue in the open-view VPR. The differences in the central values of J0 and J45 were 0.064 ± 0.237D and -0.167 ± 0.302D, respectively, further suggesting that the significantly larger differences in M were due to accommodation and not a systematic difference across devices.

Fig. 4.

Pairs of maps for the 18 subjects (in transposed order with respect to Fig. 2) comparing M (top), J0 (center), and J45 (bottom) provided by VPR with a cutout of UPER measurements in the overlapping area (left and right panels of each pair, respectively). Axes and color bar follow the same notation as in Fig. 2.

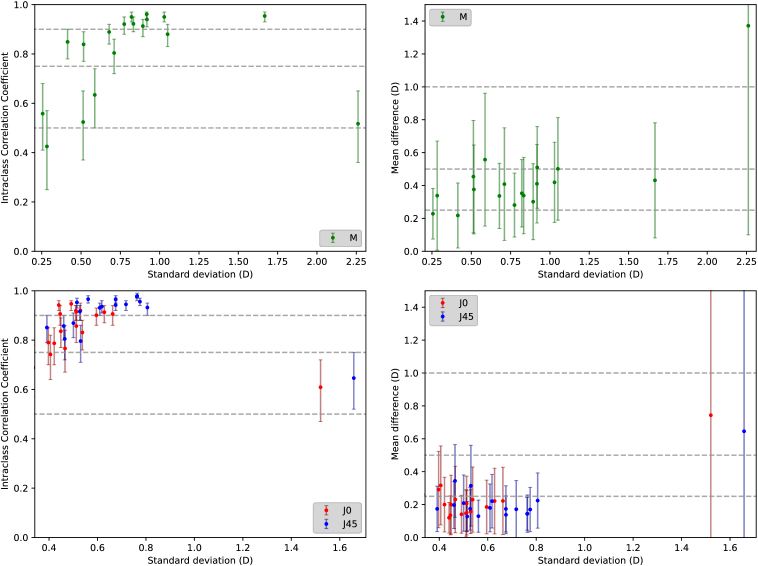
The ICC values and mean absolute differences in refraction between the instruments are shown in Fig. 5(left and right columns, respectively). Plots in the top row correspond to the spherical equivalent, M, while those below combine the information of both astigmatisms, J0 and J45. The x-axis represents the standard deviation of the corresponding refractive component in UPER maps. This choice was made under the assumption that cases showing less progression with eccentricity (i.e., flatter maps with lower standard deviations) could be more sensitive to measurement noise, resulting in lower ICC values. On the other contrary, the mean absolute differences were not expected to present this type of dependency if the impact of noise was similar across subjects.

Fig. 5.

Left: Intraclass correlation coefficient ICC(3,1) between devices for each subject’s spherical equivalent (top), and astigmatisms J0 and J45 (bottom). Dashed lines represent ICC of 0.5, 0.75, and 0.9. Right: Mean absolute differences between devices for M (top), and J0 and J45 (bottom). Dashed lines represent 0.25, 0.5, and 1 diopter differences. In all cases, the X-axis represents the standard deviation of the corresponding refraction component in the UPER map cutout. Error bars represent 95% confidence intervals.

The similarities between the instruments for each refraction component can be easily observed by visually comparing the maps in Fig. 4. Classifying the relative spherical equivalent data (Fig. 5, top left) according to the criteria by Koo et al [35], only one subject showed poor correlation between devices (ICC < 0.5), while the rest showed moderate correlation (0.5 < ICC < 0.75, four subjects), good correlation (0.75 < ICC < 0.9, five subjects) or excellent correlation (0.9 < ICC, eight subjects). We also found that subjects with smaller correlation coefficients tended to have relatively flatter maps with only one exception. This subject was an ortho-k lens user, which could explain the poorer measurements, as well as the higher difference between central and peripheral refraction. The correlations improved when considering J0 and J45 astigmatisms, as 22 and 11 comparisons showed excellent or good correlation, respectively, and only three cases were moderately correlated.

Pooling the data of all subjects, we obtained a global intraclass correlation coefficient for M of 0.812 (95% confidence interval [0.796, 0.827]), whereas for J0 and J45 the results were ICC = 0.906 (95%CI [0.861, 0.943]) and ICC = 0.932 (95%CI [0.904, 0.952]), respectively. This indicates that both instruments are measuring similar trends across different metrics and subjects in the overlapping measurement region.

The mean difference in M between devices across all subjects was 0.435 ± 0.244D, and 17 subjects showed differences smaller than 0.6D. The only outlier was the same ortho-k user with a significantly higher difference of 1.37D. On the other hand, the rest of the subjects that showed worse correlations presented similar mean absolute differences, further indicating that the decrease in correlation coefficients was probably caused by an increased impact of measurement noise in flatter maps. For J0 and J45, the mean differences across subjects were 0.231 ± 0.135D and 0.215 ± 0.119D, respectively, further demonstrating the similar behaviors of both devices.

3.2. Wide field analysis

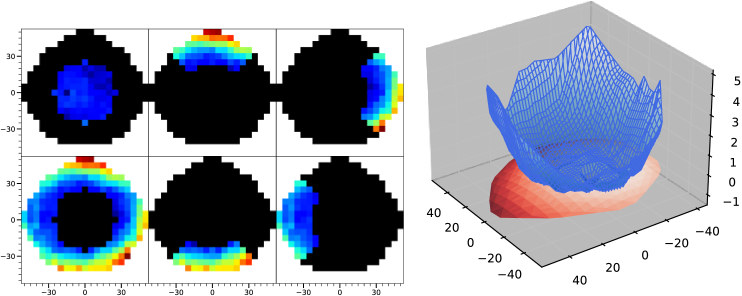
The importance of wider angles in peripheral refraction measurements was studied by comparing different regions of the complete spherical equivalent maps provided by UPER, as illustrated in Fig. 6(left). Data from the central inner region, defined as 50°-diameter circle around the fovea, was used to perform a predictive analysis by fitting them to an ellipsoidal shape and using the resulting function to estimate the expected values in a 100°-diameter circle, thus extrapolating the inner behavior of refraction to the outer region. The results were then compared separately with the measured values for the inner and outer zones. An example of this comparison can be seen in Fig. 6, right, where the relatively flat map in the inner region produced a surface fit that did not accurately represent the overall peripheral hyperopic trend for larger angles in a highly myopic subject (-7.77D central refraction).

Fig. 6.

Left panels: Zones selected for analysis. Top-left: Inner region used for the ellipsoidal fit. Bottom-left: outer region used to analyze the predictive power of the fit. The other four panels represent the four quadrants separately analyzed. Right graph: 3D plot of a refractive map. The blue surface represents the actual 100° measurement while the red surface represents the extrapolation of the ellipsoidal fit in the inner 50°. X and Y axes represent retinal angle in degrees and Z axis represents spherical equivalent in diopters.

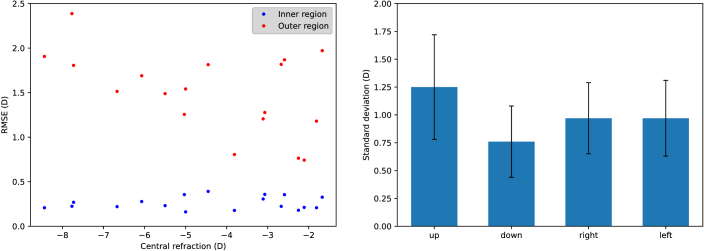
The root-mean-square error (RMSE) between the fit and data in each region is shown as a function of the subject’s central refraction in Fig. 7. (left). The mean RMSE across subjects changed from 0.26 D ± 0.07 D in the inner circle to 1.5 D ± 0.44 D in the outer ring. This suggests that the actual refraction behavior as we move further into the periphery of the retina cannot be easily extrapolated from measurements limited to the central area.

Fig. 7.

Left: Root mean squared error between fit and data for the inner region used for the fit (blue dots) and in the outer region with larger eccentricities (red dots). Right: Standard deviation across subjects of the difference between the prediction of the ellipsoidal fit and the measured values in each zone.

Additionally, the standard deviation across subjects of the RMSE between the fit and measurements in the four outer quadrants (see Fig. 6, left) is shown in Fig. 7(right). Although the differences between quadrants were not statistically significant, the RMSE for the upper retina was slightly higher on average, which might indicate that this quadrant shows tendencies that are even harder to predict.

4. Discussion

The number of data points in the full retinal map obtained by UPER changes slightly from subject to subject, mainly due to a decrease in the optical quality in the far periphery, causing some images to be discarded. An additional common trend is the lack of data on the inferior region of the retina caused by the superior eyelid blocking the path of the laser, a problem that is particularly noticeable in the eastern Asian population that comprised most of the subjects of this study. However, this should not be an insurmountable limitation, as techniques to lift the eyelid can be used. Even then, these techniques would only be required for the scan with the fixation far in the inferior retina. This single scan requires only a few seconds, reducing discomfort, and is a precaution that would only be required for some subjects.

Even with these missing points, most of the peripheral 100-degree retinal patch was obtained. While 18 eyes are not sufficient to obtain statistically significant data on the relationship between the relative maps and their central refraction, there seems to be the expected trend of higher relative hyperopia for more myopic subjects [11]. An average time of less than 10 minutes to obtain the full range with UPER is beneficial for longitudinal studies where multiple subjects need to be measured in relatively short periods of time, particularly when considering that the narrower scans with VPR were performed in a similar amount of time. The two longer measurements of more than 20 minutes were the first two subjects, implying that clinician’s familiarity with the device played an important role in the measurement time. This highlights the relevance of training to ensure that the full measurement protocol is fast and comfortable for the subjects, especially when dealing with less cooperative individuals, such as children.

While the comparison between the instruments yielded a strong correlation for all three measured refractive components, the concordance could be even stronger but for some hampering factors. For example, the angle shift that was used to match angles due to the non-coincident vertical sampling schemes was 2° at most (in that case, the average of the top and bottom neighbors was taken). Although the typical changes in the spherical equivalent across those ranges are of the order of 0.05D [21], this practice could have a small deleterious effect on the measurement comparison.

The accommodation apparently induced by UPER could cause not only an overall shift in the retinal maps, as considered here, but also produce small changes in the optical quality in the periphery that could in turn affect the comparison. However, the relationship between accommodation and changes in relative peripheral shape is not clear. Some studies suggest that an accommodation of 2.5D can result in up to 0.4D changes in relative peripheral refraction at >40° [36]. On the other hand, similar research has shown no significant differences with accommodation of 3D and up to 30° in peripheral refraction [37]. For the VPR and UPER comparison we would expect small differences, given that the largest angle is 30° horizontal while the average accommodation was approximately 1D. Nonetheless, future experiments should take into account the accommodative effect of UPER and could consider cycloplegia if absolute spherical equivalent measurements are essential.

Additionally, a stronger and more precise outlier rejection protocol for VPR should improve the overall data quality. Finally, small fixation differences between the measurements of the two devices, particularly in VPR, where the external fixations had to be set manually, may have affected the final comparison. Any movement relative to each other, of the device or the post with the vertical fixations, can slightly alter the fixation position, making the setup less stable than the internally controlled fixation in UPER.

Correcting some or all of these issues should increase the ICC and reduce the mean absolute difference between the instruments, thus improving the comparison between devices. On the other hand, we do not expect any of them to have a great impact on the ability of both instruments to accurately show the trends in peripheral refraction, particularly when compared to the range of the relative spherical equivalent results, which can change in excess of 5 D between central refraction and 50-degree periphery.

Although ellipsoidal functions have been shown to be good overall descriptors of retinal shape [5], the best fit of smaller regions of the retinal map depends on the subject for near emmetropic cases [26] and the overall shape changes depending on central refraction [6]. This best-fit discrepancy should artificially increase the RMSE for both the inner and outer regions, with a stronger impact on the latter, as it is more dependent on an accurate prediction.

However, the differences between and within groups of different central refractive values show the difficulty in predicting the actual behavior of the far periphery on a case-to-case basis. This is more impactful for emmetropes, where the change in refractive trends between smaller retinal sections and further regions of the periphery is subject dependent [26]. This becomes particularly important in myopia prevention, where children that are close to emmetropia would probably present flatter retinas and therefore larger sections of the periphery would be required to detect trends that could be used as predictors for myopia progression.

Zonal analysis did not show a statistically significant difference in the predictive capability (or lack thereof) of the central fit in the different regions of the periphery, but this study was limited to a small number of subjects. The results in the bottom retinal region were also skewed by the fact that most subjects had missing data in that region. However, the increased standard deviation of the difference between the central prediction and peripheral data found in the superior retina suggests that this region might be more difficult to predict. This is an interesting fact that could be worth studying in the future, as smaller eccentricities of this region in particular have been suggested in the literature as an indicator of myopia progression in children [22].

5. Conclusion

A recently presented peripheral refractor, UPER, was compared with a previous-generation instrument, VPR, which is widely employed in clinical settings for the same purpose. The older device was initially devised to measure in the horizontal meridian, but it has been used to produce rectangular 60°x35° peripheral refraction maps, at the cost of using an external, manually set fixation arrangement. UPER, on the other hand, performs a 2-dimensional scan and internally changes the fixation to increase the measurement range to a retinal patch of 100° in diameter.

Correlation analysis showed good agreement between the devices in the overlapping region, validating the new instrument. Furthermore, wide-field analysis suggests that the presence of retinal refractive trends in the far periphery (30° to 50° eccentricities) cannot be easily predicted from data in the limited patch covered by VPR while falling into the measurement range of the new instrument.

In conclusion, with its improved characteristics, UPER could be an important tool in multiple research and clinical fields, with a particular mention to myopia control. This could help to better understand the potential role of peripheral refraction in the onset and progression of myopia in children, which in turn could lead to the development of new early diagnostics and prevention strategies.

Funding

Agencia Estatal de Investigación10.13039/501100011033 (PID2023-146439OB); Centro para el Desarrollo Tecnológico Industrial10.13039/501100001872 (IDI-20220740); Fundación Séneca10.13039/100007801 (21402/FPl/20); Ministry of Science and Technology of the People's Republic of China10.13039/501100002855 (2022YFE0124600).

Disclosures

Some of the authors are co-inventors in a patent application of the described instrument.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.