Network analysis: An overview for mental health research

Abstract

Network approaches to psychopathology have become increasingly common in mental health research, with many theoretical and methodological developments quickly gaining traction. This article illustrates contemporary practices in applying network analytical tools, bridging the gap between network concepts and their empirical applications. We explain how we can use graphs to construct networks representing complex associations among observable psychological variables. We then discuss key network models, including dynamic networks, time‐varying networks, network models derived from panel data, network intervention analysis, latent networks, and moderated models. In addition, we discuss Bayesian networks and their role in causal inference with a focus on cross‐sectional data. After presenting the different methods, we discuss how network models and psychopathology theories can meaningfully inform each other. We conclude with a discussion that summarizes the insights each technique can provide in mental health research.

1. INTRODUCTION

The contemporary landscape of mental health research increasingly recognizes the intricate complexity of mental disorders as biopsychosocial systems (Davies & Roache, 2017). This recognition reflects a significant shift from traditional models, acknowledging that mental health issues cannot be fully understood through isolated symptoms or singular causal pathways; instead, they are products of complex interactions among biological, psychological, and social factors (Freedman, 1995; Fried, 2022). This systems perspective underscores the dynamic nature of mental health, where each component influences and is influenced by others in a constantly evolving network (Borsboom, 2017a).

Network approaches have highlighted a critical gap in traditional methods in clinical research. Historically, clinical approaches have often considered mental health through a more reductionist lens, which has its merits in some contexts but tends to oversimplify the multifaceted and interconnected nature of mental disorders (Kendler et al., 2011). The need for methodologies that can holistically address the complexity of these systems has become increasingly apparent, driving innovation and paradigmatic shifts in mental health research (Borsboom, Deserno, et al., 2021).

Network models have emerged as a fitting response to this need, offering a methodological framework that naturally accommodates the complexity of mental health disorders (Borsboom, 2017b; Ebrahimi, 2023; Fried et al., 2017). Network models not only serve as descriptive tools but also stand on their own as valuable tools for hypothesis generation. The ability to generate hypotheses about influential pathways within the network opens up new avenues for understanding how changes in one aspect of the system might ripple through and impact the overall mental health of an individual (Borsboom & Cramer, 2013; McNally, 2016). This has led to a growing interest in network psychometrics, which aims to model correlational patterns in psychological phenomena—such as symptoms, traits, affects, behaviors, cognitions, desires, abilities, and environments—in terms of interactions among their basic constituents (Borsboom, Deserno, et al., 2021). Over the last few decades, several psychological phenomena, including intelligence (Van Der Maas et al., 2006), personality (Cramer et al., 2012), psychopathology (Borsboom & Cramer, 2013), and attitudes (Dalege et al., 2016), have been reconceptualized as networks. This shift has necessitated the development of innovative methodologies to explore their properties under this new lens, further advancing our understanding of mental health in its full complexity.

The evolution of statistical methods in network psychometrics has significantly enriched the psychometrician's toolbox, providing a diverse array of tools that can be used in many scenarios. A few examples of such tools include network models for cross‐sectional (Briganti et al., 2023; Epskamp, Waldorp, et al., 2018; Marsman & Haslbeck, 2023; Van Borkulo et al., 2014) and panel data (Epskamp, 2020), community detection and dimensionality reduction tools (Christensen et al., 2023; Golino & Epskamp, 2017), and inference measures (Huth, de Ron, et al., 2023; Jones, Ma, & McNally, 2021; Williams & Mulder, 2020).

In this article, we offer a comprehensive overview of the current landscape of network analysis in mental health research, bridging theoretical network constructs and their empirical applications in the field. First, we briefly introduce the most commonly used framework: undirected network estimation in cross‐sectional data using frequentist estimation techniques. We elected to keep the introduction on these methods brief as other introductory texts already discuss these methods in detail (e.g., Borsboom, Deserno, et al., 2021; Epskamp & Fried, 2018; Isvoranu et al., 2022). Following this introduction, we elaborate on new lines of research that are currently growing prominently in the field of network analysis in mental health research: psychometric network modeling, Bayesian estimation techniques, causal inference, and longitudinal data analysis. Finally, we discuss how network models can effectively enhance the description, prediction, comprehension, and treatment of mental health disorders, thereby enriching the field of psychopathology with nuanced insights and methods.

2. THE ELEMENTS OF A NETWORK

A network consists of a set of nodes and a set of edges connecting the nodes. In a statistical network model, such as the types we discuss below, nodes represent variables, and edges represent statistical relationships between these variables, such as log‐linear relationships, (partial) correlation coefficients or regression coefficients (Borsboom, van der Maas, et al., 2021; Burger, Isvoranu, et al., 2022). Network science typically starts by observing nodes and edges representing a system (e.g., social connections, the Internet, the World Wide Web, or transportation networks, to name a few examples) and then focuses on examining their properties. Psychometric networks, however, involve an additional challenge: they cannot be simply observed but must be inferred from the available data (Bringmann et al., 2019; Epskamp, Borsboom, & Fried, 2018). Nodes can define variables at different levels of abstraction, such as symptoms versus disorders and personality facets versus traits. The most informative abstraction level depends on the research question at hand. Different abstraction levels can also provide different perspectives on the same psychological phenomenon (Costantini & Perugini, 2012).

Edges can be undirected or directed, indicating symmetrical relationships among nodes or asymmetrical relationships. Edges can be weighted, but typically, special attention is also placed on whether or not edge weights are exactly equal to 0 (indicating that an edge is not included in the network). Several methods have been developed for estimating the network structure (including edges) and the edge weights (parameters associated with edges), with different approaches offering different perspectives on specific types of data (Borsboom, van der Maas, et al., 2021; Briganti et al., 2023; Costantini et al., 2015; Epskamp, Waldorp, et al., 2018; Isvoranu et al., 2022).

Most of the methods described here belong to two broad families: Pairwise Markov Random Fields (PMRFs) and Directed Acyclic Graphs (DAGs) (Ryan et al., 2022). Both represent relationships between variables but differ in their underlying structure, the types of relationships they can capture, and the assumptions they impose on the data. In PMRFs, (the absence of) undirected edges are used to represent conditional (in)dependencies between pairs of variables and are modeled using local conditional probability distributions. The presence of an edge indicates that two nodes are conditionally dependent given the others, whereas its absence indicates that they are conditionally independent. In DAGs, directed edges can also represent causal relationships between variables, with each edge pointing from a cause (or parent node) to an effect (or child node). DAGs are acyclic, meaning they contain no loops or cycles.

A DAG is a network that indicates causal relationships, and it is not necessarily tied to a statistical representation. Different statistical representations that utilize a DAG structure can be used, and the exact parameters of such a statistical DAG depend on the statistical representation chosen. The most famous statistical representation of a DAG is the Structural Equation Model (SEM), which can be used in the case data are Gaussian and in which the parameters equate to linear regression coefficients (Pearl, 1998). A parameter of zero indicates no causal effect. The larger structure of the DAG imposes several constraints on conditional independence relationships. For example, the DAG A → B → C indicates that A and C are conditionally independent given B. Note: this DAG is equivalent to the DAGs A ← B → C and A ← B ← C.

A PMRF uses an undirected network instead to encode conditional independence relationships. Continuing the example, the PMRF A — B — C also indicates that A and C are conditionally independent given B, but has no equivalent models (without introducing latent variables). The parameterization of the edges depends on the distribution of the variables, but usually takes the form of partial correlation coefficients (for Gaussian data) or (log)‐linear regression coefficients (possibly standardized or averaged) for other types of data. Epskamp, Haslbeck, et al. (2022) discuss several ways in which the parameters of a PMRF can be interpreted, ranging from descriptive (modeling pairwise interactions in a sparse manner) to predictive (showing which variables would predict each other in multiple regression models) and causal (hypothesis generating due to a close connection with causal models such as DAGs, but a PMRF can also be a causal model by itself, such as the Ising model).

While PMRFs can capture statistical associations between variables and are closely related to DAGs (Epskamp, Waldorp, et al., 2018), they do not explicitly model causal relationships: inference about causal effects requires additional assumptions or interventions beyond the statistical associations represented by the model. Conversely, DAGs are designed specifically for causal modeling and inference but cannot capture mutual causation or causal loops that may characterize some psychological phenomena without being reformulated as temporal networks (Briganti et al., 2023; Epskamp, Waldorp, et al., 2018; Haslbeck et al., 2022). PMRFs are uniquely identified (no equivalent models) and easily parameterized (allowing for weighted networks), whereas a DAG may have many equivalent models and may be harder to parameterize. PRMFs also rely on fewer assumptions than DAGs. DAGs, on the other hand, allow for stronger causal interpretations. Below, we discuss PMRFs and DAGs separately in more detail.

3. PAIRWISE MARKOV RANDOM FIELDS

3.1. The GGM, the Ising model, and the MGM

Different models can be used to define PMRFs for different types of cross‐sectional data (Epskamp, Haslbeck, et al., 2022). When data are Gaussian, the most appropriate model to use is the Gaussian graphical model (GGM; Epskamp, Waldorp, et al., 2018; Lauritzen, 1996), which, like commonly used models in factor analysis, is a model for the variance‐covariance structure of the data (Epskamp, Rhemtulla, & Borsboom, 2017):

$$\mathrm{v}\mathrm{a}\mathrm{r}\left(\mathit{x}\right)=\mathbf{\Delta }{\left(\mathit{I}-\mathbf{\Omega }\right)}^{-1}\mathbf{\Delta }.$$

Here, x represents a set of random Gaussian responses (e.g., questionnaire responses of a random person), Δ represents a diagonal scaling matrix that controls the variance of each variable, I represents an identity matrix, and Ω represents a matrix of partial correlation coefficients typically visualized and analyzed as a network structure. When data are binary, the most appropriate model to use is termed the Ising model (Marsman & Haslbeck, 2023; Van Borkulo et al., 2014), which models the probability of obtaining a particular set of responses:

$$\mathrm{Pr}\left(x\right)=\frac{1}{Z}\exp \left(\sum _i{\tau }_i{x}_i+\sum _{<i,j>}{\omega }_{ij}{x}_i{x}_j\right).$$

Here, Z represents a normalizing constant, τ _i a threshold parameter (intercept), and ω _ij a log‐linear relationship that quantifies the association between variables i and j after controlling for all other variables in the model. Again, a matrix Ω can be formed using the individual ω _ij elements, typically visualized and analyzed as a network structure. For data that contains a mixture of categorical (e.g., binary), continuous and count variables, the most appropriate model to use is the Mixed Graphical Model (MGM; Haslbeck & Waldorp, 2020), which we do not detail here.

3.2. Estimating PMRFs

Several estimation methods have been proposed and evaluated to estimate the parameters (especially the network parameters encoded in the Ω matrices) models in psychological data (Blanken et al., 2022; Huth, de Ron, et al., 2023; Isvoranu & Epskamp, 2022; Marsman & Haslbeck, 2023). The most commonly used estimation methods rely on frequentist estimates, meaning that they aim to find parameters that maximize the (pseudo/penalized) likelihood function. In maximum likelihood estimation, the parameters are chosen as the set of parameters under which the data was the most likely. Analytic standard errors can usually be obtained and used to threshold non‐significant edges or to perform more complicated model search algorithms (Blanken et al., 2022). In the case of the Ising model and the MGM, however, joint maximum likelihood estimation is usually not feasible due to the need to estimate the normalizing constant Z (which is a sum over all possible outcomes). To this end, routines that aim to estimate the Ising model or MGM models usually rely on the pseudolikelihood instead (Keetelaar et al., 2024). Pseudolikelihood estimators split the problem by estimating first a multiple (logistic) regression model per variable and subsequently combining the estimated regression parameters into a single matrix used to draw a network. Finally, many researchers make use of “LASSO regularization” which uses shrinkage to estimate network parameters that perform better in predicting new responses and follow a sparse structure (Epskamp & Fried, 2018; Tibshirani, 1996). The use of LASSO regularization, however, is not uncontroversial, and it depends on the dataset and research question if its use is warranted (Blanken et al., 2022; Isvoranu & Epskamp, 2022; Williams & Rast, 2020).

3.3. Analyzing a network structure

Once nodes are defined and network edges are estimated, further insights about network properties can be obtained. Some local indices describe the properties of individual nodes. Centrality indices, originally developed to determine the importance of individuals in social networks, have been adapted and extended to psychometric networks (Briganti et al., 2018; Costantini et al., 2015; Robinaugh et al., 2016). However, they are difficult to interpret when applied to networks involving random variables as nodes (Bringmann et al., 2019). Other local indices have been developed specifically to represent node‐level properties in psychometric networks. For example, predictability quantifies the amount of variance that a node shares with the rest of the network (Haslbeck & Waldorp, 2018). Global metrics that summarize structures as a whole, such as density, transitivity, and small‐worldness, have also been proposed (Costantini et al., 2015). Finally, community‐detection algorithms can be applied to identify groups of densely connected nodes (Fortunato, 2010), and bridge‐centrality metrics can determine the centrality of nodes acting as bridges between different communities (Jones, Ma, & McNally, 2021).

3.4. Stability and accuracy of results

Since psychometric networks are estimated from data, it is important to inspect whether the parameters of interest are estimated with sufficient accuracy before drawing inferences from the properties of a network's structure. Bootstrap and permutation‐based methods have been developed to test the accuracy of network edge and centrality estimates and other features such as communities and group differences. We refer the reader to several tutorials and introductory texts that exist on these methods (Borsboom, Deserno, et al., 2021; Christensen & Golino, 2021; Epskamp, Borsboom, & Fried, 2018; Fried et al., 2022; Van Borkulo et al., 2022).

4. NETWORK PSYCHOMETRICS

4.1. Network models and factor models

While network modeling has been proposed as an alternative to latent variable modeling techniques commonly used in psychometrics, interestingly, in some cases, there can be a full correspondence between some networks and some latent variable models, including factor and item response theory (IRT) models (Epskamp et al., 2021; Epskamp, Kruis, & Marsman, 2017; Kruis & Maris, 2016; Marsman et al., 2018; van Bork et al., 2021; Waldorp & Marsman, 2022). To this end, in general, it is impossible to determine from on observational data whether a network or a latent variable model has unambiguously generated the data at hand. If a latent variable model underlies the data, an equivalent network model would generally be highly clustered (Golino & Epskamp, 2017; Marsman et al., 2018). As such, we cannot determine from the model fit alone if a clustered network model or a latent variable model generated the data; a combination of theoretical considerations and experimental interventions is typically required (Costantini & Perugini, 2018; Epskamp, Kruis, & Marsman, 2017).

The close relationship between latent variable modeling and network modeling, however, does allow for these frameworks to be closer linked than might be thought at first glance. For example, since latent variables would emerge as clusters in an estimated network structure, community‐detection algorithms applied on networks can be used to explore the potential number of underlying latent variables (Christensen et al., 2023; Golino & Epskamp, 2017); a technique termed Exploratory Graph Analysis (EGA). In addition, the close link readily allows for metrics and methods from factor analysis to be applicable in network psychometrics, such as measurement invariance testing, fit measures and meta‐analytic methods (Epskamp, Isvoranu, & Cheung, 2022; Kan et al., 2020). These methods have been implemented in the software package psychonetrics, which can be used for network psychometrics and structural equation modeling (SEM).

4.2. Confirmatory network modeling

The close links between GGM networks and SEM and between Ising models and IRT allow for techniques commonly used in latent variable modeling to be applied in network modeling. One example of such techniques is the ability to perform a confirmatory fit of a pre‐defined network structure using confirmatory network modeling (Epskamp, Isvoranu, & Cheung, 2022; Epskamp, Rhemtulla, & Borsboom, 2017; Kan et al., 2020). Just like how in factor modeling, exploratory factor analysis (EFA) can be used to explore a factor structure and confirmatory factor analysis (CFA) can be used to fit a pre‐defined factor structure (in a new dataset), exploratory network estimation algorithms can be used to estimate a network structure, which can then be fit in a new dataset using CFA. This allows one, for example, to test if a network structure replicates (Fried et al., 2022), and for a fair comparison between (simple) factor models and (sparse) network models (Kan et al., 2020).

4.3. Latent network modeling

Many network studies include each questionnaire item as a separate node. However, there are two problems with this approach. First, the nodes in a network are treated as observed, and measurement error is not considered. Particularly at the item level, measurement error is likely to be present and may lead to spurious edges while attenuating the edge weights of truly present edges. Second, because many questionnaires focus on measuring broad constructs (e.g., a mental disorder rather than individual symptoms), there are likely to be semantically overlapping items (Fried & Cramer, 2017). In this case, the nodes in the network are no longer separate entities, making it difficult to accurately interpret the relationships between variables.

Latent network modeling (LNM; Epskamp, Rhemtulla, & Borsboom, 2017) has been developed to address these points. LNM estimates a network based on the implied latent variance‐covariance structure of the data. This allows researchers to model conditional independence relationships between latent variables without making assumptions about directionality, as in SEM, or acyclicity, as in DAGs. An advantage of LNM over estimating factor scores for each latent variable and then fitting a network on the obtained factor scores is that it avoids factor indeterminacy (Acito & Anderson, 1986; de Ron et al., 2022). The residual network model (RNM) builds on the LNM by formulating a network structure of the relationships between variables that remain after fitting an LNM (Epskamp, Rhemtulla, & Borsboom, 2017). These interactions can be interpreted as causal influences or partial overlaps between items after accounting for the latent variables in the network model. Both methods are implemented in the lrnm function of the psychonetrics R package (Epskamp, 2020).

Thus, LNM allows network analysis while accounting for measurement error, and RNM allows one to estimate a network when nodes are partially influenced by latent variables. However, one needs to estimate a larger number of parameters in a network with 10 latent nodes than in a network model with ten (observed) nodes, and this thus requires a larger amount of data. In situations where the sample size relative to the number of parameters is limited, a potential solution for combining items into a single node in the network is taking the mean or sum score, although this approach addresses the issue of semantically overlapping items it does not take measurement error into account.

4.4. Multi‐group and meta‐analytic network modeling

In addition to confirmatory and latent network modeling, a final range of methods from the factor analysis literature that can be applied to network models concern methods that investigate homogeneity and heterogeneity across multiple datasets (Epskamp, Isvoranu, & Cheung, 2022). These methods can be divided into two classes: multi‐group models and meta‐analytic models. In multi‐group modeling, multi‐group network models can be formed and used in a way that is very similar to testing for measurement invariance in factor analysis (Maassen et al., 2023; Meredith & Teresi, 2006; Millsap, 2012). These methods can, therefore, be used to perform a statistical test on whether or not a homogenous network structure can underlie responses on two (or more) datasets (Fried et al., 2022; Hoekstra et al., 2024). For a larger number of datasets, meta‐analytic Gaussian network aggregation (MAGNA; Epskamp, Isvoranu, & Cheung, 2022)—which is derived from meta‐analytic SEM (Cheung, 2015; Cheung & Chan, 2005)—can be applied to estimate one common network structure in addition to the extent of cross‐study heterogeneity. While the nascent field of network psychometrics and the large data requirements for individual network studies make it hard to obtain a sufficiently large enough number of studies to apply MAGNA, it has so far successfully been applied in the study of post‐traumatic stress‐disorder (PTSD; Isvoranu et al., 2021), a field in which the application of network modeling has been popular in the past decade.

5. THE BAYESIAN APPROACH TO NETWORK ANALYSIS

Estimating a network from data involves two fundamental questions. First, is there an edge between two nodes (i.e., an edge connecting variables A and B?)? Second, if there is an edge, how strong is the effect (i.e., the edge weight)? The first question concerns testing, while the second concerns estimation. Although a Bayesian approach can be used to answer both questions, the primary focus in this section is on whether an edge is present or absent.

The literature on the network analysis of psychological data has mostly focused on estimation, whereas hypothesis testing of whether an edge exists remains underdeveloped. Networks often lack several of their potential connections. This can be due to two reasons: the connections are missing because their effect is absent (the two variables are conditionally independent) or because there is too little information to conclude its presence. Fortunately, a test can distinguish between the evidence for edge absence and the absence of evidence: the inclusion Bayes factor. This section will provide a general overview of the Bayesian approach to network analysis, discuss Bayesian hypothesis testing using the inclusion Bayes factor, and finally offer a discussion of Bayesian Network (BN) estimation. The Bayesian methods for network analysis described here are implemented in the user‐friendly package easybgm (Huth, Keetelaar, et al., 2023).

5.1. Basics of Bayesian inference

The Bayesian approach to evaluating or testing a network structure begins with assessing how well the network structure can predict newly observed data, P(data∣structure s). Considering a network with three nodes and edges without direction, there are eight possible structures (Figure 1). The problem lies in determining which of these possible structures will produce the data that has not yet been seen. To solve this problem, a Bayesian assigns prior weights (i.e., probabilities) to each possible structure to reflect the ignorance about the exact network structure that would produce the data, P(structure s). Typically, a default choice of prior ignorance is considered, and an equal prior probability is assigned to each possible structure. That is, each of the eight structures in Figure 1 receives a prior weight of 1/8. In practice, these prior probabilities can be assigned in different ways. ¹

FIGURE 1.

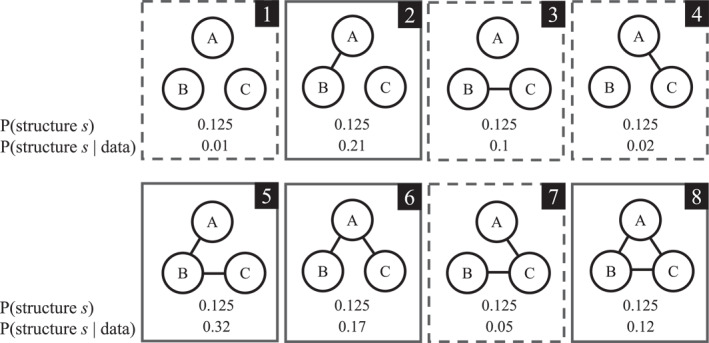
The eight possible structures for a three‐node network with their prior and posterior probabilities.

Regardless of how the prior probability was specified, Bayes' rule can be used to update prior probabilities to posterior probabilities once the data are observed:

$$\stackrel{\begin{array}{c}\text{Posterior}\text{Probability}\end{array}}{\overbrace{P(\text{structure}\mathrm{s}|\text{data})}}=\stackrel{\begin{array}{c}\text{Predictive}\\ \text{Update}\text{Factor}\end{array}}{\overbrace{\frac{P(\text{data}|\text{structure}\mathrm{s})}{P(\text{data})}}}\times \stackrel{\begin{array}{c}\text{Prior}\text{Probability}\end{array}}{\overbrace{P(\text{structure}\mathrm{s})}}$$

The predictive update factor considers how well structure s predicted the observed data relative to how well all possible network structures predicted that data. Structures that predicted the data well receive an increase in plausibility, while structures that predicted the data poorly receive a decrease in plausibility. The posterior probability resulting from this update represents all the information available about the structure after seeing the data. It conveys how plausible it was that this particular structure produced the data at hand. Figure 1 shows the posterior probability for each structure of our imaginary three‐node network.

One can imagine that with more variables, there are more potential network structures. Therefore, the posterior probability has to be divided over more potential structures, indicating less certainty that a particular structure generated the data at hand. Indeed, in practice, it may be highly uncertain which structure generated the data at hand (see, for example, the empirical analyses in Marsman & Haslbeck, 2023; Marsman et al., 2022). Fortunately, the Bayesian approach can express this uncertainty in terms of posterior probabilities, which is impossible with other approaches. If this uncertainty is ignored, researchers risk overconfidence in uncertain results (Hinne et al., 2020; Hoeting et al., 1999). This issue has received much attention in the recent network analysis literature (e.g., see Fried et al., 2018; Jones, Williams, & McNally, 2021; Marsman & Rhemtulla, 2022, for recent discussions). By acknowledging this uncertainty, the Bayesian approach allows for inference that generalizes better and is more transferable (Sekulovski, Keetelaar, Huth, et al., 2023; Williams & Mulder, 2020).

5.2. A Bayesian test for the presence or absence of edges

The structure probabilities above can be used to answer the first question of edge presence or absence in a network. There are two possible hypotheses ² for the edge between nodes A and B:

• ${\mathcal{H}}_1$: There is an edge between the variables A and B;

• ${\mathcal{H}}_0$: There is no edge between the variables A and B.

It is necessary to evaluate which hypothesis is more plausible for the data at hand, that is, whether network structures with a particular edge are better at predicting the observed data than network structures without the edge. Since no assumption is made about the rest of the network in the evaluation (i.e., whether there is an edge between variables A and C or not), all possible structures are considered simultaneously. To do this, the prior (posterior) probabilities of all structures where the edge A — B is present (shown with a solid frame in Figure 1) and of all structures where the edge A — B is absent (shown with a dashed frame) are summed to obtain the prior (posterior) probabilities for the two hypotheses. In our example in Figure 1, the prior edge inclusion probability is obtained with

$$P\left({\mathcal{H}}_1\right)=P(\text{structure}2)+P(\text{structure}5)+P(\text{structure}6)+P(\text{structure}8)=0.5$$

and the posterior edge inclusion probability with

$$\begin{array}{l}\hfill P\left({\mathcal{H}}_1|\text{data}\right)=P(\text{structure}2|\text{data})+P(\text{structure}5|\text{data})\\ +P(\text{structure}6|\text{data})+P(\text{structure}8|\text{data})=0.82.\hfill \end{array}$$

Conversely, the prior edge exclusion probability is obtained with

$$P\left({\mathcal{H}}_0\right)=P(\text{structure}1)+P(\text{structure}3)+P(\text{structure}4)+P(\text{structure}7)=0.5$$

and posterior exclusion probability with

$$P\left({\mathcal{H}}_1|\text{data}\right)=P(\text{structure}1|\text{data})+P(\text{structure}3|\text{data})+P(\text{structure}4|\text{data})+P(\text{structure}7|\text{data})=0.18.$$

The next step is to pit the competing hypotheses against each other to determine which is better at predicting the observed data. To do this, the posterior probability of inclusion is compared to the posterior probability of exclusion:

$$\underset{\begin{array}{c}\text{posterior}\\ \text{inclusion}\text{odds}\end{array}}{\underbrace{\frac{P\left({\mathcal{H}}_1|\text{data}\right)}{P({\mathcal{H}}_0|\text{data})}}}=\underset{\begin{array}{c}\text{Bayes}\\ \text{factor}\end{array}}{\underbrace{{\text{BF}}_{10}}}\times \underset{\begin{array}{c}\text{prior}\\ \text{inclusion}\text{odds}\end{array}}{\underbrace{\frac{P\left({\mathcal{H}}_1\right)}{P\left({\mathcal{H}}_0\right)}}}.$$

As before, the predictive update factor can be used to update the prior beliefs to posterior beliefs. In this case, the prior odds are updated by contrasting two hypotheses to the corresponding posterior odds using the Bayes factor, which is the primary Bayesian tool for comparing models or hypotheses (Kass & Raftery, 1995; Wagenmakers et al., 2016). The Bayes factor compares how likely the observed data are under the hypothesis that the edge A — B is included (i.e., ${\mathcal{H}}_1$) with how likely the data are under the hypothesis that this edge is excluded (i.e., ${\mathcal{H}}_0$). This is called the inclusion Bayes factor (Huth, de Ron, et al., 2023; Marsman et al., 2022; Marsman & Haslbeck, 2023; Sekulovski, Keetelaar, Huth, et al., 2023). In the example, the inclusion Bayes factor is $B{F}_{10}=\frac{0.82}{.18}/\frac{0.5}{0.5}=4.56$, which means that the data are approximately five times more likely to come from a network with the A − B edge than from a network without it (i.e., evidence for conditional dependence). Conversely, evidence for edge exclusion can be obtained by acquiring the reciprocal of the Bayes factor $B{F}_{01}=\frac{1}{B{F}_{10}}$ (the change is noted in the subscript). A Bayes factor of 1 indicates equal evidence for both hypotheses and a Bayes factor BF ₁₀ less than one indicates evidence for exclusion (i.e., conditional independence). Bayes factors are continuous measures of evidence, but categorizations have been introduced to classify them. A Bayes factor of up to three is often considered weak evidence, up to 10 is considered moderate evidence, and more than 10 is considered strong evidence (Jeffreys, 1961). Thus, in the example, the conclusion is that moderate but not compelling evidence exists for an edge between nodes A and B.

5.3. The Bayesian approach to parameter estimation

The previous section focused on answering the question of whether there is an effect of one variable on another in the network, more specifically, on whether a direct relationship between the two variables exists. However, the Bayesian approach can also answer the second question of this section and estimate network parameters such as edge weights. Suppose that structure five in Figure 1 is the most likely structure for the data, such that an edge likely exists between variables A and B in the example. The corresponding edge weight is denoted by the symbol θ _AB . As with the structures, it is essential to consider how well this parameter predicts the data at hand. Since it is a priori unknown which values generate the yet unseen data, prior plausibilities must be specified for the different values the parameter could take in the form of a continuous probability distribution, denoted p(θ _AB ). Considering, for instance, the bell‐shaped curve of a normal distribution with a mean of 0 and a variance of 1 as the prior probability distribution, the value 0 is the most plausible value the parameter could take because it is at the top of the distribution. Moving away from this value in either direction, increasingly fewer beliefs are assigned to the corresponding parameter values. The Bayes' rule can be used to update our prior probability distribution into a posterior probability distribution:

$$\stackrel{\begin{array}{c}\text{Posterior}\text{Distribution}\end{array}}{\overbrace{p\left({\theta }_{AB}|\text{data},\text{structure}5\right)}}=\stackrel{\begin{array}{c}\text{Predictive}\\ \text{Update}\text{Factor}\end{array}}{\overbrace{\frac{P\left(\text{data}|{\theta }_{AB}\right)}{P(\text{data})}}}\times \stackrel{\begin{array}{c}\text{Prior}\text{Distribution}\end{array}}{\overbrace{p\left({\theta }_{AB}|\text{structure}5\right)}}.$$

After the data is obtained, the posterior probability distribution resulting from this prediction update is all information known about the parameter at the current moment.

6. NETWORKS FROM LONGITUDINAL DATA

In psychology, understanding how processes unfold over time is often crucial and hardly possible when relying solely on cross‐sectional data (Epskamp, Hoekstra, et al., 2022). Similar to cross‐sectional networks, numerous estimation techniques are available for longitudinal data (Blanchard et al., 2023; Burger, Hoekstra, et al., 2022). If longitudinal data are available, network edges can encode different types of information. Some network models, such as the multilevel graphical vector‐autoregressive network (GVAR; Epskamp, 2020; Epskamp, Waldorp, et al., 2018), provide three types of model outputs. In temporal networks, directed edges encode information about how within‐person deviations of a node at some time point relate to within‐person deviations in itself or another node's states in the future. Contemporaneous networks, on the other hand, contain undirected edges and encode symmetric relationships among different nodes' states, encoding within‐person relationships within the same window of measurement (after controlling for temporal effects). In between‐person networks, undirected edges represent symmetric relationships between a person's typical levels of each node across time—individual differences in stable averages. Whereas the temporal and contemporaneous networks can also be estimated on a single person's longitudinal data, the between‐person network can only be estimated if longitudinal data of multiple individuals are available (Costantini et al., 2019). Network models also differ in their idiographic versus nomothetic focus. Some models focus solely on person‐specific relationships (Haslbeck & Ryan, 2022), while others integrate within‐person and between‐person phenomena, for instance, using a multilevel framework (Bringmann et al., 2013). Finally, a third class of models does not encompass inter‐individual differences in processes (Epskamp & Fried, 2018). In this section, we provide an overview of different approaches to modeling network structures in longitudinal data.

6.1. Vector autoregressive network models

In the parlance of network psychometrics, a temporal network is one where the edges represent relationships between variables over time. This definition is contrasted with the previously described cross‐sectional networks, where the edges represent some measure of contemporaneous association. There are many different kinds of temporal network models used in network psychometric research today (Blanchard et al., 2023), and most are extensions or elaborations of the vector autoregressive model (VAR; Lütkepohl, 1991), such as the commonly used GVAR model mentioned above. The VAR model is the simplest of temporal models as it poses the temporal relations between variables as being (a) linear and (b) only at a given time lag (typically at a lag of 1, though the VAR framework does allow for arbitrary lag values). A VAR model of lag 1 has the following standard form:

$${\mathit{x}}_t=\mathit{\mu }+\mathit{B}\left({\mathit{x}}_{t-1}-\mathit{\mu }\right)+{\mathit{\epsilon }}_t,$$

In which x _t is the vector of observed variables at timepoint t, μ is a vector of (person‐wise) means, B is a matrix of regression coefficients that relate the values of x _t to x _t + 1, and ɛ _t is the innovation vector. The B matrix, also termed the temporal network, is of interest because it represents how the variables in the psychometric network are related to one another over time. In addition to B , researchers are typically also interested in modeling the variance‐covariance structure of ɛ _t as a network (in which case the VAR model becomes a GVAR model), termed the contemporaneous network, to model relationships in the same window of measurement. The temporal and contemporaneous networks can be used in a graph‐theoretic sense, and various network statistics can be calculated. The above is a simple VAR and can be modified to include time trends (gradual increases or decreases in the variables), seasonal effects (cyclical changes, such as positive mood increasing during weekends), and exogenous predictors (trait level characteristics and demographics).

While VAR models, at their simplest, are useful exploratory tools capable of identifying possible dynamical relations between variables over time, caution must be taken in interpreting them as complete descriptions of a psychological process for one core reason: the standard VAR model is a stationary model. A stationary model or system is one in which the properties of the model do not change with respect to time. In the case of the standard VAR model, this results in a system where neither the relations between variables nor their expected values can ever change. Theoretically, this is a difficult set of assumptions to impose on a psychological system, as it says that no amount of disturbance, no intervention of any strength, can result in permanent change. Stationarity also implies that we cannot model behavior we are often intersted in, that is, no sudden transitions, or emergent behavior that characterize psychological phenomena (Borsboom, 2017b; Olthof et al., 2023; Wichers et al., 2019). Indeed, reducing the means and variances of symptom measures is precisely the aim of clinical treatment. Due to this property of stationarity, simple VAR models are not as useful for the identification of intervention targets via control theory (Henry et al., 2021) or for predictive modeling as a more elaborate nonstationary formal model might be (see, for instance Robinaugh, Haslbeck, Waldorp, Kossakowski, Fried, Millner, McNally, et al., 2019; Wang et al., 2023). Instead, VAR models can be used to uncover broad patterns of temporal relations in the same way an exploratory factor model can be used to explore the structure of a given construct. The VAR modeling framework has been extended in several ways that radically improve its usefulness for exploring the dynamics of psychopathology.

6.2. Time‐varying network models

The temporal networks discussed thus far have all been time‐invariant, meaning their parameters do not change over time. However, from a clinical perspective, change in a network is often precisely what researchers, patients, and therapists are interested in. A core idea of the network approach is that a network represents a system of symptoms or a system underlying symptoms (Borsboom, 2017a; Cramer et al., 2016; Haslbeck et al., 2022). Therefore, it could be expected that the network changes when the symptoms of the disorder change. This might be the case in purely observational studies, where changes in networks may be used as early warning signals for transitions to a more problematic state (Bringmann et al. (2023), van de Leemput et al. (2014), and Wichers et al. (2016, 2019, 2020), but also see Dablander et al. (2022)). However, it could also be interesting to track the impact of a given treatment by investigating how the network model changes in response to the treatment (van der Wal et al., 2022). At this time, this field of research needs models that can identify alterations in the network edges to detect such changes when moving from a healthy to a depressed network or vice versa. In other words, time‐varying models are necessary to capture changes in networks over time (Haslbeck et al., 2022).

When estimating a time‐varying (network) model, ideally, a separate “version” of the model of interest will be obtained at every time point in the measured time interval. For example, considering measures during a 2‐week interval, the model could be determined, for example, on day 4 at 11 am, on day 12 at 3 pm, or any other time point. However, estimating a model at each single time point represents a complex question. Clearly, the model cannot be estimated using data only from a given single time point. To make estimation feasible, close time points could be combined with the desired time point. This procedure is justified if a version of local stationarity is satisfied. One common form of local stationarity is that parameters are smooth functions of time, which implies that the models at time points that are very close to each other also have very similar parameters. Under this assumption, different methods can be used to estimate a time‐varying network model. Bringmann et al. (2017, 2018) proposed a method using Generalized Additive Models (GAMs; Wood, 2006), in which time serves as moderator of all parameters, which can take on almost any (smooth) shape thanks to the flexibility of GAMs. Another approach is to use some version of a moving window or kernel smoothing approach (Haslbeck & Waldorp, 2015). A simulation study comparing both methods in settings resembling typical data from Experience Sampling Methodology (ESM) studies can be found in Haslbeck et al. (2021).

Although methods based on smooth change are the most widely employed for estimating time‐varying psychopathological networks, numerous models exist that model change discretely. The simplest example of a discretely changing network involves a change point analysis. For instance, Bringmann et al. (2013) use a multilevel VAR model to analyze data before and after a treatment program (the change point). They introduce a dummy variable (with zeros for the time points before and ones after the treatment) to test parameter changes after treatment. If the change point (i.e., dummy variable) is significant, two networks are required—one representing the period before treatment and another representing the dynamics between nodes after treatment. Otherwise, if there is no change, one network representing the entire study period is sufficient, as observed in the results of Bringmann et al. (2013). Identifying a change point or the moment of discrete change without knowing its location is also possible using change point analysis (Cabrieto et al., 2018).

In some cases, the process under study may switch between different regimes, as seen in bipolar disorders shifting from a depressive to a manic state and vice versa (Hamaker et al., 2016). When a system shifts between these different regimes, change point analysis becomes inadequate because it assumes only a few definitive changes without considering back‐and‐forth transitions. In such instances, regime‐switching analysis, like threshold autoregressive modeling, proves more suitable (De Haan‐Rietdijk et al., 2016; Hamaker et al., 2009). In this variant of a time‐varying VAR model, the threshold variable is specified by the researcher and included in the network itself, while the threshold value is estimated based on the data. Alternatively, when the variable determining the regime‐switching behavior is unknown, hidden Markov models might be more appropriate (de Haan‐Rietdijk et al., 2017; Mildiner Moraga & Aarts, 2023; Zucchini & MacDonald, 2009). Other approaches can capture repeated changes that address the limitations of changepoint detection and better scale to many change points in the time series segmentation literature, for example, a method to estimate piecewise constant GGMs using a group‐fused lasso (Gibberd & Nelson, 2017).

Furthermore, methods integrating discrete and continuous changes are viable, such as a time‐varying model based on the generalized additive framework combined with change point analyses (Albers & Bringmann, 2020). Another model capable of handling both continuous and discrete changes is moderated time series analysis, where changes in the network are related to a moderator (Adolf et al., 2017; Bringmann et al., 2024; Swanson, 2020). While most network changes primarily focus on therapeutic goals over time, it is equally crucial to ascertain if specific contextual factors are associated with the change rather than solely observing whether the network changes over time. In such cases, moderation analysis proves useful (for cross‐sectional moderation networks, see Haslbeck, 2022)). Depending on whether the moderation analysis involves a discrete factor (e.g., being alone or with others) or a continuous variable (e.g., stressful events), the network can change either continuously or discretely (Bringmann, 2024; Bringmann et al., 2024).

A topic closely related to the time‐varying models discussed here is the topic of (non)‐stationarity. There are different definitions of nonstationarity, which refer to different aspects of the distribution being the same (stationarity) or not (nonstationarity) across time. While there can be infinitely many processes generating nonstationary time series, one typically distinguishes between deterministic and stochastic nonstationarity processes. The time‐varying models fall into the category of deterministic nonstationarity since all parameters are estimated to be deterministic functions of time. Similarly, time‐varying means (or trends) are also deterministic forms of nonstationarity for the same reason. A well‐known example of a process with stochastic nonstationarity is a random walk. Here, the parameters do not change over time, but the distribution does change across time (e.g., the variance goes to ∞ as t → ∞). For an accessible introduction to the topic of stationary and nonstationary time series, see Ryan, Haslbeck, and Waldorp (2023).

6.3. Network models from panel data

Dynamic network models can be constructed from different types of (intensive) longitudinal data. As different forms of data warrant distinct analytical approaches, beyond matching the research question of the investigator, the network model estimated must match the type of data to be collected or available to the researcher. Intensive longitudinal data are often measured through Ecological Momentary Assessment (Shiffman et al., 2008, EMA) or the Experience Sampling Method (Telford et al., 2012, ESM). These approaches often yield repeated‐measurement data with a high measurement frequency, including assessments that are frequently conducted hourly (e.g., every 3 h) or daily (e.g., diary studies). In contrast, more traditional longitudinal or panel data often involve fewer (frequent) measurements per person and a longer timespan between each subsequent assessment, usually measured on a weekly, monthly, or yearly timescale. Such panel datasets often include a much larger sample size (number of people) than typical in high‐intensity EMA/ESM studies.

The GVAR model has been generalized to apply to panel datasets (Epskamp, 2020) through the panelGVAR framework. This model allows for the estimation of networks based on observed variables, which may, for example, include nodes that are single items or sum scores. The panelGVAR model can further be generalized to incorporate a measurement model and, thus, latent variables as nodes in the network. Like SEM, the latent variable panelGVAR model allows nodes to be measured by multiple indicators to represent nodes as latent variables, thereby being able to address measurement error (Epskamp, 2020).

The panelGVAR is technically a GVAR model with random means (intercepts) across individuals but not random networks (slopes). As panel data both includes multiple individuals (N > 1) in addition to repeated measurements per person, network models from panel data enable the disaggregation of within‐person from between‐person effects (Curran & Bauer, 2011; Epskamp, 2020; Hamaker et al., 2015). Combined with the autoregressive and cross‐lagged effects, the VAR model enables the estimation of temporal parameters, contemporaneous effects, and between‐person effects. Similar to other dynamic network models, such as the multilevel vector autoregressive model (Bringmann et al., 2013; Epskamp, Waldorp, et al., 2018), dynamic network models from panel data result in a temporal, contemporaneous, and between‐subject network.

The directed edges in the temporal network must be interpreted in accordance with the longitudinal assessment window of the study (Borsboom, Deserno, et al., 2021). For example, suppose a study has measured depressive symptoms every month (e.g., across three or four longitudinal assessment waves). In that case, the edges of this temporal symptom network provide information on the extent to which within‐person fluctuations in the current levels of one symptom (e.g., feelings of worthlessness) predict within‐person fluctuations in another symptom (e.g., depressed mood) a month later. Correspondingly, if a study involves five (or another number of) longitudinal assessment waves with 1 week between each assessment, the directed edges in the temporal network reflect the predictive effect of one node on another a week later.

Similarly, edges in the contemporaneous network require awareness of the time distance between the assessment waves of the longitudinal study. Generally, the undirected edges in the contemporaneous network are described to reflect associations between nodes that occur within the same measurement window (i.e. occurring in a shorter temporal resolution than captured by the temporal network; Epskamp, van Borkulo, et al., 2018). Following the previous example with a weekly time lag, a positive edge between sleep difficulties and fatigue in the contemporaneous network reflects how greater sleep problems than one's average are associated with more fatigue within a weekly time window. Notably, both the temporal and contemporaneous networks embody average within‐person effects, reflecting within‐person effects that regularly occur across the sample of individuals.

Finally, the panelGVAR model further yields a between‐subject network based on person‐specific means over the study period (Epskamp, 2020). As this person‐specific mean provides information about the stable level of a variable over the study period, these nodes can be thought to represent trait‐like variables, with the association between nodes in the between‐subject network reflecting how higher levels of a variable from the mean (e.g. physical activity) compared to other individuals is associated with higher or lower level from the mean of another variable (e.g. fatigue) compared to other individuals.

As network models estimated from panel data often include longer‐term distances between assessments (e.g., weeks or months) and are usually accompanied by self‐reported measurements assessing a longer retrospective period (e.g., depressive symptoms during the past month), these network models from panel data are often suitable for addressing questions about the interplay between longer‐term symptom relationship patterns, periodic tendencies, or longer‐term habitual or behavioral patterns. Accordingly, network models from panel data provide rich sources of information on the dynamic interplay between symptoms occurring across longer periods and are suitable for a wide range of research questions across psychological domains (e.g. clinical and developmental psychology; Freichel et al., 2023; Hoffart et al., 2023).

6.4. Idiographic network comparison

In recent years, there has been a growing interest in applying VAR models to time‐series data to explore symptom dynamics at an individual level (Bringmann, 2021). This surge in interest is partly due to the aim of uncovering individual differences in symptom dynamics. However, the comparison of idiographic network structures to identify the presence of heterogeneity is a challenging endeavor in many applied settings. The applications of idiographic network analysis utilize different approaches to estimate, inspect, and interpret person‐specific network structures. Methods such as visual inspection, correlation computation, and multilevel data analysis techniques, such as mlVAR, have been employed to discover individual differences between idiographic network structures. However, these approaches cannot directly test for (in)equalities between idiographic network structures, leaving the door open to interpreting all variability in the data in terms of individual differences. However, not all variability directly results from individual differences (Hoekstra et al., 2023). Hoekstra et al. (2023) revealed that these tools might erroneously indicate heterogeneity in instances where the underlying network structures are homogenous. Such misinterpretations inflate the perceived extent of individual differences.

To address this challenge, the Idiographic Network Intervention Test (INIT) has been introduced as a novel methodology for comparing estimated idiographic network models (Hoekstra et al., 2024). INIT accommodates the comparison of idiographic network structures to determine the presence of heterogeneity, that is, individual differences between idiographic network structures, by contrasting a model assuming network equality against one that allows for heterogeneity. This methodological advance extends common model comparison practices to idiographic network estimation, providing a more rigorous testing framework to ascertain whether the observed differences between idiographic network structures are plausible given the data. By assuming homogeneity rather than heterogeneity as its null model, INIT contrasts with previous methods that used heterogeneity as the starting assumption. This shift toward a more conservative approach ensures that variance within the data is attributed to individual differences only when sufficient evidence is present. Such a cautious stance enhances the reliability of conclusions drawn from idiographic network analysis, reducing the likelihood of misattributing general variability found in time‐series data as meaningful individual differences.

The INIT methodology offers a versatile tool for analyzing the heterogeneity in idiographic network models across different contexts. In addition to enabling researchers to identify heterogeneity between the idiographic network structures of two unique individuals, INIT can be applied to examine a change in the idiographic network structure of a single individual across separate instances of time‐series data. This application allows for assessing whether an individual's network structure exhibits changes over time, providing insights into the temporal stability of idiographic network structures.

Employing INIT, van der Tuin et al. (2023) have linked the stability of symptom networks over a year to changes in psychopathology severity by examining individuals along the psychosis severity continuum. Most individuals displayed stable symptom networks alongside a decrease in psychopathological severity, indicating no direct correlation between network stability and severity change. These findings challenge the idea that psychopathology severity and idiographic networks are closely intertwined. Moreover, INIT's broader application was demonstrated by Ebrahimi et al. (2024). Investigating heterogeneity in idiographic depression symptom networks, Ebrahimi et al. (2024) found distinct symptom dynamics in a large portion of individuals (63%) with similar symptom severity. Their results highlight the nuanced and individualized nature of psychopathological experiences beyond mere severity quantification and underscore the importance of personalized approaches in understanding mental health.

6.5. Rate of change network models

Most dynamic network models use previous time points to assess how symptoms predict each other from one time point to the next. Rate‐of‐change network models offer a different perspective on symptom dynamics. Rate of change measures, such as the derivatives of each symptom's time series, provide insight into how symptoms are changing together over time—that is, whether the increases and decreases in the activation in one symptom are associated (inversely) with the increases (decreases) and decreases (increases) of other symptoms in the system. The first‐order derivatives, often referred to as velocity, can be used to estimate the rate of change and provide insight into linear and nonlinear changes in symptom activations. To estimate these derivatives, the generalized linear local approximation (GLLA; Deboeck et al., 2009) approach uses time delay embeddings or bins of time points in sequential “windows” of time Equation (1).

$$\left(\begin{array}{ccccc}\hfill x_{t=1}\hfill & \hfill x_{t=2}\hfill & \hfill x_{t=3}\hfill & \hfill x_{t=4}\hfill & \hfill x_{t=5}\hfill \\ \hfill x_{t=2}\hfill & \hfill x_{t=3}\hfill & \hfill x_{t=4}\hfill & \hfill x_{t=5}\hfill & \hfill x_{t=6}\hfill \\ \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill & \hfill \text{⋮}\hfill \\ \hfill x_{t=T-4}\hfill & \hfill x_{t=T-3}\hfill & \hfill x_{t=T-2}\hfill & \hfill x_{t=T-1}\hfill & \hfill x_{t=T}\hfill \end{array}\right)$$ (1)

The first‐order derivatives are then computed over each sequence of time for each variable using GLLA to derive how variables change over time. One surprising feature of this approach is that it is relatively robust to missing measurement points. Boker et al., 2018 demonstrated that an error introduced by a missing measurement point cancels itself out with enough time points before and after it. Consequently, GLLA can capture continuous dynamics across time at different intervals and remain robust to missing measurement points.

Another feature of using derivatives to capture the dynamics of symptoms is that nonlinear relationships can be captured. Considering two variables, one with an increasing stepwise linear time pattern and the other with a U‐shaped pattern, most linear approaches estimate this relationship as zero, given that at different time points, the U‐shaped pattern decreases and later increases when the other time series is strictly increasing. The first‐order derivative reveals that the rate of change is increasing similarly for both and, therefore, captures the (nonlinear) relationship between these two symptoms across time.

A network model can then be estimated using the derivatives of each symptom to establish the conditional relationships between symptoms as they change across time (Golino et al., 2022). These relationships can be interpreted as the extent to which two symptoms change together across time. Using each person's derivatives, networks can be estimated at the sample, group, and individual levels (with enough time points). At the individual level, a person's symptom interactions can be monitored throughout an intervention to determine the specific effects the intervention has on the individual. The group‐ and sample‐level dynamics can be used to determine the course of multiple interventions and the overall effect of an intervention (respectively).

6.6. Network intervention analysis

Network intervention analysis (NIA) was introduced in 2019 as a methodology to combine network analyses with experimental research (Blanken et al., 2019). With the introduction of mixed graphical models (Haslbeck & Waldorp, 2020), it became possible to incorporate different variable types into a single model. Leveraging this possibility, NIA incorporates a treatment allocation variable into the network. As such, the NIA allows the investigation of symptom‐specific treatment effects within a network analytical context. The upside of investigating these symptom‐specific relations using network analysis is that the interrelations between the symptoms themselves are taken into account, allowing us to differentiate between direct and indirect treatment effects.

A particular strength of combining network analysis with a randomized controlled trial is that the randomization process ensures that treatment can influence the symptoms and not vice versa. Therefore, even though the links in the network are undirected, the NIA identifies the symptoms that are directly affected by treatment.

More recently, NIA has been applied to contrast active treatment conditions. In these analyses, any identified link between the treatment allocation variable and a particular symptom reflects treatment differences. Interestingly, when applied to contrast cognitive and behavioral treatments for insomnia, it was shown that while both active treatments are indistinguishable at the overall severity level (i.e., as reflected in sum scores), NIA could reveal that the treatments showed unique patterns in the symptoms they were targeting (Blanken et al., 2021; Lancee et al., 2022). These unique effects are in line with their theoretical underpinnings and could offer opportunities for precision medicine. Accordingly, using network analyses in combination with RCTs may provide new ways to investigate treatment mechanisms.

The way NIA was introduced is only one specific example of how network analysis and experimental research designs could be combined. For each dimension (i.e., the number of assessments, type of manipulation, included variables, model type), NIA could be adapted. First, NIA can be applied to test pre‐post differences (e.g., Boschloo, Bekhuis, et al., 2019; Boschloo, Cuijpers, et al., 2019), or to reflect sequential differences throughout the treatment (e.g., Bernstein et al., 2023). Second, the framework can be generalized to incorporate any experimental condition into the networks; this approach is not restricted to RCTs. Third, the variables that are included in the networks can be varied, for example, to reflect treatment processes rather than symptoms (e.g., Lancee et al., 2022). Finally, rather than evaluating the effect of treatments on symptoms, we can model the effect of treatments on their links through moderated network models (Fishbein et al., 2023).

7. CAUSAL INFERENCE AND BAYESIAN NETWORKS

Similar to other graphical models, BNs associate a probability distribution with a graph: in this case, a DAG G = (V, E) where V is a set of nodes representing the random variables X ₁, X ₂, …, X _n , and E is a set of directed edges indicating conditional dependencies (Briganti et al., 2023). If two nodes are separated in the graph, the corresponding variables are independent in probability. The graphical separation criterion is called d‐separation in BNs and is defined as follows: two nodes X _i and X _j are d‐separated by some other node(s) S if along every path between X _i and X _j there is a node that belongs to S or, instead, there is a node that is part of an unshielded collider but does not belong to S nor do its descendants. A collider is defined as the pattern of edges X _j  → X _i  ← X _k ; if there is no edge between X _j and X _k , it is called an unshielded collider or v‐structure; if X _j and X _k are connected by an edge, it is called a shielded collider.

This definition has three important implications. First, each node X _i in a BN is conditionally independent of its nondescendants given its parents Pa(X _i ). The joint probability distribution of the network can then be expressed as

$$P\left(X_1,X_2,\text{…},X_n\right)=\prod _{i=1}^{n}P\left(X_i|Pa\left(X_i\right)\right).$$ (2)

As a result, BNs are computationally efficient, and the behavior of specific symptoms from their local distributions can easily be studied. Second, the subset of symptoms that completely explains the behavior of X _i directly from the DAG can be read: it comprises the parents, the children and the spouses of X _i . Third, d‐separation bridges from probability to causality by identifying v‐structures as a pattern of causal effects that has the unique probabilistic behavior shown in Figure 2, which makes it identifiable by purely statistical means. A practical example involving six symptoms (“Anxiety”, “Insomnia”, “Depression”, “Fatigue”, “Withdrawal” and “Irritability”) is shown for illustration in Figure 3. Overall, BNs are the original artificial intelligence model: their construction allows them to be learned automatically and to provide a working model of pathology that can be used for automated reasoning, as discussed below.

FIGURE 2.

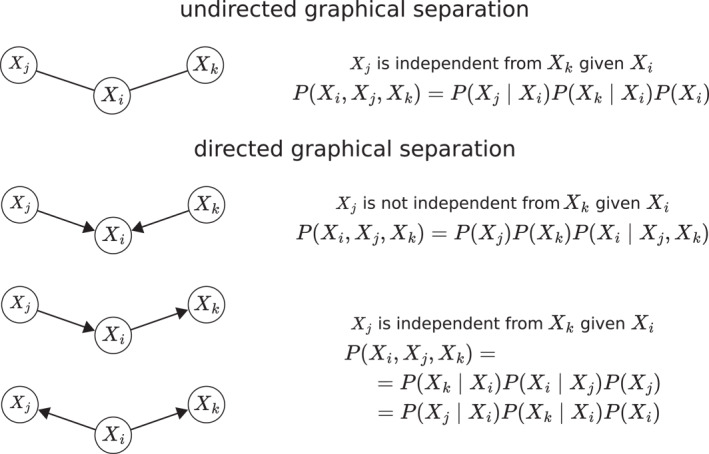
Directed and undirected graphical separation, illustrated using all possible patterns of three nodes connected by two edges.

FIGURE 3.

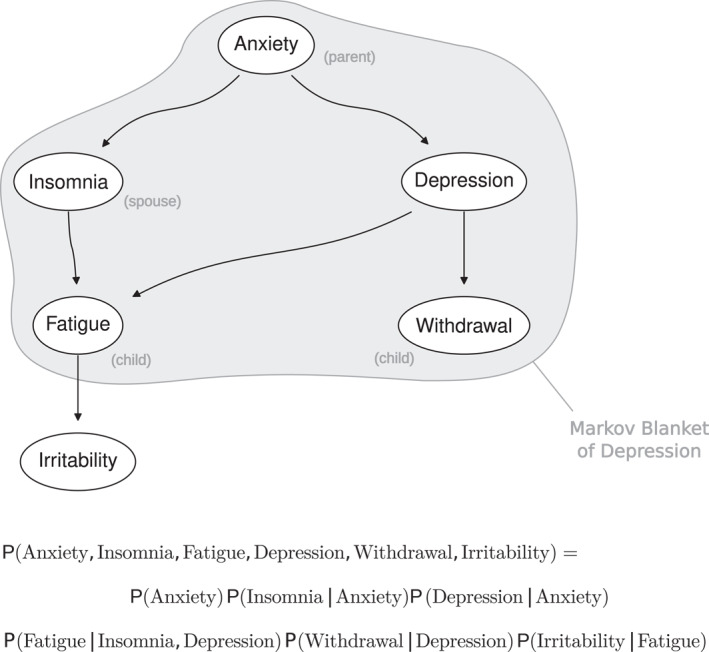
An example of a Bayesian network representing potential causal relationships in psychopathology. The directed edges illustrate hypothesized causal influences among various symptoms, such as “Anxiety” leading to “Insomnia” and “Depression” influencing “Withdrawal”. The Markov blanket of “Depression”, consisting of “Anxiety” (parent node), “Insomnia” (spouse), “Fatigue” and “Withdrawal” (children), is highlighted in gray. The local distributions defined in Equation (2) take the form shown below the network.

7.1. Principles of causal inference with Bayesian networks

Causal inference in BNs treats edges as causal relationships rather than just as statistical correlations. On the one hand, the correlation is symmetric: if X is correlated with Y, then Y is correlated with X. On the other hand, if X causes Y, an intervention on X should change the distribution of Y, but an intervention on X should not change the distribution of Y. Their semantics are very different, but we rely on d‐separation to identify whether either type of relationship exists between two variables in the DAG. In the words of Pearl, 1988: “It seems that if conditional independence judgments are byproducts of stored causal relationships, then tapping and representing those relationships directly would be a more natural and more reliable way of expressing what we know or believe about the world. This is indeed the philosophy behind causal BNs.”

As discussed above, v‐structures represent a configuration in BNs where two or more variables converge on a common effect, forming a V‐shaped structure. This configuration is particularly challenging in causal inference because it can introduce spurious associations between the converging variables when conditioning on the collider. Specifically, conditioning on a collider can open a previously closed path in the network, potentially leading to biased estimates and false causal interpretations (Rohrer, 2018). Despite these challenges, collider structures can be useful in hypothesis testing and model specification. They allow researchers to explore and control for potential sources of bias, enhancing the robustness of causal conclusions drawn from BNs (Lipsky & Greenland, 2022).

Using BNs as causal network models requires careful consideration of several essential conditions. First, the structure of the BN must accurately reflect the underlying causal relationships among the variables and that there are no cyclic relations between them. We should leverage domain knowledge available from experts and from the literature to validate the directed edges as plausible causal relationships. Second, the data used to construct the network should be representative of the population we would like to study, sufficient in quantity, and free of sampling bias and systematic patterns of missing values. Third, we should critically examine the theoretical assumptions underlying causal inference in BNs: the faithfulness condition and the absence of hidden confounders. The faithfulness condition requires that the observed probabilistic dependencies are entirely due to the causal structure of the network. The lack of hidden confounders, defined as unobserved variables that are parents of at least two observed variables, avoids the risk of edges representing spurious causal effects.

Violations of these assumptions can lead to incorrect causal interpretations. However, even if they are satisfied, causal interpretations are inherently limited when using observational data and often require supplementary experimental or longitudinal data for validation.

7.2. Estimation of Bayesian networks

The estimation of BNs integrates observed data with prior beliefs, using Bayesian inference to determine which edges are supported by the information available and to estimate the values of network parameters. To estimate the structure of the network, the constraint‐based algorithms can be employed, such as the PC algorithm (Colombo & Maathuis, 2014), which use conditional independence tests to establish conditional independencies and are designed explicitly for causal discovery; score‐based algorithms, which are general‐purpose optimization algorithms that use scoring methods for network models; and hybrid algorithms, which combine both independence tests and scoring methods for improved accuracy. These algorithms automate the model selection process in the spirit of machine learning. An overview of the algorithm, scoring methods and conditional independence tests available from the literature are described in (Kitson et al., 2023; Scutari et al., 2019). After the network structure is available, estimating the parameters of the local distributions from Equation (2) is an application of classical Bayesian statistics.

7.3. Bayesian inference in BNs

BN inference is the process of drawing conclusions from the network through belief updating or causal reasoning. These conclusions take the form of conditional independence statements or posterior probabilities and densities, and they can provide significant insights into the dependence and causal structure of the symptoms. BNs are constructed to provide a working model of reality that can be used for automated reasoning, either by replacing clinical investigations with simulation experiments (approximate inference) or by combining graphical manipulations and local computations (exact inference). In both cases, the BN represents a working model of the world that a computer can understand, and inference is automated by computer algorithms that can produce the desired conclusions, given only an event of interest and evidence on the patient's current state. Two examples of exact inference algorithms are variable elimination and junction trees, and two examples of approximate inference algorithms are logic sampling and likelihood weighting. An approachable introduction to this topic is available in (Scutari & Denis, 2021). These algorithms present computational and probabilistic challenges, especially in large networks or when dealing with rare events. They are only feasible for sparse networks or simple structures such as trees and polytrees: their computational complexity can become exponential as the number of variables increases, as is often the case in psychopathological networks.

Furthermore, exact and approximate algorithms can also be used for causal inference methods such as interventions and counterfactuals that manipulate the graphical structure of the BN (Pearl et al., 2016). Interventions simulate a clinical treatment by removing the parents of a symptom and replacing its distribution with the one that would result from the treatment. Counterfactuals augment the graphical structure with additional nodes to represent additional outcomes that have not been observed in reality to study them together with those that have.

These tools allow BNs to play a crucial role in generating hypotheses in psychopathology, especially in retrospective or cross‐sectional studies where rigorous causal analysis might not be feasible. Their ability to identify potential causal directions among variables facilitates the formulation of research hypotheses for future experimental validation.

7.4. Limitations and considerations

The use of BNs in psychopathology enhances the ability to address the complexity of mental disorders and generate hypotheses for future research despite their limitations.

The assumptions necessary for rigorous causal inference, such as the absence of latent confounding variables, are often challenging to meet in usual psychopathological data. In addition, low sample sizes can further reduce the statistical accuracy of the BN estimation process. Although progress has been made on several fronts (Bernasconi et al., 2023), resampling methods such as bootstrapping (and re‐estimating the network model multiple times) remain the most common tool for selecting only the most stable connections.

Moreover, BNs can be understood as a form of “white‐box” artificial intelligence, offering transparency in complexity investigation or hypothesis generation. Unlike other approaches such as factor analysis (Watkins, 2018), the nodes in BNs represent observed variables, such as psychopathological symptoms, facilitating the identification and investigation of potential causal relationships and avoiding the arbitrary choices required to model latent factors. BNs also build to a great extent on classical statistical models and practice and, therefore, can benefit from decades of established best practices for model estimation and validation (Scutari & Denis, 2021).

8. NETWORK MODELS AND THEORIES ABOUT PSYCHOPATHOLOGY

The previous sections introduced various network models and provided guidance on how to apply them in empirical research. This section is dedicated to zooming out and reflecting on how researchers can leverage these models to develop better theories of psychopathology, which in turn improves our understanding and treatment of mental health problems. Three core use cases are considered: (1) using network models as theories, (2) using network models to make inferences to theories, and (3) using network models to establish phenomena and develop theories (see also Haslbeck et al., 2022). We describe each in turn.

8.1. Using network models as theories

One direct way in which network models can be useful is if they serve as theories of psychopathology. Theories can be seen as representing a “target system” — the part of the real world that gives rise to something we care about (e.g., Elliott‐Graves, 2014). Considering the study of panic disorder, the target system would be the set of behavioral, cognitive, physical and social components underlying panic disorder and the relations between them (Robinaugh, Haslbeck, Waldorp, Kossakowski, Fried, Millner, McNally, et al., 2019). If a theory is a good representation of the target system, it can be used to reason about the world and predict how it evolves and behaves when intervening on it. For example, physics theories allow to put people on the moon, epidemiological models allow to predict the impact of certain public health measures, and a surgeon uses biophysical models to operate on a brain. In the case of panic disorder, a good theory would be handy because it allows us to understand the causes of mental health problems and help improve treatments (Ryan, Haslbeck, & Robinaugh, 2023).

Treating network models as theories raises the question of whether they, in fact, are good representations of the target system. This may be the case for some network models. For example, an Ising model representing a network of symptoms together with a dynamic to run on the model could, in principle, be a good theory for direct causal interactions between symptoms because it can produce a rich set of behaviors, including getting “stuck” in a state with high symptom activation, sudden transitions, and hysteresis (Cramer et al., 2016; Finnemann et al., 2021; Lunansky et al., 2021). This idea can be investigated by simulation from such a model to see if the generated data fit real‐world data, which is the case for well‐established theories in other sciences (Borsboom et al., 2022; Epstein, 2008; Smaldino, 2017).

However, at least three situations come to mind in which current network models may provide poor representations of target systems and thus make for poor theories. First, network models struggle when there is a mismatch between the data used to estimate the network model and the phenomena theories seek to explain — for instance, when we estimate a network model on cross‐sectional data, but our theory is about dynamic interactions within an individual. It is possible to bridge such levels, but this requires strong assumptions (Hamaker, 2012; Molenaar, 2004). Second, network models show poor representation when they cannot produce phenomena of interest. Suppose that mental disorders involve multiple stable states (e.g., “healthy” and “unhealthy”), sudden transitions between states, hysteresis, feedback loops and processes evolving at different time scales (e.g., short‐term benefit vs. long‐term harm). In that case, a network model should be able to produce these phenomena (e.g., in a simulation), which is not the case for many popular network models introduced in this manuscript (Haslbeck et al., 2022). However, if network models cannot investigate features our theories predict to be present in the data, this raises questions about how to bring our data to bear on our theories in the first place (Fried, 2020; Haslbeck et al., 2022). Finally, a network model may represent phenomena at the right level and be able to produce important characteristics of our theory, but it may not be directly relevant to psychopathology. For example, a model may lend itself well to capturing emotion dynamics, but this does not mean that it automatically serves as a useful theory for better understanding and treating mental disorders (Ryan, Dablander, & Haslbeck, 2023; Wichers et al., 2021).

8.2. Using network models for informing theories

A second perspective is that network models themselves may not make for adequate theories of psychopathology, but they can be useful for informing theories, that is, help with inferences about the inner workings of a system under investigation. For example, by assuming a symptom A causes another symptom B, and that data is collected on these symptoms and given that the data was generated by the system of interest, it stands to reason that network models fitted to those data should recover some information about the system, such as the A—B relation. An edge between these two symptoms can be observed in a cross‐sectional network, which could lead to the conclusion that symptom A causes symptom B (or vice versa) in a within‐person process.

However, such inferences can be more problematic than perhaps expected. The reasons why this type of inference can fail include mismatches in the data level (e.g., using between‐person data to draw inferences about within‐person target systems), functional model misspecification (e.g., assuming linear relations while the target system is nonlinear), issues with time scales (e.g., the process evolves at a faster time scale than the frequency of measurements), alternative reasons for co‐occurrence (e.g., two nodes can be related due to semantic overlap, a common cause, or a collider structure), or measurement issues (e.g., recall biases or social desirability). Haslbeck et al. (2022) illustrate this by generating data from the computational model of panic disorder by Robinaugh, Haslbeck, Waldorp, Kossakowski, Fried, Millner, McNally, et al. (2019) and fitting different network models to those data. All network models have different sets of edges, and none correspond to the causal graph of the data‐generating computational model.

How to move forward? One opportunity is working within a framework that makes clear assumptions and, based on those, guarantees that certain inferences are valid. For example, causal discovery with DAGs (Peters et al., 2017; Spirtes et al., 2000; Spirtes & Glymour, 1991) provides such a framework, but it is submitted to several constraints, as detailed in the section Causal inference and Bayesian networks. A perhaps more flexible approach is to use network models to capture phenomena, which are then used for theory building and testing. This approach will be discussed in the following section.

8.3. Using network models to establish phenomena

Phenomena are robust, recurrent patterns in the real world (e.g., Haig, 2013). Not all phenomena require scientists or data models to uncover; for instance, humans have the capacity for language, and some people suffer from panic attacks. However, in many situations, phenomena will take the form of statistical patterns such as means, trends, variances, or—in networks—correlations, conditional correlations or other associations. For example, “symptoms are usually positively intercorrelated” is a phenomenon established through correlational analyses, and network modeling in the last decade has given the field a plethora of information on what these correlations look like. Theories seek to explain phenomena, and therefore, the third use case of network models is to establish phenomena that theories should be able to explain, thereby creating the foundation for developing and testing theories.

In practice, several guidelines for (formal) theory construction have recently been proposed (Borsboom, van der Maas, et al., 2021; Guest, 2024; Haslbeck et al., 2022; van Dongen et al., 2022). One is the Theory Construction Methodology (Borsboom, van der Maas, et al., 2021), which consists of five steps. Its first step is to clearly describe the phenomena a theory aims to explain. This highlights the value of thorough exploratory work, which, as Daniel Nettle describes, has been the groundwork for building robust theories in other sciences: “Biology had hundreds of years of taxonomy and natural history before it had formal phylogenetic models; geology had detailed maps of rocks before it accepted plate tectonics; people had been studying the motion of planets long before Newtonian mechanics, and so on”. ³ Much of the reform movements in psychology in the last decades can be seen as efforts to better establish whether phenomena exist and what shape they take. Network models capture the first two moments of a probability distribution (means and variances/covariances) and are, therefore, very well suited to capture relatively natural phenomena. This work, for example, has led to some evidence that participants with more severe psychopathology may have more densely connected networks at the group level (Lee et al., 2024).

Once a phenomenon is established, it provides clear goalposts for theory development: a theory must be able to produce the phenomenon of interest to be a viable candidate. Otherwise, the theory needs to be adapted to produce the phenomenon. Producing phenomena can be performed via formal or computational theories, which are simulations that generate data. If the theory‐generated data match the empirical data, the theory gets “money in the bank” because it provides a putative explanation (Haslbeck et al., 2022; Robinaugh et al., 2021; van Dongen et al., 2022). For example, the computational model of panic disorder by Robinaugh, Haslbeck, Waldorp, Kossakowski, Fried, Millner, McNally, et al. (2019) simulates data from a network theory, and the simulation produces four phenomena the theory set out to explain (e.g., realistic panic attacks). However, the simulation does not produce a fifth phenomenon: that some people with panic attacks never develop panic disorder, requiring further iterations of the theory.

9. DISCUSSION

The network framework has highlighted a critical gap in traditional clinical research methods, which have often taken a more reductionist view. While useful in some contexts, reductionist approaches can oversimplify the multifaceted nature of mental disorders. Network models have emerged as a fitting response and have offered a methodological framework that accommodates the complexity of mental health disorders (Borsboom et al., 2022). These models serve not only as descriptive tools but also as valuable tools for hypothesis generation, identifying influential pathways within the network, and opening new avenues for understanding how changes in one aspect of the system might impact overall mental health (Briganti, 2022).

The evolution of statistical methods in network psychometrics has significantly enriched the psychometrician's toolbox, providing tools for cross‐sectional and panel data, community detection, dimensionality reduction, and inference measures (Isvoranu et al., 2022). Over the last few several psychological phenomena, such as intelligence, personality, psychopathology, and attitudes, have been reconceptualized as networks, necessitating new methods to explore their properties: as new methods come to enrich this toolbox, new facets of mental health constructs can be analyzed.

In this paper, we offered an overview of the current landscape of network analysis in mental health research, bridging theoretical network models and their empirical applications. We introduced the most used framework: undirected network estimation in cross‐sectional data using frequentist estimation techniques. We then elaborated on new lines of research that are currently growing prominently in the field: psychometric network modeling, Bayesian estimation techniques, longitudinal models, and causal inference. Finally, we discussed how network models can effectively enhance the description, prediction, comprehension, and treatment of mental health disorders, thereby enriching the field of psychopathology.

Network modeling has been proposed as an alternative to latent variable modeling techniques commonly used in psychometrics. Interestingly, in some cases, there can be a full correspondence between some networks and some latent variable models, including factor and IRT models (Epskamp et al., 2021). This close relationship allows for frameworks to be more closely linked than initially thought. For example, EGA applied on networks can be used to investigate the potential number of underlying latent variables (Golino & Epskamp, 2017). Additionally, the close link readily allows for metrics and methods from factor analysis to be applicable in network psychometrics, such as measurement invariance testing, fit measures, and meta‐analytic methods (Epskamp, Isvoranu, & Cheung, 2022).

The evolution of network modeling has also seen the development of confirmatory network modeling techniques. The ability to perform a confirmatory fit of a pre‐defined network structure using confirmatory network modeling allows researchers to test if a network structure replicates and allows for a fair comparison between factor models and network models (Epskamp, Isvoranu, & Cheung, 2022; Epskamp, Rhemtulla, & Borsboom, 2017). Furthermore, latent network modeling has been developed to address issues such as measurement error and semantically overlapping items, allowing researchers to model conditional independence relationships between latent variables without making assumptions about directionality or acyclicity (Epskamp, Rhemtulla, & Borsboom, 2017).

The Bayesian approach to network analysis involves two primary questions: determining the presence or absence of an edge between nodes and estimating the strength of the edge if it exists. This method offers a robust framework for addressing these questions by incorporating prior knowledge and updating it with observed data. One significant advantage of Bayesian methods is their ability to express uncertainty in terms of posterior probabilities, which enhances the generalizability and transferability of inferences. Bayesian hypothesis testing, particularly through the use of the inclusion Bayes factor, helps distinguish between the absence of an effect and insufficient evidence (Huth, de Ron, et al., 2023; Marsman & Haslbeck, 2023). Despite their strengths, Bayesian methods are computationally intensive and require careful specification of prior distributions.

Understanding how processes unfold over time and within an individual is central to network theory and is impossible when relying solely on cross‐sectional data. Longitudinal data allows network edges to encode different types of information and provide insights into how variables interact over time (Blanchard et al., 2023). Various estimation techniques, such as the multilevel graphical vector‐autoregressive network model, offer three types of model outputs: temporal networks, contemporaneous networks, and between‐person networks. Temporal networks encode relationships between variables over time, contemporaneous networks encode relationships within the same measurement window, and between‐person networks encode relationships between a person's typical levels of each node across time. Such models are stationary, meaning their properties do not change over time, which is a strong assumption to impose on a psychological system. This limitation has led to the development of time‐varying network models, which can capture network changes over time, and rate of change network models, which provide insight into how symptoms change together over time (Bringmann, 2024).

The comparison of idiographic network structures to identify individual differences in symptom dynamics is a growing area of interest. However, traditional methods such as visual inspection, correlation computation, and multilevel data analysis techniques like mlVAR cannot directly test for (in)equalities between idiographic network structures. This limitation can lead to erroneous conclusions about individual differences. The Individual Network Invariance Test (INIT) addresses this by comparing models assuming network equality against those allowing for heterogeneity, thus providing a more rigorous testing framework. INIT enhances the reliability of conclusions by ensuring that variance within data is attributed to individual differences only when there is sufficient evidence (Hoekstra et al., 2024; van der Tuin et al., 2023).

Rate‐of‐change network models assess how symptoms change together over time, using first‐order derivatives (velocity) to capture the dynamics. These models are robust to missing data and can capture nonlinear relationships between symptoms. They offer valuable insights into the conditional relationships between symptoms as they evolve, allowing for monitoring at individual, group, and sample levels. This approach is particularly useful for understanding the specific effects of interventions on symptom dynamics over time (Golino et al., 2022).

NIA combines network analysis with experimental research to investigate symptom‐specific treatment effects (Bringmann et al., 2022). By incorporating a treatment allocation variable into the network, NIA allows for the differentiation between direct and indirect treatment effects (Blanken et al., 2019). This methodology has been applied to contrast active treatment conditions, revealing unique patterns in symptom targeting that align with theoretical underpinnings. NIA offers new ways to investigate treatment mechanisms and can be adapted to various experimental designs, variables, and model types.

Bayesian Networks associate a probability distribution with a DAG, where nodes represent random variables, and edges indicate conditional dependencies. BNs are computationally efficient and allow for studying specific symptoms from their local distributions. They also bridge from probability to causality by identifying v‐structures as patterns of causal effects (Briganti et al., 2023). Using BNs as causal network models requires careful consideration of several essential conditions, including accurate reflection of underlying causal relationships, representative data, and critical examination of theoretical assumptions. The estimation of BNs integrates observed data with prior beliefs, using Bayesian inference to determine which edges are supported by the information available and to estimate the values of network parameters. BN inference involves drawing conclusions from the network through belief updating or causal reasoning, providing significant insights into the dependence and causal structure of symptoms. Even without a strict causal interpretation, BNs hold value in terms of hypotheses generation in psychopathology (Briganti, 2022).

Network models can serve as theories of psychopathology, representing the behavioral, cognitive, physical, and social components underlying mental health issues and their interrelations. The adequacy of network models as theories depends on their ability to represent the target system accurately. When there is a mismatch between the data used to estimate the network model and the phenomena theories seek to explain, or when network models cannot produce phenomena of interest, they may provide poor representations of target systems (Fried, 2020). Nevertheless, network models can inform theories by helping with inferences about the inner workings of a system (Robinaugh, Haslbeck, Waldorp, Kossakowski, Fried, Millner, McNally, et al., 2019). They can capture phenomena that theories should be able to explain, thereby providing clear goalposts for theory development (Haslbeck et al., 2022). This approach involves establishing phenomena through thorough exploratory work and using formal or computational theories to simulate and match empirical data, thereby iteratively refining the theory.

The integration of network analysis into mental health research represents a significant advancement in understanding the complexity of mental disorders: by moving beyond reductionist approaches and embracing the interconnected nature of biopsychosocial systems, network models offer a robust framework for exploring, describing, and intervening in mental health. This paper has highlighted the theoretical foundations, methodological innovations, and practical applications of network models in mental health research. As the field continues to evolve, the ongoing refinement and validation of these models will be at the methodological core of advancing our understanding and treatment of mental health disorders.

AUTHOR CONTRIBUTIONS

Giovanni Briganti: Conceptualization, writing – original draft, writing – review & editing, supervision. Marco Scutari: Writing – original draft, writing – review & editing, supervision. Sacha Epskamp: Writing – original draft, writing – review & editing, supervision. Denny Borsboom: Writing – original draft, writing – review & editing, supervision. Ria H. A. Hoekstra: Writing – original draft, writing – review & editing. Hudson Fernandes Golino: Writing – original draft, writing – review & editing. Alexander P. Christensen: Writing – original draft, writing – review & editing. Yannick Morvan: Writing – original draft, writing – review & editing. Omid V. Ebrahimi: Writing – original draft, writing – review & editing. Giulio Costantini: Writing – original draft, writing – review & editing, supervision. Alexandre Heeren: Writing – original draft, writing – review & editing. Jill de‐Ron: Writing – original draft, writing – review & editing. Laura F. Bringmann: Writing – original draft, writing – review & editing. Karoline Huth: Writing – original draft, writing – review & editing. Jonas M B Haslbeck: Writing – original draft, writing – review & editing. Adela‐Maria Isvoranu: Writing – original draft, writing – review & editing. Maarten Marsman: Writing – original draft, writing – review & editing. Tessa Blanken: Writing – original draft, writing – review & editing. Allison Gilbert: Writing – original draft, writing – review & editing. Teague Rhine Henry: Writing – original draft, writing – review & editing. Eiko I. Fried: Writing – original draft, writing – review & editing, supervision. Richard J. McNally: Writing – original draft, writing – review & editing, supervision.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

ETHICS STATEMENT

Not applicable.

PATIENT CONSENT STATEMENT

Not applicable.

PERMISSION TO REPRODUCE MATERIAL FROM OTHER SOURCES

Not applicable.

CLINICAL TRIAL REGISTRATION

Not applicable.

Briganti, G. , Scutari, M. , Epskamp, S. , Borsboom, D. , Hoekstra, R. H. A. , Golino, H. F. , Christensen, A. P. , Morvan, Y. , Ebrahimi, O. V. , Costantini, G. , Heeren, A. , Ron, J. d. , Bringmann, L. F. , Huth, K. , Haslbeck, J. M. B. , Isvoranu, A.‐M. , Marsman, M. , Blanken, T. , Gilbert, A. , … McNally, R. J. (2024). Network analysis: An overview for mental health research. International Journal of Methods in Psychiatric Research, e2034. 10.1002/mpr.2034

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this study.