An Evaluation of an Algorithm for the Selection of Flexible Survival Models for Cancer Immunotherapies: Pass or Fail?

Abstract

Background and Objective

Accurately extrapolating survival beyond trial follow-up is essential in a health technology assessment where model choice often substantially impacts estimates of clinical and cost effectiveness. Evidence suggests standard parametric models often provide poor fits to long-term data from immuno-oncology trials. Palmer et al. developed an algorithm to aid the selection of more flexible survival models for these interventions. We assess the usability of the algorithm, identify areas for improvement and evaluate whether it effectively identifies models capable of accurate extrapolation.

Methods

We applied the Palmer algorithm to the CheckMate-649 trial, which investigated nivolumab plus chemotherapy versus chemotherapy alone in patients with gastroesophageal adenocarcinoma. We evaluated the algorithm’s performance by comparing survival estimates from identified models using the 12-month data cut to survival observed in the 48-month data cut.

Results

The Palmer algorithm offers a systematic procedure for model selection, encouraging detailed analyses and ensuring that crucial stages in the selection process are not overlooked. In our study, a range of models were identified as potentially appropriate for extrapolating survival, but only flexible parametric non-mixture cure models provided extrapolations that were plausible and accurately predicted subsequently observed survival. The algorithm could be improved with minor additions around the specification of hazard plots and setting out plausibility criteria.

Conclusions

The Palmer algorithm provides a systematic framework for identifying suitable survival models, and for defining plausibility criteria for extrapolation validity. Using the algorithm ensures that model selection is based on explicit justification and evidence, which could reduce discordance in health technology appraisals.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40273-024-01429-0.

Key Points for Decision Makers

Survival modelling is particularly challenging for immunotherapies, owing to the potential for long-term survival benefits. Palmer et al. published an algorithm designed to help analysts select survival models to inform economic evaluations of cancer immunotherapies.

We present a practical demonstration of the Palmer algorithm, and evaluate its performance using multiple data cuts from the CheckMate-649 trial, which investigated nivolumab plus chemotherapy versus chemotherapy alone in patients with gastroesophageal adenocarcinoma.

We show that the Palmer algorithm offers a valuable, systematic procedure for survival model selection: its use could reduce discourse in health technology assessments, leading to more efficient decision making. The algorithm could be improved with minor additions around the specification of hazard plots, the setting out of plausibility criteria and the inclusion of flexible parametric non-mixture cure models, which we show are potentially valuable in the cancer immunotherapy setting.

Introduction

Accurately estimating the survival benefits associated with new cancer treatments is essential for health technology assessment (HTA), to allow appropriate resource allocation decision making. Clinical trials generally have limited follow-up at the time of regulatory approval and HTA submission, driven by a desire to ensure timely patient access to new treatments [1]. In the absence of long-term data, extrapolation beyond observed trial periods is necessary, to estimate complete survival benefits. The choice of extrapolation method often substantially impacts estimates of survival and cost effectiveness, representing a key area of discourse and uncertainty in technology appraisals (TAs) [2–4]. Recently, Palmer et al. published an algorithm designed to help analysts select survival models to inform economic evaluations of cancer immunotherapies—a setting where extrapolation is a particular challenge owing to the potential for long-term survival benefits [5, 6]. In this paper, we present a practical demonstration and evaluation of this algorithm, henceforth referred to as the ‘Palmer algorithm’.

The National Institute for Health and Care Excellence (NICE) Decision Support Unit (DSU) published guidance on using parametric survival models in 2011 [7]. These guidelines focused on ‘standard’ parametric models, including exponential, Weibull, Gompertz, log-logistic, log normal and generalised gamma distributions. Each of these models makes assumptions about the shape of the hazard function (the risk of the event of interest [usually death] occurring over time). In particular, the exponential, Weibull and Gompertz models cannot represent ‘turning points’ in the hazard function (that is, where hazards that were previously increasing begin to decrease, or vice-versa), and log-logistic, log normal and generalised gamma models can only reflect one turning point. As a result, sometimes these models may not appropriately represent the expected hazard function.

Treatment of cancer using immunotherapy has been shown to result in delayed but durable responses, resulting in hazard functions with complex shapes [5, 8–10]. Typically, patients recruited into clinical trials are relatively healthy because of strict eligibility criteria [11, 12]. However, in trials of treatments for advanced cancers, the hazard of death is likely to increase in the short term before declining if participants respond to treatment. In the long term, hazards may increase again, due to age-related mortality. This implies multiple turning points in the hazard function, which none of the standard parametric survival models can represent. This was recognised in NICE DSU Technical Support Document 21, which described flexible methods for survival modelling [13]. Palmer et al. built on this document, providing an algorithm to guide analysts on how to determine when flexible survival models are needed, and which models to use, specifically in the context of immunotherapies. Given the impact of survival model choice on cost-effectiveness estimates, and regular disagreements around which survival models are appropriate [4], the algorithm represents a potentially valuable tool that could be used to harmonise the survival modelling undertaken for immunotherapy HTAs.

We apply the Palmer algorithm and evaluate its performance using multiple data cuts from the CheckMate-649 (CM-649) trial [14]. CM-649 investigated nivolumab plus chemotherapy versus chemotherapy alone in patients with advanced gastric, oesophageal adenocarcinoma or gastro-oesophageal junction cancer. Our methods section describes the CM-649 data, summarises the Palmer algorithm and explains our evaluation approach: we apply the algorithm to an early data cut from CM-649 (as would be typically available for an HTA) and evaluate its practicality, success in accurately predicting subsequently observed outcomes and potential for improvement. Our results section presents outcomes from our algorithm application and compares model predictions to later observed survival data. Finally, we discuss findings and suggest enhancements for the algorithm.

Methods

The CheckMate-649 Study

CM-649, an international, phase III, randomised controlled trial (RCT), randomised 789 participants to nivolumab plus chemotherapy and 792 participants to chemotherapy alone. The study has been reported in detail [14–16], and provided the pivotal evidence used in NICE TA857 [17]. Ultimately, NICE recommended nivolumab plus chemotherapy as an option for untreated human epidermal growth factor receptor 2-negative, advanced or metastatic gastric cancer, gastro-oesophageal junction or oesophageal adenocarcinoma in adults whose tumours express programmed death-ligand 1 (PD-L1) with a combined positive score (CPS) of 5 or more [17]. The PD-L1 CPS ≥ 5 subgroup constituted 473 of the participants randomised to nivolumab plus chemotherapy, and 482 of the participants randomised to chemotherapy alone.

At the time of submission, data from CM-649 had a minimum follow-up of 12.1 months (referred to as the ‘12-month’ data cut) [14]. During the appraisal, a second data cut became available, with a minimum follow-up of 24 months [16]. Subsequently, 36-month and 48-month minimum follow-up data have become available [15, 18].

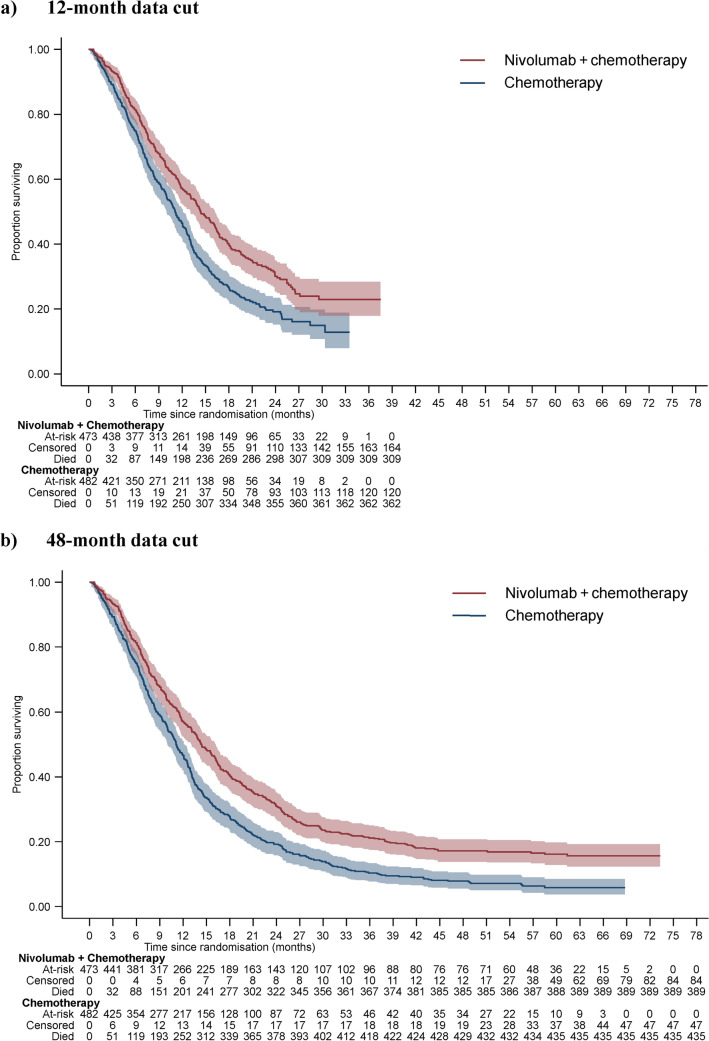
In this paper, we apply the Palmer algorithm to the 12-month data cut from CM-649 and compare model predictions to data observed in the 48-month data cut, with all analyses focused on the PD-L1 CPS ≥ 5 subgroup. Figure 1 presents overall survival data from these two data cuts. In the 12-month data cut, 70% of the participants had died, which increased to 86% in the 48-month data cut. Follow-up is clearly much longer in the 48-month data cut, the shapes of the survival curves appear more established, and there is no overlap in confidence intervals (CIs) at the tails of the curves.

Fig. 1.

CM-649 programmed death-ligand 1 combined positive score ≥5 overall survival data, 12-month and 48-month data cuts. PD-L1 programmed death-ligand 1

The Palmer Algorithm

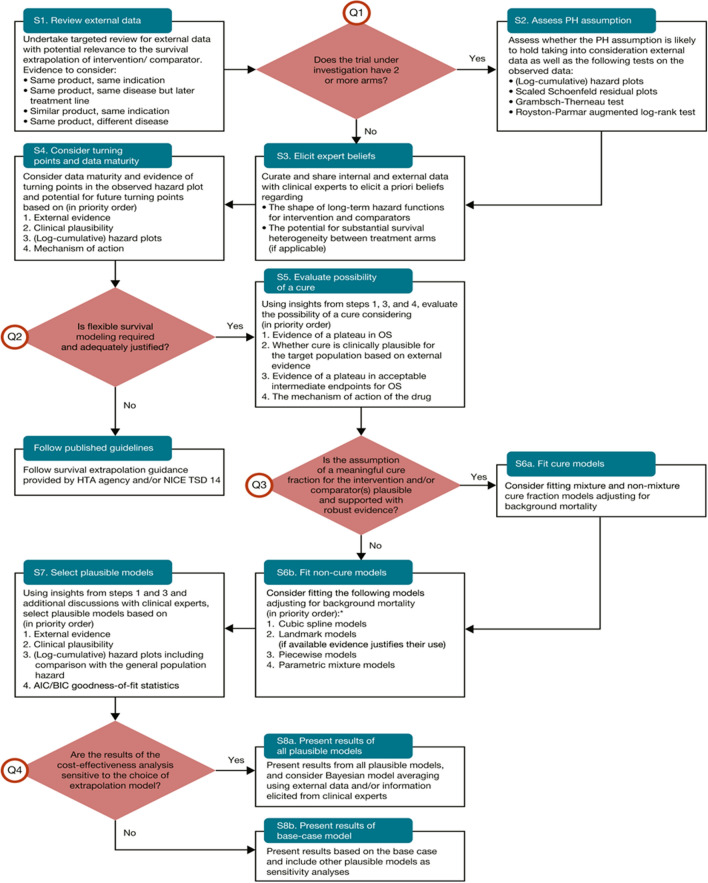
The Palmer algorithm aims to help analysts decide whether flexible survival models are required to extrapolate survival for immunotherapies, and, if so, which models should be chosen for testing. The algorithm involves 8 Steps (referred to as S1–S8) and four questions (referred to as Q1–Q4) [see Fig. 2]. Proceeding through these Steps and questions requires a detailed appraisal of the pivotal trial data as well as external data and information. Key elements include identification of relevant external data, using clinical expert input, and considering observed and expected hazard functions and the potential for long-term survival.

Fig. 2.

The Palmer algorithm. AIC Akaike Information Criterion, BIC Bayesian Information Criterion, HTA health technology assessment, NICE TSD National Institute for Health and Care Excellence Technical Support Document, PH proportional hazards, OS overall survival. Re-produced with permission from Palmer et al. [5]. This article was published in Value in Health; 26(2), Palmer S, Borget I, Friede T, Husereau D, Karnon J, Kearns B, et al. A guide to selecting flexible survival models to inform economic evaluations of cancer immunotherapies, pg. 185–92

Application and Assessment of the Palmer Algorithm

In our application of the Palmer algorithm, we utilised the fact that CM-649 provided the pivotal evidence included in NICE TA857. Given that NICE appraisals involve detailed searches and reviews of relevant evidence, we used external data sources and clinical expert opinion referred to within the appraisal documents to inform our application of the algorithm as this represents what was ‘known’ at the time. In particular, for S1 (review external data, see Fig. 2), we reviewed all the external data sources mentioned in the appraisal documents, and supplemented this with information on survival in people with cancer of the oesophagus and cancer of the stomach (diagnosed between 2015 and 2019) from the National Cancer Registration and Analysis Service, which collects data on all people living in England who are diagnosed with cancer [19]. For S3 (elicit expert beliefs), we reviewed all the expert beliefs mentioned in the appraisal documents for NICE TA857. It would not be possible to elicit a priori expert beliefs on the shape of long-term hazard functions and survival based on the 12-month CM-649 data cut given that longer term data are now available; it was therefore logical to base expert beliefs on those included in the NICE appraisal documents.

We evaluated the hazards observed in the 12-month data cut, utilising log-cumulative and smoothed hazard plots, Schoenfeld residuals, and the Grambsch-Therneau test. Additionally, we considered relevant external data and expert opinions to inform our assessment of the proportional hazards assumption (S2), our examination of turning points in the hazard function (S4), and the potential for a cure (S5). This allowed us to identify a set of candidate survival models (S6)—those that could potentially satisfy the hazard functions and survival functions expected for overall survival for nivolumab plus chemotherapy and chemotherapy alone. In addition, we defined plausibility criteria that models could be assessed by once they had been fitted. We then applied the candidate survival models to the 12-month data cut from CM-649 (PD-L1 CPS ≥ 5 population) and identified those that met our plausibility criteria (S7). We present results for each model (S8a).

To assess model performance, we compared their predictions to the pre-defined plausibility criteria and to the survival outcomes observed in the 48-month data cut. We evaluated predictions by determining whether they satisfied the plausibility criteria, and whether predicted hazard and survival functions lay within the 95% CIs of the 48-month observed data. We did not address S8b of the algorithm (presenting cost-effectiveness results) as our focus was only on survival predictions. Analyses were conducted in Stata version 17. Stpm2 was used to fit flexible parametric models and non-mixture cure (NMC) models [20], and strsmix to fit mixture cure models (MCMs) [21].

Results

Application of the Palmer Algorithm: Plausibility Criteria and Candidate Survival Models

Table 1 presents a summary of our findings for Steps S1 to S6 of the algorithm, including plausibility criteria defined based on these findings, and a set of candidate survival models considered potentially able to satisfy these criteria. A detailed commentary on the evidence and analyses underpinning these findings is provided in the Electronic Supplementary Material (ESM).

Table 1.

Application of the Palmer algorithm to the 12-month data cut from the CM-649 programmed death-ligand 1 combined positive score ≥ 5 population

Algorithm step	Issue	Evidence sources	Conclusions	Notes
S1	Review external data	First-line therapy 4 RCTs investigating immunotherapies compared to chemotherapy in populations that overlap with CM-649 [25–28] 1 meta-analysis of 4 RCTs [29] and 8 other RCTs investigating chemotherapy regimens in overlapping populations [30–37] Second-line + therapy 7 RCTs investigating either immunotherapy or chemotherapy given in populations similar to those included in CM-649 who receive subsequent therapy [38–43] Real-world data Real-world data from England [19, 44], the USA [45, 46], Canada [47] and the Netherlands [48] in populations that overlap with CM-649	Chemotherapy RCT data suggest that survival proportions of 4–7% at 4 years are plausible [29, 30] and 3% may still be alive at 9 years [29] RWE evidence suggests 5-year survival of 3–6% is plausible [19, 44–46], and around 4% of patients treated with chemotherapy may still be alive at 10 years, [46] although data for this timepoint are lacking from England, and, whilst uncertain because of censoring, data from the Royal Marsden indicate 0% survival at 9 years [44] Hazards become low for a small proportion of patients who can be expected to survive well beyond 3–5 years [19, 29, 30, 44–48] Nivolumab plus chemotherapy Studies of other immunotherapies show that survival in patients with GC and GOJ can be extended out to at least 3 years, but no evidence beyond this point Plausibility criteria Hazards will become low in the long-term, in both treatment groups Chemotherapy expected survival at 4 years: 3–7% Chemotherapy expected survival at 10 years: 1–4%	See Appendix A (ESM) for detailed information on evidence sources
S2	Assessment of proportional hazards assumption	CM-649 12-month data cut [14] ATTRACTION-4 [28] (nivolumab plus chemotherapy vs chemotherapy alone in GC and GOJ, undertaken in Japan, South Korea and Taiwan) External data and information [5, 8, 49–52]	Log-cumulative hazard, smoothed hazard, and Schoenfeld residuals plots, and Grambsch Therneau test results were not definitive as to whether the proportional hazards assumption holds in the CM-649 12-month data cut Data from ATTRACTION-4 deemed of limited use, in line with conclusions of NICE TA857 Appraisal Committee and Evidence Review Group [17, 28] External sources report that immunotherapies have delayed but durable effects: survival curves have different shapes to those associated with chemotherapy. NICE appraisals of immunotherapies consistently have not assumed proportional hazards [53] Plausibility criteria Not appropriate to assume proportional hazards - use independently fitted survival curves. Given that a small proportion of patients in both trial arms are expected to survive long term, hazards will equalise as excess disease-related hazards fall to zero	See Appendix B (ESM) for hazard and Schoenfeld residuals plots, Grambsch-Therneau test results, and commentary
S3	Eliciting expert beliefs	All expert beliefs about hazards and survival mentioned in the appraisal documents for NICE TA857 [17]	Plausibility criteria Reasonable to expect hazards that fall in the long term, for both treatment groups Hazards will equalise in the long term, in long-term survivors For chemotherapy, survival of approximately 4% at 5 years is plausible Reasonable to expect nivolumab plus chemotherapy to approximately double the long-term survival proportion For nivolumab plus chemotherapy, 20-year survival of approximately 3% is plausible Hazards are likely to remain above those in the general population, even in long-term survivors (therefore an SMR >1 is appropriate)	See Appendix C (ESM) for a summary of expert beliefs contained within NICE TA857 documents
S4	Consider turning points and data maturity	External data (summarised in S1), clinical expert beliefs (summarised in S3), and an assessment of hazards observed in CM-649	Plausibility criteria Trial data suggest an initial increase in hazards, followed by a decrease (after approximately 1 year), for both treatment groups Reasonable to expect hazards will continue to fall in the long term, for both treatment groups (see S1 and S3) Hazards will equalise in the long term, in long-term survivors (see S3) Hazards in long-term survivors will remain above those in the general population Hazards will eventually increase again in long-term survivors, due to age-related mortality	See Appendix B (ESM) for smoothed hazard plots from CM-649
S5	Evaluate possibility of a cure	Based on insights from S1, S3 and S4	Plausibility criteria Long-term disease-specific hazards may fall to zero in a small proportion of patients in both treatment groups Mortality rates will remain higher than in the background due to co-morbidities and long-term toxicities The timepoint at which disease-specific hazards fall to zero is unknown	N/A
S6	Candidate survival models	All previous steps	One turning point in the hazard function expected within the period of the data, and another turning point expected beyond the period of the data. Models must be able to reflect this Cure models are plausible and justifiable, provided they include an SMR uplift However, these may not result in credible extrapolations, fitted to 12-month data. Hence flexible non-cure models also relevant to fit Models should be fitted independently to each treatment group Candidate models: Log normal models with background mortality and SMR uplift Log-logistic models with background mortality and SMR uplift Generalised gamma models with background mortality and SMR uplift FPMs with background mortality and SMR uplift Mixture cure models (generalised gamma, log-logistic, Weibull) with background mortality and SMR uplift Non-mixture cure models (in a flexible parametric framework) with background mortality and SMR uplift	N/A

CM-649 CheckMate-649, FPM flexible parametric model, GA advanced gastric cancer, GC gastric cancer, GOJ gastro-oesophageal junction cancer, N/A Not applicable, NICE National Institute for Health and Care Excellence, RCT randomised controlled trial, RWE real-world evidence, SMR standardised mortality ratio, TA857 Technology Appraisal 857, ESM Electronic Supplementary Material

Models needed to be capable of depicting a single turning point in the hazard function over the data period as the observed hazards exhibited an initial increase, followed by a decrease after approximately 1 year. Exponential, Weibull, and Gompertz models could not capture this turning point in the hazard within the observed data period, and so were eliminated as candidates. Furthermore, models were required to incorporate an additional turning point beyond the data period to account for the eventual age-related rise in mortality risk among a small proportion of patients expected to survive beyond 10 years in both treatment groups. In these long-term survivors, it was expected that hazards would converge to rates remaining above general population levels. For this, the most appropriate standardised mortality ratio (SMR) to use was unclear. Within TA857, analyses were presented with an SMR of 1.5, though without a clear rationale [17]. We conducted analyses with SMRs of 1.5 and 2.5.

We concluded that candidate survival models included log-logistic, log normal, generalised gamma, flexible parametric models, and mixture and non-mixture cure models. We determined that models should be fitted independently to each treatment arm because it was not appropriate to assume proportional hazards. Therefore, no restriction was placed on the treatment effect over time. All models were fitted in a relative survival framework [13, 22], allowing background mortality rates with an SMR uplift to be included. For flexible parametric models, we tested models with 1–5 knots, and for MCMs we tested distributions included in standard software packages (Weibull, log-logistic, generalised gamma). For NMC models, we used a flexible parametric framework to ensure that the turning point observed within the period of the data could be captured [23, 24].

In TA857, treatment effect waning scenarios were considered, with hazards converging at 5–6.5 years, we took this into account when assessing extrapolations. Flexible parametric NMC models allow the ‘cure time-point’ to be controlled: a boundary knot is chosen, after which hazards are forced to equal the background population hazard rate (with or without an SMR applied). To align with the expectation that hazards between treatment arms may converge at 5–6.5 years, we set the boundary knot at 7 years, reflecting that hazards may fall to background population levels soon after treatment arm hazards converge. However, we also fitted these models with 10-year and 15-year boundary knots to reflect uncertainty around this assumption.

Assessment of Model Predictions

Table 2 presents survival predictions associated with each of the candidate survival models, as well as values observed in the 48-month data from CM-649. Varying SMR rates did not make a substantial difference to model estimates, but estimates generally satisfied our plausibility criteria more consistently when an SMR of 2.5 was used, and results from these models are presented in Table 2. Similarly, varying the number of knots in the flexible parametric models and NMC models did not substantially impact model estimates,– though it is notable that models that included a greater number of knots consistently produced slightly lower estimates of the incremental life-years gained associated with nivolumab plus chemotherapy compared with chemotherapy alone. We present results of models with three internal knots in Table 2, which were those that provided estimates closest to our pre-defined plausibility criteria. Complete results for all models are presented in Appendix D of the ESM.

Table 2.

Candidate model survival estimates, observed values, and plausible ranges

Model		RMST(4 years)	RMST(5.5 years)	Mean survival (50 years)	Incremental life years gained	Survival %						AIC		Cure %
						Year 4	Year 5	Year 6	Year 10	Year 20
Plausible range	Chemo	-	-	-	-	3% - 7%	-	-	1% - 4%	-	-		-
	Nivo	-	-	-	-	6% - 14%	-	-	2% - 8%	3%	-		-
Observed data (48-month data-cut) – figures in brackets represent 95% CIs	Chemo	1.26(1.16-1.36)	1.36(1.23-1.48)	-	-	7.9%(5.6%-10.6%)	5.9% (3.8%-8.6%)	-	-	-	-		-
	Nivo	1.66 (1.54-1.78)	1.90 (1.74-2.07)	-	-	17.2%(13.9%-20.7%)	16.2% (12.9%-19.8%)	15.6% (12.3%-19.3%)	-	-	-		-
Log normal	Chemo	1.26†	1.32†	1.41	-	6.2%*†	3.8%†	2.5%	0.6%	0.0%	841		NA
	Nivo	1.62†	1.75†	1.98	0.57	12.1%*	8.2%	5.7%	1.7%	0.2%	909
Log-logistic	Chemo	1.25†	1.32†	1.45	-	6.1%*†	4.1%†	2.9%	1.0%*	0.1%	829
	Nivo	1.59†	1.72	2.00	0.55	11.2%*	7.8%	5.6%	2.1%*	0.3%	906
Generalised gamma	Chemo	1.14	1.17	1.18	-	3.1%*	1.4%	0.6%	0.0%	0.0%	833
	Nivo	1.54†	1.64	1.76	0.58	10.0%*	6.1%	3.9%	0.8%	0.0%	909
FPM (4df)	Chemo	1.24†	1.30†	1.36	-	5.9%*†	3.5%	2.2%	0.3%	0.0%	831
	Nivo	1.60†	1.71	1.81	0.45	10.6%*	6.3%	3.8%	0.5%	0.0%	912
Mixture Cure (log normal)	Chemo	1.21†	1.27†	1.36	-	6.2%*†	3.8%†	2.5%	0.6%	0.0%	843		0.0%
	Nivo	1.57†	1.70	1.93	0.57	12.1%*	8.2%	5.7%	1.7%	0.2%	911		0.0%
Mixture Cure (generalised gamma)	Chemo	1.24†	1.42†	2.98	-	12.0%	11.5%	11.0%	8.9%	4.5%	829		13.9%
	Nivo	1.60†	1.85†	4.04	1.06	17.6%†	16.3%†	15.5%†	12.6%	6.3%	908		19.6%
Mixture Cure (Weibull)	Chemo	1.24†	1.42†	2.99	-	12.1%	11.6%	11.0%	9.0%	4.5%	827		14.0%
	Nivo	1.62†	1.91†	4.44	1.45	19.6%†	18.7%†	17.8%†	14.5%	7.3%	907		22.6%
Non-mixture cure (FPM, 4df, 7-year boundary knot)	Chemo	1.27†	1.41†	2.62	-	9.9%†	9.0%	8.5%	7.0%	3.5%	828		10.8%
	Nivo	1.66†	1.92†	4.17	1.55	18.2%†	16.8%†	15.9%†	12.9%	6.5%	908		20.1%
Non-mixture cure (FPM, 4df, 10-year boundary knot)	Chemo	1.26†	1.37†	2.29	-	8.5%†	7.3%†	6.7%	5.3%	2.6%	829		8.2%
	Nivo	1.65†	1.87†	3.75	1.46	16.6%†	14.7%†	13.5%†	10.7%	5.4%	908		16.7%
Non-mixture cure (FPM, 4df, 15-year boundary knot)	Chemo	1.25†	1.34†	1.99	-	7.4%†	6.0%†	5.2%	3.7%*	1.8%*	829		5.7%
	Nivo	1.64†	1.84†	3.33	1.34	15.4%†	13.0%†	11.5%	8.5%*	4.2%*	909		13.1%

All models used a standardised mortality ratio of 2.5; * - satisfies plausibility criteria; ^† - within range of observed data; *^† - satisfies plausibility criteria and within range of observed data. AIC - Akaike information criterion; Chemo - Chemotherapy; df - degrees of freedom (the number of degrees of freedom is one greater than the number of knots); FPM - Flexible parametric model; Nivo - Nivolumab plus chemotherapy; RMST - Restricted mean survival time

None of the models fitted to the 12-month data cut provided estimates of survival proportions at 4, 5 and 6 years that consistently fell within our pre-specified plausible range and within the 95% CIs observed in the 48-month data cut. However, there are mitigating circumstances: for both treatment arms, the point-estimate for year 4 survival in the 48-month data lay above our pre-specified plausible range (chemotherapy plausible range: 3–7%, observed: 7.9% [95% CI 5.6–10.6]; nivolumab plus chemotherapy plausible range: 6–14%, observed: 17.2% [95% CI 13.9–20.7]). This indicates that our pre-specified plausible range may have been too pessimistic and makes it difficult for models to provide estimates that are consistent with both the observed data and the plausible range.

At the 4-year timepoint, only the NMC models (with 7-year, 10-year and 15-year boundary knots) provided survival estimates that lay within the 95% CI from the observed data for both treatment arms. All other models provided estimates that lay within the observed 95% CIs for one treatment arm but not both, except the generalised gamma, which provided estimates that fell below the lower 95% limit compared with observed data for both treatment arms.

At the longest observed annual timepoints (year 5 for chemotherapy; year 6 for nivolumab plus chemotherapy), only the NMC models with 10-year boundary knots provided estimates that fell within the CIs of the observed data for both treatment arms. The log normal and log-logistic models provided estimates that fell within the CIs of the observed data for chemotherapy; however, none of the non-cure models achieved this for the nivolumab plus chemotherapy arm. Similarly MCMs provided estimates that fell within the observed CIs for one of the treatment arms, but not for both.

At the 10-year timepoint, the log-logistic model provided survival estimates that fell within our pre-specified plausible range for both treatment arms, but estimates were at the very bottom of the range (1.0 vs 1–4% for chemotherapy; 2.1 vs 2–8% for nivolumab plus chemotherapy). All other non-cure models produced estimates that were below the plausible range. In contrast the MCM and NMC generally gave long-term survival estimates higher than the plausible range, with the exceptions of the log normal MCM, which estimated a 0% cure fraction for both treatment arms and thus under-estimated survival, and the NMC models with 15-year boundary knots, which provided 10-year survival estimates within the pre-specified range for chemotherapy (3.7%) but marginally higher than the pre-specified range for nivolumab plus chemotherapy (8.5%). The 10-year survival estimates from the NMC models with 15-year boundary knots appear reasonable, given that observed 4-year survival in the 48-month data cut was above the upper bound of the pre-specified plausible range for both treatment arms.

Preferred Models

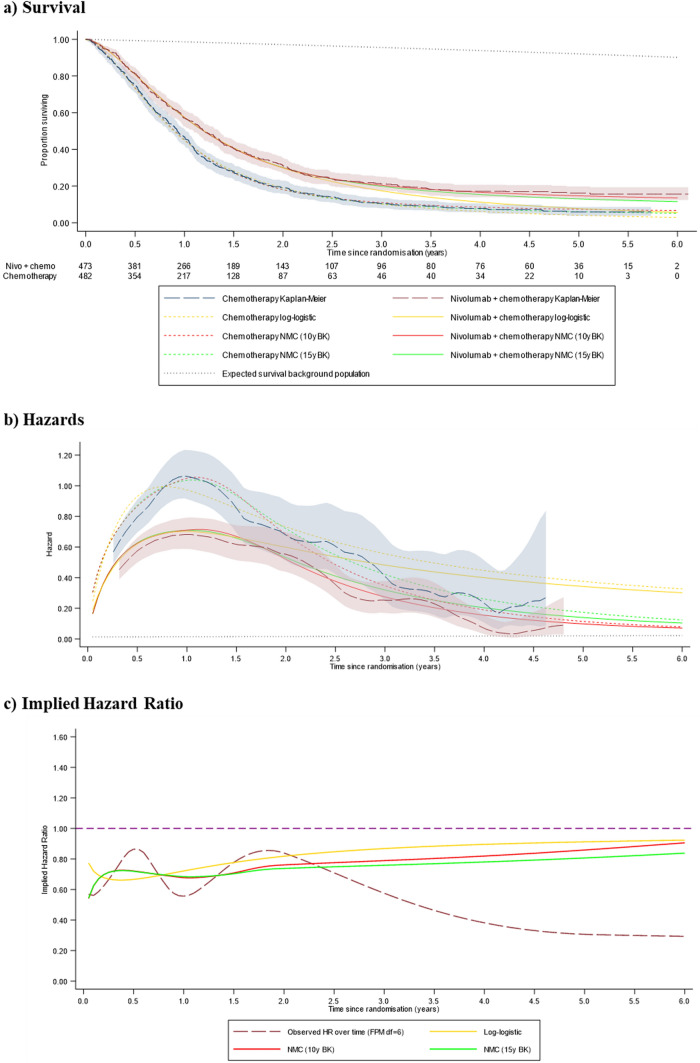
Figures 3 and 4 present (a) survival curves, (b) hazard plots and (c) implied HRs for the log-logistic and 10-year and 15-year boundary knot NMC models, representing the models we consider to have produced the most plausible survival extrapolations. Based on these results, of the non-cure models, the log-logistic models provided survival extrapolations that most closely represented pre-specified plausibility criteria. However, compared with the data observed in the 48-month data cut, these models appeared likely to have produced pessimistic extrapolations for both treatment arms, especially for nivolumab plus chemotherapy. This outcome is due to predicted hazards appearing to remain considerably too high, especially for nivolumab plus chemotherapy, tracking above the CI from the observed data.

Fig. 3.

Preferred model predictions compared to the 48-month data cut (programmed death-ligand 1 combined positive score ≥ 5), 6-year timeframe. 10y BK 10-year boundary knot, 15y BK 15-year boundary knot, df degrees of freedom (the number of degrees of freedom is one greater than the number of knots), FPM flexible parametric model, Nivo + chemo nivolumab plus chemotherapy, NMC non-mixture cure model

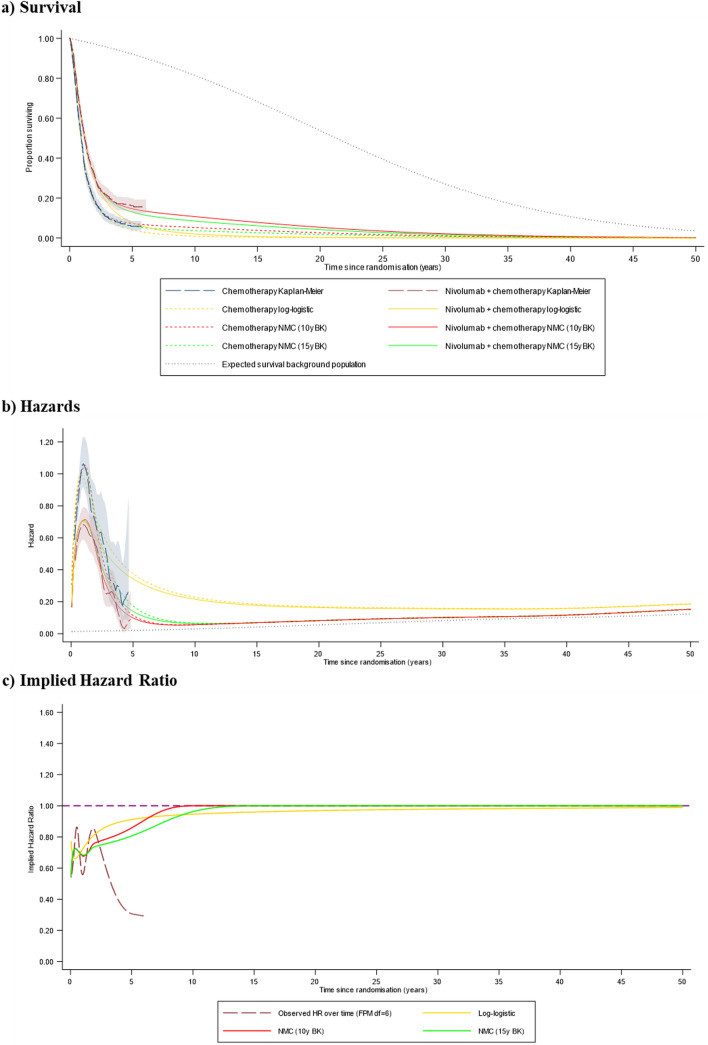
Fig. 4.

Preferred model predictions compared to the 48-month data cut (programmed death-ligand 1 combined positive score ≥ 5), 50-year timeframe. 10y BK 10-year boundary knot, 15y BK 15-year boundary knot, df degrees of freedom (the number of degrees of freedom is one greater than the number of knots), FPM flexible parametric model, NMC non-mixture cure model

Figure 3b indicates that the NMC models provided reasonable approximations of the hazards observed in the 48-month data cut, accurately representing the turning point observed in the hazard function for both treatment arms, and predicting hazards in the longer term that closely align with the observed data. Observed hazards appear to be falling towards background levels towards the end of the trial follow-up, at approximately 5 years (Fig. 4b), although convergence was not yet achieved, and hazards remained appreciably higher in the chemotherapy group. The 10-year and 15-year boundary knot NMC models predicted convergence with background hazards at 10 and 15 years, with the implied treatment effect HR converging to 1 at these timepoints. The log-logistic models projected hazards that remained substantially above background levels for the entire lifetime of even the longest term survivors. It is notable that the Weibull MCM and the NMC models provided substantially higher estimates than all other models of the life-years gained associated with nivolumab plus chemotherapy compared with chemotherapy alone.

Summary

Using plausibility criteria developed based on our application of the Palmer algorithm, we identified a range of survival models that were potentially appropriate for extrapolating survival from the 12-month data cut from CM-649 (in the PD-L1 CPS ≥ 5 population). When these models were fitted, log-logistic models seemed to provide credible extrapolations, although survival predictions from these models were towards the low end of the plausible range. Non-mixture cure models provided extrapolations that were close to plausible ranges but appeared slightly optimistic. No other models produced extrapolations that appeared plausible for both treatment arms. When compared with survival observed in the 48-month data cut from CM-649, it became apparent that survival in the trial exceeded expectations, especially in the nivolumab plus chemotherapy group, and only the NMC models appeared to provide plausible extrapolations.

Discussion

In this paper, we explored the Palmer algorithm for selecting models to extrapolate survival for immunotherapies. We evaluated its performance using multiple data cuts from the CM-649 trial. Our objectives were to assess the usability of the algorithm, identify any potential areas for improvement and evaluate whether it effectively identifies models capable of accurate extrapolation.

The Palmer algorithm offers a systematic procedure for model selection, encouraging thorough analyses and ensuring that crucial stages in the model selection process are not overlooked. Model selection steps that are implied by other guidance documents are made explicit by the algorithm. For example, while DSU Technical Support Documents on survival analysis state that external validity is crucial [7, 13], they do not outline how this should be assessed. In contrast, Steps S1–S5 of the Palmer algorithm detail explicitly what is expected with respect to survival proportions, hazard functions and treatment effects [6].

The algorithm involves extensive effort dedicated to identifying models suitable for fitting to the data, before any analyses of the pivotal trial are undertaken. This inevitably leads to a significant workload. In the context of HTA, it is our expectation that following the Palmer algorithm will increase the initial workload associated with the survival extrapolation task. However, this should result in fewer disagreements around model choice and a reduced need for additional modelling to be undertaken during the TA process, potentially leading to quicker and more efficient decision making and, where appropriate, quicker patient access to cost-effective treatments.

Our application identified several areas where we believe additions or modifications to the algorithm could be considered:

• (i)Plausibility criteria. When applying Steps S1–S5 of the algorithm, analysts are encouraged to consider key evidence and expectations around survival proportions, hazard functions and treatment effects. When completing these Steps, we felt compelled to define ‘plausibility criteria’—criteria that should be satisfied for survival models to be considered plausible. The algorithm does not explicitly state that plausibility criteria should be defined but we believe this could represent a valuable addition. We believe that this could also help clarify Step S7, which presents a priority order for criteria used to assess the plausibility of fitted models. Specifying plausibility criteria would allow these criteria to be defined more formally.
• (ii)Presentation of predicted treatment effects. Step S7 requires an assessment of the plausibility of fitted models, including hazard plots. In our application, we interpreted this as including plots of relative hazards, in line with NICE DSU Technical Support Document 21 [13]. The algorithm does not explicitly recommend these plots (whereas others are mandated), but they are important as they show what fitted models are predicting about the treatment effect over time.
• (iii)Testing the proportional hazards assumption. Step S2 of the algorithm requires an assessment of the proportional hazards assumption. We identified two issues at this Step; first, the Royston-Parmar augmented log rank test is suggested as a test of proportional hazards. However, the augmented log rank test is a test of the statistical significance of a treatment effect in the presence of non-proportional hazards, rather than a test of whether the proportional hazards assumption holds [54]. Second, Step S2 refers solely to an assessment of the proportional hazards assumption, which is only relevant when using proportional hazards models to extrapolate survival. Accelerated failure time models are also commonly used, and these assume a constant treatment effect on the time—rather than the hazards—scale when dependent models with treatment as a covariate are used. To test this assumption quantile-quantile plots are the appropriate choice [7, 55].
• (iv)Flexible parametric non-mixture cure models. Our analyses demonstrated the usefulness of these models, where cure fractions can be controlled somewhat through placement of boundary knots [23, 24]. Whilst the Palmer algorithm refers to non-mixture cure models, it does not refer to applying these in a flexible parametric framework. We believe that these offer advantages compared with standard cure models, and these should be referred to in the algorithm just as other models are signposted.
• (v)Further analyses using external data. Step S1 of the algorithm requires an extensive review of external data, but does not specify potentially useful analyses that could be undertaken using these data. For instance, when long-term data are available for the comparator treatment, the predictive accuracy of models fitted to artificially censored versions of these data could be assessed. We believe that further analyses of models fitted to relevant external data could provide useful information on their likely performance when fitted to the shorter term pivotal RCT data.
• (vi)Clarifying the priority order of model types. In S6b, the algorithm presents a priority order for flexible non-cure models (see Fig. 2). We found that the hazard function observed in CM-649 could be captured using the first priority model type (cubic spline models, also known as flexible parametric models), and therefore did not consider it necessary to fit landmark, piecewise or (non-cure) mixture models. However, the algorithm does not make clear how this decision should be made. Potentially, this could be clarified by adding that analysts should move down the list of model types if higher priority models do not provide plausible extrapolations.

In our case study, the algorithm identified a relatively wide range of models that were potentially appropriate for extrapolating the CM-649 data. However, when fitted to the data, few of these models resulted in extrapolations that met our pre-specified plausibility criteria. This may be regarded as disappointing as the algorithm identified models that did not result in plausible extrapolations. However, the algorithm ensured poor extrapolations were detected, such that implausible models could be excluded from further consideration. This might not have been possible if the algorithm had not been used and in this sense the algorithm performed well—it allowed a narrow range of models that extrapolated plausibly to be determined.

The relatively poor performance of several models is likely to be due to the short-term nature of the 12-month data cut: 70% of participants had died, and only one participant in the PD-L1 CPS ≥ 5 subgroup remained at risk at the 36-month timepoint. Using such an early data cut, it is impressive that NMC models fitted in a flexible parametric framework were able to produce plausible extrapolations. This appears to be due to the ability to exert control over the estimation of the cure fraction. Use of these models appears to have been restricted to population-level survival studies [56, 57]; we are not aware of them being used in HTAs to date. We believe that there could be considerable scope for using these models in HTAs, particularly where a long-term cure represents a reasonable assumption, but data are immature. This is especially relevant given that short-term data cuts are often used in HTA submissions, and indeed only the 12-month data cut from CM-649 was available at the initiation of TA857. However, it is very important to note that these models will not always provide valid extrapolations. If cure timepoints are placed too early, these models will over-estimate long-term survival, and over-estimates will be further exacerbated if these models are used when in fact there is not a cure [24].

Survival at 4 years in CM-649 was higher than expected in both treatment arms. An important finding was that a potential flaw in using the process recommended by the Palmer algorithm is that we may reject survival models that are extrapolating credibly, if survival exceeds all expectations—outside of pre-specified plausible ranges. This does not mean that expectations should not be used as inputs when selecting survival models, but highlights that even if we attempt to use all available information, the resulting judgements may still be inaccurate. Hence, when comparing to pre-specified criteria to determine which models extrapolate plausibly, it may be sensible to allow some leeway to avoid the exclusion of potentially accurate models.

Our research is subject to limitations. In particular, we present one case study, and repeating this research using other studies would be valuable. Further, in our study, long-term survival in the CM-649 trial remains uncertain even in the 48-month data cut, and models that accurately predict survival observed in the 48-month data cut may not extrapolate accurately further into the future. We recommend further research testing the Palmer algorithm with longer term data cuts. Fundamentally, extrapolation is necessary because longer term data are not available, but ‘true’ outcomes cannot be known until data are observed. Therefore, whilst it is crucial for HTA decision making to use appropriate extrapolation methods, long-term trial data should always be collected and estimates and decisions based on earlier data cuts should be reviewed.

In addition, because of the retrospective nature of our study, we were unable to obtain uninformed clinical expert beliefs—instead we had to rely on beliefs documented in NICE TA857 documents. We also recognise that there are many different ways in which expectations can be elicited from clinical experts [58], which should be done in an unbiased way—further research is required in this area.

A technical limitation of our study is that for some model types we considered a limited range of parametric distributions. For MCMs, we considered Weibull, log-logistic and generalised gamma distributions, which are those available in the software package we used (strsmix, in Stata [21]). We believe that these models provide a good representation of the performance of MCMs when fitted to CM-649 data, but, in theory, exponential, Gompertz and log normal MCMs could also have been fitted, and may have given different results. For NMC models, we only considered flexible parametric models because these enabled us to capture the turning point observed in the hazard function whilst also allowing us to set a range of cure timepoints. Based on our appraisal of the external information relevant for our case study, this appeared to represent a particular advantage, and indeed these models have been focused upon in a recent tutorial article describing the use of cure models for HTA [24].

Finally, the Palmer algorithm is extremely clear that external information (including external data and expert opinion) should be considered when selecting survival models. However, it does not require that this information is actually used within the fitting of models, such as by setting constraints or informative priors in a Bayesian framework [59–62]. Furthermore, there is a growing use of real-world evidence in HTAs [63], and when long-term data are available for the comparator treatment these data could be used to estimate baseline survival, with estimates of survival for patients treated with the new treatment derived using the relative treatment effect from the RCT [64]. Because the Palmer algorithm does not specifically recommend either of these approaches, we did not test them in our case study; however, further research in these areas would be valuable, and, as proposed by Palmer et al., the algorithm could be updated to include new methods as they gain traction [6].

Conclusions

The Palmer algorithm appears to be a valuable tool for identifying suitable survival models for extrapolation. The algorithm should be updated to explicitly require the definition of plausibility criteria, with other small amendments also being helpful. Consistent use of the algorithm could reduce discourse in the HTA process, potentially leading to quicker and more efficient decision making.

Supplementary Information

Below is the link to the electronic supplementary material.

Funding

Funding for this study was provided by Bristol Myers Squibb. Publication of results was not contingent on the sponsor’s approval or censorship of the manuscript.

Conflict of interest

The lead author (NRL) has a role at the University of Sheffield that is funded by Yorkshire Cancer Research (award reference number S406NL), but this work was conducted in his time as a Delta Hat Ltd employee. SH, GO, CC, IK, JB and DB were employed by Bristol Myers Squibb during the conduct of the research for this article. JB was an author of the Palmer et al. paper that proposed the algorithm evaluated in the present study, and SH, GO, CC, IK and DB have been colleagues of JB at Bristol Myers Squibb. NRL has collaborated with authors of the Palmer et al. paper in previous research.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

The data used for our analyses were from CM-649 (NCT02872116), provided by Bristol Myers Squibb to Delta Hat Ltd via a data sharing agreement. Qualified researchers may request data from Bristol Myers Squibb clinical studies. Complete details are available at https://www.bms.com/researchers-and-partners/independent-research/data-sharing-request-process.html.

Code availability

Not applicable.

Author contributions

All authors contributed to the study conception and design. Analysis was performed by NRL with support from KT. The first draft of the manuscript was written by NRL and all other authors critically revised the work. All authors read and approved the final manuscript.