Isotope-dependent site occupation of hydrogen in epitaxial titanium hydride nanofilms

Abstract

Hydrogen, the smallest and lightest element, readily permeates a variety of materials and modulates their physical properties. Identification of the hydrogen lattice location and its amount in crystals is key to understanding and controlling the hydrogen-induced properties. Combining nuclear reaction analysis (NRA) with the ion channeling technique, we experimentally determined the locations of H and D in epitaxial nanofilms of titanium hydrides from the analysis of the two-dimensional angular mappings of NRA yields. Here we show that 11 at% of H are located at the octahedral site with the remaining H atoms in the tetrahedral site. Density functional theory calculations revealed that the structures with the partial octahedral site occupation are stabilized by the Fermi level shift and Jahn-Teller effect induced by hydrogen. In contrast, D was found to solely occupy the tetrahedral site owing to the mass effect on the zero-point vibrational energy. These findings suggest that site occupation of hydrogen can be controlled by changing the isotope mixture ratio, which leads to promising manifestation of novel hydrogen-related phenomena.

The lattice location of hydrogen in titanium hydride nanofilms was identified by the channeling ¹⁵N-NRA mapping. H and D occupy the tetrahedral and octahedral sites differently because of the hydrogen Jahn-Teller effect and nuclear quantum effect.

Introduction

Hydrogen in materials finds various applications such as H storage and heterogeneous catalysis^1–3. Hydrogen also has versatile abilities to induce fascinating properties by modifying the electronic structure of host materials^4–9. The electronic and vibrational states of H depend on the location in the lattice^10,11, therefore controlling the location of hydrogen potentially leads to novel physical and chemical properties. The lattice strain potentially modulates the site energy as proposed in previous studies^12,13. Zero-point energy (ZPE) is also important for the site stability for hydrogen due to its quantum nature because of its small mass.

Titanium (Ti) is a hydrogen-absorbing metal, which forms several types of hydrides (TiH_x)^14–22. The lattice structure is schematically shown in Fig. 1d. It is known that H atoms occupy interstitial tetrahedral (T) sites rather than octahedral (O) sites in δ-phase with x above ~1.0 with a face-centered cubic (fcc) structure in bulk. As regards the electronic property, carrier polarity switching of metallic conduction in accordance with the H concentration was reported in epitaxial δ-TiH_x nanofilms, which was ascribed to the Fermi surface characteristic due to the volume change²³. It is also theoretically suggested that TiH₂ behaves as a superconductor below 6 K if the cubic structure is preserved at low temperature, which might be achieved by taking advantage of epitaxial growth of thin films²⁴. Nonetheless, conventional studies have only considered the presence of H at the T site in δ-TiH_x and have not discussed the possibility of co-occupation of the T and O sites.

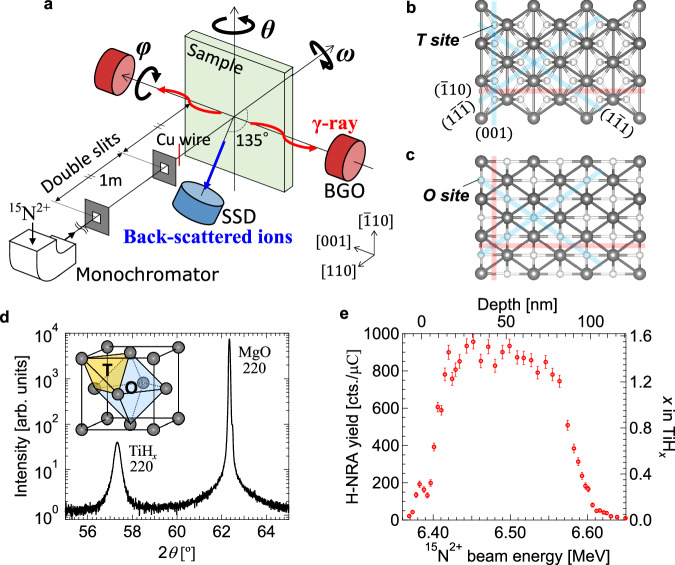
Fig. 1. Channeling ¹⁵N-NRA apparatus and sample characterization.

a Schematic illustration of the channeling ¹⁵N-NRA apparatus developed in the present study. Nuclear reaction analysis (NRA) with ¹⁵N and Rutherford backscattering spectrometry (RBS) are simultaneously performed. Top views of TiH_x(110) with H (b) at the tetrahedral (T) and (c) at the octahedral (O) sites. Black and white circles represent Ti and H atoms, respectively. Blue and red lines represent the planes in which H is located or not, respectively. d Out-of-plane θ−2θ X-ray diffraction (XRD) pattern for the 90-nm TiH_1.47(110)/MgO(110) obtained by CuKα (λ = 1.5418 Å). Inset is a schematic figure of an fcc structure and T and O sites. e Hydrogen depth profile obtained by NRA for the TiH_1.47(110) sample at random incidence. The error bars in the plots represent the statistical uncertainty.

Epitaxial nanofilms are good platforms to control the hydrogen location. Convincing structure analysis of H in nanofilms is, however, challenging because detecting H by ordinary experimental probes of electrons and x-rays is difficult due to their small cross sections except for a few advanced cases^25–27. Neutron scattering, NMR, and ion beam analysis have been conventionally used to investigate the lattice location of hydrogen^28,29, though they are not suited for nanofilms. Recently, structure analysis of H in nanofilms was performed by nuclear reaction analysis (NRA) via ¹H(¹⁵N, αγ)¹²C, which allows for depth-resolved detection of H with high sensitivity as small as 0.1 at%³⁰, combined with the ion channeling technique³¹, which is called channeling ¹⁵N-NRA. The ion channeling phenomenon is observed by reduction of the backscattering yield, which is measured by Rutherford backscattering spectrometry (RBS). Since the NRA yield under the ion channeling significantly depends on the location of H, simultaneous measurements of NRA and RBS allow us to determine the lattice location of H even in nanofilms. Furthermore, in this study, we take advantage of nuclear reactions of D with ¹⁵N to detect D. Because H and D atoms are distinguished by the energy analysis of the γ-rays emitted during the nuclear reactions, the lattice locations of the two isotopes can be analyzed by the ¹⁵N ion beam at the same time from a single specimen.

In the present study, we developed an apparatus for simultaneous measurements of NRA and RBS. We investigated the lattice location of hydrogen in epitaxial Ti hydride nanofilms from two-dimensional (2D) angular mappings of both NRA and RBS yields. Quantitatively comparing the experimental results with Monte Carlo simulations for the ion beam trajectory, 11 at% of H were found to be located at the O site with the remaining H atoms in the T site, whereas D atoms solely occupied the T site. We conducted exhaustive theoretical calculations of H configurations and corresponding electronic states of δ-TiH_x, which revealed the importance of the hydrogen Jahn–Teller effect and the ZPE of hydrogen for its site occupation.

Results

A TiH_x(110) film with a thickness of ~90 nm was fabricated on an MgO(110) substrate by reactive magnetron sputtering at 150 °C ²³. The sample was mounted on the three-axis rotation stage as schematically shown in Fig. 1a. Epitaxial growth of the δ-TiH_x was confirmed by the 220 diffraction spot in the X-ray diffraction pattern in Fig. 1d. The rocking-curve full width at half maximum value of the 220 peak was 1.4°. The H depth profile was obtained by NRA at random incidence as shown in Fig. 1e, showing that H atoms are almost uniformly distributed in the depth direction with an H/Ti atomic ratio of 1.47.

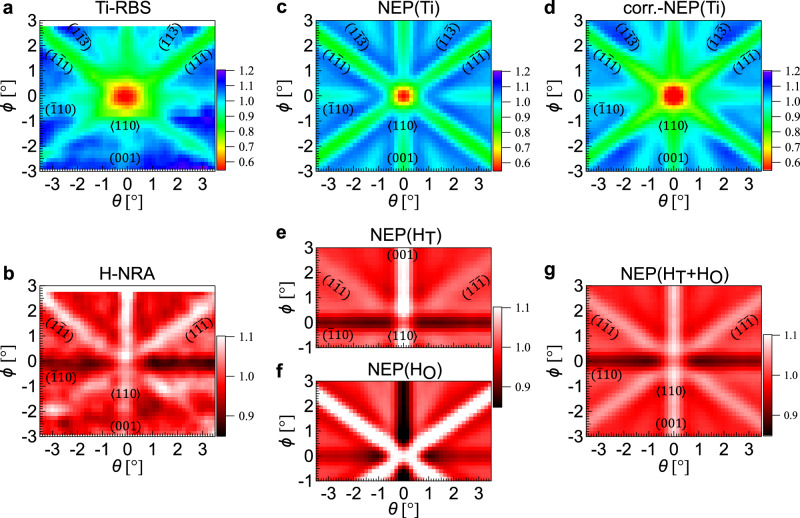
The channeling ¹⁵N-NRA experiment was performed around the normal incidence at room temperature with an incident energy of 6.45 MeV, which corresponds to a H probing depth of ~30 nm from the surface. The signal of the Ti-RBS was collected for the entire depth range. Figure 2a, b show the simultaneously obtained 2D mappings of Ti-RBS and H-NRA, respectively, as functions of incident beam angles of θ and ϕ around the <110> direction. A channeling dip corresponding to the <110> axis is clearly seen around (θ, ϕ) = (0°, 0°) in the Ti-RBS mapping in Fig. 2a. In addition, the (001), ($\overline{1}$10), (1$\overline{1}$1), (1$\overline{1}\overline{1}$), ($\overline{1}$1$\overline{3}$) and (1$\overline{1}\overline{3}$) plane channelings are identified (see Supplementary Fig. 3 and Supplementary Table 1 for the quantitative analysis of the plane assignment). In contrast, the angular dependence of the H-NRA is clearly different from the Ti-RBS as is apparent in Fig. 2b. The H-NRA yield increases in the (001), (1$\overline{1}$1), and (1$\overline{1}\overline{1}$) plane channelings while it decreases in the ($\overline{1}$10) plane channeling. This H-NRA pattern is qualitatively understood in terms of the T site occupation of H; as seen in the top views of (110) surfaces in Fig. 1b, c, while the H atoms in the O site are located between the planes of (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) but within the (001) and ($\overline{1}$10) planes formed by the host Ti atoms (Fig. 1c), the H atoms in the T site are between these planes except for the ($\overline{1}$10) plane (Fig. 1b). It is noted that the channeling patterns got blurred below ϕ = ~−1° due to the sample aging by the ion beam irradiation.

Fig. 2. Comparison of simultaneously obtained two-dimensional Ti-RBS and H-NRA mappings for the 90-nm-thick TiH_1.47 nanofilm with Monte Carlo simulations.

Two-dimensional (2D) mappings of normalized (a) Ti-RBS and (b) H-NRA yields as functions of θ and ϕ around the surface normal measured by ¹⁵N²⁺ beam with an energy of 6.45 MeV. 2D mappings of calculated nuclear close-encounter probabilities (NEP’s) for Ti (c) without and (d) with the blocking effect. 2D mappings of calculated NEP’s for the structures with H (e) at the T site (NEP(H_T)), (f) at the O site (NEP(H_O)), and (g) at both T and O sites at O-site occupation ratio z = 0.10 (NEP(H_T+H_O)). Vibrational amplitudes used in the calculations are 0.36, 0.25, and 0.45 Å for Ti, H in the T site, and H in the O site, respectively.

For the detailed analysis of the H location, we compare the experimental results with ion beam trajectory simulations using FLUX7³². The simulations estimate the average nuclear close-encounter probabilities (NEP) of ¹⁵N²⁺ ions to Ti and H atoms, which correspond to the normalized Ti-RBS and H-NRA yields, respectively. Figure 2c shows the 2D NEP mapping calculated for Ti (NEP(Ti)) with an incident energy of 6.45 MeV as functions of θ and ϕ around the <110> direction. While the dip patterns are similar to the Ti-RBS, there is a suppression in the Ti-RBS yield within θ, ϕ ≤ ±2° around the <110> axis. Considering the solid state detector (SSD) is set at 45° off from the surface normal, the blocking effect of the <100> atomic row for the back-scattered ions to the detector needs to be taken into account. Since the channeling for incoming ions is a time reversal process of the blocking for outgoing ions, the NEP(Ti) around the <110> axis is multiplied by the computed NEP(Ti) around the <100> axis with an energy of 2.04 MeV corresponding to the average energy of the scattered ions after the convolution with the instrumental function determined by the detector size. The 2D mapping of the NEP for Ti corrected by the blocking effect (corr.-NEP(Ti)) is shown in Fig. 2d, which is in good agreement with the experimental result as also shown in Supplementary Fig. 6a, showing that the beam trajectory in the nanofilm is accurately reproduced by the simulation. Note that the blocking effect does not need to be considered for the comparison of H-NRA with NEP for H, because the incident beam trajectory before the nuclear reaction is not affected.

Figure 2e, f shows NEP’s for H assuming the T and O-site occupation (NEP(H_T) and NEP(H_O)), where the H vibration amplitudes are assumed to be 0.15 and 0.20 Å, respectively. The dip and hump pattern of the H-NRA resembles the NEP(H_T) rather than the NEP(H_O) as intuitively expected from the crystal structure (Fig. 1b, c). The intensity changes in the H-NRA yield under the channeling conditions, however, are not quantitatively consistent with the NEP(H_T); while the intensity at the (001) plane channeling is clearly larger than those at the (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) plane channelings in the NEP(H_T) (Fig. 2e), the intensities are almost the same at these three plane channelings in the H-NRA (Fig. 2b). This discrepancy in the H-NRA and NEP(H_T) indicates that H atoms do not simply occupy the T site in the epitaxial TiH_1.47 nanofilm. It is noted that the beam divergence and Ti vibration amplitude in the simulations effectively reflect the crystallinity of samples and are in a trade-off relationship. We found their several combinations to practically reproduce the beam trajectory such as 0.20° and 0.43 Å, 0.25° and 0.36 Å, 0.30° and 0.29 Å, and 0.35° and 0.21 Å as shown in Supplementary Fig. 5c. In the following, the identification of the H location is comprehensively examined based on these several beam conditions.

As the origin for the discrepancy between the experimentally obtained H-NRA and the calculated NEP(H_T), we consider two possibilities: (1) off-centered occupation around the T site by H and (2) partial occupation of the O site by H. To clarify the former possibility, we investigated the dependence of NEP(H_T) on the H vibration amplitude (V_H). When H atoms randomly occupy the off-centered positions around the T site, NEP(H_T) is expected to be effectively described by large V_H. Line profiles of the normalized H-NRA and NEP(H_T)’s for various V_H’s are shown as a function of θ at each ϕ in Fig. 3a–d. As V_H is increased, i.e., as the degree of the off-centered occupation is increased, the peaks at θ = ±0.5–3.0° corresponding to the (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) plane channelings become less significant than the peak at θ = 0° of the (001) plane channeling. This is explained by the fact that the inter-plane distance of the (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) planes is narrower than that of (001). On the other hand, the weaker peak around θ = 0° at ϕ = 0° of the <110> axis channeling observed for V_H = 0.08 Å originates from the position of the T site in the <110> axis, which is deviated from the center of that axis. Figure 3e shows the mean squared error (MSE) as a function of V_H between 2D mappings of the normalized H-NRA and NEP(H_T) at ϕ = −0.6 to 2.7° (the region below ϕ = −0.6° was not used for the analysis due to the sample aging by the ion beam). They take minima at V_H = ~0.25 Å, which is larger than the zero-point vibration amplitude of 0.15 Å calculated from ZPE for TiH_1.5. Hence, it was implied that the H atoms at the T sites are slightly off centered. The relative intensities of the three peaks corresponding to the (1$\overline{1}$1), (1$\overline{1}\overline{1}$) and (001) plane channelings are, however, still not consistent with the experimental data (please compare Fig. 3a, c). The disagreement between the H-NRA and NEP(H_T) does not arise from the off-centered H around the T site.

Fig. 3. Analysis of H vibration amplitude.

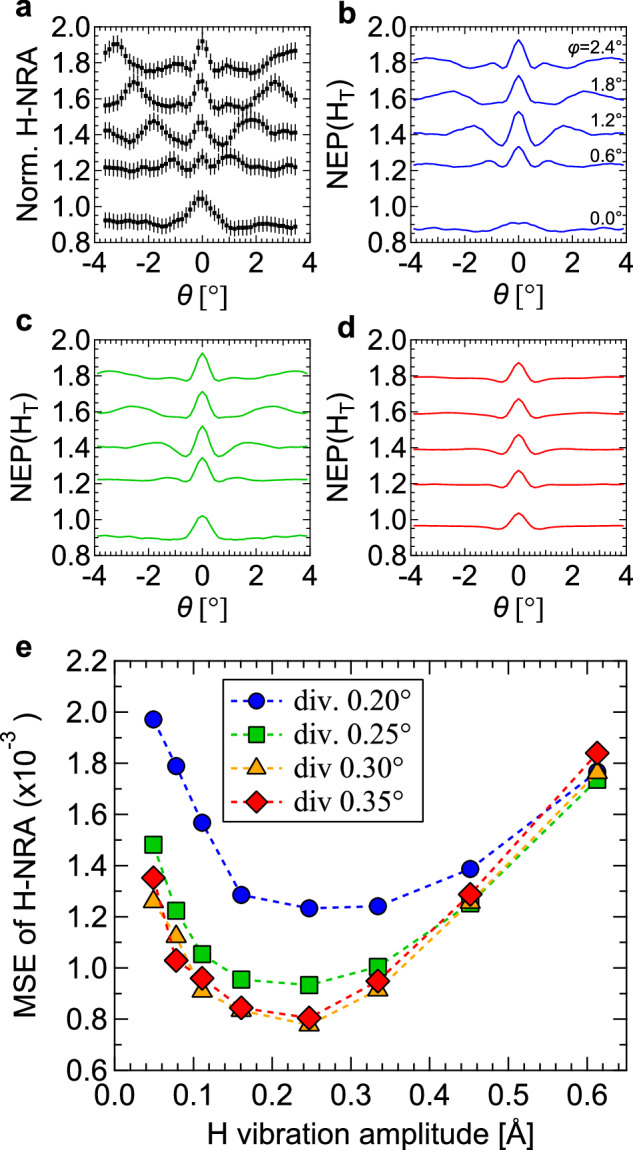
a Line profiles as a function of θ at various ϕ’s of the normalized H-NRA yield. The error bars represent the statistical uncertainty. b–d Line profiles as a function of θ at various ϕ’s of NEP(H_T)’s with different H vibration amplitudes V_H of 0.08, 0.25, and 0.61 Å, respectively, assuming the beam divergence 0.25° and the Ti vibration amplitude 0.36 Å. e Mean squared error (MSE) as a function of V_H between the 2D mappings of normalized H-NRA and NEP(H_T)’s in the ranges of θ = −3.45 to 3.45° and ϕ = −0.6 to 2.7° for the four beam divergence conditions.

We examine the possibility of (2) the partial occupation of the O site by H. Supplementary Fig. 6b compares the line profiles of the normalized H-NRA with NEP(H_T + H_O)’s at ϕ = 0.0–1.5°, where NEP(H_T + H_O)’s are obtained as NEP(H) = ((1 − z)/(1 + z) NEP(H_T) + 2z/(1 + z) NEP(H_O)) for O-site ratio z (note that the numbers of T and O sites with respect to the number of Ti atoms in the structures for NEP(H_T) and NEP(H_O) are two and one, respectively). With increasing O-site ratio, the intensity of the peak at θ = 0° of the (001) plane is suppressed while the intensities of the peaks appearing at θ = ±0.5–3.0° corresponding to the (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) planes are increased. Figure 4 shows the MSE between 2D mappings of the normalized H-NRA and NEP(H_T + H_O) at ϕ = −0.6 to 2.7° as a function of z. After optimizing the vibration amplitude of H in the O site, it is found that they take minima at 11 ± 2%. The best-fit result of NEP(H) to reproduce the H-NRA is shown in Fig. 2g. These results reveal that whereas most H atoms are located at the T site, ~10 at% of H occupy the O site in the epitaxial nanofilm.

Fig. 4. Analysis of O-site occupancy by H.

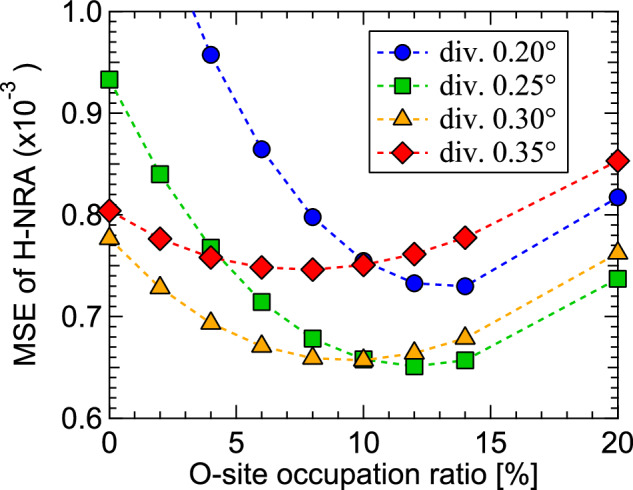
MSE as a function of the O-site occupation ratio between the 2D mappings of normalized H-NRA yield and NEP(H_T + H_O)’s in the range at θ = −3.4 to 3.4° and ϕ = −0.6 to 2.7° assuming the various beam divergence conditions. The O-site occupation ratio was calculated using the mean and standard deviation values for the four beam conditions.

We also performed the channeling ¹⁵N-NRA at the 45° oblique incidence corresponding to the <100> direction for the TiH_1.47 film (Supplementary Fig. 8). The H-NRA yield increased at the (001) plane and decreased at the (011) and (01$\overline{1}$) planes, which is in qualitative agreement with the dominant T site occupation.

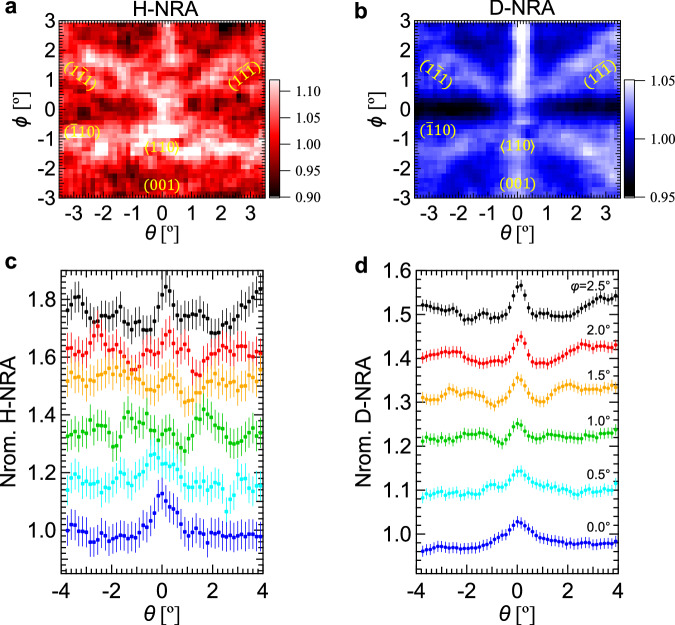
To explore the isotope effect on the lattice location, we simultaneously investigated the locations of H and D in a 100-nm-thick TiH_0.60D_1.0(110) epitaxial film by the channeling ¹⁵N-NRA (Supplementary Fig. 12). The experiment was performed around the normal incidence at an incident beam energy of 6.45 MeV. Figure 5 shows the 2D mappings of H-NRA and D-NRA and their horizontal line profiles. Increases in intensities were observed at the (001), (1$\overline{1}$1), and (1$\overline{1}\overline{1}$) plane channelings in both H-NRA and D-NRA yields. The H-NRA pattern is similar to that of the TiH_1.47 film, indicating that part of H is located at the O site with the remaining H at the T site in the TiH_0.60D_1.0(110) film. In contrast, the peak intensity in the D-NRA is significantly larger at the (001) plane than at the (1$\overline{1}$1) and (1$\overline{1}\overline{1}$) plane channelings, showing that D atoms solely occupy the T site. As a result, the ratio of hydrogen in the O site to all hydrogen (H and D) was reduced to ~4 at% in the TiH_0.60D_1.0 nanofilm.

Fig. 5. Simultaneous structure analyses of H and D in the 100-nm-thick TiH_0.60D_1.0 nanofilm.

2D mappings of normalized (a) H-NRA and (b) D-NRA yields around the surface normal measured by ¹⁵N²⁺ beam with an energy of 6.45 MeV. Their line profiles of (c) H-NRA and (d) D-NRA yields as a function of θ at various ϕ’s. The error bars represent the statistical uncertainty.

Discussion

To elucidate the origin of the partial O-site occupation by H, we investigate the stabilities of H at the T and O sites by calculating the formation energy using density functional theory (DFT). Figure 6a shows the formation energies for a supercell (s.c.) composed of Ti₈H_n with n H atoms in the T site. Also shown in the figure are the formation energies for (n − 1) H atoms in the T site and an H atom in the O site. The formation energies were calculated for all possible configurations of H. The calculations reveal that as the H concentration decreases, the energy of the lowest-energy configuration of partial O-site occupation becomes closer to that of the exclusive T-site occupation. At n = 16, the formation energy for a partial O-site occupation (labeled 15T1O) is 1.19 eV/s.c. higher than that of the exclusive T-site occupation (labeled 16 T), meaning that H is less stable at the O site than at the T site by 1.19 eV/s.c. at TiH₂. At n = 12, i.e., at TiH_1.5, the energy difference between the lowest-energy configurations for the exclusive T-site occupation (labeled 12 T) and the partial O-site occupation (labeled 11T1O) is 217 meV/s.c. This indicates that the H deficiency assists the partial O-site occupation by H. We also calculated the average displacement for the H atoms in the T sites and obtained 0.02$\pm$0.01 Å and 0.23 ± 0.03 Å for the 12T and the most stable 11T1O structures, respectively. The latter is consistent with the channeling experiment showing the slightly off-centered H atoms with V_H of 0.25 Å in the T site, further supporting the partial O-site occupation by H. We note that the relative stability of the partial O-site occupation is not significantly affected by introducing homogeneous strains in the calculations (Supplementary Fig. 11).

Fig. 6. Theoretical calculation results of Ti₈H_n.

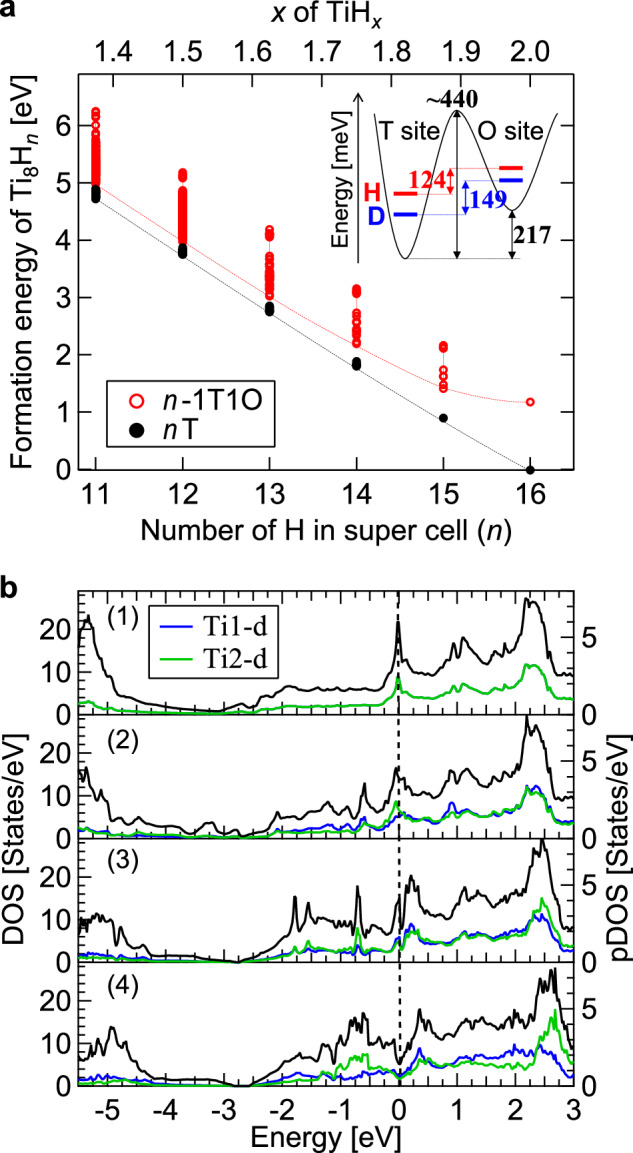
a Formation energies of Ti₈H_n as a function of the number (n) of H calculated for the structures with all H atoms in the T site (nT) and the structures with (n − 1) H atoms in the T site and one H in the O site (n − 1T1O). All possible configurations of H in the super cell were considered, and the lowest level among the configurations is displayed by dashed curves. The inset illustrates a schematic potential energy curve for H(D) in TiH(D)_1.5 and the ZPE levels for H(D). b Density of states (DOS) for (1) 16T, (2) 15T1O, (3) 12T and (4) 11T1O structures. Black curves represent the total DOS. Blue and green curves indicate the projected DOS (pDOS) for Ti1-d and Ti2-d states, respectively, where Ti1 indicates a Ti atom away from H at the T site and Ti2 indicates Ti near the H at the T site.

We discuss the microscopic mechanism that lowers the energy of the structure with the partial O-site occupation based on the electronic structure, specifically the electronic density of states (DOS). In pristine TiH₂ with H in the T site (16T), the DOS shows a sharp peak at the Fermi level originating from a van Hove singularity, mainly due to the Ti d states, as shown in Fig. 6b1 and in previous studies^23,24. When the number of H atoms is reduced from 16 to 12 (12T), four electrons are extracted from the system, resulting in an upward shift of the DOS in energy. However, the Fermi level is still located at the shoulder of the peak (Fig. 6b3). When one of the constituent H atoms at the T site of 12T is moved to an O site (11T1O) (see Supplementary Fig. 9 for detailed structures), the sharp peak at the Fermi level is split, forming a deep valley in the total DOS (so-called pseudogap) as shown in Fig. 6b4. This pseudogap formation is caused by lowering of the structural symmetry due to the co-occupation of T and O sites by H. In the most stable 11T1O structure, there are nonequivalent Ti atoms, which result in different DOS’s as shown by the pDOS’s in Fig. 6b4, and contribute to the formation of the pseudogap. On the other hand, such a split in the DOS peak around the Fermi level is not observed for the 15T1O structure (Fig. 6b2). Therefore, both the symmetry reduction due to the partial O-site occupation and the Fermi level shift owing to the H deficiency are key factors in decreasing the electronic energy, even though the lattice energy may increase. This is similar to the Jahn–Teller distortion well known in transition-metal oxides. However, this Jahn–Teller effect induced by hydrogen (i.e., the “hydrogen Jahn–Teller effect”) makes a keen contrast to the conventional Jahn–Teller effect; while oxygen atoms can be marginally displaced (<0.1 Å) due to the strong bonding with transition-metal cations in oxides, H atoms can be located in substantially different sites of T and O (>1 Å). The pseudogap feature was only found in particular H arrangements, where the H atoms are rather randomly distributed, as a consequence of the exhaustive calculations of all H arrangements for the 11T1O structures.

We considered the influence of ZPE on the stability within the harmonic approximation for the lowest-energy configurations in 12T and 11T1O structures (see Supplementary Table 2 and Supplementary Fig. 10 for details). The energy difference between the 12T and 11T1O structures is reduced to 124 meV/s.c. from 217 meV/s.c. after the ZPE correction in TiH_1.5, showing that the phonon contribution favors the O-site occupation. Due to the mass dependency in ZPE, in contrast, their energy difference is only reduced to 149 meV/s.c. in TiD_1.5. Hence, the T site is energetically more stable for D than H by 25 meV/s.c. as schematically shown by the inset in Fig. 6a, which is consistent with the different site occupancy between the two isotopes observed for the TiH_0.60D_1.0 nanofilm.

It should be noted that although the thermal effects can increase the O-site occupancy, the calculated energy difference between the 12T and 11T1O structures still seems to be slightly large to thermodynamically populate the O site by H at 11% at room temperature. Under realistic conditions, the local symmetry can be further lowered, which potentially enhances the hydrogen Jahn–Teller effect and leads to the stabilization of the partial O-site occupation.

In conclusion, we have developed an apparatus for the channeling ¹⁵N-NRA. 2D angular mappings of H(D)-NRA and Ti-RBS were obtained for epitaxial Ti hydride nanofilms. The 2D results enabled the detailed analysis of the H(D) location based on the plane channeling as well as the ordinary axial channeling with the aid of the beam trajectory simulations. It was found that ~10 at% of H atoms are located at the O site with the remaining H in the T site. The DFT calculations suggested that the hydrogen Jahn–Teller effect plays a decisive role for its lattice location, where the characteristic electronic state with an energy split around the Fermi level is realized by the Fermi level shift and the symmetry breaking due to the co-occupation of the T and O sites by hydrogen. In contrast, D atoms were found to solely occupy the T site, which reflects the mass dependence of the ZPE. These were clarified by the accurate structure analysis with the channeling ¹⁵N-NRA and the exhaustive DFT calculations. These findings demonstrate the possibility to fabricate hydrides with an arbitrary site occupancy and tune their electronic properties by controlling the isotope ratio, potentially leading to novel hydrogen-induced phenomena.

Methods

Nuclear reaction analysis (NRA) and Rutherford backscattering spectrometry (RBS)

The NRA and RBS measurements were performed in an ultrahigh vacuum chamber (base pressure ~10⁻⁶ Pa) at the 1E beam line of MALT, The University of Tokyo. The experimental setup developed in this study is schematically shown in Fig. 1a. A ¹⁵N²⁺ ion beam is accelerated to an energy of ~6.5 MeV by the 5 MV Van de Graaf tandem accelerator and delivered to a sample on the three-axis rotation stage through a pair of slits with the divergence restricted to within 0.17°. The sample is precisely rotated around three axes of θ, ω, and ϕ. The ion beam current and size on the sample were about 5 nA and 2 × 2 mm², respectively. To detect H, the γ-ray with an energy of 4.43 MeV emitted from the ¹H(¹⁵N, αγ)¹²C reaction is measured with Bi₄Ge₃O₁₂ (BGO) scintillators set at an angle of 90° to the ion beam. Since this nuclear reaction is a resonance reaction with an energy width of 1.8 keV, the depth profile of H in the sample is obtained by scanning the incident ion energy. Deuterium is also observed by the ¹⁵N²⁺ beam via ²D(¹⁵N, αγ)¹³C, ²D(¹⁵N, p)¹⁶N, and ²D(¹⁵N, nγ)¹⁶O nuclear reactions though these are non-resonant reactions and not depth-sensitive. The energies of the emitted γ-rays from these nuclear reactions are around 3.7, 6.1, and 7.1 MeV³³. H and D atoms are distinguished by the energy analysis of the emitted γ-rays (Supplementary Fig. 13). The channeling experiments were performed by systematically scanning along the θ-axis for each ϕ, starting from the positive ϕ direction. The 2D mappings of Ti-RBS and H, D-NRA were obtained after a three-point moving average of the yields in θ and ϕ directions. The ion signal backscattered from the sample is measured with a SSD set at an angle of 135° from the ion beam. After pulse-height analysis of the signal, RBS can be obtained, which reflects the depth-dependent composition in the sample by resolving the energies of backscattered ions. The energies of the backscattered ions by Ti and Mg atoms for the present configuration are calculated to be 2.1 and 0.53 MeV, respectively. RBS yields from Ti atoms in the film and Mg in the substrate were distinguished as shown in Supplementary Fig. 2a.

Simulation with FLUX7

The beam trajectories of the incident ions in crystals are calculated by the Monte Carlo methods using FLUX7³². The calculations are based on the binary collision of the incoming ions and target atoms using the Ziegler–Biersack–Littmark potential, and the ion trajectories before nuclear close encounter events are calculated. In the present study, calculations were performed for Ti hydrides consisting of Ti atoms in the fcc lattice with a lattice constant of 4.45 Å and H atoms in the T or O site. The film thickness is assumed to be 90 nm. It is noted that there is no significant difference in NEP(Ti) regardless of the H position, either at the T or O site, as shown in Supplementary Fig. 4, indicating that the beam trajectory of the incident ¹⁵N²⁺ ions is essentially determined by interaction with Ti atoms. Technically, this would be an advantage of structure analysis for hydrogen by the channeling NRA using the ¹⁵N ions with a relatively high incident energy. The blocking effect for the back-scattered ions along the <100> axis was taken into account by multiplying the computed NEP(Ti) around the <100> axis with an energy of 2.04 MeV corresponding to the average energy of the scattered ions after convolution with the instrumental function. The instrumental function was given from the detector geometry, where the SSD with a circular shape detects ions in a solid angle of 9.9 × 10⁻⁴π. For the computation of the NEP(Ti) around the <100> axis for the outgoing ions, the beam divergence and the Ti vibration amplitude were assumed to be 0.25° and 0.29 Å, respectively. Supplementary Fig. 7 shows the depth dependence of NEP(Ti) and NEP(H_T) at plane channeling conditions, showing that channeling phenomena occur within 10 nm from the surface. NEP(Ti) is obtained by averaging NEP for the entire depth region, and the NEP(H_T) and NEP(H_O) use average NEP’s at 30 ± 2.5 nm. The 2D mappings of NEP’s were obtained after a three-point moving average in θ and ϕ directions.

DFT calculation

A (√2 × 1 × √2) orthorhombic supercell of the fcc structure containing eight formula unit (f.u.) was constructed to investigate the H occupation at the T and O sites. Its basal plane corresponds to the fcc (110) surface. The lattice parameters of the unstrained cell on the (110) surface were set as a = 6.1782  Å, b = 4.3687 Å, and c = 6.1782 Å in Fig. 6, based on the theoretically optimized lattice parameter of pristine TiH₂. We also simulated the effects of the uniaxial strain caused by an MgO substrate³⁴ by adjusting the in-plane lattice constants of TiH_1.5 as shown in Supplementary Fig. 11. In these calculations, all possible patterns of the H occupation were considered by a combinatorial structure generation approach by using the Supercell program³⁵ for various numbers of H atoms (n) from 11 to 16. For each n, two patterns of the H configuration were considered; (1) all H atoms occupy the T site (nT) and (2) (n − 1) H atoms occupy the T site and one H atom occupies an O site (n − 1T1O). We generated 1, 1, 7, 12, 42, and 61 structures for the nT (n = 16–11) configuration and 2, 16, 46, 154, 314, and 592 structures for the n − 1T1O configuration. In total, 1248 structures were generated. To evaluate the structural stability, we used the projector augmented wave method³⁶ as implemented in the VASP code³⁷. The Perdew–Burke–Ernzherof exchange-correlation functional for solids (PBEsol)³⁸ was employed. The total energy was evaluated by using the tetrahedron method with Blöchl corrections³⁹ with an 8 × 12 × 8 k-point mesh after the atomic positions were fully optimized in each structure. The formation energy was calculated as E_f = E(TiH_2-δ) − E(TiH₂) + δ/2 E(H₂), where E(TiH_2-δ), E(TiH₂), and E(H₂) are the total energies of TiH_2-δ, TiH₂, and gas-phase H₂, respectively. The ZPE was calculated based on the harmonic phonon frequencies obtained using the finite-different method as implemented in the Phonopy code⁴⁰. For the phonon calculations, a (2 × 2 × 2) supercell with 64 f.u. was used.

Author contributions

T.O., D.S., and K.F. conceived the idea of the channeling NRA and developed the apparatus. The channeling NRA experiment was performed by T.O. and Y.S. T.O. performed the Monte Carlo simulations and analyzed the experimental data. Y.K., R.S., and T.H. fabricated the samples. K.Y. and I.H. conducted the DFT calculations. T.O., K.Y., and K.F. interpreted the theoretical results. K.F. supervised the overall research. T.O., K.Y., and K.F. wrote the manuscript and supplementary information, which were reviewed by all other authors.

Peer review

Peer review information

Nature Communications thanks Hajime Kimizuka and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support this article are present in the manuscript and the supplementary information. The data used to reproduce the results of DFT calculations are available at the Materials Cloud Archive [10.24435/materialscloud:je-ev].  Source data are provided with this paper.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53838-6.