Understanding Defect-Mediated Ion Migration in Semiconductors using Atomistic Simulations and Machine Learning

Abstract

Ion migration in semiconductor devices is facilitated by the presence of point defects and has a major influence on electronic and optical properties. It is important to understand and identify ways to mitigate photoinduced and electrically induced defect-mediated ion migration in semiconductors. In this Perspective, we discuss the fundamental mechanisms of defect-mediated ion migration and diffusion as understood through atomistic simulations. The discussion covers a variety of case studies from the literature, with a special focus on metal halide perovskites, important materials for solar absorption and related optoelectronic applications. Tuning the perovskite composition and dimensionality and applying systematic strains are identified as ways to suppress phase segregation and ion migration. This Perspective delves into first-principles modeling approaches for defect migration and diffusion, presenting detailed case studies on the diffusion of defects and dopants in CdTe, hydrogen impurities in halide perovskites, and halogen migration in hybrid perovskites and emphasizing the importance of organic cations. The discussion further extends to accelerating the prediction of migration pathways and barriers through machine learning approaches, particularly the application of crystal-graph neural networks. By combining theoretical insights with practical case studies, this Perspective aims to provide an understanding of defect-mediated ion migration and suggestions for next-generation semiconductor discovery while considering ion migration suppression as one of many design objectives.

Introduction

In the quest for clean energy sources, photovoltaic (PV) technology stands as the leading solution since it effectively converts sunlight into electricity and reduces dependence on fossil fuels. For improving the efficiency and stability of solar cells, it is important to accelerate the development of novel PV materials. Some of the most attractive semiconductor PV absorbers currently include metal halide perovskites and chalcogenide compounds such as CdTe, owing to their excellent optoelectronic properties, comparable efficiency with Si-based technology, and low cost.¹⁻³ Further improvement in the properties of perovskite and chalcogenide semiconductors will likely lead to the creation of a new era of the solar energy market consistent with the principles of cost-efficiency and environmental friendliness.

ABX₃ halide perovskites are especially promising as PV absorbers because they display high visible light absorption, long carrier lifetimes, and tunable bandgap and defect properties.^4,5 Perovskite solar cells have rapidly scaled their efficiency to the level of more conventional and widely researched Si-based PV technologies. However, major issues still persist, such as the stability when exposed to light, heat, and moisture, and general long-term degradation. In particular, ion migration in perovskites is considered as one of the causes of performance degradation with time.^6,7 The migration of charged ions, mainly halide anions, in the crystal lattice may lead to defects and recombination centers that eventually decrease the efficiency and the life cycle of the solar cell.⁸

Chalcogenide semiconductors such as CdTe, CIGS (typically referring to Cu(In,Ga)Se₂, sometimes to Cu(In,Ga)S₂)), CZTS (Cu₂ZnSnS₄), and related binary, ternary, and quaternary compositions form another promising class of materials for next-generation PV devices.⁹⁻¹⁹ These compounds are appreciated for their ability to absorb visible light efficiently, low cost, and conduciveness to be doped both p-type and n-type.^{9−11,20−23} However, unavoidable native defects such as vacancies, self-interstitials, and antisites will influence their electronic properties, potentially creating deep defect levels and aiding in defect-based diffusion, which could be harmful or beneficial for performance. For instance, migration of dopants could potentially reduce the annealing temperature required for processing conditions, whereas migration of vacancies or interstitials can reduce the stability and reliability of chalcogenide-based solar cells, leading to poor performance.²⁴

Defects and impurities are critical factors influencing the processing, functionality, and reliability of semiconductor devices.²⁵⁻²⁹ Controlling the diffusion of dopants and impurities, as well as their interaction with native defects, is essential for advancing next-generation semiconductors used not only in solar cells, but also electronics, sensors, power devices, and quantum technology.^30,31 Understanding diffusion mechanisms and barriers provides valuable insights into how defects impact the performance of electronic devices, revealing which sites they are most likely to exist in as well as possible segregation and stability of ionic species and defect-related phases.³² Density functional theory (DFT) computations provide an accurate way to estimate formation energies and binding energies of point defects, and simulate probable defect/ion migration pathways and energetic barriers.³³⁻³⁵ Migration can be simulated at the atomistic level using the nudged elastic band (NEB) method with DFT or using ab initio molecular dynamics (AIMD), yielding possible transition states and the relative likelihood of different processes. Such atomistic calculations form the foundation for developing detailed diffusion models which rely on Kinetic Monte Carlo, the Cluster Expansion method, and Phase Field approaches.³⁶

In this perspective article, we explore the topic of defect-mediated ion migration in semiconductors, emphasizing the use of first-principles-based DFT and molecular dynamics (MD) simulations in gaining fundamental insights. Using perovskites and CdTe as examples, we discuss both experimental and computational efforts to quantify ion migration and its effects on properties and performance. We also discuss how the computational expense of accurate first-principles simulations, especially when considering large supercells and advanced levels of theory, could be tackled by integrating computational data with machine learning (ML) models. Predictions at quantum mechanical accuracy but accelerated by ML and tied with experimental feedback will help drive the design of novel semiconductors with tolerance to defects and undesired ion migration, in addition to other properties of interest. We note that CdTe (as well as related systems such as CdSe_xTe_1–x and doped CdTe²⁷) and lead halide perovskites (both purely inorganic and hybrid organic–inorganic³⁷) are among the most promising solar cell absorbers after Si-based technology due to their high efficiency and relatively low-cost production.^27,37,38 Both classes of materials, despite their structural differences, are heavily influenced by the diffusion of ions, which can significantly affect the device performance and long-term stability.³⁰ Thus, we largely use these materials as examples for this article but emphasize that the insights gained are broadly applicable across multiple semiconductor classes, especially those used as PV absorbers where photoinduced ion diffusion may be important.

Diffusion Mechanisms

This section briefly discusses the mechanisms behind the diffusion of ions or defects in solid-state materials.³⁹ The movement of atoms or molecules through a lattice is driven by concentration gradients and can be described by Fick’s laws of diffusion. Fick’s first law states that the flux of atoms J is proportional to the concentration gradient ∇C:

where D is the diffusion coefficient. Fick’s second law describes how the concentration changes over time:

These principles underpin the understanding of diffusion mechanisms, which can be classified into three main types.

• Interstitial Diffusion: This involves atomic or molecular species moving through interstitial sites (free spaces between atoms) in the lattice. For example, H_i (Hydrogen interstitial) diffusing through Pd crystals is important in H storage, diffusion in ceramics, and catalysis.⁴⁰

• Substitutional Diffusion: This happens when atoms or molecules diffuse by replacing (substituting) atoms in the lattice. An example is Cu atoms diffusing in an Au lattice by substituting Au atoms (Cu_Au).⁴¹

• Vacancy Diffusion: This occurs when atoms or molecules move from a lattice site to a neighboring vacant site on the way to another lattice site. For example, the diffusion of Si through its lattice can be facilitated by missing Si atoms (V_Si).⁴² This type of diffusion is important in processes such as sintering, creep in metals, and the typical migration behavior of dopants in semiconductors.

Defect-Mediated Ion Migration in Perovskites: Case Studies

Ion Migration in Mixed Halide Perovskites

3D crystalline halide perovskites with the general formula ABX₃ may contain large monovalent inorganic or organic cations at the A site, divalent cations such as Pb or Sn at the B site, and typically I, Br, or Cl at the X site. The highest power conversion efficiencies achieved to date from perovskite solar cells comes from a combination of FA (formamidinium), MA (methylammonium), and Cs at the A site, I and Br at the X site, and Pb at the B site.⁴⁴⁻⁴⁸ Despite excellent efficiencies, the long-standing obstacle to commercializing perovskite solar cells is their photostability and film degradation.⁴⁹ For bulk films of mixed halide perovskites, such as MAPb(Br_1–xI_x)₃^50,51 and CsPb(Br_1–xI_x)₃⁵²⁻⁵⁴ that have some of the highest reported PV efficiencies, there has been clear evidence of light-induced phase segregation which causes a red shift in the photoluminescence (PL) spectra.⁵⁵⁻⁵⁸ When exposed to continuous light with an energy larger than the bandgap, mixed iodide-bromide perovskites commonly display halide segregation, resulting in the formation of I-rich and Br-rich domains. Considering Cl ions mixed at the X-site as well, this segregation can be represented as follows:⁵⁷⁻⁵⁹

1

The I ions tend to accumulate at the grain boundaries^60,61 and form separate I-rich domains, also creating and stabilizing vacancies, dangling bonds,⁶² and impurities. This phase segregation is majorly driven by the propensity of photogenerated charge carriers to migrate toward lower energy regions upon illumination. The rate constant (k_segregation) for segregation can be expressed using the Arrhenius equation as⁴³((Figure 1(f))):

2

3

Figure 1.

(a) Spectroscopic investigation of absorption changes in mixed halide perovskite compositions varying with excitation intensity (8–160 mW cm^–2), elucidating the dynamics of light-induced halide segregation. (b) Analysis of the rate constant ln(k) as a function of excitation intensity, providing insights into the kinetics of the segregation process. (c) Quantitative determination of the quantum efficiency for halide segregation, offering a measure of the photophysical conversion efficacy. (d) Temperature-dependent study of differential absorption spectra of mixed halide compositions under constant irradiation (25 mW cm^–2) across a range of temperatures (10, 15, 22, 35, and 40 °C), revealing the influence of temperature on segregation dynamics. (e) Temporal analysis of bleach growth kinetics as a function of temperature for insight into the thermally activated nature of the segregation process. (f) Arrhenius plot of ln(k) against (1/T) for light-induced halide ion segregation, enabling the extraction of the activation energy and pre-exponential factor. Reproduced with permission from ref (43). Copyright 2021 Wiley.

A in Equation 2 is a prefactor and E_{a,segregation} is the activation energy barrier for Br/I segregation that depends on the energy gradient (ΔE_light) between the Br/I domains as determined by the photoinduced carrier density. ΔE_remixing is the activation energy for halogen ion migration between the two domains. The segregation is effective when the photoinduced excitation energy is greater than the mixing entropy.⁵⁹ The energy difference ΔE_light refers to the gradient that exists due to the carrier density-dependent energy between the I-rich and Br-rich domains. As there is more incident light, the absorption of photons promotes carriers from the valence band to the conduction band, increasing the overall carrier density. The valence band maximum is higher in energy in the I-rich domains as compared to the overall mixed-halide phase as the former has a lower band gap. This promotes the transport of holes to the I-rich domains under illuminated conditions, which creates an energy gradient between the Br/I domains.⁶³E_{a, segregation} is the energy barrier for ion movement leading to segregation, while ΔE_remixing refers to the energy difference required for ions to remix after segregation. Although these activation energies influence ion migration under thermal conditions, ΔE_light modulates the electronic environment of the sample under photoexcitation. As reported by Cho et al.,⁴³Figure 1(a) shows the increasing bleach (or disappearance of mixed halide absorption) with increasing excitation intensity, leading to increased segregation and higher segregation rates (k_segregation) at higher intensities (Figure 1(b)). To calculate the extent of segregation, the quantum efficiency (QE) of segregation is defined as⁴³

4

Here, η_mixed represents the moles of mixed halide phases disappeared due to segregation and η_photons represents the moles of input photons from the photoexcitation that depend on the excitation intensity and time duration. As the excitation intensity increases from 8 to 160 mW cm^–2, QE decreases from 25% to 3% (Figure 1(c)), corroborating the nonlinear dependency of ln(k_segregation) with the excitation intensity. Figure 1(d) shows the increased segregation at higher temperatures due to increased carrier mobility, which can be well understood from Equation 2. Higher temperatures lower the activation barrier and enhance the segregation rate, which leads to the quicker formation of separate halide-rich domains resulting in shorter lifetimes as the system approaches equilibrium, like shown in Figure 1(e).The observed decrease in Q.E. with increasing excitation intensity can be explained by considering the thermal effects induced by higher photon flux. As the excitation intensity increases, more carriers are generated, and the energy density within the system rises. This elevated energy density can lead to localized heating effects, promoting nonradiative recombination processes and, in turn, reducing the overall Q.E. Furthermore, this thermal energy can enhance defect migration or ion remixing, particularly in systems where ion diffusion is sensitive to temperature changes. As ions migrate or remix, they can create additional nonradiative recombination centers, further lowering the Q.E.

The I-rich domains, characterized by a narrower bandgap relative to their Br-rich counterparts, act as efficient exciton trapping centers. The localization of excitons in these lower bandgap regions leads to radiative recombination events at reduced energies compared to the initial mixed-halide composition.^63,66 Consequently, this phenomenon induces a red shift in the PL spectrum. Interestingly, it was observed that upon storing the segregated phases in the dark, there is complete recovery of the mixed-halide compositions, leading to recreation of the original homogenized solution.^43,67 This dark recovery is governed by the entropy-driven halide ion mixing in the absence of a photoinduced gradient. For the retention of the homogeneous phase, the mixed halides should have a high activation energy for segregation and low activation energy for recovery.

Another experimental study by Hoke et al.⁶⁴ demonstrated that phase segregation in mixed halide perovskites occurs under continuous illumination, resulting in a reversible shift in the absorption edge and a decrease in device performance over time. Similarly, Singh et al.⁶⁸ explored the effects of halide phase segregation on the stability and efficiency of perovskite PV devices. The authors analyzed the degradation of mixed-halide perovskites, focusing on how I^– and Br^– phases segregate under illumination, causing significant shifts in the electronic structure and energy levels of the sample. X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS) reveal that photochemical degradation is more prominent in mixed-halide compositions with higher Br content, leading to diminished device stability and performance. Draguta et al.⁶³ also elucidated the underlying microscopic processes of ion-mediated phase segregation in MAPb(Br_1–xI_x)₃ using spectroscopic measurements and theoretical modeling, finding that the phase segregation was driven by the hole migration due to differences in valence band alignment, which leads to separation of iodide-rich and bromide-rich regions.

Role of Cl in Suppressing Phase Segregation

As discussed previously, in mixed halide perovskites, ion migration is predominantly governed by the diffusion of iodine (V_I) and bromine (V_Br) vacancies. The migration energy barriers (E_m) for V_I and V_Br are 0.58 eV⁶⁹ and 0.27 eV³¹ respectively, in their respective phases (MAPbI₃, MAPbBr₃), as calculated from density functional theory (DFT)⁷⁰ (Table 1). Incorporating Cl in I/Br mixed halide perovskites has been shown to inhibit halide ion migration and enhance the stability of solar cells under operational conditions.⁷¹ Cl in small concentrations (0–10%) enhances both charge carrier lifetime and mobility in mixed halide perovskite films compared to their unalloyed counterparts, without altering the crystallographic domain size.^59,71,72 Cho et al.^43,59 demonstrated that presence of Cl mitigates photoinduced phase segregation in MA-based mixed halide perovskites. In bulk MAPb(Cl_0.5I_0.5)₃ films, the inclusion of Cl elevates the activation energy (E_a, Equation 2) for Cl/I segregation to 38.2 ± 0.6 kJ mol^–1,⁴³ approximately 10 kJ mol^–1 higher than the Br/I segregation energy (E_a = 28.9 ± 1.1 kJ mol^–1)⁷³ in MAPb(Br_0.5I_0.5)₃ films. Similarly, 8% Cl addition to MAPb(Cl_xBr_0.5(1–x)I_0.5(1–x))₃ increases the activation energy barrier to 33.1 ± 1.5 kJ mol^–1,⁵⁹ approximately 4 kJ mol^–1 higher than that of the Br/I mixed perovskite (Figure 2(a)).

Table 1. Summary of Computed Defect Energetics and Migration Barriers from the Literature.

material	defect	defect formation energy (eV)	migration barrier (Em) (eV)
CdTe	As+1i	2.7832	0.0532
	As0i	3.4032	0.2732
	As-1i	4.6532	0.4532
MAPbI3	V–I	3.4485	0.5869
	V+MA	5.7285	0.8469
	H +i	0.0923	0.3423
MASnI3	H +i	0.5423	0.4123
MAPbBr3	VBr	1.2531	0.2731
	Bri	1.6431	0.3431
	surface Bri		0.1431
FAPbBr3	VBr	1.2831	0.3331
	Bri	1.8231	0.2431
	surface Bri		0.3931
CsPbI3	VI		0.58105
CsPbBr3	VBr	2.67106	0.43105

Figure 2.

(a) Activation energy diagrams for MAPb(Br_0.5I_0.5)₃, MAPb(Cl_0.05Br_0.475I_0.475)₃, and MAPb(Cl_0.5Br_0.5)₃, showing the relative feasibility of photoinduced phase segregation and reversible dark recovery. (b) Pb–X bond strength plotted against the perovskite tolerance factor.⁴³ Permission to reuse the figures was obtained from Wiley. Reproduced with permission from ref (43). Copyright 2021 Wiley.

The increased energy barrier can be attributed to the polarizability of the Pb-X (Cl, Br, I) bonds and the thermodynamic stabilization of the [PbX₆]^4– octahedra. The enhanced polarity of I^– ions, coupled with their capacity to accommodate neutral I at interstitial sites, facilitates halide ion migration throughout the perovskite film. Bond length increases in the order Pb–Cl < Pb–Br < Pb–I,⁶⁶ while bond energy decreases from Cl to I (Figure 2(b)). The stronger Pb–Cl bonds, associated with higher binding energy, contribute to the increased activation energy barrier for Cl-ion mobilization. Increasing Cl content leads to greater stabilization of the [PbX₆]^4– frameworks, consequently restricting halogen ion mobility. The dark recovery of mixed halides is governed by the entropy-driven halide remixing.⁴³

From Figure 2(a), it can be observed that with increasing Cl content, the activation energy for dark recovery decreases from 53.5 ± 3.8 kJ mol^–1 for MAPb(Br_0.5I_0.5)₃ to 41.9 ± 1.8 kJ mol^–1 for MAPb(Cl_0.5Br_0.5)₃. In MAPb(Cl_0.5Br_0.5)₃, a temperature-dependent reduction in recovery time was observed, decreasing from 50 min at room temperature (22 °C) to 10 min at elevated temperature (80 °C). This acceleration of the dark remixing process with temperature can be attributed to enhanced thermally activated halogen ion transport at higher temperatures. The recovery time of segregated phases also depends majorly on the duration and intensity of incident irradiation. Longer irradiation time or higher excitation exhibited higher recovery times for the segregated phases. The inclusion of Cl^– in the precursor solution likely plays a critical role during the film formation process, influencing the crystallization kinetics, grain growth, and resulting film morphology. By optimizing the morphology, Cl^– can lead to smoother films with fewer defects, better coverage, and enhanced grain boundary passivation, all of which contribute to improved charge transport and reduced recombination rates. This explanation aligns with the notion that Cl^– primarily affects the perovskite morphology, rather than its final incorporation into the crystal lattice.⁷⁴ Cl^–, compared to larger halide anions such as I^– and Br^–, exhibits stronger and shorter bonds with Pb²⁺ due to its smaller ionic radius, larger electronegativity, and lower polarizability,⁷⁵ which makes the lattice more rigid and makes the Cl-mixed phase less polarizable to external electric fields (photon irradiation). This results in fewer halide vacancies and reduced ion migration pathways. Additionally, the incorporation of Cl in the perovskite lattice can increase the overall lattice stability by strengthening the Pb-X bonds and reducing lattice distortions, further inhibiting the formation and movement of halide vacancies.

Similarly, the addition of dual Cl additives (MACl/CsCl) stabilizes FAI-based perovskite films,⁷⁶ due to a significant reduction of microstrain and crystal distortion-induced defects compared to pristine films or those containing a single Cl additive. The activation energy for phase segregation increases from 40.2 kJ mol^–1 to 59.2 kJ mol^–1 with Cl additives. The incorporation of MACl/CsCl in a 3:2 ratio resulted in a significant enhancement of PV efficiency from 20.92% in pristine films to 22.94%. Overall, with the addition of Cl, the increased activation barrier for photoinduced segregation and the decrease in the activation barrier for dark recovery aided the homogeneous retention of the mixed halide phase. DFT calculations quantitatively confirmed the activation energy for ion migration in the presence of dual Cl additives. The activation energy for the pristine perovskite was 0.41 eV (39.56 kJ/mol). With the addition of chloride additives (either single MACl or dual MACl/CsCl), the activation energy increased to a maximum of 0.57 eV (55 kJ/mol), showing improved ion migration suppression compared to the single additive. Various MACl/CsCl ratios were tested, with the best performance and stability observed at intermediate concentrations (MACl/CsCl = 3:2).

It should be noted that perovskite chlorides tend to show larger bandgaps beyond the PV-suitable range, and the addition of Cl to mixed halide perovskites could result in an undesirable bandgap.^37,77,78 Cl-containing perovskites also tend to have more problematic defect behavior due to deeper levels within the wider bandgap, resulting in a possible increase in nonradiative recombination centers.^78,79 Thus, while Cl may help tackle the issue of ion migration and general stability, it may adversely affect other crucial properties, and multiobjective optimization would be required to determine the ideal Cl mixing fraction.

Dimensionality Reduction as a Means to Restrict Ion Migration

2D perovskites have emerged as promising materials for optoelectronic applications, even though they currently show lower solar cell efficiencies as compared to their 3D counterparts.⁸⁰⁻⁸² The incorporation of bulky organic cations in these structures imparts hydrophobic properties and facilitates defect passivation, resulting in significantly enhanced long-term environmental stability and resistance to moisture corrosion.^83,84 Xiao et al.⁸⁵ reported suppressed ion migration in quasi-2D Ruddleson-Popper (RP) phase of BA₂MA₂Pb₃I₁₀ (BA = Butylammonium) in the in-plane direction due to an increase in the energy required to form a vacancy as compared to 3D perovskites. The n = 3 structure was used for the 2D compound, where n represents the number of layers. Specifically, this indicates a perovskite system with three repeating layers of octahedral units, which forms a quasi-2D structure. Such layered systems are commonly denoted by their layer number (n), where higher values of n correspond to more bulk-like structures.

In 3D MAPbI₃ single crystals, a temperature-dependent conductivity transition is observed. Below 280 K, electronic conduction dominates with an activation energy of 22 ± 2 meV, which is within the shallow charge trap depth range. Above 280 K, ionic conductivity prevails, exhibiting an activation energy of 0.83 eV in dark conditions. Notably, under 0.25 sun illumination, this activation energy decreases to 0.33 eV, indicating significantly increased ion migration. The quasi-2D BA₂MA₂Pb₃I₁₀ perovskite samples exhibited markedly different behavior. No transition between electronic and ionic conduction was observed, regardless of illumination conditions. A consistent activation energy of 25 ± 3 meV was measured, indicating electronic conduction and a carrier trap depth comparable to 3D perovskites. The absence of a conductivity transition up to 350 K implies negligible in-plane ion migration in these quasi-2D perovskite single crystals. The origin of this suppressed ion migration can be attributed to the high vacancy formation energy in the quasi-2D perovskite. DFT computations reveal significant differences in defect formation energies between 3D and quasi-2D perovskites. For methylammonium vacancy (V_MA), the formation energies are 5.72 eV in MAPbI₃ and 6.94 eV in BA₂MA₂Pb₃I₁₀, and for iodine vacancy (V_I), the formation energies are 3.44 and 5.46 eV in MAPbI₃ and BA₂MA₂Pb₃I₁₀, respectively, as also listed in Table 1. For typical point defects, the formation rate is given by an Arrhenius relationship,⁸⁶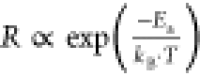, where E_a is the activation energy for defect formation, k_B is the Boltzmann constant, and T is the temperature (in Kelvin). For 3D perovskites, defect formation energies tend to be lower, leading to higher defect formation rates compared to 2D systems. In contrast, 2D perovskites, with their layered structures and enhanced crystalline robustness, tend to be more defect-tolerant and thus exhibit lower defect formation rates at room temperature. Thus, the reduced dimensionality of perovskite phases can help suppress certain defect-related processes.

Cho et al.⁸⁷ also reported suppressed ion migration with increased activation energy barrier in the 2D RP phase of 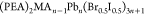(PEA = phenylethylammonium). It was observed that the activation energy barrier for halide exchange increases from 57.8 ± 2.4 kJ mol^–1 (n = 10) to 71.5 ± 2.0 kJ mol^–1 (n = 1) with decreasing number of layers n (Figure 3). The n = 1 film showed a lower diffusion coefficient (6.7 × 10^–16 cm²s^–1, 60 °C) as compared to the n = 6 (1.2 × 10^–15 cm²s^–1, 60 °C) or n = 10 (1.8 × 10^–15 cm²s^–1, 60 °C) films due to the increased fraction of organic layers suppressing halide ion movement and enhancing long-term stability. While the organic layers in 2D RP perovskites effectively suppress halide ion movement and enhance stability by impeding vertical ion migration, ion diffusion in the horizontal (in-plane) direction remains relatively unrestricted.⁸⁸ This horizontal diffusion could still lead to ion migration and degradation over time, which is detrimental to the long-term stability of the material. As suggested by Xiao et al.,⁸⁵ the higher defect formation energy of V_I and V_MA in quasi-2D BA₂MA₂Pb₃I₁₀ as compared to (CH₃NH₃)PbI₃ leads to reduced defect density that suppresses the ion-migration not only in the out-of-plane direction but also in the in-plane direction. To address this, future research on 2D RP perovskites should emphasize not only the advantages of reduced vertical diffusion but also consider strategies to limit horizontal ion migration. This could involve engineering approaches to further improve grain boundary passivation or adopting different organic spacers that may influence in-plane ion movement. Lin et al.⁸⁹ also suggested an increase in the overall activation barrier in 2D (BA)₂(MA)₃Pb₄I₁₃ which might be due to the presence of organic spacers at the grain boundaries. Such considerations are crucial to fully realizing the potential of 2D RP perovskites for enhanced long-term stability in device applications. Overall, tuning the perovskite dimensionality is a promising avenue for enhanced resistance to halide migration, stemming from the presence of organic cations and the confined mobility of halides within layered structures.

Figure 3.

(a) Arrhenius plots showing ln(k) as a function of 1/T for 2D lead halide perovskite films of varying dimensionality: n = 10, 6, and 1. (b) Activation energy plotted as a function of the number of layers (n).⁸⁷ Reproduced from ref (87). Copyright 2020 American Chemical Society.

Atomistic Modeling of Defect Migration

Experimental techniques for characterizing diffusion in semiconductors, such as secondary ion mass spectrometry (SIMS) and deep-level transient spectroscopy (DLTS), provide valuable intuition on the diffusion profiles of ions/defects, but come with certain limitations.⁹⁰ These methods are time-consuming and expensive, require complicated sample preparation, and often lack the atomic-scale resolution necessary to fully understand the underlying mechanisms of defect migration. Furthermore, experimental approaches may not always capture the intricate details of defect interactions and the influence of various environmental factors on the diffusion process.

DFT computations offer a powerful complement to experimental techniques, providing detailed atomic-level insights that can significantly accelerate the study of defect-related energetics and migration pathways. DFT can be used to accurately calculate defect formation energy, defect binding energy, and energy barriers associated with the migration of vacancies or interstitials, which are essential for understanding defect behavior in semiconductors. The defect formation energy is the energy cost for creating an isolated defect and can be calculated as a function of defect charge, Fermi level, and chemical potential conditions:^79,91−96

5

Here, E_tot(X^q) is the total DFT energy of the defect-containing supercell X in a charge state q, E_tot(bulk) is the total energy of the pristine supercell, n_i represents the number of atoms exchanged with reservoirs of chemical potentials μ_i for any species i, E_VBM is the valence band maximum (VBM), E_F is the Fermi level or electron chemical potential which ranges from the VBM to the conduction band minimum (CBM), and Δq is a finite-size charge correction.⁹⁷Figure 4(a) shows a defect formation energy plot for CdTe under Cd-rich conditions, picturing low-energy native defects V_Cd and V_Te (vacancies of Cd and Te) and extrinsic substitutional defects As_Te and Cl_Te.^25,27,95Figure 4(a) also shows that various defects exist in multiple charge states within the bandgap, and the points (E_F) where the slope of the E_f vs E_F plot changes represent charge transition levels. V_Cd and V_Te are stable acceptor and donor defects respectively that pin the equilibrium E_F close to the middle of the bandgap (indicative of intrinsic type conductivity), whereas As_Te and Cl_Te act as compensating defects that push the equilibrium E_F to the left, having an overall p-type effect. Such defect diagrams enable the identification of all low-energy defects, their most likely charge states, possible defect complexes and compensation, and the chemical potential conditions necessary to stabilize particular defects.

Figure 4.

(a) DFT-computed formation energy of selected low-energy point defects in CdTe under Cd-rich chemical potential conditions, showing the equilibrium Fermi level (E_F) pinned by the lowest energy acceptors and donors. (b) Regular vs climbing image-nudged elastic band (Cl-NEB) method, which shows that Cl-NEB yields the saddle points while demonstrating the minimum energy path (MEP) in as few images as possible. Figure (b) is taken from MatGPT (https://www.materialssquare.com).

The optimized defect geometries in suitable charge states can be used as the starting point for simulating the migration of ionic species via vacancy, interstitial, or substitutional hopping mechanisms. For finding the minimum-energy pathway (MEP) for hopping processes, transition-state theory must be applied.^39,98,99 The total energy calculated as a function of the position of the hopping atom, where the surrounding host atoms are allowed to relax, maps out a potential energy surface (PES). The PES will reveal the saddle point and the corresponding migration barrier (E_m), but accurate results necessitate sampling a large number of atomic positions. A more efficient approach to finding the MEP is the nudged elastic band (NEB) method,^98,99 which simulates a series of transition states between two known states to effectively reveal the lowest energy needed for an atomic-scale diffusion process.

An NEB calculation involves the following steps:

• Atomic configurations for the initial and final states of the diffusion process (or reaction) are first defined; these states will be local minima on the PES.

• A series of intermediate images (structures) are generated between the initial and final states through linear interpolation of atomic positions. These images represent the path along which the system should move from the initial to the final state.

• Spring forces between adjacent images are introduced to ensure that they remain evenly spaced along the reaction coordinate. These forces do not affect the energy landscape but help to maintain an even distribution of images.

• A constrained optimization is performed where each image is allowed to relax only perpendicular to the path connecting the images. The atomic forces in each geometry is a combination of the true force (gradient of the PES) and the spring force. The perpendicular component of the true force and the parallel component of the spring force are used to update the positions of the atoms in each image.

After initial relaxation, the highest energy image (the saddle point) can be further refined using the climbing-image NEB (Cl-NEB) method as pictured in Figure 4(b). In this step, the forces along the reaction path for the highest energy image are inverted, causing a climb up to the transition state. This allows for a more accurate determination of the transition state and the associated energy barrier. The NEB calculation is considered converged when the forces on all images fall below a predefined threshold, indicating that the MEP has been accurately determined. Scripts for NEB calculations are very conveniently implemented in various DFT software packages such as VASP¹⁰⁰ (Vienna Ab initio Simulation Package). Users would need to refer to the specific documentation for details on input parameters and execution. Applications of NEB include the study of diffusion of point defects and impurities in semiconductors, chemical reactions on surfaces, phase transitions in materials, and transition states in catalytic processes.

In addition to DFT, less expensive classical MD simulations¹⁰¹ are extensively used to study diffusion in solid-state materials. While DFT provides detailed insights into the electronic structure and energetics of defect migration, MD simulations offer a complementary approach by modeling the time evolution of atomic interactions under realistic temperature and pressure conditions. MD simulations utilize classical or semiempirical interatomic potentials to capture the dynamical behavior of atoms, enabling the estimation of the mean square displacement (MSD) of atoms over time as well as the diffusion coefficient (D) via the Einstein relation.¹⁰² The MSD is computed as

6

where r(t) is the position of a particle at time t and r₀ is its initial position. The angle brackets denote an average over all particles and different time origins. D can be determined from the MSD as

7

By simulating the atomic trajectories over extended periods of time, MD simulations provide valuable information on the kinetic pathways and mechanisms of diffusion processes, complementing the static, energy-focused perspective of DFT. Also, temperature effects are crucial for understanding defect migration and the 0K defect formation energy should be replaced by the Gibbs free energy of formation by taking into account temperature, volume, and pressure dependence. The 0K defect formation energy refers to what is being computed from DFT, where the temperature is not a factor and we are only concerned with the internal energy. Thermal effects are excluded and we are simply investigating the energetics of defects in an idealized, static system without additional factors of temperature-induced vibrations or excitations. However, in real-world applications, temperature effects become critical, especially under operating conditions, and the modeling approach must be modified to taken them into account. If convenient interatomic potentials are available, MD simulations could be performed on very large systems to simulate migration pathways; for higher accuracy when potentials may not be available, ab initio molecular dynamics (AIMD) simulations could be applied but using smaller supercells and typically for smaller time periods. AIMD is a computational technique where atomic trajectories are calculated using forces derived from quantum mechanical principles, typically based on DFT.¹⁰³ This method allows for the simulation of material behavior at finite temperatures, capturing the dynamic evolution of atomic positions and enabling the study of defect migration and ion diffusion under realistic conditions. Because of the heavy expense and weak scaling of quantum mechanics, AIMD simulations are typically only performed for tens of picoseconds or so, as opposed to MD simulations from classical force-fields which can be performed for several nanoseconds.

Atomistic Modeling of Defect-Mediated Diffusion and Ion Migration: Case Studies

Diffusion of Defects and Dopants in CdTe

The study from Hatton et al.³² investigates the potential of As doping in CdTe to enhance solar cell efficiency by increasing hole concentration. DFT computations were used to study the diffusion characteristics of As in zinc-blende (ZB) and wurtzite (WZ) structures of CdTe as well as in Σ3 and Σ9 grain boundary (GB) structures. As_i in ZB CdTe forms split-interstitial configurations with Te atoms, exhibiting a hopping barrier (E_m) of approximately 0.27 and 0.45 eV for neutral and negatively charged interstitials respectively, while positively charged interstitials have a very low E_m of about 0.05 eV, as presented in Table 1. In WZ structures, similar low diffusion barriers were observed. Overall, it was found that single As_i has low diffusion barrier, enabling migration even at room temperature, and with proper incorporation strategies, such as Cl saturation followed by As doping, desired p-type doping could be achieved without negatively impacting the bandgap.

Another study on the doping and diffusion of Group V elements in CdTe solar cells demonstrates significant advancements over traditional Cu doping, which suffers from low hole densities and instability due to ion migration.³³ The study also utilizes DFT calculations and experimental techniques such as X-ray Photoelectron Spectroscopy (XPS) and Time-Resolved Photoluminescence (TRPL). These methods reveal that Group V dopants P, As, Sb, and Bi can effectively diffuse through CdTe with E_m between 0.4 and 0.8 eV, similar to Cd_i atoms, indicating that high-temperature annealing may not be necessary. The findings show that As-doped CdSe_xTe_1–x films achieve hole densities exceeding 2 × 10¹⁵ cm^–3, significantly higher than Cu-doped films. Cd_i is a key native defect species in CdTe, influencing the electrical properties and performance of CdTe, especially in terms of n-type doping and compensation mechanisms. The diffusion of Cd_i occurs through interstitial pathways and can contribute to the formation of unwanted deep levels in the bandgap, potentially degrading device performance.

Another study by Colegrove et al.¹⁰⁴ performed both experimental and DFT predictions for As diffusion in CdTe, revealing a strong agreement between the two approaches in terms of the diffusion mechanism and activation energy. Experimental results indicate that unlike P, As does not undergo fast interstitial diffusion but instead follows a substitutional mechanism, with an activation energy of approximately 2.18 eV for bulk diffusion. DFT calculations corroborate these findings, predicting an activation energy greater than 2.1 eV. This close alignment between theoretical and experimental results enhances confidence in using DFT to accurately model As diffusion in CdTe. Interstitial pathways are less favorable than substitutional pathways for As in CdTe due to the larger size of As atoms, which causes significant lattice strain when occupying interstitial sites. Substitutional doping is more energetically stable, as As atoms replace Te atoms, fitting more naturally into the lattice and minimizing distortions.

Diffusion of Hydrogen (H) Impurities in Halide Perovskites

The diffusion of H-related impurities, both atomic and molecular, plays a critical role in the performance and stability of hybrid perovskite solar cells. Common sources of H include residual gases in the deposition environment, contamination during growth or processing, and H passivation treatments.^107,108 In thin-film deposition techniques such as chemical vapor deposition (CVD) or sputtering, H-containing precursors or residual H in the vacuum chamber can unintentionally introduce H into the material. Once present, H can significantly impact defect dynamics, often passivating dangling bonds or interacting with native defects, thereby altering defect formation energies and migration pathways.⁶⁴ H impurities in halide perovskites, including H⁺_i, H^-_i, and H₂, can be generated through various processes depending on the chemical and environmental conditions. For example, H⁺_i can form when H atoms donate their electrons and interact with halide vacancies, while H^-_i results from H atoms gaining electrons, typically in reducing environments. H₂ can form through the recombination of H atoms, particularly in voids or under high-pressure conditions. The migration pathways for these H species are closely tied to the presence of halide vacancies and grain boundaries, which are common in perovskites, and external factors like moisture or light exposure can significantly influence the formation and mobility of these impurities. H_i are also known to be amphoteric defects, such that they form both positively charged H⁺_i and negatively charged H^-_i defects, often creating a + 1/-1 transition level in the band gap or close to the band edges. Thus, H_i migration in perovskites must be studied in both charge states.

Atomic H_i in hybrid perovskites such as MAPbI₃ and MASnI₃ are found to be electrically active negative-U defects, contributing significantly to ionic conductivity.²³ The diffusion of H⁺_i ions is faster than for H^-_i, as evidenced from the lower barriers for the former. DFT computations show H⁺_iE_m values of 0.34 eV in MAPbI₃ and 0.41 eV in MASnI₃, as shown in Figure 5(a) and Table 1. This rapid diffusion leads to several detrimental effects, including hysteresis, device polarization, and reduced charge separation efficiency, ultimately degrading the solar cell performance. On the other hand, molecular H₂ is electrically inactive and diffuses with relatively low barriers due to its chemical inertness and the structural porosity of the perovskite lattice. The study also suggests that controlling the concentration of H_i through synthesis modifications, such as adding extra I or alloying with Sn, can effectively mitigate the adverse effects of fast H diffusion, thereby enhancing the stability and efficiency of perovskite solar cells.

Figure 5.

(a, b) DFT-computed diffusion energy barriers for hydrogen interstitials in the positive (H ⁺_i, red) and negative (H ^-_i, green) charge states in MAPbI₃ and MASnI₃, respectively. Since H is an amphoteric defect, it is important to evaluate its diffusion in either charge state. It is seen that H ⁺_i shows a significantly lower diffusion energy barrier. The atomistic configurations of the initial, transition, and final states for the migration of (c) H ⁺_i and (d) H ^-_i in MAPbI₃ are pictured.²³ Color coding: I is brown, Pb is gray, and the H impurity is red. Reproduced from ref (23). Copyright 2022 American Chemical Society.

Halogen Migration in Hybrid Perovskites: The Organic Cation Matters

Halogen migration in hybrid halide perovskites such as MAPbBr₃ and FAPbBr₃ remains a critical challenge affecting their stability and performance. Oranskaia et al.³¹ used DFT computations to investigate the influence of different organic cations (MA and FA) on Br-related defect formation and migration, specifically considering Br vacancy (V_Br) and interstitial (Br_i). Their work revealed that MAPbBr₃ exhibits lower defect formation energy for both V_Br and Br_i compared to FAPbBr₃, indicating a higher concentration of defects in MAPbBr₃ under certain growth conditions. This suggests that MAPbBr₃ is more prone to defect formation which can adversely impact its stability and subsequent electronic performance. DFT shows that E_m for V_Br in MAPbBr₃ is 0.27 eV, which is lower than the 0.33 eV calculated for FAPbBr₃, as shown in Figure 6(a–d) and presented in Table 1. On the other hand, for Br_i, E_m is calculated to be 0.34 eV in MAPbBr₃ and 0.24 eV in FAPbBr₃. The lower E_m of V_Br in MAPbBr₃ facilitates faster ion migration, which can lead to degradation of the optoelectronic properties over time.

Figure 6.

(a) Structural models showing migration pathways for bromine vacancy (V_Br) in MAPbBr₃ and FAPbBr₃. (b) DFT-computed migration energy barriers for V_Br in MAPbBr₃ and FAPbBr₃. (c) Structural models showing migration pathways for the bromine interstitial (Br_i) in MAPbBr₃ and FAPbBr₃. (d) DFT-computed migration energy barriers for Br_i in MAPbBr₃ and FAPbBr₃. The relative energy is referenced to the minimum energy of the optimized crystal structure before ion migration.³¹ Reproduced from ref (31). Copyright 2018 American Chemical Society.

The study also explored defect migration on the surfaces of these perovskites, particularly focusing on PbBr₂-terminated surfaces which are typically found to be more favorable than MABr or FABr terminations. E_m for Br_i on the MAPbBr₃ surface is remarkably low at 0.14 eV and much higher at 0.39 eV for FAPbBr₃. A critical factor affecting ion migration is the strength of H bonding between the organic cations and Br anions. It is shown that FA exhibits stronger H bonding with Br compared to MA, which contributes to the higher E_m for Br_i in FAPbBr₃, thereby reducing the rates of ion migration and potentially enhancing long-term photo and thermal stability. Moreover, the rotation barriers of the organic cations also play a key role; the lower rotation barrier of MA allows for easier reorientation, which stabilizes Br_i and facilitates ion migration. The choice of organic cation in a hybrid halide perovskite compound is clearly of great importance in controlling defect-mediated ion migration. Incorporating organic cations with stronger H bonding and more restricted motion within the inorganic framework can effectively suppress ion migration, which can lead to improved stability and performance of perovskite solar cells.

Effects of Lattice Strain on Ion Diffusion Dynamics

The residual strain in a perovskite film from fabrication plays a major role in governing the ion migration dynamics and affects the performance and stability.^109−111 Cheenady et al.¹⁰⁵ studied the effects of uniaxial, biaxial and isotropic states of compressive and tensile strain on cubic CsPbX₃ (X = Br, I) using MD and NEB simulations. As illustrated in Figure 7(a–d), the energy barriers for vacancy-assisted halide ion migration exhibit complex behavior under both isotropic and biaxial stress states. In the unstrained state, E_m for CsPbI₃ and CsPbBr₃ calculated from DFT are 0.58 and 0.43 eV, respectively, as also presented in Table 1. In CsPbI₃, E_m shows a nonmonotonic response to compressive strain, initially increasing at 0.01 strain before returning to near-unstrained levels at 0.02 strain. Conversely, tensile strains consistently reduce the barrier. In CsPbBr₃, the barrier width decreases under tensile strain and slightly increases under compression. CsPbI₃ demonstrates an opposite trend in the barrier width.

Figure 7.

Variation in energy barrier height for vacancy-assisted halogen ion migration in CsPbI₃ under (a) isotropic and (b) biaxial states of stress and in CsPbBr₃ under (c) isotropic and (d) biaxial states of stress. The energy barriers for tensile (T), compressive (C), and unstrained conditions are shown in red, blue, and black, respectively. (e) Halogen ion migration barriers in CsPbBr₃ (dashed lines) and CsPbI₃ (solid lines) under isotropic and biaxial stress conditions. (f) The deviation in the minimum energy path (MEP) during the migration of I^– to a vacant site under biaxial tension (blue curve) and biaxial compression (red curve).¹⁰⁵ Reproduced with permission from ref (105). Copyright 2023 American Institute of Physics.

Figure 7(e) reveals that CsPbBr₃ consistently maintains lower barrier compared to CsPbI₃ under similar conditions, regardless of the stress state. Both compounds exhibit a universal trend of decreasing E_m with increasing tensile strain, irrespective of the stress state. A similar reduction in barrier (0.67 to 0.57 eV) was reported in CsPbI₂Br under 1.5% biaxial tensile strain by Xiu et al.,¹¹² using DFT. The increase (decrease) in E_m under compressive (tensile) strain can be explained by the MEP from an initial position to a vacant position. The substantial changes in the trajectory at 700 K (temperature at which MD simulations were performed) from MEP (at 0 K) can be attributed to thermal vibration-induced deviations. Under biaxial and isotropic compressive stress, traversing the deviated trajectory becomes energetically unfavorable due to shrinkage in lattice volume and corresponding bond lengths, thereby increasing E_m.

Sarkar et al.¹¹³ highlighted intriguing mechanisms for pressure-induced halide migration in FA_0.875Cs_0.125PbI₂Br. Under ambient conditions, Br ions preferentially migrate to Br-vacancies (V_Br), initiating phase segregation. However, applied external pressure alters this landscape significantly. In equatorial (100) and (010) planes, cross-ion migration becomes energetically favorable as strain increases, with I ions filling V_Br sites and vice versa. This process maintains overall halide distribution randomness, counteracting phase segregation. However, if the pressure is increased > 1 GPa, the Pb atoms are compressed together and form a Pb–Pb dimer-type configuration. This leads to very high steric hindrance and inhibits all kinds of halide migration. The pressure-induced acceleration of cross-ion migration coupled with suppressed axial diffusion due to Pb–Pb dimer formation maintains the stochastic distribution of halogen ions within the perovskite lattice, effectively mitigating halide phase segregation. Pressures exceeding 1 GPa can be achieved under high-pressure experimental setups or during material synthesis. Techniques such as diamond anvil cells (DAC) and shock wave compression are commonly used to generate pressures in the GPa range or higher.¹¹⁴ These high-pressure conditions are often employed to study phase transitions, defect dynamics, or material properties under extreme environments. In the context of semiconductor processing, pressures in this range can also occur during high-temperature annealing under gas pressure or in certain thin-film deposition techniques where stress is induced in the material. However, these conditions are typically rare and controlled, as most practical semiconductor devices operate under ambient or near-ambient pressure.

Accelerated Prediction of Defect-Mediated Ion Migration

While traditional computational methods such as DFT have provided invaluable insights into defect energetics and ion migration mechanisms in semiconductors, they can be computationally expensive and time-consuming, especially when investigating large chemical spaces or simulating long-time scales. Ionic compounds, including halides and chalcogenides, often exhibit intricate bonding environments and defect chemistry, making it crucial to accurately capture long-range interactions and subtle electronic effects. Large supercells are required to minimize defect–defect interactions and accurately simulate isolated defects, but they introduce a massive computational burden when calculating defect formation energies and migration pathways.^95,97 DFT computations even with semilocal GGA (generalized gradient approximation) functionals¹¹⁵ are very expensive and scale with the cube of the number of atoms, which often makes them prohibitively expensive for simulating alloyed compositions and defect complexes which require really large supercells. Furthermore, GGA functionals are inaccurate for electronic band edges and band gap, which necessitates the use of nonlocal hybrid functionals,¹¹⁶ which are orders of magnitude more expensive than GGA.

These computational limitations are felt across all types of crystalline semiconductors, and thus, ML approaches are essential for accelerating prediction at high accuracy. ML models provide the ability to quickly predict material properties and defect behavior by learning from high-quality DFT training data sets.^117−119 Specifically, ML can accelerate the screening of beneficial or harmful defects in solid-state materials, such that in-depth and expensive computations only need to be performed at the end on the most promising systems. However, the application of ML to materials science comes with its own set of challenges. First, constructing a reliable model requires large amounts of accurate training data, often difficult to generate for complex systems with numerous defect configurations and requiring very large supercells. Additionally, ensuring that the model generalizes well beyond the training set to make accurate predictions for unseen cases is nontrivial. In the case of ion migration, ML methods must not only capture the static properties of materials but also predict dynamic behavior. In this section, we discuss how ML methods can effectively be used to accelerate the prediction and understanding of defect-mediated migration.

Examples from the Literature

Combining DFT data sets with ML models that encode compositional and physical descriptors or entire crystal structures as input enables the accelerated prediction of energies and other properties at DFT accuracy. Such ML models are capable of capturing the underlying structure–property relationships in materials by learning from the training data, such that new predictions could be made without the need for expensive DFT. “DFT-ML” approaches not only help speed up predictions but also open new avenues for the exploration and design of novel semiconductors. Depending on the quantity and quality of DFT data used for training, ML models could be developed to either directly predict properties of interest such as defect formation energy, defect levels, or ion migration barriers, or to yield force fields or interatomic potentials that can be used to optimize defect structures and obtain the relevant energies of local minima and transition state configurations.^97,121,122

Pols et al.¹²⁰ investigated the migration of defects in halide perovskites such as CsPbI₃ and CsPbBr₃ using DFT, and utilized the resulting data for training machine-learned force fields (MLFFs). An on-the-fly active learning (AL) scheme was employed to train the MLFFs, such that high-error atomic configurations identified during MD simulations (run using the MLFF) triggered additional DFT calculations. Results from the new DFT calculations were continuously incorporated in the training set to improve the accuracy of the MLFF. Figure 8(a) shows a CsPbI₃ supercell with an I vacancy, which is part of the training data set. The FLARE++ (Fast Learning of Atomistic Rare Events)¹²³ package was used to implement the training process for the MLFF, utilizing sparse Gaussian process (SGP) models to map local atomic environments. When the Bayesian error estimate exceeded a predefined threshold, a new DFT calculation was performed and the forces and energies were collected and incorporated in the training set. This iterative process refined the MLFFs, making them capable of accurately predicting the forces and energies for large-scale MD simulations as shown in Figure 8(b). The trained MLFFs were then used to simulate defect migration in CsPbI₃ and CsPbBr₃, revealing that interstitial defects migrate faster than vacancies due to shorter migration paths and that defects in CsPbI₃ exhibit higher mobility than those in CsPbBr₃, as pictured in Figure 8(c). This methodology bridges the gap between the high accuracy of DFT and the efficiency required for large supercell and high-throughput simulations, providing detailed insights into defect dynamics essential for improving the stability of halide perovskites in optoelectronic applications.

Figure 8.

(a) Crystal structure of bulk CsPbI₃ with an iodide vacancy (V_I), which is marked by an empty purple circle; the local defect region is highlighted using a red dashed circle. (b) Parity plot for the atom-decomposed force components from the vacancy-trained MLFF model compared to DFT ground truth. (c) Temperature evolution of self-diffusion coefficients of halogen vacancies (V_X; empty squares and cirlces) and halogen interstitials (I_X; filled squares and circles) in CsPbX₃.¹²⁰ Reproduced with permission under a CC BY 4.0 license from ref (120). Copyright 2023 Royal Society of Chemistry.

The use of MLFFs offers a promising approach for simulating defect migration pathways, particularly when using large supercells.^124,125 One of the key benefits of MLFFs is their ability to significantly reduce computational cost by approximating the potential energy surface based on training from a limited set of DFT-calculated data. This reduction in cost enables simulations of larger systems and longer time scales than what is feasible with conventional DFT. However, there are important trade-offs in terms of accuracy and computational efficiency that need to be considered. Conventional DFT, especially when using hybrid functionals like HSE06,¹¹⁶ provides highly accurate defect energetics. However, their computational expense grows significantly with system size, scaling with the cube of the number of atoms. MLFFs, on the other hand, are trained on high-quality DFT data and can approximate the forces and energies with much lower computational overhead. For large supercells, MLFFs can simulate defect migration pathways orders of magnitude faster than conventional DFT while still capturing the essential physics of atomic interactions. However, when highly accurate defect energetics are needed, conventional DFT remains the most reliable approach. A hybrid strategy could be adopted, where MLFFs are used for rapid screening across dozens of configurations, yielding potentially low-energy structures which can then be studied with DFT, and eliminating all unfavorable configurations which do not need to be optimized with DFT. This balance allows for both the scalability of MLFFs and the precision of DFT.

Generalizing MLFF models to complex multicomponent systems such as quaternary chalcogenides (e.g., Cu₂ZnSnS₄ or Cu₂ZnSnSe₄) would require significant model training and optimization with large quantities of training data. MLFF models trained on simpler systems may not adequately capture the intricate interactions between different cations (e.g., Cu, Zn, Sn) and anions (e.g., S, Se) in quaternary systems. This complexity leads to a broader variety of possible defect types, such as cation exchange, antisite defects, and vacancies at multiple atomic sites, all of which interact differently with the surrounding lattice. Additionally, the variations in atomic size, charge states, and bonding environments in quaternary chalcogenides make it difficult for a single MLFF model, trained on a narrow set of simpler data, to predict defect migration accurately across the entire compositional space. Expanding training data sets and incorporating hybrid approaches will be crucial for improving the accuracy of MLFFs in predicting defect migration in these more complex materials.^126,127

Crystal Graph Neural Networks: An Avenue for Quick Defect Predictions

Methods based on crystal graph-based neural networks (GNNs) are enormously powerful for predicting energies, forces, and other properties such as band gaps of solid-state materials, directly from an entire crystal structure used as input. There are various types of GNN models available in the literature which may be adapted to new material systems and retrained; they are especially suited for studying defects and ion migration because of their ability to accurately predict energies for large supercell structures. One of the earliest published GNN algorithms is the crystal graph convolutional neural network (CGCNN), developed by Xie et al.¹²⁸ CGCNN takes a crystal structure as input, converts it into a graph where atoms are nodes and bonds are edges, and applies convolutional layers to extract key features. These features are used to predict material properties such as formation energy or bandgap. Materials graph network (MEGNet), developed by Chen et al.,¹²⁹ uses elemental embeddings to encode chemical trends, which helps in making predictions for materials with limited training data. It uses graph networks to learn both the structure and chemical properties of materials. Atomistic line graph neural network (ALIGNN), developed by Choudhary et al.,¹³⁰ improves upon existing methods by considering not only pairwise interactions (bond lengths) but also three-body interactions (bond angles). This helps it better capture both local and long-range correlations within the crystal, improving predictions for more complex material properties.

In our recent work, we developed a framework for predicting and screening native defects and functional impurities in a chemical space comprising canonical group IV, III–V, and II–VI ZB semiconductors.⁹⁷ This framework leverages crystal graph-based neural networks (GNNs) trained on high-throughput DFT data generated by our group over the years.^{25−27,95,131} By utilizing an innovative method of sampling partially optimized defect configurations from DFT calculations (many of which would, incidentally, be close to transition states during defect-mediated migration), we compiled a massive defect data set encompassing a wide range of defect types, including vacancies, self-interstitials, antisite substitutions, impurity interstitials and substitutions, and various defect complexes. This data was used as input to train predictive models based on three types of established GNN techniques as already mentioned, namely CGCNN,¹²⁸ MEGNet,¹²⁹ and ALIGNN.¹³⁰

Rigorously optimized neural network architectures enabled the instant prediction of defect formation energy across multiple charge states and chemical potential conditions, with ALIGNN showing the lowest root-mean-square error of 0.3 eV, representing a prediction accuracy of 98%. We further demonstrated that these GNN predictions could be combined with an iterative structural distortion scheme to obtain roughly optimized defect geometries at a fraction of the cost of full DFT; clearly, there are prospects of applying such an approach to accelerating the prediction of the energies of starting, final, and transition states of defect configurations for simulating defect-mediated migration processes.

For a demonstration, we applied our defect GNN models (our published model⁹⁷ was refined with more data points) to explore the diffusion of a Cd_i defect in ZB CdTe, and compared the migration profiles with DFT. We performed DFT computations using VASP 6.4.1, employing the projector augmented wave (PAW) pseudopotentials^132,133 and the Perdew–Burke–Ernzerhof (PBE) functional within the GGA for the exchange-correlation energy.¹³⁴ Cd_i diffusion was simulated using a 3 × 3 × 3 supercell of CdTe considering only the neutral state,^97,135 and the NEB method was used to obtain the migration pathway. The plane-wave basis kinetic energy cutoff was set to 500 eV and a 2 × 2 × 2 Gamma-centered k-point mesh was used to sample the Brillouin zone. For atomic relaxation, the force convergence threshold was set to −0.05 eVÅ^–1.¹³⁵ Details of the GNN model being used to predict the energies can be found in our recent publication.⁹⁷

Figure 9(a) shows the diffusion path of Cd_i in CdTe and Figure 9(b) shows the energy profiles from DFT and from GNN predictions. While the GNN predicted relative energies along the migration coordinates do not perfectly align with the DFT NEB results, GNN effectively predicts the transition state (the coordinate with the largest energy) and yields an E_m of around 0.27 eV, which matches well with the DFT predicted value of 0.30 eV. The DFT relaxations for the entire NEB process took upwards of 12 h running on 896 CPU cores, whereas the GNN predicted energies take seconds, and combining them with a systematic atomic distortion scheme to better adjust the intermediate configurations only takes a few minutes. Thus, we believe energies from GNN predictions combined with gradient-free optimizers¹³⁶ or force predictions via GNN-based interatomic potentials followed by gradient descent optimization,^{121,137−139} could become highly efficient surrogates for expensive DFT calculations and yield defect configurations, intermediate structures, and energy barriers at a fraction of the cost of full DFT. Efforts are currently underway in our research group to test GNN-predicted pathways and energy barriers for various types of defect-mediated ion migrations in a variety of semiconductors when considering suitable charge states as well.

Figure 9.

(a) Diffusion profile of Cd_i in CdTe simulated using DFT. (b) Comparison between the DFT-computed and GNN-predicted migration energy pathways for Cd_i in CdTe, shown as a function of the migration coordinate. There is a good match between the transition states and barriers from DFT and GNN.

Summary and Outlook

In this article, we provided an overview of the phenomenon of defect-mediated ion migration in semiconductors, utilizing a few case studies for technologically important semiconductors such as halide perovskites and CdTe. Migration of ions or segregation of phases in these materials is often instigated by illumination and has a clear influence on their optoelectronic properties and performance in devices such as solar cells. It is seen that Cl addition, dimensionality reduction, and systematic lattice strains or pressure are possible ways to suppress halogen ion migration in perovskites, confirmed both experimentally and from first-principles simulations. Density functional theory (DFT) can be reliably applied for studying defect energetics and diffusion pathways, especially by combining them with the nudged elastic band method or with molecular dynamics. DFT is able to accurately unveil the effects of hydrogen and halogen migration via interstitial or vacancy processes in hybrid perovskites, and the hopping of native interstitials or Arsenic dopants in CdTe. DFT combined with state-of-the-art machine learning (ML) helps accelerate the prediction of defect energetics and migration barriers. We believe that DFT-ML methods have the ability to quickly yield starting, final, and transition state defect geometries for diffusion processes in semiconductors, and will thus be instrumental for future design of improved materials with tolerance to defect formation and migration in addition to typical optoelectronic properties of interest.

The discovery of next-generation semiconductors via accelerated atomistic simulations must consider bulk stability (including possible entropic effects), electronic, optical, mechanical, magnetic, and thermal properties, and importantly, the static, dynamic, and electronic behavior of defects. We believe that crystal structure-based graph neural network models, optimized to either predict energies or properties directly or to serve as force-fields that can help generate low energy structures and perform better MD simulations, will play a major role in determining likely concentrations of native and extrinsic defects and their migration through the lattice. By suitably extending current models to new chemistries, and by exhaustive benchmarking against experimental measurements, GNN-based defect models will help design novel materials where ion migration is suppressed, native defects and impurities are unproblematic, and dopants have the desired effect. We look forward to applying such approaches for perovskite-inspired materials and various multinary chalcogenide compounds, especially with complex alloying, and anticipate that a multiobjective screening process as described here will indeed yield attractive new materials.

Data Availability Statement

All new data generated here are available as part of the Supporting Information (SI). Relevant code can be found on Github at https://github.com/msehabibur/defect_GNN_gen_1/tree/main/defect_migration.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsmaterialsau.4c00095.

• Relative energy values for a Cd interstitial defect migrating through a CdTe lattice, determined from full DFT calculations and from GNN predictions (PDF)

Author Contributions

CRediT: Md Habibur Rahman data curation, formal analysis, investigation, writing - original draft; Maitreyo Biswas data curation, formal analysis, investigation, visualization, writing - original draft; Arun Mannodi-Kanakkithodi conceptualization, funding acquisition, investigation, methodology, project administration, writing - original draft, writing - review & editing.

The authors declare no competing financial interest.

Special Issue

Published as part of ACS Materials Auspecial issue “2024 Rising Stars”.