Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Oct 31;146(45):31198–31204. doi: 10.1021/jacs.4c11211

A Gravitational-like Relationship of Dispersion Interactions is Exhibited by 40 Pairs of Molecules and Noble Gas Atoms

David Danovich †, Alexandre Tkatchenko ‡, Santiago Alvarez §, Sason Shaik †,*
PMCID: PMC11565636  PMID: 39481085

Abstract

graphic file with name ja4c11211_0008.jpg

We present computational results of many-body dispersion (MBD) interactions for 40 pairs of molecular and atomic species: hydrocarbons, silanes, corresponding fluorinated derivatives, pairs which have multiple H---H contacts between the molecules, as well as pairs having π–π interactions, and pairs of noble gases. The calculations reveal that the MBD stabilization energy (EDISP,MBD) obeys a global relationship, which is gravitational-like. It is proportional to the product of the masses of the two molecules (M1M2) and inversely proportional to the corresponding distances between the molecular centers-of-mass (RCOM-COM) or the H---H distances of the atoms mediating the interactions of the two molecules (RH–H). This relationship reflects the interactions of instantaneous dipoles, which are formed by the ensemble of bonds/atoms in the interacting molecules. Using the D4-corrected dispersion energy (EDISP,D4), which accounts for three-body interactions, we find that the EDISP,MBD and EDISP,D4 data sets are strongly correlated. Based on valence-bond modeling, the dispersion interactions occur primarily due to the increased contributions of the oscillating-ionic VB structures which maintain favorable electrostatic interactions; the [Sub—C+:H–+H:C–—Sub] and [Sub—C:–+H –H:C+—Sub] structures; Sub symbolizes general residues. This augmented contribution is complemented by simultaneously diminished-weights of the destabilizing pair of structures, [Sub—C+:H––H:C+—Sub] and [Sub—:C– H++H:C–—Sub]. The local charges are propagated to the entire ensemble of bonds/atoms by partially charging the Sub residues, thus bringing about the “gravitational-like” dependence of dispersion.

1. Introduction

Unlike hydrogen bonds, which involve localized interactions,1,2 the van der Waals (vdW) dispersion-interactions are cumulative, and may involve all the atoms/bonds in the interacting molecules. As such, dispersion is a major design factor; it is a force of nature which stabilizes condensed matter in chemistry and biology.

Indeed, dispersion interactions have attracted considerable attention in the past two decades or so.3−25 Essentially, the global dispersion interaction in molecular systems is a many-body electronic-effect that arises from electron density fluctuations in the ensemble of atoms/bonds.5,6

The presently available many-body dispersion (MBD) software,6 and Grimme’s D4 method12 can be coupled to electronic-calculation codes to calculate dispersion energies (EDISP). Doing so, we show here that the dispersion interactions between homodimers and heterodimers of alkanes and silanes (see Figure 1), including fluorinated derivatives, rings, noble atom-dimers, π–π interacting dimers, 3D objects etc., obey a gravitational-like law. Thus, EDISPis shown to be proportional to the product of the two molecular masses (M1M2), of the interacting molecules/atoms, and inversely proportional to their distances (see Figures 2 and 3). This expression emerges from the contribution of dispersion interactions by all the bonds/atoms in the studied molecules/atoms. Understanding the nature of EDISP is clearly essential.

Figure 1.

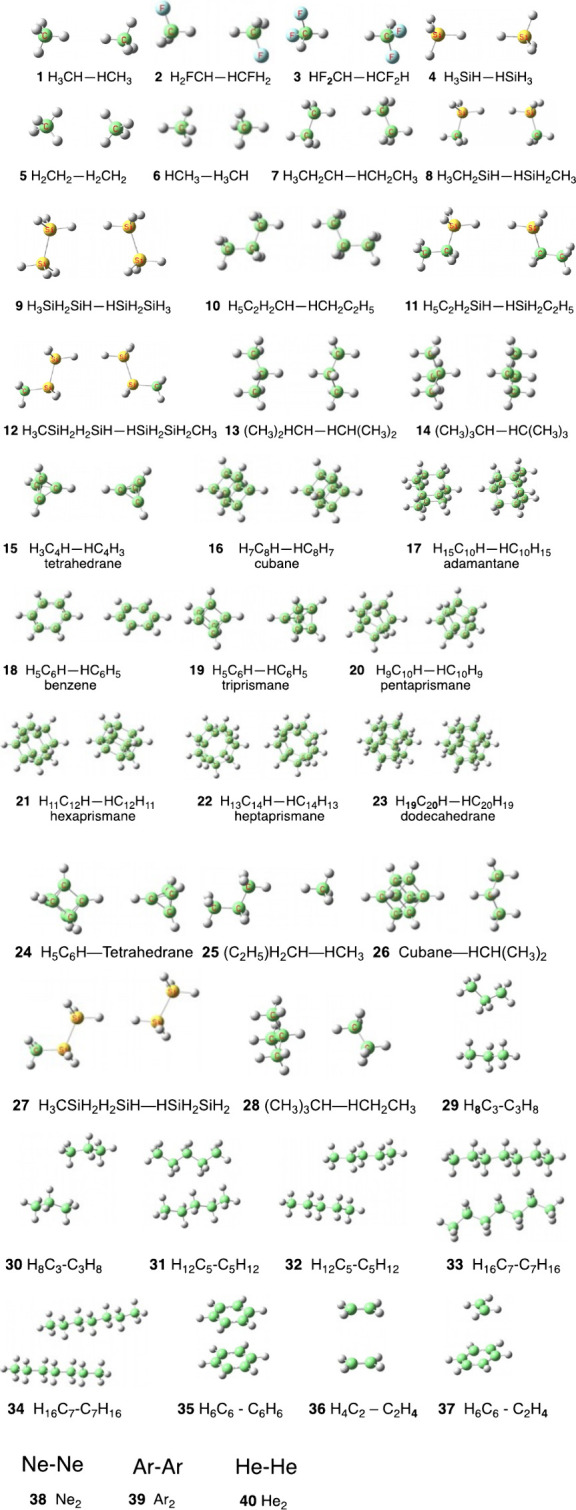
Figure 1

Open in a new tab

Homo- and heterodimers 1–40, which are studied using PBE0/cc-pVTZ with MBD and D4 dispersion corrections (C is green, F is bluish, and Si is yellow). The geometries are fully optimized at the PBE0-MBD/cc-pVTZ and PBE0-D4/cc-pVTZ levels of theory.

Figure 2.

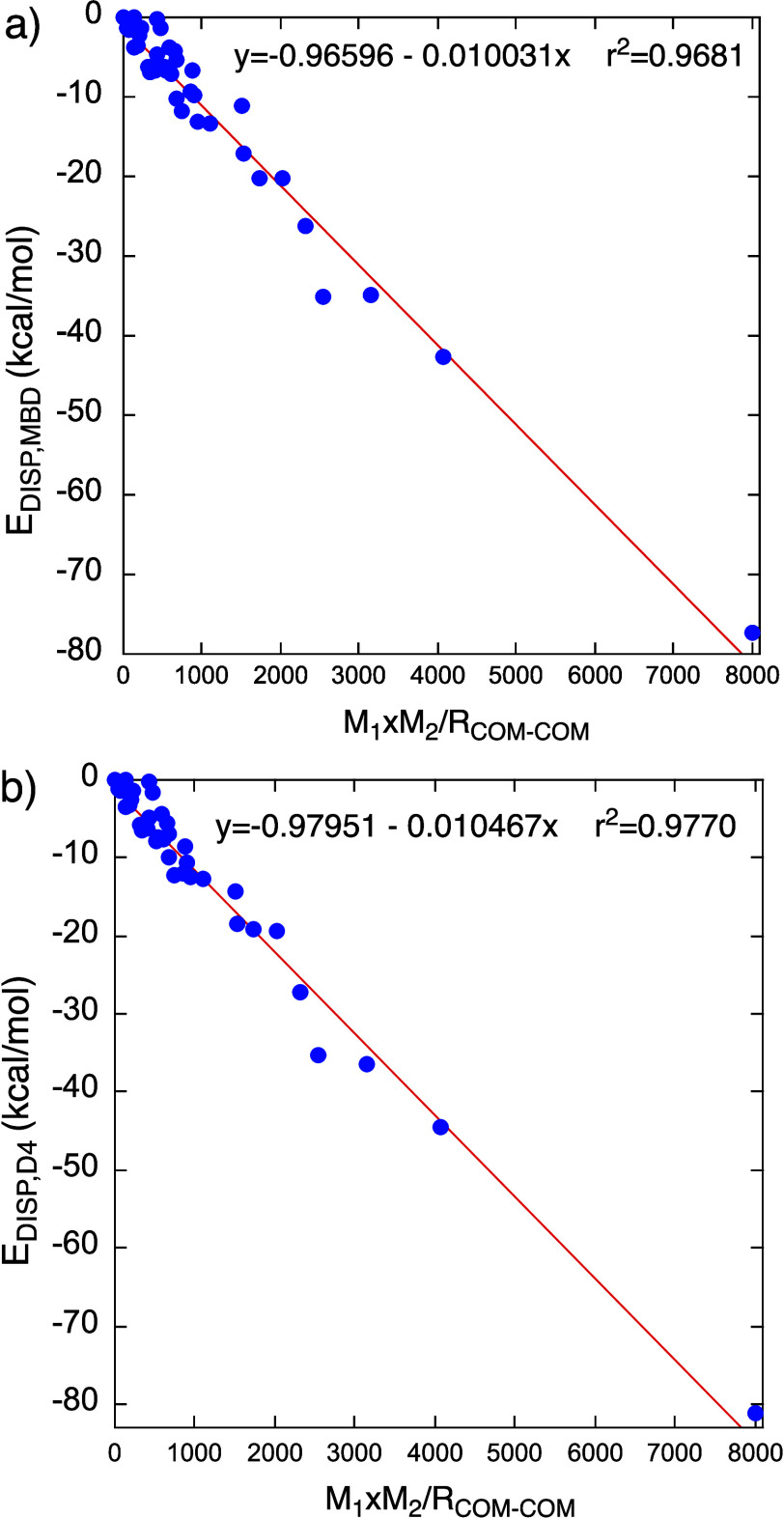
Figure 2

Open in a new tab

Dependence of the dispersion interaction energy (EDISP) on the gravitational-like expression M1M2/RCOM-COM, where M1 and M2 are the molecular masses of the molecules/atoms in the dimer and RCOM-COM is the distance between the respective centers of these masses: (a) Using the many-body dispersion (MBD) method (EDISP, MBD (kcal/mol)). (b) Using the D4 dispersion method (EDISP,D4 (kcal/mol)).

Figure 3.

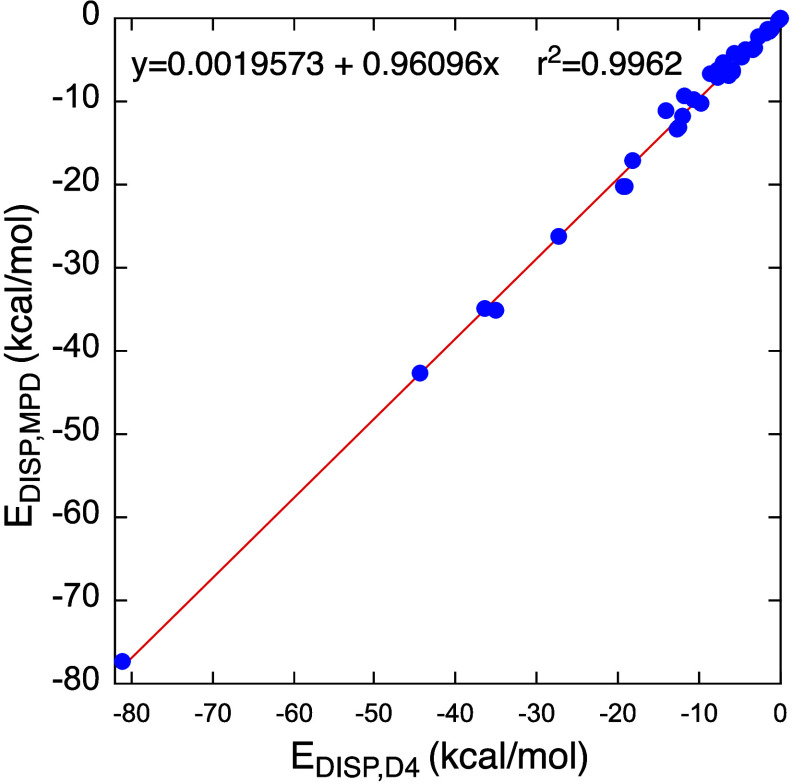
Figure 3

Open in a new tab

Correlation between dispersion energies calculated by the MBD (EDISP,MBD) vs the D4 (EDISP,D4) methods.

2. Methods

We use MBD6- and D412-coupled to density functional (DFT) calculations, PBE0/cc-pVTZ,26−28 as implemented in the QCHEM-6.02 package.29 The method is applied to 40 pairs of molecules/atoms, and demonstrates that the global dispersion energy obeys a gravitational-like law. This relationship indicates that the vdW dispersion-interaction reflects the entire ensemble of bonds/atoms in the studied dimers.5,10,17

3. Results and Discussions

3.1. Dispersion Interactions in Substituted Hydrocarbons and Higher Row Analogues

In hydrocarbons, the homopolar dihydrogen CH---HC interactions lack the electrostatic component that characterize the heteropolar dihydrogen bonds defined by Crabtree et al.30 Since the molecular-pairs studied here are all of the homopolar type, we will refer to CH---HC simply as “contacts” or “interactions”. These contacts serve as “sticky fingers” in condensed phases and in molecular dimers.13−15 Thus, for example, unlike small hydrocarbons which are gaseous molecules at room temperature (e.g., CH4), large hydrocarbons like dodecahedrane and other polyhedranes form condensed phases and solids13,14 with melting points that reach as high as 723 K.

The recent review of Rumel and Schreiner17 provides compelling evidence for the stabilizing role of dispersion and the molecular drive for creating congested geometries. Furthermore, Chen and co-workers22 showed that the drive for adaptation of congested and dispersion-stabilized molecules, persists in solvents, albeit getting somewhat attenuated. Similarly, substituted ethane molecules, which possess very long C–C bonds, that are virtually semibroken, e.g., as in hexa-(3,5-di-t-butylphenyl)-ethane,16−19 are nevertheless held together, due to the dispersion interactions of the large t-butyl substituents, which stabilize the molecule by ca. 40 kcal/mol.17−19 Moreover, graphane layers are stabilized via σ–σ and π–π dispersions (and orbital interactions) by as much as 150 kcal/mol per a pair of layers20,21

High level ab initio calculations are required to reproduce such weak CH---HC dispersion interactions.14,23−25 However, in large molecules, such as dodecahedrane, one has to use DFT calculations (herein, PBE026). DFT calculations generally (though not always31) require dispersion corrections, as an add-on to the DFT energies; hence, corresponding to DFT-D or DFT+vdW calculations.9−12,17

There are a few general dispersion-inclusive methods; one which was pioneered by Grimme and his co-workers,9−12 is the semiempirical D3 dispersion correction,11 and the more recent D4 correction12 that accounts for three-body interactions. The second type, which was formulated by Tkatchenko et al.,3−8,32−38 involves MBD effects, which in principle account for the contributions of all the atoms/bonds in the molecular ensemble. The third type was developed by Neese et al.,23−25 as part of an ab initio energy decomposition analysis, which evaluates the intermolecular dispersion interactions. As our interest is in the global dispersion energy, we use here the first two types.

Figure 1 displays the 40 dimers which are studied herein, and which involve H---H intermolecular contacts between hydrocarbons and silanes of various forms and shapes, including chains, substituted chains, rings, cages, etc. Note that 25-28 are heterodimers. In addition, some of the dimers (5, 6, 29-34) involve multiple H---H contacts. To broaden the interaction types, we added dimers 35-37, which involve π–π interactions, and noble-gas pairs 38-40. All the structures of the dimers were fully optimized without any constraints and are minima of the corresponding dimers. For most dimers, we have located the minima that possesses H---H contacts, following X-ray structures of similar systems.14 For dimers 1, 5, 6 we have checked that the dimer 6 with three H---H contacts is a global minimum, while 1 and 5 are local minima of methane dimer. Furthermore, we have verified that systems 1, 5, 6, and 29-34 are on the same correlation line regardless of the geometry. This is so, because when the geometry changes, the RCOM-COM changes accordingly.

As shown below, this variegated ensemble lies on a single correlation line, when EDISP is plotted against M1M2/R where R is the distance between the chains; R can be used as the distance across the nearest H---H contacts (RH–H) of the dimers, or preferably the RCOM-COM distance between the centers of mass (COM) of the monomers in the respective dimers in Figure 1.

The COM of each monomer in the corresponding dimer was calculated using fully optimized geometry of the dimer. RCOM-COM was calculated at the equilibrium distance between the monomers. Computational data, which affirm the superiority of this particular “gravitational” relationship, are relegated to the Supporting Information (SI) document.

These 40 dimers are subjected to calculations of the dispersion energies (EDISP) using the MBD (EDISP,MBD)5,6 and D4 (EDISP,D4)12 methods. The respective values are plotted in Figures 2a and 2b correspondingly vs M1M2/RCOM-COM, where RCOM-COM can serve as a general unbiased distance parameter. M1 and M2 are the masses of each monomer in the corresponding dimer. Finally, Figure 3 plots the dispersion energies calculated by the MBD method vs the D4 values.

It is apparent from Figure 3 that the EDISP,MBD and EDISP,D4 values correlate strongly with one another. Furthermore, the absolute magnitudes of the two dispersion quantities are close to within 1.5 kcal/mol (except of dodecahedrane dimer (23) in which the discrepancy is around 3.7 kcal/mol; see Table S2 in the SI). This includes all the dimer varieties 5, 6, and 29-34, which involve multiple H---H contacts. Clearly, MBD and D4 yield equivalent dispersion energies for the systems studied in this work. We remark that for larger molecules and supramolecular systems with more than 100 atoms, the differences between MBD and D4 may amount to more than 10 kcal/mol.36,37

Thus, the dispersion interaction here is moderately long-range, and it includes all the atoms of the monomers, by induction of charges throughout the interacting molecules.

Using the expressions for the straight-lines in Figure 2, we approximate the dispersion interactions at the PBE0-MBD/cc-pVTZ and PBE0-D4/cc-pVTZ levels, by use of eq 1 (M1 and M2 in amu (atomic mass unit), RCOM-COM in Å). This expression correlates well (r2 = 0.974) with the data in Figure 2

3.1. 1

To avoid bias, we also tried to correlate the EDISP data with the sum of the two masses (M1+M2), as well as, with the sum of masses divided by the RCOM-COMdistances. However, the qualities of these correlations are inferior to those which are obtained, respectively, with the product of the masses (M1M2) as well as with the corresponding gravitational relationship (M1M2)/R (see SI for the respective data, Figures S6a-S6c). Furthermore, we also fitted the dispersion energy to M1M2/RnCOM-COM wherein n was freely optimized. We obtained that the best correlation fitting with r2 = 0.97515 is with n = 1.2325, quite close to 1 (and so are the respective r2 values).

3.2. Origins of the Gravitational Relation in eq 1

The gravitational expression ineq 1has a profound message, namely, that molecules/noble-gas atoms, whichever they may be, interact with one another in proportion to their molecular masses. This is so because the dispersion interaction involves charge-switching in the entire ensemble of atoms/bonds in the two molecules. This mass-dependent dispersion-energy expression (eq 1) can also be derived directly from theory. Thus, based on the seminal London dispersion formula between two atoms or molecules, 1 and 2

3.2. 2

where α1and α2 are the static polarizabilities of the interacting moieties, ω is an effective oscillation frequency of the system, and R12 is the distance between the systems. The frequency ω can be written as v/R12, where v is an effective propagation speed of the vdW interaction (v is equal to the speed of light for infinite separation between the moieties). The polarizabilities of molecules, α1,2, are in turn proportional to the volume occupied by the molecules, i.e., eq 3:32

3.2. 3

where Inline graphic is the equilibrium separation distance. Substituting these expressions into the London formula at the equilibrium distance yields

3.2. 4

The appearance of the masses in eq 1 may be rationalized by the term k1k2 (eq 4), which scales with the sizes of the interacting molecules. Hence, one can rationalize the emergence of the gravitational-like potential (eq 1) for the dispersion interaction between two atoms/molecules at equilibrium separation.

3.3. Understanding the Nature of the Dispersion Interactions

To get further insight into this intriguing correlation, we use valence bond (VB) theory, and focus on the breathing orbital VB (BOVB) approach, which includes both static and dynamic electron-correlations. As such, BOVB gives rise to different orbitals for different VB structures, and hence it involves instantaneous adaptation of the state-wave function to the electron density fluctuations inherent in the ensemble of VB structures.39−41 The BOVB method was demonstrated before14 to involve dispersion corrections in hydrocarbons and to offer pictorial physical insight into the origins of these interactions. Therefore, using the VB results, we can rationalize the “gravitational-like relationship”, which we found in the DFT-MBD and DFT-D4 data, which essentially reflect the global interaction of the instantaneous oscillating dipoles that are mediated by the entire ensemble of bonds/atoms within the interacting molecules, and stabilize thereby the dimers.

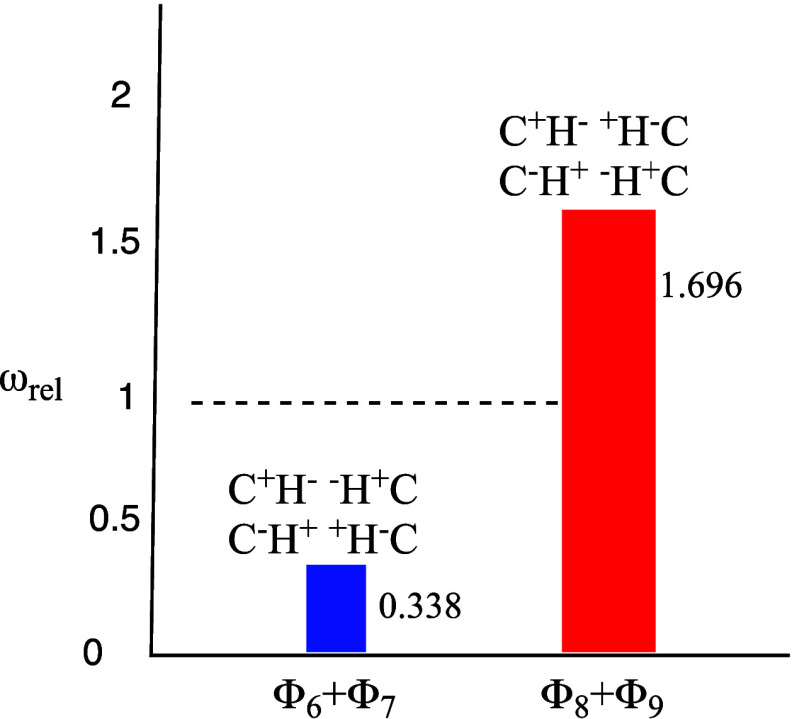
To demonstrate the origins and nature of the dispersion, we plot in Figure 4 the weight changes in the dizwitterionic VB structures in the smallest molecular pair, consisting of two methane molecules H3C–H---H–CH3 (1).14 These VB weights are shown for the equilibrium H---H distance (2.425 Å) vis-à-vis a noninteracting model, wherein the H---H distance is 22 Å.13,14

Figure 4.

Figure 4

Open in a new tab

BOVB computed relative weights, ωrel (with respect to dimer (1) at 22 Å, where ωrel = 1 which corresponds to “non-interacting monomers”), of the dizwitterionic-VB structures in the equilibrium geometry of the methane dimer H3C–H---H–CH3 (1). The relative weights of the repulsive structures, C+H–---–HC+ (Φ6) and C–H+---+HC– (Φ7), are depicted in blue, while those of the corresponding attractive ionic structures, C–H+---–HC+ (Φ8) and C+H–---+H–C (Φ9), are depicted in red. Adapted with permission from ref (14). Copyright 2013 American Chemical Society.

It is apparent that Figure 4 reveals a major change in the contributions of the dizwitterionic structures of the interacting C–H---H–C bonds (vs the noninteracting two bonds at R = 22 Å). Thus, the total weight of the two repulsive multi-ionic structures, C+H–---–HC+ (Φ6) and C–H+---+HC– (Φ7), decreases to ∼34% of its value in the 22 Å - separated methane molecules. By contrast, the weight of the two stabilizing multi-ionic structures, C–H+---–HC+ (Φ8) and C+H–---+H–C (Φ9), increases by ∼170% relative to the value in the 22 Å-separated methane molecules. As such, the major dispersion effect is brought about here, by the resonance of the following two instantaneously oscillating dipoles (C–H+---–HC+) and (C+H–---+H–C) of the interacting-moiety C–H---H–C in the H3C–H---H–CH3 dimer (1). Something that VB theory does not show is charge asymmetry which may be induced by symmetry-breaking due to mixing the two different sets of ionic structures. This is because the Hamiltonian in VB theory does not exhibit symmetry breaking effects for closed-shell species, and hence, it conserves the dizwitterionic symmetry of the H3C–H---H–CH3 complex (1).

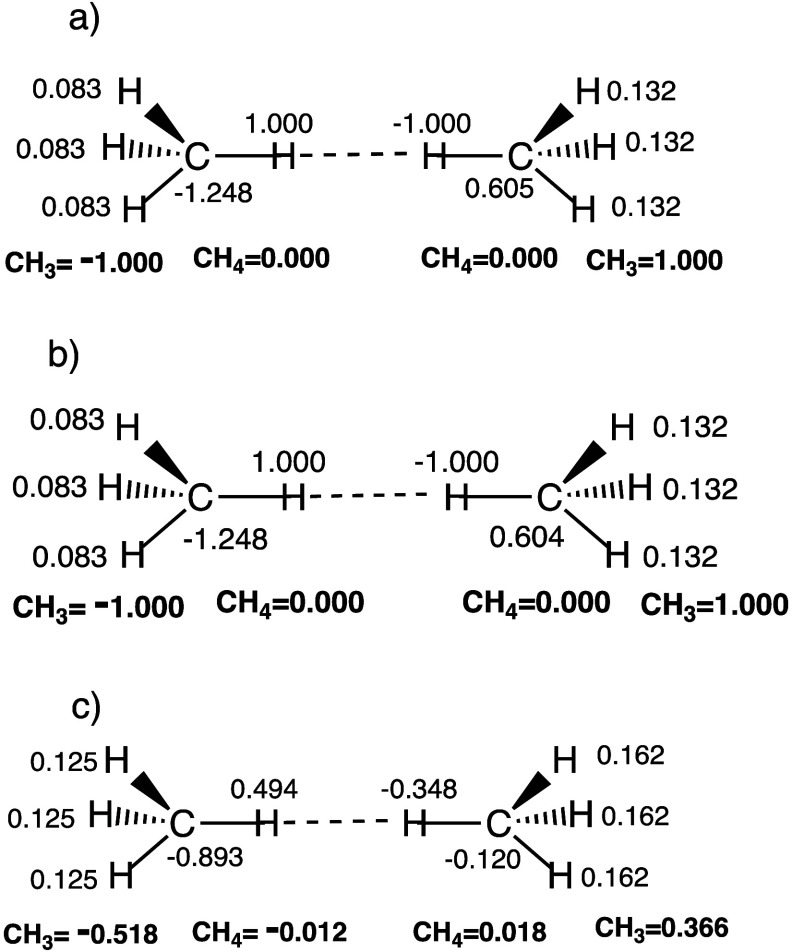
However, Figure 5 shows also charge distributions for the dizwitterionic VB structures calculated at the geometries which were optimized without (a) and with (b) MBD correction. The RH–H distance in the case of optimization without MBD correction is 2.624 Å, vs 2.425 Å in the presence of the MBD correction. Note that the total Mulliken charges on the right and left CH4 molecules are zero, but the charge distributions on the left- and right-hand CH3moieties are significantly different, and the resulting VB structures resemble multipoles. Additionally, Figure 5c shows the Löwdin charges of the same VB structure, calculated at the geometry optimized with MBD correction. It is seen that ionic structure (c) develops a dipole moment. Apparently, the charge-asymmetry of the dizwitterionic structures in (c) reflects the mixing of the instantaneously oscillating structures (C–H+---–HC+) (Φ8) and (C+H–---+H–C) (Φ9), in eq 6:

3.3. 6

This is further witnessed using e.g., tBu–H---H–tBu (13), for which the ionic VB structure in Figure 6, reflects the geometry optimized with MBD correction. The RH–H distance in the tBu–H---H–tBu dimer (13) is 2.125 Å. Thus, the Mulliken charges of the dizwitterionic VB structure in tBu–H---H–tBu, calculated at the geometry optimized with MBD correction, involves delocalization of the charges. As such, the Figure reveals that for each (CH3)3CH molecule, the molecular charges on the C-H---H-C paths of the molecules alternate and are delocalized over the ensemble of atoms in the two molecules. The global charge-delocalization in Figure 6 supports the gravitational-like relationship (eq 1).

Figure 5.

Figure 5

Open in a new tab

(a) Mulliken charges of the dizwitterionic VB structure, C–H+---–HC+ (Φ8) calculated at the VB geometry without MBD optimization. (b) Mulliken charges of the same structure calculated at the geometry optimized with MBD correction. (c) The Löwdin charges of the same VB structure calculated at the geometry optimized with MBD correction. All charges correspond to the dimer (1).

Figure 6.

Figure 6

Open in a new tab

Charges on the VB structure (H3C)3C– H+---–H +C(CH3)3 (Φ8) calculated at the geometry optimized with MBD correction. Part (a) shows Löwdin charges, and part (b) Mulliken charges. All charges correspond to the dimer (13).

Further, in addition to the emergence of oscillating dipoles in the VB wave function (Figure 6) for tBu-H---H-tBu (13), there are smaller contributions of other VB structures, which involve electronic effects due to charge transfer and bond recoupling.14 Overall, these effects reduce the Pauli repulsion between the pair of molecules and tighten their bonding. As the original work argues,14 the VB mixing of the ionic structures into the covalent structures of the hydrocarbons is larger for the dimer tBu-H---H-tBu (13), since the ionization potential of the (CH3)3C• radical is much lower than for e.g., H3C•. Thus, the stabilizing ionic structures for the tBu-H---H-tBu dimer, are closer in energy to the respective covalent structures, and hence the mutual VB mixing stabilizes the dimer.14 Indeed, while the H---H distance in the methane dimer is 2.425 Å, in the corresponding (CH3)3C–H---H-C(CH3)3 dimer (13) the distance drops to 2.125 Å (see ref (14)).

Finally, application of MBD (or D4) to the noble gas-dimers, causes rehybridization which deforms the spherical symmetry of the electron densities in the atoms. As such, for example in Ne----Ne, the dispersion interaction between the atoms is due to the 2p-3s hybridization, which creates local oscillating dipoles in the two atoms. Similarly, in Ar---Ar, 3s-3dz2-4p hybridization is possible, which will distort the spherical shape of the atomic electron density and induce dipole moments. This charge-density distortion brings about dispersion interactions, which are augmented by the resonance energy stabilization between the two induced dipolar wave function, as shown in Scheme 1.

Scheme 1. A Schematic Representation of the Resonance between the Density-Deformed Noble-Gas Atoms in the Dimer.

Scheme 1

Open in a new tab

The relative charges signify formation of dipoles.

In summary, all the above effects in pairs of molecules and in noble-gas dimers, create primarily oscillating dipoles in the two interacting molecules/atoms, which involve all the bonds, and which affect the ionic–covalent mixing energy (in the molecules). Similarly, the original MBD formulation which calculates the dispersion as a sum of fluctuating atomic-dipoles on all the atoms in the ensemble,5,12,32−35 may actually enjoy also additional covalent-ionic stabilization of the state’s wave function. Thus, while we cannot extend the VB calculations to molecules larger than the ones which we considered, the physical mechanism is extendable to the larger species in this study.

The highest dispersion energy contribution in the set of dimers in Figure 1 was found for the dodecahedrane dimer (23), ca. 77/81 kcal/mol (MBD/D4). The respective intermolecular portion of the CH---HC dispersion interaction, (which was calculated as a difference between the dispersion energy of dimer and sum of dispersion energies of the corresponding monomers), in the dodecahedrane pair is rather small (though larger than in (CH4)2, 1), and most of the dispersion interaction energy (EDISP) originates in the large dispersion energies which are induced within the monomer parts (see SI, Table S6). As we already demonstrated, our results show that the entire EDISPdata correlates best with the gravitational relationship (eq 1). In contrast, significantly poorer correlations were obtained with the sum of masses of the monomers in corresponding dimers, or with the summed-masses divided by the respective distances between the centers of masses.

Indeed, comparing the results for H3CH---HCH3 (1) vs (CH3)3CH---HC(CH3)3 (13) shows that the charge fluctuation in the larger dimer is delocalized to the entire ensemble of bonds/atoms of the interacting molecules. Furthermore, the effects of multiple H---H bridges between the chains appear to augment the atomic charges and transmit the charges to the entire molecules in the respective pairs (29–34 in Figure 1). As such, the increased molecular size enhances the stabilization energy due to increased dispersion interactions.

Thus, the dispersion interaction involves the entire ensemble of atoms/bonds in the interacting molecules, and is the root cause of the gravitational relationship of EDISP vs M1M2/RCOM-COM in Figures 2. Furthermore, the very large EDISP for the dodecahedrane pair immediately suggests that dodecahedrane will form a stable solid state, which enjoys enhanced dispersion interactions for each dodecahedrane molecule with its close neighbor molecules in the solid state. This is indeed the case for dodecahedron, and the conclusion can be generalized to other cases which involve massive molecules having high dispersion energies.13,14 Finally, using RCOM-COM in eq 1 is preferrable (to RCH-HC) since it carries information on the extent of the contact of the monomer surfaces, which depends on the anisotropy of the monomers and topology of the interaction.42

Concluding Remarks

The MBD dispersion interaction between homodimers and heterodimers of alkanes and silanes (including fluorinated derivatives, rings, noble atom-dimers, π–π interacting-dimers, 3D-objects and -cages) obey the gravitational-like law in eq 1. This expression emerges from the contribution of dispersion interactions by all the bonds/atoms in the molecules we studied. The Grimme-D4 correction produces similar dispersion interaction-energies, and a similar gravitational-like correlation for the same set of molecules (Figures 1, 3).

This correlation accounts for the fact, and the findings in this study, that larger molecules have generally larger dispersion stabilization. Thus, as the molecules grow in size the molecular masses grow, and so do the many-bonds/atom dispersion interactions in eq 1.

The straightforward statement of eq 1 is in agreement with the growth of EDISP with the increased molecular sizes, noted in the present study and elsewhere.13,14,16−25,33 Indeed, dispersion is a force of nature, which drives the aggregation of molecules to large entities and condensed phases.

Does eq 1 extend all the way to macroscopic bodies? This question has major implications which deserve further exploration.

Acknowledgments

The authors are thankful to Drs. Jorge Echeverría and Gabriel Aullón for providing us the starting structure of dimers 29–34. S.S. is thankful to Prof. P. R. Schreiner for bringing ref (17) to his attention.

Glossary

Abbreviations

MBD

many-body dispersion

D4

dispersion method (due to S. Grimme)

DFT

density functional theory

VB

valence bond,

BOVB

breathing orbital valence bond

vdW

van der Waals

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.4c11211.

  • Different computational data calculated by means of the PBE0-MBD and PBE0-D4 methods, where the interactions depend on distances between the COMs of the monomers in the corresponding dimers; dispersion energies, masses of monomers, and Mulliken and Löwdin atomic charges; Chirgwin-Coulson weights of dizwitterionic VB structures calculated with the VBSCF and BOVB methods; dependencies of dispersion energies on M1M2/R2H-H, M1M2/R2COM-COM, M1M2/RH–H; Cartesian coordinates of dimers (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

This work (by S. Alvarez) was supported by the Spanish Structures of Excellence Maria de Maeztu program (grant CEX2021-001202-M) and the Generalitat de Catalunya – AGAUR (20121-SGR-00286).

The authors declare no competing financial interest.

Supplementary Material

ja4c11211_si_001.pdf (885.1KB, pdf)

References

  1. Arunan E.; Desiraju G. R.; Klein R. A.; Sadlej J.; Scheiner S.; Alkorta I.; Clary D. C.; Crabtree R. H.; Dannenberg J. J.; Hobza P.; Kjaergaard H. G.; Legon A. C.; Mennucci B.; Nesbitt D. J. Definition of the Hydrogen Bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. 10.1351/PAC-REC-10-01-02. [DOI] [Google Scholar]
  2. Shaik S.; Danovich D.; Zare R. N. Valence Bond Theory Allows a Generalized Decription oh Hydrogen Bonding. J. Am. Chem. Soc. 2023, 145, 20132–20140. 10.1021/jacs.3c08196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Tkatchenko A.; DiStasio Jr. R. A.; Car R.; Scheffler M. Accurate and Efficient Method for Many-Body van der Waals Interactions. Phys. Rev. Lett. 2012, 108, 236402. 10.1103/PhysRevLett.108.236402. [DOI] [PubMed] [Google Scholar]
  4. Ambrosetti A.; Reilly A. M.; DiStasio R. A. Jr.; Tkatchenko A. Long-range correlation energy calculated from coupled atomic response functions. J. Chem. Phys. 2014, 140, 18A508. 10.1063/1.4865104. [DOI] [PubMed] [Google Scholar]
  5. Ambrosetti A.; Ferri N.; DiStasio Jr. R.A; Tkatchenko A. Wavelike Charge Density Fluctuation and van der Waals Interactions at the Nanoscale. Science 2016, 351, 1171–1176. 10.1126/science.aae0509. [DOI] [PubMed] [Google Scholar]
  6. Hermann J.; Stohr M.; Goger S.; Chaudhuri S.; Aradi B.; Maurer R. J.; Tkatchenko A. Lib MBD: A General-Purpose Package for Scalable Quantum Many-Body Dispersion Calculations. J. Chem. Phys. 2023, 159, 174802. 10.1063/5.0170972. [DOI] [PubMed] [Google Scholar]
  7. Liu X.; Hermann J.; Tkatchenko A. Many-Body Stabilization of Non-Covalent Interactions: Structure, Stability, and Mechanisms of Ag3Co(CN)6 Framework. J. Chem. Phys. 2016, 145, 24101. 10.1063/1.4972810. [DOI] [PubMed] [Google Scholar]
  8. Charry J.; Tkatchenko A. Van der Waals Radii of Free and Bonded Atoms from Hydrogen (Z = 1) to Organesson (Z = 118). J. Chem. Theory Comput. 2024, 20, 7469–7478. 10.1021/acs.jctc.4c00784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bursch M.; Grimme S.; Hansen A. Influence of Steric and Dispersion Interactions on Thermochemistry of Crowded (fluoro)alkyl Compounds. Acc. Chem. Res. 2024, 57, 153–163. 10.1021/acs.accounts.3c00634. [DOI] [PubMed] [Google Scholar]
  10. Grimme S.; Hansen A.; Brandenburg J. G.; Bannwarth C. Dispersion-Corrected Mean-Field Electronic Structure Method. Chem. Rev. 2016, 116, 5105–5154. 10.1021/acs.chemrev.5b00533. [DOI] [PubMed] [Google Scholar]
  11. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  12. Caldeweyher E.; Mewes J.-M.; Ehlert S.; Grimme S. Extension and Evaluation of the D4 London-Dispersion Model for Periodic Systems. Phys. Chem. Chem. Phys. 2020, 22, 8499–8512. 10.1039/D0CP00502A. [DOI] [PubMed] [Google Scholar]
  13. Echeverria J.; Aullon G.; Danovich D.; Shaik S.; Alvarez S. Dihydrogen Contacts in Alkanes are Subtle But not Faint. Nature Chem. 2011, 3, 323–330. 10.1038/nchem.1004. [DOI] [PubMed] [Google Scholar]
  14. Danovich D.; Shaik S.; Neese F.; Echeverria J.; Aullon G.; Alvarez S. Understanding the Nature of the CH···HC Interactions in Alkanes. J. Chem. Theory Comput. 2013, 9, 1977–2013. 10.1021/ct400070j. [DOI] [PubMed] [Google Scholar]
  15. Shaik S.; Alvarez S. Reply to ‘Entropic Factors Also Contribute to the High Melting of Polyhedral Alkanes. Nature Chem. 2015, 7, 89–90. 10.1038/nchem.2147. [DOI] [PubMed] [Google Scholar]
  16. Rösel S.; Balestrieri C.; Schreiner P. R. Sizing the Role of London Dispersion in the Dissociation of All-Meta Tert-Butyl Hexaphenylethane. Chem. Sci. 2017, 8, 405–410. 10.1039/C6SC02727J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Rummel L.; Schreiner P. R. Advances and Prospects in Understanding London Dispersion Interaction in Molecular Chemistry. Angew. Chem., Int. Ed. 2024, 63 (1–23), e202316364 10.1002/anie.202316364. [DOI] [PubMed] [Google Scholar]
  18. Grimme S.; Schreiner P. R. Steric Crowding Can Stabilize a Labile Molecule: Solving the Hexaphenylethane Riddle. Angew. Chem., Int. Ed. 2011, 50, 12639–12642. 10.1002/anie.201103615. [DOI] [PubMed] [Google Scholar]
  19. Rösel S.; Schreiner P. R. Computational Chemistry as a Conceptual Game Changer: Understanding the Role of London Dispersion in Hexaphenylethane Derivatives (Gomberg Systems). Isr. J. Chem. 2022, 62 (1–17), e20200002 10.1002/ijch.202200002. [DOI] [Google Scholar]
  20. Fokin A. A.; Gerbig D.; Schreiner P. R. σ/σ- and π/π-Interactions are Equally Important: Multilayered Graphanes. J. Am. Chem. Soc. 2011, 133, 20036–20039. 10.1021/ja206992j. [DOI] [PubMed] [Google Scholar]
  21. Wang C.; Mo Y.; Wagner J. P.; Schreiner P. R.; Jemmis E. D.; Danovich D.; Shaik S. The Self-Association of Graphane is Driven by London Dispersion and Enhanced by Orbital Interactions. J. Chem. Theory Comput. 2015, 11, 1621–1630. 10.1021/acs.jctc.5b00075. [DOI] [PubMed] [Google Scholar]
  22. Pollice R.; Bot M.; Kobylianskii I. J.; Shenderovich I. G.; Chen P. Attenuation of London Dispersion in Dichloromethane Solutions. J. Am. Chem. Soc. 2017, 139, 13126–13140. 10.1021/jacs.7b06997. [DOI] [PubMed] [Google Scholar]
  23. Bistoni G.; Altun A.; Wang Z.; Neese F. Local Energy Decomposition Analysis of London Dispersion Effects: From Simple Model Dimers to Complex Bimolecular Assemblies. Acc. Chem. Res. 2024, 57, 1411–1420. 10.1021/acs.accounts.4c00085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Altun A.; Neese F.; Bistoni G. Open-Shell Variant of the London Dispersion-Corrected Hartree-Fock Method (HFLD) for Quantification and Analysis of Noncovalent Interaction Energies. J. Chem. Theory Comput. 2022, 18, 2292–2307. 10.1021/acs.jctc.1c01295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Altun A.; Neese F.; Bistoni G. HFLD: A Nonempirical London Dispersion-Corrected Hartree-Fock Interaction Energies of Large Molecular Systems. J. Chem. Theory Comput. 2019, 15, 5894–5907. 10.1021/acs.jctc.9b00425. [DOI] [PubMed] [Google Scholar]
  26. Adamo C.; Cossi M.; Barone V. An Accurate Density Functional Method for the Study of Magnetic Properties: the PBE0Model. J. Mol. Struct. Theochem 1999, 493, 145–147. 10.1016/S0166-1280(99)00235-3. [DOI] [Google Scholar]
  27. Dunning T. H. Jr Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  28. Woon D. E.; Dunning T. H. Jr Gaussian-Basis Sets for Use in Correlated Molecular Calculations. III. The Atoms Aluminum Through Argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  29. Epifanovsky E.; Gilbert A. T. B.; Feng X.; Lee J.; Mao Y.; Mardirossian N.; Pokhilko P.; White A. F.; Coons M. P.; Dempwolff A. L.; et al. Software for the Frontiers of Quantum Chemistry: An Overview of Developments in the Q-Chem 5 Package. J. Chem. Phys. 2021, 155, 084801. 10.1063/5.0055522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Richardson T.; de Gala S.; Crabtree R. H.; Siegbahn P. E. M. Unconventional Hydrogen Bonds: Intermolecular B-H···H-N Interactions. J. Am. Chem. Soc. 1995, 117, 12875–12876. 10.1021/ja00156a032. [DOI] [Google Scholar]
  31. Zhao Y.; Truhlar D. G. Density Functional Theory for Reaction Energies: Test of Meta and Hybrid Meta Functionals, Range-Separated Functionals, and Other High-Performance Functionals. J. Chem. Theory Comput. 2011, 7, 669–676. 10.1021/ct1006604. [DOI] [Google Scholar]
  32. Tkatchenko A.; Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
  33. Kronik L.; Tkatchenko A. Understanding Molecular Crystals with Dispersion-Inclusive Density Functional Theory: Pairwise Corrections and Beyond. Acc. Chem. Res. 2014, 47, 3208–3216. 10.1021/ar500144s. [DOI] [PubMed] [Google Scholar]
  34. Hermann J.; DiStasio Jr. R. A.; Tkatchenko A. First-Principles Models for van der Waals Interactions in Molecules and Materials: Concepts, Theory, and Applications. Chem. Rev. 2017, 117, 4714–4758. 10.1021/acs.chemrev.6b00446. [DOI] [PubMed] [Google Scholar]
  35. Marom N.; Tkatchenko A.; Rossi M.; Gobre V. V.; Hod O.; Scheffler M.; Kronik L. Dispersion Interactions with Density-Functional Theory: Benchmarking Semiempirical and Interatomic Pairwise Corrected Density Functionals. J. Chem. Theory Comput. 2011, 7, 3944–3951. 10.1021/ct2005616. [DOI] [PubMed] [Google Scholar]
  36. Groslambert L.; Cornaton Y.; Ditte M.; Aubert E.; Pale P.; Tkatchenko A.; Djukic J.-P.; Mamane V. Affinity of Telluronium Chalcogen Bond Donors for Lewis Bases in Solution: A Critical Experimental-Theoretical Joint Study. Chem.—Eur. J. 2024, 30, e202302933 10.1002/chem.202302933. [DOI] [PubMed] [Google Scholar]
  37. Al-Hamdani Y. S.; Nagy P. R.; Zen A.; Barton D.; Kállay M.; Brandenburg J. G.; Tkatchenko A. Interactions between large molecules pose a puzzle for reference quantum mechanical methods. Nature Comm. 2021, 12, 3927. 10.1038/s41467-021-24119-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tkatchenko A.; Ambrosetti A.; DiStasio R. A. Jr. Interatomic methods for the dispersion energy derived from the adiabatic connection fluctuation-dissipation theorem. J. Chem. Phys. 2013, 138, 074106. 10.1063/1.4789814. [DOI] [PubMed] [Google Scholar]
  39. Hiberty P. C.; Humbel S.; Byrman C. P.; van Lenthe J. H. Compact Valence Bond Functions with Breathing Orbitals: Application to the Bond Dissociation Energies of F2 and HF. J. Chem. Phys. 1994, 101, 5969–5976. 10.1063/1.468459. [DOI] [Google Scholar]
  40. Hiberty P. C.; Humbel S.; Archirel P. Nature of the Differential Electron Correlation in Three-Electron Bond Dissociation. Efficiency of a Simple Two-Configuration Valence Bond Method with Breathing Orbitals. J. Phys. Chem. 1994, 98, 11697–11704. 10.1021/j100096a012. [DOI] [Google Scholar]
  41. Wu W.; Su P.; Shaik S.; Hiberty P. C. Classical Valence Bond Approach by Modern Methods. Chem. Rev. 2011, 111, 7557–7593. 10.1021/cr100228r. [DOI] [PubMed] [Google Scholar]
  42. Echeverria J.; Alvarez S. The Borderless Word of Chemical Bonding Across the Van der Waals Crust and the Valence Region. Chem. Sci. 2023, 14, 11647–11688. 10.1039/D3SC02238B. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja4c11211_si_001.pdf (885.1KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES