Cell response to extracellular matrix viscous energy dissipation outweighs high-rigidity sensing

Abstract

The mechanics of the extracellular matrix (ECM) determine cell activity and fate through mechanoresponsive proteins including Yes-associated protein 1 (YAP). Rigidity and viscous relaxation have emerged as the main mechanical properties of the ECM steering cell behavior. However, how cells integrate coexisting ECM rigidity and viscosity cues remains poorly understood, particularly in the high-stiffness regime. Here, we have exploited engineered stiff viscoelastic protein hydrogels to show that, contrary to current models of cell-ECM interaction, substrate viscous energy dissipation attenuates mechanosensing even when cells are exposed to higher effective rigidity. This unexpected behavior is however readily captured by a pull-and-hold model of molecular clutch–based cell mechanosensing, which also recapitulates opposite cellular response at low rigidities. Consistent with predictions of the pull-and-hold model, we find that myosin inhibition can boost mechanosensing on cells cultured on dissipative matrices. Together, our work provides general mechanistic understanding on how cells respond to the viscoelastic properties of the ECM.

Viscosity blunts cell response to stiff matrices in agreement with a pull-and-hold model of molecular clutch-based mechanosensing.

INTRODUCTION

The extracellular matrix (ECM) is a proteoglycan-based hydrogel supporting cells in biological tissues. Structural and biochemical signals from the ECM are essential for cell homeostasis, adhesion, migration, proliferation, and differentiation (1). However, it is now well-established that the mechanical properties of the ECM also affect the activity and fate of cells to a large extent (2, 3). A prime example is stiffness (2, 4), which, when dysregulated, is a causative factor of pathological aging (5) and diseases such as fibrosis and cancer (6, 7). Stiffness is a potent driver of mechanosensing in cells able to reinforce adhesion, for instance, by inducing nuclear translocation of the transcriptional coactivator Yes-associated protein 1 (YAP), a major proxy of their mechanobiological state (8–10).

In recent years, energy dissipation causing time-dependent relaxation of substrates under strain has been observed to influence cell behavior too (11, 12). Since the ECM is not an elastic but a viscoelastic material showing remarkable viscous energy dissipation (12), there is a fundamental interest in understanding the mechanisms by which the viscoelastic properties of the ECM are sensed by cells, including the interplay between stiffness and viscosity. Intuitively, viscosity could just make the ECM to be sensed as effectively softer, therefore countering the effect of rigidity and blunting mechanosensing in agreement with some experimental results (13, 14). However, conflicting evidence indicates that viscous stiffness can foster cell mechanosensing (11, 13, 15). Several factors may contribute to these contradicting results. For example, strategies to modulate viscoelasticity of the ECM may affect nonmechanical features that also influence cell behavior, including pore size and mesh concentration (4, 16). Similarly, plastic substrate deformation could confound results (12, 17). In this context, computational models of cell mechanosensing offer an opportunity to conceptualize molecular premises in the absence of confounding factors. Models based on the so-called molecular clutch can explain cell mechanosensing on purely elastic ECM by considering how the actomyosin cytoskeleton engages with integrins to probe substrate mechanics (4, 18). According to these models, myosin contractility propels actin retrograde flow from the cell membrane toward the nucleus, pulling on integrin-ECM bonds (the clutches) and straining the matrix. At high stiffness, the clutches experience high forces that result in the mechanical unfolding of the adaptor protein talin. Talin unfolding enables recruitment of additional proteins such as vinculin that reinforce adhesion, reducing actin retrograde flow and leading to YAP translocation to the nucleus (10, 19).

The current view emerging from molecular clutch models poses that the additional stiffness stemming from ECM viscosity can promote mechanosensing in the low-stiffness regime at the right dissipation and clutch formation timescales (13, 20, 21). These models also predict that viscous energy dissipation should play a marginal role, if any, in high-stiffness (>10 kPa) matrices where cell mechanosensing is saturated by the high rigidity. However, this prediction appears to be not compatible with limited, but contradicting, experimental data, suggesting that viscous energy dissipation can induce both increased or blunted mechanosensing in cells grown on stiff matrices (11, 14, 15). Whether these seemingly opposed behaviors are due to viscous energy dissipation, as well as the underlying molecular mechanisms, remain open questions.

To define how substrate viscous energy dissipation affects cell mechanosensing in the high-stiffness regime, here, we have engineered protein hydrogels whose viscoelasticity we tuned in the absence of noticeable nonmechanical side effects. Culturing epithelial and mesenchymal stem cells on these hydrogels, we demonstrate that substrate viscous energy dissipation leads to blunted mechanosensing even when cells grow on effectively stiffer matrices, a result that is not in agreement with conventional molecular clutch–based models of cell mechanosensing. By including a dual substrate-probing scheme, we however show that the molecular clutch model can readily capture the experimental behaviors of cells on energy-dissipating matrices.

RESULTS

Protein mechanics sets viscoelasticity of protein matrices

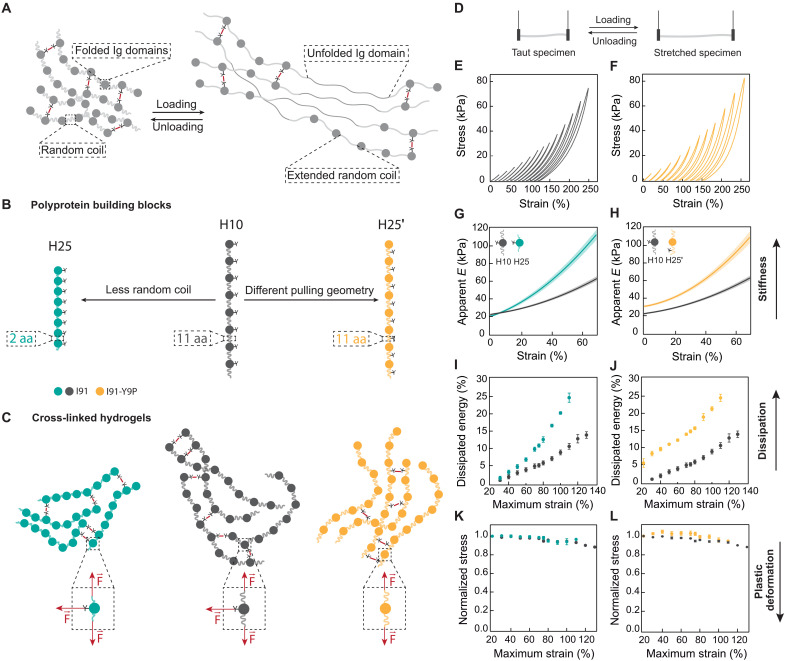
We first set out to design ECM mimetics based on recombinant protein hydrogels enabling specific modulation of viscous energy dissipation in the high-stiffness regime. In a strained protein hydrogel, mechanical forces are directly transmitted to its protein building blocks (22, 23). When under force, random coil polypeptide regions easily adapt their extension in an elastic manner, while folded domains undergo reversible unfolding and extension transitions that provide energy dissipation (Fig. 1A) (24). Hence, proteins containing a high proportion of random coil are soft and nondissipative, whereas those rich in folded domains are stiffer and dissipate more energy. On the basis of these protein mechanic principles, we introduced subtle sequence modifications into polyprotein building blocks containing eight repetitions of the I91 domain of titin separated by several amino acids in random coil structure (Fig. 1B). Key to our strategy, I91 domains have a single Tyr residue (Tyr⁹), which can be used to chemically cross-link soluble I91 polyproteins into hydrogel matrices (25). Starting from the reference building block H10, we produced H25 and H25′ counterparts by, respectively, reducing the fraction of random coil structure or placing the cross-linking tyrosine in the random coil region to alter the nanoscopic pulling geometry in the resulting hydrogel (Fig. 1, B and C; fig. S1; notes S1 to S3) (26, 27). We named the protein building blocks according to the energy the corresponding hydrogels dissipate when stretched to a ~110% final strain (see below). Circular dichroism (CD) and differential scanning fluorimetry showed that the overall β-rich structure and thermal stability of the I91 domain in the three building blocks are not affected by the length of the linkers, while the mutation Y9P required to produce H25′ leads to lower thermal stability in agreement with previous observations (figs. S2 and S3) (28).

Fig. 1. Bottom-up engineering of protein hydrogels with different viscoelastic properties.

(A) Representation of a protein hydrogel covalently cross-linked through tyrosine residues. Building blocks include immunoglobulin (Ig)–like domains and random coil regions. Under uniaxial traction, random coil regions extend elastically, and Ig domains unfold, dissipating energy. (B) Schematics of the polyprotein building blocks used in this study. The I91 Ig domain of titin was engineered into octameric repeats separated by 11 amino acid (aa)–long random coil linkers (H10, dark gray). Two more constructs were designed starting from H10. First, H25 (teal) was produced by shortening the linkers between Ig domains to only two amino acids. To build H25′ (mustard), tyrosines were mutated out from Ig domains and included as one of the 11 amino acids in the random coil linkers. (C) Schematic representation of the network structure of I91 matrices. Cross-linking takes place at tyrosine positions, leading to different mechanical force distributions (dashed insets). (D) Loading and unloading stress-strain tests used to determine apparent elastic moduli, dissipated energy, and plasticity of hydrogels. (E and F) Stress-strain curves of H10 (E) and H25′ (F) hydrogels pulled at 5 mm/s. For clarity, stress-strain curves are offset in the x axis. Actual stress-strain curves can be found in fig. S5. Curves were measured immediately one after another from low to high strains. (G and H) Strain dependency of apparent elastic moduli obtained in stress-strain experiments to 75% maximum strain. Lines represent average values, and shaded areas are SEM. (I and J) Dissipated energy is measured in stress-strain experiments to different maximum strains. (K and L) Normalized stress at 15% strain for consecutive stress-strain curves to different maximum strains. Data are obtained from four specimens of H10 and H25 and six specimens of H25′ produced in independent cross-linking reactions from two purification batches.

We cast H10, H25, and H25′ hydrogels to ~13-mm-long and 0.506-mm-diameter cylinders using the same protein concentration and cross-linking conditions. We characterized the mechanical properties of the resulting hydrogels using uniaxial traction stress-strain tests (Fig. 1D), which show hysteresis between loading and unloading cycles that are typical of viscoelastic materials as well as noticeable strain stiffening (Fig. 1, E and F) (12). Considering the challenges of modeling this mechanical behavior (29), for simplicity, we analyzed results in a model-free manner. We found that the apparent elastic modulus (E) at zero strain is ~20 kPa for H10 and H25 hydrogels and ~30 kPa for H25′ counterparts (Fig. 1, G and H). In agreement with the presence of shorter linkers, H25 hydrogels undergo more evident strain stiffening than H10 and H25′ specimens (Fig. 1G). To extract information about viscosity of the hydrogels, we determined how much energy is dissipated during loading and unloading stress-strain cycles. As expected from the higher contribution of unfolding transitions in H25 hydrogels, we found that H25 materials are more dissipative than H10 counterparts, especially at medium and large strains (Fig. 1I). H25′ hydrogels also dissipate more energy than H10 counterparts (Fig. 1J). We obtained similar conclusions from indentation experiments using atomic force microscopy (AFM) (fig. S4). Notably, subsequent loading stress-strain curves overlap to a great extent (fig. S5). The stress reached at 15% strain for every curve is always >90% of the initial value (Fig. 1, K and L), suggesting that plastic deformation for the three materials is marginal even at recovery times shorter than 5 s. In addition, we verified that the relative stiffness and energy dissipation of the three hydrogels are preserved when tensile testing is done at pulling rates varying over five orders of magnitude, supporting that H25 and H25′ are also stiffer and more dissipative than their H10 counterparts at any loading speed that may be imposed by cells when used as ECM mimetics (fig. S6). Mechanical modulation in I91 hydrogels is achieved in the absence of noticeable changes in chemical composition (figs. S1A and S7A), ultrastructure (fig. S7B), and protein stability (fig. S3). We also examined cross-linking density in the hydrogels using acid hydrolysis followed by amino acid analysis (fig. S7, C to F). As it can be expected from identical cross-linking reaction conditions, tyrosines disappear to the same extent in the three hydrogels (fig. S7, D and E), although we detected less dityrosine products in H25′ hydrolyzates (fig. S7F), raising the possibility that cross-linking in H25′ matrices could be somehow hindered.

In summary, the three engineered protein hydrogels have rigidities in the desired high-stiffness range and show negligible plastic deformation. H25 and H25′ materials are stiffer and more dissipative than H10 counterparts. These distinct mechanical properties occur alongside mostly preserved structural and chemical properties. Given these positive results, we proceeded to compare mechanosensing in cells cultured on the three matrices.

Substrate viscous energy dissipation blunts cell mechanosensing

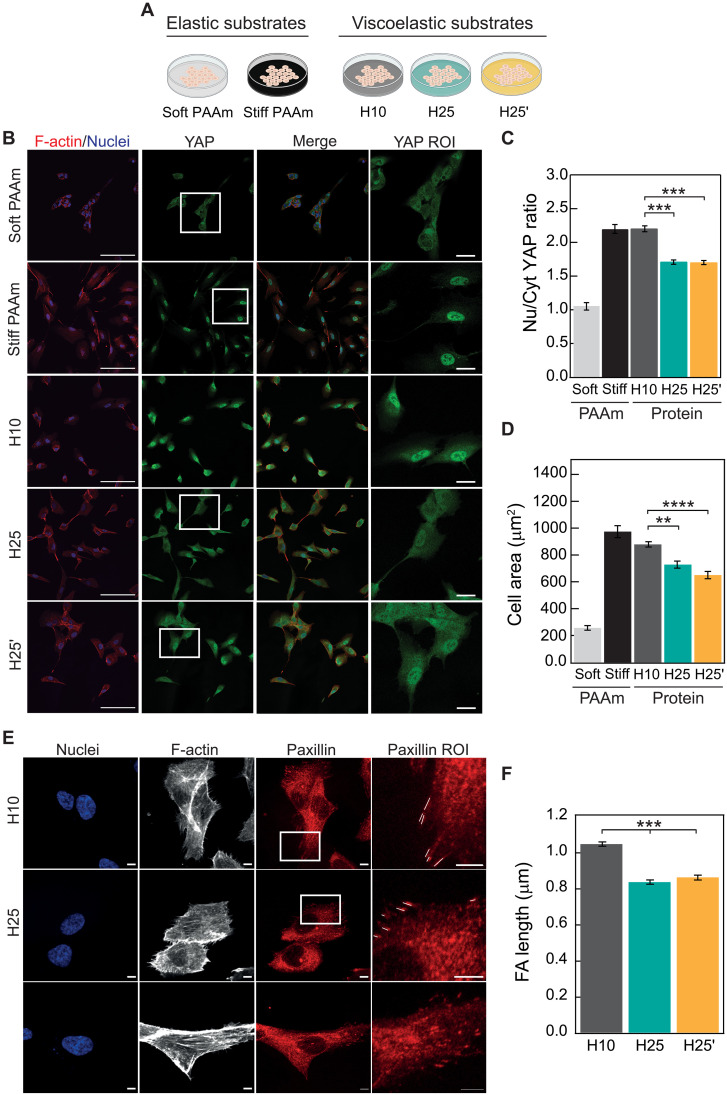
We first checked that immortalized human retinal pigment epithelial-1 (RPE-1) cells grown on H10, H25, and H25′ matrices show normal attachment and global metabolic activity (fig. S8). When RPE-1 cells are cultured on purely elastic, non-energy–dissipating polyacrylamide (PAAm) hydrogels (Fig. 2A), we observe the expected nuclear localization of YAP on stiff (~20 kPa), but not on soft (~2.8 kPa), substrates (Fig. 2, B and C) (8). YAP nuclear localization on stiff PAAm correlates with increased cell spreading (Fig. 2D) and expression of YAP target genes ANKRD1 and CTGF (fig. S9) (30). Unexpectedly, among the three protein hydrogels, the most intense nuclear YAP staining occurs in cells cultured on H10, not only the softest but also the least dissipative of them (Fig. 2, B and C). This higher nuclear localization of YAP is accompanied by more cell spreading (Fig. 2D) and higher expression levels of YAP target genes, especially when compared to H25 matrices (fig. S9), and correlates with formation of larger peripheral focal adhesions (Fig. 2, E and F), a situation also observed in elastic hydrogels (10). Using AFM indentation measurements, we confirmed that H25 matrices remain stiffer and more dissipative than H10 counterparts after cell culture (fig. S10). Supporting the generality of our observations, we obtained similar patterns of YAP activation and cell spreading in human mesenchymal stem cells (fig. S11), when RPE-1 cells are cultured on arginine-glycine-aspartic acid (RGD) peptide–coated protein hydrogels containing the minimal binding motif of fibronectin (fig. S12, A and B) (31), and when the RGD peptide is included in the sequence of protein building blocks to avoid the need for coating (H10-RGD and H25′-RGD materials; notes S4 and S5 and fig. S12, C to G).

Fig. 2. Blunted mechanosensing in cells grown on rigid viscoelastic substrates.

(A) Outline of experimental conditions. (B) Confocal immunofluorescence images of YAP localization in RPE-1 cells grown on elastic stiff or soft PAAm or on H10, H25, or H25′ protein matrices. F-actin was stained with Alexa Fluor 647-conjugated phalloidin (red; first column), and nuclei were stained with 4′,6-diamidino-2-phenylindole (DAPI; blue in merged images; first and third columns). YAP was labeled with Alexa-Fluor-488-conjugated antibody in green (second column). The fourth column shows zoomed views of the YAP region of interest (ROI) (boxed in white in the YAP column). Scale bars, 100 μm (first to third columns) and 20 μm (fourth column). (C) Quantification of nuclear versus cytoplasmic YAP distribution. (D) Cell spreading quantified as cell area. A minimum of n = 30 cells per condition were quantified in a total of four independent experiments. (E) Confocal immunofluorescence images of focal adhesions in RPE-1 cells grown on H10, H25, or H25′ matrices. Nuclei were stained with DAPI (first column), and F-actin was stained with Alexa-Fluor-647-conjugated phalloidin (second column). Paxillin in focal adhesions was labeled with Alexa-Fluor-568-conjugated antibody in red (third column). The fourth column shows zoomed views of the paxillin ROI (boxed in white in the paxillin column; focal adhesions are marked with white lines). Scale bars, 5 μm. (F) Focal adhesion (FA) length quantification. A minimum of n = 30 cells per condition were quantified in a total of three independent experiments. PAAm groups are not considered for statistical analysis in (C) and (D). Data are presented as mean ± SEM, ordinary one-way analysis of variance (ANOVA); **P < 0.01, ***P < 0.001, and ****P < 0.0001.

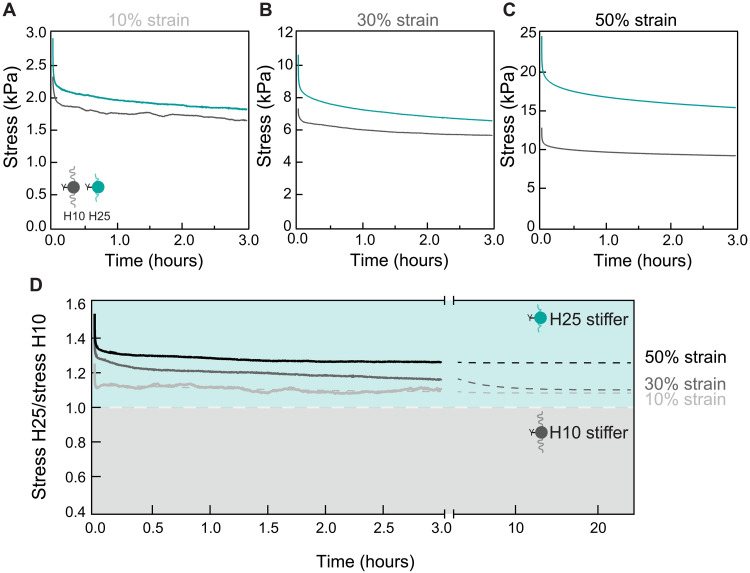
Our data showing lower YAP nuclear translocation in cells cultured on H25 and H25′ matrices suggest that ECM viscous energy dissipation blunts cell mechanosensing driven by high-stiffness matrices. Since energy dissipation leads to reduced effective stiffness, rigidity sensing mechanisms may suffice to explain our results if the actual stress sensed by cells was the highest in H10 matrices. To test this possibility, we stretched H10 and H25 hydrogels to strains between 10 and 50%, which is the range of matrix deformation typically induced by cells (32), and monitored the resulting stress for 3 hours. Results show that H25 hydrogels generate higher stress than H10 counterparts at all times and deformations despite being more dissipative (Fig. 3, A to C). Although the ratio between the stress generated by H25 and H10 hydrogels decreases with straining time as expected, H25 hydrogels are predicted to remain stiffer even after 24 hours under strain (Fig. 3D). In the context of high substrate rigidity, failure of RPE-1 cells to reinforce adhesion could explain why the stiffer H25 and H25′ induce less mechanosensing. However, we ruled out this possibility because mechanosensing remains high on cells cultured on very stiff, nondissipative glass (fig. S12, H to K). Similarly, we found no evidence of differential cytoskeletal softening, which has been shown to result in defective mechanosensing in other settings (fig. S13) (33). Hence, in combination, our results strongly support that viscous energy dissipation blunts cell mechanosensing response to stiff H25 and H25′ matrices.

Fig. 3. H25 hydrogels are effectively stiffer than H10 counterparts.

Stress relaxation of H10 (dark gray) and H25 (teal) hydrogels for 3 hours at a (A) 10%, (B) 30%, and (C) 50% strain. (D) Ratio of the stress generated by H25 and H10 hydrogels in the relaxation experiments. Ratios above 1 indicate that H25 hydrogels are stiffer than H10 counterparts. Gray dashed lines are double-exponential fits to the experimental data. Results were obtained with three H10 and three H25 specimens coming from three cross-linking reactions and two different protein purifications.

Viscous energy dissipation sensing requires actomyosin contractility

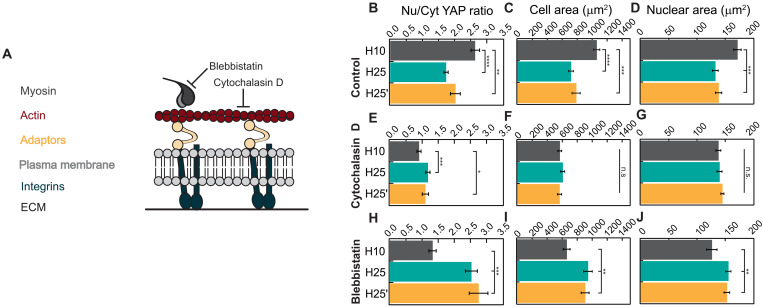
To examine the role of key components of the molecular clutch in the response of cells to substrate viscoelasticity, we examined cell mechanosensing in the presence of different specific inhibitors of the system (Fig. 4A). In agreement with results in Fig. 2 (C and D), control experiments showed higher YAP activity in RPE-1 cells cultured on H10 hydrogels, correlating with increased cell and nuclear areas (Fig. 4, B to D, and fig. S14). In cells treated with 1 μM cytochalasin D, an actin polymerization inhibitor, nuclear YAP levels decrease regardless of the substrate used (Fig. 4, B and E, and fig. S14). Under these conditions, marginal differences in YAP localization appear to follow the stiffness of the substrate although cell and nuclear areas remain unchanged (Fig. 4, E to G). Treatment with 10 μM blebbistatin, a molecule that lowers myosin pulling rates (34), results in higher YAP nuclear localization in H25 and H25′ matrices but lower in H10, as compared to control conditions in such a way that the activity of YAP now markedly follows the stiffness of the substrate (Fig. 4, B and H, and fig. S14). Under 10 μM blebbistatin treatment, YAP activity correlates with cell and nuclear areas (Fig. 4, H to J, and fig. S14). Experiments with 25 μM Rho-kinase (Rock) inhibitor Y-27632 also showed blunted cell mechanosensing in the three matrices (fig. S15), which agrees with the role of Rock promoting both actin polymerization and myosin activity (11). Together, our experiments inhibiting the actomyosin cytoskeleton indicate that the molecular clutch is involved in the blunted response to rigidity of cells cultured on viscous energy–dissipating substrates. The intriguing results with blebbistatin suggest that the speed at which myosin motors pull on clutches influences mechanosensing driven by viscoelastic substrates.

Fig. 4. Actomyosin contractility mediates cell response to viscous energy dissipation.

(A) Representation of mechanical communication between the ECM and the cytoskeleton through molecular clutches of integrins and adaptor proteins like talin. Blebbistatin and cytochalasin D treatments inhibit myosin activity and actin polymerization, respectively. (B to D) Quantification of nuclear versus cytoplasmic YAP distribution, cell spreading, and nuclear area of cells seeded on protein matrices in control conditions. (E to G) Quantification of YAP translocation to the nucleus, cell spreading, and nuclear area of cells treated with 1 μM cytochalasin D. (H to J) Quantification of YAP translocation to the nucleus, cell spreading, and nuclear area of cells treated with 10 μM blebbistatin. A minimum of 40 cells coming from three independent experiments were analyzed for quantifications in (B) to (J). Data are presented as mean ± SEM, ordinary one-way ANOVA. n.s., not significant; *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001.

A pull-and-hold model captures cell mechanosensing on viscoelastic matrices

We tested whether computational modeling of the molecular clutch could capture the two unexpected behaviors we have detected, i.e., the blunted cell response to high stiffness in energy-dissipating H25 and H25′ substrates (Fig. 2) and the recovery of mechanosensing following myosin inhibition with blebbistatin (Fig. 4). In conventional reinforceable clutch models (35), cells monotonically strain the ECM building force on the clutches, eventually unfolding talin and reinforcing adhesion if the stiffness of the substrate is high. As expected, but opposite to our experimental results, this conventional implementation of the clutch model predicts that the higher effective stiffness of H25/H25′ matrices should always result in increased force transmission across clutches, causing more frequent clutch reinforcement, higher cell traction, and, consequently, more translocation of YAP to the nucleus (fig. S16) (10). Since this prediction does not agree with our experimental results, we set out to implement an alternative model of cell mechanosensing.

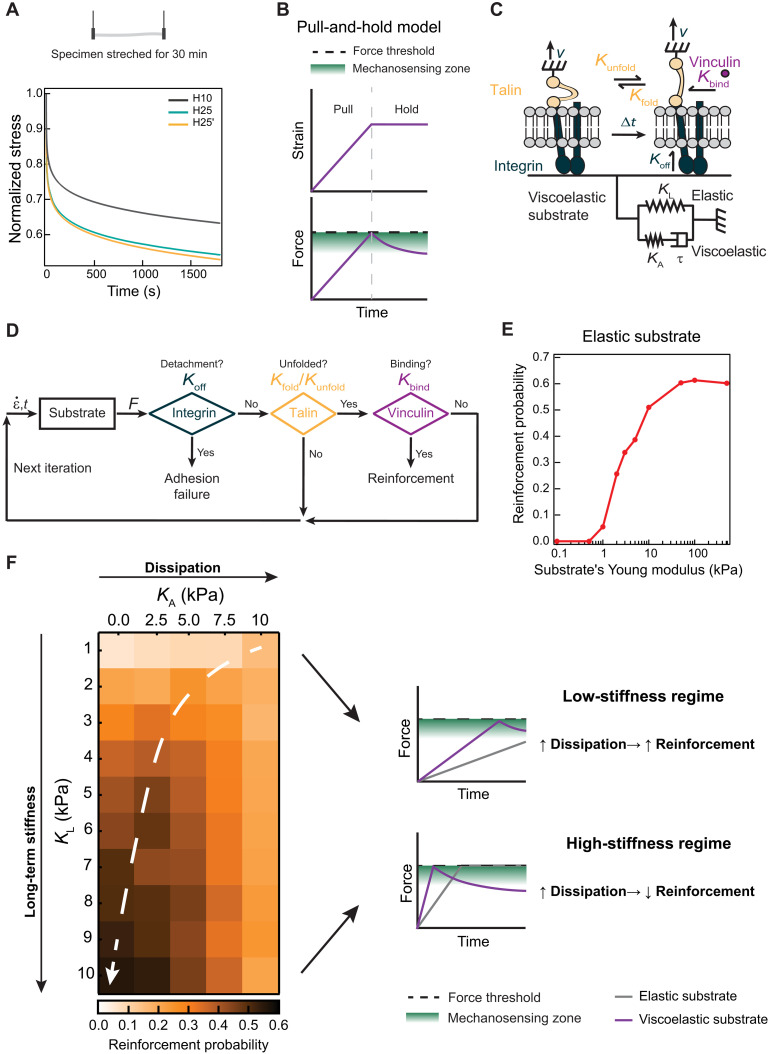
Inspired by the fact that the force generated by viscoelastic materials is inversely related to the extent of energy dissipation when probed at the same initial stress (Fig. 5A), we hypothesized that a dual cell substrate probing scheme including a switch to a stress relaxation mode at a given force threshold could produce results compatible with our experimental observations (Fig. 5B). We first implemented this “pull-and-hold” substrate probing scheme in single-chain clutch that includes four components (Fig. 5C; see Materials and Methods for details) (36):

Fig. 5. Pull-and-hold model of ECM-triggered mechanosensing.

(A) Stress relaxation at 50 kPa of H10, H25, and H25′ materials. Data obtained from three specimens of each hydrogel from independent cross-linking reactions and two purification batches. (B) Pull-and-hold substrate straining model. Initially, cells strain the substrate monotonically leading to an increase in force (pull phase). When a force threshold is reached (black dashed line), cells enter length-clamp mode (hold phase). During hold phase, the force generated by a viscoelastic substrate drops due to energy dissipation. Green indicates the region where talin unfolding, and therefore mechanosensing, is most probable. (C) Single-chain molecular clutch. A single integrin binds to a two-element generalized Maxwell-Wiechert substrate. Integrin detachment occurs according to a K_off rate. Inside the cell, talin attached to integrins can be in a folded or unfolded state according to K_unfold and K_fold rates. Vinculin binds unfolded talin given a K_bind rate. (D) Iterative Monte Carlo algorithm to estimate adhesion reinforcement. Substrate generates force according to a given strain rate ($\stackrel{·}{\mathrm{\epsilon }}$). Simulations resulting in integrin detachment are considered adhesion failures. If no detachment occurs, and if vinculin binds to talin, then the run is considered a successful reinforcement event. If there is no detachment nor vinculin binding, then a new Monte Carlo iteration starts with updated strain values. This cycle is repeated until adhesion failure or reinforcement occurs. (E) Simulated reinforcement probability for elastic substrates increases with substrate stiffness. (F) Left: Heatmap of simulated reinforcement probability according to elastic long-term stiffness (K_L) and additional viscous stiffness (K_A). The white dashed arrow highlights regions of maximum reinforcement probability for substrates with equal K_L. Right: In the low long-term stiffness regime, K_A increases overall stiffness ensuring reinforcement. In the high long-term stiffness region, viscosity leads to stress relaxation after reaching the force threshold, blunting mechanosensing.

1) a generalized Maxwell-Wiechert model viscoelastic substrate characterized by an elastic element with long-term stiffness K_L and a viscoelastic element with K_A stiffness and τ relaxation time,

2) an integrin that unbinds the substrate following a force-independent K_off rate (37),

3) a talin molecule that transduces the mechanical force generated by the actomyosin cytoskeleton and can reversibly unfold and refold in a force-dependent manner,

4) soluble vinculin, which can only bind unfolded talin according to a K_bind rate.

We ran simulations starting from an integrin-ECM–bound state and a folded talin molecule and left the system to evolve according to a kinetic Monte Carlo algorithm (Fig. 5D). In each iteration of the algorithm, force is mounted according to the mechanical properties of the substrate, which is first pulled at a fixed rate. If force on the clutch reaches the threshold, then cells do no further deform the matrix, resulting in force relaxation of viscoelastic substrates. Looking for maximal mechanosensitivity, we set the force threshold in 7.5 pN, since (i) this value is close to the most common force experienced by talin in focal adhesions (38) and (ii) the probability of vinculin binding to talin is maximal at this force (36). In each iteration, the algorithm evaluates the status of the integrin-ECM bond and the folding state of talin and whether talin-vinculin interaction has occurred. There are two possible outcomes for each simulation run, i.e., integrin can unbind the substrate (adhesion failure event) or vinculin can bind unfolded talin (reinforcement event). We ran 600 simulations per condition and calculated the associated reinforcement probability from the number of reinforcement events. We used the calculated reinforcement probability as a proxy of cell mechanosensing.

First, we verified that our minimalistic computational pull-and-hold model captures the well-established enhanced mechanosensing of cells able to reinforce adhesion when grown on purely elastic substrates as stiffness increases (Fig. 5E). Next, we studied the effect of adding gradually higher viscous dissipation to the two-element Maxwell-Wiechert substrate. Consistent with published data (20), higher probabilities of reinforcement are found when additional viscous stiffness are added to soft substrates (Fig. 5F). Notably, the viscous stiffness that optimizes reinforcement gets smaller as the long-term stiffness of the substrate increases, up to a point in which viscosity always reduces reinforcement probability (trajectory indicated by the white arrow in Fig. 5F). Hence, in the high-stiffness regime, the pull-and-hold model predicts reduced mechanosensing for more dissipative viscoelastic substrates, as we have observed in our experiments with protein hydrogels.

Results from our simulations can be rationalized in terms of the time clutches experience forces that promote talin unfolding and subsequent vinculin binding (Fig. 5, B and F). In the low-stiffness regime, purely elastic substrates are not able to build enough force to unfold talin, so the additional stiffness brought by viscosity helps to achieve higher force levels increasing probability of reinforcement. In contrast, in the high-stiffness regime, the system reaches the force threshold very soon leading to rapid force relaxation in dissipative substrates that promote the folded state of talin, precluding adhesion reinforcement.

The pull-and-hold model recapitulates mechanosensing induced by viscoelastic protein matrices

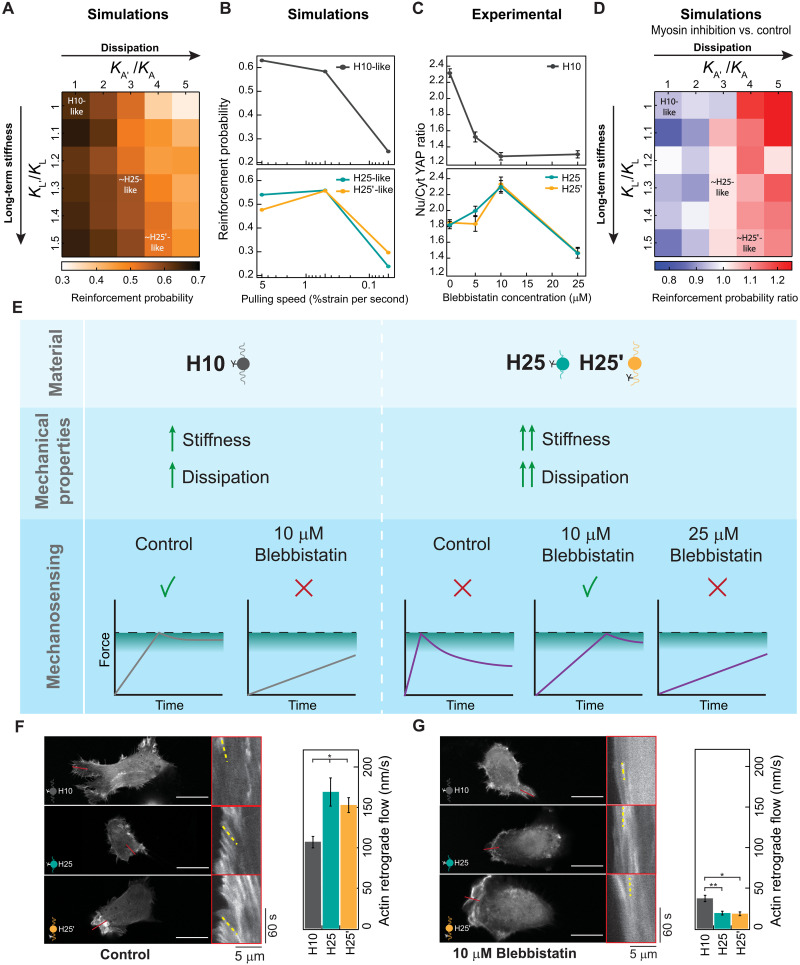
Considering our positive results with a simple two-term Maxwell-Wiechert model representation of viscoelastic substrates, we challenged the pull-and-hold model to capture differential mechanosensing triggered by matrices H10, H25, and H25′. With that aim, we first used an inverse Laplace transform procedure to extract generalized Maxwell-Wiechert model parameters representing H10 materials. This procedure identifies five relevant relaxation times, which result in good fitting of experimental data (fig. S17, A and B). Next, we ran pull-and-hold simulations considering the corresponding six-element Maxwell-Wiechert model (referred to as “H10-like parameters”; Fig. 6A and fig. S17C). Additional simulations were done to cover a 50% increase in long-term stiffness as well as 5× higher viscous stiffness so that simulations also explored parameters similar to H25 and H25′ substrates (fig. S17, D to I). Results readily show that, at these high rigidities, increasing viscosity reduces the probability of reinforcement in a way that is only marginally compensated by higher long-term stiffness (Fig. 6A and fig. S16). These results agree with the differential mechanosensing observed in cells cultured on H10 versus H25 and H25′ matrices (Fig. 2).

Fig. 6. The pull-and-hold molecular clutch model reproduces cell mechanosensing of protein viscoelastic matrices.

(A) Simulated reinforcement probability in different stiff viscoelastic substrates considering H10-like parameters as reference. Position of parameters similar to H25/H25′ materials is indicated. (B) Dependency of simulated reinforcement probability with cell pulling speed for H10-like and H25-like substrates. (C) Nuclear versus cytoplasmic YAP in cells seeded on H10, H25, or H25′ substrates and treated with increasing concentrations of blebbistatin. Data are obtained from three specimens of H10, H25, and H25′ hydrogels produced in independent cross-linking reactions from two protein purification batches. (D) Reinforcement probability ratio obtained by comparing simulations at pulling speeds of 0.5 (representing myosin inhibition) and 5 (representing control conditions) %strain per second. H10-like parameters are used as a reference and position of parameters similar to H25/H25′ materials are indicated. (E) Interpretation of cell mechanosensing in different viscoelastic substrates and under different degrees of myosin inhibition according to the pull-and-hold model. (F and G) Actin retrograde flow of cells seeded on H10, H25, or H25′ matrices in control (F) and in the presence of 10 μM blebbistatin (G). Representative static images are shown on the left of the panels, and kymographs on red boxes show actin movement toward the cell center measured in regions of interest indicated by red lines. Representative actin trajectories are highlighted in yellow. At least 30 measurements per condition were used to quantify actin retrograde flow (right). Scale bars, 20 μm. Data are presented as mean ± SEM, ordinary one-way ANOVA; *P < 0.05 and **P < 0.01.

Prompted by our results with blebbistatin (Fig. 4), we examined how reduced myosin pulling rates affect the response of the pull-and-hold molecular clutch to the three viscoelastic substrates. While lower pulling rates result in monotonically lower probability of reinforcement in the H10-like substrate, results with H25- and H25′-like parameters show a biphasic behavior in which the probability of reinforcement first increases and then drops (Fig. 6B). We confirmed that these predictions were also observed experimentally in cells treated with increasing concentrations of blebbistatin. Specifically, all tested blebbistatin concentrations decrease YAP mechanosensing in cells cultured on the H10 matrix, while a biphasic behavior is observed for H25 and H25′ matrices peaking at 10 μM blebbistatin (Fig. 6C). Next, we expanded the parameter space of the simulations at the pulling speed resulting in the highest mechanosensing in H25-like matrices and compared results with simulations at basal pulling rates. Results indicate that mechanosensing induction by low pulling rates is common for viscoelastic substrates showing high energy dissipation, whereas their long-term stiffness has little influence (Fig. 6D).

A summary of the main results of this work and the interpretation that emerges from the pull-and-hold model appear in Fig. 6E. In control conditions, the force generated by cells on H10 matrices can reach the region in which reinforcement is possible thanks to the high stiffness of the substrate. Since the H10 substrate shows limited energy dissipation, force is not relaxed much when the system reaches the force threshold switching to length-clamp mode. In contrast, in the presence of 10 μM blebbistatin, the lower myosin pulling rates prevent the clutch force from reaching the reinforcement-enabling region, resulting in blunted mechanosensing. Because of the higher stiffness of H25/H25′ materials, cells cultured on these matrices reach the force threshold sooner than when growing on H10 counterparts. However, force eventually drops as a result of the more dissipative nature of H25/H25′. Hence, when cells are grown on these substrates in control conditions, clutches spend less time in a reinforcement-permissive force range, which causes blunted mechanosensing. Under intermediate concentrations of blebbistatin, the force threshold is reached later due to the lower myosin pulling rates. This delay implies that H25/H25′ substrates dissipate more energy in the process of reaching the force threshold and therefore have less energy left to dissipate by then, an effect that is also captured in tensile testing experiments (fig. S18). As a consequence, the average force experienced by clutches increases when myosin is inhibited by 10 μM blebbistatin in cells seeded on H25/H25′ matrices, resulting in higher reinforcement probability and enhanced mechanosensing. Further inhibition of myosin by higher blebbistatin concentrations precludes the clutch from reaching the force regime for reinforcement. Further supporting our interpretation, we found that actin retrograde flow in control conditions is higher in cells seeded on H25/H25′ dissipative substrates, which are predicted to generate less opposing force (Fig. 6, E and F). In contrast, at 10 μM blebbistatin, actin flow rates are generally lower as expected but higher for the barely dissipative H10 matrix that is predicted to generate less force opposing force than H25/H25′ counterparts (Fig. 6, E and G).

DISCUSSION

Bidirectional communication between cells and the ECM is fundamental for the biology of multicellular organisms. Many examples illustrate how perturbed cell-ECM interaction can initiate, sustain, or promote disease (39–42). As expected, understanding mechanisms of interaction between cells and their surrounding matrix has driven rational development of more effective therapies in cancer (43) and cardiovascular (44) or skin (45) disease, as well as promoted the engineering of improved in vitro models of human disease (46, 47). Different mechanical features of the ECM are now widely recognized to affect cell behavior (13, 17, 48–50) and, as a result, are increasingly incorporated in biomedical applications including controlled drug release, prosthetics, and wearable biodevices (51–54). Although a focus has traditionally been put on ECM stiffness, most if not all biological tissues are not elastic but viscoelastic and undergo considerable energy dissipation under mechanical strain. Hence, exclusively “durocentric” views on how cells perceive and react upon ECM mechanics are necessarily incomplete. Over the past few years, it has become clear that the viscosity of the ECM affects cell behavior, although no consensus has been reached on the direction of modulation and the underlying mechanisms (12). Here, we have studied how cells react to viscoelasticity of the ECM in the high-stiffness regime, an underexplored territory where available theoretical models predicted little or no influence of substrate viscous energy dissipation (13, 20, 21).

First, we engineered three stiff protein ECM mimetics with tailored viscoelastic properties but preserved ultrastructure and chemical composition (Fig. 1). Next, we cultured cells on these matrices, obtaining the unanticipated result that substrate viscous energy dissipation results in reduced YAP translocation to the nucleus and lower cell spreading despite high-rigidity cues (Figs. 2 and 3). Also unexpectedly, we found that inhibition of myosin by blebbistatin can restore full steam mechanosensing in the more energy-dissipating matrices (Fig. 4). These seemingly complex behaviors are however captured by our simple molecular clutch computational model, which also reproduces experimental evidence in the literature that viscous stiffness potentiates mechanosensing in the low-stiffness regime (Figs. 5 and 6). Hence, our experimental and theoretical data provide unifying views on how cells sense ECM viscoelasticity. A fundamental insight is that myosin’s pulling rate controls how the ECM-integrin-talin molecular clutch responds to viscous energy dissipation. Hence, cells may modulate myosin activity to tune how they react to substrate viscous energy dissipation (55). Similarly, cell transformation could be contributed by changes in myosin function that breach homeostatic communication with the ECM through alteration of viscous energy dissipation sensing (56). It is also possible that not all cell types respond equally to substrate viscoelasticity due to differences in intrinsic actomyosin activity. This scenario may contribute to apparently contradictory data in the literature that were obtained using different cell models (12) .

An advantage of our minimalistic molecular clutch model is that it is based on just a few parameters, which are however enough to reproduce complex cell behaviors using reasonable inputs and in affordable computing times. Nonetheless, it goes without saying that our model cannot capture the full complexity of cell adhesion and mechanosensing, which are mediated by several hundred proteins (57, 58). For instance, vinculin can have different activation states (37), and talin has multiple domains with different mechanical and binding properties that can influence mechanosensing in intricate manners (59–61). In addition, we only considered the possibility of clutch disengagement at the integrin-ECM bond, although actin-talin and talin-integrin force-dependent interactions are expected to contribute also to the overall mechanosensing response of the clutch (62). It is also important to note that the model considers the substrate as a generalized Maxwell-Wiechert model material despite the fact that both the ECM and our protein matrices show considerable strain stiffening (Fig. 1, G and H) (12). We speculate that further refinements of the model will result in improved quantitative agreement between experiments and simulations (Fig. 6, B and C).

A distinctive assumption of the molecular clutch model presented here is that cells probe the underlying substrate using a pull-and-hold mechanism, by which they deform the substrate until they enter a length-clamp state after hitting a predefined force threshold (Fig. 5, C and D). The pull-and-hold probing scheme is conceptually different from the continuous straining considered in previous computational realizations of the molecular clutch (4, 18) and was required to explain how H25 and H25′ substrates, which are effectively more rigid, can induce less cell mechanosensing than the softer H10. If we consider a force threshold too high to be reached (15 pN), then the probability of reinforcement in the high-stiffness regime would be predicted to be high in all conditions regardless of the dissipative properties of the substrate because talin would always have a strong tendency to be unfolded (fig. S19A). In addition, at this high force threshold, myosin inhibition would cause lower reinforcement probability, regardless of energy dissipation (fig. S19B). Alternatively, if the force threshold is too low (5 pN), then talin would mostly remain in the folded state and therefore the probability of reinforcement would always be small (fig. S19, C and D). Hence, results of simulations at these extreme force thresholds indicate that, for the pull-and-hold molecular clutch model to capture the experimentally observed viscous energy dissipation sensing, the force range of talin unfolding–based reinforcement and the force threshold for switching to length-clamp must be similar.

Whether cells have length-clamp substrate pulling modes, as implied in the pull-and-hold probing scheme, has been under debate (63). The force experienced by talin in cells seeded on elastic substrates of increasing rigidities plateaus to a constant value in the high-stiffness regime, in agreement with the pull-and-hold model (38). Also consistent with our model, cell traction builds to a constant force in developing adhesions in vinculin-deficient cells not able to induce reinforcement (19). Similarly, substrate straining in nonreinforcing cells appears to reach constant plateaus (18). Hence, the results presented here add to a pool of evidence supporting that substrate deformation by cells can enter length-clamp mode. The mechanisms sustaining this manner of cell-ECM interaction remain unknown, although we speculate that they can be contributed by mechanosensing feedback loops stemming from force-dependent molecular interactions (36) and/or by the stalling properties of myosin II motors, which ensure tension maintenance at high loads due to slower adenosine diphosphate release but can result in actomyosin turnover when the underlying substrate relaxes (64, 65).

Mechanical signals are inextricably bound to cell homeostasis. Our work stresses how consideration of the viscous properties of tissues is essential to fully apprehend the cross-talk between biology and mechanics. For instance, the reported negative correlation between ECM viscosity and tumor malignancy (66) could be explained by the energy dissipation–driven inhibition of YAP that we have detected, since YAP activation typically results in more aggressive tumors (67). On the basis of our results, it is also conceivable that disruption of the homeostatic balance between substrate stiffness and viscous energy dissipation can affect cell function negatively (68). According to recent data showing that mature focal adhesions disengage when force across talin is removed (69), we cannot exclude that the cell behaviors we detect are also contributed by focal adhesion destabilization, a possibility that could be tested using matrices whose viscoelastic properties can be controlled in real time (47). We anticipate that cell mechanobiology studies are bound to exploit the ample range of stiffness and viscosity that can be engineered into protein-based ECM mimetics, including the possibility of mechanical modulation by biocompatible signals orthogonal to cell function (23).

MATERIALS AND METHODS

Polyprotein engineering

The cDNA coding for titin I91-Y9P was a gift from M. Carrión-Vázquez (Instituto Cajal, Madrid, Spain). Linker amino acids and the extra tyrosine needed for cross-linking were added by polymerase chain reaction (PCR) using the primers in table S1. The cDNA coding for I91 was provided by R. Pérez-Jiménez (CIC nanoGUNE, San Sebastián, Spain). cDNAs coding for octamers were produced following an iterative strategy of cloning using Bam HI, Bgl II, and Kpn I restriction enzymes, except for the I91₈ cDNA to produce the H10 building block, which was synthesized by GeneArt (Thermo Fisher Scientific). cDNAs were inserted in the pQE80 expression plasmid (QIAGEN, Valencia, CA, USA) using Bam HI and Bgl II restriction enzymes, and the resulting plasmids were verified by Sanger sequencing. Full polyprotein sequences can be found in notes S1 to S3. RGD-containing protein building blocks were designed by mutating H10 and H25′ sequences (notes S4 and S5) and then synthesized by GeneArt (Thermo Fisher Scientific). Polyproteins were expressed in Escherichia coli BLR (DE3). Briefly, fresh cultures [OD₆₀₀ (optical density at 600 nm) = 0.6 to 1.0] were induced with 0.4 mM (H25 and H25′) or 1 mM (H10) isopropyl β-d-1-thiogalactopyranoside for 3 hours at 37°C and at 250 rpm. Cells were lysed by a combination of tip sonication and passes through a French Press. Polyproteins were purified from the soluble fraction through Ni-NTA (nickel–nitrilotriacetic acid) agarose affinity chromatography (HisTrap FF, 5 ml) carried out in a Fast Protein Liquid Chromatography system (GE Healthcare). Proteins were eluted in 50 mM sodium phosphate (pH 7), 300 mM NaCl, and 250 mM imidazole and dialyzed against 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl. Purified polyproteins were concentrated by filtration using 2-ml Amicon Ultra 4 tubes. Purity of samples was evaluated using SDS–polyacrylamide gel electrophoresis (fig. S1A). We obtained 30 to 40 mg of polyprotein per liter of bacterial culture. Protein concentration was estimated from A₂₈₀ measurements considering theoretical extinction coefficients (table S2). Protein samples were stored at 4°C with 0.1% sodium azide.

Circular dichroism

CD spectra were collected using a Jasco J-810 spectropolarimeter. All soluble polyproteins were tested in 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl buffer in 0.1-cm-pathlength quartz cuvettes at a protein concentration of ~0.3 mg/ml. Spectra were recorded at a scanning speed of 50 nm/min and a data pitch of 0.2 nm. Averaged final spectra are the result of four accumulations. The contribution of the buffer was subtracted from each protein spectrum, which was normalized by peptide bond concentration. To study thermal denaturation, the CD signal at 215 nm was monitored as temperature increased from 25° to 85°C at a rate of 30°C/hour (0.5°C data pitch). Temperature control was achieved through a Peltier thermoelectric system.

Protein hydrogel preparation

Hydrogel gelation was achieved following a [Ru(II)(bpy)₃]²⁺-mediated photochemical cross-linking strategy targeting tyrosine residues (22, 25, 70). To this aim, 1 mM purified protein was mixed with 25% ammonium persulfate (APS) (Sigma-Aldrich) and 6.67 mM [Ru(II)(bpy)₃]²⁺ (Sigma-Aldrich). To produce cylindrical hydrogels for uniaxial traction testing, the mix was loaded into polytetrafluoroethylene (PTFE) tubing (Cole-Parmer) [d_in = 0.022 inch (0.05588 cm), d_out = 0.042 inch (0.10668 cm)] through the application of negative pressure using a 25 G needle attached to a syringe. A 2400 lm light-emitting diode (LED) white light source, with an emission maximum of 452 nm, was placed directly below the tubing to irradiate the sample for 3 hours in a cabinet at 4°C (due to local heating, the resulting reaction temperature was measured to be ~25°C). The cross-linked specimen was then taken out the PTFE tube and stored in 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl buffer at 4°C. Hydrogels prepared following this procedure can be stored for several weeks without affecting their mechanical response. To produce disk-shaped hydrogels, polyproteins were cross-linked on round glass coverslips (d = 10 mm) that had been plasma activated using a Plasma Cleaner (Harrick Plasma) for 10 min at high intensity. To this aim, 7.1 μl of the reaction mix was placed on a Gel Slick (Lonza)–coated glass slide, and then a plasma-activated coverslip was gently pushed against the protein solution. Slide-coverslip sandwiches were then transferred to the surface of the LED lamp and irradiated for 3 hours. After cross-linking, hydrogels were thoroughly washed with phosphate-buffered saline (PBS), coated with fibronectin (5 μg/ml; Sigma-Aldrich, F1141) for 1 hour at 37°C, then washed three times, and preserved in PBS at 4°C no longer than 24 hours. In control experiments in fig. S12 (A and B), RGD peptide (Sigma-Aldrich, A8052) was used instead of fibronectin. No coating was used for H10-RGD and H25′-RGD hydrogels.

Differential scanning fluorimetry

Melting curves were determined by mixing 10 μg of protein, either soluble or cross-linked hydrogels, with SYPRO Orange (Thermo Fisher Scientific, S6650) following the manufacturer’s specifications. Samples were taken to a final volume of 25 μl with 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl and were allowed to incubate with the dye for 1 hour at 4°C before being loaded into a 384-well quantitative PCR (qPCR) plate (Thermo Fisher Scientific, BC2384). The plate was then placed into a CFX384 Touch Real-Time PCR Detection System (Bio-Rad), and melting curves were obtained raising the temperature from 10° to 95°C at 3°/min. SYPRO Orange fluorescence at 570 nm increases when proteins denature until proteins aggregate, which leads to a decrease in fluorescence signal. The global minimum of the first derivative of the melting curve indicates melting temperatures.

Tensile testing

Tests were done using a home-built tensile tester inspired by Saqlain and colleagues (25). The tester consists of a SI-H KG4A force sensor (World Precision Instruments) hooked to a BAM21-LC KG Optical Force Transducer Amplifier (World Precision Instruments) and a SMAC LCA25-025-35-6F linear actuator (SMAC Moving Coil Actuators) connected to a computer through a NIDAQ USB-6002 data acquisition system (National Instruments). The force sensor and linear actuator are both connected to a pair of stainless-steel SI-TM7 general-purpose mount tweezers used to grip the specimen. For tensile testing, cylinder shaped hydrogels were fixed at both ends by the tweezers. Tensile tests were done in 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl buffer at room temperature (RT). In stress-strain tests, strain was applied and then removed at a rate of 5 mm/s, whereas in stress relaxation measurements, the strain was held constant while the load was recorded as a function of time. Apparent E was calculated from stress-strain curves performed to 75% strain as the derivative of stress (tangent modulus). Dissipated energy was evaluated from stress-strain curves carried out at increasing strain values as the ratio of the hysteresis area between the loading and unloading stress-strain curves and the area below the loading stress-strain curve.

Nanomechanical spectroscopy by AFM

AFM measurements were performed with a commercial instrument, JPK NanoWizard 3 (JPK Instruments AG, Berlin, Germany), mounted on an Axio Observer D1 inverted microscope (Carl Zeiss, Oberkochen, Germany). We used BL-AC40TS cantilevers. The force constant was calibrated using the thermal noise method (k = 0.089 N/m). The optical sensitivity was 7.2 nm/V. The nominal values for the tip’s geometry, half-angle, height, and radius, were, respectively, 18°, 7 μm, and 8 nm.

Force-distance curves (FDCs) were performed on five different positions of the hydrogel samples; 10 FDCs were acquired at each position. The FDCs were acquired by applying a triangular waveform at v = 10 μm/s with a data acquisition rate of 5 kHz. Indentation was stopped when the force reached 3 nN. The z-piezo displacement was 5 μm (closed-loop feedback). Young moduli were obtained by fitting the approach section of FDCs to the Sneddon model for a parabolic tip (71). The energy dissipated during the viscoelastic deformation was obtained from the area enclosed between the approach and retraction sections of the FDC at 150-nm indentation. Adhesion events were not considered in the analysis.

Infrared spectroscopy

Attenuated total reflection (ATR) Fourier transform infrared (FTIR) spectra were obtained using a Nicolet iS5 spectrometer equipped with an iD5 ATR complement following published protocols (72). ATR-FTIR spectra were obtained from hydrogels pressed against the diamond window at constant pressure in 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl. A background spectrum obtained while applying constant pressure to buffer was subtracted from the spectrum of each sample. All spectra were the result of averaging 32 measurements in the 550- to 4000-cm⁻¹ range, with a 4-cm⁻¹ resolution.

Scanning electron microscopy

I91 hydrogels in 50 mM sodium phosphate (pH 7.5) and 150 mM NaCl were snap-frozen in liquid nitrogen. Frozen samples were quickly transferred to a freeze dryer (VirTis) and lyophilized for 24 hours. The resulting specimens were then fractured in liquid nitrogen. The surface of the samples was coated with 6.9-nm carbon using a Leica EM ACE600 coater before observation. Imaging of the fractured end of hydrogels was performed using a Zeiss Auriga field-emission scanning electron microscope. To quantify pore size, images were processed in Fiji. An internal gradient with a radius of 15 pixels was applied to each image to better define the areas corresponding to pores. Afterward, a local threshold was applied, and the area of the thresholded pores was obtained using Fiji’s Analyze Particles plugin.

Quantification of dityrosine cross-links

For analysis of the amino acid content of soluble polyproteins and cross-linked hydrogels, samples containing 10 nmol of tyrosine were hydrolyzed in 0.2 ml of 5.7 N HCl containing 0.1% phenol and 119 μM N-Leu as an internal standard in evacuated sealed tubes at 110°C for 24 hours. Samples were then dried and washed three times with Milli-Q water. Subsequent amino acid analyses were performed on a Biochrom 20 automatic analyzer (Pharmacia) following the procedures recommended by the manufacturer.

PAAm hydrogel preparation

PAAm matrices were prepared on glass coverslips as previously described (73). Briefly, the surface of the coverslips was treated with (3-aminopropyl)triethoxysilane (APTES) (Sigma-Aldrich, 281778) to facilitate PAAm adhesion. To ensure the formation of a homogeneous PAAm layer on the glass surface, the mixture was sandwiched between the APTES-treated coverslip and a coverslip coated with Sigmacote (Sigma-Aldrich, SH25′). The PAAm mixtures were prepared using different ratios of 40% acrylamide solution (Bio-Rad, 1610140) and 2% bis-acrylamide solution (Bio-Rad, 1610142) and Sigma-Aldrich molecular biology grade water to achieve different final stiffness, as previously described (73). Final water-PAAm mixtures were cross-linked with 0.5% APS and 0.15% N,N,N′,N′-tetramethylethylenediamine (Thermo Fisher Scientific, 17919). Fifty microliters of the mixtures was added to each glass and allowed to cross-link for 30 min at RT. After cross-linking, Sigmacote-treated coverslips were removed with a surgical blade and discarded. PAAm matrices were activated twice with Sulfo-SANPAH (0.5 mg/ml) for 6 min at RT (Sigma-Aldrich, 80332), coated with fibronectin (5 μg/ml; Sigma-Aldrich, F1141) for 1 hour at 37°C, then washed three times, and preserved in PBS at 4°C no longer than 24 hours.

Cell culture

RPE-1 cells were grown in Dulbecco’s modified Eagle’s medium:Nutrient Mixture F-12 (DMEM/F12, Lonza) supplemented with 10% fetal bovine serum (FBS; Gibco, Thermo Fisher Scientific) and 1% penicillin/streptomycin (Invitrogen). Mesenchymal stem cells were grown in DMEM supplemented with 10% FBS (Gibco, Thermo Fisher Scientific) and 1% penicillin/streptomycin (Invitrogen). Cells were maintained at subconfluency on standard cell culture plates, and the medium was changed every 2 to 3 days. For cell mechanobiology experiments, RPE-1 and mesenchymal stem cells were seeded at a confluency of 50% on hydrogel surfaces and were allowed to attach for approximately 12 hours in DMEM/F12 or DMEM, respectively, supplemented with 10% FBS and 1% penicillin/streptomycin before being processed. Cells were either preserved in RNAlater (Thermo Fisher Scientific, AM7020) for RNA isolation or fixed in 4% paraformaldehyde (PFA) for immunostaining. For metabolic activity assays, cells were seeded at a confluency of 80% and cultured overnight.

Cell metabolic activity

Cell medium was replaced by Hanks’ balanced salt solution (Thermo Fisher Scientific, 14175053) supplemented with 2% FBS. 3-[4,5-Dimethylthiazol-2-yl]-2,5-diphenyl tetrazolium bromide (MTT; 5 mg/ml) in RPMI 1640 was added to the cells in a volume equal to 10% of the culture volume. Cells were incubated at 37°C and 5% CO₂ for 4 hours so MTT could be metabolized by mitochondrial dehydrogenases of viable cells, which cleave the tetrazolium ring yielding insoluble, purple MTT formazan crystals. Next, 0.1 N HCl in anhydrous isopropanol was added to the cells and used to solubilize any formazan crystals formed. Absorbance at 570 nm was measured, and background absorbance at 690 nm was subtracted. Final absorbance signal is proportional to the number of metabolically active cells.

Immunocytochemistry

Cells were washed three times with PBS and fixed with 4% PFA at RT for 10 min. Cells were then washed three times with PBS and permeabilized for 5 min with 0.2% Triton X-100 (Sigma-Aldrich) in 1% (w/v) bovine serum albumin (Sigma-Aldrich). After permeabilization, samples were incubated with FBS for 1 hour at RT. Immunostaining with anti-YAP antibody took place at 4°C overnight. Secondary antibody, phalloidin, and 4′,6-diamidino-2-phenylindole (DAPI) were incubated for 1 hour at RT. The following antibodies/reagents were used: YAP antibody (Santa Cruz Biotechnology YAP1 63.7; sc-101199), paxillin antibody (abcam; ab32084), DAPI (Invitrogen), goat anti-mouse immunoglobulin G (IgG) Alexa Fluor 488 (Invitrogen), goat anti-mouse IgG Alexa Fluor 568 (Invitrogen), goat anti-rabbit IgG Alexa Fluor 594 (Invitrogen), and Alexa Fluor 647 phalloidin to stain actin (Invitrogen). Goat anti-mouse IgG Alexa Fluor 488 (Invitrogen) was used to stain YAP in all experiments except cytoskeleton inhibition ones, where goat anti-mouse IgG Alexa Fluor 568 (Invitrogen) was used to avoid green fluorescence of blebbistatin. Goat anti-rabbit IgG Alexa Fluor 594 (Invitrogen) was used to stain paxillin in focal adhesions. For measurement of YAP nuclear localization in the absence or presence of cytoskeleton inhibitors, images of DAPI/phalloidin/YAP antibody–stained cells were taken with a 40× numerical aperture (NA) 1.40 oil immersion objective using a laser scanning confocal microscope (Zeiss, LSM700) and analyzed using ImageJ. YAP nuclear localization ratio was determined as the summed intensity of the YAP signal within a 10.8-μm² area inside the nucleus divided by the summed intensity of the YAP signal within a 10.8-μm² area inside the cytoplasm. To determine cell spreading, the outer membrane of cells was manually segmented, and ImageJ was then used to compute total cell area. DAPI staining was used to quantify nuclei. Particles above 50 μm² in size were analyzed. Length of focal adhesions was manually quantified on ImageJ. Actin’s cytoskeleton organization was estimated using the software Cytospectre using phalloidin-stained samples (74).

Real-time qPCR

Total RNA was extracted from cell samples using a combination of TRIzol (Thermo Fisher Scientific) and the RNAeasy micro kit (QIAGEN). For each sample, 150 ng of RNA was reverse-transcribed using the SuperScript IV VILO Master Mix (Thermo Fisher Scientific). qPCR of cDNA was performed with SYBR Green (Applied Biosystems) accompanied by nontemplate controls. Results were normalized to endogenous glyceraldehyde phosphate dehydrogenase and β-actin. Primer sequences can be found in table S1.

Cytoskeleton inhibition

Cytochalasin D (Sigma-Aldrich, C8273), blebbistatin (Sigma-Aldrich, B0560), or Y-27632 (Sigma-Aldrich, Y0503) were added to cells 12 hours after plating, followed by incubation for 1 hour. After incubation, cells were washed three times with PBS and prepared for immunostaining.

Computational modeling of the molecular clutch

A single-chain, pull-and-hold molecular clutch model was implemented to evaluate cell mechanosensing using Monte Carlo simulations (file S1). Viscoelastic substrates followed generalized Maxwell-Wiechert models characterized by elastic modulus K_Ai and relaxation time τ_i (see Fig. 5C representing a single viscoelastic element) (75). According to the Maxwell-Wiechert model, K_L is the elastic long-term stiffness of the material (i.e., the remaining stress at infinite time in a stress relaxation experiment), and the sum of all K_Ai (K_A) is the additional viscous stiffness of the substrate. To model purely elastic matrices, all viscous terms were removed leading to a conventional Hookean material with K_L modulus. Constitutive equations were discretized in time using a forward Euler method with the same time step as the Monte Carlo simulations. Force across clutches was calculated as the product of the stress generated by the substrate and the effective area of the clutch (values for simulation parameters are found in table S3).

In the model, cells monotonically strain the substrate until a certain force is reached. At this moment, the strain is fixed. For every run of the simulation, a kinetic Monte Carlo routine is executed (Fig. 5D). Simulations start with the integrin molecule bound to the substrate. In each iteration of the Monte Carlo, the possibility of integrin detachment from the substrate is evaluated according to its off rate, K_off. Integrin detachment is considered as an adhesion failure event. If the integrin remains attached, then the folding state of talin is evaluated according to a two-state model that considers force-dependent transition rates between folded and unfolded states (K_unfold and K_fold, respectively). If talin is unfolded, then the possibility of vinculin binding to talin is enabled according to a binding rate K_bind that is both force and vinculin concentration dependent (36). Force-dependent transitions follow the Bell-Evans model (76). Vinculin binding to talin is considered as a successful reinforcement event. If no vinculin binding occurs, a new iteration is started with updated values of strain and time. A standard strain rate ($\stackrel{·}{\mathrm{\epsilon }}$) of 5% strain/s was used for control conditions. To emulate actomyosin inhibition by blebbistatin, simulations were also run at $\stackrel{·}{\mathrm{\epsilon }}$ = 0.5 and 0.05%/s. For each simulated condition, a total of 600 simulations were run. Reinforcement probability was calculated as the ratio of all reinforcement events divided by the total number of simulation runs.

Simulations in Fig. 5 used a standard linear solid model (i.e., a two-element generalized Maxwell-Wiechert model) with a relaxation time of 10 s. Simulations based on H10 or H25/H25’s mechanical response used six-element generalized Maxwell-Wiechert models (Fig. 6 and fig. S16). To estimate relaxation times, first, we used regularized inverse Laplace transformation (MATLAB’s function rilt) on stress relaxation curves at 30% strain to obtain associated time spectra (40 data points evenly spaced in logarithmic scale from 0.01 to 1000 s, a discretization ensuring efficient convergence of the algorithm). In these spectra, each peak corresponds to the value of one relaxation time, and its amplitude is directly proportional to the corresponding K_Ai value (fig. S17). After relaxation times were obtained, values of K_Ai and K_L were manually adjusted to fit the stress relaxation curves. Simulations using a conventional molecular clutch model were done according to published protocols (35).

Actin retrograde flow measurements

To measure actin retrograde flow, cells were transfected with lifeact–green fluorescent protein (Addgene plasmid 15238) using a Lipofectamine 3000 transfection kit (Invitrogen, H10000008) 2 days before measurements. About 12 hours before measurement, cells were plated on the protein hydrogels. Cells were imaged every second for 2 min with a 20× W Plan-Apo differential interference contrast (ultraviolet) VIS-IR NA 1.0 water immersion dipping objective using a laser scanning confocal microscope (Zeiss, LSM780). For each cell, kymographs were obtained at the cell periphery, and actin speed was measured from the slope of actin features observed in the kymographs (33).

Statistical analysis

In all figures, measurements are reported as mean ± SEM. The number of independent experiments is specified in the figure legends. Statistical significance was evaluated in GraphPad Prism. Unless stated otherwise, one-way analysis of variance (ANOVA) was used to assess differences between groups. Differences were considered statistically significant at *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001.

Supplementary Materials

The PDF file includes:

Figs. S1 to S19

Tables S1 to S3

Supplementary Notes S1 to S5

Legend for file S1

References

Other Supplementary Material for this manuscript includes the following:

File S1