Abstract
Detecting adulteration in extra virgin olive oil (EVOO) is particularly challenging with oils of similar chemical composition. This study applies near-infrared hyperspectral imaging (NIR-HSI) and machine learning (ML) to detect EVOO adulteration with hazelnut, refined olive, and olive pomace oils at various concentrations (1%, 5%, 10%, 20%, 40%, and 100% m/m). Savitzky-Golay filtering, first and second derivatives, multiplicative scatter correction (MSC), standard normal variate (SNV), and their combinations were used to preprocess the spectral data, with Principal Component Analysis (PCA) reducing dimensionality. Classification was performed using Partial Least Squares-Discriminant Analysis (PLS-DA) and ML algorithms, including k-Nearest Neighbors (k-NN), Naïve Bayes, Random Forest (RF), Support Vector Machine (SVM), and Artificial Neural Networks (ANN). PLS-DA, k-NN, RF, SVM, NB, and ANN models achieved accuracy rates of 97.0–99.0%, 96.2–100%, 96.5–100%, 98.6–99.5%, 93.9–99.7%, and 99.2–100%, respectively, in discriminating between pure EVOO, adulterants, and adulterated oils. PLS-DA, RF, SVM, and ANN significantly outperformed Naïve Bayes (p < 0.05) in binary classification, with Matthews correlation coefficient (MCC) values exceeding 0.90. All the binary classifiers except Naïve Bayes, when coupled with SNV/MSC, Savitzky-Golay smoothing and derivatives, consistently achieved perfect scores (1.0) for accuracy, sensitivity, specificity, F1 score, precision, and MCC in distinguishing pure EVOO from adulterated oils. No significant differences (p > 0.05) in model performance were found between those using full spectra and those based on key variable selection. However, PLS-DA and ANN significantly outperformed k-NN, RF, and SVM (p < 0.05), with MCC values ranging from 0.95 to 1.00, indicating superior classification performance. These findings demonstrate that combining NIR-HSI with machine learning, along with key variable selection, potentially offers an effective, non-destructive solution for detecting adulteration in EVOO and combating fraud in the olive oil industry.
Keywords: Machine learning, Variable selection, Extra-virgin olive oil (EVOO), Adulteration, Authentication, Classification models
Graphical abstract
Highlights
-
•
NIR-HSI with ML effectively detects EVOO adulteration.
-
•
ANN models reach 100% accuracy in three-class oil classification on the test set.
-
•
Binary classifiers accurately distinguish pure from adulterated olive oil.
-
•
Variable selection improves model performance without significant accuracy loss.
1. Introduction
Food fraud, a growing threat to public health and consumer trust, continues to undermine the integrity of the global food system through practices such as mislabeling, adulteration, and counterfeiting (Manning, 2016). The adulteration of high-value oils, particularly extra-virgin olive oil (EVOO), is alarming, with frequent reports of dilution or substitution using cheaper alternatives (Moore et al., 2012). As awareness of this issue increases, implementing robust authentication methods to safeguard the integrity of these oils has become crucial (Medina et al., 2019; Meenu et al., 2019).
The toxic oil syndrome of the 1980s, caused by aniline-adulterated rapeseed oil mislabeled as olive oil, resulted in over 400 deaths and 20,000 illnesses, drawing significant attention to oil adulteration (Manuel Tabuenca, 1981; Philen and Posada, 1993; Posada De La Paz et al., 2001). This tragedy highlighted the severity of edible oil fraud (Casadei et al., 2021). More recently, Spanish and Italian authorities uncovered 260,000 L of counterfeit EVOO blended with lower-grade lampante oil, underscoring the ongoing challenges in the industry (Food Safety News, 2023).
EVOO is the highest-quality and most expensive olive oil, produced exclusively through mechanical or physical methods that preserve its natural composition without chemical alterations (IOC, 2010). Its global demand continues to rise due to its unique sensory qualities, nutritional value, and numerous health benefits (Drira et al., 2021; Jabeur et al., 2016). However, these factors make EVOO prone to adulteration with lower-grade olive oils such as olive-pomace, deodorized olive oils, as well as cheaper vegetable oils including hazelnut, sunflower, canola, and corn (de la Mata et al., 2012; Filoda et al., 2019; Jabeur et al., 2017; Ozcan-Sinir, 2020). The authenticity and quality of EVOO are crucial for consumer satisfaction, industry reputation, and regulatory compliance (CodexAlimentarius, 2017). Rising prices and demand have fueled an increase in adulteration, often unbeknownst to consumers while sellers profit (Moore et al., 2012). This compromises product integrity and poses health risks (Posada De La Paz et al., 2001). Robust authentication measures are essential to preserve authenticity of EVOO, protect consumer confidence, and uphold industry standards.
Adulteration of EVOO remains challenging, especially with cheaper oils such as hazelnut and lower-grade olive oils. These adulterants are chosen for their similar physicochemical properties, triacylglycerol composition, sterol content, and fatty acid profile, making detection difficult, particularly at low levels (Calvano et al., 2012). This similarity extends to minor components including phenolic compounds, tocopherols, chlorophyll, carotenoids, and volatile compounds, further masking adulteration (Chiavaro et al., 2008). Despite advances in detection technologies, fraudsters continue to develop sophisticated techniques that evade some conventional methods (Peña et al., 2005). The ability to detect and quantify adulterants depends on their concentration and similarity to EVOO (Torrecilla et al., 2010). This highlights the need for advanced, sensitive techniques capable of distinguishing pure EVOO from adulterated products.
EU authorities have raised concerns about the adulteration of EVOO with hazelnut oil. Detecting refined hazelnut oil in EVOO, particularly at concentrations below 20%, remains challenging with conventional methods (Azadmard-Damirchi, 2010; Mildner-Szkudlarz and Jeleń, 2008). This difficulty stems from the refining process, which removes filbertone, a key volatile compound in hazelnut oil, along with other minor components essential for detection (Flores et al., 2006). Both oils share similar fatty acid profiles and minor components such as tocopherols and sterols, further complicating differentiation. Unrefined hazelnut oil also poses a health risk for individuals allergic to hazelnut proteins (Arlorio et al., 2010; Martín-Hernández et al., 2008; van Hengel, 2007). To address these challenges, the International Olive Council (IOC) and CODEX STAN 33–1981 have established global guidelines for olive oil purity, quality, and authenticity, emphasizing fraud detection through innovative and effective techniques (Codex Alimentarius Commission, 2003).
Several chromatography-based methods, including high-performance liquid chromatography, high-resolution gas chromatography, and mass spectrometry, have been proposed for EVOO authentication (Calvano et al., 2012; Capote et al., 2007; Drira et al., 2021; Jabeur et al., 2017; Mildner-Szkudlarz and Jeleń, 2008; Ozcan-Sinir, 2020). These techniques quantify compounds such as fatty acids, sterols, tocopherols, and tocotrienols. A common approach is to analyze specific marker compounds. For instance, filbertone is used as a chiral marker to detect unrefined hazelnut oil. However, filbertone can be removed during refining, making some adulterations harder to detect (Flores et al., 2006). Although chromatographic techniques are highly precise, they are expensive, time-consuming, and require skilled operators. Moreover, they often use harmful chemicals, raising environmental concerns due to waste production (Aparicio and Aparicio-Ruíz, 2000). Despite these limitations, chromatography remains indispensable in certain cases, though faster and non-destructive alternatives are emerging to complement it for EVOO authentication.
In recent years, rapid spectroscopic methods, including Fourier Transform Infrared Spectroscopy (FTIR) (Rohman and Man, 2010), Raman spectroscopy (Georgouli et al., 2017; López-Díez et al., 2003), NMR (Mannina et al., 2009), and total synchronous fluorescence (Poulli et al., 2007), have emerged for detecting EVOO adulteration. These techniques offer significant advantages but are point-based, scanning small sample areas and limiting their ability to provide the spatial information essential for broader food inspection (Lohumi et al., 2015). However, when combined with chemometrics and machine learning algorithms, they offer a fast, cost-effective method for routine authentication screening (Vieira et al., 2021).
Hyperspectral imaging (HSI) is a promising tool for combating food fraud, integrating spectroscopy and imaging to provide enhanced spatial and spectral detail compared to traditional methods (Mendez et al., 2019; Rungpichayapichet et al., 2017). HSI allows for simultaneous analysis of multiple samples on a conveyor belt or scanning platform, unlike traditional methods that analyze one sample at a time. This efficiency makes HSI ideal for high-throughput industrial applications. Its flexibility also allows hyperspectral data collection from samples of varying sizes and shapes (Lohumi et al., 2015). Our recent study demonstrated the effectiveness of near-infrared HSI (NIR-HSI) in detecting and quantifying EVOO adulteration with sunflower, corn, soybean, canola, sunflower, and sesame oils, outperforming traditional methods such as FTIR, Raman, UV–Vis, and GC-MS (Malavi et al., 2023). HSI-NIR successfully distinguished various vegetable oils (Hwang et al., 2024), though its potential for detecting complex adulteration in chemically similar oils remains underexplored.
Recent developments in machine learning offer promising methods for improving discrimination, minimizing overfitting, and selecting key features for authentication studies. However, the rapid detection of EVOO adulteration using NIR-HSI and machine learning algorithms has been minimally reported, particularly when dealing with oils of similar composition such as hazelnut oil and refined olive oils. This study addresses these gaps by evaluating the efficacy of NIR-HSI (900–1700 nm) combined with chemometrics (PLS-DA) and machine learning algorithms including SVM, RF, k-NN, Naive Bayes, and ANN, for detecting EVOO adulteration with cheaper oils including hazelnut, olive pomace, and refined olive oil. Additionally, the performance of binary classification models using key spectral features is assessed, further highlighting the potential of these techniques in detecting subtle adulteration patterns in olive oil.
2. Materials and methods
2.1. Edible oil samples
The edible oil samples used in this study were sourced from certified local and international suppliers. Extra virgin olive oils (EVOO) were produced in Spain, Italy, and Greece. A total of 36 EVOO samples, 11 refined hazelnut oil (HZO) samples, 11 olive pomace oil (POO) samples, and 6 refined olive oil (ROO) samples were obtained for analysis. All samples were stored in a dark environment at 25 °C prior to analysis.
2.2. Preparation of adulteration mixtures
After the initial selection, a random subset of 20 distinct extra virgin olive oil (EVOO) samples, 4 refined hazelnut oil (HZO) samples, 4 olive pomace oil (POO) samples, and 4 refined olive oil (ROO) samples were selected for adulteration experiments. Fourteen EVOO samples were randomly selected and blended with two distinct samples of each adulterant (HZO, POO, and ROO) to create adulteration mixtures for the calibration set. The remaining six EVOO samples were blended with the remaining adulterants to form mixtures for external validation (test set). Unadulterated samples were also included in both the calibration and validation phases (Fig. 1). This setup ensured sample exclusivity, critical for effective model training, validation, and testing. Adulteration mixtures were prepared at concentrations of 0%, 1%, 5%, 10%, 20%, 40%, and 100% (mass/mass) for EVOO + HZO, EVOO + POO, and EVOO + ROO. Each sample was prepared in triplicate, yielding a total of 1995 samples.
Fig. 1.
Schematic sampling experimental design.
2.3. Hyperspectral imaging system
A near-infrared hyperspectral imaging system (NIR-HSI) (Spectral Imaging Oy Ltd, Finland) was used to scan all samples. The system operates within the 900–1700 nm spectral range, with a spectral resolution of 3 nm, generating 224 bands. The setup featured a hyperspectral camera (Fx17e Specim) positioned at a 45° angle, six 150 W tungsten halogen lamps for illumination, a moving platform (40 × 20 Specim Lab Scanner), and a computer for controlling data acquisition.
2.4. Hyperspectral image acquisition
Lumo scanner software facilitated hyperspectral image acquisition, optimizing settings for exposure time, frame rate, and platform speed. The exposure time was set to 7.00 ms, the frame rate to 19.50 Hz, and the platform speed to 2.6 mm/s. For each scan, 10 g of oil sample were placed in a 6 cm diameter plastic dish, positioned 15 cm from the focus lens. The sample was scanned line by line across the NIR spectral range (900–1700 nm) with a spectral interval of 3.5 nm. Each hypercube captured spatial data with a resolution of 672 × 512 pixels and 224 spectral bands, offering comprehensive information for oil sample analysis.
2.5. HSI image processing and extraction of the spectral profile
Black and white reference images were acquired to correct the raw HSI images, addressing dark spots and uneven illumination caused by the camera. The corrected HSI image (R) was calculated using Equation (1), where "I" represents the raw HSI image, "W" is the white reference image obtained from a standard white calibration board (reflectance value 99.9%), and "B" is the dark image acquired by closing the camera lens (reflectance value 0%). The correction and normalization processes were carried out using ENVI software (IDL 8.7.2).
| (1) |
After calibrating and normalizing the hyperspectral images, a 50 × 50 pixel region of interest (ROI) was selected from the center of each sample using IDL ENVI software (version 5.5.2). The averaged reflectance values from the pixels within the ROI were used to obtain the final reflectance for each sample. The resultant data matrix, consisting of 1995 rows and 224 columns, was then prepared for further preprocessing and statistical modeling.
2.6. Spectral preprocessing
Spectral preprocessing is essential in chemometrics for analyzing spectroscopic data, as it improves data quality by eliminating noise and irrelevant information, ultimately enhancing the performance of predictive models (Feng and Sun, 2012). In this study, both raw and preprocessed spectral data were used to develop classification models. Several preprocessing methods and their combinations were applied, including normalization, standard normal variate (SNV), multiplicative scatter correction (MSC), Savitzky-Golay smoothing, and derivatives. Normalization mapped the data to a 0 to 1 range, speeding up and simplifying the modeling process. SNV and MSC were applied to reduce spectral variability caused by scattering effects. Savitzky-Golay (SG) smoothing and derivatives were used to remove noise, smooth spectral data, eliminate baseline variations, and resolve overlapping peaks (Lohumi et al., 2015). First and second derivatives, combined with a Savitzky-Golay filter using a 7-point gap and second-order polynomial filtering, were specifically employed. All spectral preprocessing was conducted in R Studio using the "mdatools" package for chemometrics (Kucheryavskiy, 2020).
2.7. Machine learning algorithms
Principal Component Analysis (PCA) was initially employed to explore the differentiation between authentic EVOO, adulterant oils, and adulterated olive oils based on spectral variations. PCA addresses high dimensionality and is used for sample clustering, feature selection, and noise reduction in spectral data (Minaei et al., 2017). The principal components (PCs) are mutually orthogonal and capture the maximum variance in the data (Florián-Huamán et al., 2022). After PCA, various supervised models, including PLS-DA, and machine learning algorithms such as k-NN, Naïve Bayes, RF, SVM, and ANN were applied for classification.
Partial Least Squares (PLS) is considered a 'gold standard' supervised linear technique in chemometrics. It establishes a linear relationship between two datasets: X (spectra) and Y (dependent variable matrix), by compressing spectral data into orthogonal latent variables that capture the maximum covariance between X and Y (Uncu and Ozen, 2019). PLS is well-regarded for feature extraction and addressing high multi-collinearity in high-dimensional data, such as HSI spectral data (Leardi, 2018). In this study, the PLS variant, Partial Least Squares-Discriminant Analysis (PLS-DA), was initially employed for classification. More details on PLS-DA and the selection criteria for a parsimonious model can be found in our previous study (Malavi et al., 2023). After PLS-DA, other machine learning algorithms, including k-NN, Random Forest (RF), Naïve Bayes, SVM, and ANN, were further assessed for classification.
K-Nearest Neighbors (k-NN) is a well-known supervised, non-parametric machine learning algorithm for pattern recognition that relies on the hyperparameter 'k' in decision-making. In k-NN, each of the 'k' nearest neighbors has equal influence on the classification outcome. The core principle is that a sample is assigned to the category most common among its 'k' closest neighbors (Yun et al., 2021). The model calculates the distances between new samples and those in the training set, classifying them based on a majority vote. In this study, the optimal value of 'k' was determined using a grid search from 3 to 30, with step increments of 2.
The Naïve Bayes (NB) classification algorithm applies Bayes' theorem to determine the most probable class among available options. It calculates the prior probabilities of each attribute within every class, assuming mutual independence of attributes. This means that the presence of one feature is considered independent of any other feature in the class. The algorithm then uses these probabilities for classification (Barbosa et al., 2014). PCA was employed to generate independent features (PCs) for use as covariates in the classification model.
Support Vector Machine (SVM) is a supervised machine learning model based on statistical learning theory, commonly used for classification, especially with high-dimensional data such as hyperspectral imaging (HSI) due to its lower sensitivity to dimensionality (Chen et al., 2007). SVM effectively learns within high-dimensional feature spaces, even with limited training data, by mapping non-linearly separable data into a higher-dimensional space and classifying it using maximal margin hyperplanes (Zhang et al., 2011). To prevent overfitting, SVM minimizes structural risk rather than focusing solely on minimizing training errors. The optimal parameters for the SVM model in this study followed the approach by Zeng et al. (2019). Based on the findings of Xie et al. (2014), the radial basis function (RBF) kernel, which outperforms other kernels in classification, was selected. The parameter sigma (σ) defined the nonlinear mapping from the input space to the high-dimensional feature space, while the "cost of constraint violation" (C) controlled the penalty for instances falling outside the margin, balancing bias and variance. A random hyperparameter search with a tune length of 30 was conducted to fine-tune the σ and C values across 30 combinations within a predefined range.
Random Forest (RF) is an ensemble machine learning algorithm that combines multiple classification trees using two powerful randomization techniques: bootstrap aggregating and random feature selection. These methods improve accuracy and make RF resilient against overfitting (Breiman, 2001). Its popularity stems from its simplicity in training, ease of parameter tuning, ability to handle nonlinear models, and strong classification performance (Cao et al., 2012). The Gini index, which measures node impurity, is often used to split binary data in RF. The leaves of the trees represent class labels, while the nodes guide the samples to a specific class (Breiman, 2001). The random forest algorithm in this study was executed as follows.
-
a)
The RF model was initially built using default parameters: the number of trees (ntree) was set to 500, and the number of split variables (mtry) was defined as the square root of the number of variables (), following de Santana et al. (2019). The ntree value of 500 was chosen after initial tests showed that it stabilized the out-of-bag (OOB) error, indicating effective performance with minimal tuning. In this context, ntree refers to the number of trees, while mtry specifies the number of variables used to grow each tree.
-
b)
A dual approach was employed to assess and enhance model performance while minimizing overfitting and ensuring good generalization to new data. First, automatic internal validation through OOB error estimation was performed, a process intrinsic to the RF algorithm. RF generates bootstrap subsets (ntree subsets) of the dataset through bagging, using about two-thirds of the calibration samples for tree growth, while the remaining OOB samples are used for cross-validation. These OOB samples estimate model performance. RF improves the effectiveness of bagging by reducing tree correlation, with unpruned trees developed at each bootstrap iteration. At every node, mtry variables are randomly selected to identify the split that minimizes the Gini index. The final prediction is determined through majority voting across all trees.
-
c)
Rather than moving directly to external prediction, we employed ten-fold cross-validation to further optimize the model. A random search for the best-performing mtry was conducted with a tune length of 30, ensuring the simplest model selection. This extensive validation provided a robust estimate of model performance.
-
d)
Finally, the simplest model, selected using the oneSE rule, was validated with external test samples to assess its generalizability.
Artificial Neural Networks (ANNs) are powerful tools for supervised pattern recognition in complex datasets. These models simulate neural processes by using interconnected layers of nodes or neurons, allowing them to process both linear and non-linear data. In this study, we employed the nnet model, a single hidden layer feed-forward neural network. The network architecture consisted of an input layer, one hidden layer, and an output layer, trained using backpropagation with a sigmoid activation function. Model performance was optimized by fine-tuning key hyperparameters, including the number of neurons in the hidden layer and the decay parameter, which prevents overfitting by penalizing large weights. Given the risk of overfitting in ANNs, careful parameter selection was essential. The best hyperparameters were identified through grid search, cross-validation, and the oneSE rule, with neuron counts ranging from 1 to 15 and decay values of 0, 0.001, 0.01, and 0.1. The maximum number of weights (MaxNWts) was set at 1000, and the maximum iterations (maxit) at 200.
2.8. Statistical analysis
2.8.1. Training and testing of machine learning models
Machine learning models, including PLS-DA, KNN, SVM, RF, Naïve Bayes, and ANN, were developed using RStudio Posit software (version 4.3.2) with the packages “pls,” “class,” “e1071,” “randomForest,” “nnet,” and “caret” (Ai et al., 2014; Liland et al., 2022; Meyer et al., 2022). The “trainControl” function from the “caret” package enabled stratified 10-fold cross-validation, repeated 10 times (“repeatedcv”). Models were trained using the methods “pls,” “knn,” “svmRadial,” “rf,” “naiveBayes,” and “nnet,” implemented via the "train" function of the "caret" package. A random seed was set prior to running the models to ensure reproducibility. The "stats" package R Core Team (2022) was used for PCA, and all visualizations were generated using “ggplot2”.
To address the issue of class imbalance in the dataset, SMOTE (Synthetic Minority Over-sampling Technique) was applied during model training using the built-in sampling method in the caret package. Specifically, SMOTE was incorporated via the sampling = "smote" argument in the trainControl function. This approach generated synthetic samples for the minority class within each fold of the training set, ensuring that the models were trained on balanced data without affecting the external validation or test sets (Kuhn et al., 2023).
Prior to model development, the samples were split into a calibration set (1380 samples ≈ 70%) and a test set (615 samples ≈ 30%), as outlined in Section 2.2. Optimal hyperparameter selection for the calibration models was performed through exhaustive grid search or random search, combined with model tuning and 10-fold cross-validation, repeated ten times. Specifically, nine partitions were used for model calibration, while one partition served as the internal validation set. This iterative process was repeated ten times, with samples randomly assigned without replacement each time. The grid search procedure not only enabled optimal parameter selection by estimating the standard error of prediction (SE), but also improved the accuracy of prediction error estimates for the calibration models.
Typically, the "carettrain" function selects the model with the highest performance metric, such as accuracy. In this study, however, the 'one standard error rule' (oneSE), recommended by Hastie et al. (2009), was used. The oneSE rule selects the simplest model that falls within one standard error of the best-performing model, helping to reduce the risk of overfitting. The selected parsimonious model was then applied to independent test sets, which were not used during training, to simulate real-world conditions. This external validation set, consisting of unlabeled samples, was used to assess the model's reliability and prediction performance.
The "varImp" function from the 'caret' package was used to identify the most influential predictors in the predictive model (Kuhn, 2008). This function calculates the importance of each predictor using various techniques, enabling the ranking of variables and providing insights into their overall impact within each model. For instance, in the Random Forest model, both the Gini importance index and permutation importance index were used (Li et al., 2024), while in PLS, importance was determined by the weighted sums of the absolute regression coefficients. For models lacking intrinsic importance metrics, such as k-NN, SVM, and ANN, permutation tests were employed to assess the effect of feature shuffling on model accuracy. All importance scores were scaled to a maximum of 100, unless the "scale" argument in "varImp" was set to FALSE (Chen et al., 2020). Previous studies have applied the 'top N variables' approach for selecting relevant features in machine learning models (Cui et al., 2023; Kganyago et al., 2017). Following this framework, the top 20 spectral bands ranked by variable importance were used to reconstruct the binary classification models in this study.
2.8.2. Evaluation of Model performance
The performance of each binary machine learning classification algorithm was evaluated using metrics such as accuracy, sensitivity, precision, specificity, F1 score, and Matthews Correlation Coefficient (MCC), calculated from confusion matrices, as shown in equations (2), (3), (4), (5), (6), (7)) (de Santana et al., 2018; van Roy et al., 2018).
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Where TP = true positives, TN = true negatives, FN = false negatives, and FP = false positives. A classification is considered perfect when all positives (adulterated samples) are correctly identified as positives and all negatives (authentic EVOO) are classified as negatives, with all performance metrics equaling 1 (Chicco and Jurman, 2023). Accuracy measures the overall proportion of correct predictions, while sensitivity and specificity assess the model's ability to correctly identify positive and negative samples, respectively. Precision focuses on the accuracy of positive predictions, and the F1 score balances precision and sensitivity, which is particularly useful for imbalanced datasets. The Matthews Correlation Coefficient (MCC), a robust metric for assessing agreement between predicted and actual classes, was also used due to the numerical imbalance of sample groups. MCC values range from −1 to 1, where −1 indicates complete disagreement, 0 represents random chance, and 1 signifies perfect agreement between predicted and actual classes (Chicco and Jurman, 2023).
2.8.3. Comparison of model performance by inferential statistical methods
The effects of preprocessing techniques and the performance of different binary classification models were compared using Matthews correlation coefficient (MCC.p) values from the external test set. MCC.p is particularly valuable for handling class imbalances, as it provides a balanced metric that incorporates all elements of the confusion matrix: True Negatives (TN), True Positives (TP), False Negatives (FN), and False Positives (FP), offering a comprehensive measure of model effectiveness (Chicco and Jurman, 2020).
Before analysis, the MCC.p data was tested for normality using the Shapiro-Wilk test and for homogeneity of variance using Levene's test. Since the data failed to meet the assumptions of normality (p < 0.05) and homoscedasticity (p < 0.05), non-parametric statistical methods were applied. The Kruskal-Wallis H test, using the 'PMCMRplus' package (Pohlert and Pohlert, 2022), was first used to assess differences in MCC scores across multiple models and preprocessing techniques. To evaluate interactions between model types and preprocessing methods, the Aligned Rank Transform (ART) for ANOVA was applied via the "ARTool" package. This method allows the application of conventional ANOVA techniques on ranked data, facilitating robust interaction testing in a non-parametric framework (Wobbrock et al., 2011).
Dunn's Test with Bonferroni correction ("dunn.test" package) was then used for multiple comparisons to identify statistical differences between models (Dinno, 2017). Additionally, the Wilcoxon signed-rank test was conducted to determine statistical differences in MCC scores for each model, with and without variable selection. This non-parametric test was selected due to the paired nature of the data and the non-normal distribution of the differences.
3. Results and discussion
3.1. Spectral reflectance profiles of oils
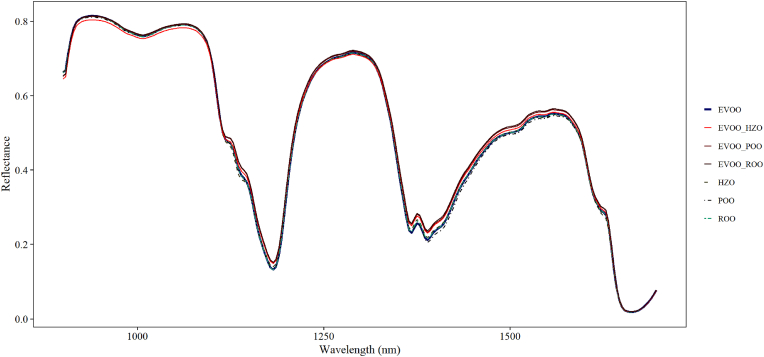
Fig. 2 presents the averaged spectral profiles of EVOO, adulterant oils, and adulterated olive oils from unprocessed HSI spectral data. These profiles display similarities, but notable variations in reflectance occur at specific wavelengths, particularly between 1114 and 1132 nm, 1139–1146 nm, 1171–1192 nm, 1360–1421 nm, and 1610–1635 nm. These peaks correspond to functional groups such as C–H, C–C, C–N, C=O, and O–H, arising from the vibrational modes of fatty acids and phenolic compounds (Choi and Moon, 2020; Xiaobo et al., 2010; Xie et al., 2014). Reflectance values for adulterated olive oils consistently exceed those of EVOO across the spectral range, likely due to the lower pigment levels, such as carotenoids and chlorophyll, caused by the refining process. In contrast, EVOO undergoes minimal processing and retains more natural pigments, resulting in lower reflectance due to compounds including polyphenols and antioxidants, which strongly absorb light in the visible and near-infrared regions (Mignani et al., 2011).
Fig. 2.
Averaged hyperspectral imaging raw spectra extra virgin olive oil (EVOO), edible oil adulterants, and adulterated olive oils.
3.2. Unsupervised learning by principal component analysis
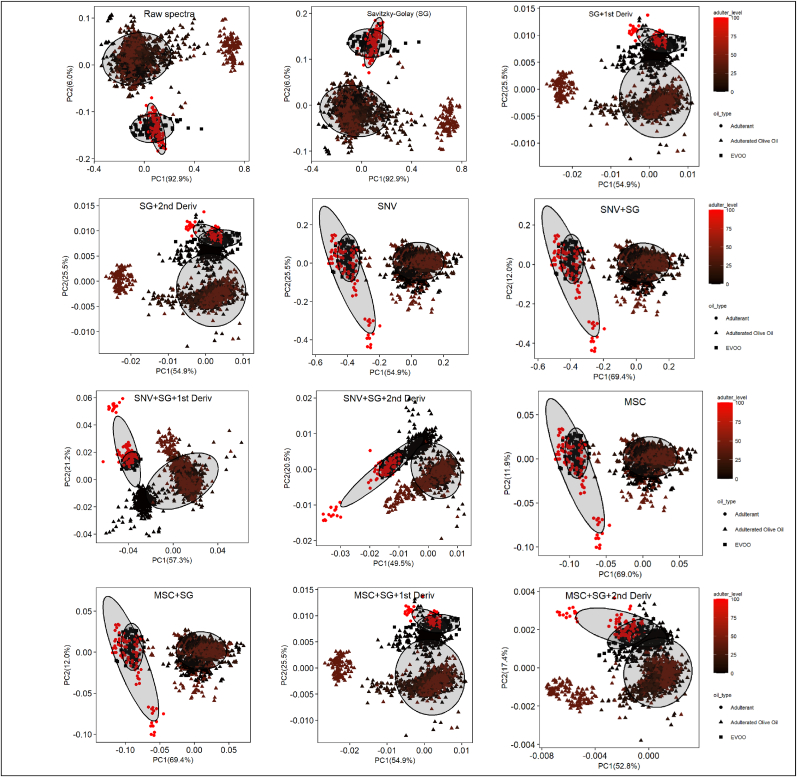
Unsupervised exploratory data analysis employing principal component analysis (PCA) was initially conducted on both raw and preprocessed spectral data. The primary objectives of PCA were to (i) visualize the samples, categorizing them as authentic EVOO, adulterants, or adulterated olive oil in a reduced-dimensional space, and (ii) identify patterns of oil groupings based on varying levels of adulteration. Fig. 3 shows the resulting plots for the first two principal components (PC1 and PC2), corresponding to each spectral preprocessing technique. PC1 and PC2 account for 98.9% of the variance in two datasets, the raw spectral data and the data treated with Savitzky-Golay alone. In contrast, the first two principal components explain 70–80% of the variance in the data subjected to other preprocessing techniques. This is likely due to noise reduction and enhanced spectral resolution from preprocessing, which distributes variance across more PCs (Feng et al., 2013). However, despite preprocessing, no significant improvement in separation among the three groups (EVOO, adulterants, adulterated oils) is observed based on PC1 and PC2. As shown in Fig. 3, EVOO and adulterants cluster closely in most principal component (PC) score plots. Additionally, some oils adulterated at 1–40% often cluster near or within the EVOO and adulterant groups, making visual separation based on adulteration levels challenging. Given these limitations in PCA visualization, advanced machine learning algorithms were applied to achieve more accurate and reliable classification.
Fig. 3.
PCA scores plots illustrate the grouping distribution of EVOO, edible oil adulterants, and adulterated olive oil using unprocessed spectra and different sets of preprocessed spectral data.
3.3. Supervised classification algorithms for full-spectrum hyperspectral imaging data
Following exploratory data analysis, machine learning algorithms using the full NIR-HSI spectral data were applied for supervised classification. The objective was to address three key questions: (i) evaluating the models' ability to distinguish between authentic and adulterated olive oil in a binary classification framework ('two Classes'), (ii) assessing the accuracy of the models in classifying pure EVOO, adulterants, and adulterated olive oils ('three Classes'), and (iii) examining the models' efficiency in differentiating among EVOO, hazelnut oil (HZO), olive pomace oil (POO), refined olive oil (ROO), and their mixtures with EVOO (EVOO + HZO, EVOO + POO, EVOO + ROO), labeled as 'seven Classes'. From an industry perspective, classification based on the exact percentage of adulteration is often less crucial than determining whether a sample is authentic or adulterated. Instead, a binary or multi-class classification (e.g., authentic vs. adulterated, or pure vs. varying adulteration types) offers more actionable insights for consumers and stakeholders. This approach better reflects real-world applications, providing clearer guidance on product authenticity and quality assurance. Thus, the models in this study were designed with these practical industry needs in mind.
3.3.1. Partial Least Squares discriminant analysis (PLS-DA)
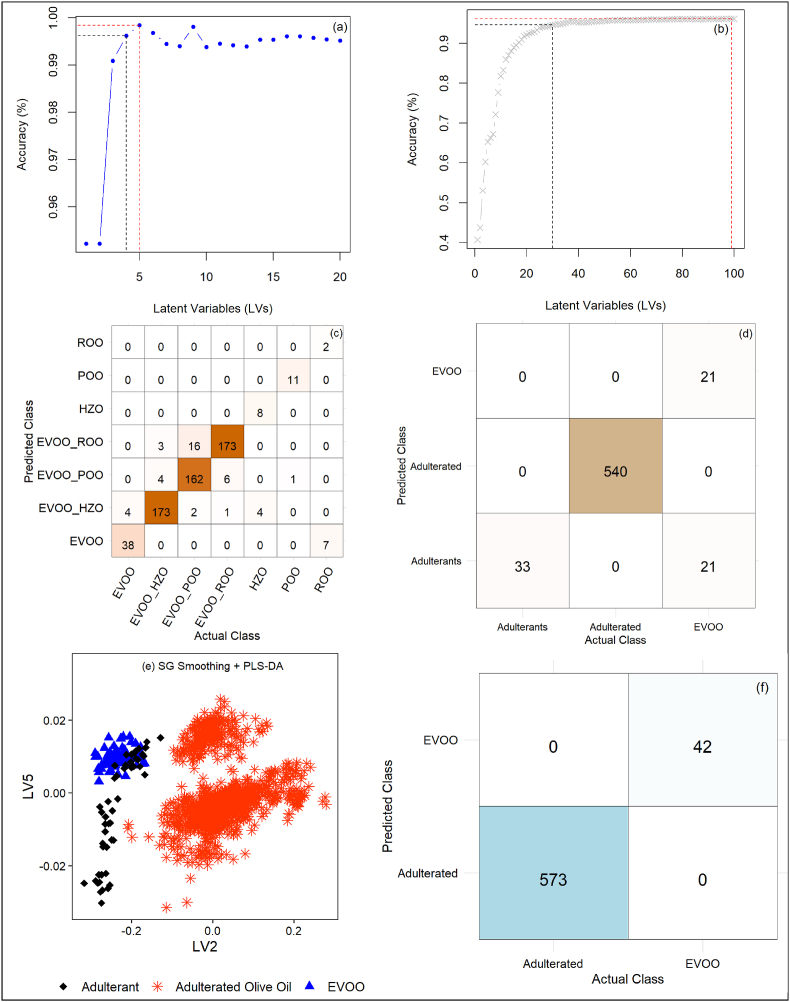
Table 1 summarizes the performance parameters for the PLS-DA classification models. To prevent overfitting, model selection focused on the simplest models with the optimal number of latent variables (LVs) based on the one-standard-error (oneSE) rule through cross-validation. For the 'three Classes' scenarios, 15 to 23 LVs were needed, while the 'two Classes' models required only 4 or 5 LVs, as shown in Table 1. In contrast, the more complex seven-class classification required 30 to 43 LVs. Adding more LVs beyond a certain threshold did not improve model performance, especially when these improvements remained within the standard error margin (Fig. 4a & b). This often leads to overfitting, where the model captures noise instead of meaningful patterns, reducing its generalization capability. These findings emphasize the importance of parsimony in model development, balancing simplicity and accuracy to avoid overfitting (Hastie et al., 2009).
Table 1.
Performance parameters of Partial Least Squares-Discriminant Analysis (PLS-DA) and K-Nearest Neighbors (KNN) classification models for cross-validation and external validation in the detection of adulteration in extra virgin olive oil (EVOO).
| Pre-processing | Model | Seven-Class Models |
Three-Class Models |
Two-Class/Binary Models |
F1.p | MCC.p | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LVs/k | ACC.cv | ACC.p | LVs/k | ACC.cv | ACC.p | LVs/k | ACC.cv | Sens.cv | Prec.cv | Spec.cv | F1.cv | ACC.p | Sens.p | Prec.p | Spec.p | ||||
| Unprocessed | PLS-DA | 33 | 95.2 | 93.5 | 22 | 99.6 | 96.6 | 5 | 99.6 | 99.8 | 99.8 | 95.0 | 99.7 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SG smoothing | PLS-DA | 33 | 95.3 | 92.2 | 23 | 99.5 | 96.8 | 5 | 99.6 | 99.8 | 99.8 | 95.2 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SG+1st deriv. | PLS-DA | 40 | 95.8 | 93.0 | 19 | 99.7 | 96.9 | 5 | 99.3 | 99.8 | 99.5 | 89.1 | 99.6 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SG+2nd deriv. | PLS-DA | 40 | 95.8 | 93.2 | 19 | 99.7 | 97.1 | 5 | 99.4 | 99.8 | 99.5 | 89.7 | 99.7 | 98.9 | 100 | 98.8 | 83.3 | 99.4 | 0.91 |
| SNV | PLS-DA | 31 | 96.1 | 94.2 | 22 | 99.8 | 96.9 | 4 | 99.6 | 99.9 | 99.7 | 93.8 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG Smoothing | PLS-DA | 41 | 95.6 | 94.8 | 22 | 99.6 | 97.9 | 4 | 99.6 | 99.9 | 99.7 | 93.8 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+1st deriv. | PLS-DA | 43 | 95.9 | 93.0 | 21 | 99.6 | 97.2 | 4 | 99.3 | 99.9 | 99.4 | 87.0 | 99.6 | 99.0 | 100 | 99.0 | 85.7 | 99.5 | 0.92 |
| SNV + SG+2nd deriv. | PLS-DA | 31 | 95.2 | 94.2 | 15 | 99.7 | 98.7 | 4 | 99.7 | 99.8 | 99.9 | 97.9 | 99.8 | 99.7 | 99.8 | 99.8 | 97.6 | 99.8 | 0.97 |
| MSC | PLS-DA | 30 | 95.6 | 93.5 | 22 | 99.7 | 96.9 | 4 | 99.6 | 99.9 | 99.7 | 93.4 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG Smoothing | PLS-DA | 34 | 95.2 | 94.3 | 22 | 99.5 | 97.6 | 4 | 99.6 | 99.9 | 99.7 | 93.8 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG+1st deriv. | PLS-DA | 40 | 95.8 | 93.0 | 19 | 99.6 | 96.9 | 5 | 99.3 | 99.8 | 99.5 | 89.1 | 99.6 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG+2nd deriv. | PLS-DA | 30 | 94.6 | 93.8 | 17 | 99.6 | 98.1 | 4 | 99.6 | 99.9 | 99.6 | 92.3 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| Unprocessed | KNN | 3 | 70.4 | 59.4 | 3 | 98.9 | 95.9 | 3 | 98.9 | 99.5 | 99.4 | 88.6 | 99.4 | 95.9 | 97.3 | 98.2 | 76.2 | 97.8 | 0.70 |
| SG smoothing | KNN | 3 | 70.1 | 59.5 | 3 | 98.9 | 95.9 | 3 | 98.9 | 99.5 | 99.4 | 87.5 | 99.4 | 95.9 | 97.4 | 98.2 | 76.2 | 97.8 | 0.70 |
| SG+1st deriv. | KNN | 3 | 80.1 | 71.5 | 3 | 99.8 | 99.4 | 3 | 99.8 | 99.8 | 99.9 | 98.3 | 99.9 | 99.4 | 99.3 | 100 | 100 | 99.6 | 0.95 |
| SG+2nd deriv. | KNN | 3 | 80.2 | 71.1 | 3 | 99.7 | 99.4 | 3 | 99.8 | 99.8 | 99.9 | 98.5 | 99.9 | 99.4 | 99.3 | 100 | 100 | 99.6 | 0.95 |
| SNV | KNN | 3 | 87.9 | 66.5 | 3 | 99.6 | 99.4 | 3 | 99.6 | 99.7 | 99.9 | 97.2 | 99.8 | 99.4 | 99.5 | 99.8 | 97.6 | 99.7 | 0.95 |
| SNV + SG Smoothing | KNN | 3 | 87.7 | 66.7 | 3 | 99.6 | 99.4 | 3 | 99.6 | 99.7 | 99.9 | 97.2 | 99.8 | 99.4 | 99.5 | 99.8 | 97.6 | 99.7 | 0.95 |
| SNV + SG+1st deriv. | KNN | 3 | 85.0 | 71.2 | 3 | 99.7 | 99.7 | 3 | 99.7 | 99.7 | 100 | 100 | 99.9 | 99.7 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| SNV + SG+2nd deriv. | KNN | 3 | 90.7 | 76.1 | 3 | 99.8 | 100 | 3 | 99.8 | 99.8 | 100 | 99.8 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | KNN | 3 | 87.9 | 66.5 | 3 | 99.6 | 99.4 | 3 | 99.6 | 99.7 | 99.9 | 97.2 | 99.6 | 99.4 | 99.5 | 99.8 | 97.6 | 99.7 | 0.95 |
| MSC + SG Smoothing | KNN | 3 | 87.7 | 66.7 | 3 | 99.6 | 99.4 | 3 | 99.6 | 99.7 | 99.9 | 97.2 | 99.8 | 99.4 | 99.5 | 99.8 | 97.6 | 99.7 | 0.95 |
| MSC + SG+1st deriv. | KNN | 3 | 87.7 | 71.5 | 3 | 99.7 | 99.4 | 3 | 99.8 | 99.8 | 99.9 | 98.3 | 99.9 | 99.4 | 99.3 | 100 | 100 | 99.6 | 0.95 |
| MSC + SG+2nd deriv. | KNN | 3 | 89.1 | 79.0 | 3 | 99.8 | 100 | 3 | 99.9 | 99.8 | 100 | 100 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
The metric values for the trained models represent averaged classification parameters of 10-fold cross-validation repeated ten times. ACC.cv = Accuracy, Sens.cv = Sensitivity, Prec.cv = Precision, Spec.cv = Specificity, and F1.cv = F1 Score for cross-validation. ACC.p = Accuracy, Sens.p = Sensitivity, Prec.p = Precision, Spec.p = Specificity, F1.p = F1 Score, and MCC.p = Matthews correlation coefficient for the external validation set (test set). SNV = Standard Normal Variate; MSC = Multiplicative Scatter Correction; SG = Savitzky-Golay smoothing; 1st deriv. = 1st derivative; 2nd deriv. = second derivative; LVs and k = an optimal number of latent variables and k-nearest neighbors for the best model after cross-validation. For the Seven-Class system, the classification involves seven groups: extra-virgin olive oil (EVOO), hazelnut oil (HZO), olive pomace oil (POO), refined olive oil (ROO), EVOO + HZO, EVOO + POO, and EVOO + ROO. The Three-Class system categorizes oils into three groups: authentic extra-virgin olive oil, edible oil adulterant (100%), or adulterated (1–40% adulteration) olive oil. The Two-Class system is a binary classification distinguishing between pure EVOO and adulterated olive oil (1–100% adulteration).
Fig. 4.
(a). The optimum number of latent variables for the MSC + SG + 2nd derivative - PLS-DA model used for binary classification and (b) is the optimum number of latent variables for the MSC + SG+2nd derivative-PLS-DA model for multi-class classification (7 classes). The simplest optimal model (represented by the black dotted line) is selected based on the 'one standard error rule,' meaning it falls within one standard error of the highest accuracy model (represented by the red dotted line). (c) A confusion matrix table showing correct classification and misclassifications by PLS-DA + raw spectra data; (e) PLS-DA plot indicating misclassification of some adulterants as EVOO with data pre-processed by SG smoothing in cross-validation; (f) A confusion matrix indicating perfect classification with one of the binary PLS-DA classification models. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
The cross-validation accuracy (ACC.cv) and external prediction accuracy (ACC.p) for the "seven-class" classification ranged from 95.2 to 96.2% and 92.2–94.8%, respectively. These results align with previous findings (Malavi et al., 2023), which reported an ACC.p of 93.8% for distinguishing EVOO from adulterants using hyperspectral imaging. The highest error rate (7.8%) occurred with PLS-DA combined with Savitzky-Golay (SG) smoothing, where 4 EVOO samples were misclassified as EVOO + HZO and 7 ROO samples as EVOO (Fig. 4c). Similarly, PLS-DA with SG+1st derivative misclassified 7 EVOO samples as EVOO + HZO, 1 as ROO, and 3 as POO. Although detecting chemically similar oils such as HZO is challenging (Zabaras, 2010), PLS-DA models reliably differentiated HZO, POO, and EVOO, without misclassifying adulterated samples (1–40%) as pure EVOO. However, models using SG, SNV, SNV+2nd derivative, MSC, and MSC+2nd derivative preprocessing misclassified 7, 1, 2, 4, and 2 ROO samples as EVOO, respectively. These results demonstrate high accuracy but reveal the challenge in distinguishing pure EVOO from ROO, with most misclassifications involving pure EVOO being labeled as mixed with HZO, POO, or ROO.
The PLS-DA models achieved an ACC.p ranging from 96.6% with raw spectral data to 98.7% using SNV + SG+2nd derivative data for distinguishing authentic EVOO from adulterants and adulterated oils. Notably, all PLS-DA models, irrespective of preprocessing techniques, correctly identified all adulterants and adulterated oils (1–40%). However, a recurring issue was the frequent misclassification of genuine EVOO as adulterated. For example, in the model utilizing raw spectral data, 50% of EVOO samples (21 cases) were incorrectly classified as adulterants (Fig. 4d). These results indicate that while PLS-DA models excel at detecting adulteration, they tend to overestimate adulteration in authentic EVOO, potentially leading to false positives (Type 1 errors) in the 'three-class' classification setup.
PLS-DA models for binary classification (two classes) performed exceptionally well in detecting adulterated olive oil. Seventy-five percent of models across various preprocessing techniques achieved 100% accuracy (ACC.p), sensitivity (Sens.p), precision (Prec.p), F1 score (F1.p), and a Matthews correlation coefficient (MCC.p) of 1.0 on external test sets (Table 1 & Fig. 4f). These models demonstrated high specificity and sensitivity, reliably identifying both pure and adulterated samples, which is crucial for the olive oil industry due to the minimal risk of misclassification. Their high precision further ensures the accurate detection of adulterated oils while minimizing false positives. These results affirm the effectiveness of PLS-DA in distinguishing authentic EVOO from oils adulterated with hazelnut, pomace, or refined olive oil. These results closely align with previous findings that achieved 100% accuracy in differentiating EVOO from sunflower, sesame, corn, canola, and safflower oils (Malavi et al., 2023).
This study marks a key advancement by successfully detecting EVOO adulteration involving refined HZO and ROO using HSI for the first time. It builds upon previous research that demonstrated the effectiveness of hyperspectral imaging and discriminant models, such as PLS-DA and LDA, in classifying various edible oils, including sesame and flavored oils (Choi and Moon, 2020; Romaniello and Baiano, 2018; Xie et al., 2014). However, some PLS-DA models showed misclassifications. For instance, using SG+2nd derivative data, the model misclassified 7 EVOO cases, reducing ACC.p to 98.9%, specificity to 83.3%, and MCC to 0.91. PLS-DA with SNV + SG+1st derivative spectra misclassified 6 EVOO samples, while SNV + SG+2nd derivative misclassified one EVOO sample and one pure ROO sample. Despite these misclassifications, the 'two-class' PLS-DA models demonstrated exceptional predictive performance on external test samples, achieving a perfect MCC.p of 1.0. Overall, this study accentuates the effectiveness of combining HSI with PLS-DA for distinguishing EVOO from adulterated oils with similar chemical profiles, such as HZO, POO, and ROO.
3.3.2. K-nearest neighbor (k-NN) classification
The k-NN algorithm, known for its simplicity and effectiveness in classification, consistently used 3 k-nearest neighbors, determined through repeated cross-validation and the 'oneSE' rule (Fig. 5a). Despite its efficiency, k-NN models demonstrated poor to moderate performance in the more complex seven-class classification tasks, with accuracy rates between 59.4% and 79.0% (Table 1). Notably, none of the models misclassified pure EVOO as adulterated with HZO, POO, or ROO (1–40%) or as pure HZO. However, when misclassifications occurred, EVOO was incorrectly labeled as pure ROO or POO. The highest error rates were found in models using raw spectra and SG smoothing alone, where 8 EVOO samples were misclassified as POO and 2 as ROO. Additionally, these models misclassified 3 cases of EVOO + HZO as pure EVOO. On the other hand, no cases of EVOO + POO or EVOO + ROO were misclassified as pure EVOO across any of the 'seven-class' k-NN models. While no POO samples were misclassified as EVOO, several ROO and HZO samples were misidentified as pure EVOO across most preprocessing techniques. For instance, models using raw and SG-smoothed data each misclassified 7 out of 9 ROO samples and 5 out of 9 HZO samples as EVOO (Fig. 5b). k-NN models are particularly sensitive to distortions in the spectral data (Zheng et al., 2014). Misclassifications in models using unprocessed or SG-smoothed data likely result from insufficient noise reduction and an inability to enhance critical spectral features, making it difficult to distinguish EVOO from adulterants. The complexity of the seven-class classification further exacerbates these challenges, as more refined and processed data are required to accurately differentiate between multiple oil types.
Fig. 5.
(a) Selection of optimal k-nearest neighbors by cross-validation and oneSE rule. The simplest optimal k-NN model (represented by the black dotted line) is selected based on the 'one standard error rule,' meaning it falls within one standard error of the highest accuracy model (represented by the red dotted line). Confusion matrixes showing misclassification by (b) ‘seven-class’ k-NN model and Savitzky-Golay data, (c) ‘three-class’ k-NN model using unprocessed spectra and (d) perfect classification by ‘two-class’ k-NN model coupled with MSC + SG+2nd derivative data. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Conversely, k-NN models demonstrated higher accuracy in the 'three-class' classification compared to the 'seven-class', with most models achieving over 96% accuracy (ACC.p). Models with SNV + SG+2nd derivative and MSC + SG+2nd derivative data achieved perfect accuracy (ACC.p of 100%). However, models using either unprocessed or only SG-smoothed data recorded the lowest accuracy (ACC.p = 95.9%), reflecting trends seen in the 'seven-class' classification. These models misclassified 10 EVOO samples as adulterants, 12 adulterants (5 HZO and 7 ROO) as EVOO, and 3 adulterated samples (EVOO + HZO, 90:10) as pure EVOO (Fig. 5c). All other k-NN models correctly identified the adulterated oils (1–40%). Most models also classified EVOO samples accurately, except those preprocessed with SNV, SNV + SG, MSC, and MSC + SG, which each misidentified one EVOO sample as adulterated. While these preprocessing techniques are effective in reducing noise and correcting baselines, they may not have fully removed scatter effects in the spectral data (Feng and Sun, 2013), contributing to the observed misclassifications.
The performance metrics for the 'two-class' k-NN predictive models ranged from ACC.p (95.9–100%), Sens.p (97.3–100%), Prec.p (98.2–100%), Spec.p (76.2–100%), and F1.p (97.8–100%). Models using MSC + SG+2nd derivative and SNV + SG+2nd derivative preprocessing achieved perfect scores across all metrics (Fig. 5d), similar to the 'three-class' models. In contrast, k-NN models based on unprocessed spectra or only Savitzky-Golay smoothing performed worse, with an MCC.p of 0.70. This highlights the importance of combining techniques, such as smoothing, removing multiplicative and additive effects, and enhancing key spectral features, to improve k-NN performance on HSI spectra (Lohumi et al., 2015). he lowest-performing models (k-NN with raw spectra and k-NN with SG-smoothed spectra) misclassified 10 out of 42 EVOO cases as adulterated, resulting in low specificity (76.2%). These models also misclassified 15 out of 573 adulterated samples as pure EVOO, reducing sensitivity to 97.3%. Similar to the 'three-class' classification, these misclassifications occurred when the models incorrectly identified pure HZO and ROO as EVOO, likely due to the spectral similarities at certain wavelengths, reflecting their close chemical profiles (Datta et al., 2022). Despite these misclassifications, the k-NN models exhibited higher precision and F1 scores, reflecting their strong ability to accurately detect adulterated oils. In comparison to related research, our use of HSI with k-NN models outperformed the results from Georgouli et al. (2017), where k-NN models paired with Raman and mid-infrared FTIR achieved classification accuracies between 69.8 and 82.3% for detecting hazelnut oil adulteration in EVOO. Our findings are consistent with those of Hwang et al. (2024), who effectively classified different vegetable oils using HSI and k-NN. Although k-NN is considered a relatively simple model, our study shows that when combined with HSI data preprocessed using SNV + SG+2nd derivative or MSC + SG+2nd derivative, it is highly effective in screening EVOO samples for authenticity.
3.3.3. Discrimination of oils by random forest classifier
Table 2 illustrates the performance of Random Forest (RF) models in classification of oil. According to Breiman (2001), both 'mtry' (variables sampled at each split) and 'ntree' (number of trees) are critical factors influencing model performance (Fig. 6a & b). While higher 'ntree' values generally improve model robustness, increasing beyond a certain point leads to diminishing returns, raising computational costs without significant performance gains. As shown in Fig. 6b, the error rate for the EVOO class initially exceeds that of adulterated oils but stabilizes with an increase in the number of trees. A forest size of 500 trees was sufficient to stabilize out-of-bag (OOB) errors across all RF models, with optimal 'ntree' values ranging from 7 to 55.
Table 2.
Random Forest (RF), Support Vector Machines (SVM), and Naïve Bayes (NB) classification model parameters for cross-validation and external validation in authenticating extra virgin olive oil.
| Pre-processing | Model | Seven-Class Models |
Three-Class Models |
Two-Class/Binary Models |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Parameters | ACC.cv | ACC.p | Optimal Parameters | ACC.cv | ACC.p | Optimal Parameters | ACC.cv | Sens. cv | Prec. cv | Spec. cv | F1.cv | ACC.p | Sens. p | Prec. p | Spec. p | F1.p | MCC.p | ||
| Unprocessed | RF | mt = 18, nt = 500 | 81.6 | 64.2 | mt = 43,nt = 500 | 99.1 | 97.7 | mt = 55,nt = 500 | 99.4 | 99.7 | 99.8 | 95.6 | 99.7 | 99.2 | 99.1 | 100 | 100 | 99.6 | 0.94 |
| SG smoothing | RF | mt = 43, nt = 500 | 81.2 | 64.0 | mt = 43,nt = 500 | 99.2 | 97.7 | mt = 72,nt = 500 | 99.5 | 99.6 | 99.8 | 96.0 | 99.7 | 99.2 | 99.1 | 100 | 100 | 99.6 | 0.94 |
| SG+1st deriv. | RF | mt = 14, nt = 500 | 92.8 | 82.1 | mt = 14, nt = 500 | 99.9 | 99.8 | mt = 7,nt = 500 | 99.8 | 100 | 99.9 | 95.7 | 99.9 | 99.9 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| SG+2nd deriv. | RF | mt = 14, nt = 500 | 93.0 | 80.2 | mt = 14, nt = 500 | 99.9 | 99.8 | mt = 7,nt = 500 | 99.8 | 100 | 99.8 | 96.7 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV | RF | mt = 43, nt = 500 | 90.3 | 71.5 | mt = 14, nt = 500 | 99.7 | 97.4 | mt = 7,nt = 500 | 99.7 | 99.9 | 99.8 | 94.9 | 99.8 | 98.0 | 99.4 | 98.4 | 78.6 | 99.0 | 0.84 |
| SNV + SG Smoothing | RF | mt = 14, nt = 500 | 90.6 | 70.7 | mt = 14, nt = 500 | 99.7 | 97.4 | mt = 7, nt = 500 | 99.7 | 99.9 | 99.8 | 95.0 | 99.8 | 98.0 | 99.5 | 98.4 | 78.6 | 99.0 | 0.84 |
| SNV + SG+1st deriv. | RF | mt = 14, nt = 500 | 94.7 | 76.4 | mt = 14,nt = 500 | 100 | 100 | mt = 7,nt = 500 | 99.9 | 100 | 99.9 | 97.3 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | RF | mt = 14, nt = 500 | 96.0 | 86.0 | mt = 14,nt = 500 | 100 | 100 | mt = 7,nt = 500 | 99.9 | 100 | 99.9 | 97.1 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | RF | mt = 43, nt = 500 | 90.8 | 71.2 | mt = 43,nt = 500 | 99.8 | 98.9 | mt = 7,nt = 500 | 99.7 | 99.9 | 99.8 | 95.0 | 99.9 | 98.5 | 99.0 | 98.0 | 71.4 | 98.4 | 0.88 |
| MSC + SG Smoothing | RF | mt = 43, nt = 500 | 90.8 | 71.4 | mt = 14,nt = 500 | 99.8 | 97.4 | mt = 7,nt = 500 | 99.7 | 99.9 | 99.7 | 94.7 | 99.9 | 99.2 | 99.3 | 99.8 | 97.8 | 98.7 | 0.90 |
| MSC + SG+1st deriv. | RF | mt = 14, nt = 500 | 92.8 | 82.1 | mt = 14,nt = 500 | 99.9 | 99.8 | mt = 7,nt = 500 | 99.8 | 100 | 99.8 | 95.7 | 99.9 | 99.7 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| MSC + SG+2nd deriv. | RF | mt = 14, nt = 500 | 96.4 | 86.2 | mt = 43,nt = 100 | 99.9 | 99.8 | mtry = 7, nt = 500 | 99.8 | 100 | 99.8 | 96.2 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| Unprocessed | SVM | C = 5, σ = 0.01 | 55.2 | 55.6 | C = 10, σ = 0.01 | 99.7 | 99.2 | C = 5, σ = 0.01 | 99.5 | 99.6 | 99.9 | 97.7 | 99.7 | 99.5 | 99.8 | 99.7 | 95.2 | 99.7 | 0.96 |
| SG smoothing | SVM | C = 10, σ = 0.01 | 55.3 | 55.6 | C = 10, σ = 0.01 | 99.7 | 99.2 | C = 5, σ = 0.01 | 99.4 | 99.5 | 99.9 | 97.8 | 99.7 | 99.4 | 99.7 | 99.7 | 95.2 | 99.7 | 0.95 |
| SG+1st deriv. | SVM | C = 5, σ = 0.01 | 60.7 | 56.6 | C = 0.05, σ = 0.01 | 99.6 | 99.4 | C = 0.5, σ = 0.01 | 99.9 | 100 | 99.8 | 97.0 | 99.9 | 98.1 | 100 | 100 | 100 | 100 | 1.00 |
| SG+2nd deriv. | SVM | C = 5, σ = 0.01 | 60.8 | 56.7 | C = 0.1, σ = 0.01 | 99.7 | 99.5 | C = 0.5, σ = 0.01 | 99.9 | 100 | 99.8 | 97.1 | 99.9 | 98.0 | 100 | 100 | 100 | 100 | 1.00 |
| SNV | SVM | C = 10, σ = 0.01 | 58.6 | 50.7 | C = 0.5, σ = 0.01 | 99.9 | 97.6 | C = 0.5, σ = 0.01 | 99.8 | 100 | 99.8 | 97.0 | 99.9 | 97.6 | 100 | 97.4 | 64.3 | 98.7 | 0.79 |
| SNV + SG Smoothing | SVM | C = 0.1, σ = 0.01 | 57.7 | 63.1 | C = 0.5, σ = 0.01 | 99.8 | 97.6 | C = 0.5, σ = 0.01 | 99.8 | 100 | 99.8 | 97.0 | 99.9 | 97.6 | 100 | 97.4 | 64.3 | 98.7 | 0.79 |
| SNV + SG+1st deriv. | SVM | C = 0.05, σ = 0.01 | 61.3 | 55.9 | C = 0.05, σ = 0.01 | 99.7 | 98.2 | C = 0.1, σ = 0.01 | 99.7 | 100 | 99.9 | 97.6 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | SVM | C = 0.05, σ = 0.01 | 63.1 | 54.0 | C = 0.5, σ = 0.01 | 99.9 | 99.0 | C = 0.05, σ = 0.01 | 99.9 | 100 | 99.9 | 99.9 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | SVM | C = 10, σ = 0.01 | 58.6 | 50.7 | C = 0.5, σ = 0.01 | 99.9 | 97.6 | C = 0.5, σ = 0.01 | 99.8 | 99.9 | 99.8 | 97.0 | 99.9 | 97.6 | 100 | 97.4 | 64.3 | 98.7 | 0.79 |
| MSC + SG Smoothing | SVM | C = 0.1, σ = 0.01 | 57.8 | 63.3 | C = 0.5, σ = 0.01 | 99.9 | 97.6 | C = 0.5, σ = 0.01 | 99.8 | 99.9 | 99.8 | 97.0 | 99.9 | 97.6 | 100 | 97.4 | 64.3 | 98.7 | 0.79 |
| MSC + SG+1st deriv. | SVM | C = 5, σ = 0.01 | 60.7 | 55.9 | C = 0.05, σ = 0.01 | 99.6 | 99.2 | C = 0.5, σ = 0.01 | 99.9 | 100 | 99.8 | 97.0 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG+2nd deriv. | SVM | C = 1, σ = 0.01 | 61.3 | 59.5 | C = 0.5, σ = 0.01 | 99.9 | 99.0 | C = 0.5, σ = 0.01 | 99.9 | 100 | 99.9 | 98.2 | 99.9 | 99.0 | 100 | 99.0 | 85.7 | 99.5 | 0.95 |
| Unprocessed | NB | lc = 0.1, ad = 0.0 | 51.0 | 48.6 | lc = 0.1, ad = 0.0 | 97.4 | 94.3 | lc = 0.1, ad = 0.0 | 96.6 | 96.5 | 99.9 | 97.2 | 98.2 | 94.1 | 93.7 | 100 | 100 | 96.8 | 0.71 |
| SG smoothing | NB | lc = 0.1, ad = 0.0 | 51.1 | 48.8 | lc = 0.1, ad = 0.0 | 97.4 | 94.3 | lc = 0.1, ad = 0.0 | 96.5 | 97.7 | 99.9 | 97.7 | 98.2 | 94.1 | 93.1 | 100 | 100 | 96.8 | 0.71 |
| SG+1st deriv. | NB | lc = 0.1, ad = 1.0 | 72.0 | 68.3 | lc = 0.1, ad = 0.0 | 99.4 | 98.9 | lc = 0.1, ad = 0.0 | 99.3 | 99.3 | 99.0 | 98.0 | 99.6 | 96.8 | 96.6 | 100 | 100 | 99.4 | 0.92 |
| SG+2nd deriv. | NB | lc = 0.1, ad = 1.0 | 72.2 | 68.2 | lc = 0.1, ad = 0.0 | 99.4 | 98.9 | lc = 0.1, ad = 0.0 | 99.2 | 99.3 | 99.9 | 97.8 | 99.6 | 98.9 | 98.8 | 100 | 100 | 99.4 | 0.92 |
| SNV | NB | lc = 0.1, ad = 0.0 | 65.6 | 60.5 | lc = 0.1, ad = 0.0 | 98.7 | 94.1 | lc = 0.1, ad = 0.0 | 98.5 | 98.4 | 100 | 99.9 | 99.2 | 95.0 | 95.3 | 99.3 | 90.5 | 97.2 | 0.70 |
| SNV + SG Smoothing | NB | lc = 0.1, ad = 0.0 | 65.7 | 60.5 | lc = 0.1, ad = 0.0 | 98.7 | 94.1 | lc = 0.1, ad = 0.0 | 98.5 | 98.4 | 100 | 99.9 | 99.2 | 95.0 | 95.3 | 99.2 | 90.5 | 97.2 | 0.70 |
| SNV + SG+1st deriv. | NB | lc = 0.1, ad = 0.0 | 80.2 | 70.5 | lc = 0.1, ad = 0.0 | 99.8 | 99.5 | lc = 0.1, ad = 0.0 | 99.3 | 99.4 | 99.9 | 98.0 | 99.6 | 99.2 | 99.3 | 99.3 | 97.6 | 99.6 | 0.94 |
| SNV + SG+2nd deriv. | NB | lc = 0.1, ad = 0.0 | 84.3 | 82.4 | lc = 0.1, ad = 0.0 | 99.7 | 97.6 | lc = 0.1, ad = 0.0 | 99.9 | 100 | 99.9 | 98.0 | 99.9 | 97.7 | 100 | 97.6 | 66.7 | 98.8 | 0.81 |
| MSC | NB | lc = 0.1, ad = 0.0 | 65.6 | 60.8 | lc = 0.1, ad = 0.0 | 98.7 | 94.1 | lc = 0.1, ad = 0.0 | 98.4 | 98.4 | 100 | 99.9 | 99.2 | 95.0 | 95.2 | 99.3 | 90.5 | 97.2 | 0.70 |
| MSC + SG Smoothing | NB | lc = 0.1, ad = 0.0 | 65.7 | 60.7 | lc = 0.1, ad = 0.0 | 98.7 | 94.4 | lc = 0.1, ad = 0.0 | 98.4 | 98.4 | 100 | 100 | 99.2 | 95.0 | 95.2 | 99.2 | 90.5 | 97.2 | 0.70 |
| MSC + SG+1st deriv. | NB | lc = 0.1, ad = 1.0 | 72.0 | 68.2 | lc = 0.1, ad = 0.0 | 99.3 | 98.9 | lc = 0.1, ad = 0.0 | 99.3 | 99.3 | 99.9 | 98.0 | 99.6 | 98.9 | 98.8 | 100 | 100 | 99.4 | 0.92 |
| MSC + SG+2nd deriv. | NB | lc = 0.1, ad = 0.0 | 84.0 | 82.1 | lc = 0.1, ad = 0.0 | 99.5 | 99.2 | lc = 0.1, ad = 0.0 | 99.5 | 99.6 | 99.9 | 98.5 | 99.8 | 99.3 | 99.8 | 99.5 | 92.9 | 99.7 | 0.95 |
The metric values for the trained models represent averaged classification parameters of 10-fold cross-validation repeated ten times. ACC.cv = Accuracy, Sens.cv = Sensitivity, Prec.cv = Precision, Spec.cv = Specificity, and F1.cv = F1 Score for cross-validation. ACC.p = Accuracy, Sens.p = Sensitivity, Prec.p = Precision, Spec.p = Specificity, and F1.p = F1 Score for the external validation set (test set). SNV = Standard Normal Variate; MSC = Multiplicative Scatter Correction; SG = Savitzky-Golay smoothing; 1st deriv. = 1st derivative; 2nd deriv. = second derivative. mt = mtry: optimal the number of features randomly sampled at each split in a decision tree within the Random Forest using cross-validation and out-of-bag error; nt = ntree, denotes the total number of decision trees created in the Random Forest ensemble based on model tuning and cross-validation. C = cost parameter, σ = Gaussian Radial Basis kernel function for SVM model. Lc = lap lace, ad = adjust parameters for the Naïve Bayes model. For the Seven-Class system, the classification involves seven groups: extra-virgin olive oil (EVOO), hazelnut oil (HZO), olive pomace oil (POO), refined olive oil (ROO), EVOO + HZO, EVOO + POO, and EVOO + ROO. The Three-Class system categorizes oils into three groups: authentic extra-virgin olive oil, edible oil adulterant (100%), or adulterated olive oil (1–40%). The Two-Class system is a binary classification distinguishing between pure EVOO and adulterated olive oil (1–100% adulteration).
Fig. 6.
(a) Model selection based on 10-fold cross-validation and oneSE rule. The simplest optimal model (represented by the blue dotted line) is selected based on the 'one standard error rule,' meaning it falls within one standard error of the highest accuracy model (represented by the red dotted line). (b) Number of trees and out-of-bag error (OOB) for RF model classifier; the red line indicates how often the model incorrectly predicts the ‘EVOO’ class while the black line reflects the frequency of incorrect predictions for the 'Adulterated' class. Confusion matrices showing correct and incorrect classifications: (c) RF-Savitzky-Golay and (d) RF-MSC + SG+2nd derivative preprocessing model for seven-class classification; (e) RF-unprocessed spectra model for three-class discrimination; and (f) RF-SNV model for binary classification. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
RF models demonstrated ACC.cv and ACC.p ranging from 81.2% to 96.4% and 64.0%–86.2%, respectively, in the seven-class classification (Table 2). The best-performing model combined MSC + SG+2nd derivative preprocessing (Fig. 6d), while the RF model using only SG preprocessing had the lowest accuracy. Models leveraging SG and derivatives correctly classified all EVOO samples, but those using SNV, SNV + SG, and MSC spectral data, misclassified 5 EVOO cases as POO. Models using raw spectra, MSC, and SG misclassified 7, 5, and 6 EVOO samples as POO, respectively. Notably, none of the adulterated oils (1–40%) were misclassified as EVOO, except for a single EVOO + ROO case in the RF-raw model. RF models also effectively distinguished adulterants, with all HZO samples correctly classified, except for RF-raw and RF-SG, which each misclassified one HZO as EVOO. Similarly, for POO, RF-raw and RF-SG models misclassified 5 and 4 cases as EVOO, respectively. SG, SNV, and SNV + SG preprocessing each led to one EVOO sample being misclassified as ROO, while RF-MSC and RF-MSC + SG misclassified 2 cases each. These misclassifications suggest that SG preprocessing alone may not adequately enhance the spectral features necessary for multi-class classification (Fig. 6c). Noise and distortions in raw data likely hinder feature extraction, further affecting model accuracy.
RF models across various preprocessing methods showed robustness in three-class discrimination tasks, with all models achieving ACC.cv above 99% and ACC.p ranging from 97.7% to 100%. Similar findings were reported by Hwang et al. (2024) in vegetable oil classification using HSI technology. RF models combining SNV + SG+1st and SNV + SG+2nd derivatives achieved a perfect ACC.p of 100%, effectively distinguishing EVOO, adulterants, and adulterated oils. All three-class RF models using Savitzky-Golay and derivatives correctly classified all 42 EVOO samples. Only the RF-unprocessed model misclassified 2 HZO and 3 ROO samples as EVOO (Fig. 6e). The highest misclassification rate of 13 out of 42 EVOO samples as adulterants occurred in models using SG alone, SNV, SNV + SG, and MSC + SG preprocessing. However, these models showed greater sensitivity in detecting adulterated oils (1–40%), with 3 cases of EVOO + HZO (10%) misidentified as pure EVOO in each case. Despite some errors, RF models consistently performed well in classifying pure and adulterated olive oils across different preprocessing techniques.
In binary classification, RF models achieved high accuracy, ranging from 99.4% to 99.9% in cross-validation and 98.0%–100% in external validation. These models balanced error types effectively, as shown by MCC values (0.84–1.00) and F1 scores exceeding 98%. Spectral treatments including SG+2nd derivative, SNV + SG+1st derivative, SNV + SG+2nd derivative, and MSC + SG+2nd derivative led to perfect performance (100%) across all metrics on the test set (Table 2), likely due to enhanced feature extraction and noise reduction. The ACC.p range in our study corroborates with de Santana et al. (2018), who used RF with FTIR-HATR spectroscopy for oil discrimination, and outperforms RF models with laser-based spectroscopy used by Gazeli et al. (2020). Eight out of twelve RF models classified all pure EVOO samples correctly, achieving 100% specificity. However, RF-SNV (Fig. 6f) and RF-SNV + SG misclassified nine EVOO cases, while RF-MSC and MSC + SG misclassified five and six, respectively. Though some models misclassified 2 to 5 adulterated oil cases as pure EVOO, they maintained high sensitivity (>99%). For example, RF-unprocessed and RF-SG each misclassified five adulterated oil cases, while RF-SG and RF-MSC + SG+1st derivative misclassified two cases. Similarly, RF-SNV, RF-SNV + SG, RF-MSC, and RF-MSC + SG each misclassified two samples.
3.3.4. Authentication of EVOO using Support Vector Machine (SVM)
SVM models showed suboptimal performance in distinguishing oils across seven classes, with ACC.p values ranging from 50.7% to 63.3%. The models using only SNV and MSC exhibited the lowest accuracy. While most SVM models correctly classified pure EVOO, those utilizing raw, SNV + SG, and MSC + SG spectra misclassified 3 EVOO samples as either EVOO + HZO or POO. Notably, none of the models misclassified EVOO + POO or EVOO + ROO as pure EVOO, but most models, except those using SNV + SG+2nd derivative and MSC + SG+2nd derivative, incorrectly labeled 2 or 3 EVOO + HZO (90:10%) samples as pure EVOO. Additionally, none of the models successfully classified all ROO samples, with 10 out of 12 models misclassifying all 9 ROO samples as EVOO. SVM models also struggled with POO, as the SVM-SNV and MSC models misclassified 5 POO cases, while SVM-SNV + SG and MSC + SG misclassified 4 cases. Pure HZO presented the greatest challenge, with 10 out of 12 models failing to classify any samples correctly. The SVM + SG model, in particular, misclassified 11 out of 12 HZO samples as pure EVOO. These misclassifications may be attributed to the radial decision boundaries formed by the SVM's RBF kernel, which can struggle with multiclass classification when significant spectral overlap occurs. The similar chemical compositions of EVOO and adulterants, particularly in triacylglycerols, fatty acids, and sterols (Mignani et al., 2011; Zabaras, 2010), make it difficult for the model to establish clear separability. This challenge is more pronounced in complex multiclass tasks with overlapping features, as seen in this study.
SVM models achieved ACC.p values ranging from 97.6% to 99.5% in classifying pure EVOO, adulterants, or adulterated samples. The MSC + SG+2nd derivative model demonstrated perfect classification of all pure and adulterated olive oil samples (1–40%). Most models accurately identified adulterated oils, but misclassifications of EVOO as adulterants occurred in all models except for SVM-SG+2nd derivative and MSC + SG+2nd derivative. Models using SNV, MSC, SNV + SG, and MSC + SG preprocessing misclassified 15 EVOO samples, while the SVM-SNV + SG+1st derivative model misclassified 7 cases. The SG+1st and SNV + SG+2nd derivative models each misclassified 2 samples. Additionally, SVM models with SG+1st, SG+2nd derivative, and MSC + SG+1st derivative preprocessing misclassified 3 EVOO + HZO (10%) samples as pure EVOO. Models using unprocessed and Savitzky-Golay smoothed spectra misclassified two ROO and one HZO sample as EVOO.
SVM models for binary classification achieved ACC.cv and ACC.p ranging from 99.4% to 99.9% and 97.6%–100%, respectively, with MCC values of 0.8–1.0, indicating high accuracy in distinguishing between authentic and adulterated olive oil. Models incorporating SG+1st derivative, SG+2nd derivative, SNV + SG+1st derivative, SNV + SG+2nd derivative, and MSC + SG+1st derivative preprocessing achieved perfect classification, demonstrating their strong potential for EVOO authentication. These results align with studies by Deng et al. (2013) and Xie et al. (2014), which reported high accuracy in discriminating sesame oils using hyperspectral imaging and SVM. Our SVM models outperformed those in other studies focused on olive oil discrimination and quality assessment (Zarezadeh et al., 2021a; Zarezadeh et al., 2021b). Notably, the radial basis function (RBF) kernel employed in our study, particularly for 'two-class' and 'three-class' classifications, delivered superior accuracy compared to the linear kernel, as reported by Gazeli et al. (2020). This further confirms the effectiveness of the RBF kernel in classification tasks, consistent with findings by Han et al. (2016) in oil adulteration studies. Despite the strong overall performance, several models struggled with identifying pure EVOO, resulting in lower specificity (64.3%). SVM-SNV, SVM-SNV + SG, SVM-MSC, SVM-MSC + SG, and SVM-MSC + SG+2nd derivative models misclassified between 6 and 15 out of 42 EVOO samples as adulterated. These misclassifications likely stem from some preprocessing techniques and models failing to capture subtle compositional differences, such as campesterol, carotenoids, and chlorophyll, between EVOO and adulterated oils (Mignani et al., 2011). While the overall accuracy remains high, these lower specificity values highlight the importance of selecting appropriate models and preprocessing techniques to reduce false positives, especially in commercial settings where the cost of misclassification can be significant.
3.3.5. Discrimination of edible oils by Naïve Bayes (NB) classifier
Table 2 shows the performance of the Naïve Bayes (NB) classifier for olive oil authentication. The 'seven-class' models ranged from poor to moderate, with ACC.cv between 51.0% and 84.3% and ACC.p between 48.6% and 82.4%. Models using raw spectra and SG-only performed worst, while NB-SNV + SG+2nd derivative and NB-MSC + SG+2nd derivative achieved the best results. NB-SG+1st derivative and NB-MSC + SG+1st derivative models perfectly classified EVOO. Most models misclassified pure EVOO as POO, except for NB-unprocessed and NB-SG, which misclassified them as HZO or POO. For example, models using SNV, SNV + SG, MSC, and MSC + SG misclassified 15 out of 42 EVOO samples as POO, while NB-unprocessed and NB-SG misclassified 13 cases. These models also misclassified 3 EVOO + HZO (90:10%) cases as EVOO and wrongly identified 7 to 12 HZO cases as EVOO. The poorest performance occurred with NB-unprocessed and NB-SG models, which misclassified all HZO cases as EVOO. Additionally, 4 to 6 POO cases were incorrectly classified as EVOO, but none misclassified EVOO + POO or EVOO + ROO (1–40%) as pure EVOO.
In the 'three-class' discrimination task, NB models exhibited higher accuracies than in the 'seven-class' task, with ACC.cv ranging from 97.4% to 99.5% and ACC.p from 94.1% to 99.5%. Only three models, those paired with SG+1st derivative, SG+2nd derivative, or MSC + SG+2nd derivative, correctly classified all authentic EVOO samples. Other models misclassified some EVOO as adulterated. The highest misclassification rates occurred with NB-raw spectra and NB-SG, each misclassifying half (21 samples) of EVOO as adulterants. Models using SNV, SNV + SG, MSC, and MSC + SG preprocessing also misclassified 15 cases. Importantly, none of the models misclassified adulterated oils (1–40%) as EVOO. However, except for NB-SNV + SG+1st derivative and MSC + SG+2nd derivative, all models misclassified some adulterant cases as EVOO. For instance, NB models pretreated with SNV, SNV + SG, MSC, and MSC + SG misclassified over half (18 cases: 9 ROO, 3 POO, 6 HZO) of adulterants as EVOO, while NB-raw and NB-SG models misclassified 11 cases (5 POO, 4 HZO, 2 ROO).
Despite its simplicity and assumption of feature independence, the NB classifier demonstrated strong performance in the 'two-class' classification scheme. ACC.cv, ACC.p, and MCC values ranged from 96.5 to 99.9%, 94.1–99.6%, and 0.70–0.95, respectively. These accuracy rates align with those reported by Zarezadeh et al. (2021b) (ACC.p = 95.5%) and slightly exceed those from an earlier study (ACC.p = 90.2%) by Zarezadeh et al. (2021a). NB models using raw spectra, SG smoothing, SG+1st derivative, SG+2nd derivative, and MSC + SG+1st derivative achieved perfect specificity (Spec.p = 100%), correctly classifying all 42 pure EVOO samples. In contrast, models with other preprocessing methods showed misclassifications. For instance, NB-SNV + SG+2nd derivative misclassified 14 EVOO samples, while models using SNV, SNV + SG, MSC, and MSC + SG+1st derivative each misclassified 4 EVOO samples as adulterated. Although NB-SNV + SG+2nd derivative had the lowest specificity, it accurately identified all adulterated oils (1–40%), achieving 100% sensitivity and precision. The highest misclassification errors (5.9%) occurred with NB-raw spectra and NB-SG, which falsely classified 36 out of 573 adulterated samples (12 HZO, 12 POO, 9 ROO, and 3 EVOO + HZO) as authentic. Other models, including NB-SNV, NB-SNV + SG, NB-MSC, and NB-MSC + SG+1st derivative, each misclassified 27 adulterated samples as EVOO. While these models performed well, there remains potential for type I and type II errors, where pure EVOO may be misclassified as adulterated, and adulterated oils as authentic.
3.3.6. Use of Artificial Neural Networks (ANN) in authentication of olive oil
Table 3 summarizes the performance metrics for the ANN models in oil classification. The optimal number of neurons ranged from 1 to 4, with most models employing an L2 regularization decay of 0.001 or 0.01 to mitigate overfitting. In the 'seven-class' classification, ANN models achieved moderate accuracy (ACC.p up to 83.4%). Most models accurately classified EVOO, but misclassifications occurred, with authentic EVOO often labeled as POO or ROO. For example, the ANN-SNV model misclassified 5 EVOO samples as POO and 2 as ROO, while ANN-SNV + SG+2nd derivative misclassified 2 EVOO cases. While no models misclassified EVOO + POO or EVOO + ROO as pure EVOO, some wrongly identified EVOO + HZO as EVOO. Specifically, ANN-SNV + SG+2nd derivative misclassified 9 EVOO + HZO cases: 2 at 10%, 1 at 20%, and 6 at 40% adulteration. Additionally, some models struggled with correctly identifying adulterants, frequently misclassifying HZO as EVOO. For instance, the ANN-MSC and ANN-unprocessed models misclassified all 12 HZO samples, while ANN-SG and ANN-SG+2nd derivative misclassified 11 HZO samples. Though models using SNV, SNV + SG, and MSC + SG preprocessing showed perfect classification, none accurately identified all ROO samples. Despite moderate overall accuracy, the tendency of ANN models to misclassify adulterants as EVOO emphasizes the complexity of the task and the challenges inherent in detecting subtle differences among oils.
Table 3.
Performance metrics of Artificial Neural Networks classifiers.
| Pre-processing | Model | Seven-Class Models |
Three-Class Models |
Two-Class/Binary Models |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Parameters | ACC.cv | ACC.p | Optimal Parameters | ACC.cv | ACC.p | Optimal Parameters | ACC.cv | Sens. cv | Prec. cv | Spec. cv | F1.cv | ACC.p | Sens. p | Prec. p | Spec. p | F1.p | MCC.p | ||
| Unprocessed | ANN | dec = 0.001,size = 2 | 73.6 | 78.9 | dec = 0.001,size = 4 | 100 | 98.9 | dec = 0.001,size = 2 | 99.7 | 100 | 99.7 | 94.5 | 99.8 | 99.7 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| SG smoothing | ANN | dec = 0.001,size = 3 | 83.6 | 79.8 | dec = 0.001,size = 4 | 100 | 100 | dec = 0.001,size = 2 | 99.6 | 100 | 99.6 | 92.5 | 99.8 | 99.7 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| SG+1st deriv. | ANN | dec = 0.001,size = 3 | 87.7 | 76.6 | dec = 0.001,size = 3 | 99.9 | 100 | dec = 0.001,size = 1 | 99.8 | 99.9 | 99.9 | 98.0 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SG+2nd deriv. | ANN | dec = 0.001,size = 3 | 87.9 | 78.3 | dec = 0.001,size = 2 | 99.6 | 100 | dec = 0.001,size = 1 | 99.8 | 99.9 | 99.9 | 99.0 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SNV | ANN | dec = 0.01,size = 3 | 92.0 | 79.5 | dec = 0.01,size = 3 | 100 | 100 | dec = 0.01,size = 1 | 99.9 | 99.9 | 99.9 | 98.5 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SNV + SG Smoothing | ANN | dec = 0.001,size = 2 | 73.0 | 68.1 | dec = 0.01,size = 3 | 100 | 100 | dec = 0.01,size = 1 | 99.9 | 99.9 | 99.9 | 98.5 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SNV + SG+1st deriv. | ANN | dec = 0.001,size = 3 | 93.7 | 83.4 | dec = 0.001,size = 2 | 99.8 | 100 | dec = 0.001,size = 1 | 99.9 | 100 | 99.9 | 98.5 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | ANN | dec = 0.001,size = 3 | 93.2 | 77.9 | dec = 0.001,size = 2 | 99.9 | 100 | dec = 0.001,size = 1 | 99.9 | 100 | 99.9 | 97.0 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | ANN | dec = 0.01,size = 2 | 71.6 | 57.1 | dec = 0.001,size = 1 | 99.2 | 98.7 | dec = 0.001,size = 2 | 99.7 | 99.9 | 99.7 | 93.5 | 99.8 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| MSC + SG Smoothing | ANN | dec = 0.001,size = 3 | 84.8 | 81.1 | dec = 0.001,size = 1 | 99.2 | 99.3 | dec = 0.001,size = 2 | 99.6 | 99.9 | 99.6 | 91.5 | 99.8 | 99.7 | 99.7 | 100 | 100 | 99.8 | 0.98 |
| MSC + SG+1st deriv. | ANN | dec = 0.001,size = 3 | 87.7 | 76.6 | dec = 0.001,size = 3 | 99.9 | 100 | dec = 0.001,size = 1 | 99.8 | 99.9 | 99.9 | 98.0 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| MSC + SG+2nd deriv. | ANN | dec = 0.001,size = 3 | 83.9 | 77.4 | dec = 0.001,size = 3 | 99.7 | 100 | dec = 0.001,size = 1 | 99.8 | 99.9 | 99.9 | 97.2 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
The metric values for the trained models represent averaged classification parameters of 10-fold cross-validation repeated ten times. ACC.cv = Accuracy, Sens.cv = Sensitivity, Prec.cv = Precision, Spec.cv = Specificity, and F1.cv = F1 Score for cross-validation. ACC.p = Accuracy, Sens.p = Sensitivity, Prec.p = Precision, Spec.p = Specificity, and F1.p = F1 Score for the external validation set (test set). SNV = Standard Normal Variate; MSC = Multiplicative Scatter Correction; SG = Savitzky-Golay smoothing; 1st deriv. = 1st derivative; 2nd deriv. = second derivative. Size is the number of optimal number of neurons in the hidden layers selected based on cross-validation and oneSE rule. Dec = decay, regularization parameter. For the Seven-Class system, the classification involves seven groups: extra-virgin olive oil (EVOO), hazelnut oil (HZO), olive pomace oil (POO), refined olive oil (ROO), EVOO + HZO, EVOO + POO, and EVOO + ROO. The Three-Class system categorizes oils into three groups: authentic extra-virgin olive oil, edible oil adulterant (100%), or adulterated (1–40% adulteration) olive oil. The Two-Class system is a binary classification distinguishing between pure EVOO and adulterated olive oil (1–100% adulteration).
Compared to other models in the study, ANN models performed best in the 'three-class' discrimination task. Nine out of twelve ANN models, utilizing various spectral preprocessing techniques, achieved 100% accuracy (ACC.p), underscoring the effectiveness of combining HSI with ANN for distinguishing EVOO from chemically similar adulterants and adulterated oils. Even models with some misclassifications maintained high accuracy, ranging between 98.9% and 99.3%. For instance, the ANN model with MSC preprocessing misclassified 7 EVOO samples as adulterants and 1 ROO as adulterated oil. Similarly, the ANN model using raw spectra misclassified 7 EVOO samples, while the model with MSC + SG preprocessing misclassified 1 ROO as EVOO, 2 adulterated oils as adulterants, and 1 EVOO sample as an adulterant. These results highlight ANN models' strong potential in complex classification tasks involving EVOO authenticity.
The ANN binary classifiers exhibited exceptional prediction accuracy, ranging from 99.7% to 100% on the external test set. Models using spectral data preprocessed with SNV or MSC, combined with Savitzky-Golay and derivatives, consistently achieved perfect classification results, with ACC.p, Sens.p, Spec.p, Prec.p, F1 score, and MCC all reaching 1.0. All 42 EVOO samples were correctly classified across all preprocessing techniques, achieving 100% specificity and precision. These findings are consistent with Aroca-Santos et al. (2016), who appied visible spectroscopy and neural networks for EVOO characterization, but they surpass the results of Zarezadeh et al. (2021a), who reported an ACC.p of 86.3% using ANN with ultrasound technology for olive oil fraud detection. Despite minimal misclassification errors (0.2%–0.3%), with only 1 or 2 out of 573 adulterated samples incorrectly identified as EVOO, the models maintained sensitivity rates between 99.7% and 100%. This demonstrates their strong ability to detect adulterated oils. Overall, the ANN models displayed robust predictive capabilities, with MCC values ranging from 0.98 to 1.0, confirming their effectiveness in distinguishing authentic EVOO from adulterated samples while minimizing both Type I and Type II errors.
3.4. Binary classification based on selected important features
Hyperspectral imaging (HSI) generates high-dimensional data, necessitating significant storage and computational resources. To enhance the practicality of HSI, selecting relevant variables simplifies models, reduces storage and processing demands, shortens training times, and minimizes the risk of overfitting, thereby addressing the challenges associated with high dimensionality (Chen et al., 2020). In the olive oil industry, food regulators focus on determining whether extra virgin olive oil (EVOO) is genuine or adulterated. Binary classification offers an efficient and reliable approach to automate quality control, optimizing computational resources while ensuring accurate results.
This study leveraged key spectral bands, identified by their 'Feature Importance Rankings', to build binary classification models (Fig. 7). These key regions span 957–975 nm, 1000–1025 nm, 1117–1157 nm, 1175–1200 nm, 1364–1421 nm, 1510–1528 nm, 1635–1642 nm, and 1650–1696 nm, corresponding to molecular vibrations. The 957–975 nm range reflects O-H stretching from hydroxyl groups or phenolics, while the 1000–1025 nm, 1117–1157 nm, and 1364–1421 nm ranges relate to C-H stretching vibrations in –CH2– and –CH3– groups of fatty acids (Xiaobo et al., 2010). The 1510–1528 nm range is attributed to O-H bending (Shang et al., 2024), and the 1635–1696 nm range corresponds to O-H stretching in phenolic compounds (Nicolaï et al., 2007).
Fig. 7.
Performance heat map displaying key features selected by models built from spectral data preprocessed with SNV + Savitzky-Golay + second derivative.
Table 4, Table 5 outline the performance of PLS-DA, k-NN, Random Forest (RF), SVM, and ANN models using selected wavelengths for discrimination of pure and adulterated olive oil. PLS-DA models demonstrated superior predictive performance, with accuracy (ACC.p) and F1 scores ranging from 99.7% to 100% and Matthews correlation coefficient (MCC) values between 0.95 and 1.00. Spectral preprocessing techniques such as SG smoothing, SNV + SG + derivatives, and MSC + SG+2nd derivative optimized classification, resulting in perfect specificity and precision, with over half the models correctly identifying all 42 EVOO samples. Misclassification rates were low (0.6%), primarily in SNV and MSC-pretreated samples, with models maintaining 99.7% sensitivity in identifying adulterated oils. Similarly, k-NN models showed strong classification performance, with ACC.p values exceeding 98%, and k-NN + SNV + SG+2nd derivative achieving 100% accuracy. MCC values ranged from 0.90 to 1.00, and F1 scores between 99.0% and 100%. While most models accurately classified EVOO, k-NN + SG misclassified 10 adulterated samples as EVOO, leading to a 1.8% error rate. Despite these minor errors, the k-NN models generally maintained high precision and specificity. RF models performed comparably well, with RF-SNV + SG+1st derivative achieving perfect accuracy (ACC.p = 100%, F1 = 100%, MCC = 1.0). However, RF-SNV + SG showed a 2.1% error rate, misclassifying 5 EVOO and 8 adulterated samples. Nonetheless, RF models maintained strong overall accuracy and predictive reliability across various preprocessing methods. SVM models also achieved high accuracy, with MCC.p values exceeding 0.95 and ACC.p rates above 98%. Misclassification rates varied from 0.5% to 2.0%, with SVM-SG+2nd derivative misclassifying 12 EVOO samples as adulterated. ANN demonstrated the highest classification performance, particularly with SG + derivatives or MSC/SNV + SG + derivatives preprocessing. Seven ANN models achieved perfect metrics, with MCC values of 1.0. The remaining models maintained strong MCC values of 0.96, with minimal misclassification (0.5%). Only 3 adulterated samples were misclassified as EVOO, underscoring the superior performance of ANN models in extracting critical spectral features for accurate classification.
Table 4.
Partial Least Squares-Discriminant Analysis (PLS-DA) and K-Nearest Neighbors (KNN) classification models based on variable selection for cross-validation and external validation in the classification of oils as either pure EVOO or adulterated olive oil.
| Pre-processing | Model | Cross-Validation |
External Validation |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LVs/k | ACC.cv | Sens.cv | Prec.cv | Spec.cv | F1.cv | ACC.p | Sens.p | Prec.p | Spec.p | F1.p | MCC.p | ||
| Unprocessed | PLS-DA | 5 | 99.5 | 100 | 99.5 | 90.0 | 99.7 | 99.7 | 99.8 | 99.8 | 97.6 | 99.8 | 0.97 |
| SG smoothing | PLS-DA | 5 | 99.4 | 100 | 99.4 | 88.4 | 99.7 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SG+1st deriv. | PLS-DA | 6 | 98.2 | 99.8 | 98.4 | 66.6 | 99.1 | 99.8 | 100 | 99.8 | 97.6 | 99.9 | 0.99 |
| SG+2nd deriv. | PLS-DA | 4 | 99.2 | 100 | 99.1 | 82.4 | 99.6 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SNV | PLS-DA | 3 | 98.6 | 99.9 | 98.7 | 73.9 | 99.3 | 99.4 | 99.7 | 99.7 | 95.2 | 99.7 | 0.95 |
| SNV + SG Smoothing | PLS-DA | 3 | 98.6 | 99.9 | 98.7 | 73.9 | 99.3 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| SNV + SG+1st deriv. | PLS-DA | 4 | 99.4 | 99.9 | 99.5 | 90.1 | 99.7 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | PLS-DA | 5 | 99.6 | 100 | 99.6 | 92.5 | 99.8 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | PLS-DA | 3 | 98.6 | 99.9 | 98.7 | 74.4 | 99.3 | 99.4 | 99.7 | 99.7 | 95.2 | 99.7 | 0.95 |
| MSC + SG Smoothing | PLS-DA | 3 | 98.6 | 99.8 | 98.7 | 73.7 | 99.3 | 99.8 | 99.5 | 100 | 100 | 99.9 | 0.99 |
| MSC + SG+1st deriv. | PLS-DA | 6 | 98.2 | 99.8 | 98.4 | 66.6 | 99.1 | 99.8 | 100 | 97.6 | 97.6 | 99.9 | 0.99 |
| MSC + SG+2nd deriv. | PLS-DA | 4 | 99.3 | 99.9 | 99.3 | 86.0 | 99.6 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| Unprocessed | KNN | 3 | 99.9 | 99.9 | 99.9 | 98.3 | 99.9 | 98.7 | 98.8 | 99.8 | 97.6 | 99.3 | 0.91 |
| SG smoothing | KNN | 3 | 99.9 | 99.9 | 99.9 | 98.3 | 99.9 | 98.2 | 98.3 | 99.8 | 97.6 | 99.0 | 0.88 |
| SG+1st deriv. | KNN | 3 | 99.3 | 99.6 | 99.7 | 93.8 | 99.6 | 98.7 | 99.0 | 99.6 | 95.3 | 99.3 | 0.90 |
| SG+2nd deriv. | KNN | 3 | 99.2 | 99.5 | 99.7 | 93.4 | 99.6 | 98.7 | 98.9 | 99.6 | 95.2 | 99.3 | 0.90 |
| SNV | KNN | 3 | 99.8 | 99.9 | 99.8 | 95.8 | 99.9 | 99.2 | 99.1 | 100 | 100 | 99.6 | 0.94 |
| SNV + SG Smoothing | KNN | 3 | 99.8 | 99.9 | 99.8 | 95.8 | 99.9 | 99.2 | 99.2 | 100 | 100 | 99.6 | 0.94 |
| SNV + SG+1st deriv. | KNN | 3 | 99.6 | 99.9 | 99.7 | 94.6 | 99.8 | 99.8 | 100 | 99.8 | 97.6 | 99.9 | 0.99 |
| SNV + SG+2nd deriv. | KNN | 3 | 99.8 | 100 | 99.8 | 95.7 | 100 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | KNN | 3 | 99.8 | 99.9 | 99.8 | 95.8 | 99.9 | 99.2 | 99.1 | 100 | 100 | 99.6 | 0.94 |
| MSC + SG Smoothing | KNN | 3 | 99.8 | 99.9 | 99.8 | 95.8 | 99.9 | 99.2 | 99.1 | 100 | 100 | 99.6 | 0.94 |
| MSC + SG+1st deriv. | KNN | 3 | 99.3 | 99.6 | 99.7 | 93.8 | 99.6 | 98.7 | 99.0 | 99.6 | 95.2 | 99.3 | 0.90 |
| MSC + SG+2nd deriv. | KNN | 3 | 99.5 | 99.8 | 99.7 | 94.0 | 99.7 | 98.9 | 99.4 | 99.3 | 90.4 | 99.4 | 0.91 |
The values represent averaged classification parameters of 10-fold cross-validation repeated ten times. ACC.cv = Accuracy, Sens.cv = Sensitivity, Prec.cv = Precision, Spec.cv = Specificity, and F1.cv = F1 Score for cross-validation. ACC.p = Accuracy, Sens.p = Sensitivity, Prec.p = Precision, Spec.p = Specificity, F1.p = F1 Score, and MCC.p = Matthews correlation coefficient for the external validation set (test set). SNV = Standard Normal Variate; MSC = Multiplicative Scatter Correction; SG = Savitzky-Golay smoothing; 1st deriv. = 1st derivative; 2nd deriv. = second derivative; LVs = optimal latent variables and k = optimal k-nearest neighbors for the best model after cross-validation.
Table 5.
Artificial Neural Network (ANN), Random Forest (RF), and Support Vector Machines (SVM) binary classification model based on variable selection for cross-validation and external validation in the classification of oils as either pure EVOO or adulterated olive oil.
| Pre-processing | Cross-Validation |
External Validation |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Optimal Parameters | ACC.cv | Sens.cv | Prec.cv | Spec.cv | F1.cv | ACC.p | Sens.p | Prec.p | Spec.p | F1.p | MCC.p | |
| Unprocessed | RF | mtry = 3, ntree = 500 | 99.5 | 99.7 | 99.8 | 95.3 | 99.8 | 99.3 | 99.3 | 100 | 100 | 99.6 | 0.95 |
| SG smoothing | RF | mtry = 3, ntree = 500 | 99.6 | 99.8 | 99.8 | 95.3 | 99.8 | 99.3 | 98.6 | 100 | 100 | 99.3 | 0.95 |
| SG+1st deriv. | RF | mtry = 5,ntree = 500 | 99.6 | 99.9 | 99.7 | 93.7 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SG+2nd deriv. | RF | mtry = 3, ntree = 500 | 99.6 | 99.9 | 99.7 | 94.3 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SNV | RF | mtry = 3, ntree = 500 | 99.5 | 99.8 | 99.6 | 92.8 | 99.7 | 99.3 | 99.5 | 99.8 | 97.6 | 99.7 | 0.95 |
| SNV + SG Smoothing | RF | mtry = 14, ntree = 500 | 99.3 | 99.7 | 99.6 | 91.6 | 99.6 | 97.9 | 98.6 | 99.1 | 88.1 | 98.9 | 0.84 |
| SNV + SG+1st deriv. | RF | mtry = 3, ntree = 500 | 99.8 | 99.9 | 99.8 | 96.5 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | RF | mtry = 3, ntree = 500 | 99.7 | 99.9 | 99.8 | 95.5 | 99.9 | 99.8 | 99.8 | 100 | 100 | 99.9 | 0.99 |
| MSC | RF | mtry = 3, ntree = 500 | 99.5 | 99.8 | 99.7 | 92.9 | 99.7 | 99.2 | 99.5 | 99.7 | 95.2 | 99.6 | 0.94 |
| MSC + SG Smoothing | RF | mtry = 3, ntree = 500 | 99.5 | 99.8 | 99.7 | 94.0 | 99.7 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC + SG+1st deriv. | RF | mtry = 7, ntree = 500 | 99.6 | 99.9 | 99.7 | 93.9 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC + SG+2nd deriv. | RF | mtry = 3, ntree = 500 | 99.4 | 99.9 | 99.5 | 90.6 | 99.7 | 98.9 | 99.3 | 99.5 | 92.9 | 99.4 | 0.91 |
| Unprocessed | SVM | Cost = 50, σ = 0.01 | 99.8 | 99.9 | 99.9 | 98.3 | 99.9 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SG smoothing | SVM | Cost = 50, σ = 0.01 | 99.8 | 99.9 | 99.9 | 97.6 | 99.9 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SG+1st deriv. | SVM | Cost = 10, σ = 0.01 | 99.1 | 99.5 | 99.6 | 91.8 | 99.6 | 98.2 | 99.7 | 98.4 | 78.6 | 99.0 | 0.85 |
| SG+2nd deriv. | SVM | Cost = 10, σ = 0.01 | 99.3 | 99.6 | 99.6 | 92.4 | 99.6 | 98.0 | 100 | 97.9 | 71.4 | 99.0 | 0.84 |
| SNV | SVM | Cost = 5, σ = 0.01 | 99.6 | 99.8 | 99.8 | 95.0 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SNV + SG Smoothing | SVM | Cost = 5, σ = 0.01 | 99.6 | 99.9 | 99.7 | 94.7 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SNV + SG+1st deriv. | SVM | Cost = 5, σ = 0.01 | 99.2 | 99.7 | 99.5 | 90.7 | 99.6 | 98.9 | 99.5 | 99.3 | 90.5 | 99.4 | 0.91 |
| SNV + SG+2nd deriv. | SVM | Cost = 1, σ = 0.01 | 99.6 | 99.7 | 99.9 | 98.4 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC | SVM | Cost = 5, σ = 0.01 | 99.6 | 99.9 | 99.7 | 94.9 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC + SG Smoothing | SVM | Cost = 5, σ = 0.01 | 99.6 | 99.9 | 99.7 | 94.6 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC + SG+1st deriv. | SVM | Cost = 10, σ = 0.01 | 99.1 | 99.5 | 99.6 | 91.8 | 99.6 | 98.2 | 99.7 | 98.4 | 78.6 | 99.0 | 0.85 |
| MSC + SG+2nd deriv. | SVM | Cost = 1, σ = 0.01 | 99.5 | 99.8 | 99.6 | 92.1 | 99.7 | 99.4 | 99.3 | 100 | 100 | 99.6 | 0.95 |
| Unprocessed | ANN | decay = 0.001, size = 1 | 99.4 | 99.7 | 99.7 | 94.5 | 99.7 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SG smoothing | ANN | decay = 0.001, size = 1 | 99.4 | 99.7 | 99.7 | 95.0 | 99.7 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SG+1st deriv | ANN | decay = 0.001, size = 1 | 99.8 | 99.9 | 99.9 | 98.5 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SG+2nd deriv. | ANN | decay = 0.001, size = 1 | 99.8 | 99.9 | 99.9 | 99.9 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV | ANN | decay = 0.001, size = 2 | 99.6 | 99.9 | 99.7 | 93.9 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SNV + SG Smoothing | ANN | decay = 0.001, size = 2 | 99.6 | 99.9 | 99.7 | 94.6 | 99.8 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| SNV + SG+1st deriv. | ANN | decay = 0.001, size = 1 | 99.8 | 99.9 | 99.9 | 98.8 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| SNV + SG+2nd deriv. | ANN | decay = 0.001, size = 1 | 99.9 | 100 | 99.9 | 98.3 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC | ANN | decay = 0.001, size = 1 | 99.5 | 99.7 | 99.8 | 95.2 | 99.7 | 99.5 | 99.5 | 100 | 100 | 99.7 | 0.96 |
| MSC + SG Smoothing | ANN | decay = 0.001, size = 1 | 99.9 | 100 | 99.9 | 98.7 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG+1st deriv. | ANN | decay = 0.001, size = 1 | 99.8 | 99.9 | 99.9 | 97.8 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
| MSC + SG+2nd deriv. | ANN | decay = 0.001, size = 1 | 99.8 | 99.9 | 99.8 | 96.9 | 99.9 | 100 | 100 | 100 | 100 | 100 | 1.00 |
The values represent averaged classification parameters of 10-fold cross-validation repeated ten times. ACC.cv = Accuracy, Sens.cv = Sensitivity, Prec.cv = Precision, Spec.cv = Specificity, and F1.cv = F1 Score for cross-validation. ACC.p = Accuracy, Sens.p = Sensitivity, Prec.p = Precision, Spec.p = Specificity, and F1.p = F1 Score for the external validation set (test set). SNV = Standard Normal Variate; MSC = Multiplicative Scatter Correction; SG = Savitzky-Golay smoothing; 1st deriv. = 1st derivative; 2nd deriv. = second derivative Lc = lap lace, ad = adjust for the best model after cross-validation.
3.5. Comparison of binary classification models: effects of spectral preprocessing and feature selection
The Aligned Rank Transform Analysis of Variance (ART ANOVA) identified the ‘model type’ as the only significant factor (F = 6.487, p = 0.021) affecting the performance of binary classifiers using full spectra data (224 variables) (Fig. 8). There was no significant interaction between 'model type' and preprocessing techniques (F = 0.473, p = 0.932), indicating that model performance remains independent of spectral pretreatment. PLS-DA, SVM, RF, and ANN models significantly outperformed the Naïve Bayes model (χ2 = 27.16, p < 0.05), though differences between k-NN and NB models were not statistically significant (p = 0.347). Similarly, 'model type' had a significant effect (F = 8.531, p = 0.019) on the Matthews correlation coefficient (MCC.p) results in models using selected important variables. ANN models significantly outperformed k-NN (p = 0.0004), RF (p = 0.0073), and SVM (p = 0.0055), while PLS-DA outperformed k-NN (p = 0.0010), RF (p = 0.0144), and SVM (p = 0.0110). However, there was no significant difference between the performances of ANN and PLS-DA (p > 0.05). The superior performance of PLS-DA and ANN can be attributed to their robustness in handling complex data patterns and their ability to extract essential features from spectral data, making them particularly effective at distinguishing subtle differences between pure and adulterated oils. This capability highlights their suitability for accurate and efficient food authentication applications.
Fig. 8.
Box Plots demonstrating MCC values based on model type and spectral preprocessing techniques. The symbol  on each plot indicates the mean MCC value.
on each plot indicates the mean MCC value.
The overall (combined) and individual model performance (except for Naïve Bayes) was compared using full-length spectra and selected features. The Wilcoxon signed-rank test indicated no significant difference in model performance before and after variable selection (p = 0.424). Performance remained consistent across individual models, including PLS-DA (p = 0.797), k-NN (p = 0.444), RF (p = 0.824), SVM (p = 0.472), and ANN (p = 0.188). This suggests that even with fewer but relevant variables, the models retain essential predictive information. Thus, employing a simplified model offers advantages such as lower computational costs and faster processing times without sacrificing accuracy, making them suitable for practical, real-world applications.
3.6. Comparison of HSI and machine learning with advanced spectroscopic techniques
The performance of HSI and ML algorithms was compared with other spectroscopic techniques to validate their application in combating olive oil fraud. Squeo et al. (2019) achieved 96–100% accuracy using FTIR and LDA to distinguish EVOO from virgin olive oil based on ethyl ester content. However, the specificity rate with SIMCA (40–67%) was significantly lower than the models in our study, which reported specificity values up to 100%. Similarly, Mossoba et al. (2017) applied FT-NIR and PLS to successfully detect ROO adulteration in commercial EVOO. Georgouli et al. (2017) reported accuracies of 82% for Raman and 69% for FTIR using CLPP and k-NN to identify HZO in EVOO at low concentrations. While their classification was based on percentage adulteration, our multi-class classification models outperformed their results.
Front-face total fluorescence spectroscopy combined with second-order chemometric methods demonstrated the potential to detect adulteration in EVOO, with detection limits of about 15% for ROO and 3% for POO (Durán Merás et al., 2018). In contrast, the HSI-NIR and ML models in our study detected adulteration as low as 1%. Furthermore, Zade et al. (2023) proposed a classification strategy combining PLS-DA and DD-SIMCA with Raman spectroscopy, achieving 100% accuracy, sensitivity, and specificity in detecting HZO adulteration in EVOO. These comparisons highlight the effectiveness of NIR-HSI in detecting adulteration, particularly at lower concentrations, and emphasize the advantages of combining HSI with machine learning.
Tachie et al. (2024) used ATR-FTIR and machine learning models to classify pure oils and margarines. However, our models outperformed theirs, which achieved 97% accuracy with k-NN, 93% with logistic regression, 83% with SVM, 53% with LightGBM, and 50% with a decision tree. In contrast, Hwang et al. (2024) demonstrated the potential of HSI and ML for classifying edible vegetable oils, achieving over 98.9% accuracy, comparable to fatty acid composition-based methods. Similarly, Aqeel et al. (2024) reported even higher accuracy using hyperspectral identification and ML techniques. These findings align with our current results and underscore the effectiveness of NIR-HSI combined with machine learning for detecting oil adulteration.
3.7. Pixel-level visualization of adulteration using Spectral Angle Mapper (SAM) and Spectral Information Divergence (SID) classification
Hyperspectral imaging, though commonly applied to heterogeneous samples, also demonstrates potential for use with homogeneous samples such as edible oils (Aqeel et al., 2024). In this study, Spectral Angle Mapper (SAM) and Spectral Information Divergence (SID) were used to detect and map adulteration levels in EVOO ranging from 0% to 100%. SAM calculates the spectral angle between reference and pixel spectra, with smaller angles indicating closer matches, while SID measures spectral divergence, where lower values suggest higher similarity (Qin et al., 2009). As shown in Fig. 9, scattered red, pink, and brown pixels at 0% adulteration, indicate misclassifications, suggesting that pure EVOO may be falsely flagged as adulterated due to noise and overlapping spectral feautures. At 1% adulteration, both SAM and SID detect the presence of the adulterants, but overestimation occurs, especially in SAM, where the adulterant color is more prominent than expected. As adulteration levels increase (5–40%), the maps more clearly the presence of adulterants, with their respective colors dominating the image. Both classifiers effectively detect adulteration, showing no misclassifications up to 40% adulteration. However, at 100% adulteration, residual blue pixels persist, particularly in the SID classification, indicating that pure adulterants are frequently misclassified as pure EVOO. The subtle spectral differences caused by chemical similarity make it challenging for these techniques to distinguish between pure EVOO and pure adulterants.
Fig. 9.
Pixel-based classification maps showing the detection of EVOO adulteration using Spectral Angle Mapper (SAM) and Spectral Information Divergence (SID) at adulteration levels of 0%, 1%, 5%, 10%, 20%, 40%, and 100%. Blue represents pure EVOO, while red, pink, and brown indicate the presence of adulterants (hazelnut, olive pomace, and refined olive oils, respectively). The progression from blue to adulterant colors illustrates how the classifiers detect increasing levels of adulteration. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
While SAM and SID effectively detect adulteration at levels between 1% and 40%, they struggle with separating pure EVOO from pure individual adulterants such as hazelnut, olive pomace, and refined olive oils. To overcome these limitations, future studies should explore pixel-level machine learning techniques including Convolutional Neural Networks (CNNs) or deep learning to capture finer spectral details. Hybrid or ensemble models could also improve detection performance, particularly in areas where SAM and SID struggle in performance, enhancing pixel-based adulteration detection in EVOO.
4. Conclusions
In summary, this study successfully integrates near-infrared hyperspectral imaging (NIR-HSI) with advanced machine learning (ML) techniques to effectively detect adulteration in extra virgin olive oil (EVOO), particularly involving chemically similar oils such as refined olive oil (ROO), olive pomace oil (POO), and hazelnut oil (HZO).
ANN models excelled in this study, achieving 100% accuracy across most preprocessing techniques in three-class classification. Furthermore, models such as kNN + SNV + SG+2nd derivative, kNN + MSC + SG+2nd derivative, RF + SNV + SG+1st derivative, and RF + SNV + SG+2nd derivative also attained 100% classification accuracy in discrimination of pure EVOO, adulterants and adulterated olive oil. Other models performed robustly as well, consistently exceeding 97% accuracy.
Binary classification models performed exceptionally well in distinguishing pure EVOO from adulterated samples. Preprocessing techniques including SNV and MSC, combined with Savitzky-Golay (SG) smoothing and derivatives, outperformed models based on raw spectral data. Remarkably, RF, kNN, PLS-DA, and ANN consistently achieved 100% accuracy, sensitivity, precision, F1 scores, and a perfect MCC of 1.0 with these preprocessing methods.
The study further demonstrated that models built on selected key features, including k-NN, SVM, PLS-DA, RF, and ANN, matched the performance of those using full-length spectra, highlighting the potential to streamline computational processes without compromising accuracy. This approach offers greater efficiency and scalability for larger datasets in practical applications.
Ultimately, integrating NIR-HSI with machine learning techniques provides a powerful, highly sensitive method for detecting EVOO adulteration, even at levels as low as 1%. This approach shows great potential for enhancing the authenticity and quality control of extra virgin olive oil, particularly in the ongoing fight against food fraud.
CRediT authorship contribution statement
Derick Malavi: Conceptualization, Methodology, Investigation, Data curation, Formal analysis, Writing – original draft, and, Visualization. Katleen Raes: Supervision, Writing – review & editing. Sam Van Haute: Conceptualization, Writing – review & editing, Supervision, Project administration.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors acknowledge the financial support provided by Ghent University (Belgium) and Ghent University Global Campus (South Korea).
Data availability
Data are available on GitHub at https://github.com/DNMalavi/NIR-HSI-ML-for-EVOO-Fraud-Detection.
References
- Ai F.F., Bin J., Zhang Z.M., Huang J.H., Wang J.B., Liang Y.Z., Yu L., Yang Z.Y. Application of random forests to select premium quality vegetable oils by their fatty acid composition. Food Chem. 2014;143:472–478. doi: 10.1016/j.foodchem.2013.08.013. [DOI] [PubMed] [Google Scholar]
- Aparicio R., Aparicio-Ruíz R. Authentication of vegetable oils by chromatographic techniques. J. Chromatogr. A. 2000;881(1–2):93–104. doi: 10.1016/S0021-9673(00)00355-1. [DOI] [PubMed] [Google Scholar]
- Aqeel M., Sohaib A., Iqbal M., Rehman H.U., Rustam F. Hyperspectral identification of oil adulteration using machine learning techniques. Curr. Res. Food Sci. 2024;8(February) doi: 10.1016/j.crfs.2024.100773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arlorio M., Coisson J.D., Bordiga M., Travaglia F., Garino C., Zuidmeer L., van Ree R., Giuffrida M.G., Conti A., Martelli A. Olive oil adulterated with hazelnut oils: simulation to identify possible risks to allergic consumers. Food Addit. Contam. 2010;27(1):11–18. doi: 10.1080/02652030903225799. [DOI] [PubMed] [Google Scholar]
- Aroca-Santos R., Cancilla J.C., Pariente E.S., Torrecilla J.S. Neural networks applied to characterize blends containing refined and extra virgin olive oils. Talanta. 2016;161:304–308. doi: 10.1016/j.talanta.2016.08.033. [DOI] [PubMed] [Google Scholar]
- Azadmard-Damirchi S. Food Additives and Contaminants Review of the use of phytosterols as a detection tool for adulteration of olive oil with hazelnut oil Review of the use of phytosterols as a detection tool for adulteration of olive oil with hazelnut oil. Food Addit. Contam. 2010;27(1):1–10. doi: 10.1080/02652030903225773. [DOI] [PubMed] [Google Scholar]
- Barbosa R.M., Nacano L.R., Freitas R., Batista B.L., Barbosa F. The use of decision trees and Naïve Bayes algorithms and trace element patterns for controlling the authenticity of free-range-pastured hens' eggs. J. Food Sci. 2014;79(9):C1672–C1677. doi: 10.1111/1750-3841.12577. [DOI] [PubMed] [Google Scholar]
- Breiman L. Random forests. Random Forests. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Calvano C.D., De Ceglie C., D'Accolti L., Zambonin C.G. MALDI-TOF mass spectrometry detection of extra-virgin olive oil adulteration with hazelnut oil by analysis of phospholipids using an ionic liquid as matrix and extraction solvent. Food Chem. 2012;134(2):1192–1198. doi: 10.1016/j.foodchem.2012.02.154. [DOI] [PubMed] [Google Scholar]
- Cao D.S., Huang J.H., Liang Y.Z., Xu Q.S., Zhang L.X. Tree-based ensemble methods and their applications in analytical chemistry. TrAC, Trends Anal. Chem. 2012;40(2):158–167. doi: 10.1016/j.trac.2012.07.012. [DOI] [Google Scholar]
- Capote F.P., Jiménez J.R., De Castro M.D.L. Sequential (step-by-step) detection, identification and quantitation of extra virgin olive oil adulteration by chemometric treatment of chromatographic profiles. Anal. Bioanal. Chem. 2007;388(8):1859–1865. doi: 10.1007/s00216-007-1422-9. [DOI] [PubMed] [Google Scholar]
- Casadei E., Valli E., Panni F., Donarski J., Farrús Gubern J., Lucci P., Conte L., Lacoste F., Maquet A., Brereton P., Bendini A., Gallina Toschi T. Emerging trends in olive oil fraud and possible countermeasures. Food Control. 2021;124 doi: 10.1016/j.foodcont.2021.107902. [DOI] [Google Scholar]
- Chen Q., Zhao J., Fang C.H., Wang D. Feasibility study on identification of green, black and Oolong teas using near-infrared reflectance spectroscopy based on support vector machine (SVM) Spectrochimica Acta - Part A: Molecular and Biomolecular Spectroscopy. 2007;66(3):568–574. doi: 10.1016/j.saa.2006.03.038. [DOI] [PubMed] [Google Scholar]
- Chen R.C., Dewi C., Huang S.W., Caraka R.E. Selecting critical features for data classification based on machine learning methods. Journal of Big Data. 2020;7(1) doi: 10.1186/s40537-020-00327-4. [DOI] [Google Scholar]
- Chiavaro E., Vittadini E., Rodriguez-Estrada M.T., Cerretani L., Bendini A. Differential scanning calorimeter application to the detectionof refined hazelnut oil in extra virgin olive oil. Food Chem. 2008;110(1):248–256. doi: 10.1016/j.foodchem.2008.01.044. [DOI] [PubMed] [Google Scholar]
- Chicco D., Jurman G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020;21(1):1–13. doi: 10.1186/s12864-019-6413-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chicco D., Jurman G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. BioData Min. 2023;16(1):1–23. doi: 10.1186/s13040-023-00322-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi J.Y., Moon K.D. Non-destructive discrimination of sesame oils via hyperspectral image analysis. J. Food Compos. Anal. 2020;90(January) doi: 10.1016/j.jfca.2020.103505. [DOI] [Google Scholar]
- Codex Alimentarius Commission . CODEX STAN 33, 1981. FAO/WHO; January: 2003. Codex Standards for olive oils, and olive pomace oils; pp. 50–55. [DOI] [Google Scholar]
- CodexAlimentarius Codex stan 33-1981. Standard for olive oils and olive pomace oils. Codex Alimentarius. 2017;91(5):1689–1699. [Google Scholar]
- Cui Y., Lu W., Xue J., Ge L., Yin X., Jian S., Li H., Zhu B., Dai Z., Shen Q. Machine learning-guided REIMS pattern recognition of non-dairy cream, milk fat cream and whipping cream for fraudulence identification. Food Chem. 2023;429(July) doi: 10.1016/j.foodchem.2023.136986. [DOI] [PubMed] [Google Scholar]
- Datta D., Mallick P.K., Bhoi A.K., Ijaz M.F., Shafi J., Choi J. Hyperspectral image classification: potentials, challenges, and future directions. Comput. Intell. Neurosci. 2022;2022 doi: 10.1155/2022/3854635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Mata P., Dominguez-Vidal A., Bosque-Sendra J.M., Ruiz-Medina A., Cuadros-Rodríguez L., Ayora-Cañada M.J. Olive oil assessment in edible oil blends by means of ATR-FTIR and chemometrics. Food Control. 2012;23(2):449–455. doi: 10.1016/j.foodcont.2011.08.013. [DOI] [Google Scholar]
- de Santana F.B., Borges Neto W., Poppi R.J. Random forest as one-class classifier and infrared spectroscopy for food adulteration detection. Food Chem. 2019;293:323–332. doi: 10.1016/j.foodchem.2019.04.073. July 2018. [DOI] [PubMed] [Google Scholar]
- de Santana F.B., Mazivila S.J., Gontijo L.C., Neto W.B., Poppi R.J. Rapid discrimination between authentic and adulterated andiroba oil using FTIR-HATR spectroscopy and random forest. Food Anal. Methods. 2018;11(7):1927–1935. doi: 10.1007/s12161-017-1142-5. [DOI] [Google Scholar]
- Deng S., Xu Y., Li L., Li X., He Y. A feature-selection algorithm based on Support Vector Machine-Multiclass for hyperspectral visible spectral analysis. J. Food Eng. 2013;119(1):159–166. doi: 10.1016/j.jfoodeng.2013.05.024. [DOI] [Google Scholar]
- Dinno A. CRAN Repository; 2017. Package ‘dunn.test.’; pp. 1–7.https://cran.r-project.org/web/packages/dunn.test/dunn.test.pdf [Google Scholar]
- Drira M., Guclu G., Portolés T., Jabeur H., Kelebek H., Selli S., Bouaziz M. Safe and fast fingerprint aroma detection in adulterated extra virgin olive oil using gas chromatography–olfactometry-mass spectrometry combined with chemometrics. Food Anal. Methods. 2021;14(10):2121–2135. doi: 10.1007/s12161-021-02034-z. [DOI] [Google Scholar]
- Durán Merás I., Domínguez Manzano J., Airado Rodríguez D., Muñoz de la Peña A. Detection and quantification of extra virgin olive oil adulteration by means of autofluorescence excitation-emission profiles combined with multi-way classification. Talanta. 2018;178(October 2017):751–762. doi: 10.1016/j.talanta.2017.09.095. [DOI] [PubMed] [Google Scholar]
- Feng Y., Sun D. Application of Hyperspectral Imaging in Food Safety Inspection and Control : A Review Application of Hyperspectral Imaging in Food Safety Inspection and Control : A Review. 2012:37–41. doi: 10.1080/10408398.2011.651542. June 2013. [DOI] [PubMed] [Google Scholar]
- Feng Y.Z., Elmasry G., Sun D.W., Scannell A.G.M., Walsh D., Morcy N. Near-infrared hyperspectral imaging and partial least squares regression for rapid and reagentless determination of Enterobacteriaceae on chicken fillets. Food Chem. 2013;138(2–3):1829–1836. doi: 10.1016/j.foodchem.2012.11.040. [DOI] [PubMed] [Google Scholar]
- Feng Y.Z., Sun D.W. Near-infrared hyperspectral imaging in tandem with partial least squares regression and genetic algorithm for non-destructive determination and visualization of Pseudomonas loads in chicken fillets. Talanta. 2013;109:74–83. doi: 10.1016/j.talanta.2013.01.057. [DOI] [PubMed] [Google Scholar]
- Filoda P.F., Fetter L.F., Fornasier F., Schneider R.D.C.D.S., Helfer G.A., Tischer B., Teichmann A., da Costa A.B. Fast methodology for identification of olive oil adulterated with a mix of different vegetable oils. Food Anal. Methods. 2019;12(1):293–304. doi: 10.1007/s12161-018-1360-5. [DOI] [Google Scholar]
- Flores G., Ruiz Del Castillo M.L., Herraiz M., Blanch G.P. Study of the adulteration of olive oil with hazelnut oil by on-line coupled high performance liquid chromatographic and gas chromatographic analysis of filbertone. Food Chem. 2006;97(4):742–749. doi: 10.1016/j.foodchem.2005.06.008. [DOI] [Google Scholar]
- Florián-Huamán J., Cruz-Tirado J.P., Fernandes Barbin D., Siche R. Detection of nutshells in cumin powder using NIR hyperspectral imaging and chemometrics tools. J. Food Compos. Anal. 2022;108(January) doi: 10.1016/j.jfca.2022.104407. [DOI] [Google Scholar]
- Food Safety News. (2023). Spanish and Italian investigators uncover olive oil fraud. Retrieved February 2024, from https://www.foodsafetynews.com/2023/12/spanish-and-italian-investigators-uncover-olive-oil-fraud/.
- Gazeli O., Bellou E., Stefas D., Couris S. Laser-based classification of olive oils assisted by machine learning. Food Chem. 2020;302(April 2019) doi: 10.1016/j.foodchem.2019.125329. [DOI] [PubMed] [Google Scholar]
- Georgouli K., Martinez Del Rincon J., Koidis A. Continuous statistical modelling for rapid detection of adulteration of extra virgin olive oil using mid infrared and Raman spectroscopic data. Food Chem. 2017;217:735–742. doi: 10.1016/j.foodchem.2016.09.011. [DOI] [PubMed] [Google Scholar]
- Han Z., Wan J., Deng L., Liu K. 2016. Oil Adulteration Identification by Hyperspectral Imaging Using QHM and ICA; pp. 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T., Tibshirani R., Friedman J. Springer series in statistics the elements of statistical learning. Math. Intell. 2009;27(2):83–85. [Google Scholar]
- Hwang J., Choi K.O., Jeong S., Lee S. Machine learning identification of edible vegetable oils from fatty acid compositions and hyperspectral images. Curr. Res. Food Sci. 2024;8(December 2023) doi: 10.1016/j.crfs.2024.100742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IOC International trade standard applying to olive oils and olive-pomace oils international trade standard applying to olive oils and olive-pomace oils. COI/T.15/NC No 3/Rev. 5. Coi/T.15/Nc, No3/REV. 2010;12:17. https://www.internationaloliveoil.org/what-we-do/chemistry-standardisation-unit/standards-and-methods/ [Google Scholar]
- Jabeur H., Drira M., Rebai A., Bouaziz M. Putative markers of adulteration of higher-grade olive oil with less expensive pomace olive oil identified by gas chromatography combined with chemometrics. J. Agric. Food Chem. 2017;65(26):5375–5383. doi: 10.1021/acs.jafc.7b00687. [DOI] [PubMed] [Google Scholar]
- Jabeur H., Zribi A., Bouaziz M. Extra-virgin olive oil and cheap vegetable oils: distinction and detection of adulteration as determined by GC and chemometrics. Food Anal. Methods. 2016;9(3):712–723. doi: 10.1007/s12161-015-0249-9. [DOI] [Google Scholar]
- Kganyago M., Odindi J., Adjorlolo C., Mhangara P. Selecting a subset of spectral bands for mapping invasive alien plants: a case of discriminating parthenium hysterophorus using field spectroscopy data. Int. J. Rem. Sens. 2017;38(20):5608–5625. doi: 10.1080/01431161.2017.1343510. [DOI] [Google Scholar]
- Kucheryavskiy S. Mdatools – R package for chemometrics. Chemometr. Intell. Lab. Syst. 2020;198(January) doi: 10.1016/j.chemolab.2020.103937. [DOI] [Google Scholar]
- Kuhn M. Building predictive models in R using the caret package. J. Stat. Software. 2008;28(5):1–26. doi: 10.18637/jss.v028.i05. [DOI] [Google Scholar]
- Kuhn M., Wing J., Weston S., Williams A., Keefer C., Engelhardt A., Cooper T., Mayer Z., Kenkel B., Benesty M., Lescarbeau R., Ziem A., Scrucca L., Tang Y., Candan C., Hunt T., Maintainer . Predictive Analytics with KNIME. 2023. Classification and regression trees. [DOI] [Google Scholar]
- Leardi R. Modern Techniques for Food Authentication. second ed. Elsevier Inc; 2018. Chemometric methods in food authentication. [DOI] [Google Scholar]
- Li Y., Logan N., Quinn B., Hong Y., Birse N., Zhu H., Haughey S., Elliott C.T., Wu D. Fingerprinting black tea: when spectroscopy meets machine learning a novel workflow for geographical origin identification. Food Chem. 2024;438(October 2023) doi: 10.1016/j.foodchem.2023.138029. [DOI] [PubMed] [Google Scholar]
- Liland K.H., Mevik B.H., Wehrens R., Hiemstra P., Liland M.K.H., Suggests M.A.S.S. {pls}: partial least squares and principal component regression. 2022. https://cran.ms.unimelb.edu.au/web/packages/pls/pls.pdf
- Lohumi S., Lee S., Lee H., Cho B.K. A review of vibrational spectroscopic techniques for the detection of food authenticity and adulteration. Trends Food Sci. Technol. 2015;46(1):85–98. doi: 10.1016/j.tifs.2015.08.003. [DOI] [Google Scholar]
- López-Díez E.C., Bianchi G., Goodacre R. Rapid quantitative assessment of the adulteration of virgin olive oils with hazelnut oils using Raman spectroscopy and chemometrics. J. Agric. Food Chem. 2003;51(21):6145–6150. doi: 10.1021/jf034493d. [DOI] [PubMed] [Google Scholar]
- Malavi D., Nikkhah A., Raes K., Van Haute S. Hyperspectral imaging and chemometrics for authentication of extra virgin olive oil : a comparative approach with FTIR. Foods. 2023;12(429) doi: 10.3390/foods12030429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mannina L., D'Imperio M., Capitani D., Rezzi S., Guillou C., Mavromoustakos T., Vilchez M.D.M., Fernández A.H., Thomas F., Aparicio R. 1H NMR-based protocol for the detection of adulterations of refined olive oil with refined hazelnut oil. J. Agric. Food Chem. 2009;57(24):11550–11556. doi: 10.1021/jf902426b. [DOI] [PubMed] [Google Scholar]
- Manning L. Food fraud: policy and food chain. Curr. Opin. Food Sci. 2016;10(2):16–21. doi: 10.1016/j.cofs.2016.07.001. [DOI] [Google Scholar]
- Manuel Tabuenca J. Toxic-allergic syndrome caused by ingestion of rapeseed oil denatured with aniline. Lancet. 1981;318(8246):567–568. doi: 10.1016/S0140-6736(81)90949-1. [DOI] [PubMed] [Google Scholar]
- Martín-Hernández C., Bénet S., Obert L. Determination of proteins in refined and nonrefined oils. J. Agric. Food Chem. 2008;56(12):4348–4351. doi: 10.1021/jf7036888. [DOI] [PubMed] [Google Scholar]
- Medina S., Perestrelo R., Silva P., Pereira J.A.M., Câmara J.S. Trends in Food Science & Technology Current trends and recent advances on food authenticity technologies and chemometric approaches. Trends Food Sci. Technol. 2019;85(December 2018):163–176. doi: 10.1016/j.tifs.2019.01.017. [DOI] [Google Scholar]
- Meenu M., Cai Q., Xu B. A critical review on analytical techniques to detect adulteration of extra virgin olive oil. Trends Food Sci. Technol. 2019;91(September 2018):391–408. doi: 10.1016/j.tifs.2019.07.045. [DOI] [Google Scholar]
- Mendez J., Mendoza L., Cruz-Tirado J.P., Quevedo R., Siche R. Trends in application of NIR and hyperspectral imaging for food authentication. Sci. Agropecu. 2019;10(1):143–161. doi: 10.17268/sci.agropecu.2019.01.16. [DOI] [Google Scholar]
- Meyer D., Dimitriadou Evgenia, Hornik Kurt, Weingessel Andreas, Leisch Friedrich, Chih-Chung Chang C.-C.L. Package ‘e1071. 2022. https://cran.r-project.org/web/packages/e1071/index.html
- Mignani A.G., Ciaccheri L., Ottevaere H., Thienpont H., Conte L., Marega M., Cichelli A., Attilio C., Cimato A. Visible and near-infrared absorption spectroscopy by an integrating sphere and optical fibers for quantifying and discriminating the adulteration of extra virgin olive oil from Tuscany. Anal. Bioanal. Chem. 2011;399(3):1315–1324. doi: 10.1007/s00216-010-4408-y. [DOI] [PubMed] [Google Scholar]
- Mildner-Szkudlarz S., Jeleń H.H. The potential of different techniques for volatile compounds analysis coupled with PCA for the detection of the adulteration of olive oil with hazelnut oil. Food Chem. 2008;110(3):751–761. doi: 10.1016/j.foodchem.2008.02.053. [DOI] [Google Scholar]
- Minaei S., Kiani S., Ayyari M., Ghasemi-Varnamkhasti M. A portable computer-vision-based expert system for saffron color quality characterization. Journal of Applied Research on Medicinal and Aromatic Plants. 2017;7(December 2016):124–130. doi: 10.1016/j.jarmap.2017.07.004. [DOI] [Google Scholar]
- Moore J.C., Spink J., Lipp M. Development and application of a database of food ingredient fraud and economically motivated adulteration from 1980 to 2010. J. Food Sci. 2012;77(4) doi: 10.1111/j.1750-3841.2012.02657.x. [DOI] [PubMed] [Google Scholar]
- Mossoba M.M., Azizian H., Fardin-Kia A.R., Karunathilaka S.R., Kramer J.K.G. First application of newly developed FT-NIR spectroscopic methodology to predict authenticity of extra virgin olive oil retail products in the USA. Lipids. 2017;52(5):443–455. doi: 10.1007/s11745-017-4250-5. [DOI] [PubMed] [Google Scholar]
- Nicolaï B.M., Beullens K., Bobelyn E., Peirs A., Saeys W., Theron K.I., Lammertyn J. Nondestructive measurement of fruit and vegetable quality by means of NIR spectroscopy: a review. Postharvest Biol. Technol. 2007;46(2):99–118. doi: 10.1016/j.postharvbio.2007.06.024. [DOI] [Google Scholar]
- Ozcan-Sinir G. Detection of adulteration in extra virgin olive oil by selected ion flow tube mass spectrometry (SIFT-MS) and chemometrics. Food Control. 2020;118(April) doi: 10.1016/j.foodcont.2020.107433. [DOI] [Google Scholar]
- Peña F., Cárdenas S., Gallego M., Valcárcel M. Direct olive oil authentication: detection of adulteration of olive oil with hazelnut oil by direct coupling of headspace and mass spectrometry, and multivariate regression techniques. J. Chromatogr. A. 2005;1074(1–2):215–221. doi: 10.1016/j.chroma.2005.03.081. [DOI] [PubMed] [Google Scholar]
- Philen R.M., Posada M. Toxic oil syndrome and eosinophilia-myalgia syndrome: may 8-10, 1991, world health organization meeting report. Semin. Arthritis Rheum. 1993;23(2):104–124. doi: 10.1016/S0049-0172(05)80017-4. [DOI] [PubMed] [Google Scholar]
- Pohlert T., Pohlert M.T. 2022. Package ‘ PMCMR. [Google Scholar]
- Posada De La Paz M., Philen R.M., Borda I.A. Toxic oil syndrome: the perspective after 20 years. Epidemiol. Rev. 2001;23(2):231–247. doi: 10.1093/oxfordjournals.epirev.a000804. [DOI] [PubMed] [Google Scholar]
- Poulli K.I., Mousdis G.A., Georgiou C.A. Rapid synchronous fluorescence method for virgin olive oil adulteration assessment. Food Chem. 2007;105(1):369–375. doi: 10.1016/j.foodchem.2006.12.021. [DOI] [Google Scholar]
- Qin J., Burks T.F., Ritenour M.A., Bonn W.G. Detection of citrus canker using hyperspectral reflectance imaging with spectral information divergence. J. Food Eng. 2009;93(2):183–191. doi: 10.1016/j.jfoodeng.2009.01.014. [DOI] [Google Scholar]
- R Core Team The R stats package. 2022. https://stat.ethz.ch/R-manual/R-devel/library/stats/html/00Index.html
- Rohman A., Man Y.B.C. Fourier transform infrared (FTIR) spectroscopy for analysis of extra virgin olive oil adulterated with palm oil. Food Res. Int. 2010;43(3):886–892. doi: 10.1016/j.foodres.2009.12.006. [DOI] [Google Scholar]
- Romaniello R., Baiano A. Discrimination of flavoured olive oil based on hyperspectral imaging. 2018. [DOI] [PMC free article] [PubMed]
- Rungpichayapichet P., Nagle M., Yuwanbun P., Khuwijitjaru P., Mahayothee B., Müller J. Prediction mapping of physicochemical properties in mango by hyperspectral imaging. Biosyst. Eng. 2017;159:109–120. doi: 10.1016/j.biosystemseng.2017.04.006. 2011. [DOI] [Google Scholar]
- Shang Y., Bao L., Bi H., Guan S., Xu J., Gu Y., Zhao C. Authenticity discrimination and adulteration level detection of camellia seed oil via hyperspectral imaging technology. Food Anal. Methods. 2024 doi: 10.1007/s12161-024-02577-x. [DOI] [Google Scholar]
- Squeo G., Grassi S., Paradiso V.M., Alamprese C., Caponio F. FT-IR extra virgin olive oil classification based on ethyl ester content. Food Control. 2019;102(January):149–156. doi: 10.1016/j.foodcont.2019.03.027. [DOI] [Google Scholar]
- Tachie C.Y.E., Obiri-Ananey D., Alfaro-Cordoba M., Tawiah N.A., Aryee A.N.A. Classification of oils and margarines by FTIR spectroscopy in tandem with machine learning. Food Chem. 2024;431(July 2023) doi: 10.1016/j.foodchem.2023.137077. [DOI] [PubMed] [Google Scholar]
- Torrecilla J.S., Rojo E., Domínguez J.C., Rodríguez F. A novel method to quantify the adulteration of extra virgin olive oil with low-grade olive oils by UV-Vis. J. Agric. Food Chem. 2010;58(3):1679–1684. doi: 10.1021/jf903308u. [DOI] [PubMed] [Google Scholar]
- Uncu O., Ozen B. A comparative study of mid-infrared, UV–Visible and fluorescence spectroscopy in combination with chemometrics for the detection of adulteration of fresh olive oils with old olive oils. Food Control. 2019;105(April):209–218. doi: 10.1016/j.foodcont.2019.06.013. [DOI] [Google Scholar]
- van Hengel A.J. Declaration of allergens on the label of food products purchased on the European market. Trends Food Sci. Technol. 2007;18(2):96–100. doi: 10.1016/j.tifs.2006.07.012. [DOI] [Google Scholar]
- van Roy J., Wouters N., De Ketelaere B., Saeys W. Semi-supervised learning of hyperspectral image segmentation applied to vine tomatoes and table grapes. J. Spectr. Imaging. 2018;7:1–18. doi: 10.1255/jsi.2018.a7. [DOI] [Google Scholar]
- Vieira L.S., Assis C., de Queiroz M.E.L.R., Neves A.A., de Oliveira A.F. Building robust models for identification of adulteration in olive oil using FT-NIR, PLS-DA and variable selection. Food Chem. 2021;345(August 2020) doi: 10.1016/j.foodchem.2020.128866. [DOI] [PubMed] [Google Scholar]
- Wobbrock J.O., Findlater L., Gergle D., Higgins J.J. The aligned rank transform for nonparametric FactorialAnalyses using only ANOVA proced. The New York Times. 2011:1–5. [Google Scholar]
- Xiaobo Z., Jiewen Z., Povey M.J.W., Holmes M., Hanpin M. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta. 2010;667(1–2):14–32. doi: 10.1016/j.aca.2010.03.048. [DOI] [PubMed] [Google Scholar]
- Xie C., Wang Q., He Y. Identification of different varieties of sesame oil using near-infrared hyperspectral imaging and chemometrics algorithms. PLoS One. 2014;9(5) doi: 10.1371/journal.pone.0098522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yun J., Cui C., Zhang S., Zhu J., Peng C., Cai H., Yang X., Hou R. Use of headspace GC/MS combined with chemometric analysis to identify the geographic origins of black tea. Food Chem. 2021;360(May) doi: 10.1016/j.foodchem.2021.130033. [DOI] [PubMed] [Google Scholar]
- Zabaras D. Olives and Olive Oil in Health and Disease Prevention. Elsevier Inc; 2010. Olive oil adulteration with hazelnut oil and analytical approaches for its detection. [DOI] [Google Scholar]
- Zade S.V., Forooghi E., Jannat B., Hashempour-baltork F., Abdollahi H. A combined classification modeling strategy for detection and identification of extra virgin olive oil adulteration using Raman spectroscopy. Chem. Intell. Lab. Syst. 2023;240:104903. [Google Scholar]
- Zarezadeh M.R., Aboonajmi M., Ghasemi Varnamkhasti M. Fraud detection and quality assessment of olive oil using ultrasound. Food Sci. Nutr. 2021;9(1):180–189. doi: 10.1002/fsn3.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarezadeh M.R., Aboonajmi M., Varnamkhasti M.G., Azarikia F. Olive oil classification and fraud detection using E-nose and ultrasonic system. Food Anal. Methods. 2021;14(10):2199–2210. doi: 10.1007/s12161-021-02035-y. [DOI] [Google Scholar]
- Zeng Tan, Matsunaga, Shirai Generalization of parameter selection of SVM and LS-SVM for regression. Machine Learning and Knowledge Extraction. 2019;1(2):745–755. doi: 10.3390/make1020043. [DOI] [Google Scholar]
- Zhang X.-F., Zou M.-Q., Qi X.-H., Liu F., Zhang C., Yin F. Quantitative detection of adulterated olive oil by Raman spectroscopy and chemometrics. 2011. [DOI]
- Zheng W., Fu X., Ying Y. Spectroscopy-based food classification with extreme learning machine. Chemometr. Intell. Lab. Syst. 2014;139:42–47. doi: 10.1016/j.chemolab.2014.09.015. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data are available on GitHub at https://github.com/DNMalavi/NIR-HSI-ML-for-EVOO-Fraud-Detection.