The molecular architecture of the desmosomal outer dense plaque by integrative structural modeling

Abstract

Desmosomes mediate cell–cell adhesion and are prevalent in tissues under mechanical stress. However, their detailed structural characterization is not available. Here, we characterized the molecular architecture of the desmosomal outer dense plaque (ODP) using Bayesian integrative structural modeling via the Integrative Modeling Platform. Starting principally from the structural interpretation of a cryo‐electron tomography (cryo‐ET) map of the ODP, we integrated information from x‐ray crystallography, an immuno‐electron microscopy study, biochemical assays, in silico predictions of transmembrane and disordered regions, homology modeling, and stereochemistry information. The integrative structure was validated by information from imaging, tomography, and biochemical studies that were not used in modeling. The ODP resembles a densely packed cylinder with a plakophilin (PKP) layer and a plakoglobin (PG) layer; the desmosomal cadherins and PKP span these two layers. Our integrative approach allowed us to localize disordered regions, such as the N‐terminus of PKP and the C‐terminus of PG. We refined previous protein–protein interactions between desmosomal proteins and provided possible structural hypotheses for defective cell–cell adhesion in several diseases by mapping disease‐related mutations on the structure. Finally, we point to features of the structure that could confer resilience to mechanical stress. Our model provides a basis for generating experimentally verifiable hypotheses on the structure and function of desmosomal proteins in normal and disease states.

1. INTRODUCTION

Desmosomes are large, 300 nm‐long protein assemblies that connect the keratin intermediate filaments of adjacent cells. They mediate cell–cell adhesion and play a crucial role in maintaining tissue integrity for tissues under mechanical stress, such as heart and epithelial tissues. They also play critical roles in cell signaling and tissue differentiation. Dysfunction of desmosomes has been implicated in skin and heart diseases, auto‐immune diseases, and cancers (Garrod & Chidgey, 2008; Green & Simpson, ²⁰⁰⁷; Kowalczyk & Green, ²⁰¹³).

The ultra‐structure of desmosomes shows its organization in three areas: the extracellular core region (EC), and two intracellular regions: the outer dense plaque (ODP), and the inner dense plaque (IDP) (Figure 1a) (Delva et al., 2009). The EC is made up of the desmosomal cadherins (DCs), desmoglein (DSG), and desmocollin (DSC), which interact with similar molecules in adjacent cells to achieve cell–cell adhesion. The ODP, which spans 15–20 nm, is a protein‐dense cytoplasmic region between the EC and IDP that is immediately adjacent to the plasma membrane. Here, members of the armadillo family—plakoglobin (PG) and plakophilin (PKP), members of the plakin family—desmoplakin (DP), and the cytoplasmic tails of the desmosomal cadherins interact. The ODP functions to regulate cadherins since it contains several phosphorylation sites and binding sites for regulatory proteins (Badu‐Nkansah & Lechler, 2020; Garrod & Chidgey, ²⁰⁰⁸). Recent proteomics studies have identified several regulatory proteins that are seen in the ODP (Badu‐Nkansah & Lechler, 2020). Desmoplakin links to the keratin intermediate filaments in the IDP at the cytoplasmic end of the desmosome (Garrod & Chidgey, 2008; Kowalczyk & Green, ²⁰¹³).

FIGURE 1.

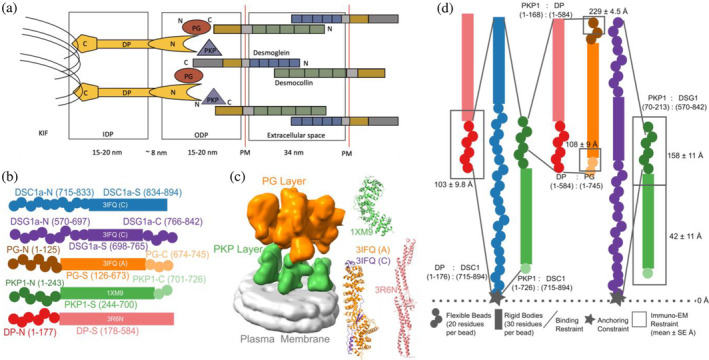
Representation and restraints used for integrative modeling of the desmosomal ODP. (a) The desmosome connects the extracellular space external to the plasma membrane (PM) and the keratin intermediate‐filament (KIF) cytoskeleton. It comprises three regions: the extracellular space, and two intracellular regions: the outer dense plaque (ODP), and the inner dense plaque (IDP). (b) The isoforms used in modeling the desmosomal ODP of stratified epithelia and the representation of the different protein domains as rigid bodies with known structures (rectangles with PDB ID and chain name) or flexible beads (circles). The domains with known structure are usually denoted by a suffix ‐S after the protein (e.g., DP‐S), while the termini are denoted by ‐N or ‐C suffixes after the protein (e.g., DP‐N). (c) Three types of restraints are shown. 1. Binding restraints between interacting protein domains are depicted by a pair of lines connecting the boundaries of each interacting domain pair. 2. Immuno‐EM restraint for localizing protein termini depicted by rectangles around the restrained protein terminus, and 3. Anchoring constraint for localizing the transmembrane region of the cadherins depicted by stars. The color scheme follows that in panel (a). (d) (Left) The cryo‐ET density map (EMD‐1703) used for modeling is shown with the PKP and the PG layers segmented. The density corresponding to the plasma membrane was not used for modeling. (Right) The PDB structures used, are colored according to panel (a). See also 4. Methods, Figure S1, Tables S1 and S2.

A detailed structural characterization of the ODP is not yet available. A molecular map based on immuno‐electron microscopy is known (North et al., 1999). However, this map provides the distances of plaque protein termini from the plasma membrane; it does not provide information on the three‐dimensional arrangement of the proteins. A 32 Å density map obtained from cryo‐electron tomography (cryo‐ET) of the ODP, which shows its organization in two layers, has been determined by (Al‐Amoudi et al., 2011). This is also the most comprehensive structural study on the ODP so far. However, the resolution of the cryo‐ET map did not allow to unambiguously fit the known structures of plaque proteins and protein complexes. Moreover, domains of unknown structure, comprising a significant portion of the ODP, were not modeled. These domains make up about 40% of the protein sequences of the stratified epithelial desmosomal ODP (Figure 1b, Table S1). In this study, we built a more complete model of the ODP, including domains of unknown structure, by combining the data from cryo‐electron tomography and immuno‐EM experiments with an array of known biophysical, biochemical, and cell biological experimental data, bioinformatics predictions, and physical principles (Figure 1, Tables S2 and S3) (Bonné et al., 2003; Bornslaeger et al., ²⁰⁰¹; Hatzfeld et al., ²⁰⁰⁰; Kowalczyk et al., ¹⁹⁹⁹; Smith & Fuchs, ¹⁹⁹⁸).

Structures of large protein assemblies such as desmosomes are challenging to characterize using a single experimental method such as x‐ray crystallography or cryo‐electron microscopy. Purifying the component proteins is difficult since several of these are membrane proteins. Here we applied integrative structural modeling via IMP (Integrative Modeling Platform; https://integrativemodeling.org) to characterize the molecular architecture of the ODP (Alber et al., 2007; Rout & Sali, ²⁰¹⁹; Russel et al., ²⁰¹²). In this approach, we combined information from experiments along with physical principles, statistical inference, and prior models for structure determination. Several assemblies have been determined using this approach, including the yeast nuclear pore complex (Alber et al., 2007; Kim et al., ²⁰¹⁸), 26S proteasome (Lasker et al., 2012), yeast centrosome (Viswanath, Bonomi, et al., 2017), and chromatin‐modifying assemblies (Arvindekar et al., 2022; Robinson et al., ²⁰¹⁵). Importantly, the Bayesian inference framework allowed us to rigorously and objectively combine multiple sources of experimental data at different spatial resolutions by accounting for the data uncertainty. It also facilitated the modeling of full‐length proteins, including regions of unknown structure and/or disorder along with regions of known and/or readily modeled atomic structure.

Based primarily on the structural interpretation of the cryo‐ET density map of the ODP (Al‐Amoudi et al., 2011), we integrated information from an immuno‐electron microscopy study, several x‐ray crystallography studies, biochemical studies based on yeast two‐hybrid, co‐immunoprecipitation, in vitro overlay, and in vivo co‐localization assays, in silico sequence‐based predictions of transmembrane and disordered regions, homology modeling, and stereochemistry information to obtain the integrative structure of the desmosomal ODP (Figures 1 and 2, Tables S1–S3). Our structure was further validated by additional information super‐resolution imaging, newer tomograms, and biochemical studies not used in modeling (Sikora et al., 2020; Smith & Fuchs, ¹⁹⁹⁸; Stahley et al., ²⁰¹⁶) (Table S3A). Our approach allowed us to localize disordered regions such as the N‐terminus of plakophilin and the C‐terminus of plakoglobin in the context of regions of known structure. We refine known protein–protein interactions in the ODP, provide structure‐based hypotheses for defective cell–cell adhesion associated with pathogenic mutations seen in skin diseases and cancers, and identify aspects of the desmosome structure that could possibly confer robustness to mechanical stress. Further, our integrative structure is more complete in terms of the sequence coverage of the ODP proteins compared to other structures, for example, based on cryo‐electron tomography, which lack the disordered domains of ODP proteins (Al‐Amoudi et al., 2011) (e.g., PKP1‐N). The current work forms a basis for generating experimentally verifiable hypotheses on the structure and function of desmosomal proteins. Finally, modeling the desmosome necessitated the development of new methods for integrative modeling of systems with ambiguity, that is, multiple protein copies. These methods are implemented in the open‐source Integrative Modeling Platform (https://integrativemodeling.org) and are available for use in other investigations (Russel et al., 2012).

FIGURE 2.

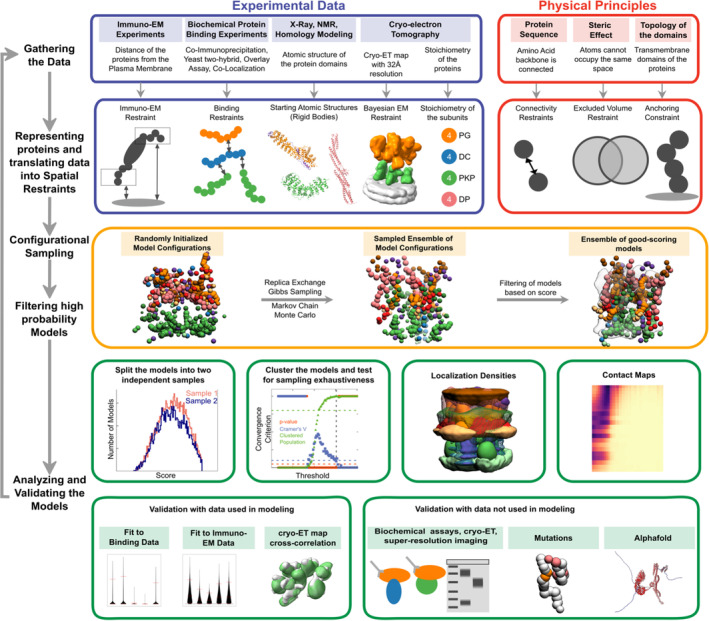
Integrative modeling of the desmosomal ODP. From top to bottom, the rows describe the input information (first), how the input information is encoded into spatial restraints (second), the sampling procedure (third), the analysis (fourth), and the validation of the results (fifth).

2. RESULTS AND DISCUSSION

2.1. Summary of the integrative modeling workflow

The expression of isoforms of the ODP subunits is tissue‐dependent (Delva et al., 2009; Green & Simpson, ²⁰⁰⁷). Below, we detail the integrative structure of the desmosomal ODP corresponding to the upper epidermis, comprising of plakoglobin (PG), desmoplakin (DP1, henceforth DP), plakophilin (PKP1a, henceforth PKP1), desmocollin (DSC1a, henceforth DSC1), and desmoglein (DSG1a, henceforth DSG1) (Figure 1b, Table S1). The chosen isoforms are the predominant ones in stratified epithelia, and as a simplifying assumption, our model contains a single isoform of each modeled protein (Garrod & Chidgey, 2008; Green & Simpson, ²⁰⁰⁷). The upper epidermis was chosen since the corresponding isoforms were associated with the most biochemical data. Further, the tomography data and immuno‐EM data also correspond to epithelial tissue.

The protein domains constituting the desmosomal ODP and the corresponding terminology used henceforth are shown (Figure 1b, Table S1). The stoichiometry of these proteins was determined using a previously published cryo‐ET map (4. Methods) (Al‐Amoudi et al., 2011). Integrative modeling proceeded in four stages (Figure 2, 4. Methods). Data from x‐ray crystallography, cryo‐electron tomography, immuno‐electron microscopy, and biochemical assays was integrated with in silico sequence‐based predictions of transmembrane and disordered regions, homology modeling, and stereochemistry information (Figure 1c,d, Tables S2 and S3).

Each protein was represented by a series of spherical beads along the backbone, each bead denoting a fixed number of residues. Protein domains with x‐ray structures or homology models (such as the PKP1 armadillo repeat domain) were represented at 30 residues per bead and modeled as rigid bodies, whereas domains without known atomic structure (such as the PKP1‐N) were coarse‐grained at 20 residues per bead and modeled as flexible strings of beads (Figure 1b,d, Table S1, 4. Methods). Data from immuno‐EM was used to restrain the distance of protein termini from the plasma membrane, cryo‐ET density maps were used to restrain the localization of ODP proteins, and the data from biochemical assays restrained the distance between interacting protein domains (Figure 1c,d, 4. Methods). Starting with random initial configurations for the rigid bodies and flexible beads, 180 million models were sampled using Replica Exchange Gibbs Sampling MCMC, from a total of 50 independent runs. At each step, models were scored based on agreement with the immuno‐EM, cryo‐ET density map, and biochemical data, together with additional stereochemical restraints such as cylinder restraints, connectivity, and excluded volume (see 4. Methods).

About 24,866 good‐scoring models were selected for further analysis (see 4. Methods, Stage 4 for details). These models were clustered based on structural similarity and the precision of the clusters was estimated (Arvindekar et al., 2022; Saltzberg et al., ²⁰²¹; Viswanath, Chemmama, et al., ²⁰¹⁷) (Figure S2). The quality of the models was assessed by the fit to input data, as well as to data not used in modeling (Figures S3 and S4, Tables S2 and S3, 4. Methods). The models are consistent with all the input information, including the information from protein–protein binding assays, immuno‐EM maps, and the cryo‐ET map (Figure S3, Table S2, 4. Methods). The models are also consistent with information not used in the modeling, such as data from protein–protein binding assays, and newer super‐resolution imaging and cryo‐electron tomography experiments (Figure S4, Table S3A, 4. Methods). Further analysis included the identification of protein–protein interfaces via contact maps and rationalizing skin and cancer‐related diseases involving ODP proteins via mapping of known missense, pathogenic mutations on the integrative structure (Figures 4 and 5, Figure S5, Tables S4 and S5, 4. Methods).

FIGURE 4.

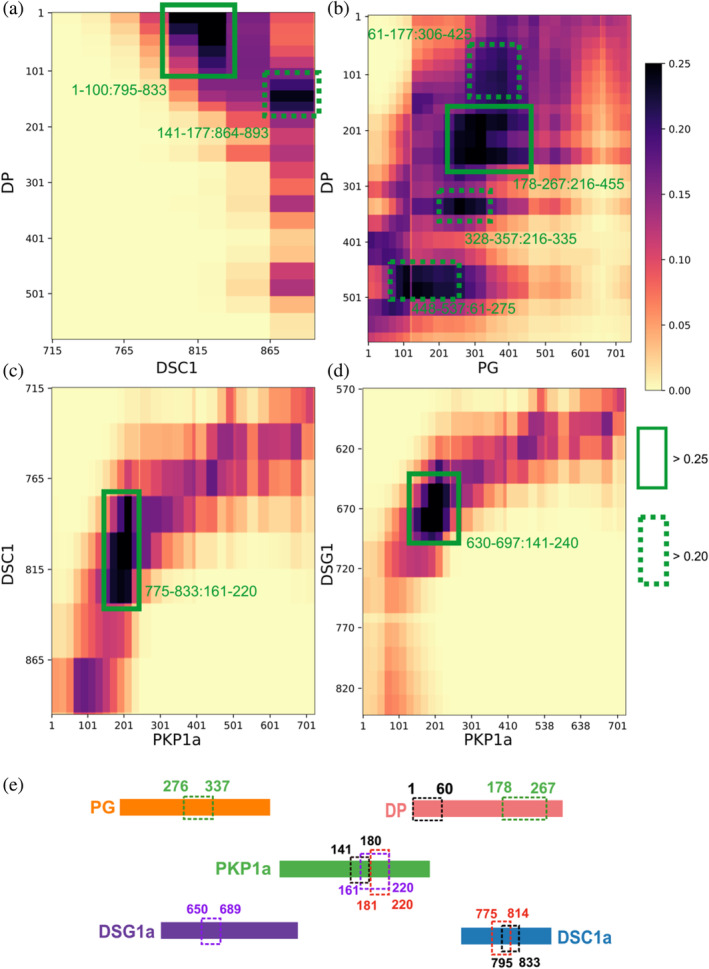
Novel ODP protein–protein interfaces. Protein–protein contact maps for DP‐DSC1 (a), DP‐PG (b), DSC1‐PKP1 (c), and DSG1‐PKP1 (d) pairs. Maps are colored by the proportion of the models in the major cluster where the corresponding bead surfaces are within contact distance (10 Å). Rectangles with solid green (broken green) lines outline novel contacts present in >25% (>20%) of the models. Interacting residues are marked in green text in the format Y‐axis protein residues: X‐axis protein residues. (e) Summary of high‐confidence protein–protein interactions from the integrative model. Dashed rectangles of the same color denote a protein–protein interaction; the interacting residues are marked in the same color. For example, DP 178–267 interacts with PG 276–337 (green rectangle). See also Figure S5, Table S4.

FIGURE 5.

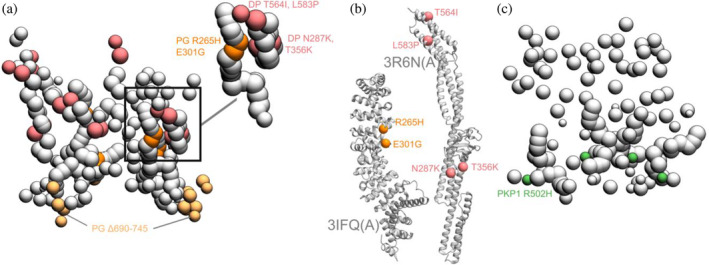
Disease‐associated mutations mapped onto the integrative structure. (a) Cluster center bead model showing mutations in PG and DP. Mutations in DP‐S (pink), PG‐S (orange), and PG‐C (light orange) are colored as per Figure 1. Remaining beads of DP and PG are shown in gray. The top right shows a zoomed‐in version of a novel predicted PG‐DP interface harboring disease mutations. (b) PG‐S and DP‐S mutations mapped onto the corresponding structures 3IFQ(A) and 3R6N(A) (Choi et al., 2009; Choi & Weis, ²⁰¹¹). (c) Bead model showing mutations in PKP1‐S (green). See also Table S5.

2.2. Integrative structure of the desmosomal ODP in the upper epidermis

Integrative modeling of the desmosomal ODP in the upper epidermis resulted in a single cluster of 24,016 models (97% of 24,866 models), with a model precision of 67 Å. Model precision is the variability of models in this cluster and is computed as the average RMSD of the cluster models to the cluster centroid (Figure 3, Figure S2, 4. Methods). The model precision is lower than the resolution of the ODP cryo‐ET map (32 Å) (Al‐Amoudi et al., 2011). This is mostly due to the fact that the integrative model localizes 55% more residues than the map, the majority of which are on disordered and flexible regions. To confirm this, the precision was calculated separately for regions with known structures, such as DP‐S, PG‐S, PKP1‐S (“stable core,” comprising 60% of the beads), and disordered regions, such as PKP1‐N, DP‐N, PG‐N, PG‐C, DSC1, and DSG1 (“disordered” region, comprising 40% of the beads). This classification was based on disorder predictions from PSIPRED (Buchan & Jones, 2019) (Figure S6). The precision of the disordered region was lower at 77 Å (0.45 Å precision per bead), compared to that of the stable core at 48 Å (0.19 Å precision per bead). The precision of the stable core remains approximately the same as in the previous cryo‐electron tomography study (Al‐Amoudi et al., 2011). However, some disordered regions, such as parts of DSC1, DSG1, and PKP1‐N localized at high precision and/or formed extensive interactions with proteins in the PG layer of the stable core (Figure 3, Figure 4, Table S4).

FIGURE 3.

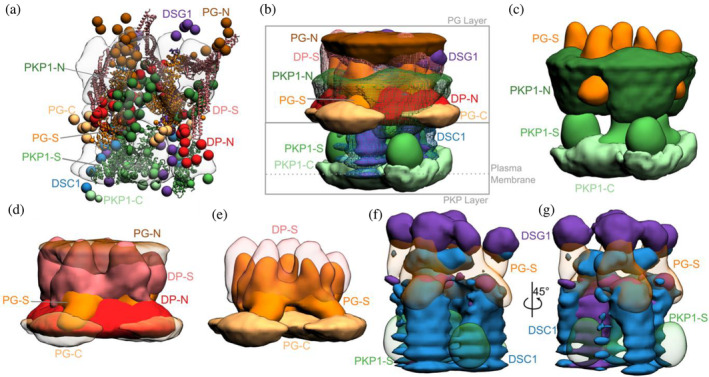
Integrative structure of the desmosomal ODP. (a) The cluster center bead model for the major structural cluster with the cryo‐ET map (EMD‐1703) superimposed in translucent gray. (b) Localization densities of the major cluster. The densities are at a cutoff of approximately 15% for PKP1‐C, PKP1‐S, PG‐S, DP‐S, DSC1, and DSG1 and around 30% for disordered termini regions (PKP1‐N, PG‐N, DP‐N, PG‐C). (c) Localization densities for PKP1 layer (PG‐S density is shown for reference). (d) Localization densities for PG‐layer. (e) The densities for PG‐S and DP‐S with PG‐C as a reference. (f, g) Localization densities for the cadherins. Panel (g) is a rotated view of panel (f). See also Figure 4, Figures S2–S5, Movie S1.

Other factors that contribute to low precision include low‐resolution, sparse, and noisy input information. For example, the protein–protein binding data are on the domain level and not the residue level, we have fewer than 10 protein–protein binding restraints. All these sources of uncertainty in the input information are reflected in the model precision.

Nevertheless, these models fit well with the input information used in modeling (Figure S3, Table S2, 4. Methods). They were further corroborated by their agreement with information not used for modeling (Figure S4, Table S3). A subset of this information is orthogonal to the input information and nontrivial for the models to satisfy (validation data, Table S3A), while another subset is consistent with the input information and hence satisfied by the model by construction (Table S3B) (4. Methods). The resulting integrative structures were visualized in two ways: a bead model representing the centroid of the major cluster (Figure 3a), and a localization probability density map, representing the localization of protein domains by specifying the probability of a voxel (3D volume) being occupied by a domain in the set of structurally superposed cluster models (Figure 3b–g).

Overall, the desmosomal ODP resembles a densely packed cylinder with two layers, the PG layer on top of the PKP layer (Figure 3a,b). A striking feature of the ODP model is that the two layers are not distinct and well‐separated. Rather, the desmosomal cadherins and PKP1 span both layers. The N‐terminus of PKP1 penetrates the PG layer while the rest of the protein is in the PKP layer (Figure 3b).

2.2.1. PKP layer

PKP1‐C is the region of the ODP closest to the plasma membrane. This region has low precision in the integrative model as shown by the spread of the localization densities (Figure 3b,c). PKP1‐S, the armadillo repeat domain of PKP1, is juxtaposed between PKP1‐C and PKP1‐N, at high precision (Figure 3b,c). This is consistent with PKP1‐S localization in cryo‐ET maps (Al‐Amoudi et al., 2011). PKP1‐N extends from PKP1‐S in the PKP layer to the middle of the PG layer, forming interfaces with several proteins in the PG layer (see also protein–protein interfaces) (Figure 3b,c). Its density is spread out, that is, it has low precision, consistent with the idea that it is a disordered domain (Figure 3b,c) (Al‐Amoudi et al., 2011).

2.2.2. PG layer

PKP1‐N, DP‐N, and PG‐C form the approximate boundary between the PKP and PG layers (Figure 3b–d). The last two are approximately equidistant from the plasma membrane, consistent with previous immuno‐EM studies (North et al., 1999; Table S2B).

PG‐S and DP‐S, the armadillo repeat and plakin domains of PG and DP, respectively, seem to localize in approximately the same region and physically interact (see also protein–protein interfaces from the integrative model) (Figure 3b–e). Previously, PG‐S and DP‐S were hypothesized to form a regular zigzag arrangement, with both domains approximately equidistant to the plasma membrane (Al‐Amoudi et al., 2011). In contrast, in our integrative structure, the centers of PG‐S and DP‐S are at slightly different distances from the membrane (Figure 3d,e). On average, PG‐S is slightly closer to the plasma membrane and DP‐S is slightly closer to the cytoplasmic end. Also, there is no regular orientation to either PG‐S or DP‐S, although based on the localization densities, these domains appear to prefer an orientation where their long axis is approximately perpendicular to the membrane (Figure 3d,e). The lack of regular orientations could be because these domains are flexible and dynamic. Alternatively, the orientation could be regular, but there is not enough data at present to suggest a regular orientation.

The cytoplasmic end of the desmosomal ODP is occupied by PG‐N. The PG layer protein termini with unknown structure, PG‐N, DP‐N, and PG‐C, are localized at low precision (Figure 3d).

2.2.3. Desmosomal cadherins

The desmosomal cadherins extend from the membrane end of the ODP, through the space in the PKP layer, toward the PG layer, interacting with PG, DP, as well as PKP1 (see also protein–protein interfaces) (Figure 3b,f,g). DSG1 being longer, extends longer at the cytoplasmic end of the PG layer, close to PG‐N, where it is localized at low precision. Whereas, DSC1 extends until PG‐S in the middle of the PG layer (Figure 3b,f,g).

2.3. Protein–protein interfaces from the integrative model

To enable the discovery of protein–protein interfaces in the desmosomal ODP, we computed contact maps and predicted interfaces between protein pairs (Figure 4a–e, Figure S5, Table S4, 4. Methods). Our contact maps denote the percentage of models in the cluster in which the corresponding bead surfaces are within contact distance (10 Å). The contact maps are consistent with the localization of PG and PKP1 in separate layers and with the structures of known ODP sub‐complexes, for example, the PG‐desmosomal cadherin complexes (Figure S5, Table S4). Analysis of the set of top 2%–5% contacts, which likely excludes contacts made randomly, enabled us to refine previously known interactions (Figure 4, Figure S5, Table S4, 4. Methods). The newly predicted interfaces are consistent with the input biochemical binding information and refine the latter, providing higher‐resolution information due to the integration of additional sources of information in the modeling. They form an extensive set of concrete hypotheses for future experiments (Figure 4, Figure S5, Table S4). Below, we discuss some of these novel interfaces in light of the role of desmosomal subunits in maintaining robust cell–cell adhesion, assembly of desmosomes, and desmosome‐related diseases.

2.4. Insights into the molecular basis of desmosome‐related diseases

Next, we hypothesized the structural basis for desmosomal defects in skin diseases and cancer by mapping disease‐associated mutations on our integrative structure. These hypotheses would need to be verified experimentally in future studies. Specifically, we mapped known pathogenic missense mutations on desmosomal subunits that are associated with Naxos disease, Carvajal syndrome, or cancers (Figure 5, Table S5, 4. Methods). Both Naxos disease and Carvajal syndrome are characterized by abnormalities in epithelial tissue including palmoplantar keratoderma (thickened skin) and woolly hair (Boulé et al., 2012; Den Haan et al., ²⁰⁰⁹; Erken et al., ²⁰¹¹; Keller et al., ²⁰¹²; Marino et al., ²⁰¹⁷; McKoy et al., ²⁰⁰⁰; Pigors et al., ²⁰¹⁵; Whittock et al., ²⁰⁰²).

2.4.1. PG mutations in Naxos disease

The missense mutations PG R265H and PG E301G seen in Naxos disease are in the armadillo repeat domain of PG (Figure 5a,b, Table S5). These mutations are in the newly predicted PG‐DP interface and known PG‐DSG1 interface, and may result in disruption of these interfaces (Figures 4 and 5a,b). Additionally, since they are in the armadillo domain, these mutations may also affect the folding and stability of this domain, and therefore desmosome assembly.

On the other hand, the truncation mutation PG Δ690‐745 is in the disordered PG C‐terminus (Figure 5a). The latter is known to regulate the size of the desmosome; deletion of PG‐C results in desmosomes that are larger than usual (Palka & Green, 1997). This truncation mutation may therefore affect desmosome assembly by altering the mechanism by which PG‐C regulates desmosome size, for example, by modifying interactions with regulatory proteins.

2.4.2. DP mutations in Carvajal syndrome and skin fragility/woolly hair (SF/WH) syndrome

The DP missense mutations N287K (SF/WH syndrome) and T356K, T564I, and L583P (Carvajal Syndrome) are in the spectrin homology domain of DP (Figure 5a,b, Table S5) as well as the newly predicted PG‐DP interface (Figures 4 and 5a, Table S4). These mutations may alter the integrity of the DP‐PG interface as well as the folding and stability of the spectrin domain.

2.4.3. Cancers

The PKP1 R502H missense mutation is in the armadillo repeat domain of PKP1 and might affect the folding and stability of PKP1 in the ODP (Figure 5c, Table S5). It is noteworthy that this residue is not resolved in the x‐ray structure of PKP1, PDB: 1XM9 (Choi & Weis, 2005). It is part of a larger flexible loop with missing residues, suggesting the conformational flexibility of this region.

The other mutations associated with these diseases could not be readily rationalized by our structure (Table S5). In summary, three reasons can be identified for the pathogenicity of these mutations. They alter the folding and/or stability of ODP proteins, they disrupt protein–protein interfaces in the ODP, or they modify the binding properties of functionally important disordered protein domains in the ODP. All three types of mutations may disrupt the assembly and stability of the ODP, thereby affecting cell–cell adhesion. However, these mutations could also be pathogenic due to their effects on other functions such as cell signaling (Garrod & Chidgey, 2008). Given the low model precision and the mapping to approximate interfaces and localizations, further experiments are required to validate the impact of these mutations.

Besides, the structure of cardiac desmosomes is likely similar to that of the modeled epithelial desmosome. Therefore, our model could also be used to determine the structural basis of the numerous mutations related to cardiac diseases (e.g., ARVC). However, we restricted the mutation analysis to epithelial diseases since our integrative structure is based on epithelial tissue isoforms (cardiac tissues consist of a slightly different set of isoforms (Delva et al., 2009; Green & Simpson, ²⁰⁰⁷)) (Figure 1, Table S1).

2.5. PKP‐N penetrates the PG layer

Our models indicate that PKP1‐N penetrates the PG layer and a conserved 40‐residue segment in PKP1‐N interacts with several ODP proteins. In our integrative structure, the N‐terminus of PKP1 (PKP1‐N) penetrates from the PKP layer to the PG layer and the two layers are not well‐separated (Figure 3a–c, Figure 6). In contrast, PG and PKP were seen in two distinct layers in cryo‐ET density maps (Al‐Amoudi et al., 2011). The densities in these maps were likely contributed by regions of known structure (e.g., PG‐S and PKP1‐S). PKP1‐N, being disordered, is possibly flexible and heterogeneous, leading to smoothing out of its densities upon averaging (Figure S6). In integrative modeling via IMP, regions of unknown structure can be modeled alongside regions of known structure. By combining biochemical binding data along with structural (cryo‐ET) data, our approach allowed us to localize disordered domains like PKP1‐N.

FIGURE 6.

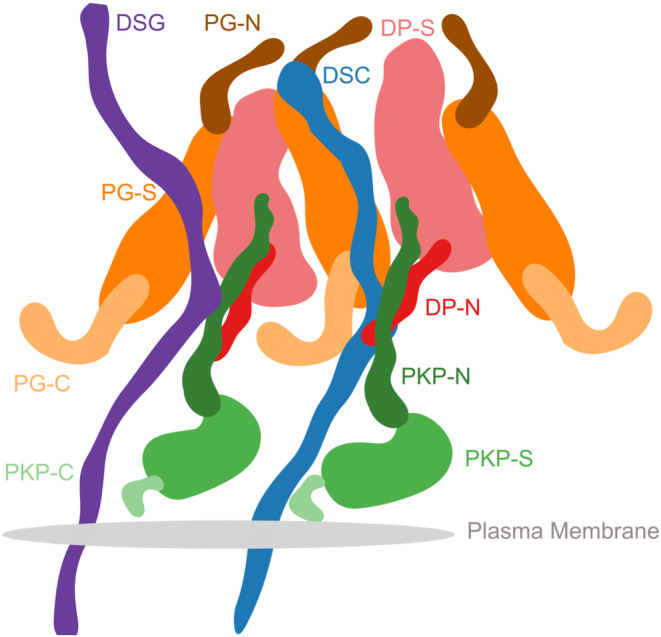
Schematic of the desmosome ODP. Schematic showing the salient features of the protein organization and protein–protein interfaces in the ODP. Wavy thick lines represent potentially disordered regions without known structure (DC, PKP‐N, PG‐N, DP‐N, PKP‐C, PG‐C). Larger shapes represent regions with known structures (PG‐S, DP‐S, PKP‐S). This is an artistic representation of Figure 3.

In our structure, PKP1‐N mediates interactions with several ODP proteins (Figure 4, Figure 6), implying that PKP plays a more integral role in desmosome function and assembly. Specifically, PKP1^181‐220 interacts with DSC1^775‐814, and PKP1^161‐220 with DSG1^650‐689; notably, both desmosomal cadherins share binding sites on PKP1 (Figure 4). Also, PKP1^141‐180 interacts with DP^1‐60 at a slightly lower, but still stringent, contact map cutoff (top 5% of all contacts, Figure S5, Table S4). Interestingly, this 40 residue stretch in PKP1‐N, PKP1^161‐200, interacts with DP as well as the cadherins, and sequence analysis suggests that this sequence in PKP1‐N is conserved (Figure S6).

This is consistent with studies that show that PKP1 enhances recruitment of other desmosomal proteins, increasing desmosome size, and promoting desmosome assembly. For example, (Bornslaeger et al., 2001; Kowalczyk et al., ¹⁹⁹⁹; Sobolik‐Delmaire et al., ²⁰⁰⁶) showed that PKP1 clusters DP, (Hatzfeld et al., 2000) showed that PKP1 interacts with DP as well as desmosomal cadherins, and keratins, and (Tucker et al., 2014) showed that PKP1 interacts with DP and DSG3. PKP1 is also essential for clustering DSG1 and DSG3 (Fuchs et al., 2019). Two of the above studies mention that the amino tip of PKP1, PKP1^1‐70 (Hatzfeld et al., 2000), and PKP1^1‐34 (Sobolik‐Delmaire et al., 2006), recruits DP. In our models, although PKP1^141‐180 (middle of PKP1‐N), is the most probable PKP1‐binding region (i.e., highest confidence contact) for DP, the amino‐tip of PKP1 is also proximal to DP and is among the top 5% of PKP1‐DP contacts (Table S4). This region is also predicted to bind to DP based on Alphafold (See Comparison to Alphafold). In summary, our models indicate that PKP1‐N, specifically the conserved region PKP1^161‐200, could be involved in the recruitment and/or subsequent stabilization of other ODP proteins.

2.6. PG‐C extends outward from the ODP

In our integrative structure, the C‐terminus of PG, PG^674‐745, extends outward, suggesting that it can form lateral connections with other proteins (Figure 3d, Figure 6). It is known to play a role in regulating the size of the desmosome. Deletion of the PG C‐terminus resulted in larger desmosomes due to lateral association (Palka & Green, 1997). Moreover, this deletion was also associated with Naxos disease and defects in tissue integrity, highlighting the importance of PG‐C (McKoy et al., 2000).

The mechanism by which PG‐C regulates the size of desmosomes remains to be elucidated. It is predicted to be intrinsically disordered (IDR) (Figure S6). PG^683‐687 in this region is predicted to be a MoRF (molecular recognition feature), which is a motif in a disordered protein sequence that recognizes and binds to another protein (Disfani et al., 2012). The presence of the MoRF may allow PG‐C to bind to itself, that is, PG‐S, or to other proteins to enable regulation of desmosome size. In particular, the former mechanism, that is, IDR tails competitively binding to domains of the same protein to inhibit their function, is well‐known for several enzymes and single‐stranded DNA‐binding proteins (Uversky, 2013). Finally, this region also contains a phosphosite (PG S730), suggesting that phosphorylation could potentially be another mechanism by which the desmosome size is regulated (Bian et al., 2014).

2.7. The plakin domain of DP interacts with the armadillo repeats of PG

Our integrative structure identifies an interaction between the plakin domain of DP and the armadillo repeat domain of PG, DP^178‐267, and PG^276‐335 (Figure 4). DP‐S appears to encapsulate PG‐S in the densities (Figure 3e, Figure 6). This interaction could provide a robust mechanism for desmosomes to anchor intermediate filaments (IF) and withstand mechanical stress. In fact, PG‐DP binding is shown to be required for effective IF anchoring in desmosomes. PG knockout cells showed defective anchoring of IF (Acehan et al., 2008). Both the DP plakin domain and the PG arm domain are conserved across vertebrates, suggesting this interaction could also be conserved (Green et al., 2020; Smith & Fuchs, ¹⁹⁹⁸). Further, a mutation in this region, PG E301G, was associated with Naxos disease and defects in epithelial tissue, further alluding to the importance of this interaction (Figure 5, Table S5).

Moreover, this interaction could be important for desmosome assembly. In transient expression experiments in COS cells, PG was shown to be required for DP recruitment to cell borders (Kowalczyk et al., 1999). In our models, the DP binding region of PG overlaps with its cadherin‐binding region, consistent with the fact that these three ODP proteins cluster together in desmosome assembly (Figure 4) (Kowalczyk et al., 1999). Given their proximity, DP could also regulate the signaling functions of PG and PG‐mediated crosstalk between desmosomes and adherens junction (Garrod & Chidgey, 2008).

2.8. The localization and interactions of desmosomal cadherins

The desmosomal cadherins wind their way through the other proteins in the PG and PKP layers, making several interactions (Figures 3b,f,g and 6). The cadherin spacing of 7 nm from recent density maps from cryo‐electron tomograms is consistent with our model (Sikora et al., 2020) (Figure S4, 4. Methods). The cadherins appear to be embedded in the thick of the other proteins, instead of circumnavigating the other proteins. This embedding in the midst of other ODP proteins provides a stronger anchoring for the cadherins and their extracellular domains in the cytoplasm. In turn, this feature could buffer the desmosomes from mechanical stress.

Notably, DSC and DSG are different in their interactions with the other proteins. DSC1^795‐833 (the DSC1 region N‐terminal to its PG binding site) interacts with DP^1‐60 (Figure 4). Whereas, an interaction with DP is not seen for DSG1 (Figure S5). This is consistent with the input information (Figure 1, Table S2) (Smith & Fuchs, 1998). It is also consistent with experiments that showed that DSG requires PG to recruit DP, while DSC can recruit DP independently (Kowalczyk et al., 1999).

2.9. Comparison to alphafold

We also attempted to model sub‐complexes of the ODP using the Al‐based protein structure prediction method, Alphafold3 (Abramson et al., 2024) (4. Methods Stage 4).

2.9.1. AF3 model of the desmosome ODP

We first modeled a 2:2:2:1:1 DP1:PG:PKP1a:DSG1a:DSC1a complex of the ODP with Alphafold3 (AF3) (Abramson et al., 2024) (Figure S7A). The stoichiometry followed the same considerations as in the integrative modeling approach (1 desmosomal cadherin per PG, 1:1:1 stoichiometry for DP:PG:PKP1a). The number of copies of each protein was based on the maximum sequence length permitted per complex in AF3 (5000 residues). The same sequence segments as earlier were modeled (Table S1). The model confidence, as well as the average confidence in the predicted interfaces, was low as indicated by the pTM (predicted TM) score of 0.5 and the iPTM (interface predicted TM) score of 0.45 for the best‐ranked model across multiple runs. In Alphafold3, a pTM higher than 0.5 indicates a likely correct overall fold and an iPTM greater than 0.6 is likely to be a correct interface prediction, with 0.6–0.8 being a gray zone (Abramson et al., 2024). Further, no single pairwise interface prediction was reliable according to AF3, as indicated by the values of ipTMs for pairs of subunits, all less than 0.55. These confidence values indicate that the arrangement of the subunits relative to each other is possibly incorrect.

Nevertheless, there is agreement between the AF3 model and the integrative model in several aspects, which makes the AF3 model compelling (Figure S7A). AF3 produces a symmetric model of the desmosome (Figure S7A). The PG layer is shaped like a hollow rugby ball, widest at the center and tapering out at the ends. PG‐S and DP‐S are oriented with their long axes parallel to each other and they interleave to form the sides of the rugby ball. PKP1‐N occupies the central hollow region, forming closer contact with DP. The U‐shaped armadillo domains of the two PKP1s, PKP1‐S, cup the base of the ball. The desmosomal cadherins extend from the plasma membrane to the cytoplasm, winding their way through the armadillo domains of PKP1a at the base of the model and the armadillo domains of PG at the center of the model.

The relative localization of the N‐ and C‐termini of all proteins is consistent with the integrative model and the immuno‐EM data (North et al., 1999). The orientations of the domains with known structures, such as PG‐S, DP‐S, and PKP1‐S are also consistent with the integrative model and previous cryo‐electron tomography maps (Al‐Amoudi et al., 2011) (Figures 3 and 6). However, in the Alphafold3 model, PKP1 is closer to the PG‐DP layer compared to the integrative model and the model from cryo‐electron tomography maps (Al‐Amoudi et al., 2011). The new predictions from the AF3 model include several helical regions predicted at high confidence (pLDDT >70) for disordered regions such as DP‐N (residues 71–87, 108–128, 137–150) and PKP1‐N (residues 37–50), which are consistent with PSIPRED secondary structure predictions for this region (Figure S6B,C).

2.9.2. AF3 models of binary protein complexes in the ODP

Since the model of the full ODP from Alphafold3 was of low confidence and the prediction of interfaces was not reliable, we wanted to test if predictions of binary protein complexes would be predicted at high confidence. Therefore, we modeled the following subunit pairs with Alphafold3: PG‐DP, PG‐DSC1, PG‐DSG1, PKP1‐DSC1, PKP1‐DSG1, and PKP1‐DP. These pairs had borderline reliable predictions: PG‐DSC1, PG‐DSG1, and PKP1‐DP, with iPTM values of 0.65, 0.65, and 0.61, respectively. The predictions were below the iPTM confidence threshold for the other pairs.

The PG‐DSC1 and PG‐DSG1 structures are similar to their counterparts in the integrative model, that is, the homology models based on the PDB structure of PG‐E‐cadherin (Figure S7B,C). The Cɑ ligand RMSDs between the Alphafold model and homology model are respectively 4.3 Å (PG‐DSC1) and 4.4 Å (PG‐DSG1). The PDB structure of PG‐E‐cadherin (3IFQ) was likely part of the training set of AF3, and also accessible for AF3 to use as a template.

AF3 predicted an interface between a part of the disordered N‐terminus of PKP1 (approximately PKP1 residues 19–53) and DP (Figure S7D), predicting a potential disordered‐to‐ordered transition on binding for PKP1. The predicted interface overlaps with our contact map predictions of interfaces between DP and PKP1 (Figure 4, Figure S5, Table S4) and is also consistent with studies that show that the tip of PKP1‐N binds to DP (Kowalczyk et al., 1999; Sobolik‐Delmaire et al., ²⁰⁰⁶).

In summary, Alphafold3 did not produce a reliable model for the full desmosomal ODP but produced borderline confident interface predictions for three pairs of ODP proteins. Alphafold modeling with other stoichiometries and different combinations of fragments can be attempted to improve the current results. Predictions from AI‐based methods such as Alphafold are not integrated into the current model. Future integrative modeling can start with the predictions from Alphafold for sub‐regions that are of high confidence, incorporating these as rigid bodies or restraints. In particular, apart from the PG‐cadherin complexes, the PKP1‐DP interaction is a new prediction from Alphafold3 that can be utilized.

2.10. Limitations of the current model and future directions

Here, we attempt to discuss and quantify, where possible, the different sources of uncertainty in the modeling process. Broadly, the sources of uncertainty in modeling include uncertainty in the data, uncertainty in the representation, uncertainty in the mapping of data to restraints, and uncertainty in the sampling (Schneidman‐Duhovny et al., 2014). Uncertainty in input information may arise from noise, sparseness, ambiguity, and incoherence. Noise can result from systematic and/or random errors in measurement. Sparseness can be quantified by the number of data points relative to the degree of freedom of the system. Alternatively for volumetric data such as EM‐maps or atomic structures, sparseness can be quantified by the percentage of residues in the system that the map or structure covers. In both these cases, lower values indicate higher sparseness. Ambiguity is the uncertainty of assigning data points to unique beads, that is, the data can be satisfied by any one of several beads in the model. Incoherence refers to compositional or conformational heterogeneity in the samples used to acquire data on the system (Schneidman‐Duhovny et al., 2014). All these types of uncertainty can be quantified in terms of system size, for example, the number of residues, or spatial distance.

First, the noise in the cryo‐ET map is reflected in its resolution (32 Å) and the corresponding sparseness can be quantified by the percentage of modeled residues that the map covered (~65%) (Al‐Amoudi et al., 2011) (Figure 1b, Table S6). Second, similarly, the noise in the atomic structures can be quantified by the resolution of the corresponding experimental structures and templates for homology modeling (~3 Å) and the corresponding sparseness can be quantified by the percentage of residues with atomic structure (~65%) (Tables S1 and S6). Third, the noise in the immuno‐EM data reflects the noise in the microscopy, the uncertainty of the precise antibody‐binding site in the epitope as well as conformational heterogeneity of the antibodies, the gold labels, and the termini themselves (North et al., 1999). It is quantified in the standard error and standard deviation of the distance measurements (~10 and ~140 Å, respectively) (Table S2B). The sparseness of this data is 3.3% (20 restraints, 594 degrees of freedom in total) (Table S6). Fourth, the noise in the protein–protein binding data arises from the high false‐positive rate of the associated yeast two‐hybrid experiments as well as the uncertainty in the protein–protein binding sites within the longer queried domain; the sparseness can be quantified by 5.7% (34 restraints, 594 degrees of freedom in total) (Tables S2 and S6). The ambiguity of the protein–protein binding data also contributes to its uncertainty: each data point on two interacting protein domains can be satisfied by any pair of beads in the corresponding domains from any pair of copies of the corresponding proteins.

One source of uncertainty in the representation is the number of copies of the modeled proteins: these were determined by fitting to the cryo‐ET data, and slightly different numbers of protein copies fit the data equally well. The stoichiometry in vivo may vary, for example, due to compositional heterogeneity, adding some uncertainty. Another source of uncertainty in the representation arises from the resolutions of coarse‐grained beads for regions with known (unknown) structure which are correspondingly 30‐residue, ~9 Å radius (20‐residue beads, 7.5 Å radius) in dimension. Given the low resolution and sparsity of the input data, these coarse‐grained beads are sufficient for accurate mapping of the data to restraints and for efficient sampling. Another source of uncertainty in the representation arises from the uncertainty in the definition of rigid bodies based on known structures, which can be estimated to be a few residues (<10) per structure, at the maximum, based on the error in homology modeling. Further, one source of uncertainty in the formulation of restraints arises from the uncertainty in the mapping of data from one species and/or set of isoforms to another. This uncertainty includes the error associated with sequence alignments and is applicable for the immuno‐EM data since data from Bovine/Xenopus PG and DP were used. However, the uncertainty is negligible in this case, since the mapping between the human and Bovine/Xenopus PG and DP proteins used in the experiment is almost 1:1. Another uncertainty in the formulation of restraints arises from the uncertainty in the inter‐bead distance used in the connectivity restraint for disordered regions. This inter‐bead distance is estimated based on the radius of gyration of disordered fragments in experiments. However, the associated error here is expected to be small and the results are relatively robust to the estimates (Supporting Information Section 1.2). Finally, uncertainty in sampling can arise from insufficient sampling and is quantified in the sampling precision of 82 Å (Viswanath, Chemmama, et al., 2017). Taken together, the above analysis indicates that the lack of data, that is, data sparseness could be a key contributor to the low model precision, along with the conformational heterogeneity associated with the disordered regions.

Given the low model precision, one can use the model to infer approximate protein–protein interfaces and relative localizations of protein domains. For higher‐resolution analysis such as exact binding sites and impact of mutations, further experimental validation is required. Experiments such as chemical crosslinking by mass spectrometry can provide information on the stoichiometry of the ODP and can characterize protein–protein interfaces at higher resolution than the yeast two‐hybrid interactions used in the present study. Single particle cryo‐electron microscopy can provide higher resolution structural data of sub‐complexes than the cryo‐ET map used in the present study. Both these experiments would aid in increasing the precision of the current ODP model.

3. CONCLUSION

Here, we obtained an integrative structure of the desmosomal ODP starting primarily from the structural interpretation of a cryo‐electron tomography map of the ODP, and combining x‐ray crystal structures, distances from an immuno‐EM study, interacting protein domains from biochemical assays, bioinformatics sequence‐based predictions of transmembrane and disordered regions, homology modeling, and stereochemistry information. Our model can be used to generate experimentally verifiable hypotheses on the structure and function of desmosomal proteins. High‐resolution structural data, for example, higher‐resolution cryo‐EM maps would improve the structural characterization of the desmosome and our knowledge of the mechanistic details of cell–cell adhesion. Structural characterization of the desmosome interactome including desmosome‐associated adaptor proteins is another avenue for future work (Badu‐Nkansah & Lechler, 2020).

4. METHODS

Integrative structure determination of the desmosomal ODP proceeded through four stages (Alber et al., 2007; Rout & Sali, ²⁰¹⁹) (Figures 1 and 2). Our modeling procedure used the Python Modeling Interface of the Integrative Modeling Platform (IMP 2.17.0; https://integrativemodeling.org), an open‐source library for modeling macromolecular complexes (Russel et al., 2012), and is primarily based on previously described protocols (Arvindekar et al., 2022; Saltzberg et al., ²⁰²¹; Viswanath, Chemmama, et al., ²⁰¹⁷). Python libraries scipy (Virtanen et al., 2020) and matplotlib (Hunter, 2007) were used for analysis, GNU Parallel (Tange, 2020) was used for parallelization, UCSF Chimera v1.15 (Pettersen et al., 2004) and UCSF ChimeraX v1.5 (Pettersen et al., 2021) were used for visualization. Input data, scripts, and results are publicly available at https://github.com/isblab/desmosome and ZENODO. Integrative structures are deposited in the PDB‐DEV (https://pdb-dev.wwpdb.org).

4.1. STAGE 1: Gathering data

4.1.1. Isoforms

The ODP comprises PG (plakoglobin), PKP (plakophilin), DP (desmoplakin), and Desmosomal Cadherins (DC of two types, Desmoglein, DSG, and Desmocollin, DSC). Desmosomes from different tissues vary in the isoforms of these constituent proteins (Garrod & Chidgey, 2008; Green & Simpson, ²⁰⁰⁷). Here, we modeled the desmosomal ODPs corresponding to the stratified epithelium and containing PKP1 (Figure 1a, Table S1). For ODPs from two other tissues that we modeled (stratified epithelium containing PKP3, DSC1, DSG1, PG, and DP and basal epithelium containing PKP3, DSC2, DSG3, PG, and DP) the results were similar at the resolution of the input information (Figure 3). Epithelial desmosomes were chosen for modeling as there was more information (e.g., from protein–protein binding experiments) on epithelial isoforms than desmosomes in heart tissue. The extracellular regions of the Desmosomal Cadherins were not modeled, based on sequence annotations in Uniprot (see also (Choi et al., 2009)). Further, we do not model DSG1^843‐1049 and DP^585‐2871 as they are known to be outside the ODP (Al‐Amoudi et al., 2011; Garrod & Chidgey, ²⁰⁰⁸; Nilles et al., ¹⁹⁹¹) (Table S1).

4.1.2. Stoichiometry and number of copies

The stoichiometry of the desmosomal proteins was based on previous studies using modeling and density analysis on cryo‐electron microscopy data (Al‐Amoudi et al., 2011) (See Stage 2).

4.1.3. Atomic structures

The plakin domain of DP and armadillo domains of PG and PKP1 were modeled by their x‐ray structures (PDB: 1XM9 (PKP) (Choi & Weis, 2005), 3R6N (DP) (Choi & Weis, 2011), 3IFQ (PG) (Choi et al., 2009)), while the PG‐DSC and PG‐DSG complexes were obtained by homology modeling based on the PG‐E‐cadherin structure as the template (Choi et al., 2009), using MODELER (Šali & Blundell, 1993) and HHPRED (Gabler et al., 2020) for sequence alignment (Figure 1c, Table S1).

4.1.4. Cryo‐electron density map

We used a 32 Å density map (EMD‐1703, denoised mask without symmetrization) from cryo‐electron tomography of the ODP (Al‐Amoudi et al., 2011). The map was segmented using UCSF Chimera Segger (Pintilie et al., 2010), and the densities corresponding to the PKP and PG layers were used for modeling (Figure 1c).

4.1.5. Immuno‐EM

The distance of the N and C termini of the desmosomal proteins from the plasma membrane was informed by immuno‐electron microscopy gold‐staining experiments (Figure 1b, Table S2) (North et al., 1999). Using Clustal‐Omega (Sievers et al., 2011), the alignment between Bovine/Xenopus PG and DP (used in the experiments) and the Human PG and DP (used in modeling) is almost 1‐to‐1, and therefore, the residue ranges for the antibody‐binding regions are taken to be the same.

4.1.6. Protein–protein binding assays

The relative distance between ODP protein domains was informed by biochemical data from multiple biochemical studies, including yeast‐2‐hybrid (Bonné et al., 2003; Hatzfeld et al., ²⁰⁰⁰; Kowalczyk et al., ¹⁹⁹⁹), co‐immunoprecipitation (Bonné et al., 2003; Kowalczyk et al., ¹⁹⁹⁹), in vitro overlay assays (Smith & Fuchs, 1998), and in‐vivo co‐localization assays (Bonné et al., 2003; Bornslaeger et al., ²⁰⁰¹; Kowalczyk et al., ¹⁹⁹⁹) (Figure 1b, Tables S2 and S3).

We note that we have not used other desmosome data that is not directly informative for the integrative structural modeling of the core stratified epithelial ODP. This includes data on desmosome‐interacting proteins, data on isoforms of ODP proteins not dominant in the modeled tissue, data on the role of desmosome in signaling and regulation, and data that is too low‐resolution for our modeling (e.g., on the protein level instead of the domain or residue level).

4.2. STAGE 2: Representing the system and translating data into spatial restraints

4.2.1. Stoichiometry and number of copies, PG layer, and the desmosomal cadherins

The stoichiometry of the desmosome ODP was 1:1:1:1 for DP:PG:PKP: DC‐based on previous studies (Al‐Amoudi et al., 2011). The number of copies of each protein was based on fitting an equal number of PG and DP molecules to the PG layer of the cryo‐ET map. However, the number of PG and DP proteins that correspond to the map was unknown and computed to be four each by fitting different numbers of PG and DP molecules to the PG layer density in independent modeling runs (Supporting Information Section 1.1). We model 4 DC molecules, two each of DSC1 and DSG1.

4.2.2. Stoichiometry and number of copies, PKP layer

The PKP layer has seven distinct densities. These correspond well (average EM cross‐correlation around mean in UCSF Chimera = 0.91) to the structured ARM repeats of seven PKP molecules (Al‐Amoudi et al., 2011) (Figure S1, inset). To keep a 1:1:1:1 stoichiometry for PG:DP:PKP:DC, we selected four of these seven PKP molecules to represent in full; the central PKP and three symmetrically surrounding PKPs (Figure S1, inset).

We also represented the remaining three PKP molecules (“noninteracting” PKPs) by their structured ARM repeats alone. These PKPs participate only to satisfy the cryo‐ET map and to exclude other proteins from these locations in space. The locations and orientations of each of these PKPs were fitted based on cross‐correlation to the PKP densities in the map; subsequently, they were fixed during sampling.

4.2.3. Multi‐scale coarse‐grained bead representation

The rationale for choosing a coarse‐grained representation is based on the following requirements (Viswanath & Sali, 2019). A representation must enable efficient and exhaustive sampling of models, its resolution must be commensurate with the quantity and resolution of input information, and the resulting models should facilitate downstream biological analysis. In the current case, we have low‐resolution, sparse, noisy sparse input information, therefore, a higher‐resolution representation, for example, one‐residue per bead representation, would not be justified. Moreover, sampling with this higher resolution representation would be infeasible in days on modern supercomputers for a complex as large as the ODP; on the other hand, sampling in a shorter time would not be exhaustive.

In light of these considerations, we use the following coarse‐grained representation of the proteins where a set of contiguous amino acids in a protein is represented by a spherical bead (Figure 1a, Table S1). Domains with known atomic structures were represented by 30‐residue beads to maximize computational efficiency and modeled as rigid bodies where the relative configuration between the beads is fixed during sampling. Notably, this coarse‐graining of domains with known atomic structures is performed mainly for sampling efficiency and does not result in any loss of existing atomic structural information, as one can map these structures readily onto the rigid bodies in our model (Figure 3). In contrast, domains without known structure were coarse‐grained at 20 residues per bead and modeled as flexible strings of beads which can move relative to one another.

Next, we encoded the information gathered in stage 1 into spatial restraints that constitute a scoring function that allows scoring each model in proportion to its posterior probability. This score allows the sampling of high‐probability models that best satisfy the data.

4.2.4. EM restraints

A Bayesian EM restraint was used to incorporate the information from the cryo‐ET density map (Bonomi et al., 2019). PKP‐S, the structured region of PKP, was restrained by the PKP‐layer density; PG and DP molecules were restrained by the PG layer density. The EM restraint was not applied to regions such as PKP‐N, PKP‐C, and the desmosomal cadherins as they are either disordered and/or extended and therefore considered to be averaged out or contribute negligibly to the density in the map (Al‐Amoudi et al., 2011). The part of DC complexed with PG was included in this restraint.

4.2.5. Immuno‐EM restraints

The distances of ODP protein termini to the plasma membrane were restrained by a Gaussian restraint with the mean and standard deviation equal to the mean distance and standard error measured in immuno‐EM gold‐staining experiments (North et al., 1999). The set of restrained beads for each protein terminus corresponded to the antibody‐binding region in the experiments. The standard error of mean accounts for the variance in the distance measurements arising, for example, from random antibody orientations. The restraint score was based on the bead in the terminus that was closest to the mean distance obtained from the experiment, for each protein copy. Desmosomal Cadherins were not restrained by immuno‐EM since they form a complex with PG, which is restrained by immuno‐EM data. The complexed region is more specific than the antibody‐binding region for DSG1. Further, immuno‐EM measurements were not available for specific DSC isoforms.

4.2.6. Binding restraints

The distances between interacting protein domains were restrained by a harmonic upper bound on the minimum distance among the pairs of beads representing the two interacting domains, (the score is zero for distances less than or equal to 0, and quadratically rises above zero). For two interacting proteins A and B, ambiguity, that is, multiple copies of a protein, was factored in by adding multiple such distance restraints. For each copy of protein A, the minimum distance among all pairs of beads across all copies of B was restrained. Similarly, for each copy of protein B, the minimum distance among all pairs of beads across all copies of A was restrained. This formulation allows a protein copy to find a binding partner from any of the available copies of the other protein, potentially allowing multiple protein A copies to bind to the same protein B copy.

Different experiments provide different levels of evidence as to whether their results can be extended to in‐vivo conditions and whether the results preclude indirect binding via an intermediary protein. Restraints were therefore weighed in the order Overlay Assays = Co‐Immunoprecipitation > Yeast‐2‐Hybrid. However, the results we obtain are fairly robust to this weighting scheme and all the experimental data are individually satisfied in the final set of models (Figure S3). If multiple experiments provided data on the binding of two proteins, the highest‐resolution data (i.e., a more specific binding site) was chosen.

4.2.7. Cylindrical restraints

To keep the modeled proteins close to the positions in the cryo‐ET map, beads were restrained to lie within a cylinder of radius 150 Å that encloses the map. The restraint was implemented using a harmonic upper bound on the distance of each bead from the cylinder surface.

4.2.8. Excluded volume restraints

The excluded volume restraints were applied to each bead to represent the steric hindrance of the protein residues that disallow other residues to come in physical proximity. The bead radius was calculated assuming standard protein density (Alber et al., 2007), with beads penalized based on the extent of their overlap.

4.2.9. Sequence connectivity restraints

We applied sequence connectivity restraints on the distance between consecutive beads in a protein molecule. The restraint was encoded as a harmonic upper bound score that penalizes beads that are greater than a threshold distance apart. The threshold distance is different for each protein and the calculation is inspired by models from statistical physics (Teraoka, 2002) (Supporting Information Section 1.2). As a summary, we predict what proportion of each protein's predicted secondary structure is disordered using PSIPRED (Buchan & Jones, 2019), and compute the threshold based on this proportion, the known radii of gyration for disordered regions, and bead radii for globular proteins estimated from their density (Alber et al., 2007). For regions with known structures, the inter‐bead distances were fixed during sampling and their contribution to the restraint score was fixed across models.

Similar to prior integrative modeling studies, the overall framework is that of Bayesian inference, with the posterior being computed from a likelihood and a prior. The likelihood here comprises all restraints informed by experimental data such as the Bayesian EM restraint and non‐Bayesian restraints such as the immuno‐EM and protein–protein binding restraints. The prior comprises other restraints not based on data, such as stereochemistry and excluded volume.

4.3. STAGE 3: Structural sampling to produce an ensemble of structures that satisfies the restraints

We employed Gibbs sampling Replica Exchange Monte Carlo sampling (Arvindekar et al., 2022; Saltzberg et al., ²⁰²¹; Viswanath, Chemmama, et al., ²⁰¹⁷). The positions of the rigid bodies and flexible beads were sampled as in previous protocols, with a few customizations.

First, we implemented an Anchoring Constraint wherein the membrane‐proximal beads of the desmosomal cadherins were initialized adjacent to the membrane and were constrained to move only along the membrane plane during sampling (Figure 1b).

Second, a custom random initialization was used for the PG layer. The PG and DP rigid bodies and beads were randomized within a bounding box that tightly enclosed the PG layer density. The orientation of the long axis of the structured region of PG and DP molecules with respect to the membrane determines the polarity of each PG/DP molecule (N‐to‐C along the normal to the membrane). After the random initialization, if it was opposite of the polarity observed from immuno‐EM (North et al., 1999), this polarity was corrected by flipping the structured region along a random axis in the plane of the membrane by 180 degrees; in effect, reversing the polarity along the normal to the membrane while keeping its orientation random. For example, if a PG molecule was initialized with its N‐terminus closer to the membrane than its C‐terminus, its orientation would be flipped. This is because, owing to the high protein density of the PG layer, molecules with the incorrect polarity might not have the freedom to flip polarity during sampling.

Finally, a custom random initialization was used for the PKP layer. Each PKP was initialized around one of the molecule‐wise PKP densities with a random orientation.

The Monte Carlo moves included random translations of individual beads in the flexible segments, random translations and rotations of rigid bodies, and super‐rigid bodies, that is, groups of rigid bodies and beads of the same protein or complex. The size of these moves and the replica exchange temperature for the replicas were optimized using StOP (Pasani & Viswanath, 2021). A model was saved every 10 Gibbs sampling steps, each consisting of a cycle of Monte Carlo steps that proposed a move for every bead and rigid body once. We sampled a total of 180 million integrative models, from 50 independent runs.

4.4. STAGE 4: Analyzing and validating the ensemble of structures

The sampled models were analyzed to assess sampling exhaustiveness and estimate the precision of the structure, its consistency with input data, and consistency with data not used in modeling. We based our analysis on the protocols published earlier (Arvindekar et al., 2022; Saltzberg et al., ²⁰²¹; Viswanath, Chemmama, et al., ²⁰¹⁷; Webb et al., ²⁰¹⁸).

4.4.1. Filtering the models into a good‐scoring set

To make analysis computationally tractable and to select models that have a good score, that is, higher probability, we first selected the models to create a good‐scoring set which involved the following steps. Models were first filtered based on score equilibration and auto‐correlation decay along the MCMC runs (Supporting Information Section 2.1). Filtered models were clustered based on their restraint scores using HDBSCAN (McInnes et al., 2017), resulting in a single cluster of 37,145 models (Saltzberg et al., 2021). Subsequently, these models were filtered to choose models for which each restraint score as well as the total score is better than the corresponding mean plus 1.46 standard deviations, leading to a good‐scoring set of 24,866 models for the next stage of analysis (Arvindekar et al., 2022).

4.4.2. Clustering, precision, and localization densities

We next assessed if the sampling was exhaustive by previously established protocols which randomly divide the models into two independent sets and assess via statistical tests whether the two sets had similar scores and structures (Arvindekar et al., 2022; Saltzberg et al., ²⁰²¹; Viswanath, Chemmama, et al., ²⁰¹⁷) (Figure S2). We perform structural clustering of the models to find the minimum clustering threshold for which the sampling is exhaustive (sampling precision) as well as the mean RMSD between a cluster model and its cluster centroid (model precision) (Figure S2).

The bead‐wise RMSD calculation in the protocol was extended to consider ambiguity, that is, multiple protein copies. The RMSD between two models is the minimum RMSD among all combinations of protein copy pairings between the models. For example, two models containing four copies of PG have 4! possible bipartite pairings of PG copies among them for which the RMSD needs to be computed. This calculation of RMSD for large systems with tens of thousands of models and several identical protein copies per model is time‐consuming. It was parallelized to make it computationally efficient and implemented in the open‐source Integrative Modeling Platform (https://integrativemodeling.org), thus making it freely available for use in other studies (Russel et al., 2012).

The consideration of ambiguity was applied to all proteins except PKP. Each PKP copy was initialized to the same molecule‐wise EM density in every simulation and usually remained close to it throughout the simulation. PKP copies could be considered noninterchangeable because of the presence of fixed, noninteracting PKPs in their midst. The latter also precludes the need for alignment to a common frame of reference during RMSD calculations.

The result of integrative modeling was a single major cluster corresponding to 24,016 (96.6% of 24,866) models. The model precision, which quantifies the variability of models in the cluster, and is defined as the average RMSD of a cluster model from the cluster centroid, was 67 Å. The cluster is visualized via localization probability density maps, which specify the probability of a volume element being occupied by beads of a given domain in the set of superposed models from the cluster (Figure 3).

4.4.3. Fit to input information

To calculate the fit to data from protein–protein binding assays, we calculated the minimum distance among all bipartite pairs of beads representing all copies of interacting domains for each model in the cluster and visualized the distribution (Figures S3A and S4, Tables S2A and S3A).

To calculate the fit to immuno‐EM data (North et al., 1999) for each restrained protein terminus, we calculated the difference between the model‐predicted distance of the terminus to the plasma membrane and the corresponding mean distance from the experiment. The model‐predicted distance for a terminus was equal to the distance of the terminus bead closest to the experimental mean. The distribution of the difference for each copy of a protein for each model in the cluster was visualized (Figure S3B).

To calculate the fit to the cryo‐ET map, we computed cross‐correlation between the localization probability densities for the cluster and the segmented map for the PG and PKP layers separately (Supporting Information Section 2.2, Figure S3C). The model is consistent with all input information.

4.4.4. Fit to information not used in modeling

The information not used in modeling was divided into two subsets: a subset that is orthogonal to the input information and nontrivial for the models to satisfy (Table S3A), and a subset that is consistent with the input information and hence satisfied by the model by construction (Table S3B). The models were validated by their fit to the data in the first subset, which includes protein–protein binding, super‐resolution imaging, and cryo‐ET data; only data on the modeled desmosomal protein isoforms was used for validation (Table S3A, Figure S4).

The fit to protein–protein binding data for DP‐DP binding was calculated similarly to the fit to input protein–protein binding restraints, and the models are consistent with these data (Table S3A, Figure S4A). These data are not trivial for the models to satisfy. While observing some contact between DPs is not surprising based on the high density of the PG‐DP region, there could be alternative arrangements that would have sequestered DPs without any DP‐DP contact.

The fit to data from dSTORM super‐resolution imaging was calculated as follows. The distances of the modeled domains from the plasma membrane were obtained by starting from the dSTORM plaque‐to‐plaque measurements, subtracting the width of the intercellular space (∼34 nm), subtracting two times the plasma membrane thickness (∼4–6 nm), and dividing by two (Stahley et al., 2016) (Table S3A). These distances were compared to the distribution from our models for PG‐N (Figure S4B, Table S3A). For PG‐N, the super‐resolution imaging data and the immuno‐EM data differ in their mean distance, their uncertainties as measured by the standard deviation (super‐resolution imaging data) or standard error (immuno‐EM data), and the region of PG to which the data are applied (epitope; North: PG 1–106, Stahley: PG 30–109). These validation data are not trivial to satisfy; the models can satisfy the immuno‐EM data without satisfying the super‐resolution imaging data. A portion of the ensemble satisfies both the immuno‐EM and super‐resolution imaging data while another portion is closer to the former, presumably owing to the smaller uncertainty of the immuno‐EM restraint (Figure S4B). However, most of the models are consistent with the validation data and within one standard deviation of the latter (Figure S4B).

To calculate the fit to data from tomography, we obtained the cadherin spacing from recent cryo‐ET density maps. The distance between DSG2 and DSC2 was reported as 7 nm for the W‐shape arrangement of cadherins and compared to the distribution from our model (Sikora et al., 2020) (Table S3B, Figure S4C). The distribution of the minimum distance between the DSG1 and DSC1 membrane‐anchored beads was plotted for models in the cluster, as a proxy for the distance between adjacent cadherins at the plasma membrane. The models are consistent with the spacing from these newer tomograms (Figure S4C). Satisfying this data indirectly depends on the number of PKP1 molecules and cadherin molecules in the modeled region and other restraints. To ascertain how trivial it would be for an ensemble to satisfy this validation data, we compute a null (baseline) model where the cadherin molecules are spaced randomly in the plasma membrane. This null model contains the same number of cadherin molecules as the integrative model. The membrane‐anchored beads of the cadherins are randomly placed in the plane of the plasma membrane within a circle defined by the extent of the cryo‐ET map. Under this null model, we compute the distribution of the minimum bead‐bead distance of the membrane‐anchored beads of the cadherins DSG1 and DSC1. The null model does not satisfy the validation data and the difference between the null and model distributions can illustrate the contribution of the rest of the model, that is, the PKP1 spacing and other restraints. (Figure S4C).

We also report data not used in modeling that is consistent with the input information, and hence by construction, satisfied by the ensemble of models that fit well with the input information (Table S3B). This data provides additional support to the input information. The PG‐DP data overlaps with an input biochemical binding data point (Table S2A). The PG‐DSC1 and PG‐DSG1 data are consistent with the input homology models. The models are also consistent by construction with the data from acyl biotin exchange assays from (Roberts et al., 2016) which state that DSG1 residues 571 and 573 are membrane‐proximal and palmitoylated (Table S3B, Figure 1). The bead corresponding to residues 570–589 is membrane‐anchored in our model.

We also report a couple of exceptions: information not consistent with the input data and hence not consistent with our models (Table S3B). The first kind of exception corresponds to two data points that mention that the first few cytoplasmic residues of DSC1, in the PKP layer in our model, bind to proteins in the PG layer. The second exception pertains to the distance of DP from the plasma membrane from super‐resolution imaging (Stahley et al., 2016). DP is localized further away from the membrane than it is in our model and in (North et al., 1999), a fact that Stahley and co‐workers also comment on. This could be partly due to the uncertainty in dSTORM‐based measurement that arises from the localization precision of Alexa Fluor 647, and the primary and secondary antibody labels.

4.4.5. Contact maps

A contact between beads is defined as a surface‐to‐surface distance of 10 Å or lower. For each protein pair, we obtained the proportion of models in the cluster that have at least one contact for each bead pair across all copies of the two proteins. To filter out the significant contacts from those that might occur by chance, we identified significant contacts as those present in at least 20%–25% of the models. A 25% cutoff corresponds to approximately the top ≤2% of all possible contacts for each protein pair while a 20% cutoff corresponds to ~8% of all possible contacts for PG‐DP and ≤5% for the rest of the protein pairs. This ensures that only a small fraction of all possible bead pairs are included in our analysis with the assumption that any nontrivial contact will be consistently found across the ensemble (i.e., be above the threshold described above).

4.4.6. Mapping disease mutations

We considered two kinds of mutations to map to the integrative structure. First, disease mutations associated with defects in epithelial tissue that could be mapped to ODP protein domains and/or residues were obtained by a literature search and using databases such as OMIM and Uniprot (Online Mendelian Inheritance in Man, 2023; The UniProt Consortium et al., ²⁰²³). These mutations corresponded to those seen in Naxos disease (ARVC with palmoplantar keratoderma and woolly hair) and Carvajal syndrome (left ventricular cardiomyopathy with palmoplantar keratoderma and woolly hair) (Boulé et al., 2012; Den Haan et al., ²⁰⁰⁹; Erken et al., ²⁰¹¹; Keller et al., ²⁰¹²; Marino et al., ²⁰¹⁷; McKoy et al., ²⁰⁰⁰; Pigors et al., ²⁰¹⁵; Whittock et al., ²⁰⁰²). Second, cancer‐associated somatic, missense, confirmed pathogenic mutations on ODP proteins that occurred in five or more samples were extracted from the COSMIC database (Tate et al., 2019).

We did not consider mutations involved in cardiac disease as we model an epithelial ODP. In general, we refrained from mapping mutations across isoforms. We also did not consider mutations that could not be mapped to the protein domains, although a large number of these are known, for example, pathological differential expression of proteins.

4.4.7. Comparison to Alphafold2‐multimer and Alphafold3

We ran Alphafold3 from the web server interface with default parameters (Abramson et al., 2024; https://alphafoldserver.com/). The following complexes were modeled: a 2:2:2:1:1 DP1:PG:PKP1:DSG1:DSC1 model of the ODP, and sub‐complexes containing pairs of proteins: PG‐DP, PKP1‐DSC1, PKP1‐DSG1, PG‐DSC1, PG‐DSC1, and PKP1‐DP. For each complex, the single best‐ranked model based on the ranking score provided by Alphafold3 was chosen for analysis. For complexes where the iPTM of the best‐ranked model was lower than 0.6 (e.g., PG‐DP and the larger ODP complex with all five proteins), we reran with a different seed. The model with the best iPTM across both runs was chosen for further analysis.

For PG‐DSC1 and PG‐DSG1, the similarity of the AF3 model to the respective homology model used in the integrative modeling was determined by the ligand RMSD between the two. The ligand RMSD was calculated as the C$\mathrm{\alpha }$ RMSD of the DSC1 (or DSG1) residues, after superposing the PG chains of the two structures, using the rmsd command in ChimeraX (Pettersen et al., 2021).

For DP‐PKP1, the best‐ranked model was used to discover confidently predicted interfaces, identified as inter‐protein residue pairs in which each residue was confidently predicted (pLDDT >70), the residue pair had an accurate relative prediction (PAE <5), and the pair was at an interface (Cα‐Cα distance <10 Å).

AUTHOR CONTRIBUTIONS

Satwik Pasani: Methodology; investigation; validation; visualization; writing – original draft; writing – review and editing; software; data curation. Kavya S. Menon: Writing – review and editing; investigation; data curation; software; methodology. Shruthi Viswanath: Conceptualization; methodology; validation; visualization; writing – review and editing; writing – original draft; investigation; funding acquisition; project administration; supervision; resources.

FUNDING INFORMATION

This work has been supported by the Department of Atomic Energy (DAE) TIFR grant RTI 4006 and the Department of Science and Technology (DST) SERB grant SPG/2020/000475 from the Government of India to SV.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

Supporting information

Data S1: Supporting Information.

Movie S1: Visualization of localization density and bead models of the major cluster of the desmosomal outer plaque.

Pasani S, Menon KS, Viswanath S. The molecular architecture of the desmosomal outer dense plaque by integrative structural modeling. Protein Science. 2024;33(12):e5217. 10.1002/pro.5217

DATA AVAILABILITY STATEMENT

Files containing input data, scripts, and results are at https://github.com/isblab/desmosome and https://zenodo.org/doi/10.5281/zenodo.8035862. Integrative structures are deposited in the PDB (PDB ID: 9A8U) (https://www.wwpdb.org/pdb?id=pdb_00009a8u). Alphafold3 models are deposited in the ModelArchive: https://www.modelarchive.org/doi/10.5452/ma‐8443n (full desmosome ODP model), https://www.modelarchive.org/doi/10.5452/ma‐5u1n5 (PG‐Dsc1 model), https://www.modelarchive.org/doi/10.5452/ma‐fwvwf (PG‐Dsg1 model), and https://www.modelarchive.org/doi/ 10.5452/ma‐ic5zo (PKP1‐DP model).