Abstract
We study compactness of product of Toeplitz operators with symbols continuous on the closure of the polydisc in terms of behavior of the symbols on the boundary. For certain classes of symbols f and g, we show that is compact if and only if fg vanishes on the boundary. We provide examples to show that for more general symbols, the vanishing of fg on the whole polydisc might not imply the compactness of . On the other hand, the reverse direction is closely related to the zero product problem for Toeplitz operators on the unit disc, which is still open.
Keywords: Toeplitz operator, Compact, Bergman space, Polydisc
Introduction
Let be a bounded domain in . The Bergman space consists of all holomorphic functions on that are square integrable with respect to the Lebesgue volume measure dV. The orthogonal projection is known as the Bergman projection. For a bounded measurable function f on , the Toeplitz operator is defined as
for . We call f the symbol of .
There is an extensive literature on the study of Toeplitz operators on various domains. In this paper, we are particularly interested in the case the domain is the polydisc and compactness of product of Toeplitz operators whose symbols are continuous up to the boundary.
A classical approach to compactness of Toeplitz operators involves the Berezin transform. For finite sum of finite products of Toeplitz operators on the Bergman space of the unit disc, the Axler–Zheng Theorem [1, Theorem 2.2] characterizes compactness in terms of the behavior of the Berezin transform of the operator. In higher dimensions, the Axler–Zheng Theorem is extended to the case of the polydisc as seen in [2] and [3, p. 232], and the unit ball as shown in [4, Theorem 9.5]. Recently, there have been a few generalizations of this result in different directions. See, for instance, [5–8].
In this paper, we study compactness of products of Toeplitz operators in terms of the behavior of the symbols on the boundary. More specifically, we would like to characterize functions f, g that are continuous on such that is compact.
Coburn [9, Lemma 2] showed that on the Bergman space over unit ball , for f a continuous function on , the Toeplitz operator is compact if and only if on . Furthermore, [9, Theorem 1] established a -isomorphism satisfying
where is the Toeplitz algebra generated by and is the ideal of compact operators on . As a consequence, we see that for , the product is compact if and only if the product on .
On the polydisc , the first author [10] showed that, in the context of weighted Bergman spaces, for , the Toeplitz operator is compact if and only if f vanishes on , the (topological) boundary of . Generalizing this result, the second and the third authors in [11] proved that compactness of the Toeplitz operator with a symbol continuous on the closure of a bounded pseudoconvex domain in with Lipschitz boundary is equivalent to the symbol vanishing on the boundary of the domain.
Motivated by Coburn’s aforementioned result, one may expect that the necessary and sufficient condition for to be compact is that fg vanishes on . However, we shall see in our results and examples that while the above statement holds for a certain class of symbols, sufficiency is false in general. On the other hand, necessity is closely related with the famous “zero product problem” in the theory of Toeplitz operators on the unit disc, which is still wide open.
Main Result
Let be a finite sum of finite products of Toeplitz operators with . Coburn’s aforementioned result implies that compactness of the operator T on is equivalent to on the circle. Therefore, throughout the paper we will assume that as the case is well understood.
Before we state our results, we define the restriction operator for and as follows.
and
for and .
In our main result, we give a characterization of compactness of the finite sum of finite products of Toeplitz operators in terms of the vanishing of the operator restricted to the polydiscs in the boundary. We recall that consists of all such that for some j.
Theorem 1
Let be a finite sum of finite products of Toeplitz operators on for with . Then T is compact on if and only if
on for all and .
As an immediate corollary we get the following.
Corollary 1
Let for . Assume that for each and there exists j such that on . Then is compact on .
Applications
Let and be two functions in . We define and for . Then for any ,
and
By Theorem 1, the product is a compact operator on if and only if on and for all . Since the second condition is actually a consequence of the first, we conclude that for such f and g, the product is compact on if and only if on , which is equivalent to on .
Example 1
Let
and
Using polar coordinates, one can check that both operators and are diagonalizable with respect to the standard orthonormal basis and their eigenvalues are all strictly positive. Hence on . On the other hand, on . Then for and , we have on but is not compact on as . This example shows that the vanishing of fg on (or even on ) does not imply the compactness of .
Example 2
Take f as in Example 1 and define
Then fg is not identically zero on because and on . Yet, by Theorem 1, the product is not compact since for ,
is not the zero operator on .
Remark 1
From the previous examples we see that on is not a sufficient condition for the compactness of . Is it a necessary condition? It turns out this question is related to the zero product problem for Toeplitz operators on the disc. More specifically, as in Example 1, we see that with and , if the product is compact on , then on (which gives on ). However, it is not known if this condition implies that on . For and , we have and . So on if and only if on .
In Proposition 1 below, we show that if the symbols are harmonic along the discs in the boundary, then we have necessary and sufficient conditions for the compactness of the product of two Toeplitz operators. A function is said to be n-harmonic if
for all That is, f is harmonic in each variable separately [12, pg. 16].
Proposition 1
Let (with ) such that for , and , the functions and are -harmonic on . Then is compact if and only if on .
We note that in Example 1, both f and g depend on the same single variable. In Proposition 2 below, we give a characterization when the symbols are product of single-variable functions.
Proposition 2
Let be a finite product of Toeplitz operators on such that for and . Let . Then the following statements hold.
-
(i)
If T is a nonzero compact operator, then on .
-
(ii)
If on and F is not identically zero on , then T is compact.
Remark 2
We do not know whether (i) in Proposition 2 still holds in the case T is the zero operator. This is closely related to the zero product problem. More specifically, consider and , where . Then on if and only if on . On the other hand, on if and only if on . It is still an open problem whether on implies that on .
Remark 3
The conclusion of (ii) in Proposition 2 does not hold if F is identically zero on . Indeed, the functions f and g in Example 1 are of the type considered here and on but is not compact on .
In the proposition below, we show that when all but at most one of the symbols are polynomials, compactness of a Toeplitz product on is equivalent to the vanishing of the product of the symbols on . For this result, we need to restrict to dimension two. It would be interesting to extend the result to all . See Remark 4.
Proposition 3
Let and be polynomials in z, w and , and . Then is compact on if and only if
Proofs
Let BT(p) denote the Berezin transform of a bounded linear operator at . That is,
where
is the normalized Bergman kernel of .
We will need the following lemma whose proof is contained in the proof of Theorem 1 in [13]. We provide a sketch of the proof here for the convenience of the reader. We note that Bf denotes whenever f is a bounded function and we use the following notation: for . For functions defined on and defined on , we use to denote the function on .
Lemma 1
Suppose and . Let and define for .
-
(i)If is a bounded set in , then
-
(ii)If are functions independent of and W is any bounded operator on , then
Proof
-
(i)Let be given. By the uniform continuity of , there exists such that for all ,
Then,
However,
Then, . Since was arbitrary, we conclude that -
(ii)We note that for . We define
Since each is independent of , is independent of and hence it can be considered as an element of . Note that the set is bounded by . Furthermore, we have . It follows that
which, by (i), converges to zero as .
Proof of Theorem 1
We first make an observation. If is a bounded function on , then , while initially defined on , can be naturally considered as a Toeplitz operator with symbol acting on . This will not create any confusion due to the fact that for independent of , the function is also independent of and for all .
Let . For each j and , the function can be written as . We then expand as
Note that in the second sum, each summand has the form considered in Lemma 1(ii). We then conclude that for any ,
| 1 |
Now suppose that T is compact. Fix . Since weakly as , the compactness of T implies that as . Equation (1) then gives
| 2 |
Since
and for all , (2) implies that
Because was arbitrary, it follows that is the zero operator on . Applying the same method for other values of k, we have
on for and all .
We now prove the converse. Let with and . Since it is assumed that , equation (1) implies that . As a consequence,
The same argument is applicable for all . By Axler–Zheng Theorem for ([2] and [3, p. 232]), we conclude that T is compact on .
Proof of Corollary 1
We assume that for each and there exists j such that . Then on . Hence, Theorem 1 implies that is compact on .
Proof of Proposition 1
To prove the forward direction, we first use Theorem 1 to conclude that the operator is zero on for all and . Since the symbols and are -harmonic on , we apply [14, Theorem 1.1] (or [15, Corollary 2] in the case ) to conclude that either or . Then on as desired.
To prove the converse we argue as follows. For each and , since both and are -harmonic and their product is zero on , either or . Then on for all and . Theorem 1 now implies that is compact.
Proof of Proposition 2
We first prove (i). Assume that T is a nonzero compact operator. Then by Theorem 1 when restricted on the first coordinate, for any ,
on , where . Since T is not the zero operator, the second factor on the right hand side above is a nonzero operator. This follows from the fact that T can be written as the product
where the first factor acts on functions in and the second factor acts on functions in . Hence, . It follows that
on . The same argument applies to other coordinates and we have on .
Next we prove (ii). Assume that on and F is not identically zero on . Choose such that for all k, which implies that for all j and k. For any , since , we have
Because the second factor is nonzero, it follows that . As a result,
on , where, as before, . The same argument applies to other parts of . Then Theorem 1 implies that is compact on .
The proof of Proposition 3 hinges on several elementary facts about polynomials that we describe below. We use to denote the vector space of all polynomials in z and .
The following lemma is well known. The proof follows from the fact that if a real analytic function vanishes on a non-empty open set, it must be identically zero.
Lemma 2
Let be not identically zero. Then the set
has an empty interior.
Lemma 3
Let . Assume that there exist infinitely many such that . Then there is a polynomial such that . In particular, for all .
Proof
For non-negative integers s, t, we write
As a result, there are integers and polynomials (for ) and (for ) of a single variable such that
By the hypothesis, there exists infinitely many such that
This implies that for each j. As a consequence, all and are divisible by . We then conclude that f(z) is divisible by , from which the conclusion of the lemma follows.
Lemma 4
Let f(z, w) be a polynomial in and let . Assume that on . Then or and or .
Proof
Assume that h does not vanish identically on . By continuity, there exist a non-empty arc and a non-empty open set such that for all and . It follows that for all such and w. For each , applying Lemma 2, we conclude that for all . Then for each , since vanishes on J (which is an infinite set), Lemma 3 implies that for all . Therefore, f vanishes identically on . The proof for is similar.
Lemma 5
[[16, Corollary 1.8]] Suppose and are polynomials of in and . If on , then one of the symbols must be zero.
Proof of Proposition 3
Assume that is compact on , then by Theorem 1,
on for all . By Lemma 5, one of , , and is a zero function on . Thus, on . Similar argument works for . Therefore, on .
For the converse, by Lemma 4, one of the symbols is identically zero on . It then follows that
Similarly,
Therefore, by Theorem 1, we conclude that is compact on .
Remark 4
It is desirable to generalize Proposition 3 to for all . While Lemmas 2, 3 and 4 remain true for all n, Lemma 5 has only been known for the disc. In order to extend Proposition 3 to all , one needs to prove a several-variable version of Lemma 5. Some partial results have been obtained in the literature. For example, the main results of [17] imply that Lemma 5 holds in several variables when or when all are monomials. As a result, Proposition 3 holds on for all in the case , or in the case all and are monomials.
Acknowledgements
Trieu Le is partially supported by Simons Foundation Travel Support for Mathematicians MPS-TSM-00002303.
Author Contributions
All authors contributed equally to the manuscripts. All authors reviewed the manuscript.
Data Availability
Data sharing is not applicable to this article as no data sets were generated or analyzed in this study.
Declarations
Conflict of Interest
The authors have no conflict of interest to declare that are relevant to the content of this article.
Ethics Approval
Ethics approval is not applicable to this article as no research involving human or animal subjects was done in this study.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Axler, Sheldon, Zheng, Dechao: Compact operators via the Berezin transform. Indiana Univ. Math. J. 47(2), 387–400 (1998) [Google Scholar]
- 2.Engliš, Miroslav: Compact Toeplitz operators via the Berezin transform on bounded symmetric domains. Integral Equ. Oper. Theory 33(4), 426–455 (1999) [Google Scholar]
- 3.Choe, Boo Rim, Koo, Hyungwoon, Lee, Young Joo: Finite sums of Toeplitz products on the polydisk. Potential Anal. 31(3), 227–255 (2009) [Google Scholar]
-
4.Suárez, Daniel: The essential norm of operators in the Toeplitz algebra on
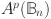 . Indiana Univ. Math. J. 56(5), 2185–2232 (2007) [Google Scholar]
. Indiana Univ. Math. J. 56(5), 2185–2232 (2007) [Google Scholar] -
5.Čučković, Željko, Şahutoğlu, Sönmez.: Axler-Zheng type theorem on a class of domains in
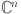 . Integral Equ. Oper. Theory 77(3), 397–405 (2013) [Google Scholar]
. Integral Equ. Oper. Theory 77(3), 397–405 (2013) [Google Scholar] -
6.Mitkovski, Mishko, Suárez, Daniel, Wick, Brett D.: The essential norm of operators on
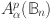 . Integral Equ. Oper. Theory 75(2), 197–233 (2013) [Google Scholar]
. Integral Equ. Oper. Theory 75(2), 197–233 (2013) [Google Scholar] - 7.Mitkovski, Mishko, Wick, Brett D.: A reproducing kernel thesis for operators on Bergman-type function spaces. J. Funct. Anal. 267(7), 2028–2055 (2014) [Google Scholar]
-
8.Čučković, Željko, Şahutoğlu, Sönmez., Zeytuncu, Yunus E.: A local weighted Axler–Zheng theorem in
 . Pacific J. Math. 294(1), 89–106 (2018) [Google Scholar]
. Pacific J. Math. 294(1), 89–106 (2018) [Google Scholar] - 9.Lewis, A.: Coburn, Singular integral operators and Toeplitz operators on odd spheres. Indiana Univ. Math. J. 23, 433–439 (1973) [Google Scholar]
- 10.Le, Trieu: On Toeplitz operators on Bergman spaces of the unit polydisk. Proc. Amer. Math. Soc. 138(1), 275–285 (2010) [Google Scholar]
-
11.Rodriguez, T.M., Şahutoğlu, S.: Compactness of Toeplitz operators with continuous symbols on pseudoconvex domains in
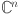 . Proc. Amer. Math. Soc. Ser. B 11, 406–421 (2024) [Google Scholar]
. Proc. Amer. Math. Soc. Ser. B 11, 406–421 (2024) [Google Scholar] - 12.Rudin, W.: Function Theory in Polydiscs. The Benjamin/Cummings Publishing Company, Reading, MA, Math. Lect. Note Ser. (1969) [Google Scholar]
- 13.Čučković, Ž., Huo, Z., Şahutoğlu, S.: On spectra of Hankel operators on the polydisc. Can. Math. Bull. (2022). 10.48550/arXiv.2207.13116
-
14.Choe, B.R., Koo, H., Lee, Y.J.: Zero products of Toeplitz operators with
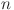 -harmonic symbols. Integral Equ. Oper. Theory 57(1), 43–66 (2007) [Google Scholar]
-harmonic symbols. Integral Equ. Oper. Theory 57(1), 43–66 (2007) [Google Scholar] - 15.Ahern, Patrick, Čučković, Željko: A theorem of Brown–Halmos type for Bergman space Toeplitz operators. J. Funct. Anal. 187(1), 200–210 (2001) [Google Scholar]
- 16.Thilakarathna, D.: Finite rank perturbations of Toeplitz products on the Bergman space of the unit disc, Ph.D. thesis, University of Toledo (2018)
- 17.Čučković, Željko, Huo, Zhenghui, Şahutoğlu, Sönmez.: Zero products of Toeplitz operators on Reinhardt domains. Canad. Math. Bull. 65(1), 170–179 (2022) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as no data sets were generated or analyzed in this study.


