Abstract
This study, for the first time, explores the integration of data science and machine learning for the classification and prediction of coronary artery calcium (CAC) scores. It focuses on tooth loss and patient characteristics as key input features to enhance the accuracy of classifying CAC scores into tertiles and predicting their values. Advanced analytical techniques were employed to assess the effectiveness of tooth loss and patient characteristics in the classification and prediction of CAC scores. The study utilized data science and machine learning methodologies to analyze the relationships between these input features and CAC scores. The research evaluated the individual and combined contributions of patient characteristics and tooth loss on the accuracy of identifying individuals at higher risk of cardiovascular issues related to CAC. The findings indicated that patient characteristics were particularly effective for tertile classification of CAC scores, achieving a classification accuracy of 75%. Tooth loss alone provided more accurate predicted CAC scores with the smallest average mean squared error of regression and with a classification accuracy of 71%. The combination of patient characteristics and tooth loss demonstrated improved accuracy in identifying individuals at higher risk with the best sensitivity rate of 92% over patient characteristics (85%) and tooth loss (88%). The results highlight the significance of both oral health indicators and patient characteristics in predictive modeling and classification tasks for CAC scores. By integrating data science and machine learning techniques, the research provides a foundation for further exploration of the connections between oral health, patient characteristics, and cardiovascular outcomes, emphasizing their importance in advancing the accuracy of CAC score classification and prediction.
Keywords: Tooth loss, Patient characteristics, Coronary artery calcification, Atherosclerosis, Data science, Machine learning
Subject terms: Biomarkers, Cardiology, Health care, Mathematics and computing
Introduction
The intersection between oral health and cardiovascular well-being has been a subject of growing interest in the medical and dental research communities1–9. Among various oral health indicators, tooth loss has emerged as a potential marker linked to systemic health conditions, including cardiovascular diseases10,11.
In an early investigation, Holmlund et al.12 presented a study with an extended follow-up period. Their aim was to explore whether various parameters of oral health exhibit an association with future mortality in distinct cardiovascular disorders. The finding highlighted a link between oral health and cardiovascular diseases, underscoring the suitability of the number of teeth as a meaningful indicator for oral health in this specific context.
Gao et al.13 found that periodontitis stands as a risk factor for coronary heart disease (CHD), establishing a positive correlation between the number of extracted teeth and CHD risk. Recognizing the significance of these factors in clinical assessments is crucial due to their association with cardiovascular risks.
Additional insights from Cheng et al.14 underscore a significant increase in the association between tooth loss and the risk of cardiovascular disease and stroke. Subgroup analyses revealed links, especially within Asian and Caucasian populations, and across both fatal and non-fatal cases. The study also identified a noteworthy dose-response relationship between tooth loss and the risk of cardiovascular disease and stroke.
Another study by De Angelis et al.15 highlighted that individuals with over 18 missing teeth face a 2.5 times greater risk of cardiovascular disease, which exhibits associations with Type 2 diabetes mellitus, underweight, and obesity. These findings affirm a connection between cardiovascular disease and oral health.
Beukers et al.16 contributed to the discourse by emphasizing tooth loss as an outcome of prevalent dental conditions, dental caries, and periodontitis, constituting 2% of the global burden of human diseases. The systematic review and meta-analyses conducted in this study demonstrated that a diminished number of teeth serves as a risk factor for atherosclerotic cardiovascular diseases and mortality.
Beyond tooth loss, patient characteristics play a pivotal role in cardiovascular risk assessment. Factors such as age, gender, body mass index (BMI), smoking habits, and comorbidities have been extensively studied in the context of cardiovascular health17. A meta-analysis by Wong et al.18 highlighted the multifactorial nature of cardiovascular risk, emphasizing the need to consider a spectrum of patient characteristics for accurate risk assessment. Research has sought to elucidate the intricate connections between tooth loss, patient characteristics, and CAC19.
CAC is a measure of the amount of calcium in the walls of the coronary arteries, which supply blood to the heart muscle20. The presence of calcium is an indicator of atherosclerosis, a condition characterized by the buildup of plaque that can lead to coronary heart disease (CHD) and potentially to heart attacks or other cardiovascular events. The CAC score, derived from a specialized CT scan, quantifies the amount of calcified plaque in the coronary arteries. This score is a valuable tool for assessing an individual’s risk of developing CHD21,22. Higher CAC scores are strongly associated with a greater risk of CHD and cardiovascular mortality, making it an important predictor for clinical outcomes.
Classifying CAC scores into tertiles and predicting these values are crucial because they provide a stratified risk assessment23,24. This stratification helps in identifying individuals at varying levels of risk, enabling tailored preventive and therapeutic strategies. By enhancing the precision of CAC score classification and prediction, this study aims to improve risk stratification, which can lead to more personalized patient care. This, in turn, can result in better management of CHD, potentially reducing the incidence of adverse cardiovascular events and improving overall patient outcomes.
The existing literature demonstrates a significant correlation between tooth loss and an increased risk of cardiovascular disease. However, these findings were primarily derived from meta-analyses or clinical studies. This study employs a data-driven approach, offering objective insights based on empirical data. This method allows for concrete evidence and measurable results, providing a more robust assessment of the impact.
In this attempt, a pioneering exploration is carried out, employing advanced data science of tensor decomposition25 and generalized additive models (GAMs)26 in machine learning to address the classification and prediction of CAC scores. In particular, the methods of tensor decomposition have been pervasively applied to many areas of life and medical sciences27–36. The focus centers on tooth loss and patient characteristics to elucidate the intricate interplay between these health indicators and the broader spectrum of cardiovascular well-being. Tensor decomposition, a powerful analytical tool, is designed to uncover multidimensional patterns within the dataset, offering an understanding of the intricate relationships that may influence CAC scores. Simultaneously, the application of GAMs provides a flexible and robust framework, capable of capturing non-linear relationships within the data. This flexibility is especially crucial in the context of medical data, where relationships between variables are often complex and multifaceted.
The primary objective of this research endeavor is to investigate the precision of classifying CAC scores into tertiles and predicting their values. By leveraging the insights provided by tooth loss and patient characteristics, this study seeks to unravel latent patterns and contribute to the evolving landscape of predictive modeling in cardiovascular health assessments.
Materials and methods
Patient data
This investigation utilized a publicly available dataset19 comprising 212 patients gathered from three hospitals located in the Netherlands, of which 114 were male. The average age of the participants was 57.8 years, with a mean body mass index (BMI) of 28 kg/
This study included the following patient characteristics: sex, age, smoking status, diabetes mellitus, hypercholesterolemia, hypertension, and BMI. These characteristics were extracted from electronic health records as documented in the referenced study19. If diabetes mellitus, hypercholesterolemia, or hypertension were not explicitly mentioned in a patient’s file but corresponding medications such as metformin, insulin, statins, or antihypertensive drugs were present, the patient was recorded as having that condition. BMI was calculated using the height and weight recorded on the day of the CT scan for the CAC score. For more detailed information on patient characteristics, coronary artery calcification, and dental pathology, the reader is referred to the original data description in the referenced study19.
The inclusion criteria for this study encompassed patients for whom both a CAC score and an orthopantomogram (OPG) were available, with both assessments recorded within a maximum period of 365 days spanning from 2009 to 2017. The CAC score, determined using the Agatston method, was measured through computed tomography scans.
The count of present teeth included all visible teeth on the OPG, encompassing third molars and radices relictae (remnants of tooth roots that remain in the jawbone after a tooth has been partially extracted or has broken off). Pontics of fixed partial dentures and prosthetic dentures were excluded from the tally of present teeth. The number of missing teeth was calculated by subtracting the count of present teeth from the expected total of 32 teeth. Dental implants were individually recorded.
The patients’ CAC scores were divided into tertiles. The first tertile consists of the lowest CAC scores, the second tertile comprises intermediate CAC scores, and the third tertile includes the highest CAC scores.
All the data were anonymized prior to access. Approval for the study was obtained from the Medical Ethical Committee (15.06107) of the Isala Hospital, Zwolle, and was also accepted by other participating hospitals. The Medical Ethical Committee waived the need for informed consent19. The methods employed in this study adhere to established ethical guidelines governing the utilization of publicly available data for research purposes. A statement regarding data availability is included following the Conclusion section.
Tensor decomposition of tooth loss and patient characteristics in coronary artery calcification
A tensor is a multiway or n-way array with different orders, where an order one tensor is a vector, an order two tensor is a matrix, and an order three tensor is a volume. An n-th order or n-way tensor takes the form of an n-hypershape.
In a general form, the elements of an n-way tensor, denoted as
| 1 |
where F represents the number of factors,
Alternatively, a tensor can be expressed as
| 2 |
where
The loading matrices
To examine the separability of tooth loss in terms of different CAC tertiles for classifying tertiles and predicting coronary artery calcium scores, two-way tensors for three cohorts of patients with different CAC tertiles, denoted as
| 3 |
where
GAM for classification and prediction of coronary artery calcification
In statistical analysis, a GAM is a type of generalized linear model where the linear response variable is influenced by unknown smooth functions of specific predictor variables. This model establishes a connection between a univariate response variable, denoted as y, and a set of predictor variables,
| 4 |
where
To accommodate non-linear effects, a GAM substitutes each linear component with a smooth function:
| 5 |
where
Equation (5) is referred to as a GAM since each smooth function is independently estimated, and the sum of these individual contributions is then combined. It is pointed out41 that GAMs exhibit great flexibility because these models allow for distinct smooth functions corresponding to each predictor. Consequently, a GAM can incorporate various techniques, such as: (a) non-linear polynomial methods for continuous predictors, (b) step functions, particularly suitable for handling categorical predictors, and (c) linear models, chosen when deemed more suitable for certain predictors.
In this study, GAM fitting was carried out by employing boosted trees42 as smooth functions for the predictors. The fitting process involved constructing a set of predictor trees during each boosting iteration, with the initial learning rate determined through Bayesian optimization. In binary classification of CAC tertiles, the GAM yielded class scores (the logit of class probabilities) by summing univariate smooth functions of the predictors. In regression tasks for predicting CAC scores, the GAM generated a response variable through the aggregation of univariate smooth functions of the predictors.
Deep learning neural networks
A deep learning neural network (DLNN) consists of multiple layers of nodes, often referred to as neurons, designed to model complex relationships in data. Each layer in the network transforms the input data before passing it on to the next, allowing the network to learn hierarchical patterns. The DLNN architecture developed in this study includes:
Input layer: This layer receives the tooth loss information (non-categorical data) as input data and feeds them into the network.
Hidden layers: These layers contain neurons that apply a series of mathematical transformations to the input data. The depth of the network is determined by the number of hidden layers, set to 32, and the neurons in these layers use activation functions ReLU to introduce non-linearity, allowing the network to capture complex patterns and relationships.
Output layer: This layer produces the CAC classification.
The DLNN was trained by adjusting the weights and biases of the neurons through a process called backpropagation, which minimized the error between the predicted and actual outcomes. This optimization was performed using stochastic gradient descent with momentum. The hyperparameters used during training included a cross-entropy loss function, a mini-batch size of thirty for each training iteration, and a maximum of fifty epochs (full passes through the data). The training data was shuffled once before training, with an initial learning rate of 0.01 and a momentum value of 0.9, which incorporated the parameter update of the previous iteration into the current iteration to improve convergence.
Classification performance metrics
Let P represent the count of instances in higher CAC tertiles, N denote the count of instances in lower CAC tertiles, TP (true positive) indicate the count of correctly classified higher tertile cases, TN (true negative) be the count of correctly classified lower tertile cases, FP (false positive) stand for the count of misclassified higher tertile cases, and FN (false negative) refer to the count of misclassified lower tertile cases.
Table 1 defines the performance measures, including accuracy (ACC), sensitivity (SEN), specificity (SPE), precision (PRE), and
Table 1.
Performance measures of binary classification.
| ACC | SEN | SPE | PRE |
|
|---|---|---|---|---|
|
|
|
|
|
|
Results
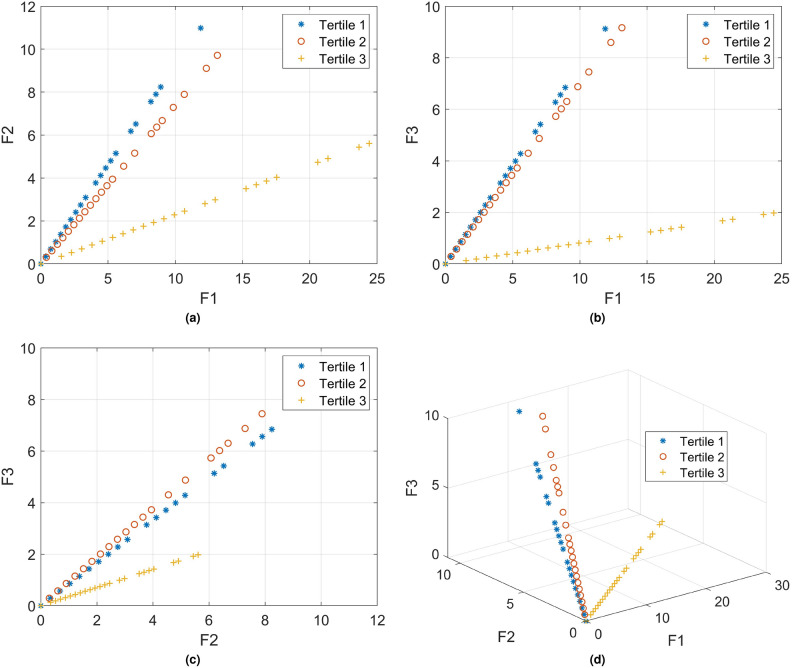
Figure 1 shows the 2D and 3D plots depicting three tensor-decomposition factors (
Fig. 1.
PARAFAC tensor-decomposition factors of patient tooth-loss model.
Table 2 shows the results obtained from a ten-fold cross-validation employing the univariate GAM for the classification of two distinct classes. In this context, class 1 includes the first tertile, whereas class 2 encompasses the second and third tertiles. The classification process used various input features, encompassing patient characteristics, tooth loss data, and the combination of patient characteristics with tooth loss information.
Table 2.
Ten-fold cross-validated GAM-based categorization of CAC into tertile 1 (class 1) and tertiles 2 & 3 (class 2).
| Input feature | %ACC | %SEN | %SPE | %PRE |
|
AUC |
|---|---|---|---|---|---|---|
| Patient characteristics | 75.00 | 84.51 | 55.71 | 79.47 | 0.82 | 0.78 |
| Tooth loss | 71.23 | 88.03 | 37.14 | 73.96 | 0.80 | 0.64 |
| Patient characteristics & tooth loss | 73.11 | 91.55 | 35.71 | 74.29 | 0.82 | 0.76 |
Similarly, Table 3 exhibits the outcomes of a ten-fold cross-validation utilizing the univariate GAM for the classification of two distinct classes. In this instance, class 2 is defined by the second tertile, while class 3 is the third tertile. The classification process incorporated a diverse set of input features, including patient characteristics, tooth loss data, and the combination of patient characteristics with tooth loss information.
Table 3.
Ten-fold cross-validated GAM-based categorization of CAC into tertile 2 (class 1) and tertile 3 (class 2).
| Input feature | %ACC | %SEN | %SPE | %PRE |
|
AUC |
|---|---|---|---|---|---|---|
| Patient characteristics | 63.38 | 59.72 | 67.14 | 65.15 | 0.78 | 0.66 |
| Tooth loss | 55.63 | 51.39 | 60.00 | 56.92 | 0.54 | 0.51 |
| Patient characteristics & tooth loss | 62.68 | 66.67 | 58.57 | 62.34 | 0.64 | 0.66 |
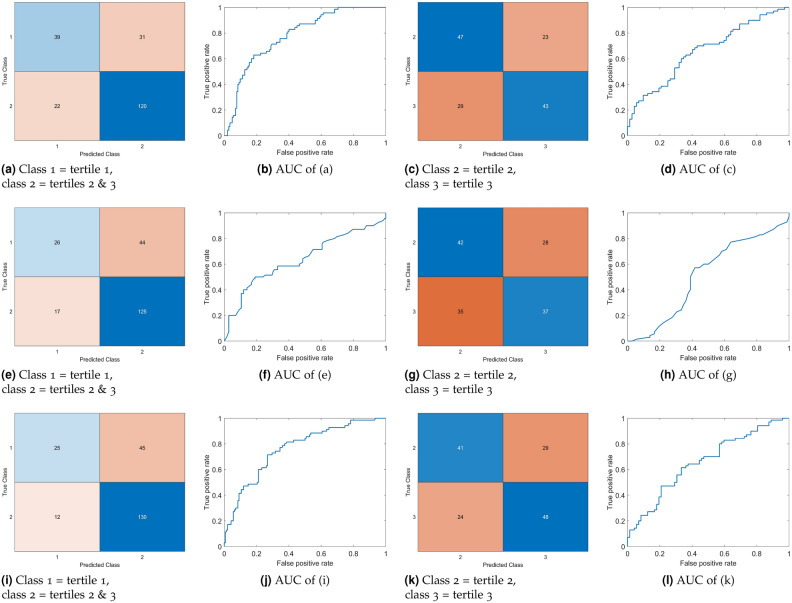
Figure 2 visually presents the confusion matrices and AUCs corresponding to the classification outcomes depicted in Tables 2 and 3.
Fig. 2.
Confusion matrices and AUCs obtained from ten-fold cross-validated GAM-based binary classification of CAC tertiles using patient characteristics (a)–(d), tooth-loss (e)–(h), and combined patient characteristics and tooth-loss (i)–(l).
In the prediction analysis, a male patient with a CAC score of 20,000 was excluded from the dataset due to its singular and notably high value, which qualifies as an outlier. Table 4 shows the ten-fold cross-validation regression errors produced from the univariate GAM, using five input scenarios: patient characteristics, patient characteristics with tooth loss (both male and female), tooth loss (both male and female), female tooth loss, and male tooth loss. Figure 3 accompanies Table 4, visually portraying the predicted and observed CAC scores as derived from the univariate GAM for regression.
Table 4.
Regression loss of ten-fold cross-validated GAM-based prediction of CAC scores.
| Input feature | Average mean squared error ( |
|---|---|
| Patient characteristics | 5.816 |
| Tooth loss | 4.823 |
| Patient characteristics & tooth loss | 6.016 |
| Male tooth loss | 5.119 |
| Female tooth loss | 4.271 |
Fig. 3.
Observed CAC scores and predicted values obtained from ten-fold cross-validated GAM for regression using: (a) patient characteristics, (b) patient characteristics with male and female tooth loss, (c) male and female tooth loss, (d) female tooth loss, and (e) male tooth loss.
Table 5 presents the CAC classification results obtained by the DLNN. The model was trained using 90% of the tooth loss data, which were well-suited for the model due to their non-categorical nature, allowing the network to capture continuous patterns effectively. The remaining 10% of the data was set aside for testing, enabling an evaluation of the model performance on unseen data.
Table 5.
DLNN-based categorization of CAC using tooth loss information.
| %ACC | %SEN | %SPE | %PRE |
|
AUC |
|---|---|---|---|---|---|
| CAC into tertile 1 (class 1) and tertiles 2 & 3 (class 2) | |||||
| 77.27 | 92.86 | 50.00 | 76.47 | 0.84 | 0.84 |
| CAC into tertile 2 (class 1) and tertile 3 (class 2) | |||||
| 60.00 | 62.50 | 57.14 | 62.50 | 0.63 | 0.54 |
Discussion
Table 2 reveals insights into the classification of CAC tertiles, where the utilization of tooth loss as an input feature (71%) stands competitively against patient characteristics (75%) in terms of accuracy. Interestingly, the combination of patient characteristics and tooth loss (73%) does not yield an improvement in classification accuracy compared to using patient characteristics alone. It is also worth noting an observation: tooth loss, when employed as a singular feature, surpasses in identifying tertiles 2 and 3 (88%), which are indicative of a higher risk of coronary artery disease, outperforming the sensitivity achieved with patient characteristics alone (85%). However, the result obtained from the combined features of patient characteristics and tooth loss achieved the highest sensitivity (92%).
The AUC value (0.64) of using tooth loss, which are lower than the patient characteristics (0.78) and the combination of both features (0.76), as a singular input to the GAM suggest a more severe trade-off between sensitivity and specificity– indicating an imbalance between sensitivity and specificity, with the classifier favoring one at the expense of the other. Precision and
The above results underscore the intricate relationship between tooth loss, patient characteristics, and their independence in the classification of CAC tertiles. The observations also suggest that the combination of tooth loss and patient characteristics information can enhance the ability to detect higher-risk categories, emphasizing the importance of considering both dental and patient-specific factors in refining the sensitivity of CAC tertile classification.
The 2D and 3D plots depicting the three PARAFAC tensor-decomposition factors derived from the tooth-loss model becomes evident in their ability to effectively distinguish between the three CAC tertiles. This observation holds meaningful implications, suggesting that tooth loss can serve as a useful feature for the classification and prediction of CAC scores. The separability demonstrated in the graphical representations underscores the potential utility of tooth loss as a valuable marker in understanding and predicting coronary artery calcium levels.
The classification between tertiles 2 and 3, as illustrated in Table 3, reveals a discernible drop in performance compared to the differentiation of tertile 1 from both tertiles 2 and 3. The performance metrics derived from the patient characteristics feature and the combination of patient characteristics and tooth loss exhibit similarities, while the metrics stemming from tooth loss alone register a lower performance.
Examining the specificities, the combined features of patient characteristics and tooth loss demonstrate enhanced capability in identifying CAC tertile 3 (67%), which is indicative of higher risk of coronary artery disease. On the other hand, patient characteristics alone exhibit superior performance in pinpointing CAC tertile 2 (67%). These differences in performance underscore the differential contributions of individual and combined features in classifying CAC tertiles, shedding light on the potential of specific feature combinations for improved predictive modeling in coronary health assessment.
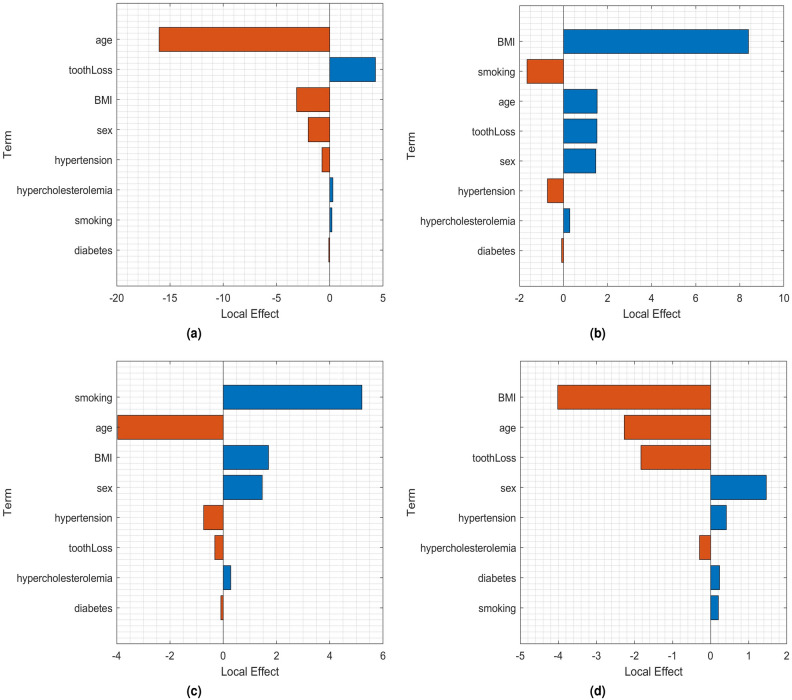
To gain a deeper understanding of the classification of CAC tertiles, Figures 4 and 5 illustrate the local and partial dependence effects43, showcasing examples of correctly and incorrectly classified CAC tertiles 2 and 3 in both male and female subjects.
Fig. 4.
Local effects in: (a) correct classification of tertile 2 for a female patient (age = 36 years, smoking = never, diabetes = no, hypercholesterolemia = no, hypertension = no, BMI = 30.3, and tooth loss = 12); (b) correct classification of tertile 3 for a male patient (age = 66 years, smoking = never, diabetes = no, hypercholesterolemia = no, hypertension = no, BMI = 22.64, and tooth loss = 32); (c) misclassifying tertile 2 as tertile 3 for a male patient (age = 73 years, smoking = never, diabetes = yes, hypercholesterolemia = yes, hypertension = yes, BMI = 25.25, and tooth loss = 7); and (d) misclassifying tertile 3 as tertile 2 for a male patient (age = 56 years, smoking = never, diabetes = no, hypercholesterolemia = no, hypertension = no, BMI = 23.99, and tooth loss = 16).
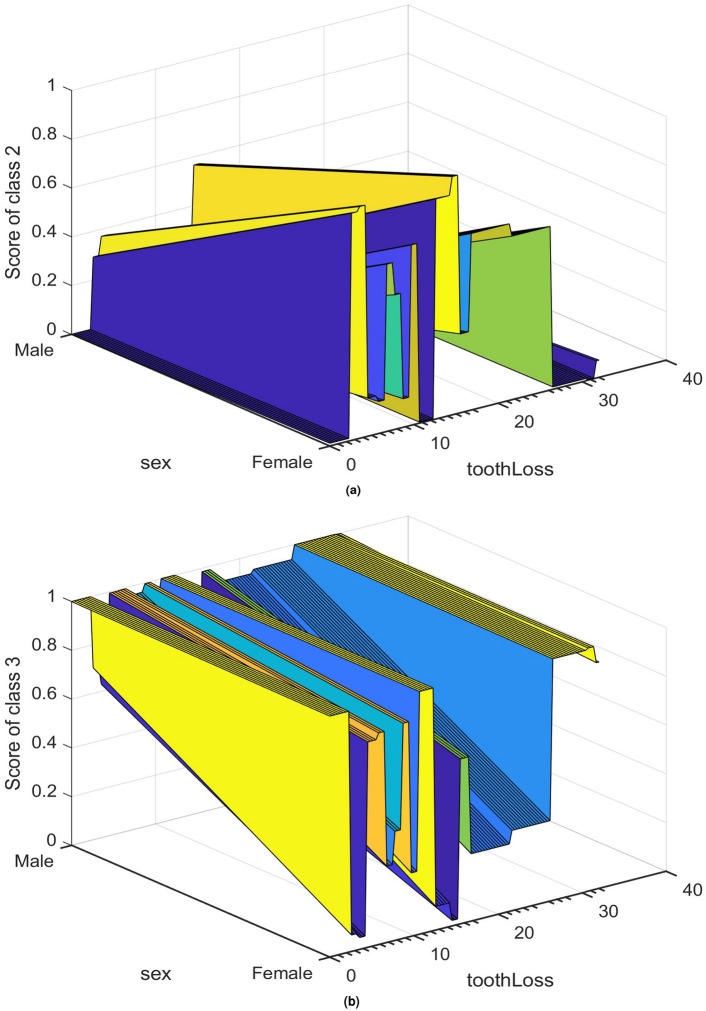
Fig. 5.
Partial effects in classifying: (a) class 2 (tertile 2), and (b) class 3 (tertile 3) in terms of tooth loss and sex.
In Fig. 4, the bar graphs represent the local effects of clinical and tooth loss attributes on GAM-based classification. Each local effect value denotes the contribution of a specific term to the classification score for a given tertile, which is the logit of the posterior probability for that tertile in the observation.
For the accurate classification of tertile 2 in a female patient (Fig. 4a), tooth loss emerges as the most influential factor. In the correct classification of tertile 3 in a male patient (Fig. 4b), BMI takes precedence, while tooth loss, age, and sex contribute equally to a positive influence. On the other hand, the misclassification of tertile 2 as tertile 3 in a male patient (Fig. 4c) is driven by smoking, BMI, and sex. Similarly, the misclassification of tertile 3 as tertile 2 in a male patient (Fig. 4d) is primarily influenced by sex and hypertension.
Moving to the partial dependence effects in Fig. 5a,b, these illustrate the partial dependence of score values for classifying tertile 2 (class 2) and tertile 3 (class 3) based on sex and tooth loss, respectively. The plots suggest that tooth loss has a more pronounced impact on the classification of tertile 2 in female patients, while tooth loss in male patients exerts a stronger influence on the classification of tertile 3.
Concerning the CAC score prediction utilizing GAM for regression, as depicted in Table 4 and Fig. 3, the inclusion of tooth loss as an independent feature yielded the smallest average mean squared error (
Regarding the prediction of male and female CAC scores, both use of patient characteristics and the combined input of patient characteristics and tooth loss resulted in largest errors. The use of individual tooth loss feature is more favorable, where the female tooth loss resulted in the smallest error. As shown in Fig. 3, large errors resulted in the regression model were mainly due to some relatively very large observed CAC scores of the patients indexed toward the right end of the plots.
In the context of CAC score prediction using GAM for regression, as shown in Table 4 and Fig. 3, the incorporation of tooth loss as an independent feature led to the lowest average mean squared error (
As depicted in Fig. 3, substantial errors in the regression model primarily arose from some exceptionally large observed CAC scores of patients situated towards the right end of the plots.
The occurrence of significant errors can be attributed to the imbalance in the dataset, leading to bias in the regression learning process. This imbalance stems from the disproportionate distribution of very small and very large CAC scores, with the majority of values falling within the category of very small scores. The dataset exhibits a skew toward these lower values, contributing to the observed imbalance.
In other words, although the accuracy of using patient characteristics is slightly higher than using tooth loss information, machine learning shows much better ability to identify coronary artery calcifications based on tooth loss information compared to patient characteristics. Additionally, Table 4 reveals that the average mean squared error of predicting CAC scores using tooth loss information is smaller than when using patient characteristics. This indicates that the predictive model performs better when leveraging tooth loss information rather than patient characteristics.
Including both age and tooth loss in the same model may lead to reduced model performance. These variables are often highly correlated because tooth loss tends to increase with age. When predictors are strongly correlated, the model may struggle to distinguish their individual effects on the response variable. Overfitting occurs when a model becomes overly complex relative to the training data, potentially capturing noise rather than true relationships. For instance, if a model attempts to capture all variations in tooth loss across different ages, it may overfit to specific patterns in the training data, leading to poor performance on new data. To mitigate potential overfitting from highly correlated predictors like age and tooth loss in a GAM, ten-fold cross-validation was applied. This technique systematically validates model performance across multiple data subsets, providing a robust assessment of how well the model generalizes to unseen data. By doing so, cross-validation enhances confidence in the model’s predictions and evaluates its overall reliability and practical usefulness in real-world applications.
This study employed ten-fold cross-validation to assess the predictive performance of the model. This method is widely recognized and utilized in the machine learning and statistical community due to its efficiency in providing an unbiased estimate of the model’s performance. Cross-validation allows for the entire dataset to be used for both training and validation purposes, ensuring that the model’s performance metrics are averaged over multiple runs. This results in a more reliable and stable estimate of the model’s accuracy. By using different subsets of the data for training and validation in each fold, cross-validation helps mitigate the risk of overfitting. This is particularly important when working with datasets where the total number of samples may not be large enough to confidently split into separate training, validation, and test sets.
While a separate test set can provide an additional layer of validation, it is not strictly necessary when cross-validation is appropriately applied. The primary goal of using cross-validation is to evaluate the model’s ability to generalize to unseen data. Since each fold serves as both training and validation set in different iterations, cross-validation effectively simulates multiple training-test splits, thus providing a robust measure of the model’s generalization capability. In scenarios where the dataset is not extensive, retaining a portion of the data as a test set can reduce the amount of data available for training the model. Cross-validation optimizes the use of all available data, enhancing the reliability of the model’s performance evaluation.
The results obtained through ten-fold cross-validation in the study have demonstrated that tooth loss and patient characteristics are indeed significant predictors of coronary artery calcification scores. This conclusion is based on consistent performance across all folds, indicating that the model is robust and reliable. The performance metrics, such as accuracy, precision,
Further discussion focuses on the performance of the DLNN in classifying CAC scores using tooth loss data. For distinguishing low CAC (tertile 1) from higher CAC (tertiles 2 & 3), the model achieved high sensitivity (93%), a solid
Although this study employs machine learning with an emphasis on prediction, this does not preclude the analysis and interpretation of the contributing factors. Machine learning has been leveraged not only to predict coronary artery calcifications but also to identify and elucidate key variables, such as tooth loss and patient characteristics, that significantly influence these predictions. This dual focus enables the study to achieve accurate forecasting while simultaneously providing a deeper understanding of the underlying risk factors.
Several closely related future directions can expand upon these findings and enhance their practical implications. One potential direction is to conduct more extensive longitudinal studies. These studies would follow participants over extended periods to observe how CAC scores evolve over time and their correlation with real-world cardiovascular outcomes. Such an approach could provide deeper insights into the long-term predictive power of CAC scoring in assessing cardiovascular risk. Another important avenue is the development and validation of improved predictive models. By integrating additional biomarkers and genetic information with CAC scores, these models can offer more precise risk assessments. This would lead to more personalized and effective prevention strategies for cardiovascular disease. Lastly, a potential future research issue involves the deeper exploration of tensor decomposition techniques to gain insights into the complex relationships between oral pathology, patient characteristics, and CAC contributing to cardiovascular disease. Tensor decomposition can help unravel multi-dimensional data structures, identifying latent patterns and interactions among these variables. Investigating how these decomposed factors correlate with cardiovascular outcomes could enhance the understanding of underlying mechanisms and improve risk stratification and targeted interventions for patients with oral health issues linked to cardiovascular disease.
In the context of classifying CAC scores, where higher scores are strongly linked to an elevated risk of CHD and cardiovascular mortality, evaluating model performance requires careful consideration of several metrics, especially in relation to the specific patient population.
One of the most critical metrics is sensitivity, which in this case refers to the ability of the model to correctly classify patients with higher CAC scores. Given the strong association between high CAC and increased risk of CHD, failing to identify these high-risk individuals could result in missed opportunities for early intervention. Sensitivity is vital because it ensures that those who need preventive care or further evaluation are not overlooked, potentially reducing cardiovascular events and mortality in the long run.
Specificity, on the other hand, measures the correct classification of lower CAC scores, identifying those at lower risk of CHD. In this population, ensuring high specificity is equally important, especially to avoid over-diagnosing low-risk individuals. If specificity is too low, many patients with lower CAC scores could be incorrectly flagged as high-risk, leading to unnecessary anxiety, follow-up tests, or even unwarranted medical treatments. This can not only create undue stress for patients but also strain healthcare resources. Therefore, in a clinical setting where resource optimization and patient well-being are critical, low specificity could be unacceptable.
While accuracy provides a general measure of how well the model performs across all classifications, it can be misleading in cases where there is class imbalance. For example, if the majority of the patient population falls into the lower CAC category, the model could achieve high accuracy simply by correctly classifying most of those cases, even if it performs poorly in detecting the more critical high-risk patients. In this case, accuracy might give a false sense of the effectiveness of the model, making it less meaningful without taking into account the balance between class outcomes.
Precision, or the positive predictive value, reflects the proportion of true positives (correctly classified higher CAC scores) out of all cases classified as positive. High precision is important for reducing false alarms, ensuring that when a patient is flagged as high-risk, there is a strong likelihood that the prediction is correct. This metric becomes especially important when considering the potential harm of unnecessary treatments or interventions for those incorrectly classified as high-risk.
The
The AUC is another valuable metric, as it measures the ability of the model to distinguish between classes across different threshold settings. A high AUC indicates that the model is effective in differentiating between high and low-risk cases, regardless of the threshold, and provides a comprehensive view of the overall performance of the model.
In this patient population, where early identification of cardiovascular risk is critical, sensitivity takes precedence to ensure high-risk patients are identified and receive timely intervention. At the same time, specificity is essential to avoid unnecessary follow-ups and interventions for patients with lower CAC scores. The ideal model, therefore, strikes a balance between these metrics, ensuring both high sensitivity to catch at-risk patients and high specificity to minimize false positives.
Metrics like the
Conclusion
The exploration of patient characteristics and tooth loss information in the classification and prediction of CAC scores has been presented and discussed in the preceding sections. The results suggest that patient characteristics is advantageous in the classification of tertiles, while tooth loss exhibits the potential for providing more accurate predicted CAC scores.
The tensor decomposition employed in this study involves breaking down a multi-dimensional array (tensor) into simpler, interpretable components. This process helps uncover hidden patterns between tooth loss information and coronary artery calcium scores, facilitating a deeper analysis of their complex relationship. With the availability of additional data that addresses the bias in small CAC scores, there is a strong anticipation that the accuracies of GAM-based score prediction and GAM-based and DNN-based tertile classification will significantly improve. The integration of patient characteristics and tooth loss emerges as a promising avenue, contributing to enhanced accuracy in identifying individuals at a higher risk of cardiovascular health issues, particularly in the realm of coronary artery calcium.
Furthermore, the methods presented in this study were tested exclusively on a single dataset from one center. To demonstrate the generalizability and robustness of these methods, it is essential to validate them using external datasets from other centers. This would help ensure that the approaches are not overfitted to the specific characteristics of the initial dataset and can be applied more broadly to diverse patient populations.
Author contributions
TDP contributed to conception, technical design, computer coding and implementation, data interpretation, drafted and critically revised the manuscript. LZ contributed to conception, data interpretation, and critically revised the manuscript. MP contributed to conception, data interpretation, and critically revised the manuscript. SH contributed to conception, data interpretation, and critically revised the manuscript. PC contributed to conception, data interpretation, and critically revised the manuscript. All authors approved the final version of the manuscript.
Data availibility
The dataset used during the current study is available in the Figshare repository (https://figshare.com/articles/dataset/S1_Data_-/13391239).
Code availability
MATLAB codes implemented in this study are freely available at the first author’s (TDP) personal website: https://sites.google.com/view/tuan-d-pham/codes, under the title “Dental and vascular diseases”.
Declarations
Competing interests
All authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kotronia, E. et al. Oral health and all-cause, cardiovascular disease, and respiratory mortality in older people in the UK and USA. Sci. Rep.11, 16452 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kotronia, E. et al. Poor oral health and inflammatory, hemostatic, and cardiac biomarkers in older age: Results from two studies in the UK and USA. J. Gerontol. A Biol. Sci. Med. Sci.76, 346–351 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Joshy, G., Arora, M., Korda, R. J., Chalmers, J. & Banks, E. Is poor oral health a risk marker for incident cardiovascular disease hospitalisation and all-cause mortality? Findings from 172 630 participants from the prospective 45 and up study. BMJ Open6, e012386 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gianos, E. et al. Oral health and atherosclerotic cardiovascular disease: A review. Am J Prev Cardiol.7, 100179 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.King, S., Chow, C. K. & Eberhard, J. Oral health and cardiometabolic disease: Understanding the relationship. Intern. Med. J.52, 198–205 (2022). [DOI] [PubMed] [Google Scholar]
- 6.Mariana, B. An updated review on the link between oral infections and atherosclerotic cardiovascular disease with focus on phenomics. Front. Physiol.13, 1101398 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aldossri, M., Farmer, J., Saarela, O., Rosella, L. & Quinonez, C. Oral health and cardiovascular disease: Mapping clinical heterogeneity and methodological gaps. JDR Clin. Transl. Res.6, 390–401 (2021). [DOI] [PubMed] [Google Scholar]
- 8.Gustafsson, N. et al. Associations among periodontitis, calcified carotid artery atheromas, and risk of myocardial infarction. J. Dent. Res.99, 60–68 (2020). [DOI] [PubMed] [Google Scholar]
- 9.Matsuyama, Y., Jurges, H. & Listl, S. Causal effect of tooth loss on cardiovascular diseases. J. Dent. Res.102, 37–44 (2023). [DOI] [PubMed] [Google Scholar]
- 10.Schwahn, C. et al. Missing, unreplaced teeth and risk of all-cause and cardiovascular mortality. Int. J. Cardiol.167, 1430–1437 (2013). [DOI] [PubMed] [Google Scholar]
- 11.Peng, J. et al. The relationship between tooth loss and mortality from all causes, cardiovascular diseases, and coronary heart disease in the general population: Systematic review and dose-response meta-analysis of prospective cohort studies. Biosci. Rep.39, BSR773 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Holmlund, A., Holm, G. & Lind, L. Number of teeth as a predictor of cardiovascular mortality in a cohort of 7674 subjects followed for 12 years. J. Periodontol.81, 870–876 (2010). [DOI] [PubMed] [Google Scholar]
- 13.Gao, S. et al. Periodontitis and number of teeth in the risk of coronary heart disease: An updated meta-analysis. Med. Sci. Monit.27, e930112 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cheng, F. et al. Tooth loss and risk of cardiovascular disease and stroke: A dose-response meta analysis of prospective cohort studies. PLoS ONE13, e0194563 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.De Angelis, F. et al. Influence of the oral status on cardiovascular diseases in an older Italian population. Int. J. Immunopathol. Pharmacol.32, 394632017751786 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Beukers, N. G. F. M., Su, N., Loos, B. G. & van der Heijden, G. J. M. G. Lower number of teeth is related to higher risks for acvd and death-systematic review and meta-analyses of survival data. Front Cardiovasc. Med.8, 621626 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Imes, C. C. & Lewis, F. M. Family history of cardiovascular disease, perceived cardiovascular disease risk, and health-related behavior: A review of the literature. J. Cardiovasc. Nurs.29, 108–129 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wong, N. D. et al. Atherosclerotic cardiovascular disease risk assessment: An American society for preventive cardiology clinical practice statement. Am. J. Prev. Cardiol.10, 100335 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Donders, H. C. M. et al. Elevated coronary artery calcium scores are associated with tooth loss. PLoS One15, e0243232 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shreya, D. et al. Coronary artery calcium score-a reliable indicator of coronary artery disease?. Cureus13, e20149 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Divakaran, S. et al. Use of cardiac CT and calcium scoring for detecting coronary plaque: Implications on prognosis and patient management. Br. J. Radiol.88, 20140594 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cheong, B. Y. C. et al. Coronary artery calcium scoring: An evidence-based guide for primary care physicians. J. Intern. Med.289, 309–324 (2021). [DOI] [PubMed] [Google Scholar]
- 23.Mannarino, T. et al. Combined evaluation of CAC score and myocardial perfusion imaging in patients at risk of cardiovascular disease: Where are we and what do the data say. J. Nucl. Cardiol.30, 2349–2360 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kitjanukit, S. et al. Coronary artery calcium (CAC) score for cardiovascular risk stratification in a Thai clinical cohort: A comparison of absolute scores and age-sex-specific percentiles. Heliyon10, e23901 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kolda, T. G. & Bader, B. W. Tensor decompositions and applications. SIAM J. Matrix Anal. Appl.51, 455–500 (2009). [Google Scholar]
- 26.Hastie, T. J. & Tibshirani, R. J. Generalized Additive Models (Chapman & Hall/CRC, Boca Raton, 1990). [Google Scholar]
- 27.Smilde, A., Bro, R. & Geladi, P. Multi-way Analysis: Applications in the Chemical Sciences (Wiley, Chichester, 2004). [Google Scholar]
- 28.Luo, Y., Ahmad, F. S. & Shah, S. J. Tensor factorization for precision medicine in heart failure with preserved ejection fraction. J. Cardiovasc. Transl. Res.10, 305–312 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pham, T. D. & Yan, H. Tensor decomposition of gait dynamics in Parkinson’s disease. IEEE Trans. Biomed. Eng.65, 1820–1827 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Zhao, J. et al. Detecting time-evolving phenotypic topics via tensor factorization on electronic health records: Cardiovascular disease case study. J. Biomed. Inform.98, 103270 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang, R., Li, S., Cheng, L., Wong, M. H. & Leung, K. S. Predicting associations among drugs, targets and diseases by tensor decomposition for drug repositioning. BMC Bioinf.20(Suppl 26), 628 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cirillo, M. D., Mirdell, R., Sjoberg, F. & Pham, T. D. Tensor decomposition for color image segmentation of burn wounds. Sci. Rep.9, 329 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Korevaar, H., Metcalf, C. J. & Grenfell, B. T. Tensor decomposition for infectious disease incidence data. Methods Ecol. Evol.11, 1690–1700 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nesaragi, N., Patidar, S. & Aggarwal, V. Tensor learning of pointwise mutual information from EHR data for early prediction of sepsis. Comput. Biol. Med.134, 104430 (2021). [DOI] [PubMed] [Google Scholar]
- 35.Ng, K. L. & Taguchi, Y. H. Identification of miRNA signatures for kidney renal clear cell carcinoma using the tensor-decomposition method. Sci. Rep.10, 15149 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Leistico, J. R. et al. Epigenomic tensor predicts disease subtypes and reveals constrained tumor evolution. Cell Rep.34, 108927 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Burdick, D. S. An introduction to tensor products with applications to multiway data analysis. Chemom. Intell. Lab. Syst.28, 229–237 (1995). [Google Scholar]
- 38.Bro, R. PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst.38, 149–171 (1997). [Google Scholar]
- 39.Harshman, R.A. Foundations of the PARAFAC procedure: model and conditions for an ‘explanatory’ multi-mode factor analysis. UCLA Working Papers in Phonetics16, 1–84 . (1970)
-
40.Carroll, J. D. & Chang, J. Analysis of individual differences in multidimensional scaling via an
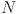 -way generalization of “Eckart-Young’’ decomposition. Psychometrika35, 283–319 (1970). [Google Scholar]
-way generalization of “Eckart-Young’’ decomposition. Psychometrika35, 283–319 (1970). [Google Scholar] - 41.Jackson, S. Machine Learning. Bookdown (2023). https://bookdown.org/ssjackson300/Machine-Learning-Lecture-Notes/ Accessed 25 January (2024).
- 42.Lou, Y., Caruana, R., & Gehrke, J. Intelligible models for classification and regression. Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’12). ACM Press, Beijing, pp. 150-158 (2012).
- 43.Goldstein, A., Kapelner, A., Bleich, J. & Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat.24, 44–65 (2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The dataset used during the current study is available in the Figshare repository (https://figshare.com/articles/dataset/S1_Data_-/13391239).
MATLAB codes implemented in this study are freely available at the first author’s (TDP) personal website: https://sites.google.com/view/tuan-d-pham/codes, under the title “Dental and vascular diseases”.