Molecular electronics: Some views on transport junctions and beyond

Abstract

The field of molecular electronics comprises a fundamental set of issues concerning the electronic response of molecules as parts of a mesoscopic structure and a technology-facing area of science. We will overview some important aspects of these subfields. The most advanced ideas in the field involve the use of molecules as individual logic or memory units and are broadly based on using the quantum state space of the molecule. Current work in molecular electronics usually addresses molecular junction transport, where the molecule acts as a barrier for incoming electrons: This is the fundamental Landauer idea of “conduction as scattering” generalized to molecular junction structures. Another point of view in terms of superexchange as a guiding mechanism for coherent electron transfer through the molecular bridge is discussed. Molecules generally exhibit relatively strong vibronic coupling. The last section of this overview focuses on vibronic effects, including inelastic electron tunneling spectroscopy, hysteresis in junction charge transport, and negative differential resistance in molecular transport junctions.

How a single molecule or an ordered network of molecules (1–7) can perform transport (8, 9) or a computation using mechanical (10), magnetic (11), or electronic (12) degrees of freedom is becoming an active field of research, after the first suggestive ideas of the 1970s (13, 14). Use of electronic and nuclear molecular degrees of freedom to create a device function embedded inside a unique molecule is a major challenge in the application of molecular electronics ideas (15, 16). Its ultimate functionality would be realized by using the physical resources inside a single molecule to integrate a full arithmetic and/or logic unit (17).

Molecular electronics entails a series of conceptual, experimental, and modeling challenges (1–7, 18–20). Those challenges concern the architecture of molecules, the interconnects and, more generally, the nanocommunication schemes within and among molecules, the chemistry, and (from a more applied point of view) nanofabrication and nanopackaging techniques.

In architecture, the main challenge is to determine whether a molecule can provide an interconnect, a switch, a transistor (13, 14, 21) or a more complex function, such as a logic gate or even a full arithmetic and logic unit (17, 92). If the ultimate miniaturization scale of an electronic device is one molecule per transistor, such hybrid molecular electronic technology might approach what is expected for future semiconductor nanoelectronics. Substantial progress in this direction has occurred since 1974, as exemplified by the contribution from Ebling et al. (22) in this Special Feature dealing with molecular rectification. Going further, if there are enough quantum resources in a single molecule to integrate more than one device function, then new computational schemes might open. These new schemes will require extensive modeling studies to select among a semiclassical architecture, forcing the molecule to behave like a traditional electronic circuit (23), a quasi-quantum one employing electronic interference effects (24) or a Hamiltonian or quantum computing-like architecture, where the intramolecular quantum dynamics of the molecule defines a computation scheme (25).

For interconnects permitting data, charge, and energy exchanges between a single molecule and the external world (the so-called nanocommunication problem), one major challenge is to create an atomically clean technology in which the fabrication precision and the positioning of a single atom, molecule, or atomic wire on a surface is better than 0.1 nm, as discussed by the Gourdon (26), Hersam (27), and Ho (28) groups in this issue of PNAS. Atomic scale precision positioning is a very active new field of research accompanied by a progressive shift from metallic to semiconducting surfaces to interconnect very precisely a single molecule to a macroscopic lead (29, 30).

The main chemical challenge may not be the synthesis of a conjugated molecular “board” to perform electronic device functions or even act as a digital logic gate. A major chemistry challenge requires equipping the board with lateral chemical groups, not contributing to the function directly but protecting the molecular electronic functionality and assembling and stabilizing the molecule on a given substrate. One example involves chemistry to maintain the molecular board away from the surface while facilitating scanning tunneling microscope single molecule manipulation (31, 32). Other chemical groups must provide a good electronic coupling between the molecular device or logic and local leads (33, 34). Aside from simple end groups, such as thiols, adding all of these lateral groups is problematic for the deposition procedure (solubility, sublimation, and self-assembly), requiring new deposition techniques. The molecular weight of these molecular facilitators may be larger than the board itself.

There is little current work on nanofabrication and nanopackaging with atomic scale precision. Molecular self assembly should permit molecules to self-build such structures as interconnect junctions (35, 36). It is fair to anticipate an explosion of activities aimed at such fabrication. Single molecular devices or logic gates will have to be packaged to transition from the laboratory to the market.

More fundamentally, molecular electronics work is contributing to the knowledge and capability base of molecular and condensed matter science. In this contribution, we focus not on elastic transport in molecular junctions, which has been recently reviewed (7–9, 19). Rather, we examine the fundamental nature of charge transport in such systems wherein the molecular entity acts as a guide/filter for charge flow. In The Superexchange Mechanism, we show that new ways of understanding the physics of signal exchange through a long molecular wire can enlarge molecular electronics by adding the language of the quantum information community. This discussion can be generalized from molecular wires interconnected to n = 2 electrodes to a larger molecule with N interfacial links.

The Superexchange Mechanism

Consider an isolated, zero-temperature molecule made of a longitudinal part (L) with a substituent group (M1) at one end of L and another group (M2) at the other end of L. When initially prepared in a quantum nonstationary state M1^––L–M2, this molecule should ideally oscillate back and forth between the forms M1^––L–M2 and M1–L–M2^–. These time-dependent Heisenberg–Rabi oscillations are the signature of a pure quantum superexchange effect (37, 38), which will then dephase, until the M1–L–M2 molecule has relaxed into a (M1–L–M2)^– state. This basic quantum phenomenon is at the origin of nearly all of the proposed and/or experimented molecular electronics device or logic functions.

The superexchange mechanism reflects the role of the molecular wire L in increasing the effective electronic coupling V₁₂ between the two quantum states M1^––M2 and M1–M2^– when M1 and M2 are maintained very far apart. In the coherent regime, the effect of the bridge L is not the creation of a classical material channel for the charge to be transferred from M1 to M2 by using stations along L (39). Rather, L facilitates tunneling by increasing the size of quantum state space (40, 41) for the quantum trajectory d(t) describing the quantum evolution of M1^––L–M2 to reach the vicinity of the target state representing M1–L–M2^–, as compared to the quantum trajectory to reach M1–M2^– starting from M1^––M2.

Optimizing an average d(t) to pass in close proximity to M1–L–M2^– starting from M1^––L–M2 or minimizing the distance between d(t) and M1–L–M2^– for a given value of t is a difficult quantum control problem. Usually, it is reduced to optimizing the W_transfer electron transfer (ET) rate between M1^––L–M2 and M1–L–M2^– (39). The electronic component of W_transfer is simply the secular frequency of the Heisenberg–Rabi nearly periodic oscillations between the M1^––L–M2 and the M1–L–M2^– states. It depends (for situations with an injection gap far exceeding thermal energy) exponentially on the length of the ligand L, on its conformation, and on the detailed properties of the virtual electronic states entering the ET process (39, 42). Those variables control the extension and quality of d(t) on the corresponding quantum state space. Reducing the d(t) characteristics to only W_transfer is a drastic reduction of the quantum properties on the ligand L. For example, the time for an electron to oscillate between M1 and M2 through a hypothetical 5-nm-long polyene ligand in a binuclear metal complex is about 1 ps (40, 41). This time can be compared to the 0.1 fs taken by a ballistic electron to run over 5 nm of a mesoscopic metallic wire (estimated from the Landauer formula, under bias V of 1 V, or from the Fermi velocity in copper). Using only W_transfer to optimize d(t) may not be enough to understand the large difference between the two processes.

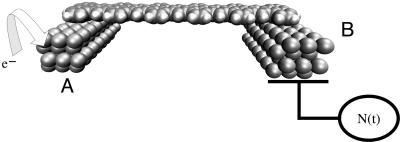
By selecting a metallic atom and bonding pattern and extending the lateral size of M1 and M2, one can use the superexchange interaction to couple two metallic pads electronically (Fig. 1). In this case, the (M1)_n–L–(M2)_n electronic coupling will depend also on a new size parameter n, n→∞ for the metal–L–metal tunnel junction case. As for n = 1, adding one electron to (M1)_n will trigger a superexchange, time-dependent process for the electron to be transferred to (M2)_n by the molecular ligand. The d(t) trajectory of this process is certainly more complex than for n = 1 and will depend on the electronic density of states of A = (M1)_n and B = (M2)_n. As a consequence, the electronic coupling V₁₂(n) between the 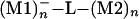and the 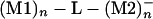states is a function of n, and the corresponding transfer rate W_reservoir differs substantially from W_transfer. Measuring V₁₂(n) for very large n is possible by using microwave-type experiments, as already practiced with mesoscopic superconductor qubits (43). The discussion in this section is dramatically modified by vibronic and dephasing processes as discussed in Decoherence and Relaxation (Inelastic Effects) and in the contribution by Ness and Fisher.

Fig. 1.

A molecular wire L adsorbed and providing electronic coupling between two metallic clusters A and B. Injecting one electron on A = (M1)_n will trigger an ET process guided by L between the state A^––L–B and A–L–B^– with B = (M2)_n. This process can be followed in time by using the electron detector N(t) before it stops because of decoherence and relaxation effects at the interface, on the molecule, and in the A and B clusters.

Source and Detection of Tunneling Electron

One heuristic physical interpretation of the tunneling regime, based on ref. 44, involves a shot–noise-like approach. Suppose now that each time a single ET event occurs between cluster A and cluster B in the A–L–B quantum system presented in Fig. 1, the transferred electron is removed from B and, immediately, another electron is provided to the cluster A, again preparing a nonstationary quantum state A^––L–B. Following this procedure, the maximum electronic current intensity measured in the external circuit is simply:

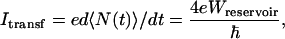[1]

with N the number operator measured on the right pad.

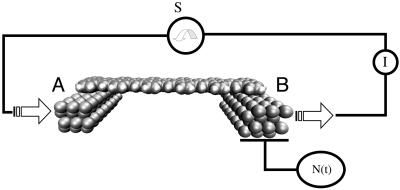
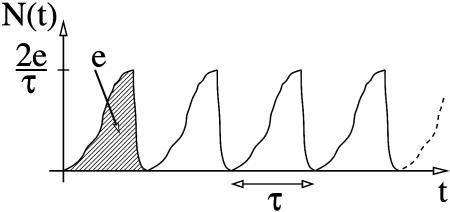
The corresponding gedanken experimental set up is presented in Fig. 2. As in Fig. 1, the set up includes a detector of single ET events able to follow in time the N(t) electron population of cluster B. A source S is now acting in synchronization with the ET events. The current (I) is calculated by performing the time average of the N(t) time-dependent signal measured at the detector. The ideal N(t) shape is a succession in time of sinusoidal arcs. The rise of each arc corresponds to the growth of the electronic population of cluster B in time, due to ET. When this population approaches its maximum, the electron is pumped out of cluster B. The maximum possible current is obtained by supposing that the source S is ideally synchronized with the ET events. This circumstance leads to a periodic N(t) signal with no interruption between each period. In this case, the current intensity depends only on the ET rate W_reservoir, which is calculated by averaging in time the ideal N(t) signal shape given in Fig. 3.

Fig. 2.

A source S is added to Fig. 1, ideally synchronized with each ET event from A to B through L. An ideal S is supposed to provide an electron at cluster A each time the previous one had been pumped out of cluster B. A macroscopic amperometer is added to measure the tunnel current density in the circuit.

Fig. 3.

The ideal N(t) time-dependent electron population on cluster B when the source S in Fig. 2 is synchronized with each ET event. As indicated, each arc is supposed to be normalized to effectively one ET at a time. τ is the full duration of the event before its fast pumping out of cluster B, τ = h/4V₁₂(n).

Of course, an ideal synchronized source S as described in Fig. 2 is not known. A source of voltage V is usually used to form a closed electrical circuit delivering electrons to the A-L-B molecular junction. In this case, the maximum tunneling current is given by the Landauer formula (45):

[2]

where X is the lead electronic conduction bandwidth and V is the bias voltage of the A–L–B tunnel junction. This current is the maximum that can be measured by the macroscopic amperometer for a given A–L–B junction. For example, a sufficient increase of the lead ohmic resistance will effectively transform the voltage source to a current source. If this lead resistance is much higher than the quantum of resistance h/2e², no electrons will be provided to the A–L–B junction. The source will be blocked by the so-called Coulomb blockade effect (46). Delivery of electrons to be transferred through the molecular wire is a very delicate process whose time dependence will not follow the N(t) ideal time sequence (Fig. 3).

Whereas delivery of electrons to the molecular wire is a classical–quantum conversion process, the detection of the electrons after its transfer through the molecular wire is a very peculiar quantum–classical measurement process, as can be demonstrated by using the Ehrenfest theorem, indicating that the current value given by (Eq. 2) results from the measurement of a specific quantum observable in the tunnel junction (47). It can be shown that this intensity is given by the quantum average over junction scattering eigenstates of the commutator [N(t)/2, H], where H is the single-electron Hamiltonian of the A–L–B tunnel junction. Both the source of tunneling electrons and detection of the transferred electrons to obtain a measurable tunneling current at the macroscopic amperometer have been studied very little, either experimentally or theoretically.

One indication of the poor performance of the actual voltage generator-interconnection lead-stray capacitance tunnel sources is the difference between the intensity given by Eqs. 1 and 2. For a short conjugated molecular wire with an effective electronic coupling V₁₂(n) between the two electrodes of 10 meV (1 eV = 1.602 × 10^–19 J), the maximum current is 1.5 μA in Eq. 1 and the scattering current is 0.2 nA in Eq. 2, where the scattering current is calculated for a bias voltage of V = 0.1 V and a lead bandwidth of 4 eV. This difference of four orders of magnitude between the two currents is an indication that the time interval between two ET events in a A-L-B tunnel junction is very large. It follows that there is no phase relation between the elementary ET events, nor a regular distribution of electron delivery to the tunnel junction over time. This Schottky noise indicates that electron delivery to the junction is a Poissonian process in time (48). Each ET event can be considered as quantum coherent [under conditions discussed in Decoherence and Relaxation (Inelastic Effects)]. The overall measured tunneling is not coherent, but noisy. There is room for extensive improvement of the source to take advantage of the fast ET rate compared with the very small rate of electron delivery to the junction.

This discussion of the source and detection of tunneling electrons may hold for any tunneling junction in the linear part of its I–V characteristic. Application to a metal/molecule/metal tunnel junction can clarify interpretation and nomenclature. First, the measured conductance of the metal–molecule–metal junction is not the “conductance of the molecule itself” nor the intrinsic ET rate through the molecular wire. It is simply the rate of delivery of electrons to the junction. Of course, this delivery rate must be lower than ET rate through the molecule to avoid any charge pile-up in the junction. Second, there is little electron flux at low-bias voltage, which (as discussed in the next section) implies that for a virtual resonance tunnel process where the bias voltage V is lower than any electronic resonance of the molecular wire, the appellation “electron transport through a molecular wire” may not describe the real process occurring in the molecular junction. Third, one can define the contact conductance as the part of the A–L–B junction conductance independent of the length of the molecular wire (49). This conductance is a measure of the ability of the molecule/metal atomic scale junction to ease both the classical–quantum conversion and the quantum measurement occurring at the junction microscopic level. Both processes are summarized in one constant, and work remains to be done to disentangle the characterization of the two processes.

A Transport Phenomenon or a Guide for Exchange Interactions

At low-bias V (as discussed in the preceding section), very few electrons are replaced on the molecular wire in the tunneling regime. Each transferred electron is localized mainly to the electrodes and not on the molecular wire: The molecular wire is not reduced or oxidized. This process is purely quantum: The molecular wire quantum states merely increase quantum state space of the A–L–B system to open a quantum trajectory representing the ET event between A and B. Without this state space expansion, the ET between A and B will be too slow. Even with it, elastic scattering at the electrode/molecule interface will reduce the value of the conductance, which is the “conductance is scattering” view of the Landauer formula (50).

When the electronic transparency increases toward unity, the electronic states of the electrodes begin to delocalize along the molecule, and a regime of ballistic transport can be reached (in the absence of vibronic coupling or resonance), where at least one excess electron can be (on average) delocalized along the molecular wire. At low transparency, a molecular wire can be better seen as a partial guide for the electronic exchange interactions between the two metallic electrodes of the A–L–B junction than as a material supporting a permanent flux of electrons (51). The large difference between the ET rate and the tunneling rate is a good piece of evidence that there is no permanent electron flux in a molecular wire junction, even if there is a permanent electronic interaction introduced by the molecular wire in A–L–B. Of course, an ET event can be viewed as an information exchange between A and B via L. The information exchanged is classical, the presence of an electron prepared in a nonstationary state and located on A. There is no known way yet to control in detail the preparation of this state, for example, by preparing a peculiar phase in the mixing of the molecular orbital involved in the definition of the A^––L–B initial state. We do not have enough control yet of the quantum state of the electrons delivered by the electrodes to the molecular wire to be able to exchange quantum information between A and B.

Many parameters characterize an exchange interaction guide: the strength of the interaction, the level of dissipation and importance of the dispersion effects, the bandwidth, the noise level, and the communication capacity of a channel formed by the molecular wire in the tunnel regime. Aside from the interaction strength (spectral density) and some vibronic components of the dissipation, none of the other parameters are accessible to simple I–V experiments because the current intensity does not provide any direct information about them.

Decoherence and Relaxation (Inelastic Effects)

Two phenomena, decoherence and relaxation, limit the quantum capability (discussed above) of a molecular wire to exchange information between metallic electrodes. Both phenomena increase with increasing temperature and length of the wire (39), which implies that the ET time between electrodes is becoming long relative to some internal characteristic time of the molecular medium defining the exchange guide.

Decoherence. Preparation of the ET process by the tunnel source on the left of the A-L-B junction creates a wave packet, which is supposed to reach the right electrode and be detected. Wave packet propagation is dispersive, so it is very difficult to optimize the chemical structure of a molecular wire to ensure perfect (quantum yield of unity) wave packet propagation. Some component of the wave packet will be phase-shifted in time, leading to a deformation of the wave packet. As a consequence, in the coherent tunneling regime with a gap, exponential decay with length of the electronic coupling V₁₂(n) = V_o(n) exp(–βL) between the electrodes through the molecular wire will occur, where β is an inverse decay length of the process (39, 52). A fascinating challenge involves finding a peculiar molecular wire structure or wave packet quantum trajectory control to approach dispersionless motion. The second order character of the Schrödinger equation is responsible for β being bound from below (53). But another second-order equation, the Maxwell equation, produces remarkable propagation behavior with material of negative refractive index (54). Might such strange behavior be induced into a quantum wave packet moving along a molecular wire? In search for a supertunnel effect, this behavior would provide a way to minimize β and to couple the A and B electrodes over large distances. A first step in this direction was to recognize that the spectral second moment describing the molecular wire electronic level distribution in energy is the second parameter controlling β after the highest occupied molecular orbital–lowest occupied molecular orbital gap of the molecular wire (39, 55).

Finding a molecular wire architecture to optimize this second-order distribution will lead to very small β. Unfortunately for this optimization of V₁₂, a simple tunneling junction does not access all virtual electronic excitations. This incompleteness is one explanation of the difference between Eqs. 1 and 2, as can be clearly observed in electronic I–V characteristics recorded on a single molecule with a scanning tunneling microscope metal surface–molecule–metal tip apex tunnel junction. The recorded spectra can usually be interpreted as tunneling through a quantum system showing only very simple monoelectronic excitations (56). How a tunneling junction is filtering (selecting) the relevant electronic virtual excitations to create a given channel is essentially an open question. Deviations from the expected simple (57) I–V curves are sometimes seen in scanning tunneling microscope I–V spectra on single molecules (29) and are not yet completely understood.

Inelastic Effects (Relaxation). Molecular electronics (1–9) differs from more traditional semiconductor electronics in several crucial ways. An important one first pointed out by Yablanovich (58) is that molecules nearly always exhibit vibronic coupling: Molecular spectra show Stokes shifts and the excited state minimum geometry of molecules is hardly ever the same as the ground state geometry, just as the behavior of molecular ions almost always differs from that of the stable molecules. The absence of such vibronic coupling in silicon is one of the important aspects of silicon semiconductors, giving stable, unchanging geometries as the electronic population changes. Because this absence is not true in molecules, molecular electronics will show several important differences from silicon electronics.

For example, in traditional semiconductors the so-called “Coulomb staircase” regime occurs when the coupling between the bridge structure, (usually a quantum dot) and the electrodes is relatively weak compared to the electronic self-energy on the dot. Under these conditions, the dot can charge multiply, lead to a “coulomb staircase.” In molecules, this charging will also change the geometries; we, therefore, do not expect a straightforward Coulomb staircase with equally spaced charging peaks, essentially because of vibronic coupling. This observation has indeed been made in measurements on conductive oligomer structures (59).

The interaction between vibrations and electronic states is responsible for many of the most important phenomena in molecular materials, including vibrational peaks in electronic spectra, nonadiabatic processes of many types, including Jahn–Teller distortions, and the characteristic activation processes associated with transport in conducting polymers (60–62). These same vibronic coupling effects are expected to be extremely important in certain aspects of molecular electronics. In this section, we very briefly discuss such vibronic coupling in inelastic electron tunneling spectroscopy (IETS), the mechanistic transition from coherent tunneling to hopping-type processes, and in some of the characteristic behaviors of transport in molecular junctions, including negative differential resistance mechanisms and hysteretic/switching behavior.

Vibronic coupling: IETS spectra and line shapes. The IETS experiment, first developed (63–67) at the Ford Laboratories in the 1950s, consists of observing vibrational side bands in the I–V characteristics of any transport medium. Because these peaks arise from electron/vibration coupling, they are expected to depend critically on the nature of this coupling. The experiment examines the dependence of the transport current on the voltage, the first derivative (conductance), and, more specifically, the second derivative of the current. In these second-derivative IETS spectra, one sees peaks that correspond to inelastic behavior, excitation of a vibrational mode on the wire.

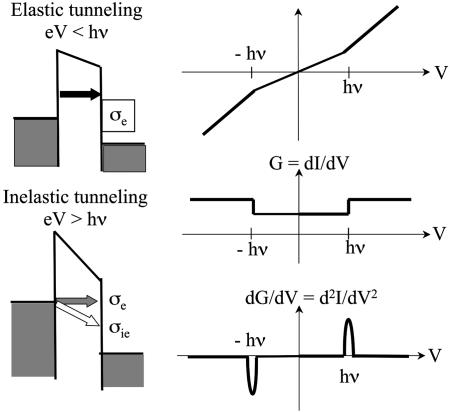
From standard textbook discussions (67), one might expect the behavior indicated in Fig. 4. Whenever the applied voltage V is large enough for an inelastic event to occur such that the current passing through a molecular wire can deposit energy corresponding to a single quantum of vibration, one should see an increase in the rate at which current flows. This behavior would be expected to give changes in slope of the current, changes in the values of the conductance, and peaks in the IETS behavior.

Fig. 4.

Schematic illustrations of the IETS measurement. The cross-sections for the elastic and inelastic tunneling are (to a first, rough approximation) additive, so that when the applied voltage exceeds a characteristic vibrational energy on the molecule, one expects to see changes of slope in the current, of value in the conductance, and peaks in the IETS (second derivative of the current) structure (M. A. Reed, personal communication).

It is useful to consider the molecular generalization of the so called Landauer–Buttiker contact time, during which the tunneling electron is actually in contact with the molecular bridge (the time in Fig. 2 between the injection and the release of this electron to the opposite electrode). A reasonable approximation (68) can be derived on the basis of the original Buttiker argument (69), extended to deal with a tight-binding type molecular wire, which yields the approximation

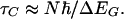[3]

The contact time, τ_c, is inversely proportional to ΔE_G, the excitation gap between the injection energy and the isolated bridge frontier orbital energy, and increases with the number, N, of repeat groups in the wire. This form is actually a straightforward generalization of the uncertainty principle, but it has important physical implications: For large gaps (for example σ-bonded systems) and short wires, τ_c will be of order 10^–16 s, far too short for significant vibronic coupling. For smaller gaps (π -electrons) and longer wires, the contact time can increase to become of the order of a vibrational period (39). One then expects adequate time for vibronic coupling to operate. Thus, for long bridges and π -type systems, vibronic coupling should be more important than for σ-type systems and short bridges, in accordance with a number of experimental observations (70, 71).

For relatively low voltages and low temperatures (conditions kT < 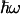and 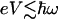, where ω is the molecular vibration frequency and V is the applied voltage), one can develop a perturbative description of the IETS spectrum (93). Here it is assumed that the vibronic coupling is weak enough that no polarons (charged distortions on the molecular bridge) occur. The current is elastic, and the inelastic part can be evaluated by low-order perturbation theory similar to the Herzberg–Teller analysis for vibrational structure in electronic spectra.

Under these conditions and from Eq. 2, the conductance can be written (A. Troisi and M.A.R., unpublished data) in the standard Landauer-type model as

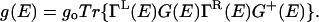[4]

Here g, g_o, Γ, G, and L denote, respectively, the conductance, the atomic unit of conductance (12.9 kΩ)^–1, the mixing of the molecular wire with the electrode on the left (L) and right (R) sides, and the Green's function (72–75) for propagation of the electron through the bridge structure. The couplings, Γ, are proportional to the escape rate of electrons from the molecule to the two electrodes. The Green's function itself is taken simply as

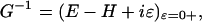[5]

where H is the full-system Hamiltonian. Expanding the conductance and the current around the geometric minimum, one can write the Green's function as

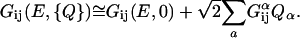[6]

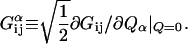[7]

The geometric derivative of Eq. 7 determines the importance of any particular vibrational normal coordinate, Q_α, in the IETS spectrum. In this sense, it is a dimensional coupling constant for the intensities.

One generally expects that a peak would appear in the IETS spectrum when the resonance condition, eV = –hω_α, occurs. The area of this peak, W_α, is

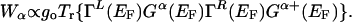[8]

Although this is an attractive formal scheme, its computational implications are difficult: One must deal with calculating the current itself, the structure, the spectral densities Γ, and the full dependence of the Green's functions (including self-energies) on the vibronic normal mode.

Troisi (A. Triosi, personal communication) considered a simplification of the problem that leads to a tractable computation and still provides both good fits to the experiment and substantial experimental insight (A. Troisi and M.A.R., unpublished data). He argues that one can glean a great deal of information about the molecular vibronic direction and its importance in IETS by ignoring, in spirit of weak coupling and perturbation theory, effects arising from the spectral densities, Γ. He then defines a “gateway” orbital, which acts as a bridge between the molecular entity and the electrode itself. These gateway orbitals are labeled λ and ρ (for left and right), and the computational analysis is restricted now in consideration of a molecule, consistent with the molecular bridge terminated by the λ and ρ orbitals.

Often, one expresses the IETS spectrum in the form of the derivative quotient:

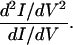which is plotted against voltage V. One then expects that there will be a peak at the resonance condition, eV = –hω_α. The peak intensity will be given by the ratio

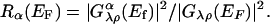[9]

Physically, this perturbative treatment treats the inelastic component as a perturbation of the elastic transport, assuming that the system is very close to equilibrium because the vibrational frequencies are all less 0.2 eV. In addition, the gateway orbital approach says that the vibrational structure on the bridge is, to a reasonable extent, separable from the spectral densities coupling the bridge to the electrodes.

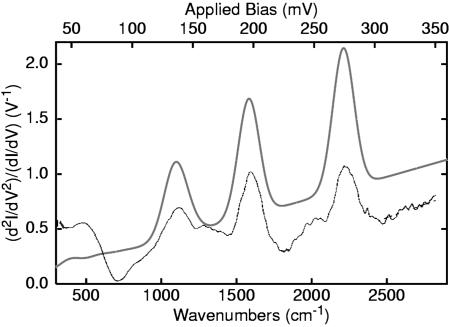
Fig. 5 shows a comparison between the experimental IETS spectrum (71) of the oligophenyleneethynylene molecule and the computation, carried out by using standard density functional theory. The three major bands of the IETS spectrum are very well produced by the simulation: The high-frequency signal near 2,211 cm^–1 is due to the triple bond symmetric stretch; the peak at 1,582 cm^–1 is due to the double bond stretch; and the C/C/C bend, largely localized on the aromatic rings, gives the major contribution to the peak at 1,100 cm^–1. Comparable results are found for other molecules.

Fig. 5.

Calculated (upper line) (A. Troisi, personal communication) and measured (lower line) (71) IETS spectra of an ortho-phenylene ethynylene molecule with a nitro substituent and gold electrodes. The peaks correspond to specific normal coordinates of the molecule.

Because no symmetry principles were involved in this calculation, propensity behaviors (numerical selection rules) are seen in the spectrum. The totally symmetric representation peaks dominate. Moreover, the coupling constants characterized in Eq. 7 index the IETS behavior very well. The appearance of peaks in the IETS spectrum, at the normal coordinates corresponding to the fully symmetric vibrations of the molecule, is strong evidence that the transport actually occurs through the molecule.

Although the simple perturbative model developed in Eqs. 4-9 provides a good general description, there are many more specific and challenging issues, for which the simple perturbative analysis may not be adequate. The first of these involves the actual line shapes for the vibronic features in the spectrum. This is a complicated problem, requiring self-consistent solutions of the self-energies for the vibrational and the electronic Green's functions (72–75). Although these line shapes provide important mechanistic insights, this analysis is outside our scope here. Significant effects occur when the vibronic coupling becomes truly strong, and the next two sections discuss the mechanistic transition from coherent tunneling to hopping behavior, and the implications of such strong coupling in determining important, unusual spectral features, such as negative differential resistance (NDR) and hysteretic/switching transport behaviors.

Mechanistic transition: Tunneling to hopping. For short molecule-transport structures, particularly those without conjugation, the Landauer–Buttiker argument of Eq. 3 suggests very weak vibronic coupling and elastic transport. This sense of the Landauer formula follows from a general non-equilibrium Green's function approach if only electronic terms are considered in the Hamiltonian. For longer bridges and smaller gaps, the vibronic coupling should become more important.

In scanning tunneling microscope measurements, pioneering work by Ho's group (76–78) has indeed shown, for a molecule on a semiconductor surface, that an entire vibrational progression can be seen in the IETS spectrum. This behavior could be analyzed by using a variant of the self-consistent Born approximation, even when the coupling can become strong, allowing more than one vibrational quantum to be involved in the inelastic current (79).

Perhaps the most striking predicted behavior is a change in the mechanism from tunneling at low temperatures and short bridges to a hopping-type (incoherent) motion for long wires and small injection barriers (39, 70). In molecular junctions, as in intramolecular ET reactions, one actually expects a mixture of two mechanisms: In the first mechanism, electrons simply tunnel across the barrier through the intervening states; as temperature increases, however, activated-type processes in which the electron is thermally excited to a higher level, thus reducing the possible tunneling distance, can become relevant (70, 80). For high fields, long wires and small injection gaps a fully activated process can occur.

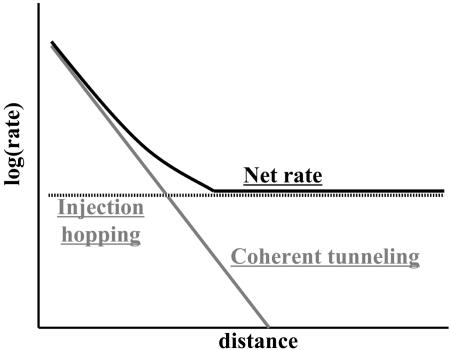
As discussed in Decoherence, the quantum ET events occurring at low temperatures lead to an exponentially decreasing current as a function of the interelectrode distance in the tunneling junction (Fig. 2). Upon activation, one expects diffuse hopping along the bridge, so that the length dependence on transport would be very shallow (generally 1/(A + BR), where A and B are constants depending on the particular experiment, and R is the distance between the electrodes) (Fig. 6). The transition from one of these mechanisms to another has been well characterized in situations like intermolecular ET processes in π -electron species and DNA (39, 81, 82). For electron transport in actual wire junctions, we know of no direct observation of the transition indicated in Fig. 6; limiting regimes have clearly been seen, from the pure tunneling behavior (49, 83–86) in small oligoalkanes and phenylene-vinylenes (all of which are tunneling) to actual conductive polymers, which transport charge (at least at high temperatures) essentially by activated mechanisms (59).

Fig. 6.

Schematic expected behavior for intramolecular ET reactions and for conductance as a function of the length of the molecular bridge. The total rate is the sum of injection hopping (incoherent motion), which is weakly distance-dependent, and coherent tunneling, which depends exponentially on distance.

Although these transitions are perhaps the most striking indication of vibronic coupling and its effects in changing ET mechanism in molecular wires and they have been extensively discussed theoretically, direct experimental confirmation is still incomplete. In actual applications, the coherent and incoherent regimes could be quite important: Simply because the transport is incoherent does not necessarily mean that substantial energy is dissipated as heat.

Polarons, NDR, and hysteric/switching behavior in molecular junctions. Vibronic effects in molecular transport junctions have been stressed very recently, both theoretically and experimentally. As indicated above, localization of the electrons can lead to incoherent tunneling processes. Datta and collaborators (87) have very recently extended earlier work concerning the effects of image forces on molecular wire transport.

Suppose that the two interfaces are inequivalent; for example, suppose that the molecule were more strongly coupled to the left A than to the right B electrode in Fig. 2. Then, localized charge on the molecule can get closer to the left electrode, building a greater image-type stabilization there and yielding an asymmetry in the overall self-consistent electrostatic potential. Formally, one can rewrite the Green's function for transport through the molecular wire as

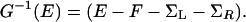[10]

Here, the last two terms are the electronic self-energies arising from interaction between the molecule and the left and right electrodes, whereas F is the Fock operator, representing the self-consistent one-electron Hamiltonian that appears for any given applied field in any given geometry.

One can construct a self-consistent solution to this problem, based on a complete neglect of differential overlap-type semiempirical argument (88). A self-consistent electrostatic potential can be found that depends on the change in electronic density on the bridge. This expression enters the Fock operator and can be in turn represented as

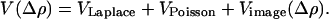[11]

The Poisson part of the equation is approximated by using the complete neglect of differential overlap potential, which contains the charging and the screening effects (ρ is the charge density). Laplace and image potentials are calculated by using a finite element method, with boundary conditions set by the local chemical potentials in the presence of the applied electrostatic potential so that any asymmetry in the potential profile can be included in an explicit fashion in terms of the self-consistent overall potential.

Application of polaron theory for device possibilities in molecular transport junctions, in particular for NDR and switching behavior, has been developed by Galperin and coworkers (89). Their simple model consists of a wire represented by a single site, containing a single electronic state and a single harmonic oscillator. This wire is placed between two electrodes, and the vibration on the molecule is allowed to interact with phonons in the environment (which could be electrodes or a solvent). The Hamiltonian can then be expressed as

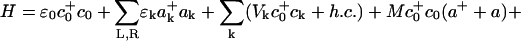[12]

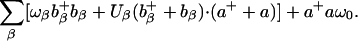Here the terms ε₀, ω₀, ε_k, ω_β are the electronic energy level on the wire, the vibrational frequency on the wire, the electronic state energies in the electrodes, and the vibrational frequency of the phonons, respectively. The coupling constants V_k, U_β, and M are respectively the injection tunneling matrix element between the molecular wire and the bridge, the phonon/vibration interaction, and the vibronic coupling on the molecule. Finally, c₀, a, c_k and b_β are the destruction operators for the bridge electronic state, bridge vibrational state, bulk electronic state, and environmental phonon, respectively. This Hamiltonian is characteristic of linear coupling to form a polaron plus an injection model at the interface.

In the spirit of the Born–Oppenheimer approximation, it is possible to separate the electronic and vibrational parts of the Hamiltonian. The electronic term then reads

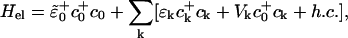[13]

Here, the renormalized site energy 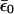depends on the occupation of the site, n₀. The renormalized energy is

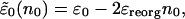[14]

where the reorganization energy is given by

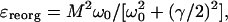[15]

with γ being the phonon lifetime.

In the wide-band limit and at steady state, one can rewrite the occupation on the level in terms of a contour integral over the lesser Green's function in the form

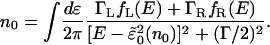[16]

Here f_L and f_R are the Fermi functions on the left and right electrodes, respectively, with the spectral density

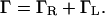[17]

Eq. 17 is the self-consistency condition: The population, n₀, on the bridge determines the polaron shifted energy 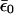, which in turn redetermines n₀. This condition becomes quite straightforward in the limit of T = 0 at equilibrium, μ_R = μ_L. Then the integral can be performed, and the result is

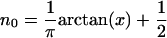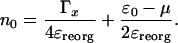[18]

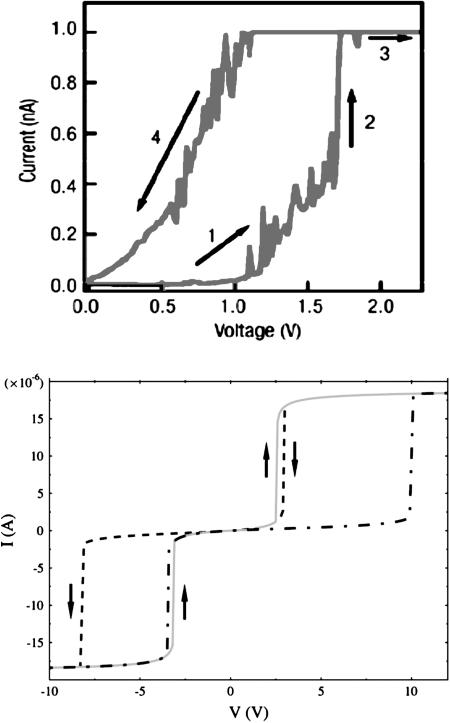
Solving these equations self-consistently yields either one or three roots. When three roots are seen, a typical hysteresis situation occurs, arising from multistability (highly reminiscent of the mean-field treatment of magnetic systems in general). Hysteresis loops might be attainable, as shown in Fig. 7.

Fig. 7.

Computed (Lower) (89) and measured (Upper) (90) hysteretic behavior in the conductance spectrum of a conjugated molecular structure. Note that Right examines only the positive voltage sweep regime.

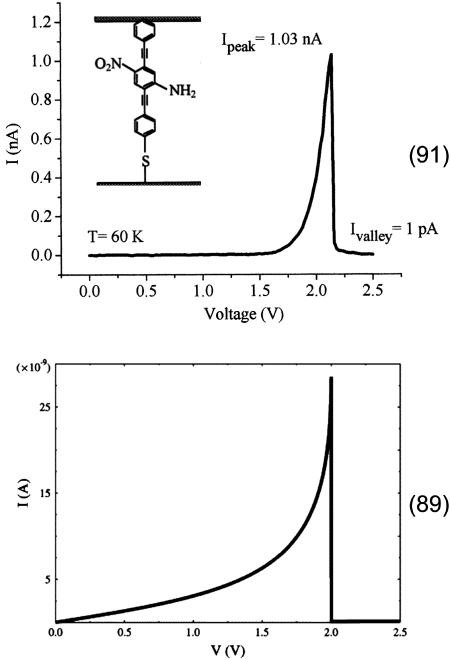
When ε₀ lies in the window between μ_L and μ_R, one would normally expect resonant tunneling to occur. If, however, polaron formation lowers the energy sufficiently by reorganization effects that 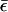drops below the chemical potential of the low-voltage electrode, then the current should abruptly turn off, as is seen in the NDR experiments. Fig. 8 shows such a prediction arising from the mean field model, compared with the experimentally observed structure. Both the temperature dependence and the voltage dependence of the calculated NDR spectrum agree with that reported in the experimental literature.

Fig. 8.

Measured (Upper) (91) and calculated (Lower) (89) negative differential resistance feature in the conductance measurement of the sketched molecule. The model explains the result based on charging of the molecular junction.

In this overview, we have focused on three topics (largely unexplored) of molecular electronics that go beyond simple transport junctions, like the question of improving the efficiency of a tunnel junction as a source of electron prepared in a quantum state superposition, the notion of the superexchange transport junction as a guide for those electrons pointing toward quantum information, and the role of vibronic coupling and inelasticity in the intramolecular events determining the physical characteristics of this guiding. The first and the last of these topics will certainly comprise major foci of the field in the near future.