Charge transport in DNA in solution: The role of polarons

Abstract

Since the discovery a decade ago of rapid photoinduced electron transfer in DNA over a distance >4 nm, a large number of experiments and theories have been advanced in the attempt to characterize the transfer, mainly of a radical cation or hole. Particularly influential experiments were carried out by Giese [Giese, B. (2000) Acc. Chem. Res. 33, 631–636] on the sequence G(A)_nGGG, where G is guanine and A is adenine. These experiments were interpreted as showing that for n > 3, after the holes tunnel through the first three As, they hop onto the bridge of As, where they are localized on a single A and travel further by hopping between neighboring As. Recent experiments of Barton and coworkers [Shao, F., O'Neill, M. A. & Barton, J. K. (2004) Proc. Natl. Acad. Sci. USA 101, 17914–17919] have, however, established that the hole wavefunctions are delocalized. One of the mechanisms based on delocalized hole wavefunctions that had been investigated, both experimentally and theoretically, is transport by polarons. For one type of polaron, the properties are determined by polarization of the surrounding medium (water and ions, in this case). Theory predicts that this type of polaron is delocalized over approximately four bases in DNA. Transport by these polarons could explain the results of Giese et al. [Giese, B., Amaudrut, J., Köhler, A.-K., Spormann, M. & Wessely, S. (2001) Nature 412, 318–320], recent experimental results of O'Neill and Barton [O'Neill, M. A. & Barton, J. K. (2004) J. Am. Chem. Soc. 126, 11471–11483] concerning the size of the region over which the hole is delocalized, and other experimental observations.

After the early experiments that showed hole transfer in DNA over a distance >4 nm (1), a number of groups showed that holes injected into DNA can travel at least 20 nm (2, 3). A wide variety of experiments and theories was produced to account for the transport. One of the basic questions at issue was whether the hole wavefunctions are localized to a single base or delocalized. An argument for localization was that the thermal motion of the bases was sufficiently strong to, in essence, negate the effect of the π bond overlap between them. Experiments of Giese et al. (4, 5) and many others were interpreted as showing that, in a series of adenines, the holes are localized on a single base and move by hopping between bases. Recently, a critical experiment has established that the holes are delocalized (6), setting up polaron motion as a major contender to explain the charge transfer over series of bases long enough to support a polaron. In what follows, I will first review briefly some of the critical experiments and calculations and then discuss the nature of polarons in DNA and how they can account for the critical experiments and other experimental data.

Some Critical Experiments and Calculations

The experimental technique that has been most used to track the motion of holes in DNA relies on the fact that a pair or triple of guanines (Gs) acts as a hole trap. The resulting G⁺ can react with water, creating a product that, with additional chemical treatment, results in readily detectable cleavage at the G⁺ sites. With this technique, injecting a hole at the left-hand G of the sequence G(A)_nGGG, Giese et al. (4) found that as n increases from 1 to 3, the percentage of holes that could penetrate to the GGG trap decreased from 97% to ≈1%. Because the energy of a hole on A is ≈0.4 eV (1 eV = 1.602 × 10^–19 J) higher than that of a hole on G for isolated A and G in solution, the researchers drew the conclusion that the holes move through the adenines by superexchange tunneling (4, 7). Generalizing this, they suggested that transport in DNA consists of holes tunneling or “hopping” between Gs (4).

Extrapolation from the result of ref. 4 for n = 3 leads to the conclusion that almost no holes should be able to penetrate four or more As. However, data of Schuster (8) and Barton and colleagues (9) showed that the holes could penetrate many more than three As. In further experiments, Giese et al. (5) found that holes could penetrate a large number of As (16 in their experiment) with almost no further attenuation than was found for 3 As. They suggested that after the hole penetrated three As, it was thermally excited onto the bridge of As and, localized to a single A at a time, traveled further by hopping between As (5).

Carrying out calculations to describe the motion of a hole from its injection onto the initial G to its hopping on the A bridge (10, 11), Bixon and Jortner (12) found that they could not account for both the rapid decrease in hole concentration over the first three As and the very gradual decrease beyond four As. They noted that the experimental observations could be accounted for if the back-recombination from A to G could somehow be prevented after n = 3. They suggested that prevention of back-recombination might be accomplished by fast configurational relaxation accompanying the thermally activated hole injection from G⁺ to the (A)_n bridge. Such a gating mechanism, they suggested, might be due to a drastic reduction of the G-A electronic coupling arising from thermal fluctuations after the hole has left G. That suggestion has been explored further by Voityuk et al. (13). They find evidence that the fluctuations facilitate hole transfer from G⁺ to A, but the effect is too small to account for the discrepancy noted in ref. 12.

An important set of experiments carried out recently by Barton and colleagues (6) showed that, contrary to the assumptions of Giese (5), Bixon, and Jortner (10–12) and many others, the wavefunction of a hole is delocalized over a number of bases, which may include cytosines (Cs) and presumably thymines (Ts) as well as Gs and As. The finding of delocalization is significant because a hole on C or T has much higher energy than a hole on G or A. In the experiments, the group used a modified C, N4-cyclopropylcytosine (^CPC), which is a fast hole trap, to at least partially overcome rapid back-charge transfer. The ^CPC, set into a DNA duplex a number of bases away from a photooxidant (e.g., an anthraquinone), showed appreciable oxidative damage on excitation of the photooxidant (4). When the trapping rates of C and G were made comparable by cyclopropyl substitution of both and the two modified bases were neighbors in the same strand, the oxidative damage of the two due to the photooxidant was found to be comparable in magnitude. Thus, the hole wavefunction is delocalized and comparable in magnitude over the two neighboring bases (6). It was concluded that charge transport is not simply a function of the relative energies of isolated bases; instead, it may require orbital mixing among the bases (6).

In another important set of experiments, O'Neill and Barton (14) investigated the distance dependence of charge transfer by using 2-aminopurine (Ap) as a photooxidant. This distance dependence was ascertained by comparing the steady-state fluorescence intensity Φ_G of the sequence Ap*(A)_nG with Φ_I, the steady-state fluorescence intensity of Ap*(A)_nI, where I is inosine, a base that cannot be oxidized by Ap*. The intensities of both sequences depend on the rate of emission and the nonradiative decay rate of Ap*. Φ_G depends also on the rate of quenching of the fluorescence due to charge transfer from Ap* to G. Therefore, the quantity [(Φ_I/Φ_G) – 1] is proportional to the quenching rate due to charge transfer (14). A plot of the measured [ln (Φ_I/Φ_G) – 1] vs. n or vs. the Ap* – G distance (= n× 0.34 nm) shows a steep decrease as n increases from 1 to 3 but then an increase around n = 4. It decreases again beyond n = 4 and has another local maximum at n = 8. Evidently, the quenching rate, and thus the charge transfer rate from Ap* to G, is larger for n = 4 than for n = 3, 5, 6, etc., and is larger for n = 8 than for n = 7, 9, 10, etc. (14). This result was interpreted by O'Neill and Barton (14) as evidence that four or five bases is the size of a region they called a domain, possessing, as a result of thermal fluctuations, at least instantaneously a specific, well-coupled conformation of DNA bases. Charge transfer through DNA was attributed to hopping among such well-stacked domains, called conformationally gated charge transfer (14). It must be noted, however, that if these well-stacked domains are the result of what might be called a lucky series of thermal fluctuations, it is not easy to see why they should all be four or five bases in length or, in fact, any particular length. In a later section, I will propose a reason for charge transfer to be faster to four As than to three, five, or six.

One of the earliest suggestions that a hole forms a polaron was based on experiments of Schuster and colleagues (2). They tracked the motion of holes introduced by ultraviolet irradiation of an anthraquinone (AQ) linked to a DNA duplex containing a number of GG traps. Although the traps were separated by base sequences of different compositions and lengths, the logarithm of the cleavage intensity at each trap (proportional to the number of holes reaching the trap) was usually found to vary linearly with the distance of the trap from the hole injection point, the AQ (2, 15). The linear relationship was interpreted as evidence that the hole wavefunction is delocalized over a number of bases, resulting in structural averaging of the DNA. The structural changes invoked included a reduction in interbase distance and a decrease in the twist angle by rotation around the axis of the helix. Despite theoretical treatment based on the same picture of a polaron (16, 17), the idea that hole transport in DNA takes place by polarons had few backers in the community of scientists focused on understanding charge transport in DNA. In the next sections, I reconsider this idea, starting from a different picture of the polaron and invoking the critical experiments outlined in this section.

The Polaron

The term polaron was introduced by the famous physicist Landau in reference to the situation of a charge moving in a polarizable medium. The charge with the accompanying polarization is called a polaron (18), the name being chosen to suggest that the pair act like a particle. The charge may be localized on a single site with the polarization spread around it, the usual situation for a polaron in three dimensions. In a one-dimensional case, the polaron is usually spread over several sites. For an excess charge, electron or hole, on the base stack of DNA, two types of polaron are possible.

One kind of polaron is based on structural distortion; this kind was referred to in the last section. Because the bases are coupled to each other by π overlap, when there is a charge on the base stack, changes in the spacing between bases create polarization and are a source of polaronic behavior. It is well documented for conducting polymers that an excess electron or a hole on a chain always forms such a polaron, extending over a number of monomers. In a calculation for a polaron on the base stack of DNA along the lines of the calculation used for conducting polymers, the important parameters are the wavefunction overlap of adjacent bases (more exactly the transfer integral, t), the rate of change of the overlap with interbase spacing, and an elastic constant. Based on what seem to be reasonable values of these parameters, the size of the polaron varied from four to six bases, depending somewhat on which bases were included (16). Its binding energy was found to vary from 0.3 to 0.03 eV as the average transfer integral t varied from 0.3 to 0.2 eV (16). Because t is probably <0.2 eV, the binding energy is small.

The second type of polaron is due to the polarization by the excess charge of the medium surrounding the DNA, water and ions. A calculation of the size of this type of polaron was carried out using a simple model by Kurnikov et al. (19). For a duplex with one strand consisting of three Gs surrounded by As, they found that the polaron was 1–3 bp in length (19). We calculated the properties of this type of polaron for the case of all bases the same [e.g., As (20)]. A Hamiltonian was set up that included, in addition to the usual term for free motion of the hole (the hopping term), a term for the change in hole energy due to the polarization of the water and ions. The effect of the environment was incorporated by considering the DNA molecule to be placed inside a cavity corresponding to the interior of the double helix, with the water and ions outside. In principle, an ion could be inside the helix, where it would have a strong effect in gating the motion of the hole (15). Experiments of O'Neill and Barton, discussed at length in ref. 14, establish that they did not see such effects due to the ions, implying that the existence of an ion inside the helix is not usual.

To obtain a first approximation for the change in hole energy due to the polarization of the environment, calculations were carried out for a spherical cavity containing just one base pair. This geometry has the advantage that analytical solutions can be obtained for the potentials and electric fields due to the various charges in the problem. The electrostatic Green's function G(r, r′) can be found by solving Poisson's equation inside and outside the cavity. For the latter region, Coulomb repulsion of the like-charged ions causes a correlation in their positions, resulting in a screening of their fields with a characteristic decay length 1/κ_D, where

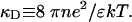Here, n is the ion density, e is the charge on the electron, ε is the dielectric constant of the medium, k is the Boltzmann constant, and T is the absolute temperature. Solving Poisson's equation for the space inside and outside the cavity and incorporating the usual boundary conditions led to the potential inside the sphere differing from that in the absence of water and ions by

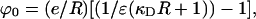where R is taken to be the radius of the helix and ε = 78. For a 1 M solution of Na⁺ ions, κ_D = 0.1/Å and κ_DR = 1. It can be seen that for such large ε, the first term in the square brackets is negligible whatever the value of κ_D. Thus, the effect of the ions drops out because of the high dielectric constant of water. It is apparent that the effect of the ions can be neglected whatever the shape of the cavity.

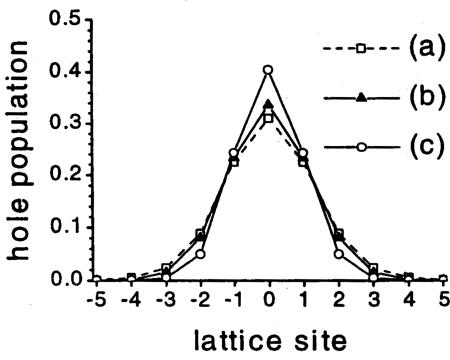
Dropping out the effect of the ions, we then calculated the effect of the surrounding water for a cylindrical cavity, obviously a better approximation for DNA. We assumed that the bases are lined up along the axis of the cylinder, with the distance between them given by the value for B-DNA, 3.4 Å. The potential in the interior of the helix was then found by solving Laplace's equation with appropriate boundary conditions. The only parameters involved in the solution are the dielectric constant of water, the diameter of the helix, and the transfer integral t_0. The result was insensitive to the value of the transfer integral, which was varied from 0.1 to 0.3 eV. The resulting probability distribution, |ψ_n|², for the hole is shown as curve b in Fig. 1. For comparison, also shown is curve a, which is the population profile for a polaron due to changes in base spacing, with t₀ = 0.2 eV and the other parameters chosen as in ref. 20, and curve c, the profile for a polaron in water and having distortion due to changes in base spacing in addition.

Fig. 1.

Hole population ψ ² vs. base position for a stationary state formed by interaction with base-spacing distortion only (curve a), environment only (curve b), or both (curve c). [Reproduced with permission from ref. 20 (Copyright 2002, American Physical Society).]

It is seen that the polaron is essentially contained in four sites, although it would be larger in curve a for a smaller value of t₀, which would agree better with recently calculated values for the transfer integral (21–23). Most significant are the calculated binding energies. For the polaron in water without distortion, for t₀ = 0.1 eV, the binding energy is 0.56 eV. For the polaron due to changes in base spacing only, the binding energy was found to be 0.057 eV, and it might be smaller with more accurate values of the parameters. For the polaron in water, with base-spacing distortion in addition, the binding energy is 0.62 eV. It is possible that the polaron in water will be subject to other structural changes that could increase the binding energy. Based on these numbers, I judge that it would be a good approximation to neglect the distortion due to changes in base spacing in calculations for the polaron in water. The numbers given here were obtained for a polaron on a series of As, but I believe the effect of base-spacing distortion will be small compared with that of water for any sequence.

It seems that a hole polaron including guanines surrounded by other bases could be somewhat smaller, as was found in ref. 19, because the Gs provide a deeper well. The other properties that depend on sequence are the transfer integral and the difference in hole energy between neighboring bases. The transfer integral has, for simplicity, been assumed to have the same value t₀ for any pair of adjacent sites, which is, of course, not correct. However, although the transfer integral was found to have a considerable effect on the length of the polaron due to chain distortion (16), it did not have a big effect for the polaron due to water. As was noted above, change in the transfer integral from 0.1 to 0.3 eV had little effect on the properties of the polaron due to water. It is expected that calculations for the properties of polarons in water with sequences other than all As will not find major differences in length due to the different sequences. The quantity that is expected to vary a great deal with sequence is the hopping rate, to which I will return subsequently.

One last point to be made here is that, with a binding energy of >0.5 eV, the polaron in water is a robust particle. Molecular dynamics calculations, which show the structure of DNA greatly altered in very short times, are usually done for a situation with no charge present, and thus no polarization, and may be misleading.

Motion of Polarons

Polaron motion is expected to take place in two ways: by drift and by hopping. Drift motion can take place in a series of like bases, such as an (A)_n sequence with n ≥ 4. We have carried out simulations of the drift motion for polarons arising from base-spacing distortion in DNA (17). The motion resulted from either a small applied electric field or from giving each base a small amount of energy in the simulation. The shape of the polaron was chosen to be that of curve a in Fig. 1 and did not change in the motion. For an (A)_n polaron with n ≥ 4, the motion was found to take place by the polaron wavefunction moving one base ahead in the direction of motion and simultaneously dropping the last base. The same behavior had been seen in simulations of polaron motion in conducting polymers. The simulation for the base spacing-distorted polaron gave the result that for a constant applied field of 5.8 × 10³ V/cm, the polaron moved seven bases, or 2.4 nm, in 138 ps (17), corresponding to an average velocity of 2 × 10³ cm/s. Although simulations have not yet been carried out for polarons in DNA due to water, it is expected that their drift motion will have similar properties, the only significant difference being the drag due to the water slowing down the drift motion (20).

A number of experiments have been carried out by Kawai et al. (24) and Takada et al. (25) to study the kinetics of hole motion along a series of As. Typically, the source of the hole was an acceptor molecule with an excited state having high enough reduction potential to ionize A. The acceptor was conjugated to a DNA that provided a series of As following the acceptor. After excitation by a laser flash, the formation and decay of the acceptor-excited state were monitored by observing its transient absorption. Charge separation was found to occur very rapidly (24). In one set of experiments, where there were four to eight As between the acceptor and a donor molecule, the number of holes arriving at the donor decreased only slightly as the number of As increased, essentially as had been found in the experiments of Giese et al. (5). From the yield measured at the donor, under the assumption that the holes hopped between adjacent As, it was determined that the rate constant for A hopping is 2 × 10¹⁰ s^–1 (25). With 0.34 nm covered in each hop, the rate constant translates into a velocity of 6.8 × 10² cm/s, not far from what was calculated above for the average velocity of the base spacing-distorted polaron in the electric field.

In another set of experiments, the dependence of the transfer rate k of the photoinduced holes on the number n of As traversed was studied. For a carrier executing a one-dimensional random walk with n steps of equal length, it has been shown that k has a weak dependence on distance, specifically (7)

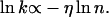[1]

If there is no bias, theory shows that η = 2. For a bias that attracts the hole to the later steps (e.g., the potential well of a GGG trap), theory predicts η < 2. In studies of propagation of photoinduced holes through a set of samples with n = 1–5, Kawai et al. (24) found that the resulting ln k vs. ln n could be fitted to a straight line with a slope of 1.5 (24). Takada et al. (25) described similar measurements for a set of samples with n = 5–8. They also found a linear relation between ln k and ln n, in their case with a slope of 1.7, and also attributed it to localized hole hopping between adjacent As.

Consider what the plot of ln k vs. ln n should be. For n = 1–3, the propagating entity should be a hole isolated to a single base and hopping between bases, and Eq. 1 should clearly be valid. For n = 4 and beyond, when the polaron is formed, the polaron motion should also be a random walk in one dimension and, as discussed earlier, the change in position for each step should be a single A. Thus, Eq. 1 should still apply, although the slope of ln k vs. ln n should be different from that for hopping by localized holes. The results of Takada et al. (25) are consistent with these ideas. For the Kawai et al. (24) results to fit, there should be a different slope after n = 4. The experimental points of the Kawai et al. (24) work are somewhat scattered, and there is not a clear change of slope at n = 4. It is noteworthy that the slopes reported in refs. 24 and 25 are different and that the values of η are in both cases <2, indicating that there is an electric field operative, although certainly not a uniform one. Further experiments of this kind on samples with n = 1–8 would be useful.

Significance of the Critical Experiments

We return to the problem of transport in the sequence G(A)_nGGG. For n = 1, 2, or 3, the fraction of holes injected from the G at the left that arrive at the GGG trap decreases by about a factor of 8 for each additional A (4, 5). This decrease has been seen as the result of back-recombination and superexchange tunneling (4, 7). The apparent change in mechanism at n = 4, characterized by little further attenuation as n increases from 3 to 4 and beyond, can be attributed to the formation of the polaron characteristic of a series of As in water. I suggest that, because of the lowering of the hole energy in the polaron, the initial G is no longer an effective hole trap. I noted earlier that the binding energy calculated for the polaron due to water is 0.5 eV (i.e., the energy level of the hole in the polaron lies 0.5 eV below the energy level of the hole on a single A on the bridge). For an isolated G in water, the hole energy has been measured as being 0.4 eV lower than the hole energy on an isolated A in water (26, 27). If that were still the case for G and A on a DNA chain, the energy of a hole on the polaron would be 0.1 eV lower than its energy on G. If the energy difference between a hole on G and one on A in the DNA chain were only 0.2 eV, as suggested by our calculations (28, 29) and by Bixon and Jortner (10, 11), the energy of the hole on the polaron would be 0.3 eV lower than that on G. In either case, the initial G could no longer compete with the polaron for the hole.

Because a hole on GGG is lower in energy than a hole on G by 0.077 eV (30), if the energy difference between a hole on G and a hole on A were 0.4 eV, the energy of a hole on GGG would still be approximately kT higher than its energy on the polaron. If the energy difference were only 0.2 eV, the energy of the hole on GGG would be ≈0.2 eV higher than on the polaron. In either case, the size of environmental fluctuations found by Voityuk et al. (13), with the standard deviations of the G value being ≈0.3–0.4 eV (13), is large enough to allow holes to transfer from the polaron to GGG, where they could interact with water, etc. Of course, fluctuations of this magnitude could result in some holes going from the polaron into the G trap. However, the exponential dependence of the probabilities on the ratio of the energy difference to kT makes the probability of the holes ending up in the GGG trap very much larger.

For the sequence Ap(A)_nG studied by O'Neill and Barton (14), charge transfer is initiated by the creation of Ap*, which is capable of oxidizing A or G. Thus, superexchange tunneling and exergonic hopping onto the bridge of As need not be invoked (14). Experiments such as those described earlier, where the steady-state fluorescence intensity of Ap*(A)_nG was compared with that of Ap*(A)_nI, demonstrate that charge injection into DNA from a photooxidant is sensitive to distant bases (n ≤ 10) (14). This fact was cited in ref. 14 as evidence for domains, described as extended π orbitals formed by thermally induced coherent base motions, vs. polarons on the grounds that “a polaron forms only in response to the charge after it is injected.” In the case of conducting polymers, it was anticipated that a carrier enters the polymer (in this case from a metal contact) as a polaron when the appropriate chain configuration is prepared by fluctuations, rather than going into the free conduction or valence band with subsequent formation of the polaron (31, 32). It was later shown by a theoretical calculation that injection into a fluctuation-prepared polaron state is the more probable process; the polaron state has lower energy than the band edge (33). This injection is another example of conformationally gated charge transfer. It should also be true for DNA for n ≥ 4, permitting a polaron state to be formed, that the polaron state is formed by injection of the carrier into a fluctuation-prepared state. This fact, plus the fact that the domains deduced by O'Neill and Barton (14) from the distance dependence of the rate of quenching are delocalized over approximately four sites, as is the polaron due to interaction of DNA with water, indicates that the domains should be identified as polarons. The one difference between the properties of a polaron and those cited for domains is that the latter are supposed to exist in the absence of a charge. It is not clear how this property of domains could be proved; nor is it clear that it is necessary to explain charge hopping, as will be discussed further below.

The fact, seen in Fig. 7 of ref. 14, that the quenching rate has a peak at n = 4 can be seen to be the result of conformationally gated charge transfer. When n equals the number of As in the polaron, there is only one possible position for the center of the polaron created by the hole jumping from Ap* onto the stack. When n increases by unity, there are two possible positions for the center: the same position as was taken for the n = 4 case and the position one A farther from Ap*. The fluctuations that favor these two sites must compete, and it is expected that it takes longer for one of them to build up sufficiently to gate the hole. Thus, the quenching rate for Ap* is smaller for n = 5 than for n = 4, as seen in Fig. 7 of ref. 14. Similar arguments can be made for the peaks at n = 6 and n = 7 to be smaller than that at n = 4. The fact that there is a second peak in Fig. 7 of ref. 14 four sites farther from Ap*, at n = 8, suggests that after the hole becomes a polaron on site 4, it can hop to the more distant site.

A great deal of informative data on charge transfer of holes has been published by Schuster and colleagues (2, 8, 15). Although they maintained that they were observing transport of polarons arising from base-spacing distortion, while the polarons were undoubtedly at least mainly due to the interaction with water, this fact in no way taints their data. Recently, they obtained some interesting results on DNA with periodic sequences (A_nGG)_m on one strand and the complementary sequence on the other strand of the duplex (34). Periodic sequences are expected to produce the highest hopping rates because the matrix element for hopping depends on how well the wavefunction in the hopped-to state matches that in the original state. The holes were introduced through the photooxidant anthraquinone at the head of the strand. Because the sequences were all mixtures of different bases, all of the transport observed was by hopping, characterized by Schuster and colleagues (2, 8, 15) as phonon-assisted hopping, rather than drift. In our calculations for base spacing-distorted polarons on sequences with a GG within a series of As, we found the polaron to essentially occupy four sites, as AGGA, with the wavefunction much larger on the Gs than on the As (28, 29). It is expected that the wavefunction of the polaron would be essentially the same when it is due to water. In their recent investigations, Schuster and colleagues (34) found that the fastest hopping occurred in the sequence [(A)₂GG]_m, where, apart from an initial A, the sequence, rewritten, is (AGGA)₆. This finding is analogous to the situation found by O'Neill and Barton (14) where the fastest transport was found for (AAAA) repeated. When additional As were added between the (AGGA)s, the hopping was found to be slower (34), also analogous to what was found for the all-A sequences in ref. 14. The reason for the slower hopping seen with additional As between AGGA sequences could be the same as that advanced above for the slowing effect of additional As between AAAA sequences. Much less is understood about hopping involving other sequences (e.g., the finding that hopping between sequences involving Ts is slower, in general, than between those involving As). A clear example is Schuster and coworkers' (34) finding that hopping between TGGTs is slower than hopping between AGGAs. A possible explanation, open to experiment, is that the hole wavefunction is partly on the A complementary to T because it has much lower energy there.

In the final analysis, what is the difference between conformationally gated charge transport and phonon-assisted hopping? In the words of ref. 14, conformationally gated charge transport requires “thermally induced coherent base motions” to set up “charge-transfer active conformations that allow the charge to hop among domains.” Thermally induced coherent base motions could be called phonons or superpositions of phonons. The statement from ref. 14 could just as well describe “phonon-assisted polaron hopping” if “hopping among domains” were replaced by “polaron hopping” in view of the identity of “domain” (as used in ref. 14) and “polaron.”

In conclusion, it appears that hole transport in DNA through regions of approximately four or more As, and, in some cases, regions of such length including Gs as well as As, takes place through polarons. The polarons can move by drifting when all of the bases are the same or by hopping. It is very likely that transport of excess electrons in DNA in solution takes place through polarons also. For a single duplex DNA strand in air or vacuum, it is unlikely that polarons are involved in transport because, without water, the environment of the bases is not very polarizable. However, the situation for a “rope” consisting of many duplexes may be different because of the polarizability of the DNA itself, as well as the incorporation of water into the rope.