Solitary wave solutions and sensitivity analysis to the space-time β-fractional Pochhammer–Chree equation in elastic medium

Abstract

Solitary wave solutions to the nonlinear evolution equations have recently attracted widespread interest in engineering and physical sciences. In this work, we investigate the fractional generalised nonlinear Pochhammer–Chree equation under the power-law of nonlinearity with order m. This equation is used to describe longitudinal deformation wave propagation in an elastic rod. In this study, we have secured a variety of exact solitary wave solutions by the assistance of the recently developed technique known as modified generalized exponential rational function method. Exact solutions of various categories, such as bright-dark, bright, mixed, singular, dark, complex, and combined solitons, are extracted. The applied approach is highly efficient and has a significant computational capability to efficiently tackle the solutions with a high degree of accuracy in nonlinear systems. To analyze the governing system, the equation under investigation is converted to an ordinary differential equation through the application of a suitable wave transformation with a \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\beta$$\end{document}-derivative. In addition to illustrate the behavior of the solution at various parameter values, we generate 2D and 3D graphs that incorporate pertinent parameters. Moreover, the Galilean transformation is employed to investigate the sensitivity analysis. This research’s results have the potential to enhance comprehension of the nonlinear dynamic characteristics displayed by the defined system and to verify the efficacy of the strategies that have been implemented. The results obtained are a substantial contribution to the comprehension of nonlinear science and nonlinear wave fields that are associated with higher dimensions.

Introduction

Nonlinear partial differential equations (NLPDEs) have a considerable influence on the study of nonlinear physical sciences. These equations are often used to elucidate many intricate natural phenomena. NLPDEs are mainly used to characterize the behaviors of waves in the form of solitons and solitary waves. As a result, the investigation of nonlinear waves plays a substantial role in our daily lives and in a variety of research fields, including hydrodynamics¹, fluid dynamics and mechanics², earth science³, solid-state physics⁴, water waves⁵, chaos theory⁶, quantum mechanics⁷, and many others. These expanded models encouraged a multitude of potential research projects and significantly elucidated the physical properties of engineering and physics applications. Consequently, the study of NLPDEs has consistently attracted considerable interest in recent years. Nonlinear differential equations represent various scientific experimental models. To comprehend the intrinsic characteristics of the nonlinear model, analytical and accurate solutions to the models are essential. It is necessary to investigate the solutions and characteristics of NLPDEs in order to understand the structure they represent. Researchers have developed a number of efficient methods using symbolic computations to ensure the accuracy of soliton solutions to NLPDEs. Numerous problem-solving methods have their own advantages and requirements when used in management models. NLPDEs are now widely recognized as the most comprehensive way for defining the physical significance of nonlinear scenarios occurring in the fields of science and engineering.

Numerous studies have demonstrated the characteristics of soliton solutions and their applications in various scientific and technological domains. Soliton theory is a significant field of research in the fields of applied mathematics and mathematical physics. Solitons are wave bundles that are self-sustaining and maintain their shape while traveling at a constant speed, as defined by mathematics and physics. There are numerous varieties of solitons, including dark, bright, peakons, anti-kink, kink, temporal, spatiotemporal, spatial, and singular. There have been numerous investigations that have demonstrated the diverse characteristics of soliton solutions and their applications in scientific and technological fields⁸. Numerous disciplines, such as fluid dynamics, plasma physics, nonlinear optics, coastal engineering, and communications engineering, have significant uses for soliton solutions. They are essential for the advancement of global communication. Advanced analytical and numerical strategies have been devised by mathematicians to ascertain the soliton solutions of various NLPDEs. Soliton waves are gaining significance in a variety of fields, such as nonlinear optics, optical fibers, and ferromagnetic materials. This multidisciplinary approach, which integrates mathematics, computer science, and physics, demonstrates the dynamic nature of scientific research when it is applied to real-world issues. By acquiring a more thorough comprehension of soliton waves, researchers may make progress in these fields and investigate novel applications.

Exact solutions are of significant importance in the investigation of physical behaviors in a variety of physical systems, as they provide a foundation for subsequent research and investigations. Characterizing the behaviors of any physical system as an ordinary differential equation (ODE) or PDE is the only feasible way of obtaining an exact solution. The preponderance of natural or industrial complex phenomena can be modeled using NLPDEs or FNLPDEs. In order to achieve analytic solutions to these issues, different methodologies and strategies have been developed by a number of academicians, such that, truncated Painlevé approach⁹, Master stability function¹⁰, improved F-expansion function method¹¹, Lie symmetry technique¹², simplest equation technique¹³, networking of higher of higher order systems¹⁴, iterative transform method¹⁵, Intelligent Detection Method¹⁶, Hirota bilinear method¹⁷, Lie classical approach¹², Adomian decomposition technique¹⁸, bifurcation analysis¹⁹, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$tan\left( \frac{\phi }{2}\right)$$\end{document} technique²⁰, multiple exp-function approach²¹, Bernoulli \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\frac{G^{\prime }}{G}$$\end{document}-expansion method²², generalized exponential rational function method²³, tanh-coth method²⁴, the inverse scattering method²⁵, the Backlund transformation²⁶, logarithmic transformation²⁷ and some other analytic methods^28–33.

Consequently, the model in concern has not been investigated using the proposed methodology, despite a comprehensive examination of the existing literature. Therefore, the current study aims to make use of this analytical methodology to clarify the complex dynamics that are inherent in the generalized nonlinear Pochhammer–Chree (PC) equation. Pochhammer³⁴ and Chree³⁵ simultaneously deduced the equation of motion in cylindrical coordinates to characterize the propagation of a sinusoidal wave with frequency f through an infinitely long homogeneous, isotropic cylinder with a uniform cross-section. Inspired by the work of Pochhammer and Chree, a frequency equation was formulated and introduced by Love³⁶ and numerical solution presented by Bancroft³⁷. This study aims to improve the understanding of these intricacies and contribute to advances in the field of analysis of complex phenomena by implementing the proposed method. Here, our main goal is to study various soliton solutions of the fractional PC equation by applying an integration method called the modified generalized exponential rational function method (mGERFM)³⁸. Furthermore, the applied method is well suited for nonlinear complex models, as it enable obtaining results in a simple and straightforward manner and is capable of generating a variety of new results and providing guidance for organizing them.

The article is structured as follows: Section “Fractional order derivative” covers the fundamental definitions and some of the most significant properties of fractional derivative. Section “The governing equation” provides the governing generalized nonlinear PC equation, while Section “Extraction of solutions for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$m=1$$\end{document}” presents the computation of numerous soliton solutions employing the suggested technique mGERFM with various graphs. Section “Sensitivity analysis” provides sensitivity analysis, while Section “Discussion and concluding remarks” offers the concluding remarks.

Fractional order derivative

Fractional differential equation are equations where the derivatives have fractional orders instead of integer orders. Soliton’s theory presents a multitude of fractional, nonlinear challenges. Researchers use fractional calculus and the development of innovative operators, such as Atangana Baleanu derivative³⁹, Riemann-Liouville derivative⁴⁰, and Caputo derivative⁴¹, to solve some of the most important contemporary problems. The fractional models exhibit superior precision and accuracy in comparison to their integer-order counterparts, closely matching the experimental data. The fractional form facilitates the implementation of sophisticated optimization and control strategies that enhance the overall performance of a system. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\beta$$\end{document}-derivative has been applied by researchers, providing a more precise understanding of the behavior of solitary waves in nonlinear systems⁴². Fractional derivative is advantageous for the comprehension and analysis of a diverse array of various nonlinear systems⁴³.

Definition 1

Suppose that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\kappa (t): [c,\infty )\rightarrow {\mathbb {R}}$$\end{document}, then the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\beta$$\end{document}-derivative⁴⁴ of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\kappa$$\end{document} is given as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr{D}}_{t}^{\beta } \left\{ {\kappa \left( t \right)} \right\} = \mathop {\lim }\limits_{{\epsilon \rightarrow 0}} \frac{{\kappa \left( {t + \epsilon \left( {t + \frac{1}{{\Gamma \left( \beta \right)}}} \right)} \right)}}{\epsilon },\;\;\;\beta \in \left( {0,1} \right]$$\end{document} 1

Theorem 1

⁴⁴ Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\kappa$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$h\ne 0$$\end{document} are two \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\beta$$\end{document}-differentiable functions such that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$0<\beta \le 1$$\end{document}. Then:

1. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr {D}}_{t}^{\beta }\left( c\{\kappa (t)\}+d\{ h(t)\}\right) =c{\mathscr {D}}_{t}^{\beta }\{\kappa (t)\}+d{\mathscr {D}}_{t}^{\beta }\{h(t)\},~\text { for all } c,~d\in {\mathbb {R}}$$\end{document}.

2. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr {D}}_{t}^{\beta }\left( \{\kappa (t)\}\times \{h(t)\}\right) = \{h(t)\}{\mathscr {D}}_{t}^{\beta }\left( \{\kappa (t)\}\right) +\{\kappa (t)\}{\mathscr {D}}_{t}^{\beta }\left( \{h(t)\}\right)$$\end{document}.

3. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr {D}}_{t}^{\beta }\left( \frac{\{\kappa (t)\}}{\{h(t)\}}\right) =\frac{\{h(t)\}{\mathscr {D}}_{t}^{\beta }\{\kappa (t)\}-\{\kappa (t)\}{\mathscr {D}}_{t}^{\beta }\{h(t)\}}{\left( \{h(t)\}\right) ^2}$$\end{document}.

4. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr {D}}_{t}^{\beta }\{\kappa (t)\}=\frac{d\{\kappa (t)\}}{dt}\left( t+\frac{1}{\Gamma (\beta )}\right) ^{1-\beta }$$\end{document}.

5. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\mathscr {D}}_{t}^{\beta }\{c(t)\}=0, ~~ {where }$$\end{document} c(t) is a constant

The governing equation

Integral systems are indispensable for the analysis of various types of nonlinear equations due to their applicability across a wide range of scientific disciplines. These systems are highly applicable in the fields of nanophysics and applied magnetism, as well as possessing remarkable geometric and gauge invariance properties. Among many integrable system, the generalized nonlinear fractional PC equation^45–48 read as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} {\mathscr {D}}_{tt}^{2\beta }u-{\mathscr {D}}_{ttxx}^{4\beta }u-{\mathscr {D}}_{xx}^{2\beta }\left( \alpha u+\eta u^{m+1}+\gamma u^{2m+1}\right) =0, \end{aligned}$$\end{document} 2

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$u=u(x, t),$$\end{document} is a real valued function that denotes the displacement field, characterizing the longitudinal wave propagation within elastic rods and the exponent \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$m\ge 1$$\end{document} is the parameter of the power-law nonlinearity and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\alpha ,~ \eta ,~\gamma$$\end{document} are real constants. Additionally, the exact solutions of Eq. (2) are generated through the application of various methods. For instance, in⁴⁵, the authors investigated various types of soliton solutions by employing the analytical technique known as the modified simple equation method. In⁴⁶, the aforementioned model is examined using the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi ^6$$\end{document}-model expansion method. In⁴⁷, the modified extended tanh-function method is employed to extract new exact solutions, while the exp-function method is employed to analyze new solutions of the fractional PC equation in⁴⁸. In the subsequent section, we derive the various solutions of the proposed model.

Extraction of solutions for m = 1

To solve Eq. (2), for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$m=1$$\end{document}, we have

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} {\mathscr {D}}_{tt}^{2\beta }u-{\mathscr {D}}_{ttxx}^{4\beta }u-{\mathscr {D}}_{xx}^{2\beta }\left( \alpha u+\eta u^{2}+\gamma u^{3}\right) =0. \end{aligned}$$\end{document} 3

Subsequently, consider

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u= & u(x,t)=\Phi (\xi ); \end{aligned}$$\end{document} 4

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \xi= & \frac{k}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta }-\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta },~~~ \end{aligned}$$\end{document} 5

where k is a scaler parameter and v is the wave speed. By employing the aforementioned transformations in Eq. (3), we obtain the following:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} -k^2 v^2 \Phi ^{(4)}(\xi )+\Phi {\prime \prime }(\xi ) \left( -\alpha k^2-3 \gamma k^2 \Phi (\xi )^2-2 \eta k^2 \Phi (\xi )+v^2\right) -2 k^2 \Phi {\prime }(\xi )^2 (\eta +3 \gamma \Phi (\xi ))=0. \end{aligned}$$\end{document} 6

Furthermore, we get the nonlinear ordinary differential equation (ODE) as follows by integrating Eq. (6) twice and setting the integration constant to zero:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} -k^2 v^2 \Phi {\prime \prime }(\xi )-\gamma k^2 \Phi (\xi )^3-\eta k^2 \Phi (\xi )^2+ \left( v^2-\alpha k^2\right) \Phi (\xi )=0. \end{aligned}$$\end{document} 7

Moreover, the suggested method is applied to analyze the Eq. (7). Using the balance principle between the terms \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi {\prime \prime }(\xi )$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi ^3(\xi )$$\end{document} in Eq. (7), \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$n=1$$\end{document} is achieved.

Application of the method

The applied method is versatile approach applicable to a wide range of nonlinear differential equations of different types. The mGERFM³⁸ solution is given as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \begin{aligned} \Phi (\xi )=d_0+\sum _{r=1}^{n}d_{r}\Bigg (\frac{\Omega '(\xi )}{\Omega (\xi )}\Bigg )^{r}+\sum _{r=1}^{n}f_{r}\Bigg (\frac{\Omega '(\xi )}{\Omega (\xi )}\Bigg )^{-r}, \end{aligned} \end{aligned}$$\end{document} 8

where

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \Omega (\xi )=\frac{r_1 e^{s_1 \xi }+r_2 e^{s_2 \xi }}{r_3 e^{s_3 \xi }+r_4 e^{s_4 \xi }}. \end{aligned}$$\end{document} 9

In this study, we have taken the few families from the suggested reference and some other families have been selected by considering the appropriate values for r and s, which produce the function \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=\frac{r_1 e^{s_1 \xi }+r_2 e^{s_2 \xi }}{r_3 e^{s_3 \xi }+r_4 e^{s_4 \xi }},$$\end{document} different and therefore the variety of solutions will be extracted. Moreover, Eq. (8) is stated as follows for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$n=1$$\end{document}:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \Phi (\xi )=d_{0}+d_{1}\Bigg (\frac{\Omega '(\xi )}{\Omega (\xi )}\Bigg )+f_{1}\Bigg (\frac{\Omega '(\xi )}{\Omega (\xi )}\Bigg )^{-1}. \end{aligned}$$\end{document} 10

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, 1, 1, 0]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[0, -1, 0, 0]$$\end{document}, in Eq. (9), provides \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=1+e^{-\xi }$$\end{document}, and inserting Eq. (10) in Eq. (7) offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= -\frac{3 \sqrt{2\alpha } k}{\sqrt{\gamma \left( k^2-1\right) }},f_1= -2d_0,d_1= 0,\eta = \frac{d_0}{\sqrt{2} },v= -\frac{\sqrt{\alpha } k}{\sqrt{1-k^2}}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= -\frac{3 \sqrt{2\alpha } k}{\sqrt{\gamma \left( k^2-1\right) }},f_1= 0,~d_1= -3d_0,~\eta = \frac{d_0}{\sqrt{2} },~v= \frac{\sqrt{\alpha } k}{\sqrt{1-k^2}}$$\end{document}, then we get:

The exponential soliton solution

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_1(x, t)=-\frac{3 \sqrt{2\alpha } k \exp \left( \frac{k \left( \frac{\sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{1-k^2}}+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) }{\sqrt{\gamma \left( k^2-1\right) } \left( 3 \exp \left( \frac{k \left( \frac{\sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{1-k^2}}+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) +2\right) }. \end{aligned}$$\end{document} 11

The explicit hyperbolic solution

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_2(x, t)=-\frac{\sqrt{2\alpha } k \left( \cosh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\sinh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) \right) }{\sqrt{\gamma k^2-\gamma } \left( \cosh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\sinh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\cosh \left( \frac{k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) }. \end{aligned}$$\end{document} 12

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Choosing \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[2, 0, 1, 1]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[0, 0, 1, -1]$$\end{document}, in Eq. (9), offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=\text {sech}(\xi )$$\end{document} while incorporating Eqs. (10) and (7) implies that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= \frac{6 \left( k^2+1\right) v^2}{\eta k^2},\gamma = -\frac{\eta ^2 k^2}{18 \left( k^2+1\right) v^2},d_1= -\frac{6 \sqrt{\left( k^2+1\right) v^4}}{\eta k},\alpha = \left( -\frac{5}{k^2}-4\right) v^2,f_1=0$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= \frac{6 \left( 4 k^2+1\right) v^2}{\eta k^2},\gamma =-\frac{\eta ^2 k^2}{18 \left( 4 k^2+1\right) v^2},d_1= \frac{6 \sqrt{\left( 4 k^2+1\right) v^4}}{\eta k},\alpha = \left( -\frac{5}{k^2}-16\right) v^2,f_1= d_1$$\end{document} and the following solutions are expressed as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_3(x, t)=\frac{6 \left( k \sqrt{\left( 4 k^2+1\right) v^4} \left( \coth ^2\left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +1\right) \tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\left( 4 k^2+1\right) v^2\right) }{\eta k^2}, \end{aligned}$$\end{document} 13

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_4(x, t)=\frac{6 \left( 2 k \sqrt{\left( 4 k^2+1\right) v^4} \coth \left( \frac{2 \left( v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) +\left( 4 k^2+1\right) v^2\right) }{\eta k^2}. \end{aligned}$$\end{document} 14

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Suppose \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1,-1,2,0]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[2, 0, 0, 0]$$\end{document}, then the Eq. (9), offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=e^{-2 \xi } \text {sech} (\xi )$$\end{document} and on managing the Eqs. (10) and (7) provide\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= 0,\gamma = -\frac{2 v^2}{d_1^2},\alpha = \left( \frac{1}{k^2}-4\right) v^2,\eta = -3\gamma ,d_0= 3 d_1$$\end{document}, along with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= d_0,\gamma = -\frac{18 v^2}{d_0^2},~\alpha = \left( \frac{1}{k^2}-4\right) v^2,\eta = \frac{18 v^2}{d_0},d_1= 0$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= 3 d_1,\gamma = -\frac{2 v^2}{d_1^2},\alpha = \left( \frac{1}{k^2}+12 \sqrt{7}-28\right) v^2,\eta =-\gamma ,d_0= \left( \sqrt{7}+1\right) d_1$$\end{document} the explicit solitary wave solutions are

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_5(x, t)=d_1 \left( \tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +1\right) , \end{aligned}$$\end{document} 15

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_6(x, t)=\frac{d_0 \left( \tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) -1\right) }{\tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) -2}, \end{aligned}$$\end{document} 16

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_7(x, t)=d_1 \left( \tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\frac{3}{\tanh \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) -2}+\sqrt{7}-1\right) . \end{aligned}$$\end{document} 17

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} On selecting \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, 1, 2, 0]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[i, -i, 0, 0]$$\end{document}, then the Eq. (9), gives \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=\cos (\xi )$$\end{document}, Eqs. (10) and (7) provide \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_1= \frac{d_0}{\sqrt{2}},~f_1= \frac{d_0}{\sqrt{2}},~\eta = \frac{12 v^2}{d_0},~k= \frac{v}{\sqrt{\alpha +8 v^2}},~\gamma = -\frac{4 v^2}{d_0^2}$$\end{document} the soliton solution as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_{8}(x, t)=\frac{d_0 \cot \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{v \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta \sqrt{\alpha +8 v^2}}\right) }{\sqrt{2}}+\frac{d_0 \tan \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{v \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta \sqrt{\alpha +8 v^2}}\right) }{\sqrt{2}}+d_0. \end{aligned}$$\end{document} 18

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, 1, 1, 0]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[3, 2, 0, 0]$$\end{document}, then the Eq. (9), gives \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=e^{2 \xi }+e^{3 \xi }$$\end{document}, Eqs. (10) and (7) provide \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= -\frac{3 \sqrt{2\alpha } k}{\sqrt{\gamma \left( k^2-1\right) }},~f_1= -2d_0,~d_1= 0,~\eta = \frac{3 \sqrt{\alpha } \gamma k}{ \sqrt{2\gamma \left( k^2-1\right) }},~v= -\frac{\sqrt{\alpha } k}{\sqrt{1-k^2}}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= -\frac{3 \sqrt{2\alpha } k}{\sqrt{\gamma \left( k^2-1\right) }},~f_1= 0,~d_1= -3d_0,~\eta = \frac{3 \sqrt{\alpha } \gamma k}{\sqrt{2\gamma \left( k^2-1\right) }},~v= \frac{\sqrt{\alpha } k}{\sqrt{1-k^2}}$$\end{document}, then we have:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_{9}(x, t)= & -\frac{3 \sqrt{2\alpha } k \exp \left( \frac{k \left( \frac{\sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{1-k^2}}+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) }{\sqrt{\gamma \left( k^2-1\right) } \left( 3 \exp \left( \frac{k \left( \frac{\sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{1-k^2}}+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) +2\right) }, \end{aligned}$$\end{document} 19

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_{10}(x, t)= & -\frac{\sqrt{2\alpha } k \left( \cosh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\sinh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) \right) }{\sqrt{\gamma \left( k^2-1\right) } \left( \cosh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\sinh \left( \frac{\sqrt{\alpha } k \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta \sqrt{1-k^2}}\right) +\cosh \left( \frac{k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) }. \end{aligned}$$\end{document} 20

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} On selecting \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, -1, i, i]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[i, -i, 0, 0]$$\end{document}, then the Eq. (9), gives \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=\sin (\xi )$$\end{document}, Eqs. (10) and (7) provide \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\alpha = \left( \frac{1}{k^2}-8\right) v^2,d_1= \frac{d_0}{\sqrt{2}},f_1= \frac{d_0}{\sqrt{2}},\gamma = -\frac{4 v^2}{d_0^2},\eta = \frac{12 v^2}{d_0}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\alpha = \left( \frac{1}{k^2}-8\right) v^2,d_0= -\sqrt{2} f_1,d_1=f_1,~\gamma = -\frac{2 v^2}{f_1^2},\eta = -\frac{6 \sqrt{2} v^2}{f_1}=$$\end{document}, we obtain the solution as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_{11}(x, t)=\frac{1}{2} d_0 \left( \sqrt{2} \left( -\cot \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) -\sqrt{2} \tan \left( \frac{v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +2\right) , \end{aligned}$$\end{document} 21

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_{12}(x, t)=-\left( f_1 \left( 2 \csc \left( \frac{2 \left( v \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-k \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }\right) }{\beta }\right) +\sqrt{2}\right) \right) . \end{aligned}$$\end{document} 22

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Numerical simulation:

See Figs. 1 and 2.

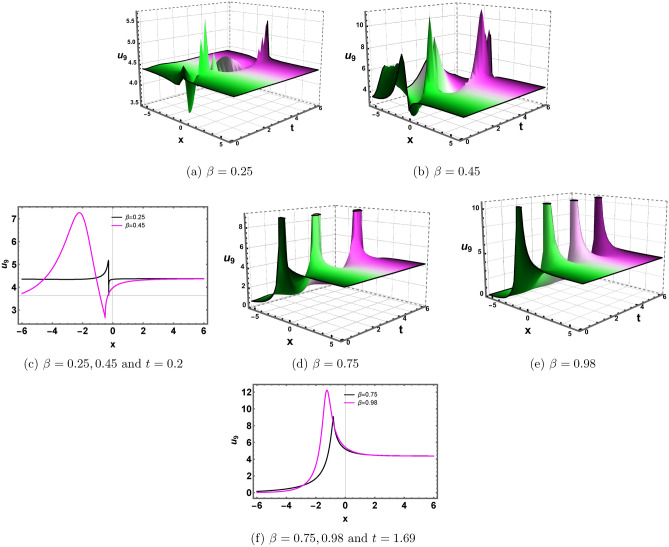
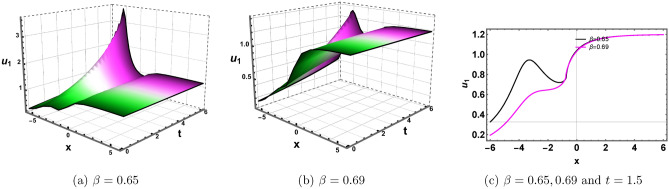
Fig. 1.

Plots of Eq. (19) for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\alpha =2.8, \gamma =1.2, k=1.15$$\end{document}.

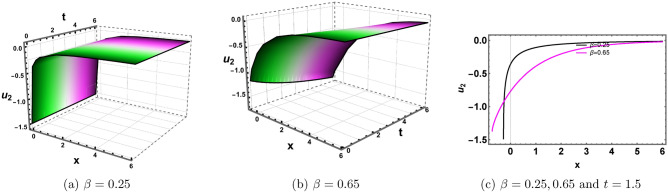
Fig. 2.

Plots of Eq. (20) for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$k=1.2, \alpha =0.01, \gamma =0.2$$\end{document}.

Solutions for m = 2

For \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$m=2$$\end{document}, Eq. (2), read as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} {\mathscr {D}}_{tt}^{2\beta }u-{\mathscr {D}}_{ttxx}^{4\beta }u-{\mathscr {D}}_{xx}^{2\beta }\left( \alpha u+\eta u^{3}+\gamma u^{5}\right) =0. \end{aligned}$$\end{document} 23

Next, we apply the transformation described by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u=u(x,t)=\Phi (\xi ); \end{aligned}$$\end{document} 24

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & \xi =\frac{1}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta }-\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta },~~~ \end{aligned}$$\end{document} 25

where c is the wave speed. Using the above relation in Eq. (23), we acquire:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} c^2\Phi ^{\prime \prime }-c^2\Phi ^{(iv)}-\left( \alpha \Phi +\eta \Phi ^{3}+\gamma \Phi \right) ^{\prime \prime }=0. \end{aligned}$$\end{document} 26

Moreover, the nonlinear ODE is obtained by integrating Eq. (26) twice and setting the integration constant to zero:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \left( c^2-\alpha \right) \Phi -c^2\Phi ^{\prime \prime }-\eta \Phi ^3-\gamma \Phi ^5=0. \end{aligned}$$\end{document} 27

When homogeneous balance principle is applied to the terms \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi ^{\prime \prime }$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi ^5$$\end{document}, the result is \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$n=\frac{1}{2}$$\end{document}, which is not an integer. In order to extract the solitary wave solutions, n must be an integer. Therefore, taking \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi (\xi )=\Psi ^{\frac{1}{2}}(\xi )$$\end{document} in Eq. (27) implies

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} 4\left( c^2-\alpha \right) \Psi ^2-2c^2\Psi \Psi ^{\prime \prime }+c^2\left( \Psi ^{\prime }\right) ^2-4\eta \Psi ^3-4\gamma \Psi ^{4}=0. \end{aligned}$$\end{document} 28

The balance principle between the terms \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Psi \Psi ^{\prime \prime }$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Psi ^4$$\end{document} in Eq. (28) , resulting in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$n=1$$\end{document}. Furthermore, solving Eq. (28) by applying the proposed method and completing the analogous process described in section “Application of the method”, we have the following solutions:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Plugging \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, 1, 1, 0]$$\end{document} along with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[0, -1, 0, 0]$$\end{document}, in Eq. (9), results in \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=1+e^{-\xi }$$\end{document}, and inserting Eq. (10) in Eq. (28) provides\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_1= d_0,~\gamma = -\frac{3 \eta }{4 d_0},~f_1= 0,c=- \sqrt{d_0\eta },~\alpha = \frac{3 d_0 \eta }{4}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_0= 0,~\gamma = -\frac{3 c^2}{4 d_1^2},~\eta =-\frac{c^2}{d_1},~f_1= 0,\alpha = \frac{3 c^2}{4}$$\end{document} then we get:

The exponential soliton solution

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_1(x, t)=\frac{d_0 e^{\frac{\sqrt{d_0 \eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }}}{e^{\frac{\sqrt{d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }+\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }}+1}. \end{aligned}$$\end{document} 29

The explicit hyperbolic solution

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_2(x, t)=-\frac{d_1 \left( \cosh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) }{\cosh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\beta }-\frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +1}. \end{aligned}$$\end{document} 30

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Further, taking \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[2, 0, 1, 1]$$\end{document} with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[0, 0, 1, -1]$$\end{document}, in Eq. (9), gives \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=\text {sech}(\xi )$$\end{document} and incorporating Eqs. (10) and (28) offer \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_1= -\frac{d_0}{2},\gamma = -\frac{3 \eta }{8 d_0},\alpha = -\frac{1}{8} \left( 3 d_0 \eta \right) ,c= \frac{\sqrt{d_0\eta }}{2 \sqrt{2}},f_1= -\frac{d_0}{2}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$d_1= 0,\gamma = -\frac{3 \eta }{8 d_0},\alpha = 0,~c= \frac{\sqrt{d_0\eta }}{\sqrt{2}},~f_1= d_0$$\end{document} then the solutions are as follows:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_3(x, t)=\frac{1}{2} d_0 \Bigg (\coth \left( \frac{4 \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }-\sqrt{2d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{4 \beta }\right) ~~~~~~~~ ~~~~~~~~~~~~~~~~\nonumber \\+\tanh \left( \frac{4 \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }-\sqrt{2 d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{4 \beta }\right) +2\Bigg ), \end{aligned}$$\end{document} 31

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_4(x, t)=d_0 \tanh \left( \frac{\sqrt{d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{2} \beta }+\frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +d_0. \end{aligned}$$\end{document} 32

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, -1, i,i]$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[i, -i, 0, 0]$$\end{document}, in Eq. (9), offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )= \sin (\xi )$$\end{document} and on solving Eqs. (10) and (28) offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\alpha =-\frac{1}{2} \left( d_0 \eta \right) ,~c= -\frac{\sqrt{d_0\eta }}{2 \sqrt{2}},~d_1= -\frac{d_0}{2},~f_1= -\frac{d_0}{2},~\gamma = -\frac{3 \eta }{8 d_0}$$\end{document} then we get:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_5(x, t)=-\frac{1}{2} d_0 \left( \cot \left( \frac{\sqrt{2d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }+4 \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{4 \beta }\right) -1\right) ^2~~~~~~\nonumber \\\left( \tan \left( \frac{\sqrt{2d_0\eta } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }+4 \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{4 \beta }\right) \right) . \end{aligned}$$\end{document} 33

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Suppose \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[2, 0, 1, 1]$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[-2, 0, 1, -1]$$\end{document}, then Eq. (9), provides \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=e^{-2 \xi } sech (\xi )$$\end{document} while Eqs. (10) and (28) offers \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= \frac{12 \left( \sqrt{3}-1\right) c^2}{\eta },~\gamma = -\frac{3 \left( \sqrt{3}+2\right) \eta ^2}{128 c^2},~\alpha = 6 \left( 2 \sqrt{3}-3\right) c^2,~d_0= -\frac{8 \left( \sqrt{3}-3\right) c^2}{\eta },~d_1= \frac{4 \left( \sqrt{3}-1\right) c^2}{\eta }$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= 0,~\gamma = -\frac{3 \eta ^2}{16 c^2},~\alpha = 0,~d_0= -\frac{2 c^2}{\eta },~d_1= -\frac{2 c^2}{\eta }$$\end{document} the solutions as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_6(x, t)=\frac{4 c^2 \left( \left( \sqrt{3}-1\right) \tanh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\frac{3 \left( \sqrt{3}-1\right) }{\tanh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) -2}-4 \sqrt{3}+8\right) }{\eta }, \end{aligned}$$\end{document} 34

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} & u_{7}(x, t)=-\frac{2 c^2 \left( \tanh \left( \frac{c \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) -1\right) }{\eta }. \end{aligned}$$\end{document} 35

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Let \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$r=[1, 1, 1, 0]$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$s=[3, 2, 0, 0]$$\end{document}, then the Eq. (9), gives \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Omega (\xi )=e^{2 \xi }+e^{3 \xi }$$\end{document}, Eqs. (10) and (28) provide \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= -3 d_0,~d_1= 0,~\eta = -\frac{8 \alpha }{3 d_0},~c= \frac{2 \sqrt{\alpha }}{\sqrt{3}},~\gamma = -\frac{4 \alpha }{d_0^2}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$f_1= 0,~d_1= -\frac{d_0}{2},~\eta = -\frac{8 \alpha }{3 d_0},~c= \frac{2 \sqrt{\alpha }}{\sqrt{3}},~\gamma = -\frac{4 \alpha }{d_0^2}$$\end{document}, then we have:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_{8}(x, t)=\frac{1}{2} d_0 \left( \frac{1}{\frac{2}{3} \exp \left( \frac{2 \sqrt{3} \sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }-3 \left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{3 \beta }\right) +1}-1\right) , \end{aligned}$$\end{document} 36

where the hyperbolic solution is written as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} u_{9}(x, t)=-\frac{d_0 \left( \cosh \left( \frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) }{2 \left( \cosh \left( \frac{2 \sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{3} \beta }\right) +\sinh \left( \frac{2 \sqrt{\alpha } \left( \frac{1}{\Gamma (\beta )}+t\right) ^{\beta }}{\sqrt{3} \beta }\right) +\cosh \left( \frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) +\sinh \left( \frac{\left( \frac{1}{\Gamma (\beta )}+x\right) ^{\beta }}{\beta }\right) \right) }. \end{aligned}$$\end{document} 37

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\bullet$$\end{document} Numerical simulation:

See Figs. 3 and 4

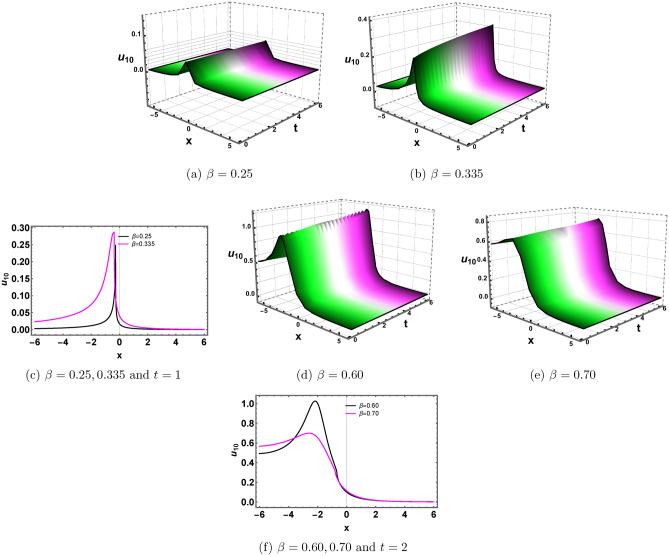
Fig. 3.

Plots of Eq. (29) for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\gamma =-0.03, d_0=1.2$$\end{document}.

Fig. 4.

Plots of Eq. (30) for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$c=0.3, d_1=2$$\end{document}.

Sensitivity analysis

This section explores the sensitivity analysis of the proposed model. Applying the Galilean transformation, Eq. (7) can be reconfigured into two separate systems of equations. Under the assumption that \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\phi ^{\prime }=Q$$\end{document}, Eq. (7) can then be formulated subsequently.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \left. \ \begin{array}{ll} \dfrac{d\Phi }{d\xi }=Q,\\ \\ \dfrac{dQ}{d\xi }=A\Phi (\xi )^{3}+B\Phi (\xi )^{2}+C\Phi (\xi ), \end{array}\right\} \end{aligned}$$\end{document} 38

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$A=\frac{-\gamma }{ v^{2}}, ~B=\frac{-\eta k}{ v^{2}}$$\end{document} and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$C=\frac{v^{2}-\alpha k^{2}}{k^{2} v^{2}}$$\end{document}.

The system (38) is solved using the Runge-Kutta method by applying the suitable parameter values for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$k=1, v=0.7, \eta =0.5, \alpha =0.22, \gamma =0.8$$\end{document}.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textit{Case 01}$$\end{document} Two possible solutions are depicted in Fig. 5: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document} in red (solid line) and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.07)$$\end{document} in navy blue (solid line) .

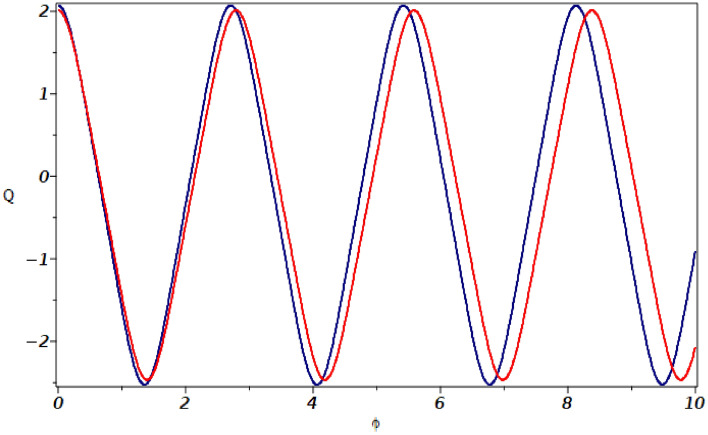
Fig. 5.

Sensitivity analysis of system (38) with initial conditions \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document} in red (solid line) and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(R, \Phi )=(0, 2.07)$$\end{document} in navy blue (solid line).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textit{Case 02}$$\end{document} In Fig. 6\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document} in red and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.1)$$\end{document} in green.

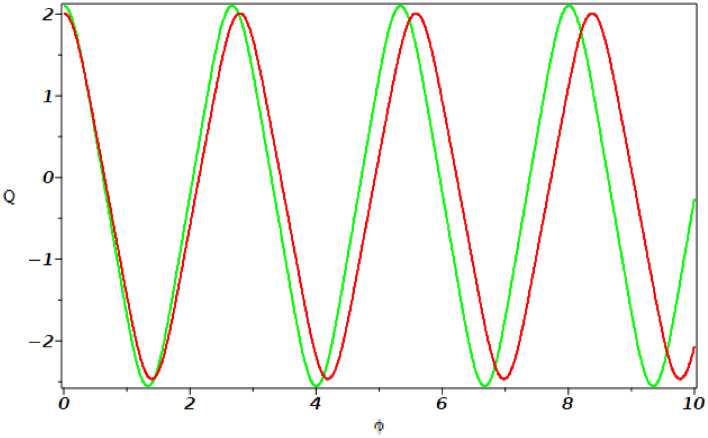
Fig. 6.

Sensitivity analysis of system (38) with initial conditions \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document} in red and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$((Q, \Phi ))=(0, 2.1)$$\end{document} in green.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textit{Case 03}$$\end{document} Similarly, Fig. 7 illustrates two solution curves. First set is characterized by initial values of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.07)$$\end{document} in navy blue (solid line), while second set is characterized by initial values of \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.1)$$\end{document} in green (solid line).

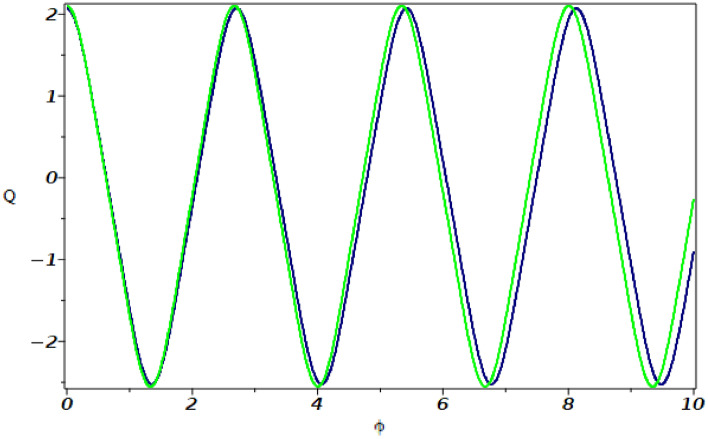
Fig. 7.

Sensitivity analysis of system (38) with initial conditions \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.07)$$\end{document} in navy blue (solid line) and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.1)$$\end{document} in green (solid line).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textit{Case 04}$$\end{document} Figure 8 demonstrates three solutions: red, navy blue, and green, which are denoted by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.07)$$\end{document}, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.1)$$\end{document}, respectively. Upon observing the figures, it becomes evident that minor alterations in the initial conditions have a negligible impact on the stability of the solution.

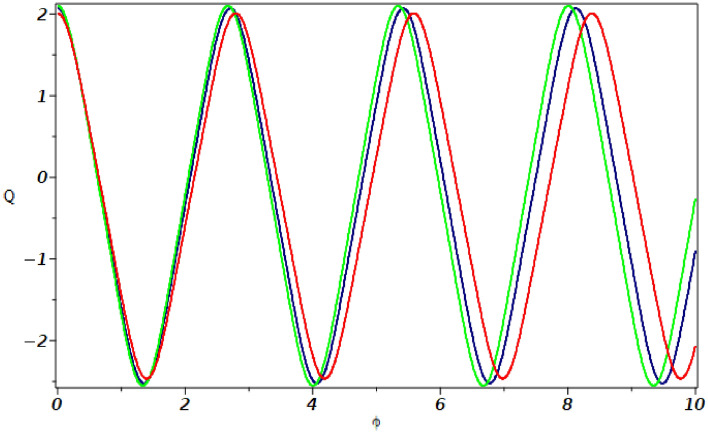
Fig. 8.

Sensitivity analysis of system (38) with initial conditions. Three solutions, red, navy blue, and green, indicated by \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.01)$$\end{document}, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.07)$$\end{document} and, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(Q, \Phi )=(0, 2.1)$$\end{document} respectively.

Discussion and concluding remarks

The PC equation, a mathematical framework for modeling nonlinear longitudinal wave propagation in elastic media, is widely applicable in various fields of physics and engineering. In particular, the equations include nonlinear effects associated with scenarios involving high-amplitude wave motion. Researchers have extensively employed the PC equation to investigate a wide range of real-world phenomena. Examples of these phenomena include transverse vibrations in structures, large-amplitude seismic wave propagation, nonlinear acoustics in pipes, tubes, and granular materials, as well as solitons and solitary wave dynamics. The PC equation’s versatility in encapsulating wave motion in elastic medium is demonstrated in biomechanics and biofluids, revealing its nonlinear physics of wave motion. The present study aims to enhance comprehension of the diverse physical systems described by the PC equation across multiple disciplines by offering solutions and insights into this fundamental model. The generalized nonlinear PC equation has been thoroughly examined in this study with the aid of the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\beta$$\end{document} fractional derivative. A variety of solitary wave solutions have been secured by the considering the recently introduced integration method called mGERFM. The comprehension of the PC equation is substantially improved by the identification of these novel solitary wave solutions. Their unique properties align with traditional wave theory concepts while also bringing innovative advancements to the field. The identification of these unconventional wave patterns highlights the success of computational methods used to reveal complex details. Moreover, the obtained solutions have been depicted in the Figs. 1, 2, 3, 4 for observing the physical movement and fractional parametric effect. Visualizing the solitary wave solutions of the model using different graphical styles is essential for comprehending the shapes and features of the waves, as well as for simplifying complex mathematical concepts. Visual representations of the solutions, such as graphs with various parameter values, aid in understanding the mathematical solutions derived from the problem. These graphical aids facilitate a more intuitive understanding of wave dynamics, including the shapes, magnitudes, and propagation patterns of the solitary waves. Furthermore the sensitivity analysis is also observed and shown in the Figs. 5, 6, 7, 8.

As a result, our study’s findings are particularly important in understanding the propagation of longitudinal waves through elastic rods. Through nonlinear wave dynamics, the solitary waves have the capacity to influence material behaviors and applications associated with energy transmission. This research work can serve as a basis for exploring various potential solutions, encouraging further research on other profiles. New research enhances understanding of solitary waves governed by PC equations, revealing unexpected changes that were previously unnoticed. This broadens the spectrum of known solutions and enriches the theoretical foundation of wave physics.

Author contributions

J.M.: Writing-original draft, Methodology; U.Y.: Formal analysis, Software; E.H.: Qualitative Analysis; Q.A.: Visualization, Validation; M.S.: Writing - original draft; Writing - review & editing; K.K.: Writing - review, Supervision, Formal analysis; A.Z.J.: Formal analysis and Graphics.

Data availability

All data that support the findings of this study are included in the article.

Declarations

Competing interest

The authors declare no competing interests.