A PDZ tandem repeat folds and unfolds via different pathways

Abstract

Protein folding and unfolding experiments are interpreted under the assumption of microscopic reversibility, that is, that at equilibrium one process is the reverse of the other. Single‐domain proteins illustrate the validity of such an interpretation, although reversibility does not necessarily hold under the different conditions typically used for folding and unfolding experiments. In fact, more complex proteins, which often exhibit irreversible unfolding, are generally considered not amenable to folding kinetics studies. Here, the X11 PDZ1‐PDZ2 tandem repeat allows us to reveal the different folding and unfolding pathways at play under different experimental conditions, thus reconciling the apparent contradiction between theory and experiment.

1. INTRODUCTION

Despite decades of intense research, our current understanding of the protein folding reaction is based primarily on single‐domain systems. While multidomain proteins constitute the vast majority of the human proteome (Batey and Clarke 2006), they are typically very difficult to study experimentally and have largely escaped a detailed characterization (Rajasekaran and Kaiser 2024). Indeed, in such cases, it is not uncommon to observe that (un)folding behaves as an irreversible reaction and/or is characterized by a multiphasic behavior, both kinetically and at equilibrium, which generally prevents a quantitative representation.

Two recurring effects have been highlighted in studies comparing the folding of multidomain constructs with their respective isolated constituent domains. First, it has been observed that adjacent domains can transiently populate misfolded kinetic traps (Borgia et al. 2015; Gautier et al. ²⁰²⁰; Lafita et al. ²⁰¹⁹; Malagrinò et al. ²⁰²²; Tian and Best ²⁰¹⁶; Visconti et al. ²⁰²¹; Wright et al. ²⁰⁰⁵). Such misfolding events appear to be promoted by the presence of two simultaneously denatured units and are favored by a high sequence similarity between the domains, possibly implying transient domain swapping (Tian and Best 2016; Wright et al. ²⁰⁰⁵). On the other hand, the presence of folded elements in the vicinity of a domain could contribute to minor structural perturbations along the folding pathway, which are more relevant for the early events of folding rather than for the late events (Gautier and Gianni 2022; Pagano et al. ²⁰²¹).

A vexing problem is represented by the observed cooperativity of the folding reaction in multidomain systems. In fact, while isolated protein domains often fold well and independently of each other, there is limited evidence suggesting that some multidomain constructs fold and unfold as a single cooperative unit (Gruszka et al. 2016; Laursen et al. ²⁰²¹; Santorelli et al. ²⁰²³). Remarkably, the effects recapitulated above can be observed even when the individual domains are able to fold efficiently when expressed in isolation, thereby raising unresolved questions about the transient thermodynamic interactions that occur between these structural subunits. Currently, there are no established guidelines for predicting whether individual domains fold independently or cooperatively at the super‐tertiary level.

One common type of multidomain organization in proteins involves tandem repeats, where structurally homologous domains are arranged in a contiguous assembly (Jung et al. 2016; Pena‐Francesch and Demirel ²⁰¹⁹; Valle‐Orero et al. ²⁰¹⁵). We have previously shown that in the case of PDZ tandem repeats the folding of each domain tends to occur independently of the other, as observed in the case of whirlin (Gautier et al. 2020; Pagano et al. ²⁰²¹) or sPDZD2 (Malagrinò et al. 2022). Contrary to these cases, however, the folding of the tandem PDZ1‐PDZ2 from X11 (X11 PDZ1‐PDZ2), also comprising two homologous PDZ domains (Figure 1a), displays a remarkable cooperativity and folds and unfolds as a single unit (Santorelli et al. 2023). The X11 family of proteins, also known as Mint proteins, plays a critical role in synaptic vesicle trafficking and regulation of amyloid precursor protein (APP) metabolism (Miller et al. 2006). These proteins interact with amyloid precursor protein, influencing its cleavage and processing, which is significant in understanding neurodegenerative diseases such as Alzheimer's. Such roles are played thank to the synergic interaction of X11 with the amyloid precursor protein, via a PTB domain, and with presenelin, through PDZ domains (Wu et al. 2020). Of note, the X11 PDZ domains consist of 5 β‐strands (designated A through E) and 2 α‐helices—one long and one short. The two domains are connected by a short linker and by a C‐terminal auto‐inhibitory tail that forms the conventional PDZ peptide‐COOH interaction and energetically links the two adjacent PDZ domains (Long et al. 2005). The two linkers constrain the two PDZ domains to form a compact interface rich in hydrophobic residues. Truncation of the C‐terminal auto‐inhibitory tail abolishes the folding and unfolding cooperativity and leads to the decoupling of the (un)folding of the individual PDZ domains (Santorelli et al. 2023).

FIGURE 1.

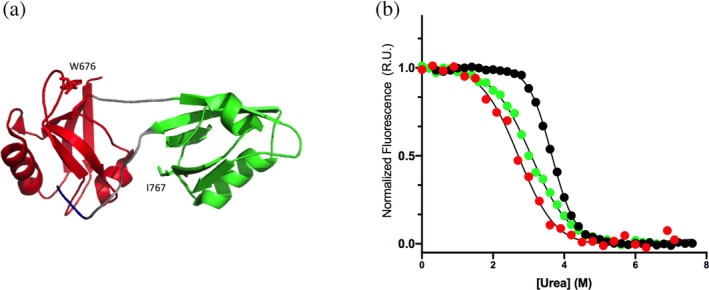
(a) Three‐dimensional structure of the tandem of PDZ1 (in red) and PDZ2 (in green) of X11 (PDB:1u3b). Residues W676 and I767 are shown in sticks. In this work, I767 was mutated to W to spectroscopically follow the folding and unfolding reaction of PDZ2 domain. (b) Equilibrium unfolding curves of isolated PDZ1 domain (in red), isolated PDZ2 domain (in green) and of the tandem construct (in black). All the three curves were fitted with a sigmoidal function, highlighting the cooperative nature of the unfolding reaction in all the constructs.

The previous characterization of the folding of X11 PDZ1‐PDZ2 was particularly instructive in rationalizing the molecular basis of the observed cooperativity of multidomain folding (Santorelli et al. 2023). Nevertheless, an intrinsic experimental limitation arose from the presence of a single tryptophan residue in PDZ1, with PDZ2 containing no fluorescent probes, which prevented a complete characterization of the mechanism of folding. In this work, we describe the folding behavior of a fluorescent variant of X11 PDZ1‐PDZ2 containing a tryptophan residue in each of the PDZ domains, thereby filling in the gaps that were not previously accessible experimentally. Strikingly, data reveal that the tandem construct folds via one pathway but unfolds by a different one. We support this finding by performing folding and unfolding molecular dynamic simulations, by using the so‐called multi‐eGO approach (Bačić Toplek et al. 2024; Scalone et al. ²⁰²²), that appear consistent with such experimental observations.

2. RESULTS AND DISCUSSION

2.1. Designing a fluorescent variant of X11 PDZ1‐PDZ2 that allows following the folding and unfolding of PDZ2

A perceptive strategy to address the folding of tandem repeats involves examining their behavior in comparison to that of their constituent isolated domains. In the case of X11 PDZ1‐PDZ2, although PDZ1 displays a Trp residue at position 676, PDZ2 lacks an experimentally accessible fluorescent probe. Consequently, we resorted to engineering a fluorescent variant of PDZ2 that could act as a reporter of folding both in isolation and in the X11 PDZ1‐PDZ2 construct. Yet, the latter construct proved to be reluctant in tolerating such a mutation with eight out of nine site‐directed variants displaying poor expression levels and/or negligible change in fluorescence upon (un)folding (namely L755W, L759W, F761W, L771W, M772W, V797W, I791W, V812W). Nevertheless, as described below, the mutant I767W represented a good pseudo‐wild‐type to perform folding studies both in the isolated PDZ2 and in the X11 PDZ1‐PDZ2 construct. Consequently, we will refer to this variant, denoted as X11 PDZ1‐PDZ2*, in all the subsequent sections of this work.

The fluorescence‐monitored equilibrium (un)folding transitions of PDZ1, PDZ2*, and PDZ1‐PDZ2* are reported in Figure 1b. As previously observed in the case of wild‐type X11 PDZ1‐PDZ2 (Santorelli et al. 2023), also in the case of X11 PDZ1‐PDZ2* the observed cooperativity appears much more pronounced than that observed for its constituent isolated domains, suggesting that this molecule behaves as a single cooperative unit. A quantitative analysis of the curves by following a two‐state model returns an m _D‐N value of 1.9 ± 0.1 kcal mol⁻¹ M⁻¹ for PDZ1‐PDZ2*, as compared to a value of 1.1 ± 0.1 and 1.08 ± 0.05 kcal mol⁻¹ M⁻¹ for PDZ1 and PDZ2*, respectively. Since the m value is proportional to the change in the accessible surface area upon (un)folding (Myers et al. 1995), a nearly doubled value for X11 PDZ1‐PDZ2* confirms that this construct behaves as a single cooperative unit despite its constituent domains are competent for independent folding. Furthermore, the thermodynamic stabilities of PDZ2* and X11 PDZ1‐PDZ2* were 3.3 ± 0.4 and 7.0 ± 0.7 kcal mol⁻¹, as compared to 4.0 ± 0.2 and 8.8 ± 0.4 kcal mol⁻¹ in the case of PDZ2 and X11 PDZ1‐PDZ2, confirming that mutation Ile767Trp returns a marginal change in protein stability and represents a good probe to address folding. Furthermore, the far‐UV CD spectrum of the I767W variant, in comparison to that of the wild‐type protein (reported in Figure S1, Supporting Information), confirms that the mutation correspond to a negligible rearrangement of three‐dimensional structure within the tandem, providing additional evidence that X11 PDZ1‐PDZ2* represents a good pseudo‐wild‐type to perform folding studies.

2.2. The kinetics of folding of X11 PDZ1‐PDZ2* reveals the presence of distinct folding and unfolding intermediates

To shed light on the mechanism of folding of X11 PDZ1‐PDZ2*, we performed kinetic experiments on the tandem and analyzed them in comparison to PDZ1 and PDZ2*. Because of the complexity of the observed results on X11 PDZ1‐PDZ2*, we will first discuss the (un)folding of this construct and then address the behavior of the individual domains, with emphasis on the elements that allow clarifying the underlying mechanism.

The folding and unfolding kinetics of X11 PDZ1‐PDZ2* were studied by fluorescence‐equipped stopped‐flow experiments in buffer Hepes 50 mM, pH 7.5 at 37°C. At all the investigated conditions, the observed time courses were consistent with the sum of two exponential phases. A semi‐logarithmic plot of the two observed phases versus denaturant concentration, commonly denoted as “chevron plot,” measured for X11 PDZ1‐PDZ2* is reported in Figure 2a. A comparison of the observed dependence on X11 PDZ1‐PDZ2* with wild‐type X11 PDZ1‐PDZ2 readily explains the presence of two phases. In fact, these constructs show nearly identical dependence of the slow phase. On the other hand, introduction of a Trp residue in PDZ2 results in the appearance of the fast phase, both in refolding and unfolding, that can be therefore unambiguously assigned to the folding events related to the latter domain.

FIGURE 2.

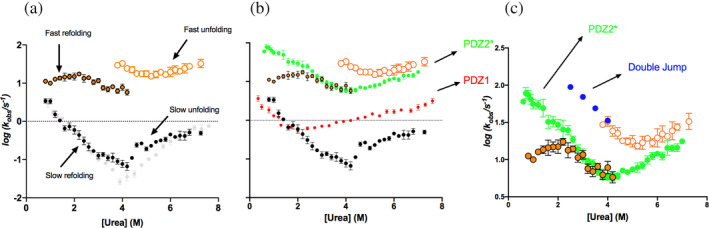
(a) Chevron plot of the X11 PDZ1‐PDZ2* construct (slow phase in black, fast phase recorded in refolding experiments in filled orange circles, fast phase recorded in unfolding experiments in empty orange circles) superimposed to the chevron plot of wild‐type X11 PDZ1‐PDZ2 (in gray). (b) Chevron plot of the X11 PDZ1‐PDZ2* construct (same color code as panel a) superimposed to the chevron plots obtained for the isolated PDZ1 (in red) and PDZ2* (in green). (c) Double mixing experiments performed to monitor the refolding of PDZ2* (blue circles) with the C‐terminal tail bound to a native PDZ1 (see text for details). The obtained k _obs are in agreement with those obtained in the unfolding of the X11 PDZ1‐PDZ2* tandem (empty orange circles).

From a qualitative inspection of Figure 2a it emerges that, while the slow phase conforms to a classical chevron, displaying a deviation from linearity (roll‐over effect, signature of the presence of an intermediate) (Parker et al. 1995; Travaglini‐Allocatelli et al. ²⁰⁰³) in the unfolding branch, the fast phase appears more complex. First, the presence of a double exponential behavior both in the folding and unfolding reactions is a particularly surprising characteristic. In fact, when and if folding involves the accumulation of a partially folded low‐energy intermediate, observed kinetics should be biphasic and the apparent (un)folding limb of the chevron plot should display a deviation from linearity that is proportional to a factor equal to 1/(1 + K _eqI) (Capaldi et al. 2001; Fersht et al. ¹⁹⁹²; Khorasanizadeh et al. ¹⁹⁹⁶; Parker et al. ¹⁹⁹⁵). Consequently, the presence of two phases should be limited to the denaturant concentration range where the intermediate is stable enough to be accumulated. We note that by investigating the data in Figure 2a and by considering solely the unfolding of X11 PDZ1‐PDZ2*, such a concentration range should be limited to [urea] > 4M. In fact, under such conditions, the fast phase reports of a two‐state chevron (referring to the pre‐equilibrium between N and I), with the slow phase displaying a detectable roll‐over effect. Conversely, biphasic time courses are also present at [urea] < 4M. Hence, a simple three‐state mechanism, previously proposed for X11 PDZ1‐PDZ2 (Santorelli et al. 2023), appears inconsistent with the overall behavior reported in Figure 2 and the presence of biphasic behavior also in the refolding experiments represents a peculiar and unexpected effect that demands additional clarifications. Second, while in the case of the slow phases the folding and unfolding experiments yield to similar rate constants, the fast phases of the two processes do not match. This finding suggests that the folding and unfolding experiments, while displaying a fast phase occurring in a similar time window and with similar relative amplitude, report of two different intermediates.

To test the robustness of the two effects reported above, we resorted to performing kinetic folding and unfolding experiments at different experimental conditions. Hence, we explored the folding and unfolding behavior of X11 PDZ1‐PDZ2* at different pH values, ranging from pH 4.5 to 9.5. These data are reported in Figure S2. Notably, the data conformed to what was observed at neutral pH at all the investigated conditions. This finding confirms that the presence of biphasic folding and unfolding time courses and the mismatch between the folding and unfolding fast phases are genuine and robust effects that demand to be properly addressed. We will examine these effects in detail below.

2.3. The study of the folding of individual domains helps in addressing the behavior of X11 PDZ1‐PDZ2*

A valuable method for understanding the folding of complex multidomain systems is to compare the observed behavior with that of its constituent isolated domains (Haq et al. 2012; Hultqvist et al. ²⁰¹³; Laursen et al. ²⁰²⁰; Visconti et al. ²⁰²¹). Therefore, in analogy to what was described above for X11 PDZ1‐PDZ2*, we subjected PDZ1 and PDZ2* to folding and unfolding stopped‐flow experiments. It is noteworthy that in both cases, the folding and unfolding time courses were consistent with a single exponential decay under all conditions examined.

The chevron plots of the two isolated domains, superposed to that of X11 PDZ1‐PDZ2*, are reported in Figure 2b. Overall, it is evident that, while the fast phase primarily reports the events related to the (un)folding of PDZ2*, the slow phase may be assigned to PDZ1. This finding is consistent with what was previously observed on wild‐type X11 PDZ1‐PDZ2 which shows the slow phase only (Santorelli et al. 2023).

The comparison between the slow phase of X11 PDZ1‐PDZ2* with the folding of PDZ1 in isolation is reminiscent of what was previously observed for the wild‐type X11 PDZ1‐PDZ2. Also in this case, the refolding of the tandem is parallel to that of the isolated domain and displays a similar value of k_F ⁰. Conversely, the unfolding arm reports a detectable stabilization and is characterized by a roll‐over effect. Such an effect reports of the accumulation of a transient intermediate where PDZ2 is denatured, while PDZ1 is folded (see fig. 3 of Santorelli et al. ²⁰²³). We previously noted that such effects are due to the presence of an auto‐inhibitory C‐terminal tail that thermodynamically couples the individual domains.

Notably, the inspection of the fast‐unfolding phase of X11 PDZ1‐PDZ2* (open orange circles in Figure 2b) in comparison to PDZ2* (green circles in Figure 2b) indicates that the unfolding of the isolated domain displays very similar rate constants, while the folding rate constants calculated from unfolding and refolding experiments on the tandem differ substantially. In fact, in the case of X11 PDZ1‐PDZ2* the refolding branch of the fast phase obtained from unfolding is about 5 times faster than that obtained from the refolding experiments, with the latter being compatible with the value obtained for PDZ2* in isolation. These effects lead to a detectable mismatch of the two branches and will be addressed in detail in the next section, thanks to the employment of double jump experiments and site‐directed mutagenesis. Additionally, it is worth noting that at low denaturant concentrations, the apparent folding rate constant of X11 PDZ1‐PDZ2* displays a decrease compared to the expected value. This effect, which has been previously observed on different systems (Borgia et al. 2015; Gautier et al. ²⁰²⁰; Lafita et al. ²⁰¹⁹; Malagrinò et al. ²⁰²²; Tian and Best ²⁰¹⁶; Visconti et al. ²⁰²¹; Wright et al. ²⁰⁰⁵), might be due to the transient interaction between the two denatured units.

2.4. The internal binding of the auto‐inhibitory tail stabilizes PDZ2 and is responsible for the apparent mismatch between folding rate constants

Previous experiments on X11 PDZ1‐PDZ2 suggested that, during unfolding, the denaturation of the second PDZ domain precedes the unbinding of the auto‐inhibitory C‐terminal tail from PDZ1 (Santorelli et al. 2023). Therefore, we hypothesized that the apparent discrepancy between the folding rate constants of PDZ2* in the context of the tandem, measured from folding and unfolding experiments, might be due to the presence of the auto‐inhibitory tail. In particular, when the tail is bound by PDZ1, a lower conformational entropy of the denatured state of PDZ2 could be assumed, resulting in an increased folding rate constant of PDZ2. To test this hypothesis, we designed a sequential mixing (double‐jump) experiment where X11 PDZ1‐PDZ2* was subjected to interrupted unfolding. The rationale of the experiment was to (i) first accumulate the intermediate displaying a denatured PDZ2* and a native PDZ1 with the bound tail and (ii) interrupt the unfolding by mixing with refolding buffer to monitor the folding rate constant of PDZ2* with a bound tail (and possibly a restrained denatured state). Hence, the protein in 2M urea was first mixed with 8M urea to obtain a final concentration of 5M urea, then, after a controlled delay time, refolding at different final urea concentrations. Two representative interrupted unfolding traces obtained at final 2.5M urea concentrations at different delay times are reported in Figure S3. It is evident the refolding at short delay times (e.g., 0.2 s) is faster than that observed at long delay times (e.g., 240 s). Hence, we fitted the different time courses to a sum of two exponential decays, while sharing the observed rate constants. Very interestingly, the amplitude of the fast refolding phase decreases with increasing delay time, as opposed to what observed for the slow refolding phase (Figure S3). Gratifyingly, as reported in Figure 2c, the fast folding rate constants of PDZ2* obtained from the double jump experiment were in agreement with those obtained in the unfolding of the X11 PDZ1‐PDZ2* tandem.

To further confirm our hypothesis and provide additional evidence to prove that the apparent mismatch between the folding branches of PDZ2 arises from the internal binding of the auto‐inhibitory tail, we resorted to destabilize such intramolecular interaction via site‐directed mutagenesis. In the case of X11, it was previously suggested that the hydrophobic nature of the C‐terminal amino acid, I837, is critical to stabilize the internal binding of the tail (Jensen et al. 2018; Long et al. ²⁰⁰⁵). This conclusion was previously put forward thanks to comparative ITC analysis of C‐terminal variants of X11 PDZ1‐PDZ2 (Jensen et al. 2018). Hence, we produced the variants I837V, I837A, and I837G and subjected them to folding and unfolding experiments. The resulting chevron plots are shown in Figure 3. In agreement with our expectations, destabilization of the binding results in a reduced mismatch of the fast phases, with the variants I837A and I837G showing no mismatch. This finding further confirms that the apparent acceleration of the folding rate constant in PDZ2* obtained from unfolding experiments and the detectable mismatch between folding and unfolding experiments is due to the internal binding of the auto‐inhibitory tail. Remarkably, a double jump experiment on the I837G mutant returned a folding rate constant that was independent on the delay time (as opposed to what observed for PDZ1‐PDZ2*).

FIGURE 3.

Folding and unfolding kinetic experiments of (a) I837V variant, (c) I837A variant, (d) I837G variant. The progressive destabilization of the binding of the C‐terminal tail to the PDZ1 domain, caused by the truncation of the side chain of the I837 residue, results in a reduced mismatch of the fast phases in unfolding and refolding experiments.

2.5. PDZ1‐PDZ2* folds and unfolds via different pathways

As noted above, the presence of double exponential time‐courses in both folding and unfolding experiments in the case of X11 PDZ1‐PDZ2* is inconsistent with the recently proposed sequential three‐state model and demands additional considerations. In this respect, it is of special interest to comment on the magnitudes of the observed rate constants in the light of the structural and thermodynamic properties of X11 PDZ1‐PDZ2* and to consider the unfolding and refolding mechanisms individually. In fact, the analysis of PDZ1 and PDZ2* expressed in isolation highlights how the (un)folding reactions of the latter domain are faster than that of the former at all the investigated conditions (see Figure 2b). However, since the binding of the auto‐inhibitory tail may only occur when PDZ1 is folded (Long et al. 2005), it is evident that, as detailed below, the time evolutions of the folding and unfolding reactions may display inherent differences.

When native X11 PDZ1‐PDZ2* is challenged with high concentrations of denaturant, the overall reaction is characterized by the accumulation of an intermediate displaying PDZ2* in its denatured state and the auto‐inhibitory tail bound to PDZ1 (see Figure 4). On the other hand, when the denatured tandem is mixed with refolding buffer, since PDZ2* is fully competent to fold in isolation and is faster than PDZ1, the overall apparent time course would correspond to two phases that can be assigned to (i) a faster phase corresponding to the folding of PDZ2*; (ii) a slower phase representing the folding of PDZ1. The intramolecular binding of the auto‐inhibitory tail, which is optically silent, most likely occurs downhill of the main barrier. Figure 4 graphically summarizes these structural considerations and highlights the inherent differences between the folding and unfolding reactions observed for X11 PDZ1‐PDZ2*.

FIGURE 4.

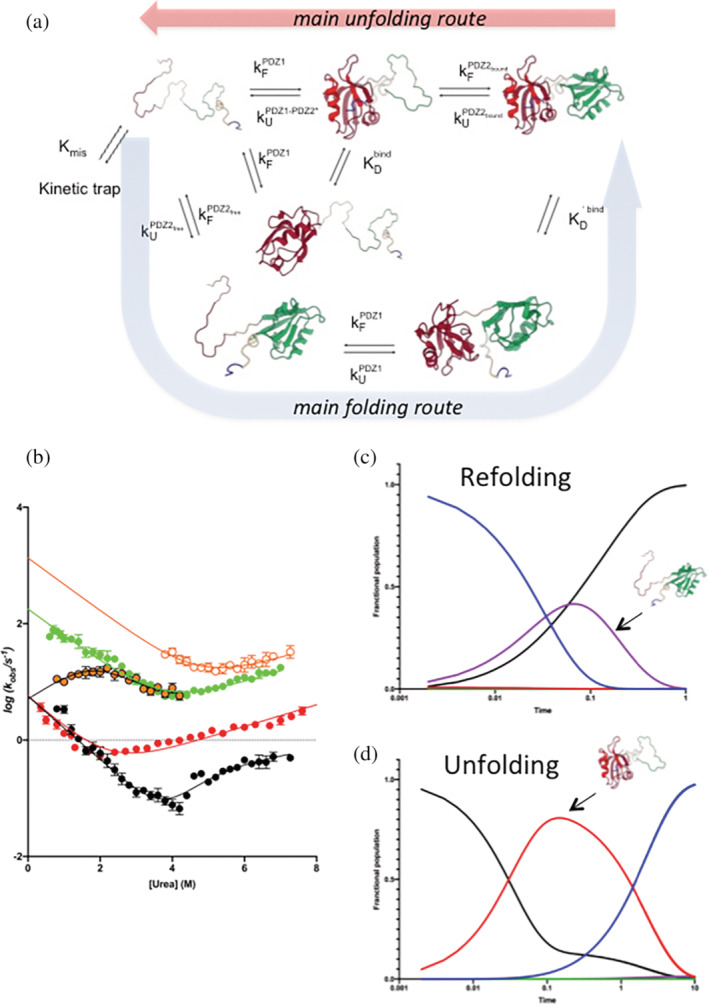
(a) Alternative pathways for the folding and unfolding processes of the X11 PDZ1‐PDZ2 tandem, with microscopic and equilibrium rate constants of the reactions involved. (b) Global analysis of the chevron plots obtained for the X11 PDZ1‐PDZ2* construct (in black) and for PDZ1 and PDZ2 in isolation (in red and green, respectively). The system of equations used to fit data is described in detail in the text. (c, d) Simulations of folding and unfolding time course of X11 PDZ1‐PDZ2* at zero and high (6.8M) denaturant concentrations (see details in the text).

The emerging picture of the kinetic folding mechanism of PDZ1‐PDZ2* is very complex and requires the consideration of alternative pathways. However, the ability to measure the different folding and unfolding phases at different denaturant concentrations, together with the ability to study the folding of PDZ1 and PDZ2* in isolation, allows us to address the underlying mechanism from a quantitative perspective. We have therefore written a minimal kinetic scheme, which we report in Figure 4. Accordingly, the apparent data can be fitted to the following system of equations:

$$\left\{\begin{array}{c}\log \left({k_{\mathrm{obs}}}^1\right)=\log \left(k_F^{\mathrm{PDZ}1}\cdot e^{-m_F^{\mathrm{PDZ}1}\cdot \left[\text{urea}\right]}+\frac{k_U^{\mathrm{PDZ}1-\mathrm{PDZ}2*}\cdot e^{-m_U^{\mathrm{PDZ}1-\mathrm{PDZ}2*}\cdot \left[\text{urea}\right]}}{\left(1+\frac{k_U^{\mathrm{PDZ}{2}_{\text{bound}}}}{k_F^{\mathrm{PDZ}{2}_{\text{bound}}}}\right)\cdot e^{-m_{\mathrm{Tot}}^{\mathrm{PDZ}{2}_{\text{bound}}}\cdot \left[\text{urea}\right]}}\right)\\ \log \left({k_{\mathrm{obs}}}^2\right)=\log \left(k_F^{\mathrm{PDZ}{2}_{\text{bound}}}{e}^{-m_F^{\mathrm{PDZ}{2}_{\text{bound}}}\cdot \left[\text{urea}\right]}+k_U^{\mathrm{PDZ}{2}_{\text{bound}}}{e}^{\left(m_{\mathrm{Tot}}^{\mathrm{PDZ}{2}_{\text{bound}}}-m_F^{\mathrm{PDZ}{2}_{\text{bound}}}\right)\cdot \left[\text{urea}\right]}\right)\\ \log \left({k_{\mathrm{obs}}}^3\right)=\log \left(k_F^{\mathrm{PDZ}{2}_{\text{free}}}{e}^{-m_F^{\mathrm{PDZ}{2}_{\text{free}}}\cdot \left[\text{urea}\right]}+k_U^{\mathrm{PDZ}{2}_{\text{free}}}{e}^{\left(m_{\mathrm{Tot}}^{\mathrm{PDZ}{2}_{\text{free}}}-m_F^{\mathrm{PDZ}{2}_{\text{free}}}\right)\cdot \left[\text{urea}\right]}\right)\\ \log \left({k_{\mathrm{obs}}}^4\right)=\log \left(k_F^{\mathrm{PDZ}1}\cdot e^{-m_F^{\mathrm{PDZ}1}\cdot \left[\text{urea}\right]}+k_U^{\mathrm{PDZ}1}{e}^{m_U^{\mathrm{PDZ}1}\cdot \left[\text{urea}\right]}\right)\\ \log \left({k_{\mathrm{obs}}}^5\right)=\log \left(\frac{k_F^{\mathrm{PDZ}{2}_{\text{free}}}\cdot e^{-m_F^{\mathrm{PDZ}{2}_{\text{free}}}\cdot \left[\text{urea}\right]}}{\left(1+K_{\mathit{mis}}\cdot e^{-m_{\mathit{mis}}\cdot \left[\mathit{\text{urea}}\right]}\right)}+k_U^{\mathrm{PDZ}{2}_{\text{free}}}{e}^{\left(m_{\mathrm{Tot}}^{\mathrm{PDZ}{2}_{\text{free}}}-m_F^{\mathrm{PDZ}{2}_{\text{free}}}\right)\cdot \left[\text{urea}\right]}\right)\end{array}\right\},$$

where k _obs ¹ to k _obs ⁵ refer to: (i) the slow phase observed in folding and unfolding experiments of X11 PDZ1‐PDZ2*; (ii) the fast phase observed for X11 PDZ1‐PDZ2* in unfolding experiments; (iii) the chevron plot of PDZ2 in isolation; (iv) the chevron plot of PDZ1 in isolation; (v) the fast refolding phase observed for X11 PDZ1‐PDZ2*. The microscopic rate constants defined in the above system are explicitly stated in the scheme described in Figure 4, where the global fit to the experimental data is also reported. The obtained parameters are listed in Table S1.

Taking advantage of the fitting procedure reported above, we simulated the folding and unfolding time course of X11 PDZ1‐PDZ2* at zero and high (6.8M) denaturant concentrations. These simulations were obtained by applying the numerical values of the microscopic rate constants obtained at the two different experimental conditions, using the kinetic simulator Copasi (University of Connecticut). In practice, the kinetic scheme depicted in Figure 4a was implemented into Copasi. Then, the numerical value of each microscopic rate constant was calculated at zero and 6.8M [urea] by taking advantage of the fitting parameters listed in Table S1. These values were inserted in Copasi to obtain the predicted time courses for the folding and unfolding of X11 PDZ1‐PDZ2*, which are shown in Figure 4c,d. It is evident that, in agreement with expectations, unfolding occurs primarily via the accumulation of an intermediate displaying a denatured PDZ2 and a native PDZ1 (bound to the C‐terminal auto‐inhibitory tail), whereas refolding follows a completely different pathway, with folding of PDZ2 preceding that of PDZ1. Based on these observations, it can be concluded that X11 PDZ1‐PDZ2* folds and unfolds via two different pathways.

2.6. The folding and unfolding reactions of X11 PDZ1‐PDZ2 by multi‐ eGO molecular dynamics simulations

To further support the experimental work reported above, we performed molecular dynamics simulations using our recently developed multi‐eGO model (Bačić Toplek et al. 2024; Scalone et al. ²⁰²²). The multi‐eGO model is system‐dependent, atomistic, and uses only one effective mean‐field interaction, described by the Lennard‐Jones potential, which is obtained by combining several pieces of information according to Bayes. Briefly, we first simulated the native state fluctuations of X11 PDZ1‐PDZ2 using a conventional molecular mechanics force field, and then trained our multi‐eGO model of X11 PDZ1‐PDZ2 by combining the above data with two reference simulations, the first describing only the local geometry and self‐excluded volume of the chain, and the second describing the random motion of the auto‐inhibitory tail with both domains folded (see section 4). Two energy scales were then applied to the interactions of the auto‐inhibitory tail with its binding site in PDZ1 and all other interactions, respectively. The resulting model was then used to run 200 folding and unfolding simulations at either 310 or 380 K, respectively. Note that the temperature is used here as a proxy for the effect of the denaturant. Also, note that the times below are nominal due to the simplified nature of the multi‐eGO model.

In Figure 5 we compare the (un)folding kinetics of the two domains as well as the correlation between (un)folding and binding kinetics of the auto‐inhibitory tail. PDZ1 unfolds significantly slower than PDZ2, as shown by the distribution of the difference in their unfolding times in Figure 5a. Furthermore, in most cases, the unbinding of the auto‐inhibitory tail follows the unfolding of PDZ2 (cf., Figure 5b). Thus, the most likely unfolding pathway is characterized by the unfolding of PDZ2, the unbinding of the auto‐inhibitory tail and finally the unfolding of PDZ1, in agreement with the analysis of the in vitro kinetics (cf., Figure 5c). In contrast to unfolding, folding shows a different picture; indeed, the difference in folding times of PDZ1 and PDZ2 shown in Figure 5d is normally distributed around 0, indicating that the two domains fold on a similar time scale. Here, in most cases, the binding of the auto‐inhibitory tail to PDZ1 follows the folding of PDZ2, with only a small fraction of simulations showing the binding of the auto‐inhibitory tail to PDZ1 before the folding of PDZ2 (cf., Figure 5e,f). This is again consistent with the picture obtained from the kinetic experiments. Remarkably, the multi‐eGO model is trained only on the native state fluctuations, suggesting how the differences in the folding and unfolding pathways are inherently encoded in the energetic of the folded protein. It should also be noted that the stochastic asymmetry in the folding and unfolding pathways does not violate microscopic reversibility, since folding and unfolding are simulated under different conditions.

FIGURE 5.

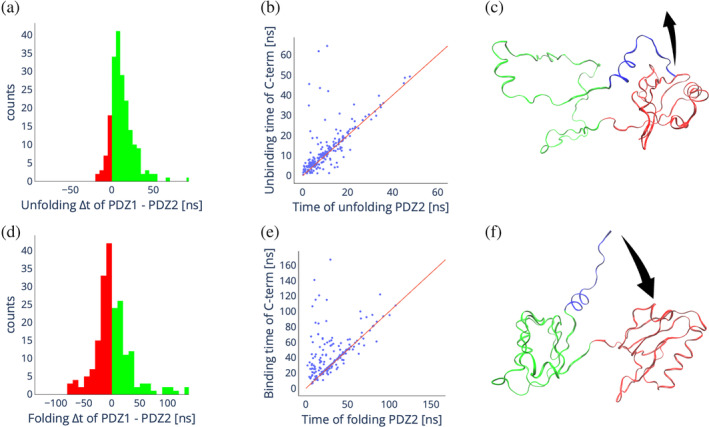
In silico unfolding and folding of X11 PDZ1‐PDZ. (a) Distribution of the difference in unfolding times of PDZ2 and PDZ1 from 200 unfolding simulations. Green bars indicate positive differences, meaning PDZ1 unfolds slower than PDZ2, red bars indicate negative differences, meaning PDZ2 unfolds slower than PDZ1. (b) Scatter plot showing the correlation between the unfolding time of PDZ2 and the unbinding time of the C‐terminal auto‐inhibitory tail of PDZ1. (c) Schematic of the most common unfolding pathway. (d) Distribution of the difference in folding times of PDZ2 and PDZ1 from 200 folding simulations. Green bars indicate positive differences, meaning PDZ1 folds slower than PDZ2, red bars indicate negative differences, meaning PDZ2 folds slower than PDZ1. (e) Scatter plot showing the correlation between the folding time of PDZ2 and the binding time of the auto‐inhibitory tail to PDZ1. (f) Schematic of the most common folding pathway.

Given the agreement of the multi‐eGO simulations with the experimental (un)folding kinetics, we challenged the model to interrogate the role of the binding of the auto‐inhibitory tail on the process. We performed 200 folding simulations of the isolated PDZ2 domain as well as 200 folding simulations starting from configurations where PDZ2 is unfolded, PDZ1 is folded, and the auto‐inhibitory tail is bound to PDZ1 (representing the double jump experiments). Remarkably, as shown in Figure 6a, the folding of PDZ2 restrained by the binding of the auto‐inhibitory tail to PDZ1 is significantly faster than its folding in isolation, with the latter being on average faster than PDZ2 folding in tandem. While binding may accelerate folding under intermediate denaturation conditions, it is plausible that it may also be responsible for PDZ2 misfolding under fully denaturing conditions. A detailed analysis of the small fraction of folding simulations where the binding of the tail precedes the folding of PDZ2 (points below the diagonal in Figure 5e) reveals a well‐defined PDZ2 misfolded state that is transiently populated after the folding of PDZ1 and the binding of the auto‐inhibitory tail to PDZ1, cf., the representative RMSD/distance plot in Figure 6b, and requires unfolding before finally folding. This state is characterized by a positional switching of the β‐strands. The β‐sheet made of strands βA, βD, and βE is disrupted in the trapped state leaving behind only the βD,E‐hairpin while βA‐strand migrates further out from the domain center. There it forms an unstable β‐sheet with the βB,C‐hairpin, which has undergone a rotation switching the relative orientations of the single strands as shown in Figure 6c,d. As the βB,C‐hairpin has stabilized in the native position of βA‐strand, the structure has to unfold first before folding to the native fold.

FIGURE 6.

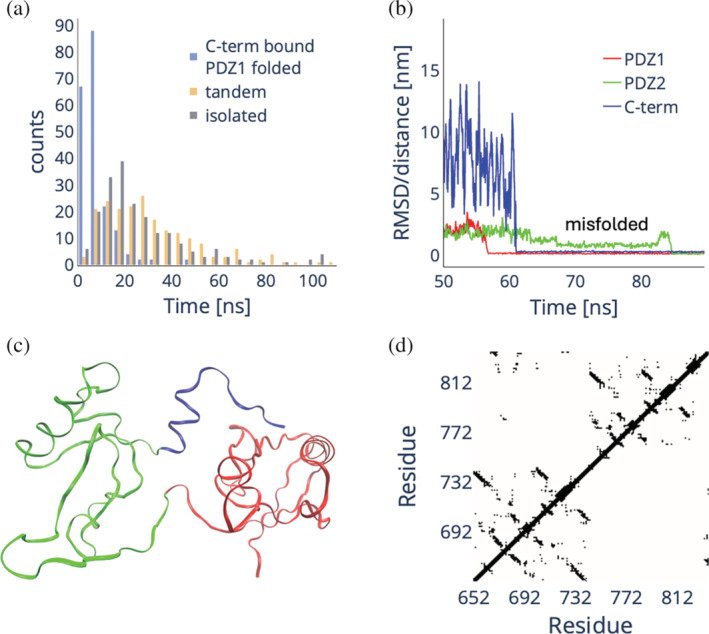
(a) Distribution of folding times of PDZ2 when in tandem with PDZ1 with the C‐terminal auto‐inhibitory tail already bound to the folded PDZ1 domain (blue), when in tandem with PDZ1 both fully denatured (lime), and when isolated (red). (b) Representative RMSD (PDZ1 and PDZ2) and distance (C‐terminal auto‐inhibitory tail) plot for a folding simulation of X11 PDZ1‐PDZ2, representing the case where the C‐terminal auto‐inhibitory tail (blue line) binds to a folded PDZ1 domain (red line) before the folding of the PDZ2 domain (green line). In this case, a misfolded intermediate is populated that must be unfolded prior to final folding. (c, d) Cartoon and contact map representation of the misfolded state. The top diagonal contact map represents the folded X11 PDZ1‐PDZ2, while the bottom diagonal represents the misfolded conformation.

3. CONCLUSIONS

The principle of microscopic reversibility states that, in a reversible reaction, the probability of any trajectory of a system equals that of the time‐reversed trajectory of the reverse reaction. Hence, to a shallow approximation, folding and unfolding are generally assumed to occur via a mechanism in which the forward reaction explores exactly the reverse of the mechanism of the opposite direction (Daggett and Fersht 2003). This assumption is, for example, at the basis of the so‐called ϕ‐value analysis (Fersht 2024; Fersht and Sato ²⁰⁰⁴). However, folding and unfolding are often studied under different conditions, for example, by changing the denaturant concentration and/or temperature, which makes the principle of microscopic reversibility theoretically violable (Bhatia and Udgaonkar 2022, 2024). These complications are even more remarkable in the case of multidomain systems, which often exhibit very elusive kinetics and complex apparent mechanisms (Hutton et al. 2015), which may lead to different folding and unfolding pathways (Moulick et al. 2019). In the case of the PDZ tandem of X11, described in our work, simulations and experiments contribute to depict a plausible scenario in which the principle of microscopic reversibility is apparently violated, giving rise to two completely different mechanisms when the folding at low denaturant and the unfolding at high denaturant are considered. Importantly, while the overall kinetic scheme recapitulated in Figure 4 is operative both in the folding and in the unfolding reactions, the apparent mismatch between pathways is essentially due to the changes in relative amplitudes, such as that the apparent mechanism is different when folding and unfolding are monitored. This is due to the presence of the intramolecular binding of the short auto‐inhibitory tail. In fact, a detectable shift between the major folding and unfolding mechanisms is caused by the context‐dependent binding of the auto‐inhibitory tail, being very stable when PDZ1 is folded and unstable when it is unfolded. Note that the violation is only apparent and can be explained by the different experimental conditions imposed by folding and unfolding, respectively. More generally, we illustrate how, in the case of multidomain systems, the stabilization of individual protein segments can be linked to the conformational assembly of another structural element. While these results provide a comprehensive, detailed view of the operating folding scenario in the case of X11, which can be successfully mapped and described, they also provide a new framework for interpreting folding and unfolding data of multidomain constructs. Future work on homologous systems will further clarify the generality of these conclusions.

4. MATERIALS AND METHODS

4.1. Protein mutagenesis, expression, and purification

The PDZ2*, X11 PDZ1‐PDZ2*, X11 PDZ1‐PDZ2*‐I837V, I837A, I837G variants were obtained by site‐directed mutagenesis QuikChange Lightning Mutagenesis Kit (Agilent technologies) following manufacturer instructions. Primers oligos were purchased from Eurofins Genomics and all sequences were confirmed by DNA sequencing.

Proteins were expressed in the Escherichia Coli BL‐21 (DE3) (BioLabs) strain. Cultures were grown in Luria Bertani medium containing 34 μg/mL kanamycin at 37°C. After induction with 1 mM IPTG (isopropyl‐β‐D‐thiogalactopyr‐anoside), cells were grown at 25°C overnight and collected by centrifugation. Pellets were resuspended in 50 mM TrisHCl pH 7.5, 300 mM NaCl, 10 mM imidazole, and protease inhibitor (Complete EDTA‐free, Roche) and sonicated. The supernatant was loaded on a HisTrap FF (GE Healthcare) column equilibrated with the same buffer. Proteins were eluted with an imidazole gradient (10 mM–1M) and collected fractions were buffer exchanged with Hepes pH 7.5, 300 mM NaCl with a HiTrap Desalting column (GE Healthcare). All the constructs in this work contain an N‐terminal His tag.

4.2. Equilibrium experiments

Fluorescence equilibrium (un)folding experiments were performed on a standard spectrofluorometer (FluoroMax single photon counting spectrofluorometer; Horiba). The proteins were excited at 280 nm, and emission spectra were recorded between 300 and 400 nm at increasing urea concentrations. Experiments were performed with all the constructs at constant concentration of 2 μM, in Hepes 50 mM at pH 7.5, at 37°C, using a quartz cuvette with a path length of 1 cm. Data were fitted using a sigmoidal transition (Fersht 1999).

4.3. Kinetic experiments

Stopped flow experiments were performed on a single‐mixing SX‐18 instrument (Applied Photophysics) monitoring the change of fluorescence emission. The excitation wavelength used was 280 nm, and the fluorescence emission was recorded by using a cut‐off glass filter (320 nm). At least five individual traces were acquired and then averaged for each experiment. The experiments were repeated in triplicates. All the averages were satisfactorily fitted with a single exponential equation. Experiments were conducted using 2 μM (after mixing) protein sample in 50 mM Hepes pH 7.5 at 37°C and different urea concentrations. Buffers used for pH dependence of PDZ1‐PDZ2* were 50 mM sodium‐acetate pH 4.5 and pH 5.5, 50 mM Bis‐Tris pH 6.5, 50 mM Tris–HCl pH 8.5, 50 mM CHES pH 9.5.

4.4. Molecular dynamics simulations

All MD simulations in this work were performed using GROMACS 2023 (Abraham et al. 2015). Multi‐eGO is a hybrid transferable/structure‐based atomic (excluding hydrogen) model defined from the combination of at least one training and one reference random‐coil simulation (Bačić Toplek et al. 2024). The training simulation can be generated using a state‐of‐the‐art conventional molecular mechanic force field, while the reference random‐coil simulation is obtained using multi‐eGO random‐coil model consisting of only bonded and Lennard‐Jones C⁽¹²⁾ repulsive interactions.

The training simulation for X11 PDZ1‐PDZ2 was run using the CHARMM22* force field (Piana et al. 2011) in TIP3P water (Jorgensen et al. 1983), using an initial structure predicted by RosettaFold2 (Baek et al. 2021) as implemented in ColabFold (Mirdita et al. 2022). The C‐terminal tail was protonated and bound to the PDZ1‐carboxylate‐binding‐loop. The system was subjected to energy minimization using the steepest descent algorithm until the maximum force converges to a value <1000 kJ/(mol nm), followed by a conjugate‐gradient minimization until the maximum force converges to a value <10 kJ/(mol nm). Subsequently, the minimized configuration was relaxed for 4 ns at a constant pressure of 1 bar and constant temperature of 310 K, keeping the protein atoms restrained to the position of the minimum energy configuration. The resulting configuration was used for a 1 μs production run at the same temperature and pressure. The simulations used the leap‐frog algorithm with a time step of 2 fs and LINCS restraints (Hess 2008) for hydrogen atoms. Non‐bonded interactions were cut off at 1 nm using PME for long‐range electrostatics. Temperature and pressure were controlled by stochastic velocity rescaling (Bussi et al. 2007) and cell rescaling (Bernetti and Bussi 2020) algorithms, respectively.

The training simulation is weighted using a reference random coil simulation that was performed for 1 μs at 310 K, which represents a self‐avoiding chain of the same sequence of the training. Training and reference simulations were analyzed to obtain interatomic distance distributions with associated contact probabilities, $P_{i,j}^{\mathrm{MD}}$ and $P_{i,j}^{\mathrm{RC}}$. Given a chosen value for the energy scale ${\epsilon }_0^{\text{intra}}$ the multi‐eGO attractive or repulsive interactions are then obtained for an i,j pair of atoms using the following functions (Bačić Toplek et al. 2024):

$${\epsilon }_{i,j}=-\frac{{\epsilon }_0^{\text{intra}}}{\ln P_{\text{threshold}}^{\mathrm{RC}}}\bullet \ln \frac{P_{i,j}^{\mathrm{MD}}}{\max \left(P_{i,j}^{\mathrm{RC}},P_{\text{threshold}}^{\mathrm{RC}}\right)},$$

$${{\tilde{C}}_{i,j}}^{\left(12\right)}=\begin{array}{l}+\frac{{\epsilon }_0^{\text{intra}}}{\ln P_{\text{threshold}}^{\mathrm{RC}}}{r_{\min }}_{\mathrm{MD}}^{12}\ln \left(\frac{P_{i,j}^{\mathrm{MD}}}{\max \left(P_{i,j}^{\mathrm{RC}},P_{\text{threshold}}^{\mathrm{RC}}\right)}\right)\\ +C_{i,j}^{\left(12\right)}{\left(\frac{{r_{\min }}_{\mathrm{MD}}}{{r_{\min }}_{\mathrm{RC}}}\right)}^{12},\end{array}$$

where the second is used if the first gives an ε _i,j  < ε _min = 0.07 kJ mol⁻¹. Above, $P_{\text{threshold}}^{\mathrm{RC}}$ is a minimum probability used for regularization and $r_{\min }$ is the interaction distance. A detailed description of the model can be found in Bačić Toplek et al. (2024) and the associated code and parameters are available on GitHub.

Multi‐eGO MD simulations were performed using stochastic dynamics integration with a timestep of 5 fs and a relaxation time of 25 ps. The cutoff for the LJ interactions was set to 2.5σ _max, corresponding to 1.45 nm. A 10% larger radius was used for the neighbor lists, which were updated every 20 steps. Different ε ₀ values were then tested to maximize the agreement with the root‐mean‐square fluctuations (RMSF) of the two domains until an optimal value of 0.21 kJ mol⁻¹ was found. This choice resulted in a simulation with an unstable binding of the C‐terminal tail to the PDZ1 domain. Subsequently, a new simulation was performed using the resulting multi‐eGO force field for all the residues but the latest 15 belonging to the C‐terminal tail, the rationale being that the interaction of the tail with the PDZ1 domain should be considered as a “ligand binding” process associated to a different energy scale. This additional reference simulation was used to reweight the contacts of the tail with the remainder of the protein and an ad‐hoc energy scale value of 0.335 kJ mol⁻¹ was found to match the overall protein RMSF. A comparison of the training and multi‐eGO RMSF at 310 K is shown in Figure S4. Folding simulations were performed at 310 K starting from structures taken from the random coil simulation. Unfolding simulations were performed starting from the folded protein at 380 K. All simulations performed in this work are publicly available via Zenodo.

AUTHOR CONTRIBUTIONS

Valeria Pennacchietti: Investigation; formal analysis. Sara di Matteo: Investigation; formal analysis. Livia Pagano: Investigation; formal analysis. Fran Bačić Toplek: Investigation; formal analysis. Bruno Stegani: Investigation; formal analysis. Angelo Toto: Investigation; formal analysis. Julian Toso: Investigation; formal analysis. Elena Puglisi: Investigation; formal analysis. Riccardo Capelli: Investigation; formal analysis. Mariana Di Felice: Investigation; formal analysis. Francesca Malagrinò: Investigation; formal analysis. Carlo Camilloni: Conceptualization; investigation; funding acquisition; writing – review and editing; formal analysis; supervision. Stefano Gianni: Conceptualization; investigation; funding acquisition; writing – original draft; formal analysis; supervision.

Supporting information

Data S1. Supporting Information.

Pennacchietti V, di Matteo S, Pagano L, Toplek FB, Stegani B, Toto A, et al. A PDZ tandem repeat folds and unfolds via different pathways. Protein Science. 2024;33(12):e5203. 10.1002/pro.5203

DATA AVAILABILITY STATEMENT

Simulations data are publicly available via Zenodo with record https://doi.org/10.5281/zenodo.11176462, the multi‐eGO code and parameters are publicly available on GitHub at https://github.com/multi-ego/multi-eGO, use the beta2 tag for a snapshot of the repository associated to this paper.