Abstract
In this study, we investigate the quaternary ammonium-based ionic liquid (QAIL), methyltrioctylammonium bis(trifluoromethylsulfonyl)imide, [N1888][TFSI], utilizing small angle neutron scattering (SANS) measurements and polarizable molecular dynamics (MD) simulations to characterize the short- and long-range liquid structure. Scattering structure factors show signatures of three length scales in reciprocal space indicative of alternating polarity (k ∼ 0.44 Å–1), charge (k ∼ 0.75 Å–1), and neighboring or adjacent (k ∼ 1.46 Å–1) domains. Excellent agreement between simulation and experimental scattering structure factors validates various simulation analyses that provide detailed atomistic characterization of the different length scale correlations. The first solvation shell structure is illustrated by obtaining radial, angular, dihedral, and combined distribution functions, where two dominant spatial motifs, N+···N– and N+···O–, compete for optimal packing around the polar head of the [N1888]+ cation. Intermediate and long-range structures are governed by the balance between local electroneutrality and octyl chain networking, respectively. By computing the charge-correlation structure factor, SZZ, and the spatial extent of the octyl chain network using graph theory, the bulk-phase structure of [N1888][TFSI] is characterized in terms of electrostatic screening and apolar domain formation length scales.
1. Introduction
Ionic liquids (ILs) are multifaceted materials that have accelerated innovation in diverse domains, including carbon capture and sequestration (CCS),1 rare earth element (REE) extraction,2,3 water desalination,4 nanoparticle (NP) coating,5 rocket propulsion,6 and solar cell manufacturing.7 ILs are used as electrolytes in electrochemical applications and have garnered recent interest as replacements to typical organic electrolytes in lithium-ion batteries because of their numerous advantageous properties: broad electrochemical windows (>4 V),8,9 high thermal stabilities (250–400 °C),10 low vapor pressures, and nonflammability. Such macroscopic properties are a direct consequence of the fundamental electrostatic and structural characteristics. For example, strong intermolecular Coulombic attractive forces between cations and anions lead to large cohesive energies that dictate ion transport (i.e., high viscosity) and thermodynamics (i.e., low vapor pressure). More broadly, ILs have hypothetical tunability, where “targeted” molecular and compositional modifications—size and mass,11−14 side-chain length,15−18 conformational flexibility,11,13,18−23,23,24 charge asymmetry,25−30 chemical functionalization,23,31−35 mixture concentration and solvation36−41—can influence (and ideally control) thermophysical properties.42
The bulk-phase liquid structure plays
an instrumental role in many
of the mentioned applications of ILs. In electrochemical applications,
the interfacial IL structure in addition to the bulk structure has
an important influence on the system behavior. As a solvation shell
transitions from the bulk to an interface, the ion packing is altered,
and resulting electrical double layers (EDLs) form layers of alternating
charge for up to several nanometers away from an electrode surface.43−48 Characterizing EDL formation and behavior for ILs is an ongoing
research area.46,49,50 Notable features of the EDL, such as ion ordering and layering,
applied voltage-dependence, or electrode-surface-dependence, are commonly
explored by measuring the differential capacitance profile, 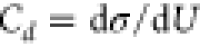 , where σ is the surface charge density,
and U is the applied voltage.46,51−61 Developing transferable EDL models across the diverse chemical composition
space of ILs remains a significant challenge, however.49,62,63 Our present work is motivated
by the importance of understanding the bulk-phase, structural characteristics
of relatively complex ILs as a prerequisite for better understanding
the interfacial structural properties of similar IL systems.64,65
, where σ is the surface charge density,
and U is the applied voltage.46,51−61 Developing transferable EDL models across the diverse chemical composition
space of ILs remains a significant challenge, however.49,62,63 Our present work is motivated
by the importance of understanding the bulk-phase, structural characteristics
of relatively complex ILs as a prerequisite for better understanding
the interfacial structural properties of similar IL systems.64,65
Quaternary ammonium cation (QA)-based ILs (QAILs) make up one structurally unique class of ILs. QAILs have drawn a burgeoning interest due to their high thermal stabilities,66 high conductivities,67 and miscibility with a wide range of solvents68,69 while benefiting from lower cost and facile synthesis.70 In the context of electrochemical interfaces, QA cations provide enhanced EDL tunability through substantial structural variation, e.g., altering Cd profiles by changing alkyl chain length,71,72 and/or functionalization, e.g., stabilizing cathodic decomposition reactions via aliphatic moieties67 or improving miscibility via introducing hydroxyethyl moieties.69 Optimal tuning remains a challenge, however, due to the complex and broad-spanning bulk-phase structural behavior that QAILs encompass. Depending on the QA ion choice, the resulting bulk phase behavior can resemble typical room temperature ILs (RTILs), IL crystals (smectic, nematic, or columnar), or even ionic plastic crystals.73
QAILs are typically composed of tetraalkylammonium-based cations, N+R4, in which aliphatic or aromatic substituents, R, link to a positive nitrogen center; the length, symmetry, and type of the R group heavily influence physical properties and crystallinity.73 Just as the well-known ansatz, “If you want to understand function, study structure!”,74 defining features of QAILs are commonly explored through their bulk-phase, structural properties.75 In the case of aprotic, tetraalkylammonium-based ILs (i.e., trialkylmethylammonium, [N1nnn]+, for some alkyl chain length n), a limited number of experimental (e.g., neutron76,77 or X-ray scattering78−84) and molecular simulation85−88 studies have sparked debate regarding the nature of their short- and long-range ordering.
Pott and Méléard79 conducted
one of the first systematic studies of [N1nnn]+ for n = 4, 6, and 8 with the common anion, bis(trifluoromethanesulfonyl)imide,
or [TFSI]−. With corroborating molecular dynamics
(MD) simulations,88 low wavevector “prepeaks”
(k ≈ 0.4–0.6 Å–1) in static X-ray scattering structure factors, S(k), were reported as signatures of a “disordered
smectic phase A”, which is indicative of interdigitated bilayers
demarcated by polar and hydrophobic regions. These conclusions suggested
that, ostensibly, [N1nnn]+-based ILs behave
like 1-alkyl-3-methylimidazolium, [Cnmim]+-based
IL crystals with 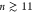 .89−91 However, upon further inspection
by Santos et al.,80 experimental and computational
analyses of temperature-dependent S(k) for [N1444][TFSI] showed no sign of mesoscopic ordering,
but rather that, the low k prepeaks were more appropriately
ascribed to the IL’s anisotropic solvation environment. Evidently,
the challenge of interpreting low k peaks has necessitated
numerous other investigations.77,82,86,87,90,92 Nonetheless, more recent efforts increasingly
agree that ILs generally exhibit three disparate S(k) domains, where low, intermediate, and high k peaks highlight the existence of nanoscale structural
heterogeneity from polar–apolar group alternation, positive–negative
charge alternation, and adjacency of neighboring cation–anion
pairs, respectively.92,93
.89−91 However, upon further inspection
by Santos et al.,80 experimental and computational
analyses of temperature-dependent S(k) for [N1444][TFSI] showed no sign of mesoscopic ordering,
but rather that, the low k prepeaks were more appropriately
ascribed to the IL’s anisotropic solvation environment. Evidently,
the challenge of interpreting low k peaks has necessitated
numerous other investigations.77,82,86,87,90,92 Nonetheless, more recent efforts increasingly
agree that ILs generally exhibit three disparate S(k) domains, where low, intermediate, and high k peaks highlight the existence of nanoscale structural
heterogeneity from polar–apolar group alternation, positive–negative
charge alternation, and adjacency of neighboring cation–anion
pairs, respectively.92,93
In this work, we contribute to the ongoing discourse on long-range structure of [N1nnn]+-based QAILs by presenting a detailed structural analysis of the methyltrioctylammonium bis(trifluoromethylsulfonyl)imide, [N1888][TFSI]. The present study is partially motivated by recent experimental investigations of [N1888][TFSI] at electrochemical interfaces, for which there are open questions regarding the interfacial IL structure.64,65,94 For instance, Klein et al.65 posit two equally plausible, yet distinct, EDL models based on neutron reflectometry (NR) experiments for various solid–[N1888][TFSI] interfaces: the interfacial structure either (1) remains indistinguishable from the bulk on an unbiased surface or (2) contains one ion-rich layer of like-species (i.e., cations or anions) near the natively charged solid surface. In this work, we conduct small angle neutron scattering (SANS) experiments on the bulk [N1888][TFSI] to investigate the liquid structure at temperatures of 300, 330, 360, and 400 K. The neutron structure factors reported here complement X-ray structure factors that have been previously reported for [N1888][TFSI] IL.79 In addition, we perform molecular dynamics (MD) simulations utilizing an ab initio, polarizable force field to characterize short- and long-range coordination environments with atomistic resolution. The structure factors computed from the MD simulations are in excellent agreement with both the experimental neutron and the X-ray scattering data, validating the reliability of subsequent simulation analysis. From the simulations, we compute radial, angular, dihedral, and combined distribution functions to illustrate the ion structuring, as well as a novel analysis of structurally heterogeneous domains using graph theory.95,96
2. Methods
2.1. Small Angle Neutron Scattering
Small angle neutron scattering experiments were conducted on the EQ-SANS instrument at Spallation Neutron Source at Oak Ridge National Laboratory.97,98 Measurements were performed at a 1.3 m sample-to-detector distance using a wavelength band defined by a minimum wavelength of 1 Å, covering scattering wavevectors ranging from 0.07 to 1.5 Å–1. The sample was loaded in a 1 mm quartz cell and measured at 300, 330, 360, and 400 K. The obtained data were reduced after correcting for the detector sensitivity and subtracting background scatterings. The data were converted into absolute scale intensities (cm–1) using a porous silica standard sample.97 Methyltrioctylammonium bis(trifluoromethylsulfonyl)imide, [N1888][TFSI] (purity 99%), was purchased from Iolitec (Alabama, US) and used as received.
2.2. Molecular Dynamics Simulations
We perform MD simulations of bulk [N1888][TFSI] IL in the NPT ensemble at 300, 400, 450, and 500 K temperatures and 1 bar pressure. The chemical structures of the ion pairs are shown in Figure 1a,b. The relatively long alkyl chains result in an overall, highly viscous (∼600 mPa s64) bulk liquid, requiring careful attention to statistical sampling in the simulations. Moreover, given the structurally complex and relatively bulky [N1888]+ cation (Figure 1a), we rigorously search for potential artifacts of finite simulation domain size, as discussed in Section 3.1. While Section 3.1 contains simulation benchmarks for a range of system sizes consisting of 200, 900, and 1600 ion pairs, unless otherwise stated, the remainder of the manuscript focuses on simulations of the 1600 ion pair system. Each simulation utilizes the previously developed SAPT-FF force field, which is an ab initio, polarizable atomistic model.99,100 Simulations are carried out with the OpenMM simulation software version 7.7.101 We utilize a dual-Langevin thermostat scheme102 for efficient treatment of Drude oscillators and set the friction coefficients for both thermostats to 1 ps–1; a Monte Carlo barostat was used for pressure coupling. Long-range electrostatics were computed using the particle mesh Ewald (PME) method,103 and van der Waals (VDW) interactions were truncated at 1.4 nm. All simulations were conducted on NVIDIA Tesla V100 GPUs for 100 ns to 1 μs of total sampling time at timesteps of 1 fs, with the longer trajectories for improved sampling at the lower temperature (e.g., 300 K); systems requiring greater sampling time were split up over several, separate MD trajectories as described in the Supporting Information. All simulation conditions are summarized in Table S1. All force field files and relevant scripts are given in the Supporting Information. A representative snapshot of the equilibrated ionic liquid system is shown in Figure 1c.
Figure 1.
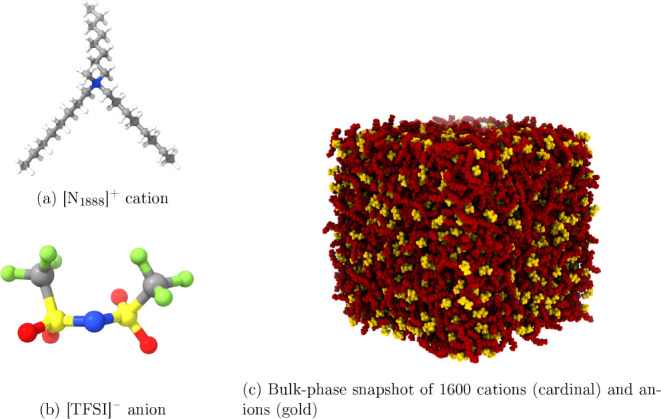
Molecular and bulk-phase structure of [N1888][TFSI] cation/anion pairs. Atoms include hydrogen (white), carbon (gray), oxygen (red), nitrogen (blue), sulfur (yellow), and fluorine (green).
2.2.1. Force Field Evaluation
To verify
force field accuracy, a number of macroscopic properties were computed
from ensemble averages of the simulation trajectory. The transferability
of bond, angle, improper dihedral, and nonbonded terms for the SAPT-FF
force field has been discussed in previous work;99,100 however, we further investigate the anion and cation proper dihedral
angles as they are a key source of conformational flexibility and
consequently affect bulk-phase behavior.13,104 As similar to other ILs,100 the population
of TFSI anions is composed of ∼67/15% cisoid (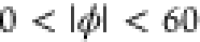 ) and transoid (
) and transoid (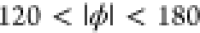 ) conformers, as shown by the “pseudo”
dihedral distribution functions (DDFs) of ϕC–S–S–C in Figure S1. Note that this is a stark
contrast from the transoid-dominated [N1444][TFSI] simulations conducted by Santos et al.80 and Lima et al!82 This behavior
is rationalized by the influence of cation/anion ion-pair interactions,
resulting in steric and packing constraints not present in the gas
phase,105 as discussed at the length by
McDaniel et al.100 Similarly, the C–C–C–C
DDFs are composed of ∼20/75% gauche (
) conformers, as shown by the “pseudo”
dihedral distribution functions (DDFs) of ϕC–S–S–C in Figure S1. Note that this is a stark
contrast from the transoid-dominated [N1444][TFSI] simulations conducted by Santos et al.80 and Lima et al!82 This behavior
is rationalized by the influence of cation/anion ion-pair interactions,
resulting in steric and packing constraints not present in the gas
phase,105 as discussed at the length by
McDaniel et al.100 Similarly, the C–C–C–C
DDFs are composed of ∼20/75% gauche (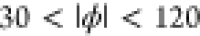 ) and trans (
) and trans (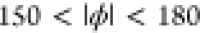 ) conformers. This distribution is in semiquantitative
agreement with quantum mechanical potential energy scans106 and numerous n-alkane conformational
statistics in bulk liquids107 (e.g., liquid
octane108,109).,
) conformers. This distribution is in semiquantitative
agreement with quantum mechanical potential energy scans106 and numerous n-alkane conformational
statistics in bulk liquids107 (e.g., liquid
octane108,109).,
Furthermore, the simulated
density (1.126 g cm–3) shows excellent agreement
within 2% of the experimental density (1.110 g cm–3).79 We also computed the liquid cohesive
energies, Ecoh, which is a fundamental
measure of how strongly bound the cations and anions are in the liquid.
For neutral organic solvents, Ecoh is
directly related to the enthalpy of vaporization ΔHvap, but for ILs, such a comparison is considerably more
complex due to ion pairing/association in the gas-phase;99 furthermore, we are not aware of experimental
ΔHvap data for the [N1888][TFSI] IL. As shown in Figure S2, the
order-of-magnitude Ecoh ∼ −550
kJ/mol and temperature-dependence are in qualitative agreement with
common alkylimidazolium ILs benchmarked in previous work.99 Interestingly, the cohesive energy of [N1888][TFSI] is ∼50–100 kJ mol–1 larger in magnitude (per ion pair) than typical alkylimidazolium/BF4-based ILs: 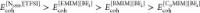 . This is consistent with the higher viscosity
of [N1888][TFSI] compared to the alkylimidazolium ILs.
The long alkyl side-chains of the [N1888]+ cation
increase the van der Waals interactions (and thus cohesive energy)
of the liquid; while a typical rule of thumb is that electrostatic
interactions should decrease for larger molecular ions, in this case,
the charge density of the [N1888]+ cation is
very localized, and TFSI anions effectively pack around the positive
nitrogen center (Section 3.4). Thus, the exact Ecoh of [N1888][TFSI] comes from the subtle interplay between nonbonded
interactions and the specific liquid structure.42 It is important to note, however, that this comparison
of energy density per ion pair is not equivalent
to comparison of volumetric energy density, due to
the disparate sizes of the ions.
. This is consistent with the higher viscosity
of [N1888][TFSI] compared to the alkylimidazolium ILs.
The long alkyl side-chains of the [N1888]+ cation
increase the van der Waals interactions (and thus cohesive energy)
of the liquid; while a typical rule of thumb is that electrostatic
interactions should decrease for larger molecular ions, in this case,
the charge density of the [N1888]+ cation is
very localized, and TFSI anions effectively pack around the positive
nitrogen center (Section 3.4). Thus, the exact Ecoh of [N1888][TFSI] comes from the subtle interplay between nonbonded
interactions and the specific liquid structure.42 It is important to note, however, that this comparison
of energy density per ion pair is not equivalent
to comparison of volumetric energy density, due to
the disparate sizes of the ions.
3. Results and Discussion
3.1. Finite-Size Effects
For computer simulations of complex liquids such as [N1888][TFSI], it is important to consider possible artifacts/finite-size effects introduced by the use of periodic simulation domains that are typically on the order of several to tens of nanometers. To circumvent larger and longer simulations, numerous corrective finite-size “scaling” methods have been developed that improve similar long-range asymptotic calculations (e.g., RDFs, Kirkwood–Buff integrals).110−123 However, finite-size scaling requires method-specific parametrization and is not necessarily transferable across all simulation analyses.124 Because [N1888][TFSI] is an electrolyte, its structural correlation functions are expected to satisfy macroscopic electrostatic screening conditions or sum rules.125 While early simulation studies of molten salts126 and ionic solutions127 emphasized the evaluation of sum rules as “an important test of the convergence of the electrolyte system to an equilibrium state”,127 to our knowledge, we report here the first example of applying sum rules to characterize finite-size effects in simulations of room-temperature ILs.
One unifying structural feature of ILs and molten salts is the anticorrelated nature of concentric coordination shells of cations and anions, which results from both charge neutrality and screening requirements.128 At a local, microscopic level, the electroneutrality condition gives rise to the following constraint on the pair-correlation or radial distribution functions,125
| 1 |
where μ and ν are types of cations
or anions, 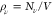 is the ion type number density
for Nν number of ions within a volume V of species ν, qν is the charge of the ion, and
is the ion type number density
for Nν number of ions within a volume V of species ν, qν is the charge of the ion, and 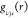 is the ion–ion radial distribution
function (RDF). Effectively, eq 1 implies that the total charge cloud surrounding a central
ion must be equal and opposite to the tagged ion’s charge,
to ensure charge neutrality.
is the ion–ion radial distribution
function (RDF). Effectively, eq 1 implies that the total charge cloud surrounding a central
ion must be equal and opposite to the tagged ion’s charge,
to ensure charge neutrality.
Electrostatic screening also markedly
dictates the long-range behavior
of the IL pair distribution functions. Being an electrolyte, the ionic
liquid is expected to exhibit electrostatic screening at long-range,
as quantified by the requirement on the dielectric response function
(in Fourier-space) that 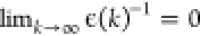 . Within linear response theory, this screening
requirement mandates conditions that the pairwise correlation functions
of the IL must satisfy. These constraints are known as the Stillinger–Lovett
sum rules, which when equivalently written in terms of the reciprocal
space, structure factor, take the form126−133
. Within linear response theory, this screening
requirement mandates conditions that the pairwise correlation functions
of the IL must satisfy. These constraints are known as the Stillinger–Lovett
sum rules, which when equivalently written in terms of the reciprocal
space, structure factor, take the form126−133
| 2 |
where ϵ∞ is the infinite frequency dielectric response. SZZ is the charge-correlation structure factor given by,
| 3 |
where ⟨···⟩ denotes an ensemble average, k is the wavevector, and
| 4 |
is the Fourier component of the microscopic charge density, where qi is the partial atomic charge, ri is the position of the atom i, and N is the total number of atoms in the system. As the electrical susceptibility is proportional to SZZ/k2,125 analysis of SZZ provides detailed insight about the electrostatic properties of the IL on microscopic length scales.134 Functionally, SZZ elucidates the length scales of the cation and anion correlations by weighting each pair correlation by the partial atomic charge, as shown in eq 4.128 We note that because the asymptotic limit of the charge correlation structure factor depends on ϵ∞, MD simulations with polarizable versus nonpolarizable force fields will fundamentally differ in their predicted ion structuring, as previously discussed in detail.128 In this work, all simulations employ a polarizable force field and thus ϵ∞ > 1, so that the right-hand side of eq 2 will be less than unity, as illustrated below.
Verifying that eq 2 is satisfied within a computer simulation of an IL or any other electrolyte is an important test of equilibrium properties. Violation of the Stillinger–Lovett condition (eq 2) would imply either that the simulation provides insufficient statistics, is not at equilibrium, or is in a metastable state, or that substantial finite-size effects exist.127 To this end, we evaluated the charge-correlation structure factor from eq 3 for three equilibrated [N1888][TFSI] systems with different computational domain sizes consisting of 200, 900, and 1600 ion pairs. Leveraging particle-mesh Ewald (PME)103 algorithms, the structure factor SZZ was calculated directly in reciprocal space based on previously described methods.128 The resulting SZZ/k2 curves are plotted in units kBT/4π for correspondence with eq 2, as shown in Figure 2 for the three different sized systems.
Figure 2.
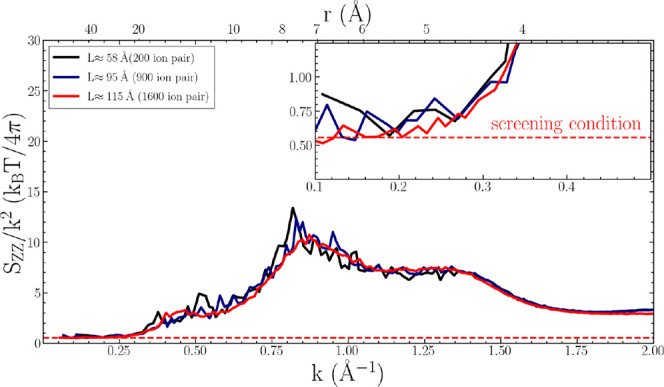
Charge-correlation structure factor SZZ for [N1888][TFSI] system sizes of length 58 Å (200 ion pairs, black curve), 95 Å (900 ion pairs, navy blue curve), and 115 Å (1600 ion pairs, red curve).
As will be discussed in further detail in later sections, the primary peaks in Figure 2 (k ∼ 0.85 Å–1) reflect length scales of real-space charge oscillations. However, the Stillinger–Lovett screening condition provides an important check on the validity of the predictions from these different system-size simulations. For various ILs (and indeed most liquids in general), the infinite frequency dielectric constant is approximately ϵ∞ ≈ 2,133,135,136 giving a value of ∼0.5 for the right-hand side of eq 2. As highlighted by the inset in Figure 2, all system sizes converge to the 1 – (ϵ∞ – 1)/ϵ∞ ≈ 0.5 asymptotic limit for typical ILs. The implications of mitigated finite size effects are significant—all subsequent static and structural analyses obey the charge sum rules and long-range electrostatic behavior of electrolytes. Nonetheless, the quantitative analysis of long-range correlations of such bulky ILs requires sufficient temporal and spatial statistics. Practically, the 1600 ion pair system provides enough of a length scale (L/2 ≈ 57.5 Å) to observe correlated behavior of the apolar domains, as will be shown in later sections. Due to these considerations, only simulation results for the large 1600 ion pair system will thus be discussed for the remainder of the paper.
3.2. Scattering Structure Factor Analysis
Like the functional form of eq 3, the X-ray and neutron scattering structure factors can be calculated from fluctuations of the microscopic number density,
| 5 |
where now microscopic number density 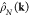 as a function of the k momentum
transfer variable is defined based on the type of scattering. In the
case of X-ray, the scattering amplitude is determined by elastic interaction
with the electron density of a sample material, resulting in
as a function of the k momentum
transfer variable is defined based on the type of scattering. In the
case of X-ray, the scattering amplitude is determined by elastic interaction
with the electron density of a sample material, resulting in
| 6 |
such that the atomic form factor, 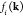 , serves
to “weight” the pairwise
correlations observed in the scattering experiment. For scattering
at small wavevectors as considered in this work, the k-dependence of
, serves
to “weight” the pairwise
correlations observed in the scattering experiment. For scattering
at small wavevectors as considered in this work, the k-dependence of 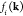 is typically small and
is typically small and 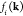 can be
approximated by the atomic number.
The asymptotic limit of the X-ray SNN is
can be
approximated by the atomic number.
The asymptotic limit of the X-ray SNN is
| 7 |
where χT is the isothermal compressibility of the liquid.
Analogously, neutron SNN is the result of elastic interactions with atomic nuclei, based on coherent scattering lengths. Thus, we calculate the scattering amplitude for the neutron structure factor by
| 8 |
where 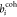 is the coherent scattering length of the
nucleus of atom i.137 Any
incoherent scattering background is ignored in the neutron SNN calculations, as it only
adds a constant background as with the experimental measurements.
is the coherent scattering length of the
nucleus of atom i.137 Any
incoherent scattering background is ignored in the neutron SNN calculations, as it only
adds a constant background as with the experimental measurements.
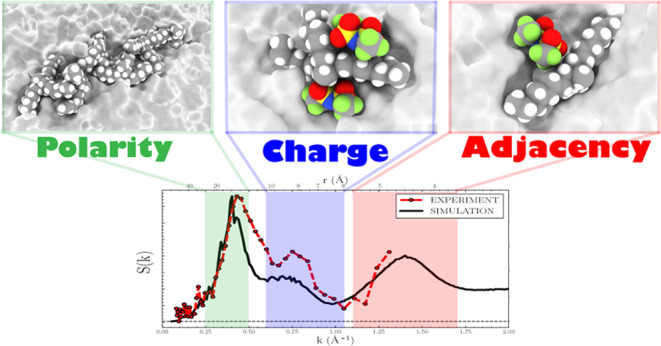
Small angle neutron scattering (SANS) experiments were performed on the bulk [N1888][TFSI] IL at four different temperatures of 300 K, 330 K, 360 K, and 400 K. The results from the SANS experiments are shown in Figure 3. The scattering is governed by three characteristic local maxima, a prepeak at k ∼ 0.44 Å–1 followed by two peaks at k ∼ 0.75 Å–1 and k ∼ 1.46 Å–1 within the k = 0.1–1.6 Å–1 range. Each peak is a feature of alternation within the bulk [N1888][TFSI], a behavior observed in common IL mixtures as well.138 At k ∼ 0.44 Å–1, the prepeak indicates the alternation of the polar (i.e., [TFSI] and the [N1111] ammonium head of [N1888]) and apolar (i.e., the octyl chains of [N1888]) groups, a feature that accounts for structural heterogeneity in a number of ILs.77,93 The strong peak at k ∼ 0.75 Å–1 reflects charge oscillation patterns between cations and anions, which is a general feature in molten salts and ILs, but the length scale for this feature is system dependent (ion size, structure, etc.).125 The final peak near k ∼ 1.46 Å–1 is attributed to correlations between adjacent atoms with strong Coulomb interactions. We follow the nomenclature by Araque et al.93 for each peak as the “polarity”, “charge”, and “adjacency” domain.
Figure 3.
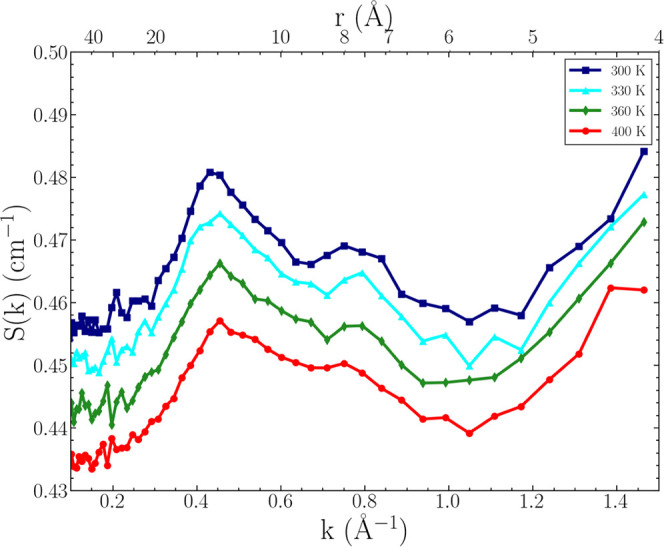
Temperature-dependent small angle neutron scattering (SANS) experimental measurements for [N1888][TFSI] ionic liquid.
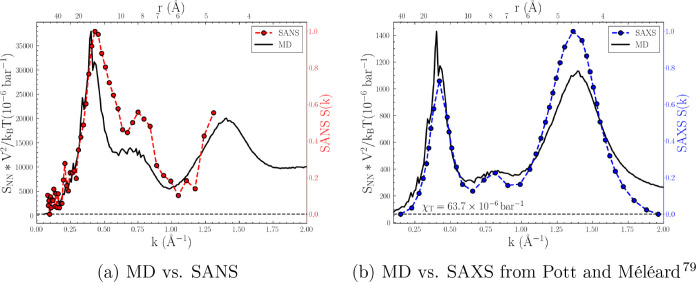
In Figure 4a, we
compare the predicted neutron structure factor from the simulations
to the experimental neutron scattering data (Figure 3) at 300 K. Additionally in Figure 4b, we compare the predicted
X-ray structure factor to previous experimental, small-angle X-ray
scattering (SAXS) data for [N1888][TFSI] reported by Pott
and Méléard.79 It is observed
that both neutron and X-ray SNN comparisons show good agreement between simulations and experiments.
The peak positions and relative error are provided in Table S2, showing ≤8% difference across
all polarity, charge, and adjacency peaks. The computed isothermal
compressibility from the X-ray SNN asymptotic limit, 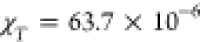 bar–1, is a reasonable
value relative to that for commonly studied, imidazolium ILs,128 but to our knowledge, there is no existing
experimental data for χT for the
[N1888][TFSI] IL. We note that there is slightly greater
error in the predicted neutron structure factor compared to that of
the X-ray when compared to experimental data (≤8% for SANS
and ≤5% for SAXS).
bar–1, is a reasonable
value relative to that for commonly studied, imidazolium ILs,128 but to our knowledge, there is no existing
experimental data for χT for the
[N1888][TFSI] IL. We note that there is slightly greater
error in the predicted neutron structure factor compared to that of
the X-ray when compared to experimental data (≤8% for SANS
and ≤5% for SAXS).
Figure 4.
Scattering structure factor comparisons between MD simulations and (4a) small angle neutron scattering (SANS) measurements and (4b) small-angle X-ray scattering (SAXS) measurements at 300 K.
Figure S4 shows the
temperature dependence
of the neutron and X-ray structure factors predicted from the simulations
and compared to the experimental data in Figure 3 as well as SAXS data from Pott and Méléard.79 Based on Figure S5, peak locations vary 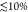 between experiment and simulation. Like
Santos et al. observed,80Figure S5 shows that at increasing length scales (or decreasing
wavevectors k), variations in peak position as a
function of temperature decrease. However, without any clear monotonic
trends, as may be generally expected, no definitive conclusions are
made regarding the temperature dependence. Santos et al.80 claim a similar conclusion, albeit at a 185–351
K range for small- and wide- angle X-ray scattering (SAXS-WAXS) measurements,
where “peak shifts are likely to be a simple consequence of
density changes in a material that has not undergone a first order
transition.”
between experiment and simulation. Like
Santos et al. observed,80Figure S5 shows that at increasing length scales (or decreasing
wavevectors k), variations in peak position as a
function of temperature decrease. However, without any clear monotonic
trends, as may be generally expected, no definitive conclusions are
made regarding the temperature dependence. Santos et al.80 claim a similar conclusion, albeit at a 185–351
K range for small- and wide- angle X-ray scattering (SAXS-WAXS) measurements,
where “peak shifts are likely to be a simple consequence of
density changes in a material that has not undergone a first order
transition.”
We also highlight the importance and complementary role of comparing SAXS and SANS experiments together. Lo Celso et al.77 showed that some neutron diffraction features, namely the initial low-k prepeak, can go undetected in SAXS measurements for certain ILs. However, the consistent prepeak–peak–peak pattern across both experimental studies shows strong evidence for structural heterogeneity due to polarity alternation in [N1888][TFSI]. Interestingly, in [N1444][TFSI], this feature was consistently missing in multiple studies,79,80,82 suggesting that the octyl chain length (∼10–11 Å) surpasses the threshold necessary for coordination of the apolar domains. We explore this hypothesis in further detail in later sections.
3.3. Partial Structure Factors
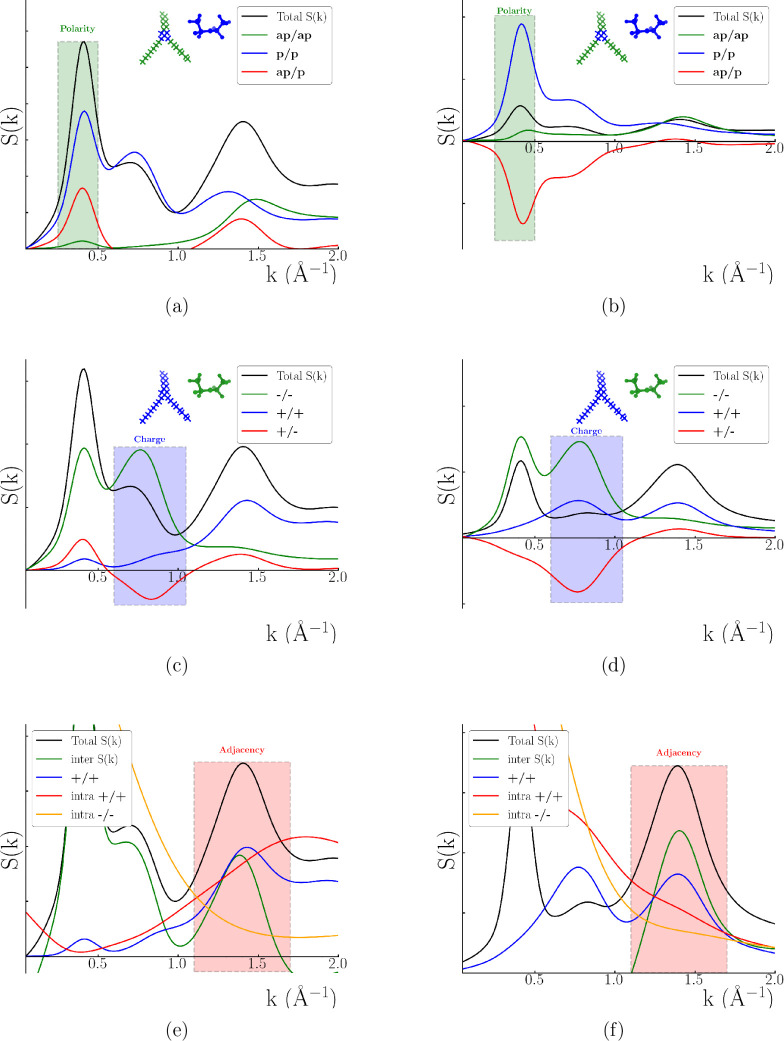
Unlike in experimental studies, the scattering structure factors computed from MD simulations can be further decomposed into partial structure factors and analyzed within wavevector-dependent partitions that elucidate the source of short- and long-range correlations. The nature of eqs 4, 6, and 8 enable partitioning schemes for the polarity,93 charge,128 and adjacency80 domains as summarized in eqs S1–S7. In Figure 5, the total neutron (a, c, e) and X-ray (b, d, f) SNN are shown with their respective partial structure factors. For ease of comparison, each partial structure factor was computed without the squared normalization term (e.g., as in eq 7).
Figure 5.
Partial neutron (left column, a, c, e) and X-ray (right column, b, d, f) scattering structure factors based on polarity (a, b), charge (c, d), and adjacency (e, f) domains. For Figures 5a–d, the colors correspond to the color of the polar/apolar or cation/anion group highlighted in the inset; the adjacency domain subfigures show the total (black), intermolecular (green), cation–cation (blue), and intramolecular anion (yellow) and cation (red) components of the structure factor.
3.3.1. Polarity Domain
The low-k prepeak (k ∼ 0.44 Å–1) is investigated via contributions from the polar–polar, polar–apolar, and apolar–apolar interactions present in [N1888][TFSI], as shown in Figure 5a,b. As highlighted in the inset, the polar components consist of the entire [TFSI] anion and cationic head, CH3N(CH2)3, while the apolar components consist of the rest of the cation tail in the octyl chain. In both the neutron and X-ray SNN, the low-k prepeak is unambiguously dominated by the polar–polar contributions. The polar–polar and apolar–polar peak–antipeak behavior observed in the X-ray SNN has been previously referred to as the “hallmark” of alternations present among “opposite-type” species.93 Thus, the peak–antipeak behavior illustrates an important structural feature, where a polar, cationic head–anion network alternates with the apolar octyl chains. The difference in relative peak heights between neutron and X-ray SNN is accounted for by the different elemental contributions to the scattering intensity, i.e., eqs 6 and 8. Namely, the partial X-ray SNN show a greater sensitivity to the high electronic density and consequently, the atomic form factors, of the TFSI anions (i.e., the “reporters of structure”92) than the neutron coherent scattering length scales.
3.3.2. Charge Domain
The intermediate peak (k ∼ 0.75 Å–1) is similarly investigated via contributions from the cation–cation, cation–anion, and anion–anion interactions. The total SNN show relatively subtle charge domain peaks (i.e., visibly a shoulder in Figure 4a and the smallest of all peaks in Figure 4b), a commonly observed feature often explained by complex interference cancellations.80,139−142 In reality, Figure 5c,d indicates definitive charge alternation based on the anion–anion and cation–anion peak–antipeak behavior, respectively. From the partial structure factor analysis, it is concluded that the anion–anion correlations are a substantial contribution to the peak (k ∼ 0.75 Å–1) in the charge domain region; this is consistent with analysis of other ILs.128 As will be discussed later, charge domain partitioning uncovers the fundamental length scale of cation–anion Coulomb interactions that align with the charge-correlation structure factor, SZZ.
3.3.3. Adjacency Domain
Lastly, the final peak at k ∼ 1.46 Å–1 can be investigated in terms of the inter- and intramolecular interactions present in the bulk-phase IL. A complimentary insight unveiled by the charge domain partitioning is the relatively large cation–cation S(k) contribution toward the high-k adjacency peak, both functionally and in relative weight, as shown in Figure 5e,f. From eq S6, the cation–cation S(k) can be simply decomposed into its relative inter- and intramolecular contributions—as shown by the red curves in Figure 5e,f, the intramolecular components were derived by sampling single molecular conformations from bulk phase trajectories, recomputing the structure factor, and scaling by the number of ions. The anion–anion intramolecular components contribute a nearly uniform background signal to the overall adjacency peak. Between the neutron and X-ray SNN, it is clear that while the intramolecular component adds a nontrivial contribution to the overall adjacency peak height, the total intermolecular components (including cation–anion cross terms) still remain the source of the k ∼ 1.46 Å–1 peak. This result is comparable to small- and wide-angle X-ray scattering and inter/intramolecular contribution comparisons for [N1444][TFSI] presented by Santos et al.,142 where intramolecular contributions only began to align with total scattering functions after k > 3 Å–1.
3.4. Domains Analysis
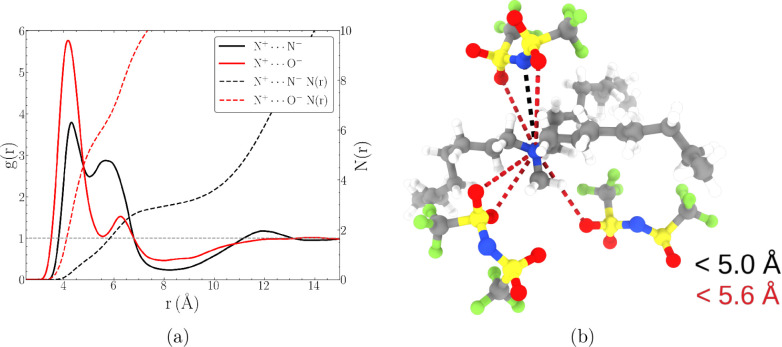
3.4.1. Real-Space Adjacency Correlation Analysis
The structural signatures
encoded by the three peaks in the structure
factors can be further investigated via real-space analyses, as done
in the ensuing sections. The adjacency domain in real-space can be
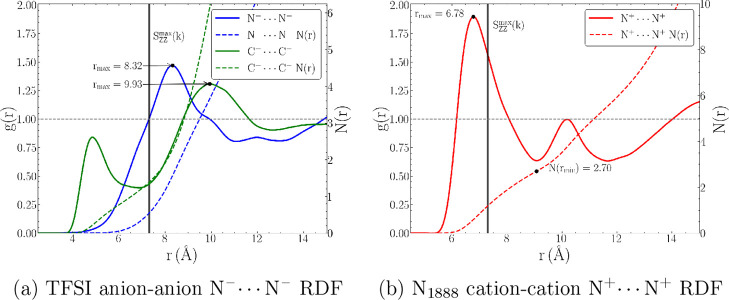
investigated by the radial distribution functions (RDFs), shown in Figure 6a. The peak heights
of the N+···O– and N+···N– are located at 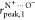 = 4.18 Å and
= 4.18 Å and 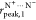 = 4.33 Å, respectively. This length
scale aligns remarkably with the adjacency peaks in Figure 4, 2π/1.46 ≈ 4.30
Å. The RDF peaks also highlight two underlining motifs where
the [TFSI] anion is facing the cation through the N– or O–, as shown in Figure 6b. The relative heights of the peaks indicate
that the N+···O– coordination
site is more favorable than the N+···N–. The running coordination numbers, N(r), provide further insight into the coordination
environment within the first solvation shell of the cation–anion
pairs. We compute the N(r) from eq 9,
= 4.33 Å, respectively. This length
scale aligns remarkably with the adjacency peaks in Figure 4, 2π/1.46 ≈ 4.30
Å. The RDF peaks also highlight two underlining motifs where
the [TFSI] anion is facing the cation through the N– or O–, as shown in Figure 6b. The relative heights of the peaks indicate
that the N+···O– coordination
site is more favorable than the N+···N–. The running coordination numbers, N(r), provide further insight into the coordination
environment within the first solvation shell of the cation–anion
pairs. We compute the N(r) from eq 9,
| 9 |
where 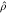 is the average number density of the observed,
anion atoms,
is the average number density of the observed,
anion atoms, 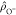 and
and 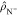 . At the first local minima of the RDFs,
the competition of the two motifs is clearly quantified by
. At the first local minima of the RDFs,
the competition of the two motifs is clearly quantified by 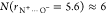 as opposed to
as opposed to 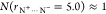 . The second local minima
are ancillary;
the secondary peaks are simply induced by the motifs in the first
peaks by the alternate atom on the same molecule.
. The second local minima
are ancillary;
the secondary peaks are simply induced by the motifs in the first
peaks by the alternate atom on the same molecule.
Figure 6.
(a) Atomistic radial distribution function (solid lines) and corresponding running coordination number (dashed lines) for N+···N– (black) and N+···O– (red) coordination sites. (b) Representative snapshot of first solvation shell consisting of three coordinated anions to single cation; black and red lines highlight coordinated N– and O– atoms coordinated with cationic nitrogen, N+ within approximate first solvation shell radius, respectively; corresponding 360 deg video provided in the Supporting Information.
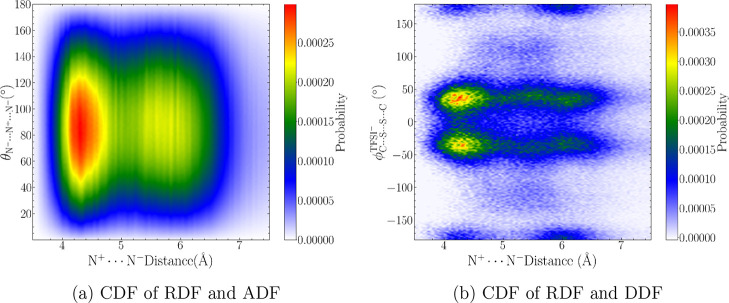
While the RDFs illustrate the connectivity of pairwise coordination, the intricate detail of the first solvation shell may be further elucidated with angular and dihedral distribution functions (ADFs and DDFs, respectively). However, ADFs and DDFs alone do not necessarily preserve the symmetries recovered from the RDFs—thus, we apply combined distribution functions (CDFs), which have shown to be a powerful tool to illustrate ion coordination using the atomistic detail provided by computer simulations.143 Concretely, Figure 7 shows a two-dimensional probability density of pairwise N+···N– distances binned with N–···N+···N– angles (Figure 7a) and proper C···S···S···C pseudodihedral angles (Figure 7b). The N+···N– motif optimally packs within the first solvation shell by forming an angle of 60° < θ < 120° with respect to a neighboring N+···N– coordination site. Just as corroborated by the snapshot in Figure 6b, anions pack within the bisector defined by the octyl chains of the [N1888]+ cation, a similar conclusion made by Lima et al.82 for a [N14444]+-based system. Moreover, Figure 7b indicates that the first solvation shell is predominantly composed of cisoid conformations based on the high density of ±45° anions at the corresponding first peak in the RDF.
Figure 7.
Combined distribution functions (CDFs) of radial distribution functions (RDFs) with (a) angular and (b) dihedral distribution functions.
Finally, we show the three-dimensional, spatial
distribution function
(SDF) calculated in TRAVIS144 to fully
illustrate the short-range cation–anion packing. As shown in Figure 8a, the solid red
(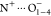 ) and solid black (N+···N–) isosurfaces highlight how the anion preferentially
occupies the space between apolar octyl chains. When plotted at the
same contour level (11.3 nm–3), the SDF isosurfaces
clearly show an increase in surface of red,
) and solid black (N+···N–) isosurfaces highlight how the anion preferentially
occupies the space between apolar octyl chains. When plotted at the
same contour level (11.3 nm–3), the SDF isosurfaces
clearly show an increase in surface of red, 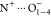 “blobs” within the first
solvation shell (∼102 Å–2) compared
to the black (∼63 Å2). The 360° video
included in the Supporting Information shows
apparent overlap of red and black isosurfaces and, thus, similarity
in the local position of the anion nitrogens and oxygens. Additionally,
the SDF in Figure 8b provides a local perspective of cation–cation coordination.
Based on the intercation carbon–carbon RDFs (Figure S7), the most apparent structuring occurs at the tail
of the octyl chains; to this end, a single terminal carbon (e.g.,
C8) was selected as a reference atom and the subsequent
SDF was computed for all possible terminal-carbon–carbon coordination
sites (C8···C1–25). The
morphological difference between the cation–anion (Figure 8a) and cation–cation
(Figure 8b) SDF isosurfaces
corroborates the “punctured sphere” versus “sleeve-like”
spatial arrangement of the polar and apolar networks, respectively.88 However, as we will further investigate in Section 3.4.3, understanding
structural nanosegregation requires analysis of apolar domain coordination globally, i.e., the local description of
cation–cation coordination provided by an SDF manifests in
long-range correlations.
“blobs” within the first
solvation shell (∼102 Å–2) compared
to the black (∼63 Å2). The 360° video
included in the Supporting Information shows
apparent overlap of red and black isosurfaces and, thus, similarity
in the local position of the anion nitrogens and oxygens. Additionally,
the SDF in Figure 8b provides a local perspective of cation–cation coordination.
Based on the intercation carbon–carbon RDFs (Figure S7), the most apparent structuring occurs at the tail
of the octyl chains; to this end, a single terminal carbon (e.g.,
C8) was selected as a reference atom and the subsequent
SDF was computed for all possible terminal-carbon–carbon coordination
sites (C8···C1–25). The
morphological difference between the cation–anion (Figure 8a) and cation–cation
(Figure 8b) SDF isosurfaces
corroborates the “punctured sphere” versus “sleeve-like”
spatial arrangement of the polar and apolar networks, respectively.88 However, as we will further investigate in Section 3.4.3, understanding
structural nanosegregation requires analysis of apolar domain coordination globally, i.e., the local description of
cation–cation coordination provided by an SDF manifests in
long-range correlations.
Figure 8.
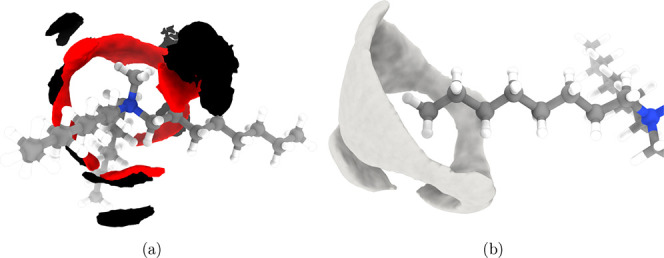
Spatial distribution functions (SDFs) of (a)  (solid red) and N+···N– (solid black) coordination sites at 11.3 nm–3 and (b) terminal carbon of one single octyl chain with every other
carbon (e.g., C8···C1–25) at 1.7 nm–3. Complete 360° videos are included
in the Supporting Information.
(solid red) and N+···N– (solid black) coordination sites at 11.3 nm–3 and (b) terminal carbon of one single octyl chain with every other
carbon (e.g., C8···C1–25) at 1.7 nm–3. Complete 360° videos are included
in the Supporting Information.
3.4.2. Charge Alternation Analysis
Beyond the first solvation shell, the intermediate and long-range structure is governed by the charge sum rules and local electroneutrality in ILs.125 While the intermediate wavevector peak (k ∼ 0.75 Å–1) in neutron and X-ray scattering factors are typically subtle or even missing, the charge correlation structure factor SZZ peak (eq 5) (as was shown in Figure 2) shows a sharp peak near the reciprocal space length scale, ∼0.85 Å–1 at 300 K. Equivalently, in real space, anion–anion (Figure 9a) and cation–cation (Figure 9b) RDFs show peaks within ∼7–10 Å in real-space, as shown in Figure 9 with the SZZ peak shown as a solid, vertical line. The atomistic RDFs involving localized negative and positive charges, N–···N– and N+···N+, respectively, span ∼7–8 Å and show excellent agreement with the SZZ peak. In previous work, this peak has been shown to identify the charge alternation length scales of common ILs,128 and for comparative purposes, Figure S6 shows the SZZ of [N1888][TFSI] (peak of ∼0.85 Å–1) compared to that of the prototypical, 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM][BF4] IL (peak of ∼1 Å–1). We also include the C–···C– (green curve in Figure 9a) as another measure of anion packing. The C–···C– exhibits a typical bifurcated peak found in the literature,128,145,146 where a peak at ∼5 Å indicates presence of hydrophobic domains on the anion (i.e., CF3) and ∼10 Å indicates longer-range coordination length scales.
Figure 9.
Radial distribution functions (RDFs) for like-species coordination, including (a) anion–anion and (b) cation–cation pairwise interactions.
Consequently, two conclusions are made evident. First, the scattering structure factor peaks, either SNN or SZZ, directly correspond to the distance between successive coordination shells (i.e., with respect to some central ion) based on like-species (i.e., cation–cation and anion–anion) coordination distances. Second, compared to the common IL, [BMIM][BF4], there is a clear shift toward larger like-species distances due to the presence of apolar octyl chains that displace charged species for favorable long-range packing.
3.4.3. Polarity Alternation Analysis
As was highlighted in the Introduction, [N1888][TFSI] is a unique IL in that it exhibits both typical charge alternation domains but also long-range ordering based on low-k scattering peaks. However, the degree of ordering is often difficult to interpret from scattering peaks alone and has evidently warranted much discussion and controversy in the literature. For example, low-k peaks similar in intensity and location have been observed in ILs that span a wide-range of phase behavior, anywhere from isotropic, smectic mesophase to near-crystalline or glass-forming liquids.75 In the case of TFSI-based ILs specifically, much insight can be drawn from the vast body of X-ray78,81,147−151 and neutron152,153 scattering studies (e.g., alkyl chain length increases ordering, hydroxyl-substitutions decreases ordering, etc.). Nonetheless, interpreting phase-behavior from scattering intensities alone is challenging, given its sensitive nature to the anion electronic structure.93 To this end, we invoke a theoretical, graph-based analysis to quantify the spatial extent of the apolar, octyl-chain network, similar to previous studies.96
Only until recently have theoretical,
graph-based analyses been used to analyze MD trajectories. For instance,
Lee et al.95 explored graph-theoretical
approaches to understand ion aggregation morphology of various salt-based
solutions. Recently, Stoppleman and McDaniel96 explored the spatial extent of hydrogen bond networks by establishing
edges between neighboring water molecules (nodes) based on O···H
distance and O···H···O angle criteria.
We build on this work to understand the spatial extent of octyl chains
within the overarching molecular simulation domain. In doing so, we
define a graph  composed of molecular nodes
composed of molecular nodes  and
criteria-based edges,
and
criteria-based edges, 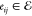 . In each frame
of the MD trajectory, we
search all [N1888]+ cations (within a cutoff)
that neighbor each other by two, tunable critical parameters: minimum
interatomic carbon–carbon distance,
. In each frame
of the MD trajectory, we
search all [N1888]+ cations (within a cutoff)
that neighbor each other by two, tunable critical parameters: minimum
interatomic carbon–carbon distance, 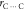 , and the minimum number of such coordination
sites, n. To determine
, and the minimum number of such coordination
sites, n. To determine 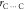 , we compute all combinations of the atomistic,
carbon–carbon RDFs and report a select few in Figure S7. In Santos et al.,80 it
was sufficient to report such an RDF to discount the interdigitated
bilayer hypothesis specifically for [N1444][TFSI] presented
by Pott and Méléard.79 However,
we use this RDF as a means to bound the
, we compute all combinations of the atomistic,
carbon–carbon RDFs and report a select few in Figure S7. In Santos et al.,80 it
was sufficient to report such an RDF to discount the interdigitated
bilayer hypothesis specifically for [N1444][TFSI] presented
by Pott and Méléard.79 However,
we use this RDF as a means to bound the 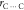 criterion in determining the overall octyl-chain
graph network. We tune n by expecting an upper bound
of 24—i.e., all octyl chains are interdigitated—and
lower bound of at least one. For each frame in the MD trajectory,
we compute the diameters, d, of all disjoint subgraphs,
criterion in determining the overall octyl-chain
graph network. We tune n by expecting an upper bound
of 24—i.e., all octyl chains are interdigitated—and
lower bound of at least one. For each frame in the MD trajectory,
we compute the diameters, d, of all disjoint subgraphs, 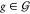 , defined as:
, defined as:
| 10 |
where 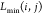 is the minimum distance (in number of nodes)
between nodes i and j for all
is the minimum distance (in number of nodes)
between nodes i and j for all 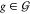 .
.
The octyl chain network is then
characterized by the probability
distribution for g to have a certain diameter, P(d). Parameter tuning was explored for 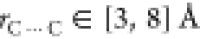 and
and 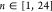 ; as expected,
extreme ends of the parameter
space (
; as expected,
extreme ends of the parameter
space (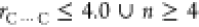 ) show very noisy and limited (if any) statistics
across the range of diameters that span the length of the simulation
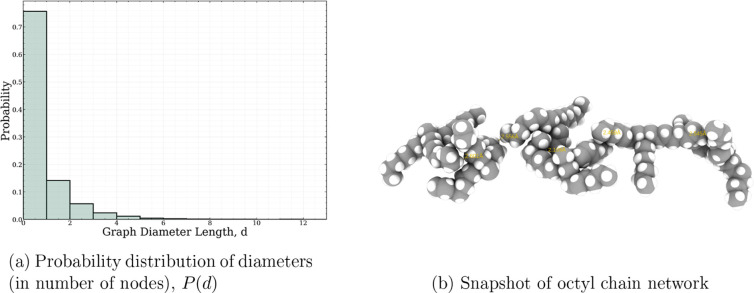
box size, 115 Å. Figure 10a thus illustrates the most representative behavior of P(d) for a selected
) show very noisy and limited (if any) statistics
across the range of diameters that span the length of the simulation
box size, 115 Å. Figure 10a thus illustrates the most representative behavior of P(d) for a selected 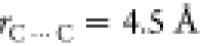 and n =
1. While small
probabilities of octyl chains appear in apolar networks that span
up to six subsequent octyl chains (e.g., Figure 10b), the predominant long-range motif is
evident by the large peak at the d = 1 node. By this
measure, the apparent low-k peak from Figure 4 can be interpreted as ∼2–3
neighboring [N1888]+ cations correlated by their
octyl chains.
and n =
1. While small
probabilities of octyl chains appear in apolar networks that span
up to six subsequent octyl chains (e.g., Figure 10b), the predominant long-range motif is
evident by the large peak at the d = 1 node. By this
measure, the apparent low-k peak from Figure 4 can be interpreted as ∼2–3
neighboring [N1888]+ cations correlated by their
octyl chains.
Figure 10.
Probability distribution of (10a) octyl chain network diameters and (10b) visual snapshot of six [N1888]+ cations connected via distance criterion.
So then why, despite its large, bulky molecular structure, does [N1888][TFSI] more so resemble an isotropic liquid than a liquid-crystalline material? Between a visual inspection from Figure 1c and quantitative analysis from Figure 10a, it is clear that nanoscale spatial heterogeneities exist; however, the degree of ordering does not lead to “orientational and/or positional long-range order in at least one direction” (e.g., periodic stacking of molecular layers), a requisite for ionic liquid crystal (ILC) or mesomorphic behavior.154 The answer is 2-fold, stemming from (1) the subtle balance between the relative apolar to polar volume, i.e., Valkyl: Vpolar(155) and (2) the crucial importance of electrostatic screening. It is known that larger Valkyl: Vpolar ratios induce higher degrees of nanosegregation of charged and uncharged domains, leading to highly ordered systems and smectic behavior.89,154 In the case of [N1888][TFSI], on one hand, the relatively large TFSI anion can generally inhibit long-range ordering due to its charge delocalization and increased configurational entropy from the low N–S torsional energy barrier.156 As an example, the study of several 1-methyl-3-(n-alkyl)imidazolium ([CnMIM]) [TFSI]−-based salts shows liquid crystal (LC) behavior only after the alkyl chain length was increased to n = 22.154 Moreover, Goossens et al.154 highlight that variations in Valkyl: Vpolar can “only show a smectic mesophase if the ionic headgroups and the alkyl chains are able to project comparable cross-sectional areas onto the ionic sublayer planes. As such, the salts with three equivalent long n-alkyl chains require larger anions than the corresponding salts with only two long n-alkyl chains to exhibit a smectic LC phase.”
4. Conclusion
We present a joint simulation and experimental study of a quaternary ammonium-based IL, [N1888][TFSI], to comprehensively characterize its bulk-phase structure. Small angle neutron scattering (SANS) experiments were conducted for a range of temperatures, and the measured structure factors were utilized to validate simulation predictions; the predicted structure factors show excellent agreement between simulation and the experiment data, as well as previously published small-angle X-ray scattering (SAXS) data.79 By partitioning the computed scattering structure factors by polar/apolar, cation/anion, and inter/intramolecular components, the reciprocal-space results indicate alternation of polarity (k ∼ 0.44 Å–1), charge (k ∼ 0.75 Å–1), and adjacency (k ∼ 1.46 Å–1) domains.
Moreover, we explore each domain via further real-space analyses. For instance, the radial distribution functions (RDFs) highlight two spatial motifs where the anion nitrogen and oxygen competitively pack around the cationic polar head. Combined distribution functions (CDFs) complete the analysis of the first solvation shell by elucidating the favorable packing of anions (1) within the bisector of the cation octyl chains and (2) in the cisoid conformation. At the intermediate range, the charge correlation structure factor, SZZ, recovers the exact length scale of the distance between subsequent solvation shells that manifest from charge oscillations. At long range, we employ a novel, graph network analysis to conclude the spatial extent of coordinated cations spanning two to three molecules, enough to show signatures of nanoscale heterogeneity but still resemble an isotropic IL.
Quaternary ammonium-based ionic liquids (QAILs) resemble a sandbox for tuning the chemical properties at electrochemical interfaces. In practice, however, their fundamental behaviors in charged and dynamic environments are inescapably linked to the static, bulk-phase liquid structure. In future work, we aim to explore the pertinent question, how does voltage modulate the electrical double layer of [N1888][TFSI] at charged interfaces? The definitive understanding of motifs and long-range phase behavior will provide a means to assess at what length scales the electrode’s presence influences the IL. Moreover, by combining both bulk-phase and interfacial studies, tunability and optimization can be made possible.
Acknowledgments
S.M.P. acknowledges support from the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Department of Energy Computational Science Graduate Fellowship under Award Number DE-SC0022158 and the NERSC ERCAP 2022 grant number ERCAP0021857. J.G.M. acknowledges partial support from the Air Force Office of Scientific Research, under award FA9550-22-1-0025. A portion of this research used resources at the Spallation Neutron Source (SNS), a Department of Energy (DOE) Office of Science User Facility operated by Oak Ridge National Laboratory. Small Angle Neutron Scattering measurements were carried out on the EQ-SANS Diffractometer at the SNS, which is sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, DOE. B.G. acknowledges partial support for beamline experiments from Breakthrough Electrolytes for Energy Storage (BEES)-an Energy Frontier Research Center (EFRC) of the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award #DE-SC0019409. J.M.K. acknowledges support from the Department of Energy Office of Science Graduate Student Research program (DOE-SCGSR).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c06255.
Summary of simulation conditions; force field benchmarks; density as function of temperature and domain size; structure factor temperature-dependence; structure factor peak location comparisons at 300 K; partial structure factor partitioning; charge-correlation structure factor and relevant RDFs; carbon–carbon atomistic RDF (PDF)
All relevant OpenMM force field files and run scripts necessary to minimally reproduce MD simulations (ZIP)
The authors declare no competing financial interest.
Supplementary Material
References
- Gurkan B. E.; de la Fuente J. C.; Mindrup E. M.; Ficke L. E.; Goodrich B. F.; Price E. A.; Schneider W. F.; Brennecke J. F. Equimolar CO2 Absorption by Anion-Functionalized Ionic Liquids. J. Am. Chem. Soc. 2010, 132, 2116–2117. 10.1021/ja909305t. [DOI] [PubMed] [Google Scholar]
- Application of Ionic Liquids on Rare Earth Green Separation and Utilization, Chen J., Ed.; Springer, 2016. [Google Scholar]
- Baxter E. T.; Zhang J.; Tan S.; Nguyen M.-T.; Zhang D.; Yuan Q.; Cao W.; Wang X.-B.; Prabhakaran V.; Glezakou V.-A.; et al. Functionalization of Electrodes with Tunable [EMIM]x[Cl]x+1- Ionic Liquid Clusters for Electrochemical Separations. Chem. Mater. 2022, 34, 2612–2623. 10.1021/acs.chemmater.1c03836. [DOI] [Google Scholar]
- Haddad A. Z.; Menon A. K.; Kang H.; Urban J. J.; Prasher R. S.; Kostecki R. Solar Desalination Using Thermally Responsive Ionic Liquids Regenerated with a Photonic Heater. Environ. Sci. Technol. 2021, 55, 3260–3269. 10.1021/acs.est.0c06232. [DOI] [PubMed] [Google Scholar]
- Hamadani C. M.; Chandrasiri I.; Yaddehige M. L.; Dasanayake G. S.; Owolabi I.; Flynt A.; Hossain M.; Liberman L.; Lodge T. P.; Werfel T. A.; et al. Improved nanoformulation and bio-functionalization of linear-dendritic block copolymers with biocompatible ionic liquids. Nanoscale 2022, 14, 6021–6036. 10.1039/D2NR00538G. [DOI] [PubMed] [Google Scholar]
- Cena N.; Blanski R. L.; Quintana A. S.; Knoerzer K. G.; Boatz J. A.; Redeker N. D.; Alabada C. D.; Marcischak J. C.; Ghiassi K. B. New room temperature ionic liquids prepared from an old phosphine: Using branching and diastereomeric mixtures to inherently benefit physical properties. J. Mol. Liq. 2023, 380, 121762. 10.1016/j.molliq.2023.121762. [DOI] [Google Scholar]
- Chao L.; Niu T.; Xia Y.; Chen Y.; Huang W. Ionic Liquid for Perovskite Solar Cells: An Emerging Solvent Engineering Technology. Acc. Mater. Res. 2021, 2, 1059–1070. 10.1021/accountsmr.1c00154. [DOI] [Google Scholar]
- Zhou Z.-B.; Matsumoto H.; Tatsumi K. Low-Melting, Low-Viscous, Hydrophobic Ionic Liquids: Aliphatic Quaternary Ammonium Salts with Perfluoroalkyltrifluoroborates. Chem.-Eur. J. 2005, 11, 752–766. 10.1002/chem.200400817. [DOI] [PubMed] [Google Scholar]
- O’Mahony A. M.; Silvester D. S.; Aldous L.; Hardacre C.; Compton R. G. Effect of Water on the Electrochemical Window and Potential Limits of Room-Temperature Ionic Liquids. J. Chem. Eng. Data 2008, 53, 2884–2891. 10.1021/je800678e. [DOI] [Google Scholar]
- Tokuda H.; Ishii K.; Susan M. A. B. H.; Tsuzuki S.; Hayamizu K.; Watanabe M. Physicochemical Properties and Structures of Room-Temperature Ionic Liquids. 3. Variation of Cationic Structures. J. Phys. Chem. B 2006, 110, 2833–2839. 10.1021/jp053396f. [DOI] [PubMed] [Google Scholar]
- Krossing I.; Slattery J. M.; Daguenet C.; Dyson P. J.; Oleinikova A.; Weingärtner H. Why Are Ionic Liquids Liquid? A Simple Explanation Based on Lattice and Solvation Energies. J. Am. Chem. Soc. 2006, 128, 13427–13434. 10.1021/ja0619612. [DOI] [PubMed] [Google Scholar]
- Slattery J. M.; Daguenet C.; Dyson P. J.; Schubert T. J. S.; Krossing I. How to Predict the Physical Properties of Ionic Liquids: A Volume-Based Approach. Angew. Chem. Int. Ed. 2007, 46, 5384–5388. 10.1002/anie.200700941. [DOI] [PubMed] [Google Scholar]
- Tsuzuki S.; Matsumoto H.; Shinoda W.; Mikami M. Effects of conformational flexibility of alkyl chains of cations on diffusion of ions in ionic liquids. Phys. Chem. Chem. Phys. 2011, 13, 5987–5993. 10.1039/c0cp02087g. [DOI] [PubMed] [Google Scholar]
- Gujt J.; Bešter-Rogač M.; Hribar-Lee B. An investigation of ion-pairing of alkali metal halides in aqueous solutions using the electrical conductivity and the Monte Carlo computer simulation methods. J. Mol. Liq. 2014, 190, 34–41. 10.1016/j.molliq.2013.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lòpez-Martin I.; Burello E.; Davey P. N.; Seddon K. R.; Rothenberg G. Anion and Cation Effects on Imidazolium Salt Melting Points: A Descriptor Modelling Study. ChemPhyschem 2007, 8, 690–695. 10.1002/cphc.200600637. [DOI] [PubMed] [Google Scholar]
- Almeida H. F. D.; Freire M. G.; Fernandes A. M.; Lopes-da Silva J. A.; Morgado P.; Shimizu K.; Filipe E. J. M.; Canongia Lopes J. N.; Santos L. M. N. B. F.; Coutinho J. A. P. Cation Alkyl Side Chain Length and Symmetry Effects on the Surface Tension of Ionic Liquids. Langmuir 2014, 30, 6408–6418. 10.1021/la501308q. [DOI] [PubMed] [Google Scholar]
- Dong K.; Liu X.; Dong H.; Zhang X.; Zhang S. Multiscale Studies on Ionic Liquids. Chem. Rev. 2017, 117, 6636–6695. 10.1021/acs.chemrev.6b00776. [DOI] [PubMed] [Google Scholar]
- Bernardino K.; Zhang Y.; Ribeiro M. C. C.; Maginn E. J. Effect of alkyl-group flexibility on the melting point of imidazolium-based ionic liquids. J. Chem. Phys. 2020, 153, 044504. 10.1063/5.0015992. [DOI] [PubMed] [Google Scholar]
- Canongia Lopes J. N.; Shimizu K.; Pádua A. A. H.; Umebayashi Y.; Fukuda S.; Fujii K.; Ishiguro S.-I. A Tale of Two Ions: The Conformational Landscapes of Bis(trifluoromethanesulfonyl)amide and N,N-Dialkylpyrrolidinium. J. Phys. Chem. B 2008, 112, 1465–1472. 10.1021/jp076997a. [DOI] [PubMed] [Google Scholar]
- Blundell R. K.; Licence P. Tuning cation-anion interactions in ionic liquids by changing the conformational flexibility of the cation. Chem. Commun. 2014, 50, 12080–12083. 10.1039/C4CC05505E. [DOI] [PubMed] [Google Scholar]
- Scarbath-Evers L. K.; Hunt P. A.; Kirchner B.; MacFarlane D. R.; Zahn S. Molecular features contributing to the lower viscosity of phosphonium ionic liquids compared to their ammonium analogues. Phys. Chem. Chem. Phys. 2015, 17, 20205–20216. 10.1039/C5CP00340G. [DOI] [PubMed] [Google Scholar]
- Endo T.; Hoshino S.; Shimizu Y.; Fujii K.; Nishikawa K. Comprehensive Conformational and Rotational Analyses of the Butyl Group in Cyclic Cations: DFT Calculations for Imidazolium, Pyridinium, Pyrrolidinium, and Piperidinium. J. Phys. Chem. B 2016, 120, 10336–10349. 10.1021/acs.jpcb.6b07166. [DOI] [PubMed] [Google Scholar]
- Philippi F.; Pugh D.; Rauber D.; Welton T.; Hunt P. A. Conformational design concepts for anions in ionic liquids. Chem. Sci. 2020, 11, 6405–6422. 10.1039/D0SC01379J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palumbo O.; Paolone A.; Philippi F.; Rauber D.; Welton T. Dynamics in Quaternary Ionic Liquids with Non-Flexible Anions: Insights from Mechanical Spectroscopy. Int. J. Mol. Sci. 2023, 24 (13), 11046. 10.3390/ijms241311046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.; Kobrak M. N. A molecular dynamics study of the influence of ionic charge distribution on the dynamics of a molten salt. J. Chem. Phys. 2009, 131 (19), 194507. 10.1063/1.3263129. [DOI] [PubMed] [Google Scholar]
- Lindenberg E. K.; Patey G. N. How distributed charge reduces the melting points of model ionic salts. J. Chem. Phys. 2014, 140 (10), 104504. 10.1063/1.4867275. [DOI] [PubMed] [Google Scholar]
- Lindenberg E. K.; Patey G. N. Melting point trends and solid phase behaviors of model salts with ion size asymmetry and distributed cation charge. J. Chem. Phys. 2015, 143 (2), 024508. 10.1063/1.4923344. [DOI] [PubMed] [Google Scholar]
- Bedrov D.; Piquemal J.-P.; Borodin O.; MacKerell A. D. J.; Roux B.; Schröder C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. 10.1021/acs.chemrev.8b00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabideau B. D.; Soltani M.; Parker R. A.; Siu B.; Salter E. A.; Wierzbicki A.; West K. N.; Davis J. H. Tuning the melting point of selected ionic liquids through adjustment of the cation’s dipole moment. Phys. Chem. Chem. Phys. 2020, 22, 12301–12311. 10.1039/D0CP01214A. [DOI] [PubMed] [Google Scholar]
- Rezaei M.; Sakong S.; Groß A. Molecular Modeling of Water-in-Salt Electrolytes: A Comprehensive Analysis of Polarization Effects and Force Field Parameters in Molecular Dynamics Simulations. J. Chem. Theory Comput. 2023, 19, 5712–5730. 10.1021/acs.jctc.3c00171. [DOI] [PubMed] [Google Scholar]
- Pringle J. M.; Golding J.; Baranyai K.; Forsyth C. M.; Deacon G. B.; Scott J. L.; MacFarlane D. R. The effect of anion fluorination in ionic liquids–physical properties of a range of bis(methanesulfonyl)amide salts. New J. Chem. 2003, 27, 1504–1510. 10.1039/B304072K. [DOI] [Google Scholar]
- Fumino K.; Wulf A.; Ludwig R. Strong, Localized, and Directional Hydrogen Bonds Fluidize Ionic Liquids. Angew. Chem. Int. Ed. 2008, 47, 8731–8734. 10.1002/anie.200803446. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Maginn E. J. The effect of C2 substitution on melting point and liquid phase dynamics of imidazolium based-ionic liquids: insights from molecular dynamics simulations. Phys. Chem. Chem. Phys. 2012, 14, 12157–12164. 10.1039/c2cp41964e. [DOI] [PubMed] [Google Scholar]
- Menges F. S.; Zeng H. J.; Kelleher P. J.; Gorlova O.; Johnson M. A.; Niemann T.; Strate A.; Ludwig R. Structural Motifs in Cold Ternary Ion Complexes of Hydroxyl-Functionalized Ionic Liquids: Isolating the Role of Cation-Cation Interactions. J. Phys. Chem. Lett. 2018, 9, 2979–2984. 10.1021/acs.jpclett.8b01130. [DOI] [PubMed] [Google Scholar]
- Niemann T.; Strate A.; Ludwig R.; Zeng H. J.; Menges F. S.; Johnson M. A. Cooperatively enhanced hydrogen bonds in ionic liquids: closing the loop with molecular mimics of hydroxy-functionalized cations. Phys. Chem. Chem. Phys. 2019, 21, 18092–18098. 10.1039/C9CP03300A. [DOI] [PubMed] [Google Scholar]
- Hanke C. G.; Lynden-Bell R. M. A Simulation Study of Water-Dialkylimidazolium Ionic Liquid Mixtures. J. Phys. Chem. B 2003, 107, 10873–10878. 10.1021/jp034221d. [DOI] [Google Scholar]
- Wu X.; Liu Z.; Huang S.; Wang W. Molecular dynamics simulation of room-temperature ionic liquid mixture of [bmim][BF4] and acetonitrile by a refined force field. Phys. Chem. Chem. Phys. 2005, 7, 2771–2779. 10.1039/b504681p. [DOI] [PubMed] [Google Scholar]
- Jiang W.; Wang Y.; Voth G. A. Molecular Dynamics Simulation of Nanostructural Organization in Ionic Liquid/Water Mixtures. J. Phys. Chem. B 2007, 111, 4812–4818. 10.1021/jp067142l. [DOI] [PubMed] [Google Scholar]
- Moreno M.; Castiglione F.; Mele A.; Pasqui C.; Raos G. Interaction of Water with the Model Ionic Liquid [bmim][BF4]: Molecular Dynamics Simulations and Comparison with NMR Data. J. Phys. Chem. B 2008, 112, 7826–7836. 10.1021/jp800383g. [DOI] [PubMed] [Google Scholar]
- Wang Y.-L.; Li B.; Sarman S.; Mocci F.; Lu Z.-Y.; Yuan J.; Laaksonen A.; Fayer M. D. Microstructural and Dynamical Heterogeneities in Ionic Liquids. Chem. Rev. 2020, 120, 5798–5877. 10.1021/acs.chemrev.9b00693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elstone N. S.; Shimizu K.; Shaw E. V.; Lane P. D.; D’Andrea L.; Demé B.; Mahmoudi N.; Rogers S. E.; Youngs S.; Costen M. L.; et al. Understanding the Liquid Structure in Mixtures of Ionic Liquids with Semiperfluoroalkyl or Alkyl Chains. J. Phys. Chem. B 2023, 127, 7394–7407. 10.1021/acs.jpcb.3c02647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippi F.; Welton T. Targeted modifications in ionic liquids - from understanding to design. Phys. Chem. Chem. Phys. 2021, 23, 6993–7021. 10.1039/D1CP00216C. [DOI] [PubMed] [Google Scholar]
- Kornyshev A. A. Double-Layer in Ionic Liquids: Paradigm Change?. J. Phys. Chem. B 2007, 111, 5545–5557. 10.1021/jp067857o. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Zhong Y.-X.; Yan J.-W.; Su Y.-Z.; Zhang M.; Mao B.-W. Probing double layer structures of Au (111)-BMIPF6 ionic liquid interfaces from potential-dependent AFM force curves. Chem. Commun. 2012, 48, 582–584. 10.1039/C1CC15463J. [DOI] [PubMed] [Google Scholar]
- Jurado L. A.; Espinosa-Marzal R. M. Insight into the Electrical Double Layer of an Ionic Liquid on Graphene. Sci. Rep. 2017, 7 (1), 4225. 10.1038/s41598-017-04576-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Souza J. P.; Goodwin Z. A. H.; McEldrew M.; Kornyshev A. A.; Bazant M. Z. Interfacial Layering in the Electric Double Layer of Ionic Liquids. Phys. Rev. Lett. 2020, 125, 116001. 10.1103/PhysRevLett.125.116001. [DOI] [PubMed] [Google Scholar]
- Wang X.; Salari M.; Jiang D.-E.; Chapman Varela J.; Anasori B.; Wesolowski D. J.; Dai S.; Grinstaff M. W.; Gogotsi Y. Electrode material-ionic liquid coupling for electrochemical energy storage. Nat. Rev. Mater. 2020, 5, 787–808. 10.1038/s41578-020-0218-9. [DOI] [Google Scholar]
- Silvester D. S.; Jamil R.; Doblinger S.; Zhang Y.; Atkin R.; Li H. Electrical Double Layer Structure in Ionic Liquids and Its Importance for Supercapacitor, Battery, Sensing, and Lubrication Applications. J. Phys. Chem. C 2021, 125, 13707–13720. 10.1021/acs.jpcc.1c03253. [DOI] [Google Scholar]
- Wu Q.; McDowell M. T.; Qi Y. Effect of the Electric Double Layer (EDL) in Multicomponent Electrolyte Reduction and Solid Electrolyte Interphase (SEI) Formation in Lithium Batteries. J. Am. Chem. Soc. 2023, 145, 2473–2484. 10.1021/jacs.2c11807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray A.; Saruhan B. Application of Ionic Liquids for Batteries and Supercapacitors. Materials 2021, 14, 2942. 10.3390/ma14112942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanjundiah C.; McDevitt S. F.; Koch V. R. Differential Capacitance Measurements in Solvent-Free Ionic Liquids at Hg and C Interfaces. J. Electrochem. Soc. 1997, 144, 3392. 10.1149/1.1838024. [DOI] [Google Scholar]
- Alam M. T.; Mominul Islam M.; Okajima T.; Ohsaka T. Measurements of differential capacitance in room temperature ionic liquid at mercury, glassy carbon and gold electrode interfaces. Electrochem. Commun. 2007, 9, 2370–2374. 10.1016/j.elecom.2007.07.009. [DOI] [Google Scholar]
- Fedorov M. V.; Kornyshev A. A. Ionic Liquid Near a Charged Wall: Structure and Capacitance of Electrical Double Layer. J. Phys. Chem. B 2008, 112, 11868–11872. 10.1021/jp803440q. [DOI] [PubMed] [Google Scholar]
- Lockett V.; Horne M.; Sedev R.; Rodopoulos T.; Ralston J. Differential capacitance of the double layer at the electrode/ionic liquids interface. Phys. Chem. Chem. Phys. 2010, 12, 12499–12512. 10.1039/c0cp00170h. [DOI] [PubMed] [Google Scholar]
- Alam M. T.; Masud J.; Islam M. M.; Okajima T.; Ohsaka T. Differential Capacitance at Au(111) in 1-Alkyl-3-methylimidazolium Tetrafluoroborate Based Room-Temperature Ionic Liquids. J. Phys. Chem. C 2011, 115, 19797–19804. 10.1021/jp205800x. [DOI] [Google Scholar]
- Wallauer J.; Drüschler M.; Huber B.; Roling B. The Differential Capacitance of Ionic Liquid/Metal Electrode Interfaces - A Critical Comparison of Experimental Results with Theoretical Predictions. Z. fur Naturforsch. B 2013, 68, 1143–1153. 10.5560/znb.2013-3153. [DOI] [Google Scholar]
- Gomes C.; Costa R.; Pereira C. M.; Silva A. F. The electrical double layer at the ionic liquid/Au and Pt electrode interface. RSC Adv. 2014, 4, 28914–28921. 10.1039/C4RA03977G. [DOI] [Google Scholar]
- Costa R.; Pereira C. M.; Silva A. F. Charge Storage on Ionic Liquid Electric Double Layer: The Role of the Electrode Material. Electrochim. Acta 2015, 167, 421–428. 10.1016/j.electacta.2015.02.180. [DOI] [Google Scholar]
- Jo S.; Park S.-W.; Shim Y.; Jung Y. Effects of Alkyl Chain Length on Interfacial Structure and Differential Capacitance in Graphene Supercapacitors: A Molecular Dynamics Simulation Study. Electrochim. Acta 2017, 247, 634–645. 10.1016/j.electacta.2017.06.169. [DOI] [Google Scholar]
- Yang J.; Lian C.; Liu H. Chain length matters: Structural transition and capacitance of room temperature ionic liquids in nanoporous electrodes. Chem. Eng. Sci. 2020, 227, 115927. 10.1016/j.ces.2020.115927. [DOI] [Google Scholar]
- Pitawela N. R.; Shaw S. K. Imidazolium Triflate Ionic Liquids’ Capacitance-Potential Relationships and Transport Properties Affected by Cation Chain Lengths. ACS Measure. Sci. Au 2021, 1, 117–130. 10.1021/acsmeasuresciau.1c00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P.; Jiao Y.; Huang J.; Chen S. Electric Double Layer Effects in Electrocatalysis: Insights from Ab Initio Simulation and Hierarchical Continuum Modeling. JACS Au 2023, 3, 2640–2659. 10.1021/jacsau.3c00410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coskun O. K.; Muñoz M.; Dongare S.; Dean W.; Gurkan B. E. Understanding the Electrode-Electrolyte Interfaces of Ionic Liquids and Deep Eutectic Solvents. Langmuir 2024, 40, 3283–3300. 10.1021/acs.langmuir.3c03397. [DOI] [PubMed] [Google Scholar]
- Klein J. M.; Squire H.; Gurkan B. Electroanalytical Investigation of the Electrode-Electrolyte Interface of Quaternary Ammonium Ionic Liquids: Impact of Alkyl Chain Length and Ether Functionality. J. Phys. Chem. C 2020, 124, 5613–5623. 10.1021/acs.jpcc.9b08016. [DOI] [Google Scholar]
- Klein J. M.; Wang H.; Sacci R. L.; Browning J. F.; Gurkan B. Smooth Modified Surfaces of Silicon for the Study of Ionic Liquid Interfaces by Neutron Reflectometry. ACS Appl. Electron. Mater. 2022, 4, 2217–2226. 10.1021/acsaelm.1c01351. [DOI] [Google Scholar]
- Wang L.; Li L.; Fan Q.; Chu T.; Wang Y.; Xu Y. Thermal stability and flammability of several quaternary ammonium ionic liquids. J. Mol. Liq. 2023, 382, 121920. 10.1016/j.molliq.2023.121920. [DOI] [Google Scholar]
- Sato T.; Masuda G.; Takagi K. Electrochemical properties of novel ionic liquids for electric double layer capacitor applications. Electrochim. Acta 2004, 49, 3603–3611. 10.1016/j.electacta.2004.03.030. [DOI] [Google Scholar]
- Kulkarni P. S.; Branco L. C.; Crespo J. G.; Nunes M. C.; Raymundo A.; Afonso C. A. M. Comparison of Physicochemical Properties of New Ionic Liquids Based on Imidazolium, Quaternary Ammonium, and Guanidinium Cations. Chem.-Eur. J. 2007, 13, 8478–8488. 10.1002/chem.200700965. [DOI] [PubMed] [Google Scholar]
- de Ferro A. M.; Reis P. M.; Soromenho M. R. C.; Bernardes C. E. S.; Shimizu K.; Freitas A. A.; Esperança J. M. S. S.; Canongia Lopes J. N.; Rebelo L. P. N. Designing the ammonium cation to achieve a higher hydrophilicity of bistriflimide-based ionic liquids. Phys. Chem. Chem. Phys. 2018, 20, 19307–19313. 10.1039/C8CP03398F. [DOI] [PubMed] [Google Scholar]
- Yang L.In Ammonium Ionic Liquids BT - Encyclopedia of Ionic Liquids, Zhang S., Ed.; Springer: Singapore, 2020; pp. 1–9. [Google Scholar]
- Pernak J.; Smiglak M.; Griffin S. T.; Hough W. L.; Wilson T. B.; Pernak A.; Zabielska-Matejuk J.; Fojutowski A.; Kita K.; Rogers R. D. Long alkyl chain quaternary ammonium-based ionic liquids and potential applications. Green Chem. 2006, 8, 798–806. 10.1039/b604353d. [DOI] [Google Scholar]
- Katakura S.; Nishi N.; Kobayashi K.; Amano K.-I.; Sakka T. Effect of Switching the Length of Alkyl Chains on Electric Double Layer Structure and Differential Capacitance at the Electrode Interface of Quaternary Ammonium-Based Ionic Liquids Studied Using Molecular Dynamics Simulation. J. Phys. Chem. C 2020, 124, 7873–7883. 10.1021/acs.jpcc.0c00795. [DOI] [PubMed] [Google Scholar]
- Jumaah F. N.; Mobarak N. N.; Hassan N. H.; Noor S. A. M.; Nasir S. N. S.; Ludin N. A.; Badri K. H.; Ahmad A.; Ito E. R. D.; Yoshizawa-Fujita M.; et al. Review of non-crystalline and crystalline quaternary ammonium ions: Classification, structural and thermal insight into tetraalkylammonium ions. J. Mol. Liq. 2023, 376, 121378. 10.1016/j.molliq.2023.121378. [DOI] [Google Scholar]
- Crick F. H.What Mad Pursuit: A Personal View of Scientific Discovery; Basic Books Inc.: New York, 1988. [Google Scholar]
- Hayes R.; Warr G. G.; Atkin R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. 10.1021/cr500411q. [DOI] [PubMed] [Google Scholar]
- Lima T. A.; Paschoal V. H.; Freitas R. S.; Faria L. F. O.; Li Z.; Tyagi M.; Zu Y.; Ribeiro M. C. C. An inelastic neutron scattering, Raman, far-infrared, and molecular dynamics study of the intermolecular dynamics of two ionic liquids. Phys. Chem. Chem. Phys. 2020, 22, 9074–9085. 10.1039/D0CP00374C. [DOI] [PubMed] [Google Scholar]
- Lo Celso F.; Appetecchi G. B.; Jafta C. J.; Gontrani L.; Canongia Lopes J. N.; Triolo A.; Russina O. Nanoscale organization in the fluorinated room temperature ionic liquid: Tetraethyl ammonium (trifluoromethanesulfonyl)(nonafluorobutylsulfonyl)imide. J. Chem. Phys. 2018, 148 (19), 193816. 10.1063/1.5016236. [DOI] [PubMed] [Google Scholar]
- Greaves T. L.; Kennedy D. F.; Mudie S. T.; Drummond C. J. Diversity Observed in the Nanostructure of Protic Ionic Liquids. J. Phys. Chem. B 2010, 114, 10022–10031. 10.1021/jp103863z. [DOI] [PubMed] [Google Scholar]
- Pott T.; Méléard P. New insight into the nanostructure of ionic liquids: a small angle X-ray scattering (SAXS) study on liquid tri-alkyl-methyl-ammonium bis(trifluoromethanesulfonyl)amides and their mixtures. Phys. Chem. Chem. Phys. 2009, 11, 5469–5475. 10.1039/b901582e. [DOI] [PubMed] [Google Scholar]
- Santos C. S.; Annapureddy H. V. R.; Murthy N. S.; Kashyap H. K.; Castner E. W. Jr.; Margulis C. J. Temperature-dependent structure of methyltributylammonium bis(trifluoromethylsulfonyl)amide: X ray scattering and simulations. J. Chem. Phys. 2011, 134 (6), 064501. 10.1063/1.3526958. [DOI] [PubMed] [Google Scholar]
- Kashyap H. K.; Santos C. S.; Daly R. P.; Hettige J. J.; Murthy N. S.; Shirota H.; Castner E. W. J.; Margulis C. J. How Does the Ionic Liquid Organizational Landscape Change when Nonpolar Cationic Alkyl Groups Are Replaced by Polar Isoelectronic Diethers?. J. Phys. Chem. B 2013, 117, 1130–1135. 10.1021/jp311032p. [DOI] [PubMed] [Google Scholar]
- Lima T. A.; Paschoal V. H.; Faria L. F. O.; Ribeiro M. C. C.; Giles C. Comparing two tetraalkylammonium ionic liquids. I. Liquid phase structure. J. Chem. Phys. 2016, 144, 224504. 10.1063/1.4953414. [DOI] [PubMed] [Google Scholar]
- Pontoni D.; DiMichiel M.; Deutsch M. Temperature evolution of the bulk nano-structure in a homologous series of room temperature ionic liquids. J. Mol. Liq. 2020, 300, 112280. 10.1016/j.molliq.2019.112280. [DOI] [Google Scholar]
- Rauber D.; Philippi F.; Kuttich B.; Becker J.; Kraus T.; Hunt P.; Welton T.; Hempelmann R.; Kay C. W. M. Curled cation structures accelerate the dynamics of ionic liquids. Phys. Chem. Chem. Phys. 2021, 23, 21042–21064. 10.1039/D1CP02889H. [DOI] [PubMed] [Google Scholar]
- Siqueira L. J. A.; Ribeiro M. C. C. Alkoxy Chain Effect on the Viscosity of a Quaternary Ammonium Ionic Liquid: Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 1074–1079. 10.1021/jp807833a. [DOI] [PubMed] [Google Scholar]
- Siqueira L. J. A.; Ribeiro M. C. C. Charge ordering and intermediate range order in ammonium ionic liquids. J. Chem. Phys. 2011, 135, 204506. 10.1063/1.3662062. [DOI] [PubMed] [Google Scholar]
- Reddy T. D. N.; Mallik B. S. Heterogeneity in the microstructure and dynamics of tetraalkylammonium hydroxide ionic liquids: insight from classical molecular dynamics simulations and Voronoi tessellation analysis. Phys. Chem. Chem. Phys. 2020, 22, 3466–3480. 10.1039/C9CP06796E. [DOI] [PubMed] [Google Scholar]
- Shimizu K.; Pádua A. A. H.; Canongia Lopes J. N. Nanostructure of Trialkylmethylammonium Bistriflamide Ionic Liquids Studied by Molecular Dynamics. J. Phys. Chem. B 2010, 114, 15635–15641. 10.1021/jp108420x. [DOI] [PubMed] [Google Scholar]
- Triolo A.; Russina O.; Bleif H.-J.; Di Cola E. Nanoscale Segregation in Room Temperature Ionic Liquids. J. Phys. Chem. B 2007, 111, 4641–4644. 10.1021/jp067705t. [DOI] [PubMed] [Google Scholar]
- Russina O.; Triolo A. New experimental evidence supporting the mesoscopic segregation model in room temperature ionic liquids. Faraday Discuss. 2012, 154, 97–109. 10.1039/C1FD00073J. [DOI] [PubMed] [Google Scholar]
- Ji Y.; Shi R.; Wang Y.; Saielli G. Effect of the Chain Length on the Structure of Ionic Liquids: from Spatial Heterogeneity to Ionic Liquid Crystals. J. Phys. Chem. B 2013, 117, 1104–1109. 10.1021/jp310231f. [DOI] [PubMed] [Google Scholar]
- Hettige J. J.; Kashyap H. K.; Annapureddy H. V. R.; Margulis C. J. Anions, the Reporters of Structure in Ionic Liquids. J. Phys. Chem. Lett. 2013, 4, 105–110. 10.1021/jz301866f. [DOI] [PubMed] [Google Scholar]
- Araque J. C.; Hettige J. J.; Margulis C. J. Modern Room Temperature Ionic Liquids, a Simple Guide to Understanding Their Structure and How It May Relate to Dynamics. J. Phys. Chem. B 2015, 119, 12727–12740. 10.1021/acs.jpcb.5b05506. [DOI] [PubMed] [Google Scholar]
- Katakura S.; Nishi N.; Kobayashi K.; Amano K.-I.; Sakka T. Surface Structure of Quaternary Ammonium-Based Ionic Liquids Studied Using Molecular Dynamics Simulation: Effect of Switching the Length of Alkyl Chains. J. Phys. Chem. C 2019, 123, 7246–7258. 10.1021/acs.jpcc.9b00799. [DOI] [Google Scholar]
- Choi J.-H.; Lee H.; Choi H. R.; Cho M. Graph Theory and Ion and Molecular Aggregation in Aqueous Solutions. Annu. Rev. Phys. Chem. 2018, 69, 125–149. 10.1146/annurev-physchem-050317-020915. [DOI] [PubMed] [Google Scholar]
- Stoppelman J. P.; McDaniel J. G. Proton Transport in [BMIM+][BF4-]/Water Mixtures Near the Percolation Threshold. J. Phys. Chem. B 2020, 124, 5957–5970. 10.1021/acs.jpcb.0c02487. [DOI] [PubMed] [Google Scholar]
- Heller W. T.; Cuneo M.; Debeer-Schmitt L.; Do C.; He L.; Heroux L.; Littrell K.; Pingali S. V.; Qian S.; Stanley C.; et al. The suite of small-angle neutron scattering instruments at Oak Ridge National Laboratory. J. Appl. Crystallogr. 2018, 51, 242–248. 10.1107/S1600576718001231. [DOI] [Google Scholar]
- Arnold O.; Bilheux J. C.; Borreguero J. M.; Buts A.; Campbell S. I.; Chapon L.; Doucet M.; Draper N.; Ferraz Leal R.; Gigg M. A.. et al. Mantid-Data analysis and visualization package for neutron scattering and μ SR experiments Nuclear Instruments And Methods In Physics Research Section A: accelerators, Spectrometers, Detectors And Associated Equipment Elsevier; 2014764156–166 10.1016/j.nima.2014.07.029 [DOI] [Google Scholar]
- McDaniel J. G.; Choi E.; Son C. Y.; Schmidt J. R.; Yethiraj A. Ab Initio Force Fields for Imidazolium-Based Ionic Liquids. J. Phys. Chem. B 2016, 120, 7024–7036. 10.1021/acs.jpcb.6b05328. [DOI] [PubMed] [Google Scholar]
- McDaniel J. G.; Son C. Y.; Yethiraj A. Ab Initio Force Fields for Organic Anions: Properties of [BMIM][TFSI], [BMIM][FSI], and [BMIM][OTf] Ionic Liquids. J. Phys. Chem. B 2018, 122, 4101–4114. 10.1021/acs.jpcb.8b01221. [DOI] [PubMed] [Google Scholar]
- Eastman P.; Swails J.; Chodera J. D.; McGibbon R. T.; Zhao Y.; Beauchamp K. A.; Wang L.-P.; Simmonett A. C.; Harrigan M. P.; Stern C. D.; et al. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PloS Comput. Biol. 2017, 13, e1005659 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamoureux G.; Roux B. Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J. Chem. Phys. 2003, 119, 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Tsuzuki S. Factors Controlling the Diffusion of Ions in Ionic Liquids. ChemPhyschem 2012, 13, 1664–1670. 10.1002/cphc.201100870. [DOI] [PubMed] [Google Scholar]
- Fujii K.; Fujimori T.; Takamuku T.; Kanzaki R.; Umebayashi Y.; Ishiguro S.-I. Conformational Equilibrium of Bis(trifluoromethanesulfonyl) Imide Anion of a Room-Temperature Ionic Liquid: Raman Spectroscopic Study and DFT Calculations. J. Phys. Chem. B 2006, 110, 8179–8183. 10.1021/jp0612477. [DOI] [PubMed] [Google Scholar]
- Ghatee M. H.; Bahrami M. Emergence of innovative properties by replacement of nitrogen atom with phosphorus atom in quaternary ammonium ionic liquids: Insights from ab initio calculations and MD simulations. Chem. Phys. 2017, 490, 92–105. 10.1016/j.chemphys.2017.04.005. [DOI] [Google Scholar]
- Schuler L. D.; Van Gunsteren W. F. On the Choice of Dihedral Angle Potential Energy Functions for n-Alkanes. Mol. Simul. 2000, 25, 301–319. 10.1080/08927020008024504. [DOI] [Google Scholar]
- Hammonds K. D.; McDonald I. R.; Ryckaert J.-P. Conformer distribution and the kinetics of trans-gauche isomerization in a model of liquid n-octane. Chem. Phys. Lett. 1993, 213, 27–31. 10.1016/0009-2614(93)85413-I. [DOI] [Google Scholar]
- Cezar H. M.; Canuto S.; Coutinho K. DICE: A Monte Carlo Code for Molecular Simulation Including the Configurational Bias Monte Carlo Method. J. Chem. Inf. Model. 2020, 60, 3472–3488. 10.1021/acs.jcim.0c00077. [DOI] [PubMed] [Google Scholar]
- Christensen S.; Peters G. H.; Hansen F. Y.; O’connell J. P.; Abildskov J. Generation of thermodynamic data for organic liquid mixtures from molecular simulations. Mol. Simul. 2007, 33, 449–457. 10.1080/08927020601177109. [DOI] [Google Scholar]
- Hess B.; van der Vegt N. F. A. Cation specific binding with protein surface charges. Proc. Int. Acad. Sci. 2009, 106, 13296–13300. 10.1073/pnas.0902904106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols J. W.; Moore S. G.; Wheeler D. R. Improved implementation of Kirkwood-Buff solution theory in periodic molecular simulations. Phys. Rev. E 2009, 80 (5), 51203. 10.1103/PhysRevE.80.051203. [DOI] [PubMed] [Google Scholar]
- Schnell S. K.; Liu X.; Simon J.-M.; Bardow A.; Bedeaux D.; Vlugt T. J. H.; Kjelstrup S. Calculating Thermodynamic Properties from Fluctuations at Small Scales. J. Phys. Chem. B 2011, 115, 10911–10918. 10.1021/jp204347p. [DOI] [PubMed] [Google Scholar]
- Wedberg R.; O’Connell J. P.; Peters G. H.; Abildskov J. Total and direct correlation function integrals from molecular simulation of binary systems. Fluid Phase Equilib. 2011, 302, 32–42. 10.1016/j.fluid.2010.10.004. [DOI] [Google Scholar]
- Perera A.; Zoranić L.; Sokolić F.; Mazighi R. A comparative Molecular Dynamics study of water-methanol and acetone-methanol mixtures. J. Mol. Liq. 2011, 159, 52–59. 10.1016/j.molliq.2010.05.006. [DOI] [Google Scholar]
- Blanco M. A.; Sahin E.; Li Y.; Roberts C. J. Reexamining protein–protein and protein–solvent interactions from Kirkwood-Buff analysis of light scattering in multi-component solutions. J. Chem. Phys. 2011, 134, 225103. 10.1063/1.3596726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly P.; van der Vegt N. F. A. Convergence of Sampling Kirkwood-Buff Integrals of Aqueous Solutions with Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 1347–1355. 10.1021/ct301017q. [DOI] [PubMed] [Google Scholar]
- Krüger P.; Schnell S. K.; Bedeaux D.; Kjelstrup S.; Vlugt T. J. H.; Simon J.-M. Kirkwood-Buff Integrals for Finite Volumes. J. Phys. Chem. Lett. 2013, 4, 235–238. 10.1021/jz301992u. [DOI] [PubMed] [Google Scholar]
- Cortes-Huerto R.; Kremer K.; Potestio R. Communication: Kirkwood-Buff integrals in the thermodynamic limit from small-sized molecular dynamics simulations. J. Chem. Phys. 2016, 145 (14), 141103. 10.1063/1.4964779. [DOI] [PubMed] [Google Scholar]
- Dawass N.; Krüger P.; Schnell S. K.; Bedeaux D.; Kjelstrup S.; Simon J. M.; Vlugt T. J. H. Finite-size effects of Kirkwood-Buff integrals from molecular simulations. Mol. Simul. 2018, 44, 599–612. 10.1080/08927022.2017.1416114. [DOI] [Google Scholar]
- Milzetti J.; Nayar D.; van der Vegt N. F. A. Convergence of Kirkwood-Buff Integrals of Ideal and Nonideal Aqueous Solutions Using Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 5515–5526. 10.1021/acs.jpcb.7b11831. [DOI] [PubMed] [Google Scholar]
- Sevilla M.; Cortes-Huerto R. Connecting density fluctuations and Kirkwood–Buff integrals for finite-size systems. J. Chem. Phys. 2022, 156, 044502. 10.1063/5.0076744. [DOI] [PubMed] [Google Scholar]
- Simon J.-M.; Krüger P.; Schnell S. K.; Vlugt T. J. H.; Kjelstrup S.; Bedeaux D. Kirkwood–Buff integrals: From fluctuations in finite volumes to the thermodynamic limit. J. Chem. Phys. 2022, 157, 130901. 10.1063/5.0106162. [DOI] [PubMed] [Google Scholar]
- Dohn A. O.; Markmann V.; Nimmrich A.; Haldrup K.; Møller K. B.; Nielsen M. M. Eliminating finite-size effects on the calculation of x-ray scattering from molecular dynamics simulations. J. Chem. Phys. 2023, 159 (12), 124115. 10.1063/5.0164365. [DOI] [PubMed] [Google Scholar]
- Hansen J.-P.; McDonald I. R. B. T.. Theory of Simple Liquids, 4 th ed.; Academic Press: Oxford, U.K, 2013. [Google Scholar]
- Hansen J. P.; McDonald I. R. Statistical mechanics of dense ionized matter. IV. Density and charge fluctuations in a simple molten salt. Phys. Rev. A 1975, 11, 2111–2123. 10.1103/PhysRevA.11.2111. [DOI] [Google Scholar]
- Caillol J. M.; Levesque D.; Weis J. J. Electrical properties of polarizable ionic solutions. II. Computer simulation results. J. Chem. Phys. 1989, 91, 5555–5566. 10.1063/1.457558. [DOI] [Google Scholar]
- McDaniel J. G.; Yethiraj A. Understanding the Properties of Ionic Liquids: Electrostatics, Structure Factors, and Their Sum Rules. J. Phys. Chem. B 2019, 123, 3499–3512. 10.1021/acs.jpcb.9b00963. [DOI] [PubMed] [Google Scholar]
- Caillol J. M. The Dielectric Constant and the Conductivity of an Electrolyte Solution at Finite Wave-Lengths and Frequencies. Europhys. Lett. 1987, 4 (2), 159. 10.1209/0295-5075/4/2/006. [DOI] [Google Scholar]
- Martin P. A. Sum rules in charged fluids. Rev. Mod. Phys. 1988, 60, 1075–1127. 10.1103/RevModPhys.60.1075. [DOI] [Google Scholar]
- Caillol J. M.; Levesque D.; Weis J. J. Electrical properties of polarizable ionic solutions. I. Theoretical aspects. J. Chem. Phys. 1989, 91, 5544–5554. 10.1063/1.457557. [DOI] [Google Scholar]
- Stillinger F. H. Jr.; Lovett R. General Restriction on the Distribution of Ions in Electrolytes. J. Chem. Phys. 1968, 49, 1991–1994. 10.1063/1.1670358. [DOI] [Google Scholar]
- McDaniel J. G.; Yethiraj A. Influence of Electronic Polarization on the Structure of Ionic Liquids. J. Phys. Chem. Lett. 2018, 9, 4765–4770. 10.1021/acs.jpclett.8b02120. [DOI] [PubMed] [Google Scholar]
- Ghorai P. K.; Matyushov D. V. Equilibrium Solvation, Electron-Transfer Reactions, and Stokes-Shift Dynamics in Ionic Liquids. J. Phys. Chem. B 2020, 124, 3754–3769. 10.1021/acs.jpcb.0c01773. [DOI] [PubMed] [Google Scholar]
- Schröder C.; Sonnleitner T.; Buchner R.; Steinhauser O. The influence of polarizability on the dielectric spectrum of the ionic liquid 1-ethyl-3-methylimidazolium triflate. Phys. Chem. Chem. Phys. 2011, 13, 12240–12248. 10.1039/c1cp20559e. [DOI] [PubMed] [Google Scholar]
- Zhang X.-X.; Liang M.; Hunger J.; Buchner R.; Maroncelli M. Dielectric Relaxation and Solvation Dynamics in a Prototypical Ionic Liquid + Dipolar Protic Liquid Mixture: 1-Butyl-3-Methylimidazolium Tetrafluoroborate + Water. J. Phys. Chem. B 2013, 117, 15356–15368. 10.1021/jp4043528. [DOI] [PubMed] [Google Scholar]
- Sears V. F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. 10.1080/10448639208218770. [DOI] [Google Scholar]
- Cabry C. P.; D’Andrea L.; Shimizu K.; Grillo I.; Li P.; Rogers S.; Bruce D. W.; Canongia Lopes J. N.; Slattery J. M. Exploring the bulk-phase structure of ionic liquid mixtures using small-angle neutron scattering. Faraday Discuss 2018, 206, 265–289. 10.1039/C7FD00167C. [DOI] [PubMed] [Google Scholar]
- Russina O.; Triolo A.; Gontrani L.; Caminiti R.; Xiao D.; Hines L. G.; Bartsch R. A.; Quitevis E. L.; Plechkova N.; Seddon K. R. Morphology and intermolecular dynamics of 1-Alkyl-3-methylimidazolium bis(trifluoromethane)sulfonylamide ionic liquids: Structural and dynamic evidence of nanoscale segregation. J. Phys.: Condens. Matter 2009, 21, 424121. 10.1088/0953-8984/21/42/424121. [DOI] [Google Scholar]
- Annapureddy H. V. R.; Kashyap H. K.; De Biase P. M.; Margulis C. J. What is the Origin of the Prepeak in the X-ray Scattering of Imidazolium-Based Room-Temperature Ionic Liquids?. J. Phys. Chem. B 2010, 114, 16838–16846. 10.1021/jp108545z. [DOI] [PubMed] [Google Scholar]
- Hardacre C.; Holbrey J. D.; Mullan C. L.; Youngs T. G. A.; Bowron D. T. Small angle neutron scattering from 1-alkyl-3-methylimidazolium hexafluorophosphate ionic liquids ([Cnmim][PF6], n = 4, 6, and 8). J. Chem. Phys. 2010, 133, 074510. 10.1063/1.3473825. [DOI] [PubMed] [Google Scholar]
- Santos C. S.; Murthy N. S.; Baker G. A.; Castner E. W. Jr. Communication: X-ray scattering from ionic liquids with pyrrolidinium cations. J. Chem. Phys. 2011, 134 (12), 121101. 10.1063/1.3569131. [DOI] [PubMed] [Google Scholar]
- Sessa F.; D’Angelo P.; Migliorati V. Combined distribution functions: A powerful tool to identify cation coordination geometries in liquid systems. Chem. Phys. Lett. 2018, 691, 437–443. 10.1016/j.cplett.2017.11.056. [DOI] [Google Scholar]
- Brehm M.; Thomas M.; Gehrke S.; Kirchner B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. 10.1063/5.0005078. [DOI] [PubMed] [Google Scholar]
- Morrow T. I.; Maginn E. J. Molecular Dynamics Study of the Ionic Liquid 1-n-Butyl-3-methylimidazolium Hexafluorophosphate. J. Phys. Chem. B 2002, 106, 12807–12813. 10.1021/jp0267003. [DOI] [Google Scholar]
- Zubeir L. F.; Rocha M. A. A.; Vergadou N.; Weggemans W. M. A.; Peristeras L. D.; Schulz P. S.; Economou I. G.; Kroon M. C. Thermophysical properties of imidazolium tricyanomethanide ionic liquids: experiments and molecular simulation. Phys. Chem. Chem. Phys. 2016, 18, 23121–23138. 10.1039/C6CP01943A. [DOI] [PubMed] [Google Scholar]
- Triolo A.; Russina O.; Fazio B.; Appetecchi G. B.; Carewska M.; Passerini S. Nanoscale organization in piperidinium-based room temperature ionic liquids. J. Chem. Phys. 2009, 130 (16), 164521. 10.1063/1.3119977. [DOI] [PubMed] [Google Scholar]
- Li S.; Bañuelos J. L.; Guo J.; Anovitz L.; Rother G.; Shaw R. W.; Hillesheim P. C.; Dai S.; Baker G. A.; Cummings P. T. Alkyl Chain Length and Temperature Effects on Structural Properties of Pyrrolidinium-Based Ionic Liquids: A Combined Atomistic Simulation and Small-Angle X-ray Scattering Study. J. Phys. Chem. Lett. 2012, 3, 125–130. 10.1021/jz2013209. [DOI] [Google Scholar]
- Rocha M. A. A.; Neves C. M. S. S.; Freire M. G.; Russina O.; Triolo A.; Coutinho J. A. P.; Santos L. M. N. B. F. Alkylimidazolium Based Ionic Liquids: Impact of Cation Symmetry on Their Nanoscale Structural Organization. J. Phys. Chem. B 2013, 117, 10889–10897. 10.1021/jp406374a. [DOI] [PubMed] [Google Scholar]
- Li S.; Bañuelos J. L.; Zhang P.; Feng G.; Dai S.; Rother G.; Cummings P. T. Toward understanding the structural heterogeneity and ion pair stability in dicationic ionic liquids. Soft Matter 2014, 10, 9193–9200. 10.1039/C4SM01742K. [DOI] [PubMed] [Google Scholar]
- Shimizu K.; Bernardes C. E. S.; Triolo A.; Canongia Lopes J. N. Nano-segregation in ionic liquids: scorpions and vanishing chains. Phys. Chem. Chem. Phys. 2013, 15, 16256–16262. 10.1039/c3cp52357h. [DOI] [PubMed] [Google Scholar]
- Deetlefs M.; Hardacre C.; Nieuwenhuyzen M.; Padua A. A. H.; Sheppard O.; Soper A. K. Liquid Structure of the Ionic Liquid 1,3-Dimethylimidazolium Bis(trifluoromethyl)sulfonylamide. J. Phys. Chem. B 2006, 110, 12055–12061. 10.1021/jp060924u. [DOI] [PubMed] [Google Scholar]
- Hardacre C.; Holbrey J. D.; Mullan C. L.; Nieuwenhuyzen M.; Youngs T. G. A.; Bowron D. T. Liquid Structure of the Ionic Liquid, 1-Methyl-4-cyanopyridinium Bis(trifluoromethyl)sulfonylimide Determined from Neutron Scattering and Molecular Dynamics Simulations. J. Phys. Chem. B 2008, 112, 8049–8056. 10.1021/jp801801j. [DOI] [PubMed] [Google Scholar]
- Goossens K.; Lava K.; Bielawski C. W.; Binnemans K. Ionic Liquid Crystals: Versatile Materials. Chem. Rev. 2016, 116, 4643–4807. 10.1021/cr400334b. [DOI] [PubMed] [Google Scholar]
- Yao B.; Paluch M.; Paturej J.; McLaughlin S.; McGrogan A.; Swadzba-Kwasny M.; Shen J.; Ruta B.; Rosenthal M.; Liu J.; et al. Self-Assembled Nanostructures in Aprotic Ionic Liquids Facilitate Charge Transport at Elevated Pressure. ACS Appl. Mater. Interfaces 2023, 15, 39417–39425. 10.1021/acsami.3c08606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley A. E.; Hardacre C.; Holbrey J. D.; Johnston S.; McMath S. E. J.; Nieuwenhuyzen M. Small-Angle X-ray Scattering Studies of Liquid Crystalline 1-Alkyl-3-methylimidazolium Salts. Chem. Mater. 2002, 14, 629–635. 10.1021/cm010542v. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.