Distortion-Corrected Posterior Ocular Shape in Myopic Eyes Assessed by Ultrawide OCT Detects Deformations Associated With Vision-Threatening Changes

Abstract

Purpose

To develop a quantitative tool for assessing the posterior ocular shape using widefield, volumetric optical coherence tomography (OCT) in eyes with myopia.

Methods

This observational, cross-sectional study included 178 eyes from 113 participants. Participants underwent a standardized eye examination, including ocular biometry and a custom ultrawide OCT. True ocular shape was reconstructed by tracing the beam propagation from the system to the posterior eye. Gaussian curvature quantified the localized ocular shape, which was further categorized into five distinct categories. An ocular shape irregularity (OSI) was calculated using principal component analysis. Linear regression with breakpoints analyzed the relationship between ocular shape parameters and axial length (AL).

Results

Increased curvature mean and variance were associated with more severe myopia (P < 0.001). Curvature categories (convex, normal, concave, and highly concave) differed significantly between the groups (all P < 0.001). Their correlations with AL revealed significant breakpoints between 27.1 and 27.2 mm. OSI, as a single metric for quantifying ocular shape distortion, was associated with more severe myopia (P < 0.001), and its correlation with AL revealed a breakpoint at 27.2 mm with a fourfold increase in slope steepness beyond this pivot. Determination of OSI was highly reproducible and could also be obtained with fewer scans.

Conclusions

Eyes exceeding 27.2 mm in length exhibit pronounced shape changes. Our framework can be seamlessly integrated into commercial OCTs for ocular shape deformation detection, which could aid in identifying eyes with pathologic myopia.

Ocular deformation in pathologic myopia (PM) is associated with axial elongation related to stretching of ocular tissues, including Bruch's membrane (BM), retinal pigment epithelium (RPE), and the sclera.^1,2 Changes in the local biomechanical properties of ocular tissue are associated with distinct deformations. These deformations include an outward pouching of the ocular wall, also known as staphyloma, and an inward pouching that can manifest as staphyloma ridges, conus ridges, or saddle-shaped or dome-shaped macula. Most ocular wall deformations manifest at or close to the posterior pole. Myopic choroidal neovascularization, the most frequently occurring complication of pathologic myopia and a leading cause of permanent vision loss, is known to commonly occur at such ridges, postulated to be due to sites of greatest biomechanical derangement. These deformations (be it outward staphyloma or inward ridges) are associated with marked morphologic changes in the macula and optic nerve, resulting in macular atrophy with irreversible vision impairment with a reduction in vision-related quality of life and a profound impact on healthcare systems as future generations may become even more myopic.^3–5 Timely monitoring of the ocular shape changes with imaging modalities is important for tracking myopia progression and potential preventative strategy planning.^6,7

Currently, the assessment of ocular shape can be achieved by magnetic resonance imaging (MRI).⁸ T1- and T2-weighted MRI contrasts intraocular fluid and uses the vitreous–retina interface to measure the ocular shape. Using a head coil and dense scanning, three-dimensional ocular MRI scans have been used to quantify different types of ocular shapes in the equatorial region⁹ and at the posterior pole.^10–13 However, MRI systems are relatively expensive and time consuming to use; thus, they are not readily employed purely for ocular evaluation in most healthcare settings.

Optical coherence tomography (OCT) allows a non-invasive, fast, volumetric scan of the posterior segment of the eye. With a resolution at least one order of magnitude higher than MRI, OCT has markedly contributed to new myopia grading systems for myopic maculopathy and myopic traction maculopathy.^6,7 Recent advancements in widefield imaging optics and enhanced image depth have further established OCT as a pivotal modality for assessing ocular shape and detecting change over time.^14–18 Although myopia progression primarily involves scleral remodeling and the choroid–sclera interface might be a more suitable target for assessing the myopia-related structural alterations, this shape boundary is referenced to the thin, smooth RPE/BM complex in OCT.^14,18–20 The RPE/BM layer is highly visible in OCT images, providing a clear, producible demarcation for segmentation in longitudinal studies. In contrast, the choroid–sclera interface has high spatial curvature variance and lower visibility, especially in eyes with thick choroid. Nevertheless, the ocular shape represented in OCT is affected by refractive optics, including optics of the system; biometrics of the eye, such as axial length (AL), anterior chamber depth, and corneal curvature; positioning of the beam versus the pupil; and the machine-to-eye distance.²¹ When optical parameters are known, tracing the beam propagation along all of the refractive optical components allows the ocular shape to be reconstructed.²² We recently developed a technology to reconstruct the true ocular shape using anatomical characteristics measured by ocular biometry and standardizing the machine-to-eye distance by aligning the pivot conjugate of the scanner to the pupil.¹⁸

In this study, we leveraged our novel technology and generated distortion-corrected, quantitative ocular curvature maps based on ultrawide volumetric OCT scans covering a field of view of more than 60°. We further categorized curvature into five categories (convex, flat, normal, concave, and highly concave) and derived a single component, ocular shape irregularity (OSI), by principal component analysis from these curvature categories. Furthermore, we aimed to investigate the association between the severities of myopia and posterior ocular curvature metrics.

Methods

Study Participants

The cross-sectional study was performed at a single tertiary eye center, the Singapore National Eye Center, Singapore, from July 2019 to October 2022. Approved by the SingHealth Centralized Institutional Review Board, the study was conducted in accordance with the tenets of the Declaration of Helsinki. Written informed consent was obtained from all participants. The results were reported according to the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) reporting guidelines. All of the eyes included in this study were categorized into non-high myopia (non-HM), high myopia (HM), and pathologic myopia (PM) groups. Moreover, subgroup I and subgroup II, subsets of non-pathologic eyes, were used for establishing a normative database and testing the repeatability of the measurements, respectively. Detailed information regarding the inclusion/exclusion criteria and their spherical equivalent (SE) refractive error ranges are listed in Table 1.

Table 1.

Definition and Inclusion Criteria of Different Groups in This Study

Group Name	SE Range (Diopter)	n	Inclusion Criteria	Exclusion Criteria	Comments
Non-high myopia (non-HM)	−5.75 to +3.25	100	Without staphyloma or myopic maculopathy stage 2 or higher*	Any prior ocular surgery, syndromic forms of myopia, vascular retinopathies, age-related macular degeneration, uveitis, or ocular trauma
High myopia (HM)	−15.75 to −6.00	58	Without staphyloma or myopic maculopathy stage 2 or higher*
Pathologic myopia (PM)	−16.75 to −6.75	20	With staphyloma or myopic maculopathy stage 2 or higher*
Subgroup I	−3.00 to −1.00	10	Without staphyloma, or myopic maculopathy stage 2 or higher*, or other eyeball distortions		Used as a normative database
Subgroup II	−7.25 to −1.00	13	Without staphyloma or myopic maculopathy stage 2 or higher*		Measured three times for repeatability test

SE, Spherical equivalent refractive error.

^*Staphyloma or myopic maculopathy stage 2 or higher, including lacquer cracks, patchy atrophies, macular neovascularization, dome-shaped macula, myopic tractional maculopathy, and high myopia-associated optic neuropathy associated with loss of best-corrected visual acuity.

Ocular Examinations

All participants were interviewed to obtain demographic data and their ocular and medical histories. A standardized eye examination included measurement of visual acuity using a logarithm of the minimum angle of resolution (logMAR) chart (Lighthouse International, New York, NY, USA), autorefractometry including keratometry (RK-5 Autorefractor Keratometer; Canon, Tokyo, Japan), and slit lamp-based biomicroscopy of the anterior and posterior ocular segments. The posterior eye segment was imaged using a MHz swept-source (SS) OCT system (Optores GmbH, Munich, Germany).²⁴ The theoretical axial resolution was ∼7 µm in tissue. For the acquisition protocol, we scanned an ultrawide field of view (raster scanning pattern; 65° in horizontal direction and 62° in sagittal direction). Each rectangle volume consisted of 1536 A-scans and 993 B-scans with an acquisition time of about 1.6 seconds.

Ocular Curvature Quantification

A flowchart of postprocessing of the OCT images is provided in Supplementary Figure S1, and all postprocessing was performed utilizing custom MATLAB algorithms (MathWorks, Natick, MA, USA). The RPE/BM line in each single B-scan was segmented automatically based on graph theory and dynamic programming.²⁵ Specifically, the RPE/BM from a central scan was initially segmented, and this segmentation was iteratively extended to adjacent scans. In this process, each scan utilized the RPE/BM location from its neighboring scan as a reference, ensuring consistent RPE/BM determinations across the entire volume. Ocular anatomical characteristics, including AL, corneal thickness, and anterior chamber depth, were measured by ocular biometry (IOLMaster 700; Carl Zeiss Meditec, Dublin, CA, USA) and were used to construct a personalized eye model.²⁶ We used the Polan eye model²⁷ to simulate phakic gradient eye lenses, and an Ansys Zemax OpticStudio model (Ansys, Canonsburg, PA, USA) traced the light propagation from a galvo scanner to the posterior eye. The position and angle of the beam chief array relative to the optical axis from the angular position of each scanner were recorded. From the angular position of each scanner, the chief array from the Ansys Zemax OpticStudio model was supposed to be colinear with the corresponding A-scan acquired. Using this Ansys Zemax OpticStudio model, RPE/BM spatial coordinates in the OCT images were transformed and projected into an isotropic physical x,y,z space.²⁶ Gaussian curvature, an invariant topological metric for describing the stretch or compression of biological tissue or cells, quantified the ocular shape from the position of the RPE/BM line in physical space.²⁸

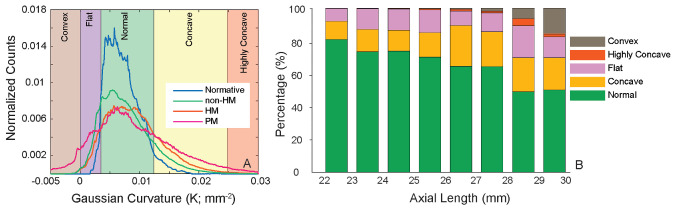
We generated curvature maps from eyes in subgroup 1 and summarized the curvature values to represent the normal curvature distribution. Subsequently, five distinct categories that represent local curvature were defined according to the normative distribution (see Fig. 2A):

• 1.Normal, within the 90% confidence interval (CI) of the normative distribution
• 2.Flat, which ranged between zero and the lower boundary of the 90% CI
• 3.Concave, which ranged from the upper boundary of the 90% CI to twice its value
• 4.Convex, which included all negative values
• 5.Highly concave, which included any values exceeding the range defined as concave

Figure 2.

(A) Histograms of the Gaussian curvature values in the normative subgroup and the myopia groups. Five distinct curvature categories were determined based on the normative curvature distribution. A full definition of each category is described in Methods. (B) Stacked bar chart of the five curvature categories sorted by AL.

The local curvature value from each pixel on the curvature map was assigned to one of the five categories, allowing each curvature map to be represented by a mixture of these categories in different proportions. Furthermore, we studied curvature distributions from the paracentral 30° region versus the non-central area, and the non-central area was further divided into four quadrants. Mean curvature and curvature variance were computed as the average and variance of all of the values obtained from each region, respectively. The variance was calculated as

$$\begin{array}{c}\hfill Variance=\frac{{\sum }_1^n{\left(k_i-\overline{k}\right)}^2}{n-1}\end{array}$$

where k_i represents the Gaussian curvature of the ith pixel, $\overline{k}$ represent the mean Gaussian curvature, and n represents the total number of pixels within the region.

Principal component analysis²⁹ was employed to extract principal components from the five curvature categories. Subsequently, the first principal component that represented the most significant pattern in curvature distribution was selected and referred to as an OSI. To illustrate the curvature maps, we used a color scheme with green representing the normal curvature, purple representing flatter areas, brown representing convex areas found in dome- or saddle-shaped macula, yellow representing concave areas, and red representing steeper and more concave areas.^14,18

Statistical Analysis

Statistical analysis was performed using R 4.0.4 (R Foundation for Statistical Computing, Vienna, Austria). Continuous variables, such as age, AL, SE, and visual acuity, are presented as mean ± SD and were compared among groups using analysis of variance (ANOVA). The χ² test was used to compare gender among groups. Curvature parameters were compared among groups using ANOVA, adjusted for age, gender, and AL. Intraclass correlation coefficients (ICCs) were utilized to test the reproducibility of the OSI parameter across triplicate measurements in subgroup II. A linear regression model with breakpoints³⁰ was used to analyze the nonlinear relationship between AL and curvature parameters. The Davies test³¹ was employed to test for a significant change in the slope at the breakpoints. The Kolmogorov–Smirnov test was used to evaluate whether the data were normally distributed; if they were, then the data were shown in a format of mean ± SD.

Results

The participant characteristics stratified by the degree of myopia and the subgroups are summarized in Table 2. Myopia groups did not differ significantly in sex (P = 0.84), but they did in age (P = 0.002), with patients in the PM group being 11.4 and 14.9 years older than those in the non-HM and HM groups, respectively. Significant differences between the groups were observed in AL, refractive error, and visual acuity (P < 0.001).

Table 2.

Characteristics of Study Participants Stratified by Myopia Severity and Subgroup

	Non-High Myopia	High Myopia	Pathologic Myopia	P *	Subgroup I	Subgroup II
Demographic parameters
Age (y), mean ± SD	47.3 ± 15.0	43.8 ± 11.3	58.9 ± 6.2	0.002	33.1 ± 5.9	35.3 ± 8.8
Gender (male/female), n	18/42	14/24	5/10	0.838	1/6	3/8
Ocular parameters, mean ± SD
AL (mm)	24.6 ± 1.5	26.8 ± 1.2	27.9 ± 1.0	<0.001	24 ± 0.4	24.7 ± 1.0
SE (D)	−2.0 ± 2.1	−8.7 ± 2.5	−10.1 ± 3.1	<0.001	−2.3 ± 0.7	−3.5 ± 1.9
Visual acuity (logMAR)	0.10 ± 0.10	0.13 ± 0.17	0.24 ± 0.14	<0.001	0	0

^*The P values were obtained with one-way ANOVA for continuous variables and χ² tests for gender.

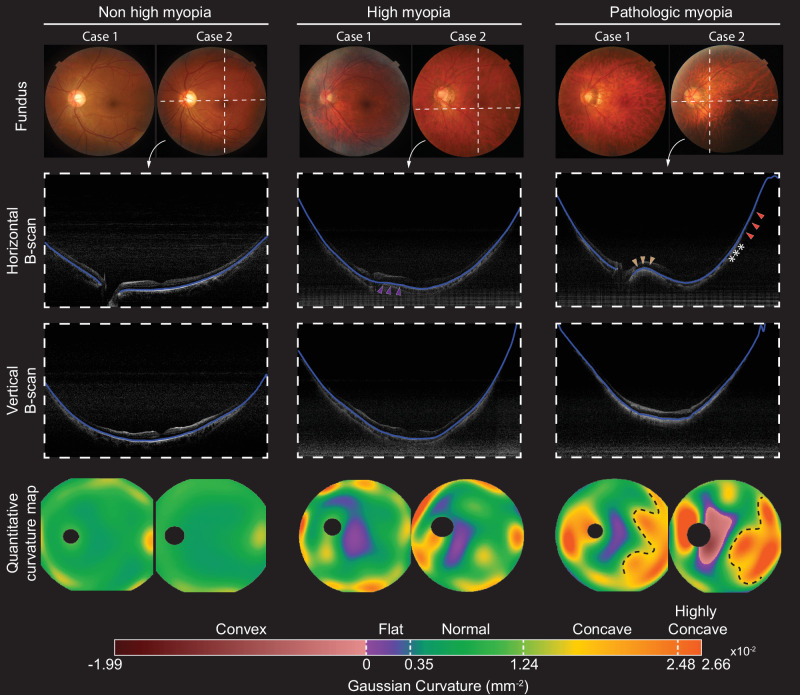
Examples of color fundus images, horizontal and vertical OCT B-scans, and ocular curvature maps in myopia groups are shown in Figure 1. From horizontal OCT B-scans, the RPE/BM line close to the optic disc appeared considerably flatter in the high myopia example compared to the low myopia example (purple arrowheads). In the PM example, a gradual transition from convexity (brown arrowheads) to high concavity (orange arrowheads) was observed from the optic disc to the macula and the temporal periphery. The curvature maps indicate that most regions in low myopic eyes were in the normal curvature range, with slight concavity being observed near the boundary of the field of view. In contrast, the curvature in eyes with HM and PM was more variable, with flat or convex curves near the macular area and patches of a concave curvature near the boundary of the field of view. Notably, a negative Gaussian curvature region indicated opposite signs of curvatures in horizontal and vertical directions. In the example of the eye with PM, a ridge-like macular shape was identified by detecting a convex curve from the horizontal scan but a concave curve from the vertical scan. Furthermore, highly concave curvatures in eyes with PM were seen in the temporal quadrants demarcated with clear boundaries (Fig. 1). As assessed from the fundus and OCT images, they were associated with staphyloma, with an abrupt change of choroidal thickness and scleral shape (ridge labeled by asterisks in horizontal OCT B-scans).³²

Figure 1.

Representative color fundus photographs (first row), OCT B-scans (middle row), and curvature maps (last row) for the various myopia groups. The OCT B-scans were taken from positions marked by the white dashed lines in the fundus photographs, and the blue lines in the B-scans indicate the segmented RPE/BM. The RPE/BM line close to the optic disc appeared considerably flatter in the example of high myopia compared to the low myopia group (purple arrowheads). In the PM example, a gradual transition from convexity (brown arrowheads) to high concavity (orange arrowheads) was observed from the optic disc to the macula and the temporal periphery. The curvature maps can visualize the boundaries of the steep retinal regions that are with staphyloma (black dashed line) with an abrupt change of choroidal thickness and scleral shape (ridge labeled by asterisks). A horizontally orientated dome-shaped macula is discernible in the region with negative curvature.

The histogram of the normal curvature from subgroup 1 is shown in the blue curve in Figure 2A. The lower and higher boundaries of the 90% CI were 0.0035 mm^–2 and 0.0124 mm^–2, respectively. The histograms from the myopic groups are shown in Figure 2A for direct comparison. The non-HM group exhibited a slightly broader curvature distribution compared to the normative subgroup, whereas the HM group showed a tendency toward more concave curvature. Interestingly, the PM group displayed a much broader distribution than the other groups, with a significant extension into both the convex and highly concave ranges. Figure 2B depicts the percentage stacked bar chart of the five curvature categories based on AL, and the bars are separated by millimeter (mm). The mean and SD values for each sub-bar are included in Supplementary Table S1.

The reproducibility test was performed in 13 eyes from subgroup 2. ICC values were 0.93 for flat, 0.93 for normal, and 0.91 for concave, but they were 0.66 for highly concave and 0.28 for convex because of the lack of pathologic eyes. The ICC value for OSI was 0.93, indicating that OSI is a highly reproducible metric for ocular shape quantification. A Bland–Altman plot comparing the OSI values computed from the first two repeated scans is shown in Supplementary Figure S2.

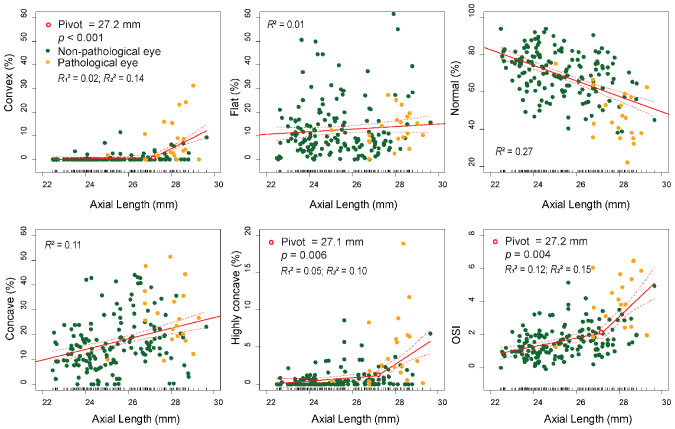
The correlations between curvature parameters and AL are summarized in Table 3, and scatterplots of the curvature categories and OSI with regard to AL are shown in Figure 3. Regression models with breakpoints automatically determined the breakpoints at AL values where the slope changed. The mean curvature and three curvature categories (normal, flat, and concave) had linear relationships with regard to AL, as the Davies test on a breakpoint on these categories was not statistically significant. Overall, an increase in AL was associated with an increase of convex curvature, and the slope of the convex increased 30-fold from 0.15%/mm to 4.59%/mm at the pivot point of 27.2 mm (P < 0.001) (Fig. 3B). Similarly, the slope of the highly concave category increased more than eightfold from 0.22%/mm to 1.88%/mm at the pivot point of 27.1 mm (P = 0.006) (Fig. 3C). OSI represented 49% of the variance among the five curvature categories, and the OSI slope magnitude increased by more than fourfold at an AL of >27.2 mm (0.26 OSI/mm, AL < 27.2 mm; 1.22 OSI/mm, AL > 27.2 mm; P = 0.004).

Table 3.

Correlation Between Curvature Parameters With Axial Length

		Correlation With AL
	Definition	Pivot (AL), P*	R2 Values**
Mean curvature (×10–2 mm–2)	Average of all the values obtained from the entire field of view	None	R2 = 0.11
Curvature variance (×10–4 mm–4)	Variance of all the values obtained from the entire field of view	27.2 mm, P = 0.002	R12 = 0.09; R22 = 0.13
Curvature category
Convex	Includes all negative values	27.2 mm, P < 0.001	R12 = 0.02; R22 = 0.14
Flat	Ranges between 0 and lower boundary of 90% CI	None	R2 = 0.01
Normal	Within the 90% CI of the normative distribution	None	R2 = 0.27
Concave	Ranges from the upper boundary of the 90% CI to twice its value	None	R2 = 0.11
Highly concave	Includes any values exceeding the range defined as concave	27.1 mm, P = 0.006	R12 = 0.05; R22 = 0.10
Curvature principal component (AU)
OSI	The first principal component from PCA of curvature categories	27.2 mm, P = 0.004	R12 = 0.12; R22 = 0.15

^*The P values were calculated from the Davies test.

^**The R values are reported for each segment of fitting: two values are reported for segmented linear regression models and one value for linear regression models.

Figure 3.

Two curvature categories (concave and highly concave) and OSI represent non-constant regression parameters with regard to AL. Nonlinear relationships between curvatures and AL were fitted by a segmented linear regression model using the Regression Models with Break-Points R package, where the other curvature categories showed linear relationships with regard to AL. The Davies test determined the number of breakpoints. Pivotal points ranging from 27.1 mm to 27.2 mm indicated significant changes in slope magnitudes before and after the pivots. The first principal component, termed OSI, amalgamated from five curvature categories, was calculated by using PCA. The magnitude of the slope increased approximately fourfold at an AL of >27.2 mm (0.26 OSI/mm, AL < 27.2 mm; 1.22 OSI/mm, AL > 27.2 mm; P = 0.004). R² values are reported for each segment of fitting: two values are reported for segmented linear regression models and one value for linear regression models.

Results of the curvature parameters in different myopia groups are summarized in Table 4. The mean curvature increased with more severe myopia in all sectors (P < 0.02), and the curvature variance also increased with myopia severity and showed smaller P values (P < 0.001) than the mean curvature. This finding is in agreement with the broader curvature distribution shown in Figure 2A. More severe myopia was associated with higher proportions of both concave and convex curvatures (an increase of convex, concave, and highly concave categories; P < 0.001), as well as a lower proportion of normal curvature (a decrease of normal category; P < 0.001). OSI, a single value for evaluating ocular deformation, can also substantially contrast the PM group from the other groups (P < 0.001).

Table 4.

Result of Ocular Curvature Analysis Stratified by Myopia Severities

	Non-High Myopia, Mean ± SD	High Myopia, Mean ± SD	Pathologic Myopia, Mean ± SD	P
Mean curvature (×10−2 mm−2)
Entire FOV 60°	0.80 ± 0.17	0.92 ± 0.16	0.97 ± 0.27	0.008
Central 30°	0.51 ± 0.19	0.57 ± 0.17	0.65 ± 0.36	0.001
Pericentral	0.88 ± 0.20	1.01 ± 0.19	1.13 ± 0.31	<0.001
Superior	0.80 ± 0.19	0.92 ± 0.17	0.96 ± 0.29	0.001
Inferior	0.79 ± 0.16	0.86 ± 0.15	0.93 ± 0.30	0.019
Nasal	0.80 ± 0.16	0.91 ± 0.16	0.94 ± 0.25	0.003
Temporal	0.78 ± 0.17	0.89 ± 0.16	0.94 ± 0.27	0.001
Curvature variance (×10−4 mm−4)
Entire FOV 60°	0.41 ± 0.12	0.50 ± 0.18	0.82 ± 0.34	<0.001
Central 30°	0.20 ± 0.09	0.25 ± 0.13	0.51 ± 0.32	<0.001
Pericentral	0.39 ± 0.14	0.49 ± 0.23	0.87 ± 0.44	<0.001
Superior	0.43 ± 0.12	0.51 ± 0.17	0.82 ± 0.34	<0.001
Inferior	0.42 ± 0.11	0.48 ± 0.17	0.82 ± 0.35	<0.001
Nasal	0.40 ± 0.12	0.50 ± 0.18	0.78 ± 0.34	<0.001
Temporal	0.41 ± 0.12	0.50 ± 0.18	0.80 ± 0.30	<0.001
Proportion of curvature category (%)
Convex	0.53 ± 1.08	1.04 ± 2.57	7.83 ± 9.44	<0.001
Flat	13.07 ± 11.14	9.40 ± 8.48	12.98 ± 7.31	0.019
Normal	71.62 ± 11.69	66.56 ± 11.88	47.47 ± 13.59	<0.001
Concave	14.38 ± 9.59	21.90 ± 10.23	27.16 ± 11.97	<0.001
Highly concave	0.57 ± 1.33	1.08 ± 1.52	4.27 ± 2.11	<0.001
Curvature principal component (AU)
OSI	1.43 ± 0.87	1.96 ± 1.07	4.27 ± 2.11	<0.001

^*The P values were obtained with one-way ANOVA for continuous variables.

Discussion

We have introduced a quantitative approach to mapping true ocular curvature using widefield, volumetric OCT scans acquired from a MHz SS-OCT system. Ocular shape abnormalities, presumably resulting from biomechanical tissue changes, such as macular ridges (staphyloma ridges or conus ridges), saddle-shaped or dome-shaped macula, and staphyloma, were associated with a curvature deviation from its normal distribution. The OSI parameter showed a nonlinear relationship with AL that could be fitted with two linear segments and a breakpoint at an AL of 27.2 mm.

Curvature maps can reveal the morphological abnormalities of the macula, such as a dome-shaped configuration or macular ridges, which are poorly identifiable by ophthalmoscopy.¹⁴ Macular ridges and a dome-shaped macular configuration can affect 11% to 15% of highly myopic eyes, independently of the presence of staphylomas.^33,34 They can be associated with sight-threatening complications such as RPE changes, macular neovascularization, retinoschisis, and serous macula detachment.^35,36 A dome-shaped macula is defined as macular elevation in all meridians, whereas a ridge- or saddle-shaped macula shows elevation in only one meridian, commonly observed in the horizontal meridian compared to the vertical meridian.³⁷ Ellabban et al.³⁸ described two outward concavities with a horizontal ridge in 42 eyes out of 51 eyes as one variant of a dome-shaped macula, now termed a ridge-shaped macula. The OCT scans of these eyes showed a convex configuration of RPE/BM in the sagittal direction and flat RPE/BM in the horizontal direction. In the other nine eyes, a uniform dome-shaped convexity was reported, with both horizontal and sagittal OCT scans showing a convex configuration.³⁹ The negative Gaussian curvature from curvature maps indicates convexity in one direction and concavity in the other; therefore, it is more of a saddle shape or ridge shape than a dome shape. The quantitative curvature map can provide a confident classification of inward bulging types, which are hypothesized to correlate with changes in Bruch's membrane and sclera.^35,39

The ultrawide OCT overcomes the limitations of fundus photography, sonography, and 3D MRI to accurately determine the presence and extent of different staphyloma types, such as narrow macula, wide macula, inferior staphyloma, and peripapillary staphyloma.^10,11,40 The quantitative curvature showed that the highly concave regions of a steep retina were associated with staphyloma. Moreover, we could quantify a posterior outward bowing and demarcate the edges of the steep retinal region. Ultrawide OCT scans have been reported to show choroidal changes near the staphyloma boundary: a gradual thinning from the periphery to the edge followed by a gradual rethickening toward the posterior pole, whereas the sclera showed a gradual thickening and inward protrusion.¹⁶ This inward protrusion of the sclera appeared as a convex region in the curvature map. A posterior staphyloma has rarely been detected in young patients with high myopia.⁴¹ A choroidal and scleral thinning at the posterior pole accompanies the development of a staphyloma in older age.^32,42 This observation agrees with findings made in our study in which patients with pathologic myopia were older than patients of the other groups. Our study showed that the slope of the linear relationship between OSI and AL was fourfold higher when AL exceeded a value of 27.2 mm. This pivotal point agrees with previous reports from Brian and Curtin⁴³ that staphylomas were not detected in eyes with an AL of <26.5 mm using ultrasound measurements. The prevalence of staphylomas increased to 1.4% when the AL ranged between 26.5 mm and 27.4 mm, and it increased to 71.4% in eyes with an AL ranging between 33.5 mm and 36.6 mm. Similarly, a study on a Japanese cohort with an AL of >26.5 mm showed an increased prevalence of posterior staphylomas.⁴⁴

This study has several limitations. First, this was a prospective cross-sectional study performed in a single center, and the different myopic groups were not age matched. Second, the current method was applied on a commercially available prototype because the image distortion correction algorithm requires details of the optical designs that require sharing or collaboration with the vendor; validation on other widefield OCT images would require knowledge of the optical designs of those specific devices. Third, the size of our normative database is small (n = 10), and the eyes included in the subgroup were not emmetropic. The normal curvature range could thus have been overestimated. The reproducibility test was only conducted on eyes without pathologic myopia. Finally, the field of view is not wide enough to cover the equator or mid-peripheral regions, which are hypothesized to be sensitive sites for tissue stretching caused by myopia.^23,45

In conclusion, ultrawide, volumetric OCT images can quantitatively assess the ocular shape. A pivotal point at an AL of 27.2 mm may suggest an excessive biomechanical shift at high degrees of myopia. The technology can be implemented on standard commercial OCT machines and serve as an efficient, low-cost, robust screening tool for discerning and monitoring ocular shape deformations in various ocular diseases. Moving forward, longitudinal follow-up may be conducted to shed light on the intricate relationship between local curvature deformation and myopia progression and vision-threatening features—for example, development of choroidal neovascularization or development or progression of either degenerative or tractional forms of pathologic myopia.